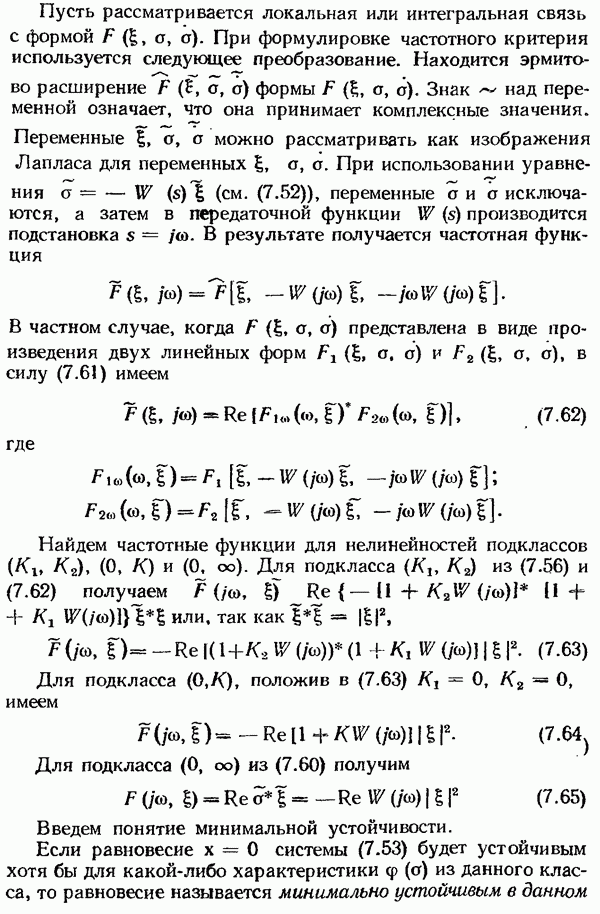| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 9.4. Спектральные плотности случайных процессов
При исследовании автоматических систем управления удобно пользоваться еще одной характеристикой стационарного случайного процесса, называемой спектральной плотностью. Во многих случаях, особенно при изучении преобразования стационарных случайных процессов линейными системами управления, спектральная плотность оказывается более удобной характеристикой, чем корреляционная функция. Спектральная плотность  случайного процесса
случайного процесса  определяется как преобразование Фурье корреляционной функцией
определяется как преобразование Фурье корреляционной функцией  , т. е.
, т. е.

Если воспользоваться формулой Эйлера  то (9.52) можно представить как
то (9.52) можно представить как

Так как  нечетная функция
нечетная функция  то в последнем выражении второй интеграл равен нулю. Учитывая, что
то в последнем выражении второй интеграл равен нулю. Учитывая, что  четная функция
четная функция  получаем
получаем

Так как  то из (9.53) следует, что
то из (9.53) следует, что

Таким образом, спектральная плотность  является действительной и четной функцией частоты о). Поэтому на графике спектральная плотность всегда симметрична относительно оси ординат.
является действительной и четной функцией частоты о). Поэтому на графике спектральная плотность всегда симметрична относительно оси ординат.
Если спектральная плотность известна, то по формуле обратного преобразования Фурье можно найти соответствующую ей корреляционную функцию:

Используя (9.55) и (9.38), можно установить важную зависимость между дисперсией  и спектральной плотностью
и спектральной плотностью  случайного процесса:
случайного процесса:

Термин «спектральная плотность» обязан своим происхождением теории электрических колебаний. Физический смысл спектральной плотности можно пояснить следующим образом.
Пусть  — напряжение, приложенное к омическому сопротивлению 1 Ом, тогда средняя мощность
— напряжение, приложенное к омическому сопротивлению 1 Ом, тогда средняя мощность  рассеиваемая на этом сопротивлении за время
рассеиваемая на этом сопротивлении за время  равна
равна

Если увеличивать интервал наблюдения  до бесконечных пределов и воспользоваться (9.30), (9.38) и (9.55) при
до бесконечных пределов и воспользоваться (9.30), (9.38) и (9.55) при  то можно формулу для средней мощности записать так:
то можно формулу для средней мощности записать так:

Равенство (9.57) показывает, что средняя мощность сигнала может быть представлена в виде бесконечной суммы бесконечно малых слагаемых  , которая распространяется на все частоты от 0 до
, которая распространяется на все частоты от 0 до 
Каждое элементарное слагаемое этой суммы играет роль мощности, соответствующей бесконечно малому участку спектра, заключенному в пределах от  до
до  Каждая элементарная мощность —
Каждая элементарная мощность —  пропорциональна значению функции
пропорциональна значению функции  для данной частоты
для данной частоты  Следовательно, физический смысл спектральной плотности состоит в том, что она характеризует распределение мощности сигнала по частотному спектру.
Следовательно, физический смысл спектральной плотности состоит в том, что она характеризует распределение мощности сигнала по частотному спектру.
Спектральная плотность может быть найдена экспериментально через среднюю величину квадрата амплитуды гармоник реализации случайного процесса. Приборы, применяемые для этой цели и состоящие  анализатора спектра и вычислителя среднего значения квадрата амплитуды гармоник, называются спектрометрами. Экспериментально находить спектральную плотность сложнее, чем корреляционную функцию, поэтому на практике чаще всего спектральную плотность вычисляют но известной корреляционной функции с помощью формулы (9.52) или (9.53).
анализатора спектра и вычислителя среднего значения квадрата амплитуды гармоник, называются спектрометрами. Экспериментально находить спектральную плотность сложнее, чем корреляционную функцию, поэтому на практике чаще всего спектральную плотность вычисляют но известной корреляционной функции с помощью формулы (9.52) или (9.53).
Взаимная спектральная плотность  двух стационарных случайных процессов
двух стационарных случайных процессов  определяется как преобразование Фурье от взаимной корреляционной функции
определяется как преобразование Фурье от взаимной корреляционной функции  т. е.
т. е.

По взаимной спектральной плотности можно, применяя к (9.58) обратное преобразование Фурье, найти выражение для взаимной корреляционной функции:

Взаимная спектральная плотность  является мерой статистической связи между двумя стационарными случайными процессами:
является мерой статистической связи между двумя стационарными случайными процессами:  Если процессы
Если процессы  некоррелированы и имеют равные нулю средние значения, то взаимная спектральная плотность равна нулю, т. е.
некоррелированы и имеют равные нулю средние значения, то взаимная спектральная плотность равна нулю, т. е.

В отличие от спектральной плотности  взаимная спектральная плотность
взаимная спектральная плотность  не является четной функцией о и представляет собой не вещественную, а комплексную функцию.
не является четной функцией о и представляет собой не вещественную, а комплексную функцию.
рассмотрим некоторые свойства спектральных плотностей 
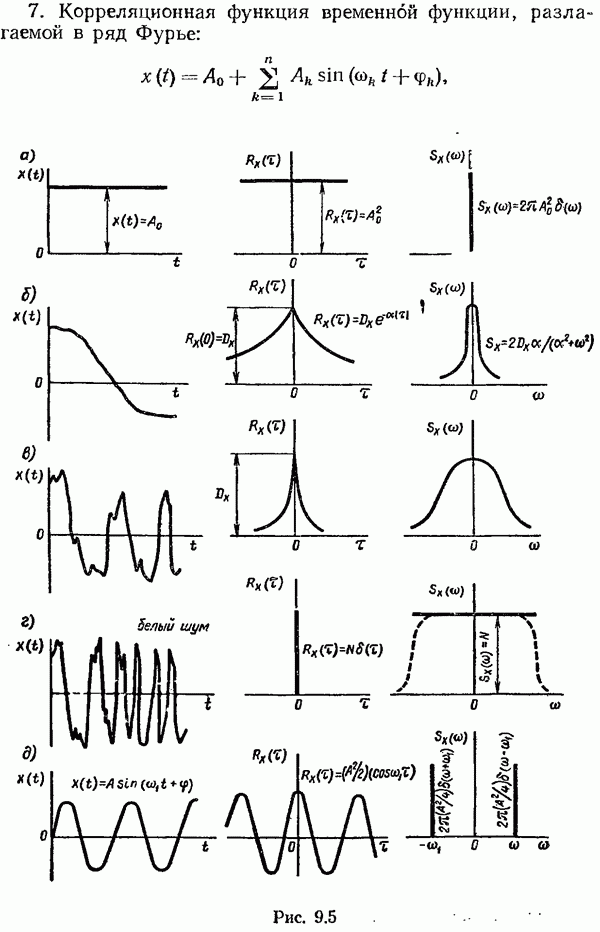
1 Спектральная плотность чистого случайного процесса, или белого шума, постоянна во всем диапазоне частот (см. рис. 9.5, г):

Действительно, подставляя в (9.52) выражение (9.47) для корреляционной функции белого шума, получим

Постоянство спектральной плотности белого шума во всем бесконечном диапазоне частот, полученное в последнем выражении, означает, что энергия белого шума распределена по всему спектру равномерно, а суммарная энергия процесса равна бесконечности. Это указывает на физическую нереализуемость случайного процесса типа белого шума. Белый шум является математической идеализацией реального процесса. В действительности частотный спектр  западает на очень высоких частотах (как показано пунктиром на рис. 9.5, г). Если, однако, эти частоты настолько велики, что при рассмотрении какого-либо конкретного устройства они не играют роли (ибо лежат вне полосы частот, пропускаемых этим устройством), то идеализация сигнала в виде белого шума упрощает рассмотрение и поэтому вполне целесообразна.
западает на очень высоких частотах (как показано пунктиром на рис. 9.5, г). Если, однако, эти частоты настолько велики, что при рассмотрении какого-либо конкретного устройства они не играют роли (ибо лежат вне полосы частот, пропускаемых этим устройством), то идеализация сигнала в виде белого шума упрощает рассмотрение и поэтому вполне целесообразна.
Происхождение термина «белый шум» объъясняется аналогией такого процесса с белым светом, имеющим одинаковые интенсивности всех компонент, и тем, что случайные процессы типа белого шума впервые были выделены при исследовании тепловых флуктуациоиных шумов в радиотехнических устройствах.
2. Спектральная плотность постоянного сигнала  представляет собой
представляет собой  -функцию, расположенную в начале координат (см. рис. 9.5, а), т. е.
-функцию, расположенную в начале координат (см. рис. 9.5, а), т. е.

Чтобы доказать это, допустим, что спектральная плотность имеет вид (9.62), и иандем по (9.55) соответствующую ей корреляционную функцию. Так как

то при  получаем
получаем

Это (в соответствии со свойством 5 корреляционных функций) означает, что сигнал, соответствующий спектральной плотности, определяемой (9.62), является постоянным сигналом, равным 
Тот факт, что спектральная плотность  представляет собой
представляет собой  -функцию при
-функцию при  означает, что вся мощность постоянного сигнала сосредоточена на нулевой частоте, что и следовало ожидать.
означает, что вся мощность постоянного сигнала сосредоточена на нулевой частоте, что и следовало ожидать.
3. Спектральная плотность периодического сигнала  представляет собой две
представляет собой две  -функции, расположенные симметрично относительно начала кординат при
-функции, расположенные симметрично относительно начала кординат при  (см. рис. 9.5, д), т. е.
(см. рис. 9.5, д), т. е.

Чтобы доказать это, допустим, что спектральная плотность имеет вид (9.63), и найдем по (9.55) соответствующую ей корреляционную функцию:

Это (в соответствии со свойством 6 корреляционных функций) означает, что сигнал, соответствующий спектральной плотности определяемой (9.63), является периодическим сиг налом, равным 
Тот факт, что спектральная плотность  представляет собой две
представляет собой две  -функции, расположенные при
-функции, расположенные при  означает, что вся мощность периодического сигнала сосредоточена на двух частотах:
означает, что вся мощность периодического сигнала сосредоточена на двух частотах:  Если рассматривать спектральную плотность только в области положительных частот, то получим,
Если рассматривать спектральную плотность только в области положительных частот, то получим,

Рис. 9.9
что вся мощность периодического сигнала будет сосредоточена на одной частоте  .
.
4. Спектральная плотность временной функции, разлагаемой в ряд Фурье  имеет на основании изложенного выше вид
имеет на основании изложенного выше вид

Этой спектральной плотности соответствует линейчатый спектр (рис. 9.9) с  -функциями, расположенными на положительных и отрицательных частотах гармоник. На рис. 9.9
-функциями, расположенными на положительных и отрицательных частотах гармоник. На рис. 9.9  -функции условно изображены так, что их высоты показаны пропорциональными коэффициентам при единичной
-функции условно изображены так, что их высоты показаны пропорциональными коэффициентам при единичной  -функции, т. е. величинам и
-функции, т. е. величинам и 
Заметим, что спектральная плотность  как это следует из (9.64), не содержит, так же как и корреляционная функция, определяемая (9.44), никаких сведений о фазовых сдвигах отдельных гармонических составляющих.
как это следует из (9.64), не содержит, так же как и корреляционная функция, определяемая (9.44), никаких сведений о фазовых сдвигах отдельных гармонических составляющих.
5. Спектральная плотность случайного процесса, не содержащего периодической составляющей, представляет собой график без ярко выраженных пиков (см. рис. 9.5, б, в).
В этом случае спектральная плотность часто аппроксимируется следующим аналитическим выражением:

где  — дисперсия случайного процесса;
— дисперсия случайного процесса;  — параметр затухания;
— параметр затухания;  — постоянный коэффициент.
— постоянный коэффициент.
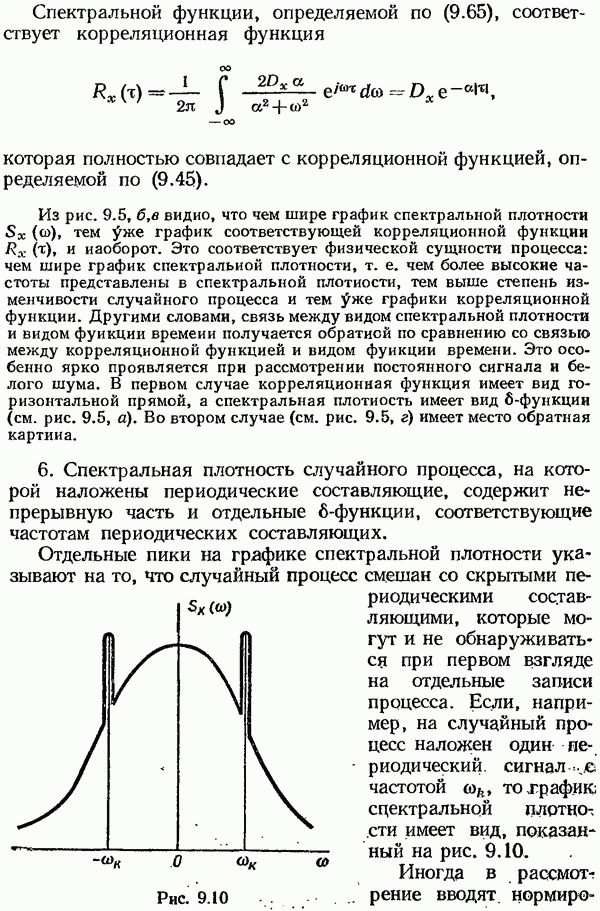
Спектральной функции, определяемой по (9.65), соответствует корреляционная функция

которая полностью совпадает с корреляционной функцией, определяемой по (9.45).
Из рис. 9.5, б, в видно, что чем шире график спектральной плотности  тем уже график соответствующей корреляционной функции
тем уже график соответствующей корреляционной функции  и наоборот. Это соответствует физической сущности процесса: чем шире график спектральной плотности, т. е. чем более высокие частоты представлены в спектральной плотности, тем выше степень изменчивости случайного процесса и тем же графики корреляционной функции. Другими словами, связь между видом спектральной плотности и видом функции времени получается обратной по сравнению со связью между корреляционной функцией и видом функции времени. Это особенно ярко проявляется при рассмотрении постоянного сигнала и белого шума. В первом случае корреляционная функция имеет вид горизонтальной прямой, а спектральная плотность имеет вид
и наоборот. Это соответствует физической сущности процесса: чем шире график спектральной плотности, т. е. чем более высокие частоты представлены в спектральной плотности, тем выше степень изменчивости случайного процесса и тем же графики корреляционной функции. Другими словами, связь между видом спектральной плотности и видом функции времени получается обратной по сравнению со связью между корреляционной функцией и видом функции времени. Это особенно ярко проявляется при рассмотрении постоянного сигнала и белого шума. В первом случае корреляционная функция имеет вид горизонтальной прямой, а спектральная плотность имеет вид  -функции (см. рис. 9.5, а). Во втором случае (см. рис. 9.5, г) имеет место обратная картина.
-функции (см. рис. 9.5, а). Во втором случае (см. рис. 9.5, г) имеет место обратная картина.
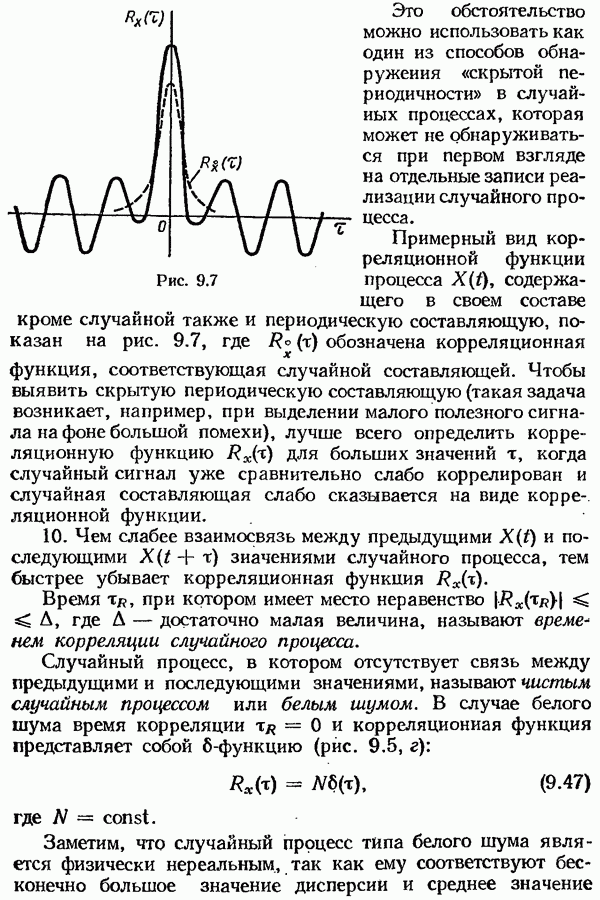
6. Спектральная плотность случайного процесса, на кото рой наложены периодические составляющие, содержит непрерывную часть и отдельные  -функции, соответствующие частотам периодических составляющих.
-функции, соответствующие частотам периодических составляющих.
Отдельные пики на графике спектральной плотности указывают на то, что случайный процесс смешан со скрытыми периодическими составляющими, которые могут и не обнаруживаться при первом взгляде на отдельные записи процесса. Если, например, на случайный процесс наложен один периодический сигнал с частотой  то график; сцектральной плотности имеет вид, показанный на рис. 9.10,
то график; сцектральной плотности имеет вид, показанный на рис. 9.10,
Иногда в рассмотрение вводят нормированную

Рис. 9.10
спектральную плотность  являющуюся изображением Фурье нормированной корреляционной функции (9.48):
являющуюся изображением Фурье нормированной корреляционной функции (9.48):

Нормированная спектральная плотность имеет размерность времени.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 7. НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
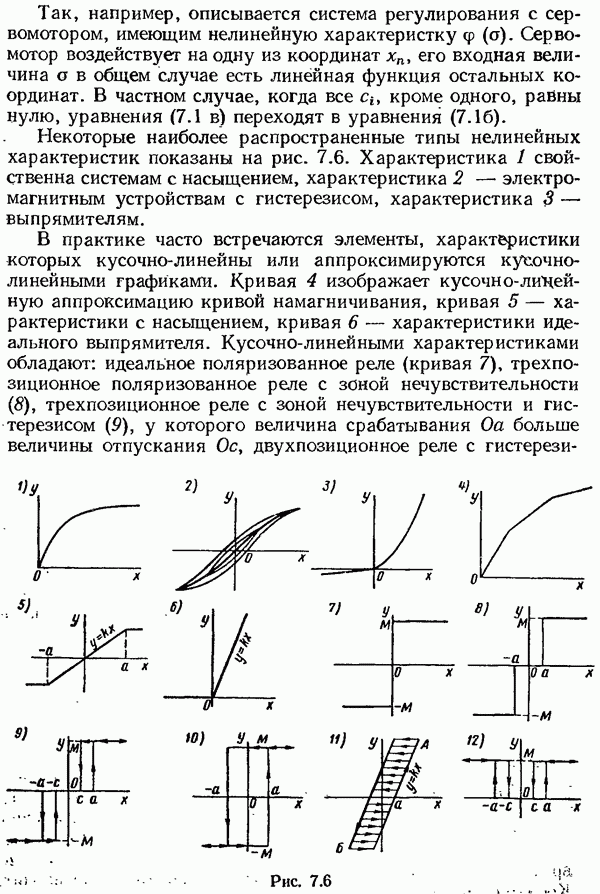
- § 7.1. Основные типы. нелинейных систем и характеристик
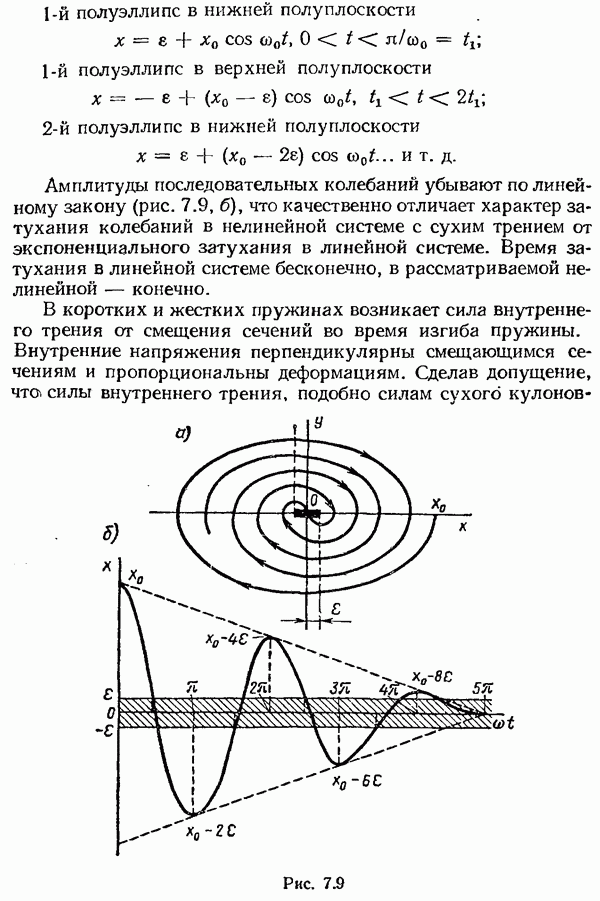
- § 7.2. Изображение движений в фазовой плоскости
- Линейная консервативная система второго порядка.
- Система с сухим кулоновским трением.
- Система с отрицательной восстанавливающей силой.
- Линейная колебательная система с вязким трением.
- Линейная апериодическая система с вязким трением.
- § 7.3. Автоколебания. Метод точечных преобразований
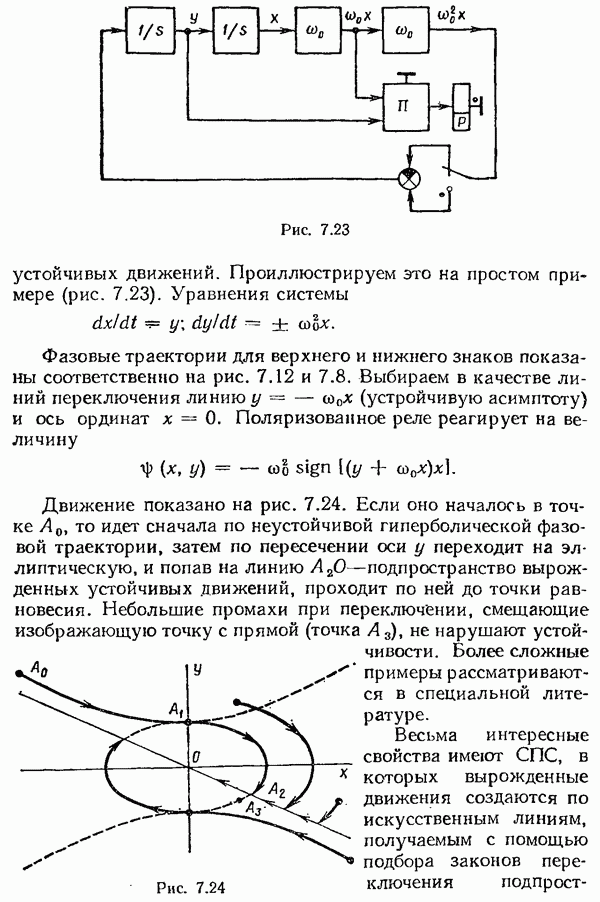
- § 7.4. Системы с переменной структурой
- § 7.5. Метод «припасовывания» граничных значений
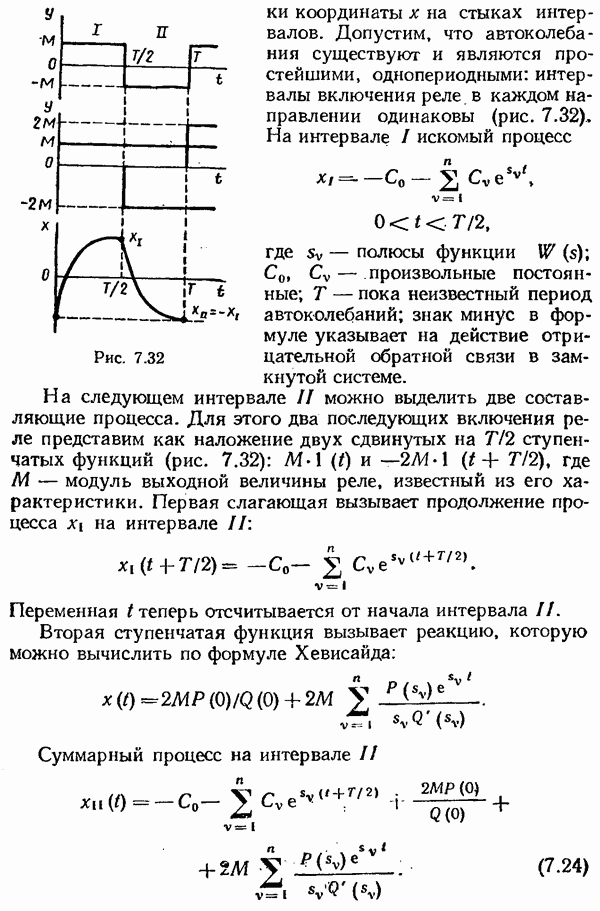
- § 7.6. Приближенное исследование автоколебаний. Метод эквивалентной линеаризации
- § 7.7. Метод гармонического баланса
- § 7.8. Устойчивость в малом, большом и целом
- § 7.9. Второй (прямой) метод Ляпунова
- § 7.10. Абсолютная устойчивость
- Квадратичный критерий абсолютной устойчивости.
- Круговой критерий устойчивости.
- Критерий В. М. Попова.
- Примечание к критерию Попова.
- Гипотезы М. Айзермана и Р. Калмана.
- Определение автоколебаний.
- Упрощенный критерий колебательности.
- Глава 8. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- § 8.1. Понятие об импульсных системах автоматического управления
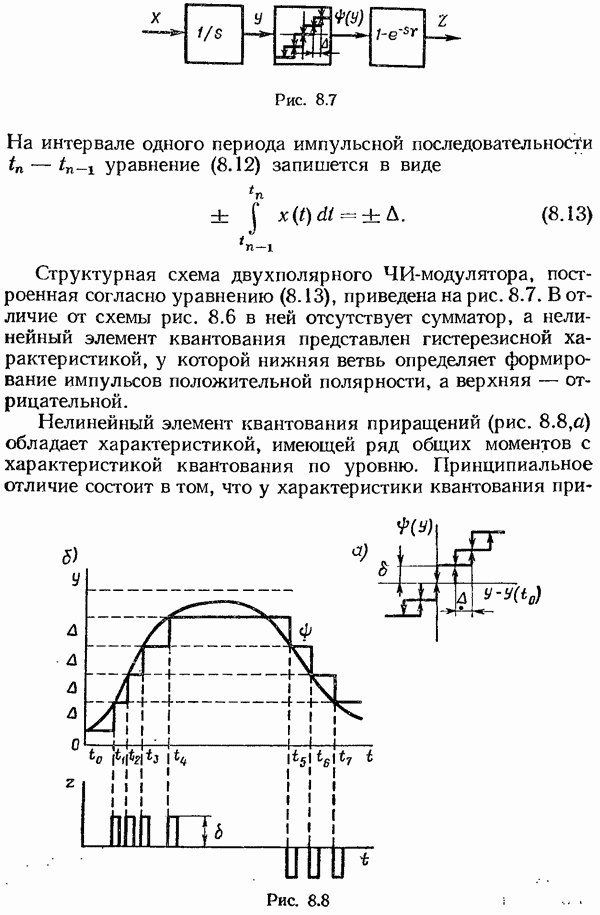
- Структура и уравнения импульсных модуляторов.
- Структурная схема амплитудно-импульсного модулятора.
- Структурная схема частотно-импульсного модулятора.
- Структурная схема широтно-импульсного модулятора.
- Структурные схемы частотно-импульсных к широтно- импульсных модуляторов 1-го рода.
- Структурная схема системы управления с импульсной модуляцией. Классификация систем управления с импульсной модуляцией.
- § 8.2. Исследование устойчивости и качества систем управления с амплитудноимпульсной модуляцией
- Передаточная функция импульсной системы.
- Дискретное преобразование Лапласа и его основные свойства.
- Частотные характеристики импульсной системы.
- Исследование устойчивости систем с амплитудно-импульсной модуляцией.
- Алгебраический критерий устойчивости (аналог критерия Гурвица).
- Частотный критерий устойчивости (аналог критерия Найквиста).
- Исследование качества систем с амплитудно-импульсной модуляцией.
- Непрерывное регулирование как граница импульсного регулирования.
- § 8.3. Исследование динамики цифровых систем автоматического управления
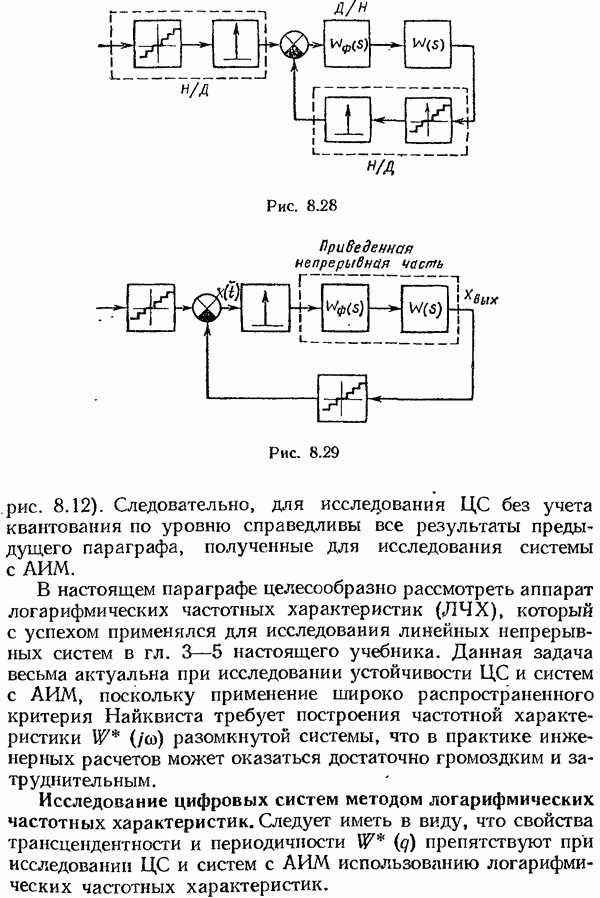
- Исследование цифровых систем методом логарифмических частотных характеристик.
- Исследование цифровых систем с непрерывной передачей данных.
- Исследование цифровых систем с учетом квантования по уровню и по времени.
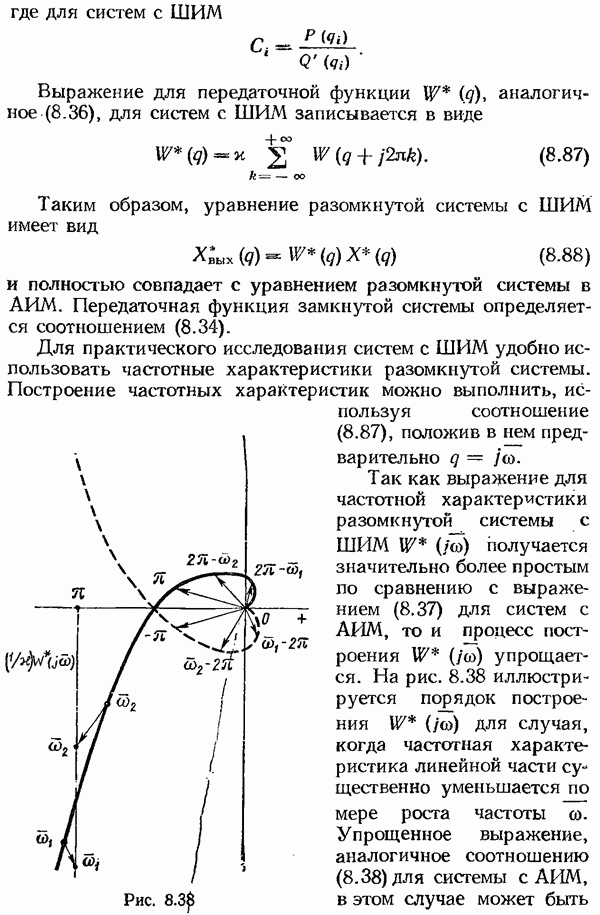
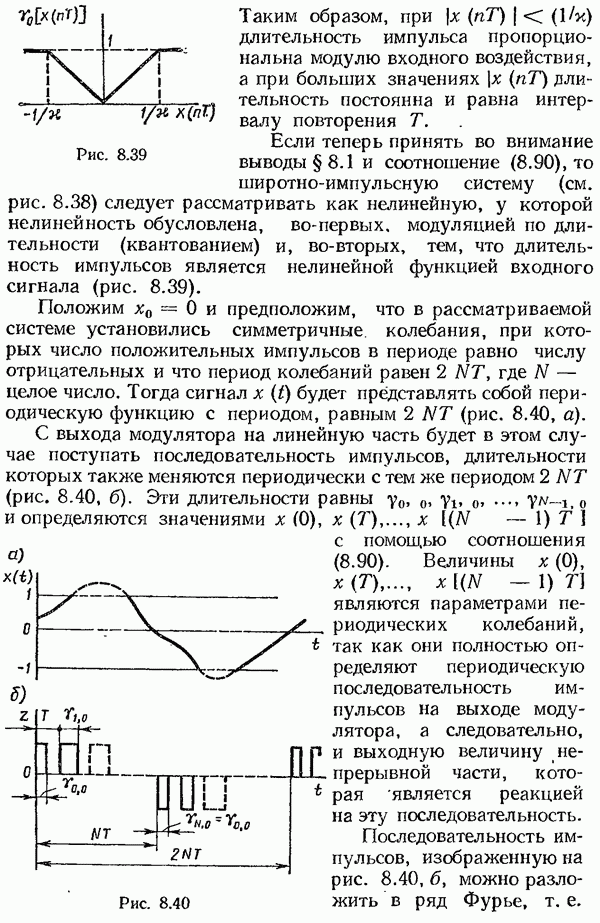
- § 8.4. Исследование систем с широтноимпульсной модуляцией
- Исследование периодических колебаний в системах с широтно-импульсной модуляцией.
- § 8.5. Исследование систем с частотно-импульсной модуляцией
- Исследование устойчивости в целом частотно-импульсных систем 2-го рода.
- Исследование периодических режимов в системах с ИЧИМ.
- Исследование периодических колебаний в системах с ИЧИМ 1-го рода.
- Глава 9. СЛУЧАЙНЫЕ ПРОЦЕССЫ В АВТОМАТИЧЕСКИХ СИСТЕМАХ УПРАВЛЕНИЯ
- § 9.2. Случайные процессы и их основные статистические характеристики
- § 9.3. Корреляционные функции случайных процессов
- § 9.4. Спектральные плотности случайных процессов
- § 9.5. Связь между корреляционными функциями и спектральными плотностями случайного процесса на входе и выходе линейной системы
- § 9.6. Расчет линейных систем при случайных воздействиях
- Аналитический метод определения дисперсии ошибки.
- Графоаналитическое определение дисперсии ошибки.
- § 9.7. Синтез линейных систем с минимальной средней квадратической ошибкой
- Синтез при произвольной структуре системы.
- Оптимальный фильтр Винера.
- Оптимальный фильтр Калмана—Бьюси.
- § 9.8. Случайные процессы в линейных импульсных системах
- § 9.9. Нелинейное преобразование случайных сигналов
- § 9.10. Статистическая линеаризация нелинейных элементов
- § 9.11. Расчет нелинейных систем методом статистической линеаризации
- Расчет замкнутых нелинейных систем.
- Глава 10. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
- Общая постановка задачи оптимального управления
- Примеры постановки задач оптимального управления.
- Классификация задач оптимального управления
- § 10.2. Метод классического вариационного исчисления (метод множителей Лагранжа)
- Уравнения Эйлера—Лагранжа.
- Задачи с подвижными концами и фиксированным временем
- Задача с нефиксированным временем.
- § 10.3. Принцип максимума Понтрягина. Условие нормальности. Теорема об n интервалах. Вырожденные и особые задачи
- Задача с подвижными концами
- Задача максимального быстродействия
- Условие нормальности.
- Теорема об n интервалах.
- Задача с ограничением на фазовые координаты
- Вырожденные задачи
- Особые задачи
- § 10.4. Метод динамического программирования. Теорема Болтянского. Метод Кротова
- Принцип оптимальности
- Функция и уравнение Беллмана
- Проблема обоснования метода динамического программирования и достаточные условия оптимальности
- Метод Кротова [11]
- Принцип оптимальности Кротова.
- § 10.5. Управляемость и наблюдаемость. Наблюдатели
- Управляемость линейных стационарных объектов.
- Стабилизируемость.
- Управляемость при наличии ограничения на управление.
- Наблюдаемость и восстанавливаемость
- Обнаруживаемость
- Наблюдатели
- Наблюдатели пониженного порядка.
- § 10.6. Методы синтеза оптимальных систем с обратной связью. Синтез оптимальных линейных систем по интегральному квадратичному критерию
- Синтез оптимальных линейных систем по интегральному квадратичному критерию
- Векторное дифференцирование.
- Синтез оптимального линейного регулятора выхода.
- § 10.7. Стохастические оптимальные системы. Методы синтеза. Методы оптимальной оценки состояния. Принцип разделимости
- Метод динамического программирования
- Синтез стохастической оптимальной линейной системы при полной информации о состоянии
- Синтез стохастических оптимальных систем управления при неполной информации
- Наблюдатель Калмана—Бьюси при цветном шуме объекта.
- Наблюдатель Калмана—Бьюси при цветном шуме наблюдения.
- Сингулярная (вырожденная) задача линейного оптимального оценивания.
- Линеаризованный наблюдатель Калмана—Бьюси.
- Стохастическая линейная оптимальная система управления при неполной информации. Принцип разделимости
- § 10.8. Оптимальные дискретные системы
- Синтез оптимальной линейной системы при квадратном критерии
- Стохастическая оптимальная линейная система при полной информации о состоянии.
- Наблюдатель (оцениватель, фильтр) Калмана.
- О расходимости фильтров и методах их регуляризации.
- Глава 11. АДАПТИВНЫЕ АВТОМАТИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
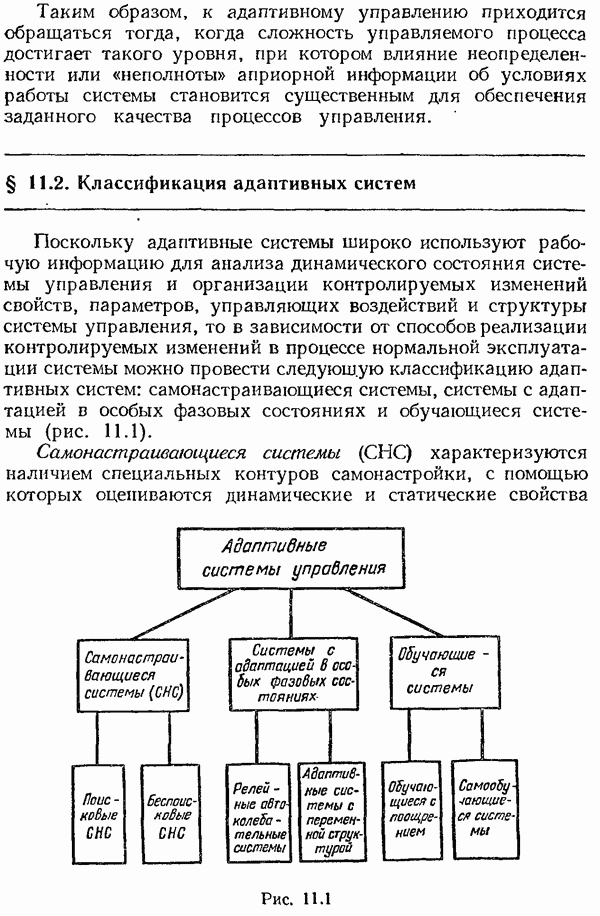
- § 11.2. Классификация адаптивных систем
- § 11.3. Самонастраивающиеся системы
- Принципы построения поисковых самонастраивающихся систем.
- Регулярные методы поиска экстремума
- Метод градиента.
- Метод наискорейшего спуска.
- Методы экстраполяционного поиска.
- Методы случайного поиска
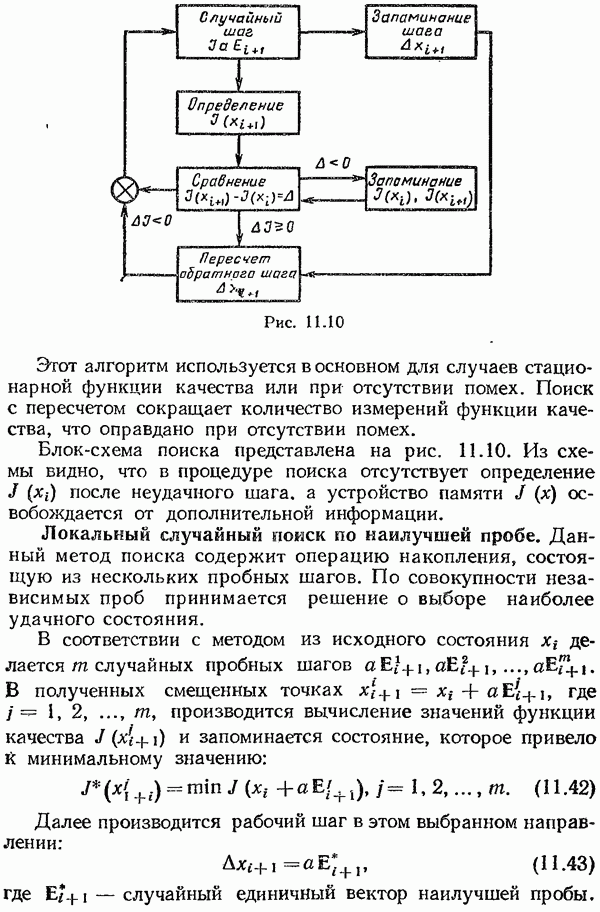
- Локальный случайный поиск с пересчетом.
- Локальный случайный поиск по наилучшей пробе.
- Локальный случайный поиск по статистическому градиенту.
- Глобальный случайный поиск с независимым выбором плотности распределения пробных шагов.
- Примеры поисковых самонастраивающихся систем
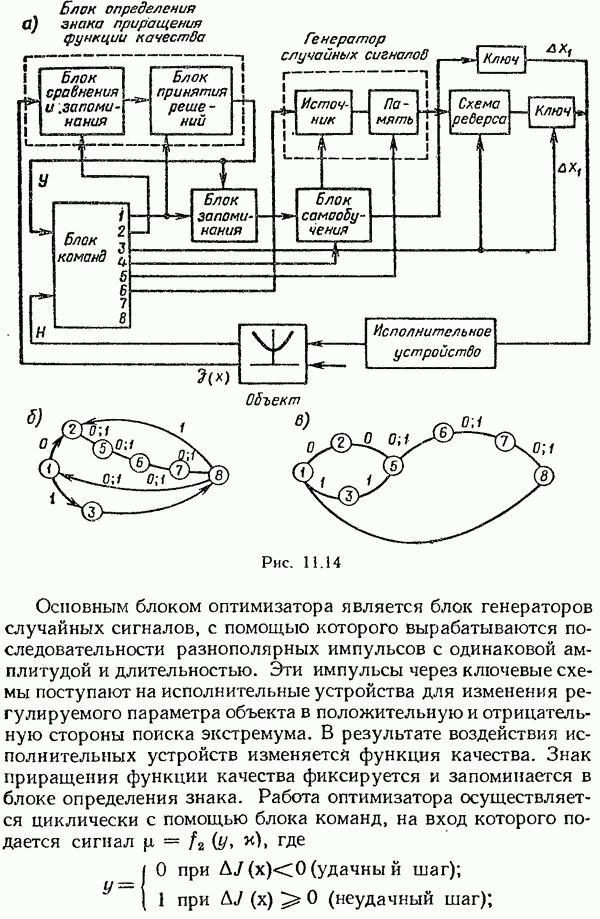
- Многоканальный статистический оптимизатор со случайным поиском.
- Принцип инвариантности.
- Принцип эталонной модели.
- Принципы определения градиента функции качества.
- Принципы идентификации динамических свойств системы управления.
- Примеры беспоисковых самонастраивающихся систем
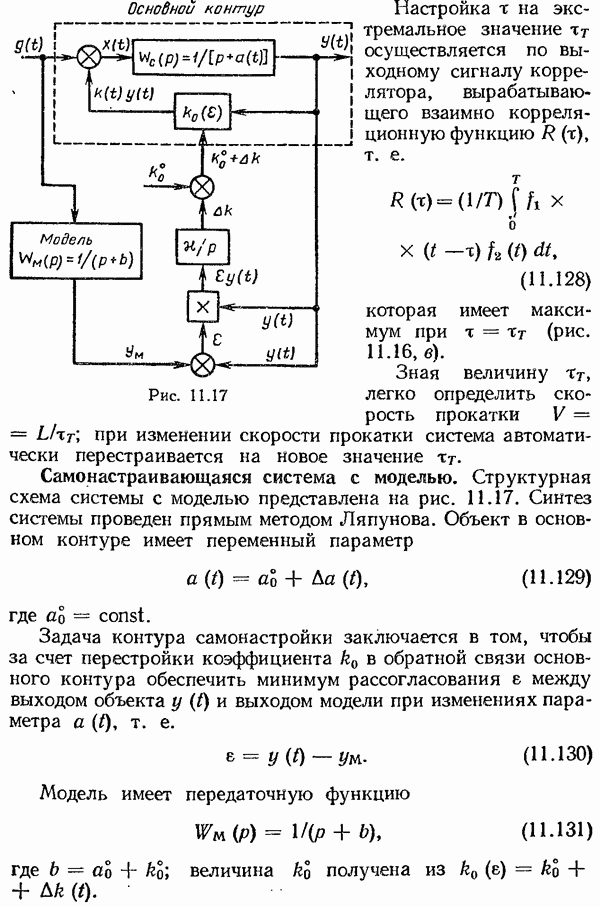
- Самонастраивающаяся система с моделью.
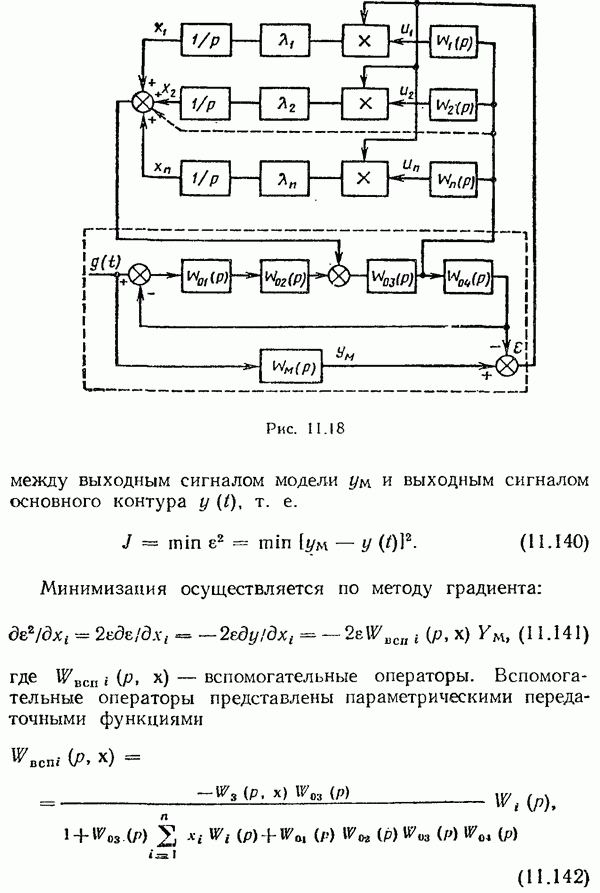
- Градиентная самонастраивающаяся система.
- § 11.4. Системы с адаптацией в особых фазовых состояниях
- Адаптивные системы с переменной структурой.
- Адаптивная система с переменной структурой, использующая информацию о внутренних координатах.
- § 11.5. Обучающиеся системы
- Метод секущих плоскостей.
- Метод потенциальных функций.
- Вероятностные алгоритмы обучения.
- Самообучение.
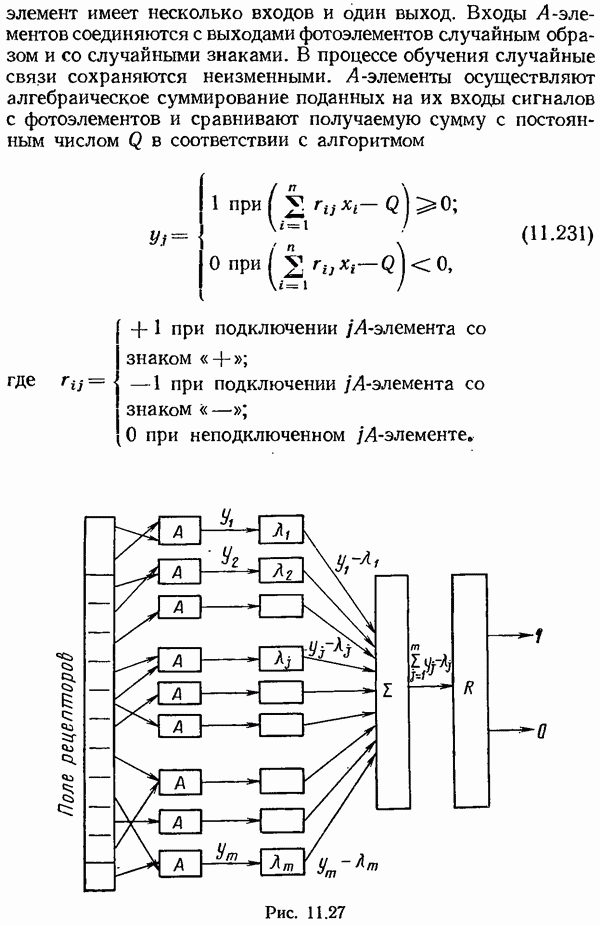
- Персептронная модель автоматической классификации.
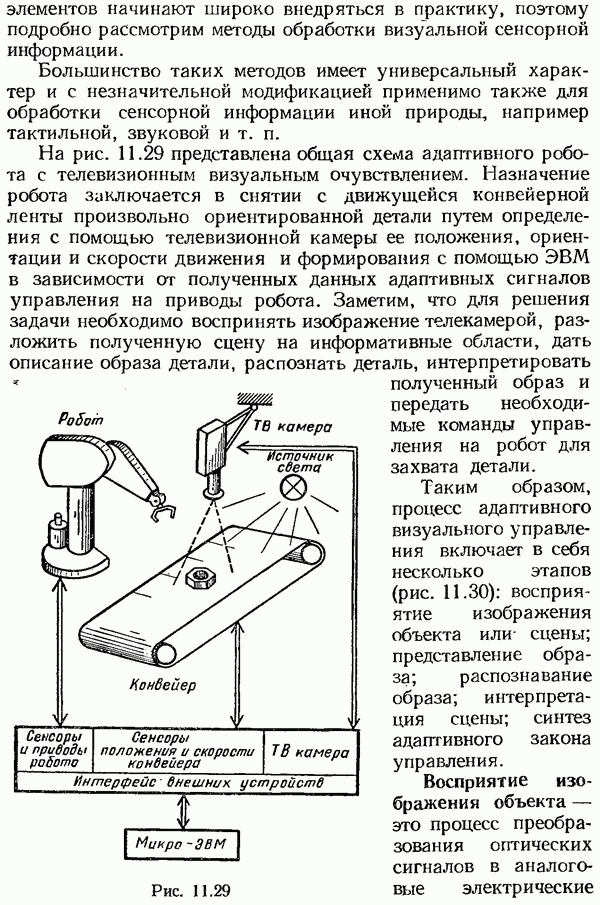
- § 11.6. Адаптивные робототехнические системы
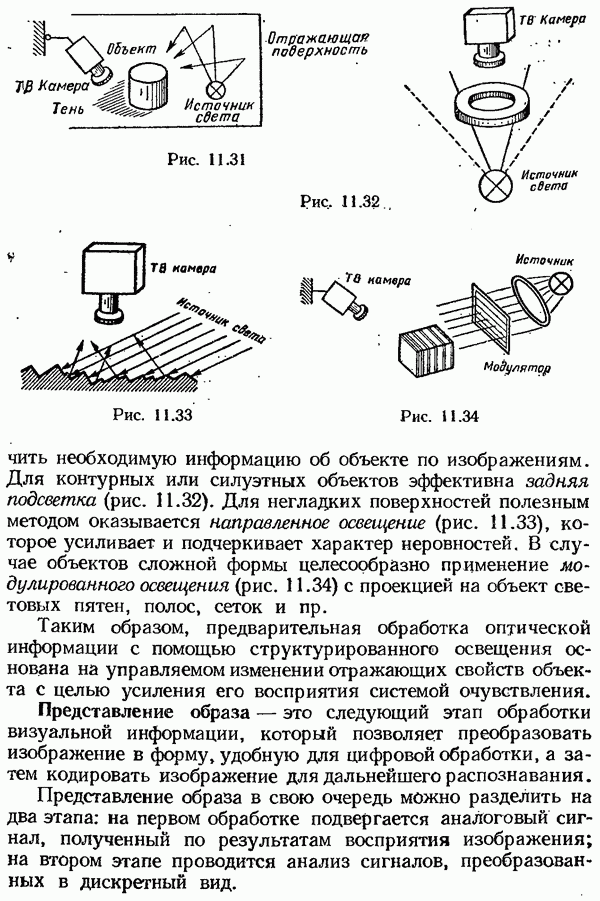
- Методы обработки сенсорной информации для адаптивного управления роботами.
- Восприятие изображения объекта
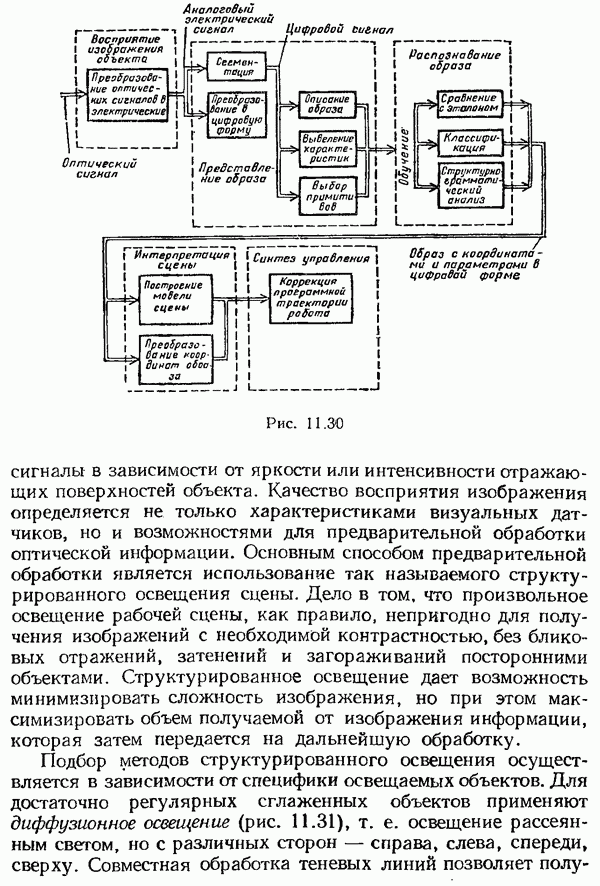
- Представление образа
- ЗАКЛЮЧЕНИЕ
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ