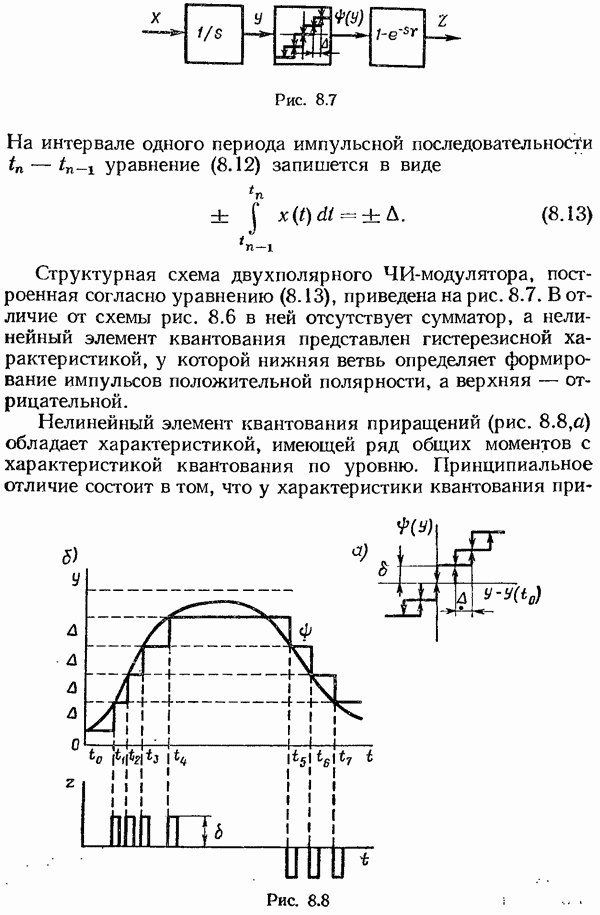
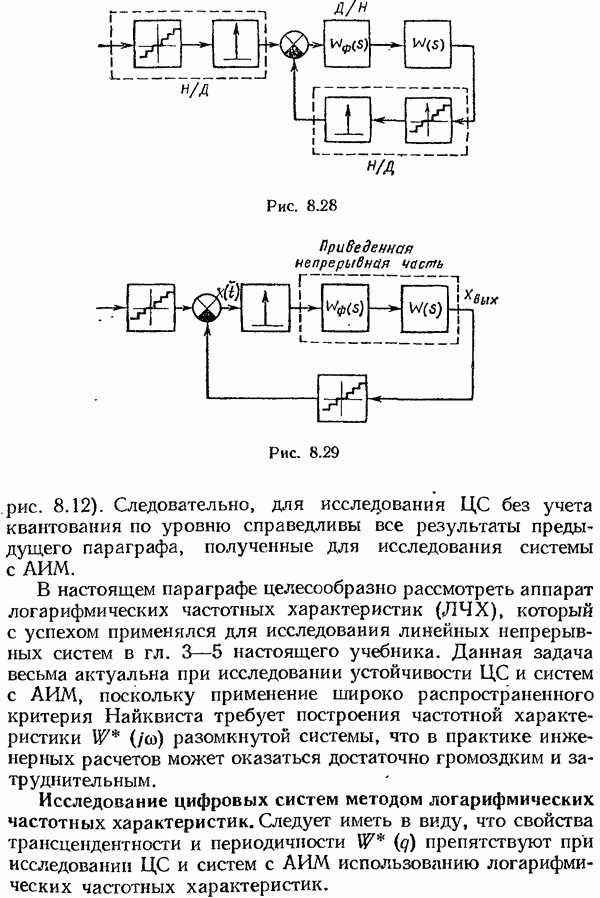
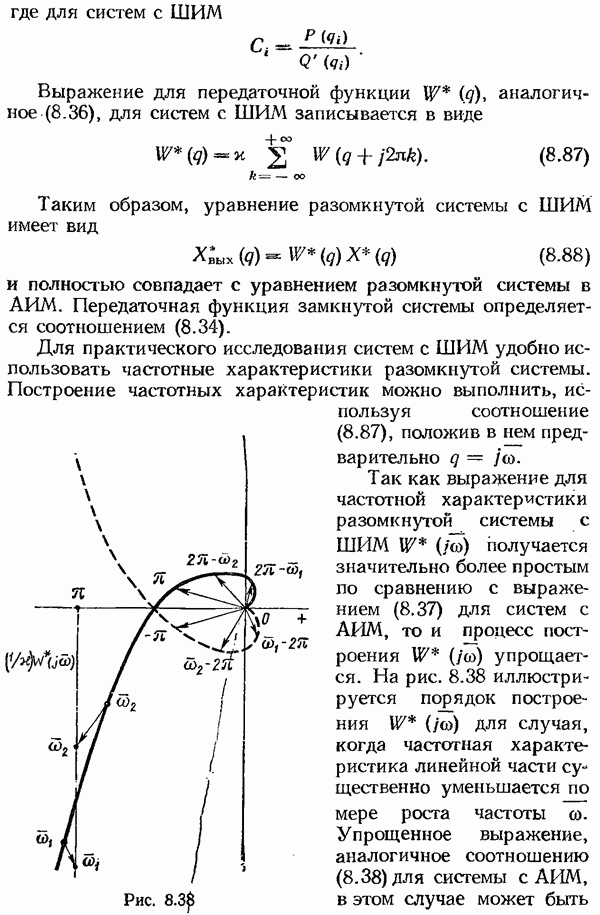
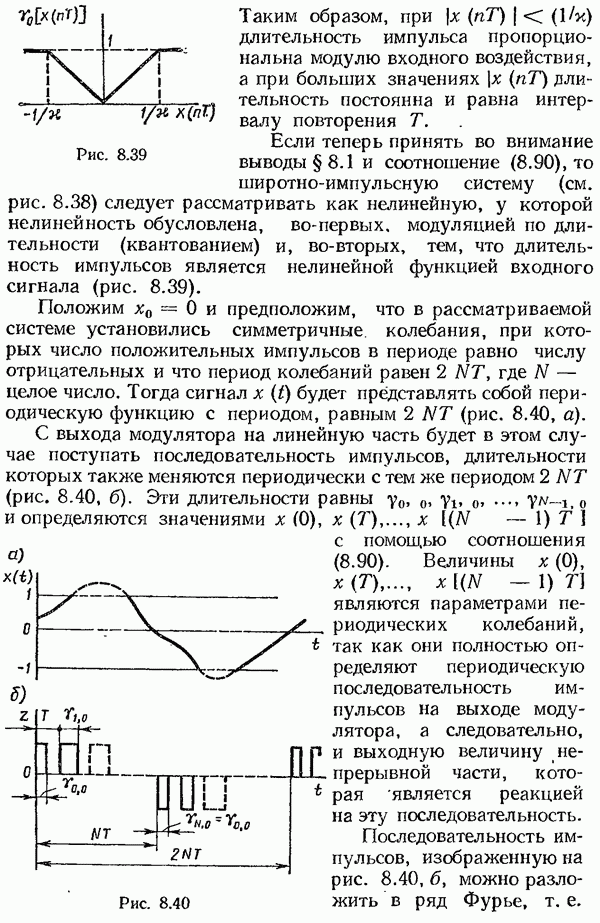
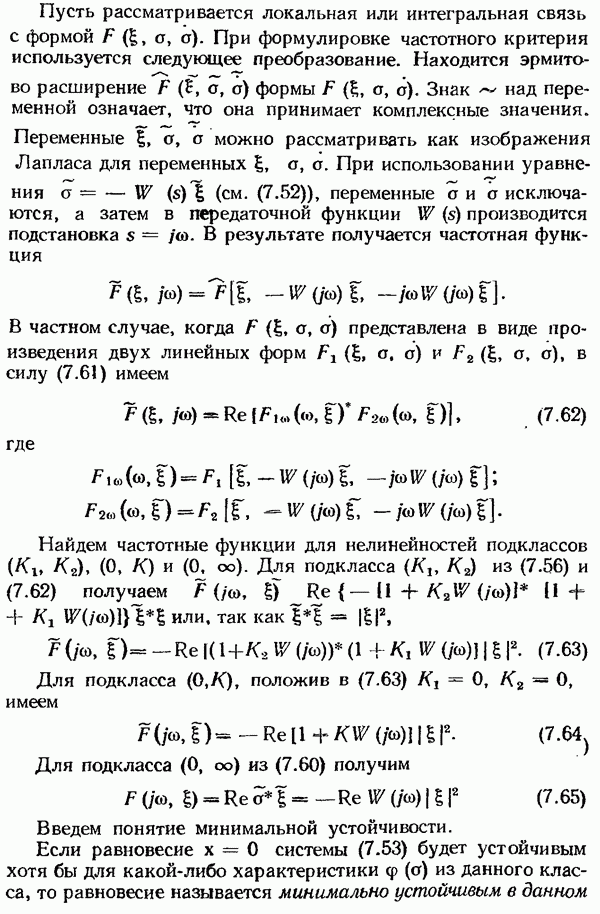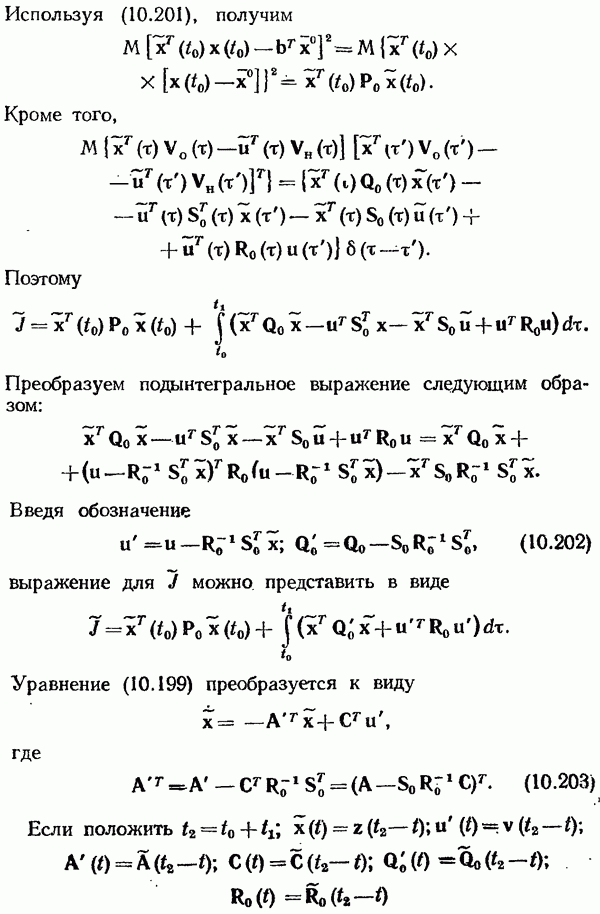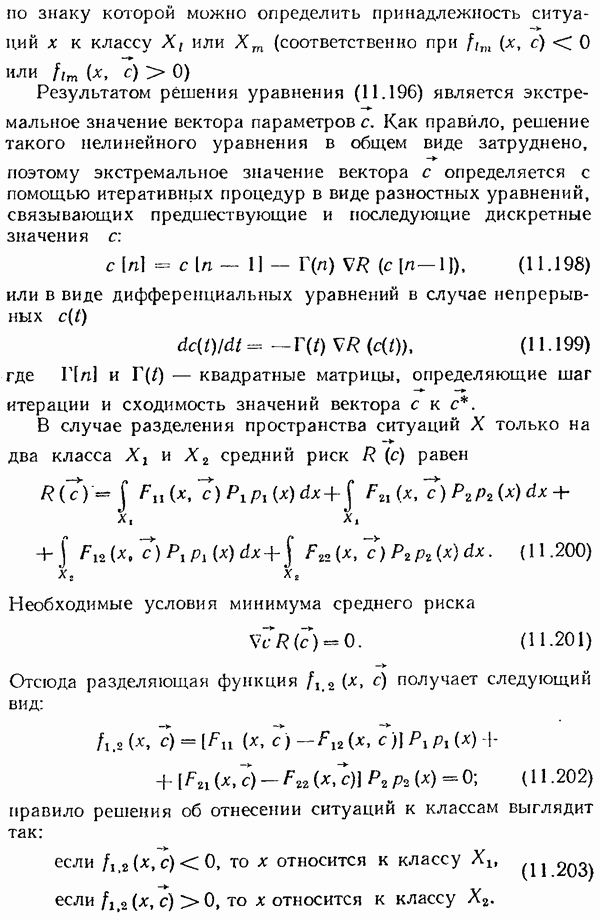| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
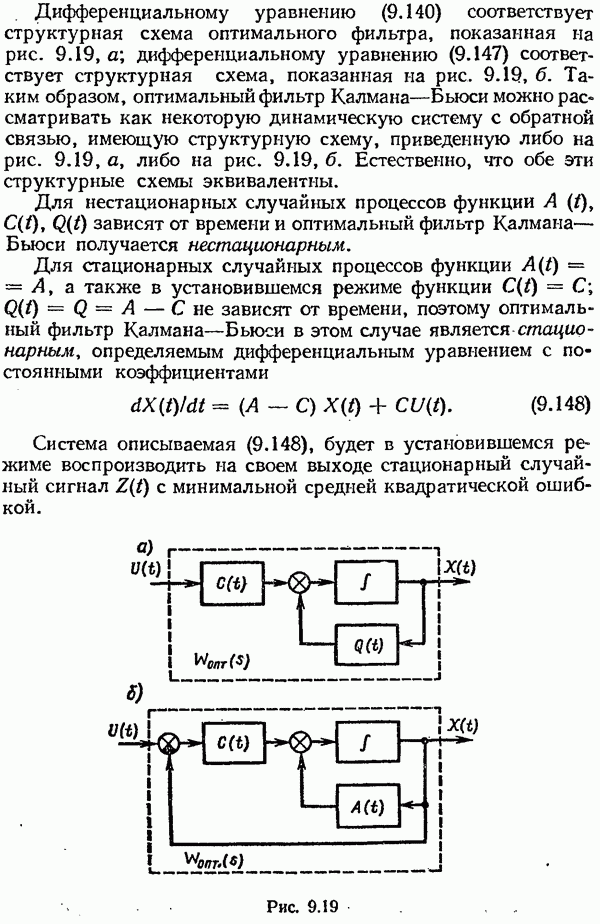
Гипотезы М. Айзермана и Р. Калмана.
Устойчивость в гурвицевом угле. Заменим в системе (7.52) нелинейный элемент линейной отрицательной обратной связью:

Тогда образуется линейная замкнутая система, характеристический полином которой будет

где  — числитель,
— числитель,  — знаменатель передаточной функции
— знаменатель передаточной функции 
Эту систему называют системой сравнения. Пусть при выполнении неравенства

полином (7.85) гурвицев, т. е. замкнутая линейная система устойчива. Наименьшее  и наибольшее
и наибольшее  значения
значения  при которых система попадает на границу устойчивости, ограничивают угол
при которых система попадает на границу устойчивости, ограничивают угол  называемый гурвицевым углом.
называемый гурвицевым углом.
В процессе развития теории абсолютной устойчивости были высказаны две гипотезы.
Гипотеза М. Айзермана.
Пусть даны уравнений (7.53), нелинейность принадлежит сектору  и для всех
и для всех  матрица
матрица  гурвицева. Тогда нелинейная система абсолютно устойчива. Иными словами, по гипотезе М. Айзермана, угол
гурвицева. Тогда нелинейная система абсолютно устойчива. Иными словами, по гипотезе М. Айзермана, угол  равен гурвицеву углу
равен гурвицеву углу  , т. е. система абсолютно устойчива в гурвицевом угле.
, т. е. система абсолютно устойчива в гурвицевом угле.
Гипотеза оказалась в общем случае неверной (для нее был указан противоречащий пример). Тогда была выдвинута гипотеза Р. Калмана.
Гипотеза Р. Калмана.
Пусть в уравнениях (7.53) нелинейность удовлетворяет условиям

и для всех  матрица
матрица  гурвицева. Тогда нелинейная система абсолютно устойчива.
гурвицева. Тогда нелинейная система абсолютно устойчива.
Г ипотеза оказалась неверной в общем случае.
Но для многих видов передаточных функций линейных частей гипотезы либо М. Айзермана, либо Р. Калмана могут выполняться. Отыскание условий, при которых выполняются эти гипотезы, представляют существенный интерес для практики, так как абсолютная устойчивость нелинейных систем, для которых гипотезы выполняются, может исследоваться по линейным критериям. Можно сказать, что такие системы абсолютно устойчивы, если они минимально устойчивы.
Представим частотную характеристику  линейной части в виде
линейной части в виде

где — передаточный коэффициент линейной части;  «нормированная» частотная характеристика с передаточным коэффициентом, равным единице. Выберем
«нормированная» частотная характеристика с передаточным коэффициентом, равным единице. Выберем  достаточно малым так, чтобы характеристика
достаточно малым так, чтобы характеристика  а следовательно, и
а следовательно, и
 располагались правее прямой
располагались правее прямой  (рис. 7.42). Пусть характеристика пересекает отрицательную вещественную полуось и крайняя левая (т. е. наиболее удаленная от начала координат) точка пересечения соответствует частоте
(рис. 7.42). Пусть характеристика пересекает отрицательную вещественную полуось и крайняя левая (т. е. наиболее удаленная от начала координат) точка пересечения соответствует частоте  . Пусть частотная характеристика
. Пусть частотная характеристика  такова, что касательная к ней в точке, соответствующей
такова, что касательная к ней в точке, соответствующей  не имеет пересечений с кривой, т. е. характеристика
не имеет пересечений с кривой, т. е. характеристика  лежит правее этой касательной, как показано на рис. 7.42. Назовем касательную
лежит правее этой касательной, как показано на рис. 7.42. Назовем касательную  правее которой расположена кривая, предельной касательной. Проведем через точку
правее которой расположена кривая, предельной касательной. Проведем через точку  на вещественной оси прямую, параллельную предельной касательной. Очевидно, что для нелинейностей из сектора
на вещественной оси прямую, параллельную предельной касательной. Очевидно, что для нелинейностей из сектора  эта прямая будет также прямой Попова. Начнем увеличивать
эта прямая будет также прямой Попова. Начнем увеличивать  Тогда размер характеристики будет увеличиваться, но форма ее будет сохраняться и предельная касательная будет перемещаться влево параллельно самой себе (пунктирные кривая и касательная на рисунке). Когда
Тогда размер характеристики будет увеличиваться, но форма ее будет сохраняться и предельная касательная будет перемещаться влево параллельно самой себе (пунктирные кривая и касательная на рисунке). Когда  достигнет такой величины, что левая точка пересечения характеристики попадет в точку
достигнет такой величины, что левая точка пересечения характеристики попадет в точку  на вещественной оси, будет иметь место равенство
на вещественной оси, будет иметь место равенство  Кривая Найквиста разомкнутой системы
Кривая Найквиста разомкнутой системы  таким образом, пройдет через критическую точку —1, 0 и устойчивость линейной замкнутой системы нарушится. Но одновременно и предельная касательная совпадет с прямой Попова и нарушится условие Попова для абсолютной устойчивости нелинейной системы из класса
таким образом, пройдет через критическую точку —1, 0 и устойчивость линейной замкнутой системы нарушится. Но одновременно и предельная касательная совпадет с прямой Попова и нарушится условие Попова для абсолютной устойчивости нелинейной системы из класса  . В данном случае верхняя граница гурвицева угла совпадает с углом
. В данном случае верхняя граница гурвицева угла совпадает с углом  . Нижняя граница, правда, не совпадает, но нас она не интересует, поэтому мы назовем данную систему абсолютно устойчивой в гурвицевом угле. Гипотеза М. Айзермана для нее справедлива в положительной части гурвицева угла.
. Нижняя граница, правда, не совпадает, но нас она не интересует, поэтому мы назовем данную систему абсолютно устойчивой в гурвицевом угле. Гипотеза М. Айзермана для нее справедлива в положительной части гурвицева угла.
Пусть теперь характеристика  такова, что предельная касательная
такова, что предельная касательная  к ней не проходит через крайнюю левую точку пересечения характеристики с отрицатель ной вещественной полуосью (рис. 7.43). В процессе возрастания
к ней не проходит через крайнюю левую точку пересечения характеристики с отрицатель ной вещественной полуосью (рис. 7.43). В процессе возрастания  при некотором его значении
при некотором его значении  предельная
предельная

Рис. 7.42

Рис. 7.43.
касательная совместится с прямой Попова и условие Попова для абсолютной устойчивости нарушится, хотя линейная замкнутая система с тем же значением  будет еще устойчивой. Нарушение ее устойчивости произойдет при значении
будет еще устойчивой. Нарушение ее устойчивости произойдет при значении  когда точка, соответствующая
когда точка, соответствующая  к частотной характеристике, попадет в точку —
к частотной характеристике, попадет в точку —  Система с такой характеристикой
Система с такой характеристикой  не будет абсолютно устойчивой в гурвицевом угле, и для нее несправедливы ни гипотеза М. Айзермана, ни гипотеза Р. Калмана.
не будет абсолютно устойчивой в гурвицевом угле, и для нее несправедливы ни гипотеза М. Айзермана, ни гипотеза Р. Калмана.
С помощью описанных построений можно в плоскости  построить секторы абсолютной устойчивости
построить секторы абсолютной устойчивости  асболютной неустойчивости
асболютной неустойчивости  и неопределенности. Вещественная ось и прямая
и неопределенности. Вещественная ось и прямая  ограничивают в первом квадранте сектор абсолютной устойчивости
ограничивают в первом квадранте сектор абсолютной устойчивости  (рис. 7.44). Прямая
(рис. 7.44). Прямая  является нижней границей сектора абсолютной неустойчивости
является нижней границей сектора абсолютной неустойчивости  (заштрихован однократно), в котором линейная система неустойчива и не соблюдены условия Попова. Между прямыми
(заштрихован однократно), в котором линейная система неустойчива и не соблюдены условия Попова. Между прямыми  заключен сектор неопределенности, в котором линейная система сравнения устойчива, но достаточное условие абсолютной устойчивости не соблюдается и мы не можем утверждать, что система абсолютно устойчива, но и не можем сказать, что она неустойчива.
заключен сектор неопределенности, в котором линейная система сравнения устойчива, но достаточное условие абсолютной устойчивости не соблюдается и мы не можем утверждать, что система абсолютно устойчива, но и не можем сказать, что она неустойчива.
Графоаналитический метод позволяет легко определить, будет ли система абсолютно устойчивой в гурвицевом угле (или его положительном секторе), но аналитическое определение этого весьма сложно. В настоящее время установлено, что нелинейная система из класса  устойчива в гурвицевом угле, если линейная часть состоит из любого числа последовательно включенных устойчивых звеньев первого порядка.
устойчива в гурвицевом угле, если линейная часть состоит из любого числа последовательно включенных устойчивых звеньев первого порядка.
В случае дифференцируемых монотонно возрастающих нелинейных характеристик из класса  , одновременно удовлетворяющих неравенствам
, одновременно удовлетворяющих неравенствам  линейная часть может кроме упомянутых звеньев первого порядка иметь в последовательной цепи любое число колебательных звеньев, передаточные функции которых имеют комплексные полюсы
линейная часть может кроме упомянутых звеньев первого порядка иметь в последовательной цепи любое число колебательных звеньев, передаточные функции которых имеют комплексные полюсы

Рис. 7.44
с отношением мнимой части к вещественной, не превышающим 3 [5].
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 7. НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
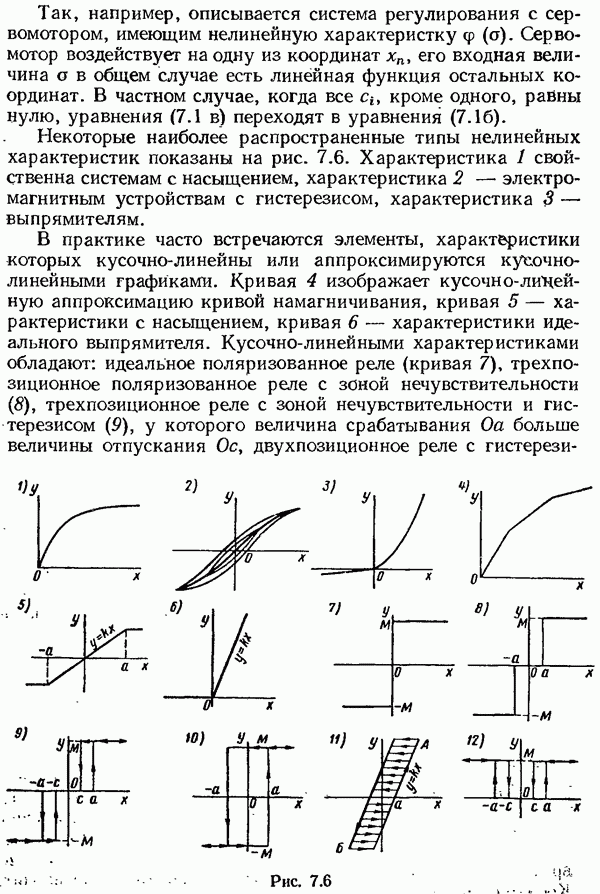
- § 7.1. Основные типы. нелинейных систем и характеристик
- § 7.2. Изображение движений в фазовой плоскости
- Линейная консервативная система второго порядка.
- Система с сухим кулоновским трением.
- Система с отрицательной восстанавливающей силой.
- Линейная колебательная система с вязким трением.
- Линейная апериодическая система с вязким трением.
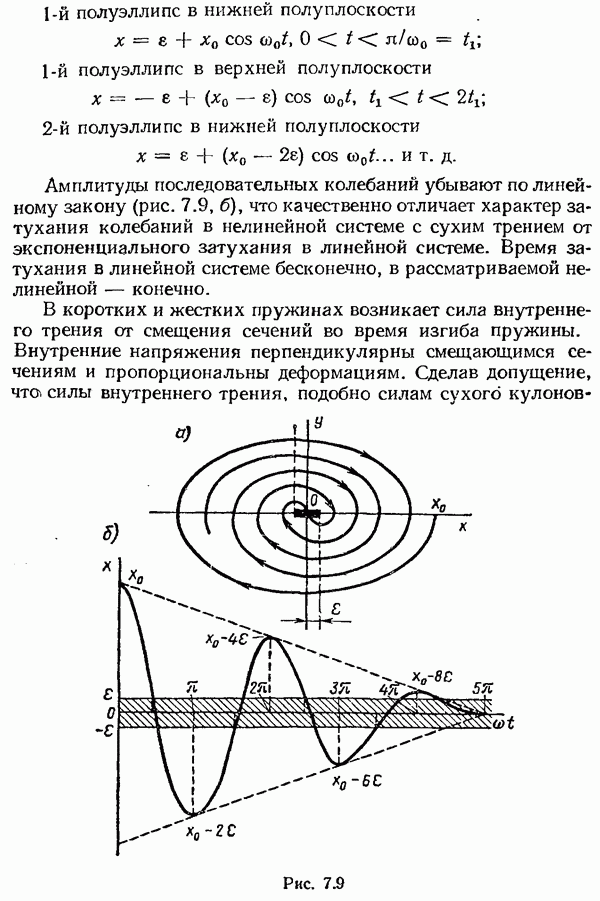
- § 7.3. Автоколебания. Метод точечных преобразований
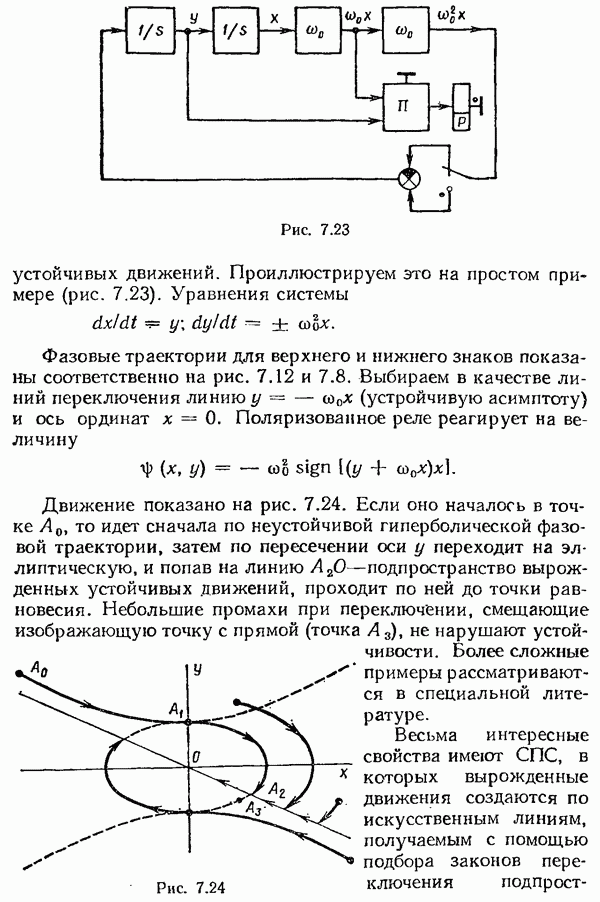
- § 7.4. Системы с переменной структурой
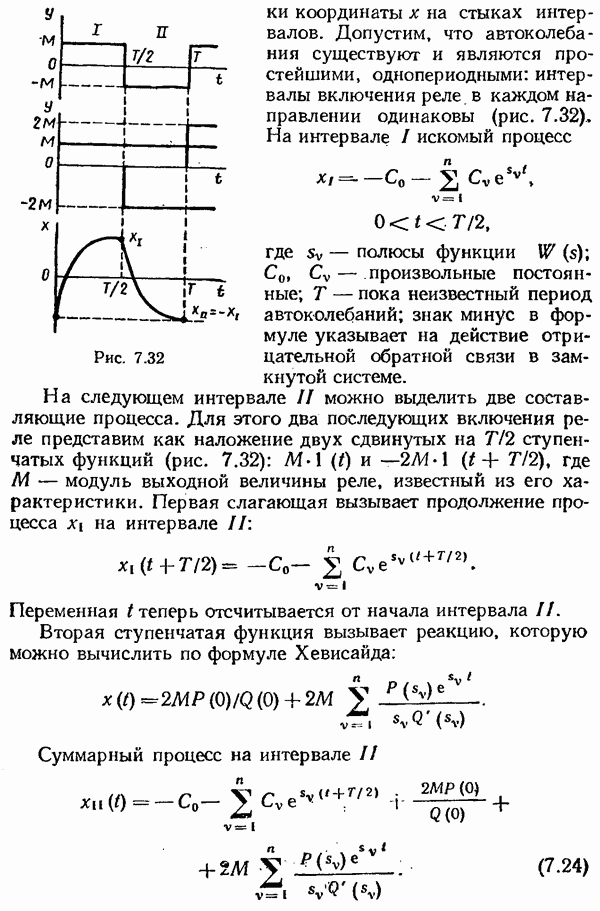
- § 7.5. Метод «припасовывания» граничных значений
- § 7.6. Приближенное исследование автоколебаний. Метод эквивалентной линеаризации
- § 7.7. Метод гармонического баланса
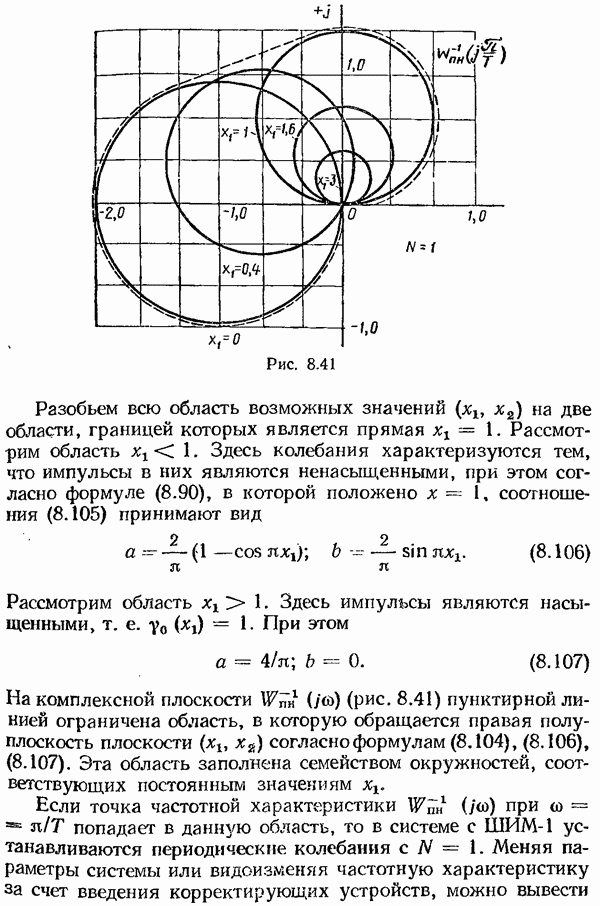
- § 7.8. Устойчивость в малом, большом и целом
- § 7.9. Второй (прямой) метод Ляпунова
- § 7.10. Абсолютная устойчивость
- Квадратичный критерий абсолютной устойчивости.
- Круговой критерий устойчивости.
- Критерий В. М. Попова.
- Примечание к критерию Попова.
- Гипотезы М. Айзермана и Р. Калмана.
- Определение автоколебаний.
- Упрощенный критерий колебательности.
- Глава 8. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
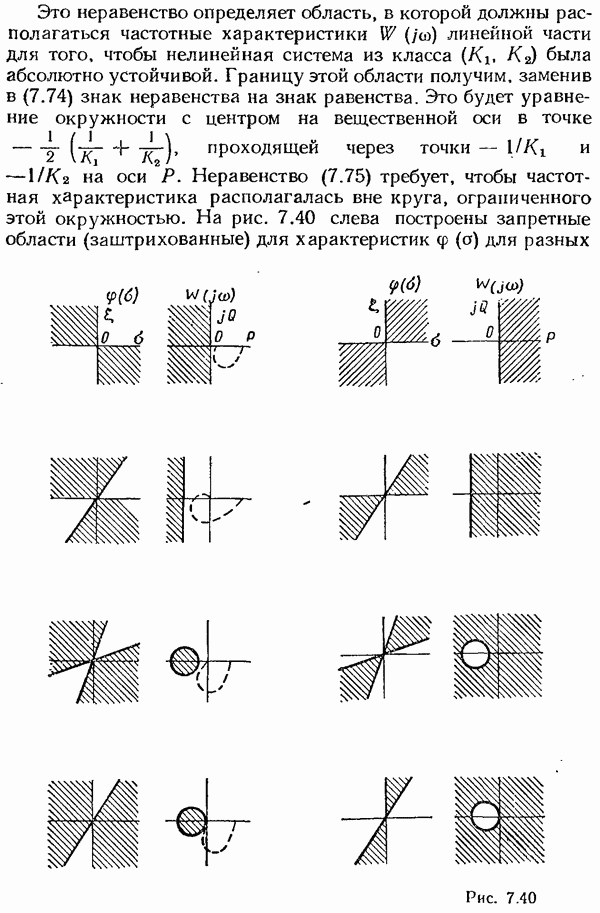
- § 8.1. Понятие об импульсных системах автоматического управления
- Структура и уравнения импульсных модуляторов.
- Структурная схема амплитудно-импульсного модулятора.
- Структурная схема частотно-импульсного модулятора.
- Структурная схема широтно-импульсного модулятора.
- Структурные схемы частотно-импульсных к широтно- импульсных модуляторов 1-го рода.
- Структурная схема системы управления с импульсной модуляцией. Классификация систем управления с импульсной модуляцией.
- § 8.2. Исследование устойчивости и качества систем управления с амплитудноимпульсной модуляцией
- Передаточная функция импульсной системы.
- Дискретное преобразование Лапласа и его основные свойства.
- Частотные характеристики импульсной системы.
- Исследование устойчивости систем с амплитудно-импульсной модуляцией.
- Алгебраический критерий устойчивости (аналог критерия Гурвица).
- Частотный критерий устойчивости (аналог критерия Найквиста).
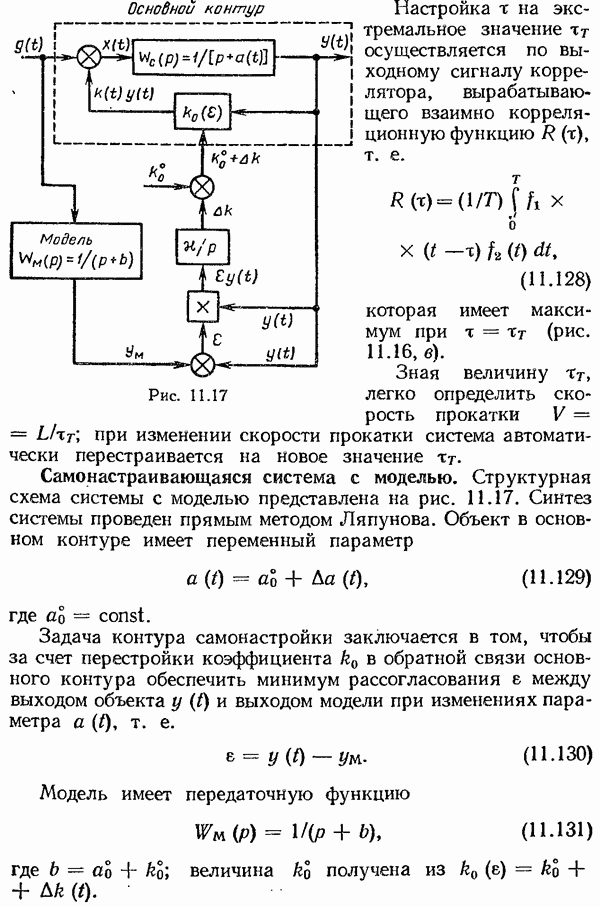
- Исследование качества систем с амплитудно-импульсной модуляцией.
- Непрерывное регулирование как граница импульсного регулирования.
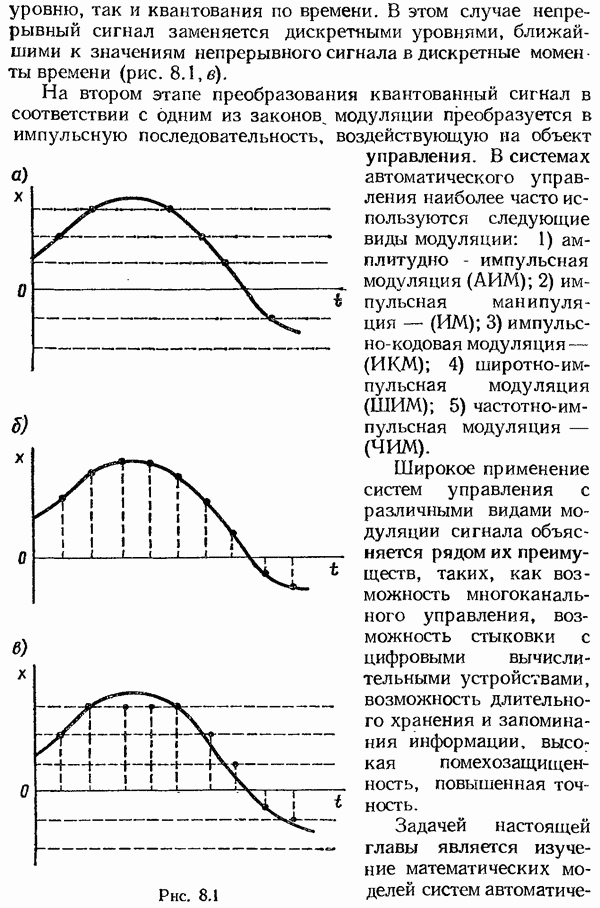
- § 8.3. Исследование динамики цифровых систем автоматического управления
- Исследование цифровых систем методом логарифмических частотных характеристик.
- Исследование цифровых систем с непрерывной передачей данных.
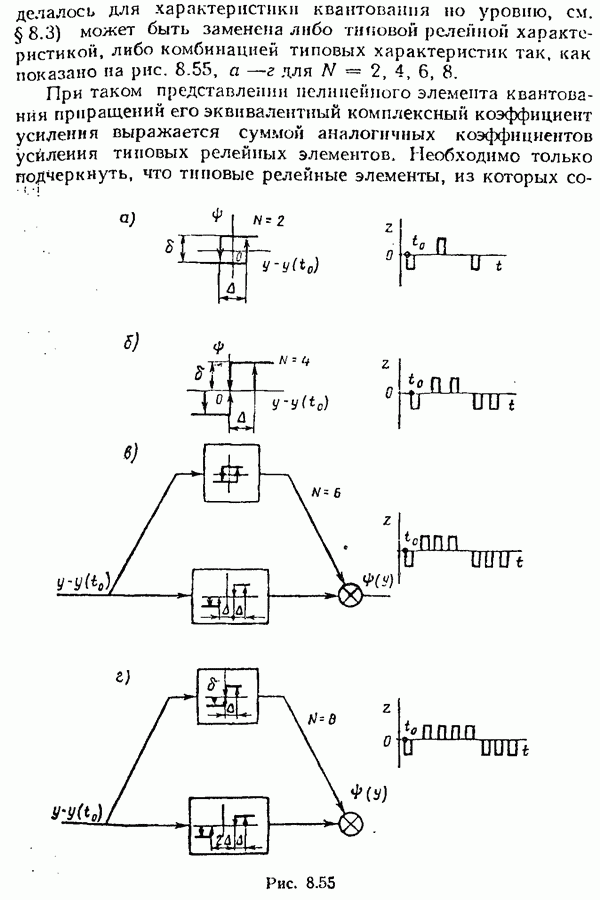
- Исследование цифровых систем с учетом квантования по уровню и по времени.
- § 8.4. Исследование систем с широтноимпульсной модуляцией
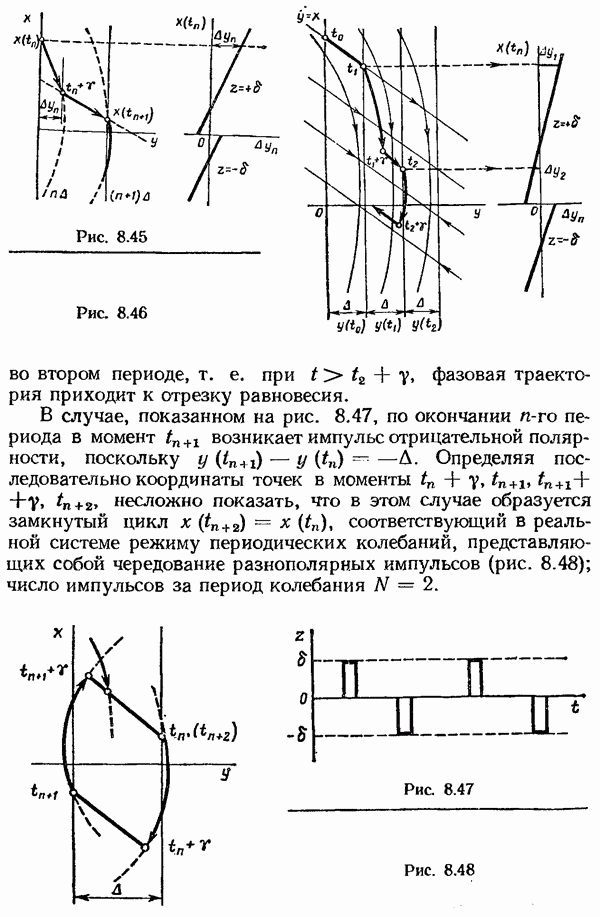
- Исследование периодических колебаний в системах с широтно-импульсной модуляцией.
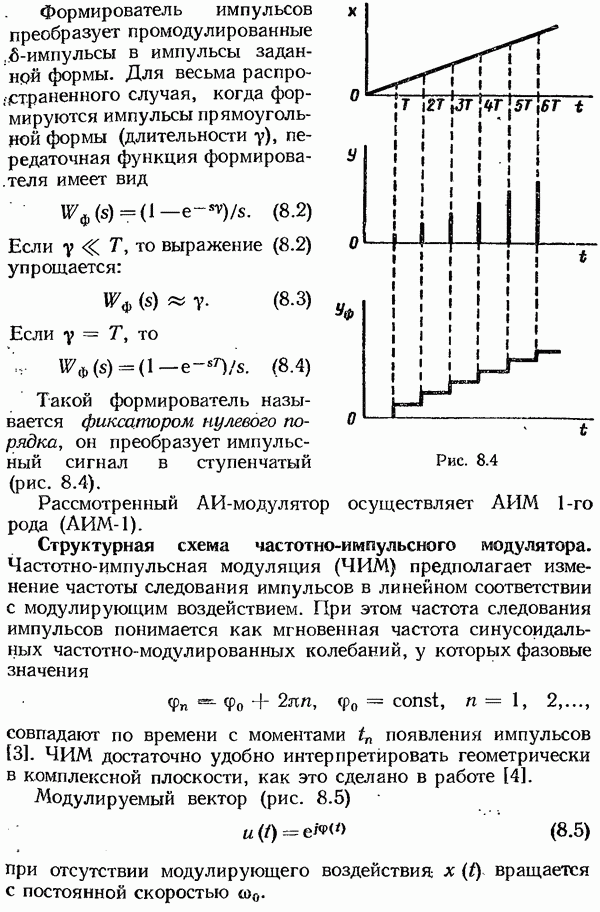
- § 8.5. Исследование систем с частотно-импульсной модуляцией
- Исследование устойчивости в целом частотно-импульсных систем 2-го рода.
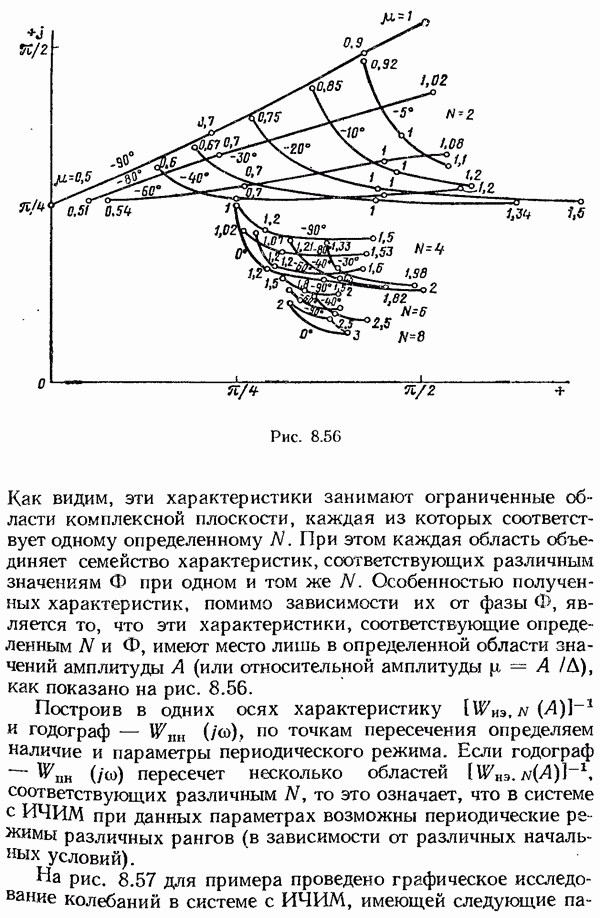
- Исследование периодических режимов в системах с ИЧИМ.
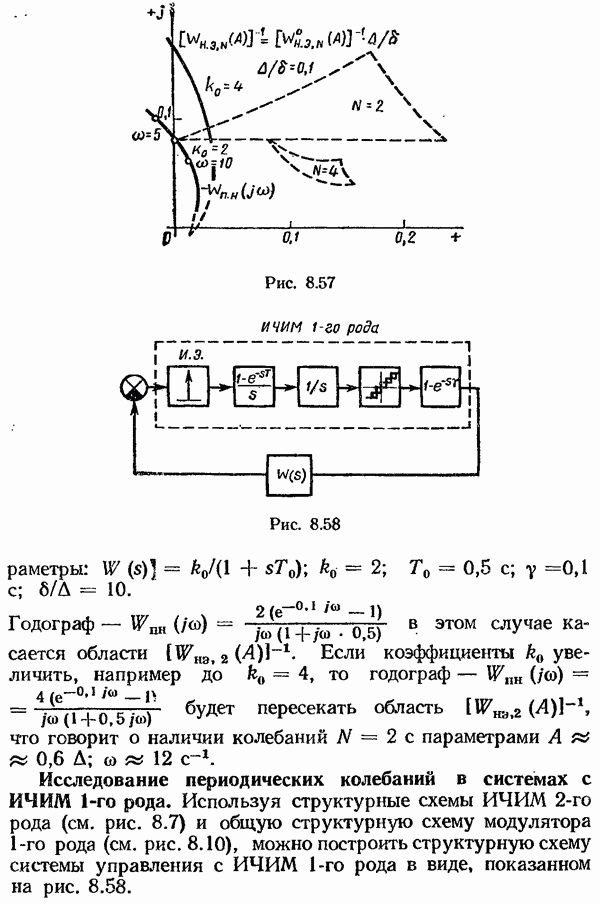
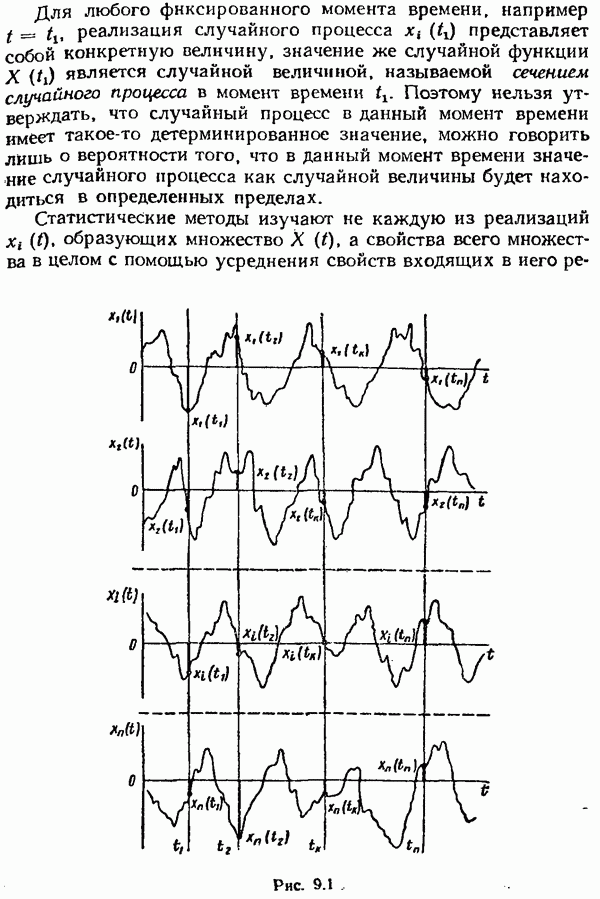
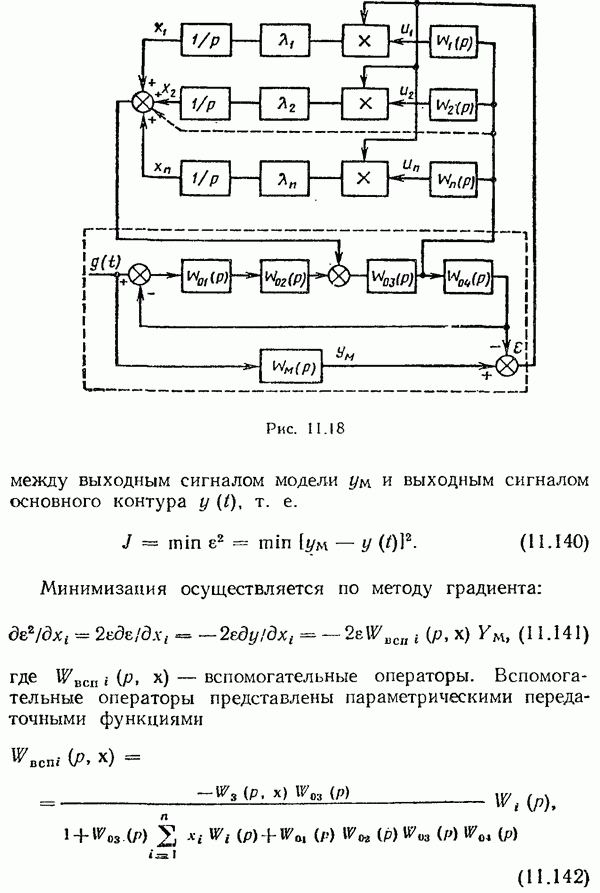
- Исследование периодических колебаний в системах с ИЧИМ 1-го рода.
- Глава 9. СЛУЧАЙНЫЕ ПРОЦЕССЫ В АВТОМАТИЧЕСКИХ СИСТЕМАХ УПРАВЛЕНИЯ
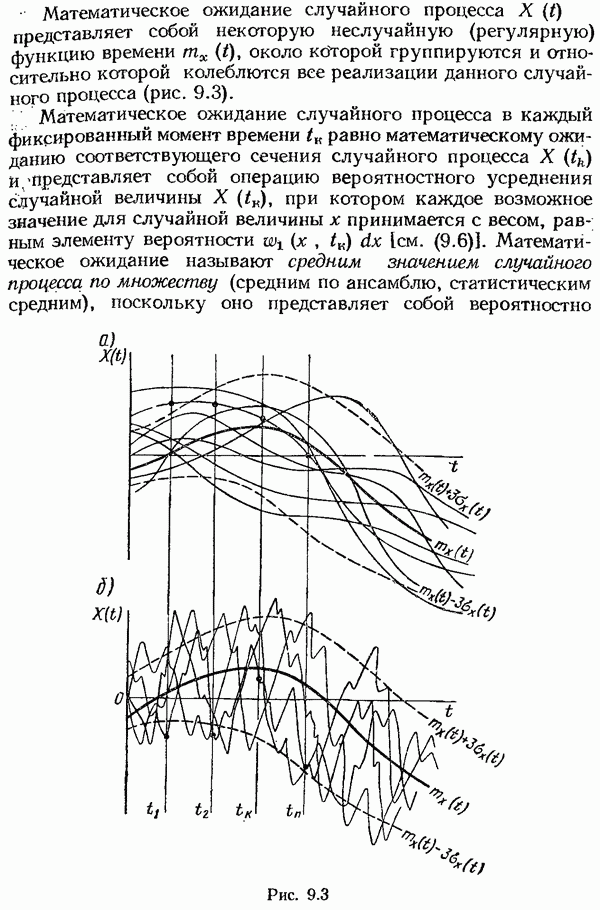
- § 9.2. Случайные процессы и их основные статистические характеристики
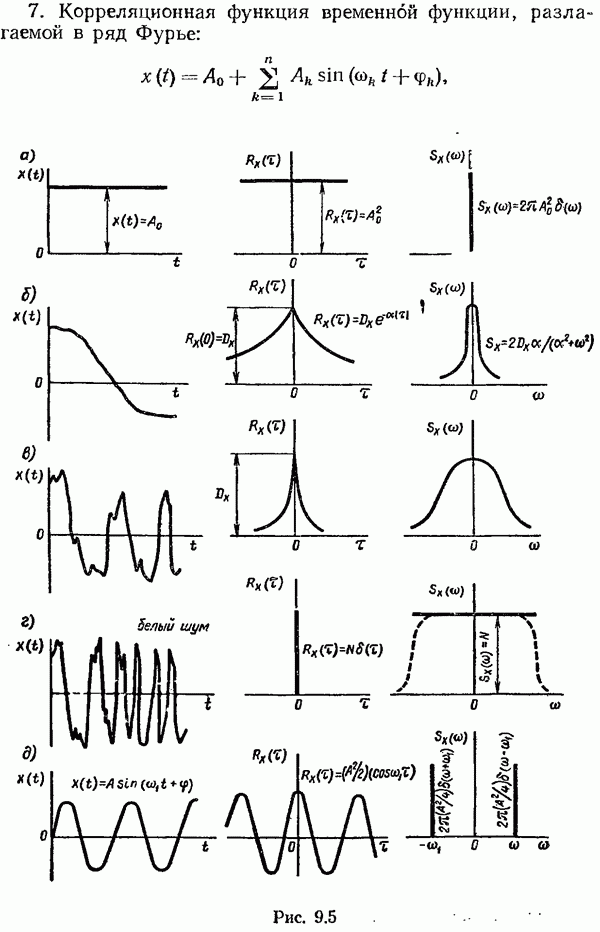
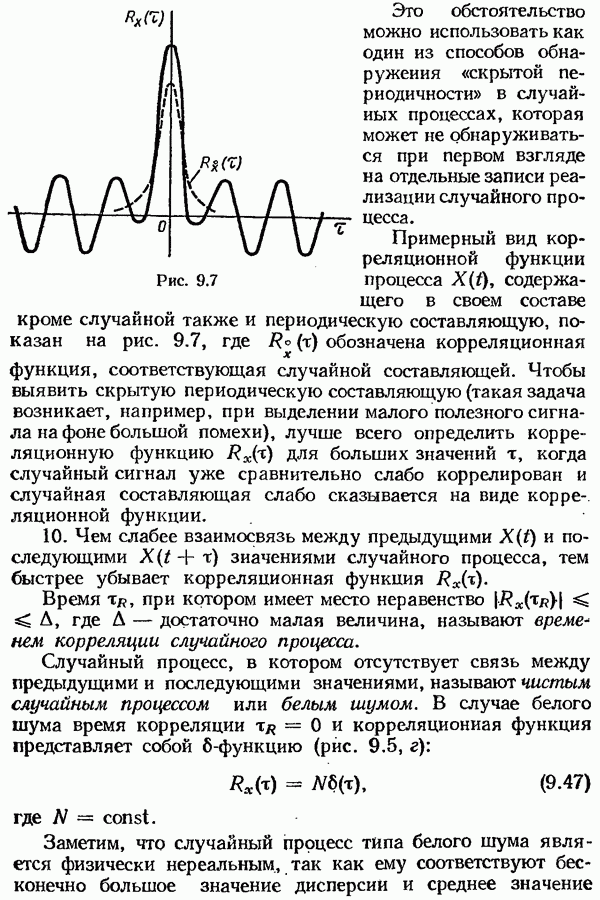
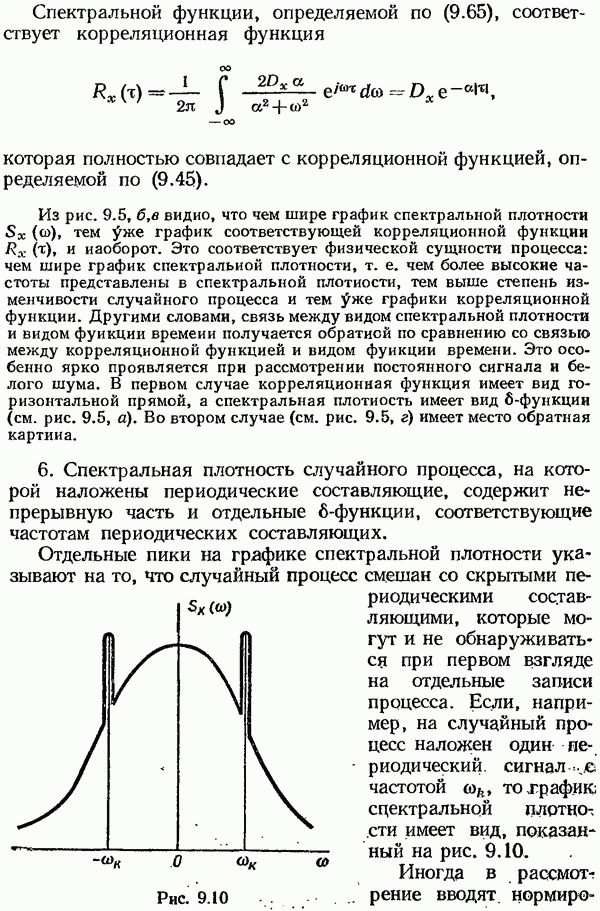
- § 9.3. Корреляционные функции случайных процессов
- § 9.4. Спектральные плотности случайных процессов
- § 9.5. Связь между корреляционными функциями и спектральными плотностями случайного процесса на входе и выходе линейной системы
- § 9.6. Расчет линейных систем при случайных воздействиях
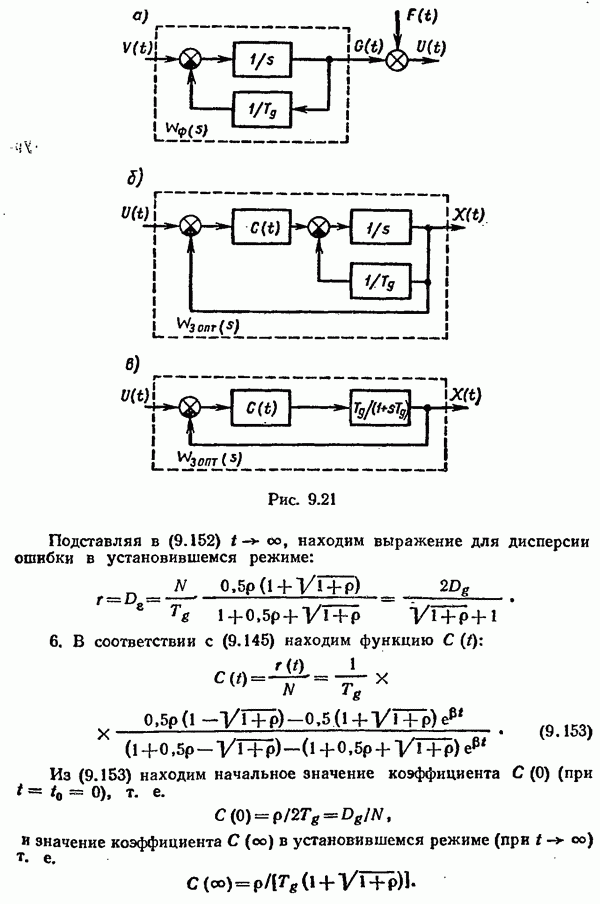
- Аналитический метод определения дисперсии ошибки.
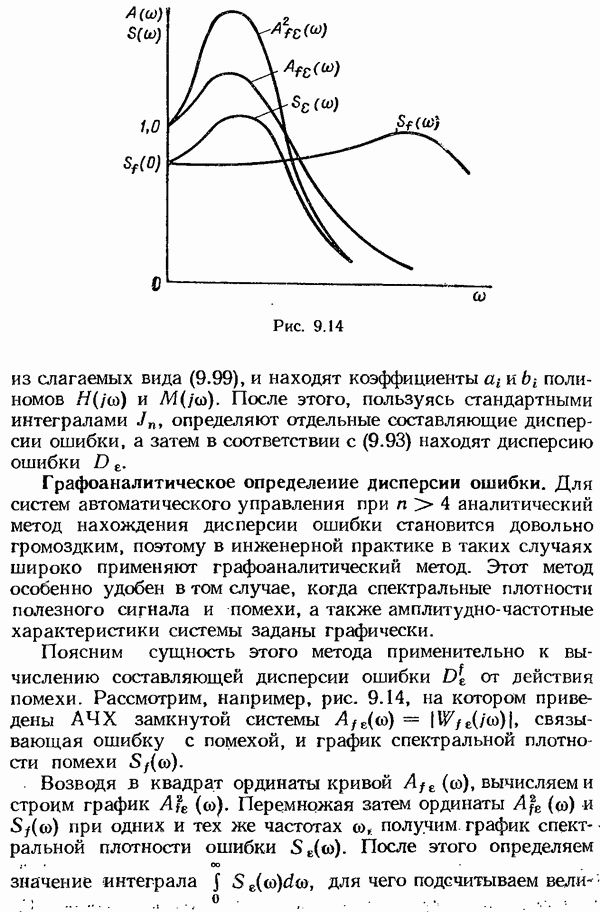
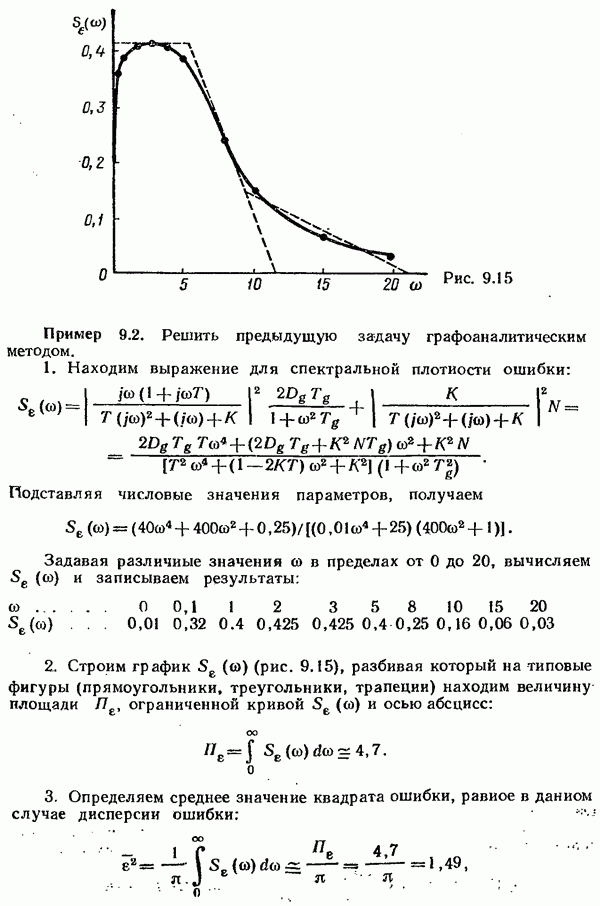
- Графоаналитическое определение дисперсии ошибки.
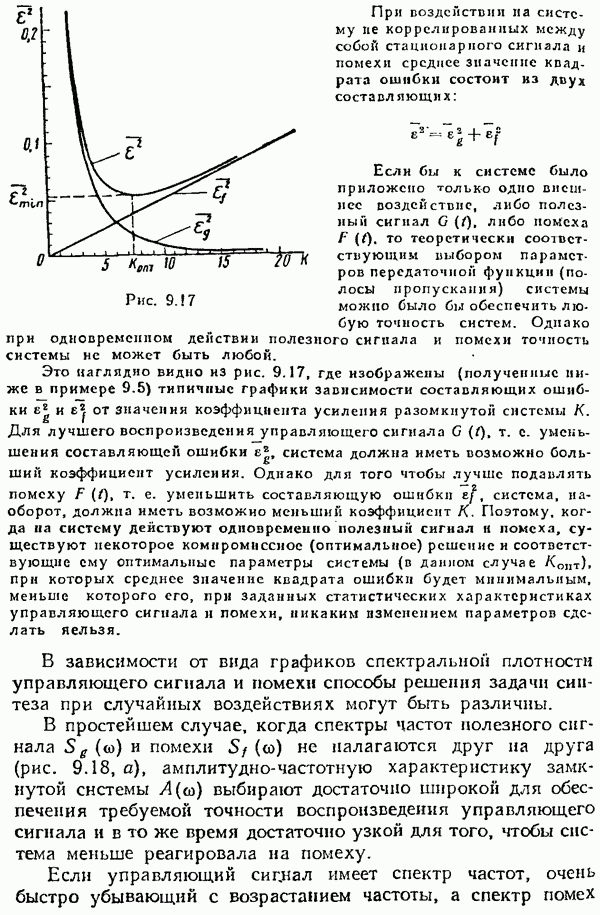
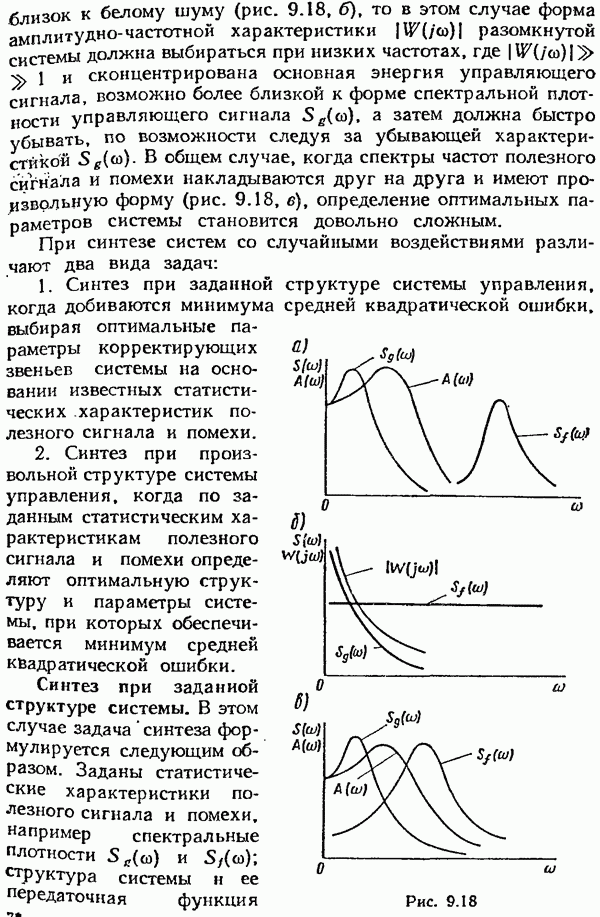
- § 9.7. Синтез линейных систем с минимальной средней квадратической ошибкой
- Синтез при произвольной структуре системы.
- Оптимальный фильтр Винера.
- Оптимальный фильтр Калмана—Бьюси.
- § 9.8. Случайные процессы в линейных импульсных системах
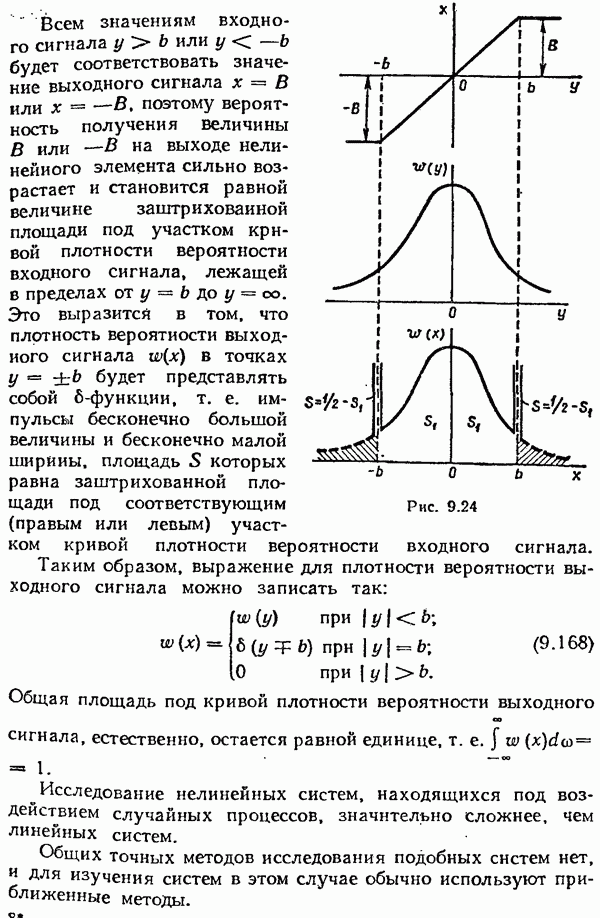
- § 9.9. Нелинейное преобразование случайных сигналов
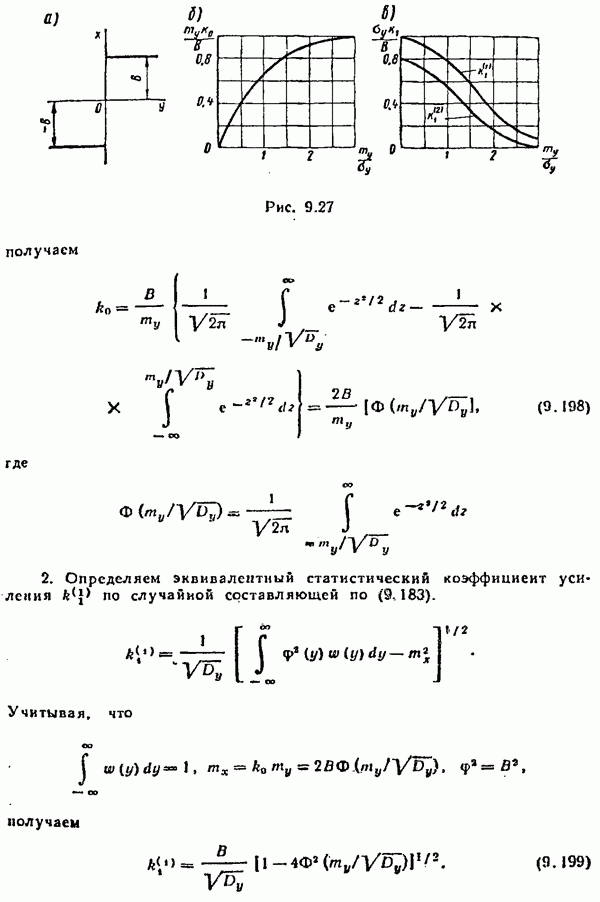
- § 9.10. Статистическая линеаризация нелинейных элементов
- § 9.11. Расчет нелинейных систем методом статистической линеаризации
- Расчет замкнутых нелинейных систем.
- Глава 10. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
- Общая постановка задачи оптимального управления
- Примеры постановки задач оптимального управления.
- Классификация задач оптимального управления
- § 10.2. Метод классического вариационного исчисления (метод множителей Лагранжа)
- Уравнения Эйлера—Лагранжа.
- Задачи с подвижными концами и фиксированным временем
- Задача с нефиксированным временем.
- § 10.3. Принцип максимума Понтрягина. Условие нормальности. Теорема об n интервалах. Вырожденные и особые задачи
- Задача с подвижными концами
- Задача максимального быстродействия
- Условие нормальности.
- Теорема об n интервалах.
- Задача с ограничением на фазовые координаты
- Вырожденные задачи
- Особые задачи
- § 10.4. Метод динамического программирования. Теорема Болтянского. Метод Кротова
- Принцип оптимальности
- Функция и уравнение Беллмана
- Проблема обоснования метода динамического программирования и достаточные условия оптимальности
- Метод Кротова [11]
- Принцип оптимальности Кротова.
- § 10.5. Управляемость и наблюдаемость. Наблюдатели
- Управляемость линейных стационарных объектов.
- Стабилизируемость.
- Управляемость при наличии ограничения на управление.
- Наблюдаемость и восстанавливаемость
- Обнаруживаемость
- Наблюдатели
- Наблюдатели пониженного порядка.
- § 10.6. Методы синтеза оптимальных систем с обратной связью. Синтез оптимальных линейных систем по интегральному квадратичному критерию
- Синтез оптимальных линейных систем по интегральному квадратичному критерию
- Векторное дифференцирование.
- Синтез оптимального линейного регулятора выхода.
- § 10.7. Стохастические оптимальные системы. Методы синтеза. Методы оптимальной оценки состояния. Принцип разделимости
- Метод динамического программирования
- Синтез стохастической оптимальной линейной системы при полной информации о состоянии
- Синтез стохастических оптимальных систем управления при неполной информации
- Наблюдатель Калмана—Бьюси при цветном шуме объекта.
- Наблюдатель Калмана—Бьюси при цветном шуме наблюдения.
- Сингулярная (вырожденная) задача линейного оптимального оценивания.
- Линеаризованный наблюдатель Калмана—Бьюси.
- Стохастическая линейная оптимальная система управления при неполной информации. Принцип разделимости
- § 10.8. Оптимальные дискретные системы
- Синтез оптимальной линейной системы при квадратном критерии
- Стохастическая оптимальная линейная система при полной информации о состоянии.
- Наблюдатель (оцениватель, фильтр) Калмана.
- О расходимости фильтров и методах их регуляризации.
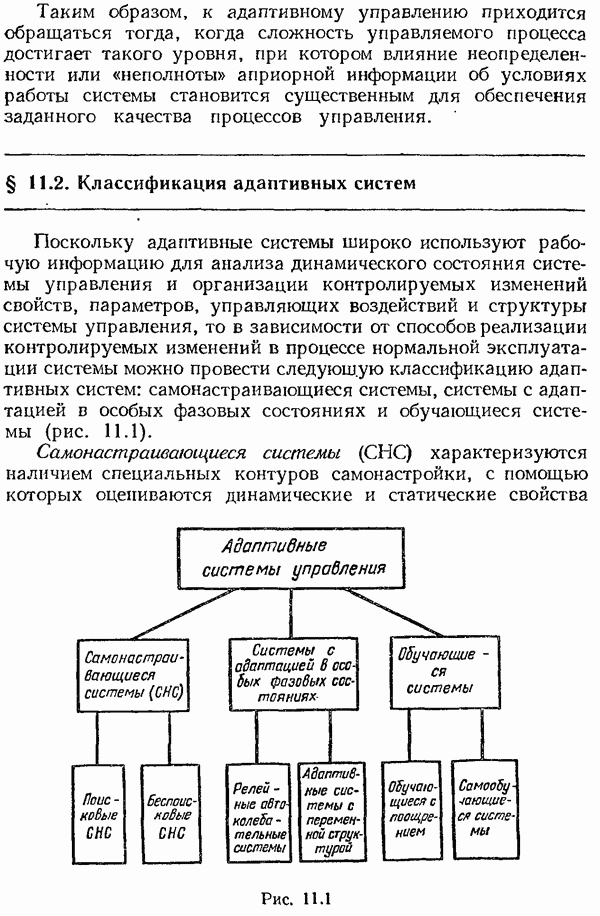
- Глава 11. АДАПТИВНЫЕ АВТОМАТИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
- § 11.2. Классификация адаптивных систем
- § 11.3. Самонастраивающиеся системы
- Принципы построения поисковых самонастраивающихся систем.
- Регулярные методы поиска экстремума
- Метод градиента.
- Метод наискорейшего спуска.
- Методы экстраполяционного поиска.
- Методы случайного поиска
- Локальный случайный поиск с пересчетом.
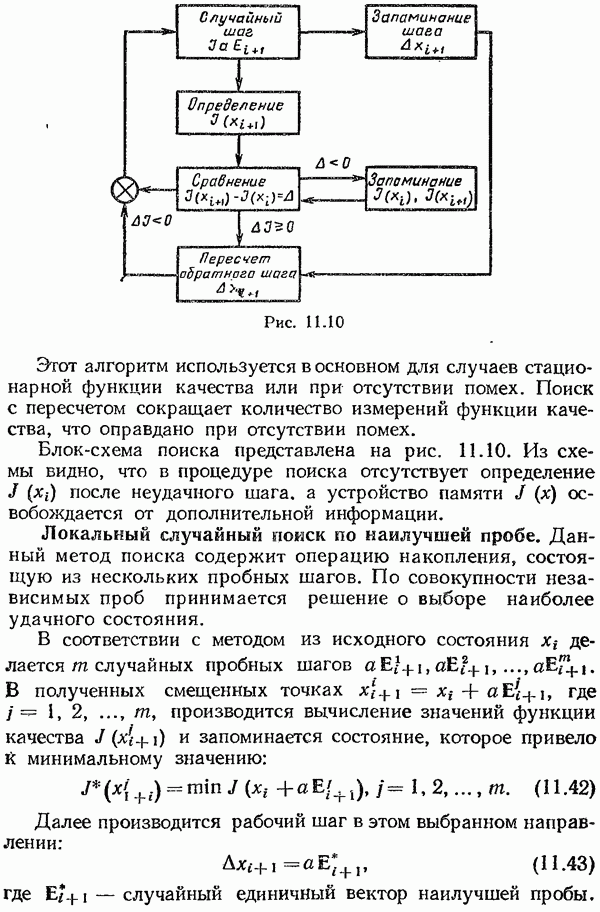
- Локальный случайный поиск по наилучшей пробе.
- Локальный случайный поиск по статистическому градиенту.
- Глобальный случайный поиск с независимым выбором плотности распределения пробных шагов.
- Примеры поисковых самонастраивающихся систем
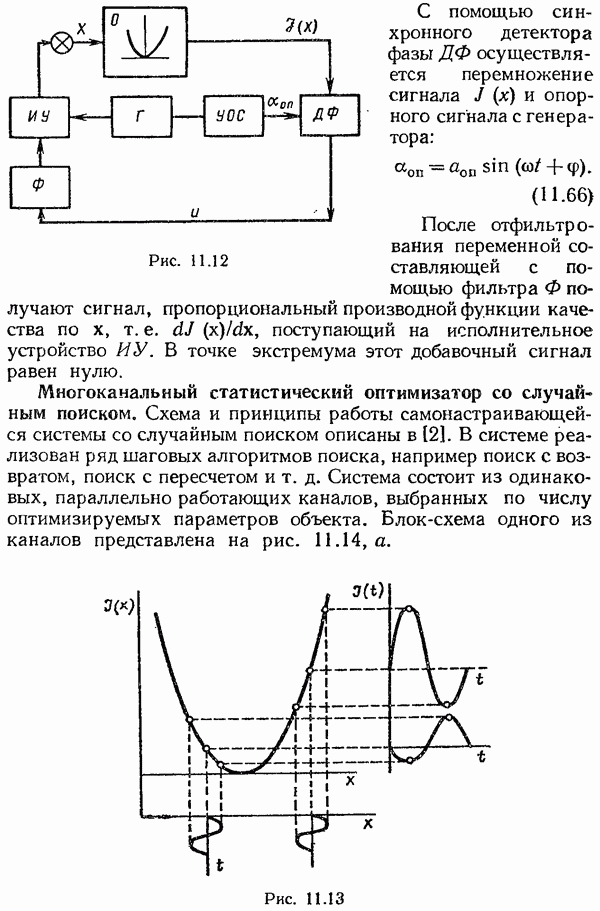
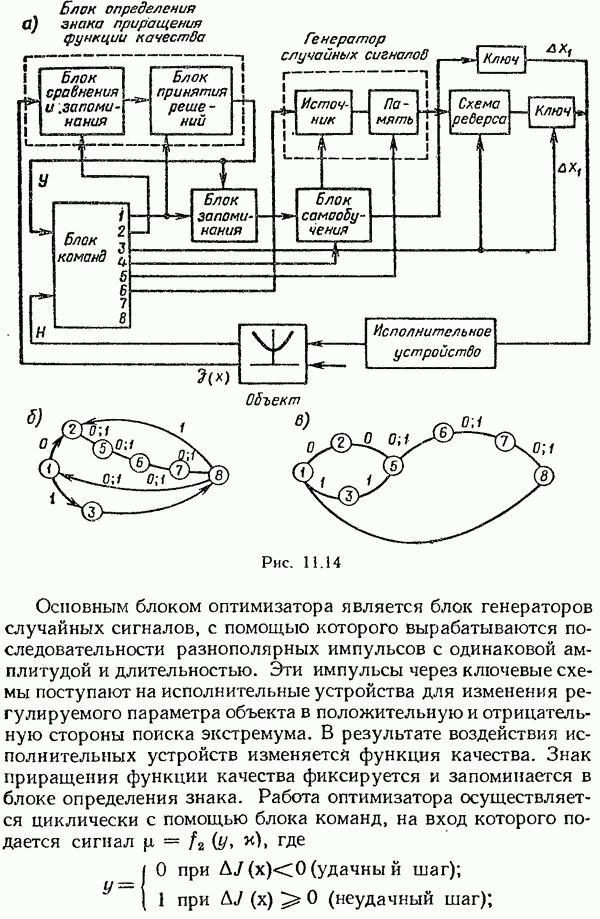
- Многоканальный статистический оптимизатор со случайным поиском.
- Принцип инвариантности.
- Принцип эталонной модели.
- Принципы определения градиента функции качества.
- Принципы идентификации динамических свойств системы управления.
- Примеры беспоисковых самонастраивающихся систем
- Самонастраивающаяся система с моделью.
- Градиентная самонастраивающаяся система.
- § 11.4. Системы с адаптацией в особых фазовых состояниях
- Адаптивные системы с переменной структурой.
- Адаптивная система с переменной структурой, использующая информацию о внутренних координатах.
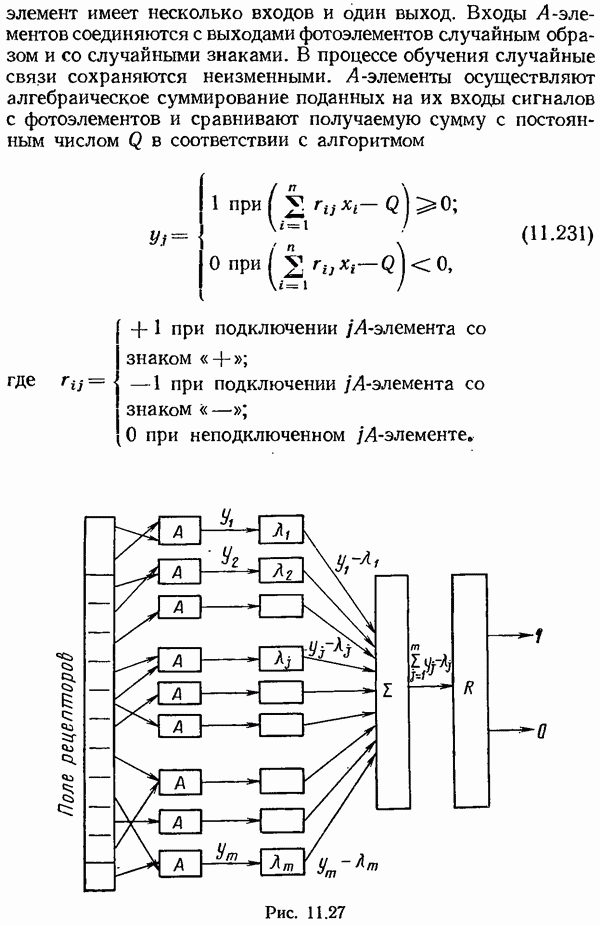
- § 11.5. Обучающиеся системы
- Метод секущих плоскостей.
- Метод потенциальных функций.
- Вероятностные алгоритмы обучения.
- Самообучение.
- Персептронная модель автоматической классификации.
- § 11.6. Адаптивные робототехнические системы
- Методы обработки сенсорной информации для адаптивного управления роботами.
- Восприятие изображения объекта
- Представление образа
- ЗАКЛЮЧЕНИЕ
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ