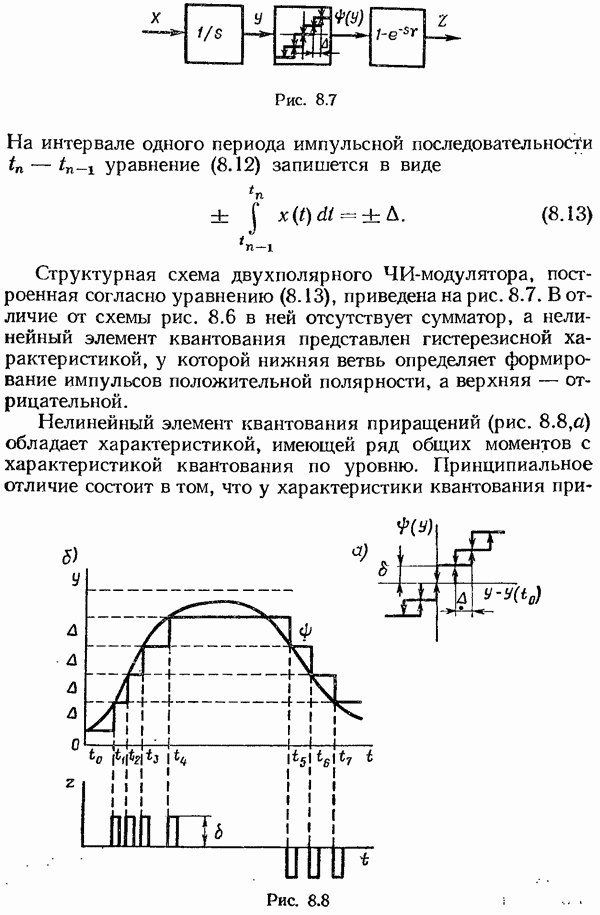
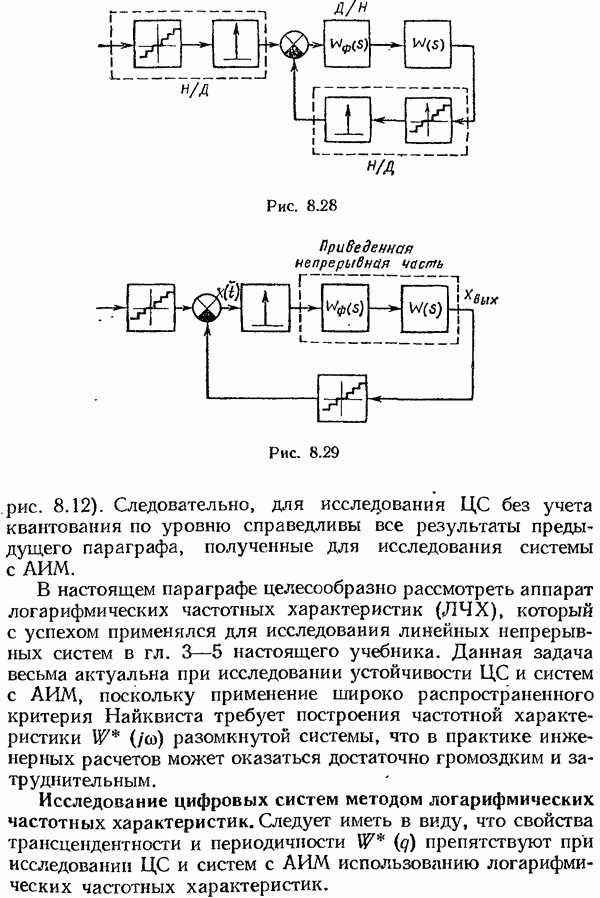
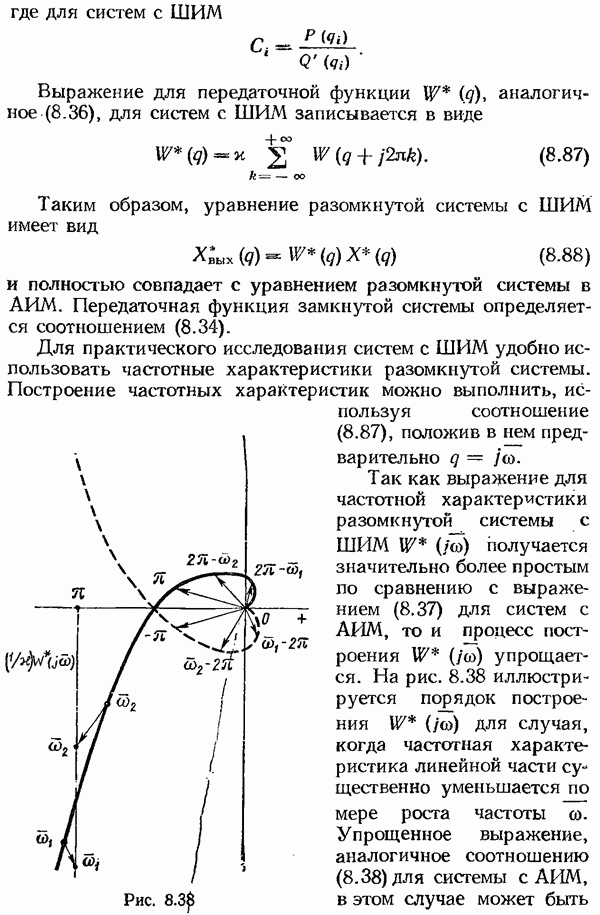
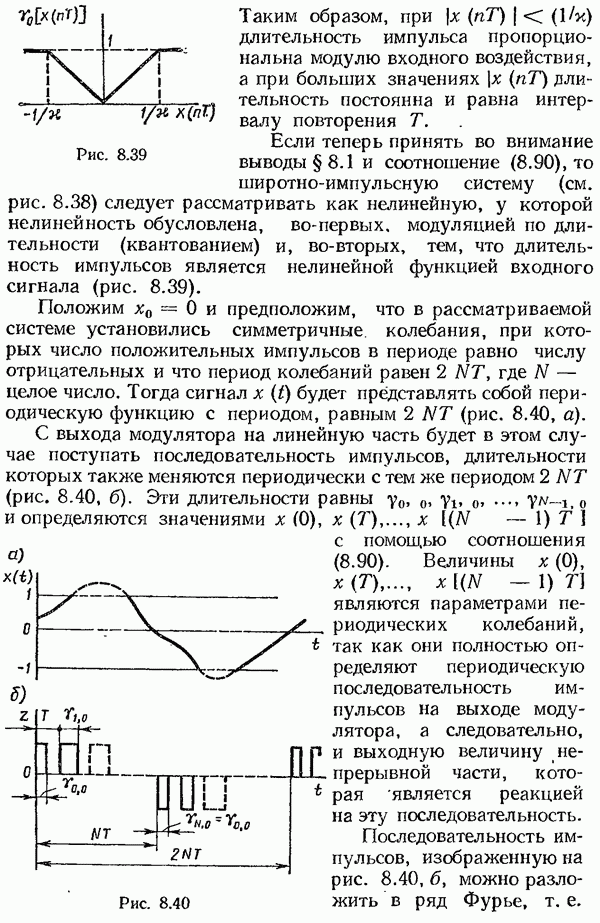
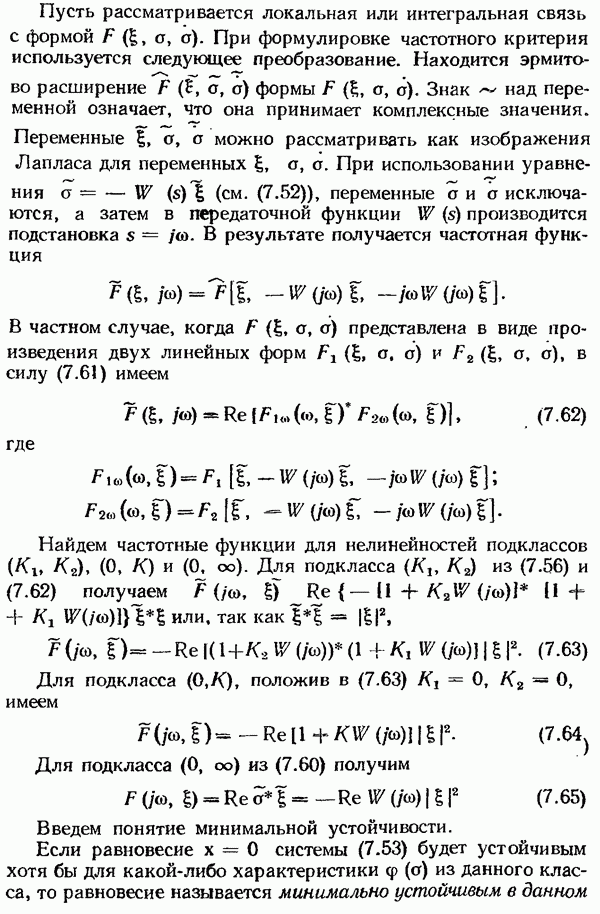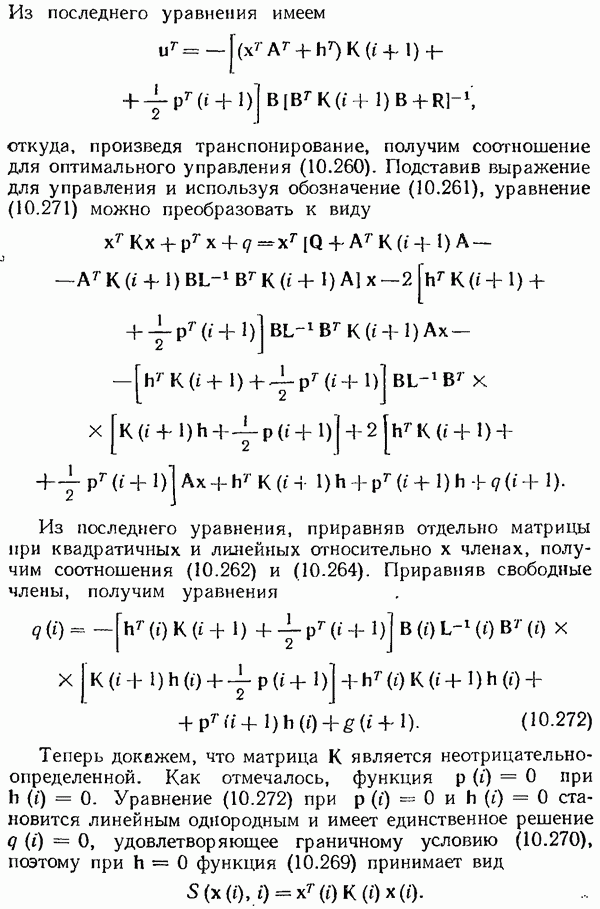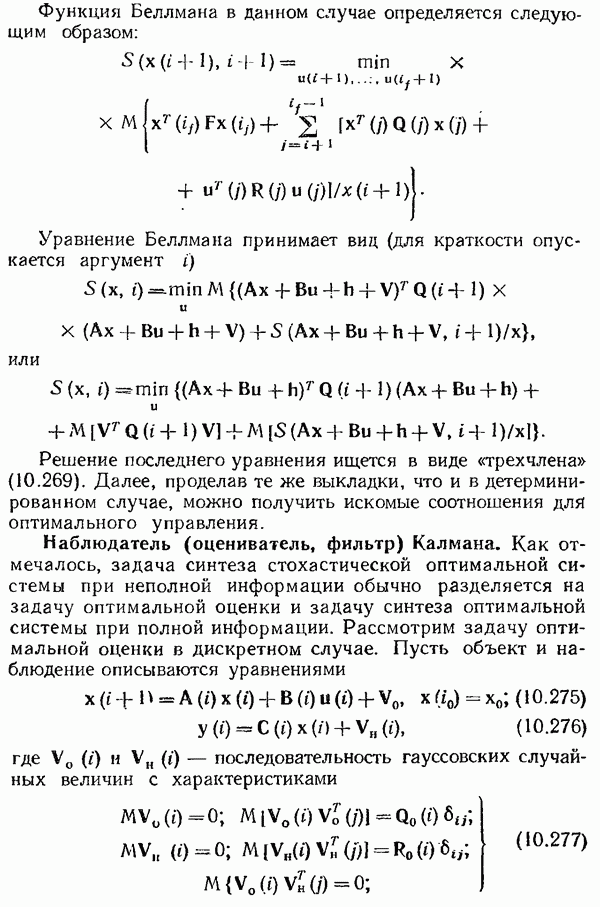| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 9.3. Корреляционные функции случайных процессов
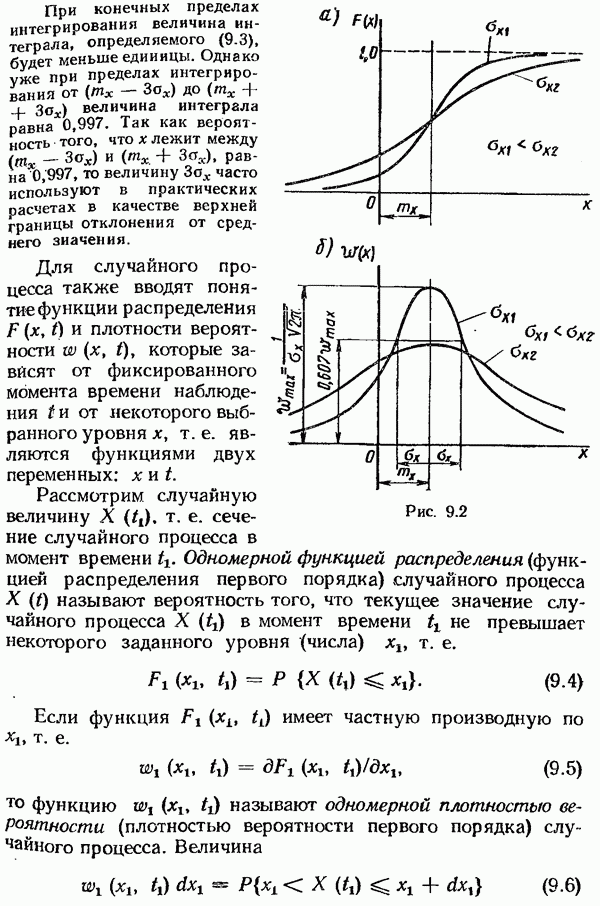
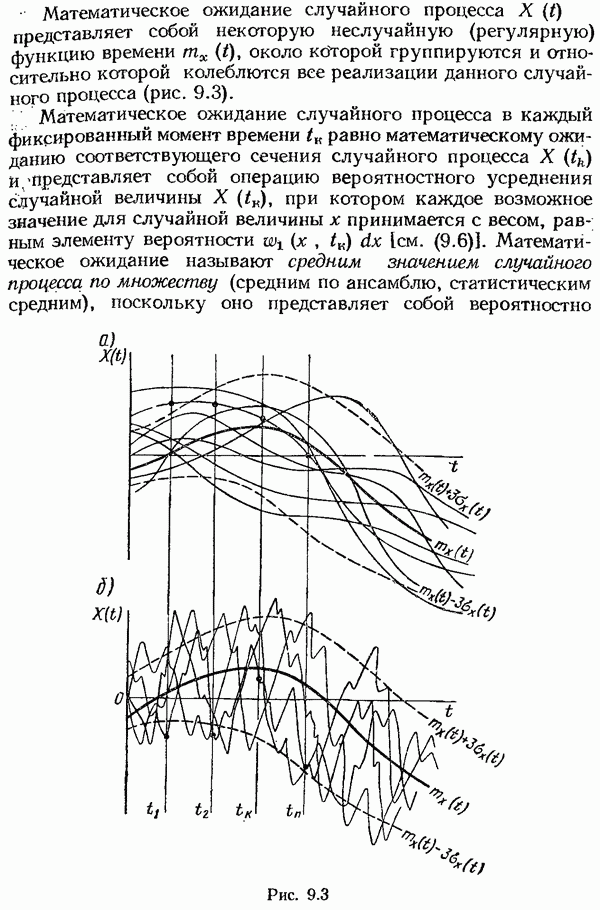
Математическое ожидание и дисперсия являются важными характеристиками случайного процесса, но они не дают достаточного представления о том, какой характер будут иметь отдельные реализации случайного процесса. Это хороню видно из рис. 9.3, где показаны реализации двух случайных процессов, совершенно различных по своей структуре, хотя и имеющих
одинаковые значения математического ожидания и дисперсии. Штриховыми линиями на рис. 9.3 показаны значения  для случайных процессов.
для случайных процессов.
Процесс, изображенный на рис. 9.3, а, от одного сечения к другому протекает сравнительно плавно, а процесс на рис. 9.3, б обладает сильной изменчивостью от сечения к сечению Поэтому статистическая связь между сечениями в первом случае больше, чем во втором, однако ни по математическому ожиданию, ни по дисперсии этого установить нельзя.
Чтобы в какой-то мере охарактеризовать внутреннюю структуру случайного процесса, т. е. учесть связь между значениями случайного процесса в различные моменты времени или, иными словами, учесть степень изменчивости случайного процесса, необходимо ввести понятие о корреляционной (автокорреляционной) функции случайного процесса.
Корреляционной функцией случайного процесса  называют неслучайную функцию двух аргументов
называют неслучайную функцию двух аргументов  которая для каждой пары произвольно выбранных значений аргументов (моментов времени)
которая для каждой пары произвольно выбранных значений аргументов (моментов времени)  равна математическому ожиданию произведения двух случайных величин
равна математическому ожиданию произведения двух случайных величин  соответствующих сечений случайного процесса:
соответствующих сечений случайного процесса:

где  — двумерная плотность вероятности;
— двумерная плотность вероятности;  — центрированный случайный процесс;
— центрированный случайный процесс;  — математическое ожидание (среднее значение) случайного процесса.
— математическое ожидание (среднее значение) случайного процесса.
Различные случайные процессы в зависимости от того, как изменяются их статистические характеристики с течением времени, делят на стационарные и нестационарные. Разделяют стационарность в узком смысле и стационарность в широком смысле.
Стационарным в узком смысле называют случайный процесс  если его n-мерные функции распределения и плотности вероятности при любом
если его n-мерные функции распределения и плотности вероятности при любом  не зависят от сдвига всех точек
не зависят от сдвига всех точек
 вдоль оси времени на одинаковую величину
вдоль оси времени на одинаковую величину  т. е.
т. е.

Это означает, что два процесса  имеют одинаковые статистические свойства для любого
имеют одинаковые статистические свойства для любого  т. е. статистические характеристики стационарного случайного процесса неизменны во времени.
т. е. статистические характеристики стационарного случайного процесса неизменны во времени.
Стационарный случайный процесс — это своего рода аналог установившегося процесса в детерминированных системах. Любой переходный процесс не является стационарным.
Стационарным в широком смысле называют случайный процесс  математическое ожидание которого постоянно:
математическое ожидание которого постоянно:

а корреляционная функция зависит только от одной переменной — разности аргументов  при этом корреляционную функцию обозначают
при этом корреляционную функцию обозначают

Процессы, стационарные в узком смысле, обязательно стационарны и в широком смысле; однако обратное утверждение, вообще говоря, неверно.
Понятие случайного процесса, стационарного в широком смысле, вводится тогда, когда в качестве статистических характеристик случайного процесса используются только математическое ожидание и корреляционная функция. Часть теории случайных процессов, которая описывает свойства случайного процесса через его математическое ожидание и корреляционную функцию, называют корреляционной теорией.
Для случайного процесса с нормальным законом распределения математическое ожидание и корреляционная функция полностью определяют его n-мерную плотность вероятности.
Поэтому для нормальных случайных процессов понятия стационарности в широком и узком смысле совпадают.
Теория стационарных процессов разработана наиболее полно и позволяет сравнительно просто производить расчеты для многих практических случаев. Поэтому допущение о стационарности иногда целесообразно делать также и для тех случаев, когда случайный процесс хотя и нестационарен но на рассматриваемом отрезке времени работы системы статистические характеристики сигналов не успевают сколько-нибудь существенно измениться. В дальнейшем, если не будет оговорено особо, будут рассматриваться случайные процессы, стационарные в широком смысле.
При изучении случайных процессов, стационарных в широком смысле, можно ограничиться рассмотрением только процессов с математическим ожиданием (средним значением), равным нулю, т. е.  так как случайный процесс с ненулевым математическим ожиданием представляют как сумму процесса с нулевым математическим ожиданием и постоянной неслучайной (регулярной) величиной, равной математическому ожиданию этого процесса (см. далее § 9.6).
так как случайный процесс с ненулевым математическим ожиданием представляют как сумму процесса с нулевым математическим ожиданием и постоянной неслучайной (регулярной) величиной, равной математическому ожиданию этого процесса (см. далее § 9.6).
При  выражение для корреляционной функции
выражение для корреляционной функции

В теории случайных процессов пользуются двумя понятиями средних значений. Первое понятие о среднем значении — это среднее значение по мнооюеству (или математическое ожидание), которое определяется на основе наблюдения над множеством реализацчй случайного процесса в один и тот же момент времени. Среднее значение по множеству принято обозначать волнистой чертой над выражением, описывающим случайную функцию:

В общем случае среднее значение по множеству является функцией времени 
Другое понятие о среднем значении — это среднее значение по времени, которое определяется на основе наблюдения за отдельной реализацией случайного процесса  на протяжении
на протяжении

Рис. 9.4
достаточно длительного времени Т. Среднее значение по времени обозначают прямой чертой над соответствующим выражением случайной функции и определяют по формуле:

если этот предел существует.
Среднее значение по времени в общем случае различно для отдельных реализаций множества, определяющих случайный процесс. Вообще говоря, для одного и того же случайного процесса среднее по множеству и среднее по времени значения различны. Однако существует класс стационарных случайных процессов, называемых эргодическими, для которых среднее по множеству равно среднему по времени, т. е.

Корреляционная функция  эргодического стационарного случайного процесса
эргодического стационарного случайного процесса  неограниченно убывает по модулю при
неограниченно убывает по модулю при 
Однако надо иметь в виду, что не всякий стационарный случайный процесс является эргодическим, например случайный процесс  каждая реализация которого
каждая реализация которого  постоянна во времени (рис. 9.4), является стационарным, но не эргодическим. В этом случае средние значения, определенные по одной реализации и в результате обработки множества реализаций, не совпадают. Один и тот же случайный процесс в общем случае может быть эргодическим по отношению к одним статистическим характеристикам и неэргодическим по отношению к другим. В дальнейшем будем считать, что по отношению ко всем статистическим характеристикам условия эргодичности выполняются.
постоянна во времени (рис. 9.4), является стационарным, но не эргодическим. В этом случае средние значения, определенные по одной реализации и в результате обработки множества реализаций, не совпадают. Один и тот же случайный процесс в общем случае может быть эргодическим по отношению к одним статистическим характеристикам и неэргодическим по отношению к другим. В дальнейшем будем считать, что по отношению ко всем статистическим характеристикам условия эргодичности выполняются.
Свойство эргодичности имеет очень большое практическое значение. Для определения статистических свойств некоторых объектов, если трудно осуществить одновременное наблюдение за ними в произвольно выбранный момент времени (например, при наличии одного опытного образца), его можно заменить длительным наблюдением за одним объектом. Иными словами, отдельная реализация эргодического случайного
процесса на бесконечном промежутке времени полностью определяет весь случайный процесс с его бесконечными реализациями. Собственно говоря, этот факт лежит в основе описанного ниже метода экспериментального определения корреляционной функции стационарного случайного процесса по одной реализации.
Как видно из (9.25), корреляционная функция представляет собой среднее значение по множеству. Для эргодических случайных процессов корреляционную функцию можно определить как среднее по времени от произведения  , т. е.
, т. е.

где  — любая реализация случайного процесса; х - среднее значение по времени, определяемое по (9.28).
— любая реализация случайного процесса; х - среднее значение по времени, определяемое по (9.28).
Если среднее значение случайного процесса равно нулю  то
то

Основываясь на свойстве эргодичности, можно дисперсию  [см. (9.19)] определить как среднее по времени от квадрата центрированного случайного процесса, т. е.
[см. (9.19)] определить как среднее по времени от квадрата центрированного случайного процесса, т. е.

Сравнивая выражения (9.30) и (9.32) при  можно установить очень важную связь между дисперсией и корреляционной функцией — дисперсия стационарного случайного процесса равна начальному значению корреляционной функции:
можно установить очень важную связь между дисперсией и корреляционной функцией — дисперсия стационарного случайного процесса равна начальному значению корреляционной функции:

Из (9.33) видно, что дисперсия стационарного случайного процесса постоянна, а следовательно, постоянно и среднее квадратическое отклонение:

Статистические свойства связи двух случайных процессов  можно характеризовать взаимной корреляционной функцией
можно характеризовать взаимной корреляционной функцией  которая для каждой пары произвольно выбранных значений аргументов
которая для каждой пары произвольно выбранных значений аргументов  равна
равна

Для эргодических случайных процессов вместо (9.35) можно записать

где  — любые реализации стационарных случайных процессов
— любые реализации стационарных случайных процессов  соответственно.
соответственно.
Взаимная корреляционная функция  характеризует взаимную статистическую связь двух случайных процессов
характеризует взаимную статистическую связь двух случайных процессов  в разные моменты времени, отстоящие друг от друга на промежуток времени
в разные моменты времени, отстоящие друг от друга на промежуток времени  . Значение
. Значение  характеризует эту связь в один и тот же момент времени.
характеризует эту связь в один и тот же момент времени.
Из (9.36) следует, что

Если случайные процессы  статистически не связаны друг с другом и имеют равные нулю средние значения, то их взаимная корреляционная функция для всех
статистически не связаны друг с другом и имеют равные нулю средние значения, то их взаимная корреляционная функция для всех  равна нулю. Однако обратный вывод о том, что если взаимная корреляционная функция равна нулю, то процессы независимы, можно сделать лишь в отдельных случаях (в частности, для процессов с нормальным законом распределения), общей же силы обратный закон не имеет.
равна нулю. Однако обратный вывод о том, что если взаимная корреляционная функция равна нулю, то процессы независимы, можно сделать лишь в отдельных случаях (в частности, для процессов с нормальным законом распределения), общей же силы обратный закон не имеет.
Заметим, что корреляционные функции могут вычисляться и для неслучайных (регулярных) функций времени. Однако когда говорят о корреляционной функции  регулярной функции
регулярной функции  то под этим понимают просто результат формального
то под этим понимают просто результат формального
применения к регулярной функции  операции, выражаемой интегралом:
операции, выражаемой интегралом:

Приведем некоторые основные свойства корреляционных функций 
1. Начальное значение корреляционной функции [см. (9.33)] равно дисперсии случайного процесса:

2. Значение корреляционной функции при любом  не может превышать ее начального значения, т. е.
не может превышать ее начального значения, т. е.

Чтобы доказать это, рассмотрим очевидное неравенство  из которого следует
из которого следует 
Находим средние значения по времени от обеих частей последнего неравенства:

Таким образом, получим неравенство 
3. Корреляционная функция есть четная функция  , т. е.
, т. е.

Это вытекает из самого определения корреляционной функции. Действительно,

поэтому на графике корреляционная функция всегда симметрична относительно оси ординат.
4. Корреляционная функция суммы случайных процессов  определяется выражением
определяется выражением

где  — взаимные корреляционные функции
— взаимные корреляционные функции
Действительно,

5. Корреляционная функция постоянной величины  равна квадрату этой постоянной величины
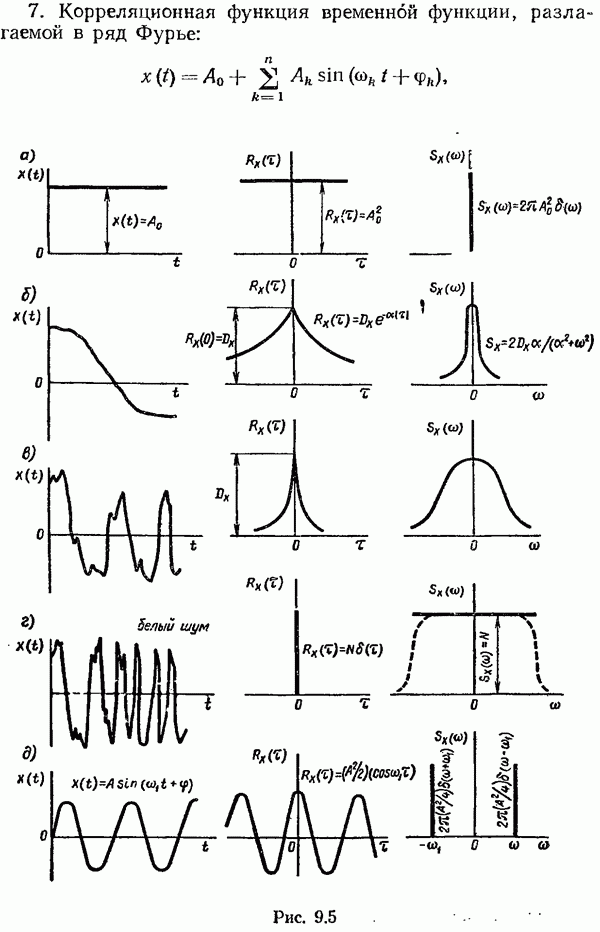
равна квадрату этой постоянной величины  (рис. 9.5, а), что вытекает из самого определения корреляционной функции:
(рис. 9.5, а), что вытекает из самого определения корреляционной функции:

6. Корреляционная функция периодической функции, например  представляет собой косинусоиду (рис. 9-5, 5), т. е.
представляет собой косинусоиду (рис. 9-5, 5), т. е.

имеющую ту же частоту  что и
что и  и не зависящую от сдвига фазы
и не зависящую от сдвига фазы 
Чтобы доказать это, заметим, что при нахождении корреляционных функций периодических функций  можно использовать следующее равенство:
можно использовать следующее равенство:

где  — период функции
— период функции 
Последнее равенство получается после замены интеграла с пределами от —Т до Т при Т со суммой отдельных интегралов с пределами от  до
до  , где
, где  и использования периодичности подынтегральных функций.
и использования периодичности подынтегральных функций.
Тогда, учитывая сказанное выше, получим т.

7. Корреляционная функция временной функции, разлагаемой в ряд Фурье:

Рис. 9.5 (см. скан)

Рис. 9.6.
имеет на основании изложенного выше следующий вид:

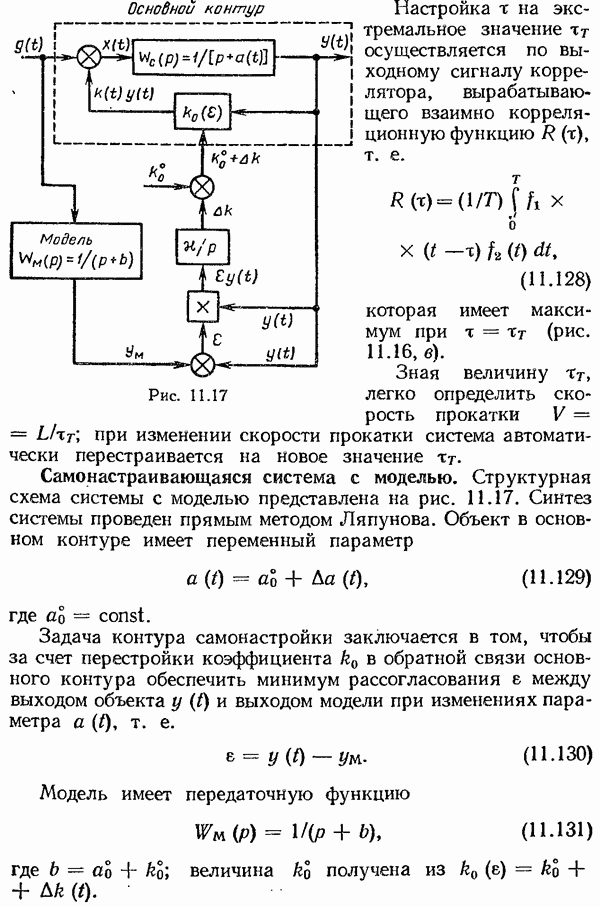
8. Типичная корреляционная функция стационарного случайного процесса имеет вид, представленный на рис. 9.6. Ее можно аппроксимировать следующим аналитическим выражением:

С ростом  связь между
связь между  ослабевает и корреляционная функция становится меньше. На рис. 9.5, б, в приведены, например, две корреляционные функции и две соответствующие им реализации случайного процесса. Легко заметить, что корреляционная функция, соответствующая случайному процессу с более тонкой структурой, убывает быстрее Другими словами, чем более высокие частоты присутствуют в случайном процессе, тем быстрее убывает соответствующая ему корреляционная функция.
ослабевает и корреляционная функция становится меньше. На рис. 9.5, б, в приведены, например, две корреляционные функции и две соответствующие им реализации случайного процесса. Легко заметить, что корреляционная функция, соответствующая случайному процессу с более тонкой структурой, убывает быстрее Другими словами, чем более высокие частоты присутствуют в случайном процессе, тем быстрее убывает соответствующая ему корреляционная функция.
Иногда встречаются корреляционные функции, которые могут быть аппроксимированы аналитическим выражением

где  — дисперсия;
— дисперсия;  — параметр затухания;
— параметр затухания;  — резонансная частота.
— резонансная частота.
Корреляционные функции подобного вида имеют, например, случайные процессы типа турбулентности атмосферы, фединга радиолокационного сигнала, углового мерцания цели и т. п. Выражения (9.45) и (9.46) часто используются для аппроксимации корреляционных функций, полученных в результате обработки экспериментальных данных.
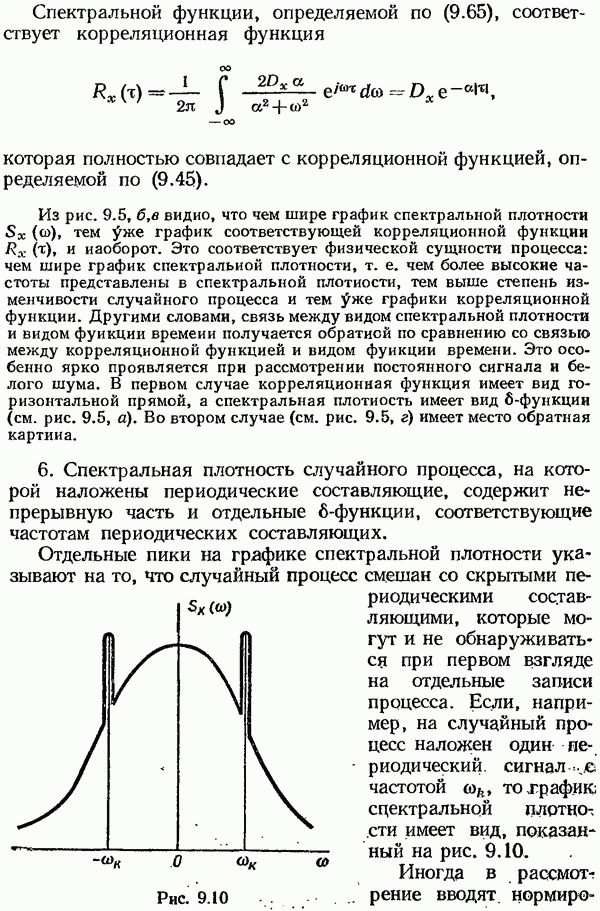
9. Корреляционная функция Стационарного случайного процесса, на которой наложена периодическая составляющая с частотой  также будет содержать периодическую составляющую той же частоты.
также будет содержать периодическую составляющую той же частоты.

Рис. 9.7
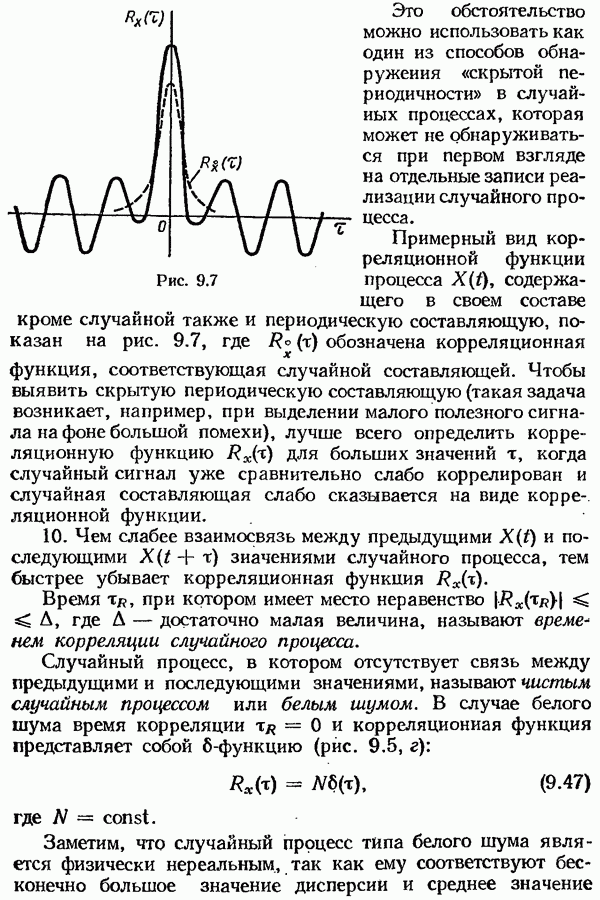
Это обстоятельство можно использовать как один из способов обнаружения «скрытой периодичности» в случайных процессах, которая может не обнаруживаться при первом взгляде на отдельные записи реализации случайного процесса.
Примерный вид корреляционной функции процесса  содержащего в своем составе кроме случайной также и периодическую составляющую, показан на рис. 9.7, где
содержащего в своем составе кроме случайной также и периодическую составляющую, показан на рис. 9.7, где  обозначена корреляционная функция, соответствующая случайной составляющей. Чтобы выявить скрытую периодическую составляющую (такая задача возникает, например, при выделении малого полезного сигнала на фоне большой помехи), лучше всего определить корреляционную функцию
обозначена корреляционная функция, соответствующая случайной составляющей. Чтобы выявить скрытую периодическую составляющую (такая задача возникает, например, при выделении малого полезного сигнала на фоне большой помехи), лучше всего определить корреляционную функцию  для больших значений
для больших значений  когда случайный сигнал уже сравнительно слабо коррелирован и случайная составляющая слабо сказывается на виде корреляционной функции.
когда случайный сигнал уже сравнительно слабо коррелирован и случайная составляющая слабо сказывается на виде корреляционной функции.
10. Чем слабее взаимосвязь между предыдущими  и последующими
и последующими  значениями случайного процесса, тем быстрее убывает корреляционная функция
значениями случайного процесса, тем быстрее убывает корреляционная функция 
Время  при котором имеет место неравенство
при котором имеет место неравенство  где
где  — достаточно малая величина, называют временем корреляции случайного процесса.
— достаточно малая величина, называют временем корреляции случайного процесса.
Случайный процесс, в котором отсутствует связь между предыдущими и последующими значениями, называют чистым случайным процессом или белым шумом. В случае белого шума время корреляции  и корреляционная функция представляет собой
и корреляционная функция представляет собой  -функцию (рис. 9.5, г):
-функцию (рис. 9.5, г):

где 
Заметим, что случайный процесс типа белого шума является физически нереальным, так как ему соответствуют бесконечно большое значение дисперсии и среднее значение
квадрата случайной величины  а следовательно, и бесконечно большая мощность.
а следовательно, и бесконечно большая мощность.
При решении практических задач часто пользуются нормированной корреляционной функцией

Нормированная корреляционная функция удобна тем, что всегда  Иногда в рассмотрение вводят нормированную взаимную корреляционную функцию
Иногда в рассмотрение вводят нормированную взаимную корреляционную функцию

причем можно показать, что 
Экспериментальное определение корреляционных функций.
Пусть имеется экспериментальная запись (осциллограмма) реализации  некоторого случайного процесса на достаточно длинном интерва
некоторого случайного процесса на достаточно длинном интерва  времени. В общем случае это может быть запись реализации случайного процесса с наложенной на него регулярной составляющей. На основании (9.31) корреляционная функция
времени. В общем случае это может быть запись реализации случайного процесса с наложенной на него регулярной составляющей. На основании (9.31) корреляционная функция  соответствующая записи
соответствующая записи  может быть приближенно вычислена следующим образом.
может быть приближенно вычислена следующим образом.
Весь интервал Т записи осциллограммы делится на I равных частей, длительность которых  выбирается такой, чтобы реализация
выбирается такой, чтобы реализация  мало изменялась на протяжении интервала
мало изменялась на протяжении интервала  (рис. 9.8).
(рис. 9.8).
Значение ординаты реализации к  на некотором отрезке
на некотором отрезке  обозначим
обозначим  а значение ординаты этой же кривой, но смещенной на величину
а значение ординаты этой же кривой, но смещенной на величину  обозначим
обозначим  .
.
Задаваясь различными значениями  находим для различных значений
находим для различных значений  среднее значение произведения ординат
среднее значение произведения ординат  . Приближенное значение корреляционной функции
. Приближенное значение корреляционной функции

В (9.50) уменьшение интервала Т на величину  обусловлено тем, что ординаты
обусловлено тем, что ординаты  известны только до
известны только до 

Рис. 9.8
Чем меньше длительность отрезков  и чем больше величина интервала Т, тем точнее выражение (9.50) соответствует корреляционной функции
и чем больше величина интервала Т, тем точнее выражение (9.50) соответствует корреляционной функции  Для получения ошибки не более
Для получения ошибки не более  должно выполняться неравенство
должно выполняться неравенство 
Приведенный способ определения корреляционной функции по экспериментально полученной реализации случайного процесса довольно трудоемок, поэтому на практике обычно корреляционные функции находят с помощью специальных приборов — корреляторов, которые автоматически вычисляют средние произведения двух ординат осциллограмм, находящихся друг от друга на расстоянии  .
.
Если запись реализации  (осциллограмма) соответствует случайному процессу, среднее значение которого равно к, то экспериментально найденная по ней эквивалентная корреляционная функция
(осциллограмма) соответствует случайному процессу, среднее значение которого равно к, то экспериментально найденная по ней эквивалентная корреляционная функция  также будет содержать постоянную составляющую, которая (на основании свойств 4 и 5 корреляционных функций) равна
также будет содержать постоянную составляющую, которая (на основании свойств 4 и 5 корреляционных функций) равна  Связь между корреляционной функцией
Связь между корреляционной функцией  случайного процесса и эквивалентной корреляционной функцией
случайного процесса и эквивалентной корреляционной функцией  определяется выражением
определяется выражением

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
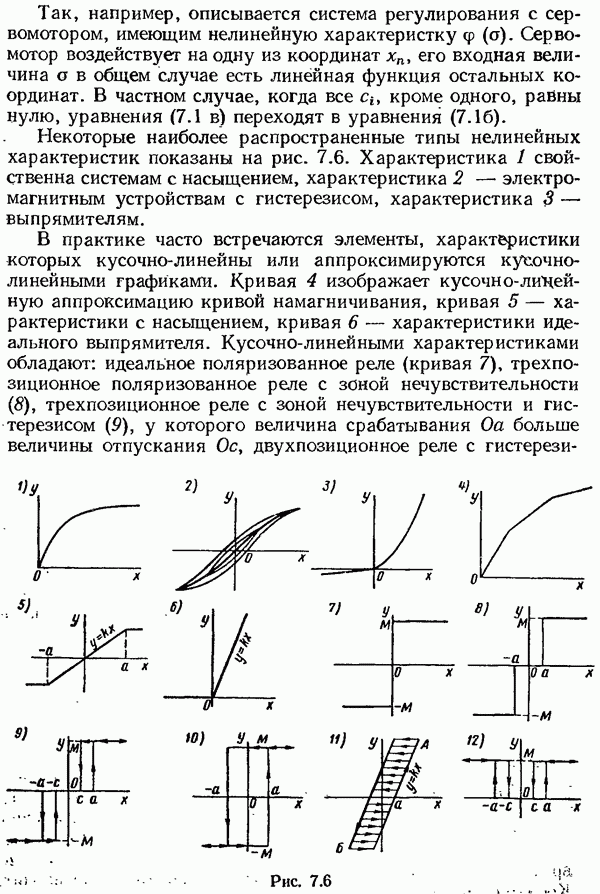
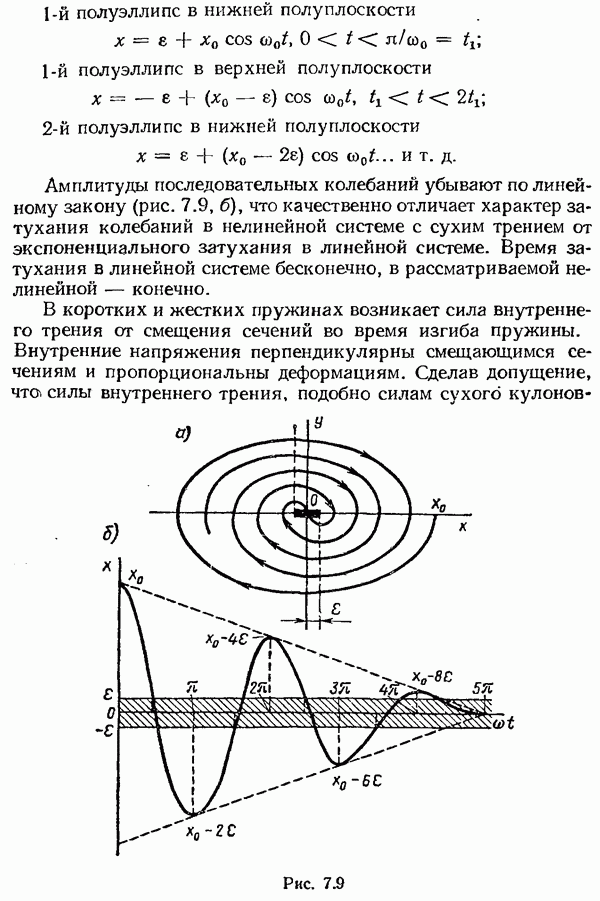
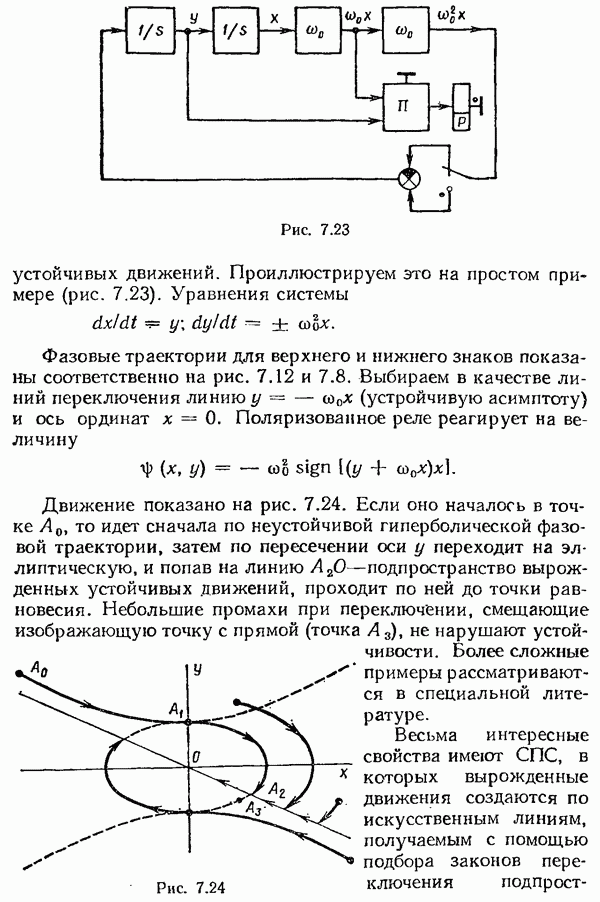
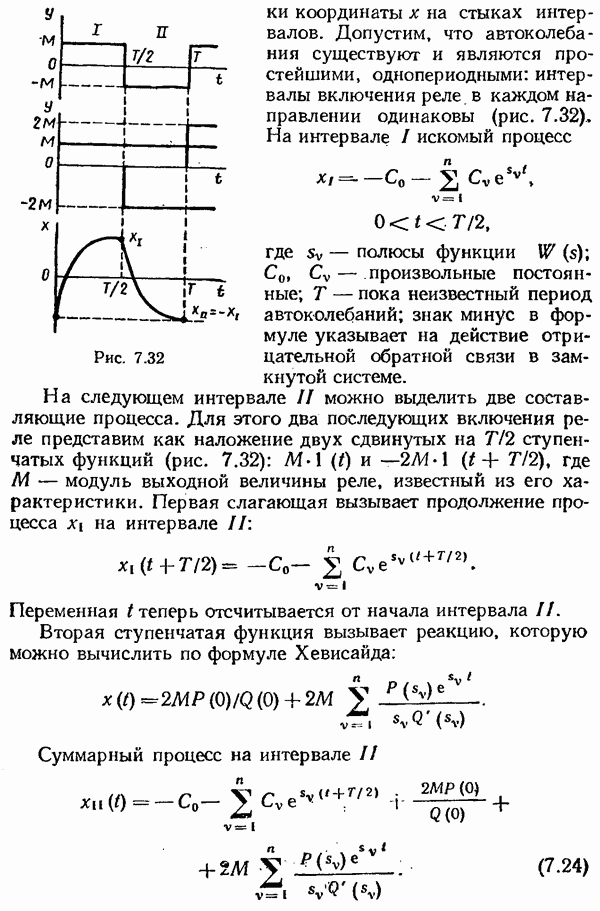
- Глава 7. НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- § 7.1. Основные типы. нелинейных систем и характеристик
- § 7.2. Изображение движений в фазовой плоскости
- Линейная консервативная система второго порядка.
- Система с сухим кулоновским трением.
- Система с отрицательной восстанавливающей силой.
- Линейная колебательная система с вязким трением.
- Линейная апериодическая система с вязким трением.
- § 7.3. Автоколебания. Метод точечных преобразований
- § 7.4. Системы с переменной структурой
- § 7.5. Метод «припасовывания» граничных значений
- § 7.6. Приближенное исследование автоколебаний. Метод эквивалентной линеаризации
- § 7.7. Метод гармонического баланса
- § 7.8. Устойчивость в малом, большом и целом
- § 7.9. Второй (прямой) метод Ляпунова
- § 7.10. Абсолютная устойчивость
- Квадратичный критерий абсолютной устойчивости.
- Круговой критерий устойчивости.
- Критерий В. М. Попова.
- Примечание к критерию Попова.
- Гипотезы М. Айзермана и Р. Калмана.
- Определение автоколебаний.
- Упрощенный критерий колебательности.
- Глава 8. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- § 8.1. Понятие об импульсных системах автоматического управления
- Структура и уравнения импульсных модуляторов.
- Структурная схема амплитудно-импульсного модулятора.
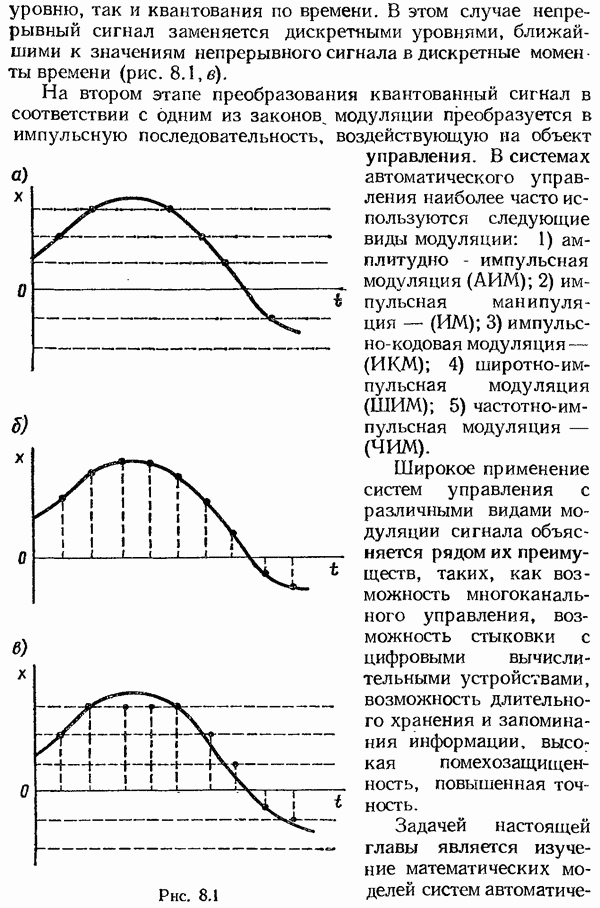
- Структурная схема частотно-импульсного модулятора.
- Структурная схема широтно-импульсного модулятора.
- Структурные схемы частотно-импульсных к широтно- импульсных модуляторов 1-го рода.
- Структурная схема системы управления с импульсной модуляцией. Классификация систем управления с импульсной модуляцией.
- § 8.2. Исследование устойчивости и качества систем управления с амплитудноимпульсной модуляцией
- Передаточная функция импульсной системы.
- Дискретное преобразование Лапласа и его основные свойства.
- Частотные характеристики импульсной системы.
- Исследование устойчивости систем с амплитудно-импульсной модуляцией.
- Алгебраический критерий устойчивости (аналог критерия Гурвица).
- Частотный критерий устойчивости (аналог критерия Найквиста).
- Исследование качества систем с амплитудно-импульсной модуляцией.
- Непрерывное регулирование как граница импульсного регулирования.
- § 8.3. Исследование динамики цифровых систем автоматического управления
- Исследование цифровых систем методом логарифмических частотных характеристик.
- Исследование цифровых систем с непрерывной передачей данных.
- Исследование цифровых систем с учетом квантования по уровню и по времени.
- § 8.4. Исследование систем с широтноимпульсной модуляцией
- Исследование периодических колебаний в системах с широтно-импульсной модуляцией.
- § 8.5. Исследование систем с частотно-импульсной модуляцией
- Исследование устойчивости в целом частотно-импульсных систем 2-го рода.
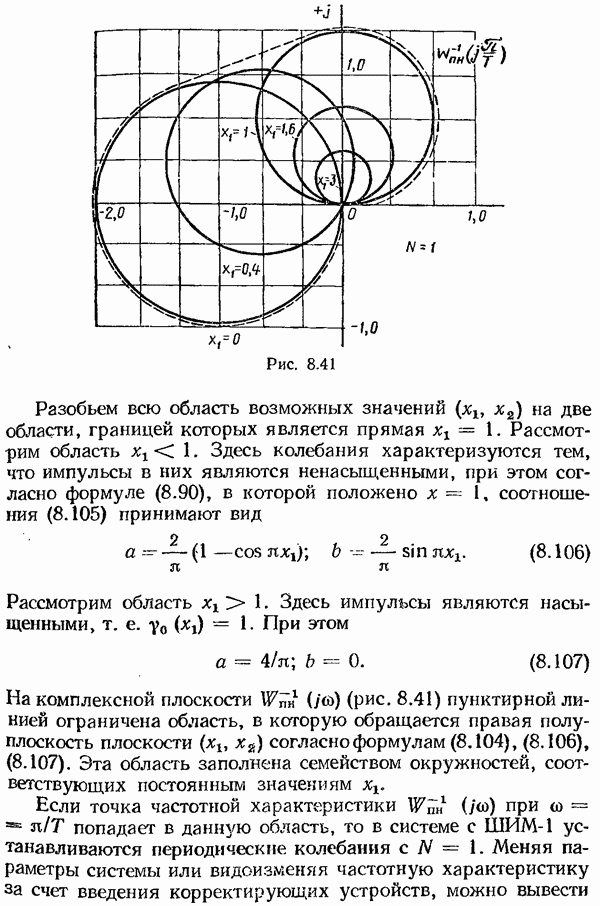
- Исследование периодических режимов в системах с ИЧИМ.
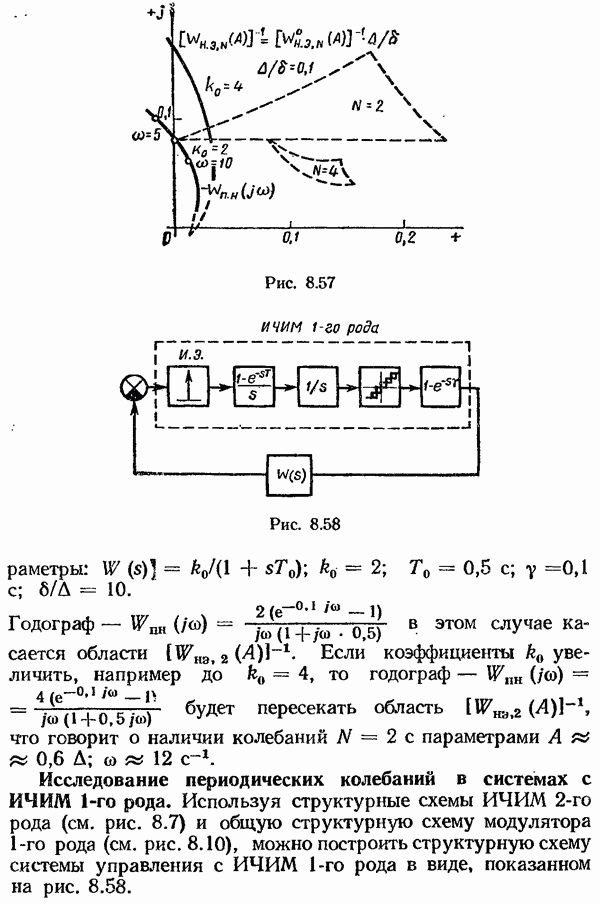
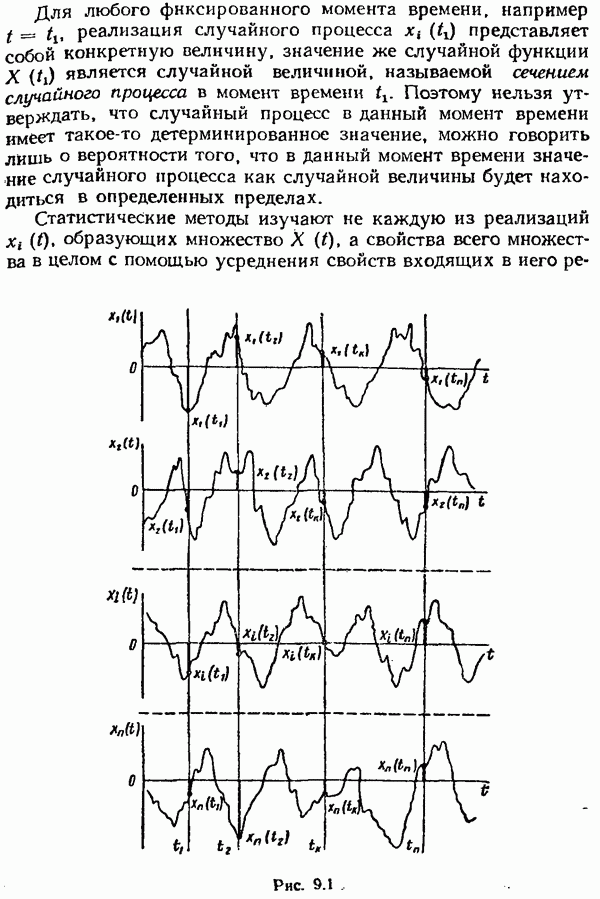
- Исследование периодических колебаний в системах с ИЧИМ 1-го рода.
- Глава 9. СЛУЧАЙНЫЕ ПРОЦЕССЫ В АВТОМАТИЧЕСКИХ СИСТЕМАХ УПРАВЛЕНИЯ
- § 9.2. Случайные процессы и их основные статистические характеристики
- § 9.3. Корреляционные функции случайных процессов
- § 9.4. Спектральные плотности случайных процессов
- § 9.5. Связь между корреляционными функциями и спектральными плотностями случайного процесса на входе и выходе линейной системы
- § 9.6. Расчет линейных систем при случайных воздействиях
- Аналитический метод определения дисперсии ошибки.
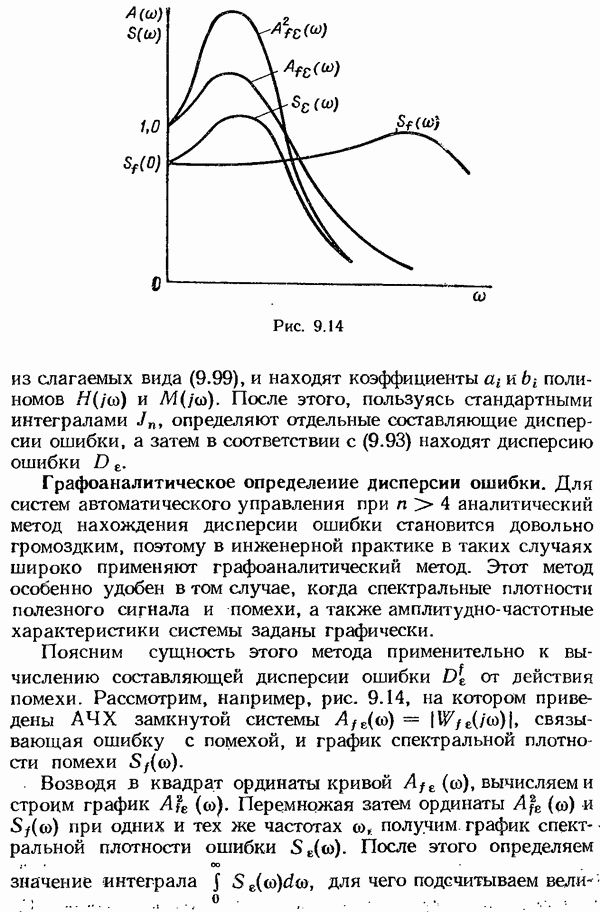
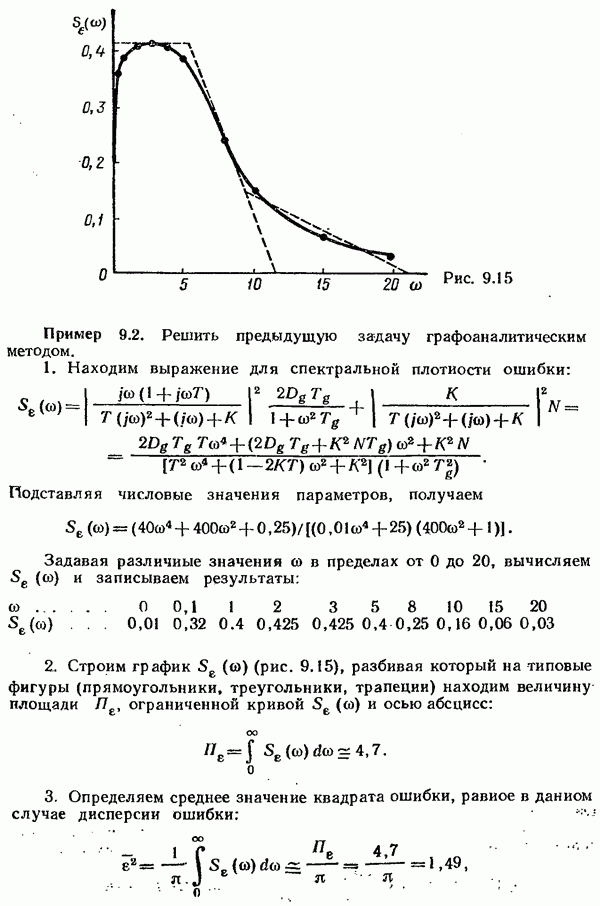
- Графоаналитическое определение дисперсии ошибки.
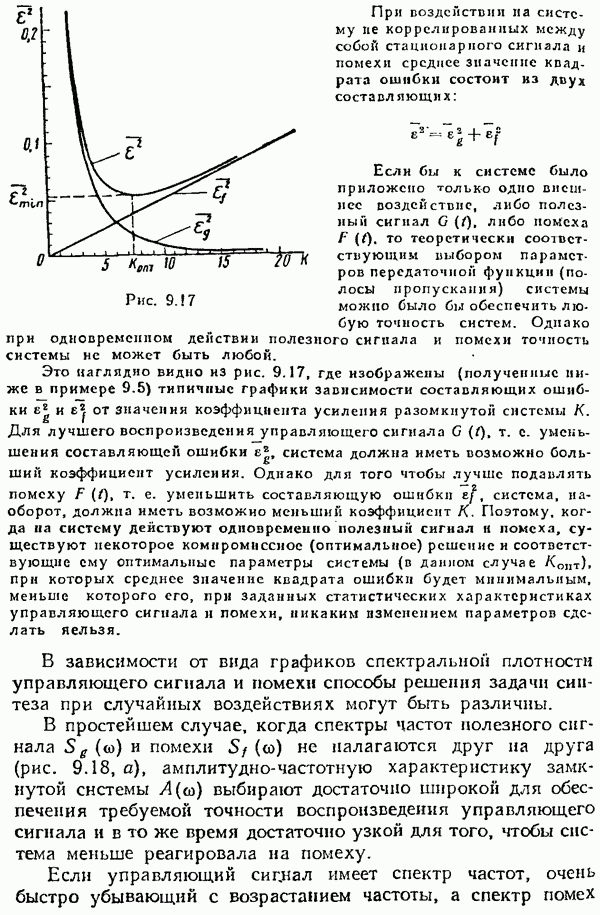
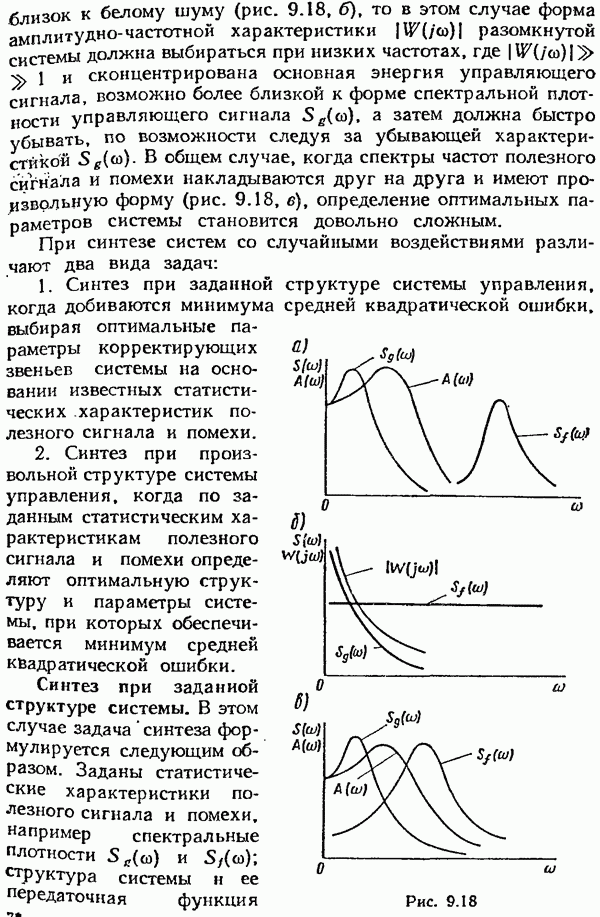
- § 9.7. Синтез линейных систем с минимальной средней квадратической ошибкой
- Синтез при произвольной структуре системы.
- Оптимальный фильтр Винера.
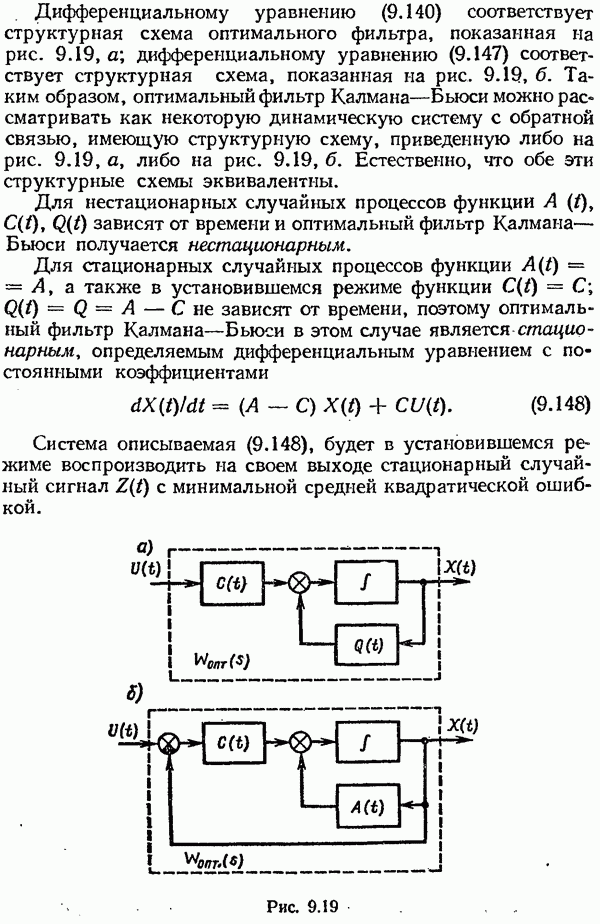
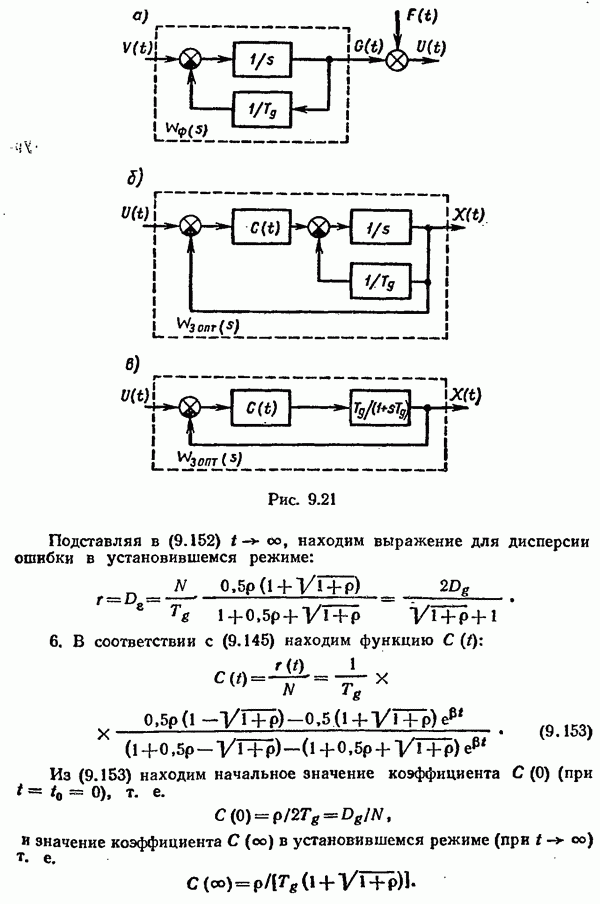
- Оптимальный фильтр Калмана—Бьюси.
- § 9.8. Случайные процессы в линейных импульсных системах
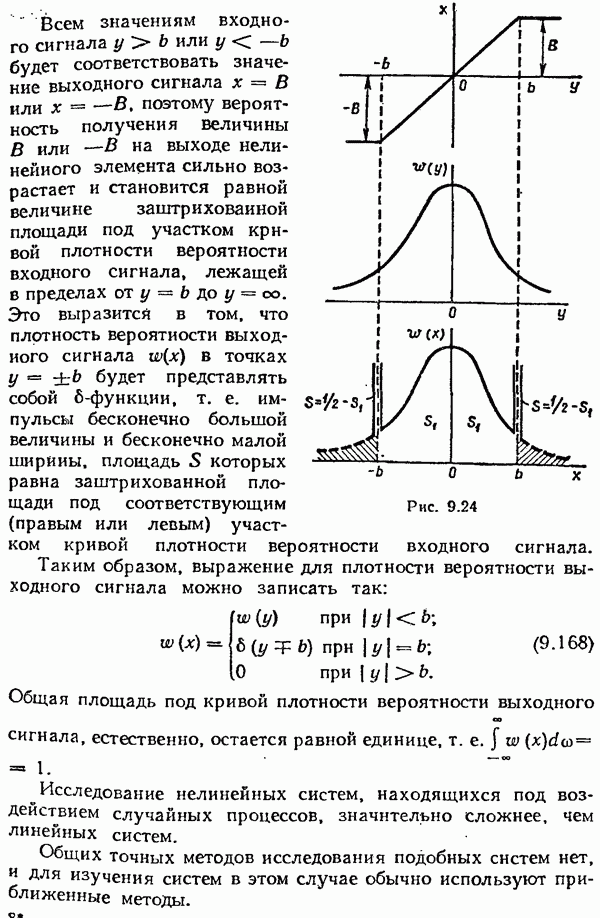
- § 9.9. Нелинейное преобразование случайных сигналов
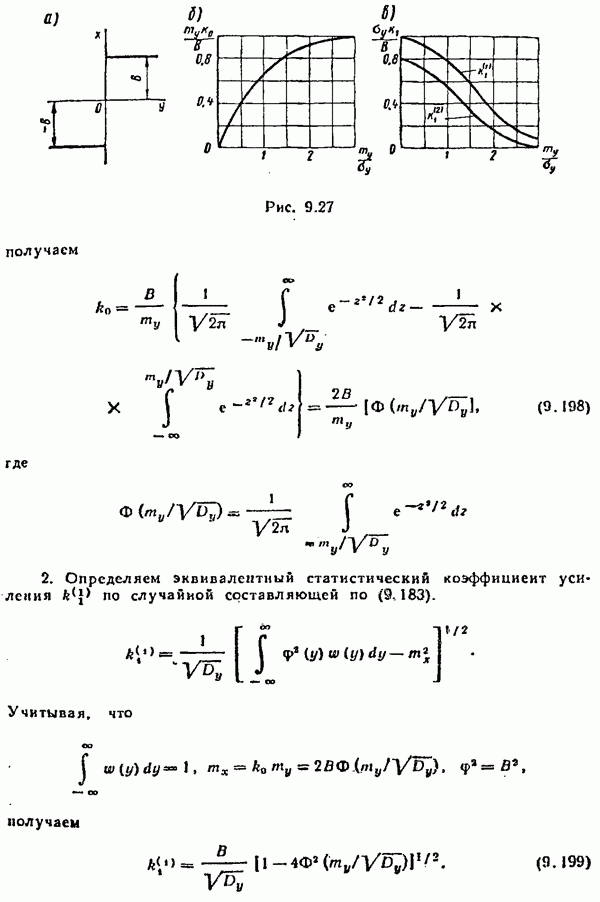
- § 9.10. Статистическая линеаризация нелинейных элементов
- § 9.11. Расчет нелинейных систем методом статистической линеаризации
- Расчет замкнутых нелинейных систем.
- Глава 10. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
- Общая постановка задачи оптимального управления
- Примеры постановки задач оптимального управления.
- Классификация задач оптимального управления
- § 10.2. Метод классического вариационного исчисления (метод множителей Лагранжа)
- Уравнения Эйлера—Лагранжа.
- Задачи с подвижными концами и фиксированным временем
- Задача с нефиксированным временем.
- § 10.3. Принцип максимума Понтрягина. Условие нормальности. Теорема об n интервалах. Вырожденные и особые задачи
- Задача с подвижными концами
- Задача максимального быстродействия
- Условие нормальности.
- Теорема об n интервалах.
- Задача с ограничением на фазовые координаты
- Вырожденные задачи
- Особые задачи
- § 10.4. Метод динамического программирования. Теорема Болтянского. Метод Кротова
- Принцип оптимальности
- Функция и уравнение Беллмана
- Проблема обоснования метода динамического программирования и достаточные условия оптимальности
- Метод Кротова [11]
- Принцип оптимальности Кротова.
- § 10.5. Управляемость и наблюдаемость. Наблюдатели
- Управляемость линейных стационарных объектов.
- Стабилизируемость.
- Управляемость при наличии ограничения на управление.
- Наблюдаемость и восстанавливаемость
- Обнаруживаемость
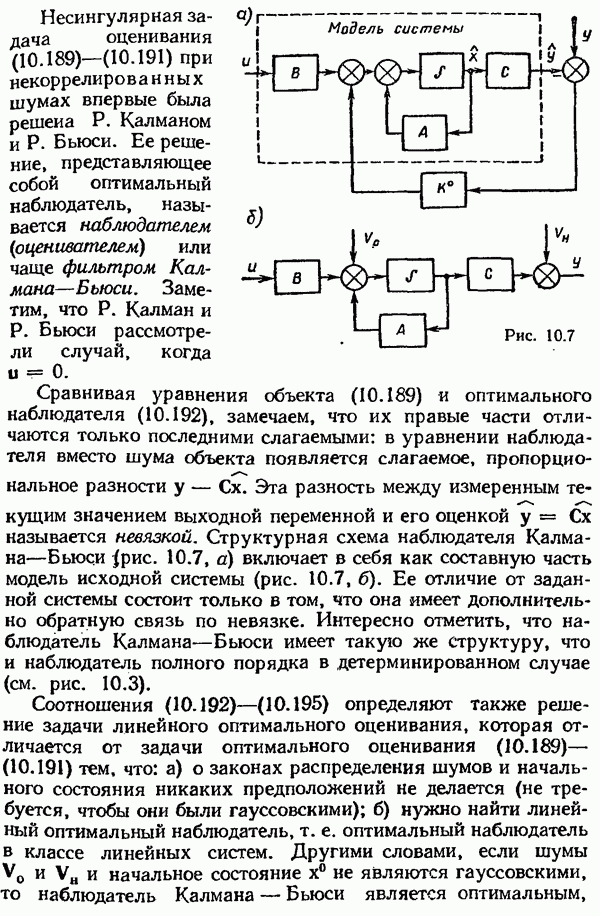
- Наблюдатели
- Наблюдатели пониженного порядка.
- § 10.6. Методы синтеза оптимальных систем с обратной связью. Синтез оптимальных линейных систем по интегральному квадратичному критерию
- Синтез оптимальных линейных систем по интегральному квадратичному критерию
- Векторное дифференцирование.
- Синтез оптимального линейного регулятора выхода.
- § 10.7. Стохастические оптимальные системы. Методы синтеза. Методы оптимальной оценки состояния. Принцип разделимости
- Метод динамического программирования
- Синтез стохастической оптимальной линейной системы при полной информации о состоянии
- Синтез стохастических оптимальных систем управления при неполной информации
- Наблюдатель Калмана—Бьюси при цветном шуме объекта.
- Наблюдатель Калмана—Бьюси при цветном шуме наблюдения.
- Сингулярная (вырожденная) задача линейного оптимального оценивания.
- Линеаризованный наблюдатель Калмана—Бьюси.
- Стохастическая линейная оптимальная система управления при неполной информации. Принцип разделимости
- § 10.8. Оптимальные дискретные системы
- Синтез оптимальной линейной системы при квадратном критерии
- Стохастическая оптимальная линейная система при полной информации о состоянии.
- Наблюдатель (оцениватель, фильтр) Калмана.
- О расходимости фильтров и методах их регуляризации.
- Глава 11. АДАПТИВНЫЕ АВТОМАТИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
- § 11.2. Классификация адаптивных систем
- § 11.3. Самонастраивающиеся системы
- Принципы построения поисковых самонастраивающихся систем.
- Регулярные методы поиска экстремума
- Метод градиента.
- Метод наискорейшего спуска.
- Методы экстраполяционного поиска.
- Методы случайного поиска
- Локальный случайный поиск с пересчетом.
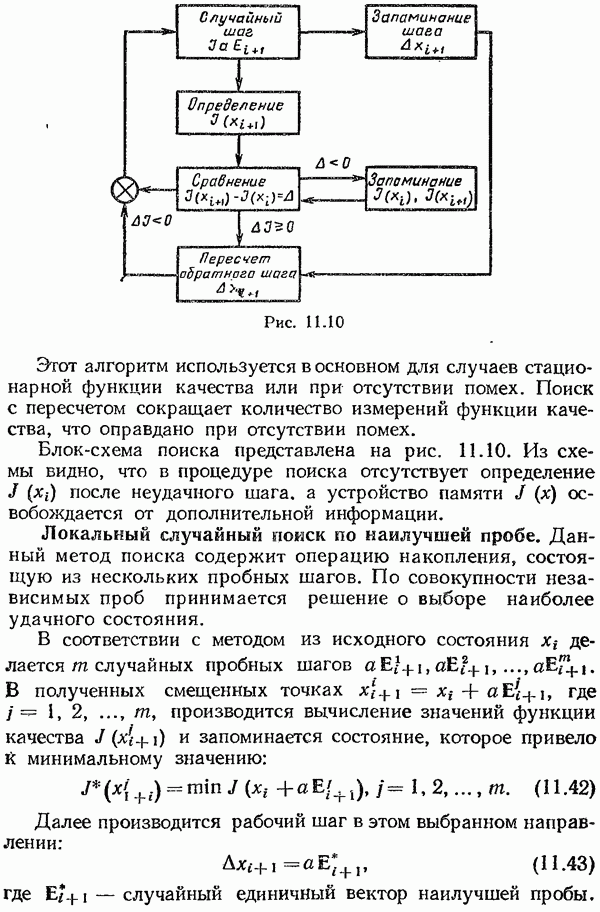
- Локальный случайный поиск по наилучшей пробе.
- Локальный случайный поиск по статистическому градиенту.
- Глобальный случайный поиск с независимым выбором плотности распределения пробных шагов.
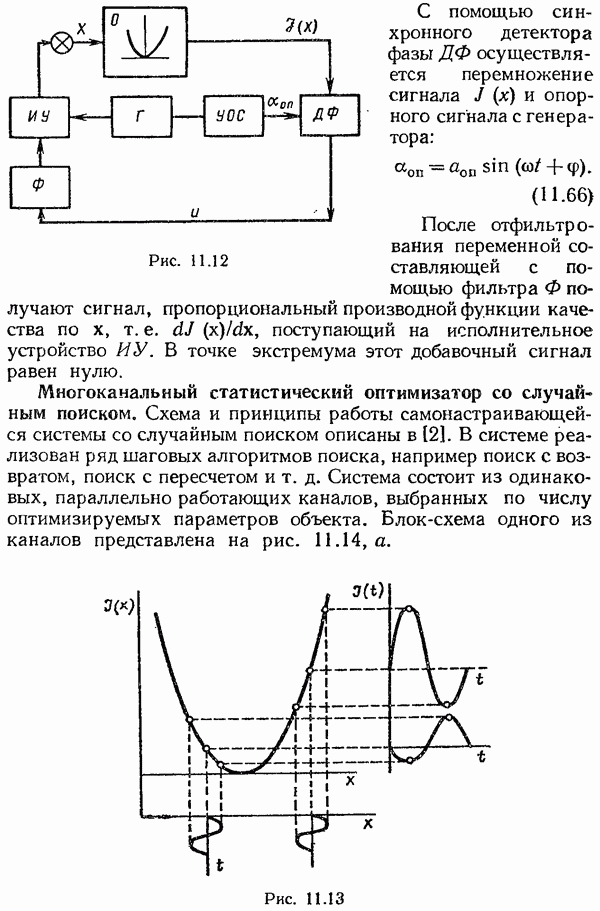
- Примеры поисковых самонастраивающихся систем
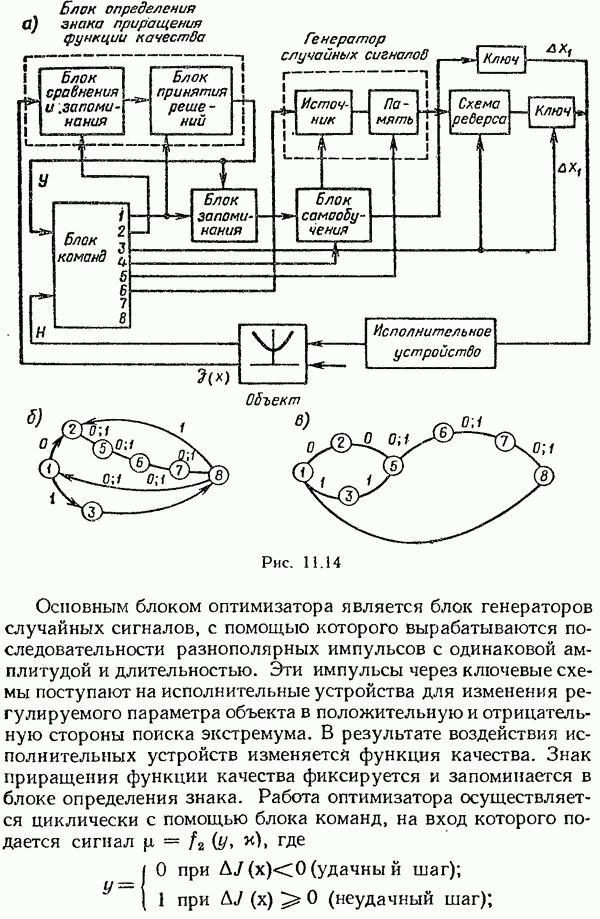
- Многоканальный статистический оптимизатор со случайным поиском.
- Принцип инвариантности.
- Принцип эталонной модели.
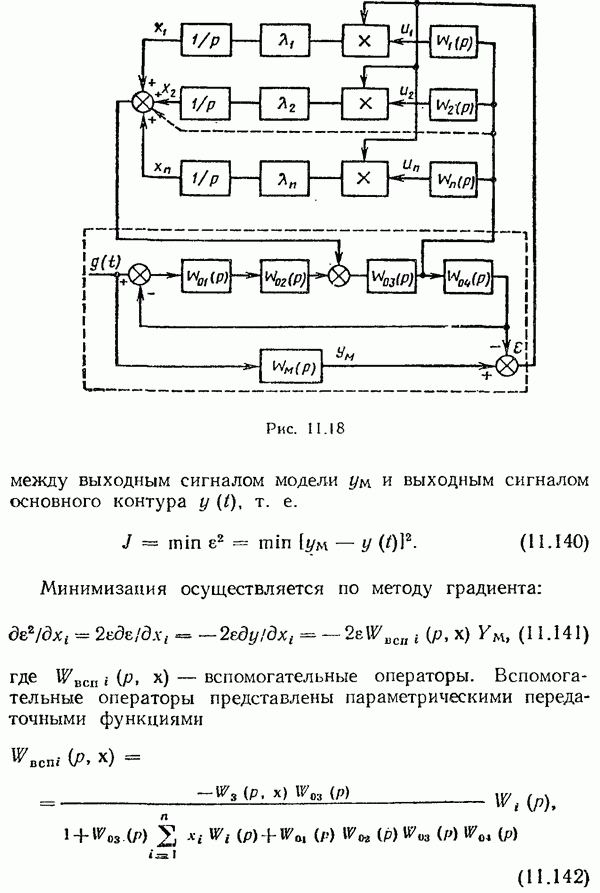
- Принципы определения градиента функции качества.
- Принципы идентификации динамических свойств системы управления.
- Примеры беспоисковых самонастраивающихся систем
- Самонастраивающаяся система с моделью.
- Градиентная самонастраивающаяся система.
- § 11.4. Системы с адаптацией в особых фазовых состояниях
- Адаптивные системы с переменной структурой.
- Адаптивная система с переменной структурой, использующая информацию о внутренних координатах.
- § 11.5. Обучающиеся системы
- Метод секущих плоскостей.
- Метод потенциальных функций.
- Вероятностные алгоритмы обучения.
- Самообучение.
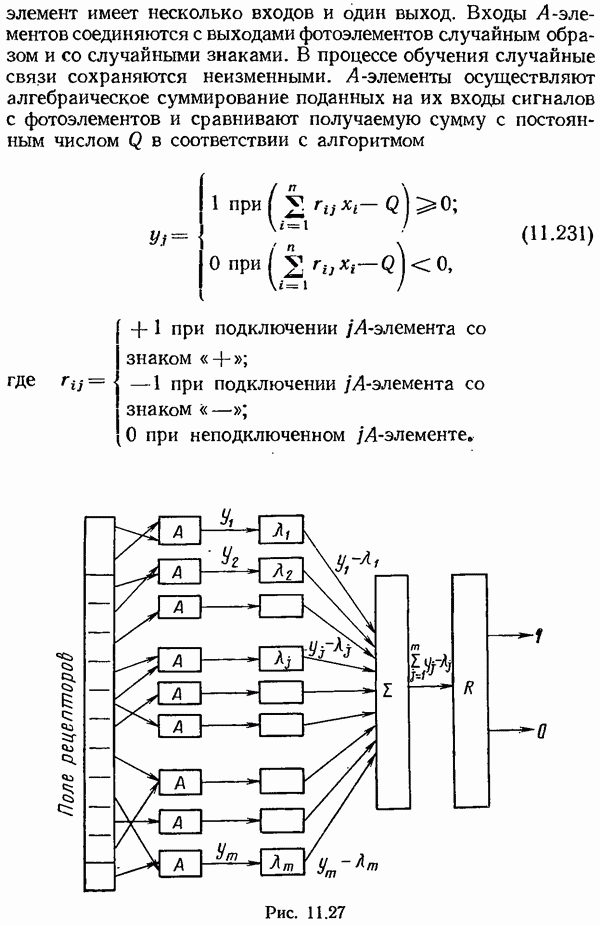
- Персептронная модель автоматической классификации.
- § 11.6. Адаптивные робототехнические системы
- Методы обработки сенсорной информации для адаптивного управления роботами.
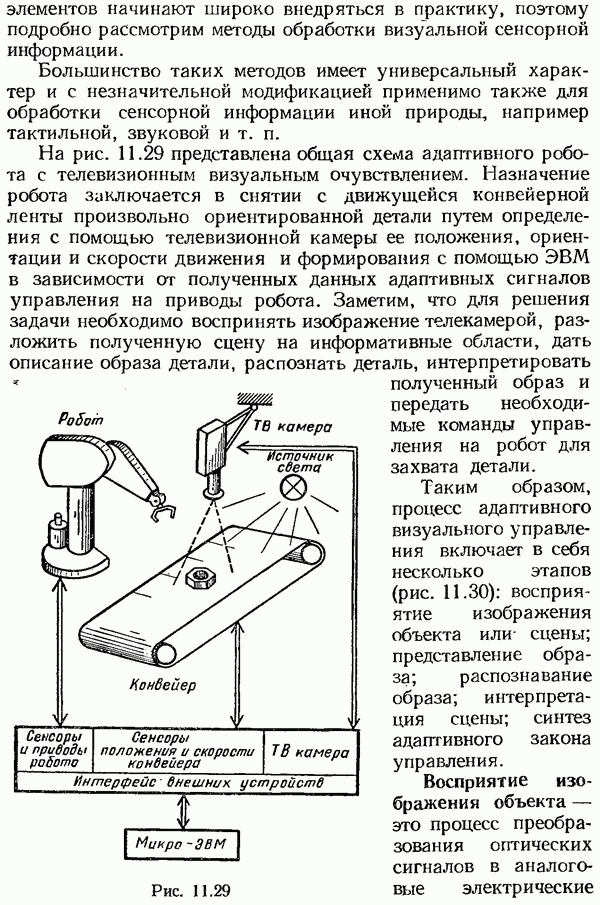
- Восприятие изображения объекта
- Представление образа
- ЗАКЛЮЧЕНИЕ
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ