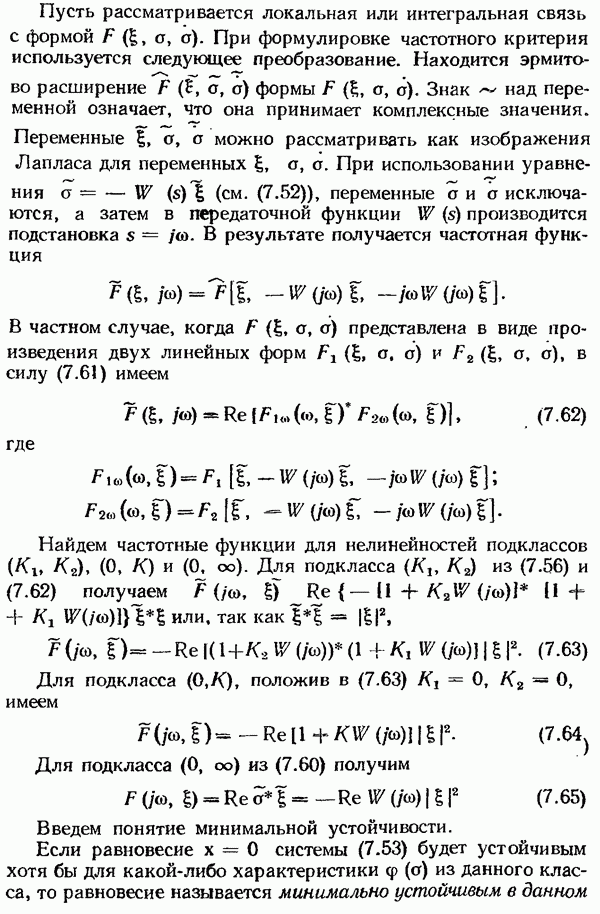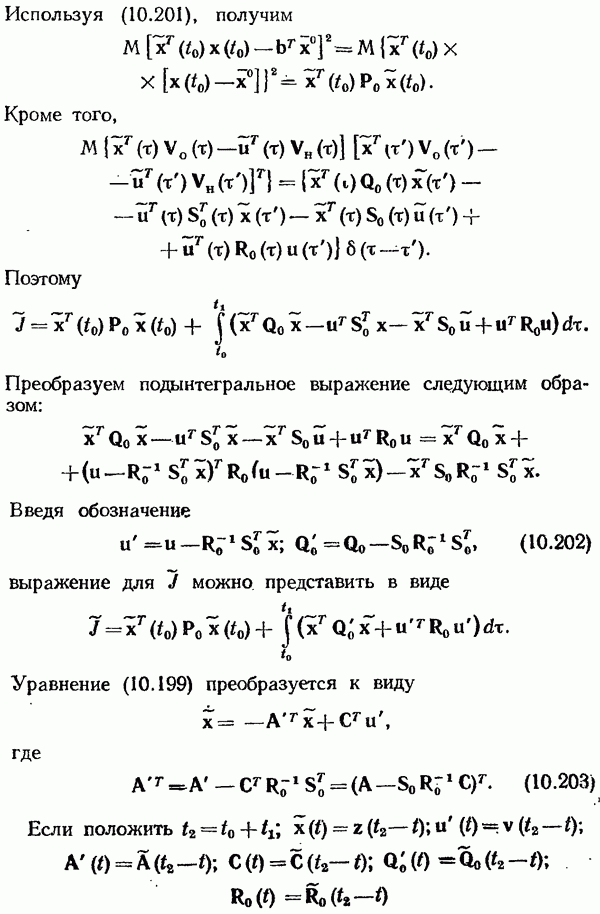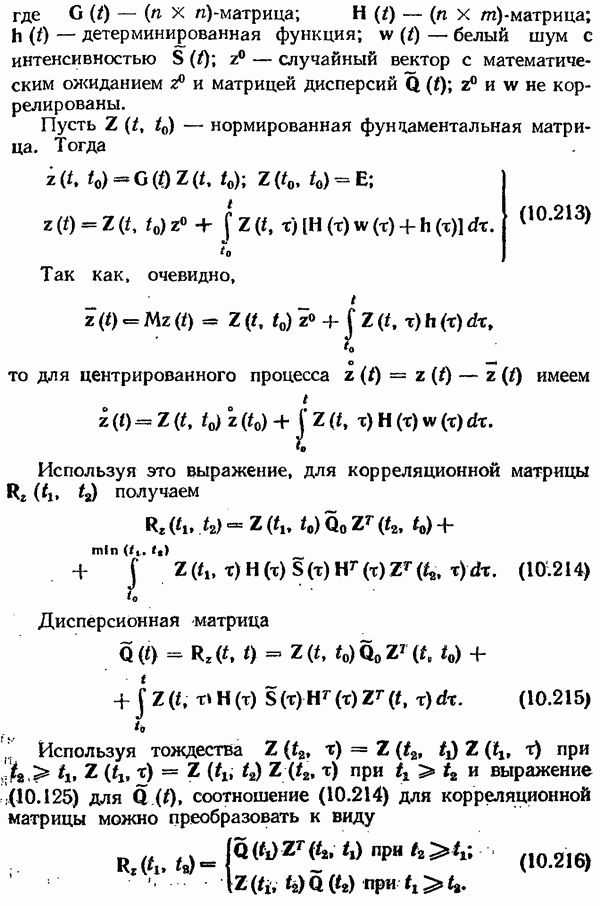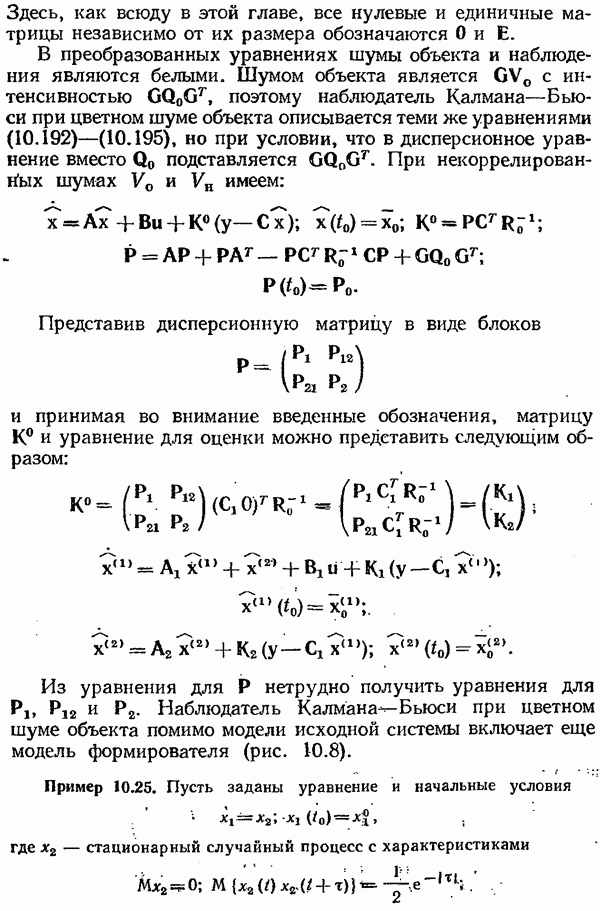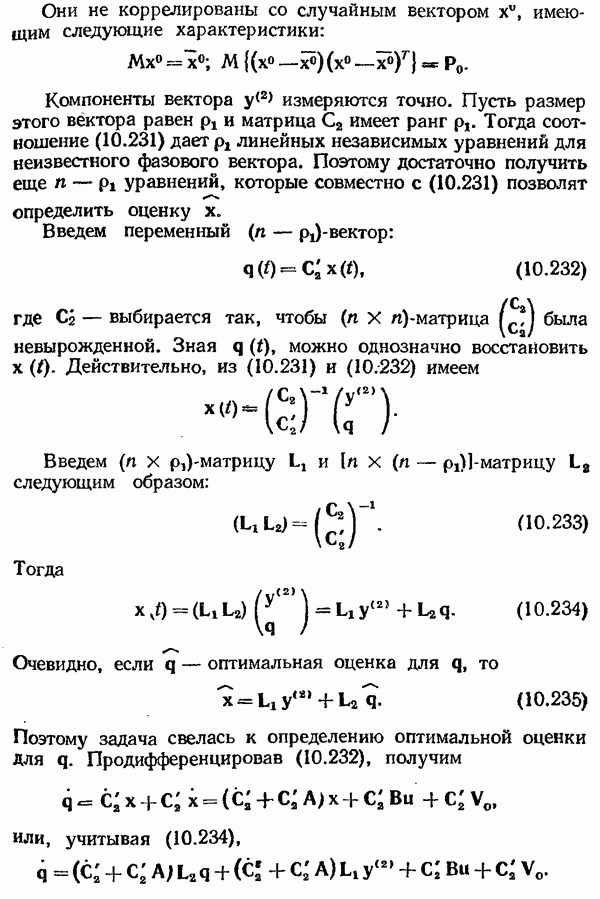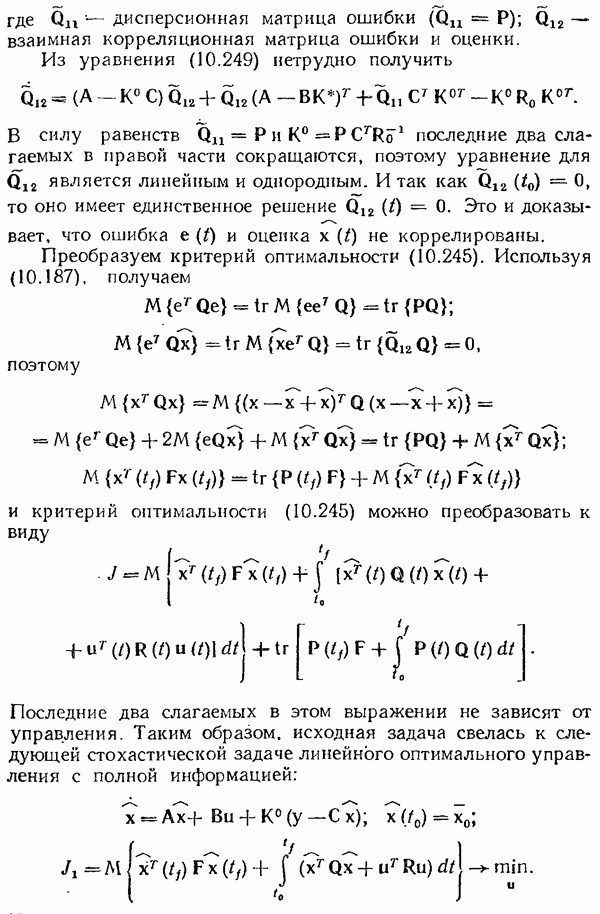| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Синтез стохастических оптимальных систем управления при неполной информации
Измерение (наблюдение), как правило, всегда сопровождается помехами, и состояние системы никогда точно не известно, поэтому более практичной является стохастическая задача оптимального управления при неполной информации о состоянии системы. Эта задача намного сложнее, и для ее решения часто используют эвристический прием (метод разделения), при котором стохастическая задача синтеза при неполной информации разделяется на две задачи: задачу оптимальной оценки состояния и детерминированную задачу синтеза или стохастическую задачу синтеза при полной информации. В общем случае система, синтезированная таким приемом, не обязательно является оптимальной. Но возможно, что, как, например, при линейных уравнениях объекта и наблюдения и среднеквадратичном критерии, метод разделения позволяет синтезировать оптимальную систему управления. Таким образом, со стохастической задачей оптимального управления тесно связана задача оптимальной оценки. Перейдем к рассмотрению этой задачи.
Наблюдатель (оцеииватель, фильтр) Калмана-Бьюси.
Рассмотрим следующую задачу оптимального оценивания (восстановления). Пусть объект и наблюдение описываются уравнениями

где  — гауссовские белые шумы с характеристиками
— гауссовские белые шумы с характеристиками

 гауссовская случайная величина с характеристиками
гауссовская случайная величина с характеристиками

 — неотрицательно-определенные симметричные матрицы
— неотрицательно-определенные симметричные матрицы  — положительно-определенная симметричная матрица
— положительно-определенная симметричная матрица 
Случайные процессы и  называются соответственно шумом объекта и шумом наблюдения или измерения. Они не коррелированы со случайной величиной
называются соответственно шумом объекта и шумом наблюдения или измерения. Они не коррелированы со случайной величиной  Требуется, используя измеренные значения выходной переменной
Требуется, используя измеренные значения выходной переменной  на интервале
на интервале  найти несмещенную оценку
найти несмещенную оценку  обеспечивающую минимум среднего квадрата ошибки:
обеспечивающую минимум среднего квадрата ошибки:

Условие  т. е. условие положительной определенности матрицы интенсивности шума наблюдения, означает, что ни одна компонента выходной переменной
т. е. условие положительной определенности матрицы интенсивности шума наблюдения, означает, что ни одна компонента выходной переменной  не измеряется точно. В этом случае задача оценивания называется несингулярной [10]. Таким образом, задача (10.189)-(10.191) является несингулярной задачей оценивания (фильтрации).
не измеряется точно. В этом случае задача оценивания называется несингулярной [10]. Таким образом, задача (10.189)-(10.191) является несингулярной задачей оценивания (фильтрации).
Ее решение, т. е. несмещенная оптимальная оценка  определяется из уравнения
определяется из уравнения

где матрица коэффициентов усиления

В (10.193) Р является дисперсионной матрицей ошибки  и находится из так называемого дисперсионного уравнения:
и находится из так называемого дисперсионного уравнения:

Если шумы объекта и наблюдения не коррелированы  то из (10.193) и (10.194) получаем
то из (10.193) и (10.194) получаем


Рис. 10.7
Несингулярная задача оценивания (10.189)-(10.191) при некоррелированных шумах впервые была решена Р. Калманом и Р. Бьюси. Ее решение, представляющее собой оптимальный наблюдатель, называется наблюдателем (оценивателем) или чаще фильтром Калмана—Бьюси. Заметим, что Р. Калман и Р. Бьюси рассмотрели случай, когда 
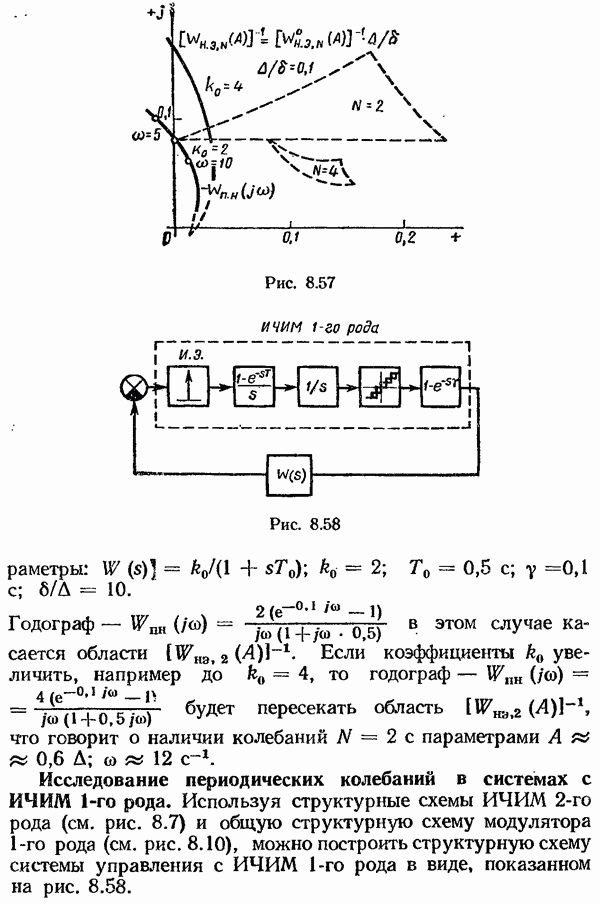
Сравнивая уравнения объекта (10.189) и оптимального наблюдателя (10.192), замечаем, что их правые части отличаются только последними слагаемыми: в уравнении наблюдателя вместо шума объекта появляется слагаемое, пропорциональное разности  Эта разность между измеренным текущим значением выходной переменной и его оценкой
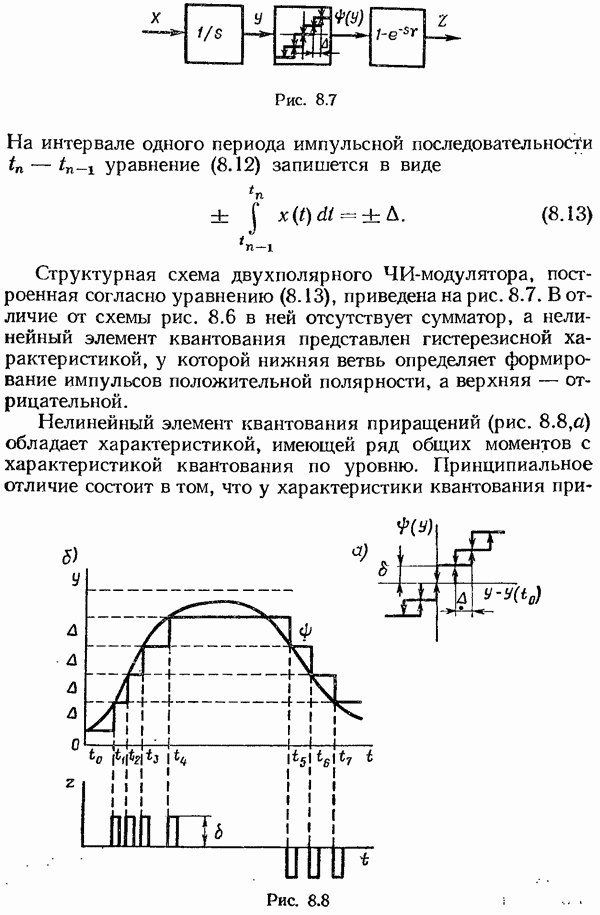
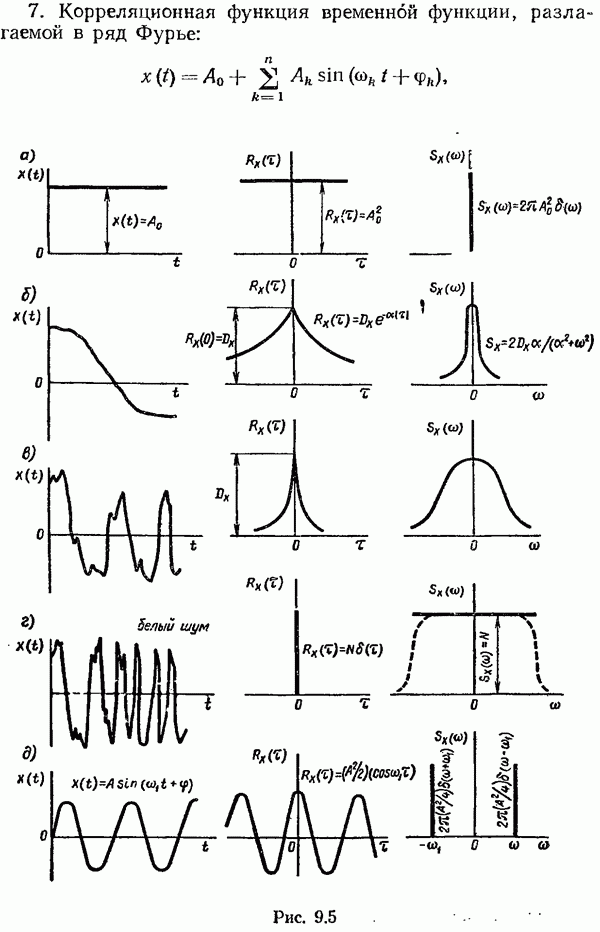
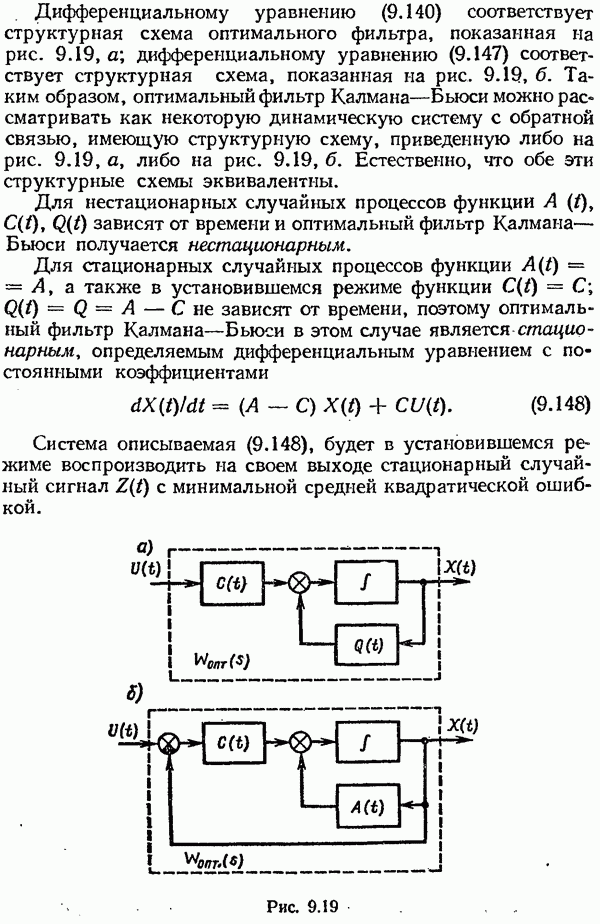
Эта разность между измеренным текущим значением выходной переменной и его оценкой  называется невязкой. Структурная схема наблюдателя Калмана—Бьюси (рис. 10.7, а) включает в себя как составную часть модель исходной системы (рис. 10.7, б). Ее отличие от заданной системы состоит только в том, что она имеет дополнительно обратную связь по невязке. Интересно отметить, что наблюдатель Калмана—Бьюси имеет такую же структуру, что и наблюдатель полного порядка в детерминированном случае (см. рис 10.3)
называется невязкой. Структурная схема наблюдателя Калмана—Бьюси (рис. 10.7, а) включает в себя как составную часть модель исходной системы (рис. 10.7, б). Ее отличие от заданной системы состоит только в том, что она имеет дополнительно обратную связь по невязке. Интересно отметить, что наблюдатель Калмана—Бьюси имеет такую же структуру, что и наблюдатель полного порядка в детерминированном случае (см. рис 10.3)
Соотношения (10.192)-(10.195) определяют также решение задачи линейного оптимального оценивания, которая отличается от задачи оптимального оценивания (10.189)- (10.191) тем, что: а) о законах распределения шумов и начального состояния никаких предположений не делается (не требуется, чтобы они были гауссовскими); б) нужно найти линейный оптимальный наблюдатель, т. е. оптимальный наблюдатель в классе линейных систем. Другими словами, если шумы  и
и  и начальное состояние
и начальное состояние  не являются гауссовскими, то наблюдатель Калмана — Бьюси является оптимальным,
не являются гауссовскими, то наблюдатель Калмана — Бьюси является оптимальным,
вообще говоря, только среди линейных наблюдателей (систем).
Покажем, что наблюдатель Калмана—Бьюси является линейным оптимальным наблюдателем. Достаточно доказать, что оценка, определяемая наблюдателем Калмана—Бьюси, минимизирует функционал

при произвольном  -векторе а. Действительно, если оценка
-векторе а. Действительно, если оценка  минимизирует функционал (10.196) при произвольном а, то она, очевидно, минимизирует функционалы
минимизирует функционал (10.196) при произвольном а, то она, очевидно, минимизирует функционалы

которые получаются из (10.196) при соответствующем выборе вектора а, и соответственно сумму

представляющую средний квадрат ошибки оценивания (10.191).
Сначала примем  Воспользуемся схемой доказательства, основанной на преобразовании задачи линейного оптимального оценивания к задаче оптимального управления [16]. Так как отыскивается линейный оптимальный наблюдатель, то линейная комбинация
Воспользуемся схемой доказательства, основанной на преобразовании задачи линейного оптимального оценивания к задаче оптимального управления [16]. Так как отыскивается линейный оптимальный наблюдатель, то линейная комбинация  как и сама оценка
как и сама оценка  представляет собой линейный функционал от функции
представляет собой линейный функционал от функции  которая является входным воздействием искомого наблюдателя:
которая является входным воздействием искомого наблюдателя:

Найдем весовую функцию и  и постоянный вектор
и постоянный вектор  при которых оценка
при которых оценка  определяемая последним соотношением, является несмещенной и оптимальной в смысле минимума критерия (10.196).
определяемая последним соотношением, является несмещенной и оптимальной в смысле минимума критерия (10.196).
Подставим в (10.197) выражение для  из (10.190):
из (10.190):

Введем векторную переменную х, определяемую уравнением

при граничном условии

Очевидно,

Так как в силу уравнений (10.188) и (10.199) (напомним, что рассматривается случай 

то

Вычитая из этого соотношения (10.198), получим

откуда

Из последнего равенства следует, что при

оценка  линейной комбинации
линейной комбинации  определяемая соотношением (10.197), будет несмещенной при всех а и
определяемая соотношением (10.197), будет несмещенной при всех а и  Из него также следует, что
Из него также следует, что

Используя (10.201), получим

Кроме того,

Поэтому

Преобразуем подынтегральное выражение следующим образом:

Введя обозначение

выражение для 7 можно представить в виде

Уравнение (10.199) преобразуется к виду

где

Если положить 

и ввести новую независимую переменную  уравнение и граничное условие для х и выражение для
уравнение и граничное условие для х и выражение для  преобразуются к виду
преобразуются к виду

Таким образом, задача линейного оптимального оценивания свелась к задаче оптимального управления (10.204), где нужно найти «управление»  минимизирующее критерий
минимизирующее критерий  . Задача (10.204) эквивалентна задаче оптимального управления (10.120), (10.121) при
. Задача (10.204) эквивалентна задаче оптимального управления (10.120), (10.121) при  причем между матрицами, входящими в условия этих задач, имеется следующее соответствие:
причем между матрицами, входящими в условия этих задач, имеется следующее соответствие:

Используя решение задачи (10.120), (10.121) при  получим [см. (10.138)]
получим [см. (10.138)]

где Р определяется из уравнения [см. (10.123), (10.125)]

Возвращаясь к независимой переменной  полученное соотношение можно записать следующим образом (заметим, что
полученное соотношение можно записать следующим образом (заметим, что

Принимая во внимание обозначения (10.202) и (10.203), получаем:

Итак, установлено, что соотношение (10.197) определяет несмещенную оптимальную оценку  если весовая функция
если весовая функция  удовлетворяет (10.205), (10.206), а постоянный вектор b — условию (10.201). Выражение для
удовлетворяет (10.205), (10.206), а постоянный вектор b — условию (10.201). Выражение для  из (10.205) и уравнение (10.206) совпадают с (10.193) и (10.194) соответственно. Следовательно, остается доказать, что оценка, определяемая из соотношения (10.197), после подстановки в него весовой функции и
из (10.205) и уравнение (10.206) совпадают с (10.193) и (10.194) соответственно. Следовательно, остается доказать, что оценка, определяемая из соотношения (10.197), после подстановки в него весовой функции и  из (10.205) удовлетворяет уравнению
из (10.205) удовлетворяет уравнению  . Подставив выражение для и из (10.205) в (10.199), получим
. Подставив выражение для и из (10.205) в (10.199), получим

Пусть  — решение матричного уравнения
— решение матричного уравнения

при единичном начальном условии

Тогда (см. § 8.2) решение уравнения  и в силу (10.200) и (10.201)
и в силу (10.200) и (10.201)


Из (10.205) и (10.209) имеем

При подстановке этого выражения и выражения (10.210) соотношение (10.197) при  преобразуется к виду
преобразуется к виду

откуда следует, что оценка

является несмещенно и доставляет минимум (10.196) при любом а. Продифференцируем (10.211) и, используя (10.208), получим

или, принимая во внимание (10.211),

Из (10.211) при  получаем
получаем 
Итак, для случая и  показали, что наблюдатель Калмана—Бьюси действительно является линейным оптимальным наблюдателем.
показали, что наблюдатель Калмана—Бьюси действительно является линейным оптимальным наблюдателем.
Перейдем к случаю  . Представим фазовый вектор в виде суммы [9]:
. Представим фазовый вектор в виде суммы [9]:  , где слагаемые удовлетворяют уравнениям
, где слагаемые удовлетворяют уравнениям

Вектор наблюдения также представим в виде двух составляющих:  где
где

Составляющие  однозначно определяются из уравнений.
однозначно определяются из уравнений.
Составляющая  легко определяется по измерениям
легко определяется по измерениям 

Таким образом, задача оптимальной оценки при  свелась к оценке
свелась к оценке  по
по  — задаче оптимальной оценки при и
— задаче оптимальной оценки при и 
Для линейной оптимальной оценки  имеем [см. (10.192)]
имеем [см. (10.192)]

где  определяется из (10.193)-(10.195).
определяется из (10.193)-(10.195).
Очевидно, оптимальная оценка  равна сумме:
равна сумме:

Продифференцировав это выражение, получим

или, принимая во внимание равенство 

На этом заканчивается доказательство, что наблюдатель Калмана—Бьюси, определяемый соотношением  является линейным оптимальным наблюдателем.
является линейным оптимальным наблюдателем.
Пример 10.24. Рассмотрим задачу определения оптимальной оценки скалярной постоянной величины х по измерениям  где
где  — белый шум с интенсивностью
— белый шум с интенсивностью 
До начала измерения известны следующие характеристики 

Искомая величина и шум независимы. Учитывая уравнение  рассматриваемую задачу можно сформулировать как задачу линейной оптимальной оценки. В данном случае
рассматриваемую задачу можно сформулировать как задачу линейной оптимальной оценки. В данном случае

и наблюдатель Калмана — Бьюси описывается уравнением

где  определяется из уравнения
определяется из уравнения

Как легко проверить,

Заметим, что хотя х — константа, ее оценка х является функцией времени: с течением времени оценка уточняется и при  стремится к х. Это следует из того, что дисперсия ошибки при
стремится к х. Это следует из того, что дисперсия ошибки при  стремится к нулю:
стремится к нулю:

Дисперсионное уравнение. Покажем, что матрица Р, определяемая из уравнения (10.194), является дисперсионной матрицей ошибок для оценки, получаемой наблюдателем Калмана—Бьюси. С этой целью сначала получим уравнение для дисперсионной матрицы стохастического процесса  описываемого уравнением
описываемого уравнением

где  детерминированная функция;
детерминированная функция;  белый шум с интенсивностью
белый шум с интенсивностью  случайный вектор с математическим ожиданием
случайный вектор с математическим ожиданием  и матрицей дисперсий
и матрицей дисперсий  не коррелированы.
не коррелированы.
Пусть  — нормированная фундаментальная матрица. Тогда
— нормированная фундаментальная матрица. Тогда

Так как, очевидно,

то для центрированного процесса  имеем
имеем

Используя это выражение, для корреляционной матрицы  получаем
получаем

Дисперсионная матрица

Используя тождества  при
при  при
при  и выражение (10.125) для
и выражение (10.125) для  соотношение (10.214) для корреляционной матрицы можно преобразовать к виду
соотношение (10.214) для корреляционной матрицы можно преобразовать к виду

Это соотношение потребуется в дальнейшем при доказательстве принципа разделения. Из (10.215) путем дифференцирования получаем следующее уравнение для дисперсионной матрицы (дисперсионное уравнение):

Из (10.215) также имеем

Теперь получим уравнение для дисперсионной матрицы ошибки. Вычитая (10.192) из (10.189), получаем уравнение для ошибки 

Начальное значение  имеет следующие характеристики:
имеет следующие характеристики:

Оно не коррелировано с шумами. Уравнение (10.219) получается из (10.212) при 

Получим выражение для интенсивности шума 

откуда

Дисперсионное уравнение (10.217) в этом случае принимает вид

Если предположить, что дисперсионная матрица оценки  и подставить выражение для
и подставить выражение для  из (10.193), то последнее уравнение преобразуется к виду (10.194). Следовательно, действительно матрица Р, определяемая из матричного уравнения
из (10.193), то последнее уравнение преобразуется к виду (10.194). Следовательно, действительно матрица Р, определяемая из матричного уравнения
Риккати в наблюдателе Калмана—Бьюси, является дисперсионной матрицей ошибки.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 7. НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
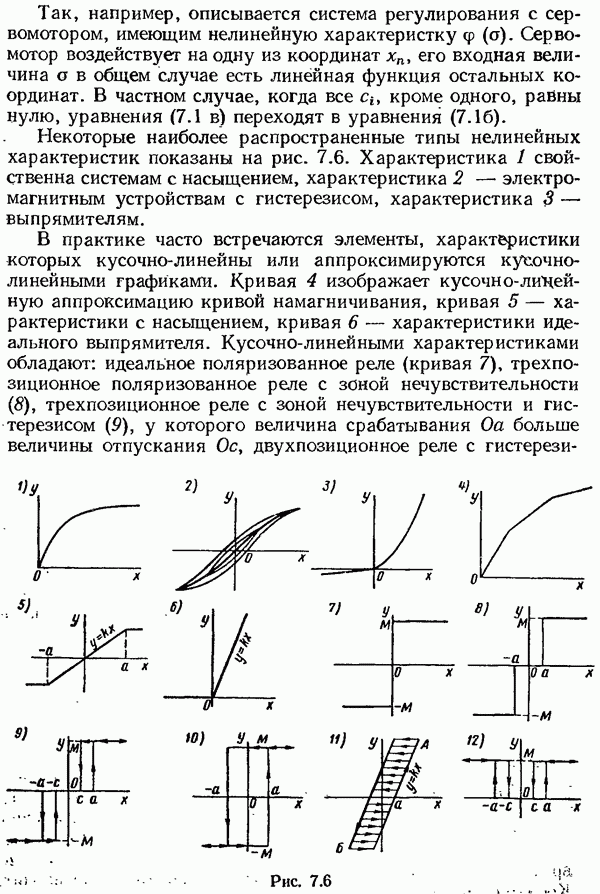
- § 7.1. Основные типы. нелинейных систем и характеристик
- § 7.2. Изображение движений в фазовой плоскости
- Линейная консервативная система второго порядка.
- Система с сухим кулоновским трением.
- Система с отрицательной восстанавливающей силой.
- Линейная колебательная система с вязким трением.
- Линейная апериодическая система с вязким трением.
- § 7.3. Автоколебания. Метод точечных преобразований
- § 7.4. Системы с переменной структурой
- § 7.5. Метод «припасовывания» граничных значений
- § 7.6. Приближенное исследование автоколебаний. Метод эквивалентной линеаризации
- § 7.7. Метод гармонического баланса
- § 7.8. Устойчивость в малом, большом и целом
- § 7.9. Второй (прямой) метод Ляпунова
- § 7.10. Абсолютная устойчивость
- Квадратичный критерий абсолютной устойчивости.
- Круговой критерий устойчивости.
- Критерий В. М. Попова.
- Примечание к критерию Попова.
- Гипотезы М. Айзермана и Р. Калмана.
- Определение автоколебаний.
- Упрощенный критерий колебательности.
- Глава 8. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
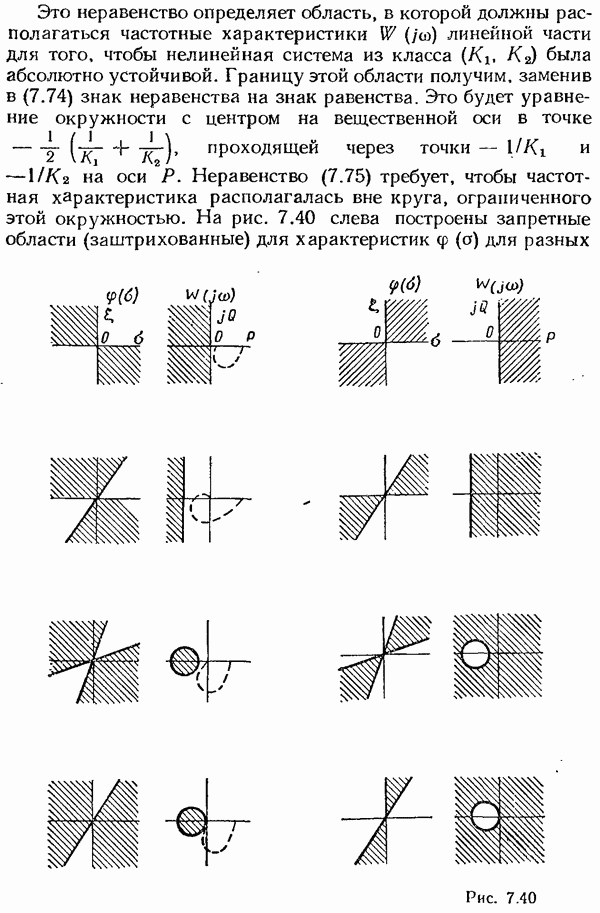
- § 8.1. Понятие об импульсных системах автоматического управления
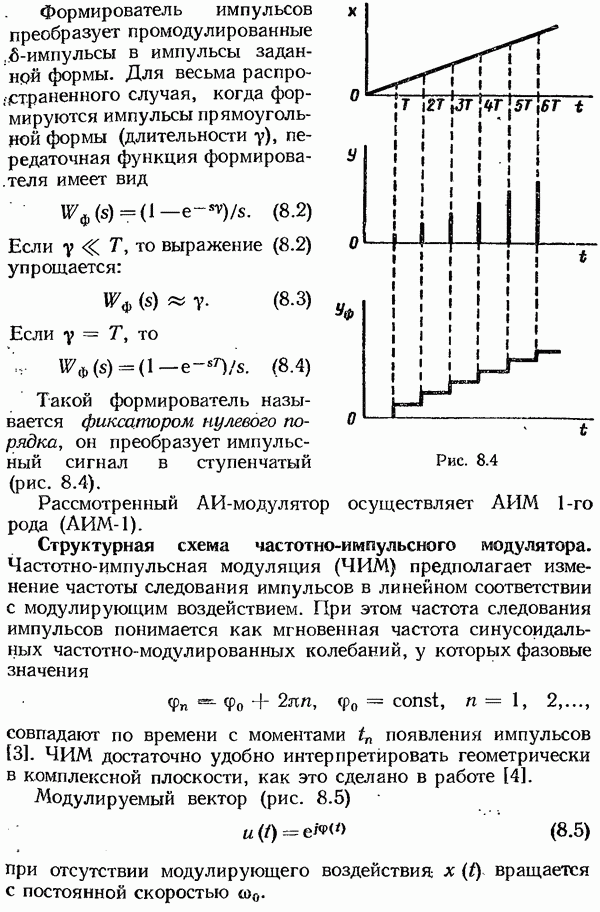
- Структура и уравнения импульсных модуляторов.
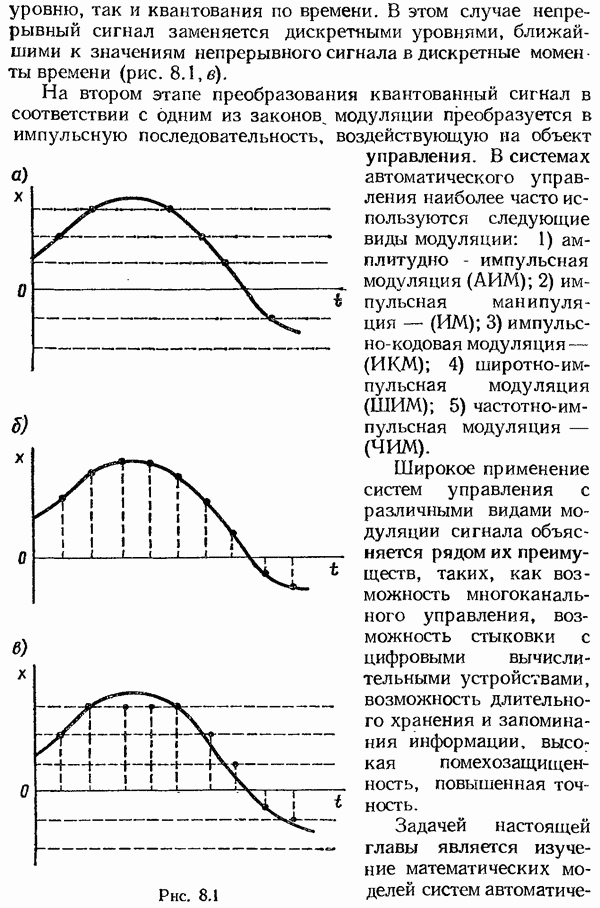
- Структурная схема амплитудно-импульсного модулятора.
- Структурная схема частотно-импульсного модулятора.
- Структурная схема широтно-импульсного модулятора.
- Структурные схемы частотно-импульсных к широтно- импульсных модуляторов 1-го рода.
- Структурная схема системы управления с импульсной модуляцией. Классификация систем управления с импульсной модуляцией.
- § 8.2. Исследование устойчивости и качества систем управления с амплитудноимпульсной модуляцией
- Передаточная функция импульсной системы.
- Дискретное преобразование Лапласа и его основные свойства.
- Частотные характеристики импульсной системы.
- Исследование устойчивости систем с амплитудно-импульсной модуляцией.
- Алгебраический критерий устойчивости (аналог критерия Гурвица).
- Частотный критерий устойчивости (аналог критерия Найквиста).
- Исследование качества систем с амплитудно-импульсной модуляцией.
- Непрерывное регулирование как граница импульсного регулирования.
- § 8.3. Исследование динамики цифровых систем автоматического управления
- Исследование цифровых систем методом логарифмических частотных характеристик.
- Исследование цифровых систем с непрерывной передачей данных.
- Исследование цифровых систем с учетом квантования по уровню и по времени.
- § 8.4. Исследование систем с широтноимпульсной модуляцией
- Исследование периодических колебаний в системах с широтно-импульсной модуляцией.
- § 8.5. Исследование систем с частотно-импульсной модуляцией
- Исследование устойчивости в целом частотно-импульсных систем 2-го рода.
- Исследование периодических режимов в системах с ИЧИМ.
- Исследование периодических колебаний в системах с ИЧИМ 1-го рода.
- Глава 9. СЛУЧАЙНЫЕ ПРОЦЕССЫ В АВТОМАТИЧЕСКИХ СИСТЕМАХ УПРАВЛЕНИЯ
- § 9.2. Случайные процессы и их основные статистические характеристики
- § 9.3. Корреляционные функции случайных процессов
- § 9.4. Спектральные плотности случайных процессов
- § 9.5. Связь между корреляционными функциями и спектральными плотностями случайного процесса на входе и выходе линейной системы
- § 9.6. Расчет линейных систем при случайных воздействиях
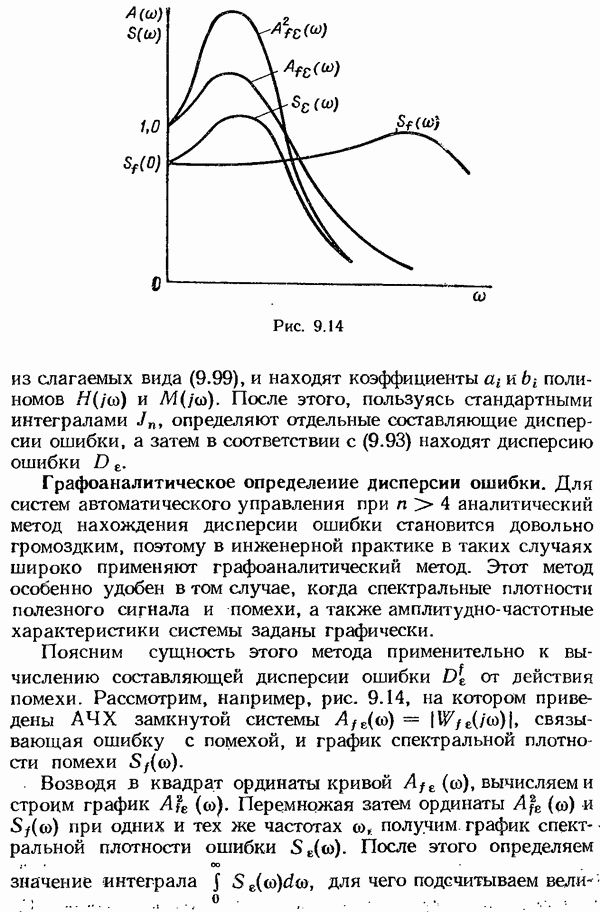
- Аналитический метод определения дисперсии ошибки.
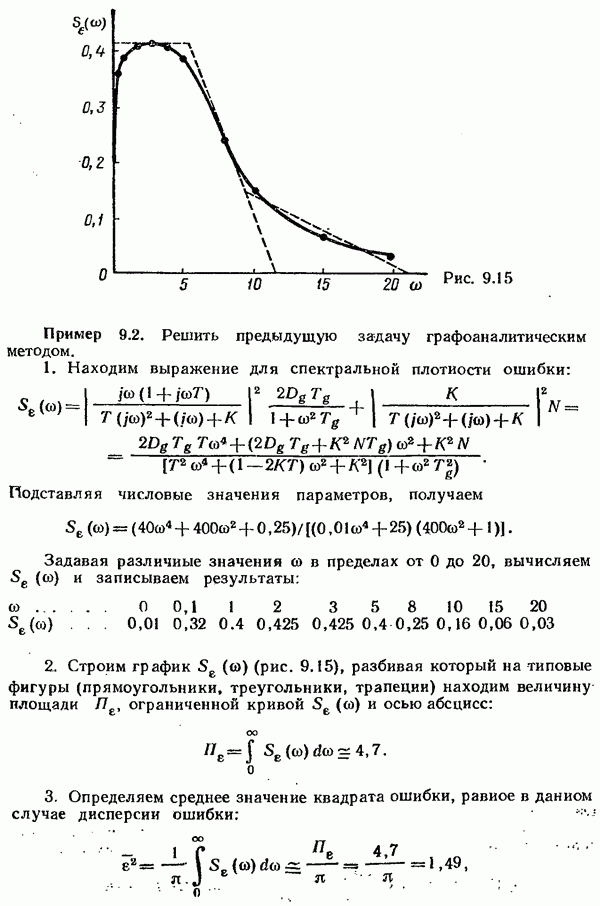
- Графоаналитическое определение дисперсии ошибки.
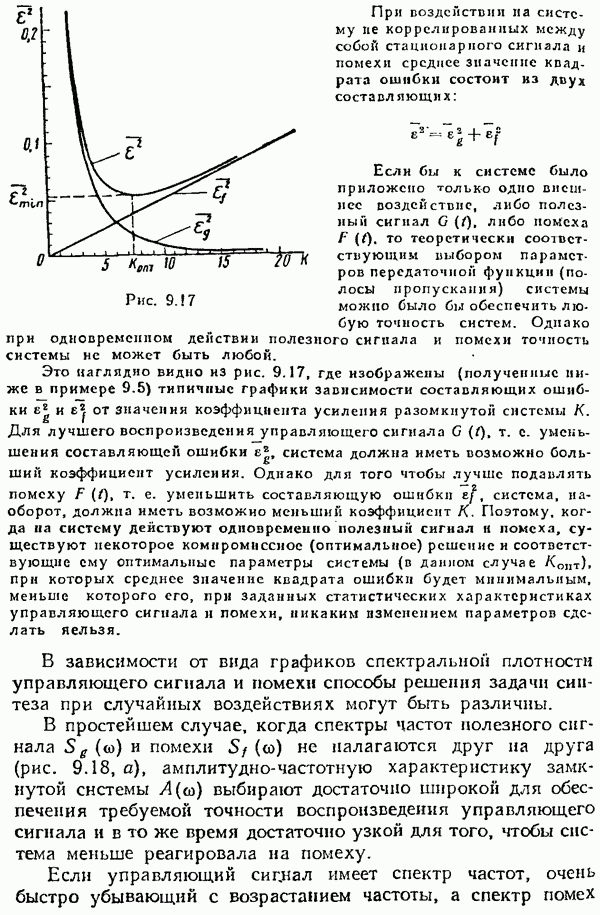
- § 9.7. Синтез линейных систем с минимальной средней квадратической ошибкой
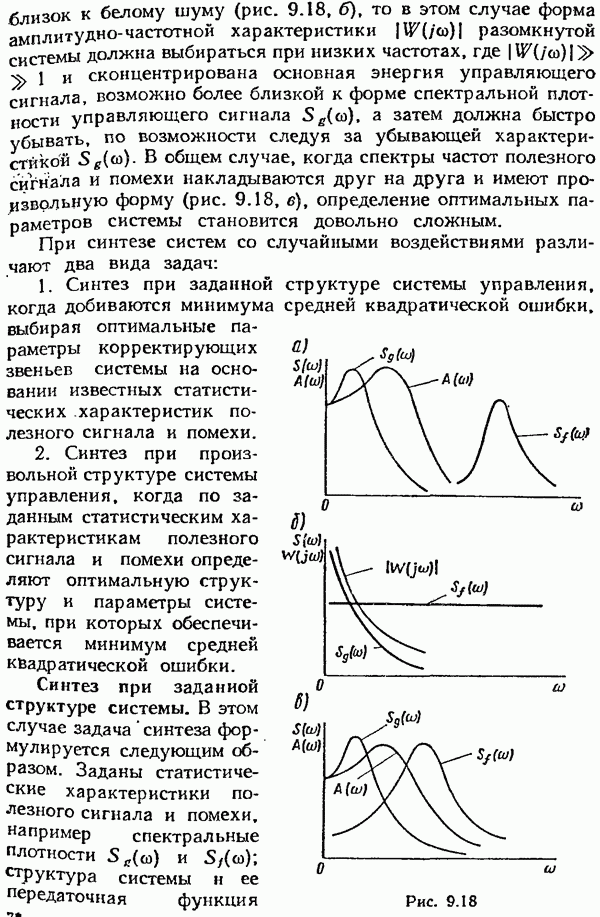
- Синтез при произвольной структуре системы.
- Оптимальный фильтр Винера.
- Оптимальный фильтр Калмана—Бьюси.
- § 9.8. Случайные процессы в линейных импульсных системах
- § 9.9. Нелинейное преобразование случайных сигналов
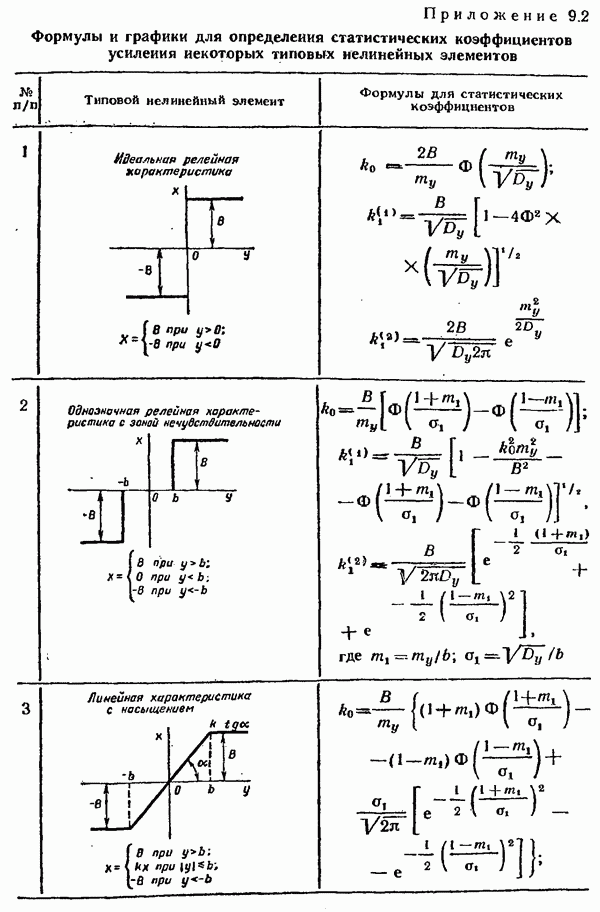
- § 9.10. Статистическая линеаризация нелинейных элементов
- § 9.11. Расчет нелинейных систем методом статистической линеаризации
- Расчет замкнутых нелинейных систем.
- Глава 10. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
- Общая постановка задачи оптимального управления
- Примеры постановки задач оптимального управления.
- Классификация задач оптимального управления
- § 10.2. Метод классического вариационного исчисления (метод множителей Лагранжа)
- Уравнения Эйлера—Лагранжа.
- Задачи с подвижными концами и фиксированным временем
- Задача с нефиксированным временем.
- § 10.3. Принцип максимума Понтрягина. Условие нормальности. Теорема об n интервалах. Вырожденные и особые задачи
- Задача с подвижными концами
- Задача максимального быстродействия
- Условие нормальности.
- Теорема об n интервалах.
- Задача с ограничением на фазовые координаты
- Вырожденные задачи
- Особые задачи
- § 10.4. Метод динамического программирования. Теорема Болтянского. Метод Кротова
- Принцип оптимальности
- Функция и уравнение Беллмана
- Проблема обоснования метода динамического программирования и достаточные условия оптимальности
- Метод Кротова [11]
- Принцип оптимальности Кротова.
- § 10.5. Управляемость и наблюдаемость. Наблюдатели
- Управляемость линейных стационарных объектов.
- Стабилизируемость.
- Управляемость при наличии ограничения на управление.
- Наблюдаемость и восстанавливаемость
- Обнаруживаемость
- Наблюдатели
- Наблюдатели пониженного порядка.
- § 10.6. Методы синтеза оптимальных систем с обратной связью. Синтез оптимальных линейных систем по интегральному квадратичному критерию
- Синтез оптимальных линейных систем по интегральному квадратичному критерию
- Векторное дифференцирование.
- Синтез оптимального линейного регулятора выхода.
- § 10.7. Стохастические оптимальные системы. Методы синтеза. Методы оптимальной оценки состояния. Принцип разделимости
- Метод динамического программирования
- Синтез стохастической оптимальной линейной системы при полной информации о состоянии
- Синтез стохастических оптимальных систем управления при неполной информации
- Наблюдатель Калмана—Бьюси при цветном шуме объекта.
- Наблюдатель Калмана—Бьюси при цветном шуме наблюдения.
- Сингулярная (вырожденная) задача линейного оптимального оценивания.
- Линеаризованный наблюдатель Калмана—Бьюси.
- Стохастическая линейная оптимальная система управления при неполной информации. Принцип разделимости
- § 10.8. Оптимальные дискретные системы
- Синтез оптимальной линейной системы при квадратном критерии
- Стохастическая оптимальная линейная система при полной информации о состоянии.
- Наблюдатель (оцениватель, фильтр) Калмана.
- О расходимости фильтров и методах их регуляризации.
- Глава 11. АДАПТИВНЫЕ АВТОМАТИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
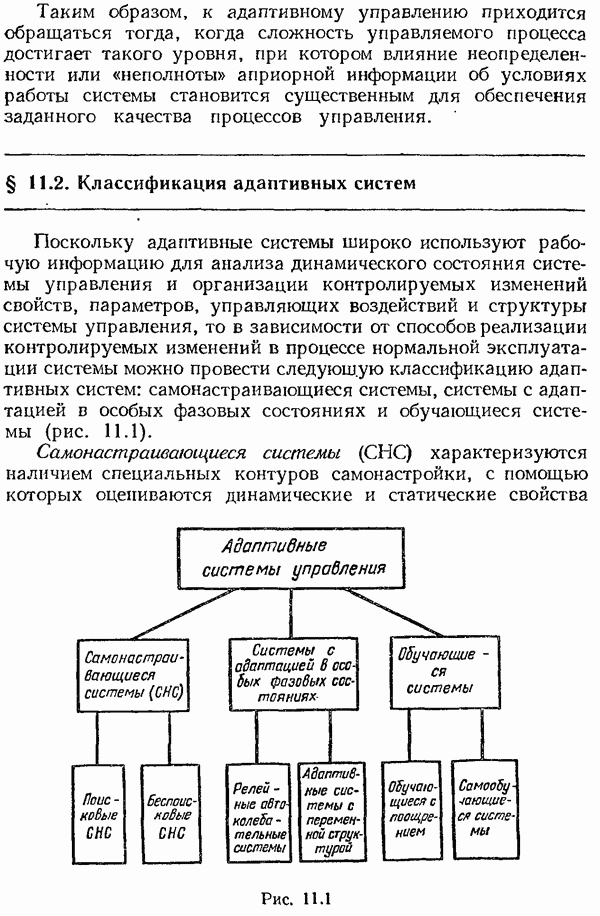
- § 11.2. Классификация адаптивных систем
- § 11.3. Самонастраивающиеся системы
- Принципы построения поисковых самонастраивающихся систем.
- Регулярные методы поиска экстремума
- Метод градиента.
- Метод наискорейшего спуска.
- Методы экстраполяционного поиска.
- Методы случайного поиска
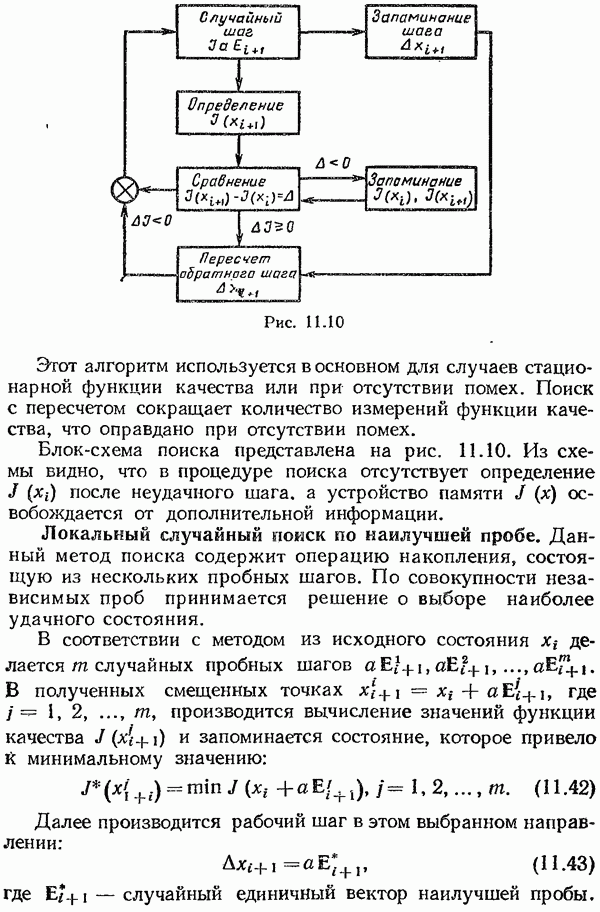
- Локальный случайный поиск с пересчетом.
- Локальный случайный поиск по наилучшей пробе.
- Локальный случайный поиск по статистическому градиенту.
- Глобальный случайный поиск с независимым выбором плотности распределения пробных шагов.
- Примеры поисковых самонастраивающихся систем
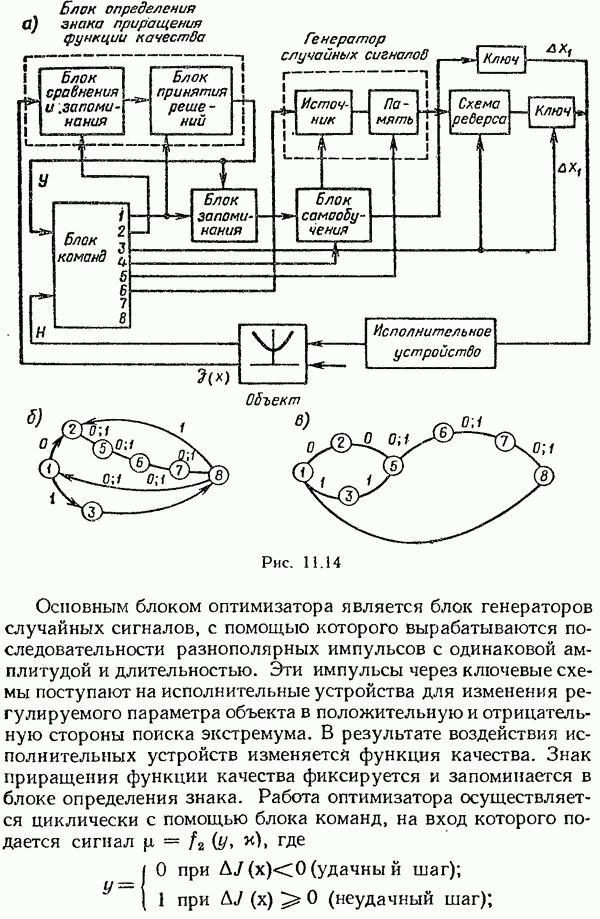
- Многоканальный статистический оптимизатор со случайным поиском.
- Принцип инвариантности.
- Принцип эталонной модели.
- Принципы определения градиента функции качества.
- Принципы идентификации динамических свойств системы управления.
- Примеры беспоисковых самонастраивающихся систем
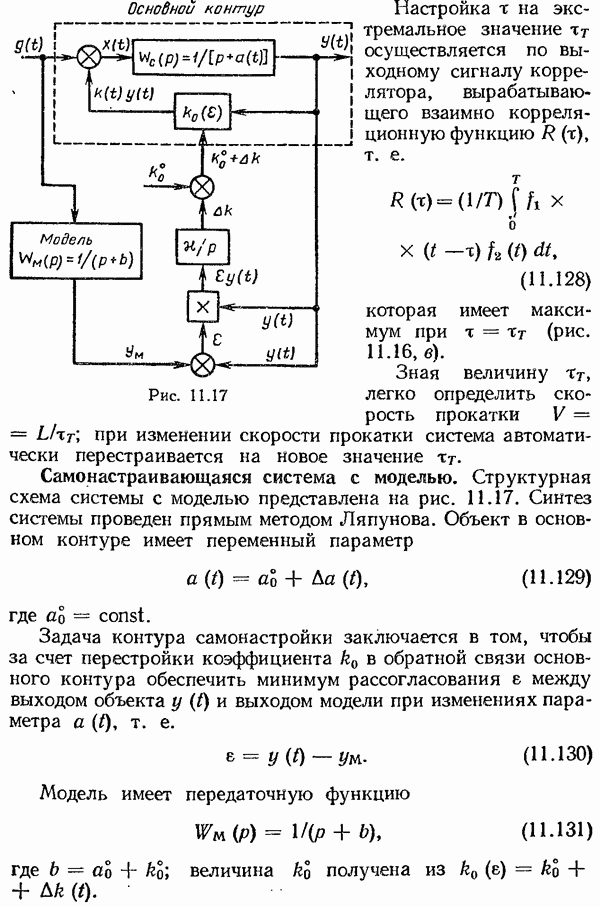
- Самонастраивающаяся система с моделью.
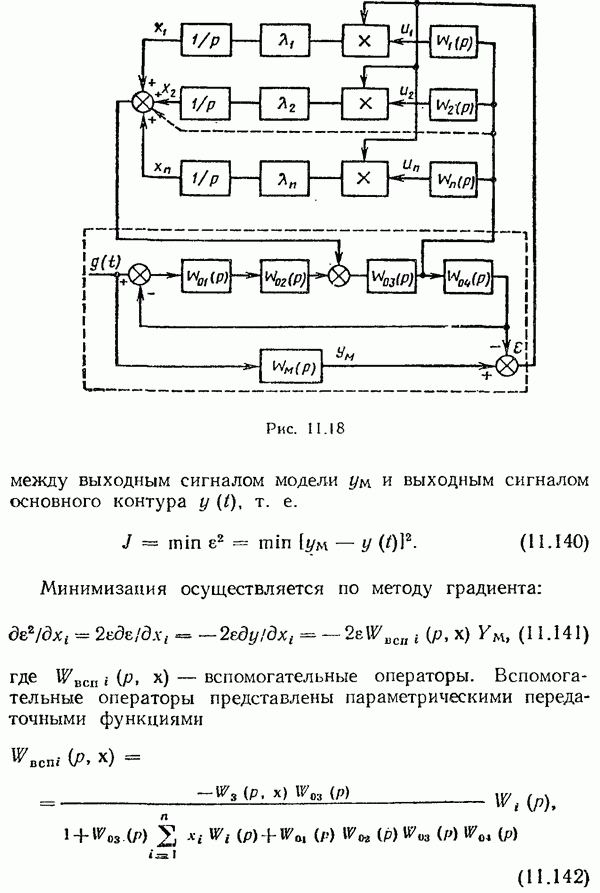
- Градиентная самонастраивающаяся система.
- § 11.4. Системы с адаптацией в особых фазовых состояниях
- Адаптивные системы с переменной структурой.
- Адаптивная система с переменной структурой, использующая информацию о внутренних координатах.
- § 11.5. Обучающиеся системы
- Метод секущих плоскостей.
- Метод потенциальных функций.
- Вероятностные алгоритмы обучения.
- Самообучение.
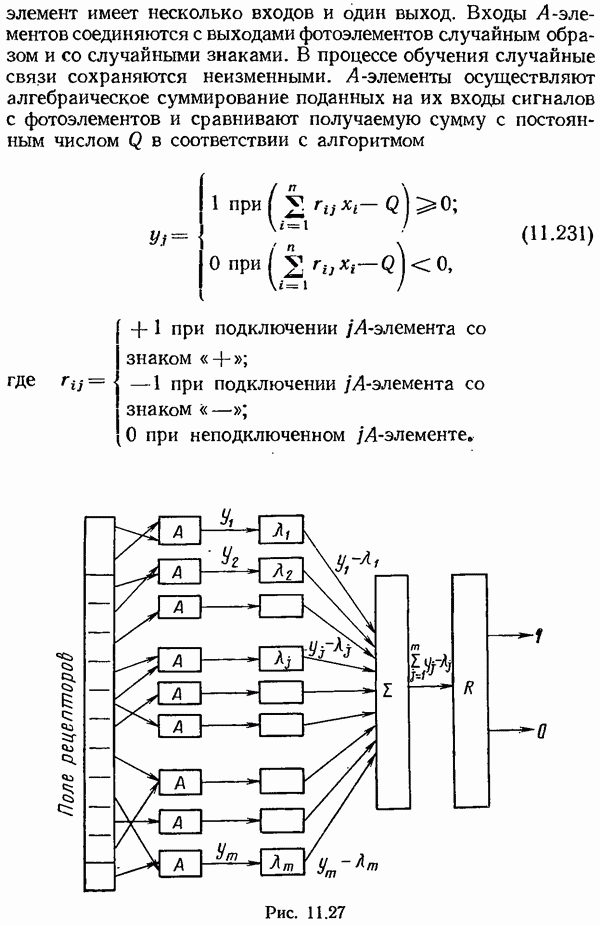
- Персептронная модель автоматической классификации.
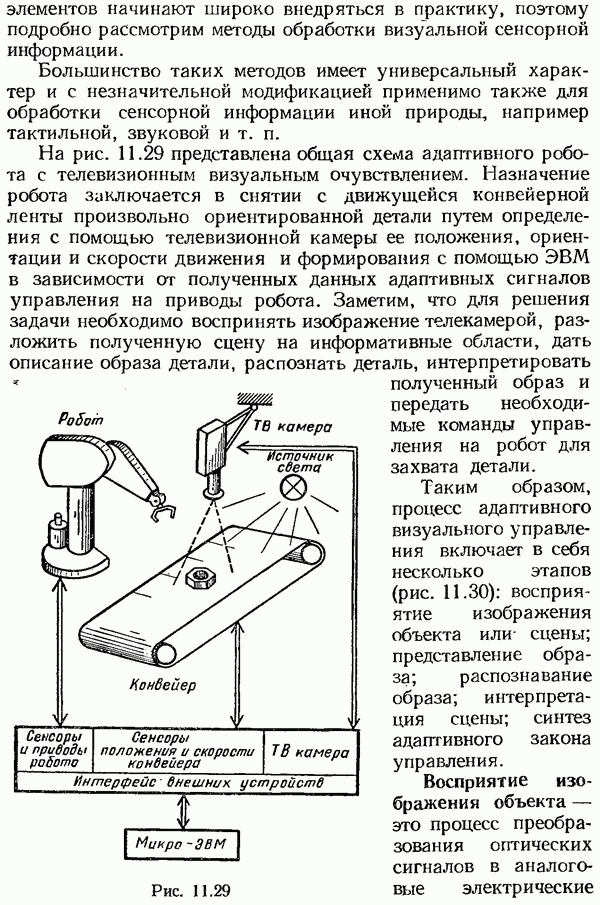
- § 11.6. Адаптивные робототехнические системы
- Методы обработки сенсорной информации для адаптивного управления роботами.
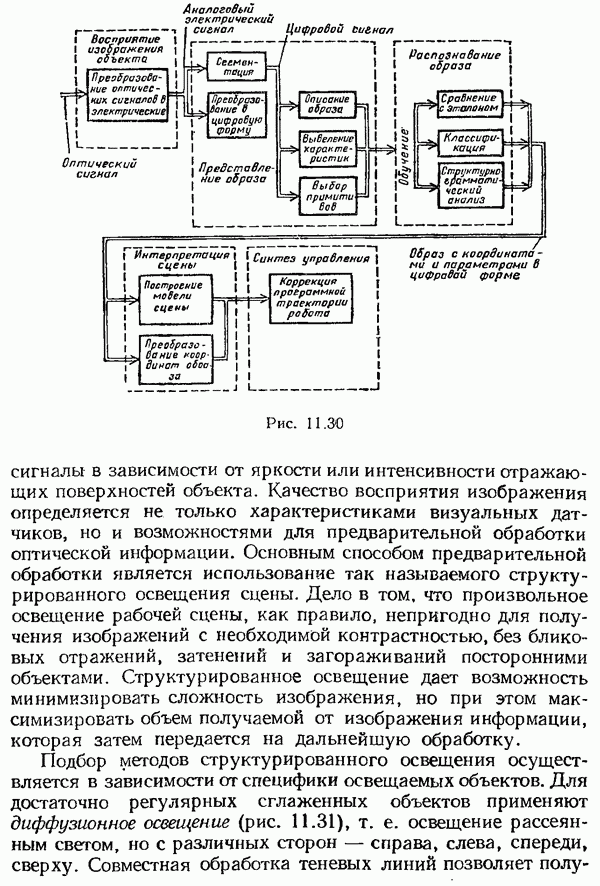
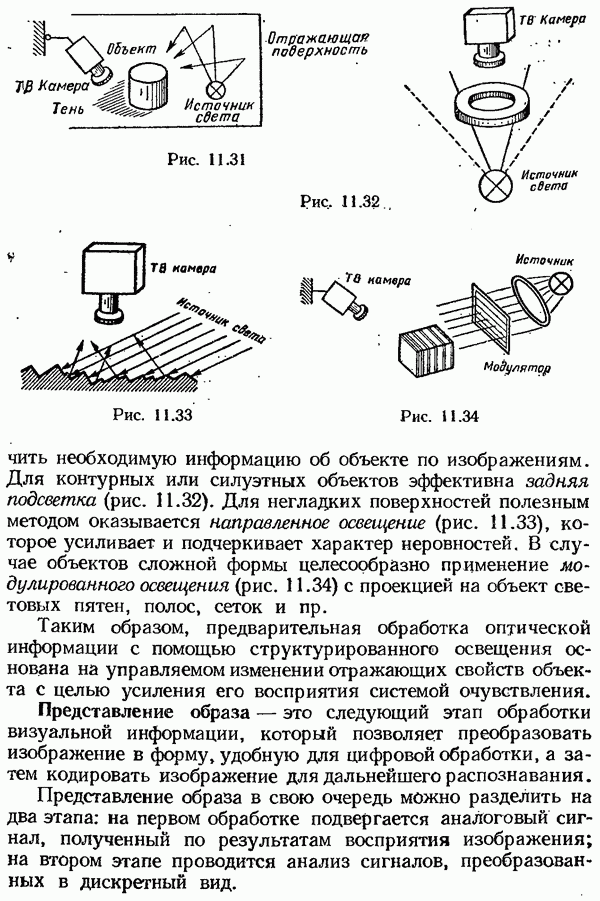
- Восприятие изображения объекта
- Представление образа
- ЗАКЛЮЧЕНИЕ
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ