| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
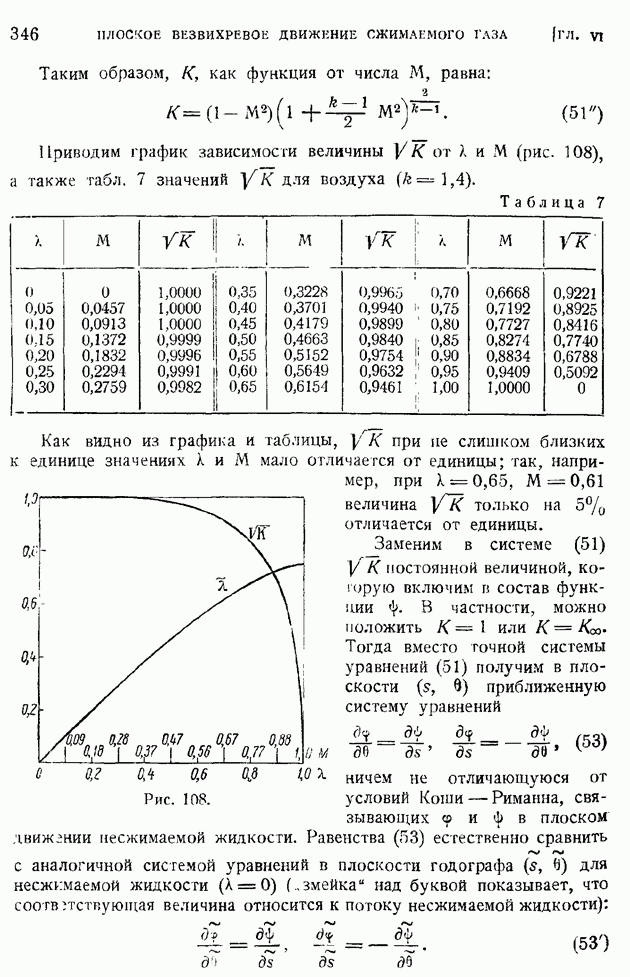
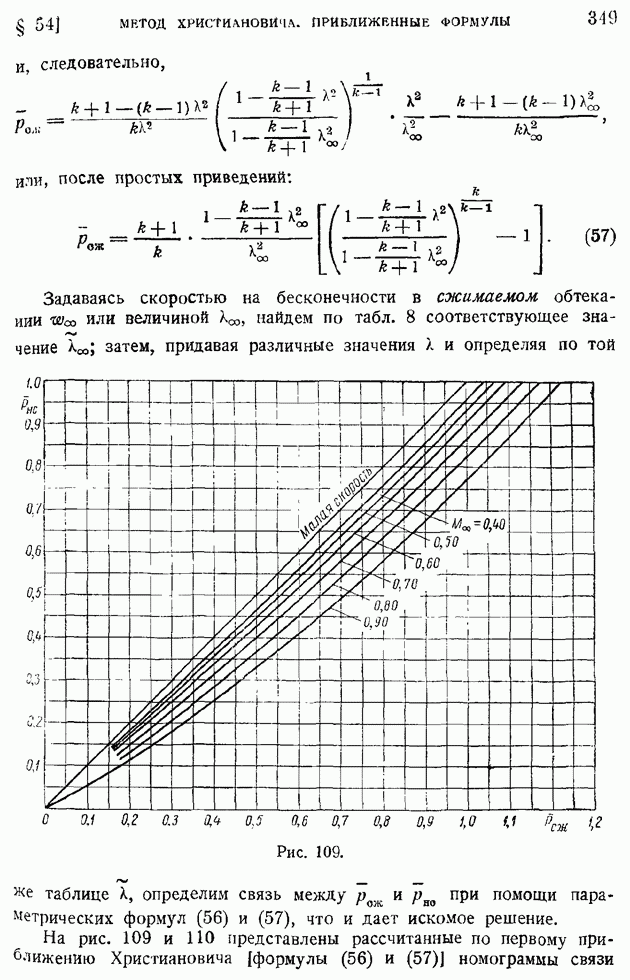
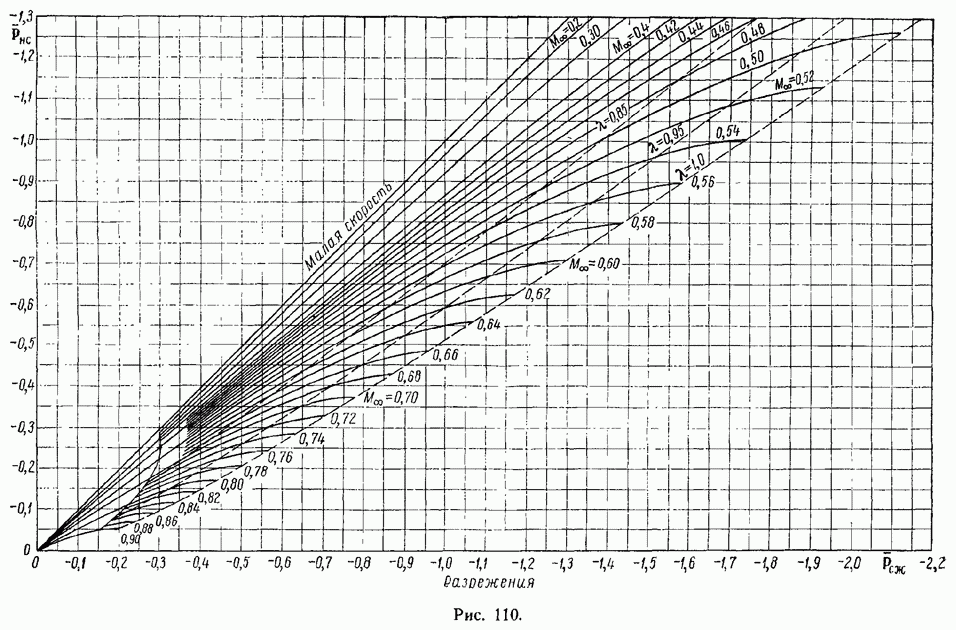
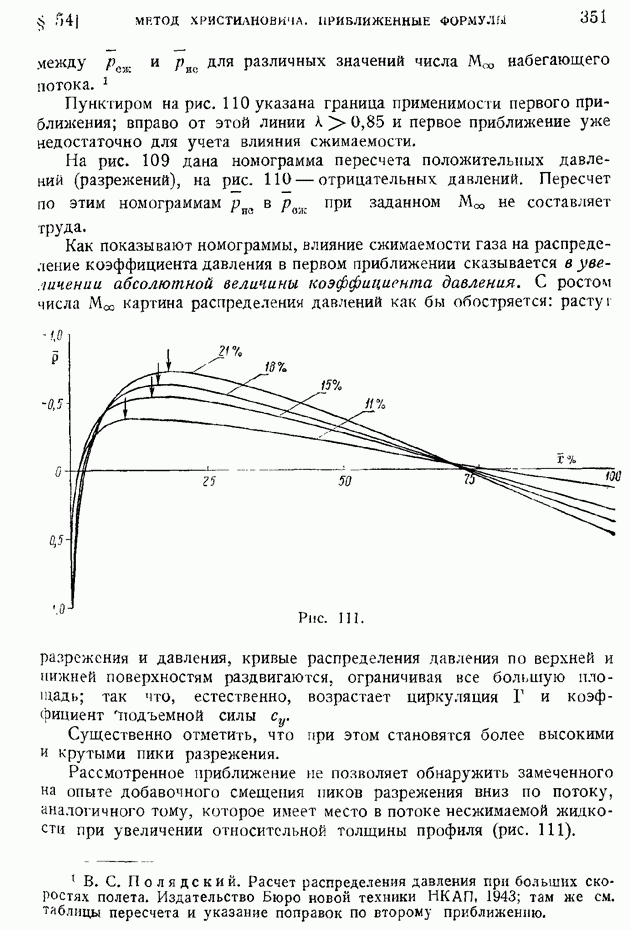
§ 100. Профильное сопротивление крыла. Разложение профильного сопротивления на сопротивление трения и сопротивление давлений. Обратное влияние пограничного слоя на распределение давлений по поверхности обтекаемого профиля
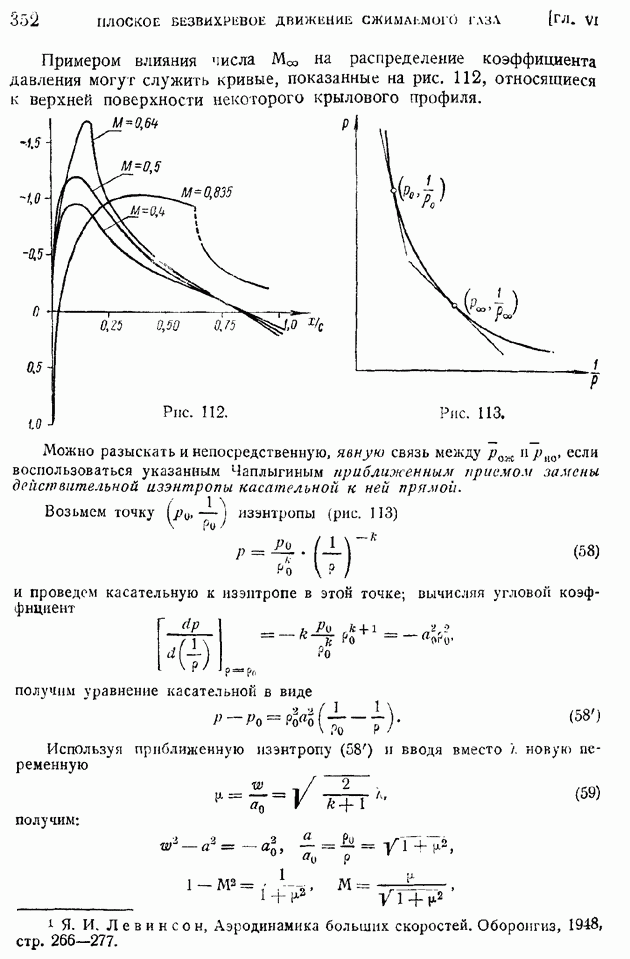
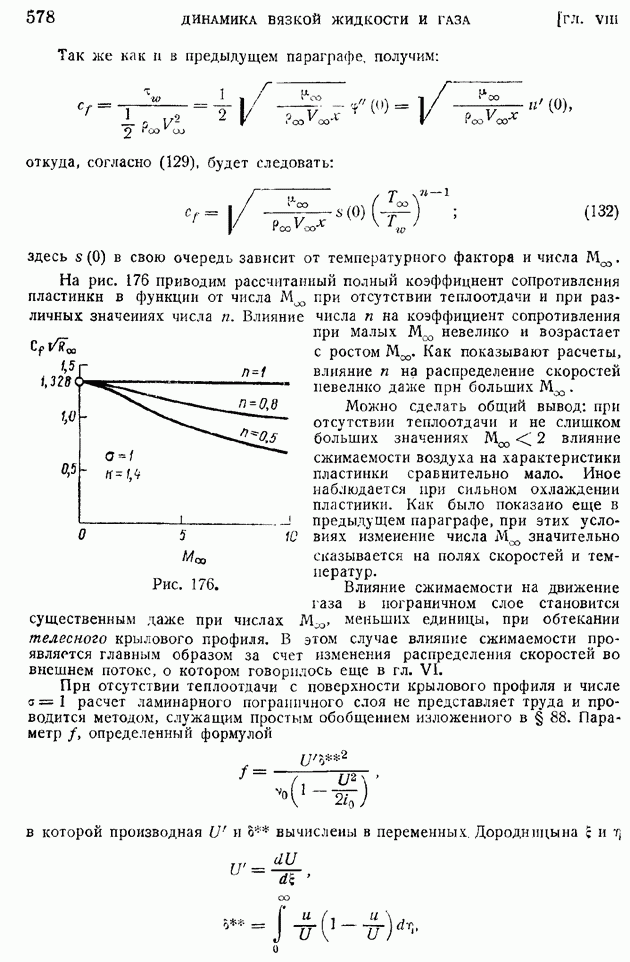
Изложенные в предыдущих параграфах упрощенные методы расчета турбулентного пограничного слоя позволяют с достаточной для практики точностью рассчитать отнесенное к единице длины вдоль размаха сопротивление цилиндрического крыла при плоском его обтекании безграничным потоком. Это сопротивление крылового профиля называют профильным сопротивлением.
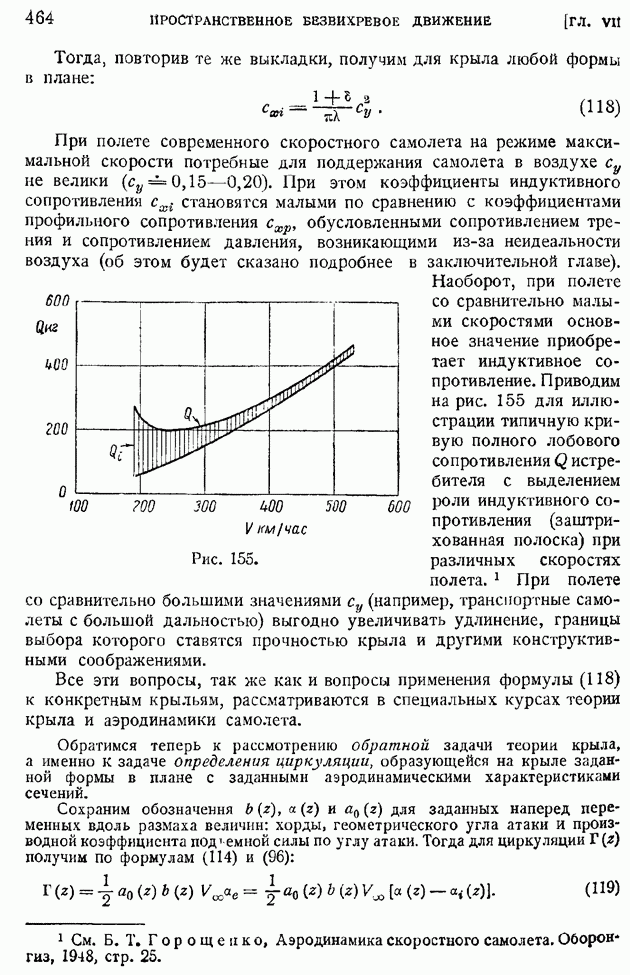
Профильное сопротивление крыла конечного размаха можно получить, складывая профильные сопротивления "плоских" сечений крыла (в смысле, разъясненном в гл. VII). Полное лобовое сопротивление крыла конечного размаха равно сумме профильного и индуктивного его сопротивлений. На режиме максимальной скорости самолета индуктивное сопротивление крыла, пропорциональное квадрату коэффициента подъемной силы, невелико, и главную часть лобового сопротивления крыла составляет его профильное сопротивление (вспомнить диаграмму сопротивлений, показанную на рис. 155, и разъяснения к ней, изложенные в § 74 гл. VII).
Прежде чем перейти к изложению методов расчета профильного сопротивления, введем понятие о двух основных составляющих профильного сопротивления: сопротивлении трения и сопротивлении давлений.
Все силы, приложенные к элементам поверхности крыла со стороны набегающего на него безграничного потока, можно разбить на касательные и нормальные.
Первые из этих сил обыкновенно называют, несколько обобщая это понятие, "трением". Такой термин полностью соответствует лишь случаю "гладкой" (в аэродинамическом, как было указано в § 95, смысле этого слова) стенки крыла, когда касательные силы определяются действительно трением в жидкости — вязкостью.
Мы сохраним тот же термин и для случая шероховатой стенки, понимая в этом случае под напряжением "трения" отнесенную к единице площади крыла сумму сил сопротивлений отдельных бугорков шероховатости.
Проекцию главного вектора приложенных к крылу касательных на направление потока на бесконечности будем называть сопротивлением трения.
Нормальные силы давления потока на поверхность крыла образуют в своей совокупности главный вектор сил давлений, проекция которого на направление потока на бесконечности называется сопротивлением давлений.
Профильное сопротивление крыла представляется суммой сопротивления трения и сопротивления давлений.
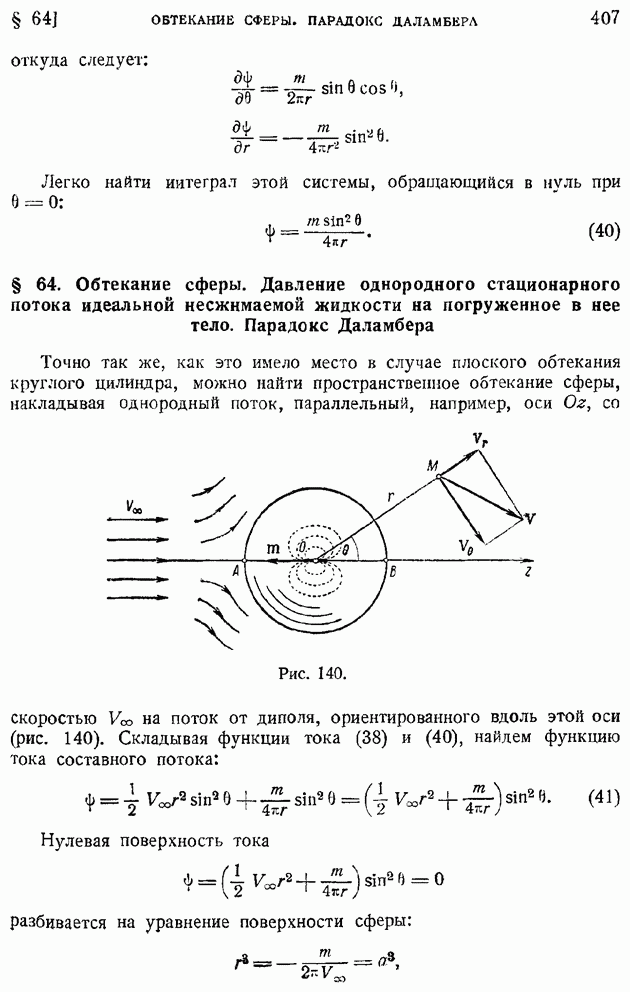
В случае безвихревого обтекания тела конечного размера безграничным потоком идеальной жидкости сопротивление давлений равняется нулю; это составляет, как известно, содержание парадокса Даламбера.
В реальной вязкой жидкости парадокс Даламбера не имеет места. Для случая очень малых рейнольдсовых чисел в этом можно было убедиться на примере задачи Стокса об обтекании шара. Для течений с большими рейнольдсовыми числами, при наличии пограничного слоя, вопрос становится менее ясным. Основное свойство пограничного слоя передавать без искажений на стенку крыла давления внешнего, безвихревого потока может навести на мысль, что парадокс Даламбера для движений с пограничным слоем сохраняет свою силу. Если бы распределение давлений во внешнем потоке в точности совпадало с тем, которое получается при безотрывном безвихревом обтекании крыла идеальной жидкостью, то сопротивление давлений, действительно, равнялось бы нулю. Однако на самом деле наблюдается следующее явление. Линии тока, вследствие подтормаживающего влияния стенки, оттесняются от поверхности крыла. Такое искажение картины течения приводит к нарушению идеального распределения давлений по поверхности крыла.
Пограничный слой, таким образом, оказывает обратное влияние на внешний поток, а не только управляется внешним потоком, как предполагалось до сих пор. Строго говоря, вообще нельзя задавать наперед распределение давлений или скоростей во внешнем потоке, так как это распределение зависит от развития пограничного слоя, а следовательно, является функцией рейнольдсова числа и других факторов обтекания (например, шероховатости поверхности). Практически, если тело обтекается без срывов и рейнольдсовы числа достаточно велики, а изменения их происходят не в слишком большом диапазоне, то пренебрежение обратным влиянием пограничного слоя на распределение давлений и скоростей во внешнем потоке оказывается допустимым.
Следует подчеркнуть, что обратное влияние пограничного слоя на внешнее обтекание особенно сильно проявляется на тех участках пограничного слоя, где слой наиболее толст, например, вблизи хвостика крыла.
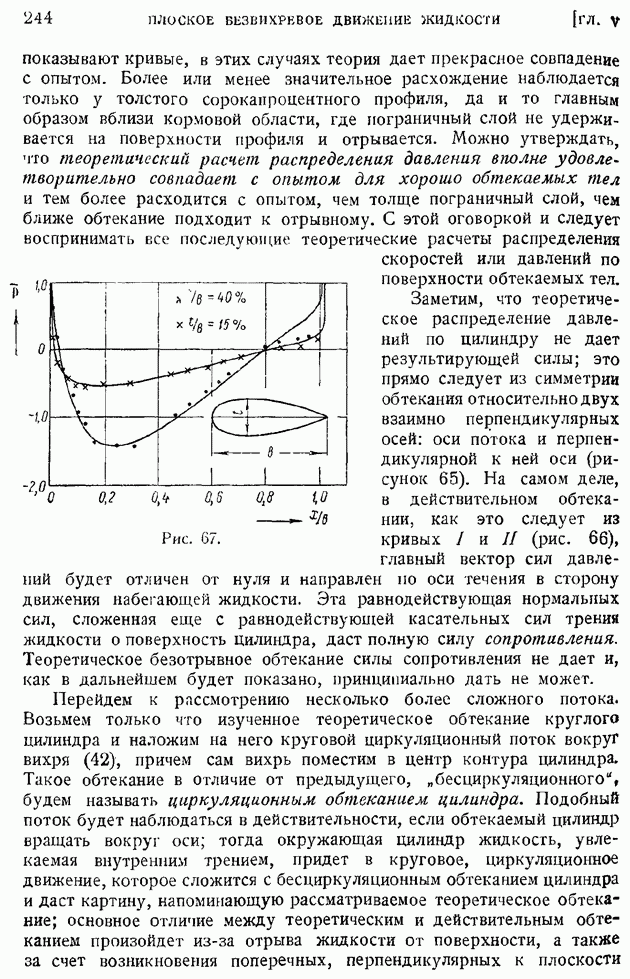
С этой точки зрения полезно вернуться к рассмотрению распределений давлений по симметричному крыловому профилю, показанных на рис. 67 гл. V. Если на пятнадцатипроцентном профиле экспериментальные точки (крестики) вблизи хвостика лишь слабо отходят от расчетной теоретической кривой, то на сорокапроцентном профиле отклонения измеренных (на рисунке — точки) давлений от рассчитанных уже очень велики. Особенно разительно сказывается обратное влияние пограничного слоя на внешний поток в случае плохо обтекаемых тел. Для иллюстрации этого факта достаточно вспомнить кривые распределения давления по круглому цилиндру,
показанные на рис. 66 гл. V. В этом случае только непосредственно в лобовой части цилиндра, не далее чем на 30—40° по обе стороны от передней критической точки, можно говорить о совпадении теоретического расчета с опытом. На остальной части поверхности цилиндра распределение давлений, рассчитанное по теории безвихревого обтекания, не имеет ничего общего с экспериментальным.
Не удивительно, что в этом случае парадокс Даламбера не выполняется, и лобовое сопротивление цилиндра определяется почти целиком сопротивлением давлений, сопротивление же трения — незначительно.
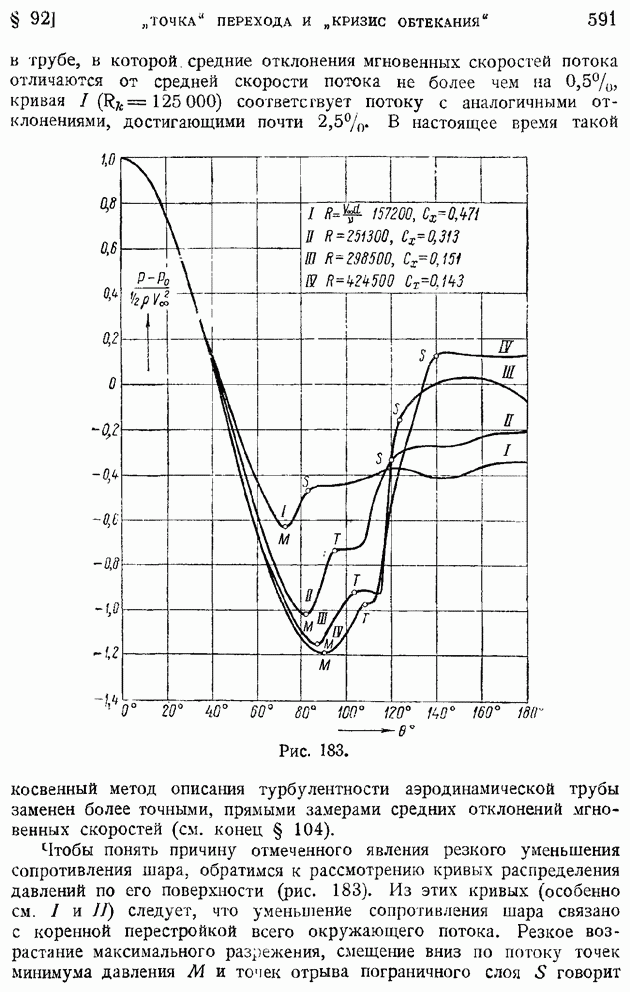
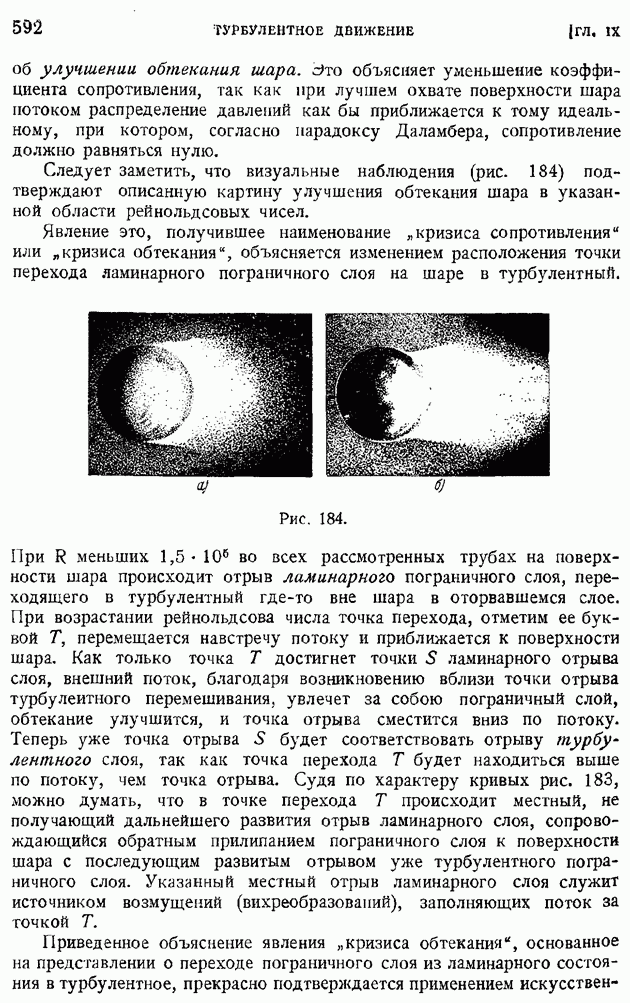
Такую же картину обратного влияния пограничного слоя на внешнее обтекание имеем и в случае шара (рис. 183). И в этом случае распределение давления оказывается сильно зависящим от рейнольдсова числа. Особенно это, конечно, сказывается вблизи "кризиса обтекания".
Распределение давлений, показанное на рис. 67, приводит к заключению, что при продольном (с нулевым углом атаки) обтекании симметричного пятнадцатипроцентного профиля сопротивление давлений будет невелико и основное значение в общем профильном сопротивлении имеет сопротивление трения.

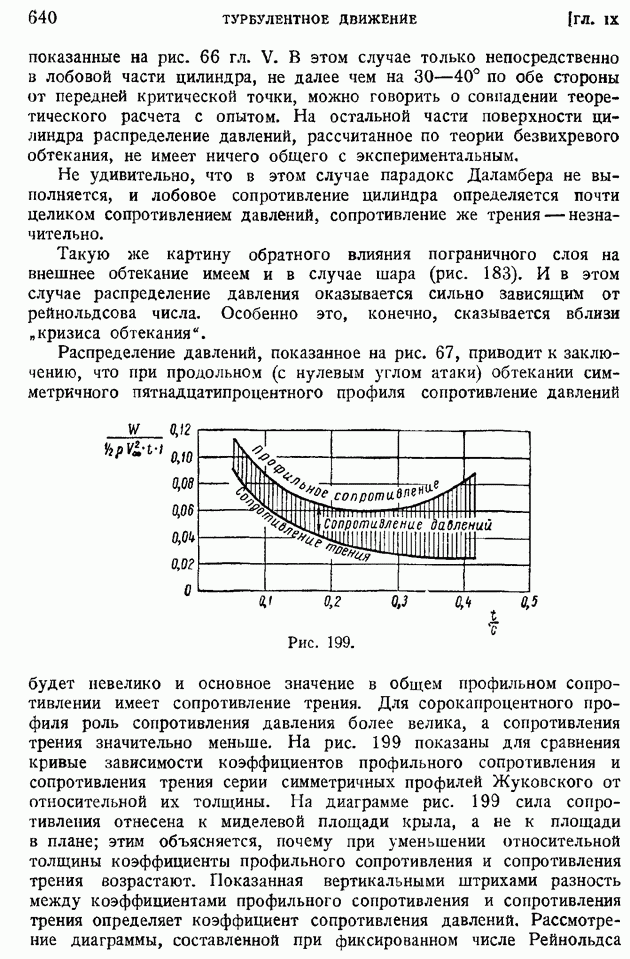
Рис. 199.
Для сорокапроцентного профиля роль сопротивления давления более велика, а сопротивления трения значительно меньше. На рис. 199 показаны для сравнения кривые зависимости коэффициентов профильного сопротивления и сопротивления трения серии симметричных профилей Жуковского от относительной их толщины. На диаграмме рис. 199 сила сопротивления отнесена к миделевой площади крыла, а не к площади в плане; этим объясняется, почему при уменьшении относительной толщины коэффициенты профильного сопротивления и сопротивления трения возрастают. Показанная вертикальными штрихами разность между коэффициентами профильного сопротивления и сопротивления трения определяет коэффициент сопротивления давлений. Рассмотрение диаграммы, составленной при фиксированном числе Рейнольдса
 Приводит к отчетливому выводу о росте роли сопротивления давления с увеличением относительной толщины профиля и, наоборот, о повышении значения сопротивления трения при переходе к тонким профилям.
Приводит к отчетливому выводу о росте роли сопротивления давления с увеличением относительной толщины профиля и, наоборот, о повышении значения сопротивления трения при переходе к тонким профилям.
Как показывают опыты, сопротивление давлений хорошо обтекаемого крылового профиля убывает с ростом рейнольдсова числа, что и естественно, так как при возрастании рейнольдсова числа толщина пограничного слоя уменьшается и внешний поток приближается к безвихревому обтеканию профиля идеальной жидкостью.
Обратное влияние пограничного слоя на внешний поток поддается не только качественному объяснению, но и количественной оценке. Поскольку в дальнейшем это не приведет к большому усложнению, будем считать жидкость не только вязкой, но и сжимаемой.

Рис. 200.
Рассмотрим какую-нибудь действительную линию тока (рис. 200а, сплошная линия), приходящую в точку  данного сечения
данного сечения  пограничного слоя и совпадающую с ней в бесконечном удалении впереди тела, и показанную на рис. 200а пунктиром линию тока безвихревого потока идеальной жидкости. Отрезок
пограничного слоя и совпадающую с ней в бесконечном удалении впереди тела, и показанную на рис. 200а пунктиром линию тока безвихревого потока идеальной жидкости. Отрезок  представляет подлежащее определению смещение действительной линии тока по отношению к идеальной. Из условия одинаковости массового расхода жидкости в сравниваемых движениях сквозь сечения
представляет подлежащее определению смещение действительной линии тока по отношению к идеальной. Из условия одинаковости массового расхода жидкости в сравниваемых движениях сквозь сечения  являющегося следствием совпадения обеих линий тока вдалеке от тела, заключим, что (через
являющегося следствием совпадения обеих линий тока вдалеке от тела, заключим, что (через  обозначены плотность и продольная скорость на внешней границе слоя)
обозначены плотность и продольная скорость на внешней границе слоя)

при составлении правой части этого равенства принято во внимание, что на протяжении малой толщины слоя плотность и скорость в безвихревом потоке идеальной жидкости могут быть приняты постоянными. Согласно последнему равенству, искомое смещение линии тока
и точке  с координатой у будет равно:
с координатой у будет равно:

На поверхности обтекаемого тела  смещение линии тока исчезает; у обоих сравниваемых потоков — действительного и идеального безвихревого — общая нулевая линия тока. При удалении от поверхности крыла смещения действительных линий тока по отношению к идеальным возрастают.
смещение линии тока исчезает; у обоих сравниваемых потоков — действительного и идеального безвихревого — общая нулевая линия тока. При удалении от поверхности крыла смещения действительных линий тока по отношению к идеальным возрастают.
На границе пограничного слоя  величина смещения достигает своего максимального значения
величина смещения достигает своего максимального значения

Если бы жидкость была несжимаема  то это смещение линии тока было бы равно известной уже по предыдущему "толщине вытеснения":
то это смещение линии тока было бы равно известной уже по предыдущему "толщине вытеснения":

Правую часть формулы (82) естественно рассматривать как обобщение понятия толщины вытеснения 2 на случай сжимаемой жидкости Итак, смещения действительных линий тока относительно линий тока безвихревого обтекания тела идеальной жидкостью определяются интегралами вида (81); на внешней границе пограничного слоя эти смещения равны по величине толщине вытеснения  . Из сказанного становится понятным происхождение термина "толщина вытеснения". Полученный результат, очевидно, одинаково применим как для ламинарного, так и для турбулентного движения.
. Из сказанного становится понятным происхождение термина "толщина вытеснения". Полученный результат, очевидно, одинаково применим как для ламинарного, так и для турбулентного движения.
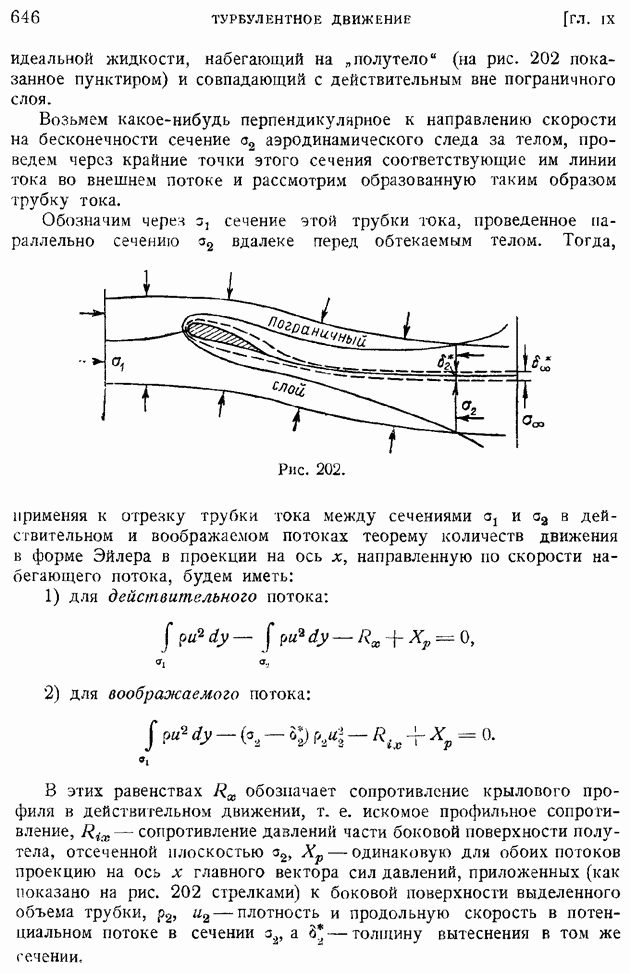
Пользуясь определением толщины вытеснения, докажем, что действительное распределение давления по поверхности крылового профиля при плоском его обтекании вязким сжимаемым газом совпадает с распределением давления при безвихревом обтекании идеальным газом полутела (рис. 201), образованного наращиванием на профиль крыла и по обе стороны от нулевой линии тока в его следе толщины вытеснения, рассчитанной по действительному распределению давления.
Для подтверждения правильности только что высказанного положения предположим, что задано плоское обтекание крылового профиля реальным (вязким и сжимаемым) газом, сопровождаемое образованием на теле пограничного слоя (а за телом — аэродинамического следа), толщина которого предполагается малой по сравнению с продольными размерами тела.
Наряду с этим действительным потоком в пограничном слое рассмотрим в той же области воображаемый потенциальный поток (в общем случае сжимаемой жидкости), который являлся бы непрерывным продолжением действительного внешнего потенциального потока на область, занятую пограничным слоем. В силу принятого предположения о малости толщины пограничного слоя, давления в построенном таким образом потенциальном потоке, а следовательно, и продольные скорости будут совпадать с давлениями и скоростями в потоке на внешней границе области пограничного слоя. Вместо характерного для движения в пограничном слое убывания скорости от некоторого значения на внешней границе слоя до нулевого значения на поверхности крыла в эквивалентном по давлениям потенциальном потоке повсюду на данной нормали будет одинаковая скорость, равная скорости на внешней границе слоя.
Отсюда сразу следует, что рассматриваемый потенциальный поток, являющийся непрерывным продолжением внешнего потенциального потока и поэтому обладающий тем же массовым расходом через сечение рассматриваемой струйки, что и действительный поток в пограничном слое, не сможет заполнить всю область пограничного слоя (включая в понятие пограничного слоя и аэродинамический след).
Для определения новой области течения рассмотрим (рис. 2006) некоторую точку  сечения пограничного слоя. Отметим сплошной линией действительную линию тока, проходящую через точку
сечения пограничного слоя. Отметим сплошной линией действительную линию тока, проходящую через точку  а пунктиром, идущим в некоторую точку
а пунктиром, идущим в некоторую точку  на той же нормали, — линию тока потенциального потока, совпадающую с только что указанной действительной вдалеке перед телом.
на той же нормали, — линию тока потенциального потока, совпадающую с только что указанной действительной вдалеке перед телом.
Обратим внимание на отличие фигурирующего воображаемого потенциального потока, совпадающего с действительным повсюду вне пограничного слоя, от ранее рассмотренного потенциального потока, имеющего с действительным лишь общую нулевую линию тока.
Как видно из рис. 200, действительные линии тока располагаются в одном случае выше идеальных, в другом, наоборот, ниже.
Составляя условие одинаковости расхода в действительном и воображаемом потенциальном потоках сквозь сечения  и
и  отсчитанные от внешней границы пограничного слоя, получим:
отсчитанные от внешней границы пограничного слоя, получим:

так что расстояние между сравниваемыми линиями тока в действительном и воображаемом движениях будет равно:

На границе пограничного слоя  и обе линии тока совпадут. При углублении в пограничный слой величина
и обе линии тока совпадут. При углублении в пограничный слой величина  будет возрастать, а воображаемые линии тока оттесняться. Когда, наконец, действительная линия тока совпадет с поверхностью крылового профиля, линия тока воображаемого безвихревого потока окажется оттесненной от поверхности на расстояние
будет возрастать, а воображаемые линии тока оттесняться. Когда, наконец, действительная линия тока совпадет с поверхностью крылового профиля, линия тока воображаемого безвихревого потока окажется оттесненной от поверхности на расстояние

равное «толщине вытеснения". Таким образом, основная, нулевая, линия тока действительного движения, разветвляющаяся в передней критической точке контура тела и в дальнейшем проходящая сквозь аэродинамический след тела, должна быть в воображаемом безвихревом потоке заменена на некоторое бесконечное "полутело", образованное наращиванием по нормали на нулевую линию тока величины "толщины вытеснения", рассчитанной по действительному распределению давления.
На рис. 201 показаны сплошной линией основной профиль и нулевая линия тока в следе за ним, а пунктиром — контур полутела, обтекание которого потенциальным потоком эквивалентно по распределению давления обтеканию профиля реальной жидкостью. Воображаемый безвихревой поток, входящий в пограничный слой через внешнюю его границу (на рисунке не показанную) с теми же скоростями, что и действительный ноток, но в дальнейшем не подвергающийся действию торможения трением, имеет виутри пограничного слоя большие скорости, чем действительный поток. Приэтом воображаемый поток не может заполнить всю область пограничного слоя, часть плоскости между нулевой линией тока и границей полутела в воображаемом течении остается не заполненной жидкостью и линия  является граничной линией тока. Таким образом, правильность высказанного ранее суждения о количественной стороне обратного влияния пограничного слоя на распределение давлений во внешнем потоке подтверждается.
является граничной линией тока. Таким образом, правильность высказанного ранее суждения о количественной стороне обратного влияния пограничного слоя на распределение давлений во внешнем потоке подтверждается.

Рис. 201.
Практически определение формы полутела и распределения давления по его поверхности следует вести по методу последовательных приближений, принимая, например, в первом приближении распределение давления соответствующим обтеканию крылового профиля и хвостовой нулевой линии тока потенциальным потоком с выполнением условия плавного обтекания задней кромки по гипотезе Жуковского.
Как уже было указано в конце § 97, приближенное определение  по теоретическому распределению
по теоретическому распределению  в задней критической точке крылового профиля, где скорость обращается в нуль, а давление восстанавливается до давления в покоящейся жидкости, становится невозможным. Опираясь на только что доказанную теорему, утверждающую, что в действительности, благодаря оттеснению линий тока указанное полное восстановление давления фактически не происходит, можем при расчете первого приближения заменить теоретическое распределение скоростей вблизи задней кромки профиля, проведенной "на глаз", прямой, экстраполирующей распределение скоростей в кормовой части профиля в точку, совпадающую с задней кромкой.
в задней критической точке крылового профиля, где скорость обращается в нуль, а давление восстанавливается до давления в покоящейся жидкости, становится невозможным. Опираясь на только что доказанную теорему, утверждающую, что в действительности, благодаря оттеснению линий тока указанное полное восстановление давления фактически не происходит, можем при расчете первого приближения заменить теоретическое распределение скоростей вблизи задней кромки профиля, проведенной "на глаз", прямой, экстраполирующей распределение скоростей в кормовой части профиля в точку, совпадающую с задней кромкой.
Используя в первом приближении теоретическое распределение давления на поверхности тела и хвостовой нулевой линии тока, соответствующее гипотезе Жуковского и исправленное только что указанным приемом вблизи задней кромки, определим по теории пограничного слоя толщину вытеснения, а затем и форму полутела в первом приближении. После этого найдем теоретическое распределение давления на поверхности полутела, новое распределение толщины вытеснения и т. д. Такого рода расчеты проводились неоднократно, но практика показала, что они связаны с исключительно трудоемкими вычислениями.
Определение сопротивления давления как проекции главного вектора сил давлений (исправленных согласно указанному выше или фактически замеренных путем дренажа поверхности крыла) на направление набегающего потока крайне неточно, так как приводит к вычислению малой разности двух сравнительно больших величин. Сопротивление давлений точнее всего определяется как разница между профильным сопротивлением и сопротивлением трения.
Доказанная только что теорема об обратном влиянии пограничного слоя на внешний поток и основанный на ней метод введения поправок на теоретическое распределение давлений устраняет недостаток формул, предложенных в § 98 и 99 для расчета элементов турбулентного пограничного слоя, и позволяет с успехом вычислять сопротивление трения.
Та же теорема оказывается полезной и для определения профильного сопротивления по излагаемому ниже приближенному методу.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Предмет механики жидкости и газа. Основные свойства «макромодели» жидкости и газа: сплошность и подвижность
- § 2. Основные методы механики жидкости и газа. Области применения и главнейшие задачи
- § 3. Краткий очерк исторического развития механики жидкости и газа. От гидромеханики древних до установления воззрений ньютонианской эпохи
- § 4. Эпоха Эйлера и Бернулли. Гидроаэродинамика в XIX в.
- § 5. Современный этап развития механики жидкости и газа
- ГЛАВА I. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
- § 6. Поле физической величины. Скалярное и векторное поля. Поверхности уровня. Векторные линин и трубки
- § 7. Мера однородности поля в данном направлении и в дайной точке. Градиевт скалярного поля и дифференциальный тензор векторного поля как меры неоднородности поля
- § 8. Задание движения сплошной среды. Поле скоростей. Линии тока и траектории
- § 9. Поле ускорений. Разложение ускорения частицы на локальную и конвективную составляющие
- § 10. Скоростное поле сплошной среды в окрестности данной точки. Угловая скорость и вихрь. Тензор скоростей деформаций и его компоненты
- § 11. Скорость объемного расширения жидкости. Интегральные представления дифференциальных операторов поля. Основные интегральные формулы
- § 12. Вихревые линии и трубки. Вторая теорема Гельмгольца. Интенсивность вихревой трубки
- § 13. Выражение интенсивности вихревой трубки через циркуляцию вектора по контуру, охватывающему трубку. Теорема об изменении циркуляции скорости во времени
- ГЛАВА II. ОСНОВНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ И РАВНОВЕСИЯ СПЛОШНОЙ СРЕДЫ
- § 14. Распределение массы в сплошной среде. Плотность и удельный вес. Напряжения. Тензор напряженности и его симметричность
- § 15. Общие уравнения динамики сплошной среды. Уравнение неразрывности. Уравнения динамики в напряжениях
- § 16. Тепловые явления в жидкостях и газах. Закон сохранения энергии и уравнение баланса энергии
- § 17. Общие уравнения равновесного состояния жидкости и газа. Равновесие воздуха в атмосфере. Приближенные барометрические формулы. Стандартная атмосфера
- § 18. Равновесие несжимаемой жидкости. Уравнение поверхности раздела. Равновесие вращающейся жидкости
- § 19. Давление тяжелой несжимаемой жидкости на поверхность тела. Сила и момент, приложенные к телу, плавающему в тяжелой жидкости. Случай вращающейся жидкости
- ГЛАВА III. ДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ И ГАЗА. ОСНОВНЫЕ УРАВНЕНИЯ И ОБЩИЕ ТЕОРЕМЫ
- § 20. Идеальная жидкость. Основные уравнения движения
- § 21. Закон сохранения энергии в движущейся идеальной жидкости. Адиабатическое движение. Сохранение энтропии
- § 22. Эйлерово представление конвективного изменения объемного интеграла. Перенос величины сквозь контрольную поверхность
- § 23. Эйлерова форма законов сохранения массы и энергии, теоремы количеств движения и момента количеств движения при стационарном движении идеальной жидкости
- § 24. Теорема об изменении кинетической энергии. Работа и мощность внутренних сил. Эйлерова форма уравнения изменения кинетической энергии
- § 25. Теорема Бернулли о сохранении полной механической энергии при стационарном баротропном движении идеальной жидкости и газа
- ГЛАВА IV. ОДНОМЕРНЫЙ ПОТОК ИДЕАЛЬНОЙ ЖИДКОСТИ
- § 26. Одномерное течение идеальной сжимаемой жидкости. Линеаризированные уравнения. Скорость распространения малых возмущений в жидкости или газе
- § 27. Изотермическая и адиабатическая скорости звука. «Конус возмущений» при сверхзвуковом движении источника возмущения. Число M и его связь с углом конуса возмущений
- § 28. Распространение непрерывных возмущений конечной интенсивности. Характеристики. Образование разрывной ударной волны
- § 29. Стоячая ударная волна или скачок уплотнения. Ударная адиабата
- § 30. Критические величины в одномерном потоке газа. Связь между скоростями до и после скачка. Изменение давления, плотности и температуры в скачке уплотнения
- § 31. Скорость распространения ударной волны. Спутное движение газа за ударной волной
- § 32. Влияние интенсивности скачка уплотнения на сжатие газа. Измерение скоростей и давлений в до- и сверхзвуковых потоках
- § 33. Одномерное движение газа по трубе переменного сечения. Истечение из резервуара большой емкости сквозь сходящееся сопло
- § 34. Одномерное течение в сопле Лаваля. Движение газа с притоком тепла
- ГЛАВА V. БЕЗВИХРЕВОЕ ДВИЖЕНИЕ ЖИДКОСТИ. ПЛОСКОЕ ДВИЖЕНИЕ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 35. Сохранение циркуляции скорости в потоке идеальной жидкости. Теорема Кельвина и Лаграижа. Безвихревое движение. Потенциал скоростей
- § 36. Интеграл Лагранжа — Коши уравнений безвихревого движения. Теорема Бернулли. Некоторые общие свойства безвихревого движения идеальной несжимаемой жидкости в односвязной области
- § 37. Плоское безвихревое движение несжимаемой жидкости. Потенциал скоростей и функция тока. Применение функций комплексного переменного. Комплексный потенциал и сопряженная скорость
- § 38. Построение полей течения по заданной характеристической Функции. Простейшие плоские потоки и их наложение
- § 39. Бесциркуляционное и циркуляционное обтекания круглого цилиндра
- § 40. Применение криволинейных координат. Бесциркуляционное и циркуляционное обтекания эллиптического цилиндра и пластинки. Задача Жуковского об обтекании решетки пластин.
- § 41. Плоское движение с отрывом струй. Разрывное обтекание пластинки и протекание жидкости сквозь отверстие
- § 42. Прямая задача в теории плоского движения идеальной несжимаемой жидкости. Применение метода конформных отображений. Гипотеза Чаплыгина о безотрывном обтекании задней кромки профиля. Формула циркуляции
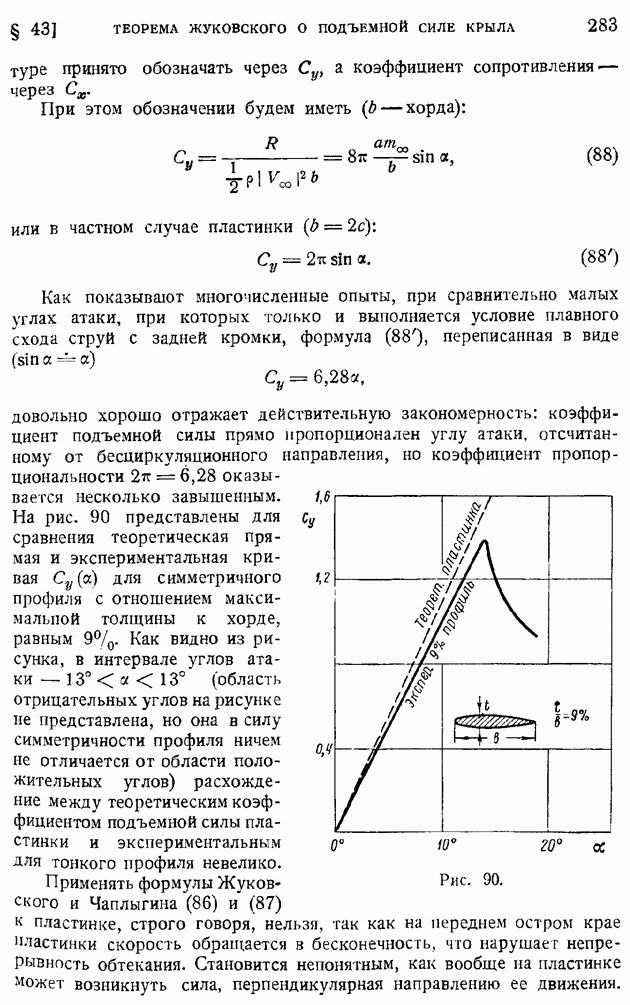
- § 43. Теорема Жуковского о подъемной силе крыла. Зависимость подъемной силы от угла атаки. Коэффициент подъемной силы
- § 44. Применение метода комплексных переменных к выводу теоремы Жуковского. Формулы Чаплыгина для главного вектора и момента сил давления потока на крыло
- § 45. Выражение главного момента сил давления потока через коэффициенты конформного отображения. Фокус крыла. Независимость от угла атаки момента относительно фокуса. Парабола устойчивости
- § 46. Частные случаи конформного отображения крылового профиля на круг. Преобразование Жуковского-Чаплыгина. Теоретические крыловые профили
- § 47. Задача об обтекании слабо изогнутой дужки произвольной формы (теория тонкого крыла)
- § 48. Определение обтекания крылового профиля произвольной формы
- § 49. Обобщение теоремы Жуковского на случай плоской решетки с бесчисленным множеством профилей
- ГЛАВА VI. ПЛОСКОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ СЖИМАЕМОГО ГАЗА
- § 50. Основные уравнения плоского стационарного безвихревого движения сжимаемого газа. Линеаризированные уравнения
- 51. Линеаризированный до- и сверхзвуковой газовый поток вдоль волнистой стенки
- § 52. Тонкое крыло в линеаризированном до- и сверхзвуковом потоках. Влияние сжимаемости газа на коэффициент подъемной силы в дозвуковом потоке. Коэффициенты подъемной силы и волнового сопротивления при сверхзвуковом потоке
- § 53. Нелинеаризированные уравнения движения идеального сжимаемого газа. Переход в плоскость годографа. Уравнения Чаплыгина
- § 54. Метод С. А. Христиановича. Приближенные формулы учета влияния сжимаемости на распределение давления
- § 55. Критическое число M и его определение по заданному распределению давления в несжимаемом обтекании. Поведение коэффициента подъемной силы и момента при около- и закритических значениях числа M
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
- § 57. Нелинеаризированный сверхзвуковой поток. «Характеристики» уравнений плоского сверхзвукового потока. Линин возмущения и их основные свойства
- § 58. Обтекание выпуклого угла сверхзвуковым потоком. Влияние угла поворота струи на ее газодинамические элементы
- § 59. Сверхзвуковой поток внутри тупого угла. Косой скачок уплотнения. Связь между газодинамическими элементами до и за косым скачком
- ГЛАВА VII. ПРОСТРАНСТВЕННОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ
- § 60. Ортогональные криволинейные координаты в пространстве. Основные дифференциальные операторы поля в криволинейных координатах
- § 61. Потенциал скоростей. Поле источника и диполя. Непрерывное распределение источников и диполей. Ньютонов потенциал. Потенциал простого и двойного слоев
- § 62. Поле скоростей вокруг заданной системы вихрей. Формула Био — Савара. Потенциал скоростей замкнутой вихревой нити. Аналогия с потенциалом двойного слоя
- § 63. Функция тока и ее связь с векторным потенциалом скоростей. Функции тока простейших течений
- § 64. Обтекание сферы. Давление однородного стационарного потока идеальной несжимаемой жидкости на погруженное в нее тело. Парадокс Даламбера
- § 65. Общие уравнения осесимметричного движения. Применение цилиндрических координат. Течение сквозь каналы
- § 66. Осесимметричное продольное обтекание тел вращения. Случай эллипсоида вращения
- § 67. Поперечное обтекание тел вращения. Пример эллипсоида вращения
- § 68. Продольное и поперечное обтекание тел вращения большого удлинения. Приближенные выражения граничных условий. Применение тригонометрических сумм для определения коэффициентов …
- § 69. Метод «особенностей». Применение непрерывно распределенных источников (стоков) и диполей для решения задачи о продольном и поперечном обтекании тел вращения
- § 70. Общий случай движения твердого тела сквозь несжимаемую идеальную жидкость. Определение потенциала скоростей. Главный вектор и главный момент сил давления потока на тело
- § 71. Коэффициенты «присоединенных масс». Свойство симметрии. «Присоединенная» кинетическая энергия. Определение «присоединенных масс» поступательно движущегося цилиндра, шара и эллипсоида
- § 72. Элементы теории крыла конечного размаха. Вихревая система крыла. Гипотеза плоских сечеиий. Геометрические и действительные углы атаки. Подъемная сила и «индуктивное сопротивление»
- § 73. Основные формулы теории «несущей линии». «Индуктивная скорость» и «индуктивный угол». Прямая задача определения подъемной силы и индуктивного сопротивления по заданному распределению циркуляции
- § 74. Крыло с минимальным индуктивным сопротивлением. Эллиптическое распределение циркуляции. Связь между коэффициентами индуктивного сопротивления и подъемной силы. Основное уравнение теории крыла и понятие о его интегрировании
- ГЛАВА VIII. ДИНАМИКА ВЯЗКОЙ ЖИДКОСТИ И ГАЗА
- § 75. Внутреннее трение и теплопроводность в жидкостях и газах. Законы Ньютона и Фурье. Влияние температуры на коэффициенты вязкости и теплопроводности. Число «сигма»
- § 76. Обобщение закона Ньютона на случай произвольного движения среды. Закон линейной связи между тензорами напряжений и скоростей деформации
- § 77. Общие уравнения движения вязкой жидкости. Динамические уравнения и уравнение баланса энергии. Граничные условия движения жидкости с треннем и теплопроводностью
- § 78. Понятие о подобии гидродинамических явлений. Безразмерные уравнения движения вязкой жидкости и газа. Условия подобия
- § 79. Ламинарное движение вязкой несжимаемой жидкости по цилиндрической трубе
- § 80. Обтекание шара при очень малых значениях числа Рейнольдса. Формула сопротивления шара по Стоксу и ее обобщения
- § 81. Вихревые линии в идеальной и вязкой жидкости. Сохраняемость вихревых линий при отсутствии внутреннего трения. Диффузия вихря в вязкой жидкости
- § 82. Одномерное прямолинейное движение сжимаемого вязкого газа. Движение внутри скачка уплотнения. Понятие о толщине скачка
- § 83. Работа внутренних сил и диссипация механической энергии в движущейся вязкой среде
- § 84. Обтекание тел жидкостью и газом при больших значениях числа Рейнольдса. Основные уравнения теории ламинарного пограничного слоя
- § 85. Ламинарный пограничный слой на пластинке, продольно обтекаемой несжимаемой жидкостью. Неизотермическое движение
- § 86. Ламинарный пограничный слой при степенном задании скорости внешнего потока
- § 87. Ламинарный пограничный слой в общем случае задания скорости внешнего потока. Применение уравнения импульсов для приближенного расчета ламинарного пограничного слоя
- § 88. Способы определения функций … Приближенный метод расчета ламинарного пограничного слоя
- § 89. Ламинарный пограничный слой на пластинке, продольно обтекаемой сжимаемым газом при больших скоростях. Случай линейной зависимости коэффициента вязкости от температуры (n = 1)
- § 90. Ламинарный пограничный слой на пластинке при любом законе связи между вязкостью и температурой и при числе … Обтекание крылового профиля потоком больших скоростей
- ГЛАВА IX. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ
- § 91. Переход ламинарного движения в турбулентное. Критическое рейнольдсово число
- § 92. Область и «точка» перехода. Явление «кризиса обтекания»
- § 93. Основные уравнения осреднеиного турбулентного движения. Тензор турбулентных напряжений
- § 94. Турбулентное движение жидкости в плоской и круглой трубе. Логарифмические формулы скоростей
- § 95. Формулы сопротивления гладких труб при турбулентном движении жидкости. Ламинарный подслой
- § 96. Влияние шероховатости стенок трубы на ее сопротивление. Предельные режимы течения. Режим установившейся шероховатости
- § 97. Турбулентный пограничный слой на продольно обтекаемой пластине. Сопротивление пластины
- § 98. Турбулентный пограничный слой на крыловом профиле при малом продольном перепаде давлений
- § 99. Турбулентный пограничный слой на крыловом профиле при значительных продольных перепадах давления
- § 100. Профильное сопротивление крыла. Разложение профильного сопротивления на сопротивление трения и сопротивление давлений. Обратное влияние пограничного слоя на распределение давлений по поверхности обтекаемого профиля
- § 101. Приближенные формулы профильного сопротивления крыла и крылового профиля в решетке
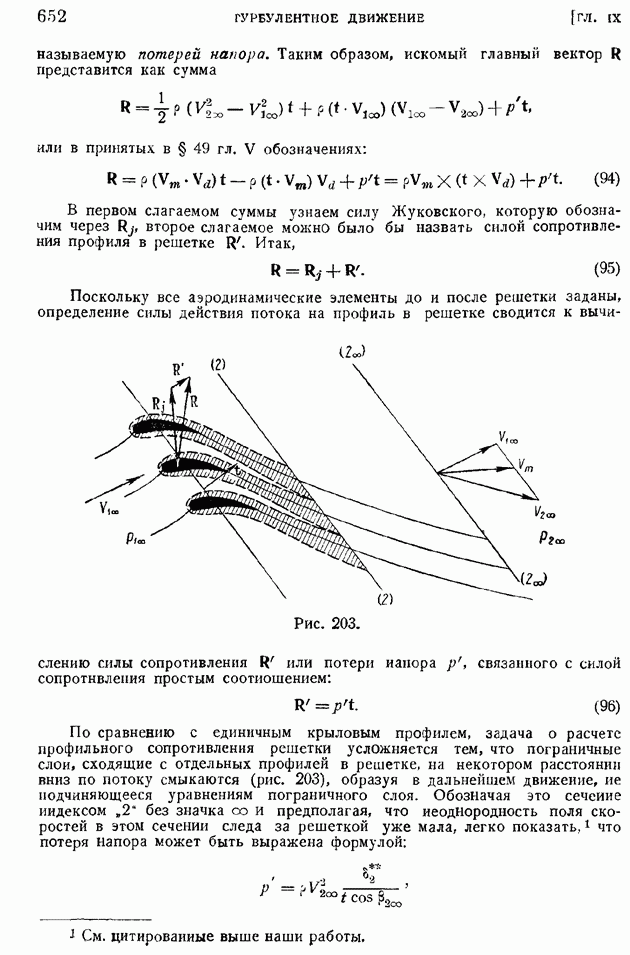
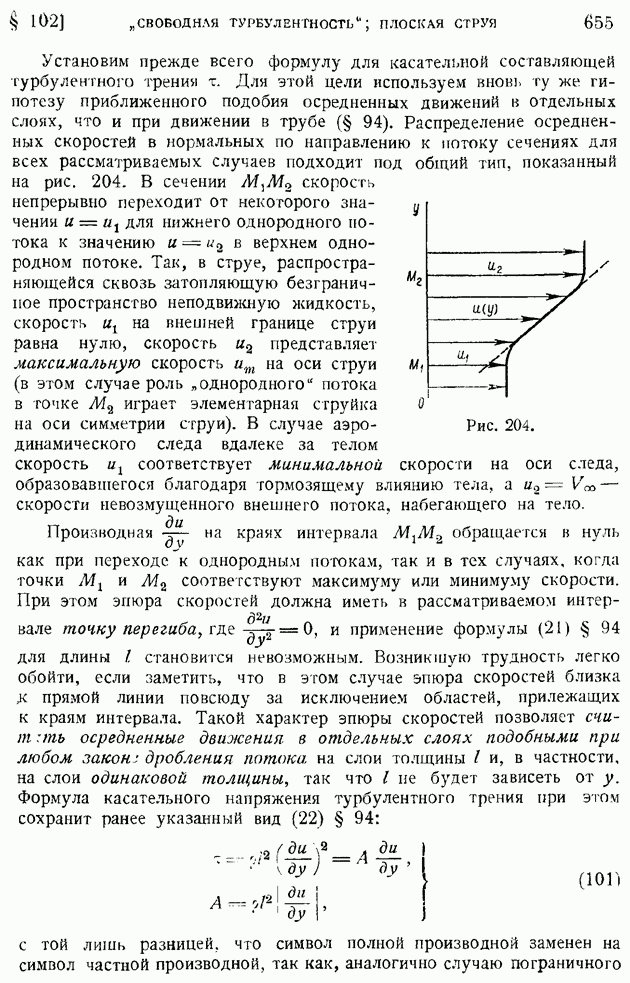
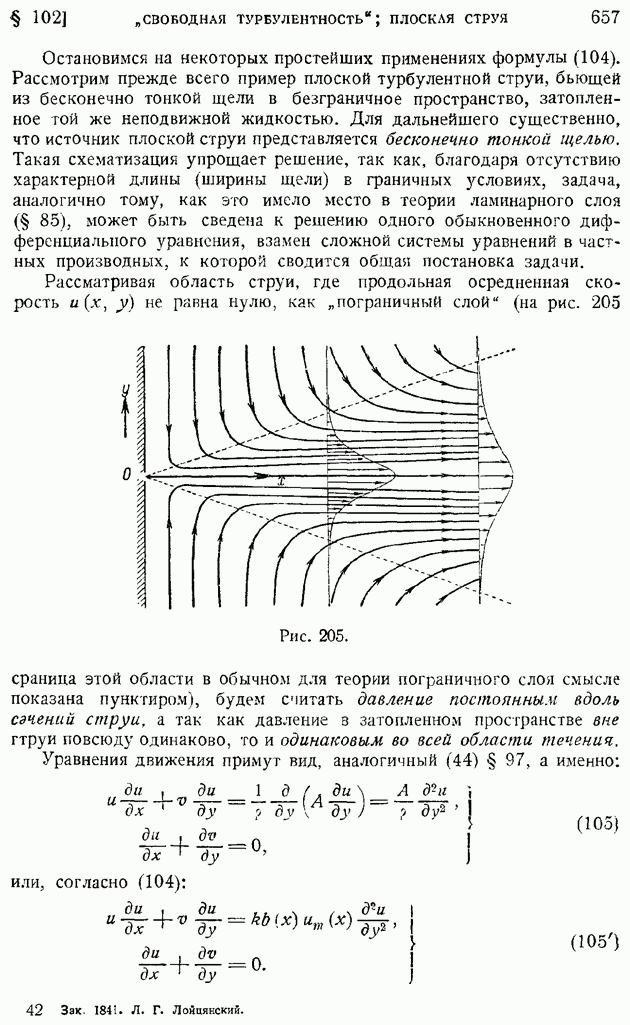
- § 102. Основные закономерности «свободной турбулентности». Плоская турбулентная струя в пространстве, заполненном той же жидкостью
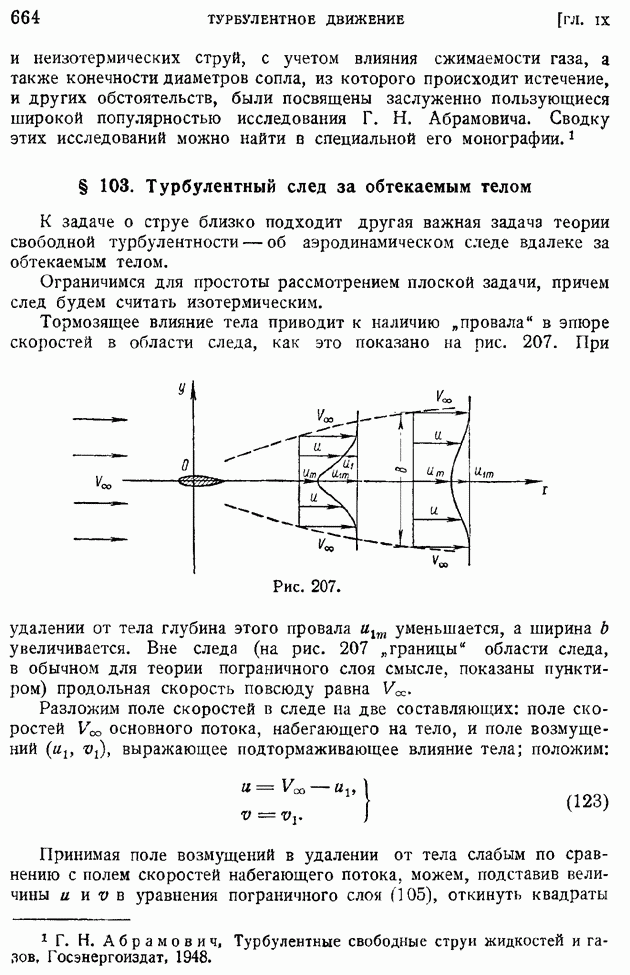
- § 103. Турбулентный след за обтекаемым телом
- § 104. Рассеяние турбулентных возмущений в жидкости. Случай изотропной и однородной турбулентности. Закон сохранения момента возмущений