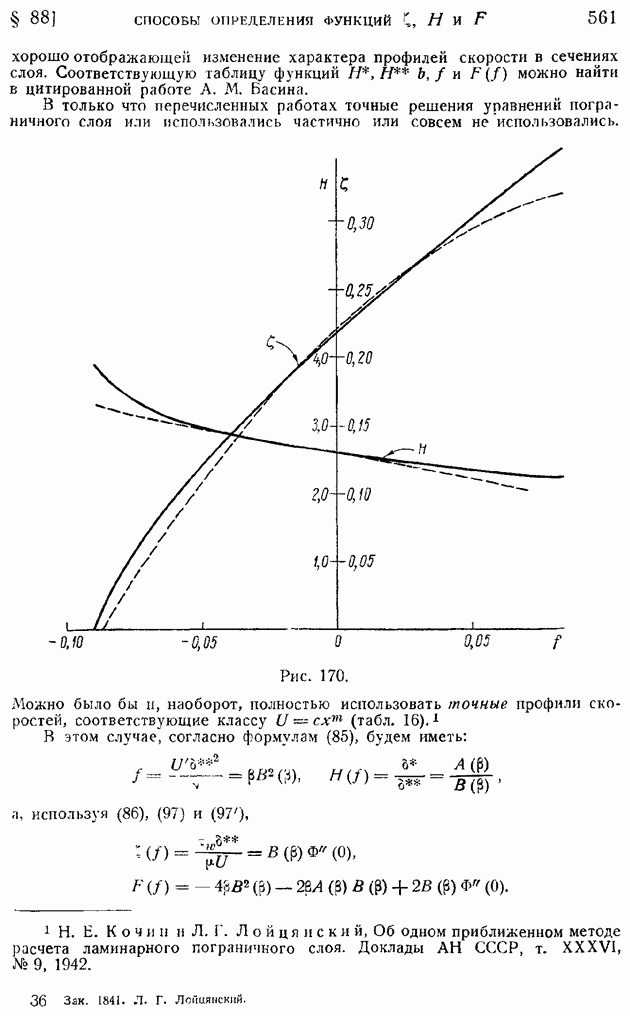| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
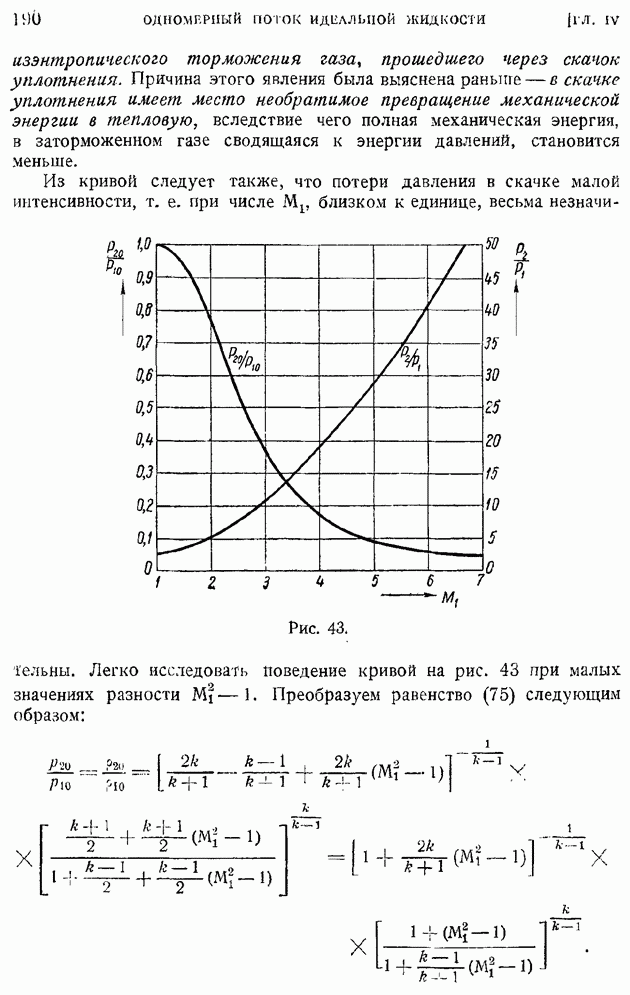
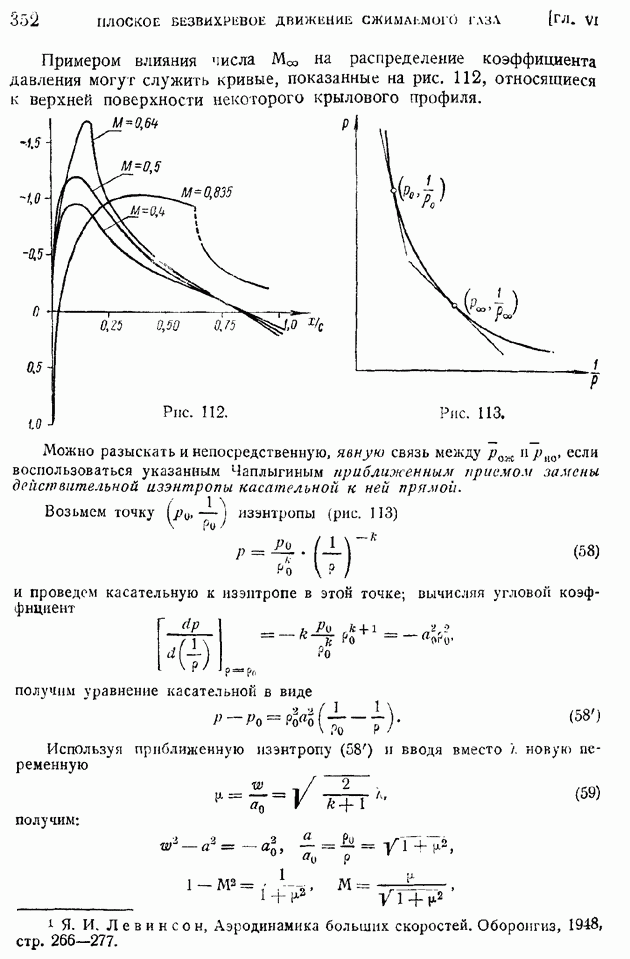
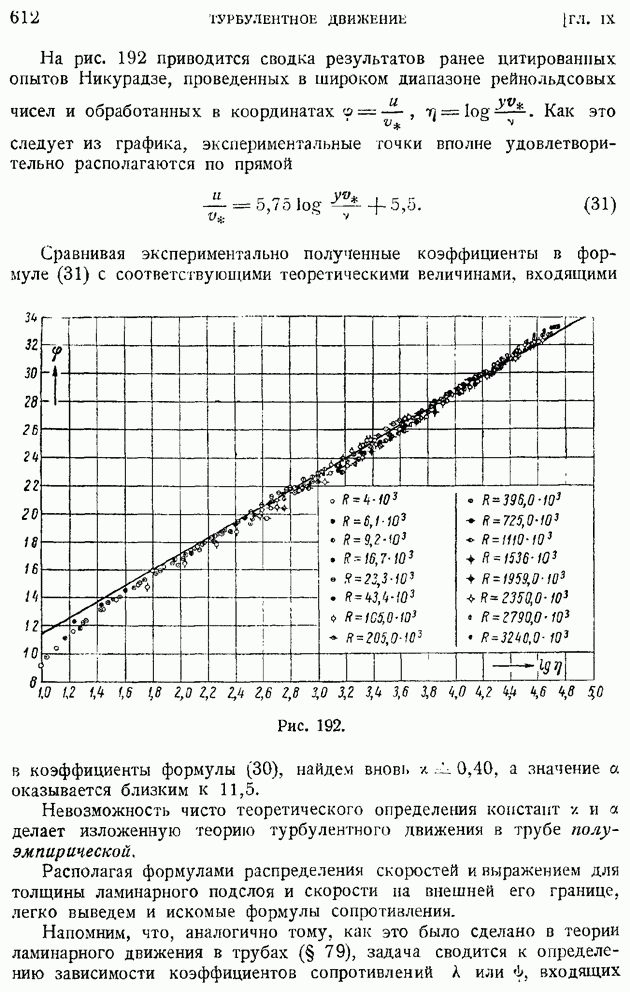
§ 43. Теорема Жуковского о подъемной силе крыла. Зависимость подъемной силы от угла атаки. Коэффициент подъемной силы
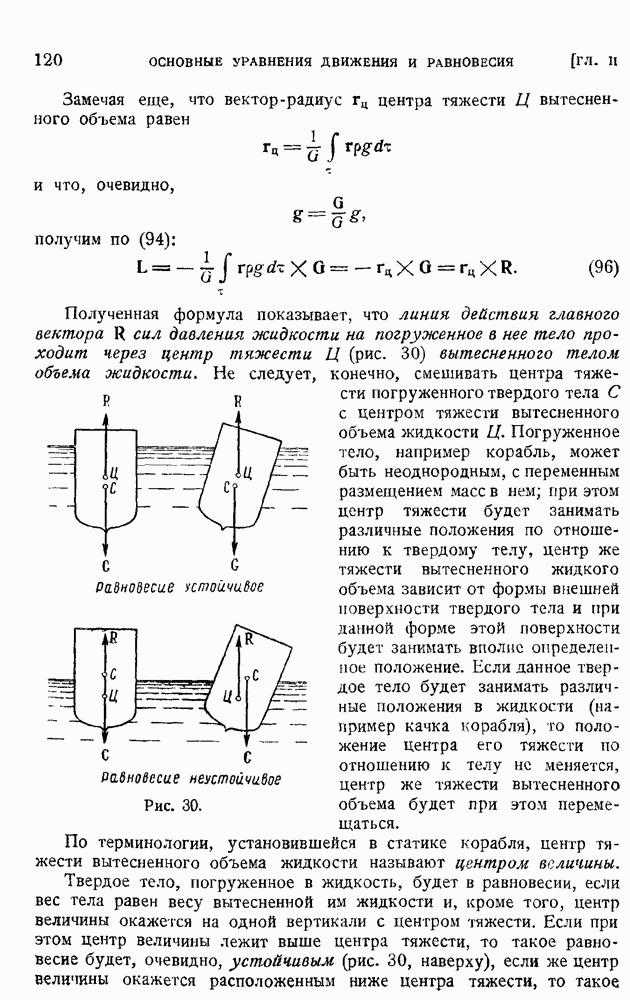
Создание общей теории воздействия плоского потока идеальной жидкости на помещенный в него крыловой профиль является заслугой великого русского ученого Н. Е. Жуковского, опубликовавшего свою известную теорему о подъемной силе крыла в 1906 г. в классическом мемуаре "О присоединенных вихрях". Н. Е. Жуковский первый установил вихревую природу сил, действующих со стороны потока на крыло, и указал на наличие простой пропорциональности между этой силой и интенсивностью вихря, "присоединенного" к обтекаемому телу.
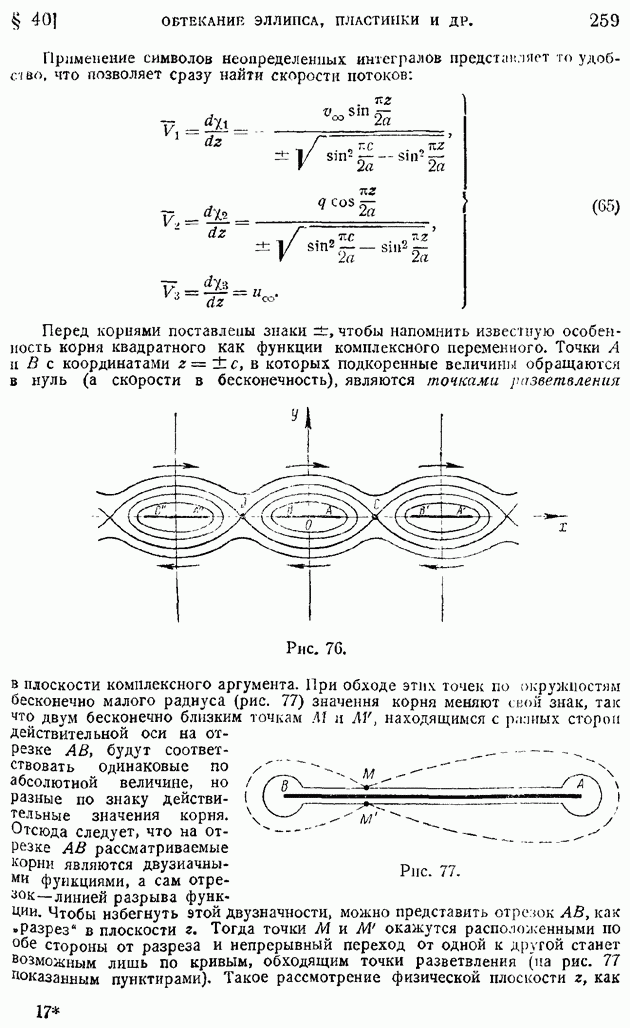
В предыдущем параграфе уже указывалось, что решение задачи об обтекании любого профиля содержит некоторый произвол: один и тот же профиль, при заданной по величине и направлению скорости набегающего на него потока, может обтекаться бесчисленным множеством образов. Все зависит от величины циркуляции скорости, вычисленной по замкнутому контуру, охватывающему обтекаемый профиль. Величина этой циркуляции, так же как и природа возникновения в идеальной жидкости вихрей, сумма интенсивностей которых должна быть равна этой циркуляции, представляла долгое время неразрешимую задачу.
Физическая причина возникновения циркуляции связана с наличием трения (вязкости) в жидкости. Как уже неоднократно упоминалось ранее, в реальной жидкости, обладающей внутренним трением, частицы, проходящие в непосредственной близости к поверхности профиля, образуют тонкий пограничный слой. В этой области резко проявляется неидеальность жидкости, движение жидкости будет вихревым, причем интенсивность вихрей может достигать больших значений, так как скорость частиц в пограничном слое резко меняется от нуля на поверхности обтекаемого тела до величины порядка скорости на бесконечности на внешней границе слоя. Так, например, на крыле самолета максимальная толщина пограничного слоя не превосходит нескольких сантиметров, в то время как разность скоростей на поверхности крыла и на внешней границе пограничного слоя достигает величины 100-200 м в секунду.
При таких значительных неоднородностях скоростного поля суммарная интенсивность вихрей по всему крылу, а следовательно, и циркуляция скорости по замкнутому контуру, охватывающему крыло, может достигать больших значений.
Теория идеальной жидкости, не учитывающая наличия трения, естественно, не могла объяснить возникновения вихрей в набегающем на трло безвихревом потоке. Для того чтобы, оставаясь в рамках теории идеального безвихревого потока, определить величину воздействия
потока на помещенное в него тело, заменим, следуя Жуковскому, контур тела замкнутой линией тока и предположим, что внутри нее происходит движение жидкости с  -вихрем, имеющим ту же интенсивность, что и сумма интенсивностей вихрей, которые образовались бы на самом деле в тонком слое на поверхности тела при обтекании его реальной жидкостью. Такой вихрь Н. Е. Жуковский назвал присоединенным к рассматриваемому твердому телу. Интенсивность "присоединенного вихря", или, что то же, циркуляция скорости по контуру, окружающему крыловой профиль, могла бы быть принципиально вычислена только при помощи расчета движения реальной жидкости в пограничном слое или при помощи некоторого дополнительного допущения об общем характере обтекания тела. По последнему пути пошел, как было указано в предыдущем параграфе, С. А. Чаплыгин, предложивший свой замечательный постулат конечности скорости на задней острой кромке крыла, позволивший определить величину "наложенной" циркуляции, или, что то же, интенсивность "присоединенного вихря".
-вихрем, имеющим ту же интенсивность, что и сумма интенсивностей вихрей, которые образовались бы на самом деле в тонком слое на поверхности тела при обтекании его реальной жидкостью. Такой вихрь Н. Е. Жуковский назвал присоединенным к рассматриваемому твердому телу. Интенсивность "присоединенного вихря", или, что то же, циркуляция скорости по контуру, окружающему крыловой профиль, могла бы быть принципиально вычислена только при помощи расчета движения реальной жидкости в пограничном слое или при помощи некоторого дополнительного допущения об общем характере обтекания тела. По последнему пути пошел, как было указано в предыдущем параграфе, С. А. Чаплыгин, предложивший свой замечательный постулат конечности скорости на задней острой кромке крыла, позволивший определить величину "наложенной" циркуляции, или, что то же, интенсивность "присоединенного вихря".
Эти две глубокие идеи великих русских аэродинамиков Н. Е. Жуковского и С. А. Чаплыгина: присоединенный вихрь и постулат конечности скорости на задней кромке крыла — легли в основу всей современной теории крыла.

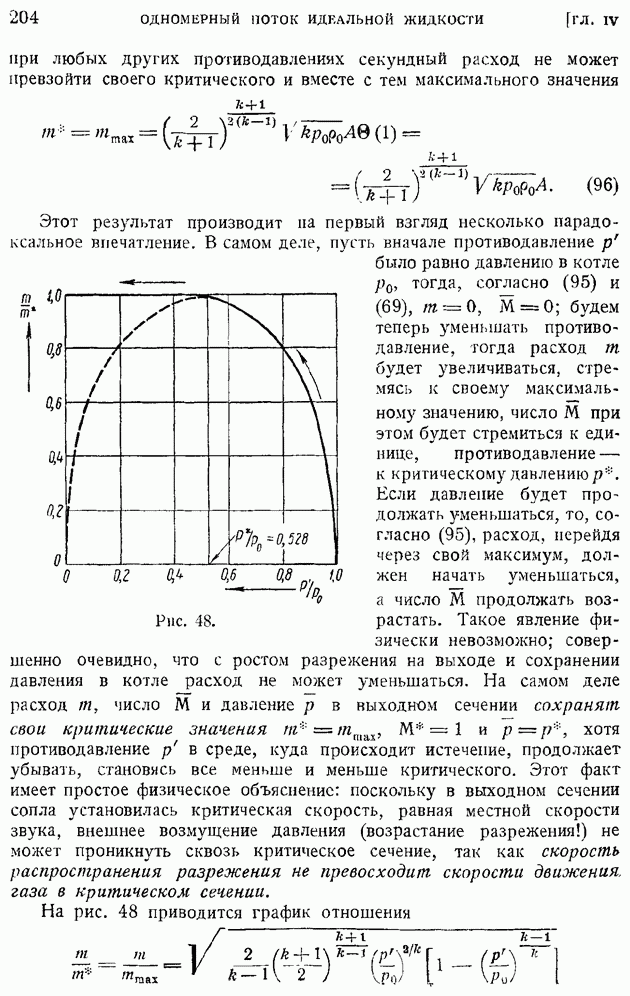
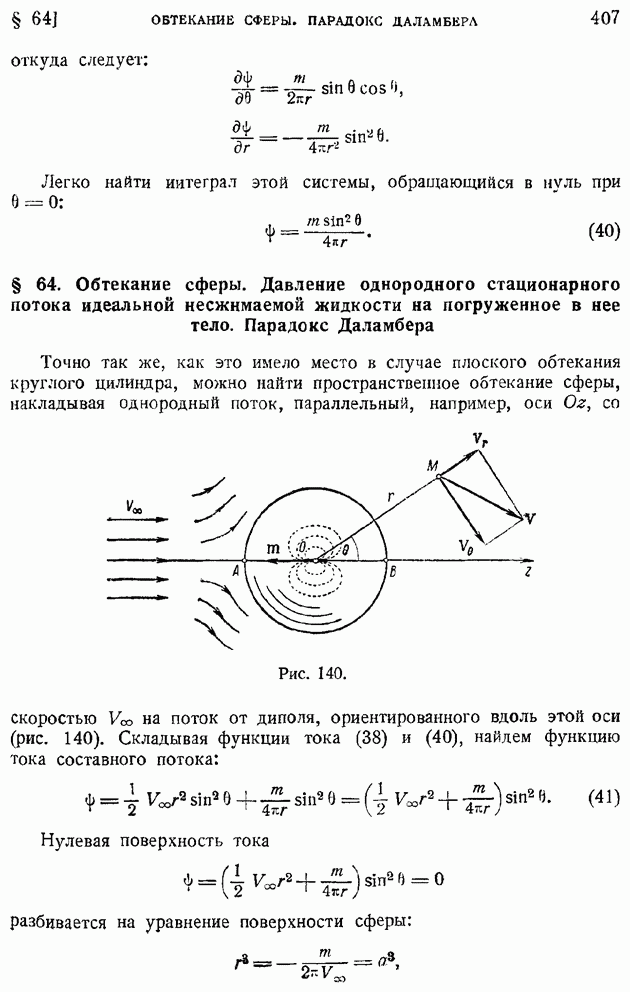
Рис. 89.
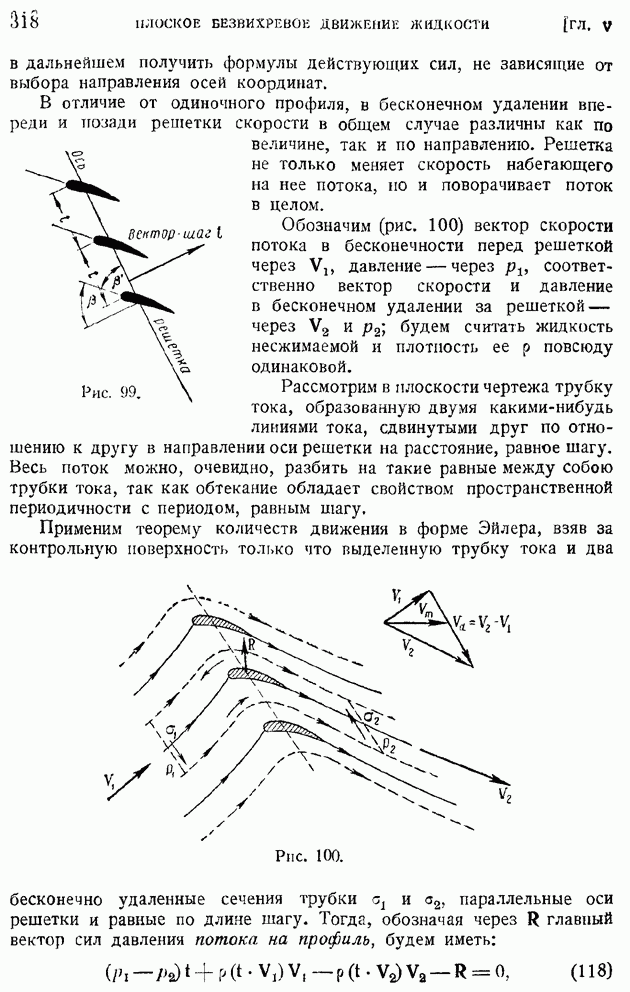
Начнем с доказательства теоремы Жуковского о подъемной силе крыла в плоскопараллельном потоке. Предлагаемое ниже векторное доказательство теоремы Жуковского только по форме отличается от классического доказательства этой теоремы, данной ее автором. Применим теорему количеств движения в форме Эйлера [§ 23, формула (38)] к объему жидкости, заключенному между поверхностью обтекаемого контура С (рис. 89) и проведенной в удалении от контура С окружностью круга  с центром в точке О и радиусом
с центром в точке О и радиусом  Пренебрегая объемными силами, будем иметь, заменяя в формуле (38) § 23,
Пренебрегая объемными силами, будем иметь, заменяя в формуле (38) § 23,
в силу плоского характера течения,  на
на 

В этом равенстве опущен, как равный нулю, перенос количества движения сквозь твердую поверхность профиля С. Первый интеграл представляет главный вектор сил давления со стороны обтекаемого тела на жидкость. Та же величина с обратным знаком определит искомый главный вектор сил давления жидкости на тело

где  нормаль, внешняя по отношению к рассматриваемому объему жидкости. Таким образом, по предыдущей формуле получим выражение искомой силы
нормаль, внешняя по отношению к рассматриваемому объему жидкости. Таким образом, по предыдущей формуле получим выражение искомой силы  через главный вектор давлений и перенос количества движения, относящийся к контуру удаленного от профиля круга
через главный вектор давлений и перенос количества движения, относящийся к контуру удаленного от профиля круга 

По теореме Бернулли

причем, как мы уже знаем, постоянная, стоящая справа, имеет в случае безвихревого движения одинаковое значение во всей области течения, а следовательно, и на круге  так что
так что

Разложим вектор скорости V на два слагаемых, положив

где  скорость в бесконечном удалении от профиля,
скорость в бесконечном удалении от профиля,  скорость возмущения, вносимого профилем в однородный плоскопараллельный поток. Относительно этой убывающей до нуля с удалением от обтекаемого тела скорости возмущений будем предполагать, что ее модуль V убывает с ростом расстояния
скорость возмущения, вносимого профилем в однородный плоскопараллельный поток. Относительно этой убывающей до нуля с удалением от обтекаемого тела скорости возмущений будем предполагать, что ее модуль V убывает с ростом расстояния  от начала координат, вблизи которого помещен профиль, как у. Это предположение соответствует наличию "присоединенного" к телу вихря и конечности Циркуляции скорости по любому замкнутому контуру, например, окружности С, длины подробнее о порядке скорости возмущения будет сказано далее.
от начала координат, вблизи которого помещен профиль, как у. Это предположение соответствует наличию "присоединенного" к телу вихря и конечности Циркуляции скорости по любому замкнутому контуру, например, окружности С, длины подробнее о порядке скорости возмущения будет сказано далее.
Подставляя указанное разложение скорости в равенство (82), получим:

По предыдущему [гл. I, формула (68)], первый интеграл равен нулю; пропадает также четвертый интеграл, так как при отсутствии источников — стоков и несжимаемости жидкости полный расход жидкости сквозь контур  равен нулю:
равен нулю:

Рассмотрим совокупность второго и пятого интегралов:

которую по известной формуле разложения тройного векторного произведения можно представить как

или, заменяя V на  что можно сделать, так как при этом добавится интеграл
что можно сделать, так как при этом добавится интеграл

тождественно равный нулю, получим

Таким образом, будем иметь следующее выражение для главного вектора сил давления потока на профиль С:

Вектор

направлен по перпендикуляру к плоскости движения, а его проекция  на этот перпендикуляр, которую мы обозначим просто через
на этот перпендикуляр, которую мы обозначим просто через  и будем считать знак входящим в определение величины
и будем считать знак входящим в определение величины  окажется равной (рис. 89)
окажется равной (рис. 89)

т. е. циркуляции скорости по контуру  или по любому другому контуру, охватывающему обтекаемый профиль. Таким образом, первое слагаемое в выражении главного вектора сил
или по любому другому контуру, охватывающему обтекаемый профиль. Таким образом, первое слагаемое в выражении главного вектора сил  не зависит от положения контура
не зависит от положения контура  остальные два имеют порядок
остальные два имеют порядок  так как подинтегральные функции представляют величины порядка -К
так как подинтегральные функции представляют величины порядка -К  а длина контура интегрирования равна
а длина контура интегрирования равна  Отсюда при переходе к пределу, когда окружность
Отсюда при переходе к пределу, когда окружность  удаляется на бесконечность
удаляется на бесконечность  следует искомая формула
следует искомая формула

где вектор  определяется как криволинейный интеграл
определяется как криволинейный интеграл

взятый по любому контуру  охватывающему обтекаемый профиль С, в частности по самому профилю С. Величина этого вектора равна циркуляции скорости по замкнутому контуру, охватывающему профиль.
охватывающему обтекаемый профиль С, в частности по самому профилю С. Величина этого вектора равна циркуляции скорости по замкнутому контуру, охватывающему профиль.
Из равенства (84) находим величину главного вектора сил давления потока на тело:

Главный вектор, как показывает формула (84), лежит в плоскости течения и направлен перпендикулярно к скорости на бесконечности в сторону, определяемую векторным произведением (84). Обычно бывает очень трудно заранее определить, в какую сторону направлен вектор Г: внутрь или наружу относительно плоскости чертежа. Если известно направление обхода контура, при котором  это направление условно называют направлением положительной циркуляции, или, короче, "направлением циркуляции" - тогда по общим правилам принятого у нас в курсе "правого винта" легко найти и сторону, в которую направлен вектор
это направление условно называют направлением положительной циркуляции, или, короче, "направлением циркуляции" - тогда по общим правилам принятого у нас в курсе "правого винта" легко найти и сторону, в которую направлен вектор  Так, если направление циркуляции совпадает с вращением по часовой стрелке, а поток набегает слева, вектор
Так, если направление циркуляции совпадает с вращением по часовой стрелке, а поток набегает слева, вектор  направлен вглубь чертежа, а сила
направлен вглубь чертежа, а сила  -вверх; это Же можно получить, если вектор скорости
-вверх; это Же можно получить, если вектор скорости  повернуть на 90° в сторону, противоположную циркуляции.
повернуть на 90° в сторону, противоположную циркуляции.
Таким образом, приходим к классической формулировке теоремы Жуковского, данной самим автором: сила давленая невихревого потока, текущего со скоростью  и обтекающего контур с циркуляцией
и обтекающего контур с циркуляцией  выражается формулой:
выражается формулой:

направление этой силы мы получим, если вектор  повернем на прямой угол в сторону, противоположную циркуляции.
повернем на прямой угол в сторону, противоположную циркуляции.
Первый вывод, который следует сделать из теоремы Жуковского, заключается в отсутствии составляющей силы, направленной вдоль движения жидкости, или, что все равно, направления движения тела по отношению к жидкости, т. е. отсутствии силы сопротивления. Этот важный факт составляет содержание парадокса Даламбера, о котором была речь в историческом очерке, помещенном во вводной части курса. Теорема Жуковского подтверждает парадокс Даламбера для любого плоского безвихревого движения идеальной жидкости как при наличии "присоединенных вихрей", так и при отсутствии их. Единственной силой, действующей на обтекаемый профиль, оказывается поперечная движению тела сила, которая может быть названа подъемной или поддерживающей силой, так как именно эта сила обеспечивает подъем аэроплана в воздух, поддерживает его крыло при горизонтальном полете.
Воспользовавшись теоремой Жуковского и постулатом Жуковского-Чаплыгина, можно по формулам (86), (80) или (81) получить выражение величины подъемной силы в виде

впервые указанном Чаплыгиным.
Входящее в эту формулу произведение  зависит от формы обтекаемого контура, так, например, по предыдущему (см. конец § 42) для пластинки
зависит от формы обтекаемого контура, так, например, по предыдущему (см. конец § 42) для пластинки  и подъемная сила оказывается равной
и подъемная сила оказывается равной

В общем случае подъемная сила, согласно (87), оказывается пропорциональной плотности жидкости, квадрату скорости набегающего потока и синусу угла атаки.
Введем коэффициент подъемной силы как отношение подъемной силы  к скоростному напору набегающего потока
к скоростному напору набегающего потока  и длине хорды. Обычно ось
и длине хорды. Обычно ось  направляют по скорости V,», тогда подъемная сила будет направлена по оси
направляют по скорости V,», тогда подъемная сила будет направлена по оси  и может быть обозначена через
и может быть обозначена через  или
или  Вот почему коэффициент подъемной силы в нашей
Вот почему коэффициент подъемной силы в нашей
литературе принято обозначать через  а коэффициент сопротивления — через
а коэффициент сопротивления — через 
При этом обозначении будем иметь  хорда):
хорда):

или в частном случае пластинки 

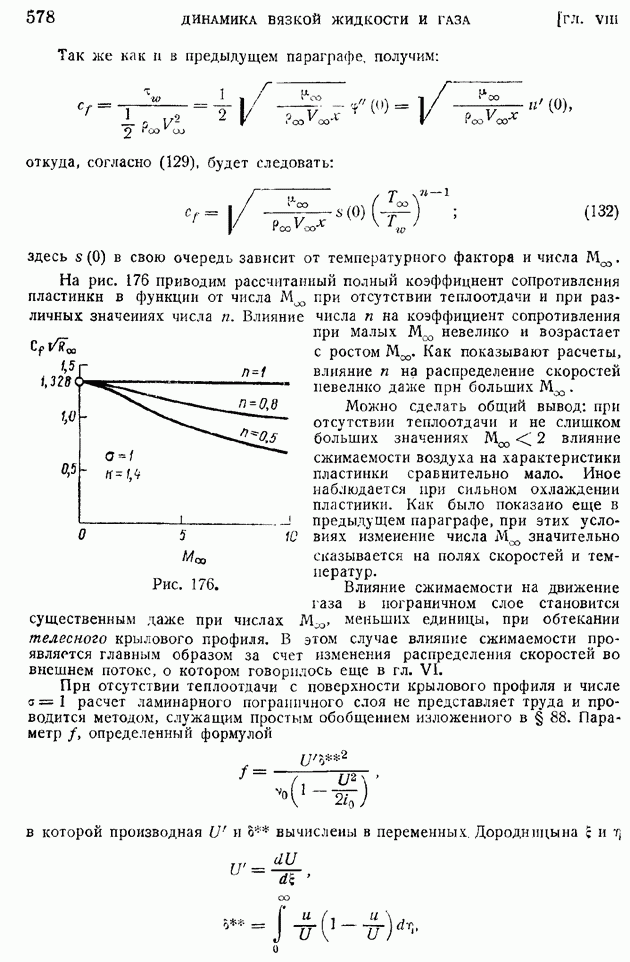
Как показывают многочисленные опыты, при сравнительно малых углах атаки, при которых только и выполняется условие плавного схода струй с задней кромки, формула (88), переписанная в виде 

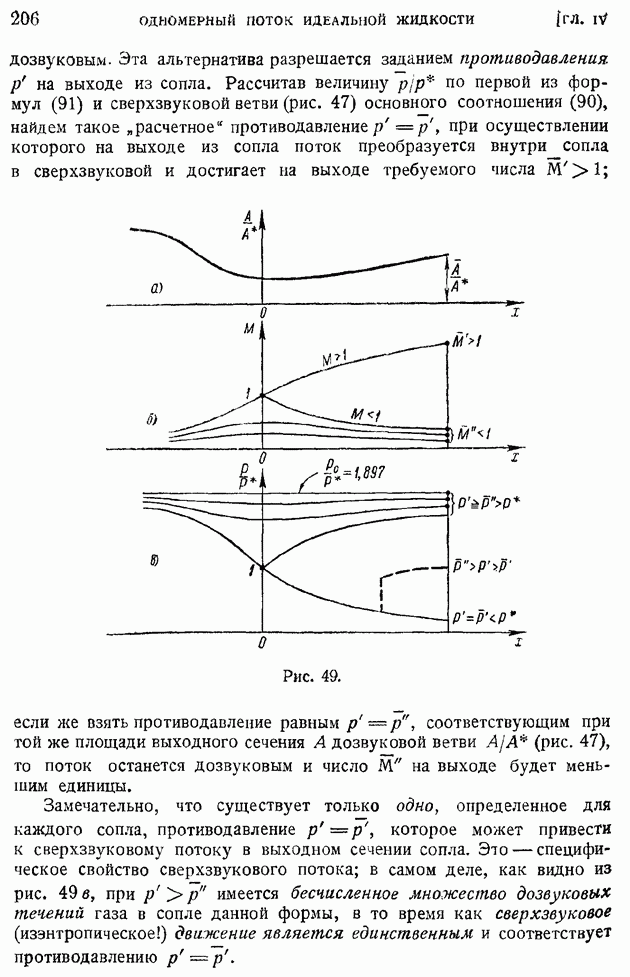
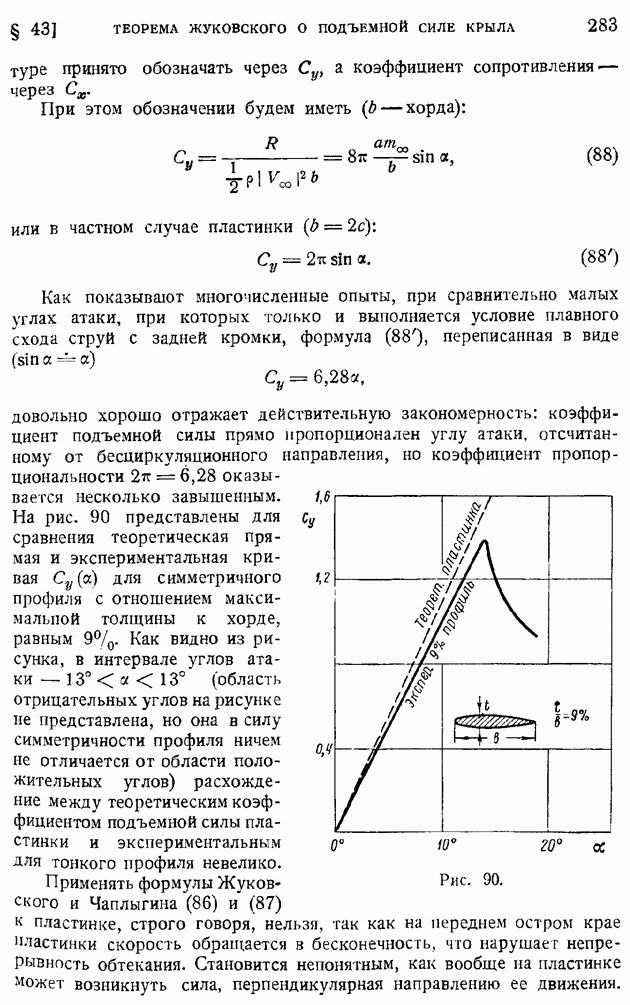
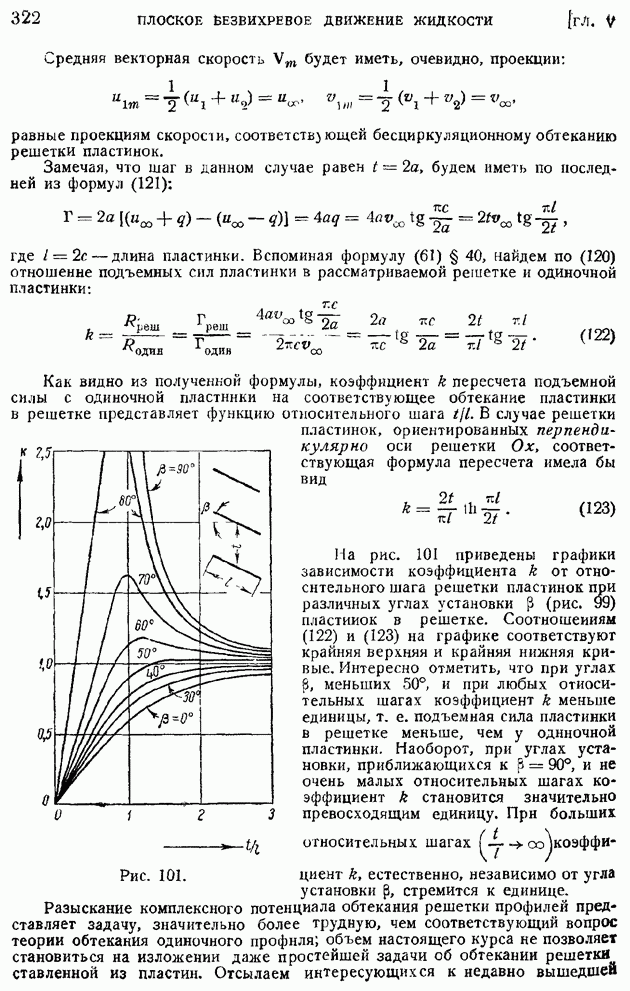
довольно хорошо отражает действительную закономерность: коэффициент подъемной силы прямо пропорционален углу атаки, отсчитанному от бесциркуляционного направления, но коэффициент пропорциональности  оказывается несколько завышенным. На рис. 90 представлены для сравнения теоретическая прямая и экспериментальная кривая
оказывается несколько завышенным. На рис. 90 представлены для сравнения теоретическая прямая и экспериментальная кривая  для симметричного профиля с отношением максимальной толщины к хорде, равным
для симметричного профиля с отношением максимальной толщины к хорде, равным  Как видно из рисунка, в интервале углов атаки —
Как видно из рисунка, в интервале углов атаки —  (область отрицательных углов на рисунке не представлена, но она в силу симметричности профиля ничем не отличается от области положительных углов) расхождение между теоретическим коэффициентом подъемной силы пластинки и экспериментальным для тонкого профиля невелико.
(область отрицательных углов на рисунке не представлена, но она в силу симметричности профиля ничем не отличается от области положительных углов) расхождение между теоретическим коэффициентом подъемной силы пластинки и экспериментальным для тонкого профиля невелико.

Рис. 90.
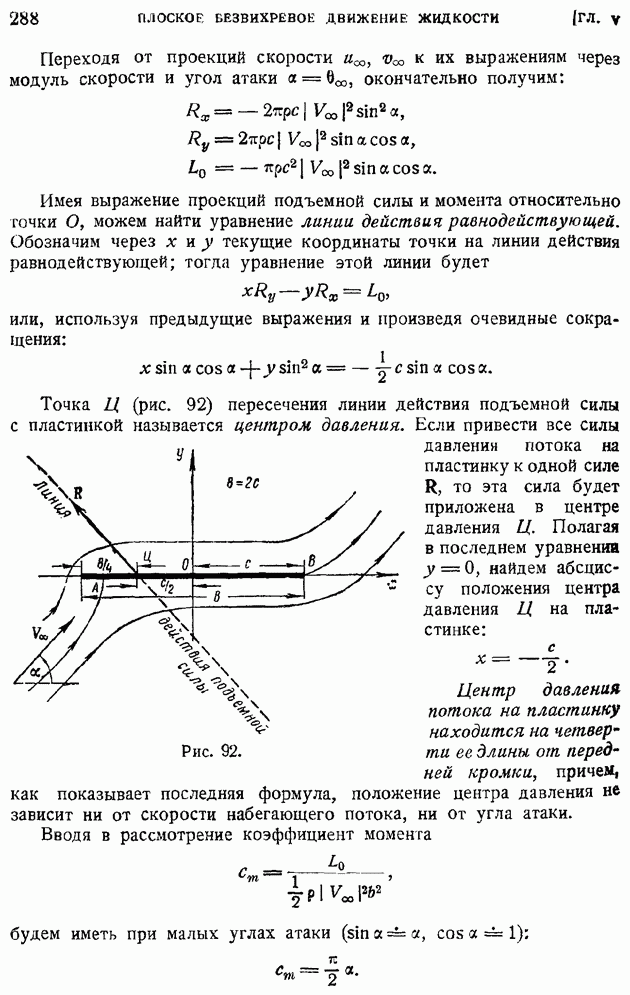
Применять формулы Жуковского и Чаплыгина (86) и (87) к пластинке, строго говоря, нельзя, так как на переднем остром крае пластинки скорость обращается в бесконечность, что нарушает непрерывность обтекания. Становится непонятным, как вообще на пластинке может возникнуть сила, перпендикулярная направлению ее движения.
Действительно, при отсутствии трения нормальные к поверхности пластинки силы давления должны дать главный вектор, направленный также по перпендикуляру к плоскости пластинки, а не к скорости на бесконечности, как этого требует теорема Жуковского. При этом, наряду с подъемной силой, имелась бы и сила сопротивления. Этот парадокс был разъяснен Жуковским во второй из ранее цитированных статей. При действительном обтекании пластинки передний ее край представляет собою на самом деле некоторую поверхность очень малого радиуса кривизны, на которой возникает значительное разрежение, приводящее к направленной против течения "подсасывающей" силе, уничтожающей сопротивление.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Предмет механики жидкости и газа. Основные свойства «макромодели» жидкости и газа: сплошность и подвижность
- § 2. Основные методы механики жидкости и газа. Области применения и главнейшие задачи
- § 3. Краткий очерк исторического развития механики жидкости и газа. От гидромеханики древних до установления воззрений ньютонианской эпохи
- § 4. Эпоха Эйлера и Бернулли. Гидроаэродинамика в XIX в.
- § 5. Современный этап развития механики жидкости и газа
- ГЛАВА I. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
- § 6. Поле физической величины. Скалярное и векторное поля. Поверхности уровня. Векторные линин и трубки
- § 7. Мера однородности поля в данном направлении и в дайной точке. Градиевт скалярного поля и дифференциальный тензор векторного поля как меры неоднородности поля
- § 8. Задание движения сплошной среды. Поле скоростей. Линии тока и траектории
- § 9. Поле ускорений. Разложение ускорения частицы на локальную и конвективную составляющие
- § 10. Скоростное поле сплошной среды в окрестности данной точки. Угловая скорость и вихрь. Тензор скоростей деформаций и его компоненты
- § 11. Скорость объемного расширения жидкости. Интегральные представления дифференциальных операторов поля. Основные интегральные формулы
- § 12. Вихревые линии и трубки. Вторая теорема Гельмгольца. Интенсивность вихревой трубки
- § 13. Выражение интенсивности вихревой трубки через циркуляцию вектора по контуру, охватывающему трубку. Теорема об изменении циркуляции скорости во времени
- ГЛАВА II. ОСНОВНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ И РАВНОВЕСИЯ СПЛОШНОЙ СРЕДЫ
- § 14. Распределение массы в сплошной среде. Плотность и удельный вес. Напряжения. Тензор напряженности и его симметричность
- § 15. Общие уравнения динамики сплошной среды. Уравнение неразрывности. Уравнения динамики в напряжениях
- § 16. Тепловые явления в жидкостях и газах. Закон сохранения энергии и уравнение баланса энергии
- § 17. Общие уравнения равновесного состояния жидкости и газа. Равновесие воздуха в атмосфере. Приближенные барометрические формулы. Стандартная атмосфера
- § 18. Равновесие несжимаемой жидкости. Уравнение поверхности раздела. Равновесие вращающейся жидкости
- § 19. Давление тяжелой несжимаемой жидкости на поверхность тела. Сила и момент, приложенные к телу, плавающему в тяжелой жидкости. Случай вращающейся жидкости
- ГЛАВА III. ДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ И ГАЗА. ОСНОВНЫЕ УРАВНЕНИЯ И ОБЩИЕ ТЕОРЕМЫ
- § 20. Идеальная жидкость. Основные уравнения движения
- § 21. Закон сохранения энергии в движущейся идеальной жидкости. Адиабатическое движение. Сохранение энтропии
- § 22. Эйлерово представление конвективного изменения объемного интеграла. Перенос величины сквозь контрольную поверхность
- § 23. Эйлерова форма законов сохранения массы и энергии, теоремы количеств движения и момента количеств движения при стационарном движении идеальной жидкости
- § 24. Теорема об изменении кинетической энергии. Работа и мощность внутренних сил. Эйлерова форма уравнения изменения кинетической энергии
- § 25. Теорема Бернулли о сохранении полной механической энергии при стационарном баротропном движении идеальной жидкости и газа
- ГЛАВА IV. ОДНОМЕРНЫЙ ПОТОК ИДЕАЛЬНОЙ ЖИДКОСТИ
- § 26. Одномерное течение идеальной сжимаемой жидкости. Линеаризированные уравнения. Скорость распространения малых возмущений в жидкости или газе
- § 27. Изотермическая и адиабатическая скорости звука. «Конус возмущений» при сверхзвуковом движении источника возмущения. Число M и его связь с углом конуса возмущений
- § 28. Распространение непрерывных возмущений конечной интенсивности. Характеристики. Образование разрывной ударной волны
- § 29. Стоячая ударная волна или скачок уплотнения. Ударная адиабата
- § 30. Критические величины в одномерном потоке газа. Связь между скоростями до и после скачка. Изменение давления, плотности и температуры в скачке уплотнения
- § 31. Скорость распространения ударной волны. Спутное движение газа за ударной волной
- § 32. Влияние интенсивности скачка уплотнения на сжатие газа. Измерение скоростей и давлений в до- и сверхзвуковых потоках
- § 33. Одномерное движение газа по трубе переменного сечения. Истечение из резервуара большой емкости сквозь сходящееся сопло
- § 34. Одномерное течение в сопле Лаваля. Движение газа с притоком тепла
- ГЛАВА V. БЕЗВИХРЕВОЕ ДВИЖЕНИЕ ЖИДКОСТИ. ПЛОСКОЕ ДВИЖЕНИЕ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 35. Сохранение циркуляции скорости в потоке идеальной жидкости. Теорема Кельвина и Лаграижа. Безвихревое движение. Потенциал скоростей
- § 36. Интеграл Лагранжа — Коши уравнений безвихревого движения. Теорема Бернулли. Некоторые общие свойства безвихревого движения идеальной несжимаемой жидкости в односвязной области
- § 37. Плоское безвихревое движение несжимаемой жидкости. Потенциал скоростей и функция тока. Применение функций комплексного переменного. Комплексный потенциал и сопряженная скорость
- § 38. Построение полей течения по заданной характеристической Функции. Простейшие плоские потоки и их наложение
- § 39. Бесциркуляционное и циркуляционное обтекания круглого цилиндра
- § 40. Применение криволинейных координат. Бесциркуляционное и циркуляционное обтекания эллиптического цилиндра и пластинки. Задача Жуковского об обтекании решетки пластин.
- § 41. Плоское движение с отрывом струй. Разрывное обтекание пластинки и протекание жидкости сквозь отверстие
- § 42. Прямая задача в теории плоского движения идеальной несжимаемой жидкости. Применение метода конформных отображений. Гипотеза Чаплыгина о безотрывном обтекании задней кромки профиля. Формула циркуляции
- § 43. Теорема Жуковского о подъемной силе крыла. Зависимость подъемной силы от угла атаки. Коэффициент подъемной силы
- § 44. Применение метода комплексных переменных к выводу теоремы Жуковского. Формулы Чаплыгина для главного вектора и момента сил давления потока на крыло
- § 45. Выражение главного момента сил давления потока через коэффициенты конформного отображения. Фокус крыла. Независимость от угла атаки момента относительно фокуса. Парабола устойчивости
- § 46. Частные случаи конформного отображения крылового профиля на круг. Преобразование Жуковского-Чаплыгина. Теоретические крыловые профили
- § 47. Задача об обтекании слабо изогнутой дужки произвольной формы (теория тонкого крыла)
- § 48. Определение обтекания крылового профиля произвольной формы
- § 49. Обобщение теоремы Жуковского на случай плоской решетки с бесчисленным множеством профилей
- ГЛАВА VI. ПЛОСКОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ СЖИМАЕМОГО ГАЗА
- § 50. Основные уравнения плоского стационарного безвихревого движения сжимаемого газа. Линеаризированные уравнения
- 51. Линеаризированный до- и сверхзвуковой газовый поток вдоль волнистой стенки
- § 52. Тонкое крыло в линеаризированном до- и сверхзвуковом потоках. Влияние сжимаемости газа на коэффициент подъемной силы в дозвуковом потоке. Коэффициенты подъемной силы и волнового сопротивления при сверхзвуковом потоке
- § 53. Нелинеаризированные уравнения движения идеального сжимаемого газа. Переход в плоскость годографа. Уравнения Чаплыгина
- § 54. Метод С. А. Христиановича. Приближенные формулы учета влияния сжимаемости на распределение давления
- § 55. Критическое число M и его определение по заданному распределению давления в несжимаемом обтекании. Поведение коэффициента подъемной силы и момента при около- и закритических значениях числа M
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
- § 57. Нелинеаризированный сверхзвуковой поток. «Характеристики» уравнений плоского сверхзвукового потока. Линин возмущения и их основные свойства
- § 58. Обтекание выпуклого угла сверхзвуковым потоком. Влияние угла поворота струи на ее газодинамические элементы
- § 59. Сверхзвуковой поток внутри тупого угла. Косой скачок уплотнения. Связь между газодинамическими элементами до и за косым скачком
- ГЛАВА VII. ПРОСТРАНСТВЕННОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ
- § 60. Ортогональные криволинейные координаты в пространстве. Основные дифференциальные операторы поля в криволинейных координатах
- § 61. Потенциал скоростей. Поле источника и диполя. Непрерывное распределение источников и диполей. Ньютонов потенциал. Потенциал простого и двойного слоев
- § 62. Поле скоростей вокруг заданной системы вихрей. Формула Био — Савара. Потенциал скоростей замкнутой вихревой нити. Аналогия с потенциалом двойного слоя
- § 63. Функция тока и ее связь с векторным потенциалом скоростей. Функции тока простейших течений
- § 64. Обтекание сферы. Давление однородного стационарного потока идеальной несжимаемой жидкости на погруженное в нее тело. Парадокс Даламбера
- § 65. Общие уравнения осесимметричного движения. Применение цилиндрических координат. Течение сквозь каналы
- § 66. Осесимметричное продольное обтекание тел вращения. Случай эллипсоида вращения
- § 67. Поперечное обтекание тел вращения. Пример эллипсоида вращения
- § 68. Продольное и поперечное обтекание тел вращения большого удлинения. Приближенные выражения граничных условий. Применение тригонометрических сумм для определения коэффициентов …
- § 69. Метод «особенностей». Применение непрерывно распределенных источников (стоков) и диполей для решения задачи о продольном и поперечном обтекании тел вращения
- § 70. Общий случай движения твердого тела сквозь несжимаемую идеальную жидкость. Определение потенциала скоростей. Главный вектор и главный момент сил давления потока на тело
- § 71. Коэффициенты «присоединенных масс». Свойство симметрии. «Присоединенная» кинетическая энергия. Определение «присоединенных масс» поступательно движущегося цилиндра, шара и эллипсоида
- § 72. Элементы теории крыла конечного размаха. Вихревая система крыла. Гипотеза плоских сечеиий. Геометрические и действительные углы атаки. Подъемная сила и «индуктивное сопротивление»
- § 73. Основные формулы теории «несущей линии». «Индуктивная скорость» и «индуктивный угол». Прямая задача определения подъемной силы и индуктивного сопротивления по заданному распределению циркуляции
- § 74. Крыло с минимальным индуктивным сопротивлением. Эллиптическое распределение циркуляции. Связь между коэффициентами индуктивного сопротивления и подъемной силы. Основное уравнение теории крыла и понятие о его интегрировании
- ГЛАВА VIII. ДИНАМИКА ВЯЗКОЙ ЖИДКОСТИ И ГАЗА
- § 75. Внутреннее трение и теплопроводность в жидкостях и газах. Законы Ньютона и Фурье. Влияние температуры на коэффициенты вязкости и теплопроводности. Число «сигма»
- § 76. Обобщение закона Ньютона на случай произвольного движения среды. Закон линейной связи между тензорами напряжений и скоростей деформации
- § 77. Общие уравнения движения вязкой жидкости. Динамические уравнения и уравнение баланса энергии. Граничные условия движения жидкости с треннем и теплопроводностью
- § 78. Понятие о подобии гидродинамических явлений. Безразмерные уравнения движения вязкой жидкости и газа. Условия подобия
- § 79. Ламинарное движение вязкой несжимаемой жидкости по цилиндрической трубе
- § 80. Обтекание шара при очень малых значениях числа Рейнольдса. Формула сопротивления шара по Стоксу и ее обобщения
- § 81. Вихревые линии в идеальной и вязкой жидкости. Сохраняемость вихревых линий при отсутствии внутреннего трения. Диффузия вихря в вязкой жидкости
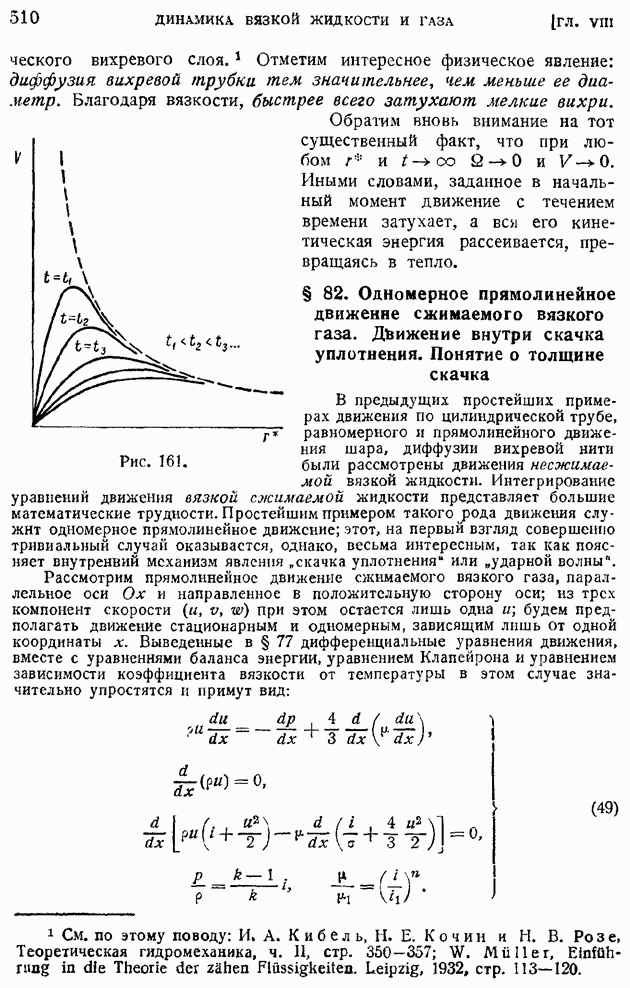
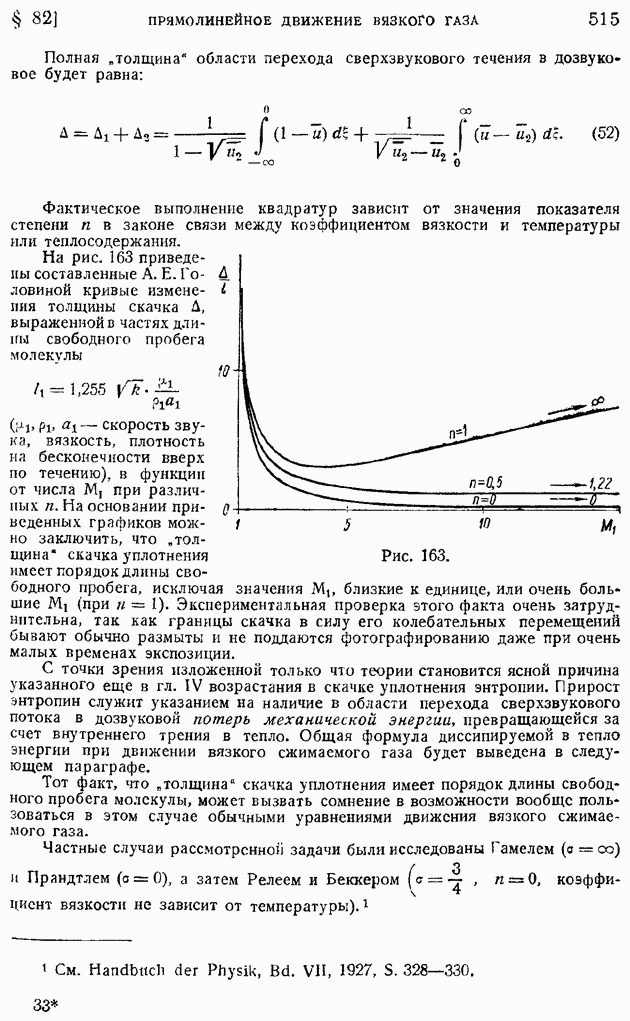
- § 82. Одномерное прямолинейное движение сжимаемого вязкого газа. Движение внутри скачка уплотнения. Понятие о толщине скачка
- § 83. Работа внутренних сил и диссипация механической энергии в движущейся вязкой среде
- § 84. Обтекание тел жидкостью и газом при больших значениях числа Рейнольдса. Основные уравнения теории ламинарного пограничного слоя
- § 85. Ламинарный пограничный слой на пластинке, продольно обтекаемой несжимаемой жидкостью. Неизотермическое движение
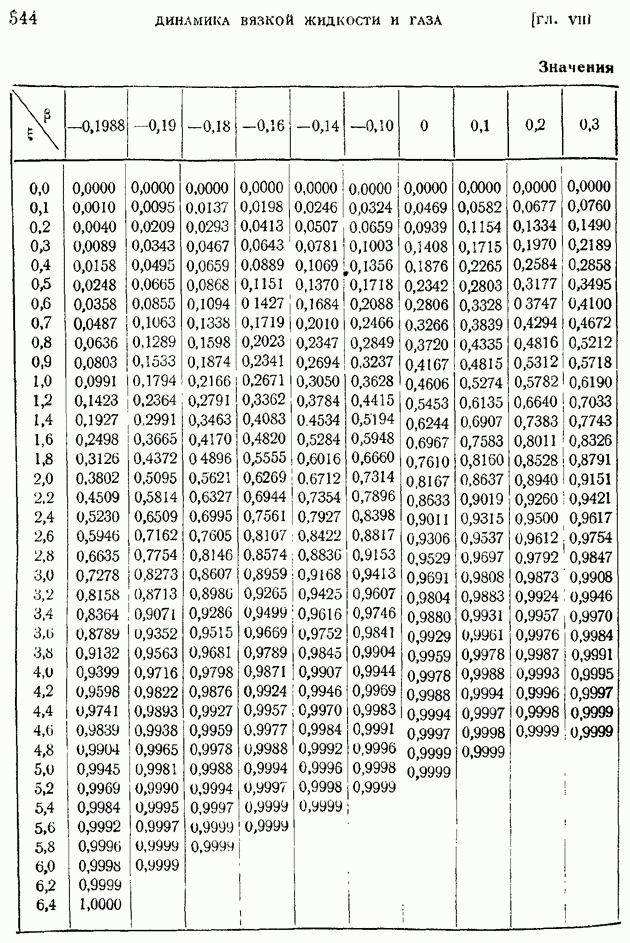
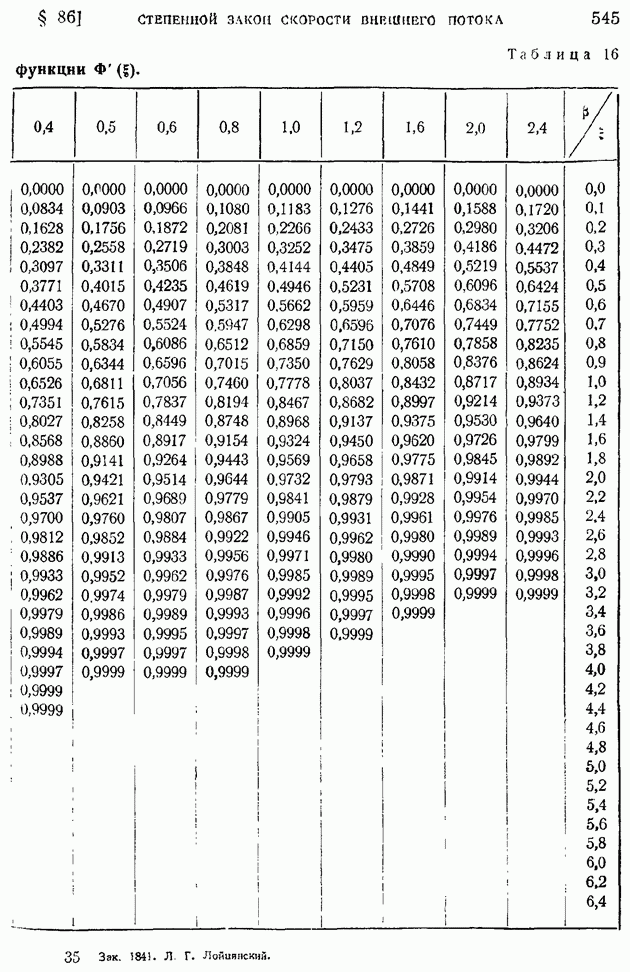
- § 86. Ламинарный пограничный слой при степенном задании скорости внешнего потока
- § 87. Ламинарный пограничный слой в общем случае задания скорости внешнего потока. Применение уравнения импульсов для приближенного расчета ламинарного пограничного слоя
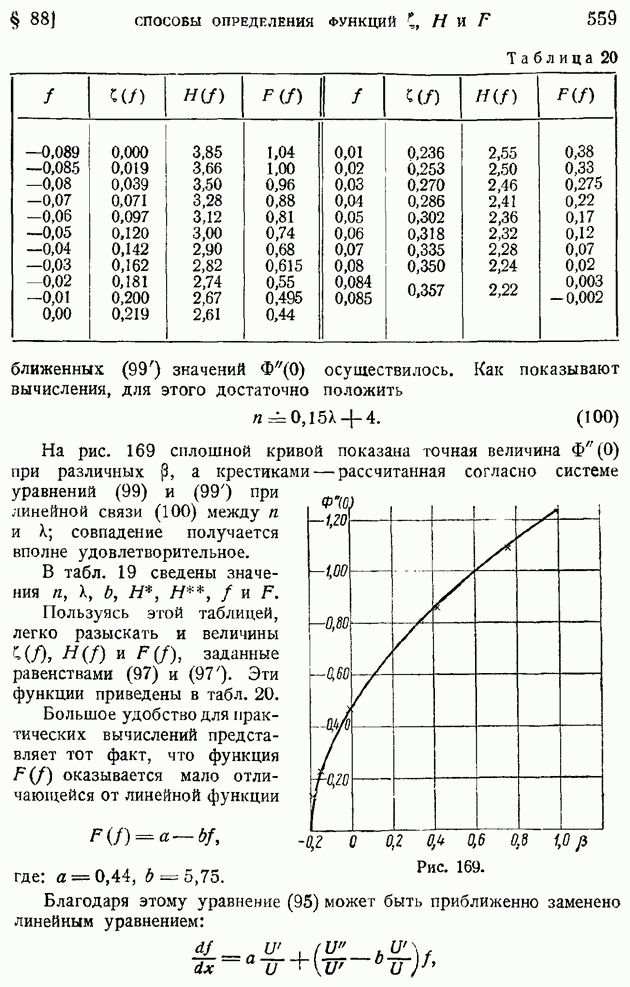
- § 88. Способы определения функций … Приближенный метод расчета ламинарного пограничного слоя
- § 89. Ламинарный пограничный слой на пластинке, продольно обтекаемой сжимаемым газом при больших скоростях. Случай линейной зависимости коэффициента вязкости от температуры (n = 1)
- § 90. Ламинарный пограничный слой на пластинке при любом законе связи между вязкостью и температурой и при числе … Обтекание крылового профиля потоком больших скоростей
- ГЛАВА IX. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ
- § 91. Переход ламинарного движения в турбулентное. Критическое рейнольдсово число
- § 92. Область и «точка» перехода. Явление «кризиса обтекания»
- § 93. Основные уравнения осреднеиного турбулентного движения. Тензор турбулентных напряжений
- § 94. Турбулентное движение жидкости в плоской и круглой трубе. Логарифмические формулы скоростей
- § 95. Формулы сопротивления гладких труб при турбулентном движении жидкости. Ламинарный подслой
- § 96. Влияние шероховатости стенок трубы на ее сопротивление. Предельные режимы течения. Режим установившейся шероховатости
- § 97. Турбулентный пограничный слой на продольно обтекаемой пластине. Сопротивление пластины
- § 98. Турбулентный пограничный слой на крыловом профиле при малом продольном перепаде давлений
- § 99. Турбулентный пограничный слой на крыловом профиле при значительных продольных перепадах давления
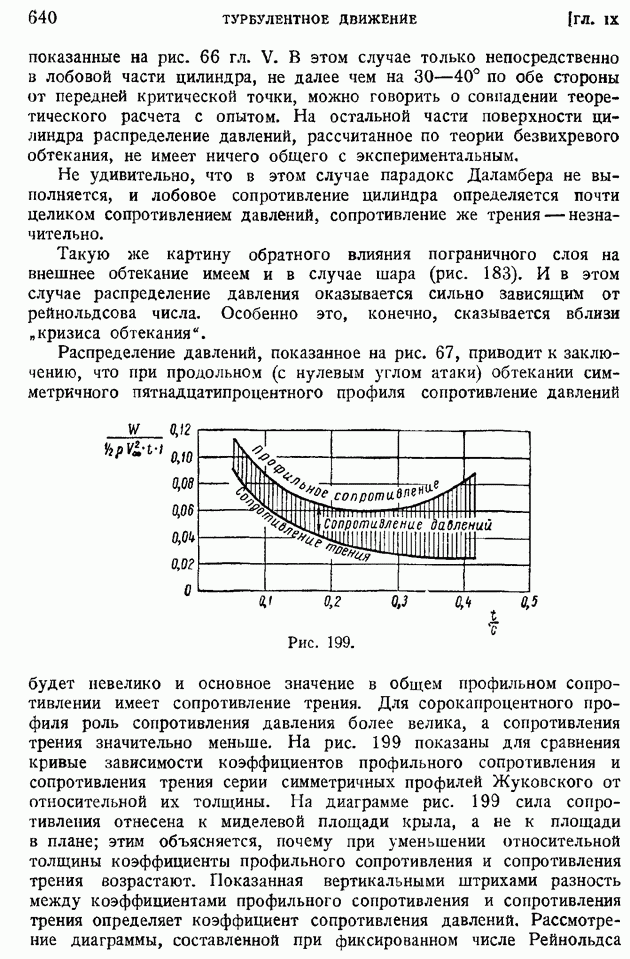
- § 100. Профильное сопротивление крыла. Разложение профильного сопротивления на сопротивление трения и сопротивление давлений. Обратное влияние пограничного слоя на распределение давлений по поверхности обтекаемого профиля
- § 101. Приближенные формулы профильного сопротивления крыла и крылового профиля в решетке
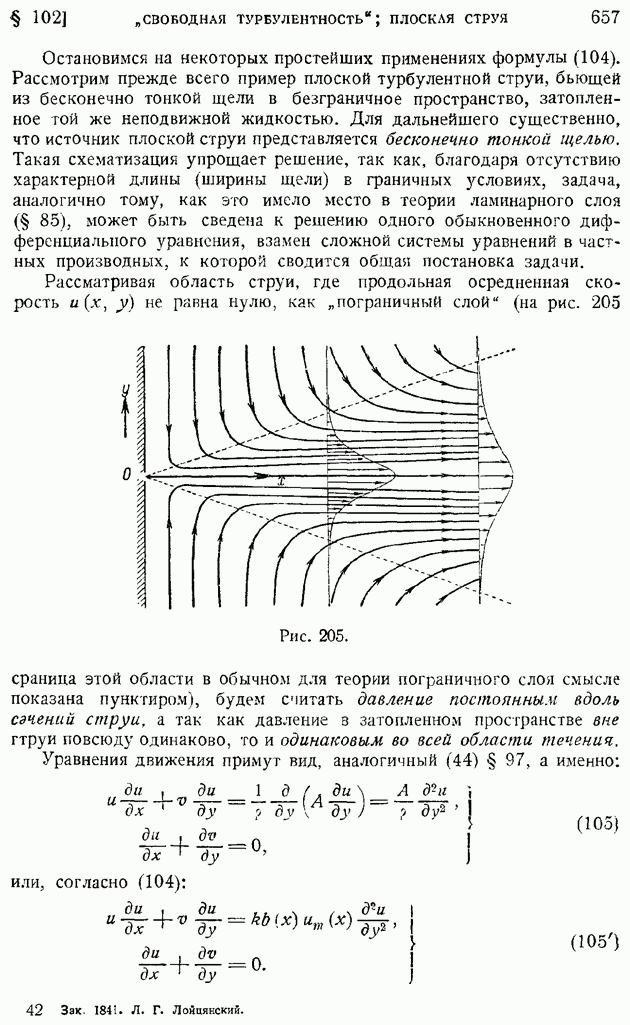
- § 102. Основные закономерности «свободной турбулентности». Плоская турбулентная струя в пространстве, заполненном той же жидкостью
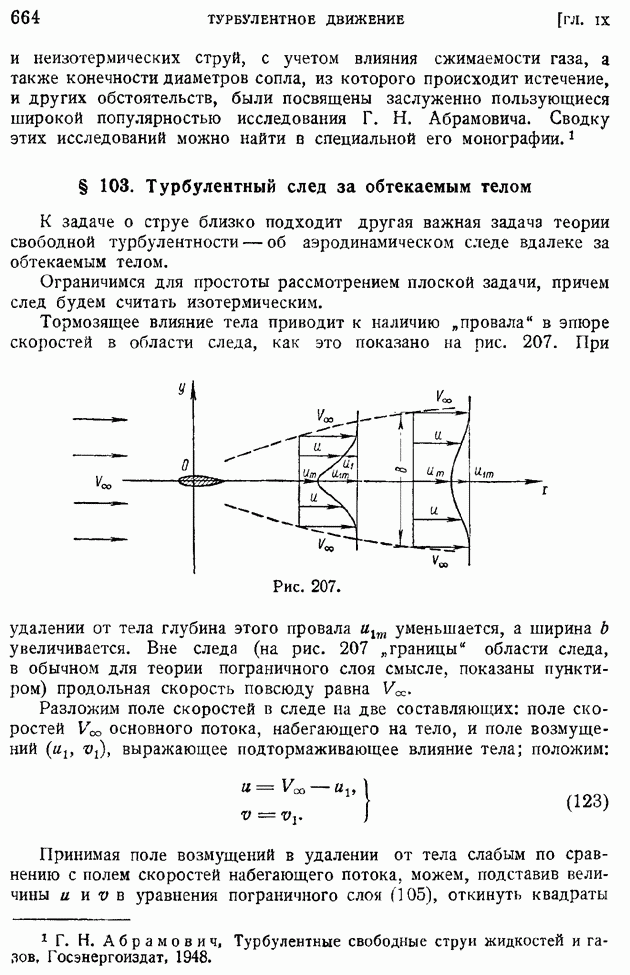
- § 103. Турбулентный след за обтекаемым телом
- § 104. Рассеяние турбулентных возмущений в жидкости. Случай изотропной и однородной турбулентности. Закон сохранения момента возмущений