| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 72. Элементы теории крыла конечного размаха. Вихревая система крыла. Гипотеза плоских сечеиий. Геометрические и действительные углы атаки. Подъемная сила и «индуктивное сопротивление»
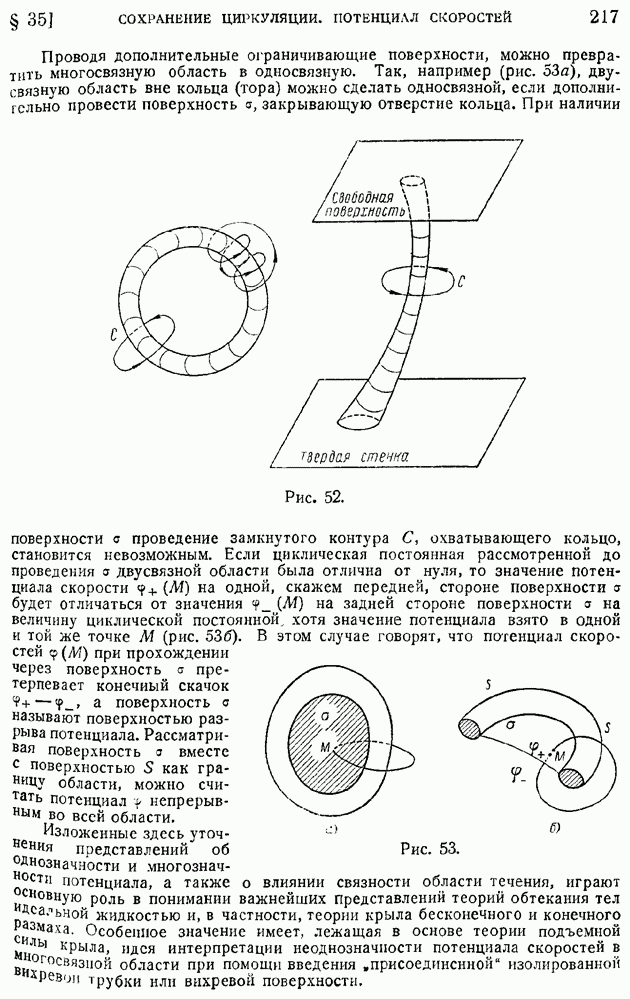
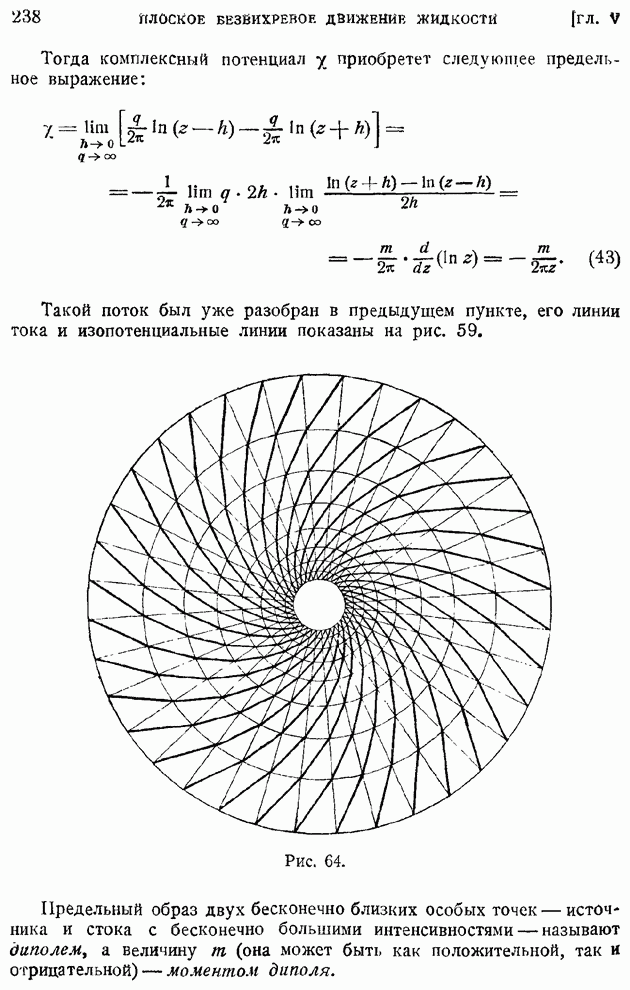
При рассмотрении плоского обтекания цилиндрического крыла бесконечного размаха уже указывалось, что на самом деле нельзя полностью пренебрегать наличием в жидкости трения. За счет внутреннего трения, особенно сильно развивающегося в тонком пограничном слое, образуются мощные вихри, совокупность которых, но гениальной идее Жуковского, может быть заменена одним "присоединенным вихрем", поясняющим возникновение подъемной силы крыла. Этот "присоединенный вихрь", в полном согласии с классической теоремой Гельмгольца (§ 12 гл. I) об одинаковости интенсивности вихревой трубки вдоль всей ее длины, не может начинаться или заканчиваться в жидкости. Совпадая по направлению с осью крыла бесконечного размаха, "присоединенный вихрь" приходит из бесконечности и в бесконечность же уходит. Интенсивность "присоединенного вихря" одинакова вдоль размаха цилиндрического крыла, одинакова и циркуляция скорости по контуру, охватывающему любое сечение крыла, и подъемная сила единицы длины крыла.
Опыт показывает, что на крыле конечного размаха, например, на крыле самолета, циркуляция не сохраняется вдоль размаха, достигая максимального своего значения где-то посередине крыла и обращаясь в нуль на его концах. Такая переменность циркуляции говорит вместе с тем и об изменениях интенсивности "присоединенной" вихревой трубки, что, как будто, находится в противоречии с ранее упомянутой теоремой Гельмгольца.
С. А. Чаплыгин еще в 1910 г. нашел причину возможности изменения интенсивности "присоединенного вихря" в сходе вихрей с поверхности крыла и дал первую теорию крыла конечного размаха; изложение этой теории появилось, повидимому, впервые лишь в специальной монографии В. В. Голубева, выпущенной в свет в 1931 г. Только спустя много лет после создания теории Чаплыгина появилась теория несущей линии Прандтля.
Сущность простейшей схемы крыла конечного размаха заключается в следующем. От основного "присоединенного" вихревого шнура крыла отделяются и уносятся потоком так называемые "свободные" вихри, оси которых в некотором удалении от крыла совпадают с линиями
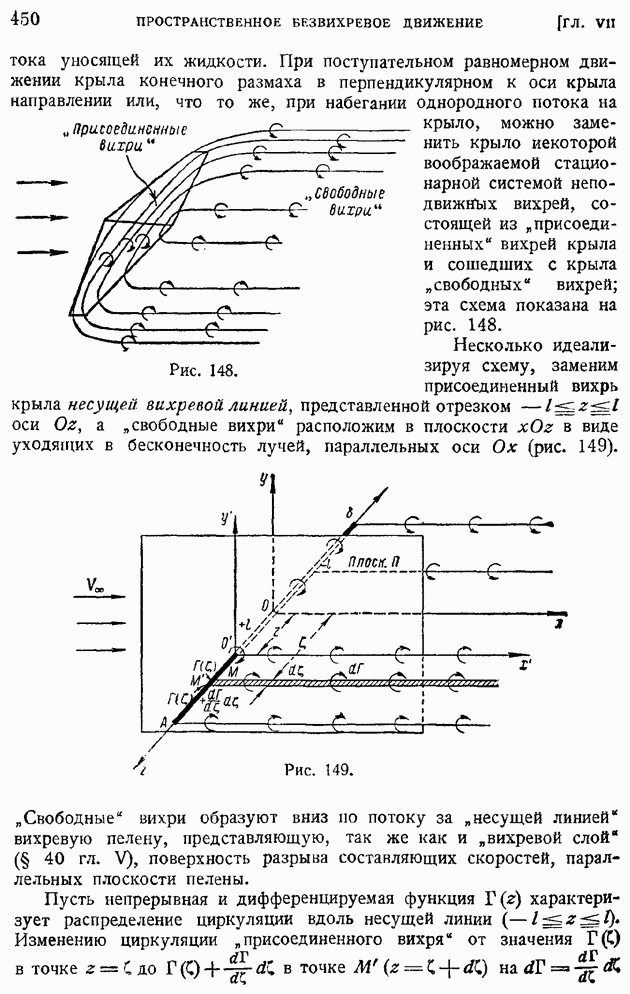
тока уносящей их жидкости. При поступательном равномерном движении крыла конечного размаха в перпендикулярном к оси крыла направлении или, что то же, при набегании однородного потока на крыло, можно заменить крыло некоторой воображаемой стационарной системой неподвижных вихрей, состоящей из "присоединенных" вихрей крыла и сошедших с крыла "свободных" вихрей; эта схема показана на рис. 148.
Несколько идеализируя схему, заменим присоединенный вихрь крыла несущей вихревой линией, представленной отрезком — оси  а "свободные вихри" расположим в плоскости
а "свободные вихри" расположим в плоскости  в виде уходящих в бесконечность лучей, параллельных оси
в виде уходящих в бесконечность лучей, параллельных оси  (рис. 149).
(рис. 149).

Рис. 148.

Рис. 149.
"Свободные" вихри образуют вниз по потоку за "несущей линией" вихревую пелену, представляющую, так же как и "вихревой слой" (§ 40 гл. V), поверхность разрыва составляющих скоростей, параллельных плоскости пелены.
Пусть непрерывная и дифференцируемая функция  характеризует распределение циркуляции вдоль несущей линии
характеризует распределение циркуляции вдоль несущей линии  Изменению циркуляции "присоединенного вихря" от значения
Изменению циркуляции "присоединенного вихря" от значения  в точке
в точке  до
до  в точке
в точке 
соответствует сход вихревой полоски (на рис. 149 заштрихованной), образующей элемент "вихревой пелены", циркуляции которого равна также 
Учитывая сошедшую, "освободившуюся" от крыла циркуляцию, убедимся, что совокупность "связанной" с крылом, "присоединенной" циркуляции и сошедшей с крыла "свободной" циркуляции при стационарном движении жидкости, в полном согласии с теоремой Гельмгольца, сохраняется неизменной.
Вихревая система крыла конечного размаха индуцирует вокруг себя некоторое поле скоростей, которое складывается с однородным набегающим потоком. В результате такого наложения создается некоторое сложное неоднородное поле скоростей, требующее для своего исследования дополнительных приближенных приемов.
Проведем через точки "несущей линии" перпендикулярные к ней плоскости, одна из которых  показана на рис. 149. Рассмотрим проекцию действительного поля скоростей в точках плоскости
показана на рис. 149. Рассмотрим проекцию действительного поля скоростей в точках плоскости  на эту плоскость и назовем соответствующий, лишенный поперечных скоростей
на эту плоскость и назовем соответствующий, лишенный поперечных скоростей  поток сечением действительного потока плоскостью
поток сечением действительного потока плоскостью  или, для краткости, плоским сечением потока.
или, для краткости, плоским сечением потока.
Плоские сечения потока только далеко впереди от "несущей линии" представляют однородные поля скоростей; в остальной области поток неоднороден, так как отдельные его точки находятся на разных расстояниях от вихревой системы крыла. Заметим еще, что плоские сечения потока отличны друг от друга, так что совокупность их не определяет плоского потока.
Рассмотрим подробнее ту часть плоского сечения, которая расположена вблизи точки О пересечения несущей линии с плоскостью сечения, или, схематически, поток вблизи сечения крыла той же плоскостью (рис. 150).

Рис. 150.
Отвлечемся на мгновение от возмущений, создаваемых крыловым профилем, т. е. элементом несущего "присоединенного" вихря.
Если бы крыло имело бесконечный размах и поток был бы строго плоским, то, удалив крыло и производимые им возмущения, мы получили бы однородное поле набегающего потока с некоторой скоростью на бесконечности  В случае крыла конечного размаха это не так. Если в плоском сечении из полного поля скоростей вычесть поле возмущений от элемента несущей линии, то оставшееся
В случае крыла конечного размаха это не так. Если в плоском сечении из полного поля скоростей вычесть поле возмущений от элемента несущей линии, то оставшееся
поле плоского сечения потока будет содержать как оонородную часть  от набегающего потока, так и добавочную неоднородную часть
от набегающего потока, так и добавочную неоднородную часть  индуцируемую "свободными вихрями" пелены, расположенными в плоскости
индуцируемую "свободными вихрями" пелены, расположенными в плоскости  Неоднородность поля этих индуктивных скоростей
Неоднородность поля этих индуктивных скоростей  - является следствием различия расстояний отдельных точек плоскости от элементов "свободных вихрей" пелены.
- является следствием различия расстояний отдельных точек плоскости от элементов "свободных вихрей" пелены.
Анализируя с количественной стороны порядок разности между рассчитанными по формуле Био - Савара индуктивными скоростями в точках плоскости  вблизи точки О и в самой точке О, можно было бы доказать, что во всех плоских сечениях потока, удаленных от концов
вблизи точки О и в самой точке О, можно было бы доказать, что во всех плоских сечениях потока, удаленных от концов  несущей линии (крыла), неоднородность поля индуктивных скоростей вблизи сечения крыла тем меньше, чем больше удлинение крыла, т. е. отношение его размаха к средней хорде.
несущей линии (крыла), неоднородность поля индуктивных скоростей вблизи сечения крыла тем меньше, чем больше удлинение крыла, т. е. отношение его размаха к средней хорде.
Таким образом, представляется допустимым для каждого плоского сечения потока ввести понятие о своей местной скорости на бесконечности  (рис, 150), равной сумме скорости потока на бесконечности перед крылом
(рис, 150), равной сумме скорости потока на бесконечности перед крылом  и "индуктивной скорости"
и "индуктивной скорости"  созданной "свободными вихрями" пелены в точке О несущей линии:
созданной "свободными вихрями" пелены в точке О несущей линии:

Имея это в виду, примем следующую "гипотезу плоских сечений": при достаточно больших удлинениях крыла конечного размаха каждое плоское сечение потока, удаленное от концов крыла, можно рассматривать как плоское обтекание полученного в пересечении крыла плоскостью крылового профиля, с "местной скоростью на бесконечности", равной сумме скоростей потока на бесконечности впереди крыла и скорости, индуцированной "свободными вихрями" пелены в соответствующей точке несущей линии.
Принятое допущение, сообщающее условным плоским сечениям потока смысл подлинных плоских движений, сводит расчет крыла конечного размаха к решению изложенной в гл. V задачи о плоском обтекании крыловых профилей и к последующему суммированию результатов по всем плоским сечениям крыла. Такое допущение имеет смысл только для крыльев значительного удлинения. Изложенная гипотеза плоских сечений неприемлема для крыльев малого удлинения.
Обозначим через а (рис. 151) угол агаки набегающего потока на бесконечности перед крылом, т. е. угол между вектором  и хордой сечения крыла. Этот угол назовем геометрическим углом атаки. Введем в рассмотрение также действительный (или эффективный) угол атаки
и хордой сечения крыла. Этот угол назовем геометрическим углом атаки. Введем в рассмотрение также действительный (или эффективный) угол атаки  как угол между "местной скоростью на
как угол между "местной скоростью на
бесконечности"  и той же хордой. Угол между скоростями
и той же хордой. Угол между скоростями  обозначим через
обозначим через  и назовем углом скоса потока или индуктивным углом. Как видно из рис. 151,
и назовем углом скоса потока или индуктивным углом. Как видно из рис. 151,

Давление плоского потока на крыловой профиль, согласно гипотезе плоских сечений и теореме Жуковского, определяется отнесенным к единице длины крыла по размаху главным вектором  равным по величине
равным по величине

где  должно быть определено, как было указано в гл. V, путем использования постулата Чаплыгина о безотрывном обтекании задней кромки сечения крыла. Вектор
должно быть определено, как было указано в гл. V, путем использования постулата Чаплыгина о безотрывном обтекании задней кромки сечения крыла. Вектор  направлен (рис. 150) по перпендикуляру к "местной скорости на бесконечности"
направлен (рис. 150) по перпендикуляру к "местной скорости на бесконечности"  в соответствующую сторону.
в соответствующую сторону.

Рис. 151.
В каждом плоском сечении пектор  будет иметь свою величину и свое направление. Желая найти подъемную силу крыла в целом, определим сначала подъемную силу сечения, как отнесенную к единице длины крыла составляющую Ну вектора
будет иметь свою величину и свое направление. Желая найти подъемную силу крыла в целом, определим сначала подъемную силу сечения, как отнесенную к единице длины крыла составляющую Ну вектора  пн направление, перпендикулярное вектору скорости потока на бесконечности V впереди крыла, а уже затем просуммируем эти составляющие, умноженные на длину элемента крыла, по всему размаху. Такое определение подъемной силы представляется вполне естественным, если обратить движение и рассматривать движение крыла конечного размаха в неподвижной жидкости. Замечательно, что при этом, наряду с подъемной силой сечения
пн направление, перпендикулярное вектору скорости потока на бесконечности V впереди крыла, а уже затем просуммируем эти составляющие, умноженные на длину элемента крыла, по всему размаху. Такое определение подъемной силы представляется вполне естественным, если обратить движение и рассматривать движение крыла конечного размаха в неподвижной жидкости. Замечательно, что при этом, наряду с подъемной силой сечения  появляется еще составляющая
появляется еще составляющая  главного вектора
главного вектора  по направлению движения, т. е. сила сопротивления. Эту, также отнесенную к единице длины крыла по размаху силу
по направлению движения, т. е. сила сопротивления. Эту, также отнесенную к единице длины крыла по размаху силу  называют индуктивным сопротивлением сечения, а сумму величин
называют индуктивным сопротивлением сечения, а сумму величин  умноженных на элемент длины крыла, вычисленную по всему размаху крыла, называют индуктивным сопротивлением крыла. Как это следует из рис. 150, имеем:
умноженных на элемент длины крыла, вычисленную по всему размаху крыла, называют индуктивным сопротивлением крыла. Как это следует из рис. 150, имеем:

Возникновение в идеальной жидкости сопротивления движению тела представляет лишь кажущееся противоречие с парадоксом Даламбера. При доказательстве правильности парадокса, Даламбера (§ 64)
было оговорено, что тело имеет ограниченные размеры и возмущающее влияние его не распространяется на бесконечность. В рассматриваемом же случае движения крыла конечного размаха образовавшаяся за крылом вихревая пелена тянется до бесконечности, производя возмущения в бесконечном удалении вниз по потоку от крыла. Легко себе представить, что в некоторой аналогии с обтеканием решетки профилей скорость на бесконечности перед крылом конечного размаха не равна скорости на бесконечности за крылом в области вихревой пелены. В этом — основное отличие теории крыла конечного размаха от теории пространственного обтекания тел вообще.

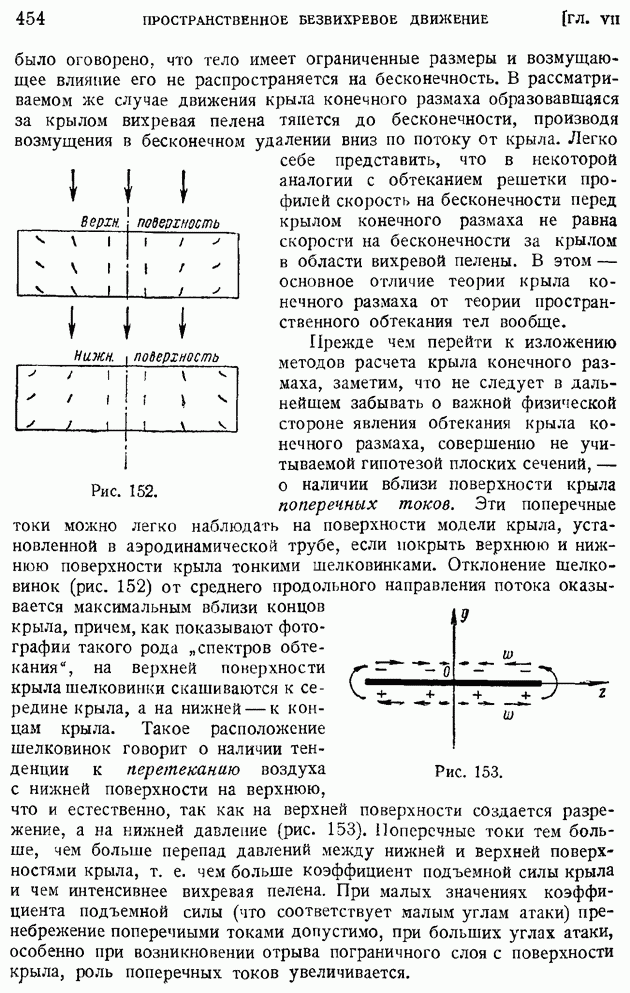
Рис. 152.

Рис. 153.
Прежде чем перейти к изложению методов расчета крыла конечного размаха, заметим, что не следует в дальнейшем забывать о важной физической стороне явления обтекания крыла конечного размаха, совершенно не учитываемой гипотезой плоских сечений, — о наличии вблизи поверхности крыла поперечных токов. Эти поперечные токи можно легко наблюдать на поверхности модели крыла, установленной в аэродинамической трубе, если покрыть верхнюю и нижнюю поверхности крыла тонкими шелковинками. Отклонение шелковинок (рис. 152) от среднего продольного направления потока оказывается максимальным вблизи концов крыла, причем, как показывают фотографии такого рода "спектров обтекания", на верхней поверхности крыла шелковинки скашиваются к середине крыла, а на нижней — к концам крыла. Такое расположение шелковинок говорит о наличии тенденции к перетеканию воздуха с нижней поверхности на верхнюю, что и естественно, так как на верхней поверхности создается разрежение, а на нижней давление (рис. 153). Поперечные токи тем больше, чем больше перепад давлений между нижней и верхней поверхностями крыла, т. е. чем больше коэффициент подъемной силы крыла и чем интенсивнее вихревая пелена. При малых значениях коэффициента подъемной силы (что соответствует малым углам атаки) пренебрежение поперечными токами допустимо, при больших углах атаки, особенно при возникновении отрыва пограничного слоя с поверхности крыла, роль поперечных токов увеличивается.
При дальнейшем изложении методов расчета крыла конечного размаха будем предполагать, что коэффициент подъемной силы невелик, вихревая пелена имеет малую интенсивность, а следовательно, малы все индуктивные скорости, малы и поперечные токи.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Предмет механики жидкости и газа. Основные свойства «макромодели» жидкости и газа: сплошность и подвижность
- § 2. Основные методы механики жидкости и газа. Области применения и главнейшие задачи
- § 3. Краткий очерк исторического развития механики жидкости и газа. От гидромеханики древних до установления воззрений ньютонианской эпохи
- § 4. Эпоха Эйлера и Бернулли. Гидроаэродинамика в XIX в.
- § 5. Современный этап развития механики жидкости и газа
- ГЛАВА I. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
- § 6. Поле физической величины. Скалярное и векторное поля. Поверхности уровня. Векторные линин и трубки
- § 7. Мера однородности поля в данном направлении и в дайной точке. Градиевт скалярного поля и дифференциальный тензор векторного поля как меры неоднородности поля
- § 8. Задание движения сплошной среды. Поле скоростей. Линии тока и траектории
- § 9. Поле ускорений. Разложение ускорения частицы на локальную и конвективную составляющие
- § 10. Скоростное поле сплошной среды в окрестности данной точки. Угловая скорость и вихрь. Тензор скоростей деформаций и его компоненты
- § 11. Скорость объемного расширения жидкости. Интегральные представления дифференциальных операторов поля. Основные интегральные формулы
- § 12. Вихревые линии и трубки. Вторая теорема Гельмгольца. Интенсивность вихревой трубки
- § 13. Выражение интенсивности вихревой трубки через циркуляцию вектора по контуру, охватывающему трубку. Теорема об изменении циркуляции скорости во времени
- ГЛАВА II. ОСНОВНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ И РАВНОВЕСИЯ СПЛОШНОЙ СРЕДЫ
- § 14. Распределение массы в сплошной среде. Плотность и удельный вес. Напряжения. Тензор напряженности и его симметричность
- § 15. Общие уравнения динамики сплошной среды. Уравнение неразрывности. Уравнения динамики в напряжениях
- § 16. Тепловые явления в жидкостях и газах. Закон сохранения энергии и уравнение баланса энергии
- § 17. Общие уравнения равновесного состояния жидкости и газа. Равновесие воздуха в атмосфере. Приближенные барометрические формулы. Стандартная атмосфера
- § 18. Равновесие несжимаемой жидкости. Уравнение поверхности раздела. Равновесие вращающейся жидкости
- § 19. Давление тяжелой несжимаемой жидкости на поверхность тела. Сила и момент, приложенные к телу, плавающему в тяжелой жидкости. Случай вращающейся жидкости
- ГЛАВА III. ДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ И ГАЗА. ОСНОВНЫЕ УРАВНЕНИЯ И ОБЩИЕ ТЕОРЕМЫ
- § 20. Идеальная жидкость. Основные уравнения движения
- § 21. Закон сохранения энергии в движущейся идеальной жидкости. Адиабатическое движение. Сохранение энтропии
- § 22. Эйлерово представление конвективного изменения объемного интеграла. Перенос величины сквозь контрольную поверхность
- § 23. Эйлерова форма законов сохранения массы и энергии, теоремы количеств движения и момента количеств движения при стационарном движении идеальной жидкости
- § 24. Теорема об изменении кинетической энергии. Работа и мощность внутренних сил. Эйлерова форма уравнения изменения кинетической энергии
- § 25. Теорема Бернулли о сохранении полной механической энергии при стационарном баротропном движении идеальной жидкости и газа
- ГЛАВА IV. ОДНОМЕРНЫЙ ПОТОК ИДЕАЛЬНОЙ ЖИДКОСТИ
- § 26. Одномерное течение идеальной сжимаемой жидкости. Линеаризированные уравнения. Скорость распространения малых возмущений в жидкости или газе
- § 27. Изотермическая и адиабатическая скорости звука. «Конус возмущений» при сверхзвуковом движении источника возмущения. Число M и его связь с углом конуса возмущений
- § 28. Распространение непрерывных возмущений конечной интенсивности. Характеристики. Образование разрывной ударной волны
- § 29. Стоячая ударная волна или скачок уплотнения. Ударная адиабата
- § 30. Критические величины в одномерном потоке газа. Связь между скоростями до и после скачка. Изменение давления, плотности и температуры в скачке уплотнения
- § 31. Скорость распространения ударной волны. Спутное движение газа за ударной волной
- § 32. Влияние интенсивности скачка уплотнения на сжатие газа. Измерение скоростей и давлений в до- и сверхзвуковых потоках
- § 33. Одномерное движение газа по трубе переменного сечения. Истечение из резервуара большой емкости сквозь сходящееся сопло
- § 34. Одномерное течение в сопле Лаваля. Движение газа с притоком тепла
- ГЛАВА V. БЕЗВИХРЕВОЕ ДВИЖЕНИЕ ЖИДКОСТИ. ПЛОСКОЕ ДВИЖЕНИЕ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 35. Сохранение циркуляции скорости в потоке идеальной жидкости. Теорема Кельвина и Лаграижа. Безвихревое движение. Потенциал скоростей
- § 36. Интеграл Лагранжа — Коши уравнений безвихревого движения. Теорема Бернулли. Некоторые общие свойства безвихревого движения идеальной несжимаемой жидкости в односвязной области
- § 37. Плоское безвихревое движение несжимаемой жидкости. Потенциал скоростей и функция тока. Применение функций комплексного переменного. Комплексный потенциал и сопряженная скорость
- § 38. Построение полей течения по заданной характеристической Функции. Простейшие плоские потоки и их наложение
- § 39. Бесциркуляционное и циркуляционное обтекания круглого цилиндра
- § 40. Применение криволинейных координат. Бесциркуляционное и циркуляционное обтекания эллиптического цилиндра и пластинки. Задача Жуковского об обтекании решетки пластин.
- § 41. Плоское движение с отрывом струй. Разрывное обтекание пластинки и протекание жидкости сквозь отверстие
- § 42. Прямая задача в теории плоского движения идеальной несжимаемой жидкости. Применение метода конформных отображений. Гипотеза Чаплыгина о безотрывном обтекании задней кромки профиля. Формула циркуляции
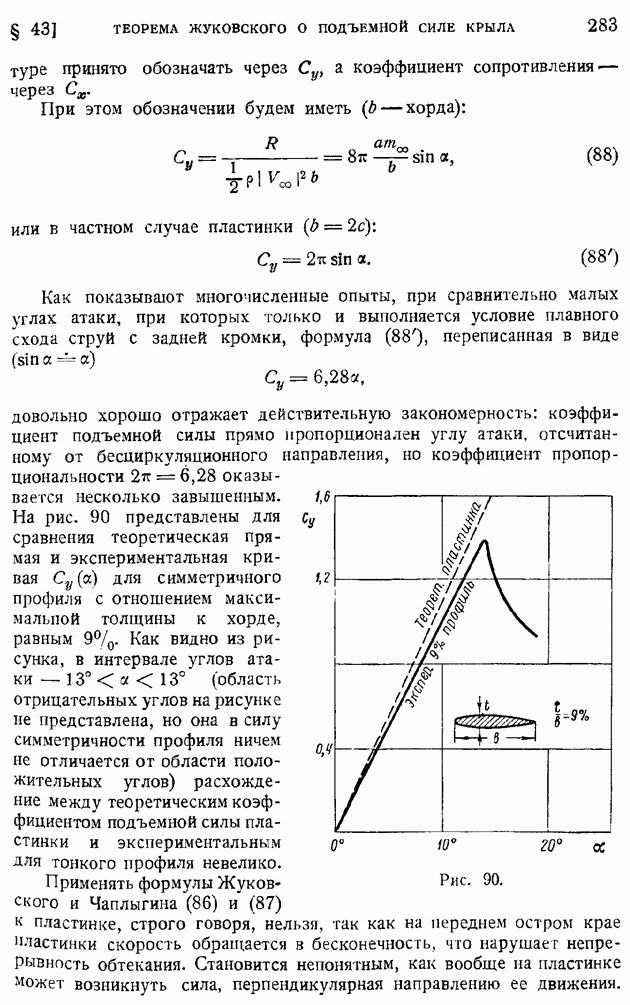
- § 43. Теорема Жуковского о подъемной силе крыла. Зависимость подъемной силы от угла атаки. Коэффициент подъемной силы
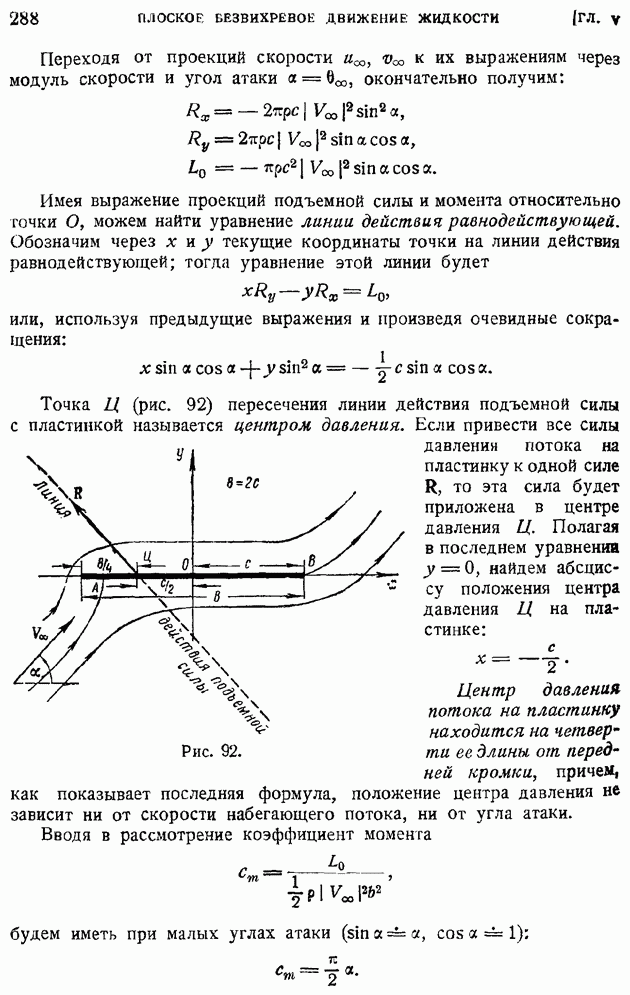
- § 44. Применение метода комплексных переменных к выводу теоремы Жуковского. Формулы Чаплыгина для главного вектора и момента сил давления потока на крыло
- § 45. Выражение главного момента сил давления потока через коэффициенты конформного отображения. Фокус крыла. Независимость от угла атаки момента относительно фокуса. Парабола устойчивости
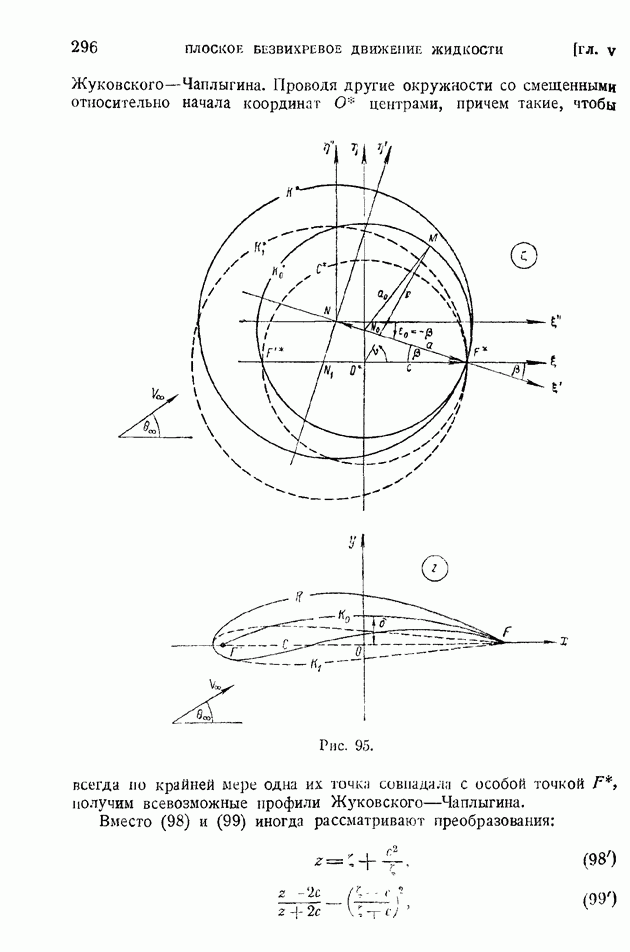
- § 46. Частные случаи конформного отображения крылового профиля на круг. Преобразование Жуковского-Чаплыгина. Теоретические крыловые профили
- § 47. Задача об обтекании слабо изогнутой дужки произвольной формы (теория тонкого крыла)
- § 48. Определение обтекания крылового профиля произвольной формы
- § 49. Обобщение теоремы Жуковского на случай плоской решетки с бесчисленным множеством профилей
- ГЛАВА VI. ПЛОСКОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ СЖИМАЕМОГО ГАЗА
- § 50. Основные уравнения плоского стационарного безвихревого движения сжимаемого газа. Линеаризированные уравнения
- 51. Линеаризированный до- и сверхзвуковой газовый поток вдоль волнистой стенки
- § 52. Тонкое крыло в линеаризированном до- и сверхзвуковом потоках. Влияние сжимаемости газа на коэффициент подъемной силы в дозвуковом потоке. Коэффициенты подъемной силы и волнового сопротивления при сверхзвуковом потоке
- § 53. Нелинеаризированные уравнения движения идеального сжимаемого газа. Переход в плоскость годографа. Уравнения Чаплыгина
- § 54. Метод С. А. Христиановича. Приближенные формулы учета влияния сжимаемости на распределение давления
- § 55. Критическое число M и его определение по заданному распределению давления в несжимаемом обтекании. Поведение коэффициента подъемной силы и момента при около- и закритических значениях числа M
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
- § 57. Нелинеаризированный сверхзвуковой поток. «Характеристики» уравнений плоского сверхзвукового потока. Линин возмущения и их основные свойства
- § 58. Обтекание выпуклого угла сверхзвуковым потоком. Влияние угла поворота струи на ее газодинамические элементы
- § 59. Сверхзвуковой поток внутри тупого угла. Косой скачок уплотнения. Связь между газодинамическими элементами до и за косым скачком
- ГЛАВА VII. ПРОСТРАНСТВЕННОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ
- § 60. Ортогональные криволинейные координаты в пространстве. Основные дифференциальные операторы поля в криволинейных координатах
- § 61. Потенциал скоростей. Поле источника и диполя. Непрерывное распределение источников и диполей. Ньютонов потенциал. Потенциал простого и двойного слоев
- § 62. Поле скоростей вокруг заданной системы вихрей. Формула Био — Савара. Потенциал скоростей замкнутой вихревой нити. Аналогия с потенциалом двойного слоя
- § 63. Функция тока и ее связь с векторным потенциалом скоростей. Функции тока простейших течений
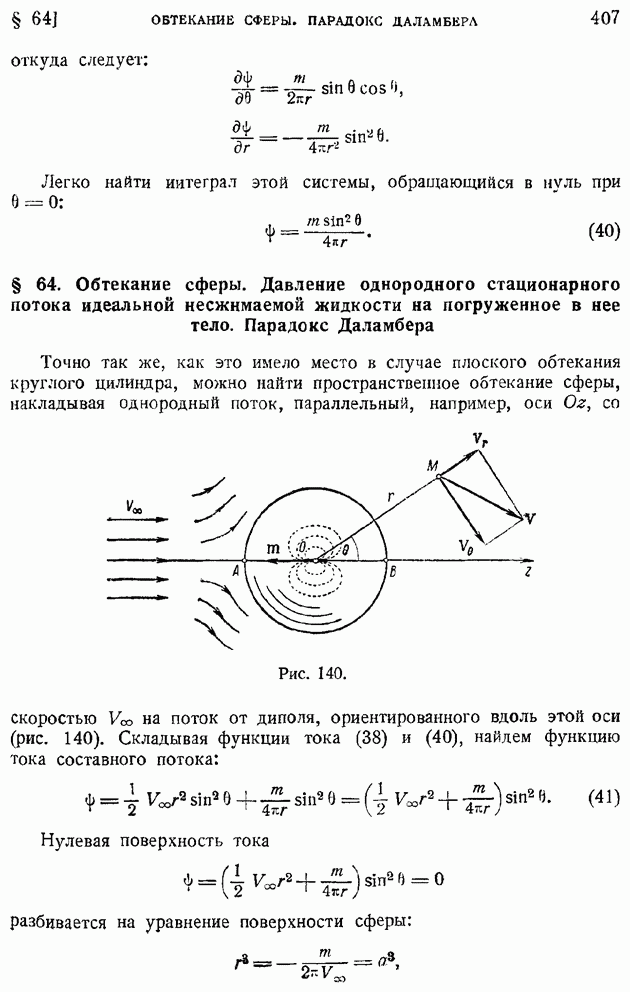
- § 64. Обтекание сферы. Давление однородного стационарного потока идеальной несжимаемой жидкости на погруженное в нее тело. Парадокс Даламбера
- § 65. Общие уравнения осесимметричного движения. Применение цилиндрических координат. Течение сквозь каналы
- § 66. Осесимметричное продольное обтекание тел вращения. Случай эллипсоида вращения
- § 67. Поперечное обтекание тел вращения. Пример эллипсоида вращения
- § 68. Продольное и поперечное обтекание тел вращения большого удлинения. Приближенные выражения граничных условий. Применение тригонометрических сумм для определения коэффициентов …
- § 69. Метод «особенностей». Применение непрерывно распределенных источников (стоков) и диполей для решения задачи о продольном и поперечном обтекании тел вращения
- § 70. Общий случай движения твердого тела сквозь несжимаемую идеальную жидкость. Определение потенциала скоростей. Главный вектор и главный момент сил давления потока на тело
- § 71. Коэффициенты «присоединенных масс». Свойство симметрии. «Присоединенная» кинетическая энергия. Определение «присоединенных масс» поступательно движущегося цилиндра, шара и эллипсоида
- § 72. Элементы теории крыла конечного размаха. Вихревая система крыла. Гипотеза плоских сечеиий. Геометрические и действительные углы атаки. Подъемная сила и «индуктивное сопротивление»
- § 73. Основные формулы теории «несущей линии». «Индуктивная скорость» и «индуктивный угол». Прямая задача определения подъемной силы и индуктивного сопротивления по заданному распределению циркуляции
- § 74. Крыло с минимальным индуктивным сопротивлением. Эллиптическое распределение циркуляции. Связь между коэффициентами индуктивного сопротивления и подъемной силы. Основное уравнение теории крыла и понятие о его интегрировании
- ГЛАВА VIII. ДИНАМИКА ВЯЗКОЙ ЖИДКОСТИ И ГАЗА
- § 75. Внутреннее трение и теплопроводность в жидкостях и газах. Законы Ньютона и Фурье. Влияние температуры на коэффициенты вязкости и теплопроводности. Число «сигма»
- § 76. Обобщение закона Ньютона на случай произвольного движения среды. Закон линейной связи между тензорами напряжений и скоростей деформации
- § 77. Общие уравнения движения вязкой жидкости. Динамические уравнения и уравнение баланса энергии. Граничные условия движения жидкости с треннем и теплопроводностью
- § 78. Понятие о подобии гидродинамических явлений. Безразмерные уравнения движения вязкой жидкости и газа. Условия подобия
- § 79. Ламинарное движение вязкой несжимаемой жидкости по цилиндрической трубе
- § 80. Обтекание шара при очень малых значениях числа Рейнольдса. Формула сопротивления шара по Стоксу и ее обобщения
- § 81. Вихревые линии в идеальной и вязкой жидкости. Сохраняемость вихревых линий при отсутствии внутреннего трения. Диффузия вихря в вязкой жидкости
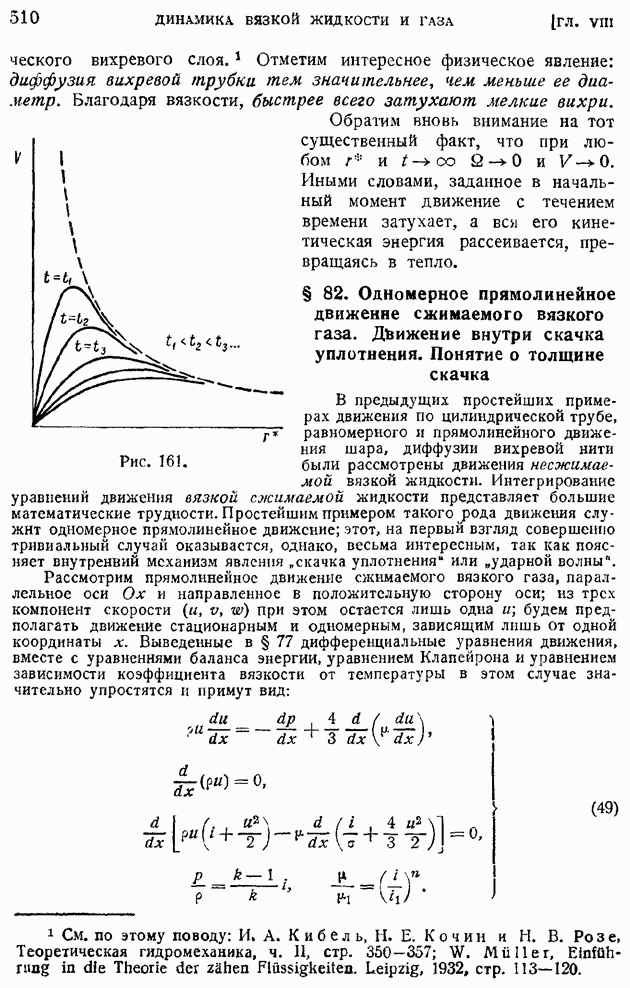
- § 82. Одномерное прямолинейное движение сжимаемого вязкого газа. Движение внутри скачка уплотнения. Понятие о толщине скачка
- § 83. Работа внутренних сил и диссипация механической энергии в движущейся вязкой среде
- § 84. Обтекание тел жидкостью и газом при больших значениях числа Рейнольдса. Основные уравнения теории ламинарного пограничного слоя
- § 85. Ламинарный пограничный слой на пластинке, продольно обтекаемой несжимаемой жидкостью. Неизотермическое движение
- § 86. Ламинарный пограничный слой при степенном задании скорости внешнего потока
- § 87. Ламинарный пограничный слой в общем случае задания скорости внешнего потока. Применение уравнения импульсов для приближенного расчета ламинарного пограничного слоя
- § 88. Способы определения функций … Приближенный метод расчета ламинарного пограничного слоя
- § 89. Ламинарный пограничный слой на пластинке, продольно обтекаемой сжимаемым газом при больших скоростях. Случай линейной зависимости коэффициента вязкости от температуры (n = 1)
- § 90. Ламинарный пограничный слой на пластинке при любом законе связи между вязкостью и температурой и при числе … Обтекание крылового профиля потоком больших скоростей
- ГЛАВА IX. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ
- § 91. Переход ламинарного движения в турбулентное. Критическое рейнольдсово число
- § 92. Область и «точка» перехода. Явление «кризиса обтекания»
- § 93. Основные уравнения осреднеиного турбулентного движения. Тензор турбулентных напряжений
- § 94. Турбулентное движение жидкости в плоской и круглой трубе. Логарифмические формулы скоростей
- § 95. Формулы сопротивления гладких труб при турбулентном движении жидкости. Ламинарный подслой
- § 96. Влияние шероховатости стенок трубы на ее сопротивление. Предельные режимы течения. Режим установившейся шероховатости
- § 97. Турбулентный пограничный слой на продольно обтекаемой пластине. Сопротивление пластины
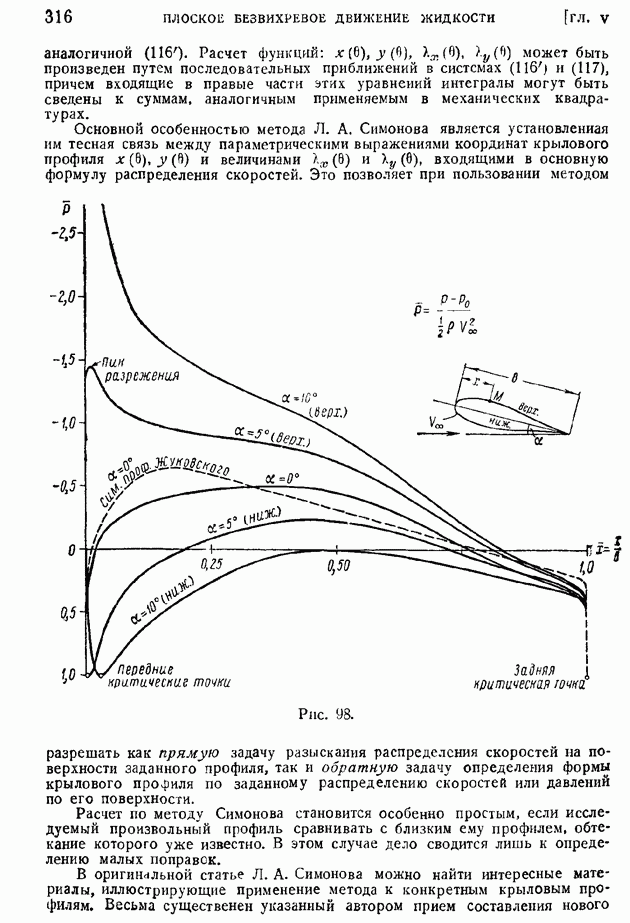
- § 98. Турбулентный пограничный слой на крыловом профиле при малом продольном перепаде давлений
- § 99. Турбулентный пограничный слой на крыловом профиле при значительных продольных перепадах давления
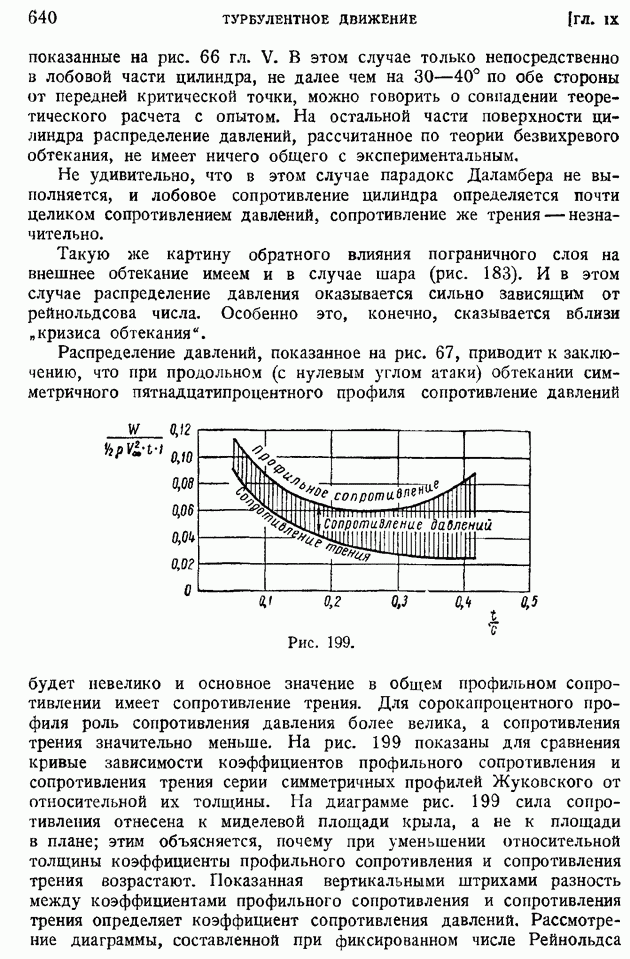
- § 100. Профильное сопротивление крыла. Разложение профильного сопротивления на сопротивление трения и сопротивление давлений. Обратное влияние пограничного слоя на распределение давлений по поверхности обтекаемого профиля
- § 101. Приближенные формулы профильного сопротивления крыла и крылового профиля в решетке
- § 102. Основные закономерности «свободной турбулентности». Плоская турбулентная струя в пространстве, заполненном той же жидкостью
- § 103. Турбулентный след за обтекаемым телом
- § 104. Рассеяние турбулентных возмущений в жидкости. Случай изотропной и однородной турбулентности. Закон сохранения момента возмущений