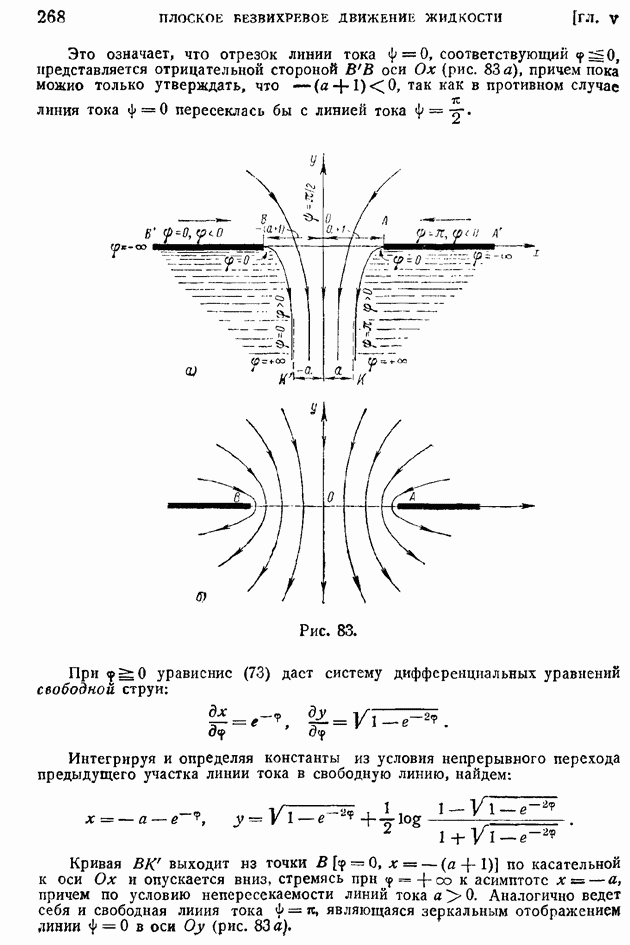
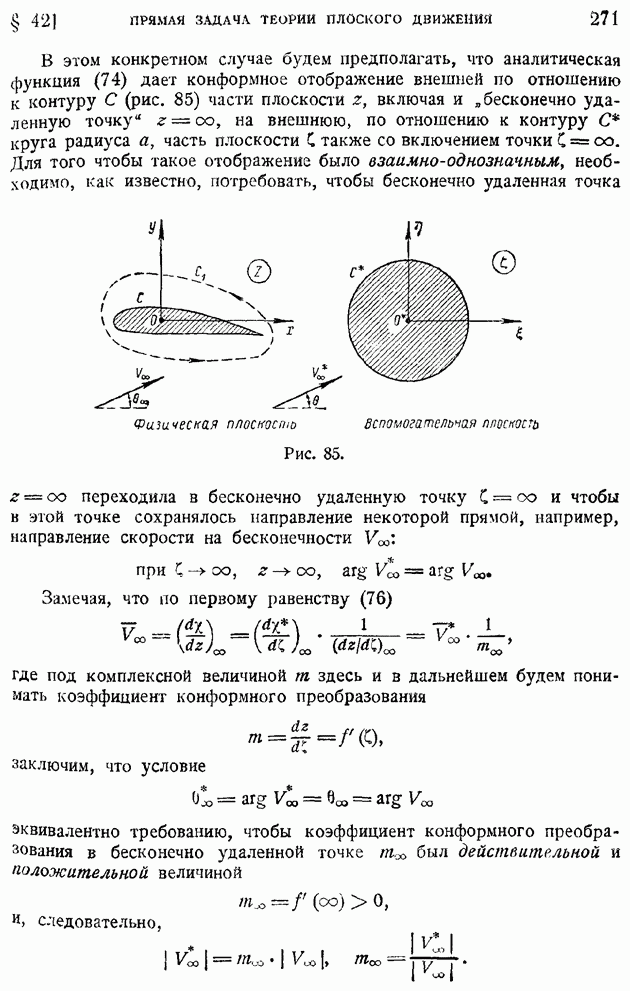
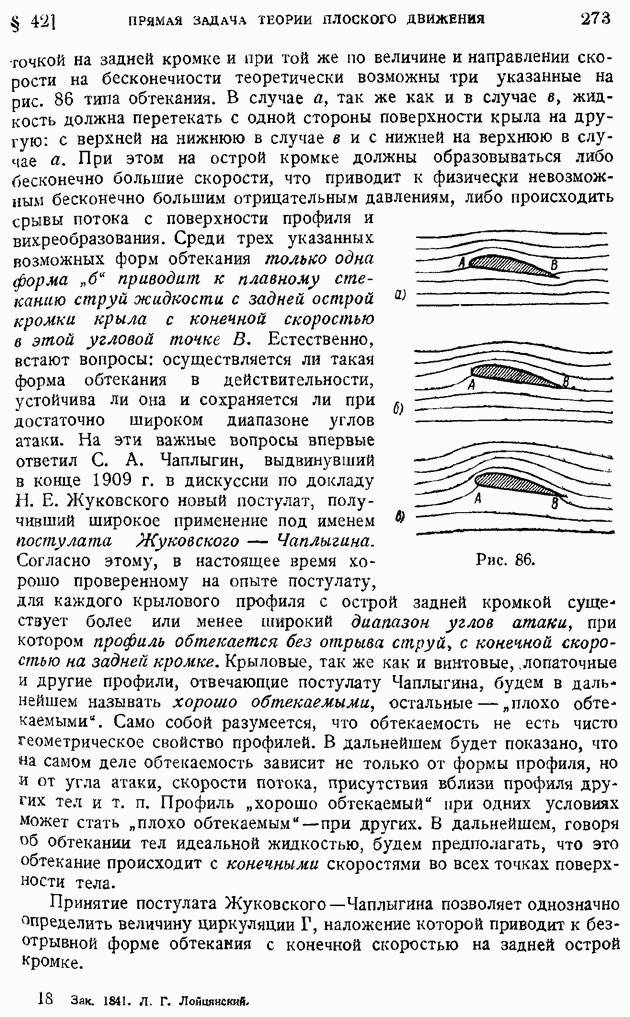
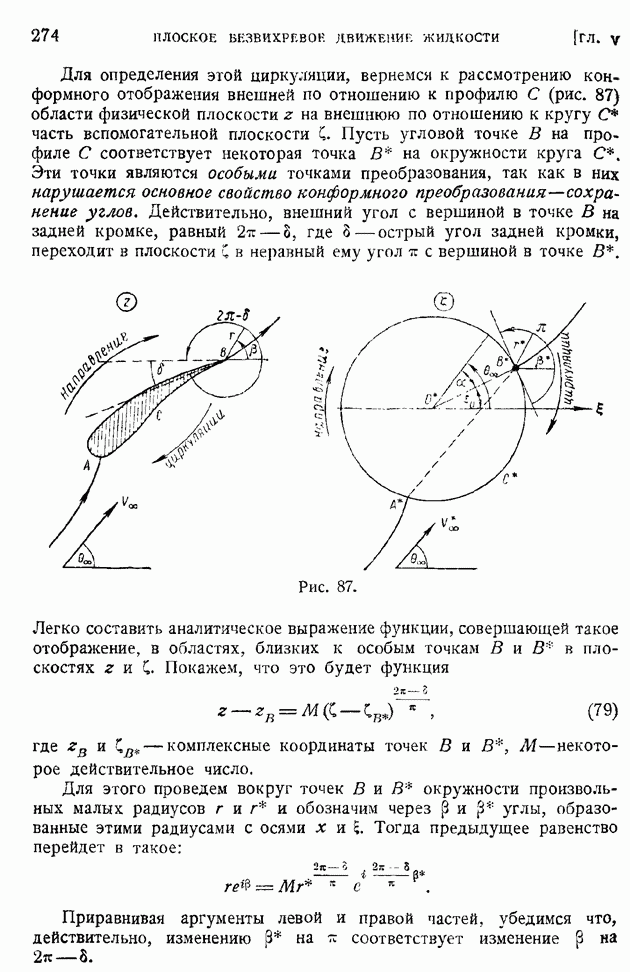
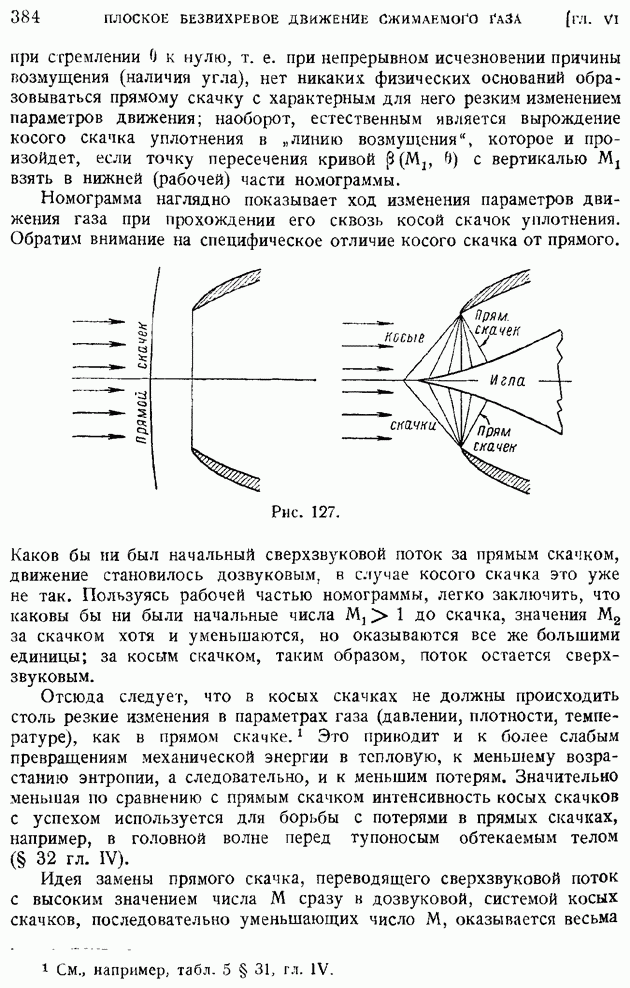
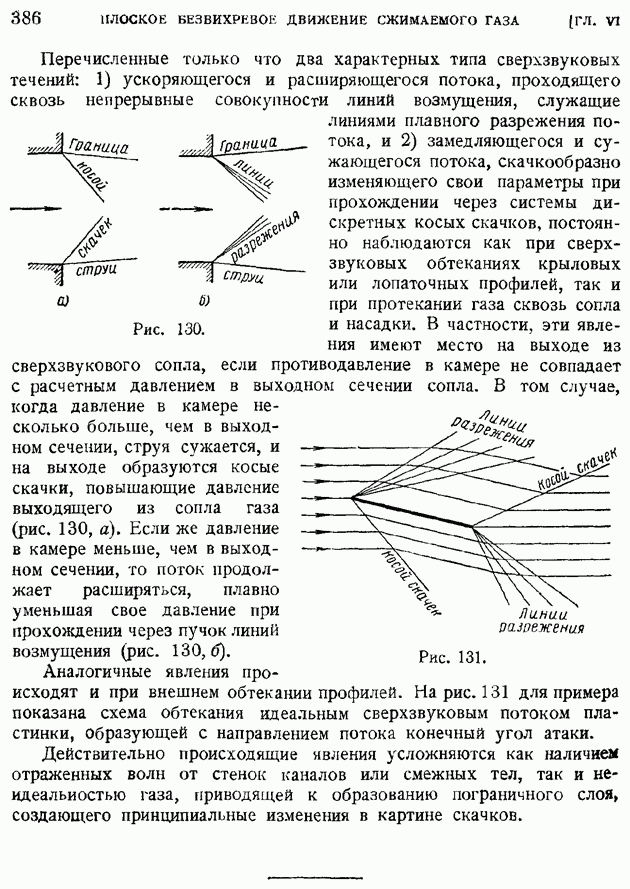
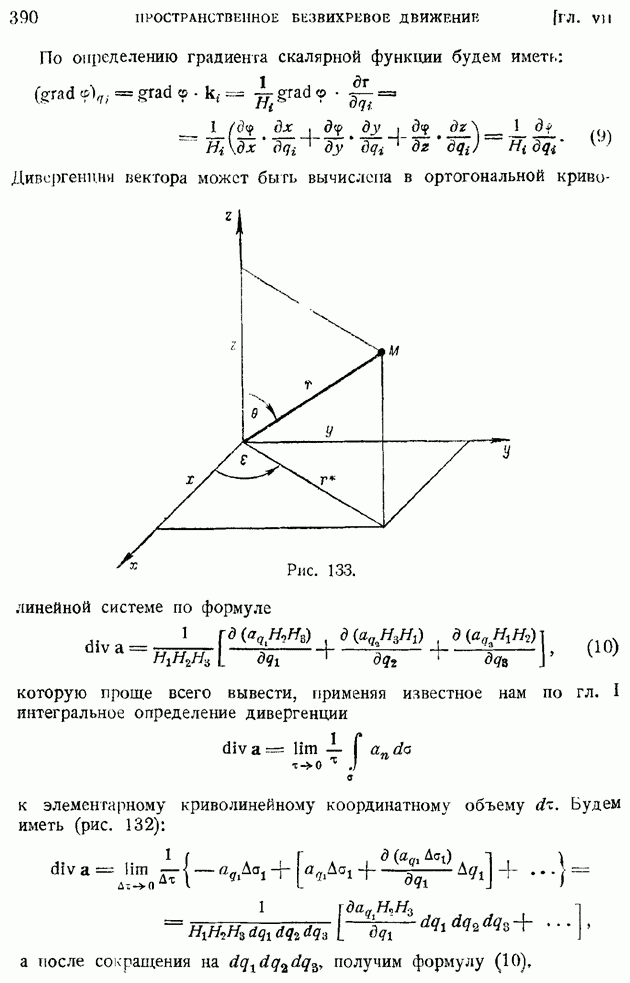
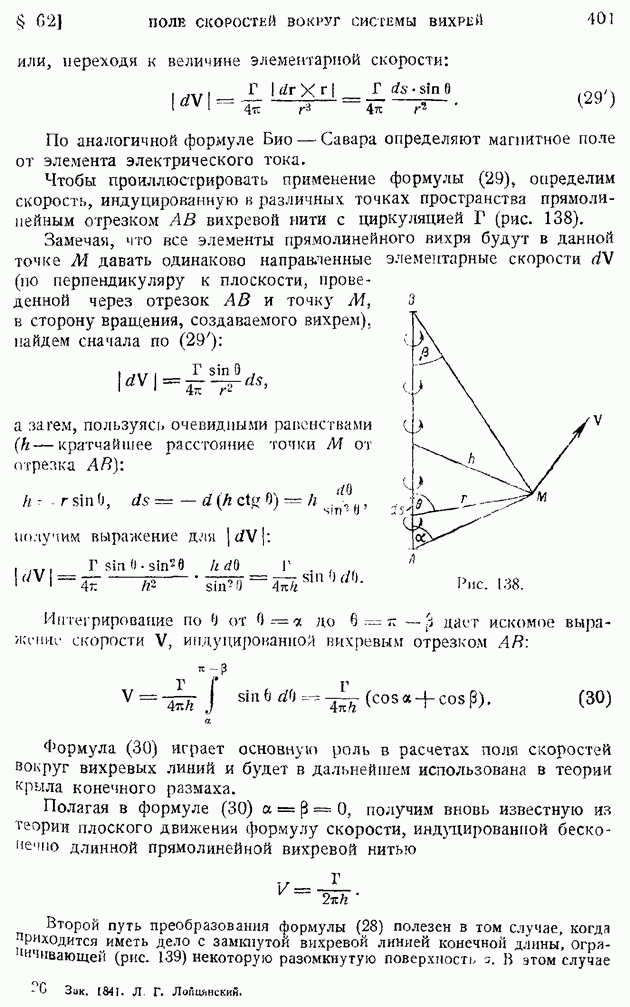
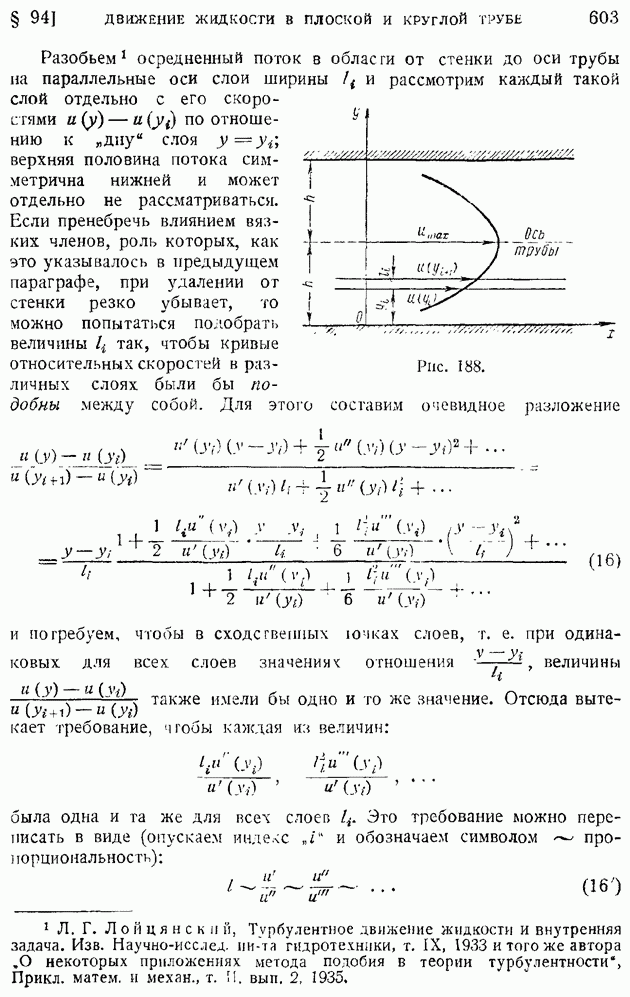
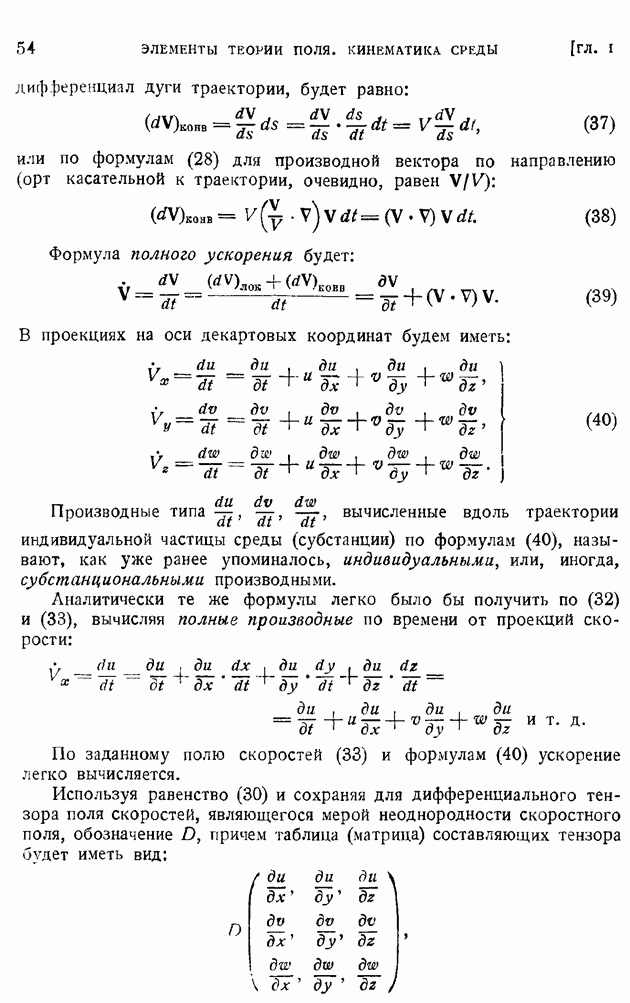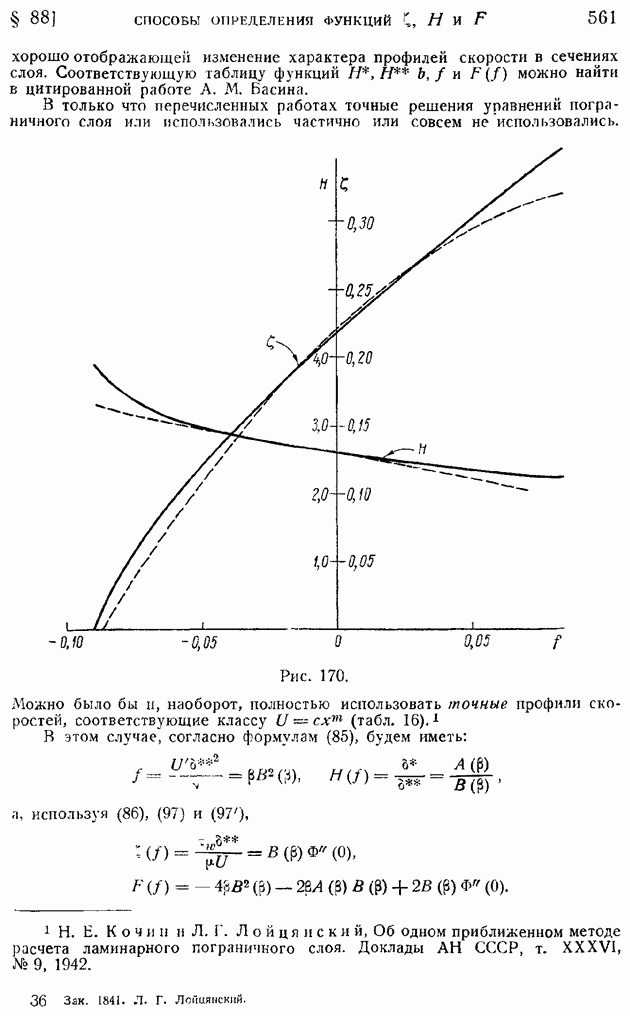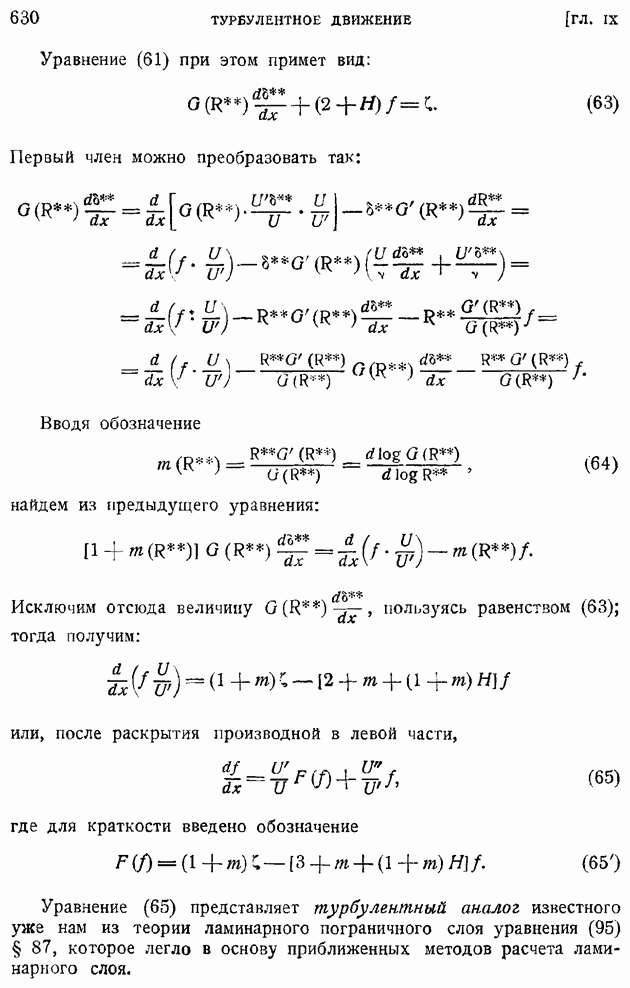| << Предыдущий параграф |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 104. Рассеяние турбулентных возмущений в жидкости. Случай изотропной и однородной турбулентности. Закон сохранения момента возмущений
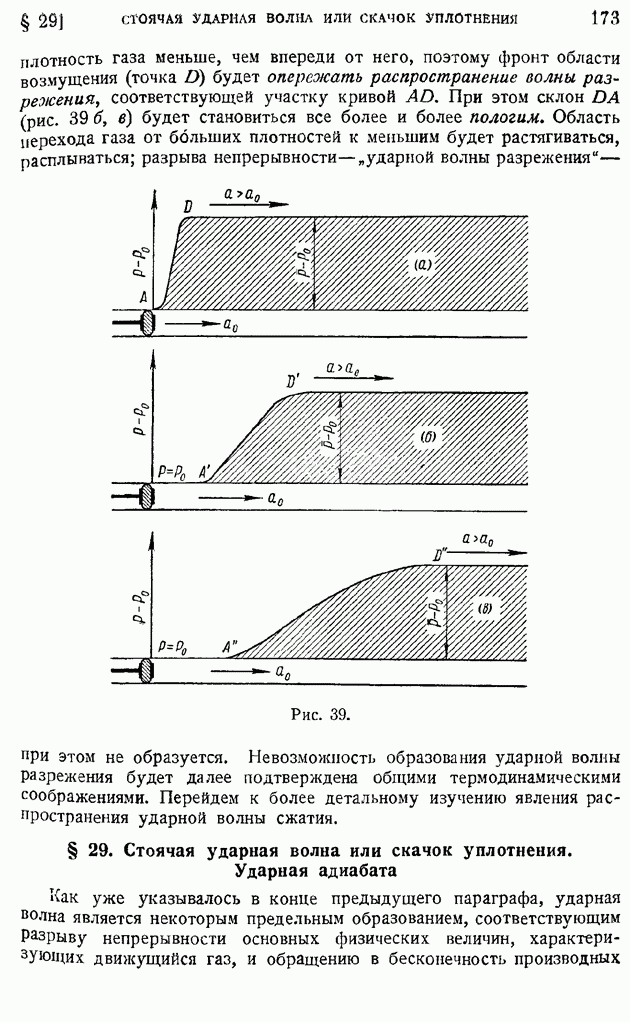
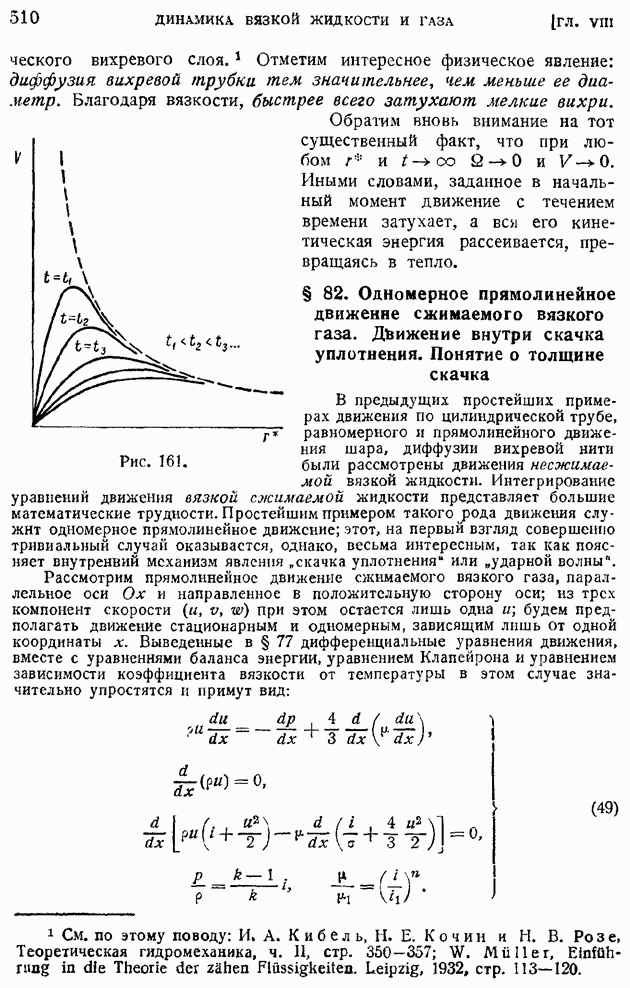
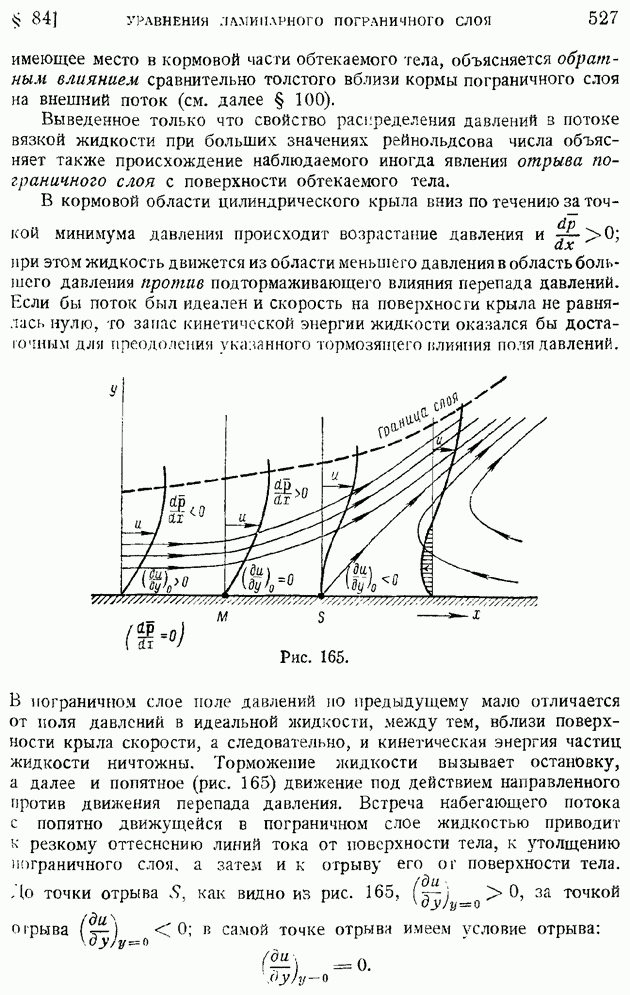
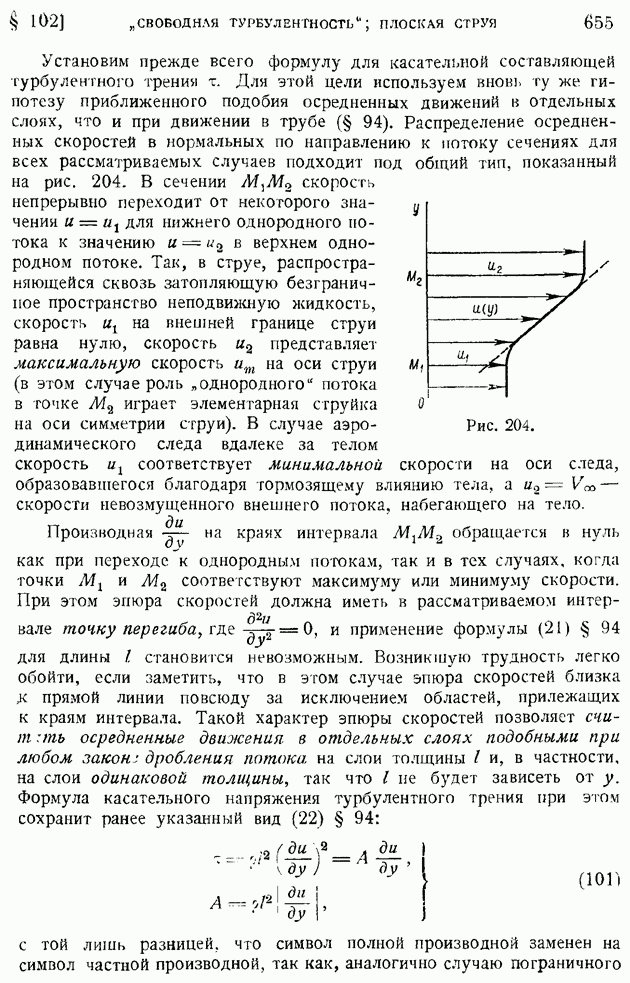
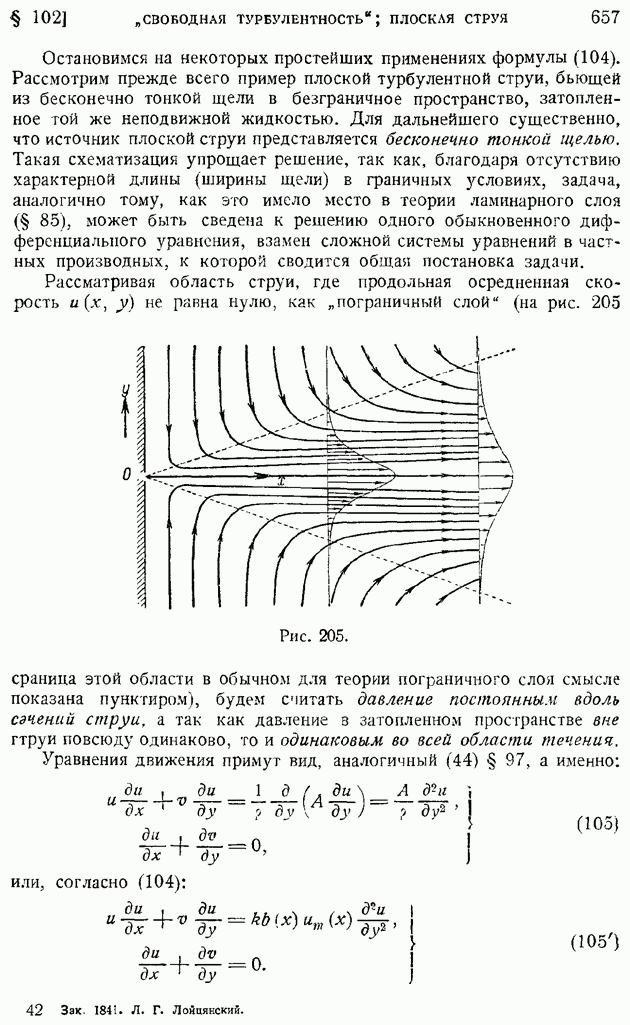
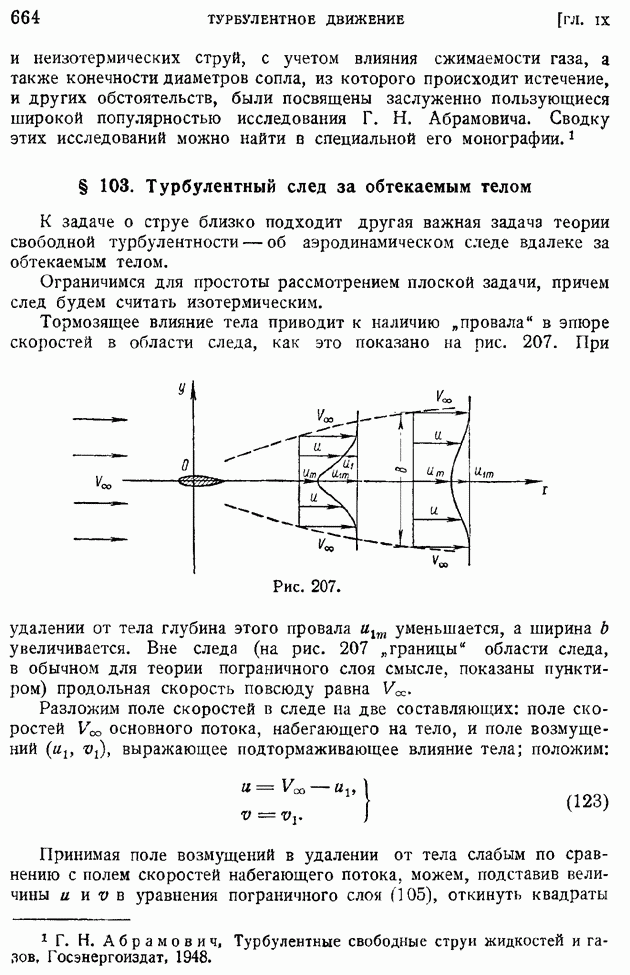
В предыдущих двух параграфах было показано, как происходит затухание неоднородности поля осредненных скоростей в турбулентной струе и следе при удалении от источника возникновения их. Не следует, однако, думать, что выравнивание поля осредненных скоростей приводит одновременно и к исчезновению пульсаций скорости, т. е. к затуханию турбулентности. Опыты показывают, что вдалеке за телом, уже после того, как практически исчезнет изображенный на рис. 207 провал скоростей, на значительном расстоянии вниз по потоку сохраняются турбулентные возмущения, энергия которых сравнительно медленно рассеивается, превращаясь благодаря вязкости жидкости в тепло.
Явление рассеяния турбулентных возмущений представляет особенно большой интерес при изучении потоков, прошедших сквозь сетки с небольшими размерами ячеек и малыми диаметрами проволоки. Такого рода сетки применяются для создания однородных, мало турбулентных потоков в рабочих участках аэродинамических труб. Возникшие в жидкости в силу различных случайностей крупные вихри при прохождении сквозь сетку разбиваются на мелкие, имеющие тот же порядок размера, что и ячейки сетки. Как уже упоминалось ранее (§ 81), диффузия вихрей происходит тем быстрее, чем вихри меньше по размерам. В силу этого обстоятельства измельченные сеткой вихри быстро затухают и в рабочем участке трубы, расположенном в некотором удалении от "фильтрующей" сетки, создается спокойный малотурбулентный поток. Потребное для успокоения потока расстояние от сетки выражается в калибрах сетки и практически не превышает тысячи калибров, что при малых размерах ячейки не является для аэродинамической трубы слишком стеснительным с конструктивной точки зрения.
Теоретическое рассмотрение явления диффузии турбулентных возмущений представляет большую сложность и требует применения тонких статистических методов. Остановимся на некоторых результатах существующих в настоящее время пока еще далеко не совершенных теорий, позволяющих все же разобраться в основных тенденциях явления.
Остановимся на случае так называемой однородной турбулентности, под которой подразумевают движение жидкости с однородным полем осредненных во времени величин, определенных в данной точке пространства, в том числе и поля осредненных скоростей. При этом предполагается, что турбулентные пульсации скоростей существуют даже и в том частном случае, когда осредненные скорости повсюду равны нулю. Чтобы охарактеризовать распределение пульсаций в потоке и их взаимную связь, обозначим через  векторы пульсаций скорости в двух каких-нибудь точках
векторы пульсаций скорости в двух каких-нибудь точках 
и  и составим, следуя замечательной идее наших советских исследователей А. А. Фридмана и Л. В. Келлера, моменты связи между пульсационными скоростями:
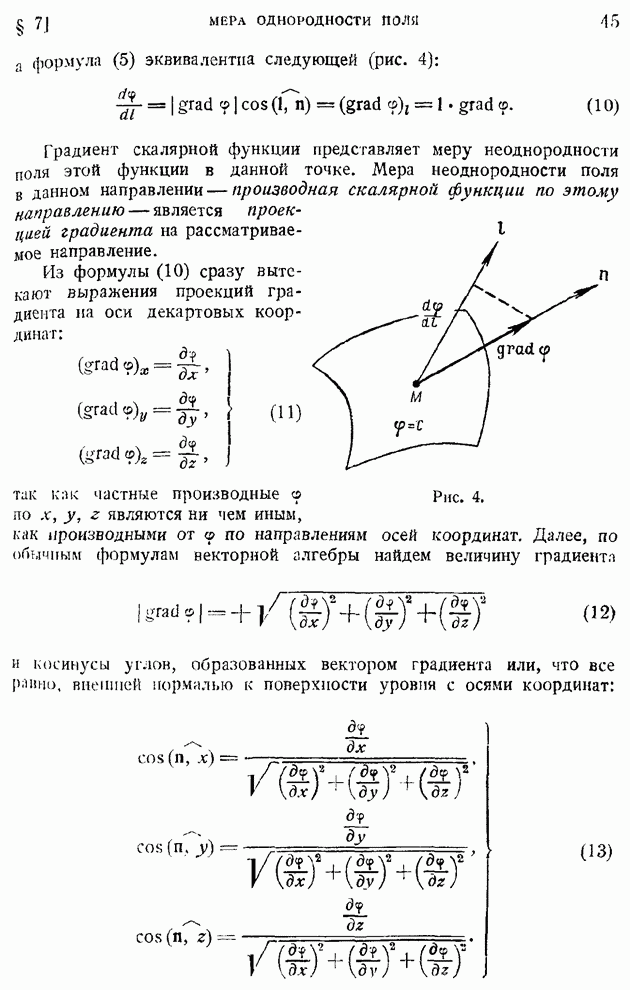
и составим, следуя замечательной идее наших советских исследователей А. А. Фридмана и Л. В. Келлера, моменты связи между пульсационными скоростями:
а) второго порядка

б) третьего порядка

Здесь подстрочные индексы означают перенумерованные оси координат, а черта сверху — осреднение во времени, подчиняющееся тем же основным равенствам, что и указанные ранее в § 93. Величины  и
и  характеризуют статистическую связанность между пульсациями скоростей в точках
характеризуют статистическую связанность между пульсациями скоростей в точках  Совокупности их образуют соответственно теизоры второго и третьего рангов.
Совокупности их образуют соответственно теизоры второго и третьего рангов.
В общем случае однородной турбулентности компоненты  являются функциями вектора
являются функциями вектора  характеризующего взаимное расположение точек
характеризующего взаимное расположение точек  и
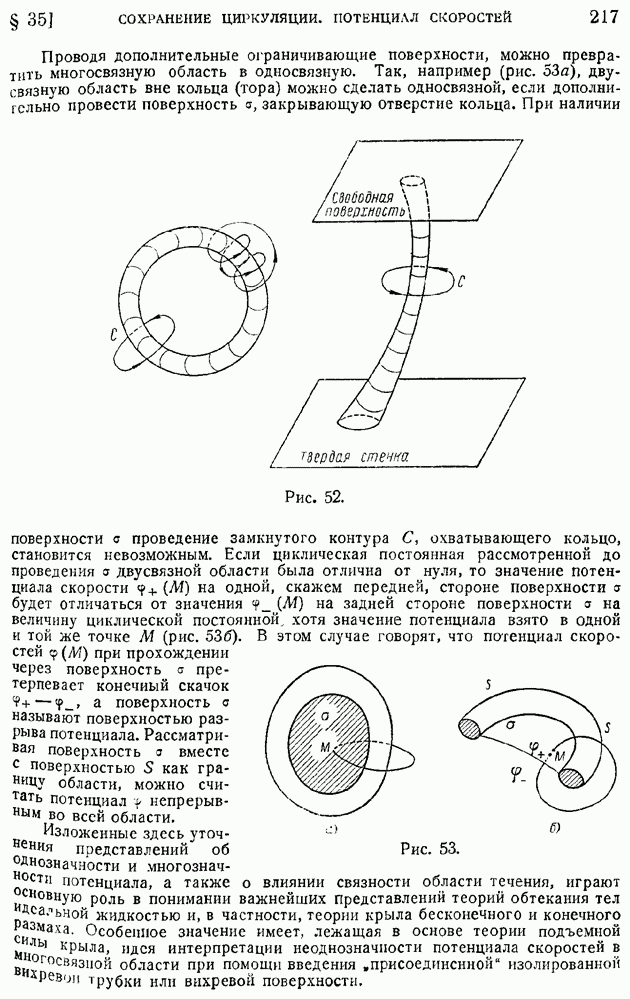
и  Предположим теперь, что в некоторый начальный момент в неподвижной жидкости, заполняющей безграничное пространство, создано непрерывное однородное поле начальных возмущений, которое с течением времени будет затухать (рассеиваться). Легко сообразить, что и в любой последующий момент времени поле затухающих во времени возмущений останется однородным. Кроме того, при равноправности любых направлений в пространстве поле возмущений окажется изотропным в том смысле, что указанные выше тензоры моментов связи будут функциями только расстояния
Предположим теперь, что в некоторый начальный момент в неподвижной жидкости, заполняющей безграничное пространство, создано непрерывное однородное поле начальных возмущений, которое с течением времени будет затухать (рассеиваться). Легко сообразить, что и в любой последующий момент времени поле затухающих во времени возмущений останется однородным. Кроме того, при равноправности любых направлений в пространстве поле возмущений окажется изотропным в том смысле, что указанные выше тензоры моментов связи будут функциями только расстояния  между точками
между точками  и не будут зависеть от направления вектора
и не будут зависеть от направления вектора 
Как показывают простые вычисления, в случае такой, однородной и изотропной, турбулентности компоненты тензора  могут быть выражены через две функции, представляющие моменты связи между составляющими скоростей пульсаций в точках
могут быть выражены через две функции, представляющие моменты связи между составляющими скоростей пульсаций в точках  1) направленными вдоль отрезка
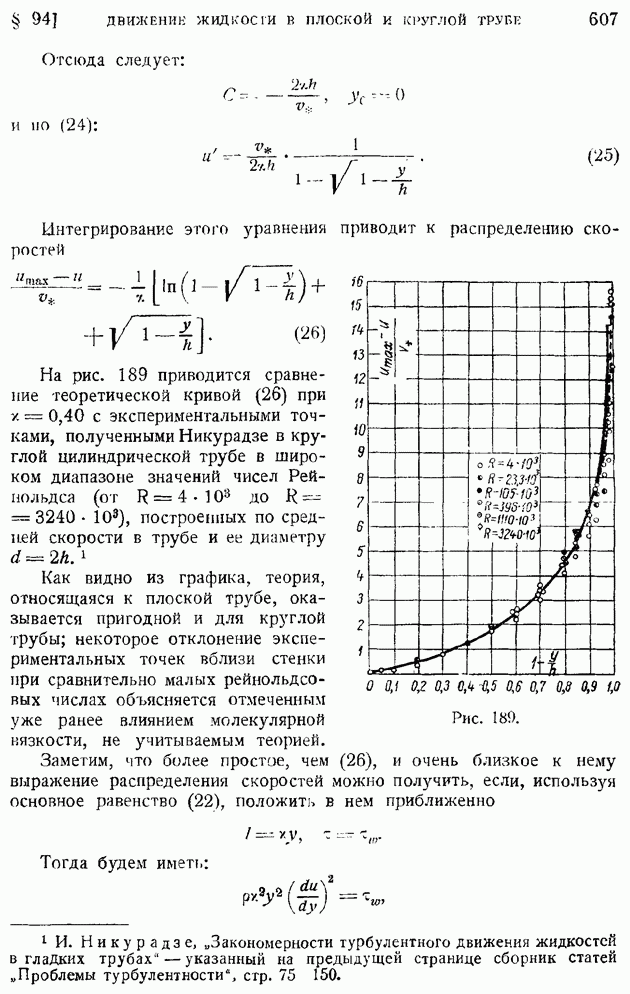
1) направленными вдоль отрезка  (продольные составляющие) и 2) нормально к этому отрезку (поперечные составляющие). Точно так же и компоненты
(продольные составляющие) и 2) нормально к этому отрезку (поперечные составляющие). Точно так же и компоненты  могут быть выражены через три величины моментов связей третьего порядка между продольными и поперечными составляющими пульсационных скоростей в точках
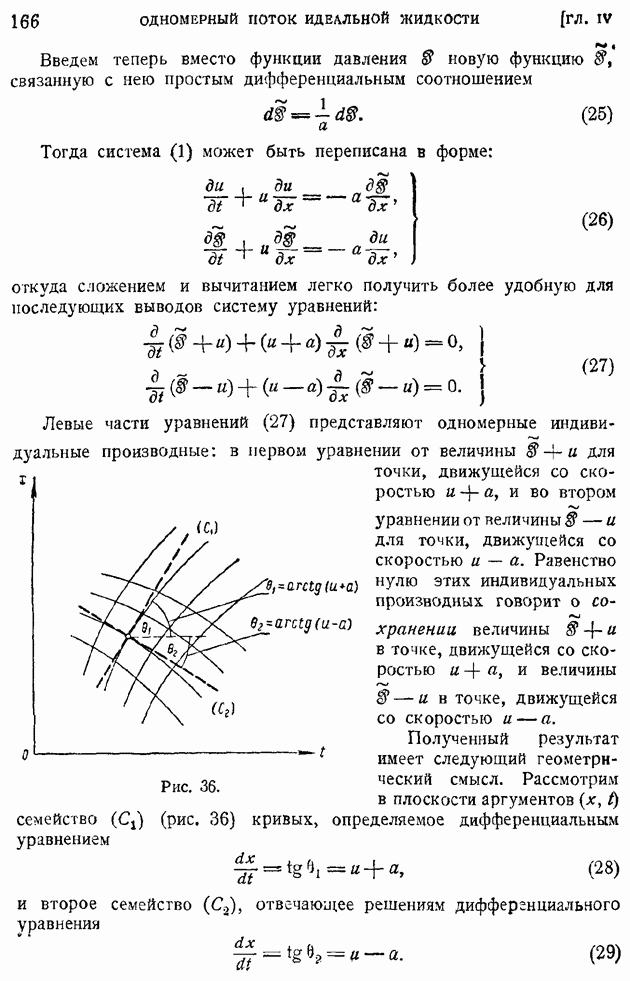
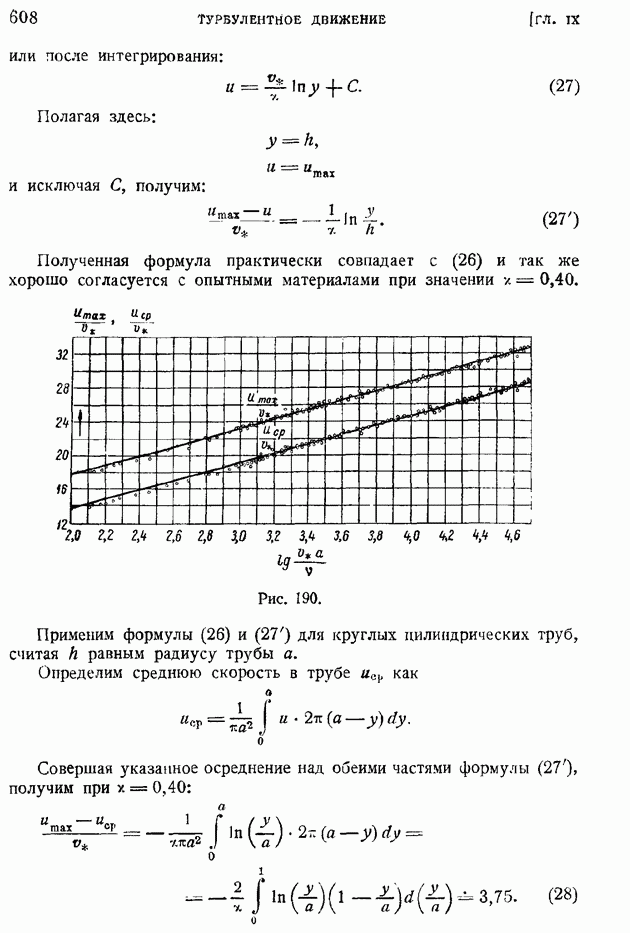
могут быть выражены через три величины моментов связей третьего порядка между продольными и поперечными составляющими пульсационных скоростей в точках 
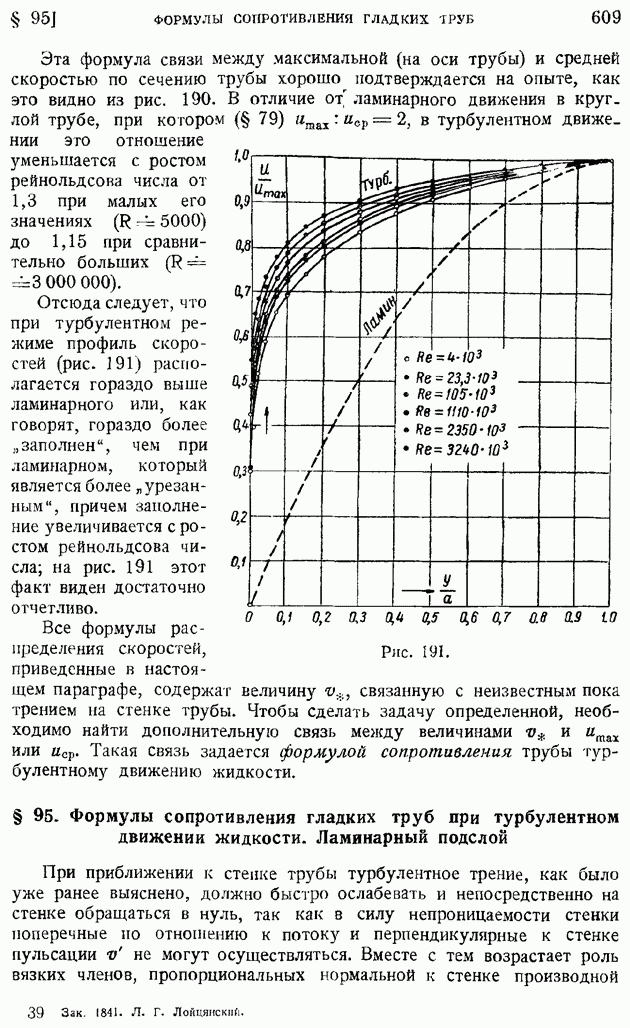
Используя осреднение уравнения неразрывности и общих динамических уравнений вязкой жидкости, удается получить одно дифференциальное уравнение в частных производных второго порядка:

с двумя неизвестными функциями  и
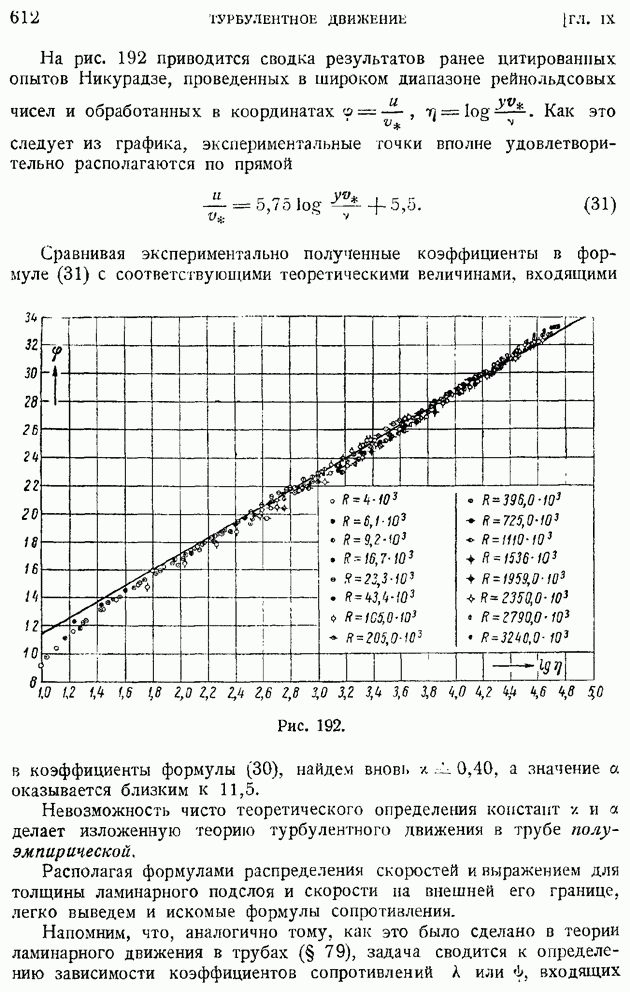
и  из которых первая
из которых первая  представляет момент связи второго порядка между продольными компонентами пульсационных скоростей в точках
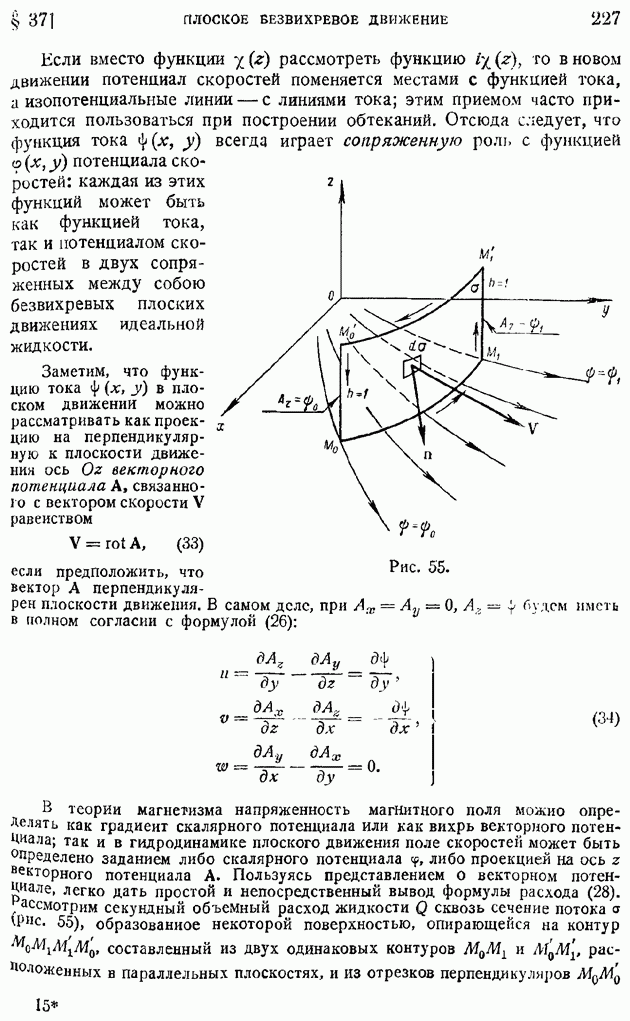
представляет момент связи второго порядка между продольными компонентами пульсационных скоростей в точках  а вторая
а вторая  момент связи третьего порядка между квадратом поперечной составляющей в точке
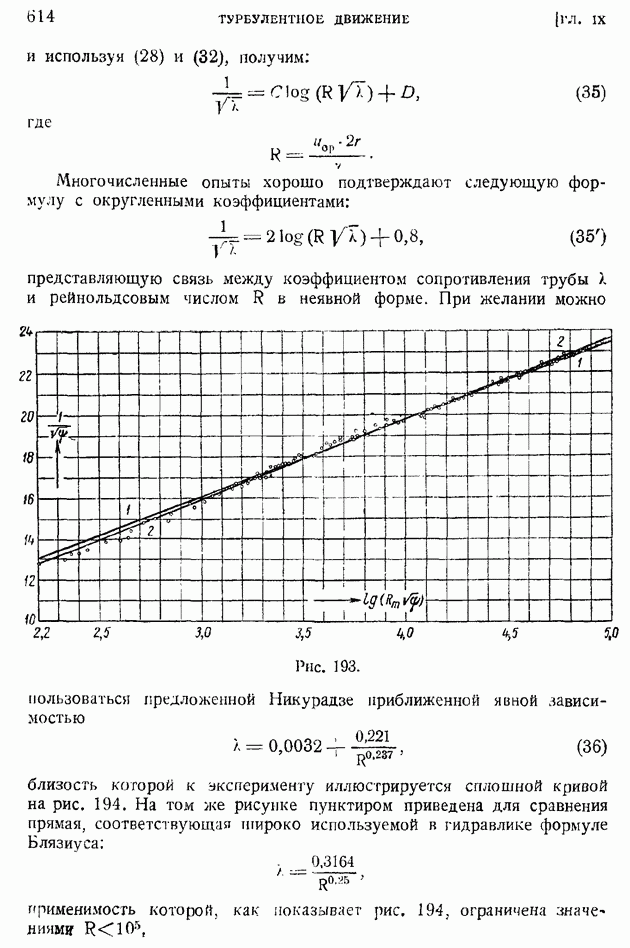
момент связи третьего порядка между квадратом поперечной составляющей в точке  и продольной — в точке
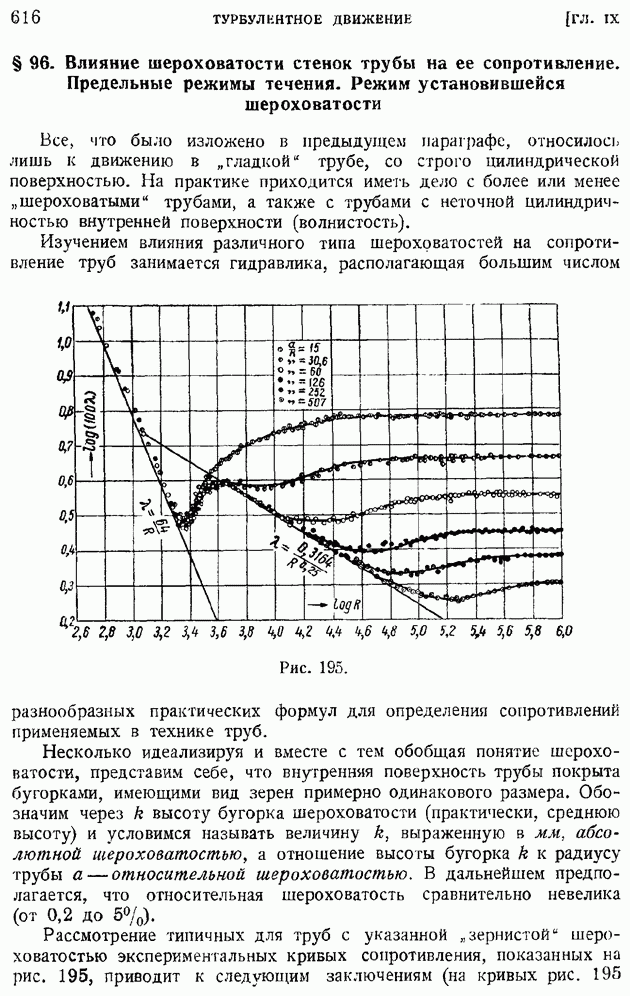
и продольной — в точке 
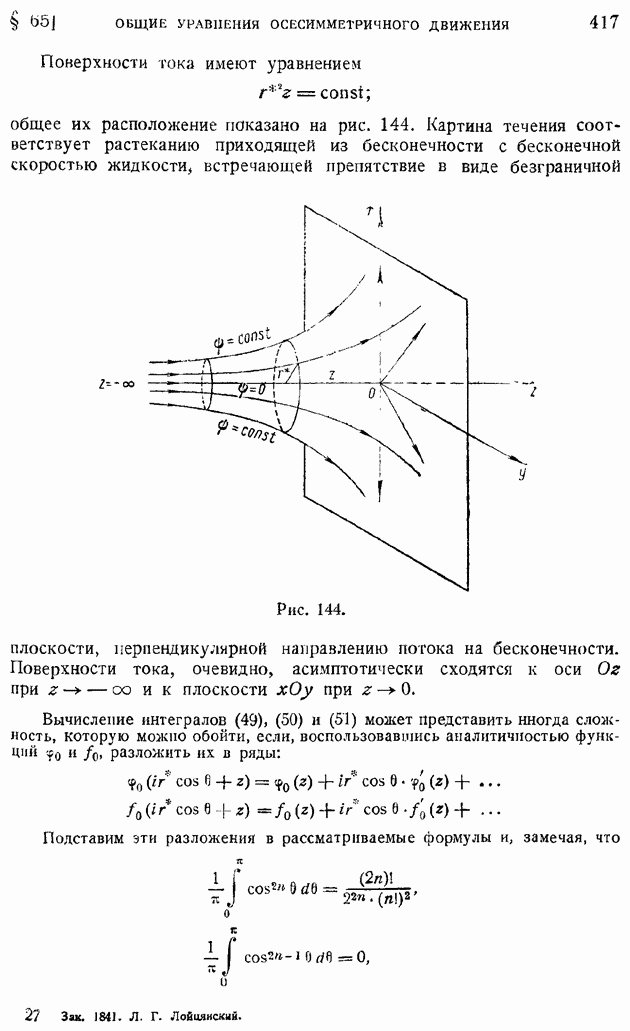
Уравнение (135) можно рассматривать как уравнение рассеяния величины  характеризующей структуру турбулентных возмущений в потоке.
характеризующей структуру турбулентных возмущений в потоке.
Рассмотрим эту функцию несколько ближе. Если устремить  к нулю, то функция
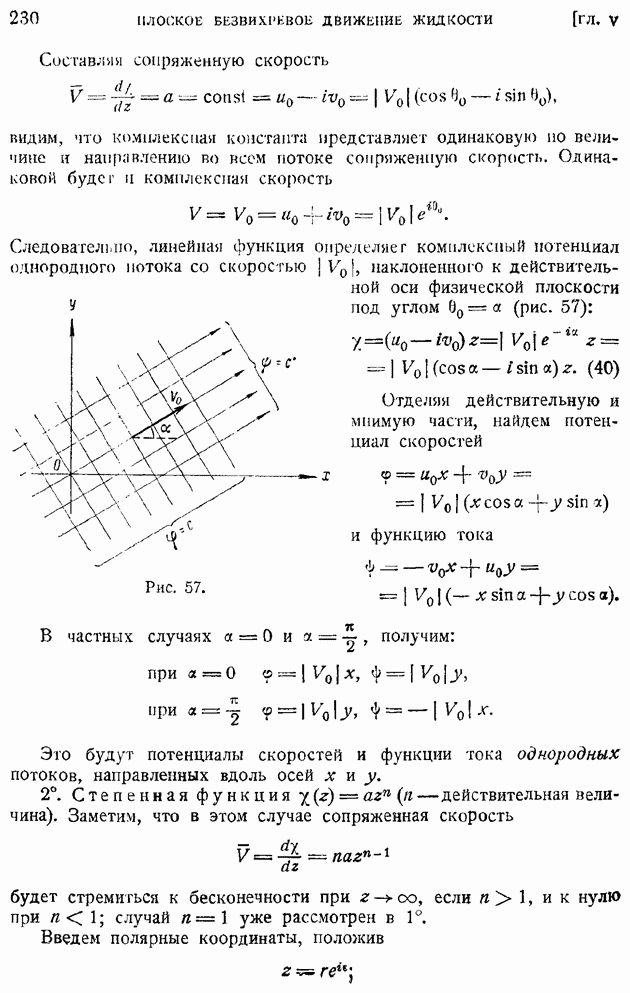
к нулю, то функция  согласно ее определению и свойству изотропности потока, превратится в среднее значение квадрата пульсации в данной точке:
согласно ее определению и свойству изотропности потока, превратится в среднее значение квадрата пульсации в данной точке:

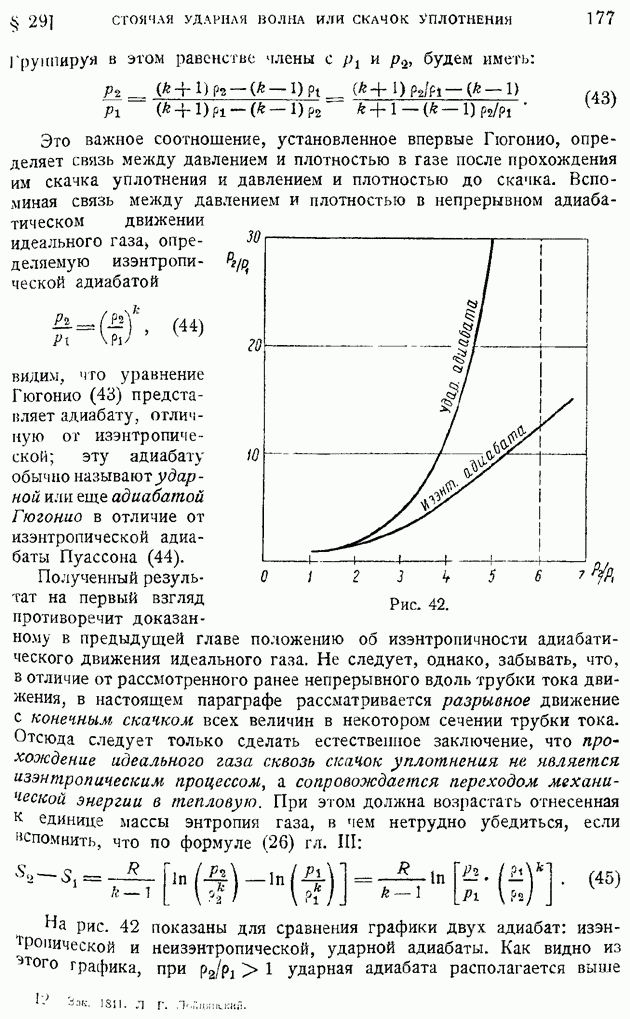
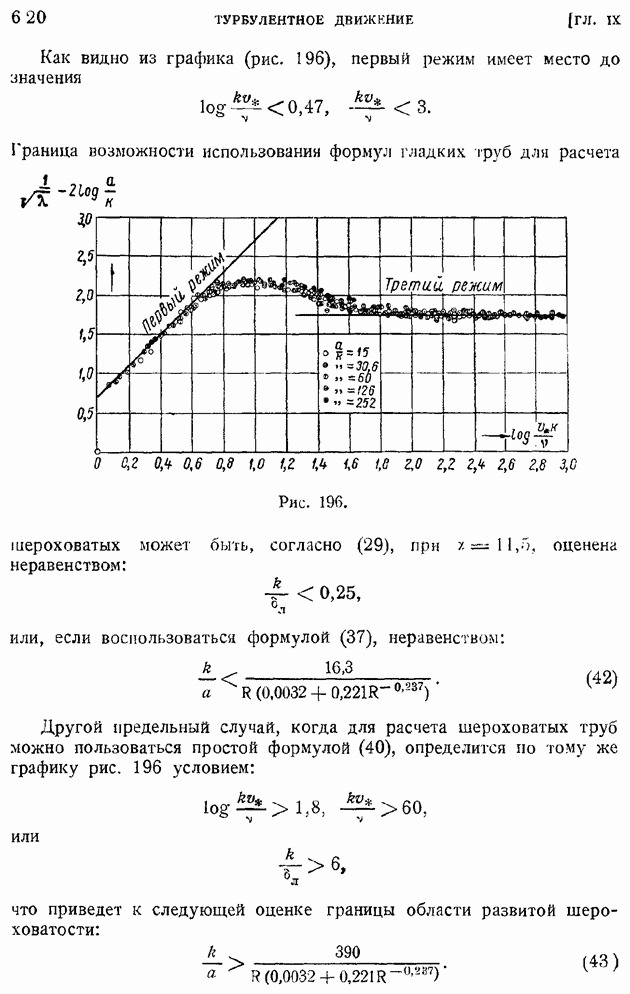
Эту величину (или квадратный корень из  принимают за меру интенсивности турбулентности в данной точке. В рассматриваемом случае однородной турбулентности величина
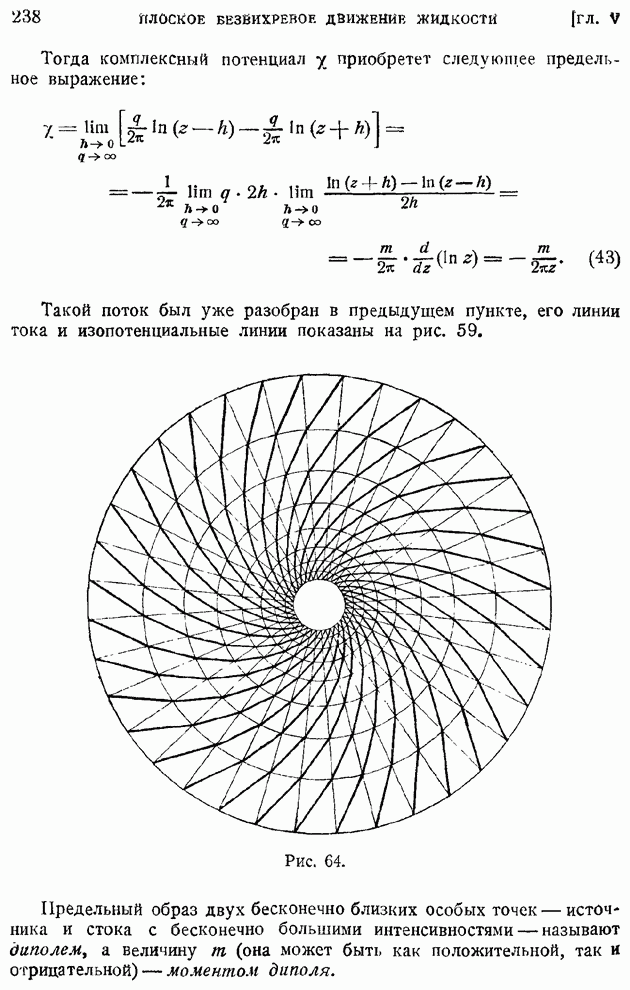
принимают за меру интенсивности турбулентности в данной точке. В рассматриваемом случае однородной турбулентности величина  одинакова во всех точках потока в данный момент времени и зависит лишь от времени. Примем в дальнейшем для краткости обозначение
одинакова во всех точках потока в данный момент времени и зависит лишь от времени. Примем в дальнейшем для краткости обозначение  и рассмотрим величину
и рассмотрим величину

носящую наименование коэффициента корреляции (связи) двух пульсирующих во времени функций  Коэффициент корреляции изменяется в пределах от нуля до единицы, причем крайние его значения соответствуют: нуль — отсутствию какой бы то ни было связи между пульсациями скорости в точках
Коэффициент корреляции изменяется в пределах от нуля до единицы, причем крайние его значения соответствуют: нуль — отсутствию какой бы то ни было связи между пульсациями скорости в точках  единица — полной связи между этими пульсациями.
единица — полной связи между этими пульсациями.
Очевидно, что при  будет
будет  при увеличении расстояния
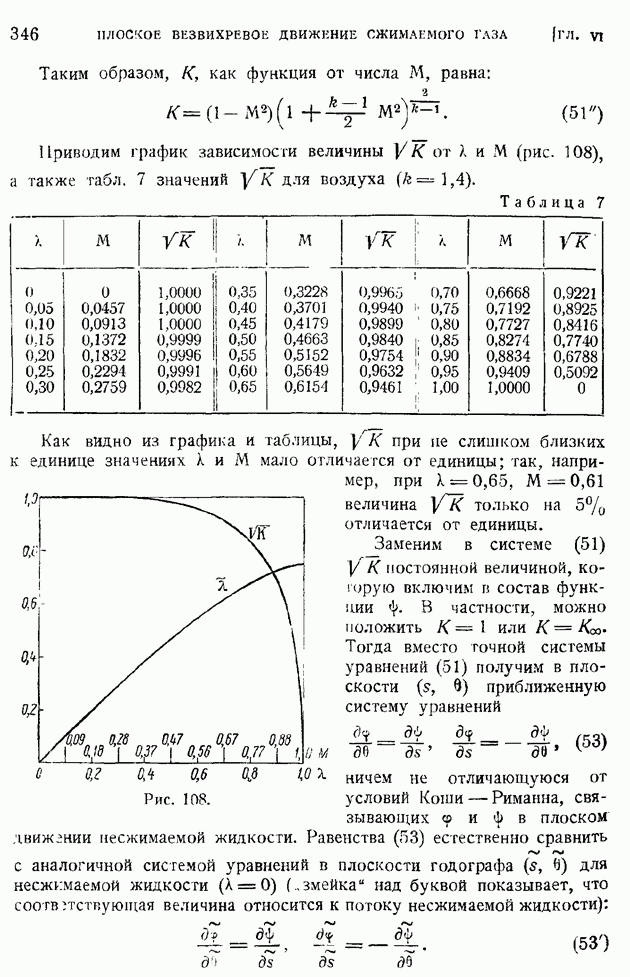
при увеличении расстояния  между точками
между точками  степень статистической связанности между пульсациями скорости быстро ослабевает и функция
степень статистической связанности между пульсациями скорости быстро ослабевает и функция  так же как
так же как  и
и  резко спадает до нулевого значения. Используя коэффициент корреляции
резко спадает до нулевого значения. Используя коэффициент корреляции  как статистическую меру связанности возмущений в двух точках потока, можно ввести понятие о масштабе турбулентности. Для этого построим интеграл
как статистическую меру связанности возмущений в двух точках потока, можно ввести понятие о масштабе турбулентности. Для этого построим интеграл

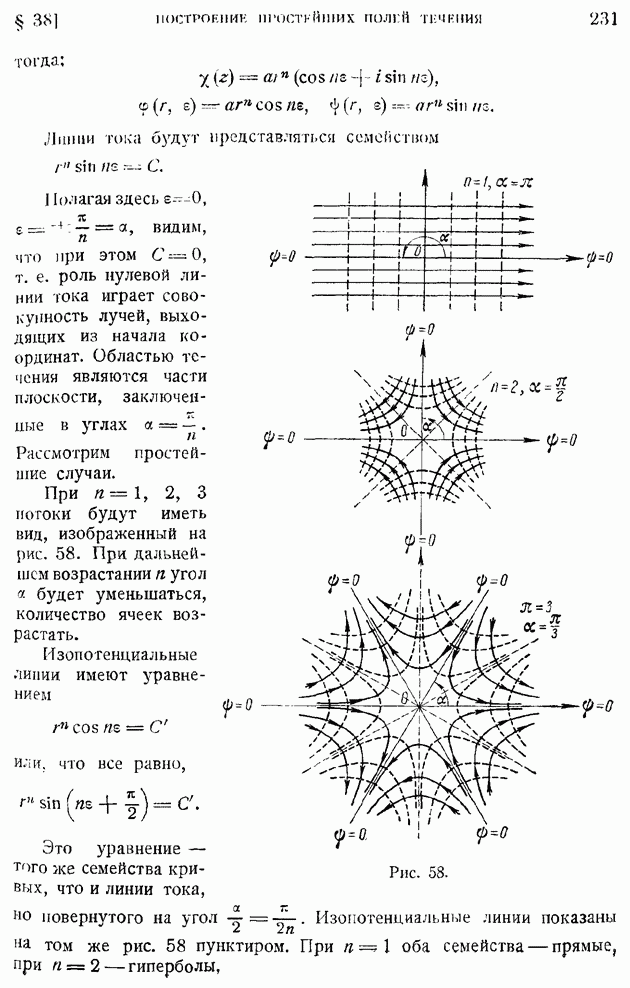
представляющий взвешенное суммирование бесконечно малых отрезков  причем за "вес" принимается как раз степень связанности
причем за "вес" принимается как раз степень связанности  пульсаций в точках
пульсаций в точках  Величину
Величину  можно принять за статистический масштаб турбулентности; в дальнейшем будет указан также еще и другой возможный масштаб турбулентности.
можно принять за статистический масштаб турбулентности; в дальнейшем будет указан также еще и другой возможный масштаб турбулентности.
Возвращаясь к уравнению (135), можем следующим образом проинтерпретировать отдельные его члены. Локальная производная от величины  по времени складывается из вязкостного (диффузионного) ее рассеяния, представленного правой частью уравнения, и конвективного изменения, определяемого выражением в левой части, зависящим от функции
по времени складывается из вязкостного (диффузионного) ее рассеяния, представленного правой частью уравнения, и конвективного изменения, определяемого выражением в левой части, зависящим от функции  При малых значениях рейнольдсова числа турбулентности
При малых значениях рейнольдсова числа турбулентности  некоторый характерный размер)
некоторый характерный размер)

конвективный член становится пренебрежимым, а задача — определенной, так как уравнение (135) переходит в уравнение относительно одной функции 

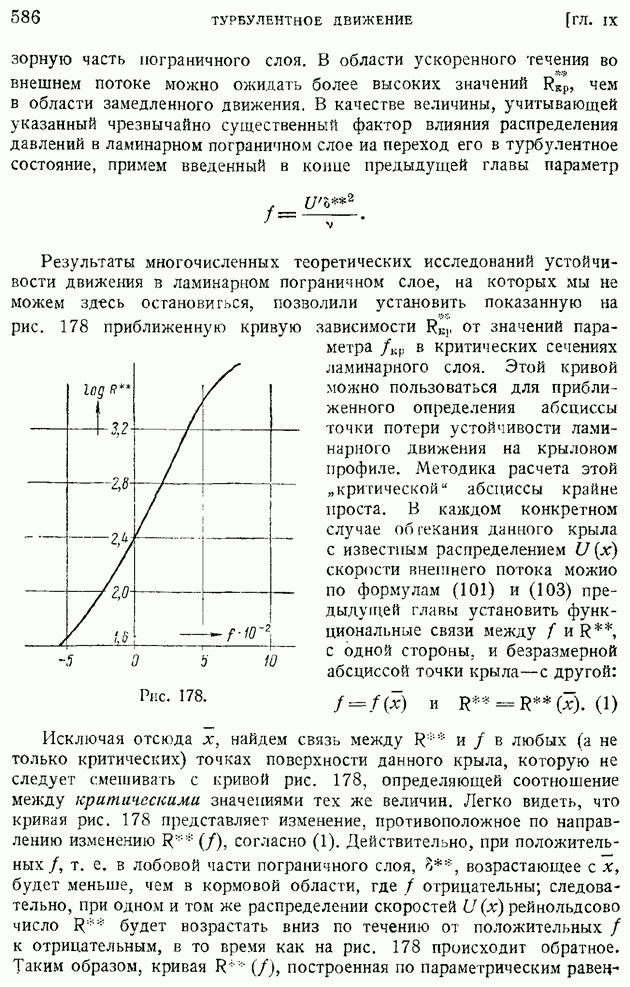
При больших значениях того же рейнольдсова числа оба члена сохраняют свое значение, и для решения задачи необходимо выдвигать дополнительные допущения.
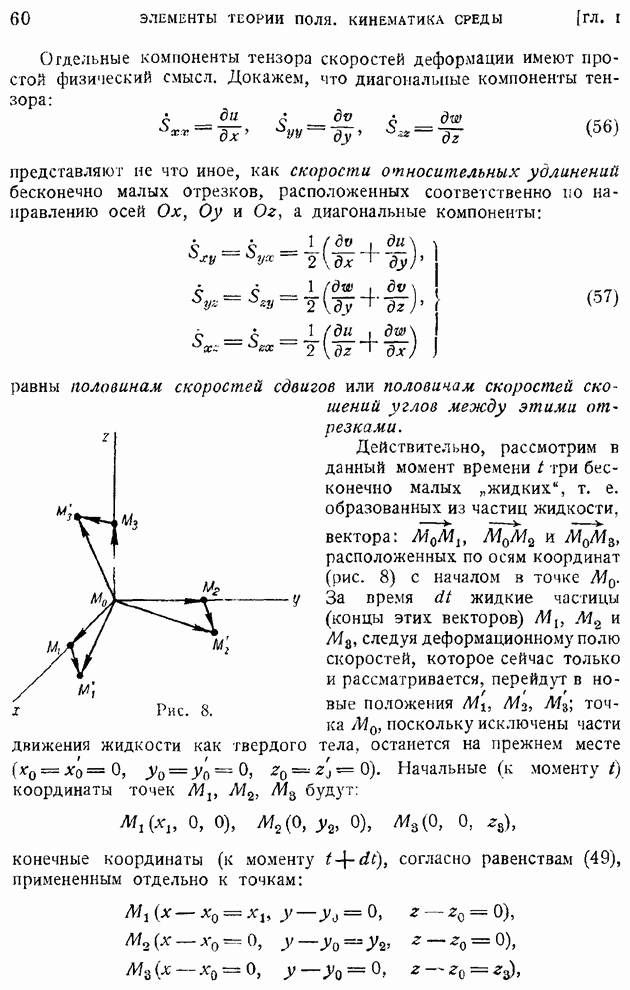
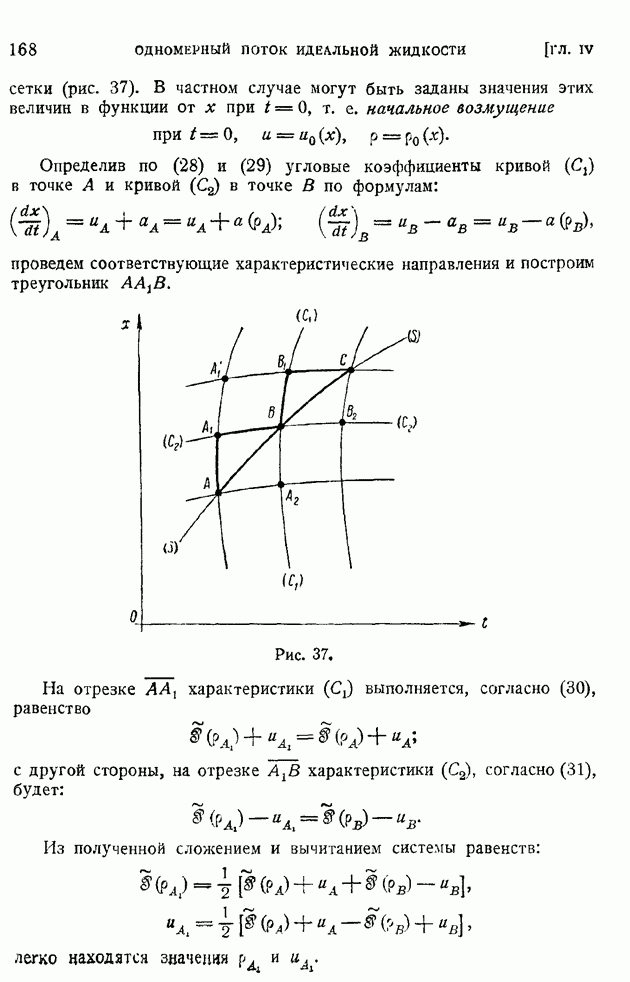
Прежде чем перейти к вопросу об интегрировании уравнения (139), установим общее соотношение, выражающее закон сохранения одной, характерной для турбулентных возмущений величины. Закон оказывается общим для затухающей однородной и изотропной турбулентности, безотносительно к тому, опускаются или нет конвективные члены.
Для вывода этого закона сохранения умножим обе части уравнения (135) на  и проинтегрируем в пределах от нуля до бесконечности. Тогда, предполагая, что функции
и проинтегрируем в пределах от нуля до бесконечности. Тогда, предполагая, что функции  удовлетворяют условиям убывания на бесконечности:
удовлетворяют условиям убывания на бесконечности:

и что соответствующие интегралы существуют, после простого интегрирования по частям получим:

откуда сразу следует искомый закон сохранения:

Величину  можно было бы назвать "моментом возмущений и говорить о законе сохранения момента возмущений. Переходя от функции
можно было бы назвать "моментом возмущений и говорить о законе сохранения момента возмущений. Переходя от функции  к коэффициенту корреляции
к коэффициенту корреляции  перепишем предыдущее равенство в виде
перепишем предыдущее равенство в виде

Входящий в это соотношение интеграл имеет размерность длины в пятой степени. Если вместо величины  определенной равенством (138), ввести в рассмотрение новый масштаб турбулентности
определенной равенством (138), ввести в рассмотрение новый масштаб турбулентности  равный
равный

то равенство (141) заменится простым соотношением

выражающим закон сохранения момента возмущений в форме: произведение средней квадратичной пульсации скорости (или среднего значения отнесенной к единице массы Жидкости кинетической энергии пульсационного движения) на пятую степень масштаба турбулентности при затухании однородной и изотропной турбулентности сохраняется.
Сохраняющаяся во времени величина момента возмущений А представляет своеобразную характеристику поля турбулентных возмущений и играет такую же роль, как, например, общее количество тепла в задаче о распространении тепла в жидкости или количество движения при удалении от источника струи или тела, образующего след.
Тепловая аналогия в данном случае оказывается особенно интересной, так как уравнение (139) можно рассматривать формально как аналог уравнения распространения тепла в пятимерном пространстве. Поскольку
уравнение (139) справедливо лишь при малых рейнольдсовых числах турбулентности, т. е. в последних стадиях затухания возмущений, что соответствует большим значениям времени  то достаточно построить простейшее решение уравнения (139), отвечающее случаю "источника". Это решение будет:
то достаточно построить простейшее решение уравнения (139), отвечающее случаю "источника". Это решение будет:

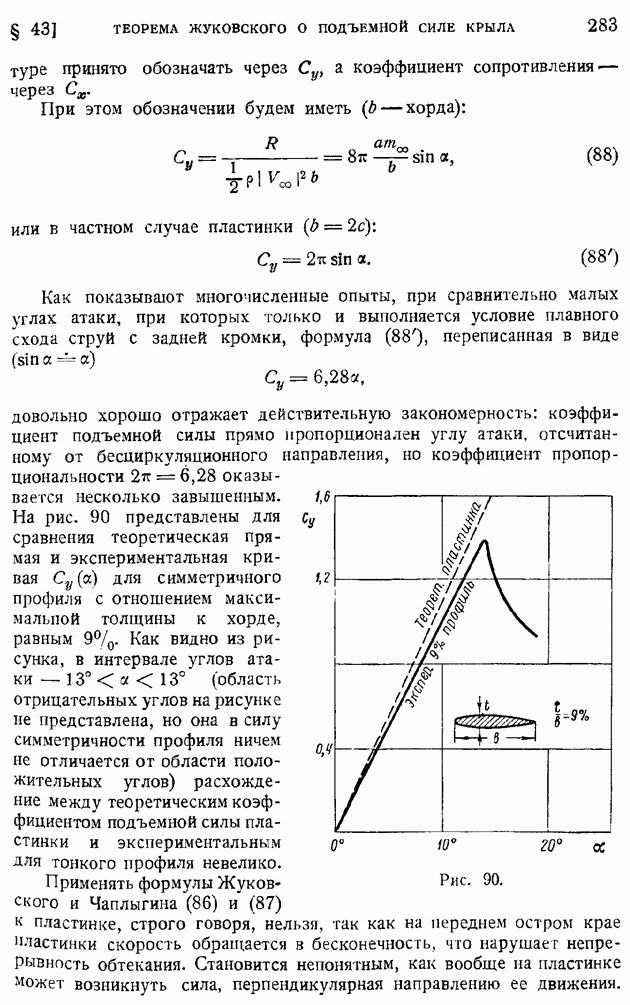
Для определения константы воспользуемся теоремой о сохранении момента возмущений. Будем иметь:

откуда найдем:

Итак, имеем:

Полагая здесь  получим, согласно (136), следующий закон убывания со временем интенсивности турбулентности:
получим, согласно (136), следующий закон убывания со временем интенсивности турбулентности:

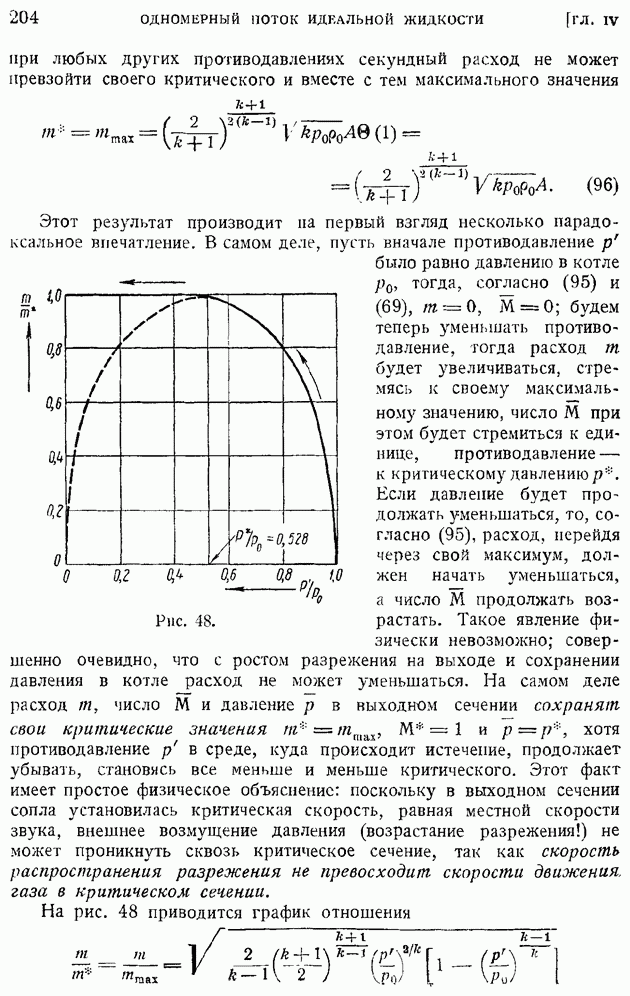
Разделив обе части (145) соответственно на (146), определим коэффициент корреляции

и
После этого нетрудно иайтн и закон возрастания со временем масштаба турбулеитности L:

Согласно (143) и (146), таков же и порядок возрастания масштаба 

Рейнольдсово число турбулентности  если в нем за линейный размер принять масштаб
если в нем за линейный размер принять масштаб  будет убывать со временем по закону:
будет убывать со временем по закону:

т. е. действительно будет малым при больших 
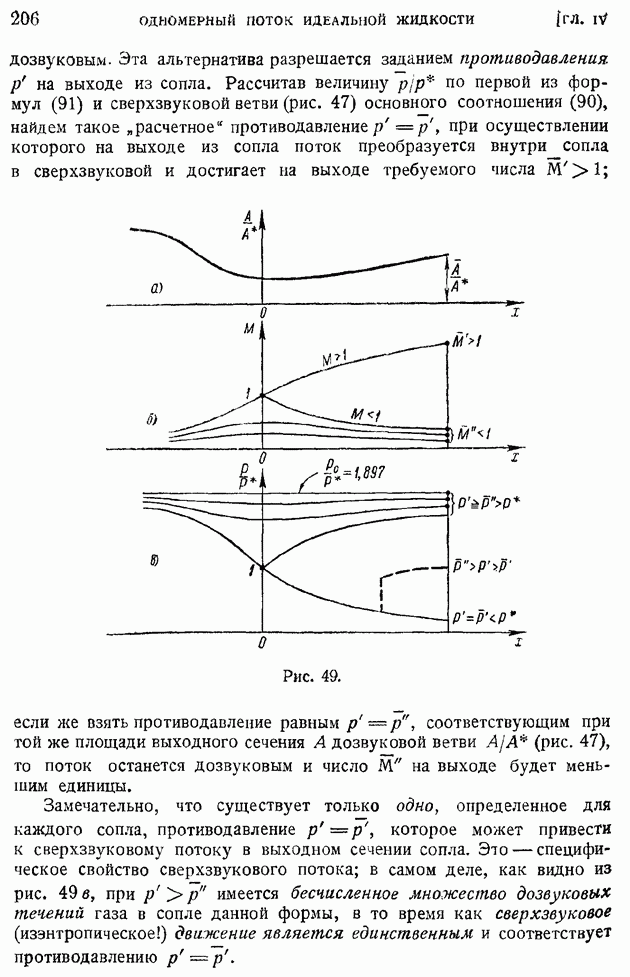
Случай больших значений рейнольдсова числа турбулентности, когда недопустимо пренебрежение конвективным членом, содержащим функцию  был при допущении о "локальном подобии" турбулентности изучен акад. А. Н. Колмогоровым, показавшим, что отвечающий формуле (142) масштаб турбулентности
был при допущении о "локальном подобии" турбулентности изучен акад. А. Н. Колмогоровым, показавшим, что отвечающий формуле (142) масштаб турбулентности  в этом случае изменяется по закону:
в этом случае изменяется по закону:

где  некоторые постоянные. Затухание интенсивности турбулентности определяется при этом формулой:
некоторые постоянные. Затухание интенсивности турбулентности определяется при этом формулой:

За доказательством этих двух важных соотношений отсылаем к цитированным выше работам А. Н. Колмогорова.
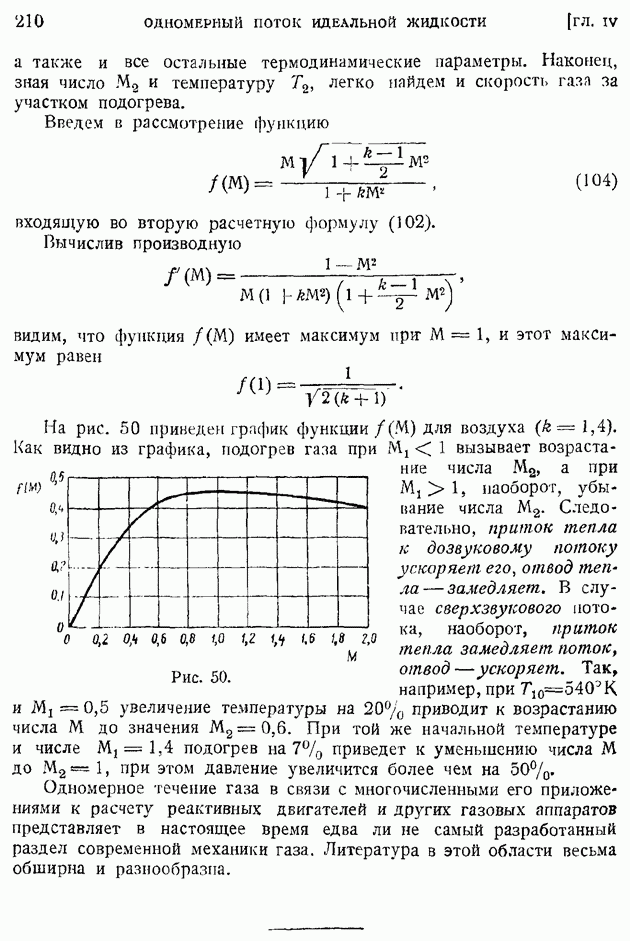
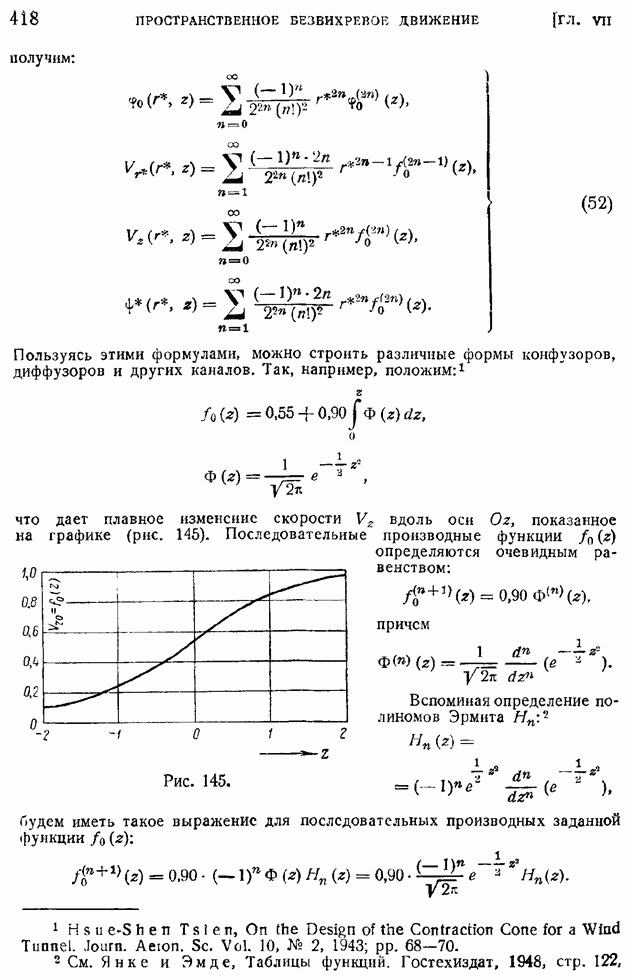
Подробный и тщательный анализ возможных решений основного уравнения (135) при различных гипотезах относительно структуры однородного, изотропного турбулентного потока был произведен Л. И. Седовым; некоторые соображения по тому же поводу в дальнейшем высказал Батчелор. Советские ученые добились больших успехов в изучении структуры турбулентных потоков; о главнейших достижениях в этой области можно прочесть в обзоре А. М. Обухова.
Вопрос о возможности применения статистических теорий турбулентности к прикладным вопросам не решен еще окончательно. Некоторые приложения этих теорий в динамической метеорологии можно найти в работах Л. В. Келлера, А. М. Обухова, М. И. Юдина, ссылки на которые помещены в только что цитироваииом обзоре А. М. Обухова.
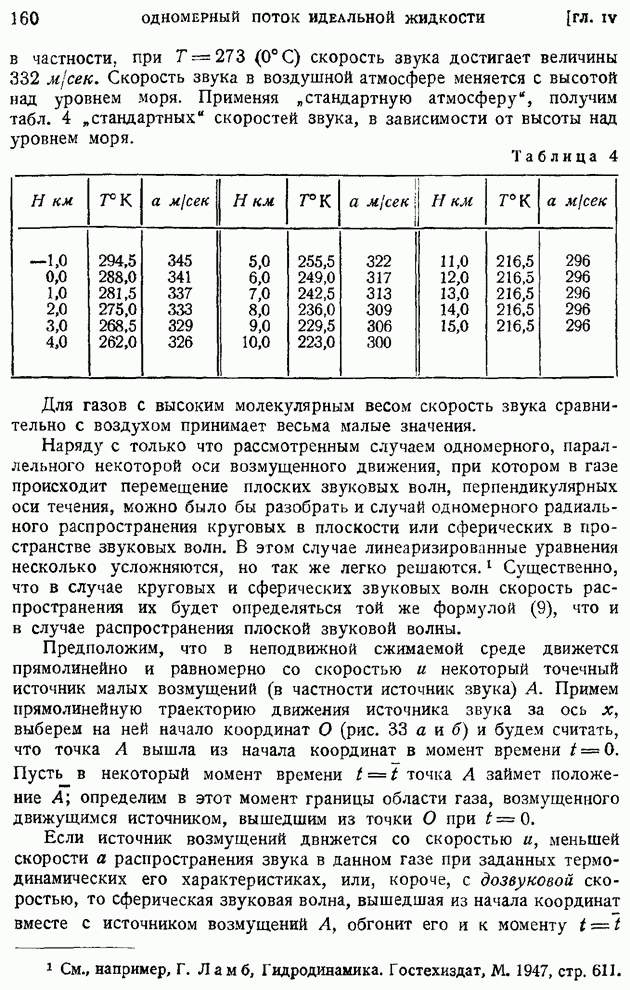
Современная техника аэродинамического эксперимента позволяет измерять не только средние, но и действительные быстро пульсирующие значения скоростей и давлений в турбулентном потоке, а также различные осредненные характеристики турбулентности потока. Для этой цели наиболее удобен тепловой анемометр или, как его еще иногда называют, анемометр с нагреваемой нитью. Устройство этого в настоящее время хорошо изученного прибора не сложно. Кусочек тонкой платиновой нити (диаметром от 0,008 до  и длины от одного до нескольких миллиметров) подогревается электрическим током и устанавливается перпендикулярно направлению воздушного потока, который ее охлаждает. Включая нить в одну из ветвей
и длины от одного до нескольких миллиметров) подогревается электрическим током и устанавливается перпендикулярно направлению воздушного потока, который ее охлаждает. Включая нить в одну из ветвей
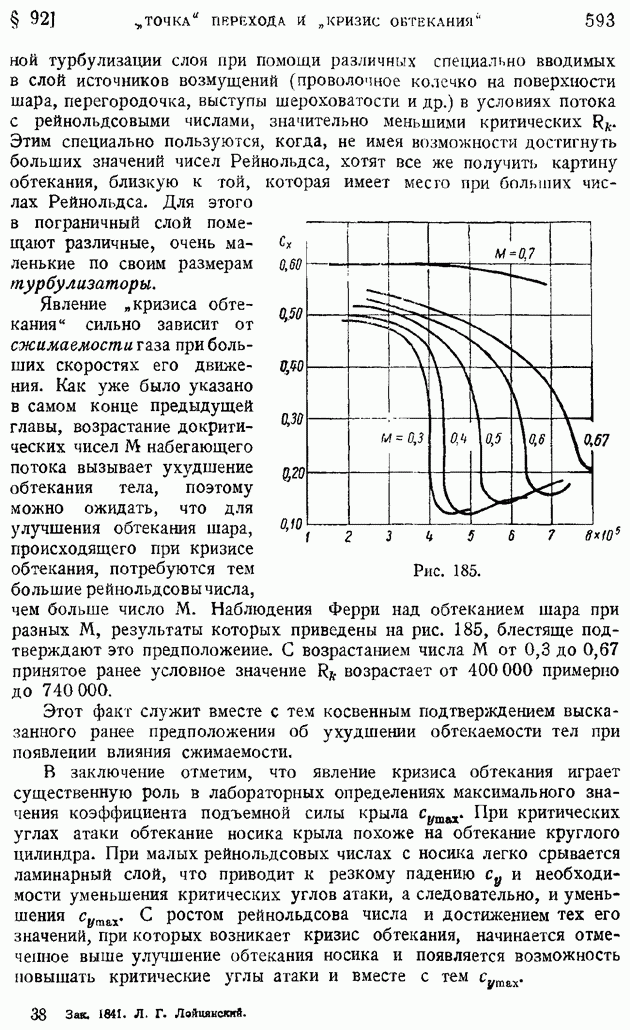
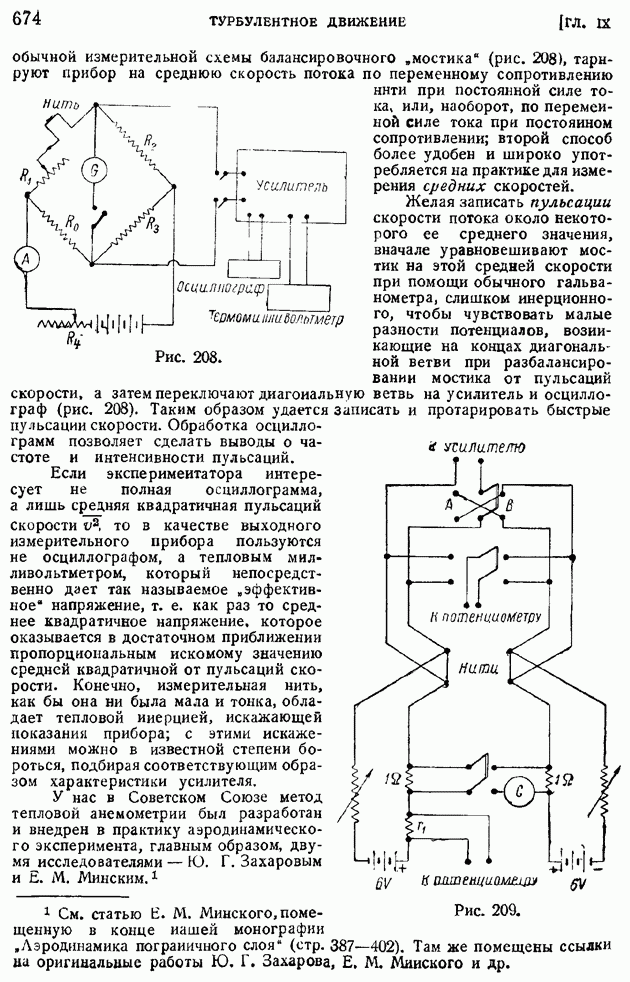
обычной измерительной схемы балансировочного "мостика" (рис. 208), тарируют прибор на среднюю скорость потока по переменному сопротивлению нити при постоянной силе тока, или, наоборот, по переменной силе тока при постоянном сопротивлении; второй способ более удобен и широко употребляется на практике для измерения средних скоростей.
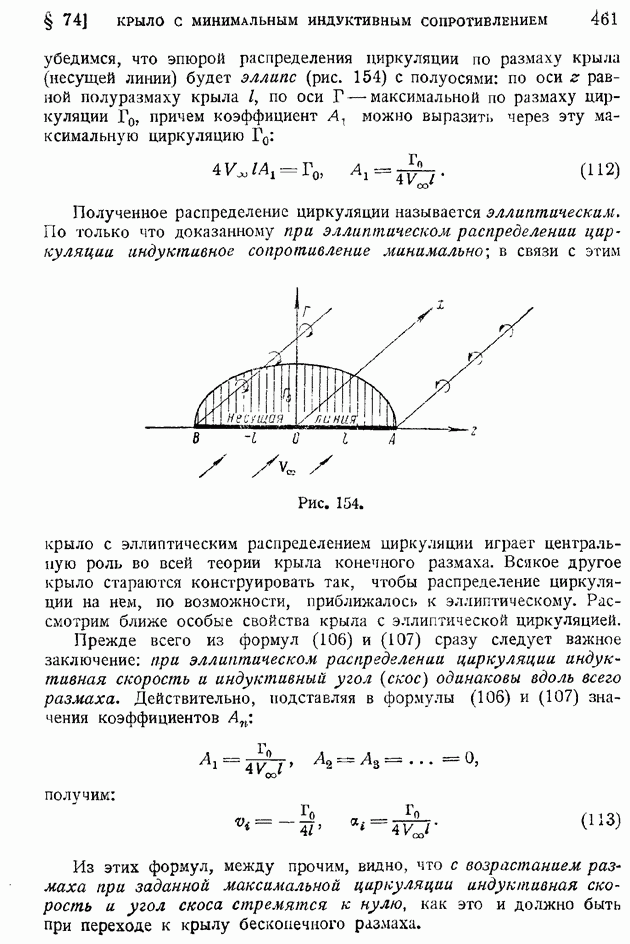
Желая записать пульсации скорости потока около некоторого ее среднего значения, вначале уравновешивают мостик на этой средней скорости при помощи обычного гальванометра, слишком инерционного, чтобы чувствовать малые разности потенциалов, возникающие на концах диагональной ветви при разбалансировании мостика от пульсаций скорости, а затем переключают диагональную ветвь на усилитель и "осциллограф (рис. 208). Таким образом удается записать и протарировать быстрые пульсации скорости. Обработка осциллограмм позволяет сделать выводы о частоте и интенсивности пульсаций.

Рис. 208.
Если экспериментатора интересует не полная осциллограмма, а лишь средняя квадратичная пульсаций скорости  то в качестве выходного измерительного прибора пользуются не осциллографом, а тепловым милливольтметром, который непосредственно дает так называемое "эффективное" напряжение, т. е. как раз то среднее квадратичное напряжение, которое оказывается в достаточном приближении пропорциональным искомому значению средней квадратичной от пульсаций скорости. Конечно, измерительная нить, как бы она ни была мала и тонка, обладает тепловой инерцией, искажающей показания прибора; с этими искажениями можно в известной степени бороться, подбирая соответствующим образом характеристики усилителя.
то в качестве выходного измерительного прибора пользуются не осциллографом, а тепловым милливольтметром, который непосредственно дает так называемое "эффективное" напряжение, т. е. как раз то среднее квадратичное напряжение, которое оказывается в достаточном приближении пропорциональным искомому значению средней квадратичной от пульсаций скорости. Конечно, измерительная нить, как бы она ни была мала и тонка, обладает тепловой инерцией, искажающей показания прибора; с этими искажениями можно в известной степени бороться, подбирая соответствующим образом характеристики усилителя.
У нас в Советском Союзе метод тепловой анемометрии был разработан и внедрен в практику аэродинамического эксперимента, главным образом, двумя исследователями — Ю. Г. Захаровым и Е. М. Минским.

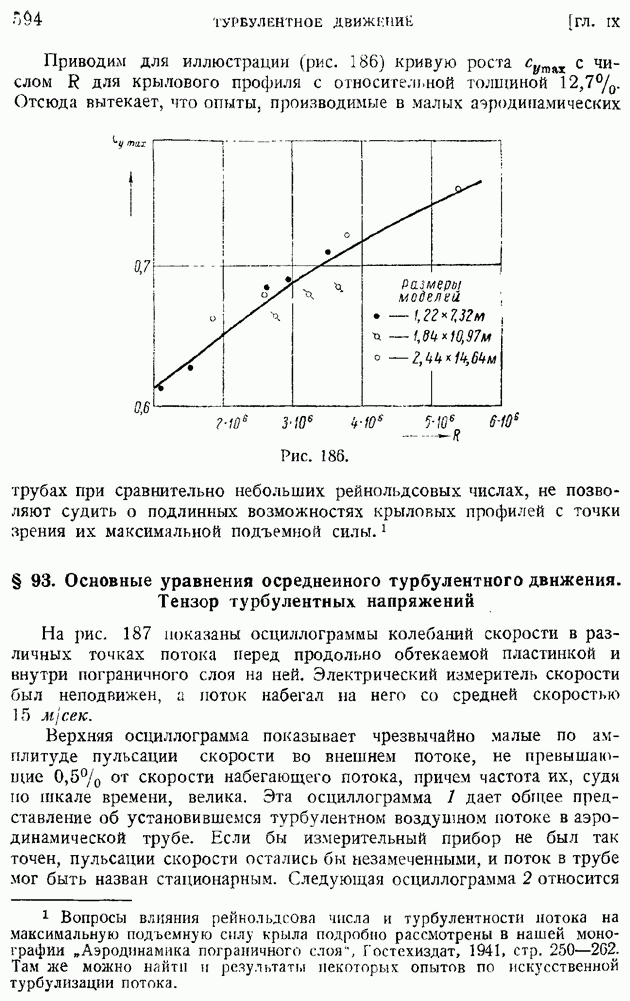
Рис. 209.
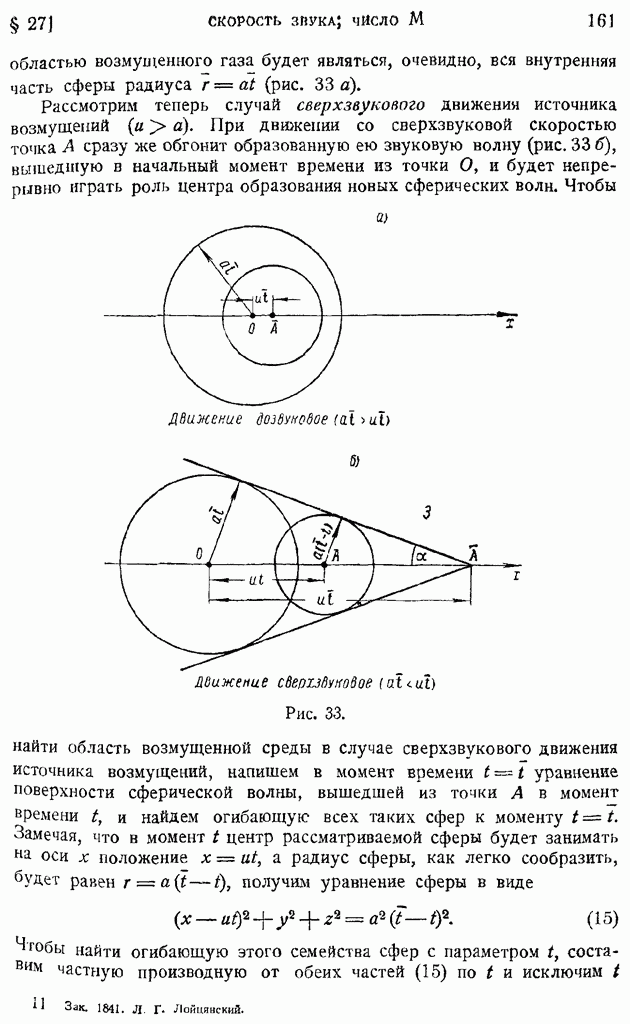
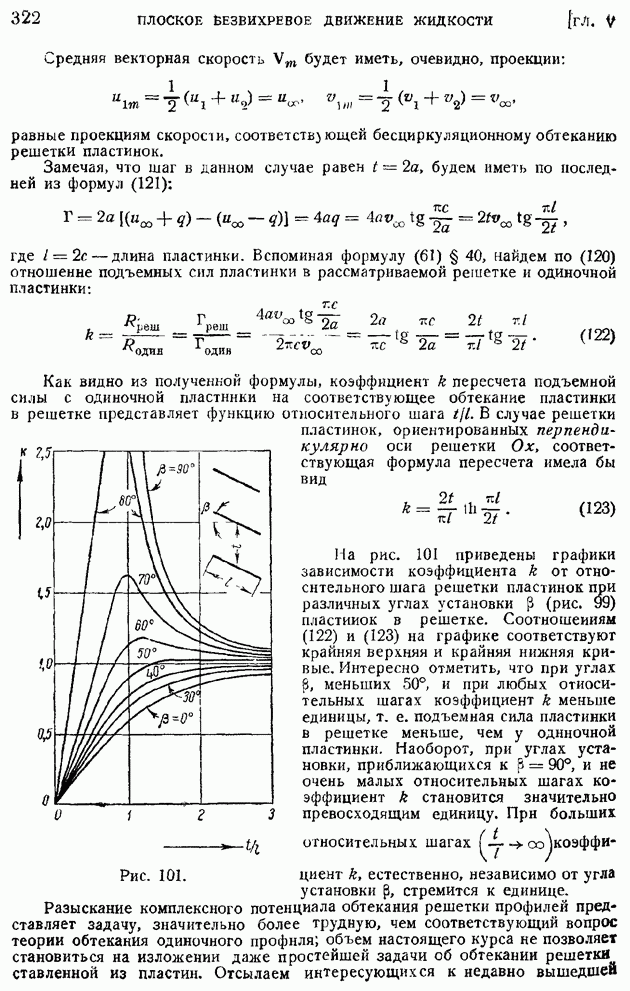
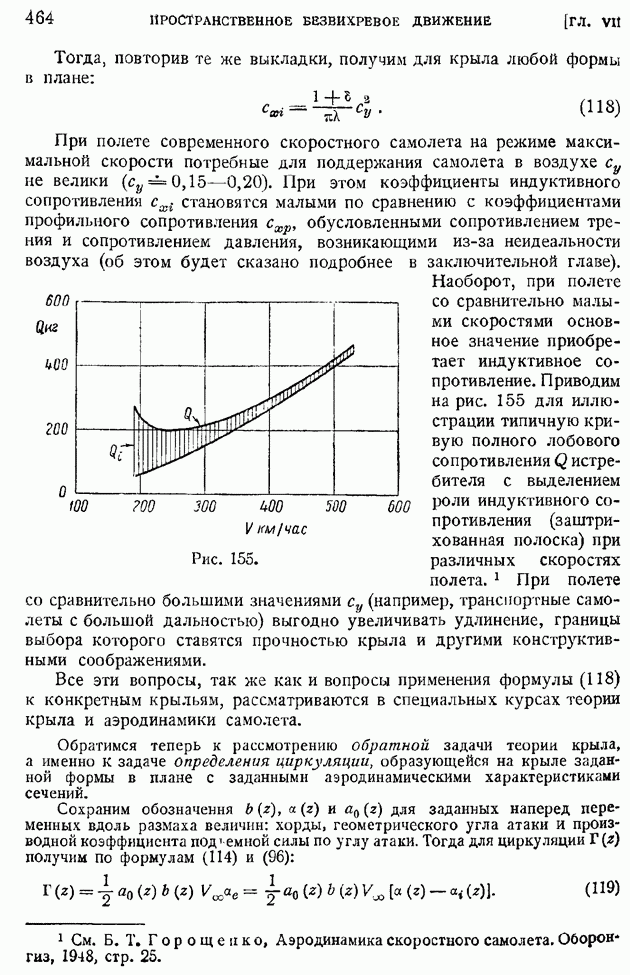
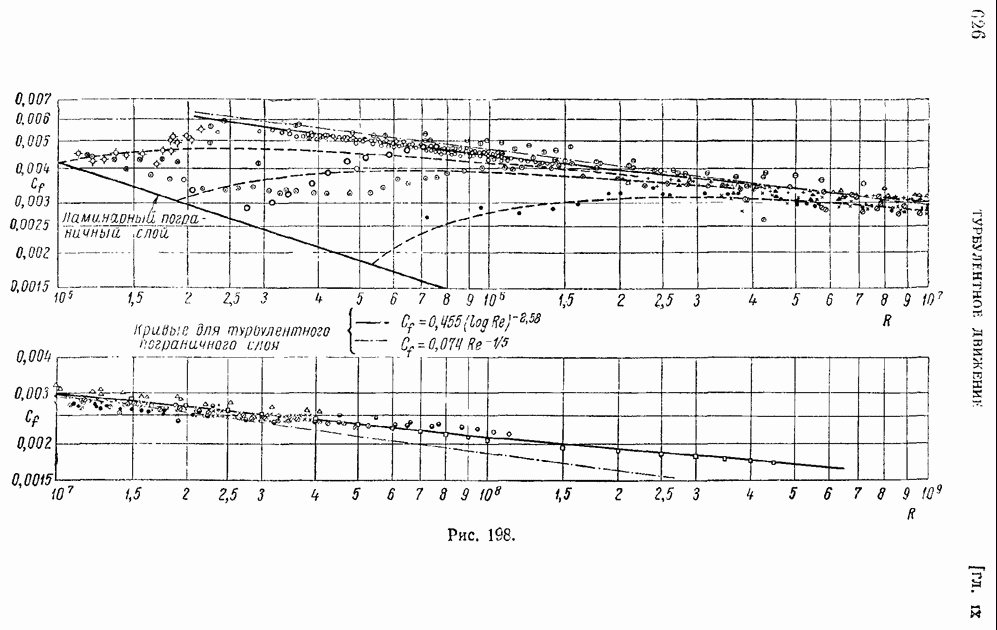
Замечательно, что тем же, но несколько усложненным методом тепловой анемометрии можно измерять величину  коэффициента корреляции, представленную формулой (137). Для этой цели используется двойная потенциометрическая схема (рис. 209) с двумя измерительными нитями, помещенными в двух смежных точках потока.
коэффициента корреляции, представленную формулой (137). Для этой цели используется двойная потенциометрическая схема (рис. 209) с двумя измерительными нитями, помещенными в двух смежных точках потока.

Рис. 210.
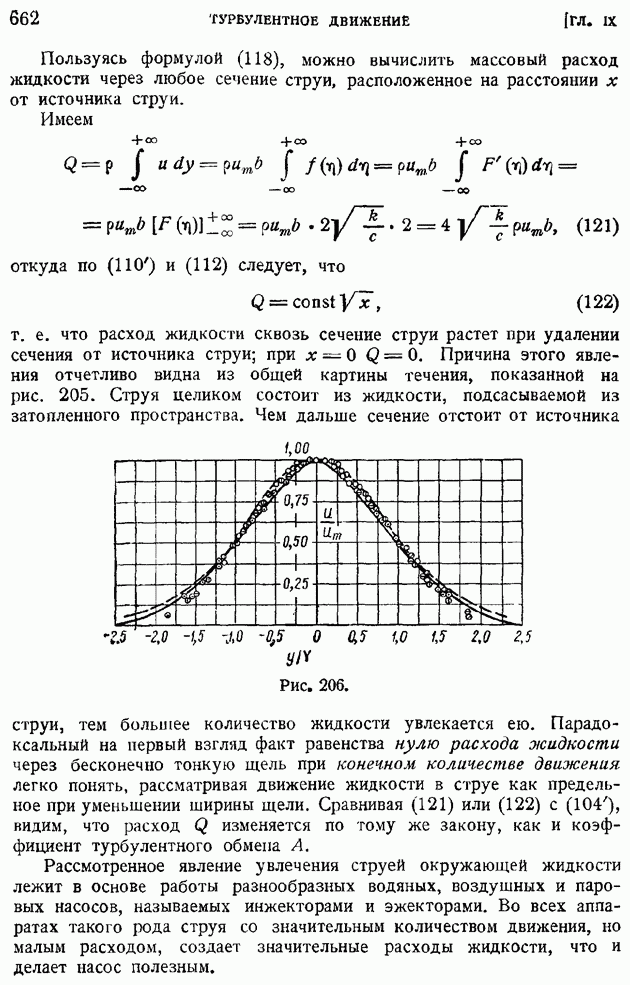
Прибор позволяет непосредственно мерить средние квадратичные от суммы и разности пульсирующих потенциалов  на концах нитей, т. е. величины
на концах нитей, т. е. величины  Вычисляя после этого отношение
Вычисляя после этого отношение

 в силу ранее упомянутой пропорциональности между напряжениями и скоростями равное
в силу ранее упомянутой пропорциональности между напряжениями и скоростями равное

получим в изотропном турбулентном потоке  искомое значение (137) коэффициента корреляции
искомое значение (137) коэффициента корреляции

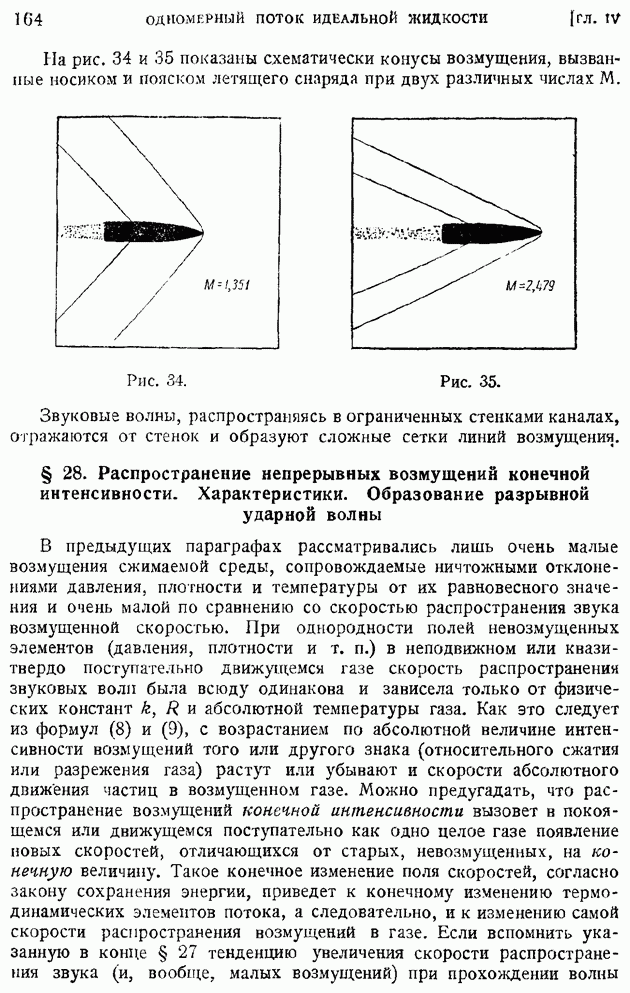
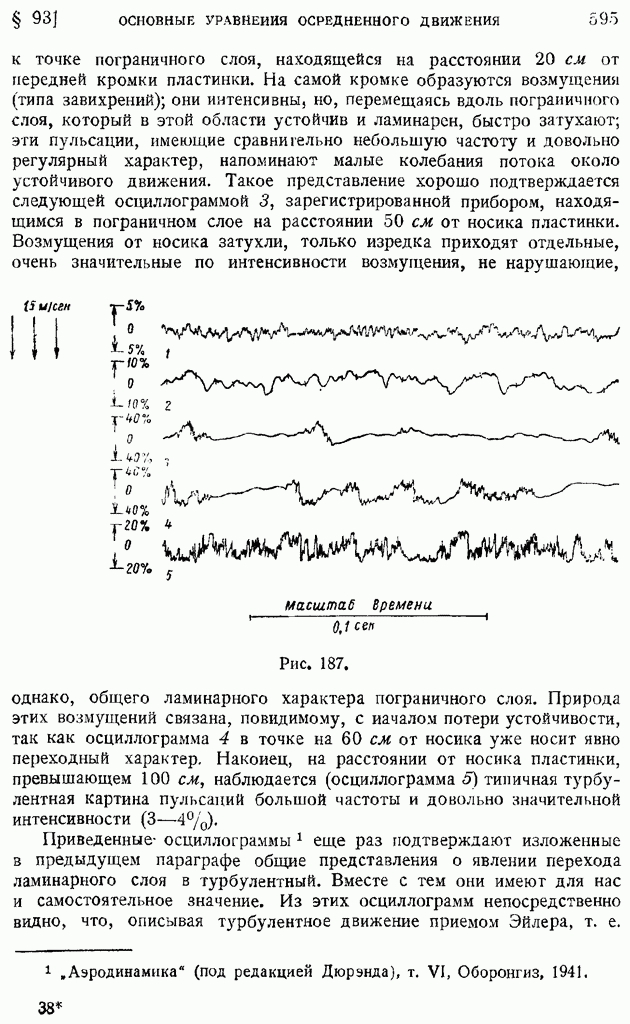
Для проведения измерения коэффициента корреляции пользуются особым зондом, в котором одна из нитей остается неподвижной в данной точке потока, а другая может перемещаться по отношению к ней при помощи микрометрического приспособления. Такого рода прибор позволяет находить величину  в функции от расстояния между нитями
в функции от расстояния между нитями  Имея такие графики уже не трудно простым интегрированием определить по ним масштабы турбулентности
Имея такие графики уже не трудно простым интегрированием определить по ним масштабы турбулентности  заданные соответственно формулами (138) и (142).
заданные соответственно формулами (138) и (142).
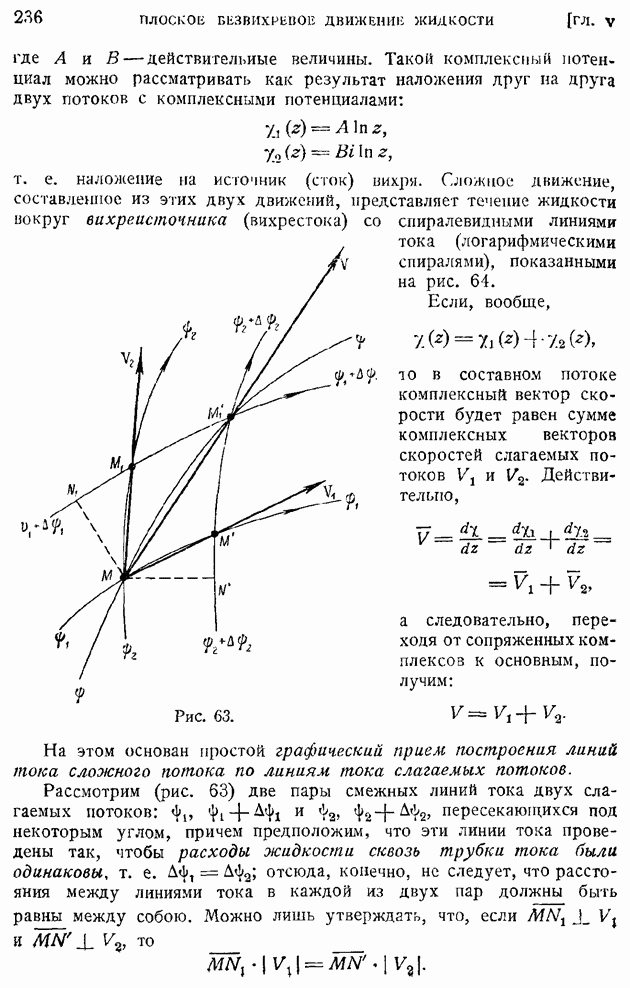
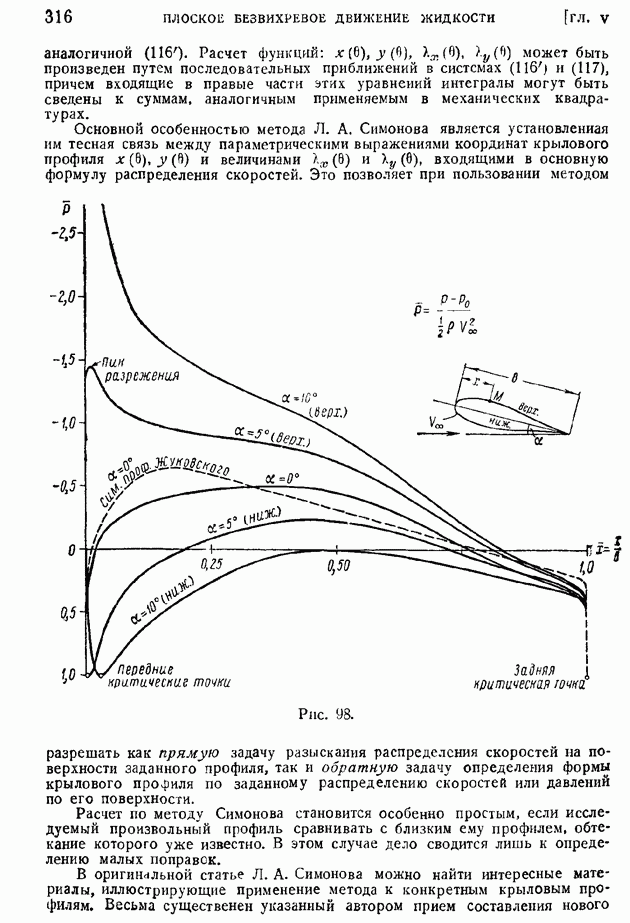
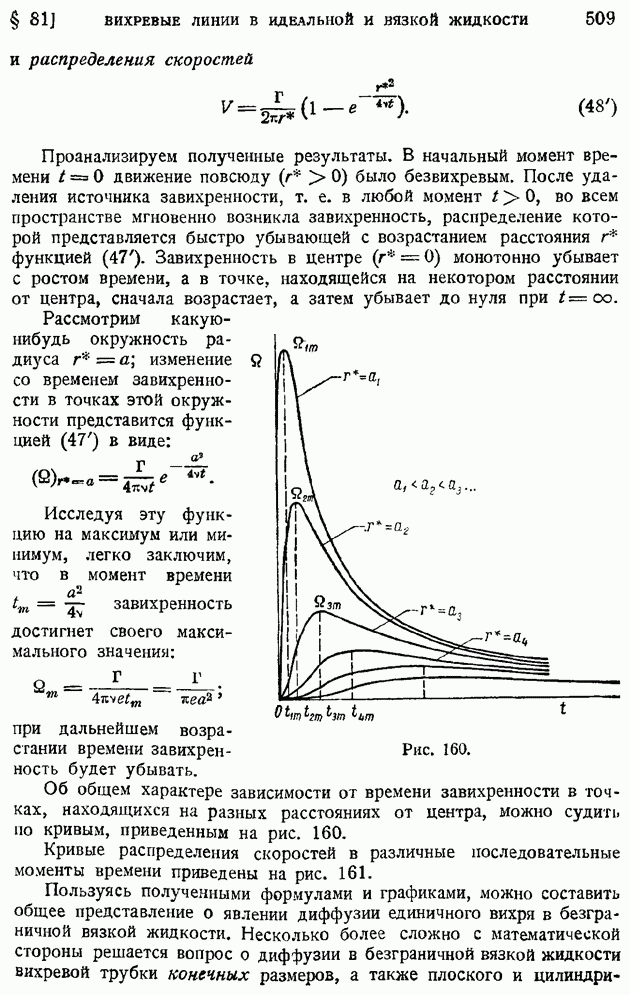
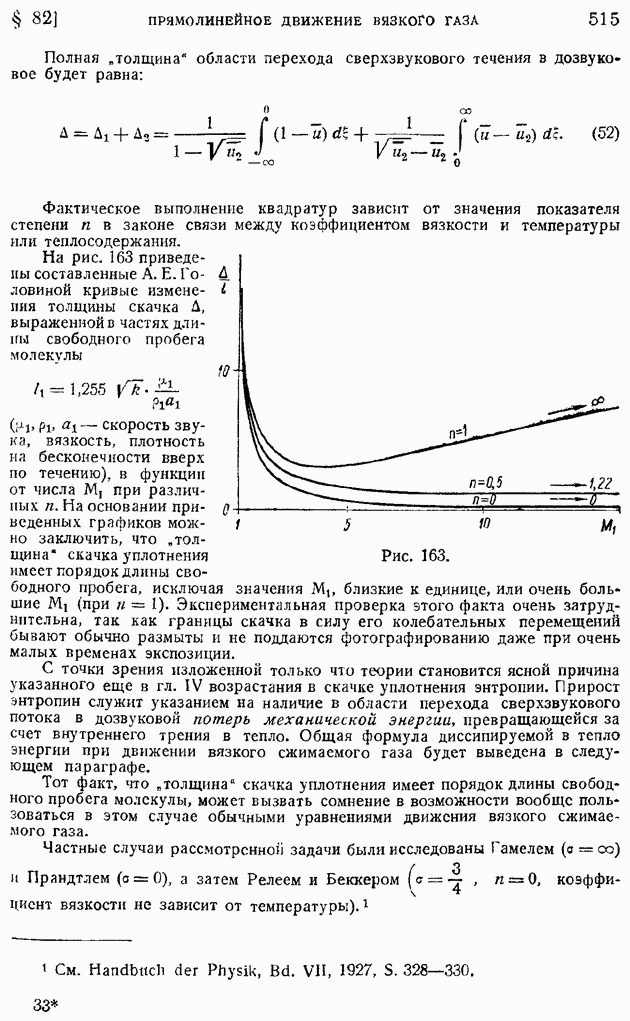
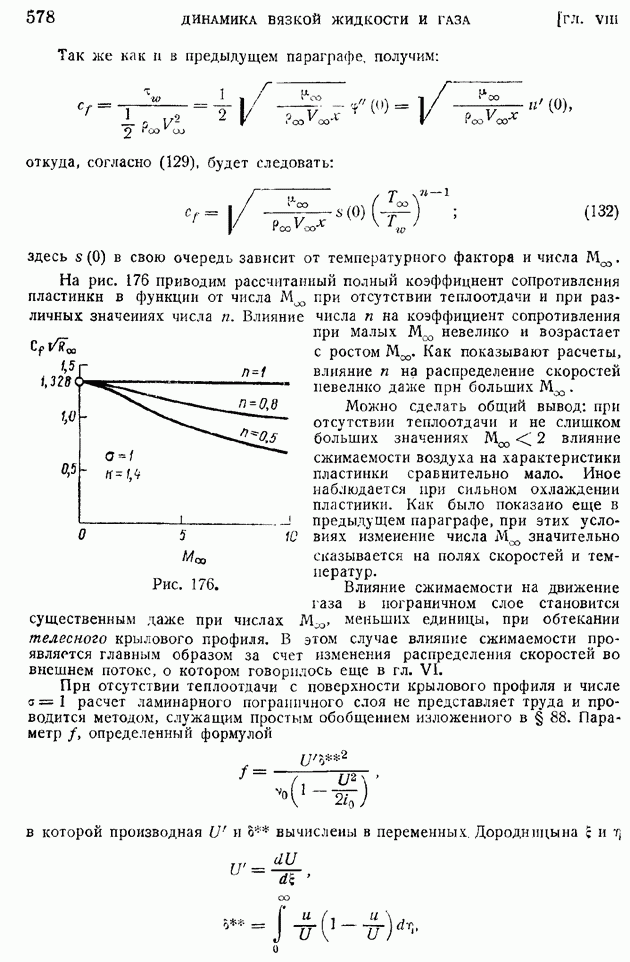
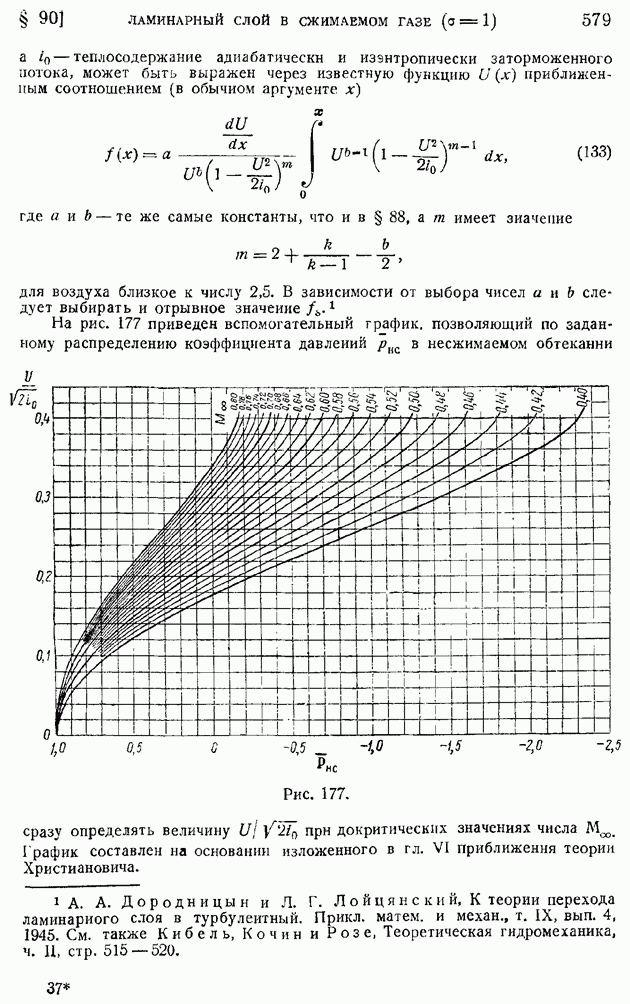
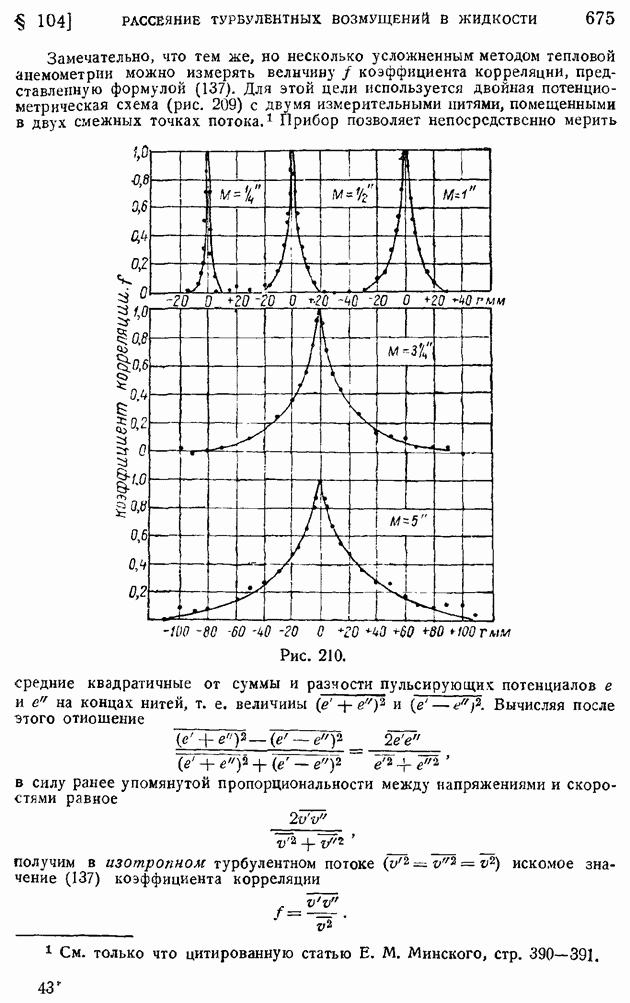
На рис. 210 показаны для иллюстрации примеры кривых изменения коэффициента корреляции  смеренных в некоторой точке потока за турбулизирующими решетками с различными размерами ячеек
смеренных в некоторой точке потока за турбулизирующими решетками с различными размерами ячеек  По характеру кривых сразу видно, что с увеличением размера ячеек растут и масштабы турбулентности. К сожалению, до настоящего времени указанные измерения еще нельзя считать в достаточной степени точными.
По характеру кривых сразу видно, что с увеличением размера ячеек растут и масштабы турбулентности. К сожалению, до настоящего времени указанные измерения еще нельзя считать в достаточной степени точными.
| << Предыдущий параграф |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Предмет механики жидкости и газа. Основные свойства «макромодели» жидкости и газа: сплошность и подвижность
- § 2. Основные методы механики жидкости и газа. Области применения и главнейшие задачи
- § 3. Краткий очерк исторического развития механики жидкости и газа. От гидромеханики древних до установления воззрений ньютонианской эпохи
- § 4. Эпоха Эйлера и Бернулли. Гидроаэродинамика в XIX в.
- § 5. Современный этап развития механики жидкости и газа
- ГЛАВА I. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
- § 6. Поле физической величины. Скалярное и векторное поля. Поверхности уровня. Векторные линин и трубки
- § 7. Мера однородности поля в данном направлении и в дайной точке. Градиевт скалярного поля и дифференциальный тензор векторного поля как меры неоднородности поля
- § 8. Задание движения сплошной среды. Поле скоростей. Линии тока и траектории
- § 9. Поле ускорений. Разложение ускорения частицы на локальную и конвективную составляющие
- § 10. Скоростное поле сплошной среды в окрестности данной точки. Угловая скорость и вихрь. Тензор скоростей деформаций и его компоненты
- § 11. Скорость объемного расширения жидкости. Интегральные представления дифференциальных операторов поля. Основные интегральные формулы
- § 12. Вихревые линии и трубки. Вторая теорема Гельмгольца. Интенсивность вихревой трубки
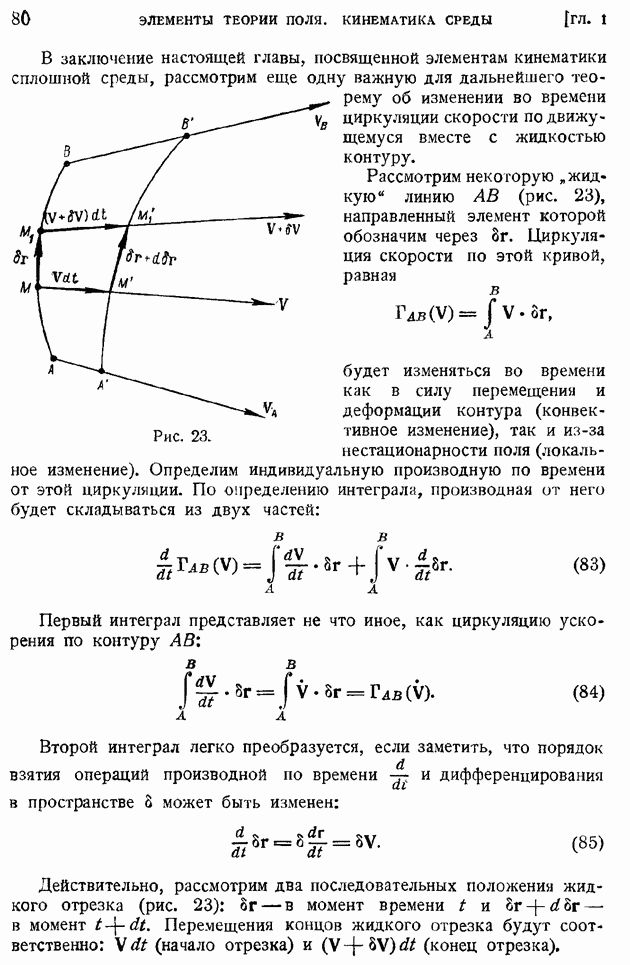
- § 13. Выражение интенсивности вихревой трубки через циркуляцию вектора по контуру, охватывающему трубку. Теорема об изменении циркуляции скорости во времени
- ГЛАВА II. ОСНОВНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ И РАВНОВЕСИЯ СПЛОШНОЙ СРЕДЫ
- § 14. Распределение массы в сплошной среде. Плотность и удельный вес. Напряжения. Тензор напряженности и его симметричность
- § 15. Общие уравнения динамики сплошной среды. Уравнение неразрывности. Уравнения динамики в напряжениях
- § 16. Тепловые явления в жидкостях и газах. Закон сохранения энергии и уравнение баланса энергии
- § 17. Общие уравнения равновесного состояния жидкости и газа. Равновесие воздуха в атмосфере. Приближенные барометрические формулы. Стандартная атмосфера
- § 18. Равновесие несжимаемой жидкости. Уравнение поверхности раздела. Равновесие вращающейся жидкости
- § 19. Давление тяжелой несжимаемой жидкости на поверхность тела. Сила и момент, приложенные к телу, плавающему в тяжелой жидкости. Случай вращающейся жидкости
- ГЛАВА III. ДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ И ГАЗА. ОСНОВНЫЕ УРАВНЕНИЯ И ОБЩИЕ ТЕОРЕМЫ
- § 20. Идеальная жидкость. Основные уравнения движения
- § 21. Закон сохранения энергии в движущейся идеальной жидкости. Адиабатическое движение. Сохранение энтропии
- § 22. Эйлерово представление конвективного изменения объемного интеграла. Перенос величины сквозь контрольную поверхность
- § 23. Эйлерова форма законов сохранения массы и энергии, теоремы количеств движения и момента количеств движения при стационарном движении идеальной жидкости
- § 24. Теорема об изменении кинетической энергии. Работа и мощность внутренних сил. Эйлерова форма уравнения изменения кинетической энергии
- § 25. Теорема Бернулли о сохранении полной механической энергии при стационарном баротропном движении идеальной жидкости и газа
- ГЛАВА IV. ОДНОМЕРНЫЙ ПОТОК ИДЕАЛЬНОЙ ЖИДКОСТИ
- § 26. Одномерное течение идеальной сжимаемой жидкости. Линеаризированные уравнения. Скорость распространения малых возмущений в жидкости или газе
- § 27. Изотермическая и адиабатическая скорости звука. «Конус возмущений» при сверхзвуковом движении источника возмущения. Число M и его связь с углом конуса возмущений
- § 28. Распространение непрерывных возмущений конечной интенсивности. Характеристики. Образование разрывной ударной волны
- § 29. Стоячая ударная волна или скачок уплотнения. Ударная адиабата
- § 30. Критические величины в одномерном потоке газа. Связь между скоростями до и после скачка. Изменение давления, плотности и температуры в скачке уплотнения
- § 31. Скорость распространения ударной волны. Спутное движение газа за ударной волной
- § 32. Влияние интенсивности скачка уплотнения на сжатие газа. Измерение скоростей и давлений в до- и сверхзвуковых потоках
- § 33. Одномерное движение газа по трубе переменного сечения. Истечение из резервуара большой емкости сквозь сходящееся сопло
- § 34. Одномерное течение в сопле Лаваля. Движение газа с притоком тепла
- ГЛАВА V. БЕЗВИХРЕВОЕ ДВИЖЕНИЕ ЖИДКОСТИ. ПЛОСКОЕ ДВИЖЕНИЕ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 35. Сохранение циркуляции скорости в потоке идеальной жидкости. Теорема Кельвина и Лаграижа. Безвихревое движение. Потенциал скоростей
- § 36. Интеграл Лагранжа — Коши уравнений безвихревого движения. Теорема Бернулли. Некоторые общие свойства безвихревого движения идеальной несжимаемой жидкости в односвязной области
- § 37. Плоское безвихревое движение несжимаемой жидкости. Потенциал скоростей и функция тока. Применение функций комплексного переменного. Комплексный потенциал и сопряженная скорость
- § 38. Построение полей течения по заданной характеристической Функции. Простейшие плоские потоки и их наложение
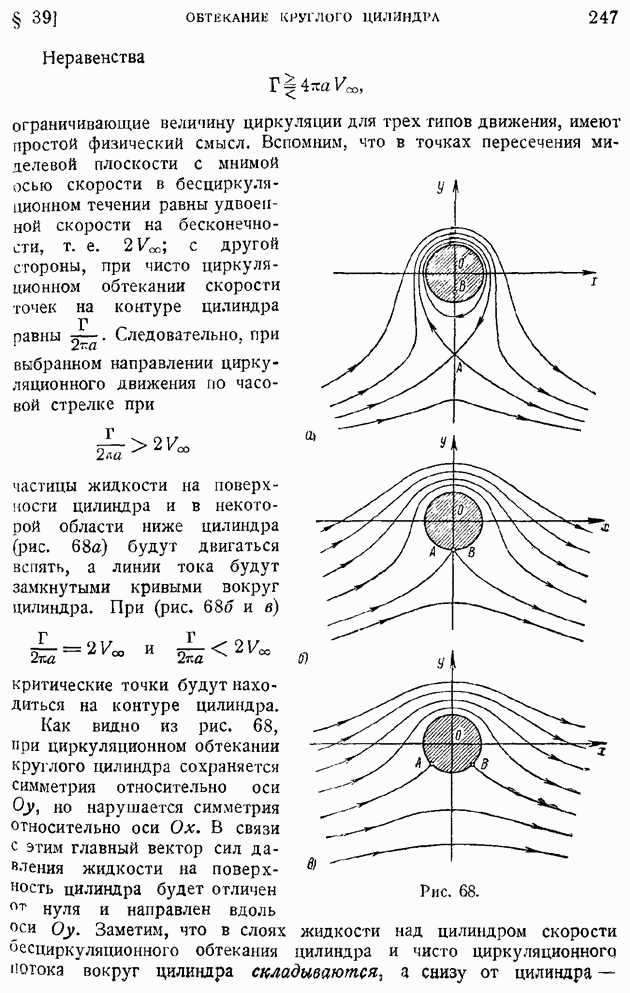
- § 39. Бесциркуляционное и циркуляционное обтекания круглого цилиндра
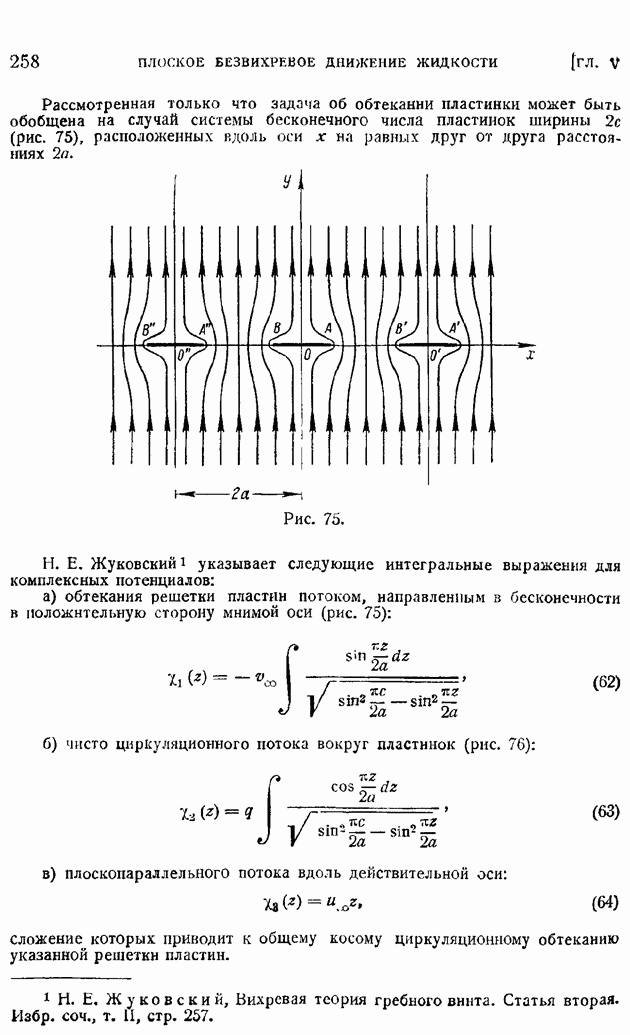
- § 40. Применение криволинейных координат. Бесциркуляционное и циркуляционное обтекания эллиптического цилиндра и пластинки. Задача Жуковского об обтекании решетки пластин.
- § 41. Плоское движение с отрывом струй. Разрывное обтекание пластинки и протекание жидкости сквозь отверстие
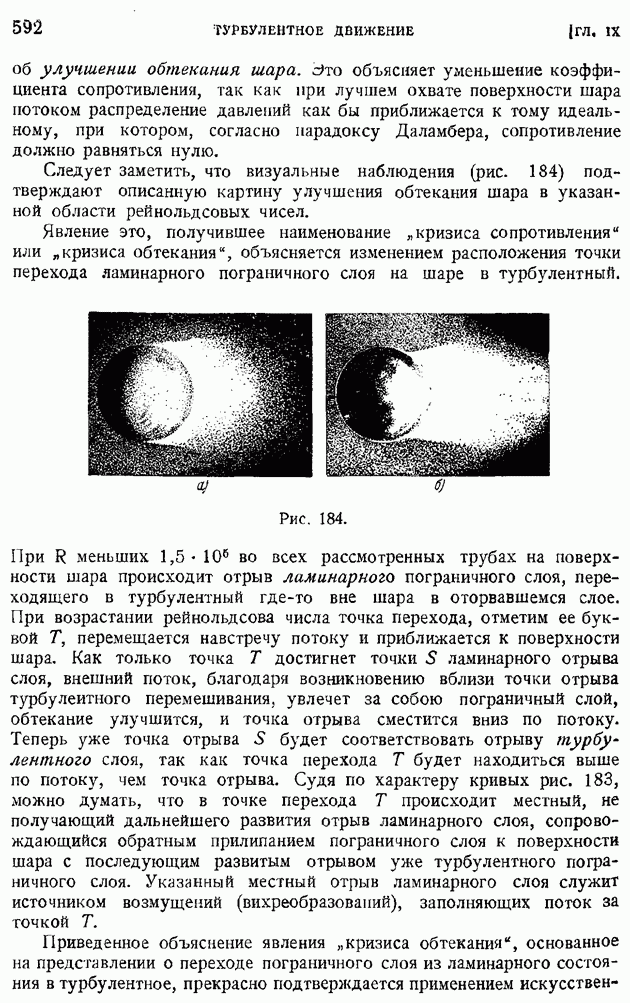
- § 42. Прямая задача в теории плоского движения идеальной несжимаемой жидкости. Применение метода конформных отображений. Гипотеза Чаплыгина о безотрывном обтекании задней кромки профиля. Формула циркуляции
- § 43. Теорема Жуковского о подъемной силе крыла. Зависимость подъемной силы от угла атаки. Коэффициент подъемной силы
- § 44. Применение метода комплексных переменных к выводу теоремы Жуковского. Формулы Чаплыгина для главного вектора и момента сил давления потока на крыло
- § 45. Выражение главного момента сил давления потока через коэффициенты конформного отображения. Фокус крыла. Независимость от угла атаки момента относительно фокуса. Парабола устойчивости
- § 46. Частные случаи конформного отображения крылового профиля на круг. Преобразование Жуковского-Чаплыгина. Теоретические крыловые профили
- § 47. Задача об обтекании слабо изогнутой дужки произвольной формы (теория тонкого крыла)
- § 48. Определение обтекания крылового профиля произвольной формы
- § 49. Обобщение теоремы Жуковского на случай плоской решетки с бесчисленным множеством профилей
- ГЛАВА VI. ПЛОСКОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ СЖИМАЕМОГО ГАЗА
- § 50. Основные уравнения плоского стационарного безвихревого движения сжимаемого газа. Линеаризированные уравнения
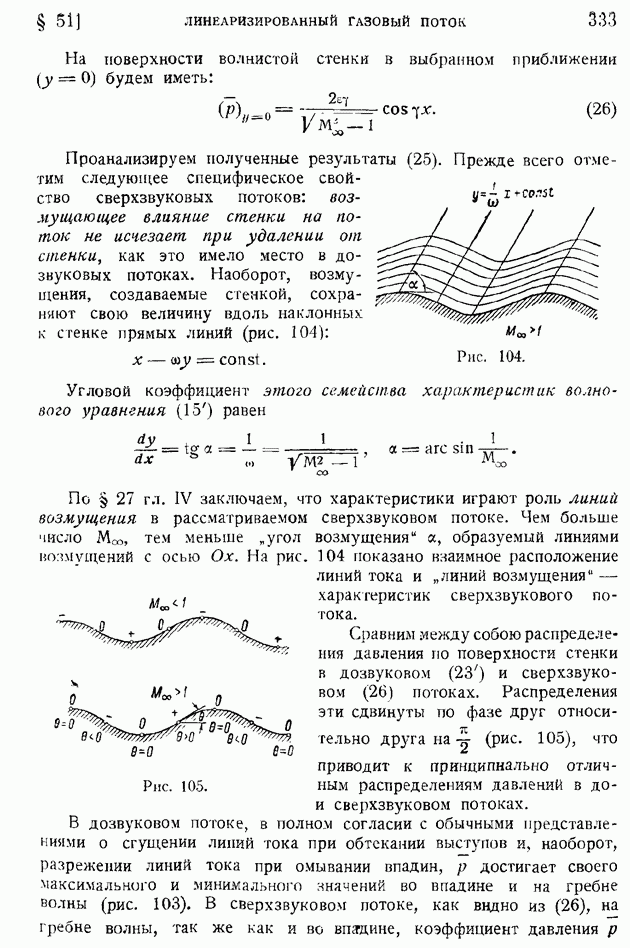
- 51. Линеаризированный до- и сверхзвуковой газовый поток вдоль волнистой стенки
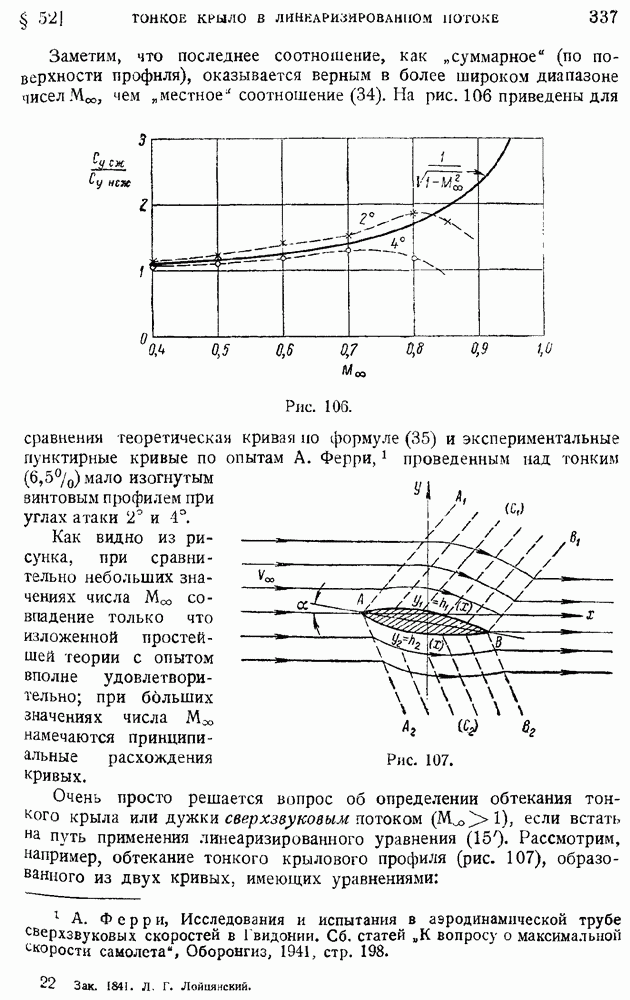
- § 52. Тонкое крыло в линеаризированном до- и сверхзвуковом потоках. Влияние сжимаемости газа на коэффициент подъемной силы в дозвуковом потоке. Коэффициенты подъемной силы и волнового сопротивления при сверхзвуковом потоке
- § 53. Нелинеаризированные уравнения движения идеального сжимаемого газа. Переход в плоскость годографа. Уравнения Чаплыгина
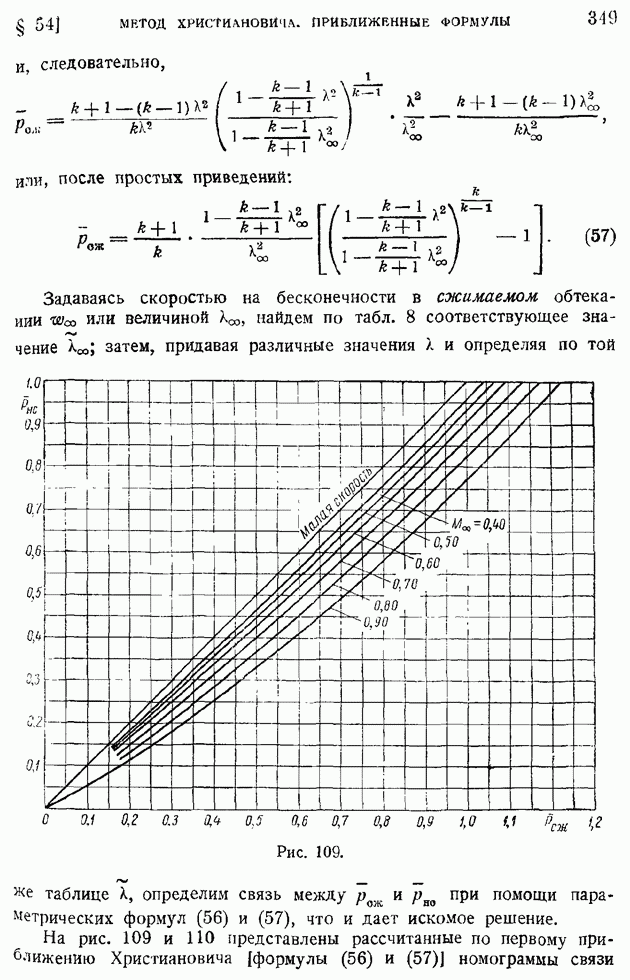
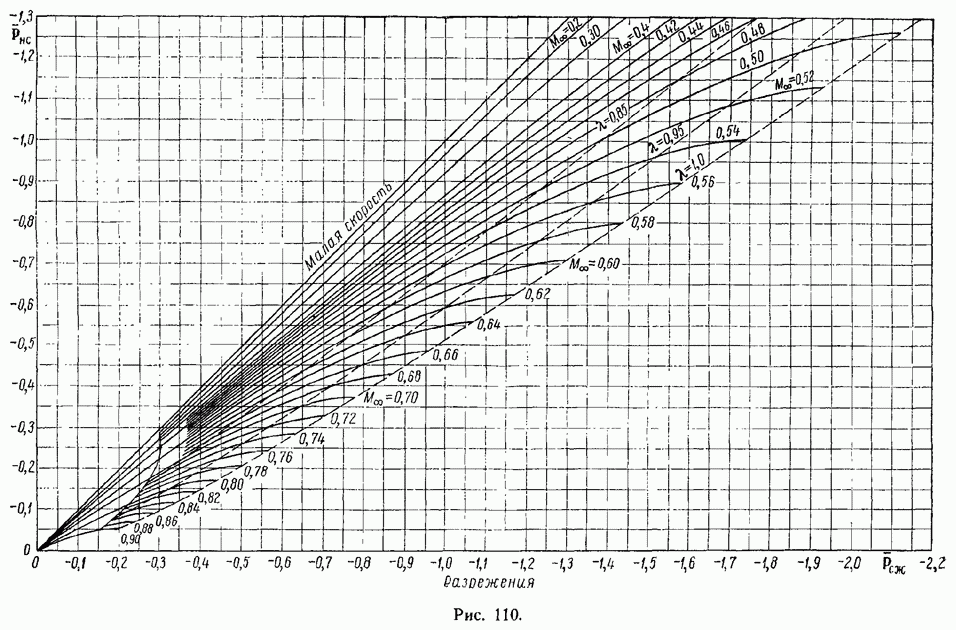
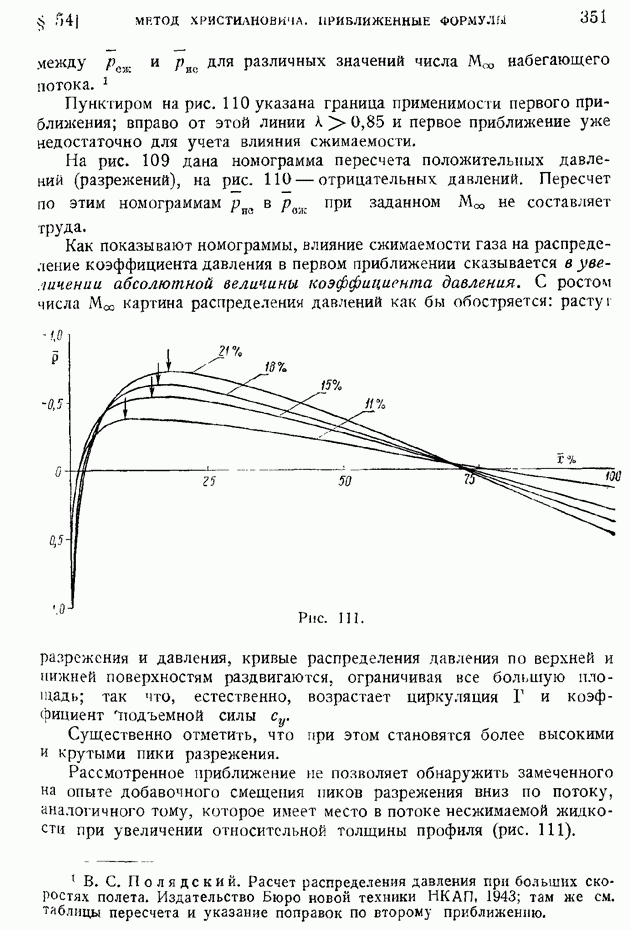
- § 54. Метод С. А. Христиановича. Приближенные формулы учета влияния сжимаемости на распределение давления
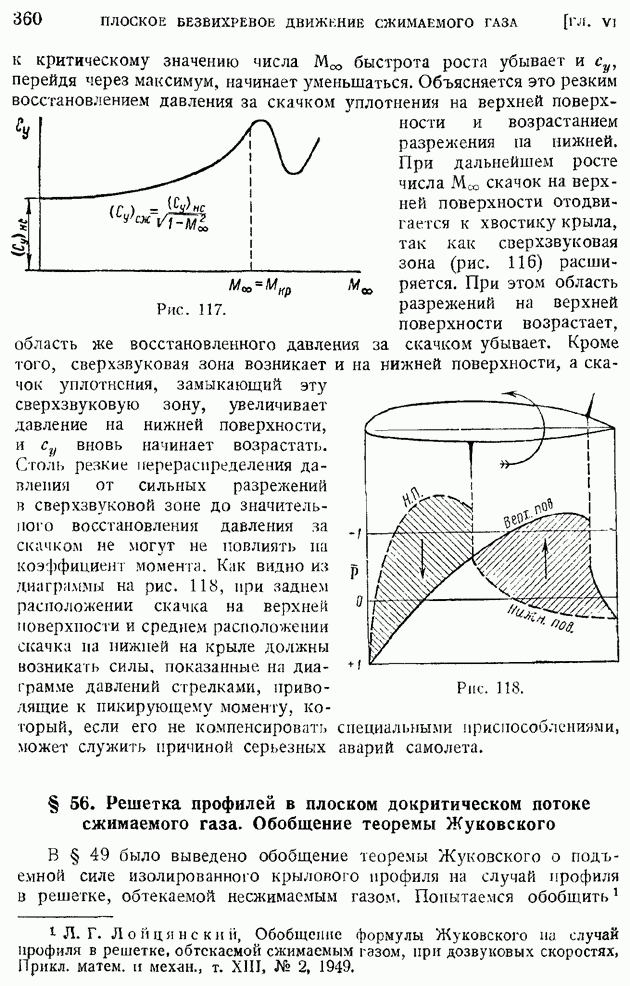
- § 55. Критическое число M и его определение по заданному распределению давления в несжимаемом обтекании. Поведение коэффициента подъемной силы и момента при около- и закритических значениях числа M
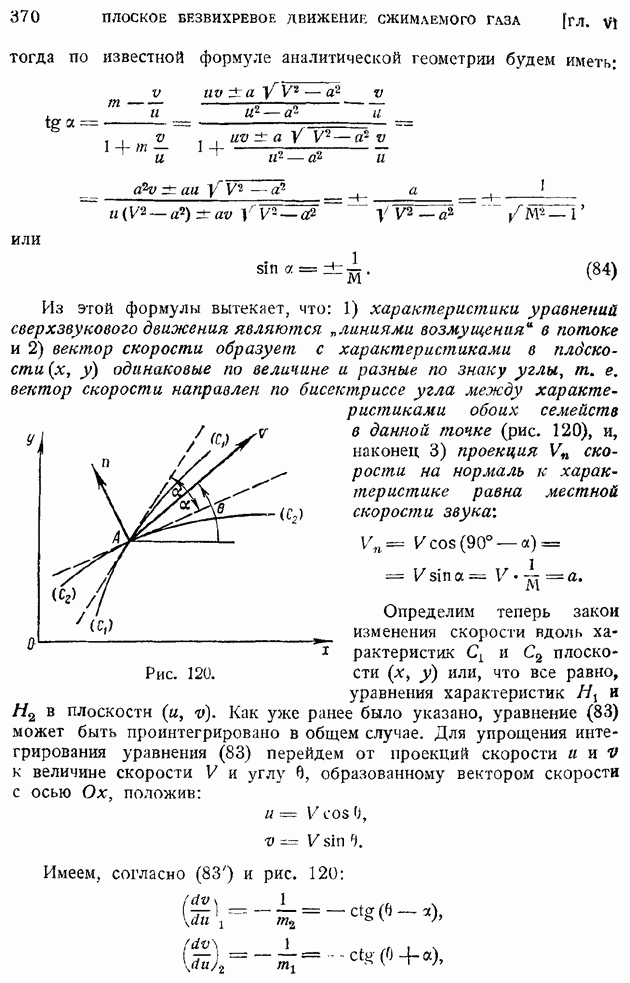
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
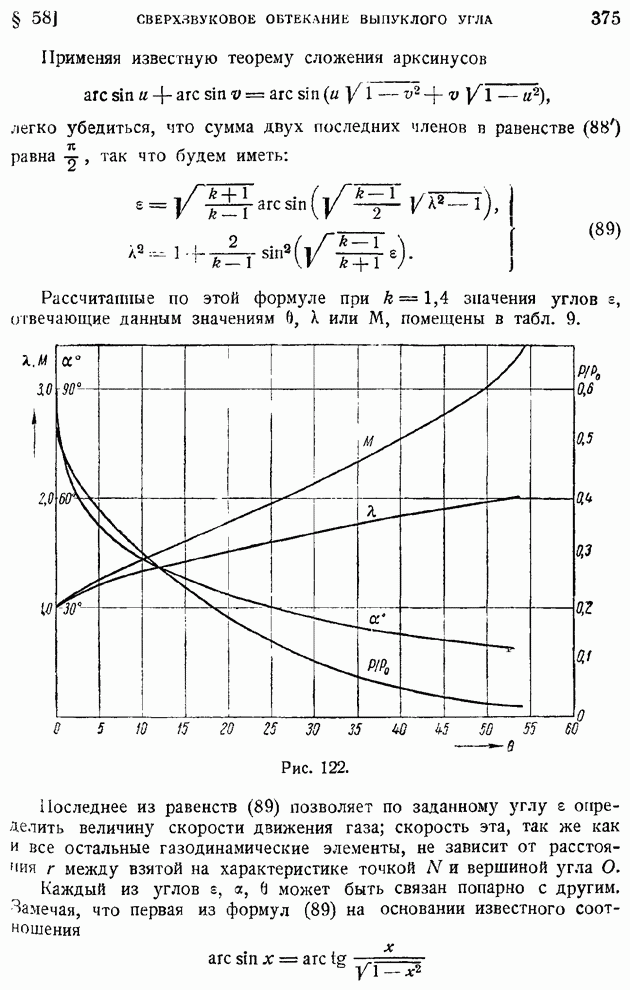
- § 57. Нелинеаризированный сверхзвуковой поток. «Характеристики» уравнений плоского сверхзвукового потока. Линин возмущения и их основные свойства
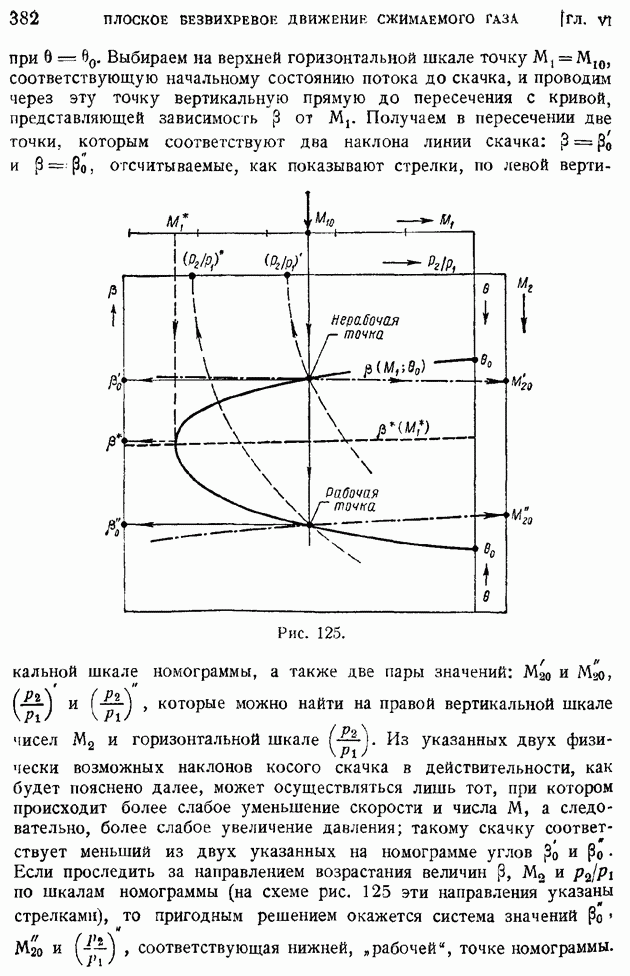
- § 58. Обтекание выпуклого угла сверхзвуковым потоком. Влияние угла поворота струи на ее газодинамические элементы
- § 59. Сверхзвуковой поток внутри тупого угла. Косой скачок уплотнения. Связь между газодинамическими элементами до и за косым скачком
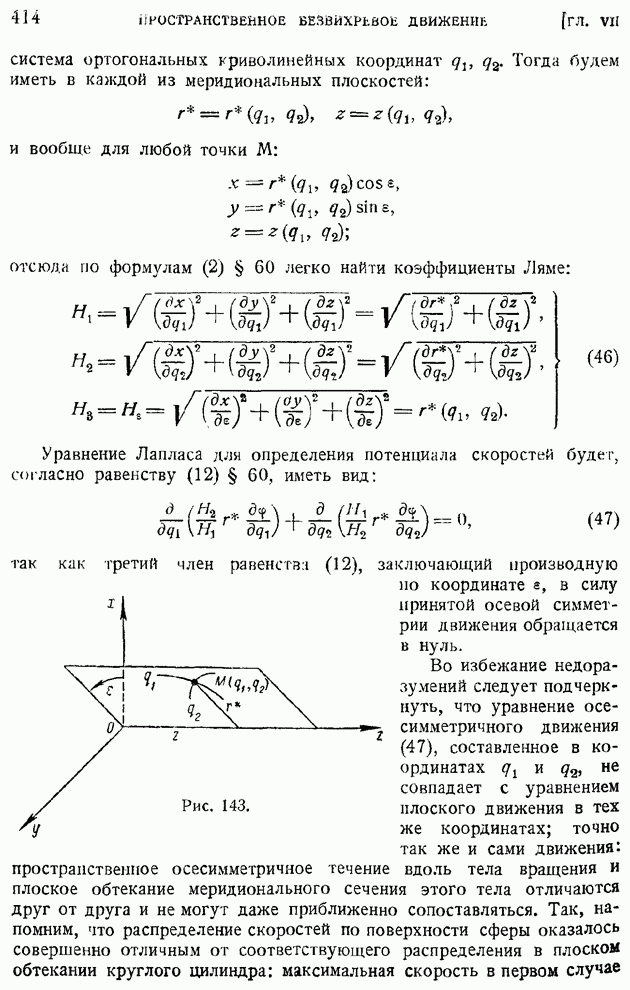
- ГЛАВА VII. ПРОСТРАНСТВЕННОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ
- § 60. Ортогональные криволинейные координаты в пространстве. Основные дифференциальные операторы поля в криволинейных координатах
- § 61. Потенциал скоростей. Поле источника и диполя. Непрерывное распределение источников и диполей. Ньютонов потенциал. Потенциал простого и двойного слоев
- § 62. Поле скоростей вокруг заданной системы вихрей. Формула Био — Савара. Потенциал скоростей замкнутой вихревой нити. Аналогия с потенциалом двойного слоя
- § 63. Функция тока и ее связь с векторным потенциалом скоростей. Функции тока простейших течений
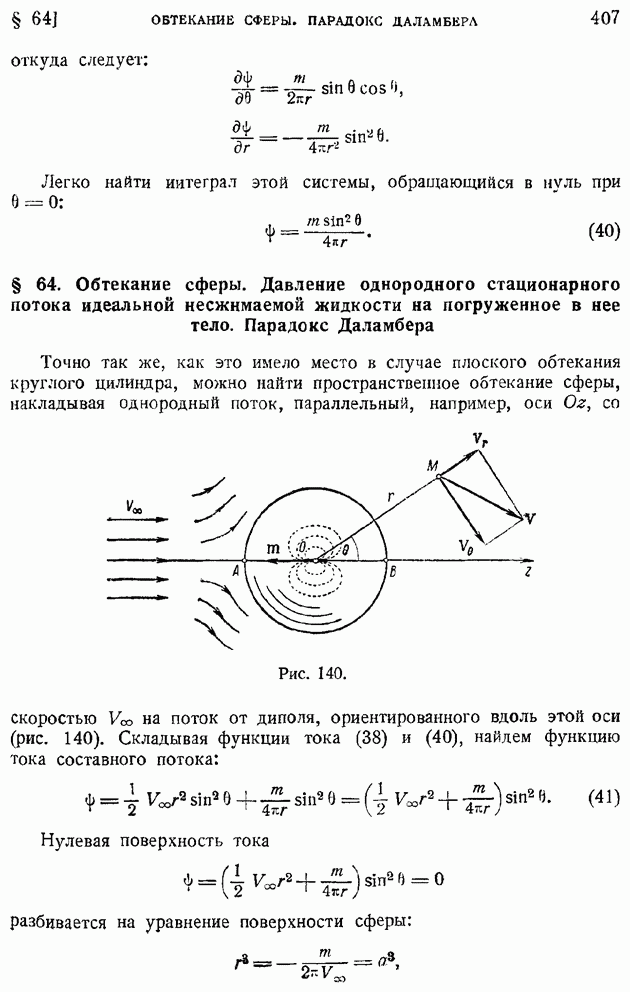
- § 64. Обтекание сферы. Давление однородного стационарного потока идеальной несжимаемой жидкости на погруженное в нее тело. Парадокс Даламбера
- § 65. Общие уравнения осесимметричного движения. Применение цилиндрических координат. Течение сквозь каналы
- § 66. Осесимметричное продольное обтекание тел вращения. Случай эллипсоида вращения
- § 67. Поперечное обтекание тел вращения. Пример эллипсоида вращения
- § 68. Продольное и поперечное обтекание тел вращения большого удлинения. Приближенные выражения граничных условий. Применение тригонометрических сумм для определения коэффициентов …
- § 69. Метод «особенностей». Применение непрерывно распределенных источников (стоков) и диполей для решения задачи о продольном и поперечном обтекании тел вращения
- § 70. Общий случай движения твердого тела сквозь несжимаемую идеальную жидкость. Определение потенциала скоростей. Главный вектор и главный момент сил давления потока на тело
- § 71. Коэффициенты «присоединенных масс». Свойство симметрии. «Присоединенная» кинетическая энергия. Определение «присоединенных масс» поступательно движущегося цилиндра, шара и эллипсоида
- § 72. Элементы теории крыла конечного размаха. Вихревая система крыла. Гипотеза плоских сечеиий. Геометрические и действительные углы атаки. Подъемная сила и «индуктивное сопротивление»
- § 73. Основные формулы теории «несущей линии». «Индуктивная скорость» и «индуктивный угол». Прямая задача определения подъемной силы и индуктивного сопротивления по заданному распределению циркуляции
- § 74. Крыло с минимальным индуктивным сопротивлением. Эллиптическое распределение циркуляции. Связь между коэффициентами индуктивного сопротивления и подъемной силы. Основное уравнение теории крыла и понятие о его интегрировании
- ГЛАВА VIII. ДИНАМИКА ВЯЗКОЙ ЖИДКОСТИ И ГАЗА
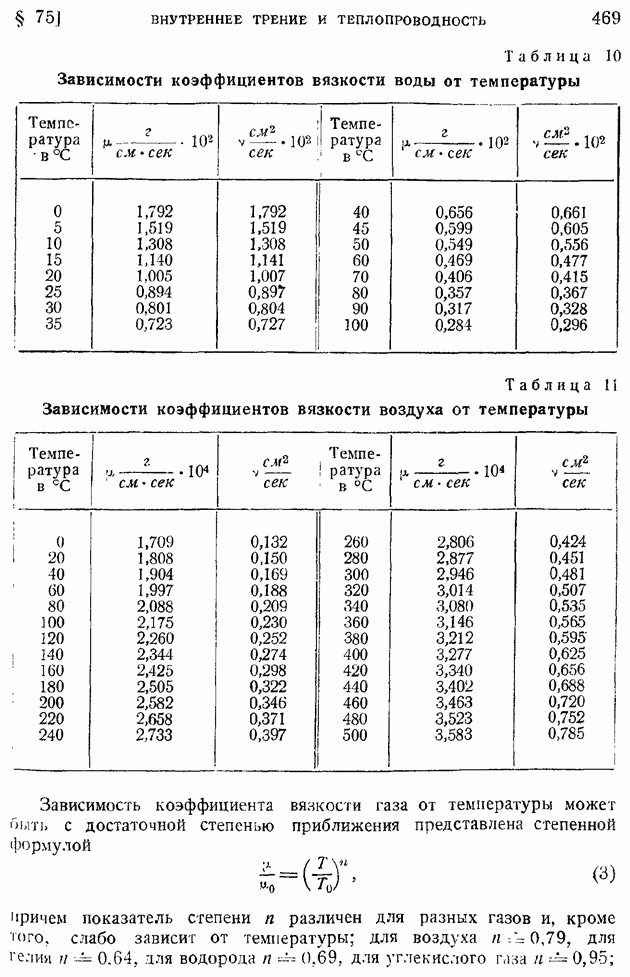
- § 75. Внутреннее трение и теплопроводность в жидкостях и газах. Законы Ньютона и Фурье. Влияние температуры на коэффициенты вязкости и теплопроводности. Число «сигма»
- § 76. Обобщение закона Ньютона на случай произвольного движения среды. Закон линейной связи между тензорами напряжений и скоростей деформации
- § 77. Общие уравнения движения вязкой жидкости. Динамические уравнения и уравнение баланса энергии. Граничные условия движения жидкости с треннем и теплопроводностью
- § 78. Понятие о подобии гидродинамических явлений. Безразмерные уравнения движения вязкой жидкости и газа. Условия подобия
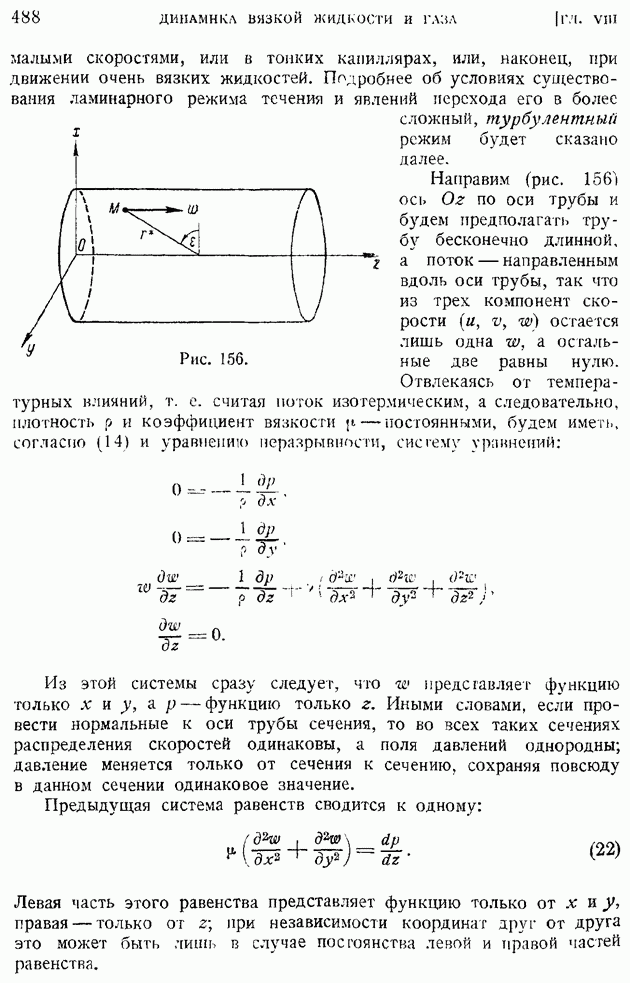
- § 79. Ламинарное движение вязкой несжимаемой жидкости по цилиндрической трубе
- § 80. Обтекание шара при очень малых значениях числа Рейнольдса. Формула сопротивления шара по Стоксу и ее обобщения
- § 81. Вихревые линии в идеальной и вязкой жидкости. Сохраняемость вихревых линий при отсутствии внутреннего трения. Диффузия вихря в вязкой жидкости
- § 82. Одномерное прямолинейное движение сжимаемого вязкого газа. Движение внутри скачка уплотнения. Понятие о толщине скачка
- § 83. Работа внутренних сил и диссипация механической энергии в движущейся вязкой среде
- § 84. Обтекание тел жидкостью и газом при больших значениях числа Рейнольдса. Основные уравнения теории ламинарного пограничного слоя
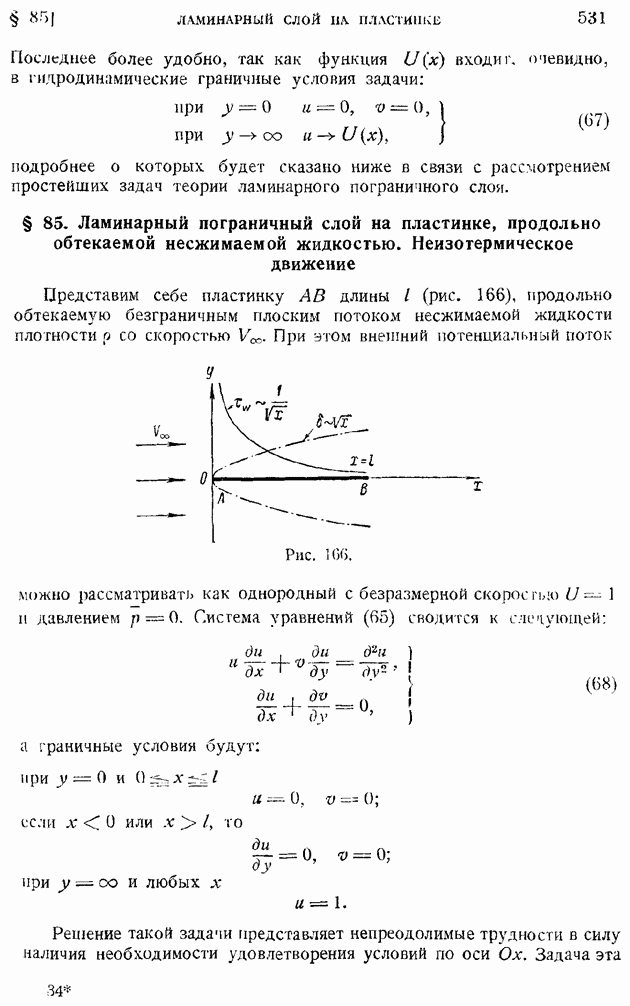
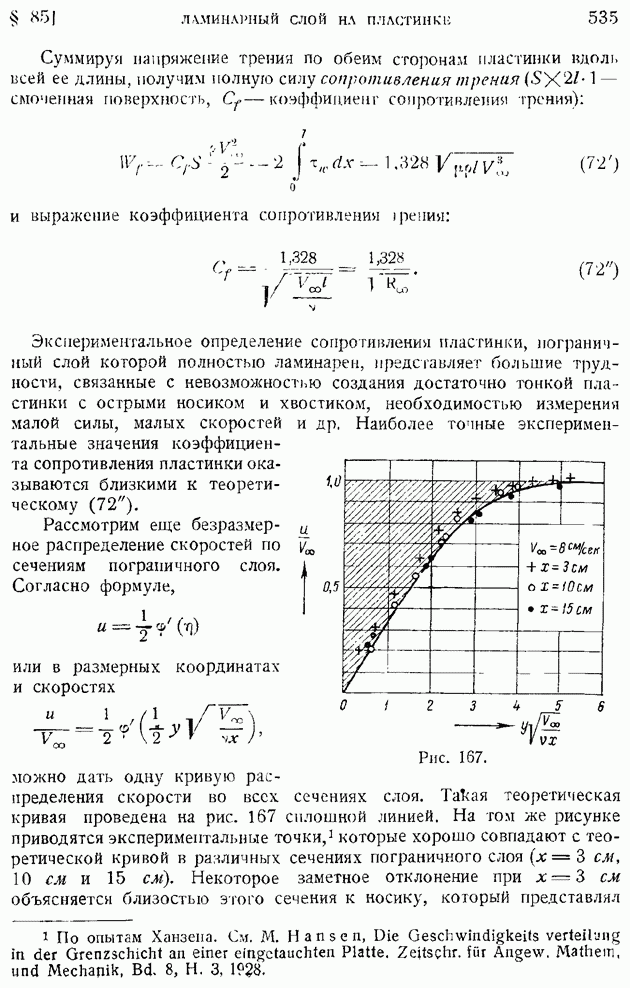
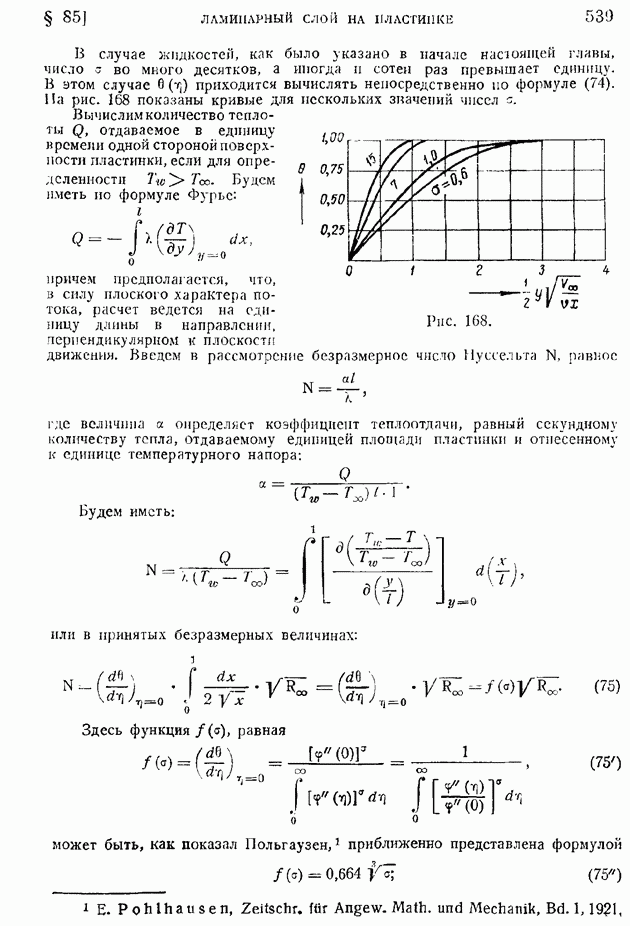
- § 85. Ламинарный пограничный слой на пластинке, продольно обтекаемой несжимаемой жидкостью. Неизотермическое движение
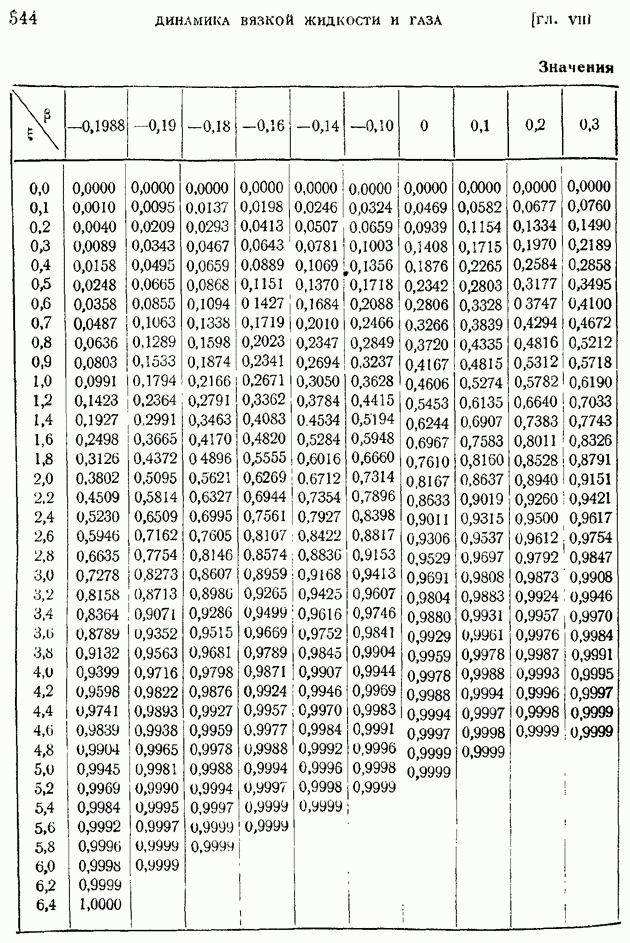
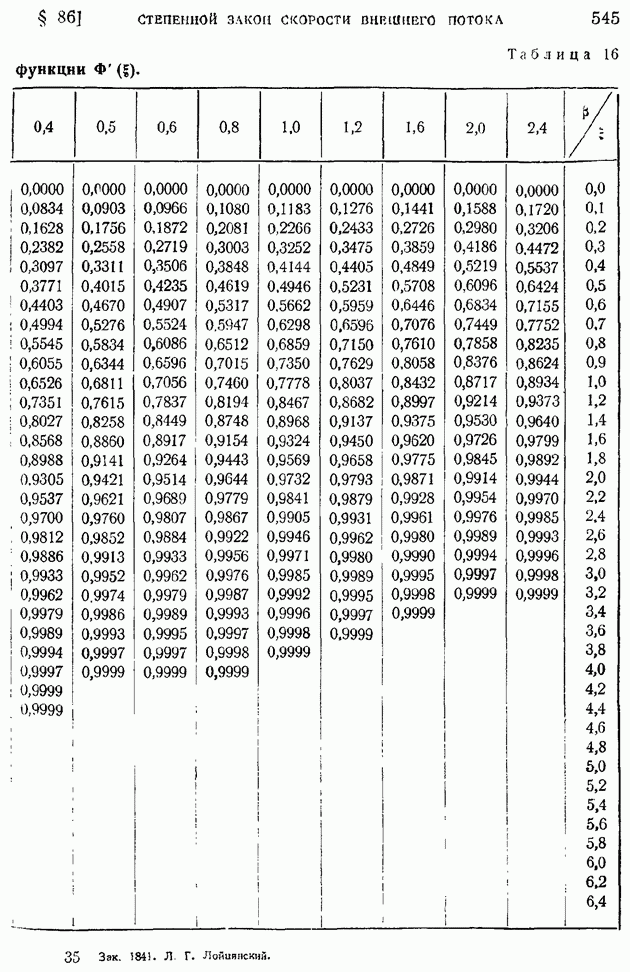
- § 86. Ламинарный пограничный слой при степенном задании скорости внешнего потока
- § 87. Ламинарный пограничный слой в общем случае задания скорости внешнего потока. Применение уравнения импульсов для приближенного расчета ламинарного пограничного слоя
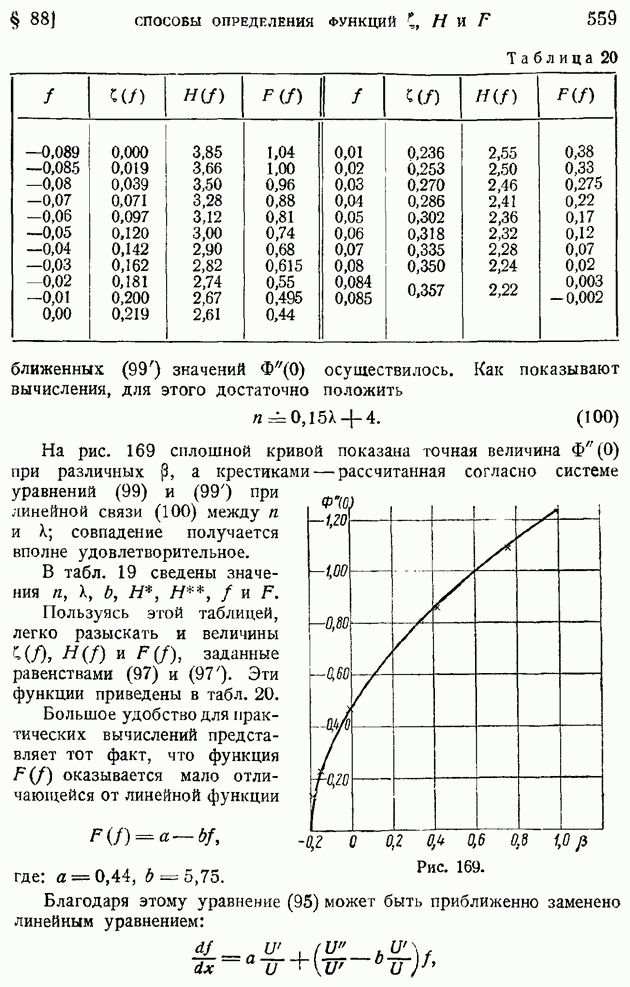
- § 88. Способы определения функций … Приближенный метод расчета ламинарного пограничного слоя
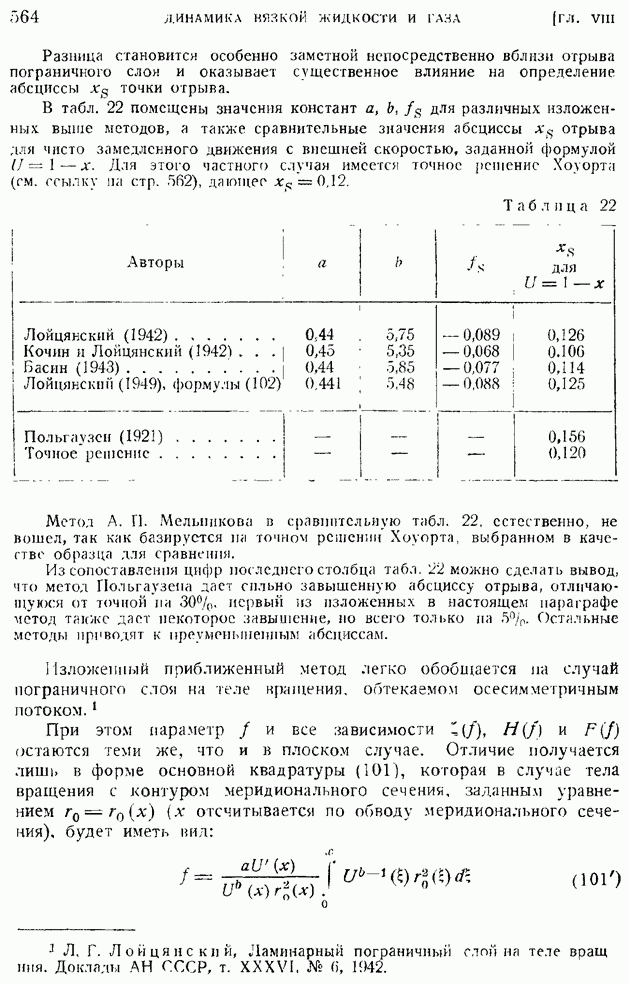
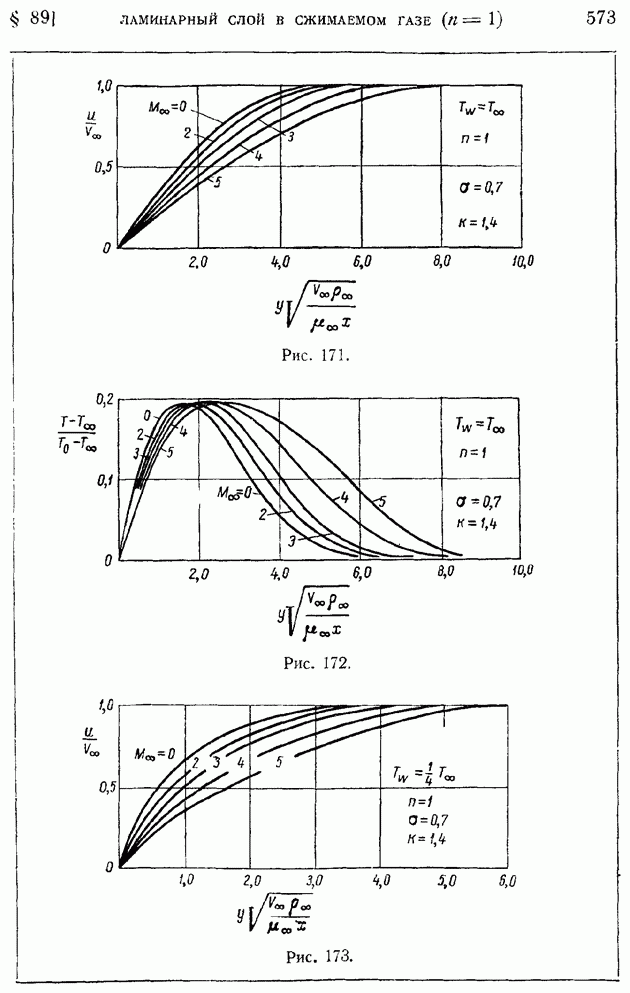
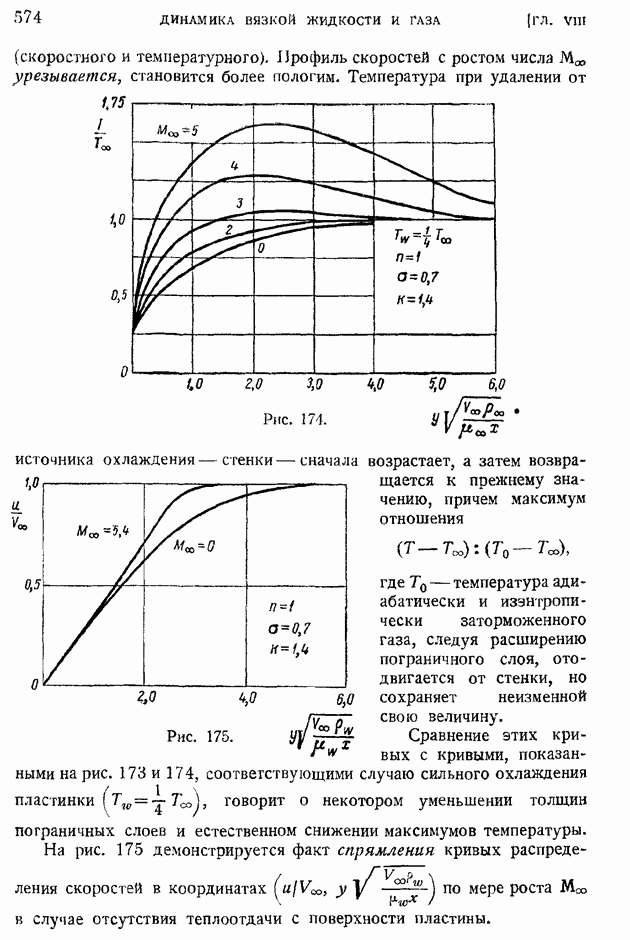
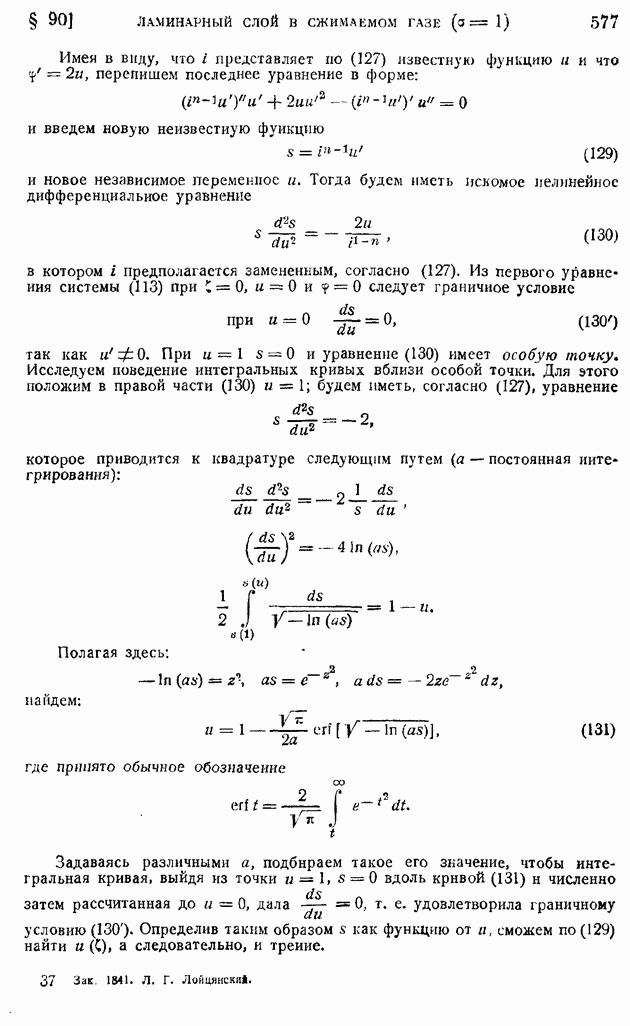
- § 89. Ламинарный пограничный слой на пластинке, продольно обтекаемой сжимаемым газом при больших скоростях. Случай линейной зависимости коэффициента вязкости от температуры (n = 1)
- § 90. Ламинарный пограничный слой на пластинке при любом законе связи между вязкостью и температурой и при числе … Обтекание крылового профиля потоком больших скоростей
- ГЛАВА IX. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ
- § 91. Переход ламинарного движения в турбулентное. Критическое рейнольдсово число
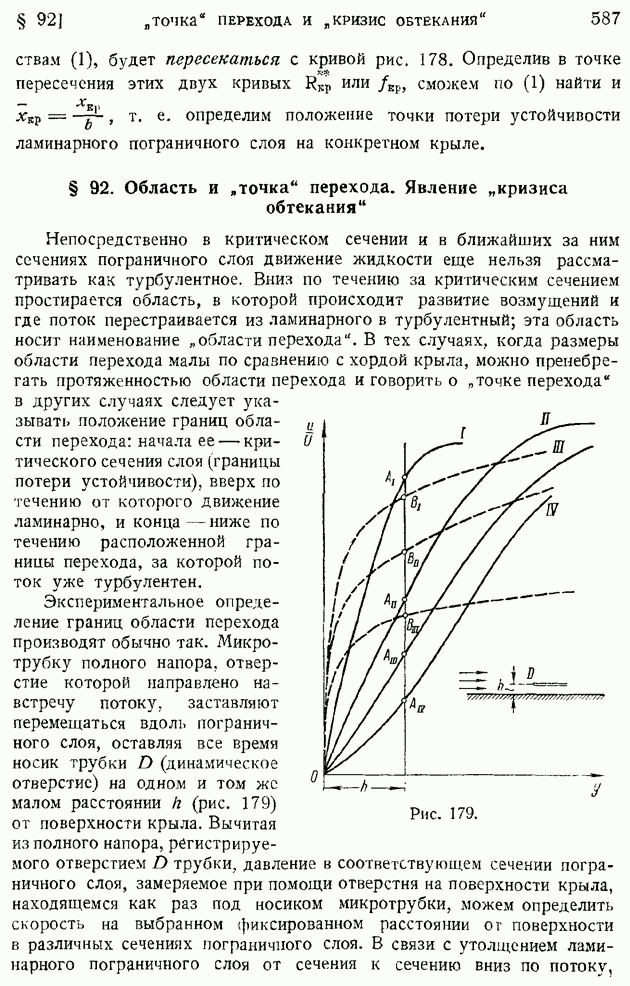
- § 92. Область и «точка» перехода. Явление «кризиса обтекания»
- § 93. Основные уравнения осреднеиного турбулентного движения. Тензор турбулентных напряжений
- § 94. Турбулентное движение жидкости в плоской и круглой трубе. Логарифмические формулы скоростей
- § 95. Формулы сопротивления гладких труб при турбулентном движении жидкости. Ламинарный подслой
- § 96. Влияние шероховатости стенок трубы на ее сопротивление. Предельные режимы течения. Режим установившейся шероховатости
- § 97. Турбулентный пограничный слой на продольно обтекаемой пластине. Сопротивление пластины
- § 98. Турбулентный пограничный слой на крыловом профиле при малом продольном перепаде давлений
- § 99. Турбулентный пограничный слой на крыловом профиле при значительных продольных перепадах давления
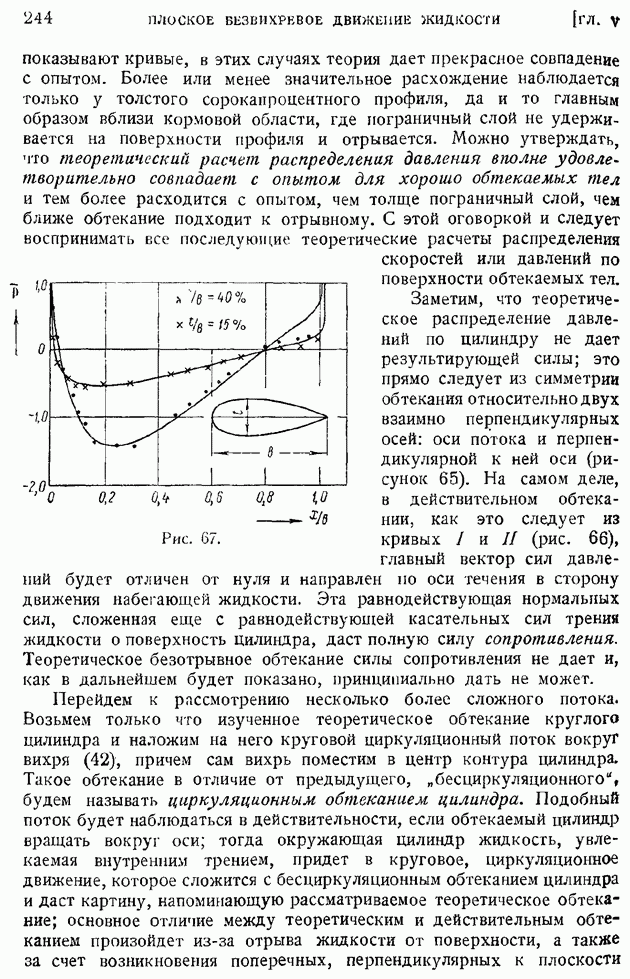
- § 100. Профильное сопротивление крыла. Разложение профильного сопротивления на сопротивление трения и сопротивление давлений. Обратное влияние пограничного слоя на распределение давлений по поверхности обтекаемого профиля
- § 101. Приближенные формулы профильного сопротивления крыла и крылового профиля в решетке
- § 102. Основные закономерности «свободной турбулентности». Плоская турбулентная струя в пространстве, заполненном той же жидкостью
- § 103. Турбулентный след за обтекаемым телом
- § 104. Рассеяние турбулентных возмущений в жидкости. Случай изотропной и однородной турбулентности. Закон сохранения момента возмущений