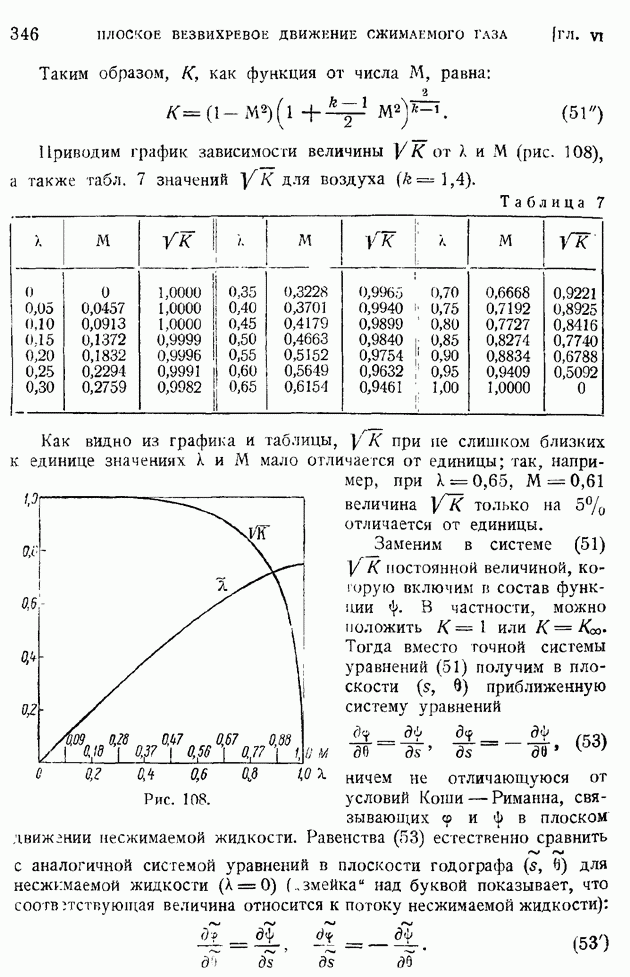
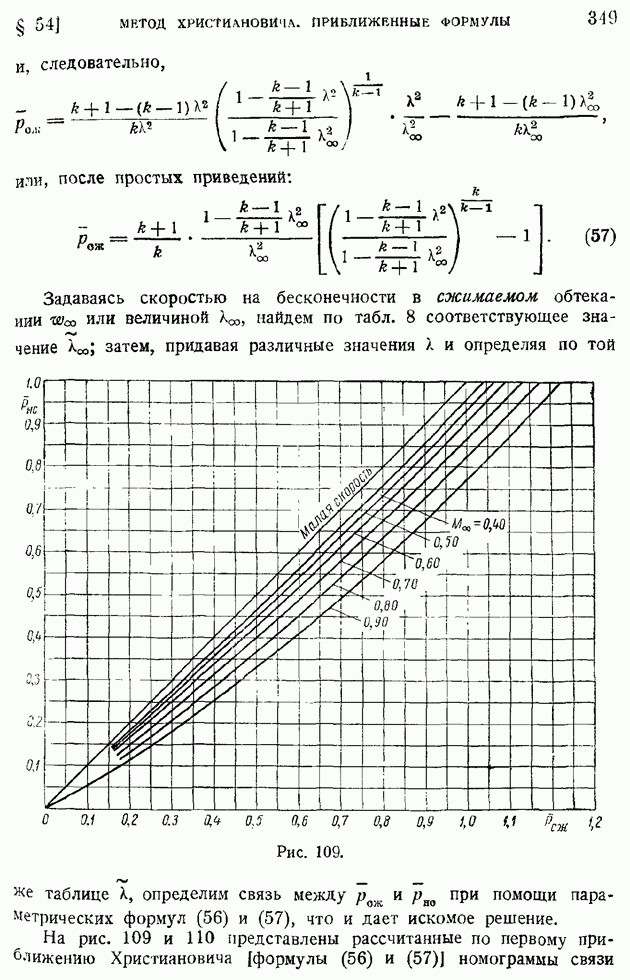
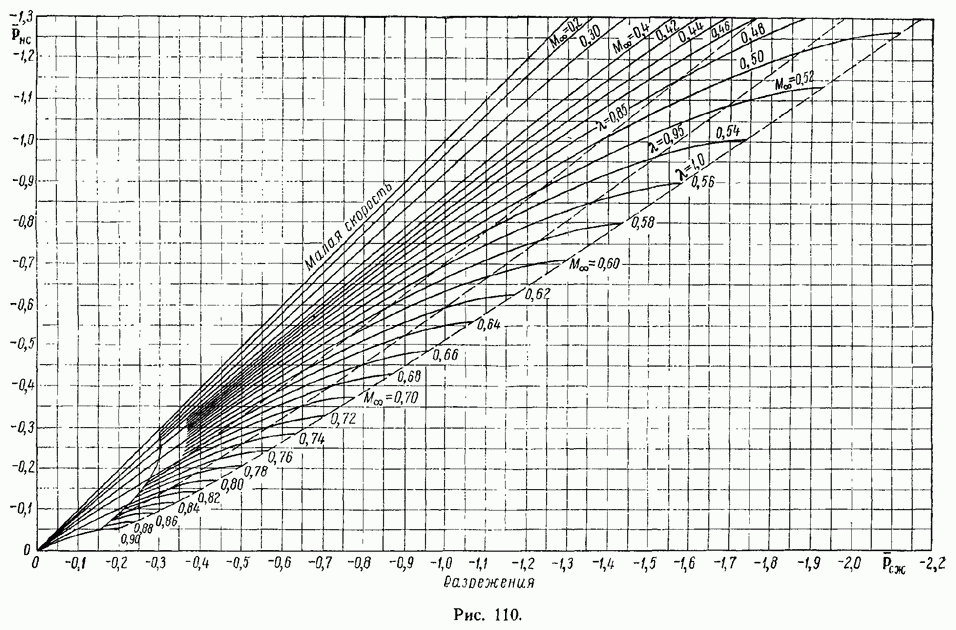
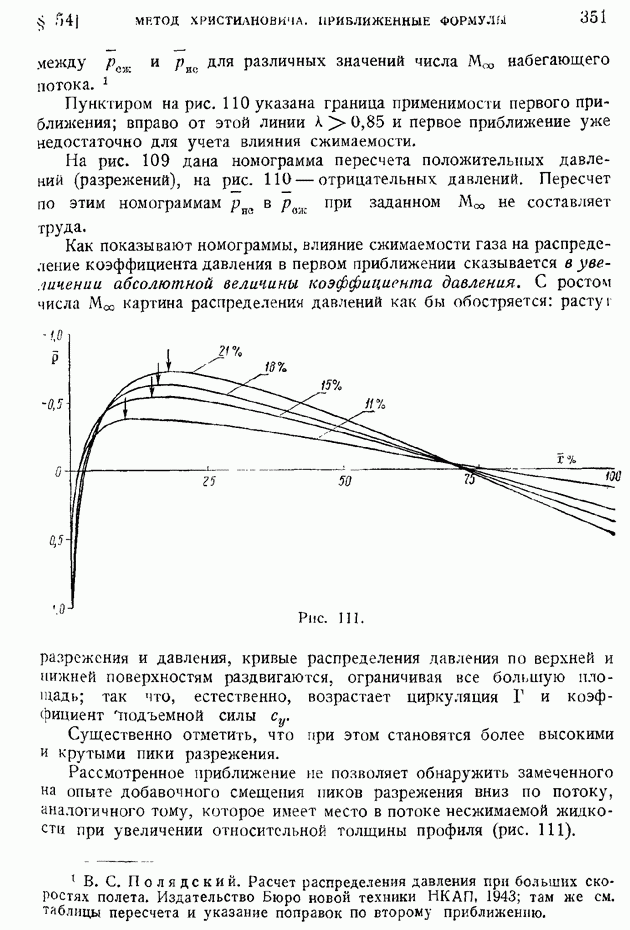
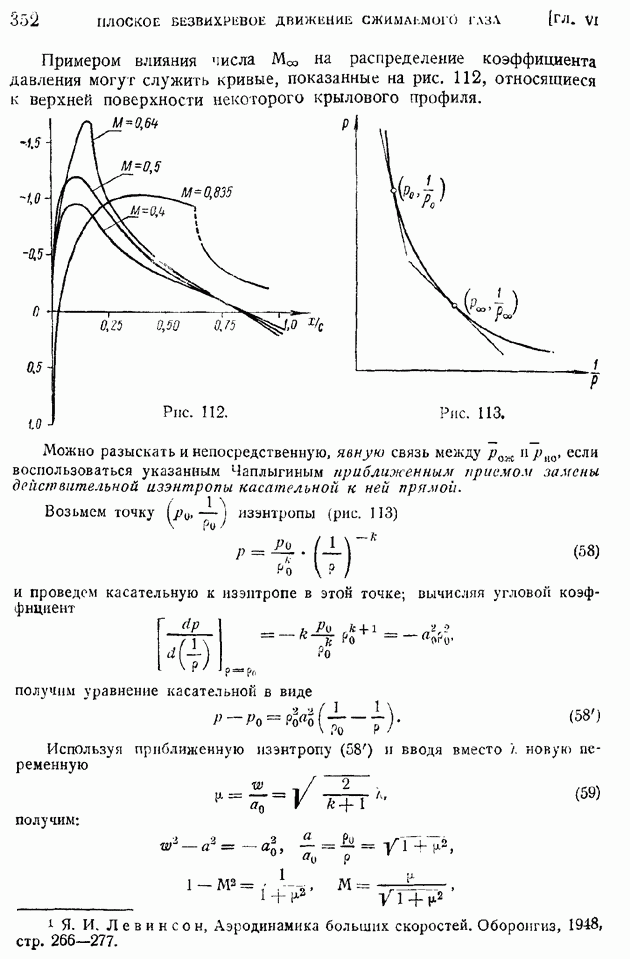
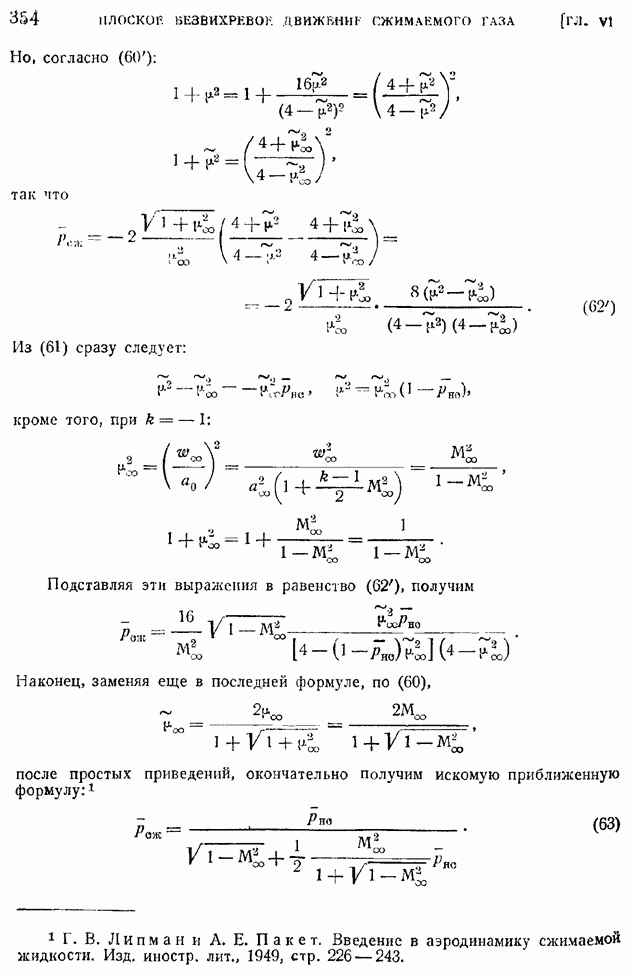
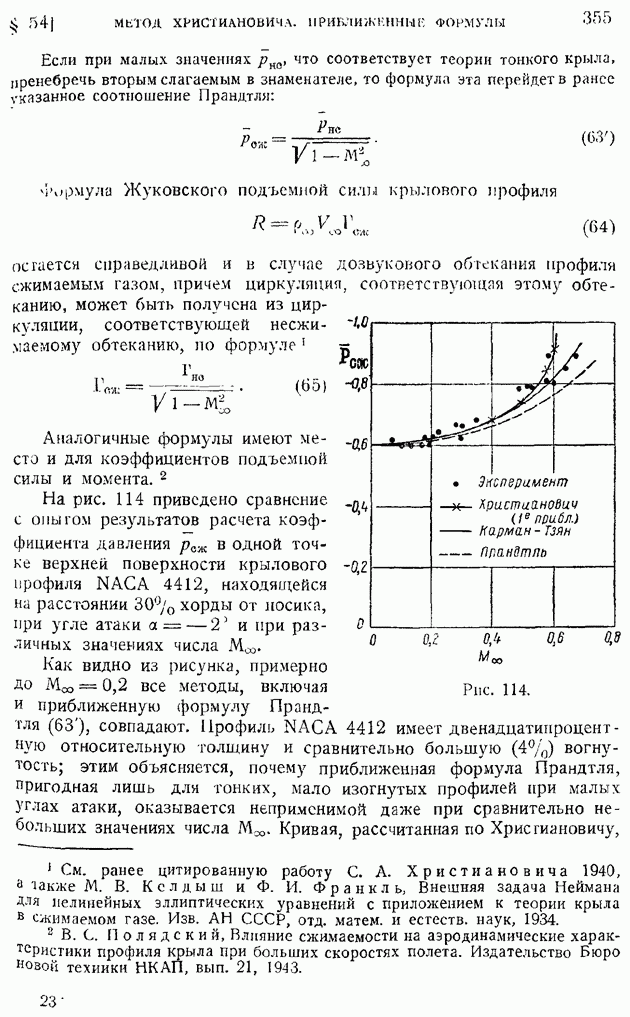
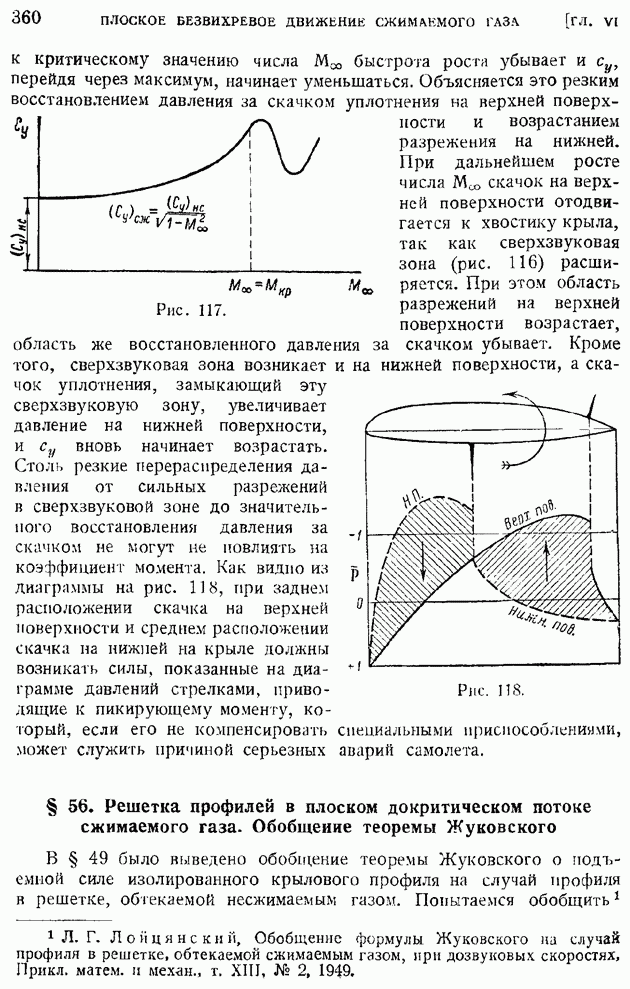
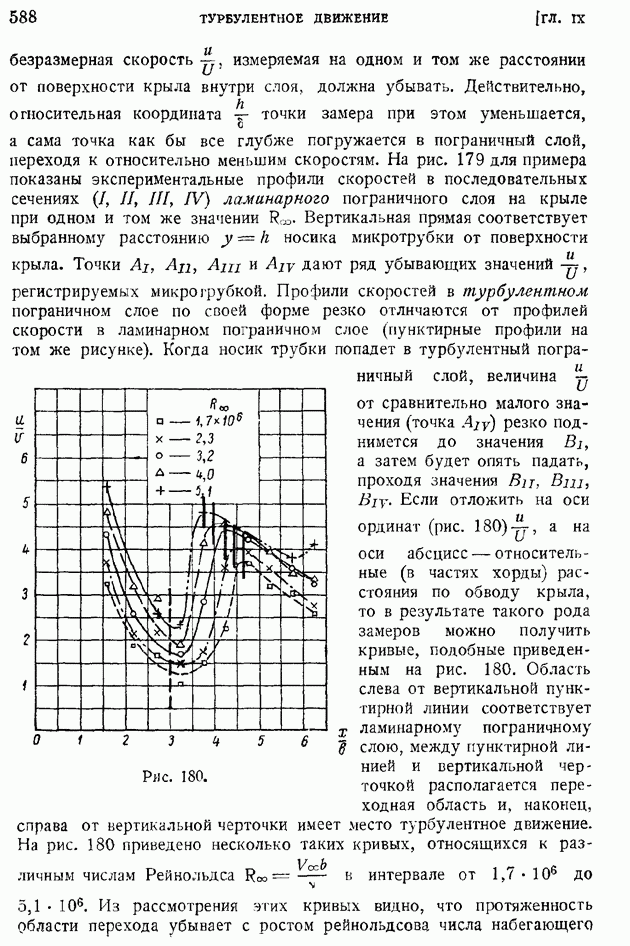
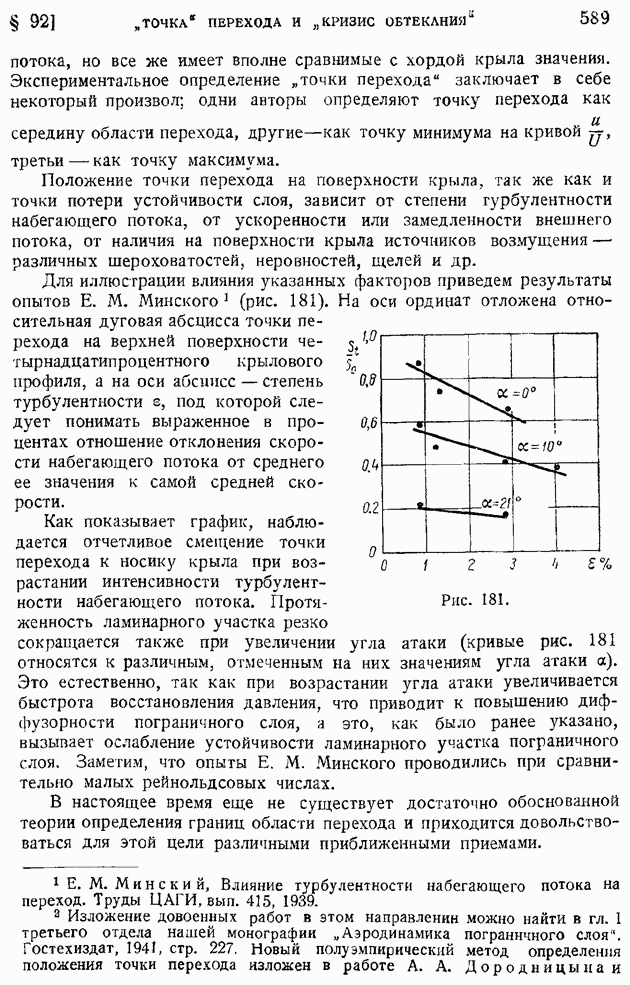
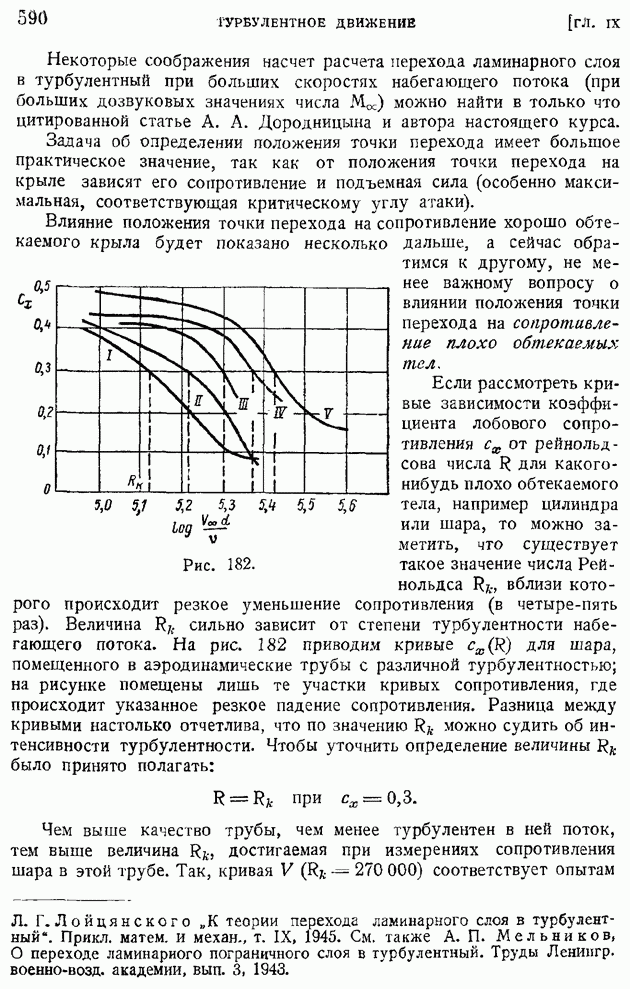
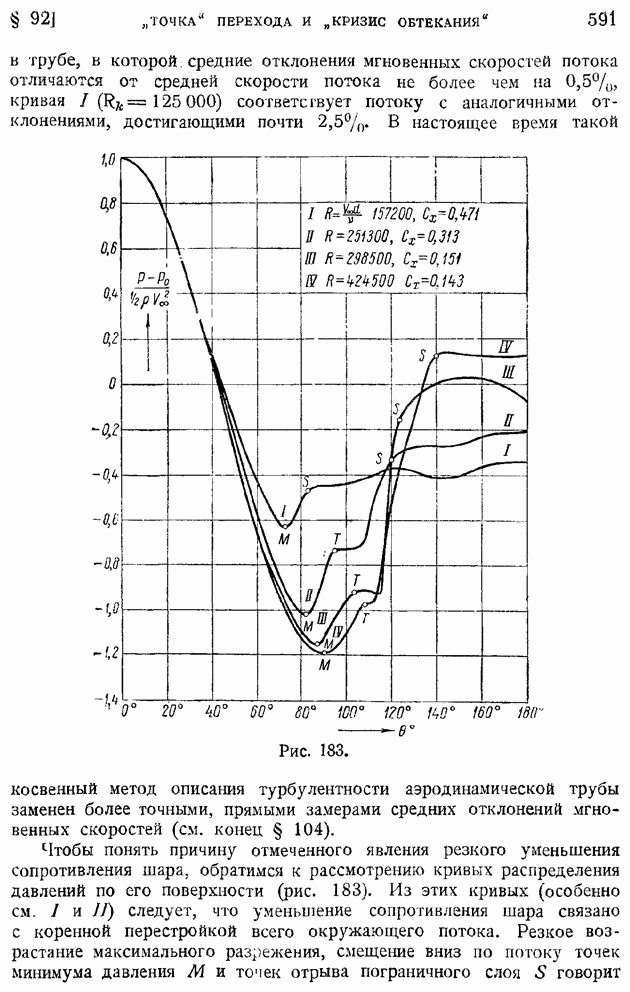
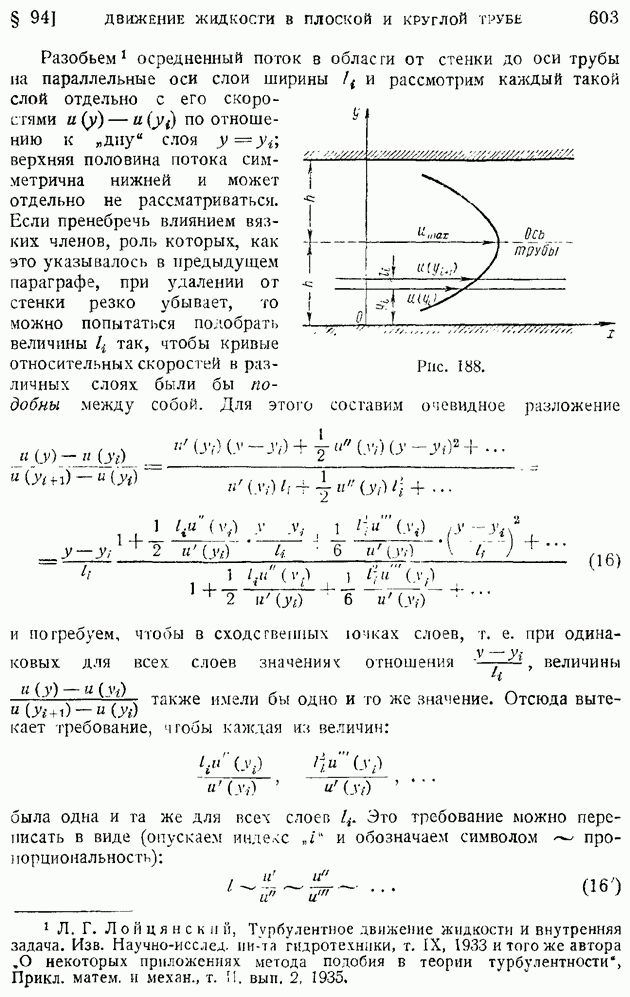
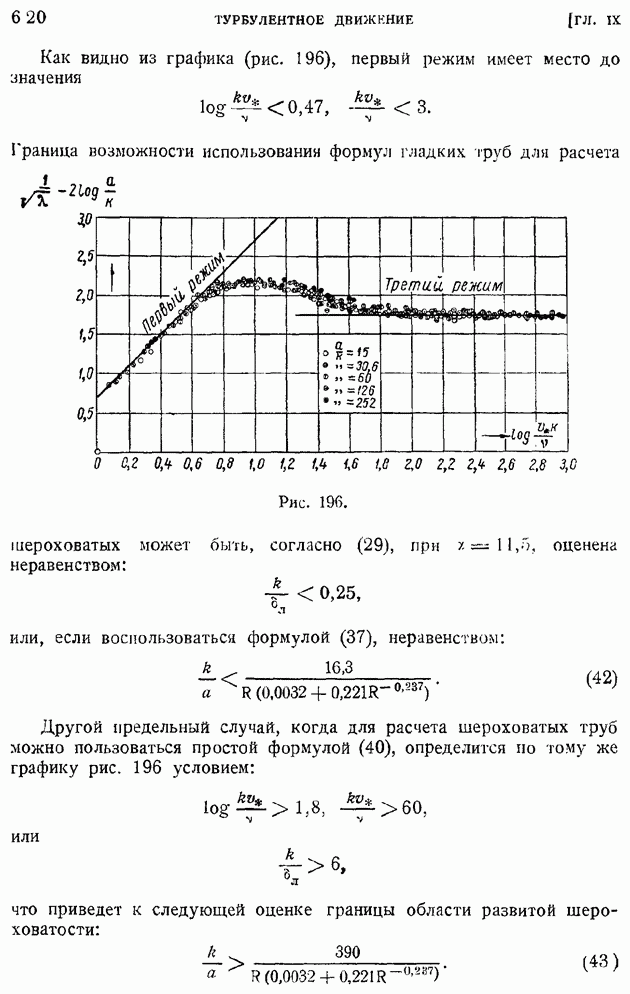
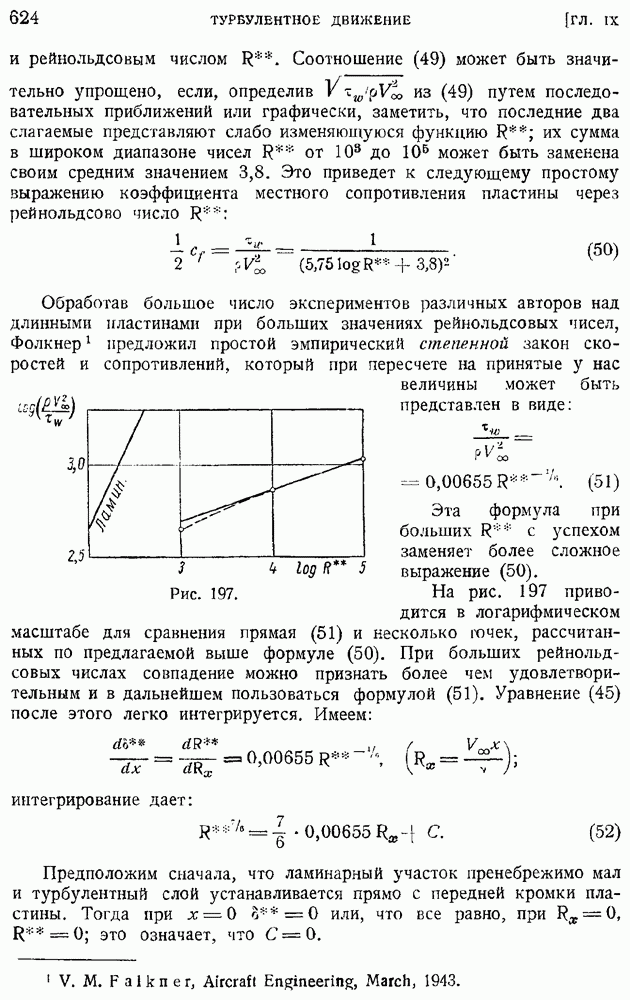
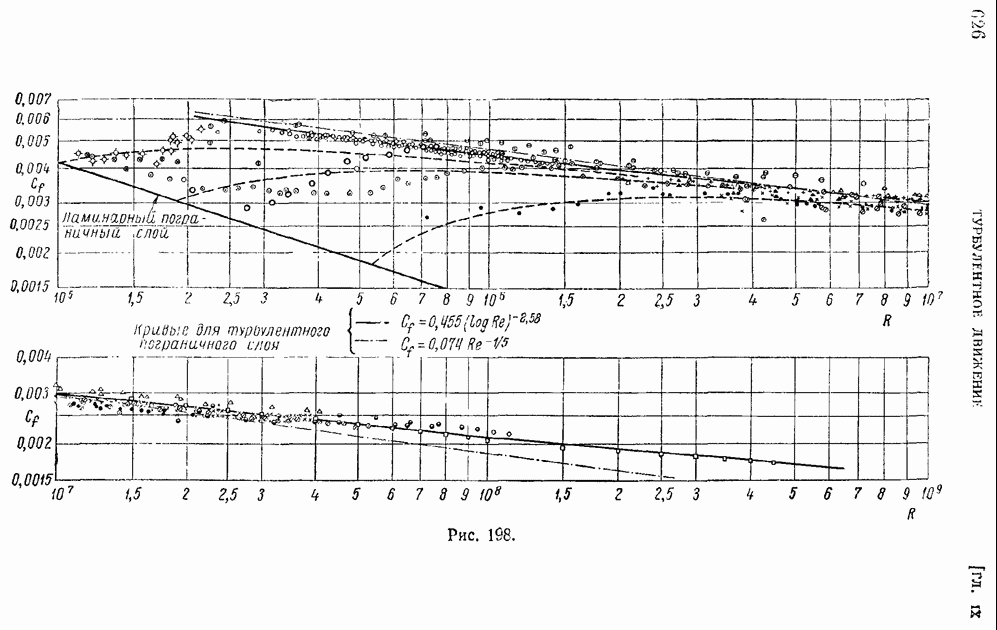
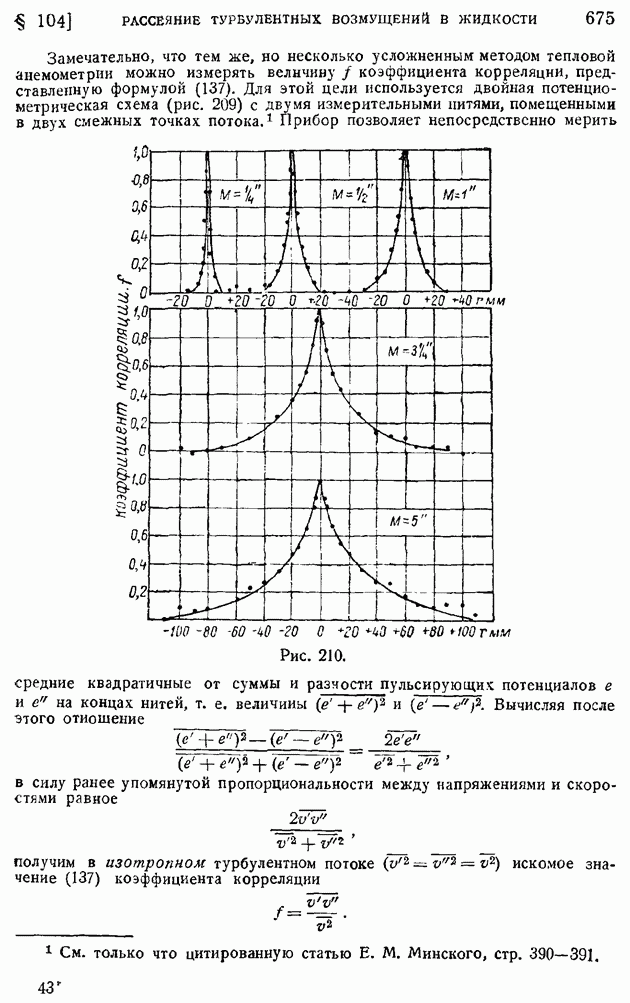
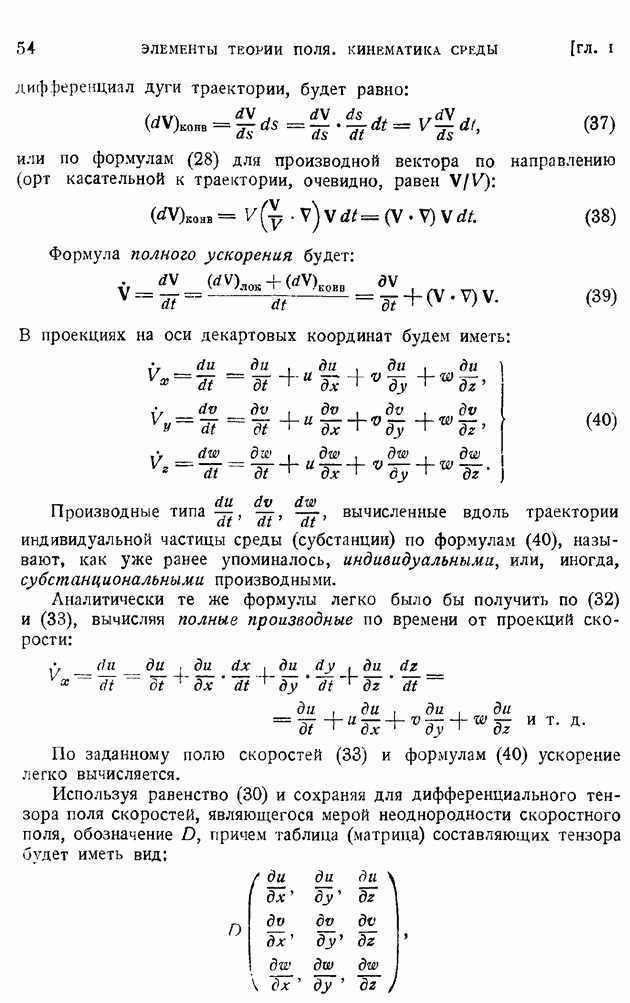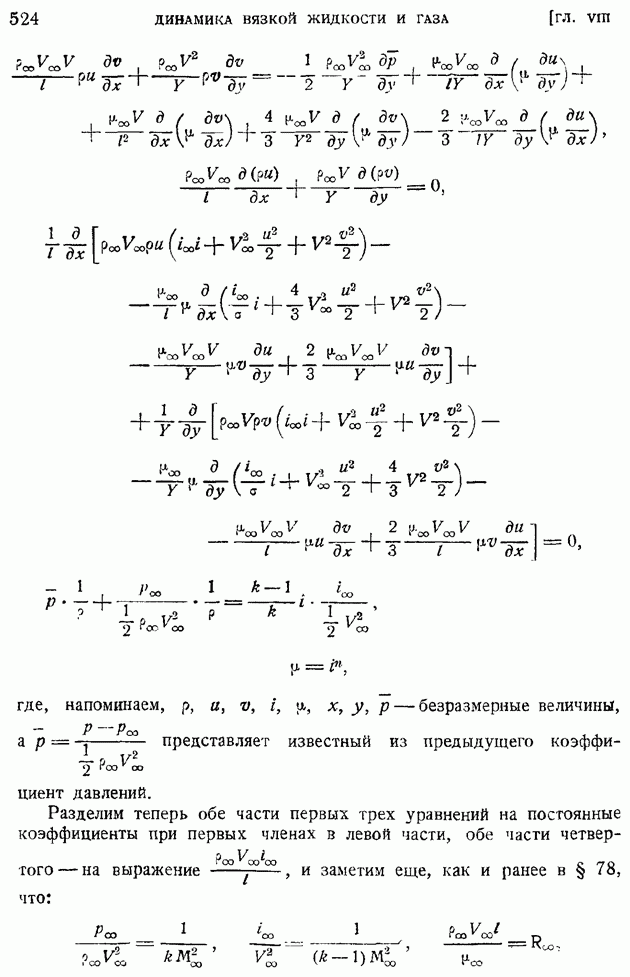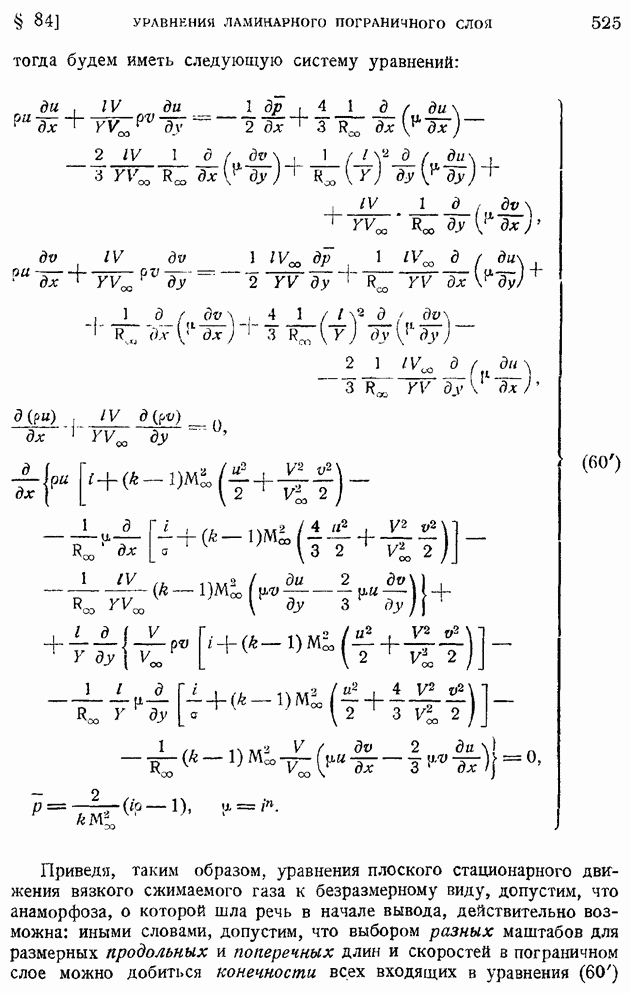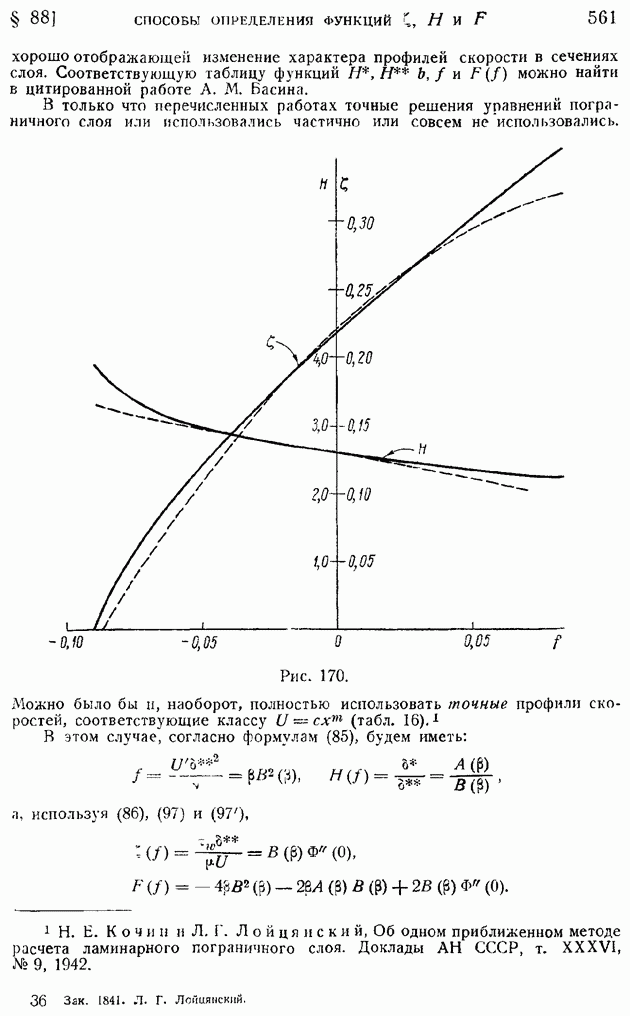| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 11. Скорость объемного расширения жидкости. Интегральные представления дифференциальных операторов поля. Основные интегральные формулы
Деформационная часть поля скоростей характеризуется еще одной важной величиной — скоростью относительного объемного расширения в данной точке, которую можно определить как предел

где  - малый объем, в котором взята точка. Эта физическая скалярная величина носит наименование дивергенции (расходимости) скоростного поля и обозначается символом
- малый объем, в котором взята точка. Эта физическая скалярная величина носит наименование дивергенции (расходимости) скоростного поля и обозначается символом  так что можно написать
так что можно написать

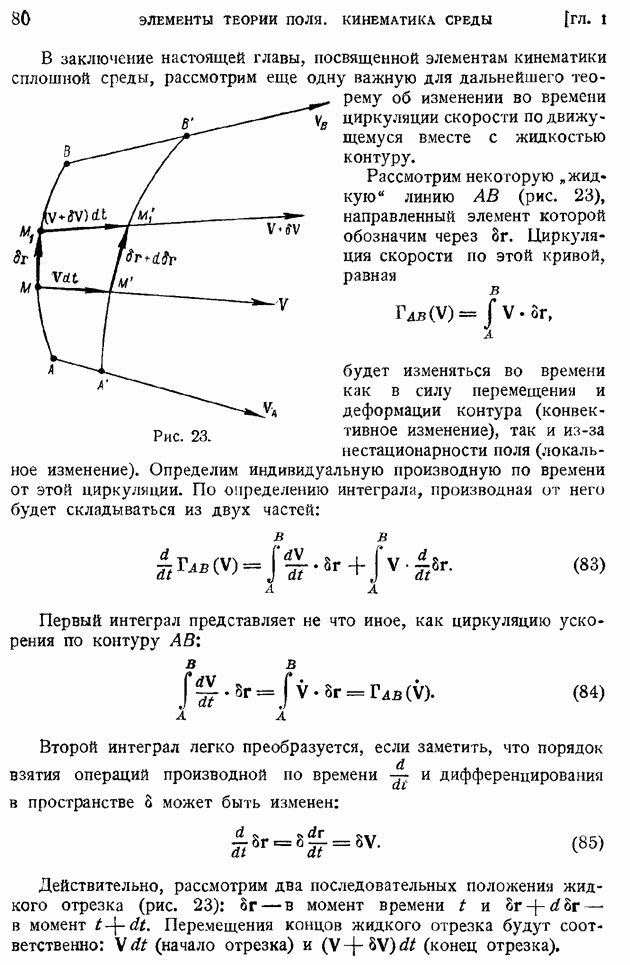
Чтобы не смешивать бесконечно малые приращения в пространстве с приращениями во времени, условимся в тех случаях, когда это может повести к недоразумениям, обозначать пространственные дифференциалы символом 8, временные —  Тогда (58) дает
Тогда (58) дает

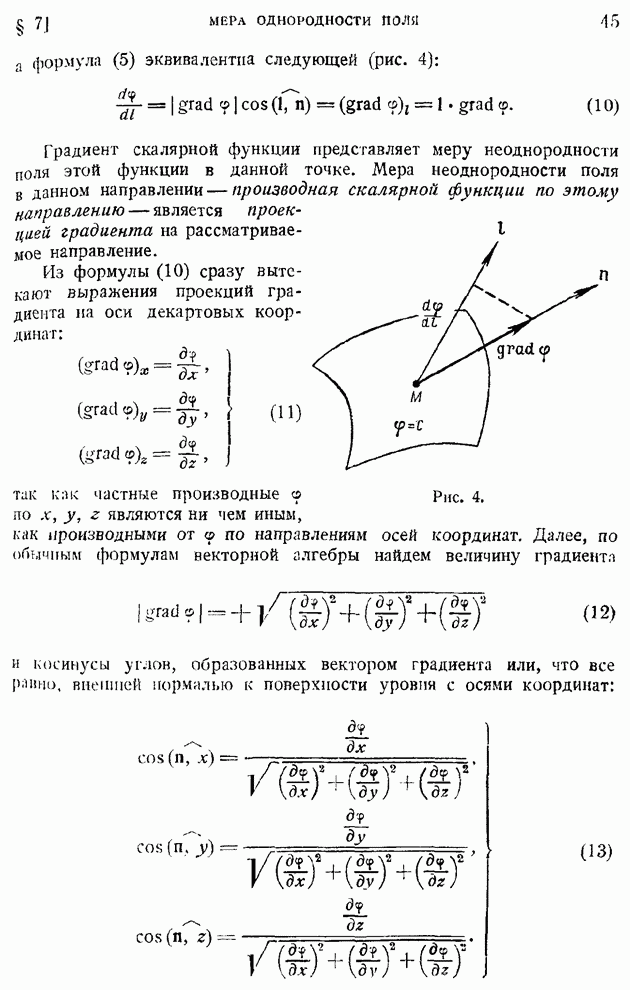
В дальнейшем часто придется находить производную по времени от элементарного объема жидкости. По (59) имеем:

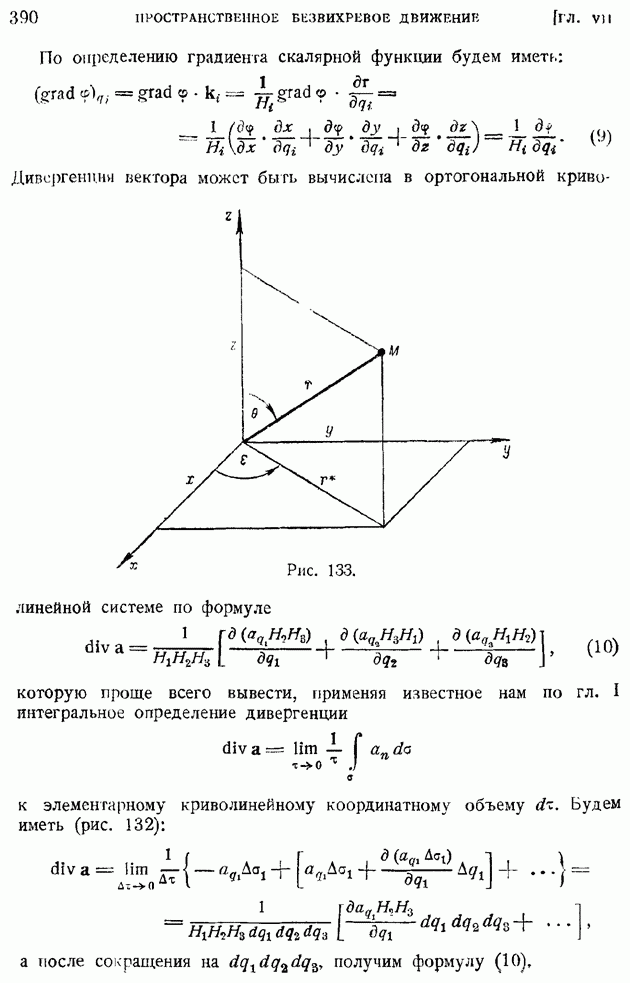
Для определения величины  воспользуемся приемом, идея которого восходит еще к Эйлеру. Возьмем в данный момент времени
воспользуемся приемом, идея которого восходит еще к Эйлеру. Возьмем в данный момент времени  элементарную трубку тока и двумя произвольно наклонными сечениями
элементарную трубку тока и двумя произвольно наклонными сечениями  выделим некоторый объем
выделим некоторый объем  За время
За время  объем сместится в положение
объем сместится в положение  вообще говоря, изменится, причем, как легко сообразить, полное изменение объема
вообще говоря, изменится, причем, как легко сообразить, полное изменение объема  в этом случае будет равно:
в этом случае будет равно:

так как объем  является общей частью объема трубки в начальный и следующий моменты. Проведем внешние по отношению к объему
является общей частью объема трубки в начальный и следующий моменты. Проведем внешние по отношению к объему  нормали
нормали  и внутреннюю нормаль
и внутреннюю нормаль  а также отметим векторы скоростей
а также отметим векторы скоростей  в сечениях
в сечениях  Тогда будем иметь:
Тогда будем иметь:

и, следовательно,


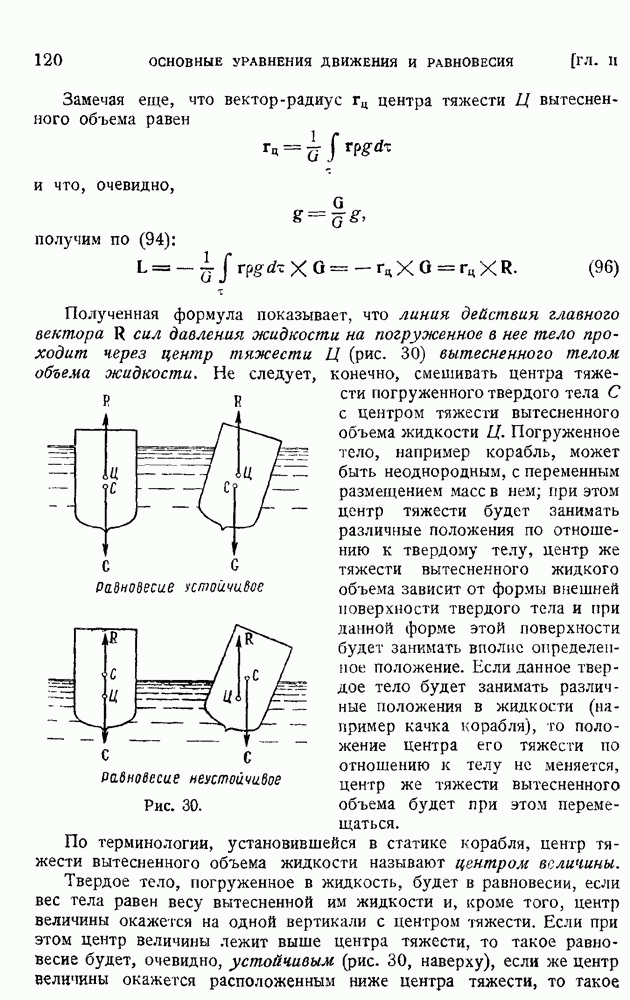
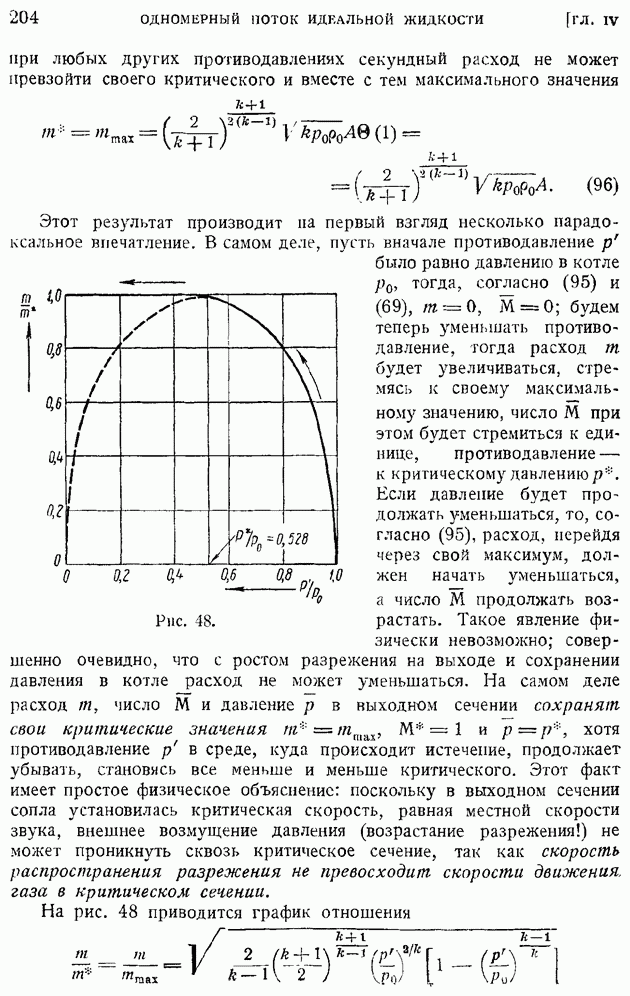
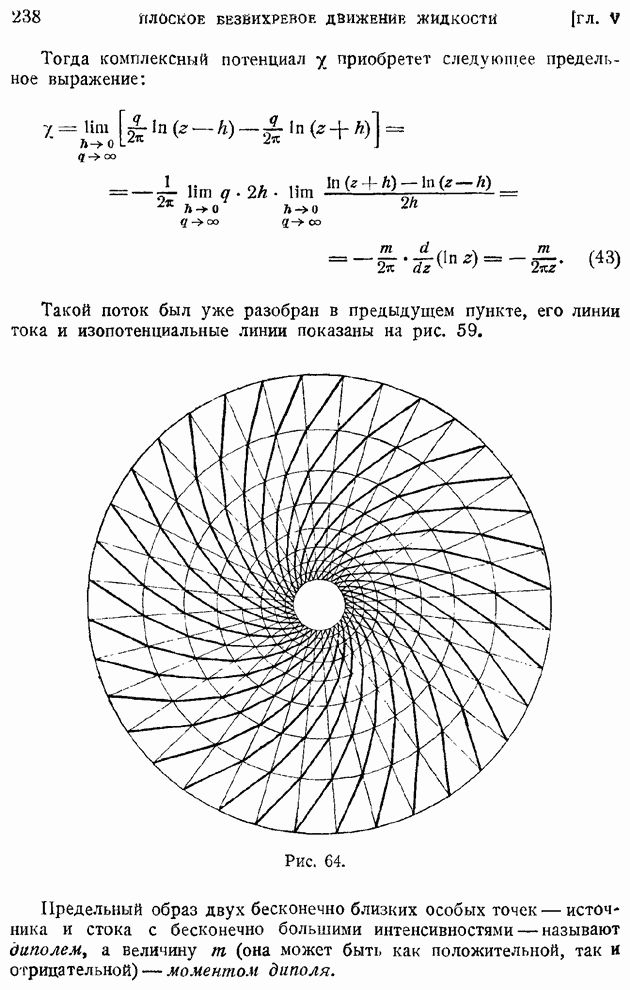
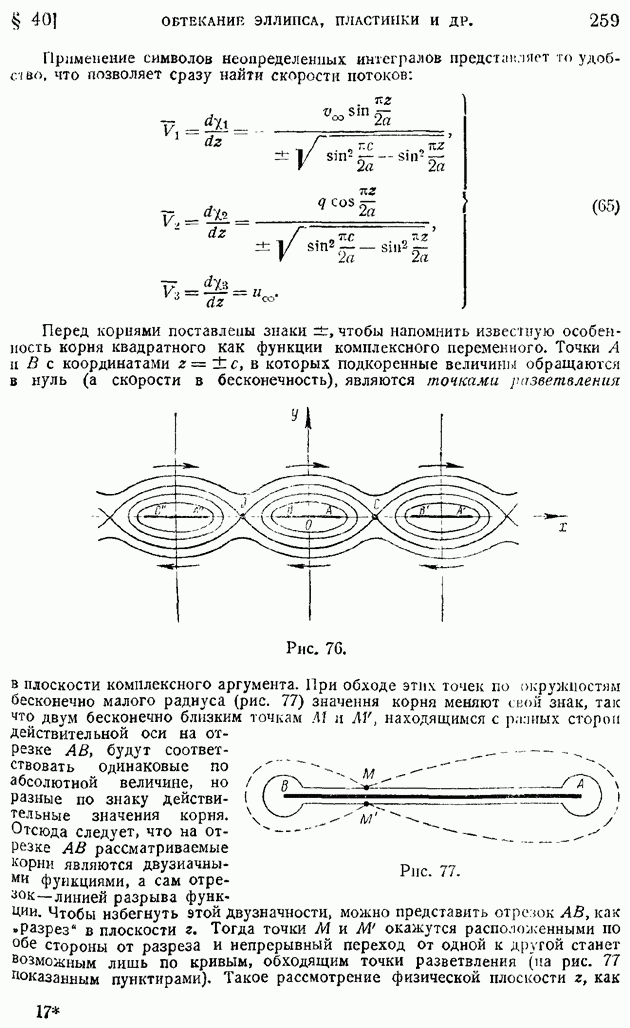
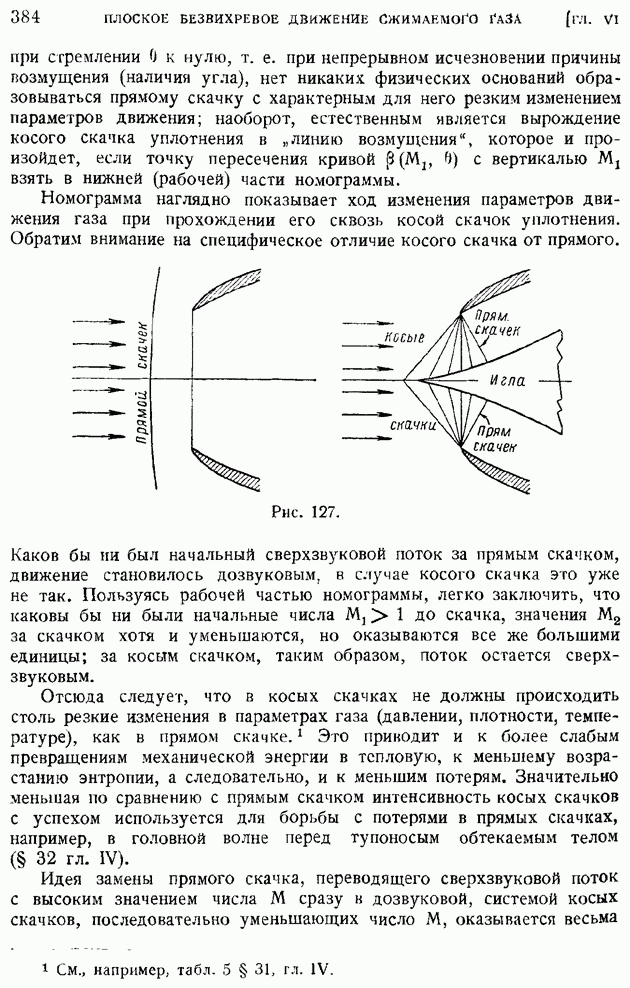
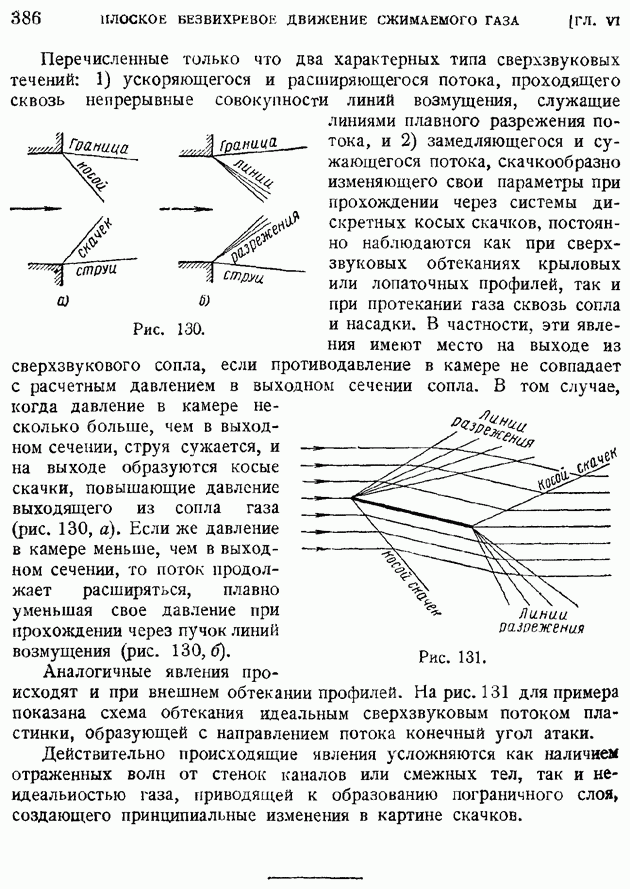
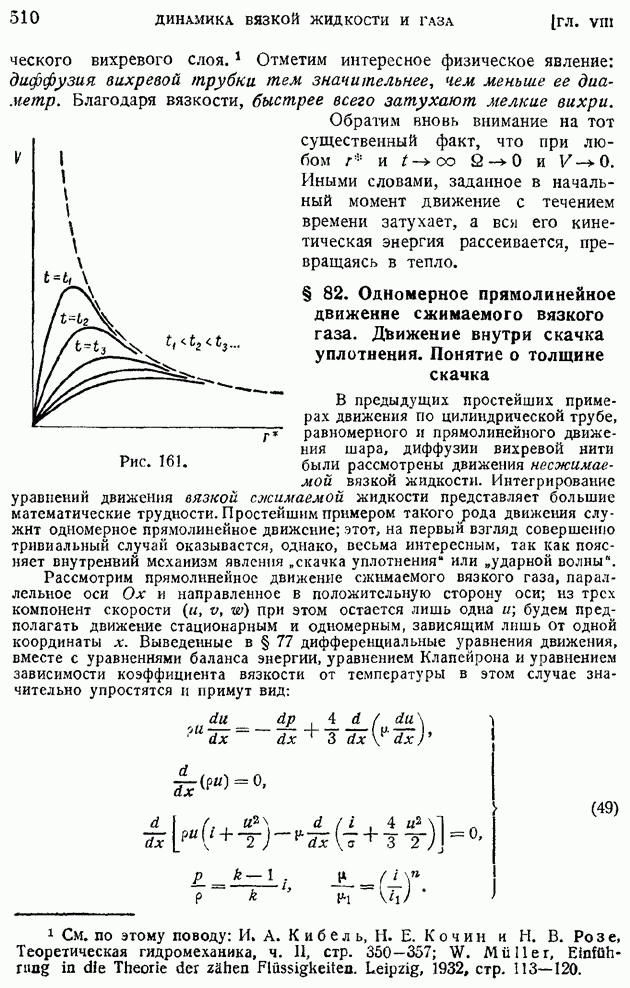
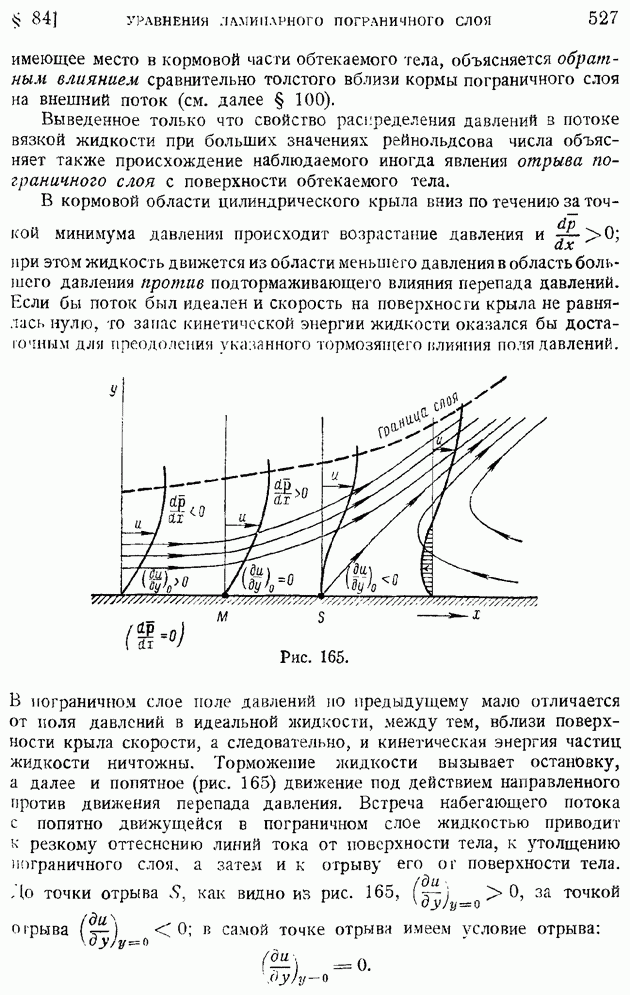
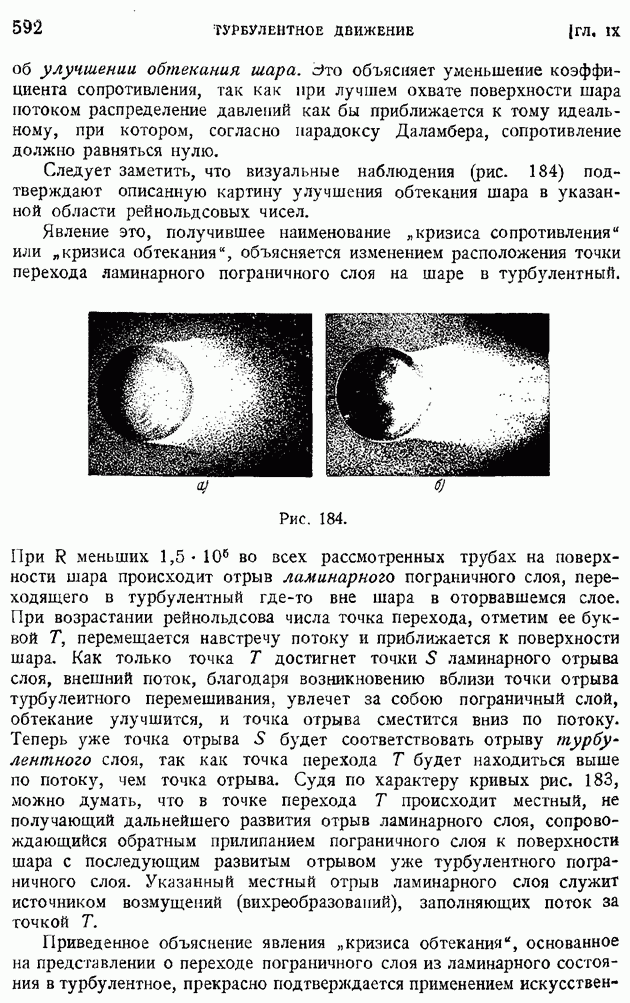
Рис. 9.
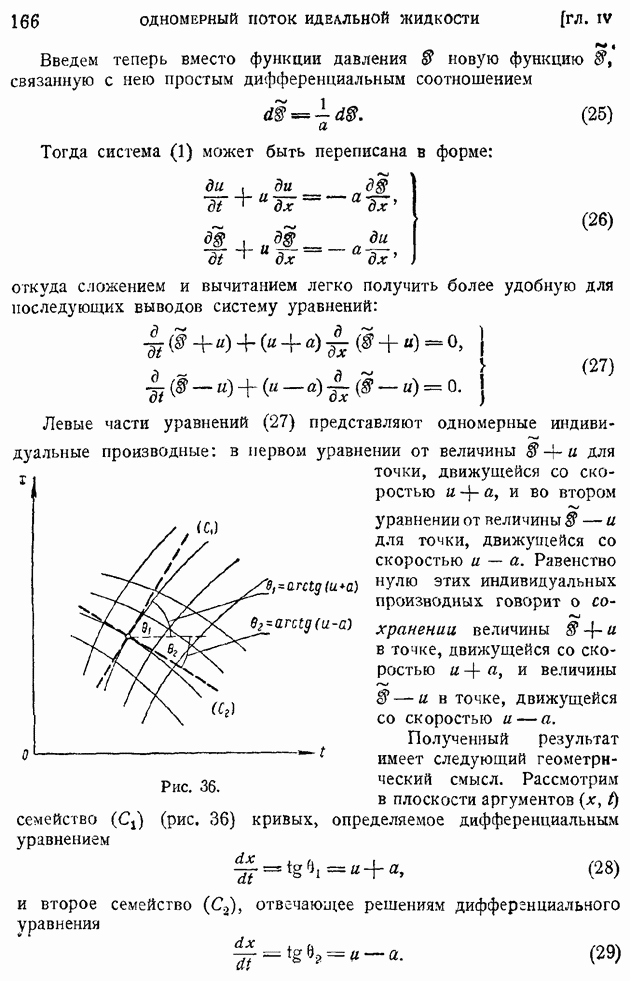
Возьмем теперь в поле скоростей любой конечный объем  разобьем его поверхностями трубок тока на бесчисленное множество элементарных объемов
разобьем его поверхностями трубок тока на бесчисленное множество элементарных объемов  при этом входные и выходные сечения
при этом входные и выходные сечения  заполнят всю поверхность о, ограничивающую объем
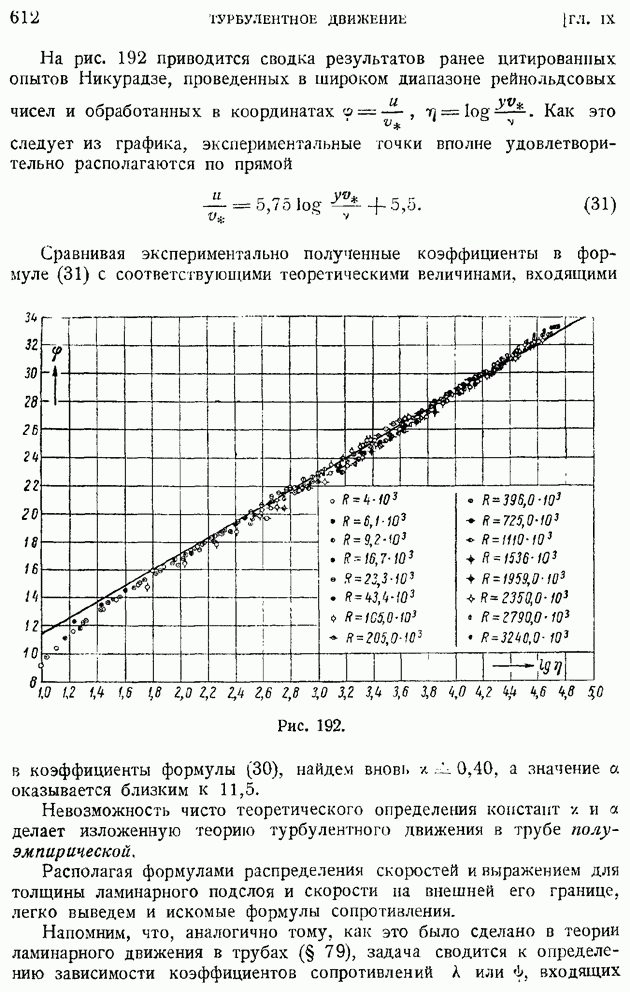
заполнят всю поверхность о, ограничивающую объем  Просуммируем равенства, подобные (60), по всем трубкам тока; тогда, очевидно, получим общую формулу для любого конечного объема:
Просуммируем равенства, подобные (60), по всем трубкам тока; тогда, очевидно, получим общую формулу для любого конечного объема:

Согласно (58), получим теперь следующее интегральное представление дивергенца скорости:

где  — поверхность, ограничивающая малый объем
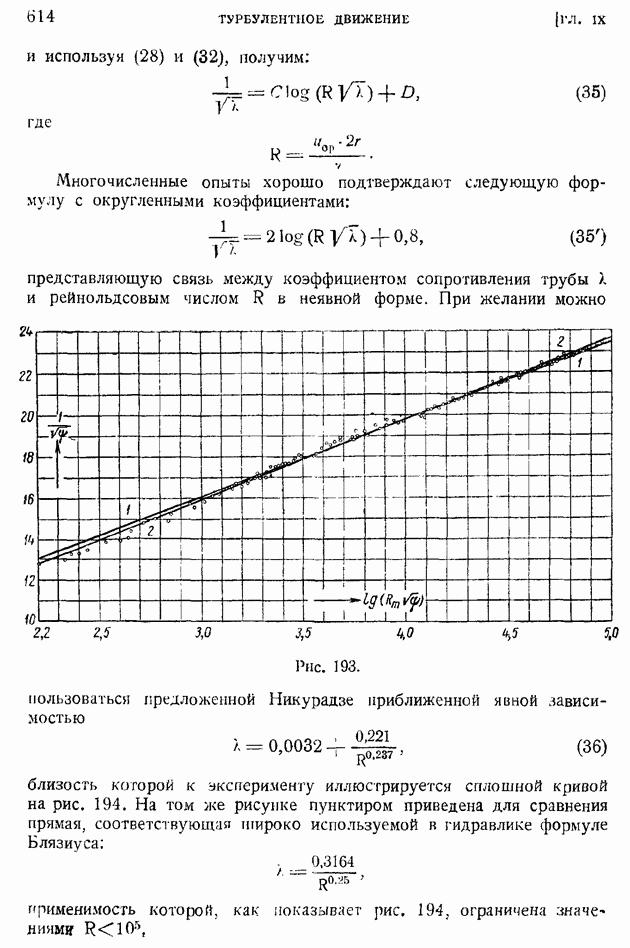
— поверхность, ограничивающая малый объем  заключающий в себе точку, в которой определяется
заключающий в себе точку, в которой определяется  при стремлении
при стремлении  к нулю поверхность
к нулю поверхность  стягивается в эту точку. Замечая, что выражение
стягивается в эту точку. Замечая, что выражение

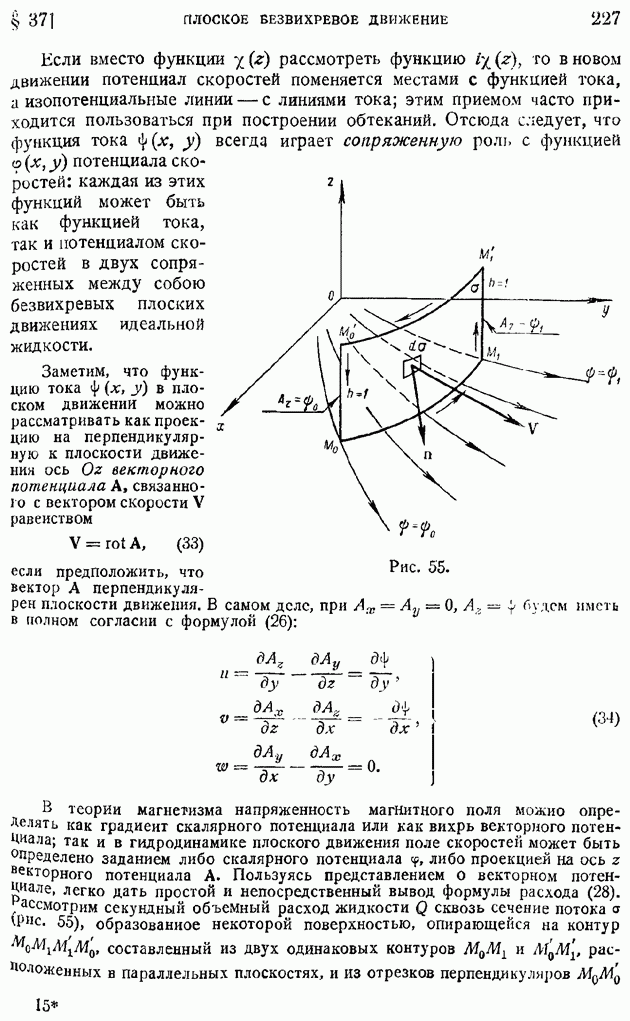
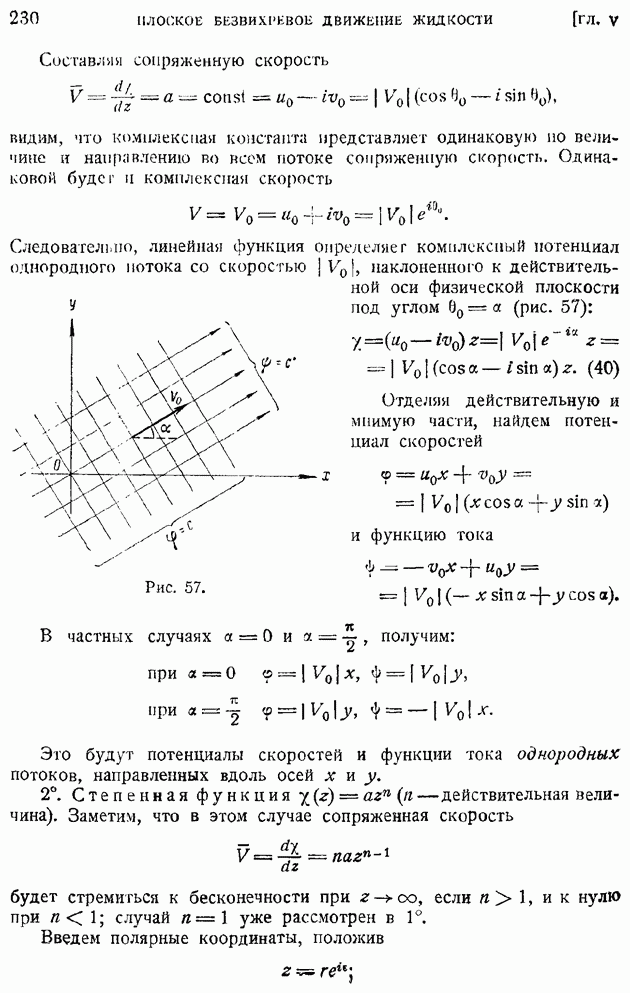
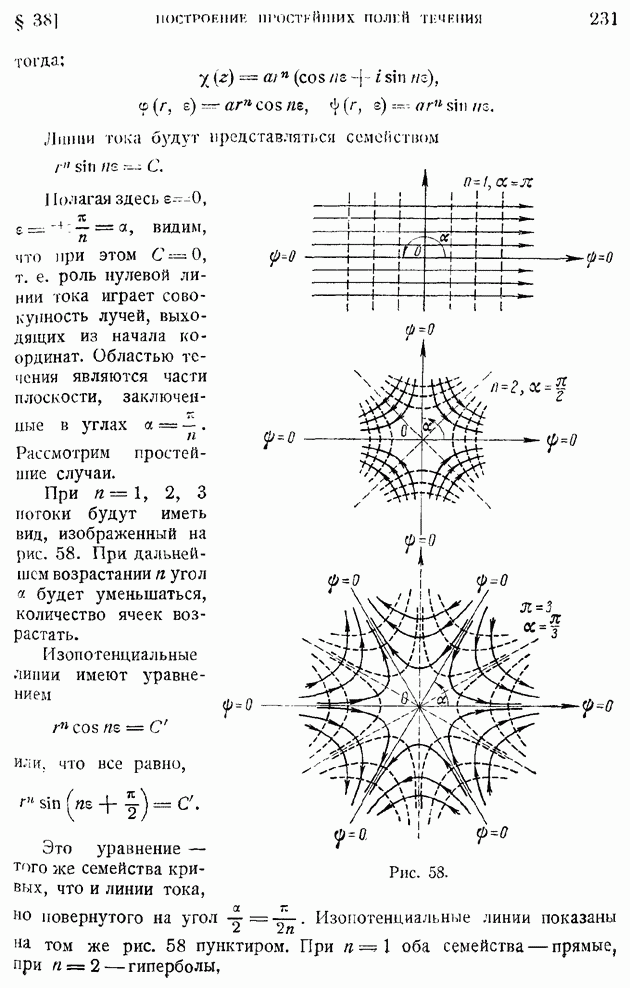
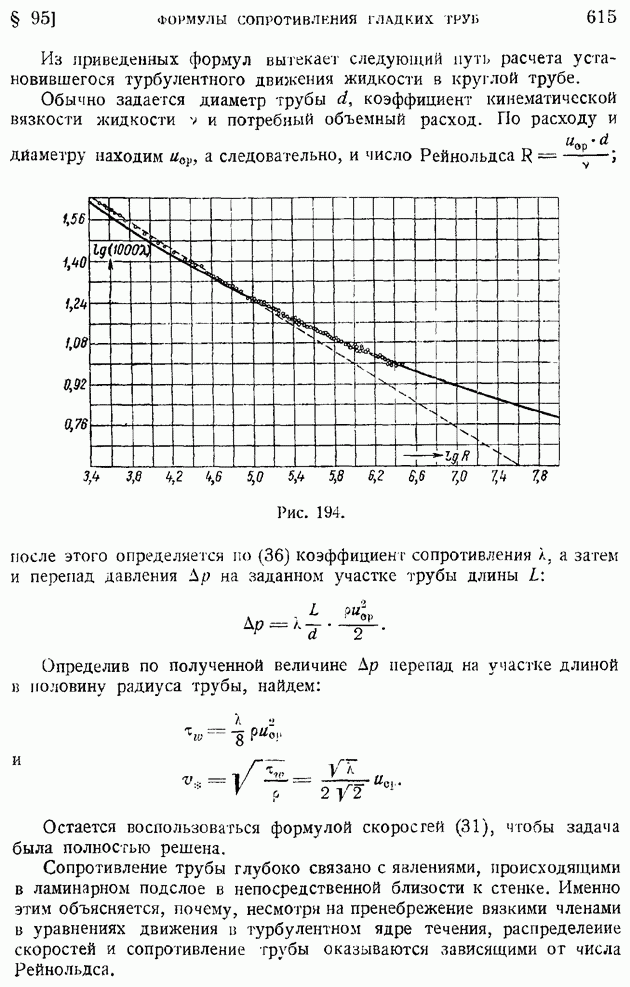
представляет секундный объемный расход жидкости сквозь замкнутую поверхность До, ограничивающую объем  содержащий внутри себя точку, в которой определится дивергенция, можем еще определить величину
содержащий внутри себя точку, в которой определится дивергенция, можем еще определить величину  как предел отношения секундного объемного расхода жидкости сквозь замкнутую поверхность к объему, ограниченному этой поверхностью, когда поверхность стягивается к точке, в которой определяется дивергенция.
как предел отношения секундного объемного расхода жидкости сквозь замкнутую поверхность к объему, ограниченному этой поверхностью, когда поверхность стягивается к точке, в которой определяется дивергенция.

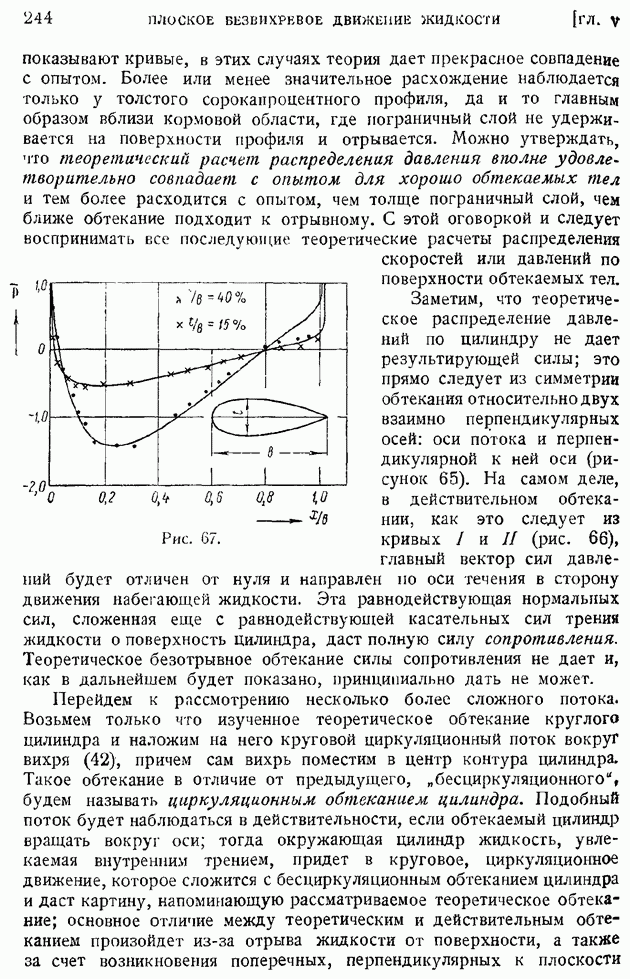
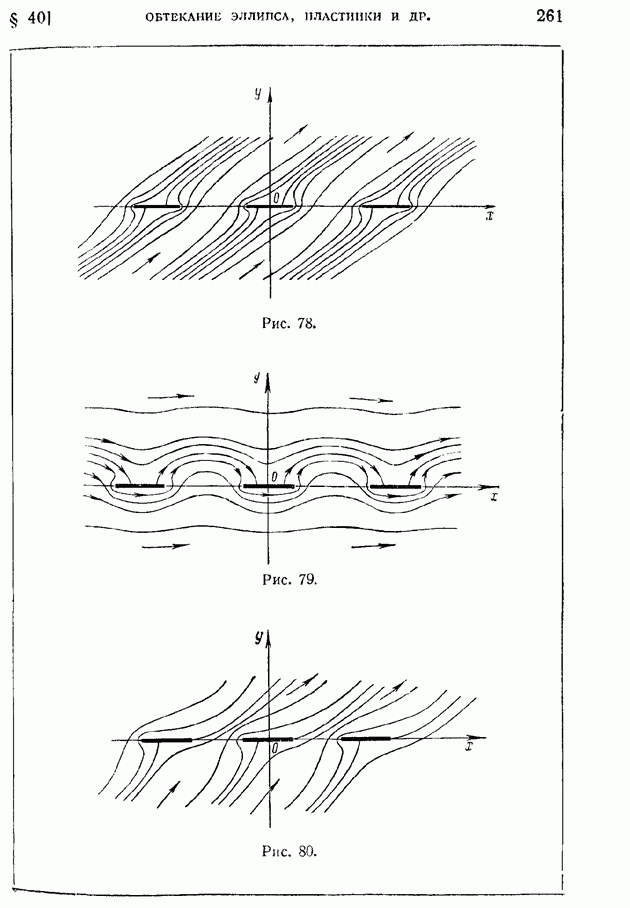
Рис. 10.
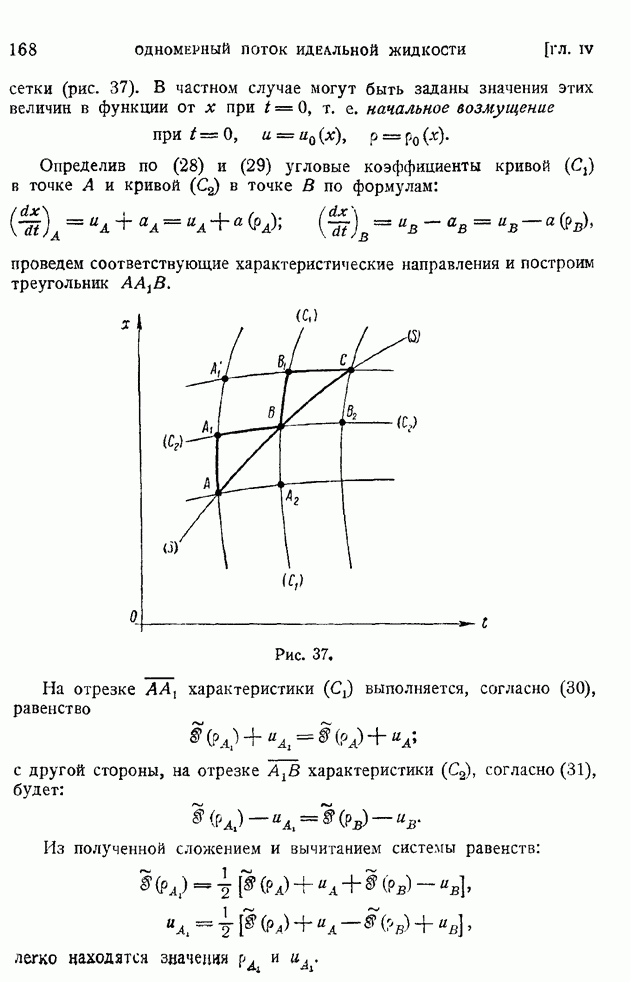
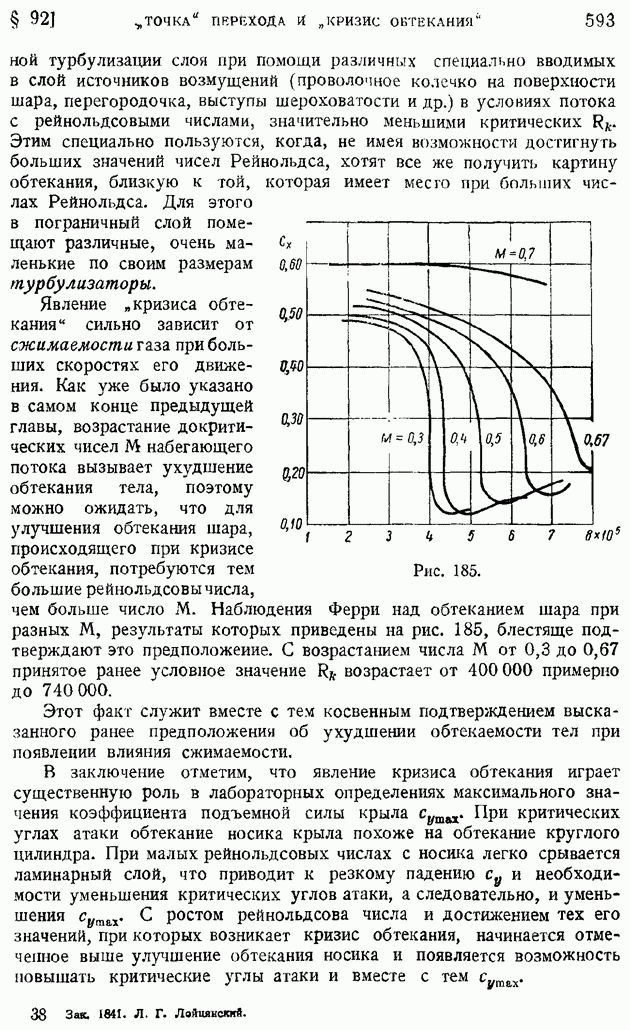
Как видно из хода доказательства, объем  совершенно произволен по форме. Выберем за
совершенно произволен по форме. Выберем за  элементарный декартов координатный параллелепипед (рис. 10); тогда, составляя непосредственно поверхностный интеграл в правой части (62) от значения
элементарный декартов координатный параллелепипед (рис. 10); тогда, составляя непосредственно поверхностный интеграл в правой части (62) от значения  по всем шести граням (эти значения показаны на рисунке), получим:
по всем шести граням (эти значения показаны на рисунке), получим:

откуда найдем искомое выражение дивергенции скорости в прямоугольных декартовых координатах:

По заданным уравнениям поля скоростей  в данный момент легко вычисляется. Для облегчения запоминания формулы (63) приведем
в данный момент легко вычисляется. Для облегчения запоминания формулы (63) приведем
ее символический вид

Раскрывая правую часть по правилу скалярного произведения и вспоминая (24), получим формулу (63).
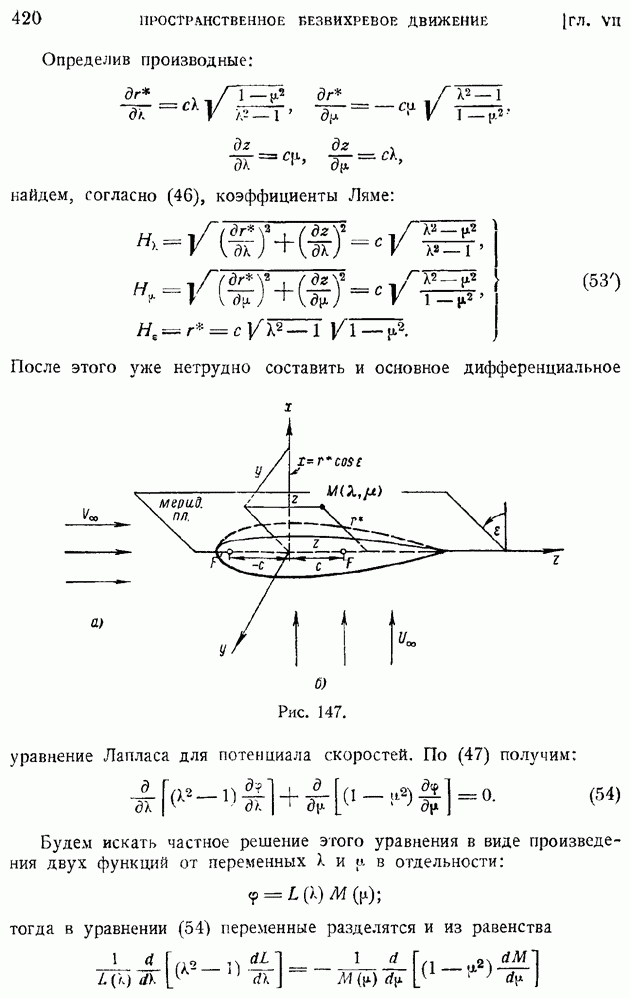
Заметим, что дивергенция может рассматриваться как некоторая общая дифференциальная операция, совершаемая над любой векторной функцией и определяемая формулами (62) и (63), куда вместо вектора V надлежит вставить дифференцируемый вектор а. В этом случае уже нельзя говорить о скорости объемного расширения, а выражение

где интеграл берется по некоторой (вообще говоря, не замкнутой) поверхности а, называют потоком вектора а через поверхность  . Если вектор а представляет скорость жидкости, то поток вектора а совпадает с объемом жидкости, протекающим через поверхность а в единицу времени, т. е. с секундным объемным расходом жидкости сквозь сечение а, что приводит к ранее данному определению дивергенции скорости.
. Если вектор а представляет скорость жидкости, то поток вектора а совпадает с объемом жидкости, протекающим через поверхность а в единицу времени, т. е. с секундным объемным расходом жидкости сквозь сечение а, что приводит к ранее данному определению дивергенции скорости.
В общем случае дивергенция вектора определяется как предел отношения потока вектора сквозь замкнутую поверхность к объему, ограниченному этой поверхностью, когда поверхность стягивается к точке, в которой определяется дивергенция, т. е.

Выражение дивергенции вектора а в декартовых прямоугольных координатах будет, аналогично (63), иметь вид:

Приведенный ранее вывод формулы (63) почти буквально можно повторить для элемента объема в любой системе криволинейных координат (полярных, цилиндрических, сферических и др.) и получить, таким образом, выражение дивергенции вектора-функции в криволинейной системе координат; это будет сделано далее в гл. VII.
Из формулы (62) легко выводится важная для дальнейшего интегральная формула, впервые указанная в 1834 г. знаменитым русским академиком М. В. Остроградским (1801—1861).
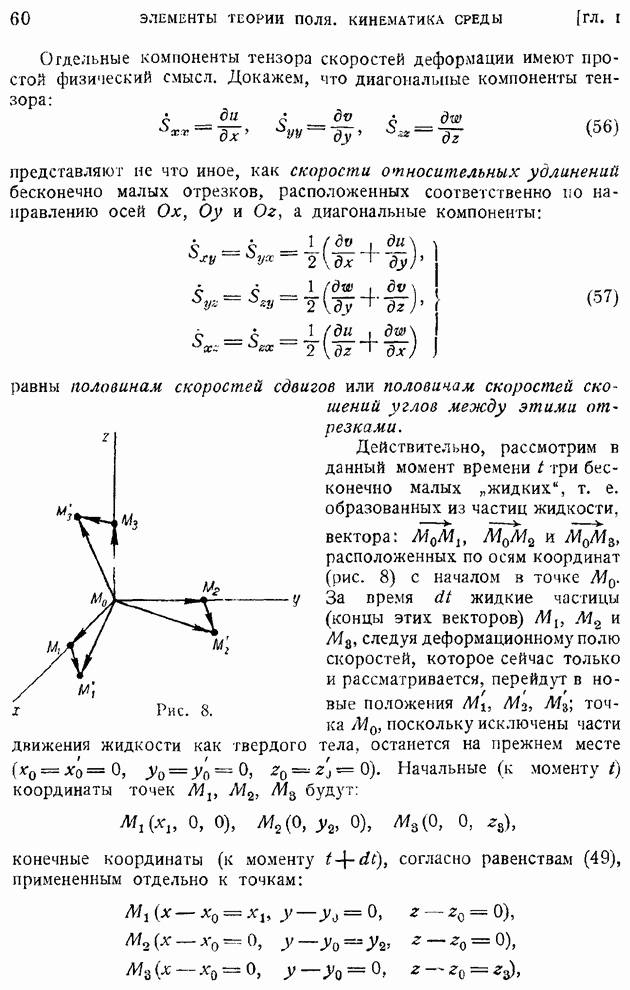
Разобьем любой конечный объем  на большое число малых объемов
на большое число малых объемов  обозначим поверхность, ограничивающую
обозначим поверхность, ограничивающую  через
через  через
через  .
.
Тогда, согласно (62), будем иметь для элементарного объема 

где  малая величина, идущая к нулю с уменьшением
малая величина, идущая к нулю с уменьшением 
Просуммируем обе части равенства (65) по всем объемам  образующим конечный объем; получим:
образующим конечный объем; получим:

В сумме, стоящей слева, взаимно сократятся все элементы интегралов, взятые по общим границам двух соседних малых объемов, так как сама вектор-функция а в силу непрерывности имеет одинаковое значение на границе со стороны какого объема не совершался бы подход к граничащей поверхности, в то же время внешняя нормаль к поверхности, ограничивающей один из малых объемов, является внутренней нормалью к той же поверхности для смежного малого объема; поэтому в рассматриваемой сумме часть слагаемых, равных между собою по величине и противоположных по знаку, сократится. Останутся лишь элементы интеграла, распространенные по внешним частям поверхности а, окружающей объем  т. е. поверхностный интеграл по поверхности а. С правой стороны, если устремить к нулю малые объемы
т. е. поверхностный интеграл по поверхности а. С правой стороны, если устремить к нулю малые объемы  останется объемный интеграл от
останется объемный интеграл от  взятый по объему
взятый по объему  так как второй член справа, как сумма малых четвертого порядка, обратится в нуль. Таким образом, получим интегральную формулу:
так как второй член справа, как сумма малых четвертого порядка, обратится в нуль. Таким образом, получим интегральную формулу:

или

Эта интегральная формула Остроградского выражает объемный интеграл от дифференциального оператора  а векторного поля через интеграл от проекции вектора на внешнюю нормаль, взятый по поверхности, ограничивающей выбранный объем. На первый взгляд кажется странным, что при любом виде векторной функции а (подчиненной лишь ограничению непрерывности и существования первых производных по координатам) объемный интеграл, вычисление которого требует знания функции во всех точках внутри объема, выражается общей формулой через поверхностный интеграл, определяемый значениями вектора-функции лишь на поверхности объема. Дело здесь в том, что под знаком объемного интеграла стоит не сама функция, а некоторый дифференциальный оператор от нее. Аналогично, беря определенный интеграл от производной функции, получают разность
а векторного поля через интеграл от проекции вектора на внешнюю нормаль, взятый по поверхности, ограничивающей выбранный объем. На первый взгляд кажется странным, что при любом виде векторной функции а (подчиненной лишь ограничению непрерывности и существования первых производных по координатам) объемный интеграл, вычисление которого требует знания функции во всех точках внутри объема, выражается общей формулой через поверхностный интеграл, определяемый значениями вектора-функции лишь на поверхности объема. Дело здесь в том, что под знаком объемного интеграла стоит не сама функция, а некоторый дифференциальный оператор от нее. Аналогично, беря определенный интеграл от производной функции, получают разность
значений функции на краях интервала, независимо от того, каков был непрерывный закон изменения функции внутри интервала.
Формула (66) в декартовой системе координат принимает обычный вид формулы Остроградского:

Если положить  т. е. применить формулу (66) к скоростному полю, то левая часть представит секундный объемный расход жидкости сквозь замкнутую поверхность а, а правая часть определит скорость увеличения объема
т. е. применить формулу (66) к скоростному полю, то левая часть представит секундный объемный расход жидкости сквозь замкнутую поверхность а, а правая часть определит скорость увеличения объема  жидкости со временем; естественно, что скорость увеличения объема равна секундному объемному расходу жидкости сквозь поверхность, окружающую этот объем.
жидкости со временем; естественно, что скорость увеличения объема равна секундному объемному расходу жидкости сквозь поверхность, окружающую этот объем.
Для облегчения запоминания формулы Остроградского, заметим, что равенство (66) можно представить символически так:

как будто орту внешней нормали в поверхностном интеграле соответствует дифференциальный оператор в объемном.
Из формулы (66) можно вывести одно, необходимое для дальнейшего равенство, если применить ее к произвольному, но однородному векторному полю постоянного по величине и направлению вектора а. Тогда получим

или, вынося постоянный вектор а за знак интеграла,

откуда, в силу произвольности вектора а, сразу следует, что для всякой замкнутой поверхности можно написать:

Чисто геометрическое доказательство этой формулы можно найти, например, в ранее указанном руководстве по векторному исчислению Н. Е. Кочина (изд. 1934 г., стр. 49). В геометрической трактовке формула (68) представляет предельную форму теоремы о равенстве нулю геометрической суммы векторов, представляющих площади граней замкнутого многогранника.
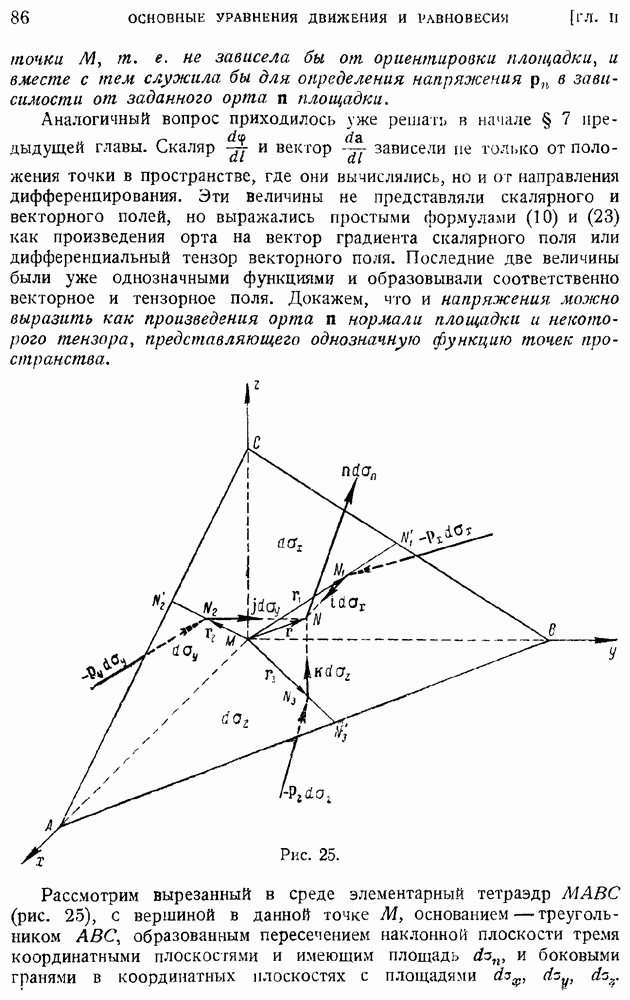
Покажем теперь, что и для остальных двух, ранее введенных дифференциальных операторов — градиента и вихря — можно вывести интегральные представления и интегральные формулы, аналогичные только что выведенным формулам (62) и (66).
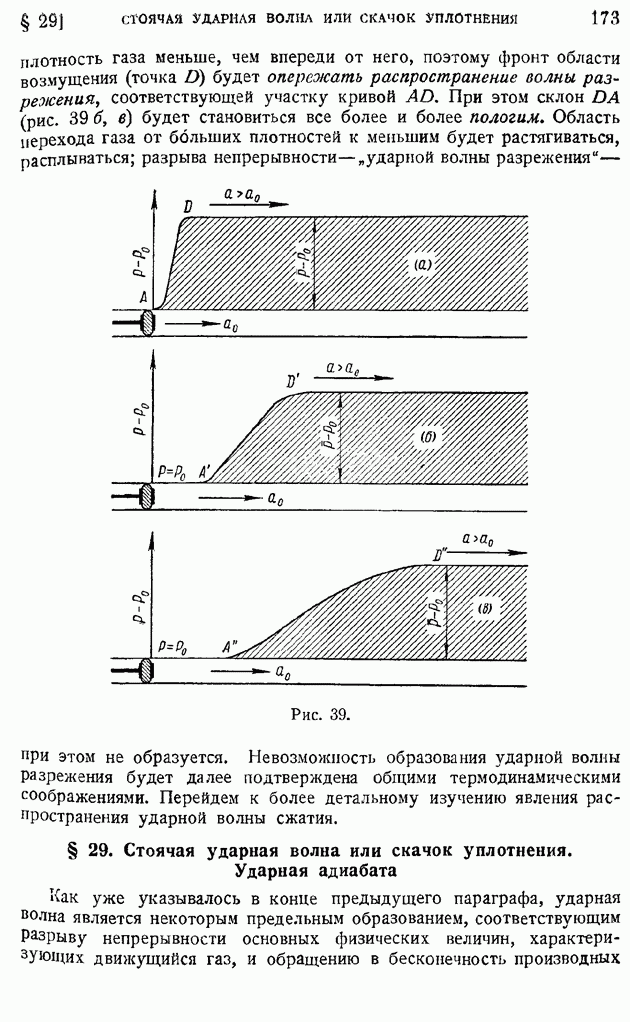
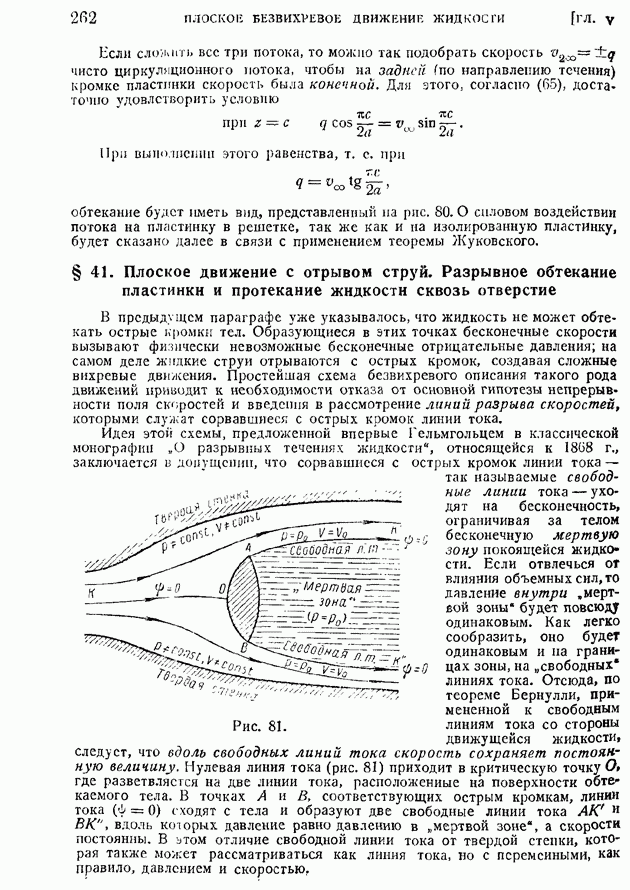
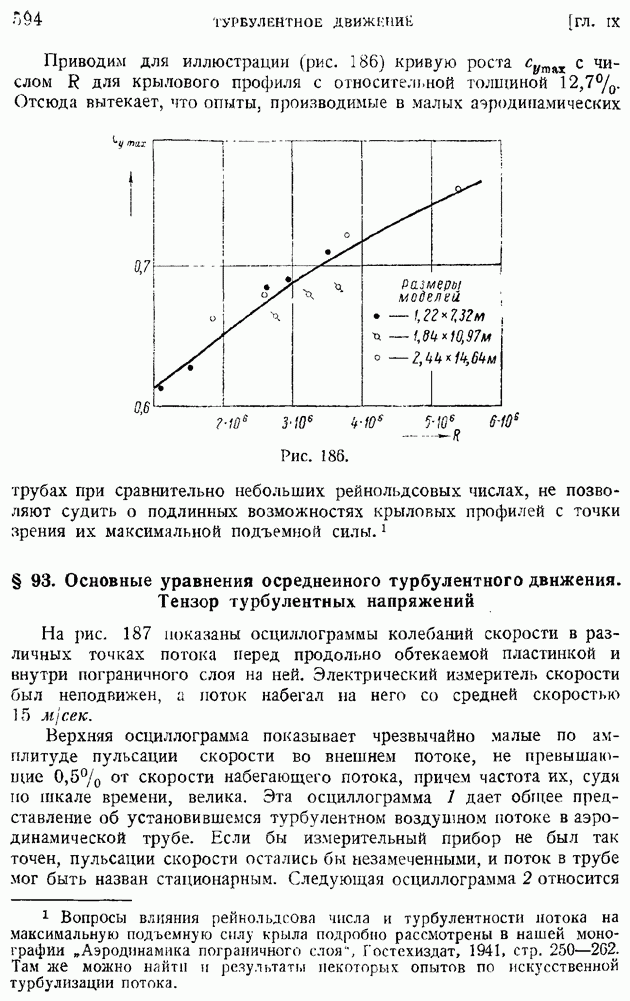
Рассмотрим в поле скалярной функции  произвольный малый объем
произвольный малый объем  (рис. 11) с поверхностью Да и рассечем его двумя смежными поверхностями уровня
(рис. 11) с поверхностью Да и рассечем его двумя смежными поверхностями уровня  находящимися друг относительно друга на расстоянии
находящимися друг относительно друга на расстоянии  отсчитанном по внешней нормали
отсчитанном по внешней нормали  проведенной через точку
проведенной через точку  первой поверхности уровня. Рассмотрим поверхностный интеграл
первой поверхности уровня. Рассмотрим поверхностный интеграл

распространенный на поверхность, окружающую объем  заключенный между проведенными поверхностями уровня и равный, в силу малости всех величин, произведению площади основания на высоту
заключенный между проведенными поверхностями уровня и равный, в силу малости всех величин, произведению площади основания на высоту  под знаком интеграла
под знаком интеграла  внешняя нормаль к поверхности интегрирования,
внешняя нормаль к поверхности интегрирования,  элемент площади поверхности.
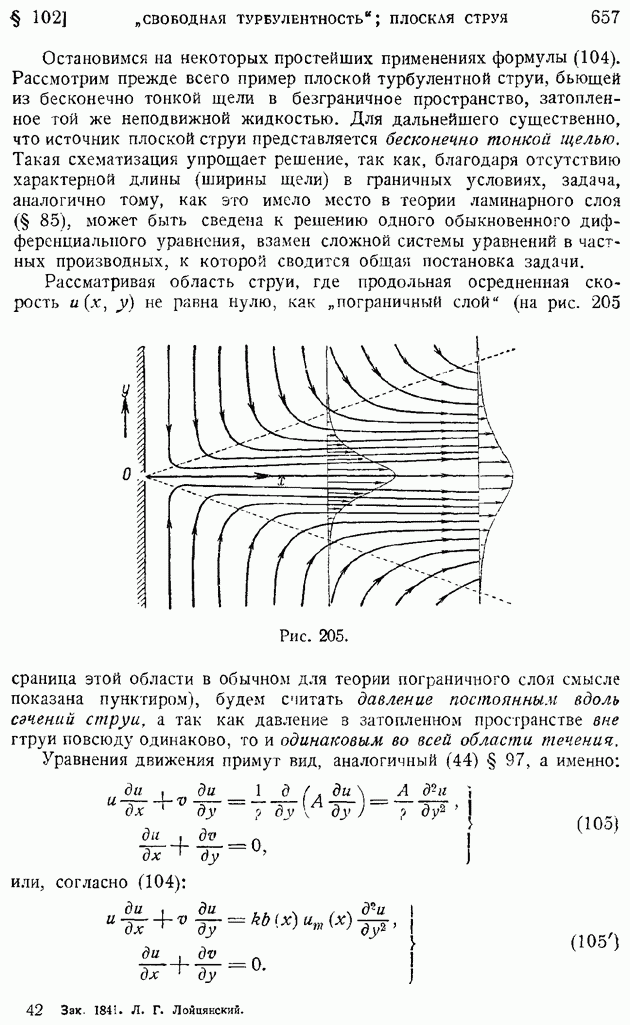
элемент площади поверхности.

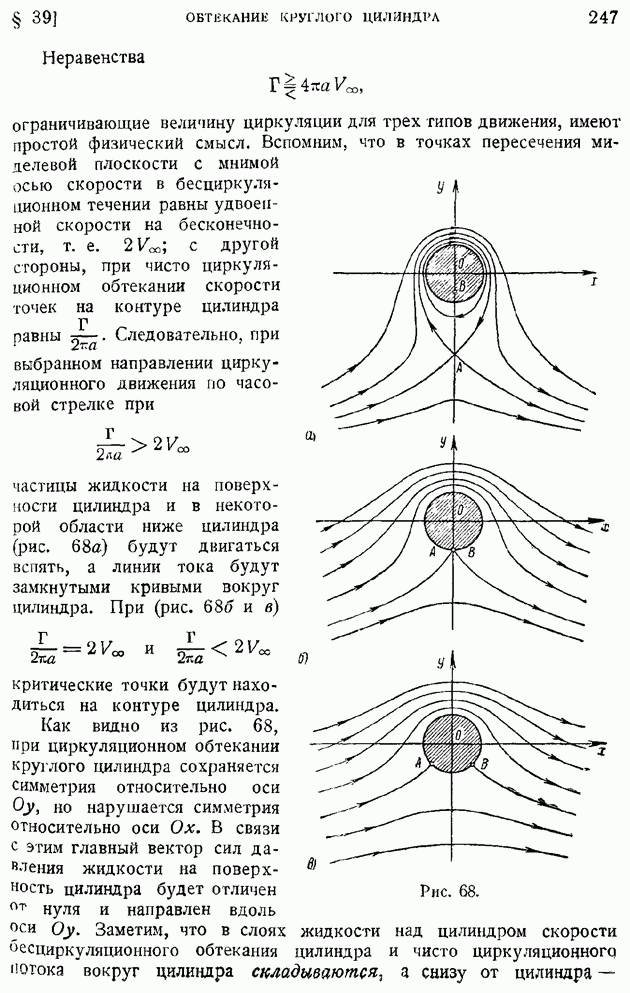
Рис. 11.
Этот интеграл может быть представлен как сумма своих элементов, рассчитанных по площадкам  кроме того, интеграла по боковой поверхности, являющейся частью (пояском) поверхности Да. Будем иметь:
кроме того, интеграла по боковой поверхности, являющейся частью (пояском) поверхности Да. Будем иметь:

так как можно считать, что по боковой поверхности рассматриваемого объема о сохраняется постоянным; с другой стороны, применяя к той же поверхности формулу (68), получим

откуда сразу следует, что выражение в скобках в правой части предыдущего равенства равно нулю, а само равенство имеет вид:

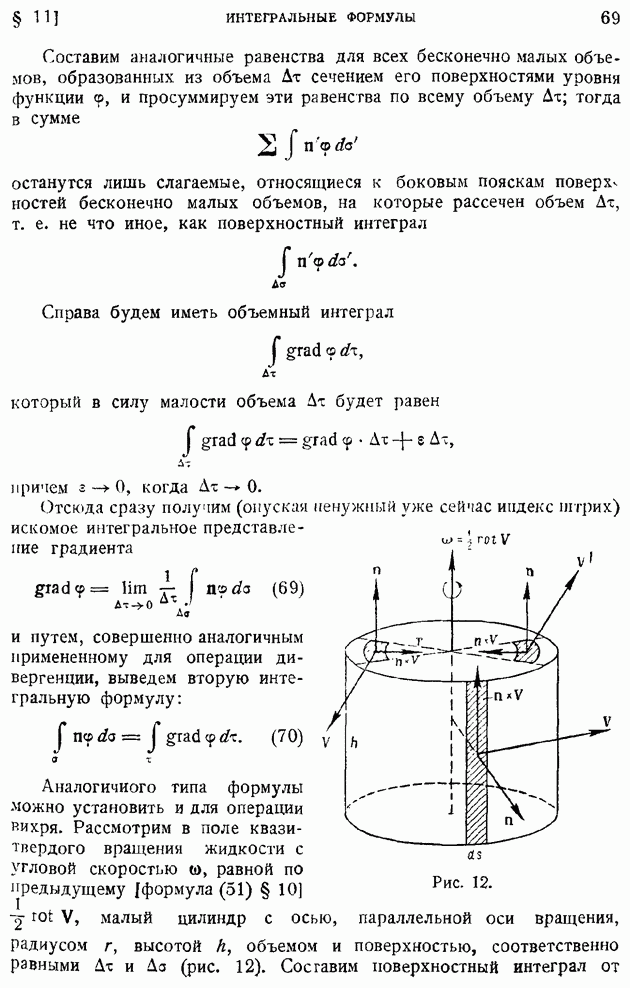
Составим аналогичные равенства для всех бесконечно малых объемов, образованных из объема  сечением его поверхностями уровня функции
сечением его поверхностями уровня функции  и просуммируем эти равенства по всему объему
и просуммируем эти равенства по всему объему  тогда в сумме
тогда в сумме

останутся лишь слагаемые, относящиеся к боковым пояскам поверх ностей бесконечно малых объемов, на которые рассечен объем  т. е. не что иное, как поверхностный интеграл
т. е. не что иное, как поверхностный интеграл

Справа будем иметь объемный интеграл

который в силу малости объема  будет равен
будет равен

причем  когда
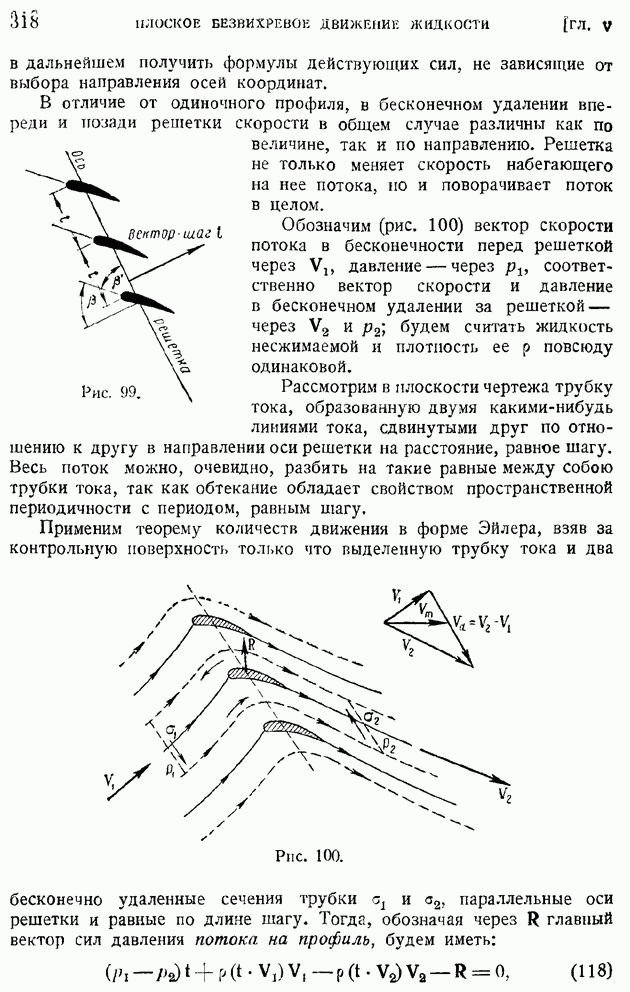
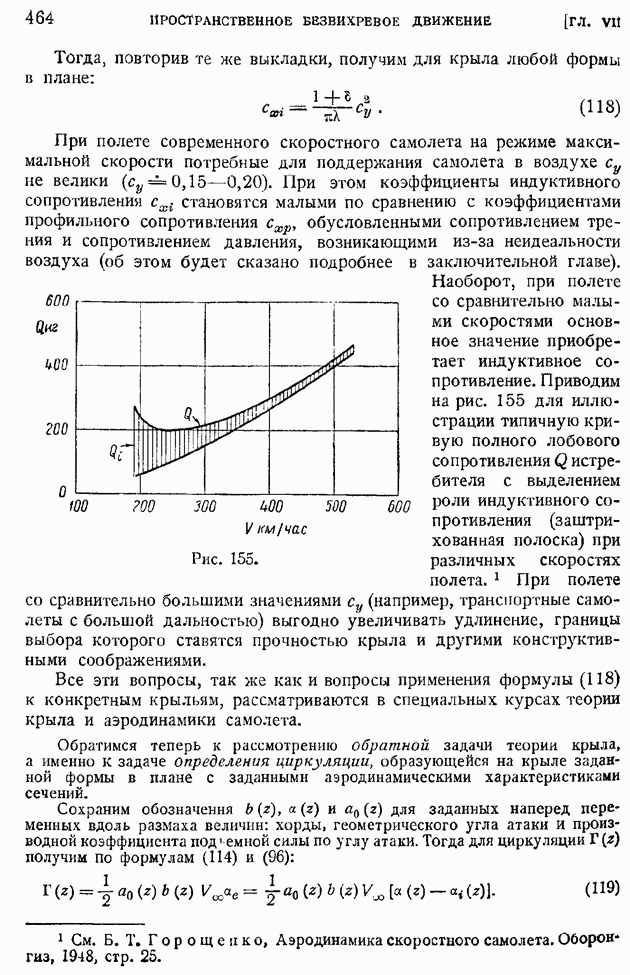
когда 
Отсюда сразу получим (опуская ненужный уже сейчас индекс штрих) искомое интегральное представление градиента

и путем, совершенно аналогичным примененному для операции дивергенции, выведем вторую интегральную формулу:


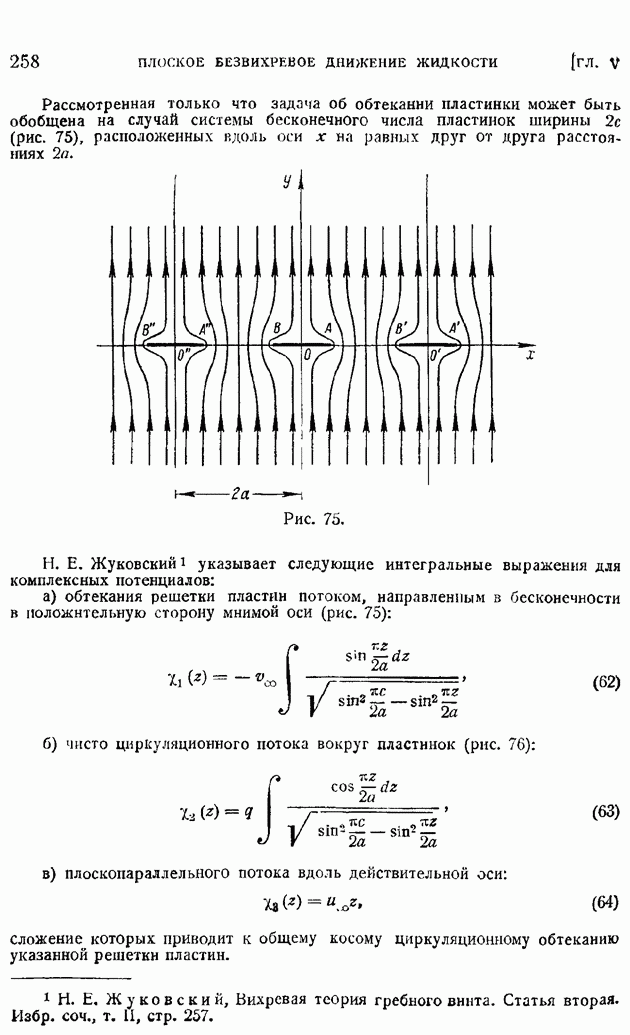
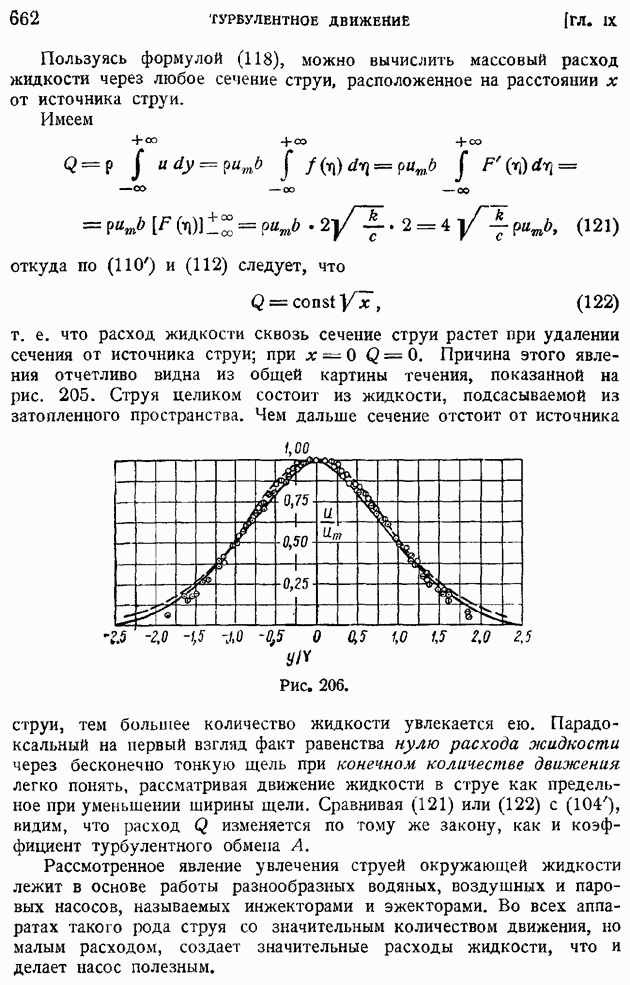
Рис. 12.
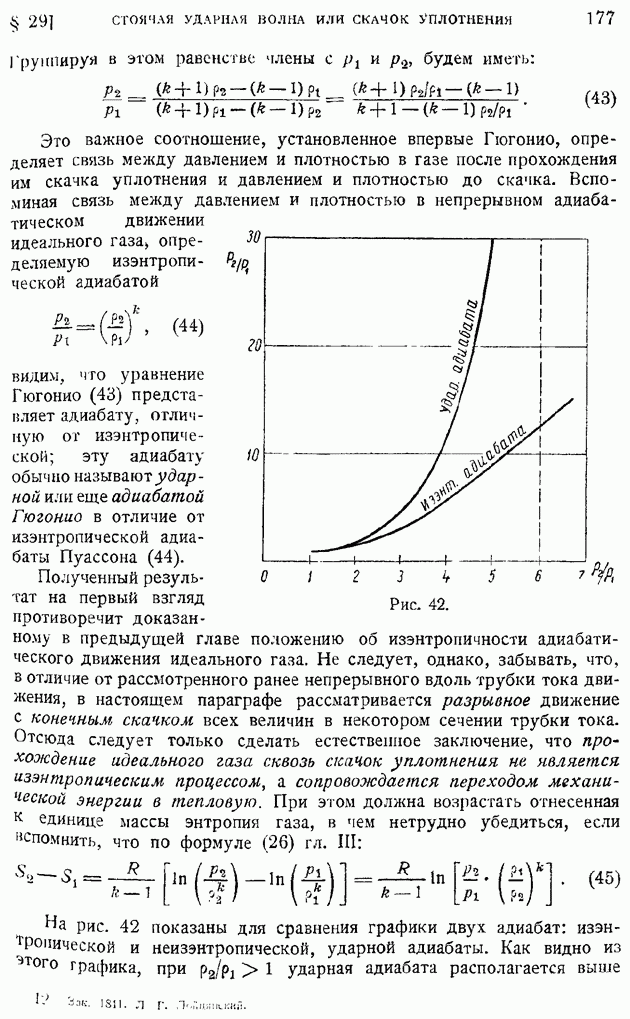
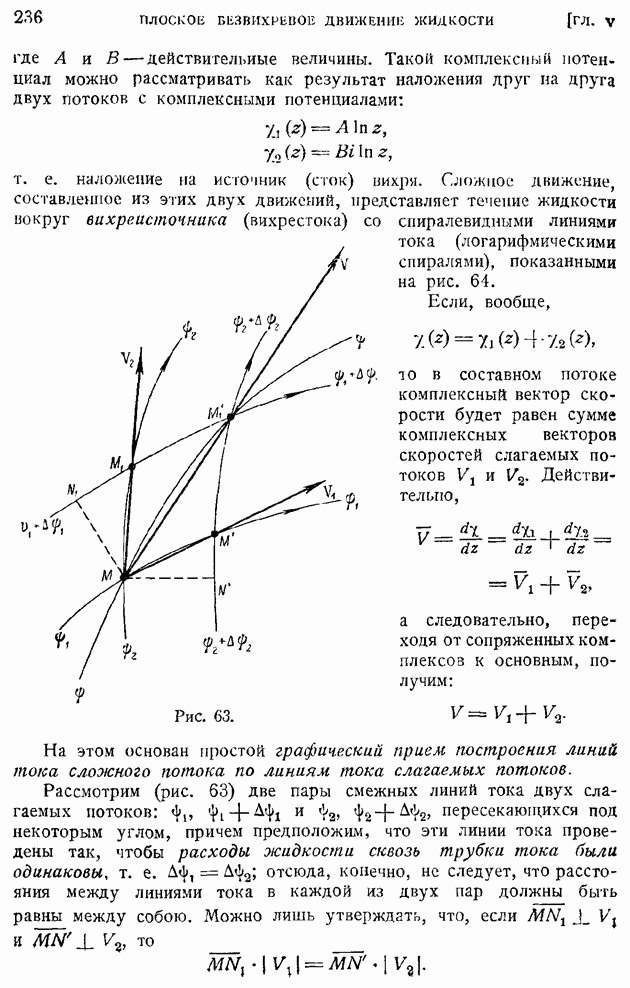
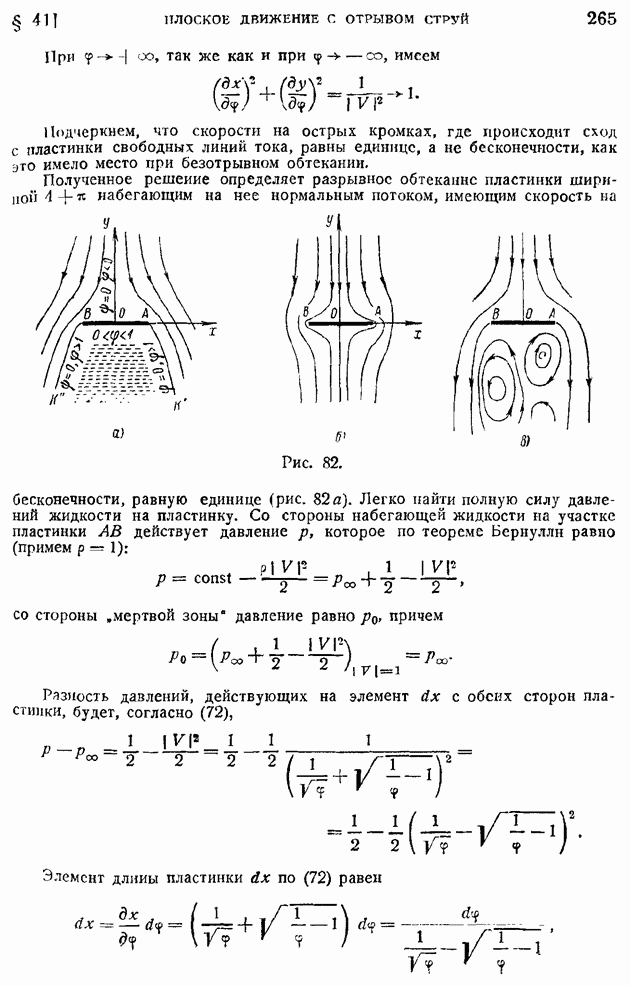
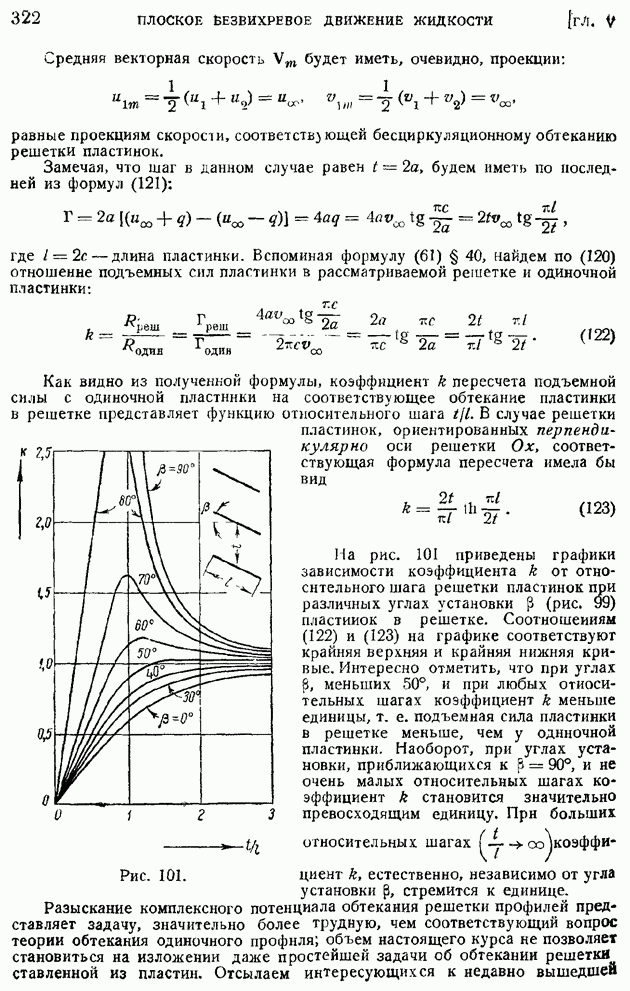
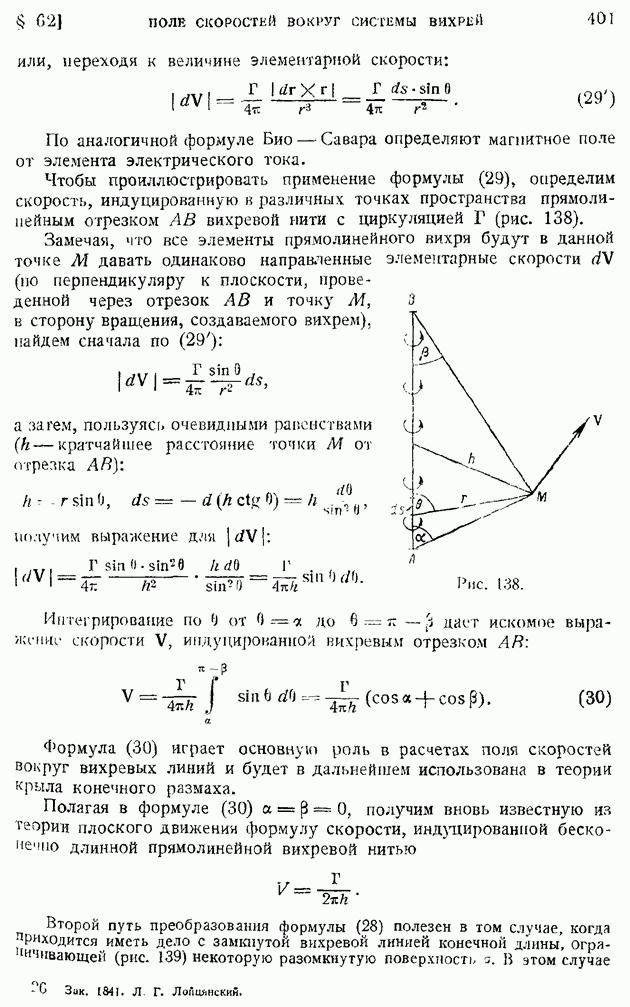
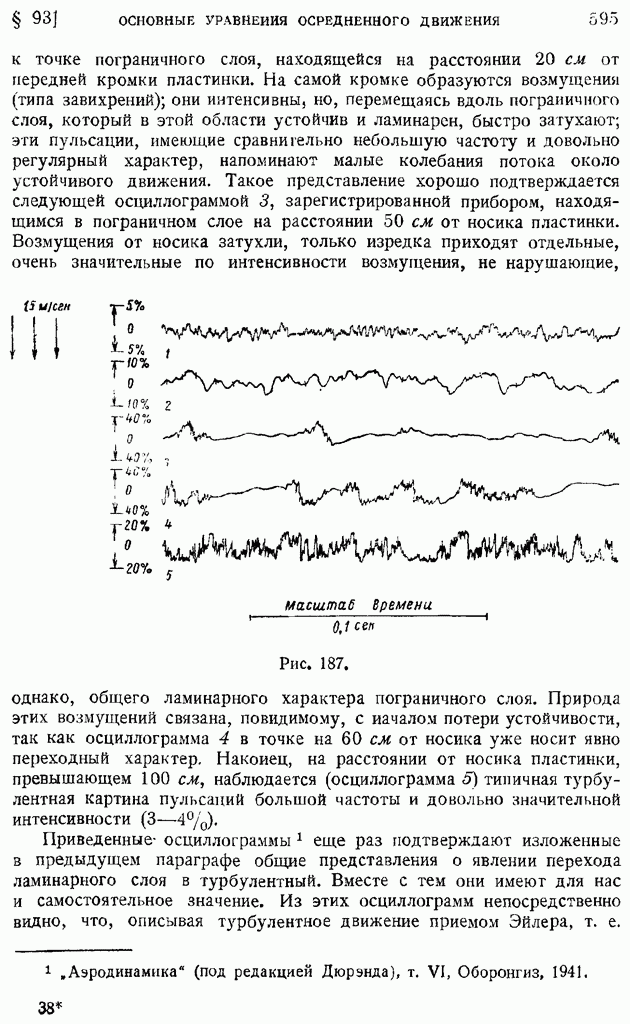
Аналогичного типа формулы можно установить и для операции вихря. Рассмотрим в поле квазитвердого вращения жидкости с угловой скоростью  равной по предыдущему [формула (51) § 10]
равной по предыдущему [формула (51) § 10]  малый цилиндр с осью, параллельной оси вращения, радиусом
малый цилиндр с осью, параллельной оси вращения, радиусом  высотой А, объемом и поверхностью, соответственно равными
высотой А, объемом и поверхностью, соответственно равными  и
и  (рис. 12). Составим поверхностный интеграл от
(рис. 12). Составим поверхностный интеграл от
векторного произведения орта внешней нормали  к поверхности этого цилиндра на вектор вращательной скорости
к поверхности этого цилиндра на вектор вращательной скорости  Тогда, выбирая, как показано на рисунке, за элемент боковой поверхности цилиндра полоску, ограниченную двумя образующими на расстоянии
Тогда, выбирая, как показано на рисунке, за элемент боковой поверхности цилиндра полоску, ограниченную двумя образующими на расстоянии  друг от друга, а в плоскостях оснований — симметричные элементы, убедимся, что искомый поверхностный интеграл сведется к следующему:
друг от друга, а в плоскостях оснований — симметричные элементы, убедимся, что искомый поверхностный интеграл сведется к следующему:

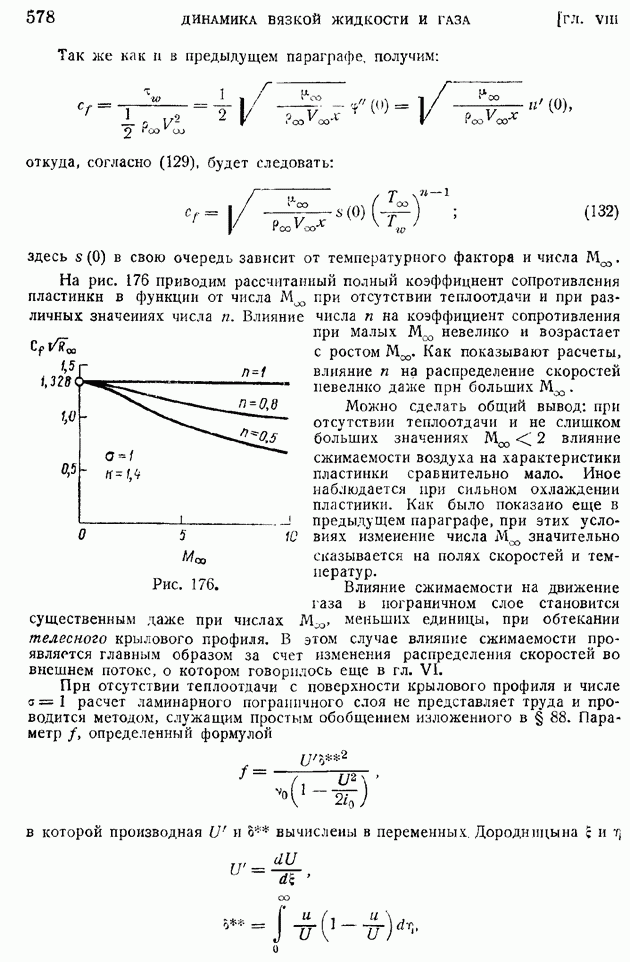
так как элементы интеграла по основаниям цилиндра взаимно сократятся.
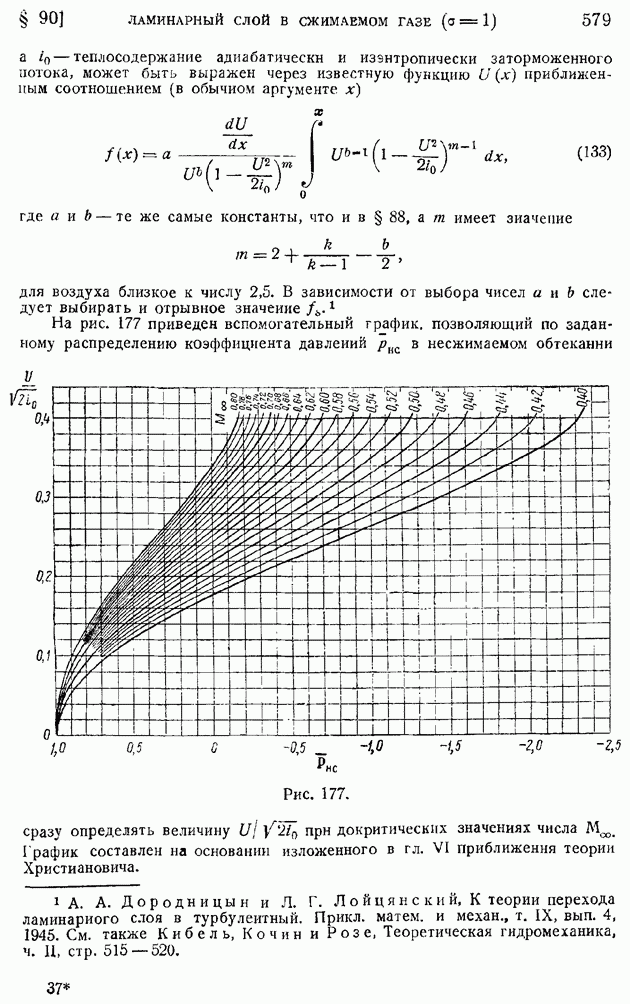
Замечая, далее, что на боковой поверхности цилиндра вектор  параллелен вектору
параллелен вектору  и равен по величине
и равен по величине  будем иметь с точностью до малых высших порядков:
будем иметь с точностью до малых высших порядков:

Отсюда следует точное равенство:

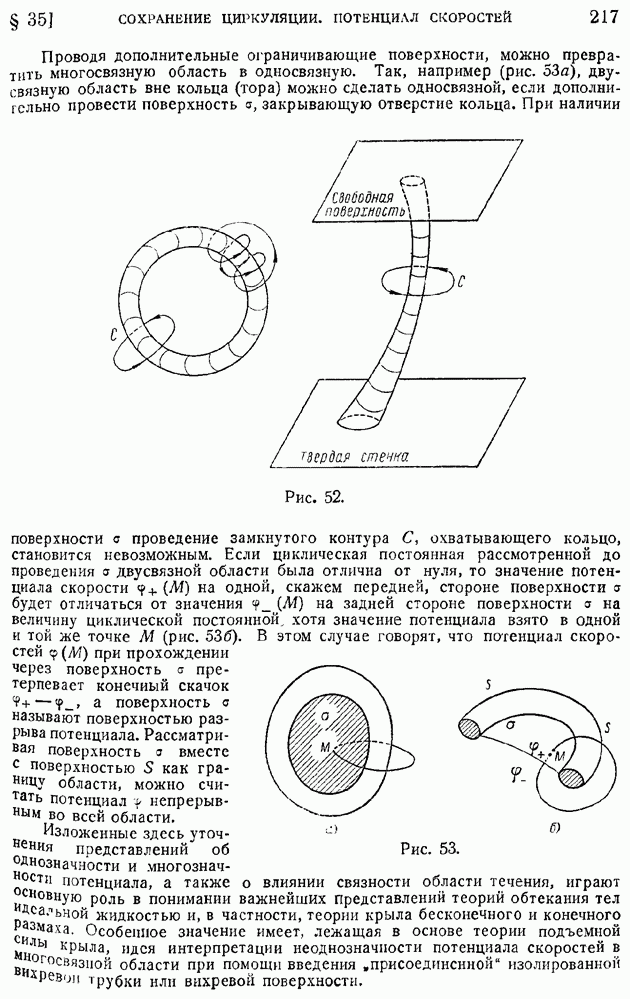
обобщая которое на случай любого векторного поля вектора а и произвольный закон стягивания поверхности  , окружающей элементарный объем
, окружающей элементарный объем  к данной точке пространства, получим следующее интегральное определение вихря вектора:
к данной точке пространства, получим следующее интегральное определение вихря вектора:

Пользуясь этим определением, легко получить выражение вихря в декартовых координатах. Для этого воспользуемся тем же приемом, что и для выражения дивергенции в декартовых координатах. Применим формулу (72) к координатному параллелепипеду с малыми сторонами  (рис. 13). Тогда, проводя непосредственное интегрирование по поверхности параллелепипеда, будем иметь в силу малости граней:
(рис. 13). Тогда, проводя непосредственное интегрирование по поверхности параллелепипеда, будем иметь в силу малости граней:

Отсюда по формуле (72), переходя к пределу, будем иметь

Проектируя на отдельные оси по правилам проектирования векторного произведения, найдем:

Легко видеть, что формулы (50) являются частным случаем этих формул при 
Приемом, аналогичным ранее использованному при выводе интегральных формул для дивергенции и градиента, из равенства (72) получим

Здесь, согласно правилу (51), вновь оправдывается символический прием для запоминания интегральных формул: орт  в поверхностном интеграле заменяется оператором V в объемном
в поверхностном интеграле заменяется оператором V в объемном

Интегральные формулы (66), (70) и (73) будут играть важную роль в выводе основных уравнений динамики жидкости и газа, а также и в некоторых кинематических вопросах.

Рис. 13.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Предмет механики жидкости и газа. Основные свойства «макромодели» жидкости и газа: сплошность и подвижность
- § 2. Основные методы механики жидкости и газа. Области применения и главнейшие задачи
- § 3. Краткий очерк исторического развития механики жидкости и газа. От гидромеханики древних до установления воззрений ньютонианской эпохи
- § 4. Эпоха Эйлера и Бернулли. Гидроаэродинамика в XIX в.
- § 5. Современный этап развития механики жидкости и газа
- ГЛАВА I. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
- § 6. Поле физической величины. Скалярное и векторное поля. Поверхности уровня. Векторные линин и трубки
- § 7. Мера однородности поля в данном направлении и в дайной точке. Градиевт скалярного поля и дифференциальный тензор векторного поля как меры неоднородности поля
- § 8. Задание движения сплошной среды. Поле скоростей. Линии тока и траектории
- § 9. Поле ускорений. Разложение ускорения частицы на локальную и конвективную составляющие
- § 10. Скоростное поле сплошной среды в окрестности данной точки. Угловая скорость и вихрь. Тензор скоростей деформаций и его компоненты
- § 11. Скорость объемного расширения жидкости. Интегральные представления дифференциальных операторов поля. Основные интегральные формулы
- § 12. Вихревые линии и трубки. Вторая теорема Гельмгольца. Интенсивность вихревой трубки
- § 13. Выражение интенсивности вихревой трубки через циркуляцию вектора по контуру, охватывающему трубку. Теорема об изменении циркуляции скорости во времени
- ГЛАВА II. ОСНОВНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ И РАВНОВЕСИЯ СПЛОШНОЙ СРЕДЫ
- § 14. Распределение массы в сплошной среде. Плотность и удельный вес. Напряжения. Тензор напряженности и его симметричность
- § 15. Общие уравнения динамики сплошной среды. Уравнение неразрывности. Уравнения динамики в напряжениях
- § 16. Тепловые явления в жидкостях и газах. Закон сохранения энергии и уравнение баланса энергии
- § 17. Общие уравнения равновесного состояния жидкости и газа. Равновесие воздуха в атмосфере. Приближенные барометрические формулы. Стандартная атмосфера
- § 18. Равновесие несжимаемой жидкости. Уравнение поверхности раздела. Равновесие вращающейся жидкости
- § 19. Давление тяжелой несжимаемой жидкости на поверхность тела. Сила и момент, приложенные к телу, плавающему в тяжелой жидкости. Случай вращающейся жидкости
- ГЛАВА III. ДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ И ГАЗА. ОСНОВНЫЕ УРАВНЕНИЯ И ОБЩИЕ ТЕОРЕМЫ
- § 20. Идеальная жидкость. Основные уравнения движения
- § 21. Закон сохранения энергии в движущейся идеальной жидкости. Адиабатическое движение. Сохранение энтропии
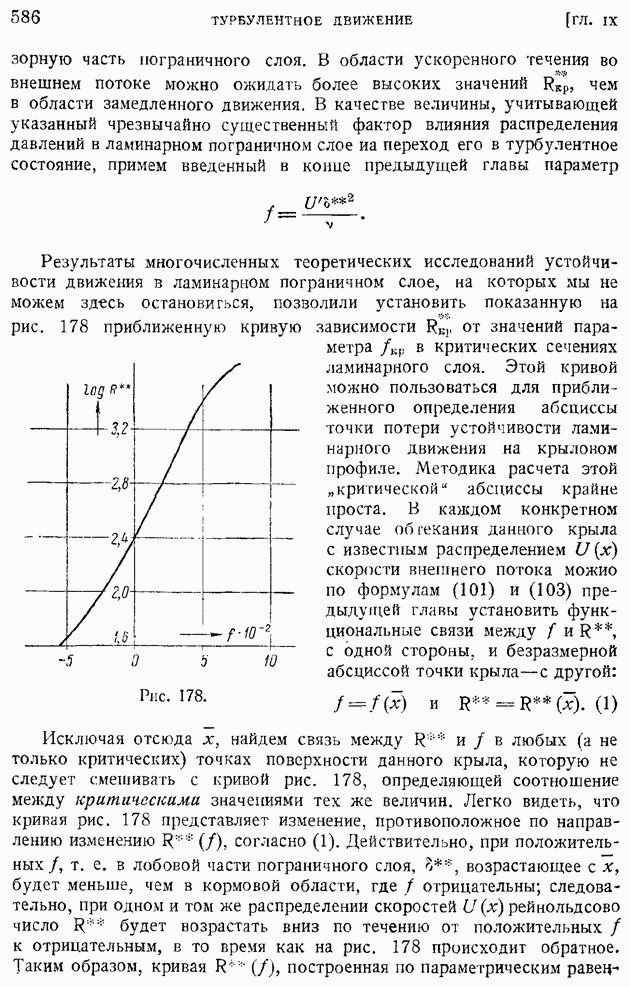
- § 22. Эйлерово представление конвективного изменения объемного интеграла. Перенос величины сквозь контрольную поверхность
- § 23. Эйлерова форма законов сохранения массы и энергии, теоремы количеств движения и момента количеств движения при стационарном движении идеальной жидкости
- § 24. Теорема об изменении кинетической энергии. Работа и мощность внутренних сил. Эйлерова форма уравнения изменения кинетической энергии
- § 25. Теорема Бернулли о сохранении полной механической энергии при стационарном баротропном движении идеальной жидкости и газа
- ГЛАВА IV. ОДНОМЕРНЫЙ ПОТОК ИДЕАЛЬНОЙ ЖИДКОСТИ
- § 26. Одномерное течение идеальной сжимаемой жидкости. Линеаризированные уравнения. Скорость распространения малых возмущений в жидкости или газе
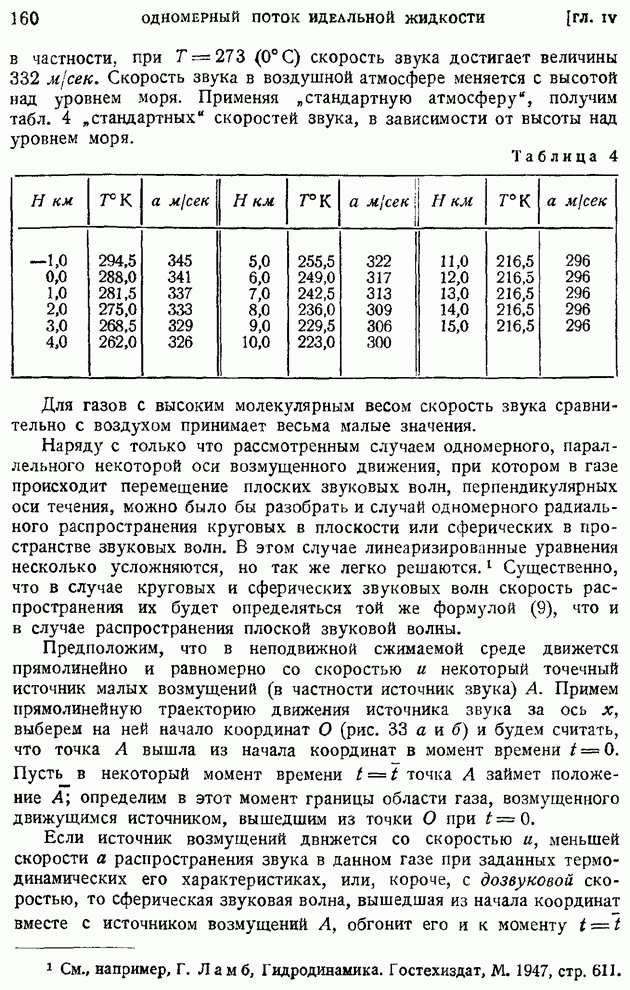
- § 27. Изотермическая и адиабатическая скорости звука. «Конус возмущений» при сверхзвуковом движении источника возмущения. Число M и его связь с углом конуса возмущений
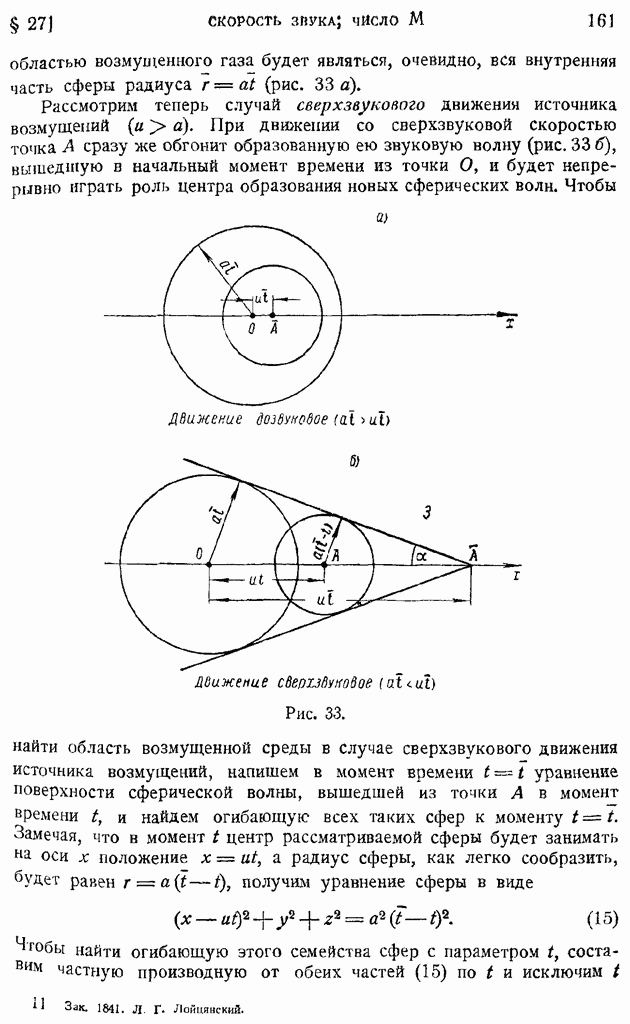
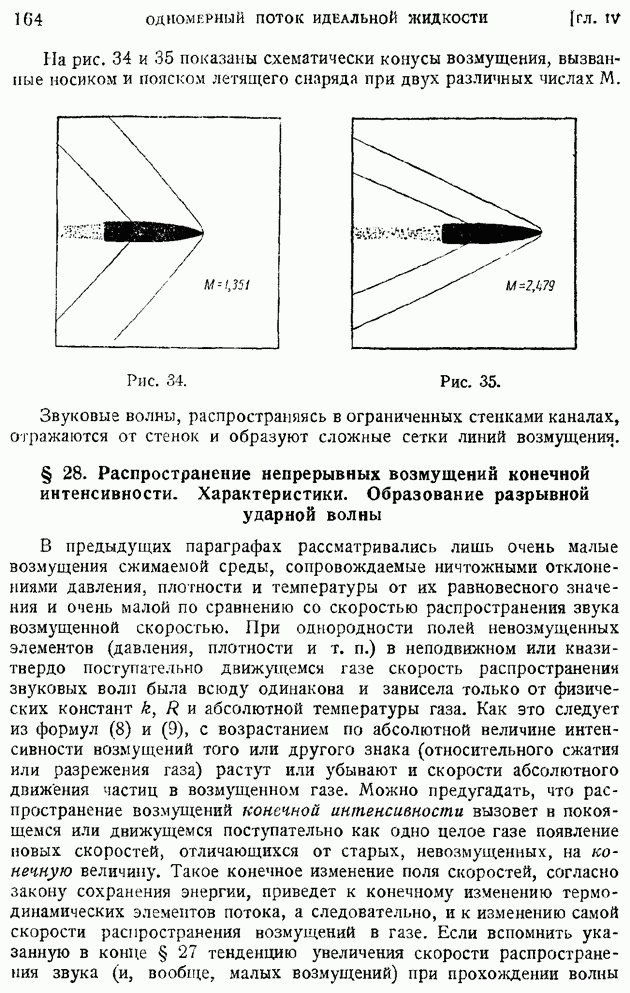
- § 28. Распространение непрерывных возмущений конечной интенсивности. Характеристики. Образование разрывной ударной волны
- § 29. Стоячая ударная волна или скачок уплотнения. Ударная адиабата
- § 30. Критические величины в одномерном потоке газа. Связь между скоростями до и после скачка. Изменение давления, плотности и температуры в скачке уплотнения
- § 31. Скорость распространения ударной волны. Спутное движение газа за ударной волной
- § 32. Влияние интенсивности скачка уплотнения на сжатие газа. Измерение скоростей и давлений в до- и сверхзвуковых потоках
- § 33. Одномерное движение газа по трубе переменного сечения. Истечение из резервуара большой емкости сквозь сходящееся сопло
- § 34. Одномерное течение в сопле Лаваля. Движение газа с притоком тепла
- ГЛАВА V. БЕЗВИХРЕВОЕ ДВИЖЕНИЕ ЖИДКОСТИ. ПЛОСКОЕ ДВИЖЕНИЕ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 35. Сохранение циркуляции скорости в потоке идеальной жидкости. Теорема Кельвина и Лаграижа. Безвихревое движение. Потенциал скоростей
- § 36. Интеграл Лагранжа — Коши уравнений безвихревого движения. Теорема Бернулли. Некоторые общие свойства безвихревого движения идеальной несжимаемой жидкости в односвязной области
- § 37. Плоское безвихревое движение несжимаемой жидкости. Потенциал скоростей и функция тока. Применение функций комплексного переменного. Комплексный потенциал и сопряженная скорость
- § 38. Построение полей течения по заданной характеристической Функции. Простейшие плоские потоки и их наложение
- § 39. Бесциркуляционное и циркуляционное обтекания круглого цилиндра
- § 40. Применение криволинейных координат. Бесциркуляционное и циркуляционное обтекания эллиптического цилиндра и пластинки. Задача Жуковского об обтекании решетки пластин.
- § 41. Плоское движение с отрывом струй. Разрывное обтекание пластинки и протекание жидкости сквозь отверстие
- § 42. Прямая задача в теории плоского движения идеальной несжимаемой жидкости. Применение метода конформных отображений. Гипотеза Чаплыгина о безотрывном обтекании задней кромки профиля. Формула циркуляции
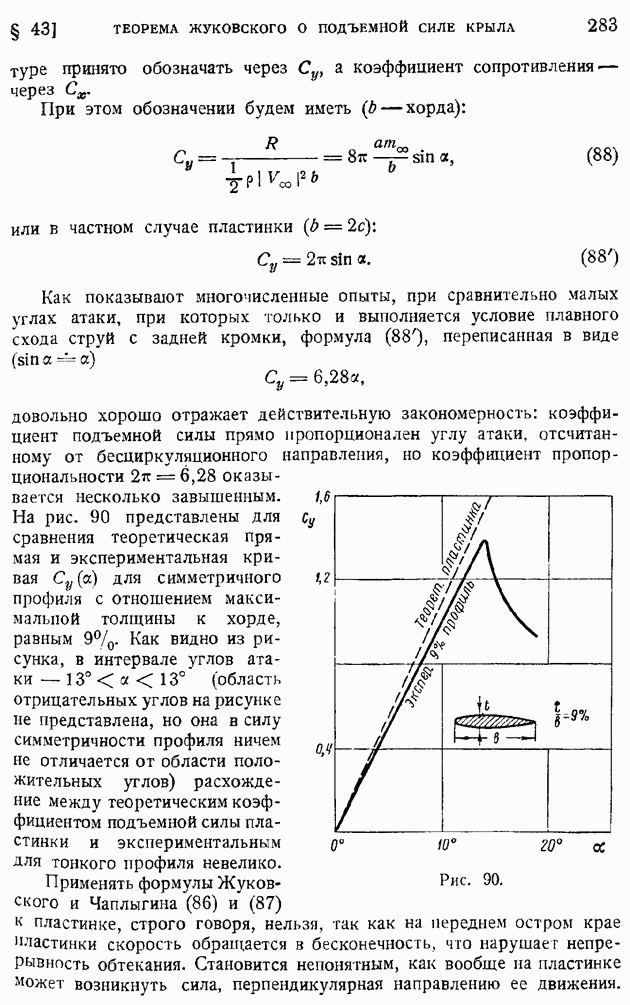
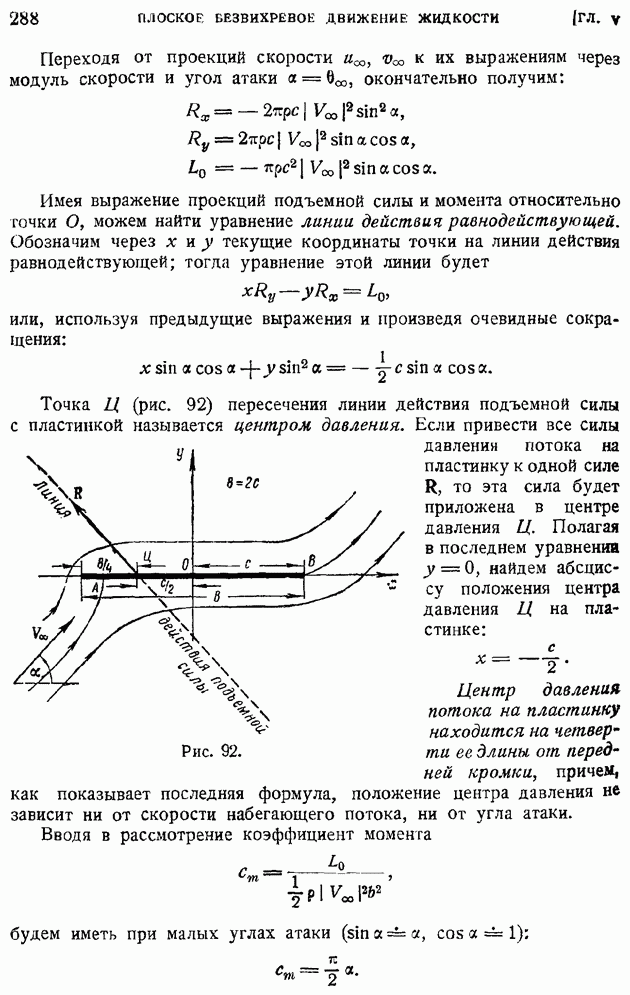
- § 43. Теорема Жуковского о подъемной силе крыла. Зависимость подъемной силы от угла атаки. Коэффициент подъемной силы
- § 44. Применение метода комплексных переменных к выводу теоремы Жуковского. Формулы Чаплыгина для главного вектора и момента сил давления потока на крыло
- § 45. Выражение главного момента сил давления потока через коэффициенты конформного отображения. Фокус крыла. Независимость от угла атаки момента относительно фокуса. Парабола устойчивости
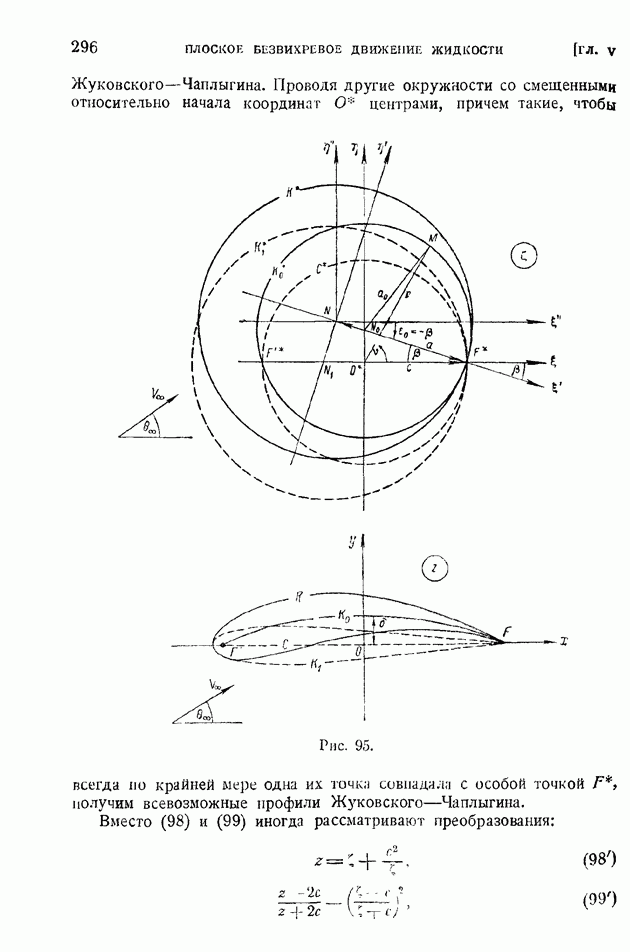
- § 46. Частные случаи конформного отображения крылового профиля на круг. Преобразование Жуковского-Чаплыгина. Теоретические крыловые профили
- § 47. Задача об обтекании слабо изогнутой дужки произвольной формы (теория тонкого крыла)
- § 48. Определение обтекания крылового профиля произвольной формы
- § 49. Обобщение теоремы Жуковского на случай плоской решетки с бесчисленным множеством профилей
- ГЛАВА VI. ПЛОСКОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ СЖИМАЕМОГО ГАЗА
- § 50. Основные уравнения плоского стационарного безвихревого движения сжимаемого газа. Линеаризированные уравнения
- 51. Линеаризированный до- и сверхзвуковой газовый поток вдоль волнистой стенки
- § 52. Тонкое крыло в линеаризированном до- и сверхзвуковом потоках. Влияние сжимаемости газа на коэффициент подъемной силы в дозвуковом потоке. Коэффициенты подъемной силы и волнового сопротивления при сверхзвуковом потоке
- § 53. Нелинеаризированные уравнения движения идеального сжимаемого газа. Переход в плоскость годографа. Уравнения Чаплыгина
- § 54. Метод С. А. Христиановича. Приближенные формулы учета влияния сжимаемости на распределение давления
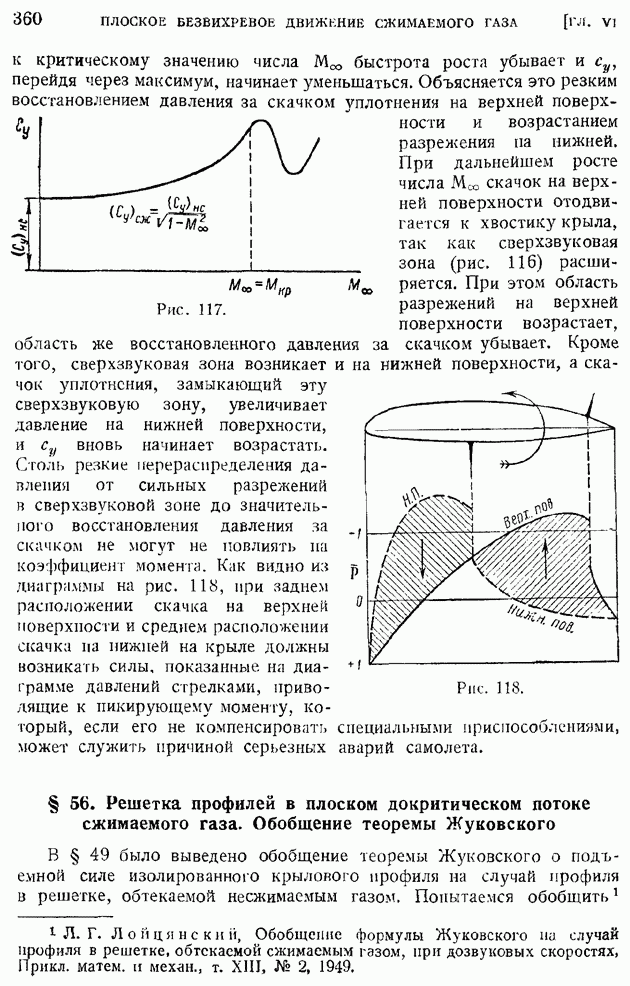
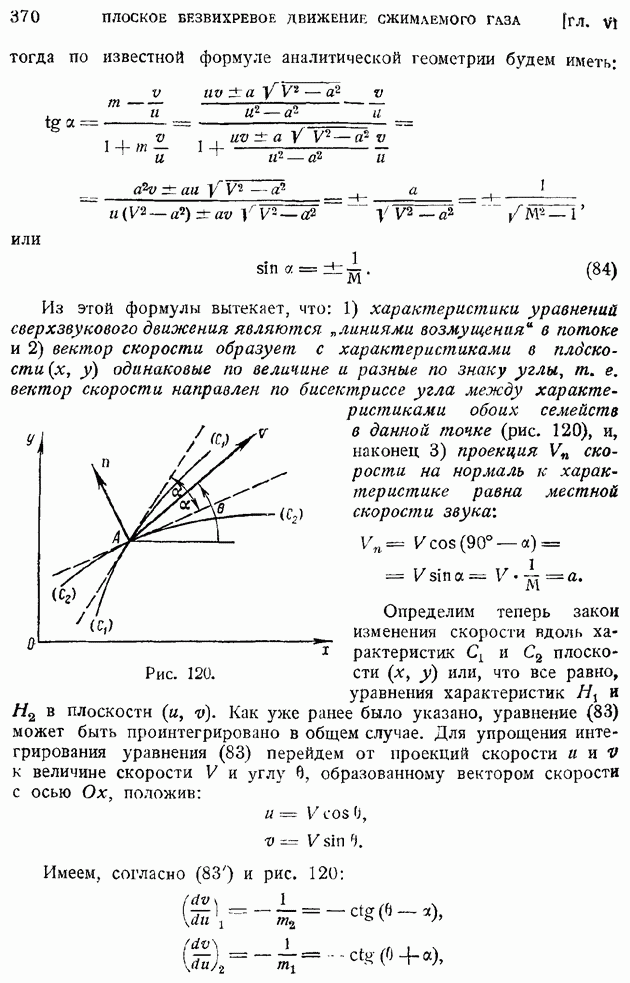
- § 55. Критическое число M и его определение по заданному распределению давления в несжимаемом обтекании. Поведение коэффициента подъемной силы и момента при около- и закритических значениях числа M
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
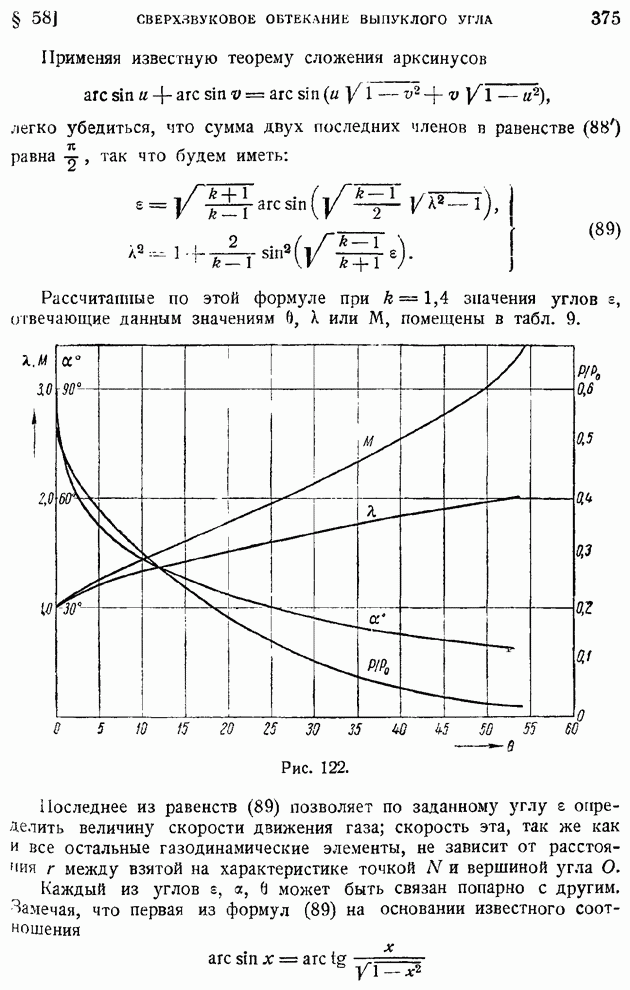
- § 57. Нелинеаризированный сверхзвуковой поток. «Характеристики» уравнений плоского сверхзвукового потока. Линин возмущения и их основные свойства
- § 58. Обтекание выпуклого угла сверхзвуковым потоком. Влияние угла поворота струи на ее газодинамические элементы
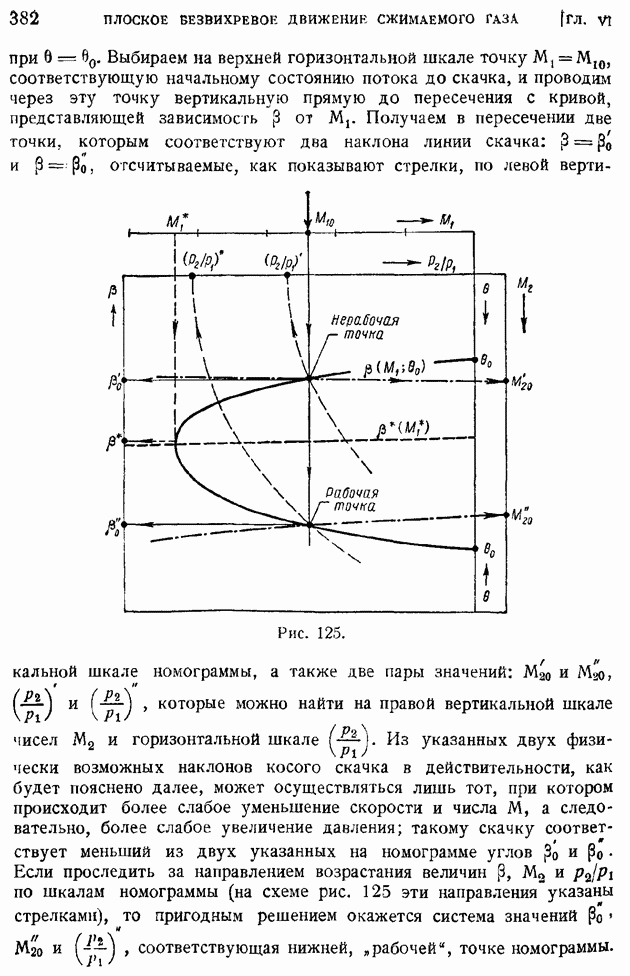
- § 59. Сверхзвуковой поток внутри тупого угла. Косой скачок уплотнения. Связь между газодинамическими элементами до и за косым скачком
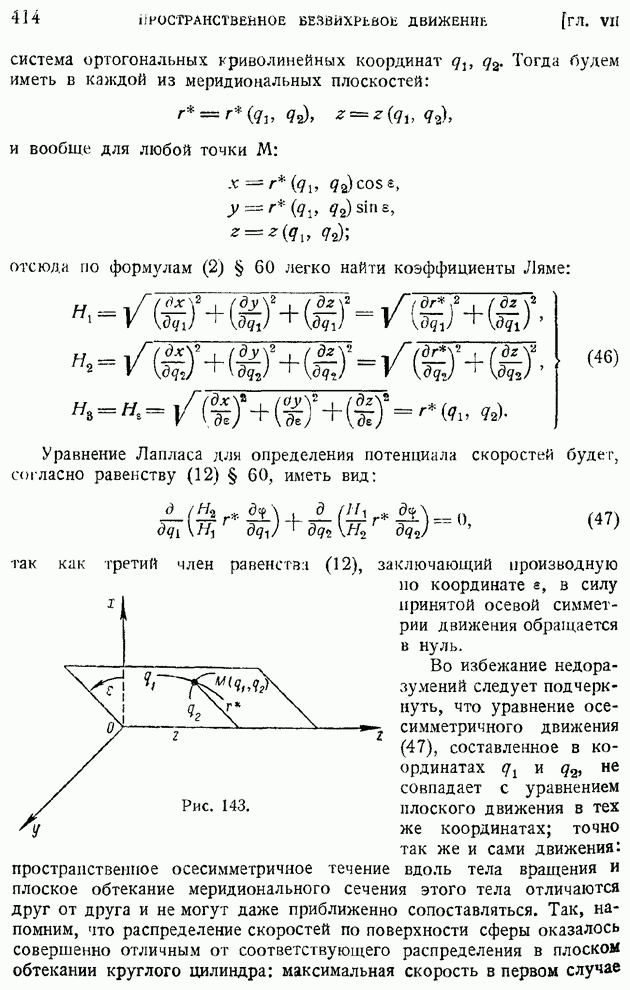
- ГЛАВА VII. ПРОСТРАНСТВЕННОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ
- § 60. Ортогональные криволинейные координаты в пространстве. Основные дифференциальные операторы поля в криволинейных координатах
- § 61. Потенциал скоростей. Поле источника и диполя. Непрерывное распределение источников и диполей. Ньютонов потенциал. Потенциал простого и двойного слоев
- § 62. Поле скоростей вокруг заданной системы вихрей. Формула Био — Савара. Потенциал скоростей замкнутой вихревой нити. Аналогия с потенциалом двойного слоя
- § 63. Функция тока и ее связь с векторным потенциалом скоростей. Функции тока простейших течений
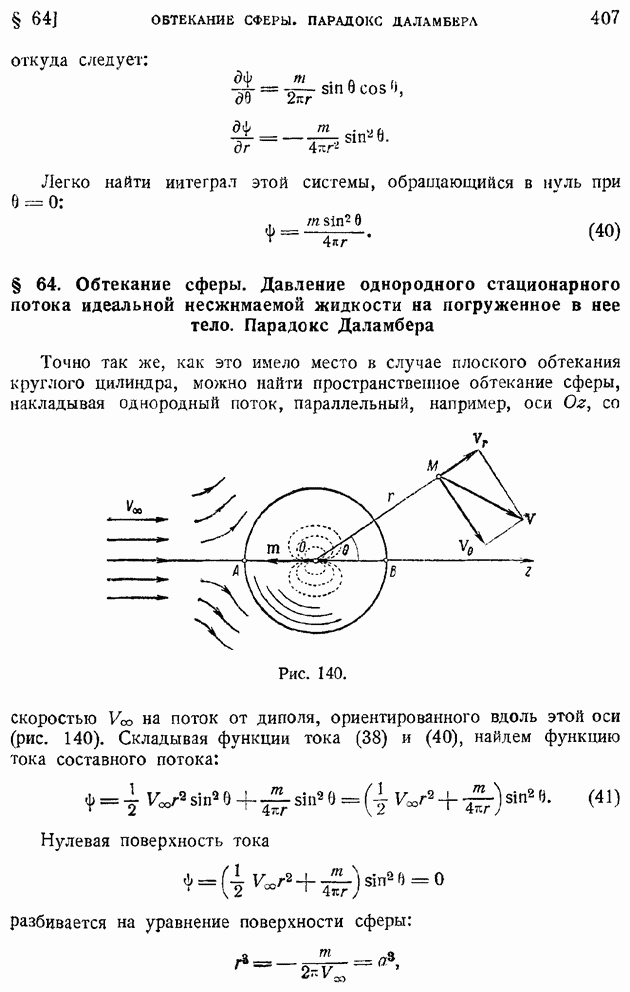
- § 64. Обтекание сферы. Давление однородного стационарного потока идеальной несжимаемой жидкости на погруженное в нее тело. Парадокс Даламбера
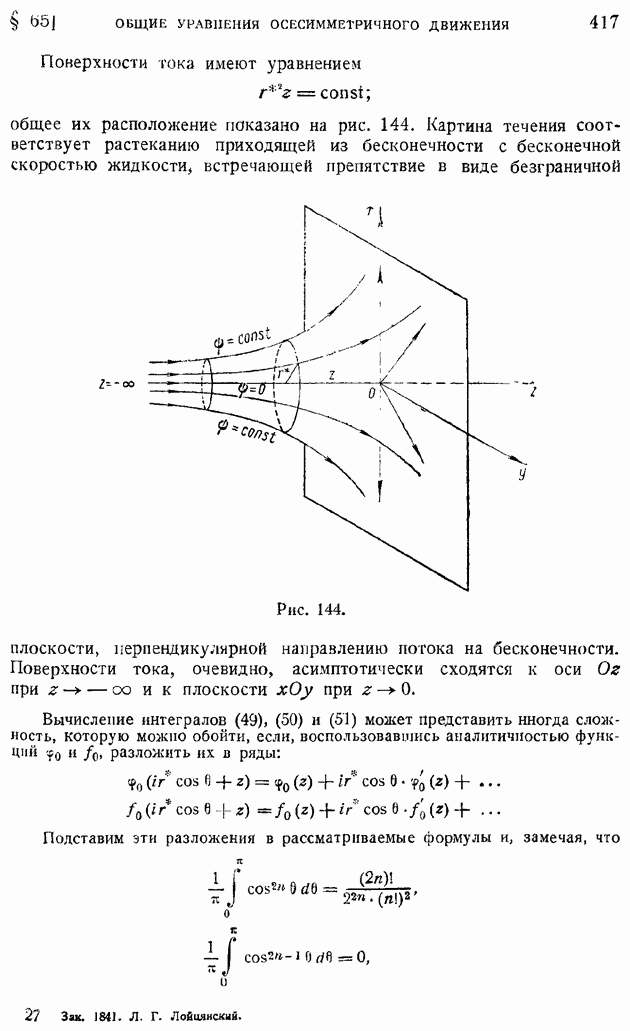
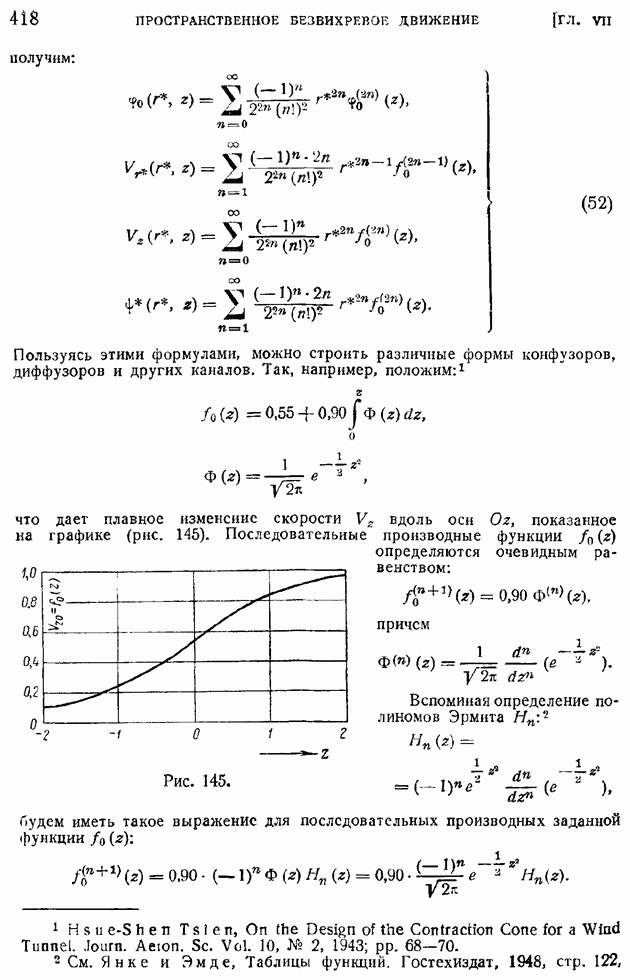
- § 65. Общие уравнения осесимметричного движения. Применение цилиндрических координат. Течение сквозь каналы
- § 66. Осесимметричное продольное обтекание тел вращения. Случай эллипсоида вращения
- § 67. Поперечное обтекание тел вращения. Пример эллипсоида вращения
- § 68. Продольное и поперечное обтекание тел вращения большого удлинения. Приближенные выражения граничных условий. Применение тригонометрических сумм для определения коэффициентов …
- § 69. Метод «особенностей». Применение непрерывно распределенных источников (стоков) и диполей для решения задачи о продольном и поперечном обтекании тел вращения
- § 70. Общий случай движения твердого тела сквозь несжимаемую идеальную жидкость. Определение потенциала скоростей. Главный вектор и главный момент сил давления потока на тело
- § 71. Коэффициенты «присоединенных масс». Свойство симметрии. «Присоединенная» кинетическая энергия. Определение «присоединенных масс» поступательно движущегося цилиндра, шара и эллипсоида
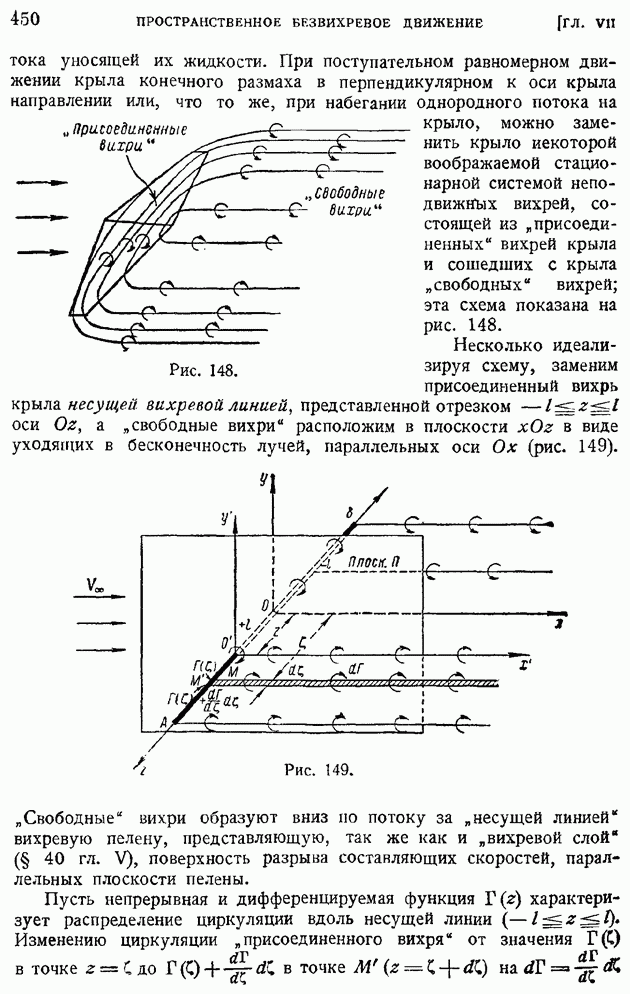
- § 72. Элементы теории крыла конечного размаха. Вихревая система крыла. Гипотеза плоских сечеиий. Геометрические и действительные углы атаки. Подъемная сила и «индуктивное сопротивление»
- § 73. Основные формулы теории «несущей линии». «Индуктивная скорость» и «индуктивный угол». Прямая задача определения подъемной силы и индуктивного сопротивления по заданному распределению циркуляции
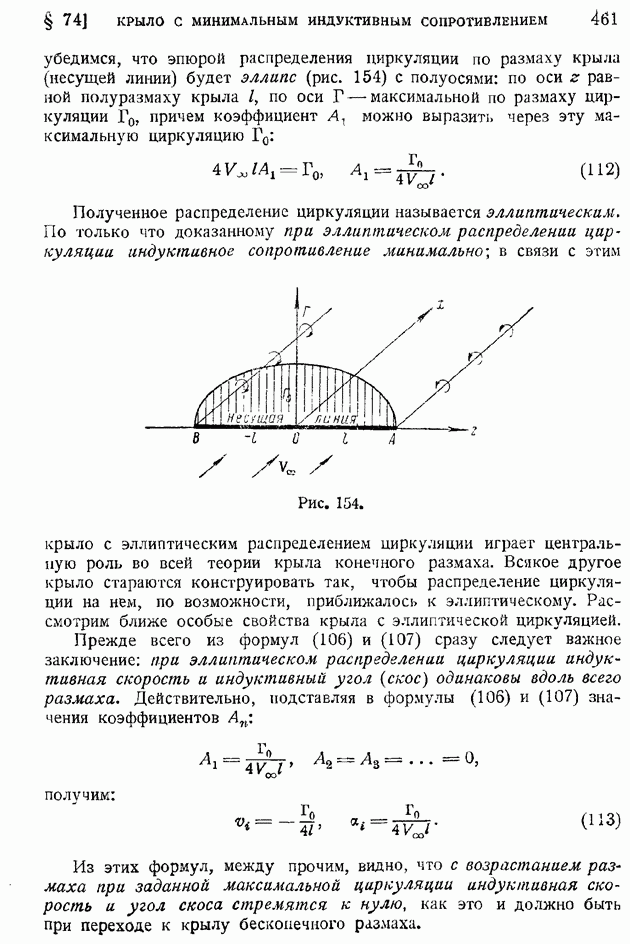
- § 74. Крыло с минимальным индуктивным сопротивлением. Эллиптическое распределение циркуляции. Связь между коэффициентами индуктивного сопротивления и подъемной силы. Основное уравнение теории крыла и понятие о его интегрировании
- ГЛАВА VIII. ДИНАМИКА ВЯЗКОЙ ЖИДКОСТИ И ГАЗА
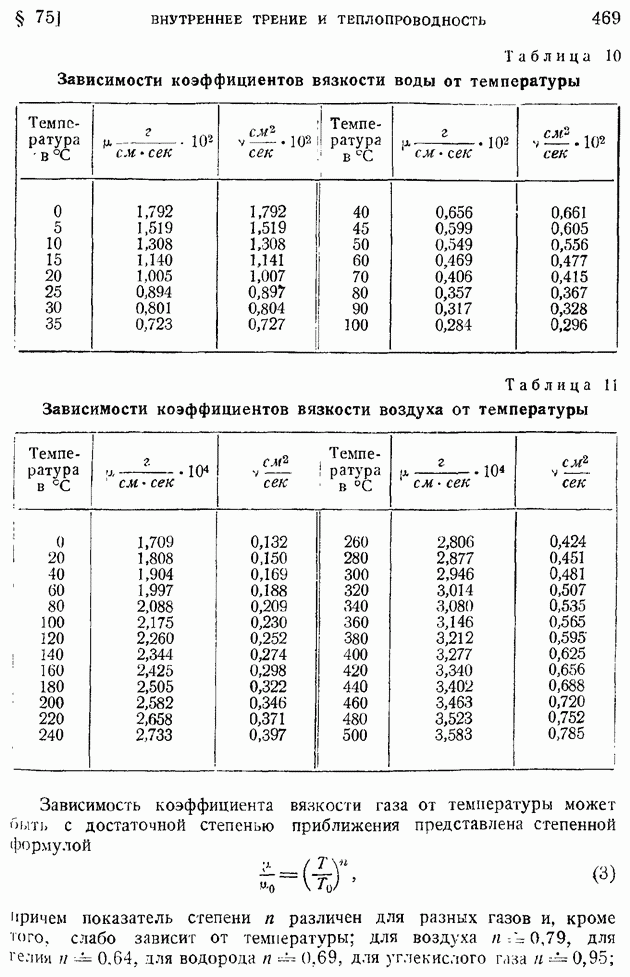
- § 75. Внутреннее трение и теплопроводность в жидкостях и газах. Законы Ньютона и Фурье. Влияние температуры на коэффициенты вязкости и теплопроводности. Число «сигма»
- § 76. Обобщение закона Ньютона на случай произвольного движения среды. Закон линейной связи между тензорами напряжений и скоростей деформации
- § 77. Общие уравнения движения вязкой жидкости. Динамические уравнения и уравнение баланса энергии. Граничные условия движения жидкости с треннем и теплопроводностью
- § 78. Понятие о подобии гидродинамических явлений. Безразмерные уравнения движения вязкой жидкости и газа. Условия подобия
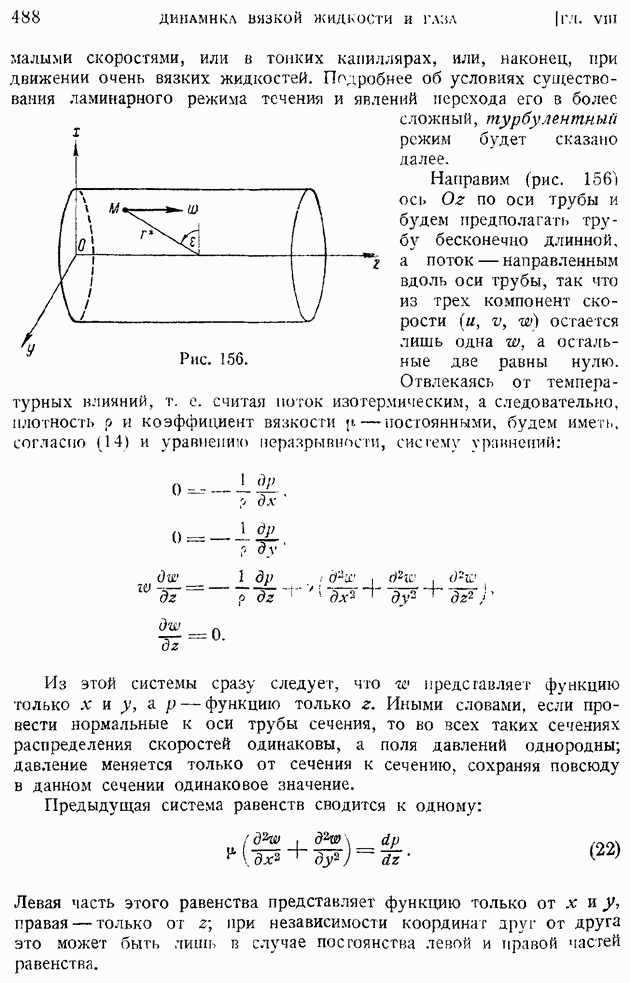
- § 79. Ламинарное движение вязкой несжимаемой жидкости по цилиндрической трубе
- § 80. Обтекание шара при очень малых значениях числа Рейнольдса. Формула сопротивления шара по Стоксу и ее обобщения
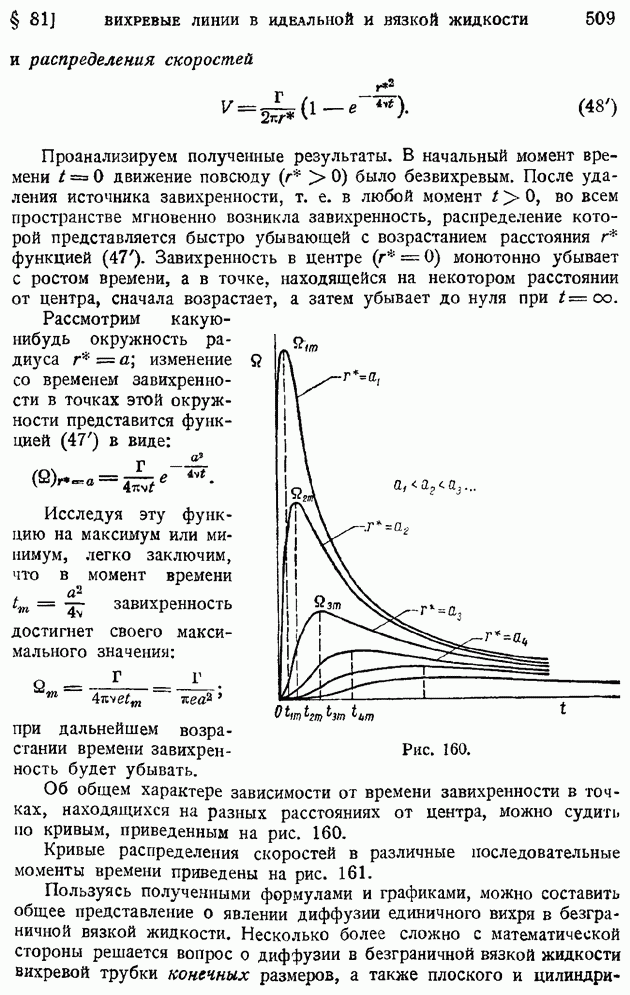
- § 81. Вихревые линии в идеальной и вязкой жидкости. Сохраняемость вихревых линий при отсутствии внутреннего трения. Диффузия вихря в вязкой жидкости
- § 82. Одномерное прямолинейное движение сжимаемого вязкого газа. Движение внутри скачка уплотнения. Понятие о толщине скачка
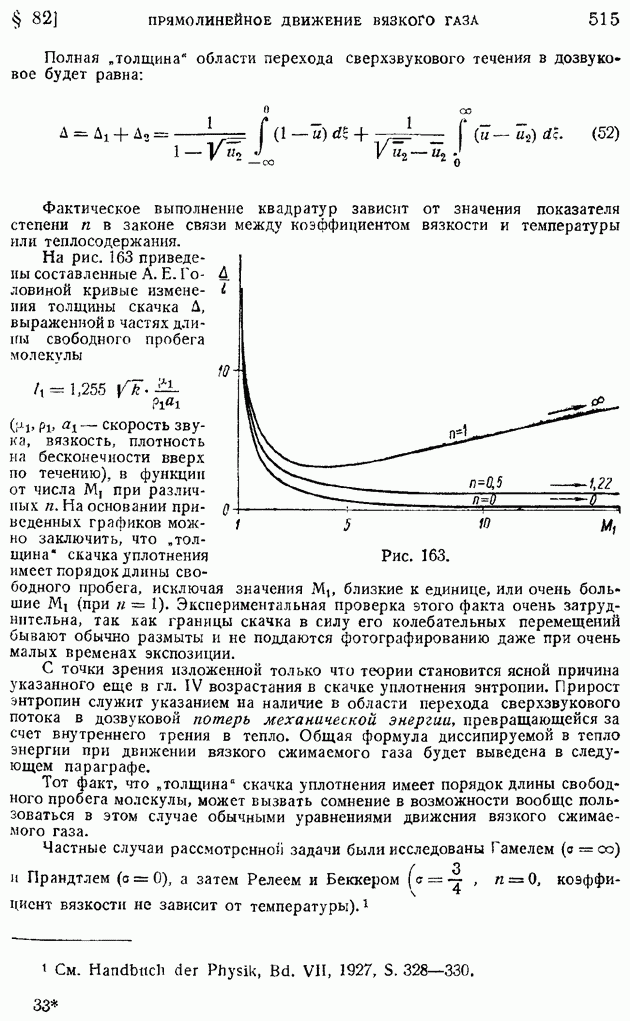
- § 83. Работа внутренних сил и диссипация механической энергии в движущейся вязкой среде
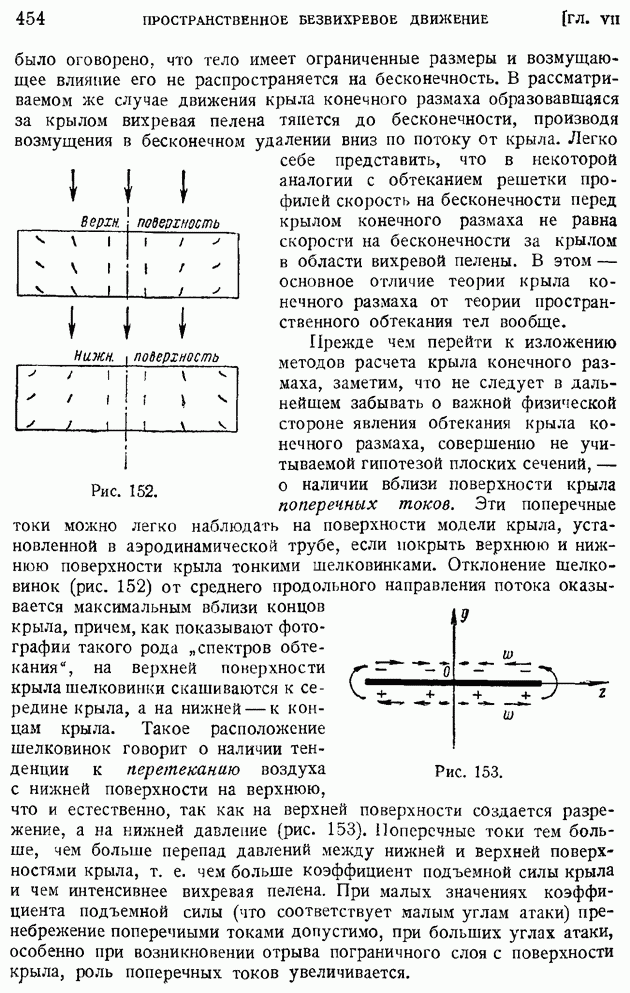
- § 84. Обтекание тел жидкостью и газом при больших значениях числа Рейнольдса. Основные уравнения теории ламинарного пограничного слоя
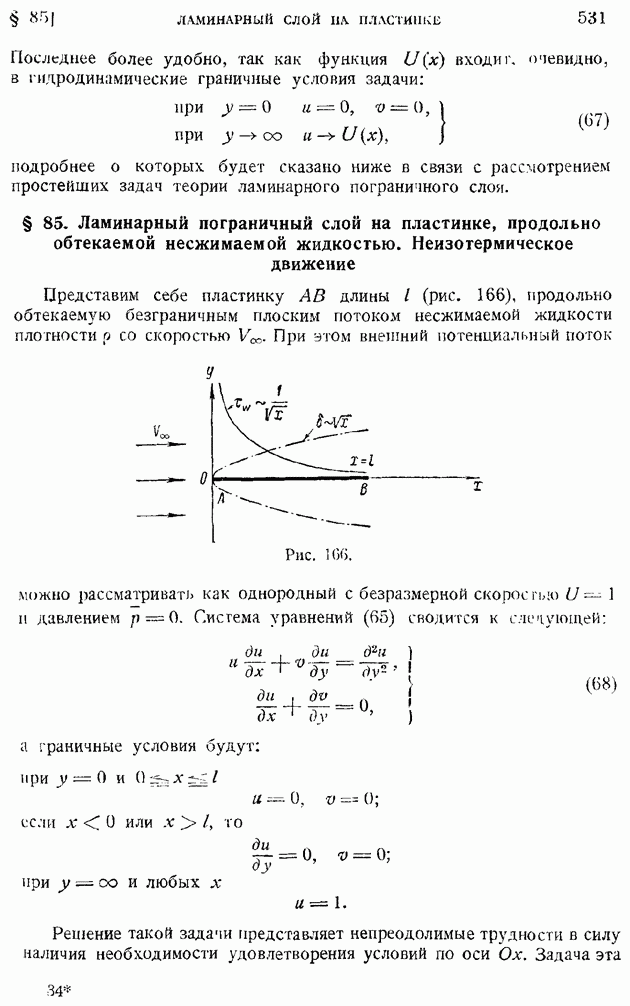
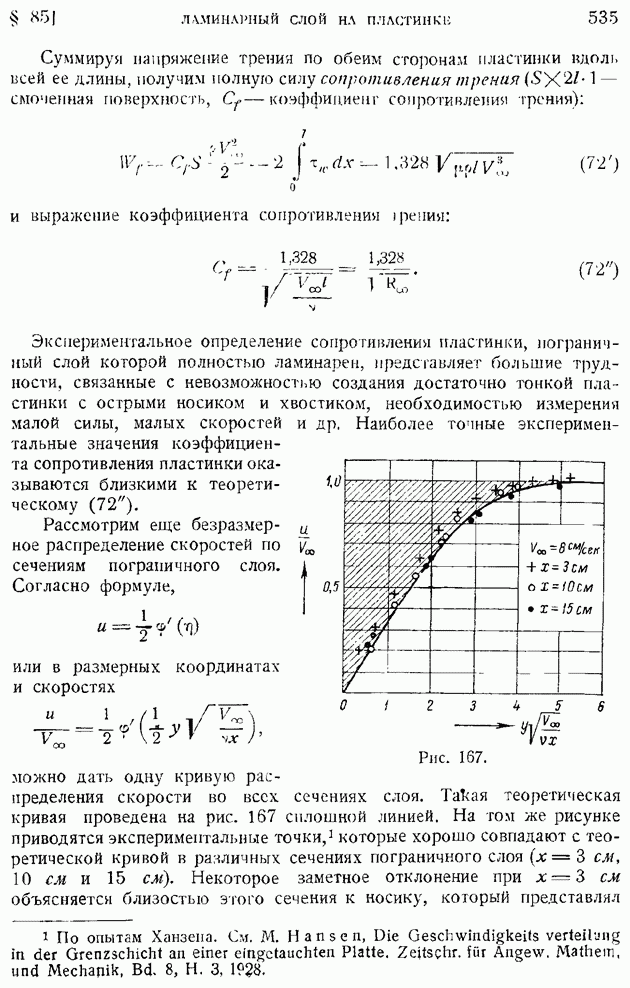
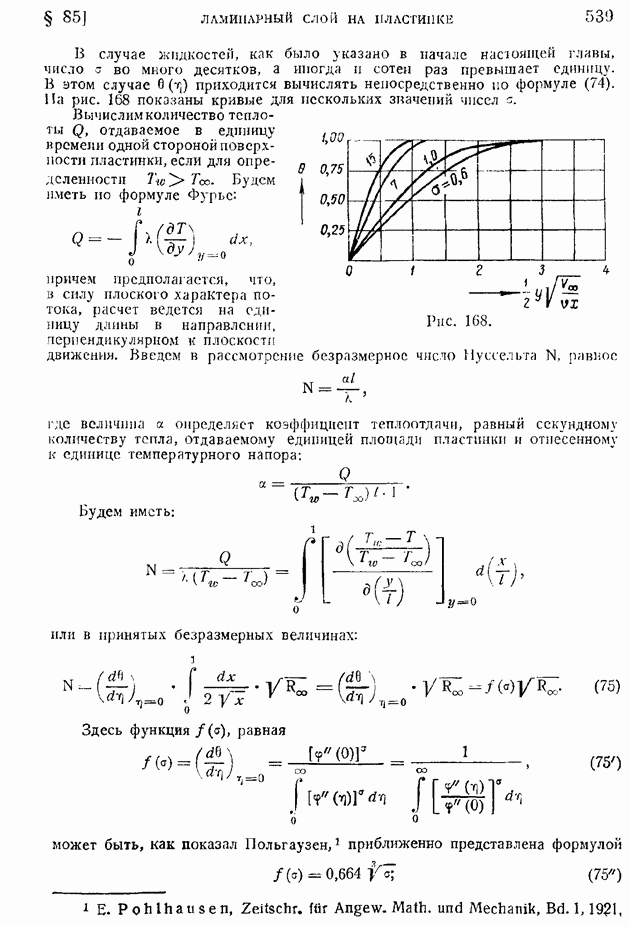
- § 85. Ламинарный пограничный слой на пластинке, продольно обтекаемой несжимаемой жидкостью. Неизотермическое движение
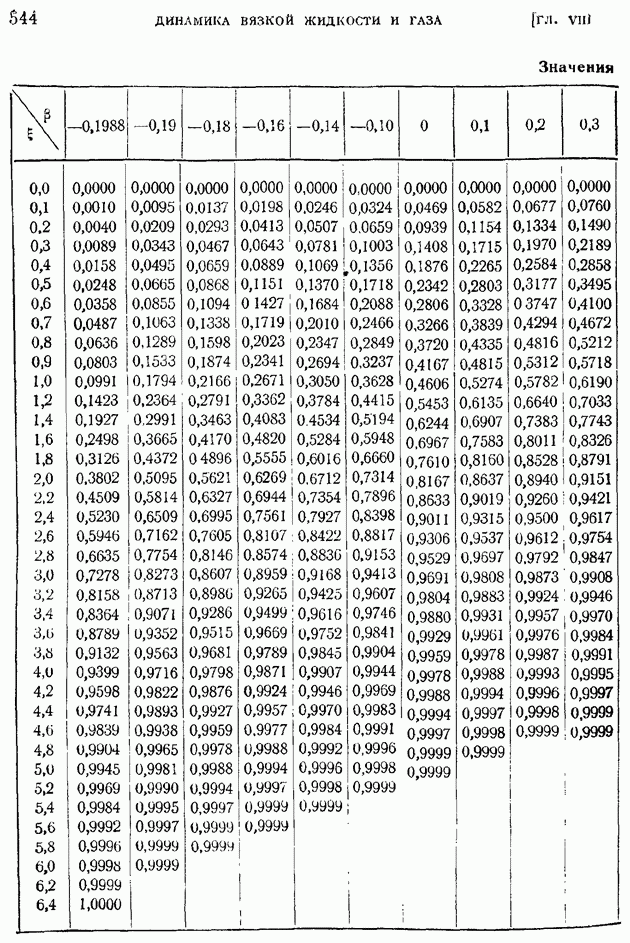
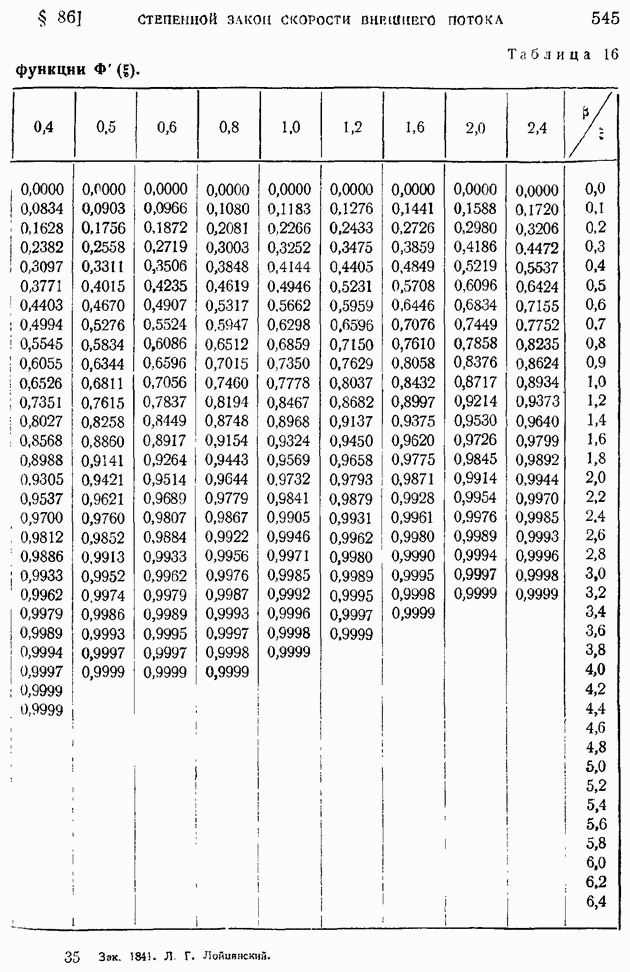
- § 86. Ламинарный пограничный слой при степенном задании скорости внешнего потока
- § 87. Ламинарный пограничный слой в общем случае задания скорости внешнего потока. Применение уравнения импульсов для приближенного расчета ламинарного пограничного слоя
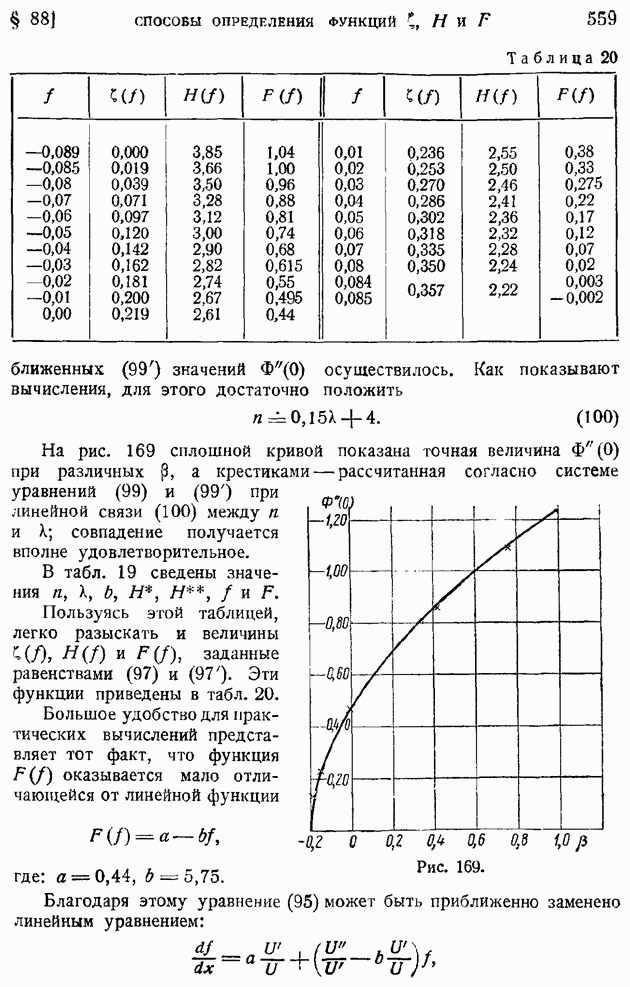
- § 88. Способы определения функций … Приближенный метод расчета ламинарного пограничного слоя
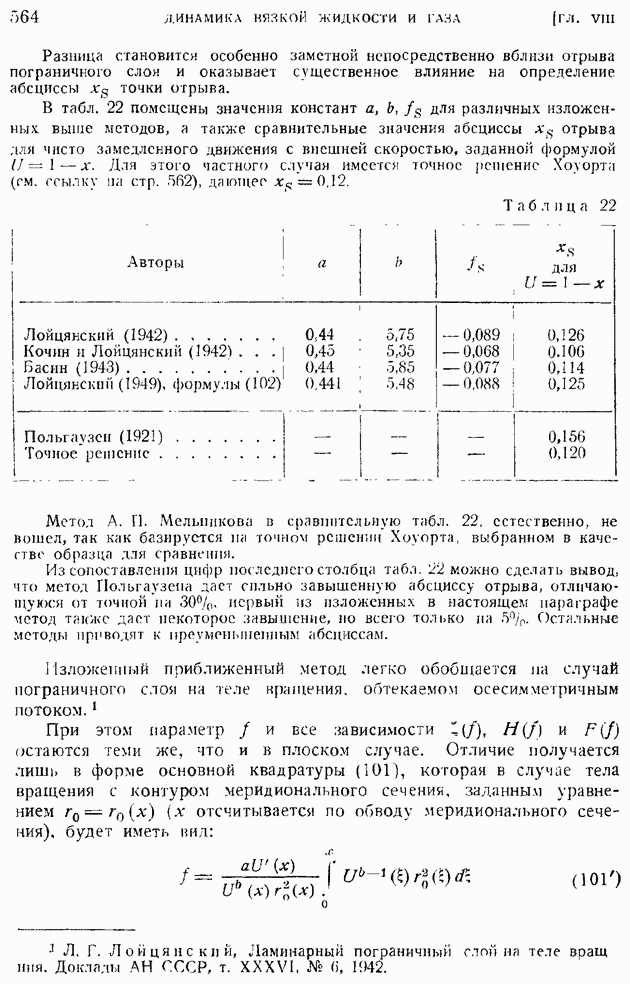
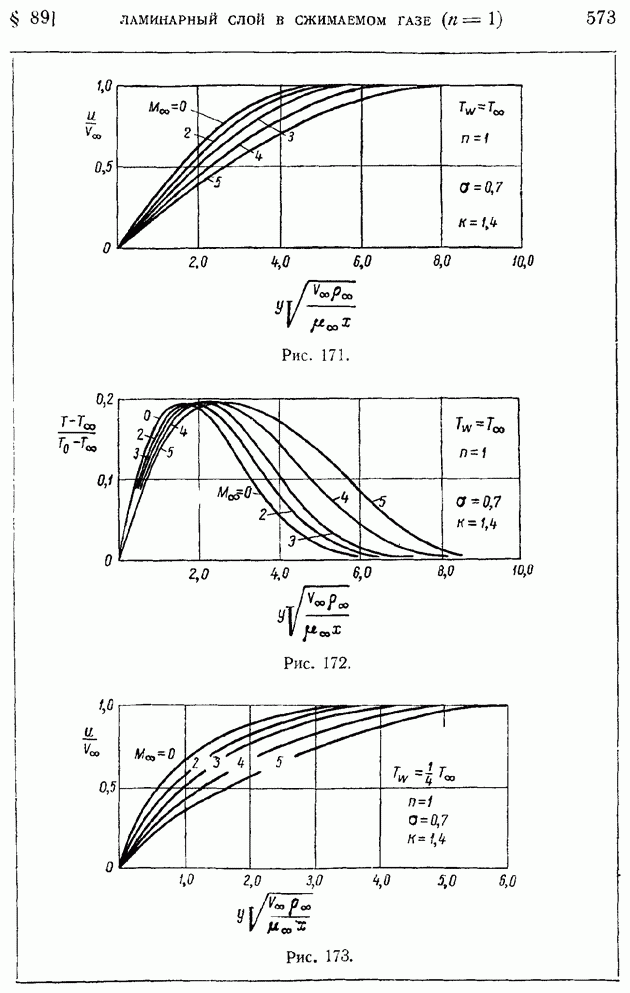
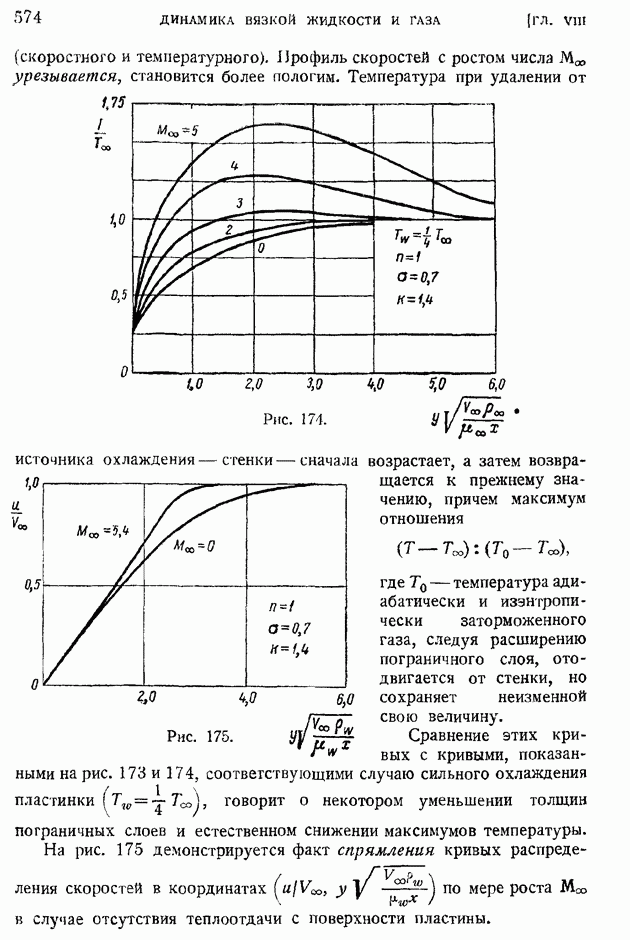
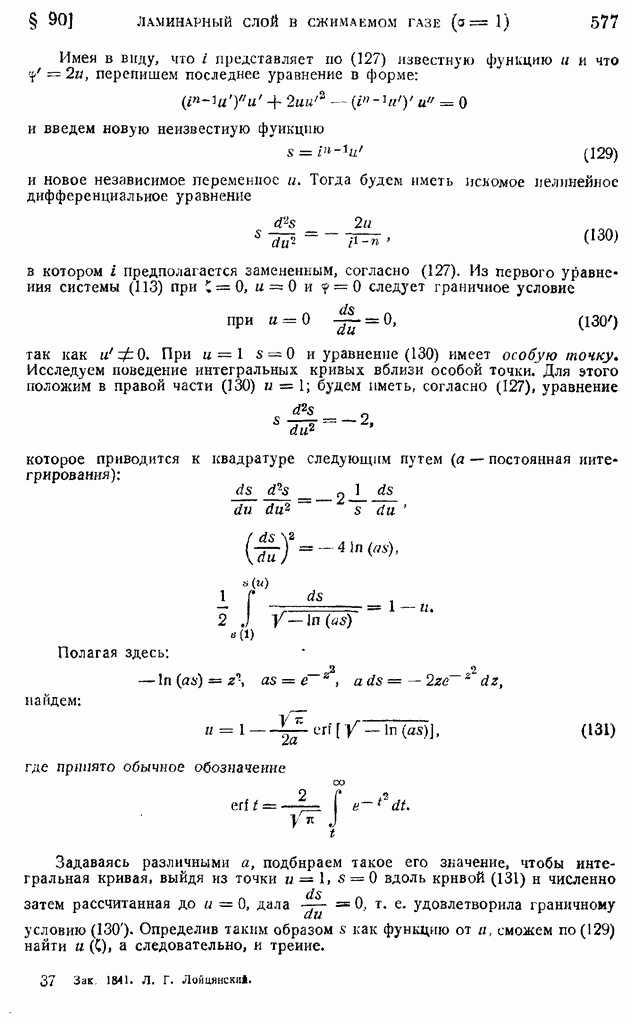
- § 89. Ламинарный пограничный слой на пластинке, продольно обтекаемой сжимаемым газом при больших скоростях. Случай линейной зависимости коэффициента вязкости от температуры (n = 1)
- § 90. Ламинарный пограничный слой на пластинке при любом законе связи между вязкостью и температурой и при числе … Обтекание крылового профиля потоком больших скоростей
- ГЛАВА IX. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ
- § 91. Переход ламинарного движения в турбулентное. Критическое рейнольдсово число
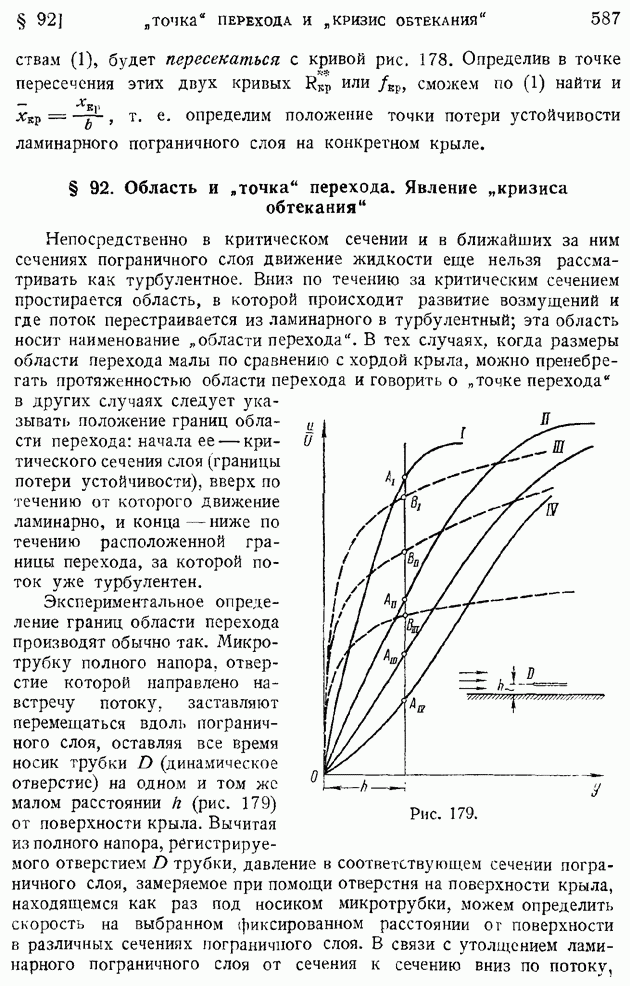
- § 92. Область и «точка» перехода. Явление «кризиса обтекания»
- § 93. Основные уравнения осреднеиного турбулентного движения. Тензор турбулентных напряжений
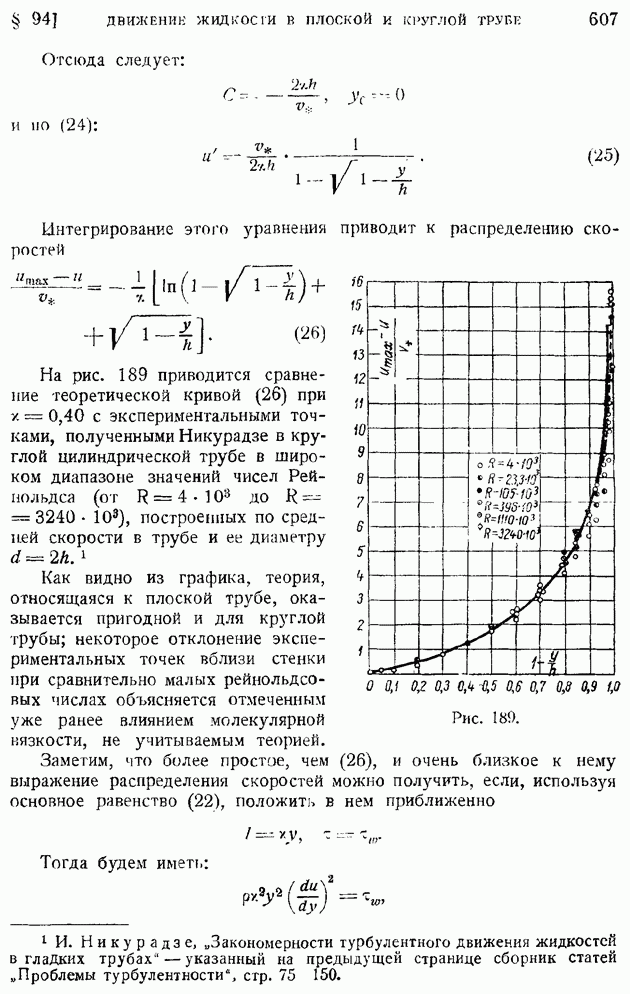
- § 94. Турбулентное движение жидкости в плоской и круглой трубе. Логарифмические формулы скоростей
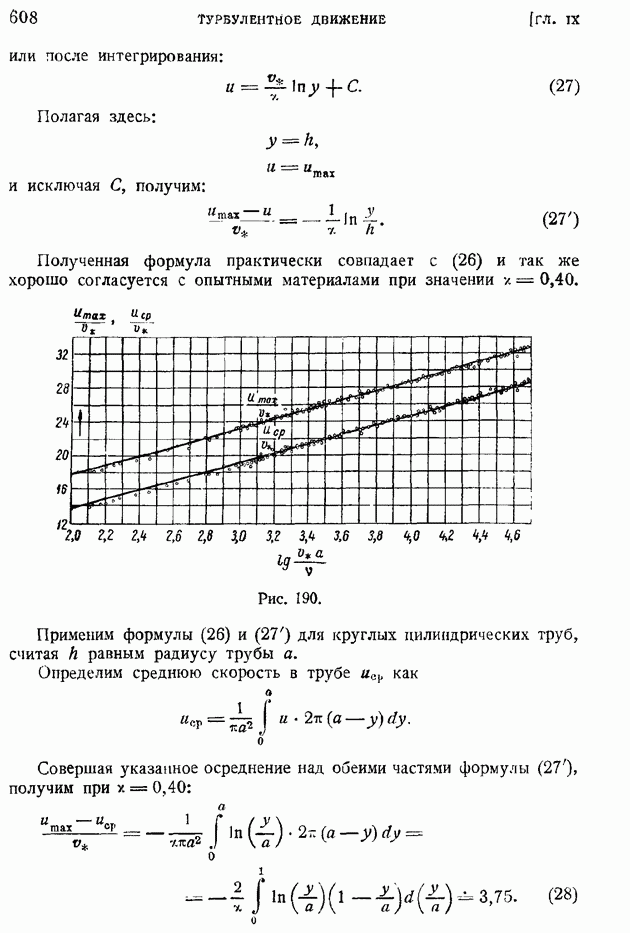
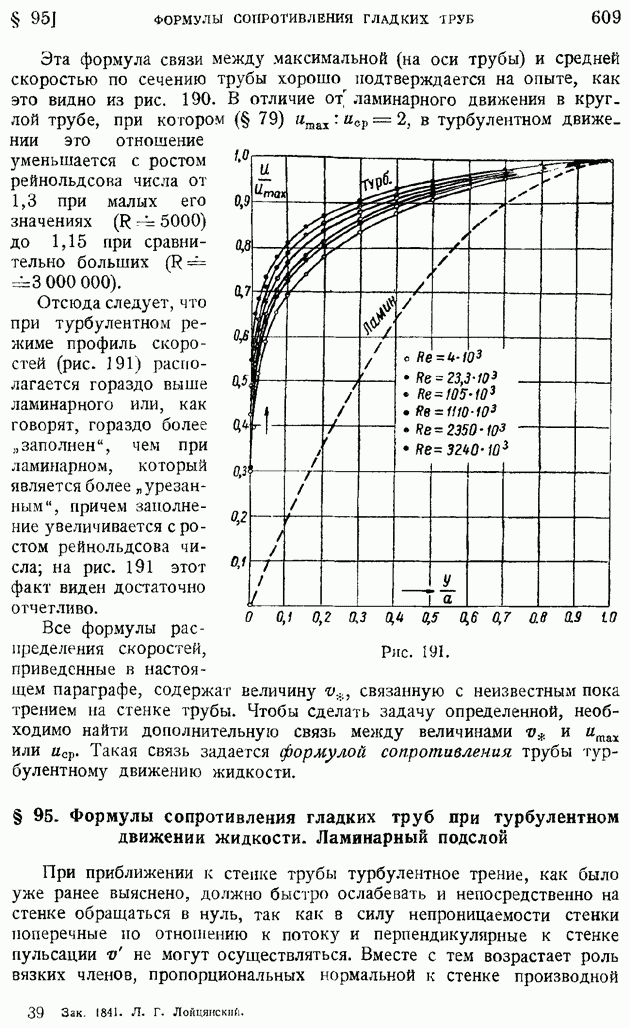
- § 95. Формулы сопротивления гладких труб при турбулентном движении жидкости. Ламинарный подслой
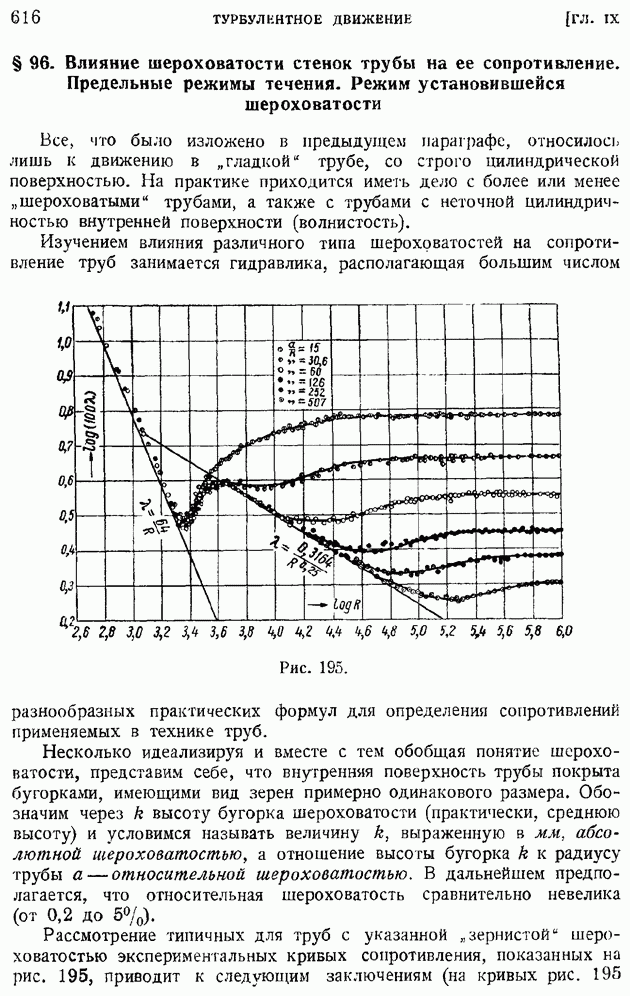
- § 96. Влияние шероховатости стенок трубы на ее сопротивление. Предельные режимы течения. Режим установившейся шероховатости
- § 97. Турбулентный пограничный слой на продольно обтекаемой пластине. Сопротивление пластины
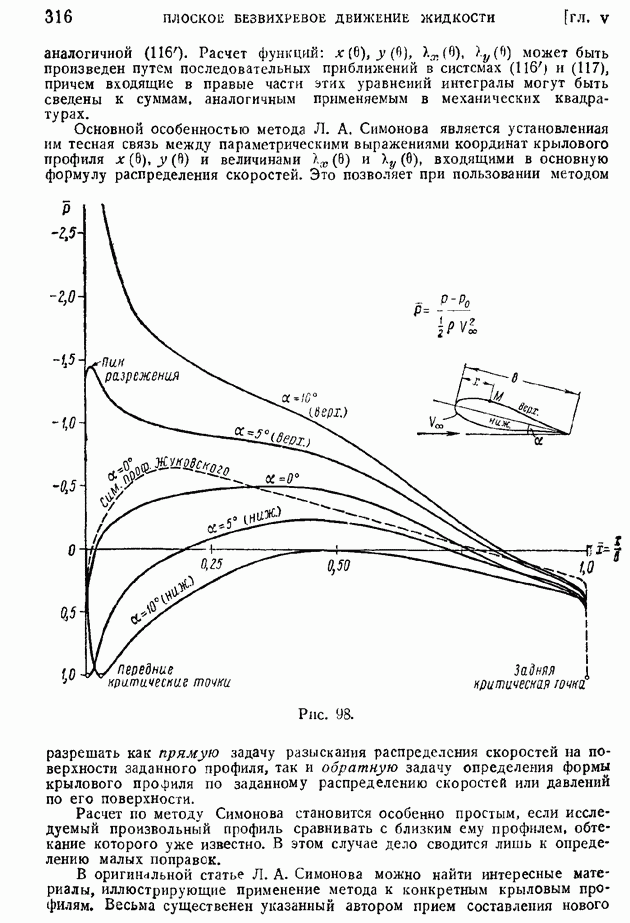
- § 98. Турбулентный пограничный слой на крыловом профиле при малом продольном перепаде давлений
- § 99. Турбулентный пограничный слой на крыловом профиле при значительных продольных перепадах давления
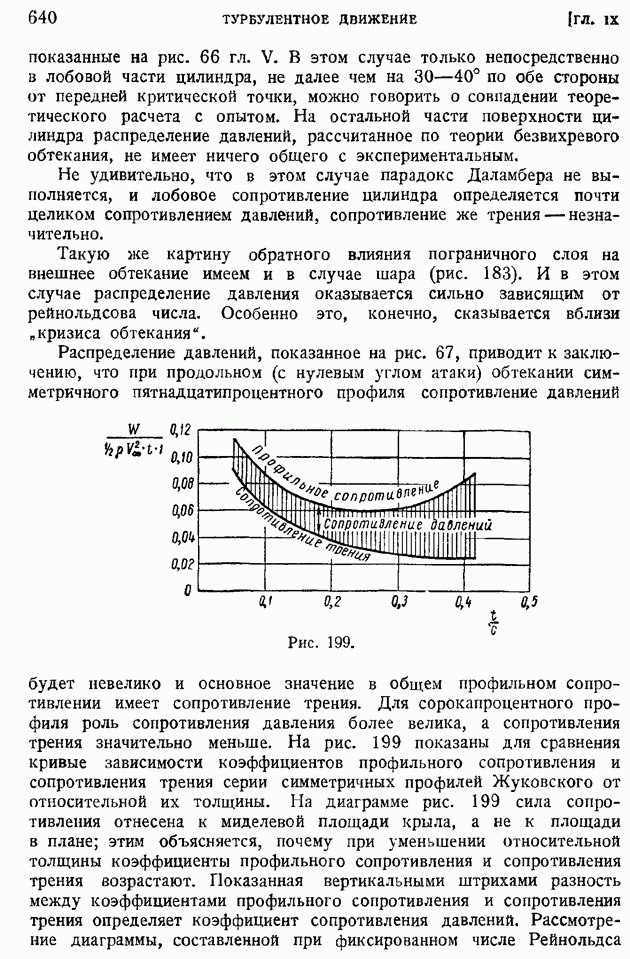
- § 100. Профильное сопротивление крыла. Разложение профильного сопротивления на сопротивление трения и сопротивление давлений. Обратное влияние пограничного слоя на распределение давлений по поверхности обтекаемого профиля
- § 101. Приближенные формулы профильного сопротивления крыла и крылового профиля в решетке
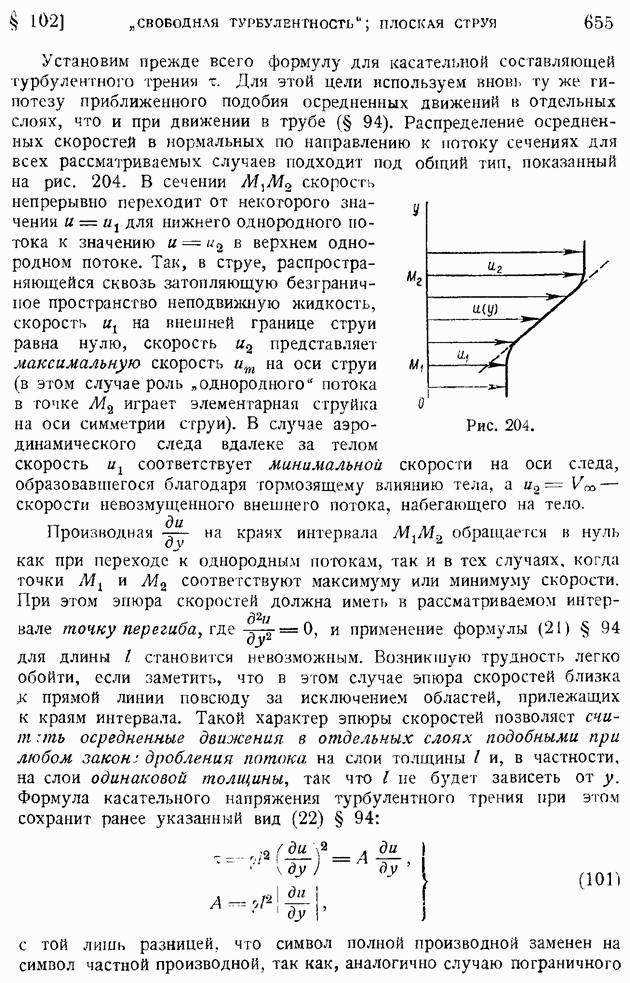
- § 102. Основные закономерности «свободной турбулентности». Плоская турбулентная струя в пространстве, заполненном той же жидкостью
- § 103. Турбулентный след за обтекаемым телом
- § 104. Рассеяние турбулентных возмущений в жидкости. Случай изотропной и однородной турбулентности. Закон сохранения момента возмущений