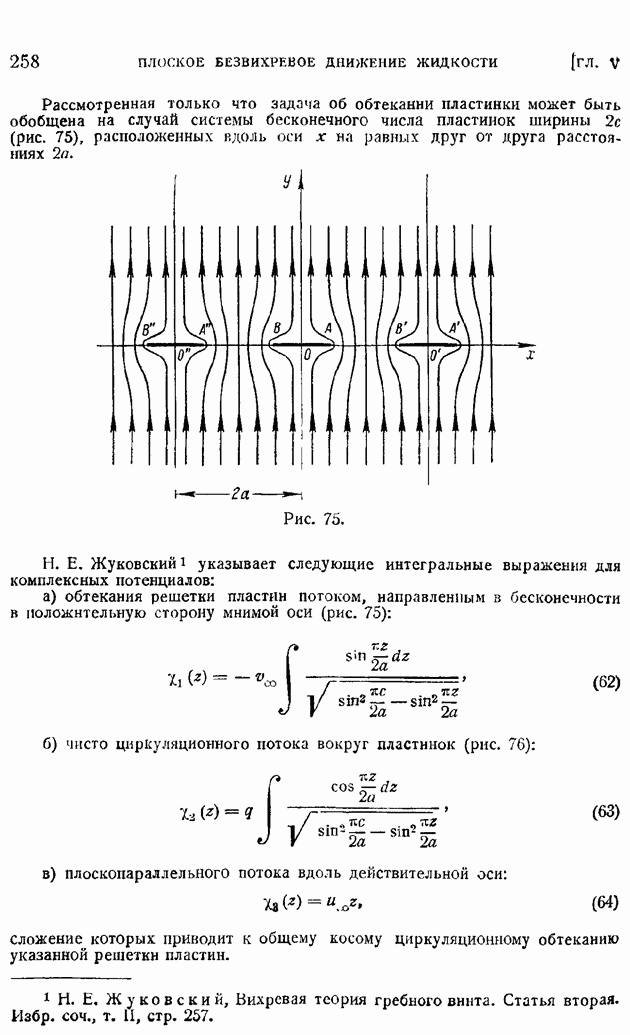
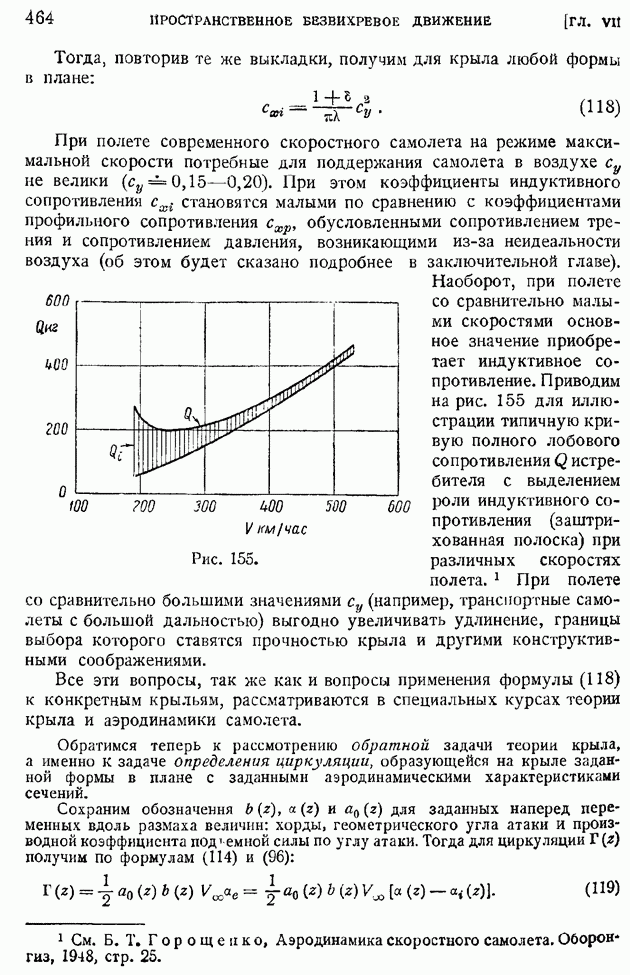
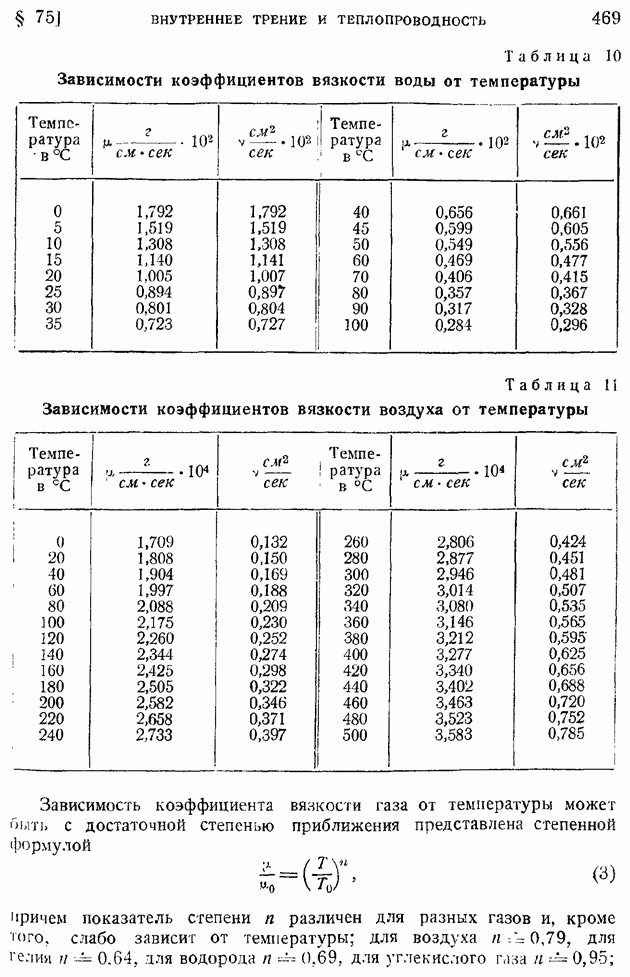
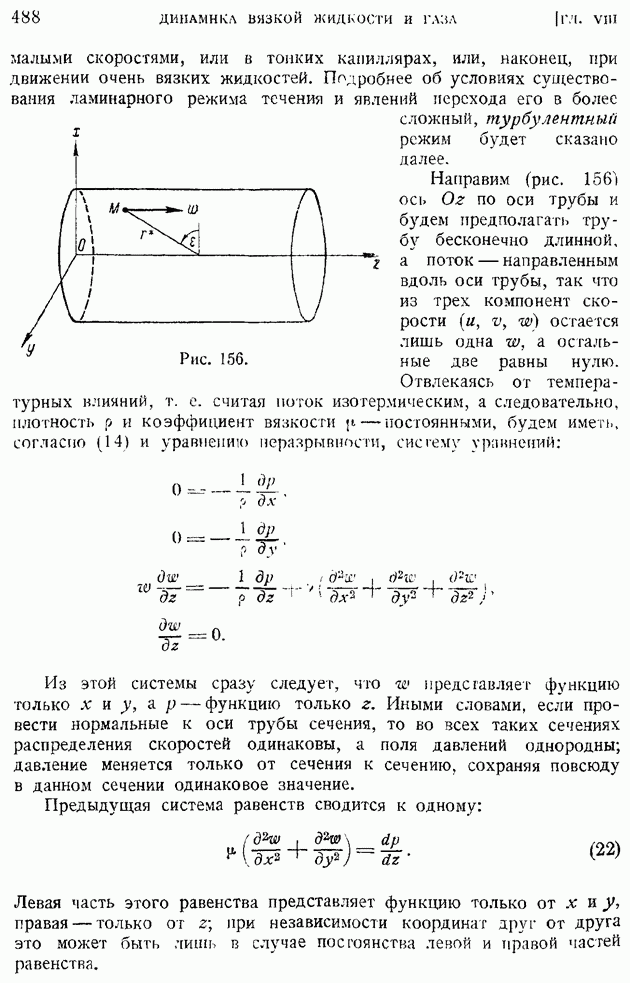
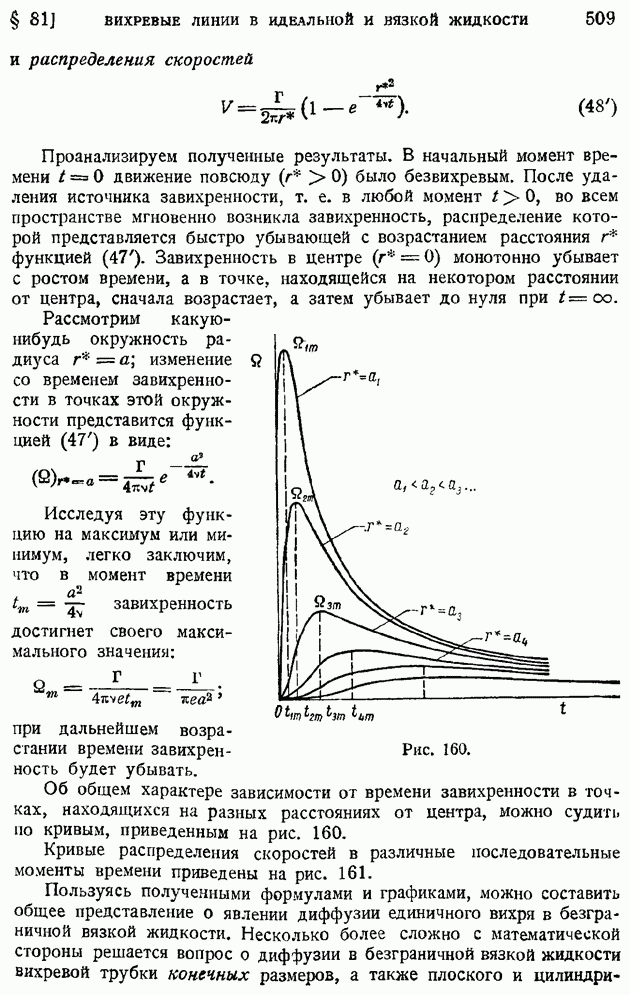
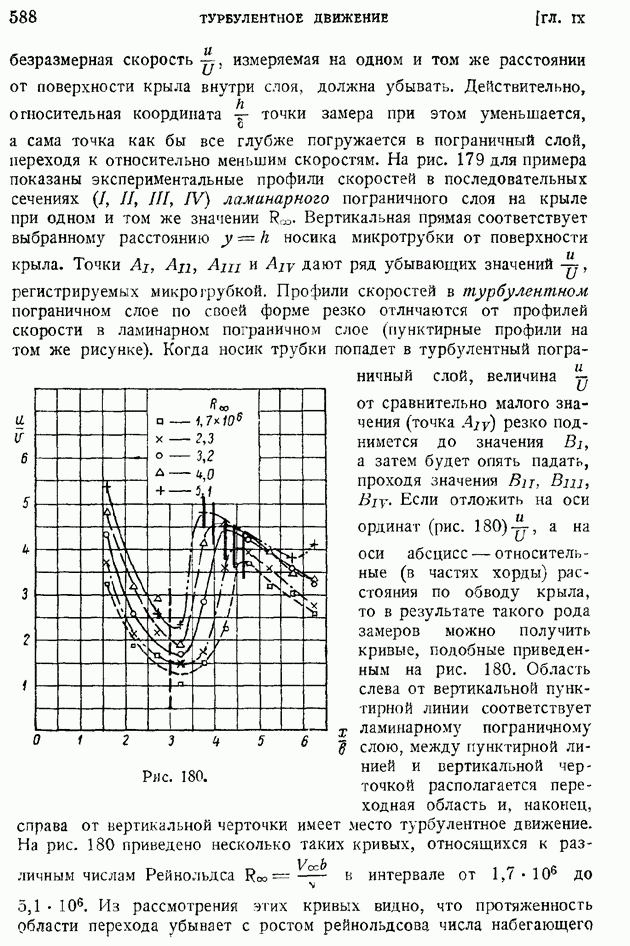
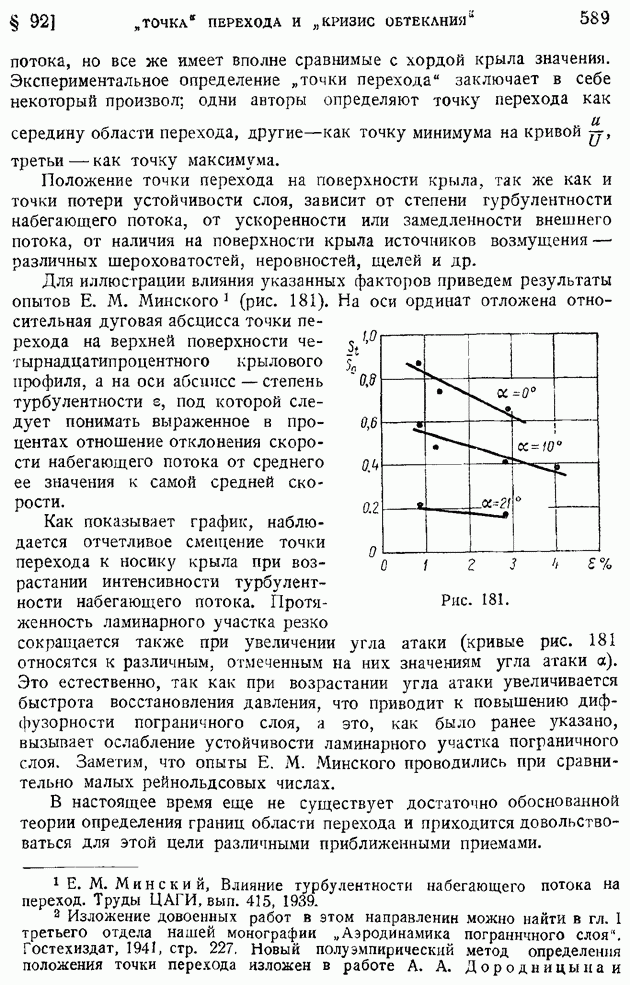
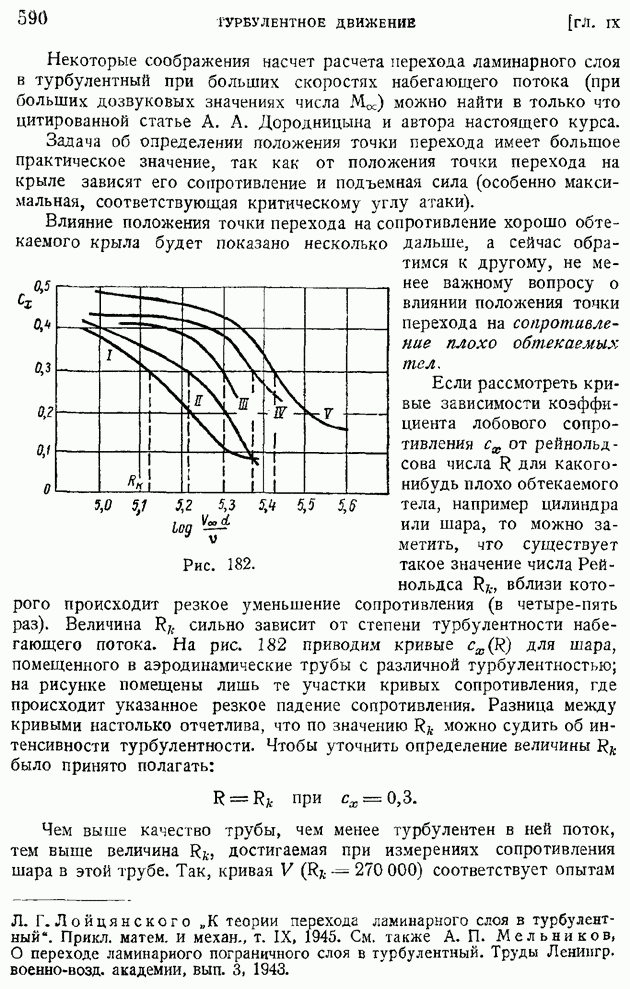
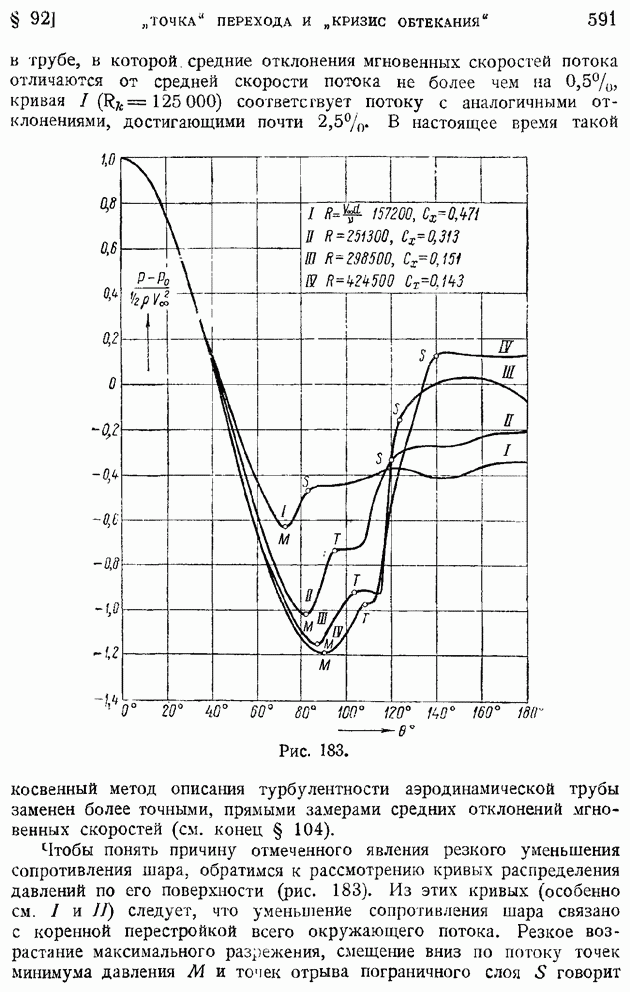
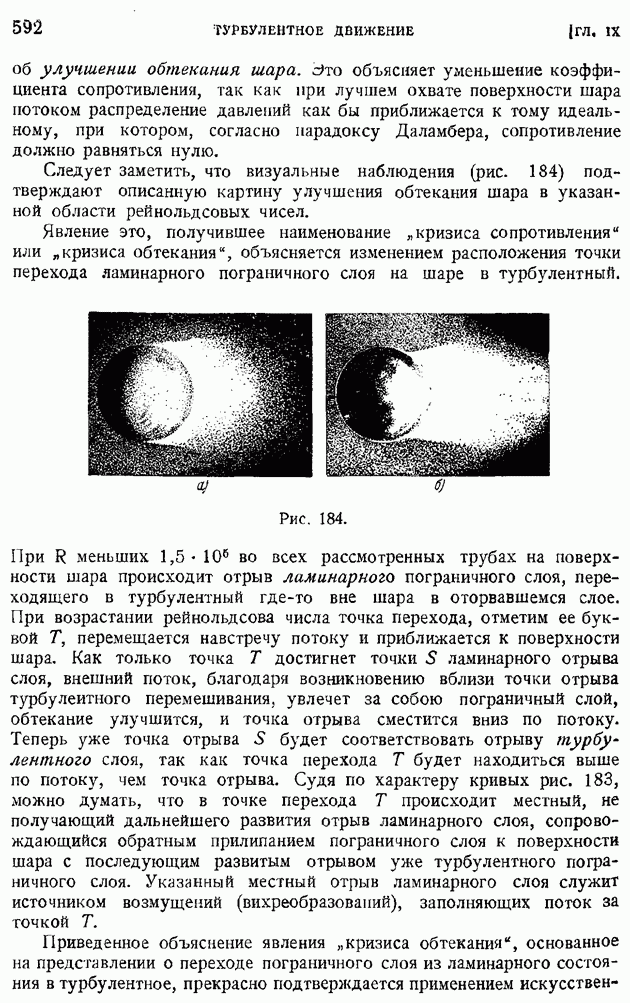
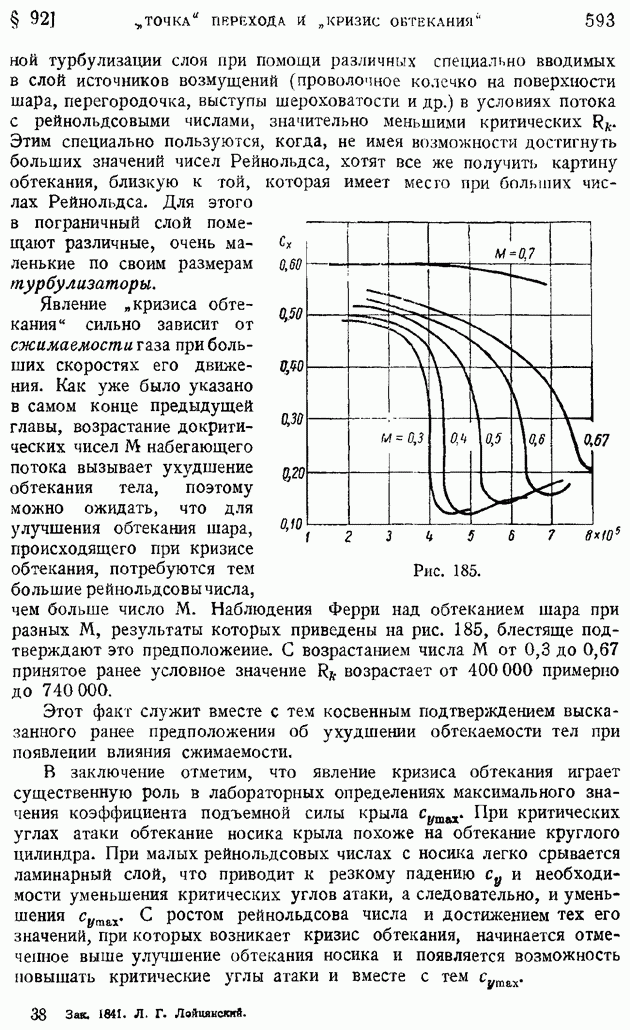
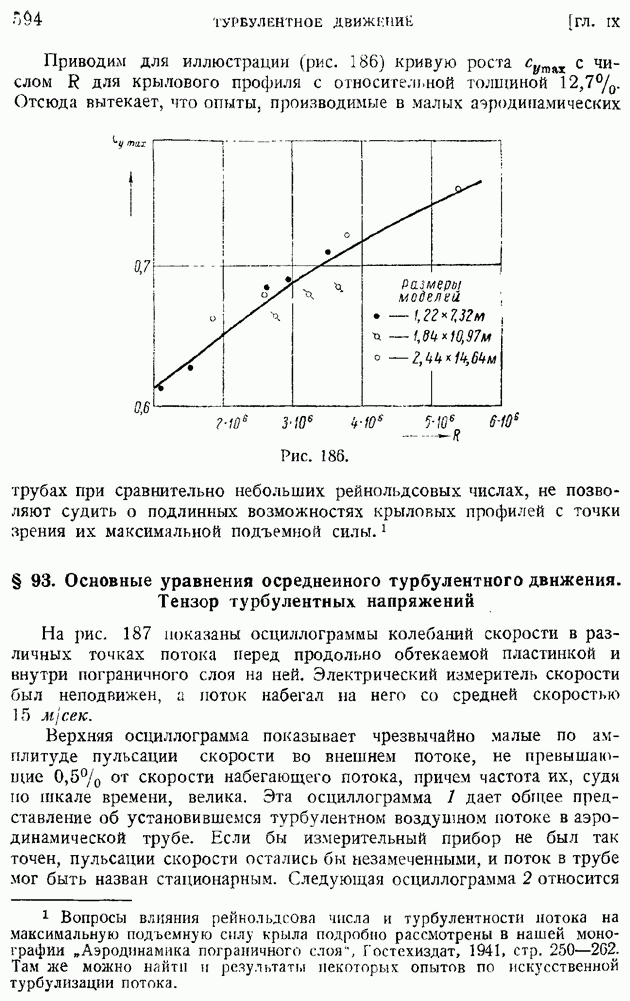
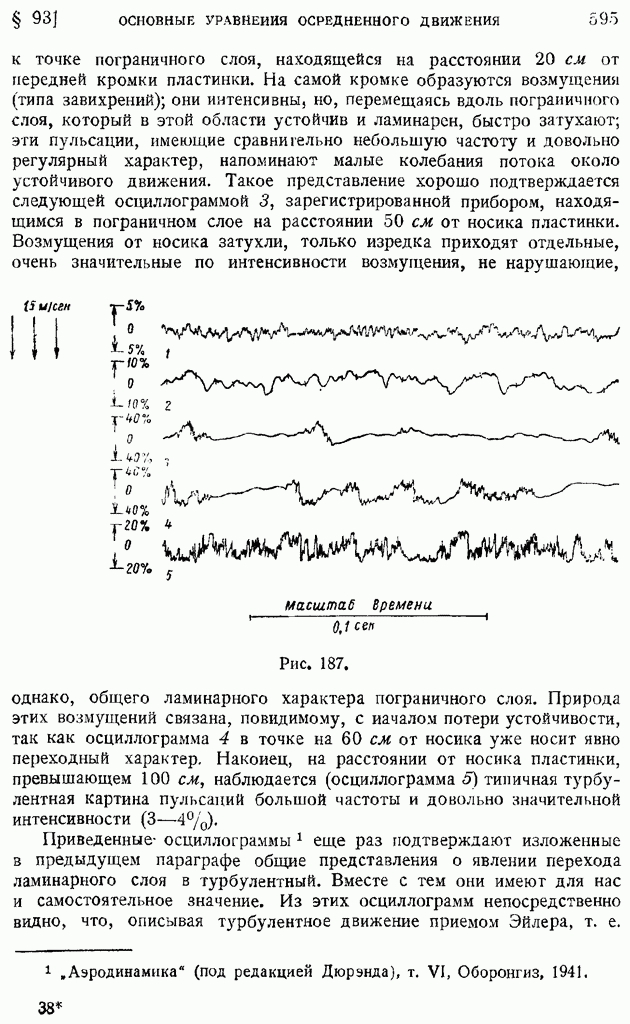
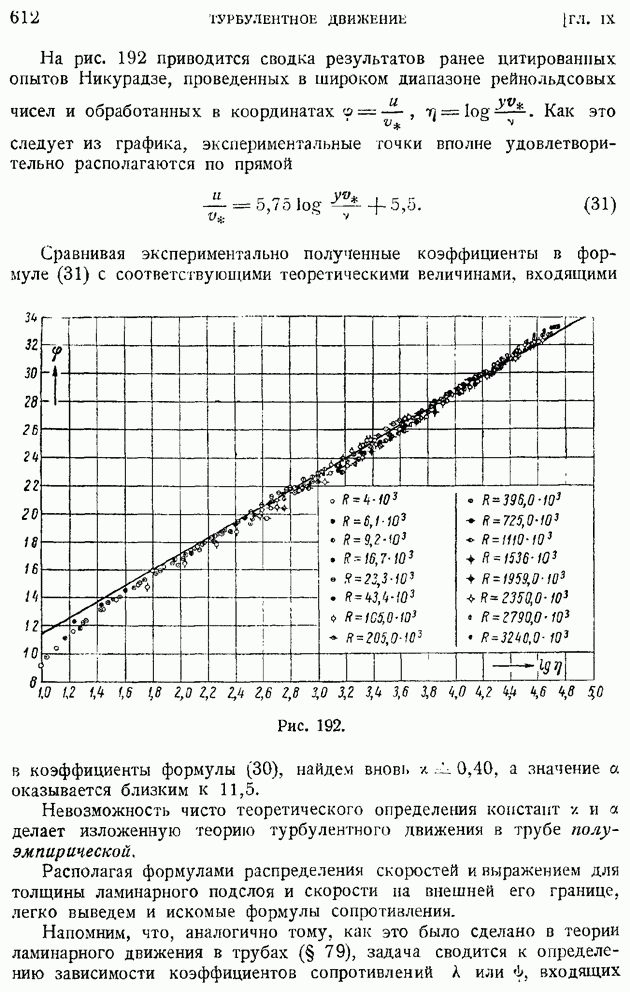
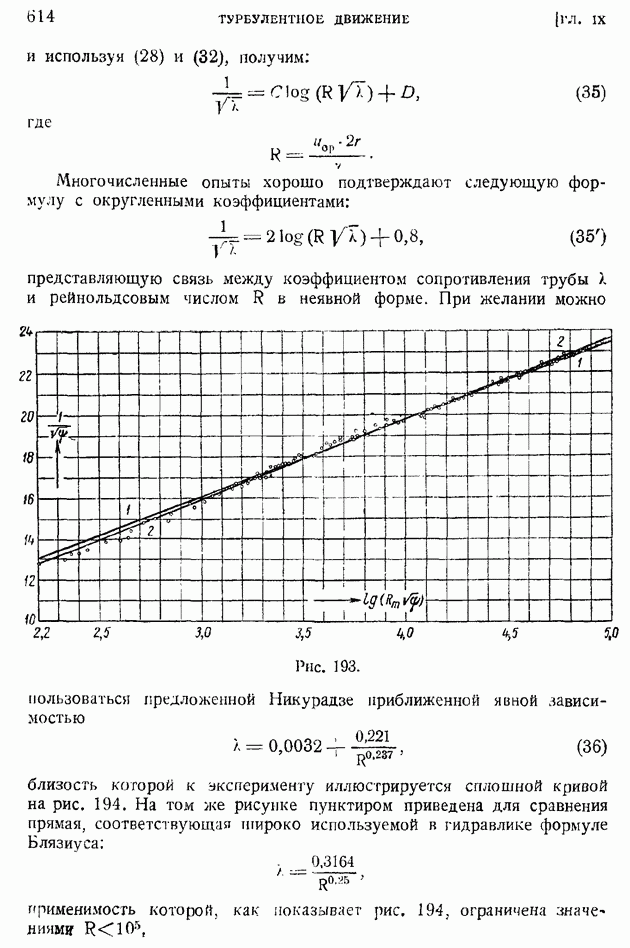
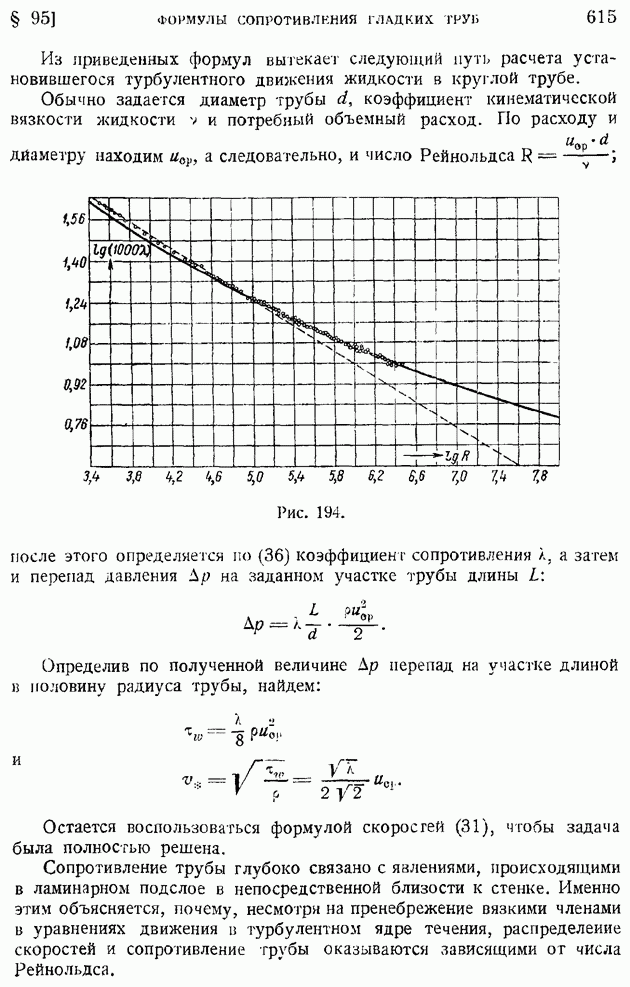
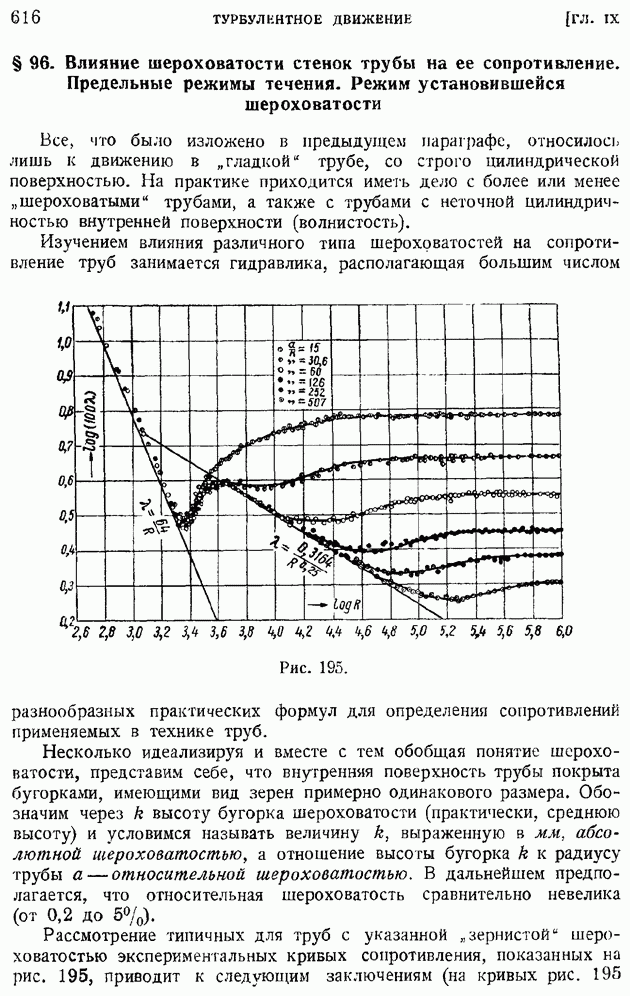
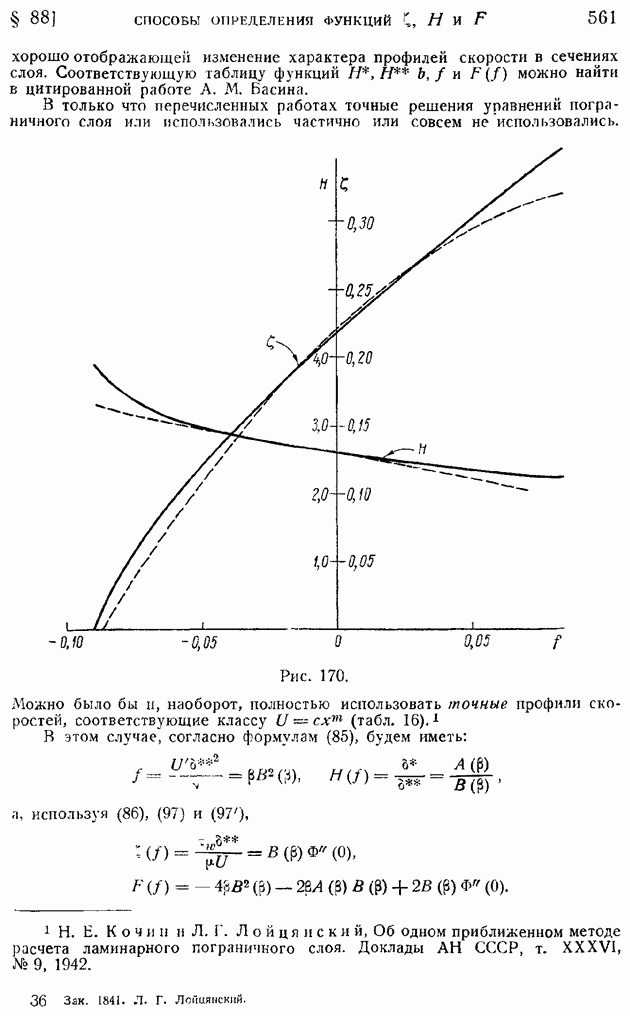| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
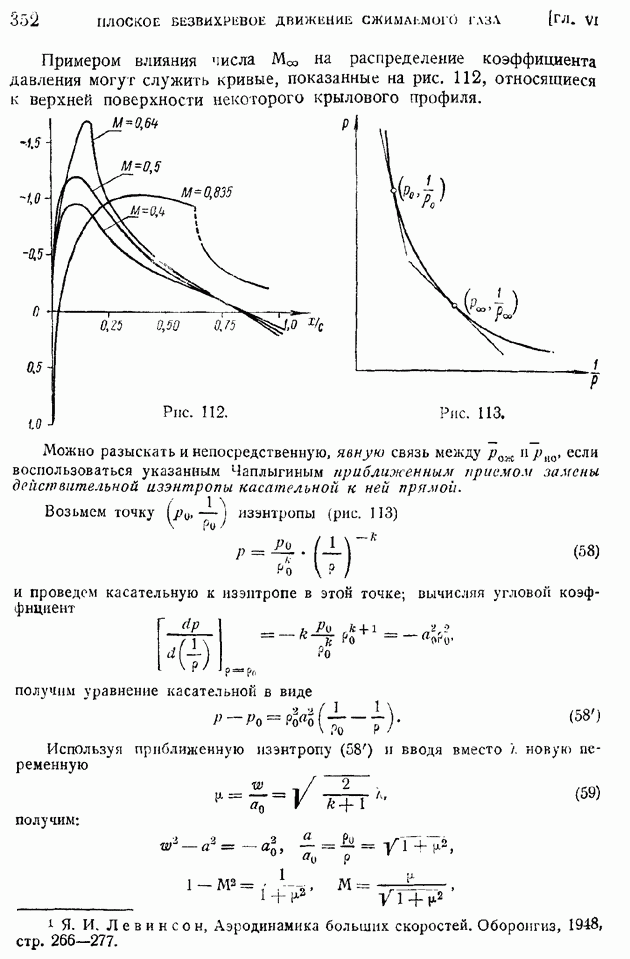
§ 39. Бесциркуляционное и циркуляционное обтекания круглого цилиндра
Наложим плоский, параллельный оси х однородный поток со скоростью  действительная положительная величина) и комплексным потенциалом
действительная положительная величина) и комплексным потенциалом

на скоростное поле диполя с комплексным потенциалом

и составим комплексный потенциал сложного движения

Чтобы найти уравнение семейства линий тока, составим функцию тока

Полагая правую часть равной различным постоянным, найдем уравнение линий тока

Нулевая линия тока

распадается на две кривые: 1) окружность:

и 2) ось х:

Выбирая произвольную до сих пор величину момента диполя равной

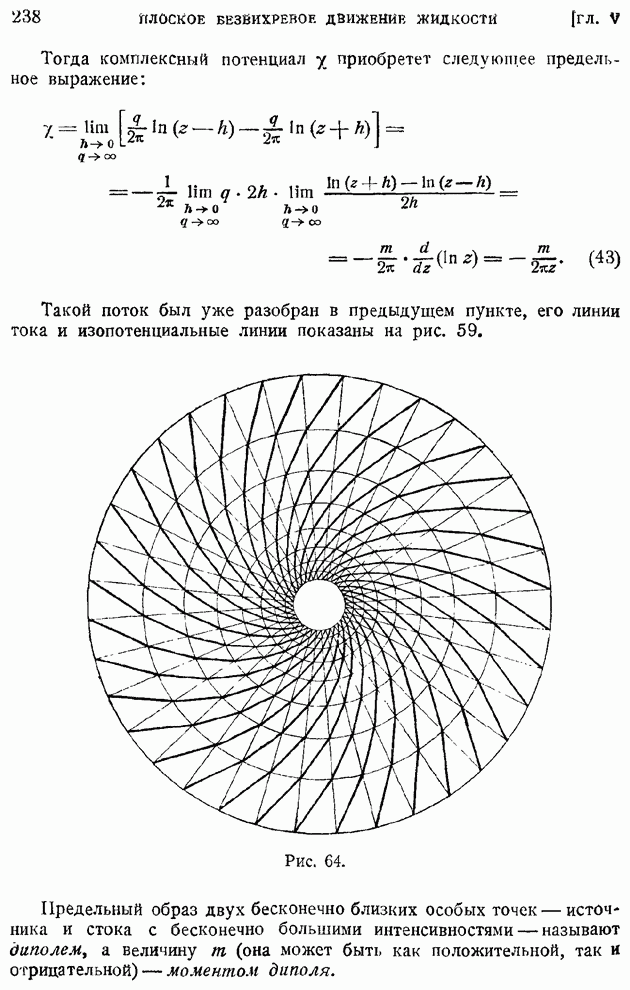
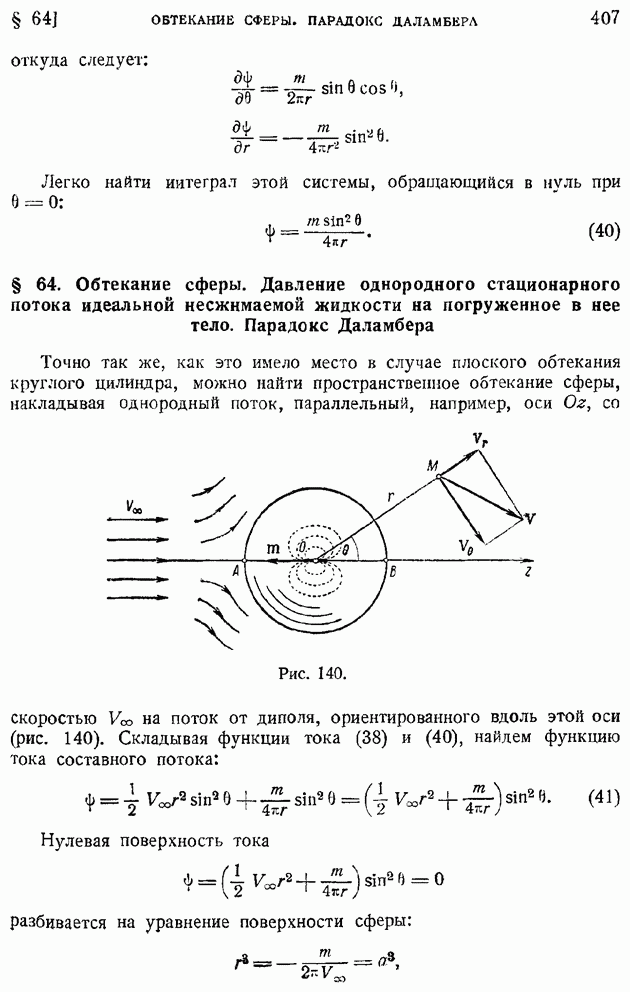
получим нулевую линию тока в виде совокупности окружности Радиуса а с центром в начале координат и оси  (рис. 65). стальные линии тока легко получить, задавая различные значения констант в уравнении
(рис. 65). стальные линии тока легко получить, задавая различные значения констант в уравнении

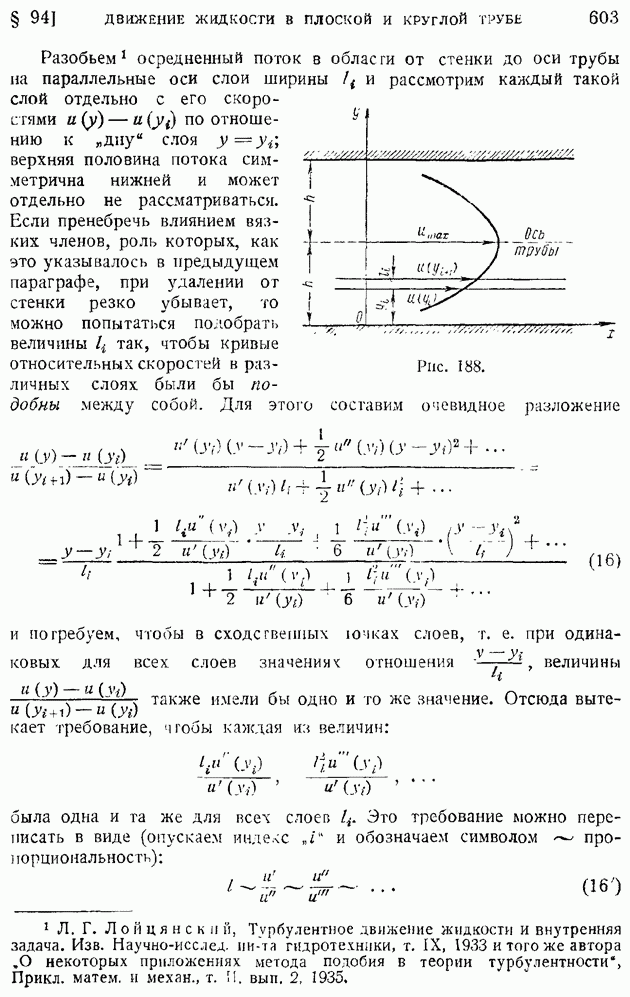
Полная картина движения состоит из двух областей — вне и внутри круга. Первую область можно рассматривать как обтекание круглого цилиндра радиуса а плоскопараллельным потоком, имеющим на бесконечности скорость этот поток имеет комплексный потенциал

Вторая область представляет картину течения, образуемого находящимся в начале координат диполем с моментом  внутри круга радиуса а; этому потоку соответствует комплексный потенциал
внутри круга радиуса а; этому потоку соответствует комплексный потенциал

Остановимся несколько подробнее на первом потоке. Найдем распределение скоростей. Имеем, по предыдущему:

По этой формуле можно найти сопряженную скорость V, а следовательно, и комплексный вектор скорости V в любой точке потока с комплексной координатой 

Рис. 65.
Определим, например, распределение скоростей по контуру обтекаемого цилиндра. Для этого положим — угол между радиусом контура цилиндра и осью 

и будем иметь по предыдущей формуле:

откуда определим модуль скорости на контуре круга

Из этой формулы следует, что при плоском безвихревом обтекании круглого цилиндра идеальной жидкостью скорости на его поверхности распределяются по закону синуса. В точках  разветвления потока
разветвления потока  скорость обращается в нуль. Точки потока, где скорость движения обращается в нуль, называют критическими точками потока. При направлении движения, указанном на рис. 65, точка А называется "передней" критической точкой, точка В — "задней".
скорость обращается в нуль. Точки потока, где скорость движения обращается в нуль, называют критическими точками потока. При направлении движения, указанном на рис. 65, точка А называется "передней" критической точкой, точка В — "задней".
Скорость на поверхности цилиндра принимает свое максимальное значение при в точках  миделееого сечения цилиндра; это максимальное значение скорости равно
миделееого сечения цилиндра; это максимальное значение скорости равно

т. е. удвоенной скорости набегающего потока (скорости на бесконечности).
Иногда приходится иметь дело с обтеканием цилиндра плоскопараллельным потоком, скорость которого  направлена под некоторым углом
направлена под некоторым углом  к оси
к оси 
Заметим, что в этом более общем случае комплексный потенциал обтекания будет иметь вид:

где Ко является уже не действительной величиной, а комплексным вектором, равным

Выражение комплексного потенциала (46) легко получить из равенства (44), если ввести в рассмотрение дополнительную плоскость  действительная ось которой наклонена к действительной оси плоскости
действительная ось которой наклонена к действительной оси плоскости  под углом Тогда в плоскости z скорость на бесконечности будет представляться действительной величиной
под углом Тогда в плоскости z скорость на бесконечности будет представляться действительной величиной  и но (44) получим:
и но (44) получим:

Подставляя сюда выражение  через
через 

докажем правильность формулы (46):

Обратимся теперь к рассмотрению соответствующего формуле (45) распределения давлений по контуру цилиндра. Для этого вспомним, что при безвихревом движении несжимаемой жидкости давление  связано с величиной скорости
связано с величиной скорости  формулой Бернулли [§ 36, равенство (12)]:
формулой Бернулли [§ 36, равенство (12)]:

Константу определим из условия на бесконечности [возвращаемся к обозначению 

тогда будем иметь, вводя безразмерный коэффициент давления 

Из формулы (47) следует, что распределение по контуру цилиндра безразмерного коэффициента давления  не зависит ни от размеров цилиндра, ни от величины скорости и давления на бесконечности. Вот почему так удобно пользоваться этим коэффициентом при изучении давления потока на поверхности обтекаемого жидкостью цилиндра. В дальнейшем будет показано, как эти свойства коэффициента давления распространяются и на тела других форм.
не зависит ни от размеров цилиндра, ни от величины скорости и давления на бесконечности. Вот почему так удобно пользоваться этим коэффициентом при изучении давления потока на поверхности обтекаемого жидкостью цилиндра. В дальнейшем будет показано, как эти свойства коэффициента давления распространяются и на тела других форм.
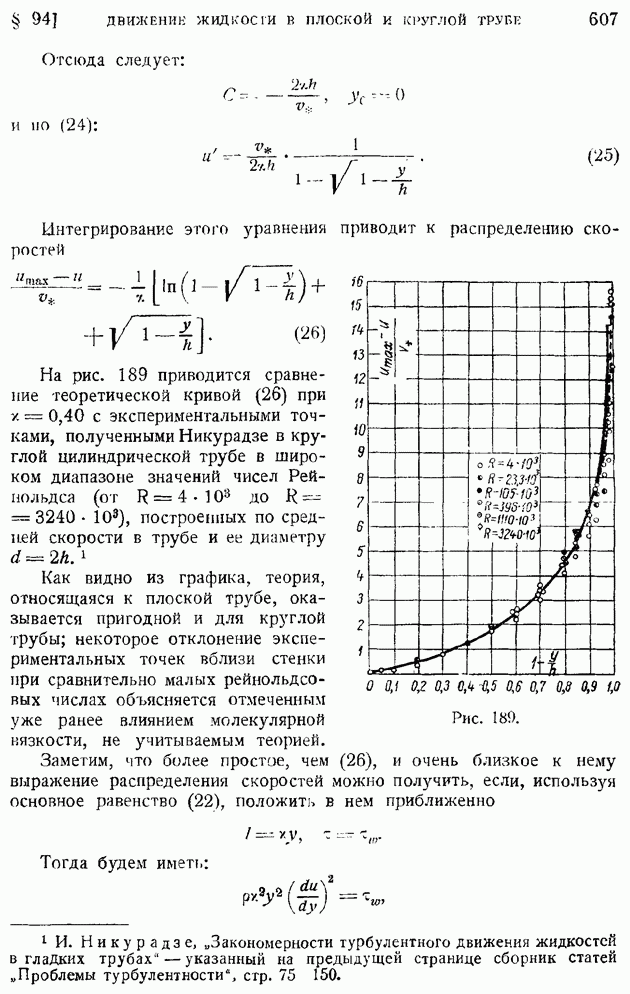
Вернемся к формуле (47) и условимся угол  отсчитывать от передней критической точки А против часовой стрелки. Тогда график теоретического распределения
отсчитывать от передней критической точки А против часовой стрелки. Тогда график теоретического распределения  согласно (47), представится нижней кривой на рис. 66. В лобовой критической точке
согласно (47), представится нижней кривой на рис. 66. В лобовой критической точке  имеем
имеем  ; размерное давление
; размерное давление  в этой точке равно полному напору набегающего потока, т. е. сумме давления
в этой точке равно полному напору набегающего потока, т. е. сумме давления  и скоростного напора
и скоростного напора  набегающего потока. При
набегающего потока. При  т. е. в миделевой плоскости, коэффициент
т. е. в миделевой плоскости, коэффициент  приобретает максимальное по абсолютной величине отрицательное значение
приобретает максимальное по абсолютной величине отрицательное значение  В этих точках на поверхности цилиндра наблюдается максимальное разрежение. Давление здесь меньше чем
В этих точках на поверхности цилиндра наблюдается максимальное разрежение. Давление здесь меньше чем  (например, атмосферное при продувке цилиндра в аэродинамической трубе с открытой рабочей частью) на три скоростных напора. На участке
(например, атмосферное при продувке цилиндра в аэродинамической трубе с открытой рабочей частью) на три скоростных напора. На участке  теоретическая кривая повторяет кривую для
теоретическая кривая повторяет кривую для 
Экспериментально замеренное распределение давления не подтверждает эту теоретическую кривую. В зависимости от некоторых условий, о которых будет идти речь в конце курса, на опыте получаются две разных формы кривых распределения давления  и II на рис. 66), но даже и более близкая к теоретической кривая I
и II на рис. 66), но даже и более близкая к теоретической кривая I
нее же находится в резком расхождении с теорией. Причиной этого расхождения служит отсутствие в действительности безотрывного плавного обтекания цилиндра, подобного теоретическому обтеканию, показанному на рис. 65. На самом деле цилиндр представляет собою плохо обтекаемое тело. Набегающий поток, разветвившись в передней критической точке А (рис. 66), омывает поверхность цилиндра лишь до точек  находящихся примерно на
находящихся примерно на  до миделевой плоскости — в случае кривой давлении
до миделевой плоскости — в случае кривой давлении  и на
и на  в случае
в случае  после чего поток отрывается, уступая место жидкости, подсасывающейся из кормовой области.
после чего поток отрывается, уступая место жидкости, подсасывающейся из кормовой области.

Рис. 66.
И в том и в другом случае получаются картины обтекания, далекие от безотрывного обтекания всей поверхности от передней А до задней В критических точек, предписываемого теорией безвихревого движения идеальной жидкости.
Как будет показано в дальнейшем, образовавшийся из-за наличия внутреннего трения в жидкости пограничный слой не выдерживает резкого восстановления давления при  отрывается и искажает всю картину обтекания. Об этом подробно будет рассказано в главе о движении вязкой жидкости.
отрывается и искажает всю картину обтекания. Об этом подробно будет рассказано в главе о движении вязкой жидкости.
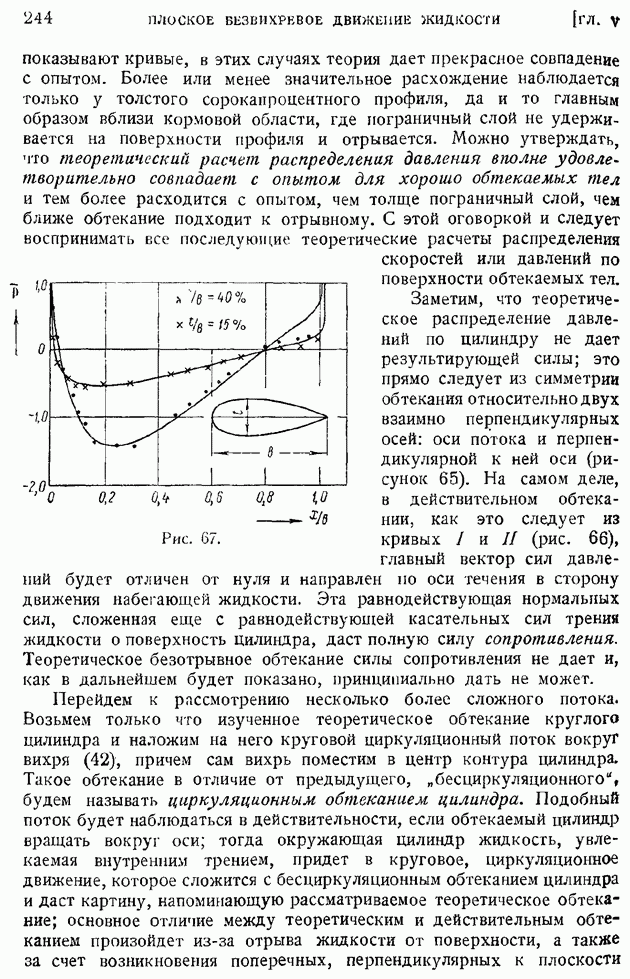
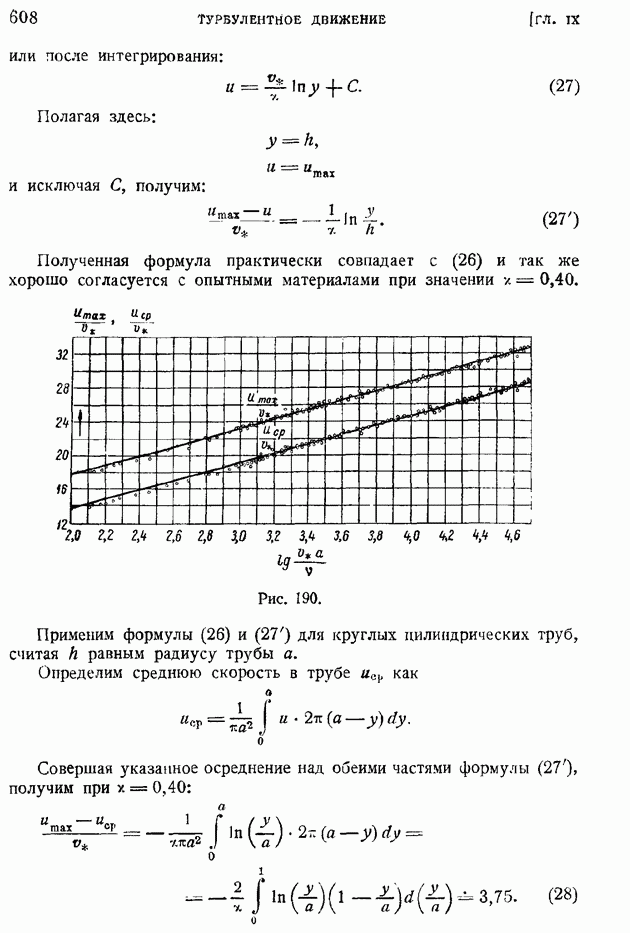
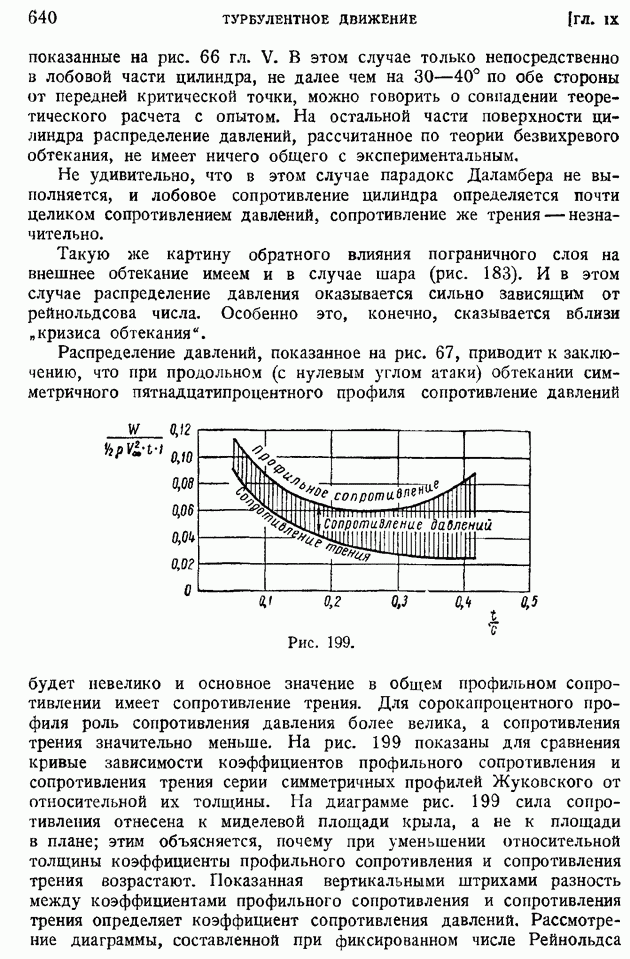
Выло бы, однако, неправильно сделать отсюда вынод, что теория безвихревого движения идеальной жидкости вообще не может применяться для описания действительных обтеканий. На рис. 67 приведены кривые распределения давления по поверхности двух "хорошо обтекаемых" симметричных профилей Жуковского. Один профиль имеет относительную толщину  другой
другой  Как
Как
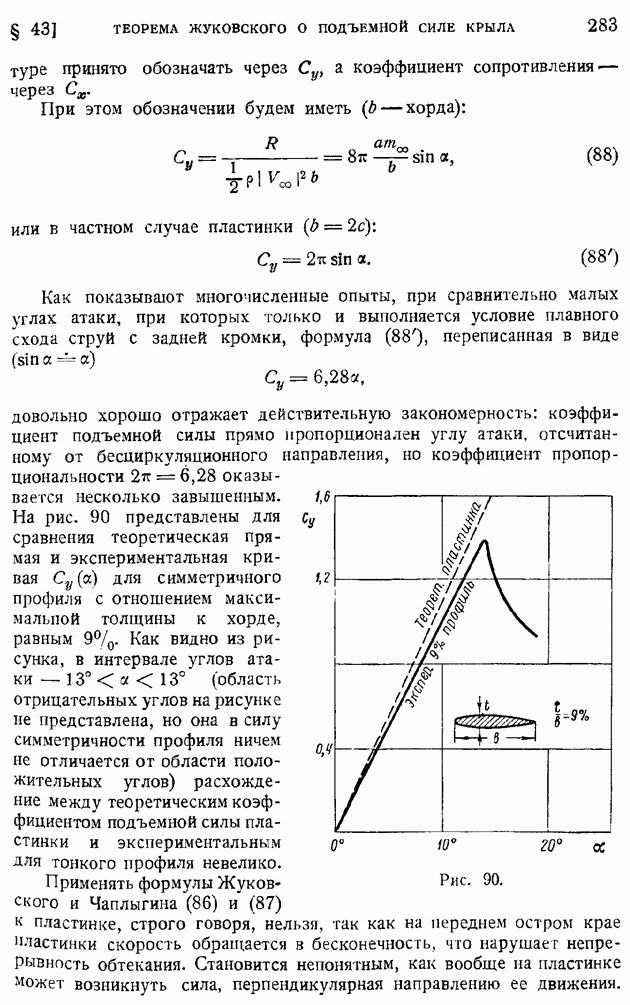
показывают кривые, в этих случаях теория дает прекрасное совпадение с опытом. Более или менее значительное расхождение наблюдается только у толстого сорокапроцентного профиля, да и то главным образом вблизи кормовой области, где пограничный слой не удерживается на поверхности профиля и отрывается. Можно утверждать, что теоретический расчет распределения давления вполне удовлетворительно совпадает с опытом для хорошо обтекаемых тел и тем более расходится с опытом, чем толще пограничный слой, чем ближе обтекание подходит к отрывному. С этой оговоркой и следует воспринимать все последующие теоретические расчеты распределения скоростей или давлений по поверхности обтекаемых тел.
Заметим, что теоретическое распределение давлений по цилиндру не дает результирующей силы; это прямо следует из симметрии обтекания относительно двух взаимно перпендикулярных осей: оси потока и перпендикулярной к ней оси (рисунок 65). На самом деле, в действительном обтекании, как это следует из кривых I и II (рис. 66), главный вектор сил давлений будет отличен от нуля и направлен по оси течения в сторону движения набегающей жидкости. Эта равнодействующая нормальных сил, сложенная еще с равнодействующей касательных сил трения жидкости о поверхность цилиндра, даст полную силу сопротивления. Теоретическое безотрывное обтекание силы сопротивления не дает и, как в дальнейшем будет показано, принципиально дать не может.

Рис. 67.
Перейдем к рассмотрению несколько более сложного потока. Возьмем только что изученное теоретическое обтекание круглого цилиндра и наложим на него круговой циркуляционный поток вокруг вихря (42), причем сам вихрь поместим в центр контура цилиндра. Такое обтекание в отличие от предыдущего, "бесциркуляционного", будем называть циркуляционным обтеканием цилиндра. Подобный поток будет наблюдаться в действительности, если обтекаемый цилиндр вращать вокруг оси; тогда окружающая цилиндр жидкость, увлекаемая внутренним трением, придет в круговое, циркуляционное движение, которое сложится с бесциркуляционным обтеканием цилиндра и даст картину, напоминающую рассматриваемое теоретическое обтекание; основное отличие между теоретическим и действительным обтеканием произойдет из-за отрыва жидкости от поверхности, а также за счет возникновения поперечных, перпендикулярных к плоскости
теоретического течения вторичных потоков, сопровождающих в действительности циркуляционное течение.
Комплексный потенциал циркуляционного обтекания цилиндра напишем в виде

что при  соответствует направлению циркуляционного движения по часовой стрелке.
соответствует направлению циркуляционного движения по часовой стрелке.
Определим сопряженную скорость

и найдем положение критических точек, решая уравнение

или, что то же, квадратное уравнение

Корни его будут:

В зависимости от величины циркуляции возможны три типа обтекания:
1°. Циркуляция достаточно велика, а именно

В этом случае под знаком радикала будет стоять отрицательная величина, и можно написать

Оба корня квадратного уравнения мнимы, причем модуль одного больше радиуса цилиндра, другого — меньше; действительно, корень

имеет модуль

второй корень

имеет модуль

меньший чем выражение, которое получим справа, если заменим в знаменателе  на меньшую величину а, т. е.
на меньшую величину а, т. е.

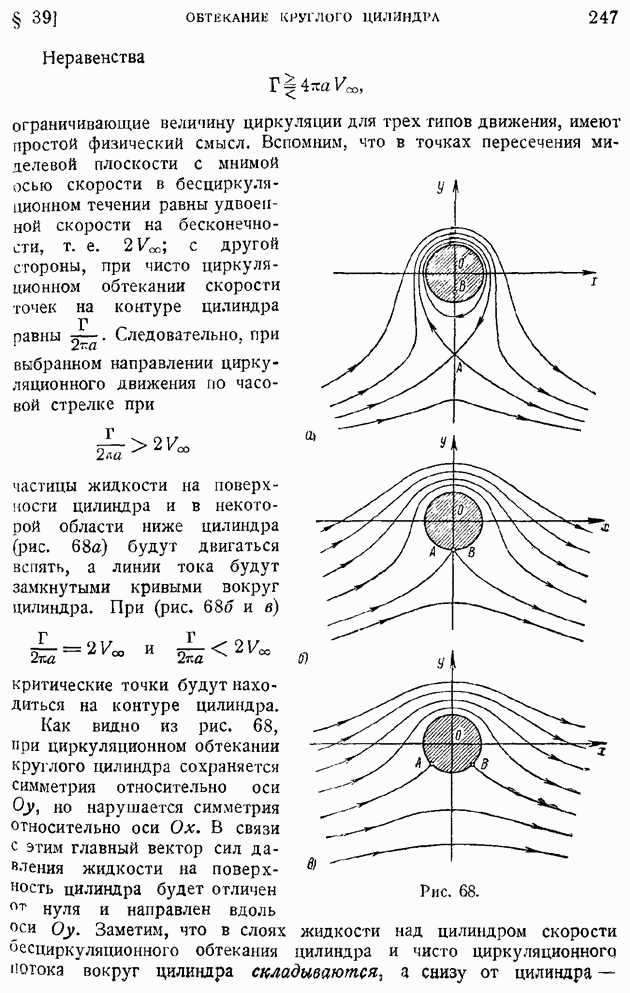
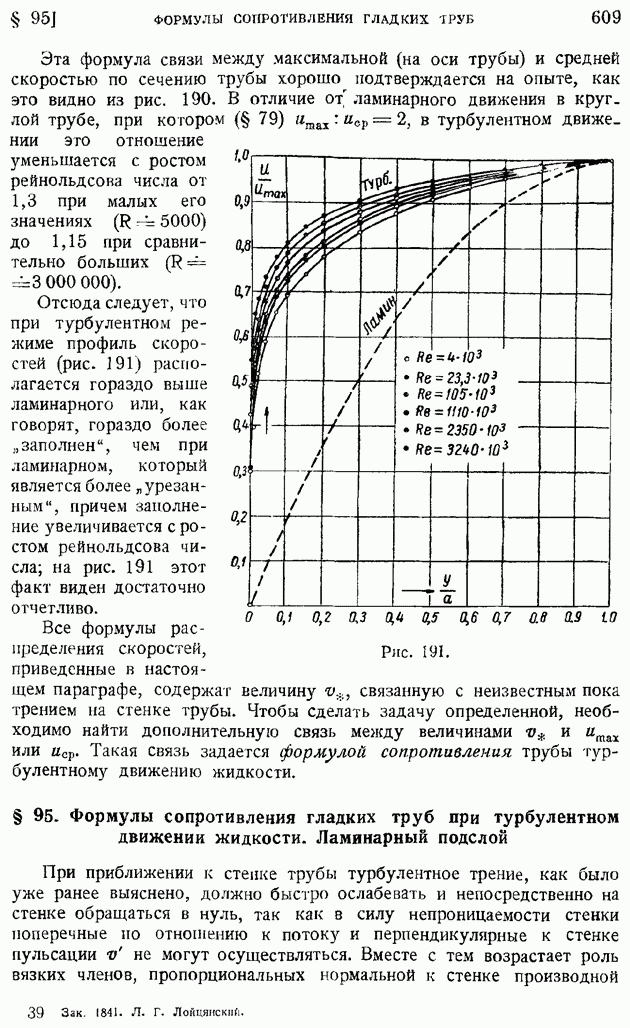
Первый корень  дает критическую точку А (рис. 68а), лежащую на отрицательной стороне мнимой оси вне цилиндра, второй — критическую точку В, лежащую на той же оси внутри цилиндра.
дает критическую точку А (рис. 68а), лежащую на отрицательной стороне мнимой оси вне цилиндра, второй — критическую точку В, лежащую на той же оси внутри цилиндра.
2°. Предельный случай

дает двойной корень

в этом случае обе критические точки  попадают в одну, расположенную на контуре цилиндра в точке пересечения контура с мнимой осью (рис. 686).
попадают в одну, расположенную на контуре цилиндра в точке пересечения контура с мнимой осью (рис. 686).
3°. Наконец, в случае малой циркуляции

комплексные корни

имеют общую ординату — мнимую часть:

и отличающиеся знаками абсциссы:

также по модулю меньшие а.
Положение критических точек  показано на рис. 68в. При дальнейшем уменьшении циркуляции
показано на рис. 68в. При дальнейшем уменьшении циркуляции  точки
точки  будут раздвигаться, стремясь занять свои предельные положения на диаметре круга при
будут раздвигаться, стремясь занять свои предельные положения на диаметре круга при 
Неравенства

ограничивающие величину циркуляции для трех типов движения, имеют простой физический смысл. Вспомним, что в точках пересечения миделевой плоскости с мнимой осью скорости в бесциркуляционном течении равны удвоенной скорости на бесконечности, т. е.  с другой стороны, при чисто циркуляционном обтекании скорости точек на контуре цилиндра равны
с другой стороны, при чисто циркуляционном обтекании скорости точек на контуре цилиндра равны  Следовательно, при
Следовательно, при  выбранном направлении циркуляционного движения по часовой стрелке при
выбранном направлении циркуляционного движения по часовой стрелке при

частицы жидкости на поверхности цилиндра и в некоторой области ниже цилиндра (рис. 68а) будут двигаться вспять, а линии тока будут замкнутыми кривыми вокруг цилиндра. При (рис. 686 и в)

критические точки будут находиться на контуре цилиндра.

Рис. 68.
Как видно из рис. 68, при циркуляционном обтекании круглого цилиндра сохраняется симметрия относительно оси  но нарушается симметрия относительно оси
но нарушается симметрия относительно оси  В связи с этим главный вектор сил давления жидкости на поверхность цилиндра будет отличен
В связи с этим главный вектор сил давления жидкости на поверхность цилиндра будет отличен  нуля и направлен вдоль оси
нуля и направлен вдоль оси  Заметим, что в слоях жидкости над цилиндром скорости бесциркуляционного обтекания цилиндра и чисто циркуляционного потока вокруг цилиндра складываются, а снизу от цилиндра —
Заметим, что в слоях жидкости над цилиндром скорости бесциркуляционного обтекания цилиндра и чисто циркуляционного потока вокруг цилиндра складываются, а снизу от цилиндра —
вычитаются. Отсюда следует, что над цилиндром скорости больше чем снизу; это видно и по плотности линий тока — над цилиндром линии тока сгущаются, под цилиндром, наоборот, разрежаются. При этом, согласно теореме Бернулли, давление на верхней половине цилиндра меньше, на нижней — больше, следовательно, главный вектор сил давления должен быть направлен по оси  вверх. Найдем величину этой, перпендикулярной к направлению движения силы
вверх. Найдем величину этой, перпендикулярной к направлению движения силы  Имеем
Имеем

где контурный интеграл вычисляется по положительному обходу окружности. По теореме Бернулли

На контуре круга, согласно (49):

откуда

Замечая, что интеграл по замкнутому контуру от постоянной составляющей давления С, как архимедова сила в однородном поле давлений, равен нулю, получим:

Интегралы легко вычисляются; имеем:

Из всех интегралов отличен от нуля лишь второй в выражении  так что:
так что:

Как и в случае бесциркуляционного обтекания цилиндра, при циркуляционном обтекании сопротивления нет  но зато появилась поперечная сила
но зато появилась поперечная сила  равная, по (50), произведению плотности жидкости на скорость набегающего потока и на циркуляцию. Формула (50) является частным случаем общей теоремы Жуковского, относящейся к любому обтекаемому контуру; доказательство этой теоремы будет дано ниже.
равная, по (50), произведению плотности жидкости на скорость набегающего потока и на циркуляцию. Формула (50) является частным случаем общей теоремы Жуковского, относящейся к любому обтекаемому контуру; доказательство этой теоремы будет дано ниже.
Возникновение поперечной силы при обтекании вращающегося артиллерийского снаряда набегающим воздухом было обнаружено еще в середине XVIII в.
Роторы Флетнера, представляющие собою вращающиеся цилиндрические башни, размещенные на палубе корабля, создают при наличии набегающего ветра перпендикулярную к направлению ветра силу, движущую корабль. Аналогичный эффект наблюдается на закрученных теннисных и футбольных мячах и во многих других случаях.
Как будет показано в дальнейшем, задача о циркуляционном обтекании круглого цилиндра имеет основное значение. К этой задаче будут сводиться все остальные случаи обтекания замкнутых контуров и, в частности, задача об обтекании крыла.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Предмет механики жидкости и газа. Основные свойства «макромодели» жидкости и газа: сплошность и подвижность
- § 2. Основные методы механики жидкости и газа. Области применения и главнейшие задачи
- § 3. Краткий очерк исторического развития механики жидкости и газа. От гидромеханики древних до установления воззрений ньютонианской эпохи
- § 4. Эпоха Эйлера и Бернулли. Гидроаэродинамика в XIX в.
- § 5. Современный этап развития механики жидкости и газа
- ГЛАВА I. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
- § 6. Поле физической величины. Скалярное и векторное поля. Поверхности уровня. Векторные линин и трубки
- § 7. Мера однородности поля в данном направлении и в дайной точке. Градиевт скалярного поля и дифференциальный тензор векторного поля как меры неоднородности поля
- § 8. Задание движения сплошной среды. Поле скоростей. Линии тока и траектории
- § 9. Поле ускорений. Разложение ускорения частицы на локальную и конвективную составляющие
- § 10. Скоростное поле сплошной среды в окрестности данной точки. Угловая скорость и вихрь. Тензор скоростей деформаций и его компоненты
- § 11. Скорость объемного расширения жидкости. Интегральные представления дифференциальных операторов поля. Основные интегральные формулы
- § 12. Вихревые линии и трубки. Вторая теорема Гельмгольца. Интенсивность вихревой трубки
- § 13. Выражение интенсивности вихревой трубки через циркуляцию вектора по контуру, охватывающему трубку. Теорема об изменении циркуляции скорости во времени
- ГЛАВА II. ОСНОВНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ И РАВНОВЕСИЯ СПЛОШНОЙ СРЕДЫ
- § 14. Распределение массы в сплошной среде. Плотность и удельный вес. Напряжения. Тензор напряженности и его симметричность
- § 15. Общие уравнения динамики сплошной среды. Уравнение неразрывности. Уравнения динамики в напряжениях
- § 16. Тепловые явления в жидкостях и газах. Закон сохранения энергии и уравнение баланса энергии
- § 17. Общие уравнения равновесного состояния жидкости и газа. Равновесие воздуха в атмосфере. Приближенные барометрические формулы. Стандартная атмосфера
- § 18. Равновесие несжимаемой жидкости. Уравнение поверхности раздела. Равновесие вращающейся жидкости
- § 19. Давление тяжелой несжимаемой жидкости на поверхность тела. Сила и момент, приложенные к телу, плавающему в тяжелой жидкости. Случай вращающейся жидкости
- ГЛАВА III. ДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ И ГАЗА. ОСНОВНЫЕ УРАВНЕНИЯ И ОБЩИЕ ТЕОРЕМЫ
- § 20. Идеальная жидкость. Основные уравнения движения
- § 21. Закон сохранения энергии в движущейся идеальной жидкости. Адиабатическое движение. Сохранение энтропии
- § 22. Эйлерово представление конвективного изменения объемного интеграла. Перенос величины сквозь контрольную поверхность
- § 23. Эйлерова форма законов сохранения массы и энергии, теоремы количеств движения и момента количеств движения при стационарном движении идеальной жидкости
- § 24. Теорема об изменении кинетической энергии. Работа и мощность внутренних сил. Эйлерова форма уравнения изменения кинетической энергии
- § 25. Теорема Бернулли о сохранении полной механической энергии при стационарном баротропном движении идеальной жидкости и газа
- ГЛАВА IV. ОДНОМЕРНЫЙ ПОТОК ИДЕАЛЬНОЙ ЖИДКОСТИ
- § 26. Одномерное течение идеальной сжимаемой жидкости. Линеаризированные уравнения. Скорость распространения малых возмущений в жидкости или газе
- § 27. Изотермическая и адиабатическая скорости звука. «Конус возмущений» при сверхзвуковом движении источника возмущения. Число M и его связь с углом конуса возмущений
- § 28. Распространение непрерывных возмущений конечной интенсивности. Характеристики. Образование разрывной ударной волны
- § 29. Стоячая ударная волна или скачок уплотнения. Ударная адиабата
- § 30. Критические величины в одномерном потоке газа. Связь между скоростями до и после скачка. Изменение давления, плотности и температуры в скачке уплотнения
- § 31. Скорость распространения ударной волны. Спутное движение газа за ударной волной
- § 32. Влияние интенсивности скачка уплотнения на сжатие газа. Измерение скоростей и давлений в до- и сверхзвуковых потоках
- § 33. Одномерное движение газа по трубе переменного сечения. Истечение из резервуара большой емкости сквозь сходящееся сопло
- § 34. Одномерное течение в сопле Лаваля. Движение газа с притоком тепла
- ГЛАВА V. БЕЗВИХРЕВОЕ ДВИЖЕНИЕ ЖИДКОСТИ. ПЛОСКОЕ ДВИЖЕНИЕ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 35. Сохранение циркуляции скорости в потоке идеальной жидкости. Теорема Кельвина и Лаграижа. Безвихревое движение. Потенциал скоростей
- § 36. Интеграл Лагранжа — Коши уравнений безвихревого движения. Теорема Бернулли. Некоторые общие свойства безвихревого движения идеальной несжимаемой жидкости в односвязной области
- § 37. Плоское безвихревое движение несжимаемой жидкости. Потенциал скоростей и функция тока. Применение функций комплексного переменного. Комплексный потенциал и сопряженная скорость
- § 38. Построение полей течения по заданной характеристической Функции. Простейшие плоские потоки и их наложение
- § 39. Бесциркуляционное и циркуляционное обтекания круглого цилиндра
- § 40. Применение криволинейных координат. Бесциркуляционное и циркуляционное обтекания эллиптического цилиндра и пластинки. Задача Жуковского об обтекании решетки пластин.
- § 41. Плоское движение с отрывом струй. Разрывное обтекание пластинки и протекание жидкости сквозь отверстие
- § 42. Прямая задача в теории плоского движения идеальной несжимаемой жидкости. Применение метода конформных отображений. Гипотеза Чаплыгина о безотрывном обтекании задней кромки профиля. Формула циркуляции
- § 43. Теорема Жуковского о подъемной силе крыла. Зависимость подъемной силы от угла атаки. Коэффициент подъемной силы
- § 44. Применение метода комплексных переменных к выводу теоремы Жуковского. Формулы Чаплыгина для главного вектора и момента сил давления потока на крыло
- § 45. Выражение главного момента сил давления потока через коэффициенты конформного отображения. Фокус крыла. Независимость от угла атаки момента относительно фокуса. Парабола устойчивости
- § 46. Частные случаи конформного отображения крылового профиля на круг. Преобразование Жуковского-Чаплыгина. Теоретические крыловые профили
- § 47. Задача об обтекании слабо изогнутой дужки произвольной формы (теория тонкого крыла)
- § 48. Определение обтекания крылового профиля произвольной формы
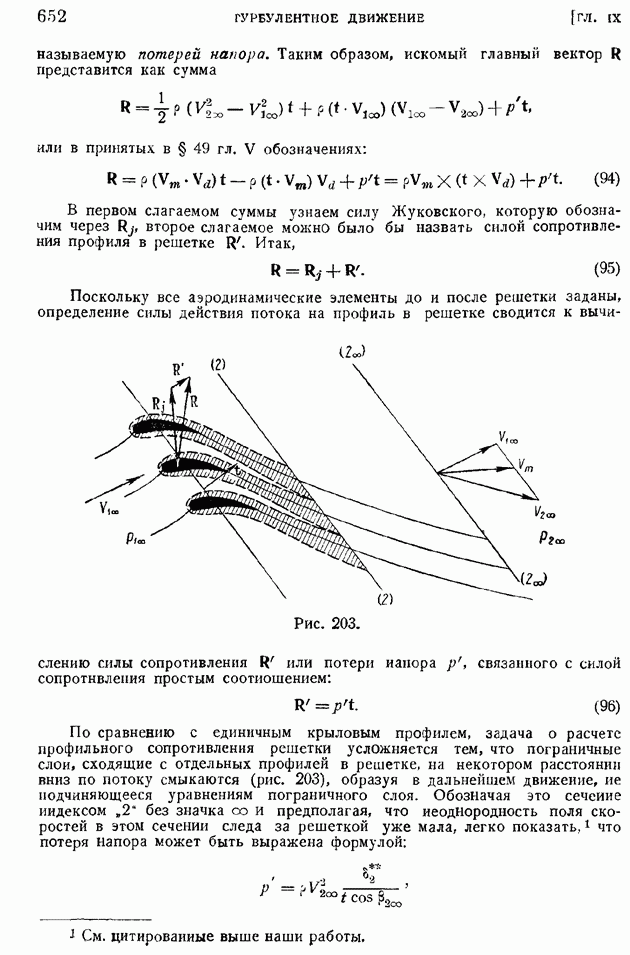
- § 49. Обобщение теоремы Жуковского на случай плоской решетки с бесчисленным множеством профилей
- ГЛАВА VI. ПЛОСКОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ СЖИМАЕМОГО ГАЗА
- § 50. Основные уравнения плоского стационарного безвихревого движения сжимаемого газа. Линеаризированные уравнения
- 51. Линеаризированный до- и сверхзвуковой газовый поток вдоль волнистой стенки
- § 52. Тонкое крыло в линеаризированном до- и сверхзвуковом потоках. Влияние сжимаемости газа на коэффициент подъемной силы в дозвуковом потоке. Коэффициенты подъемной силы и волнового сопротивления при сверхзвуковом потоке
- § 53. Нелинеаризированные уравнения движения идеального сжимаемого газа. Переход в плоскость годографа. Уравнения Чаплыгина
- § 54. Метод С. А. Христиановича. Приближенные формулы учета влияния сжимаемости на распределение давления
- § 55. Критическое число M и его определение по заданному распределению давления в несжимаемом обтекании. Поведение коэффициента подъемной силы и момента при около- и закритических значениях числа M
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
- § 57. Нелинеаризированный сверхзвуковой поток. «Характеристики» уравнений плоского сверхзвукового потока. Линин возмущения и их основные свойства
- § 58. Обтекание выпуклого угла сверхзвуковым потоком. Влияние угла поворота струи на ее газодинамические элементы
- § 59. Сверхзвуковой поток внутри тупого угла. Косой скачок уплотнения. Связь между газодинамическими элементами до и за косым скачком
- ГЛАВА VII. ПРОСТРАНСТВЕННОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ
- § 60. Ортогональные криволинейные координаты в пространстве. Основные дифференциальные операторы поля в криволинейных координатах
- § 61. Потенциал скоростей. Поле источника и диполя. Непрерывное распределение источников и диполей. Ньютонов потенциал. Потенциал простого и двойного слоев
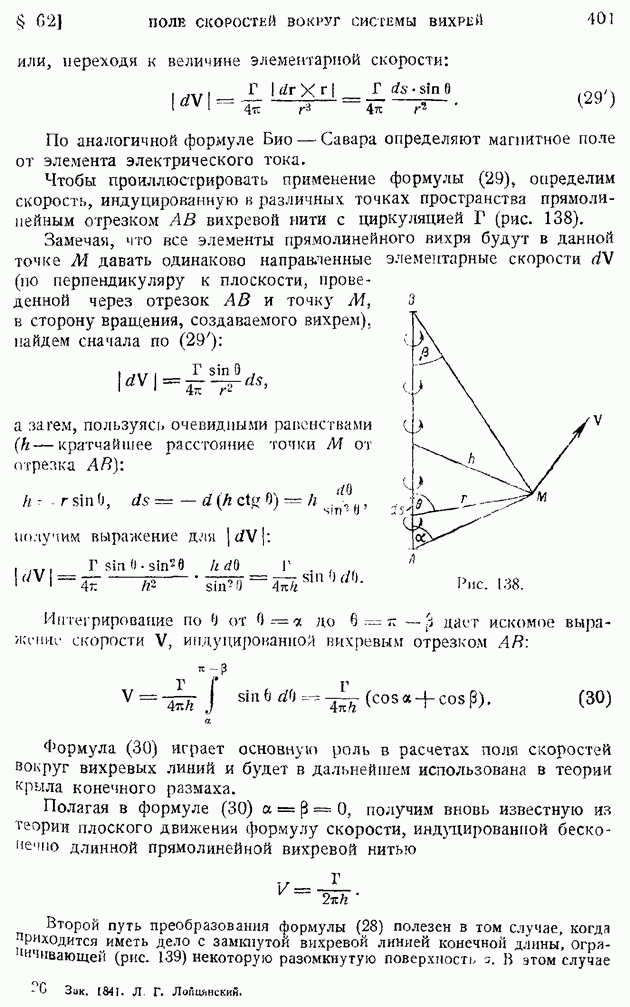
- § 62. Поле скоростей вокруг заданной системы вихрей. Формула Био — Савара. Потенциал скоростей замкнутой вихревой нити. Аналогия с потенциалом двойного слоя
- § 63. Функция тока и ее связь с векторным потенциалом скоростей. Функции тока простейших течений
- § 64. Обтекание сферы. Давление однородного стационарного потока идеальной несжимаемой жидкости на погруженное в нее тело. Парадокс Даламбера
- § 65. Общие уравнения осесимметричного движения. Применение цилиндрических координат. Течение сквозь каналы
- § 66. Осесимметричное продольное обтекание тел вращения. Случай эллипсоида вращения
- § 67. Поперечное обтекание тел вращения. Пример эллипсоида вращения
- § 68. Продольное и поперечное обтекание тел вращения большого удлинения. Приближенные выражения граничных условий. Применение тригонометрических сумм для определения коэффициентов …
- § 69. Метод «особенностей». Применение непрерывно распределенных источников (стоков) и диполей для решения задачи о продольном и поперечном обтекании тел вращения
- § 70. Общий случай движения твердого тела сквозь несжимаемую идеальную жидкость. Определение потенциала скоростей. Главный вектор и главный момент сил давления потока на тело
- § 71. Коэффициенты «присоединенных масс». Свойство симметрии. «Присоединенная» кинетическая энергия. Определение «присоединенных масс» поступательно движущегося цилиндра, шара и эллипсоида
- § 72. Элементы теории крыла конечного размаха. Вихревая система крыла. Гипотеза плоских сечеиий. Геометрические и действительные углы атаки. Подъемная сила и «индуктивное сопротивление»
- § 73. Основные формулы теории «несущей линии». «Индуктивная скорость» и «индуктивный угол». Прямая задача определения подъемной силы и индуктивного сопротивления по заданному распределению циркуляции
- § 74. Крыло с минимальным индуктивным сопротивлением. Эллиптическое распределение циркуляции. Связь между коэффициентами индуктивного сопротивления и подъемной силы. Основное уравнение теории крыла и понятие о его интегрировании
- ГЛАВА VIII. ДИНАМИКА ВЯЗКОЙ ЖИДКОСТИ И ГАЗА
- § 75. Внутреннее трение и теплопроводность в жидкостях и газах. Законы Ньютона и Фурье. Влияние температуры на коэффициенты вязкости и теплопроводности. Число «сигма»
- § 76. Обобщение закона Ньютона на случай произвольного движения среды. Закон линейной связи между тензорами напряжений и скоростей деформации
- § 77. Общие уравнения движения вязкой жидкости. Динамические уравнения и уравнение баланса энергии. Граничные условия движения жидкости с треннем и теплопроводностью
- § 78. Понятие о подобии гидродинамических явлений. Безразмерные уравнения движения вязкой жидкости и газа. Условия подобия
- § 79. Ламинарное движение вязкой несжимаемой жидкости по цилиндрической трубе
- § 80. Обтекание шара при очень малых значениях числа Рейнольдса. Формула сопротивления шара по Стоксу и ее обобщения
- § 81. Вихревые линии в идеальной и вязкой жидкости. Сохраняемость вихревых линий при отсутствии внутреннего трения. Диффузия вихря в вязкой жидкости
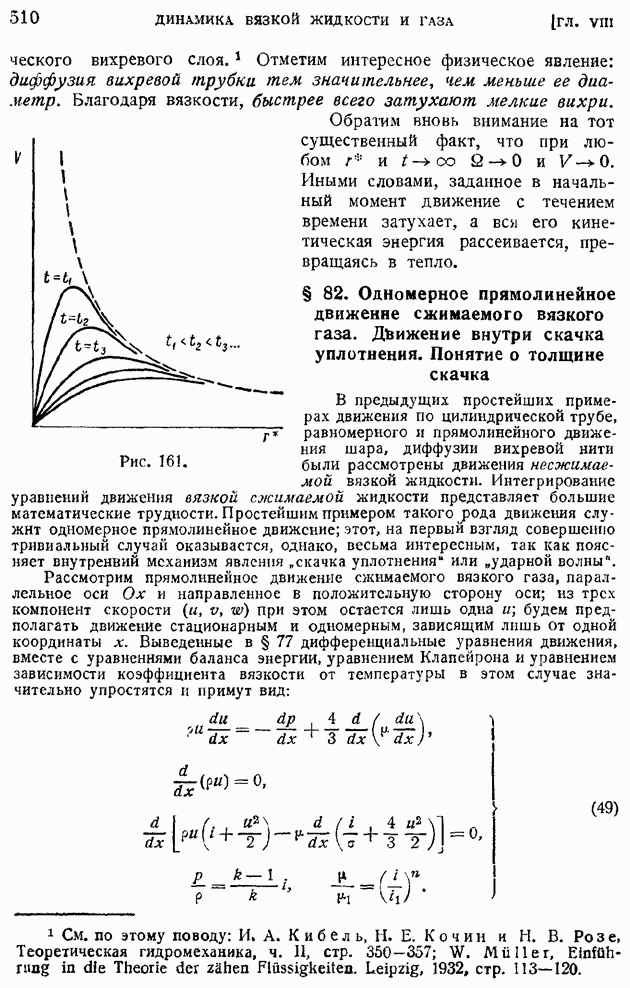
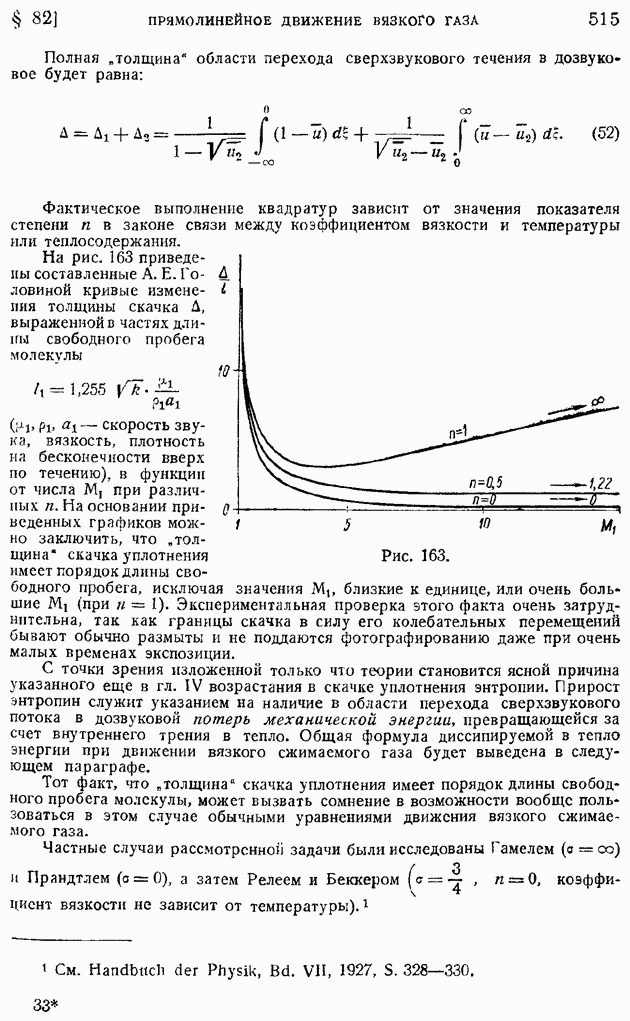
- § 82. Одномерное прямолинейное движение сжимаемого вязкого газа. Движение внутри скачка уплотнения. Понятие о толщине скачка
- § 83. Работа внутренних сил и диссипация механической энергии в движущейся вязкой среде
- § 84. Обтекание тел жидкостью и газом при больших значениях числа Рейнольдса. Основные уравнения теории ламинарного пограничного слоя
- § 85. Ламинарный пограничный слой на пластинке, продольно обтекаемой несжимаемой жидкостью. Неизотермическое движение
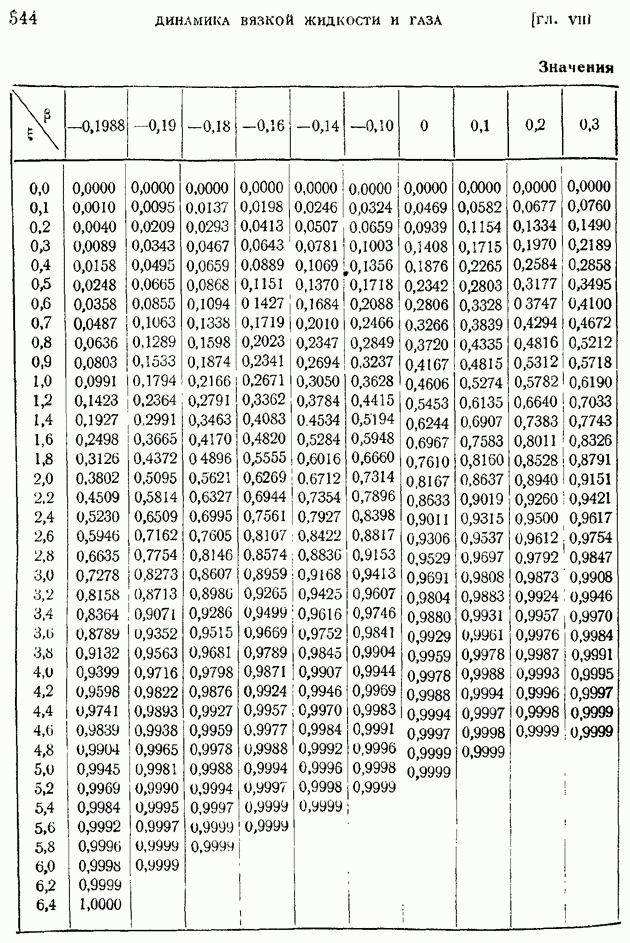
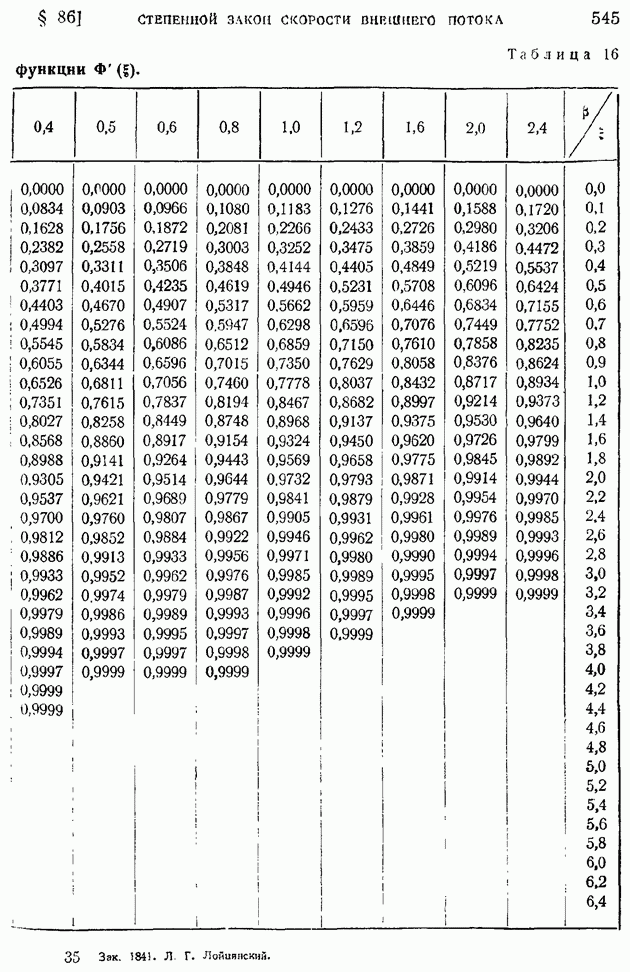
- § 86. Ламинарный пограничный слой при степенном задании скорости внешнего потока
- § 87. Ламинарный пограничный слой в общем случае задания скорости внешнего потока. Применение уравнения импульсов для приближенного расчета ламинарного пограничного слоя
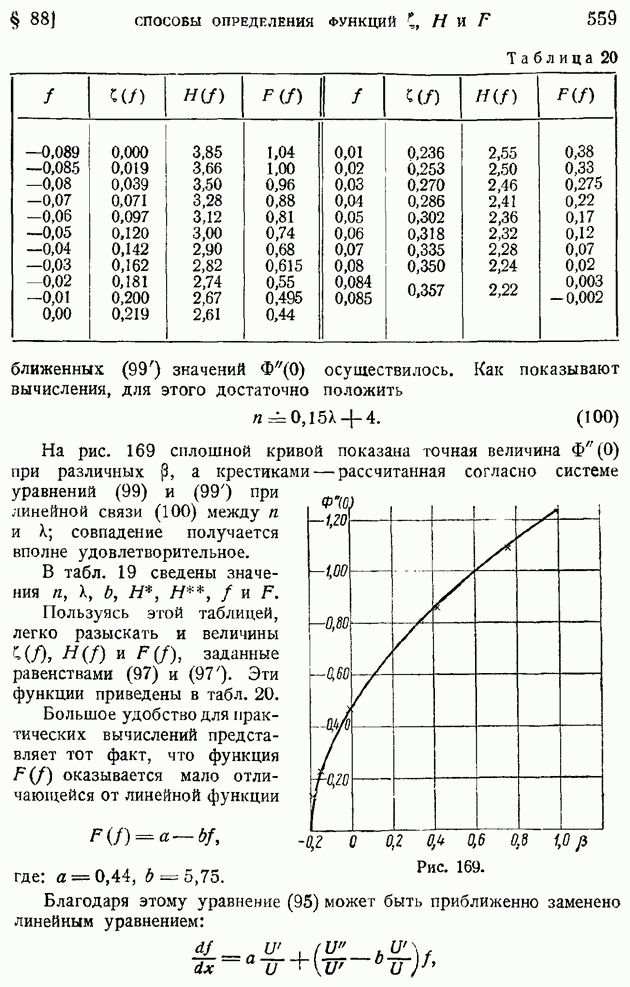
- § 88. Способы определения функций … Приближенный метод расчета ламинарного пограничного слоя
- § 89. Ламинарный пограничный слой на пластинке, продольно обтекаемой сжимаемым газом при больших скоростях. Случай линейной зависимости коэффициента вязкости от температуры (n = 1)
- § 90. Ламинарный пограничный слой на пластинке при любом законе связи между вязкостью и температурой и при числе … Обтекание крылового профиля потоком больших скоростей
- ГЛАВА IX. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ
- § 91. Переход ламинарного движения в турбулентное. Критическое рейнольдсово число
- § 92. Область и «точка» перехода. Явление «кризиса обтекания»
- § 93. Основные уравнения осреднеиного турбулентного движения. Тензор турбулентных напряжений
- § 94. Турбулентное движение жидкости в плоской и круглой трубе. Логарифмические формулы скоростей
- § 95. Формулы сопротивления гладких труб при турбулентном движении жидкости. Ламинарный подслой
- § 96. Влияние шероховатости стенок трубы на ее сопротивление. Предельные режимы течения. Режим установившейся шероховатости
- § 97. Турбулентный пограничный слой на продольно обтекаемой пластине. Сопротивление пластины
- § 98. Турбулентный пограничный слой на крыловом профиле при малом продольном перепаде давлений
- § 99. Турбулентный пограничный слой на крыловом профиле при значительных продольных перепадах давления
- § 100. Профильное сопротивление крыла. Разложение профильного сопротивления на сопротивление трения и сопротивление давлений. Обратное влияние пограничного слоя на распределение давлений по поверхности обтекаемого профиля
- § 101. Приближенные формулы профильного сопротивления крыла и крылового профиля в решетке
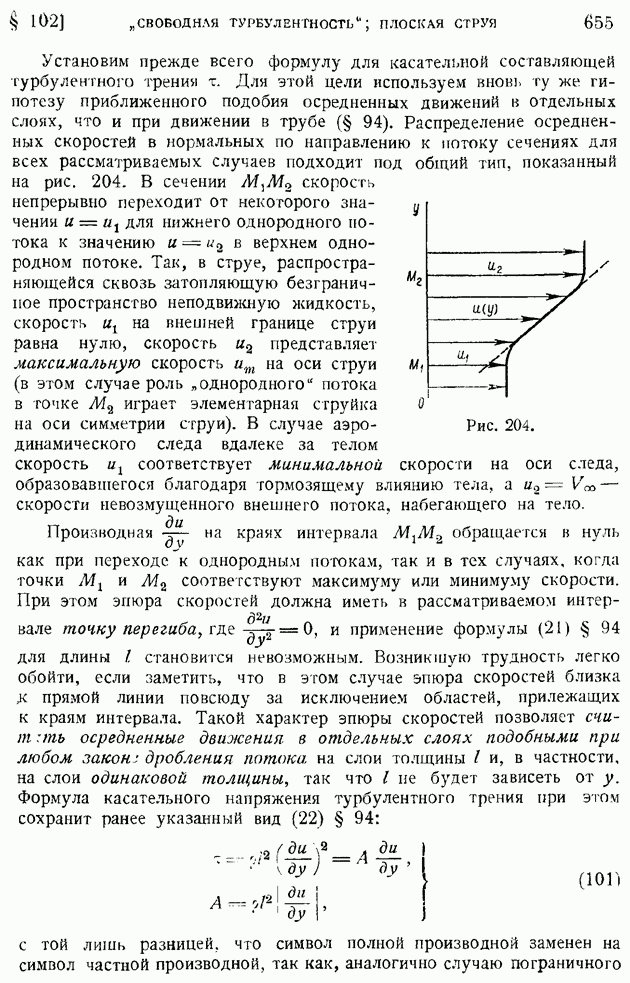
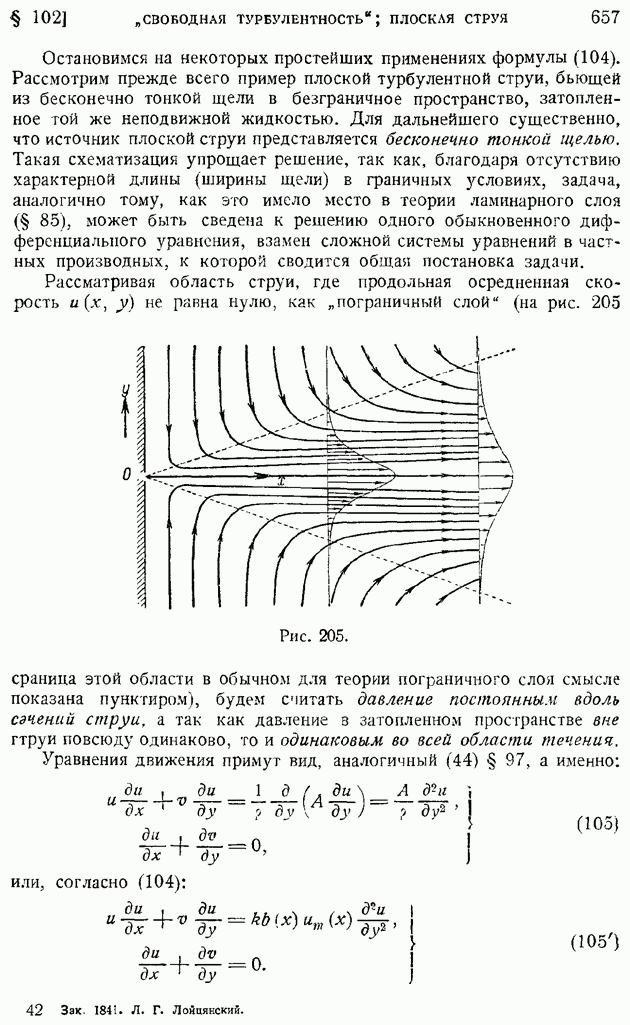
- § 102. Основные закономерности «свободной турбулентности». Плоская турбулентная струя в пространстве, заполненном той же жидкостью
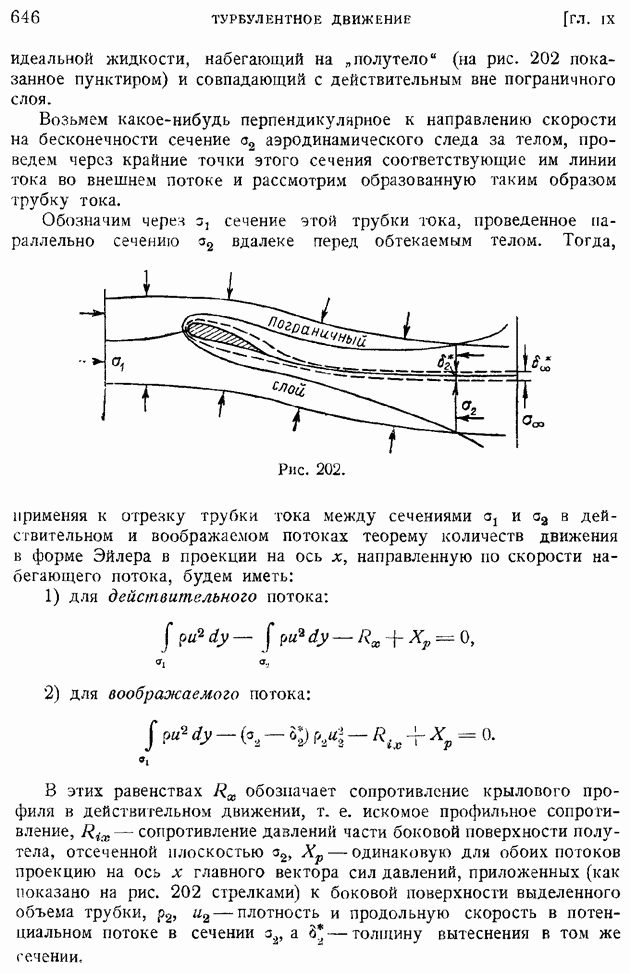
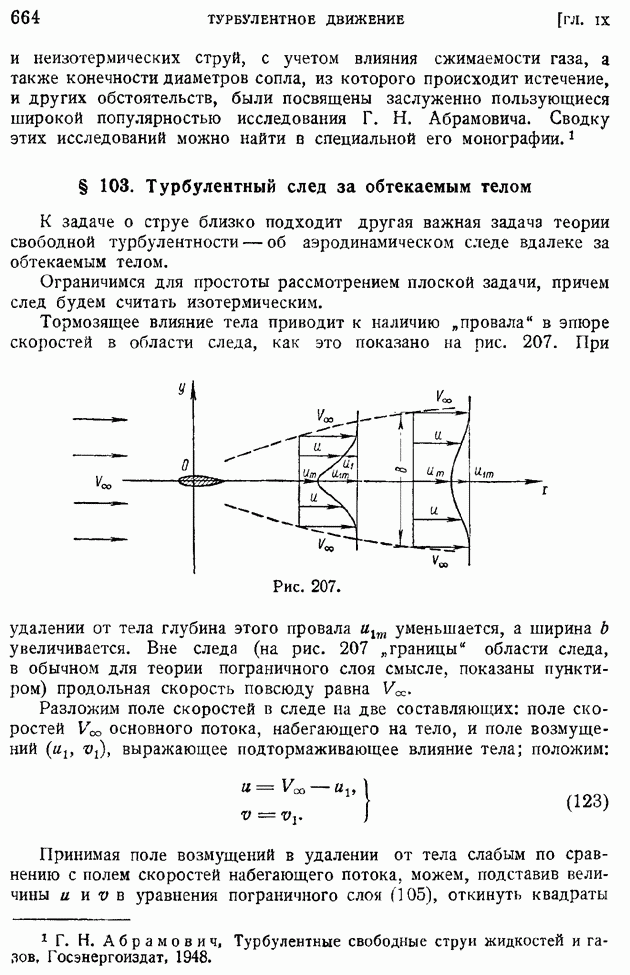
- § 103. Турбулентный след за обтекаемым телом
- § 104. Рассеяние турбулентных возмущений в жидкости. Случай изотропной и однородной турбулентности. Закон сохранения момента возмущений