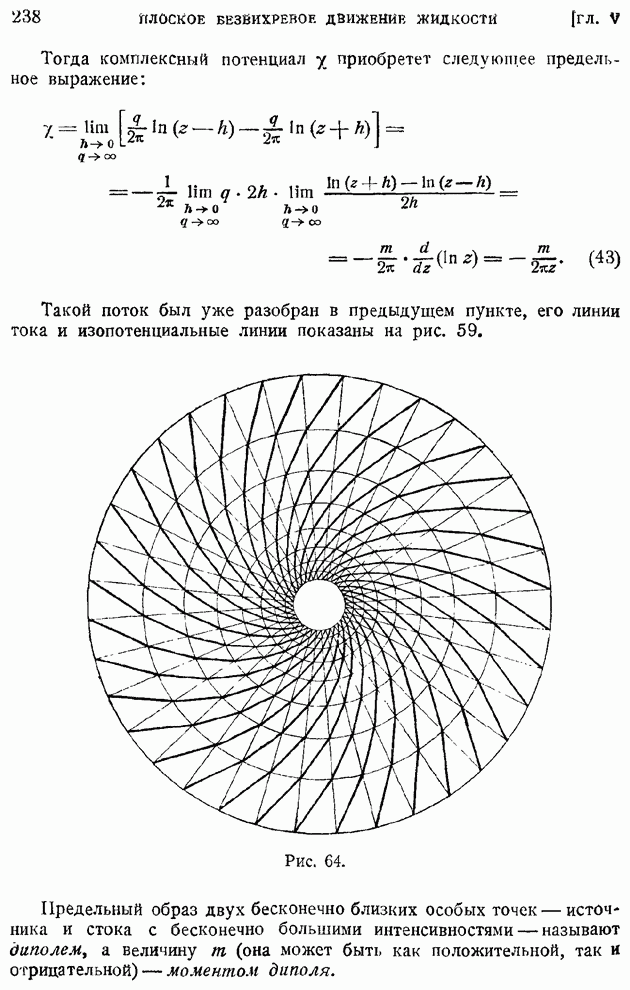
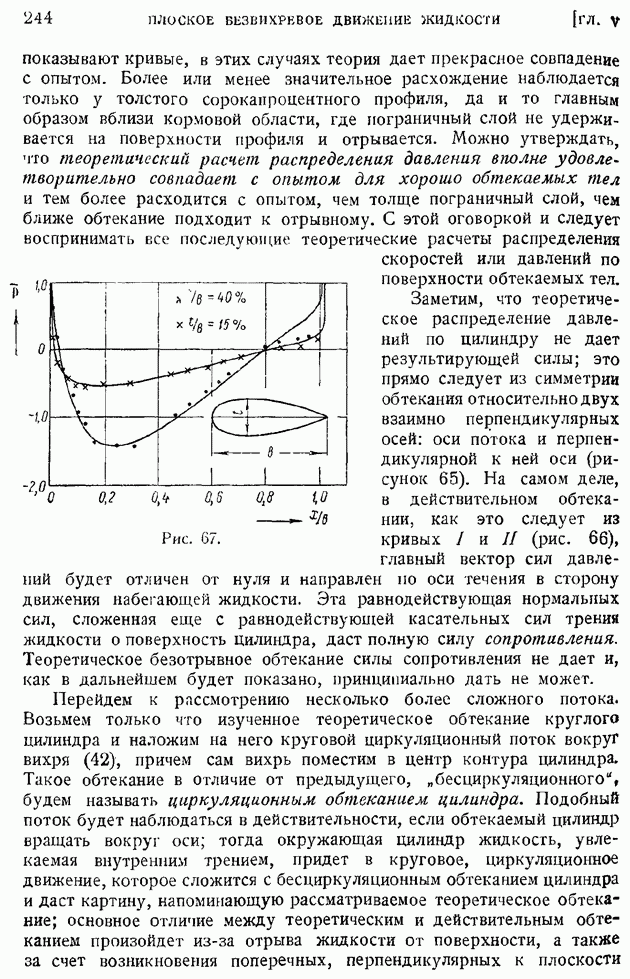
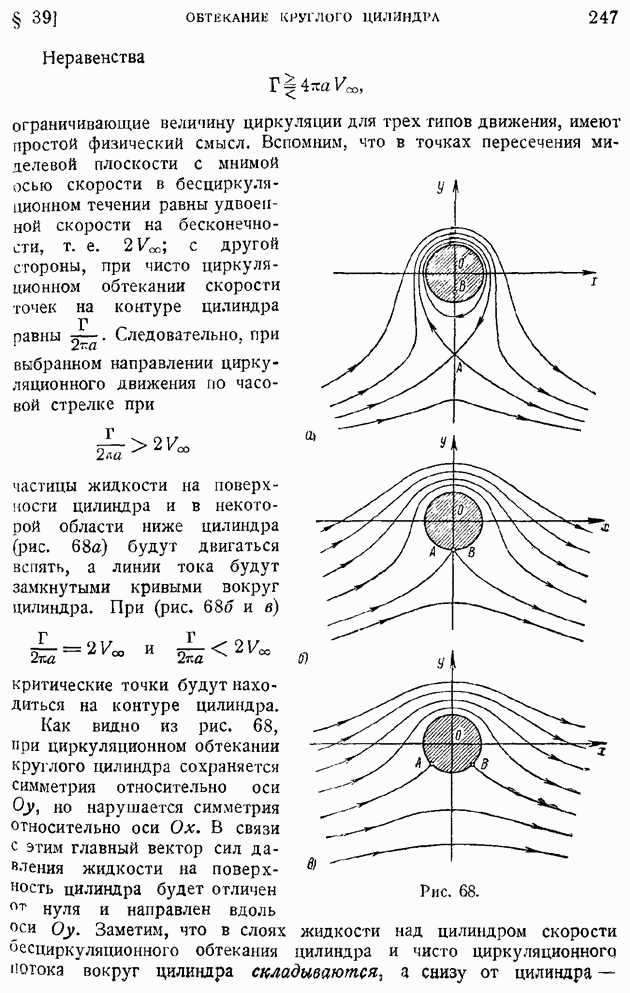
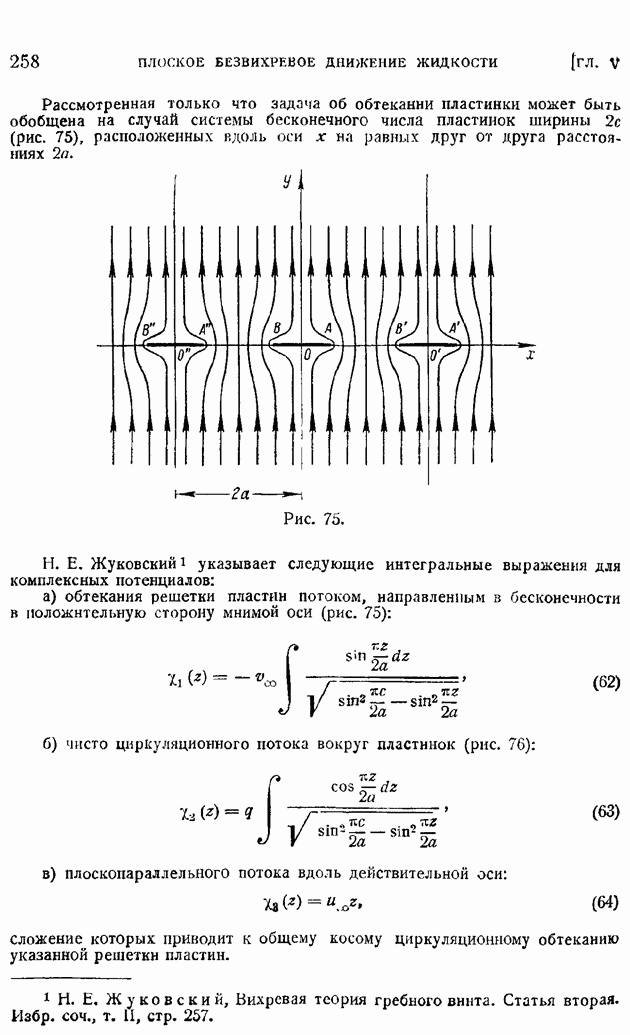
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 17. Общие уравнения равновесного состояния жидкости и газа. Равновесие воздуха в атмосфере. Приближенные барометрические формулы. Стандартная атмосфера
Согласно основному свойству жидкостей и газов — легкой подвижности, — при равновесии отсутствуют касательные силы сопротивления взаимному скольжению жидких объемов друг по отношению к другу по площадкам их соприкосновения, а действуют лишь нормальные к этим площадкам силы.
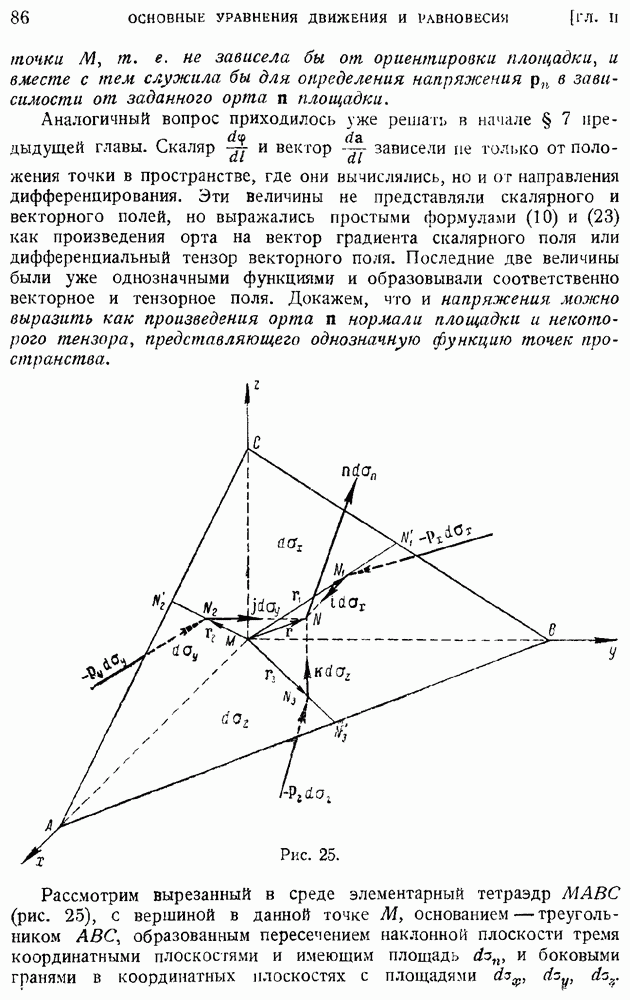
Таким образом, при равновесии жидкости или газа векторы напряжений, приложенные к трем координатным и одной наклонной к ним площадке (§ 14), будут равны:

а касательные компоненты напряжений равны нулю:

Подставляя значения напряжений в основную систему равенств (10), найдем:

откуда сразу следует

Общее значение нормальных напряжений, приложенных в данной точке жидкости к площадке любого направления, назовем давлением в данной точке жидкости или газа и обозначим через  в знак того, что вектор напряжения направлен противоположно орту нормали к площадке:
в знак того, что вектор напряжения направлен противоположно орту нормали к площадке:

что соответствует сжатию выделенного объема. Давление  такой же физический скаляр, как плотность, температура и др.
такой же физический скаляр, как плотность, температура и др.
Тензор напряженности  при равновесии среды имеет таблицу.
при равновесии среды имеет таблицу.

Симметричный тензор компоненты которого отвечают условиям:

называют единичным тензором или тензорной единицей. Последние равенства должны выполняться, очевидно, независимо от выбора системы координат, т. е. единичный тензор должен оставаться единичным при любом направлении взаимно перпендикулярных декартовых осей координат; это можно было бы показать и непосредственно на основании формул преобразования компонент тензора при изменении направления осей координат (см., например, ранее цитированный курс векторного и тензорного исчисления Н. Е. Кочина).
Формула (12) вместе с (52) и (53) дает очевидную систему равенств:

из которых, между прочим, видно, что

так что умножение орта  на тензорную единицу приводит к тому же вектору, — общее свойство умножения любого вектора на тензорную единицу, в чем легко убедиться, проделав операцию умножения по ранее установленному в гл. I правилу (20),
на тензорную единицу приводит к тому же вектору, — общее свойство умножения любого вектора на тензорную единицу, в чем легко убедиться, проделав операцию умножения по ранее установленному в гл. I правилу (20),
Чтобы вывести уравнения равновесия среды, т. е. ее относительного покоя, рассмотрим уравнения движения, частным случаем которых при равенстве нулю всех скоростей должны являться уравнения равновесия.
Уравнение неразрывности (22) сведется при этом к первому условию равновесия

т. е. к стационарности поля плотностей среды.
Уравнения в напряжениях (29) на основании таблицы (53) дают следующую систему основных уравнений равновесия среды

называемых уравнениями Эйлера равновесия жидкости или газа. Система (56), очевидно, эквивалентна одному векторному уравнению

которое можно было и сразу вывести из (37), заметив, что но (53), (31), (55) и интегральной формуле (70) гл. I:

Наконец, уравнение баланса энергии (45) дает тепловое условие равновесия жидкости или газа

которое, при наличии только теплопроводности приводится но (48) к уравнению:

а при возможности считать коэффициент теплопроводности постоянным [см. формулу (49)] к уравнению:

где постоянный коэффициент а называют коэффициентом температуропроводности.
Рассмотрим подробнее основное уравнение равновесия в векторной форме (57). Простыми операциями из него можно исключить плотность и давление. Для этого возьмем сначала от обеих частей векторного равенства (57) операцию вихря  тогда
тогда  пропадет, так как
пропадет, так как  будем иметь
будем иметь

или, раскрывая скобки по известному правилу векторного анализа, получаем

Умножим теперь обе части этого равенства скалярно на  тогда, заметив, что второе слагаемое, как векторное произведение, перпендикулярно своему сомножителю
тогда, заметив, что второе слагаемое, как векторное произведение, перпендикулярно своему сомножителю  найдем следующее общее ограничение, накладываемое на класс сил, под действием которых возможно равновесие жидкости или газа:
найдем следующее общее ограничение, накладываемое на класс сил, под действием которых возможно равновесие жидкости или газа:

или, в проекциях на оси декартовых координат:

К числу объемных сил, удовлетворяющих условию (62), относятся прежде всего силы, имеющие потенциал 11, так как для них

В этом случае, как легко усмотреть из равенства (61),

откуда следует, что силовые линии поля потенциальных объемных сил ортогональны изостерам (поверхностям одинаковой плотности), а также, что изостеры совпадают с изопотенциальными поверхностями силового поля.
Из (57) следует еще, что при равновесии среды силовые линии перпендикулярны изобарам (поверхностям одинакового давления). Таким образом, вообще, при равновесии жидкости или газа под действием потенциального поля объемных сил изопотенциальные поверхности поля совпадают с изобарами и изостерами.
Можно доказать и обратное предложение: если изобары совпадают с изостерами, то равновесие жидкости или газа, возможно только под действием потенциального поля объемных сил. Действительно, по условию,

или по (57)

отсюда, на основании (61), вытекает

Ихли в движущемся или покоящемся газе плотность является функцией только давления, то такой процесс движения или равновесия называется баротропным. Из предыдущего следует, что баротропное равновесие газа возможно при наличии только потенциальных сил, так как при условии  изобары и изостеры, очевидно, совпадут; следовательно, как только что было показано, силовое поле должно быть потенциальным.
изобары и изостеры, очевидно, совпадут; следовательно, как только что было показано, силовое поле должно быть потенциальным.
Более общее условие (62) имеет смысл требования существования в силовом поле поверхностей, ортогональных к силовым линиям, причем эти поверхности в общем случае не должны совпадать с изостерами.
Система уравнений (57), как уравнений в полных дифференциалах, представляет лишь одну связь между двумя неизвестными величинами  уравнение
уравнение  - также одно уравнение с двумя неизвестными
- также одно уравнение с двумя неизвестными  Чтобы сделать систему уравнений равновесия определенной, необходимо добавить еще уравнение состояния газа, называемое обычно уравнением Клапейрона:
Чтобы сделать систему уравнений равновесия определенной, необходимо добавить еще уравнение состояния газа, называемое обычно уравнением Клапейрона:

и уравнение зависимости коэффициента теплопроводности от температуры:

Если равновесие баротропно, то

Это имеет место, например, в следующих случаях:
1) газ несжимаем, т. е. имеет повсюду одинаковую плотность

2) равновесие изотермическое, при котором

а следовательно, по (64):

3) равновесие адиабатическое (без притока тепла извне), отвечающее известной из курса термодинамики адиабате:

где  показатель адиабаты, равный отношению теплоемкостей газа при постоянном давлении
показатель адиабаты, равный отношению теплоемкостей газа при постоянном давлении  и постоянном объеме с; для воздуха
и постоянном объеме с; для воздуха  Значения величин
Значения величин  относятся к какой-нибудь одной характерной точке покоящегося газа.
относятся к какой-нибудь одной характерной точке покоящегося газа.
Задача сводится, таким образом, к решению уравнений (57) и (59) при тех или иных дополнительных связях между термодинамическими элементами  и
и 
Останавливаясь лишь на случае баротропного равновесия газа в потенциальном силовом поле, напишем уравнение равновесия в виде:

Введем в рассмотрение функцию давления

градиент ее по (70) равен:

При баротропности равновесия газа функция давлений  играет роль потенциала или потенциальной энергии поля отнесенных к единице массы главных векторов поверхностных сил, сводящихся в случае равновесия к силам давления. Можно сказать также, что функция давлений представляет потенциальную энергию интенсивности объемного действия поля давлений.
играет роль потенциала или потенциальной энергии поля отнесенных к единице массы главных векторов поверхностных сил, сводящихся в случае равновесия к силам давления. Можно сказать также, что функция давлений представляет потенциальную энергию интенсивности объемного действия поля давлений.
Действительно, в полном соответствии с обычной связью между векторным силовым полем и его потенциальной энергией, имеем по (70):

Итак, при баротропном равновесии среды объемное действие среды на выделенное в ней "единичное тело" (единицу объема или массы) образует потенциальное поле с потенциалом, зависящим только от характера баротропности процесса.
Уравнение равновесия (69) может быть переписано в форме

откуда следует, что при равновесии среды во всех точках ее выполняется равенство

В качестве иллюстрации рассмотрим приближенные уравнения равновесия атмосферы под действием силы тяжести. В этом случае, направляя ось z вертикально вверх и помещая начало координат на уровне моря, будем иметь  некоторая высота над уровнем моря):
некоторая высота над уровнем моря):

Функция  для изотермического случая будет определяться на «сновании (66) так:
для изотермического случая будет определяться на «сновании (66) так:

Условие приближенного равновесия атмосферы между пунктами  по (71) можно написать в виде:
по (71) можно написать в виде:

где  значения давления и плотности на высотах
значения давления и плотности на высотах  и над уровнем моря. Формула (73) представляет простейшую
и над уровнем моря. Формула (73) представляет простейшую
барометрическую формулу, позволяющую приближенно определят), высоту пункта над уровнем моря по измеренному барометром давлению в этом пункте, если известны  при
при 
Полагая  можем придать формуле (73) простой вид:
можем придать формуле (73) простой вид:

Формулу (73) или (73) можно применять с большой точностью, если разбить весь интервал ее применения на малые промежуточные интервалы  и в начале каждого следующего интервала
и в начале каждого следующего интервала  пользоваться новым значением отношения
пользоваться новым значением отношения  исправленным на новую температуру
исправленным на новую температуру  но формуле
но формуле

и новым значением  вычисленным по (73) из равенства
вычисленным по (73) из равенства

Обычно поступают несколько проще. Обозначим разность двух близких высот  через
через  разность соответствующих им давлений
разность соответствующих им давлений  через тогда равенство (73), согласно (66), примет вид:
через тогда равенство (73), согласно (66), примет вид:

где под  будем понимать среднюю температуру воздуха в интервале
будем понимать среднюю температуру воздуха в интервале 

Отсюда найдем 

или, пользуясь разложением логарифма в ряд,

Можно еще перейти от абсолютных температур к обычным по формуле

и получить приближенную формулу:

Замечая, что для сухого воздуха

приведем формулу (74) к такому окончательному виду:

удобному для практических измерений.
При технических расчетах пользуются обычно так называемой стандартной атмосферой, согласно которой в нижних слоях атмосферы — в тропосфере  температуру принимают падающей
температуру принимают падающей  значения 15° С вблизи уровня моря на
значения 15° С вблизи уровня моря на  на каждый километр, а давление на уровне моря — равным 760 мм рт. ст. В стратосфере
на каждый километр, а давление на уровне моря — равным 760 мм рт. ст. В стратосфере  температура считается одинаковой и равной -56,5° С.
температура считается одинаковой и равной -56,5° С.
Формулы расчета для тропосферы получаются из следующей системы уравнений:

где газовая постоянная  для сухого воздуха равна
для сухого воздуха равна 
Интегрирование этой системы уравнений не составляет труда. Имеем:

Отсюда следует  атмосферное давление на уровне моря, принимаемое равным 760 мм рт. ст.), что
атмосферное давление на уровне моря, принимаемое равным 760 мм рт. ст.), что

или, подставляя числа,

Для стратосферы начальная температура принимается равной — 56,5°С и интегрирование проводится так же, как и для изотермического случая.
Не составляет труда получение барометрической формулы и для адиабатического равновесия.
В этом случае, обозначая через  и
и  — давление и плотность на уровне моря
— давление и плотность на уровне моря  по (68) и (70) легко найдем
по (68) и (70) легко найдем

после чего по (71) получим барометрическую формулу:

В рассмотренном одноразмерном случае (безграничная атмосфера, изменяющаяся вдоль оси  ) тепловое условие равновесия в предположении стационарности температурного поля примет вид
) тепловое условие равновесия в предположении стационарности температурного поля примет вид

что приводит к линейному распределению температуры, в частности, к постоянству ее но высоте. Это условие выполняется как при изотермическом равновесии, так и в случае "стандартной" атмосферы. При адиабатичности процесса условие теплового равновесия не выполняется.
Нетрудно построить барометрическую формулу изотермического равновесия и с учетом поля тяготения, если заметить, что в этом случае потенциал массовых сил может быть принят равным

где а — радиус Земли,  - ускорение на уровне моря. По (71) будем иметь
- ускорение на уровне моря. По (71) будем иметь

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Предмет механики жидкости и газа. Основные свойства «макромодели» жидкости и газа: сплошность и подвижность
- § 2. Основные методы механики жидкости и газа. Области применения и главнейшие задачи
- § 3. Краткий очерк исторического развития механики жидкости и газа. От гидромеханики древних до установления воззрений ньютонианской эпохи
- § 4. Эпоха Эйлера и Бернулли. Гидроаэродинамика в XIX в.
- § 5. Современный этап развития механики жидкости и газа
- ГЛАВА I. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
- § 6. Поле физической величины. Скалярное и векторное поля. Поверхности уровня. Векторные линин и трубки
- § 7. Мера однородности поля в данном направлении и в дайной точке. Градиевт скалярного поля и дифференциальный тензор векторного поля как меры неоднородности поля
- § 8. Задание движения сплошной среды. Поле скоростей. Линии тока и траектории
- § 9. Поле ускорений. Разложение ускорения частицы на локальную и конвективную составляющие
- § 10. Скоростное поле сплошной среды в окрестности данной точки. Угловая скорость и вихрь. Тензор скоростей деформаций и его компоненты
- § 11. Скорость объемного расширения жидкости. Интегральные представления дифференциальных операторов поля. Основные интегральные формулы
- § 12. Вихревые линии и трубки. Вторая теорема Гельмгольца. Интенсивность вихревой трубки
- § 13. Выражение интенсивности вихревой трубки через циркуляцию вектора по контуру, охватывающему трубку. Теорема об изменении циркуляции скорости во времени
- ГЛАВА II. ОСНОВНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ И РАВНОВЕСИЯ СПЛОШНОЙ СРЕДЫ
- § 14. Распределение массы в сплошной среде. Плотность и удельный вес. Напряжения. Тензор напряженности и его симметричность
- § 15. Общие уравнения динамики сплошной среды. Уравнение неразрывности. Уравнения динамики в напряжениях
- § 16. Тепловые явления в жидкостях и газах. Закон сохранения энергии и уравнение баланса энергии
- § 17. Общие уравнения равновесного состояния жидкости и газа. Равновесие воздуха в атмосфере. Приближенные барометрические формулы. Стандартная атмосфера
- § 18. Равновесие несжимаемой жидкости. Уравнение поверхности раздела. Равновесие вращающейся жидкости
- § 19. Давление тяжелой несжимаемой жидкости на поверхность тела. Сила и момент, приложенные к телу, плавающему в тяжелой жидкости. Случай вращающейся жидкости
- ГЛАВА III. ДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ И ГАЗА. ОСНОВНЫЕ УРАВНЕНИЯ И ОБЩИЕ ТЕОРЕМЫ
- § 20. Идеальная жидкость. Основные уравнения движения
- § 21. Закон сохранения энергии в движущейся идеальной жидкости. Адиабатическое движение. Сохранение энтропии
- § 22. Эйлерово представление конвективного изменения объемного интеграла. Перенос величины сквозь контрольную поверхность
- § 23. Эйлерова форма законов сохранения массы и энергии, теоремы количеств движения и момента количеств движения при стационарном движении идеальной жидкости
- § 24. Теорема об изменении кинетической энергии. Работа и мощность внутренних сил. Эйлерова форма уравнения изменения кинетической энергии
- § 25. Теорема Бернулли о сохранении полной механической энергии при стационарном баротропном движении идеальной жидкости и газа
- ГЛАВА IV. ОДНОМЕРНЫЙ ПОТОК ИДЕАЛЬНОЙ ЖИДКОСТИ
- § 26. Одномерное течение идеальной сжимаемой жидкости. Линеаризированные уравнения. Скорость распространения малых возмущений в жидкости или газе
- § 27. Изотермическая и адиабатическая скорости звука. «Конус возмущений» при сверхзвуковом движении источника возмущения. Число M и его связь с углом конуса возмущений
- § 28. Распространение непрерывных возмущений конечной интенсивности. Характеристики. Образование разрывной ударной волны
- § 29. Стоячая ударная волна или скачок уплотнения. Ударная адиабата
- § 30. Критические величины в одномерном потоке газа. Связь между скоростями до и после скачка. Изменение давления, плотности и температуры в скачке уплотнения
- § 31. Скорость распространения ударной волны. Спутное движение газа за ударной волной
- § 32. Влияние интенсивности скачка уплотнения на сжатие газа. Измерение скоростей и давлений в до- и сверхзвуковых потоках
- § 33. Одномерное движение газа по трубе переменного сечения. Истечение из резервуара большой емкости сквозь сходящееся сопло
- § 34. Одномерное течение в сопле Лаваля. Движение газа с притоком тепла
- ГЛАВА V. БЕЗВИХРЕВОЕ ДВИЖЕНИЕ ЖИДКОСТИ. ПЛОСКОЕ ДВИЖЕНИЕ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 35. Сохранение циркуляции скорости в потоке идеальной жидкости. Теорема Кельвина и Лаграижа. Безвихревое движение. Потенциал скоростей
- § 36. Интеграл Лагранжа — Коши уравнений безвихревого движения. Теорема Бернулли. Некоторые общие свойства безвихревого движения идеальной несжимаемой жидкости в односвязной области
- § 37. Плоское безвихревое движение несжимаемой жидкости. Потенциал скоростей и функция тока. Применение функций комплексного переменного. Комплексный потенциал и сопряженная скорость
- § 38. Построение полей течения по заданной характеристической Функции. Простейшие плоские потоки и их наложение
- § 39. Бесциркуляционное и циркуляционное обтекания круглого цилиндра
- § 40. Применение криволинейных координат. Бесциркуляционное и циркуляционное обтекания эллиптического цилиндра и пластинки. Задача Жуковского об обтекании решетки пластин.
- § 41. Плоское движение с отрывом струй. Разрывное обтекание пластинки и протекание жидкости сквозь отверстие
- § 42. Прямая задача в теории плоского движения идеальной несжимаемой жидкости. Применение метода конформных отображений. Гипотеза Чаплыгина о безотрывном обтекании задней кромки профиля. Формула циркуляции
- § 43. Теорема Жуковского о подъемной силе крыла. Зависимость подъемной силы от угла атаки. Коэффициент подъемной силы
- § 44. Применение метода комплексных переменных к выводу теоремы Жуковского. Формулы Чаплыгина для главного вектора и момента сил давления потока на крыло
- § 45. Выражение главного момента сил давления потока через коэффициенты конформного отображения. Фокус крыла. Независимость от угла атаки момента относительно фокуса. Парабола устойчивости
- § 46. Частные случаи конформного отображения крылового профиля на круг. Преобразование Жуковского-Чаплыгина. Теоретические крыловые профили
- § 47. Задача об обтекании слабо изогнутой дужки произвольной формы (теория тонкого крыла)
- § 48. Определение обтекания крылового профиля произвольной формы
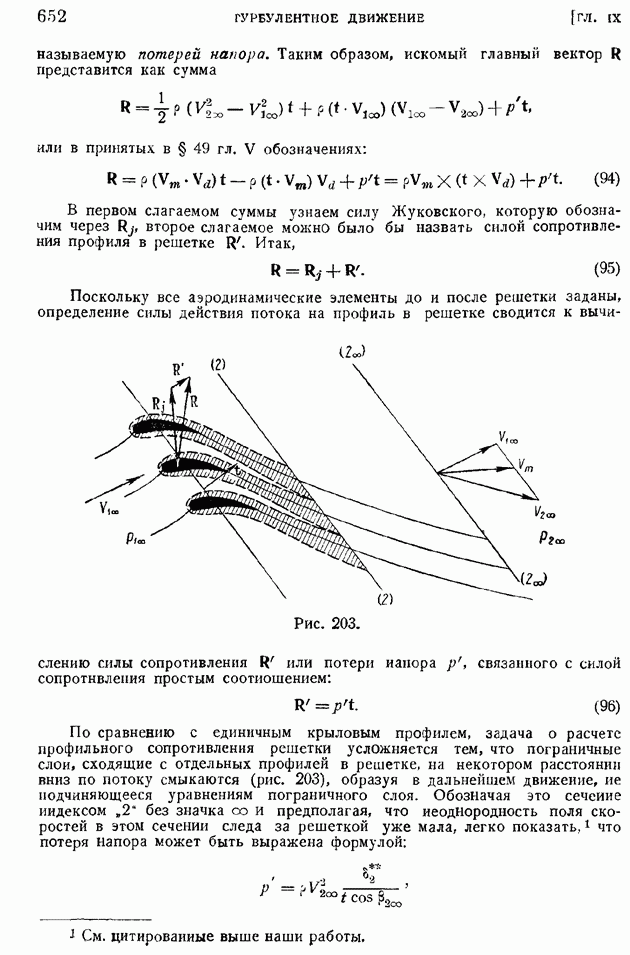
- § 49. Обобщение теоремы Жуковского на случай плоской решетки с бесчисленным множеством профилей
- ГЛАВА VI. ПЛОСКОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ СЖИМАЕМОГО ГАЗА
- § 50. Основные уравнения плоского стационарного безвихревого движения сжимаемого газа. Линеаризированные уравнения
- 51. Линеаризированный до- и сверхзвуковой газовый поток вдоль волнистой стенки
- § 52. Тонкое крыло в линеаризированном до- и сверхзвуковом потоках. Влияние сжимаемости газа на коэффициент подъемной силы в дозвуковом потоке. Коэффициенты подъемной силы и волнового сопротивления при сверхзвуковом потоке
- § 53. Нелинеаризированные уравнения движения идеального сжимаемого газа. Переход в плоскость годографа. Уравнения Чаплыгина
- § 54. Метод С. А. Христиановича. Приближенные формулы учета влияния сжимаемости на распределение давления
- § 55. Критическое число M и его определение по заданному распределению давления в несжимаемом обтекании. Поведение коэффициента подъемной силы и момента при около- и закритических значениях числа M
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
- § 57. Нелинеаризированный сверхзвуковой поток. «Характеристики» уравнений плоского сверхзвукового потока. Линин возмущения и их основные свойства
- § 58. Обтекание выпуклого угла сверхзвуковым потоком. Влияние угла поворота струи на ее газодинамические элементы
- § 59. Сверхзвуковой поток внутри тупого угла. Косой скачок уплотнения. Связь между газодинамическими элементами до и за косым скачком
- ГЛАВА VII. ПРОСТРАНСТВЕННОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ
- § 60. Ортогональные криволинейные координаты в пространстве. Основные дифференциальные операторы поля в криволинейных координатах
- § 61. Потенциал скоростей. Поле источника и диполя. Непрерывное распределение источников и диполей. Ньютонов потенциал. Потенциал простого и двойного слоев
- § 62. Поле скоростей вокруг заданной системы вихрей. Формула Био — Савара. Потенциал скоростей замкнутой вихревой нити. Аналогия с потенциалом двойного слоя
- § 63. Функция тока и ее связь с векторным потенциалом скоростей. Функции тока простейших течений
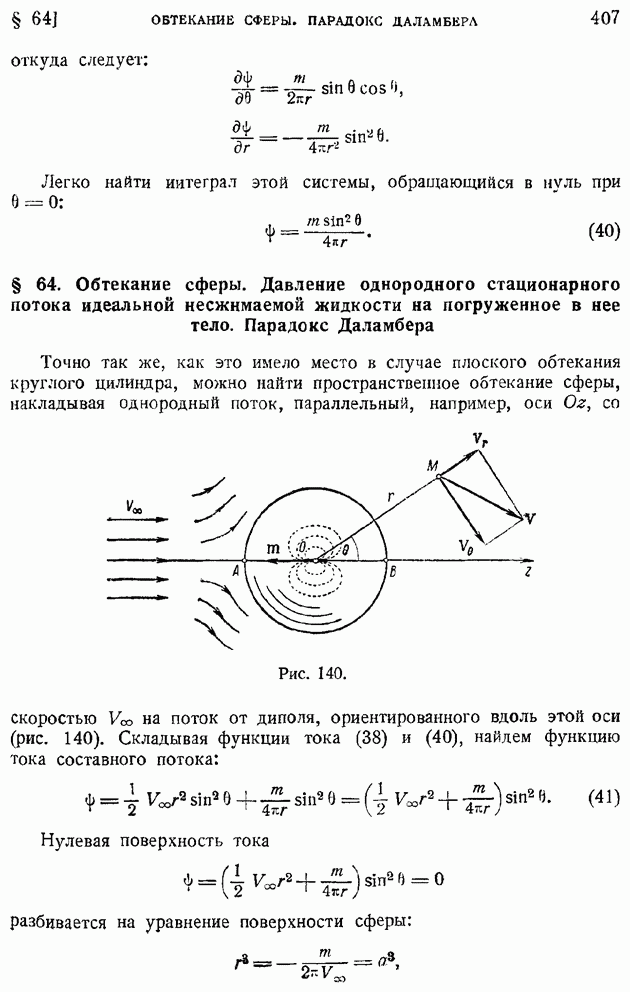
- § 64. Обтекание сферы. Давление однородного стационарного потока идеальной несжимаемой жидкости на погруженное в нее тело. Парадокс Даламбера
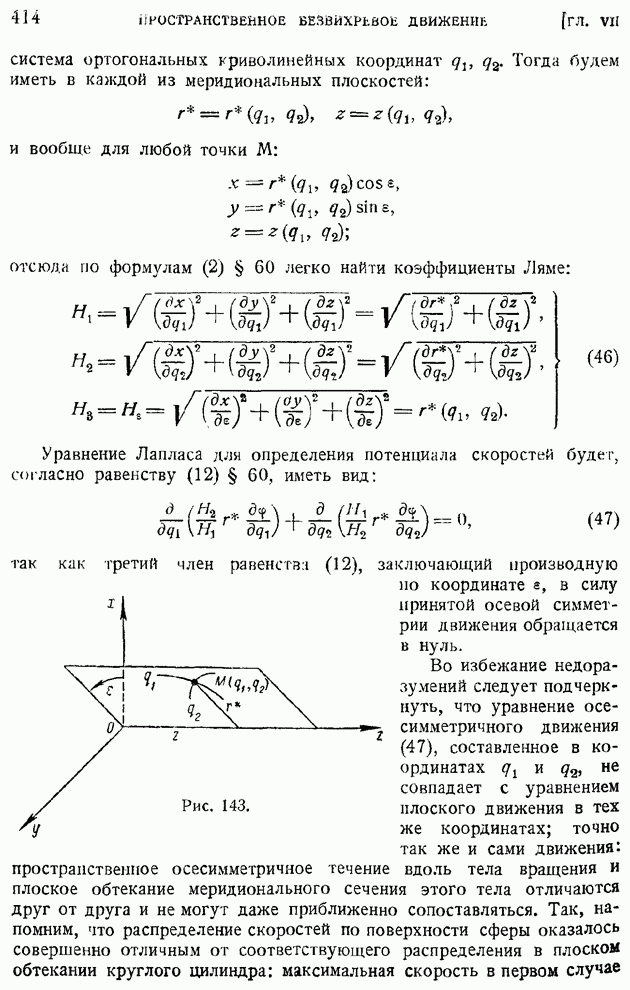
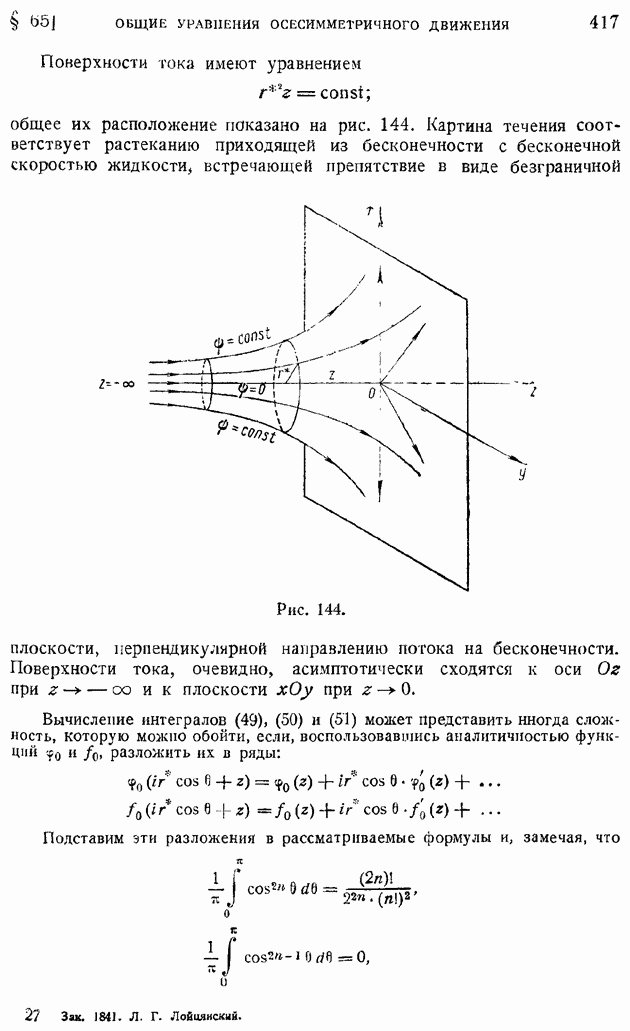
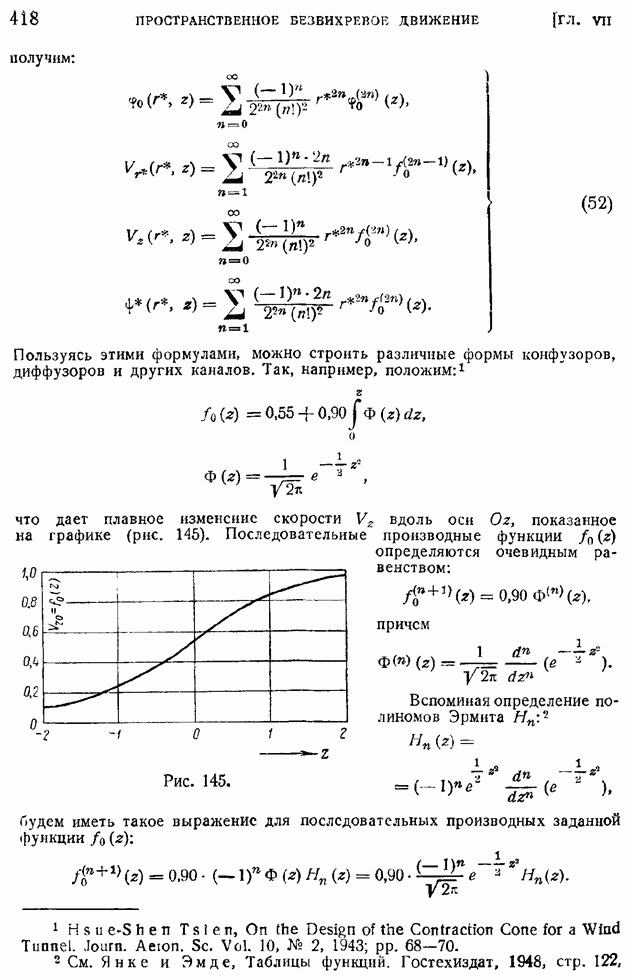
- § 65. Общие уравнения осесимметричного движения. Применение цилиндрических координат. Течение сквозь каналы
- § 66. Осесимметричное продольное обтекание тел вращения. Случай эллипсоида вращения
- § 67. Поперечное обтекание тел вращения. Пример эллипсоида вращения
- § 68. Продольное и поперечное обтекание тел вращения большого удлинения. Приближенные выражения граничных условий. Применение тригонометрических сумм для определения коэффициентов …
- § 69. Метод «особенностей». Применение непрерывно распределенных источников (стоков) и диполей для решения задачи о продольном и поперечном обтекании тел вращения
- § 70. Общий случай движения твердого тела сквозь несжимаемую идеальную жидкость. Определение потенциала скоростей. Главный вектор и главный момент сил давления потока на тело
- § 71. Коэффициенты «присоединенных масс». Свойство симметрии. «Присоединенная» кинетическая энергия. Определение «присоединенных масс» поступательно движущегося цилиндра, шара и эллипсоида
- § 72. Элементы теории крыла конечного размаха. Вихревая система крыла. Гипотеза плоских сечеиий. Геометрические и действительные углы атаки. Подъемная сила и «индуктивное сопротивление»
- § 73. Основные формулы теории «несущей линии». «Индуктивная скорость» и «индуктивный угол». Прямая задача определения подъемной силы и индуктивного сопротивления по заданному распределению циркуляции
- § 74. Крыло с минимальным индуктивным сопротивлением. Эллиптическое распределение циркуляции. Связь между коэффициентами индуктивного сопротивления и подъемной силы. Основное уравнение теории крыла и понятие о его интегрировании
- ГЛАВА VIII. ДИНАМИКА ВЯЗКОЙ ЖИДКОСТИ И ГАЗА
- § 75. Внутреннее трение и теплопроводность в жидкостях и газах. Законы Ньютона и Фурье. Влияние температуры на коэффициенты вязкости и теплопроводности. Число «сигма»
- § 76. Обобщение закона Ньютона на случай произвольного движения среды. Закон линейной связи между тензорами напряжений и скоростей деформации
- § 77. Общие уравнения движения вязкой жидкости. Динамические уравнения и уравнение баланса энергии. Граничные условия движения жидкости с треннем и теплопроводностью
- § 78. Понятие о подобии гидродинамических явлений. Безразмерные уравнения движения вязкой жидкости и газа. Условия подобия
- § 79. Ламинарное движение вязкой несжимаемой жидкости по цилиндрической трубе
- § 80. Обтекание шара при очень малых значениях числа Рейнольдса. Формула сопротивления шара по Стоксу и ее обобщения
- § 81. Вихревые линии в идеальной и вязкой жидкости. Сохраняемость вихревых линий при отсутствии внутреннего трения. Диффузия вихря в вязкой жидкости
- § 82. Одномерное прямолинейное движение сжимаемого вязкого газа. Движение внутри скачка уплотнения. Понятие о толщине скачка
- § 83. Работа внутренних сил и диссипация механической энергии в движущейся вязкой среде
- § 84. Обтекание тел жидкостью и газом при больших значениях числа Рейнольдса. Основные уравнения теории ламинарного пограничного слоя
- § 85. Ламинарный пограничный слой на пластинке, продольно обтекаемой несжимаемой жидкостью. Неизотермическое движение
- § 86. Ламинарный пограничный слой при степенном задании скорости внешнего потока
- § 87. Ламинарный пограничный слой в общем случае задания скорости внешнего потока. Применение уравнения импульсов для приближенного расчета ламинарного пограничного слоя
- § 88. Способы определения функций … Приближенный метод расчета ламинарного пограничного слоя
- § 89. Ламинарный пограничный слой на пластинке, продольно обтекаемой сжимаемым газом при больших скоростях. Случай линейной зависимости коэффициента вязкости от температуры (n = 1)
- § 90. Ламинарный пограничный слой на пластинке при любом законе связи между вязкостью и температурой и при числе … Обтекание крылового профиля потоком больших скоростей
- ГЛАВА IX. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ
- § 91. Переход ламинарного движения в турбулентное. Критическое рейнольдсово число
- § 92. Область и «точка» перехода. Явление «кризиса обтекания»
- § 93. Основные уравнения осреднеиного турбулентного движения. Тензор турбулентных напряжений
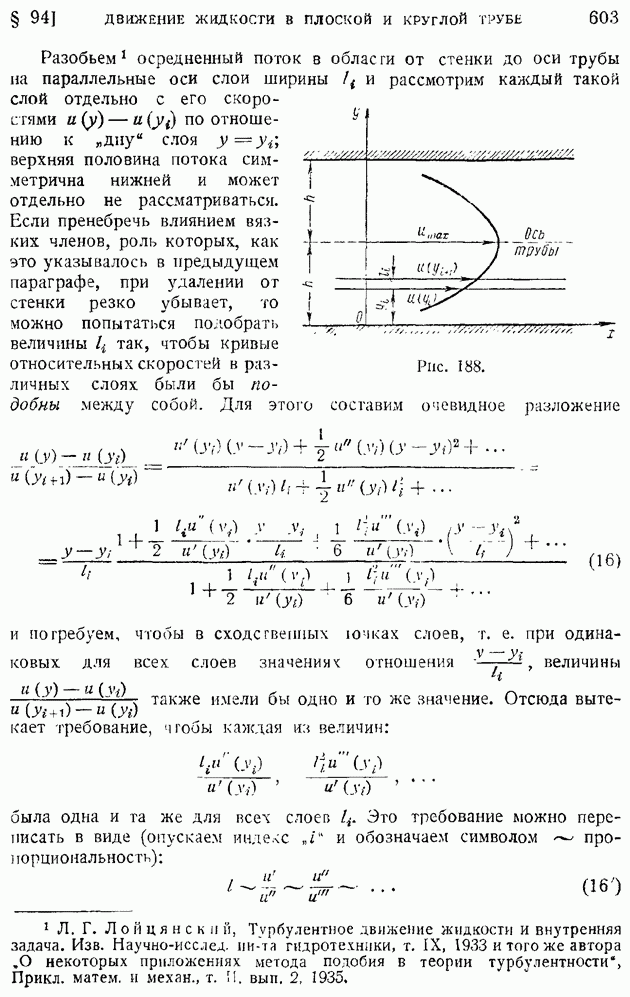
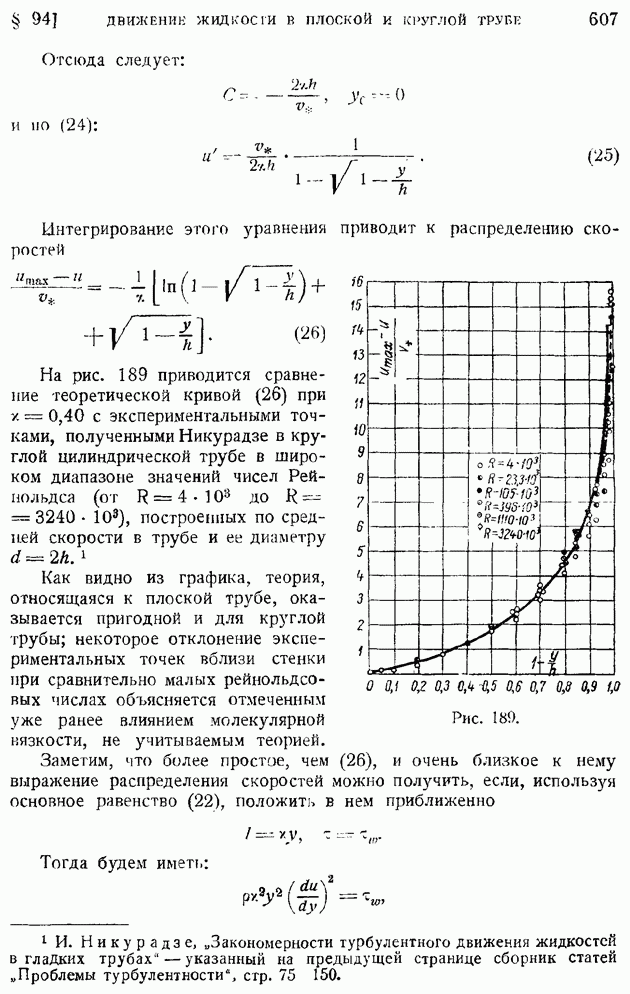
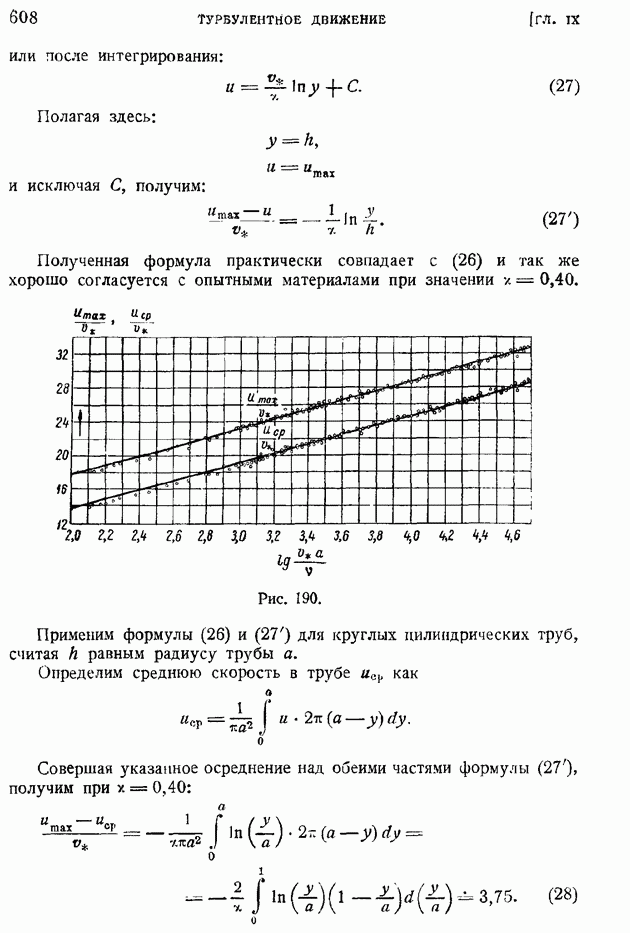
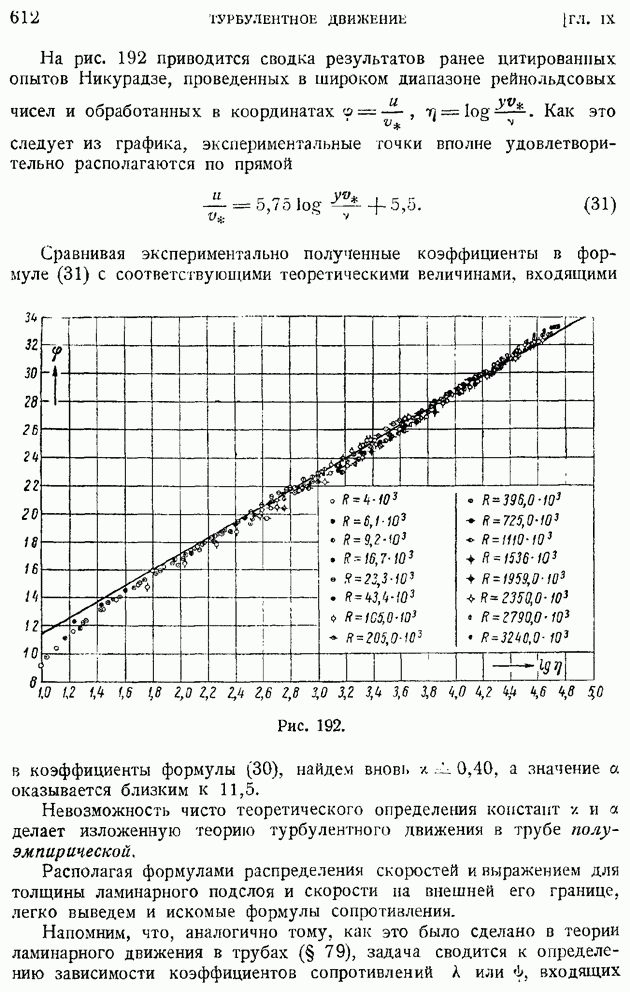
- § 94. Турбулентное движение жидкости в плоской и круглой трубе. Логарифмические формулы скоростей
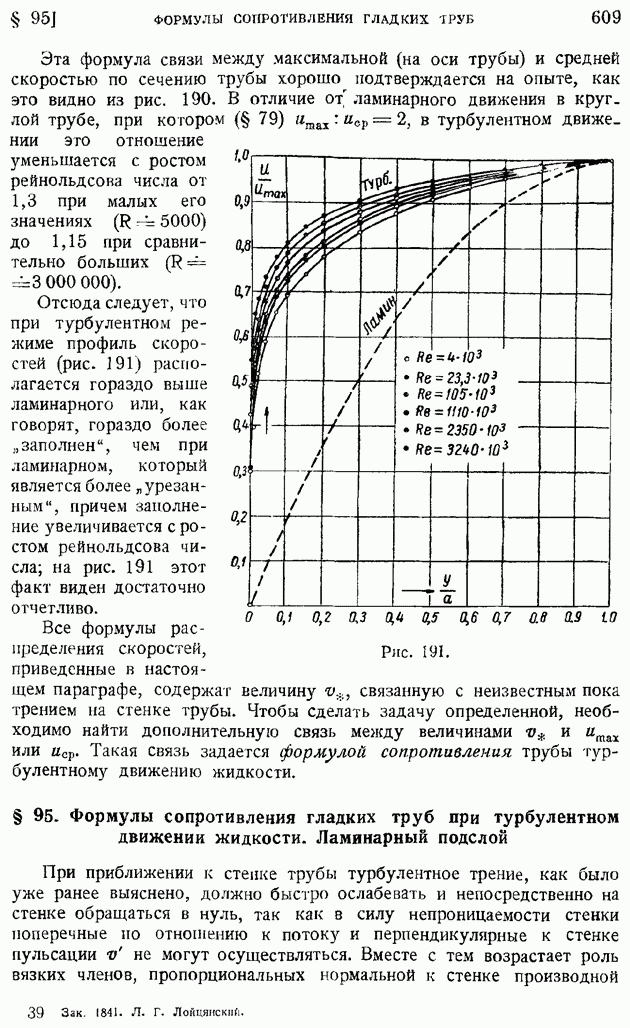
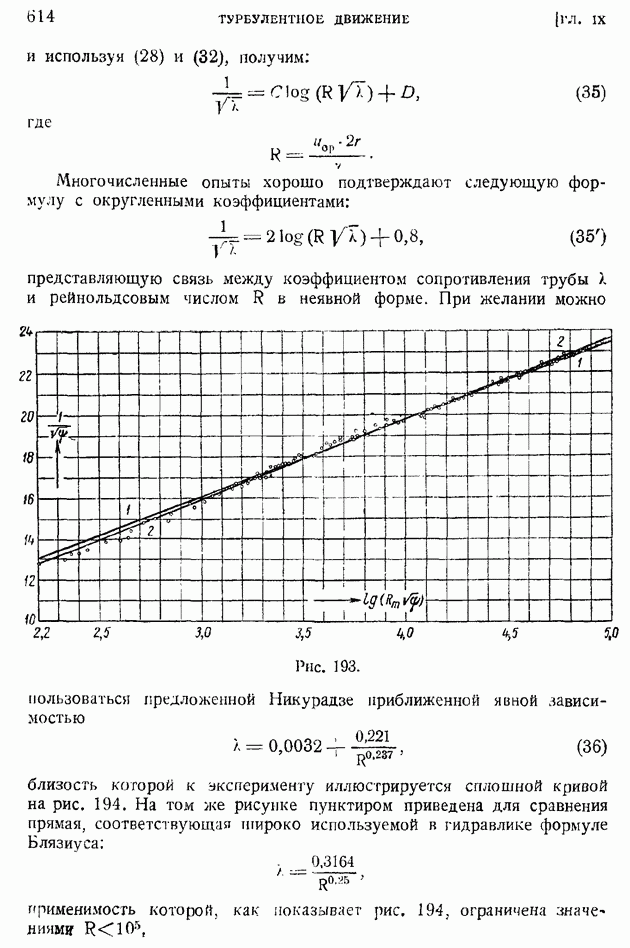
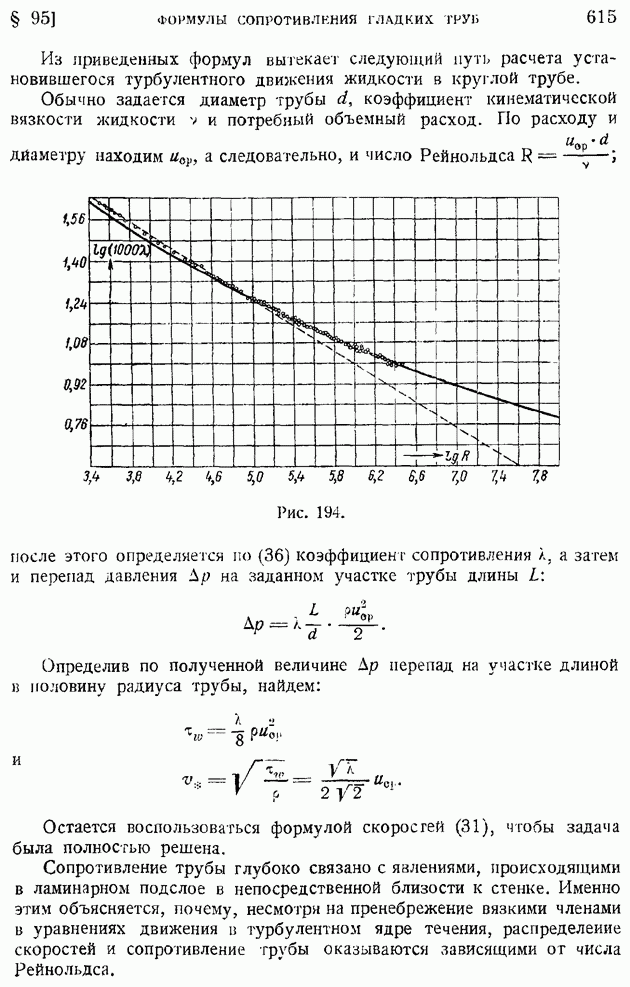
- § 95. Формулы сопротивления гладких труб при турбулентном движении жидкости. Ламинарный подслой
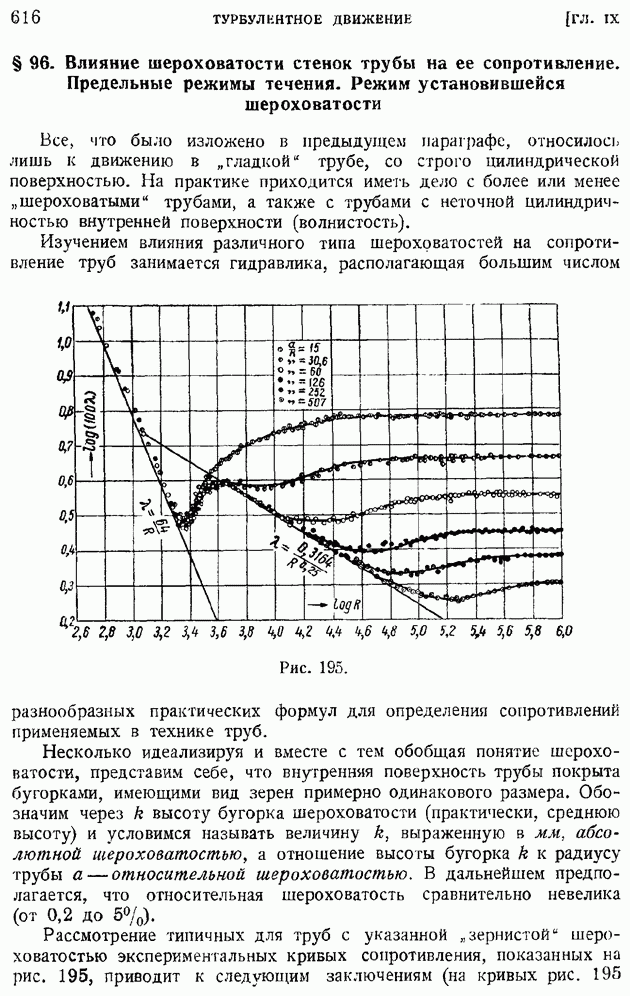
- § 96. Влияние шероховатости стенок трубы на ее сопротивление. Предельные режимы течения. Режим установившейся шероховатости
- § 97. Турбулентный пограничный слой на продольно обтекаемой пластине. Сопротивление пластины
- § 98. Турбулентный пограничный слой на крыловом профиле при малом продольном перепаде давлений
- § 99. Турбулентный пограничный слой на крыловом профиле при значительных продольных перепадах давления
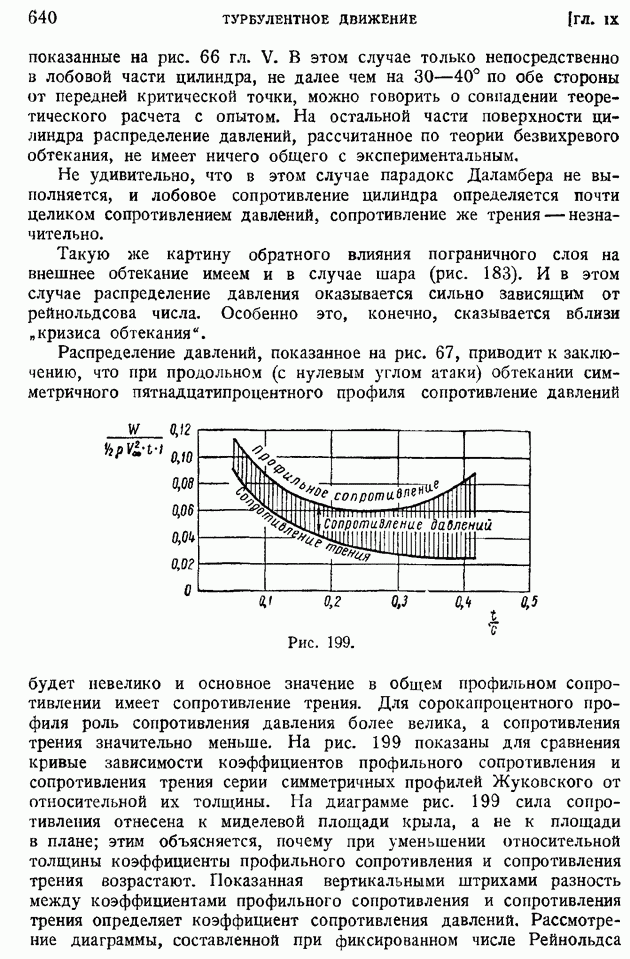
- § 100. Профильное сопротивление крыла. Разложение профильного сопротивления на сопротивление трения и сопротивление давлений. Обратное влияние пограничного слоя на распределение давлений по поверхности обтекаемого профиля
- § 101. Приближенные формулы профильного сопротивления крыла и крылового профиля в решетке
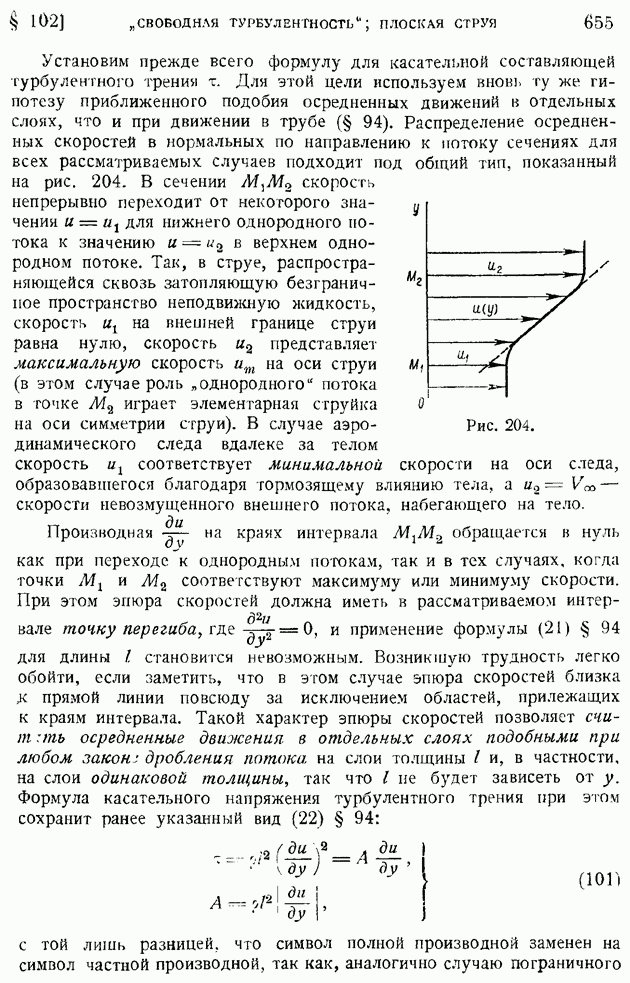
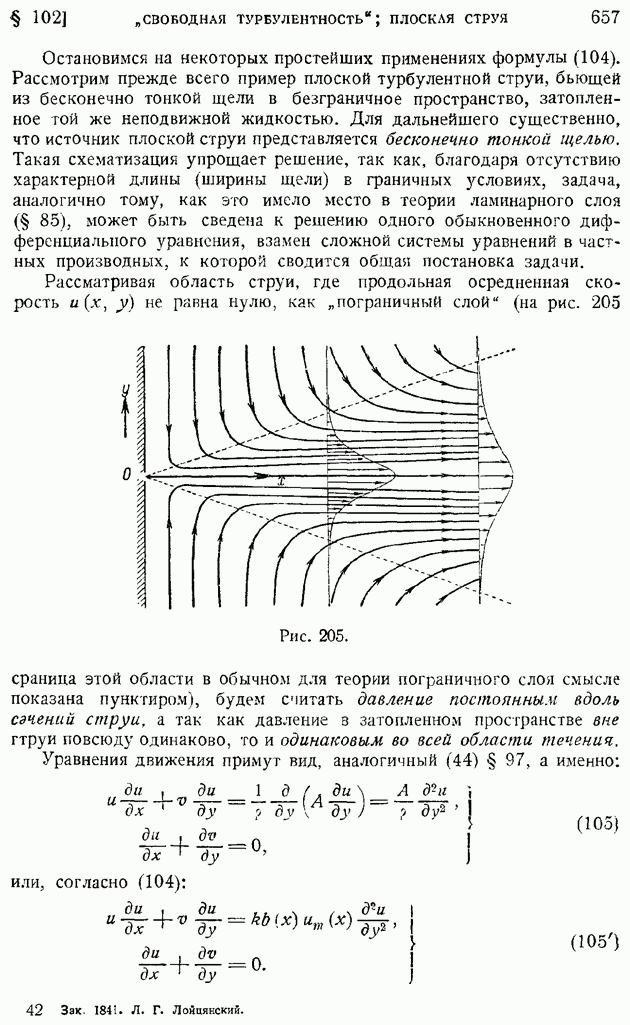
- § 102. Основные закономерности «свободной турбулентности». Плоская турбулентная струя в пространстве, заполненном той же жидкостью
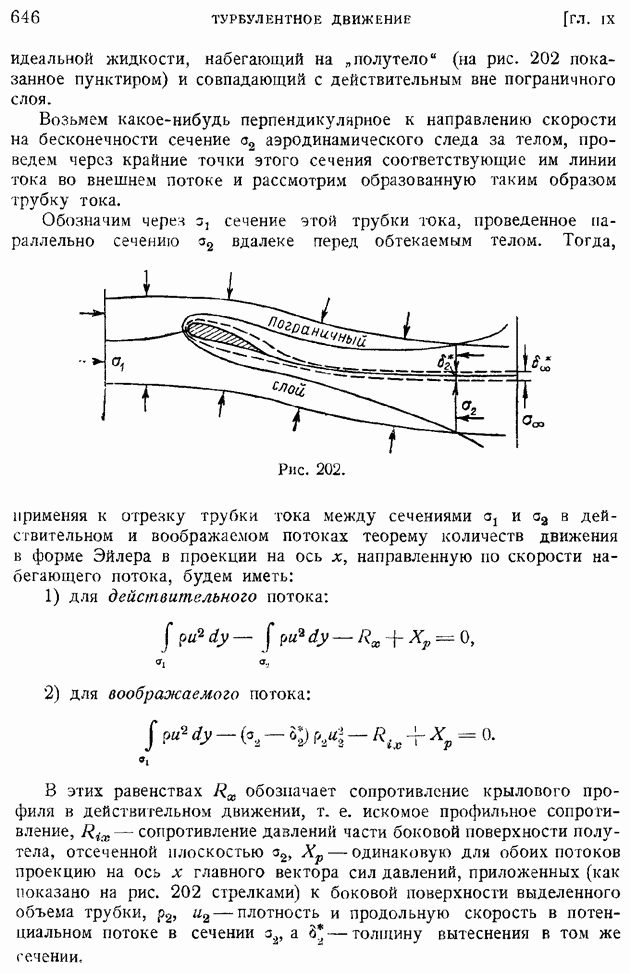
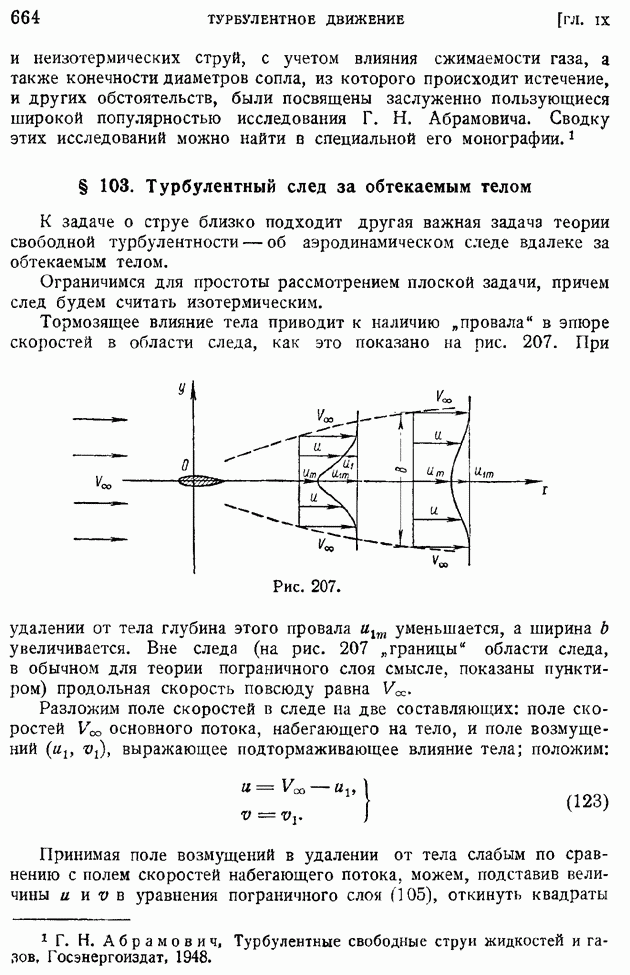
- § 103. Турбулентный след за обтекаемым телом
- § 104. Рассеяние турбулентных возмущений в жидкости. Случай изотропной и однородной турбулентности. Закон сохранения момента возмущений