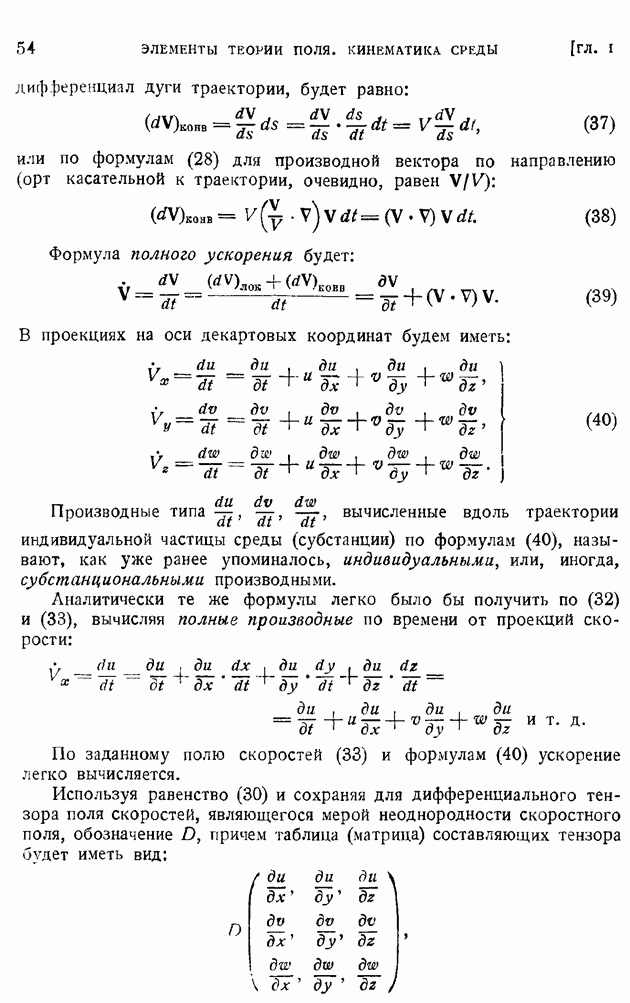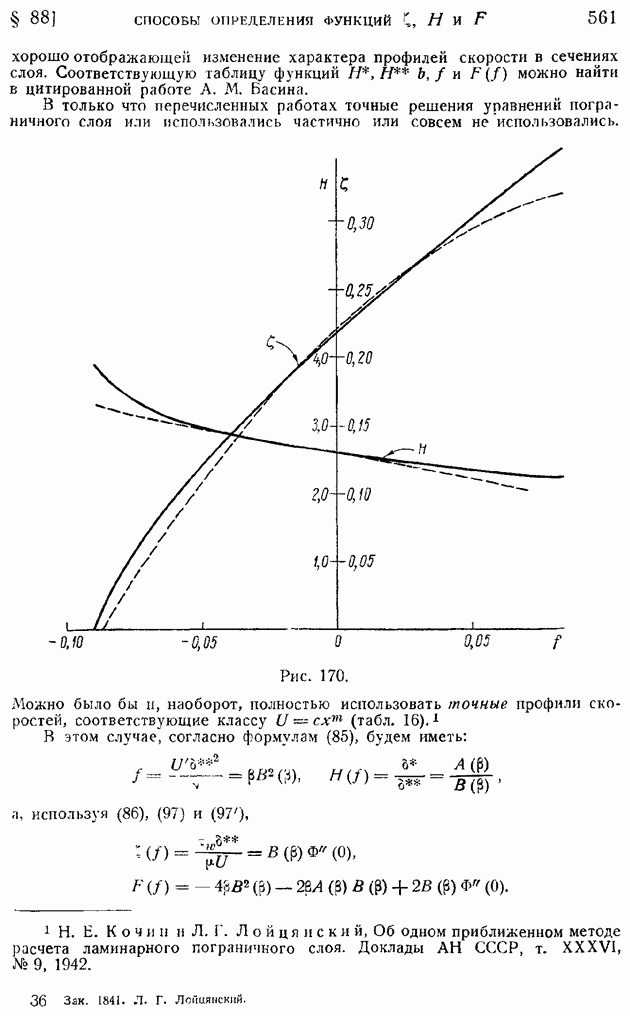| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
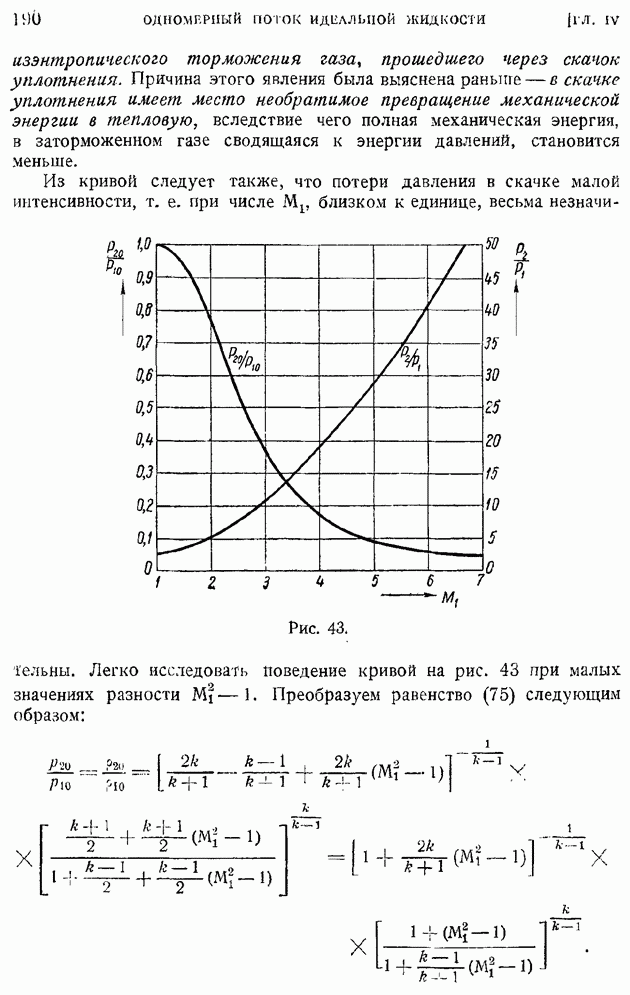
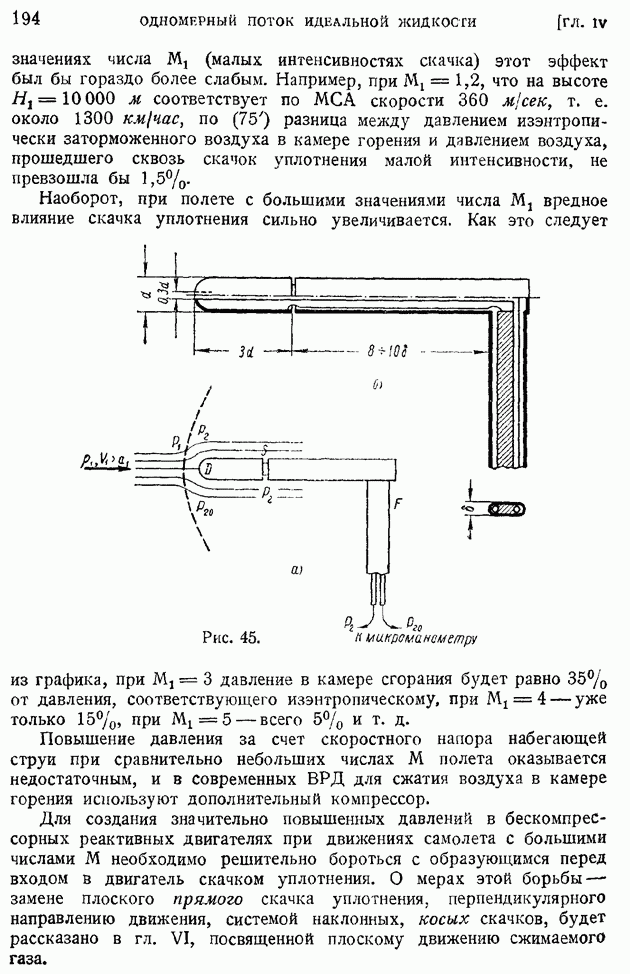
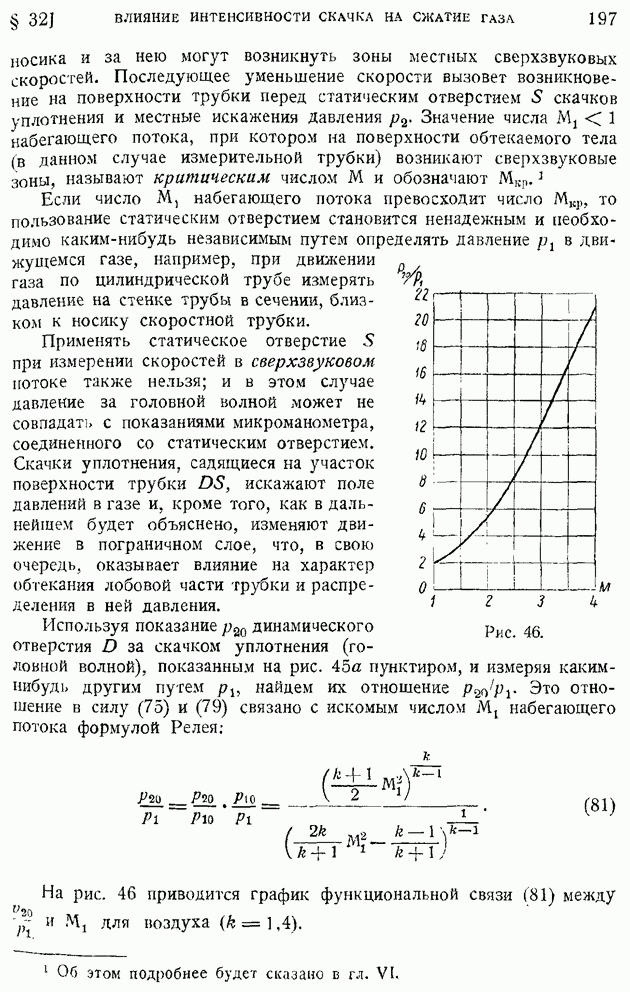
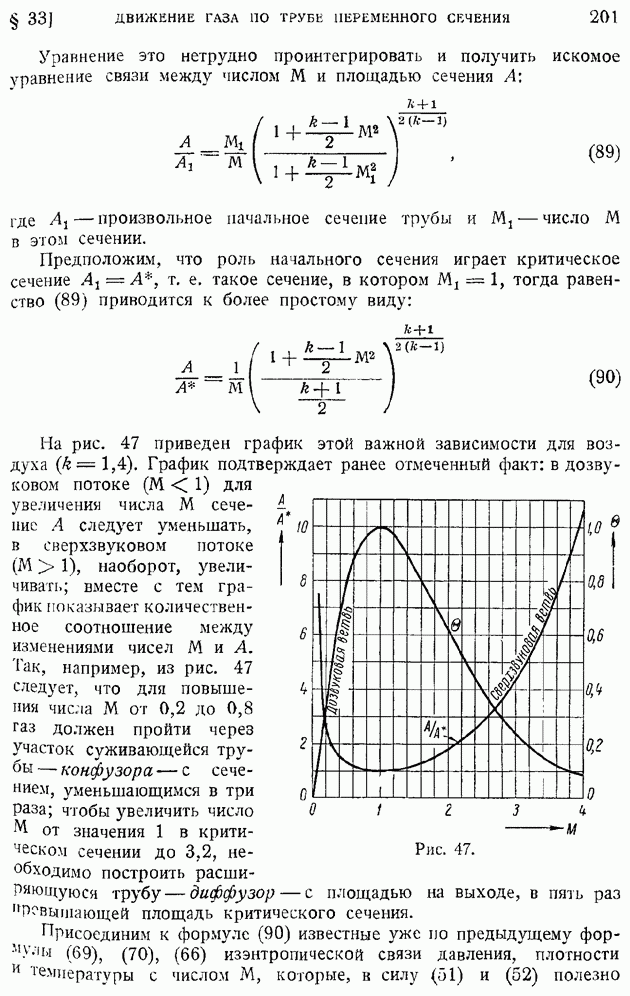
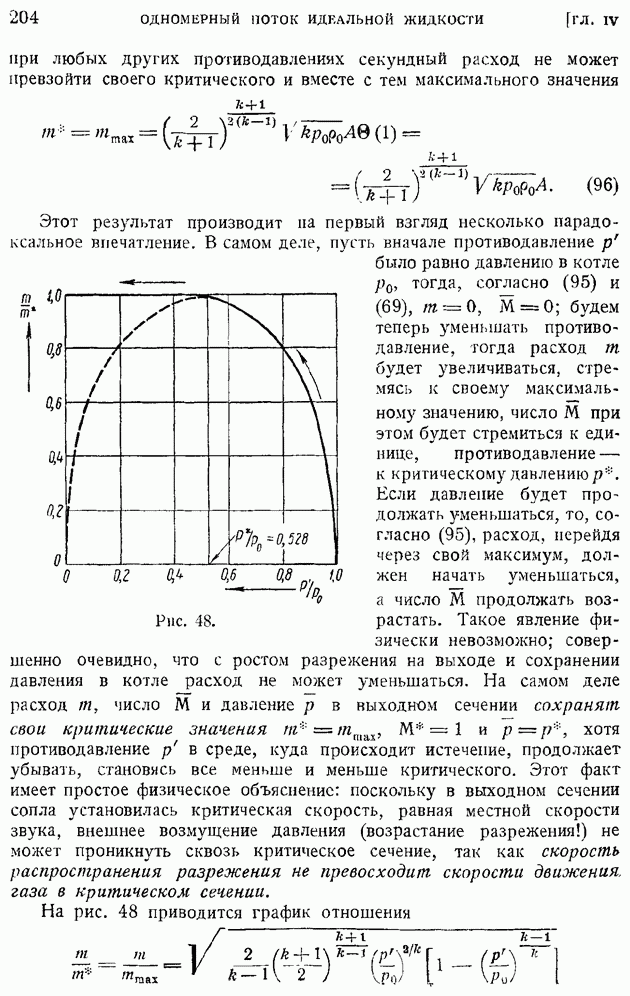
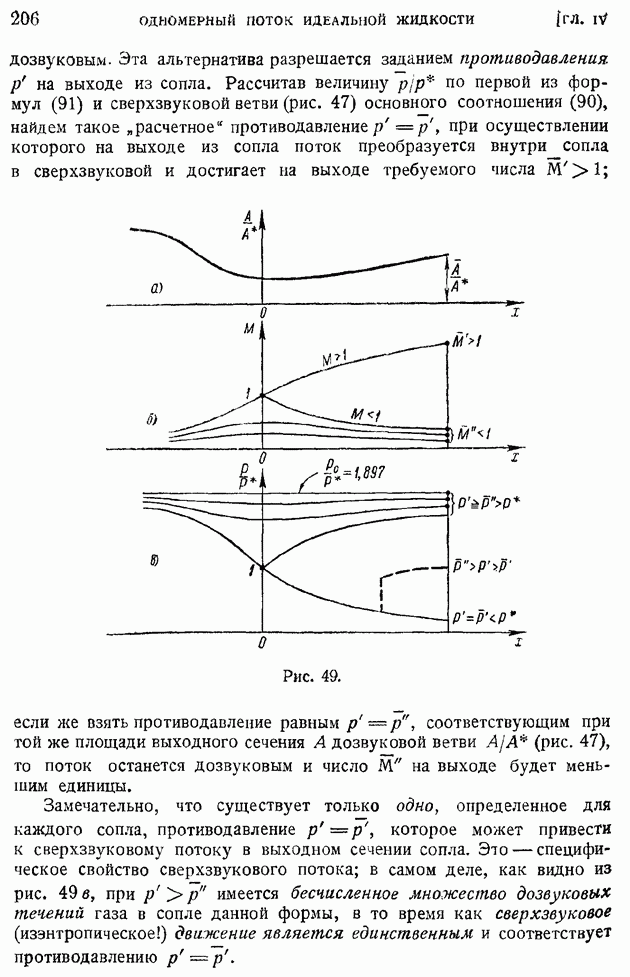
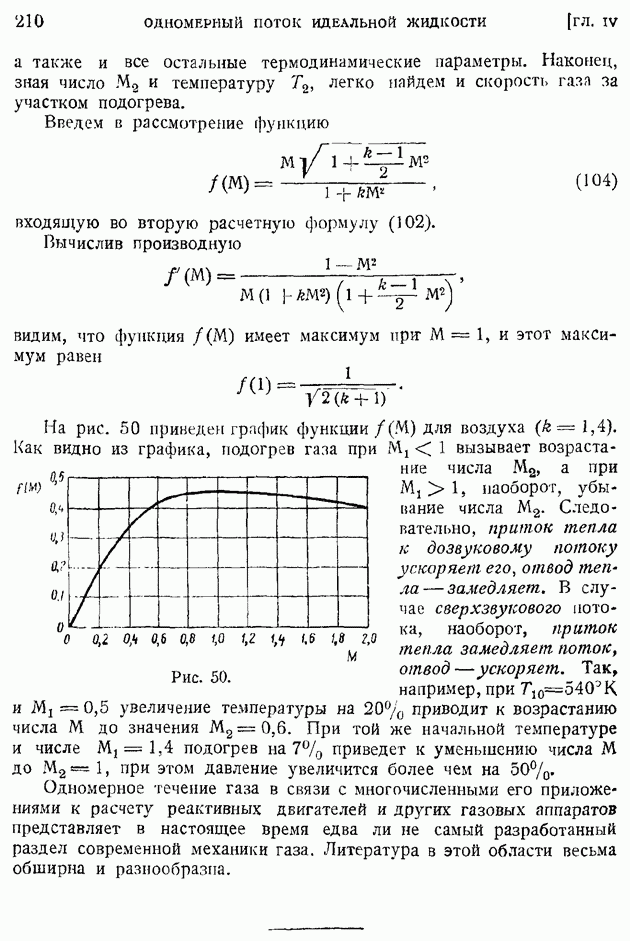
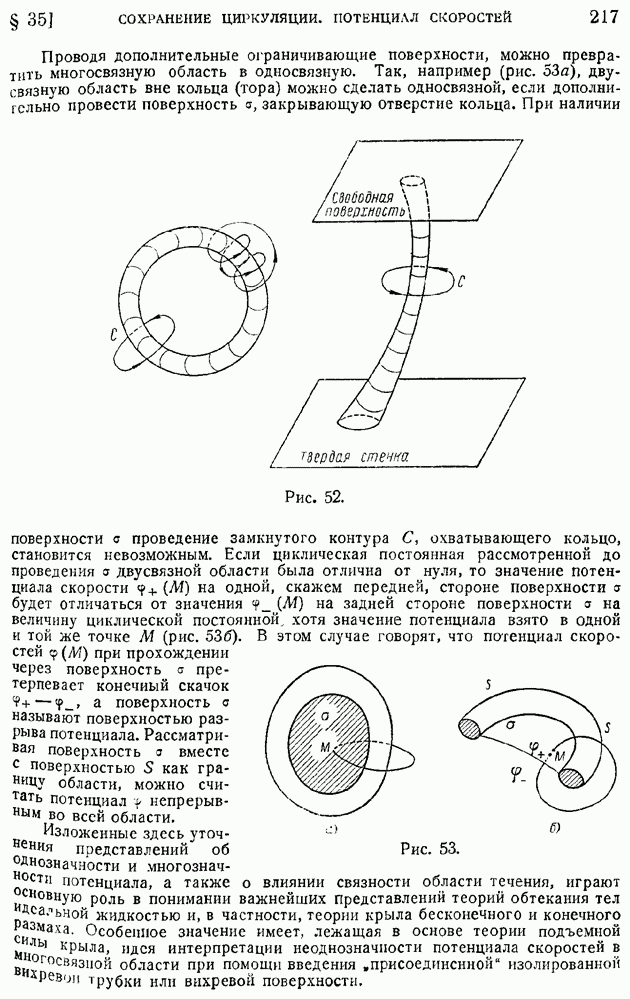
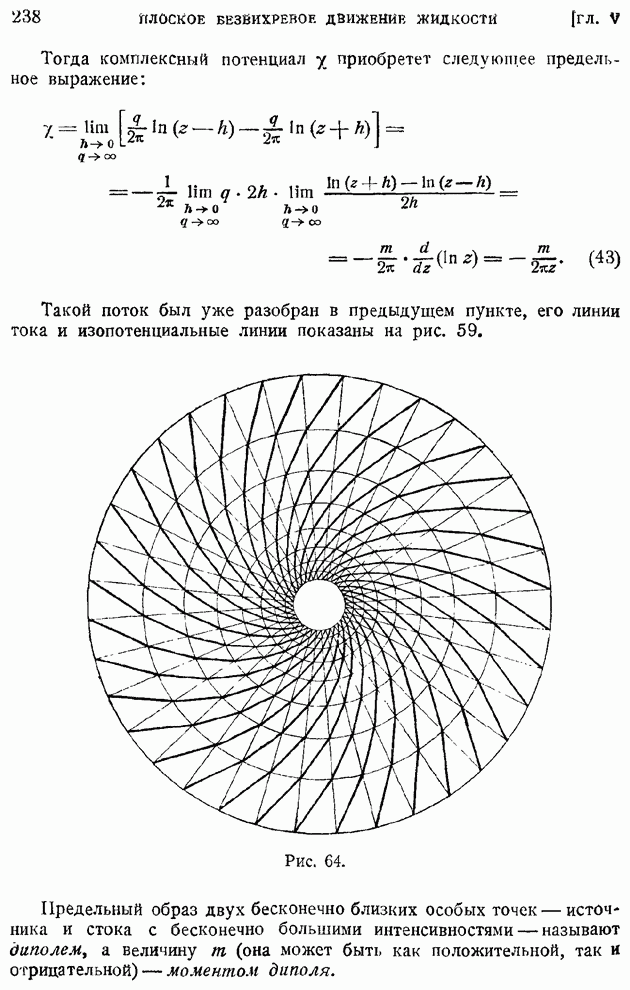
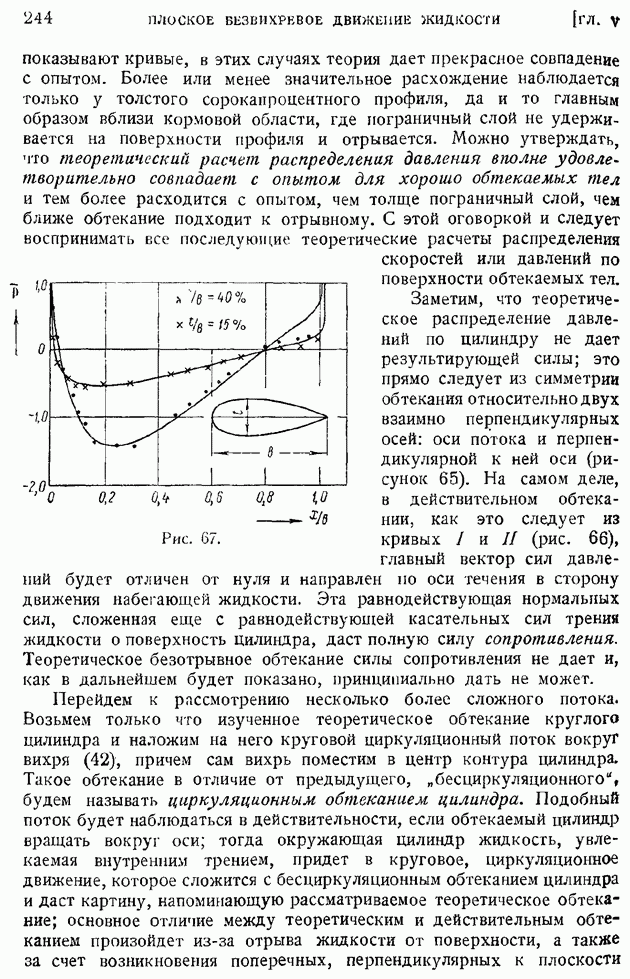
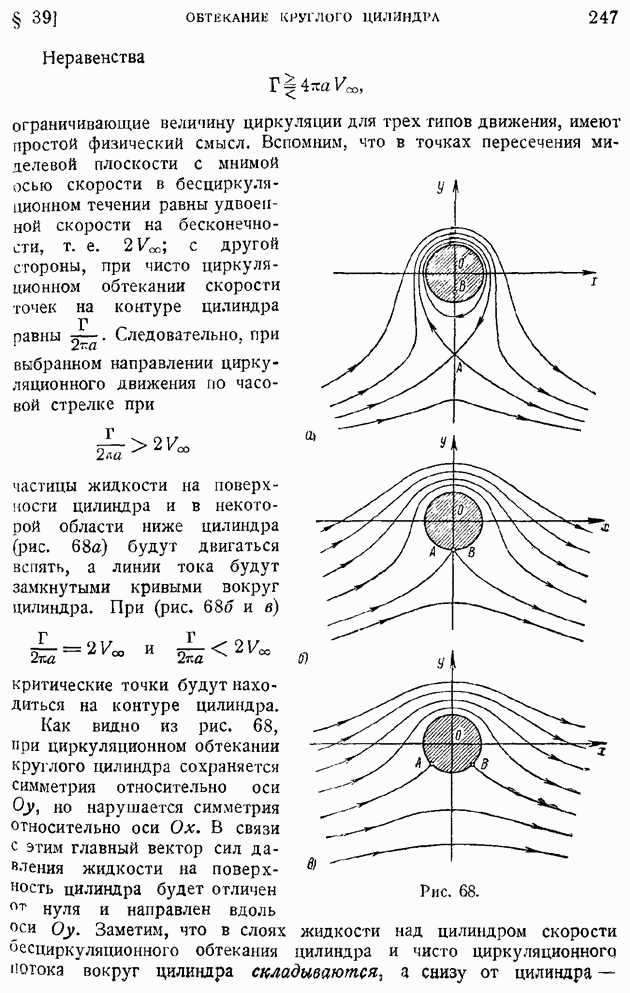
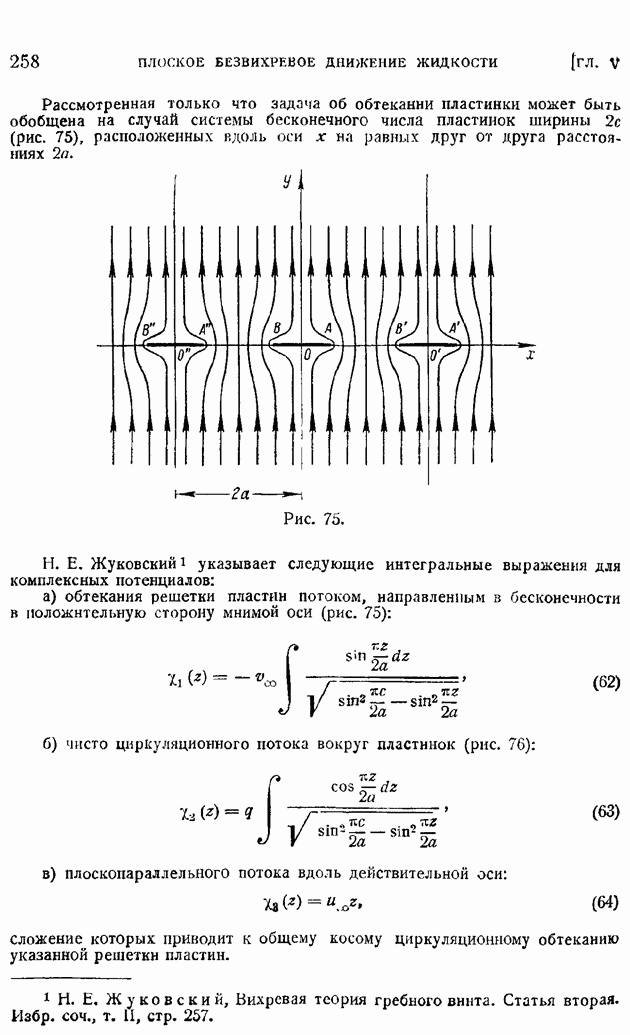
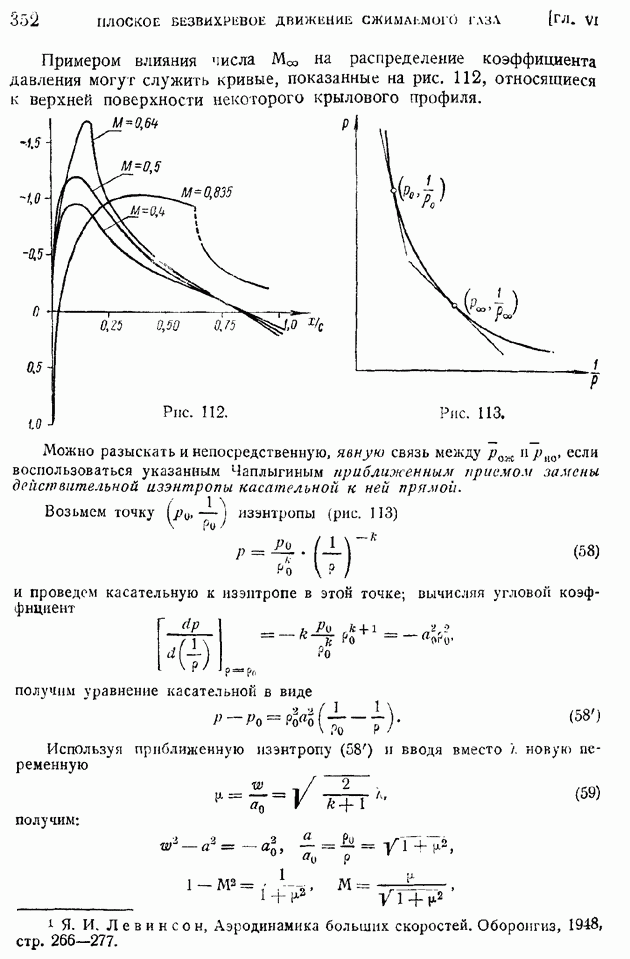
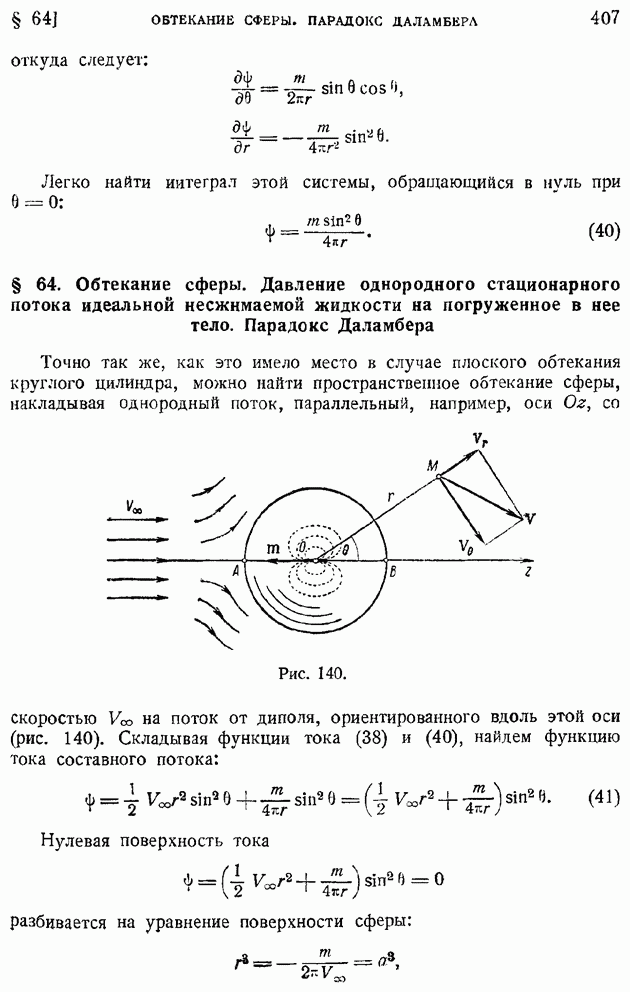
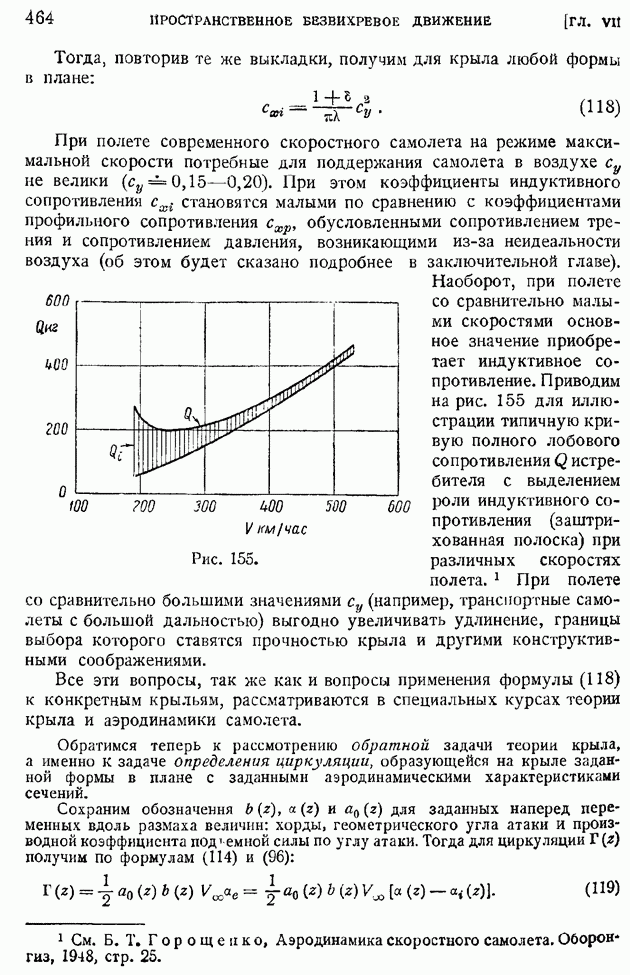
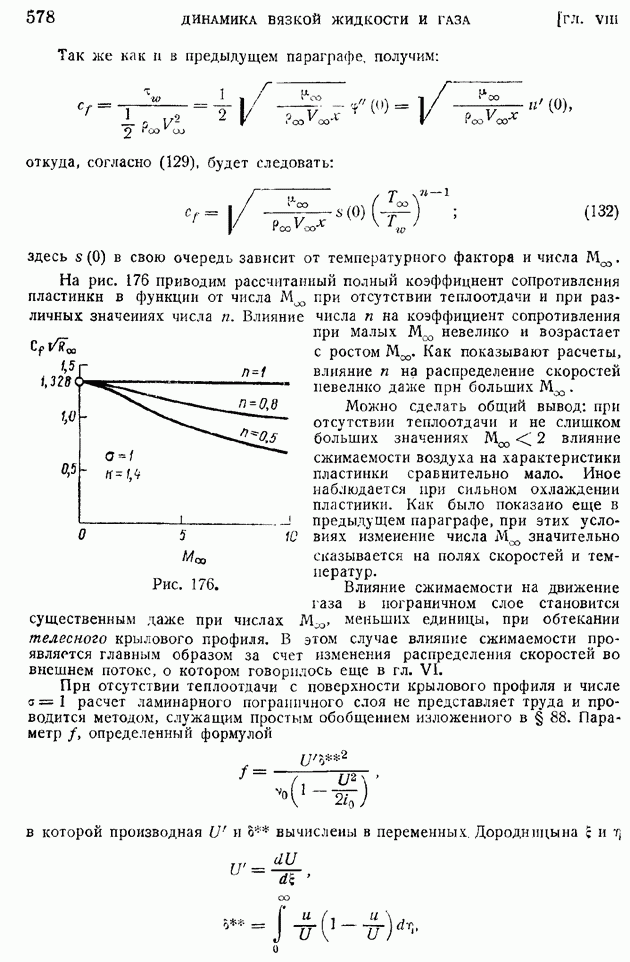
§ 92. Область и «точка» перехода. Явление «кризиса обтекания»
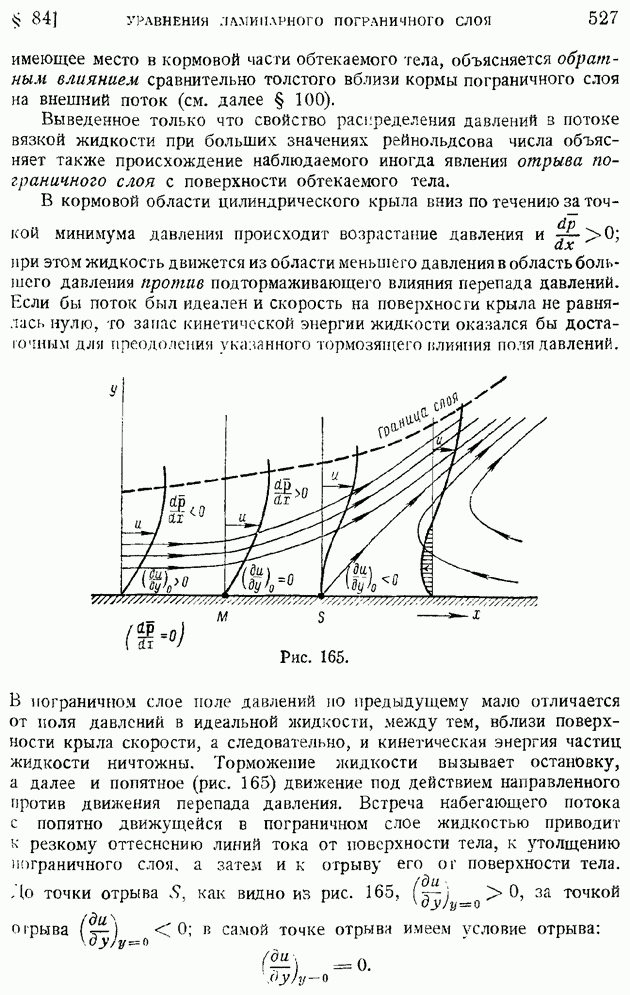
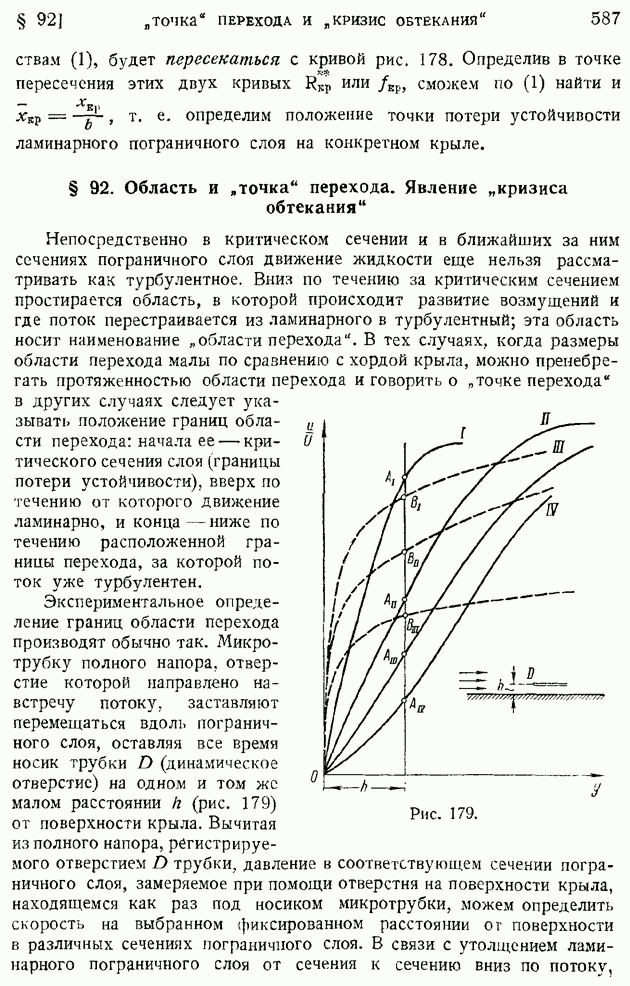
Непосредственно в критическом сечении и в ближайших за ним сечениях пограничного слоя движение жидкости еще нельзя рассматривать как турбулентное. Вниз по течению за критическим сечением простирается область, в которой происходит развитие возмущений и где поток перестраивается из ламинарного в турбулентный; эта область носит наименование "области перехода". В тех случаях, когда размеры области перехода малы по сравнению с хордой крыла, можно пренебрегать протяженностью области перехода и говорить о "точке перехода" в других случаях следует указывать положение границ области перехода: начала ее — критического сечения слоя (границы потери устойчивости), вверх по течению от которого движение ламинарно, и конца — ниже по течению расположенной границы перехода, за которой поток уже турбулентен.

Рис. 179.
Экспериментальное определение границ области перехода производят обычно так. Микротрубку полного напора, отверстие которой направлено навстречу потоку, заставляют перемещаться вдоль пограничного слоя, оставляя все время носик трубки  (динамическое отверстие) на одном и том же малом расстоянии
(динамическое отверстие) на одном и том же малом расстоянии  (рис. 179) от поверхности крыла. Вычитая из полного напора, регистрируемого отверстием
(рис. 179) от поверхности крыла. Вычитая из полного напора, регистрируемого отверстием  трубки, давление в соответствующем сечении пограничного слоя, замеряемое при помощи отверстия на поверхности крыла, находящемся как раз под носиком микротрубки, можем определить скорость на выбранном фиксированном расстоянии
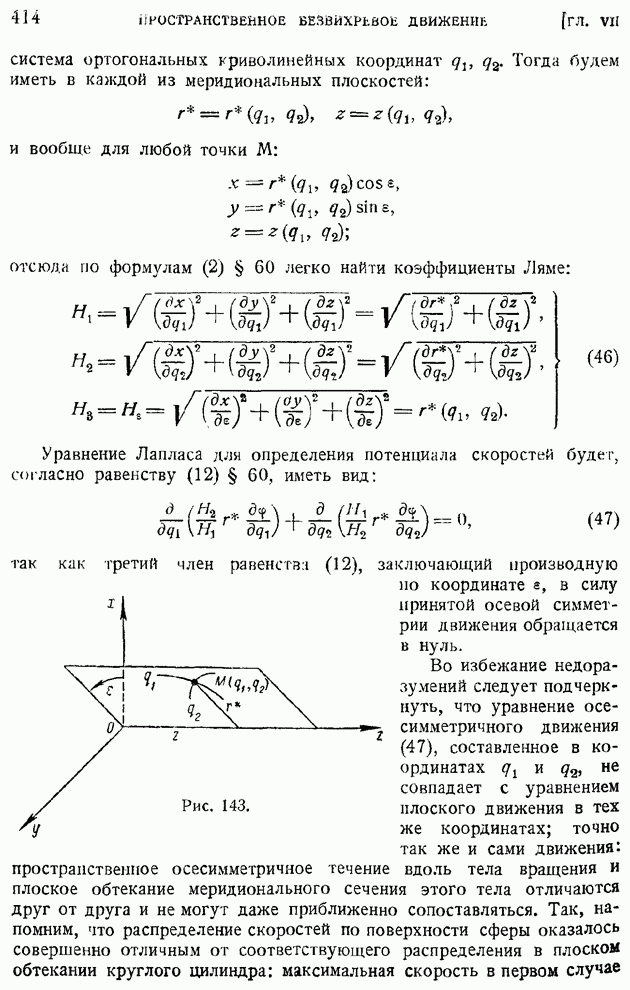
трубки, давление в соответствующем сечении пограничного слоя, замеряемое при помощи отверстия на поверхности крыла, находящемся как раз под носиком микротрубки, можем определить скорость на выбранном фиксированном расстоянии  поверхности в различных сечениях пограничного слоя. В связи с утолщением ламинарного пограничного слоя от сечения к сечению вниз по потоку.
поверхности в различных сечениях пограничного слоя. В связи с утолщением ламинарного пограничного слоя от сечения к сечению вниз по потоку.
безразмерная скорость  измеряемая на одном и том же расстоянии от поверхности крыла внутри слоя, должна убывать. Действительно, относительная координата у точки замера при этом уменьшается, а сама точка как бы все глубже погружается в пограничный слой, переходя к относительно меньшим скоростям. На рис. 179 для примера показаны экспериментальные профили скоростей в последовательных сечениях
измеряемая на одном и том же расстоянии от поверхности крыла внутри слоя, должна убывать. Действительно, относительная координата у точки замера при этом уменьшается, а сама точка как бы все глубже погружается в пограничный слой, переходя к относительно меньшим скоростям. На рис. 179 для примера показаны экспериментальные профили скоростей в последовательных сечениях  ламинарного пограничного слоя на крыле при одном и том же значении
ламинарного пограничного слоя на крыле при одном и том же значении  Вертикальная прямая соответствует выбранному расстоянию
Вертикальная прямая соответствует выбранному расстоянию  носика микротрубки от поверхности крыла. Точки
носика микротрубки от поверхности крыла. Точки  дают ряд убывающих значений регистрируемых микрогрубкой. Профили скоростей в турбулентном пограничном слое по своей форме резко отличаются от профилей скорости в ламинарном пограничном слое (пунктирные профили на том же рисунке). Когда носик трубки попадет в турбулентный пограничный слой, величина — от сравнительно малого значения (точка
дают ряд убывающих значений регистрируемых микрогрубкой. Профили скоростей в турбулентном пограничном слое по своей форме резко отличаются от профилей скорости в ламинарном пограничном слое (пунктирные профили на том же рисунке). Когда носик трубки попадет в турбулентный пограничный слой, величина — от сравнительно малого значения (точка  ) резко поднимется до значения
) резко поднимется до значения  а затем будет опять падать, проходя значения
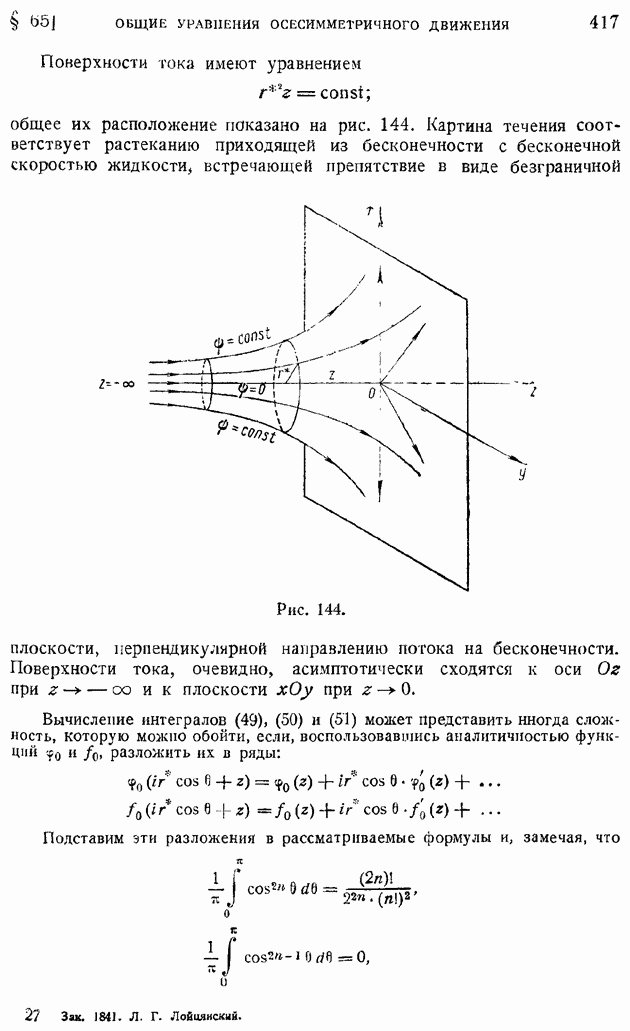
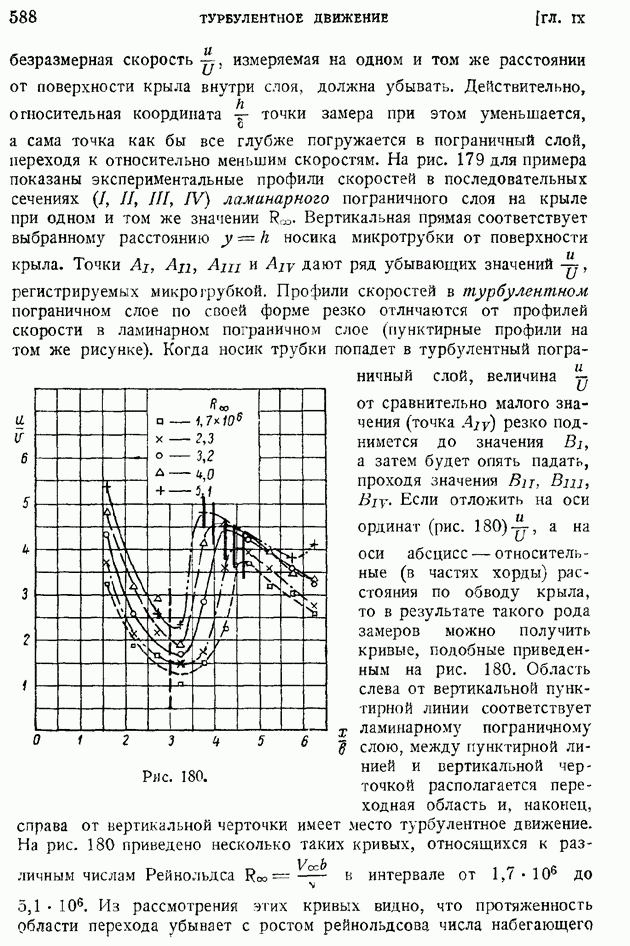
а затем будет опять падать, проходя значения  Если отложить на оси ординат (рис. 180), а на оси абсцисс — относительные (в частях хорды) расстояния по обводу крыла, то в результате такого рода замеров можно получить кривые, подобные приведенным на рис. 180. Область слева от вертикальной пунктирной линии соответствует ламинарному пограничному слою, между пунктирной линией и вертикальной черточкой располагается переходная область и, наконец, справа от вертикальной черточки имеет место турбулентное движение. На рис. 180 приведено несколько таких кривых, относящихся к различным числам Рейнольдса
Если отложить на оси ординат (рис. 180), а на оси абсцисс — относительные (в частях хорды) расстояния по обводу крыла, то в результате такого рода замеров можно получить кривые, подобные приведенным на рис. 180. Область слева от вертикальной пунктирной линии соответствует ламинарному пограничному слою, между пунктирной линией и вертикальной черточкой располагается переходная область и, наконец, справа от вертикальной черточки имеет место турбулентное движение. На рис. 180 приведено несколько таких кривых, относящихся к различным числам Рейнольдса  интервале от
интервале от  до
до  Из рассмотрения этих кривых видно, что протяженность Области перехода убывает с ростом рейнольдсова числа набегающего
Из рассмотрения этих кривых видно, что протяженность Области перехода убывает с ростом рейнольдсова числа набегающего

Рис. 180.
потока, но все же имеет вполне сравнимые с хордой крыла значения. Экспериментальное определение "точки перехода" заключает в себе некоторый произвол; одни авторы определяют точку перехода как середину области перехода, другие — как точку минимума на кривой  третьи — как точку максимума.
третьи — как точку максимума.
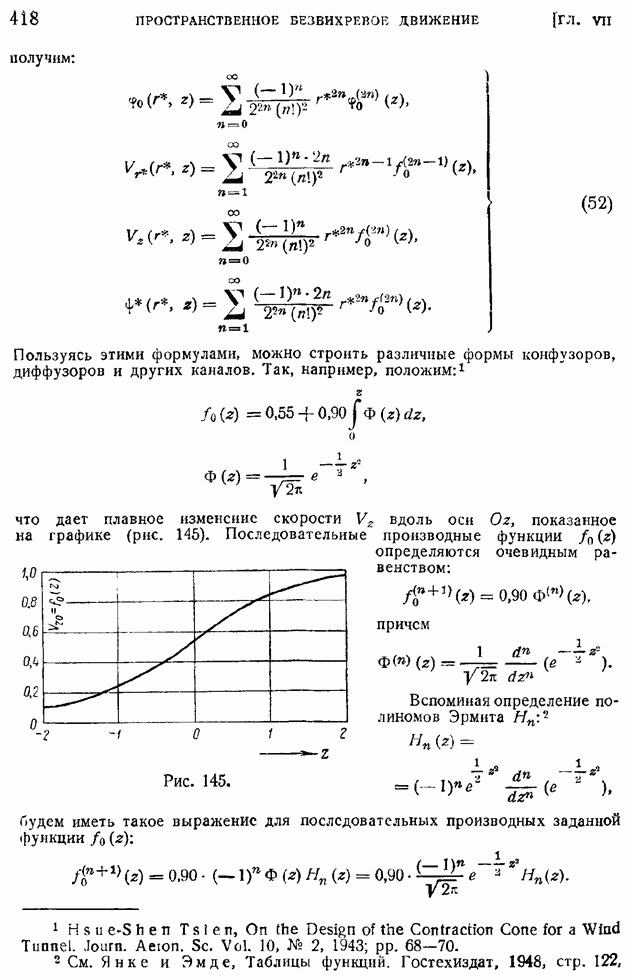
Положение точки перехода на поверхности крыла, так же как и точки потери устойчивости слоя, зависит от степени турбулентности набегающего потока, от ускоренности или замедленности внешнего потока, от наличия на поверхности крыла источников возмущения — различных шероховатостей, неровностей, щелей и др.

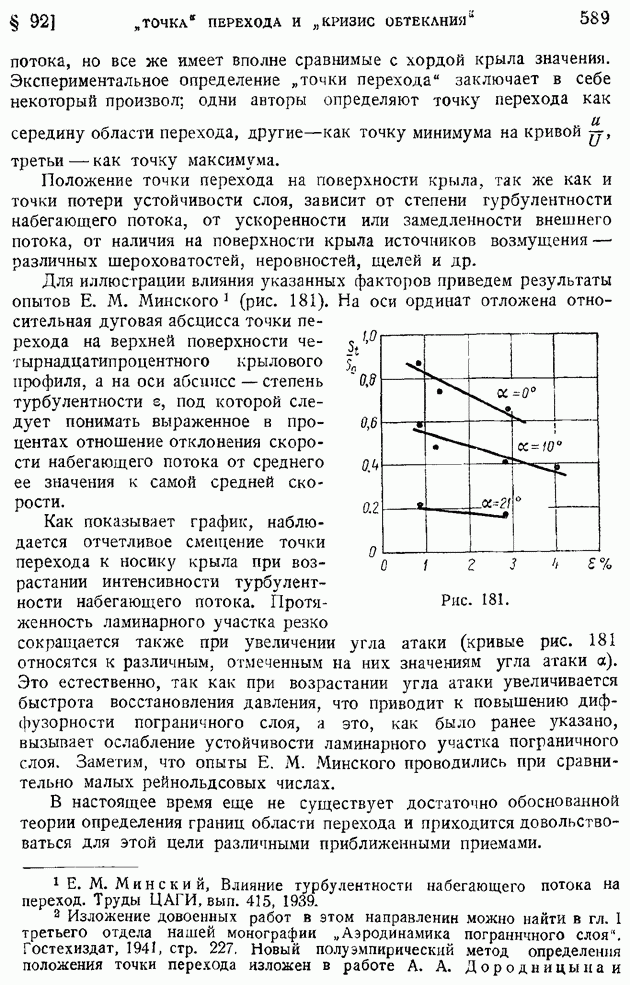
Рис. 181.
Для иллюстрации влияния указанных факторов приведем результаты опытов Е. М. Минского (рис. 181). На оси ординат отложена относительная дуговая абсцисса точки перехода на верхней поверхности четырнадцатипроцентного крылового профиля, а на оси абсписс — степень турбулентности  под которой следует понимать выраженное в процентах отношение отклонения скорости набегающего потока от среднего ее значения к самой средней скорости.
под которой следует понимать выраженное в процентах отношение отклонения скорости набегающего потока от среднего ее значения к самой средней скорости.
Как показывает график, наблюдается отчетливое смещение точки перехода к носику крыла при возрастании интенсивности турбулентности набегающего потока. Протяженность ламинарного участка резко сокращается также при увеличении угла атаки (кривые рис. 181 относятся к различным, отмеченным на них значениям угла атаки а). Это естественно, так как при возрастании угла атаки увеличивается быстрота восстановления давления, что приводит к повышению диффузорности пограничного слоя, а это, как было ранее указано, вызывает ослабление устойчивости ламинарного участка пограничного слоя. Заметим, что опыты Е. М. Минского проводились при сравнительно малых рейнольдсовых числах.
В настоящее время еще не существует достаточно обоснованной теории определения границ области перехода и приходится довольствоваться для этой цели различными приближенными приемами.
Некоторые соображения насчет расчета перехода ламинарного слоя в турбулентный при больших скоростях набегающего потока (при больших дозвуковых значениях числа  можно найти в только что цитированной статье А. А. Дородницына и автора настоящего курса.
можно найти в только что цитированной статье А. А. Дородницына и автора настоящего курса.
Задача об определении положения точки перехода имеет большое практическое значение, так как от положения точки перехода на крыле зависят его сопротивление и подъемная сила (особенно максимальная, соответствующая критическому углу атаки).
Влияние положения точки перехода на сопротивление хорошо обтекаемого крыла будет показано несколько дальше, а сейчас обратимся к другому, не менее важному вопросу о влиянии положения точки перехода на сопротивление плохо обтекаемых тел.

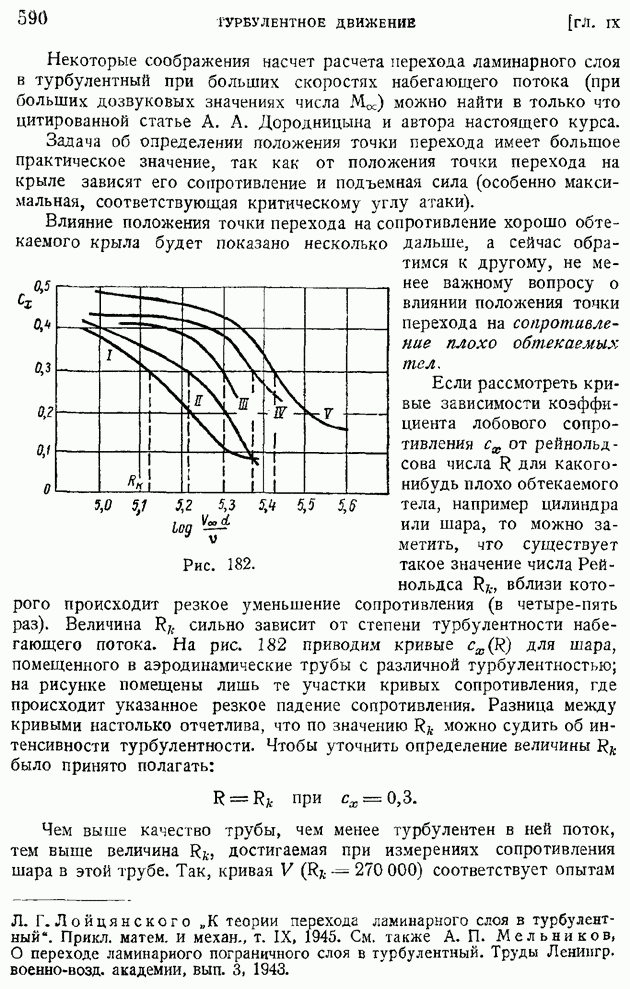
Рис. 182.
Если рассмотреть кривые зависимости коэффициента лобового сопротивления  от рейнольдсова числа
от рейнольдсова числа  для какого-нибудь плохо обтекаемого тела, например цилиндра или шара, то можно заметить, что существует такое значение числа Рейнольдса
для какого-нибудь плохо обтекаемого тела, например цилиндра или шара, то можно заметить, что существует такое значение числа Рейнольдса  вблизи которого происходит резкое уменьшение сопротивления (в четыре-пять раз). Величина
вблизи которого происходит резкое уменьшение сопротивления (в четыре-пять раз). Величина  сильно зависит от степени турбулентности набегающего потока. На рис. 182 приводим кривые
сильно зависит от степени турбулентности набегающего потока. На рис. 182 приводим кривые  для шара, помещенного в аэродинамические трубы с различной турбулентностью; на рисунке помещены лишь те участки кривых сопротивления, где происходит указанное резкое падение сопротивления. Разница между кривыми настолько отчетлива, что по значению
для шара, помещенного в аэродинамические трубы с различной турбулентностью; на рисунке помещены лишь те участки кривых сопротивления, где происходит указанное резкое падение сопротивления. Разница между кривыми настолько отчетлива, что по значению  можно судить об интенсивности турбулентности. Чтобы уточнить определение величины было принято полагать:
можно судить об интенсивности турбулентности. Чтобы уточнить определение величины было принято полагать:

Чем выше качество трубы, чем менее турбулентен в ней поток, тем выше величина  достигаемая при измерениях сопротивления шара в этой трубе. Так, кривая
достигаемая при измерениях сопротивления шара в этой трубе. Так, кривая  соответствует опытам
соответствует опытам
в трубе, в которой средние отклонения мгновенных скоростей потока отличаются от средней скорости потока не более чем на 0,5%, кривая  соответствует потоку с аналогичными отклонениями, достигающими почти 2,5%.
соответствует потоку с аналогичными отклонениями, достигающими почти 2,5%.
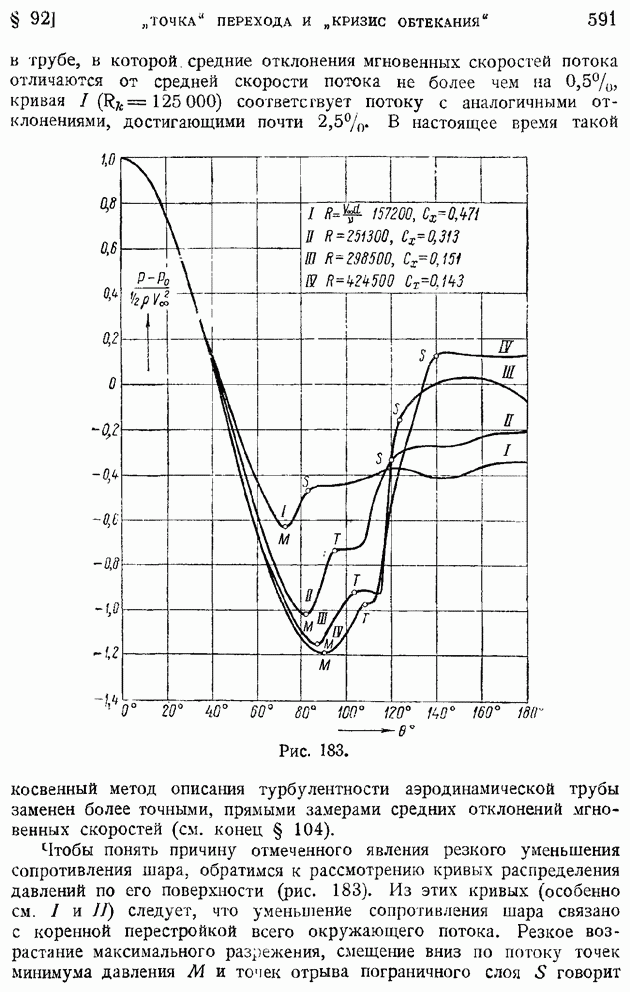
Рис. 183. (см. скан)
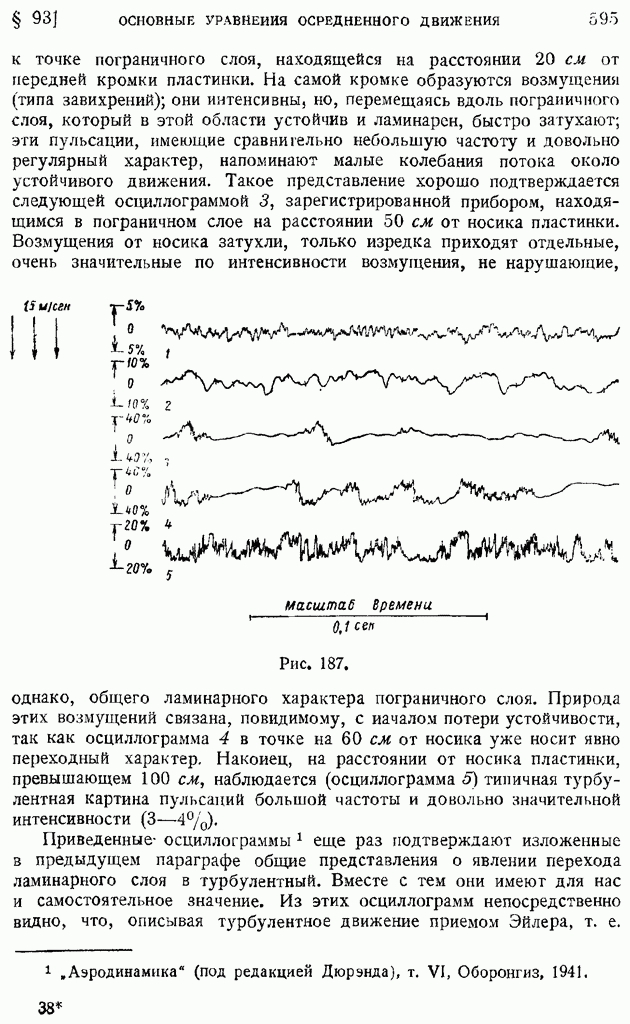
В настоящее время такой косвенный метод описания турбулентности аэродинамической трубы заменен более точными, прямыми замерами средних отклонений мгновенных скоростей (см. конец § 104).
Чтобы понять причину отмеченного явления резкого уменьшения сопротивления шара, обратимся к рассмотрению кривых распределения давлений по его поверхности (рис. 183). Из этих кривых (особенно см. I и II) следует, что уменьшение сопротивления шара связано с коренной перестройкой всего окружающего потока. Резкое возрастание максимального разрежения, смещение вниз по потоку точек минимума давления  и точек отрыва пограничного слоя 5 говорит
и точек отрыва пограничного слоя 5 говорит
об улучшении обтекания шара. Это объясняет уменьшение коэффициента сопротивления, так как при лучшем охвате поверхности шара потоком распределение давлений как бы приближается к тому идеальному, при котором, согласно парадоксу Даламбера, сопротивление должно равняться нулю.
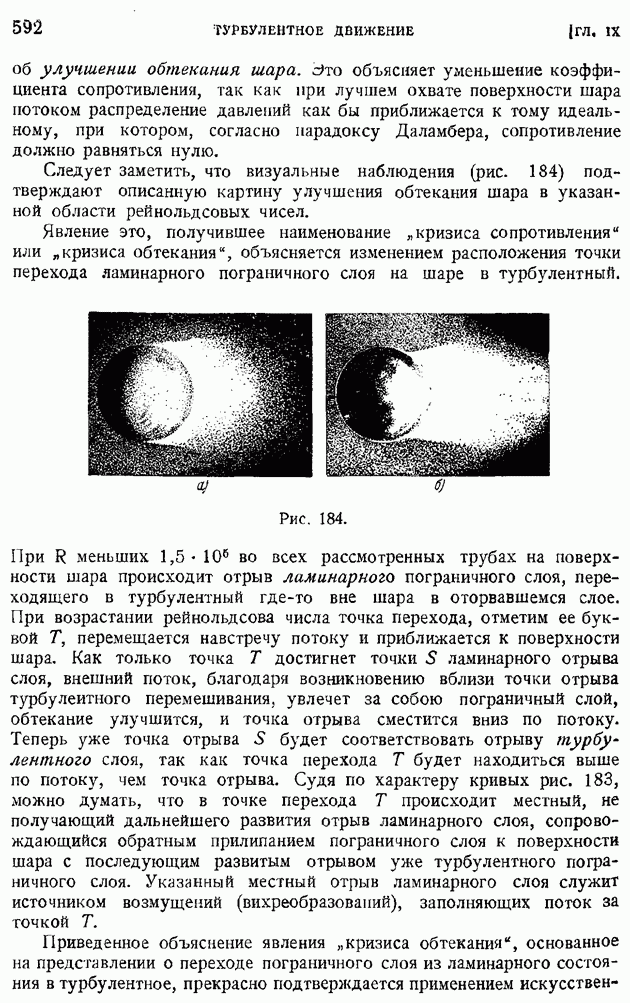
Следует заметить, что визуальные наблюдения (рис. 184) подтверждают описанную картину улучшения обтекания шара в указанной области рейнольдсовых чисел.
Явление это, получившее наименование "кризиса сопротивления" или "кризиса обтекания", объясняется изменением расположения точки перехода ламинарного пограничного слоя на шаре в турбулентный.

Рис. 184.
При  меньших 1,5- 106 во всех рассмотренных трубах на поверхности шара происходит отрыв ламинарного пограничного слоя, переходящего в турбулентный где-то вне шара в оторвавшемся слое. При возрастании рейнольдсова числа точка перехода, отметим ее буквой
меньших 1,5- 106 во всех рассмотренных трубах на поверхности шара происходит отрыв ламинарного пограничного слоя, переходящего в турбулентный где-то вне шара в оторвавшемся слое. При возрастании рейнольдсова числа точка перехода, отметим ее буквой  перемещается навстречу потоку и приближается к поверхности шара. Как только точка
перемещается навстречу потоку и приближается к поверхности шара. Как только точка  достигнет точки 5 ламинарного отрыва слоя, внешний поток, благодаря возникновению вблизи точки отрыва турбулентного перемешивания, увлечет за собою пограничный слой, обтекание улучшится, и точка отрыва сместится вниз по потоку. Теперь уже точка отрыва
достигнет точки 5 ламинарного отрыва слоя, внешний поток, благодаря возникновению вблизи точки отрыва турбулентного перемешивания, увлечет за собою пограничный слой, обтекание улучшится, и точка отрыва сместится вниз по потоку. Теперь уже точка отрыва  будет соответствовать отрыву турбулентного слоя, так как точка перехода
будет соответствовать отрыву турбулентного слоя, так как точка перехода  будет находиться выше по потоку, чем точка отрыва. Судя по характеру кривых рис. 183, можно думать, что в точке перехода
будет находиться выше по потоку, чем точка отрыва. Судя по характеру кривых рис. 183, можно думать, что в точке перехода  происходит местный, не получающий дальнейшего развития отрыв ламинарного слоя, сопровождающийся обратным прилипанием пограничного слоя к поверхности шара с последующим развитым отрывом уже турбулентного пограничного слоя. Указанный местный отрыв ламинарного слоя служит источником возмущений (вихреобразовапий), заполняющих поток за точкой
происходит местный, не получающий дальнейшего развития отрыв ламинарного слоя, сопровождающийся обратным прилипанием пограничного слоя к поверхности шара с последующим развитым отрывом уже турбулентного пограничного слоя. Указанный местный отрыв ламинарного слоя служит источником возмущений (вихреобразовапий), заполняющих поток за точкой 
Приведенное объяснение явления "кризиса обтекания", основанное на представлении о переходе пограничного слоя из ламинарного состояния в турбулентное, прекрасно подтверждается применением
искусственной турбулизации слоя при помощи различных специально вводимых в слой источников возмущений (проволочное колечко на поверхности шара, перегородочка, выступы шероховатости и др.) в условиях потока с рейнольдсовыми числами, значительно меньшими критических  Этим специально пользуются, когда, не имея возможности достигнуть больших значений чисел Рейнольдса, хотят все же получить картину обтекания, близкую к той, которая имеет место при больших числах Рейнольдса. Для этого в пограничный слой помещают различные, очень маленькие по своим размерам турбулизаторы.
Этим специально пользуются, когда, не имея возможности достигнуть больших значений чисел Рейнольдса, хотят все же получить картину обтекания, близкую к той, которая имеет место при больших числах Рейнольдса. Для этого в пограничный слой помещают различные, очень маленькие по своим размерам турбулизаторы.

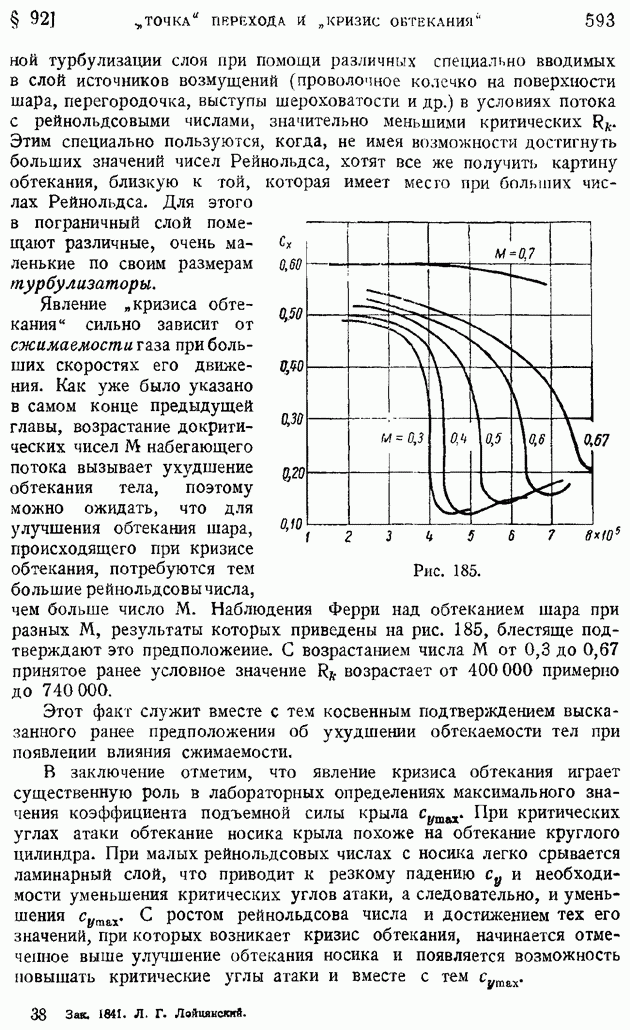
Рис. 185.
Явление "кризиса обтекания" сильно зависит от сжимаемости газа при больших скоростях его движения. Как уже было указано в самом конце предыдущей главы, возрастание докритических чисел  набегающего потока вызывает ухудшение обтекания тела, поэтому можно ожидать, что для улучшения обтекания шара, происходящего при кризисе обтекания, потребуются тем большие рейнольдсовы числа, чем больше число
набегающего потока вызывает ухудшение обтекания тела, поэтому можно ожидать, что для улучшения обтекания шара, происходящего при кризисе обтекания, потребуются тем большие рейнольдсовы числа, чем больше число  Наблюдения Ферри над обтеканием шара при разных
Наблюдения Ферри над обтеканием шара при разных  результаты которых приведены на рис. 185, блестяще подтверждают это предположение. С возрастанием числа
результаты которых приведены на рис. 185, блестяще подтверждают это предположение. С возрастанием числа  от 0,3 до 0,67 принятое ранее условное значение
от 0,3 до 0,67 принятое ранее условное значение  возрастает от
возрастает от  примерно до 740 000.
примерно до 740 000.
Этот факт служит вместе с тем косвенным подтверждением высказанного ранее предположения об ухудшении обтекаемости тел при появлении влияния сжимаемости.
В заключение отметим, что явление кризиса обтекания играет существенную роль в лабораторных определениях максимального значения коэффициента подъемной силы крыла сутга. При критических углах атаки обтекание носика крыла похоже на обтекание круглого цилиндра. При малых рейнольдсовых числах с носика легко срывается ламинарный слой, что приводит к резкому падению  и необходимости уменьшения критических углов атаки, а следовательно, и уменьшения сута. С ростом рейнольдсова числа и достижением тех его значений, при которых возникает кризис обтекания, начинается отмеченное выше улучшение обтекания носика и появляется возможность повышать критические углы атаки и вместе с тем сутгх.
и необходимости уменьшения критических углов атаки, а следовательно, и уменьшения сута. С ростом рейнольдсова числа и достижением тех его значений, при которых возникает кризис обтекания, начинается отмеченное выше улучшение обтекания носика и появляется возможность повышать критические углы атаки и вместе с тем сутгх.
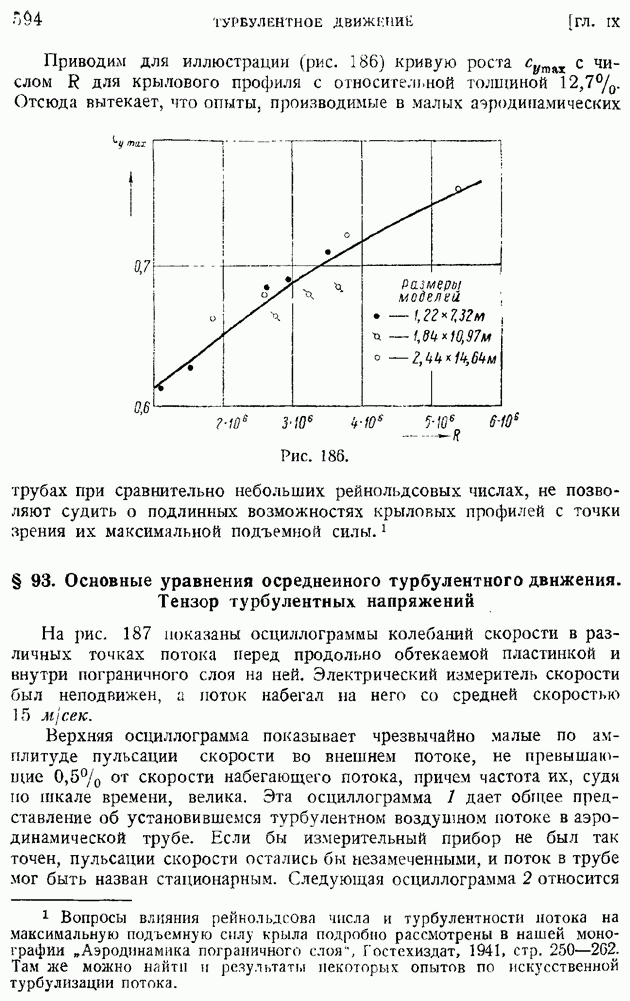
Приводим для иллюстрации (рис. 186) кривую роста  с числом
с числом  для крылового профиля с относительной толщиной
для крылового профиля с относительной толщиной 

Рис. 186.
Отсюда вытекает, что опыты, производимые в малых аэродинамических трубах при сравнительно небольших рейнольдсовых числах, не позволяют судить о подлинных возможностях крыловых профилей с точки зрения их максимальной подъемной силы.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Предмет механики жидкости и газа. Основные свойства «макромодели» жидкости и газа: сплошность и подвижность
- § 2. Основные методы механики жидкости и газа. Области применения и главнейшие задачи
- § 3. Краткий очерк исторического развития механики жидкости и газа. От гидромеханики древних до установления воззрений ньютонианской эпохи
- § 4. Эпоха Эйлера и Бернулли. Гидроаэродинамика в XIX в.
- § 5. Современный этап развития механики жидкости и газа
- ГЛАВА I. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
- § 6. Поле физической величины. Скалярное и векторное поля. Поверхности уровня. Векторные линин и трубки
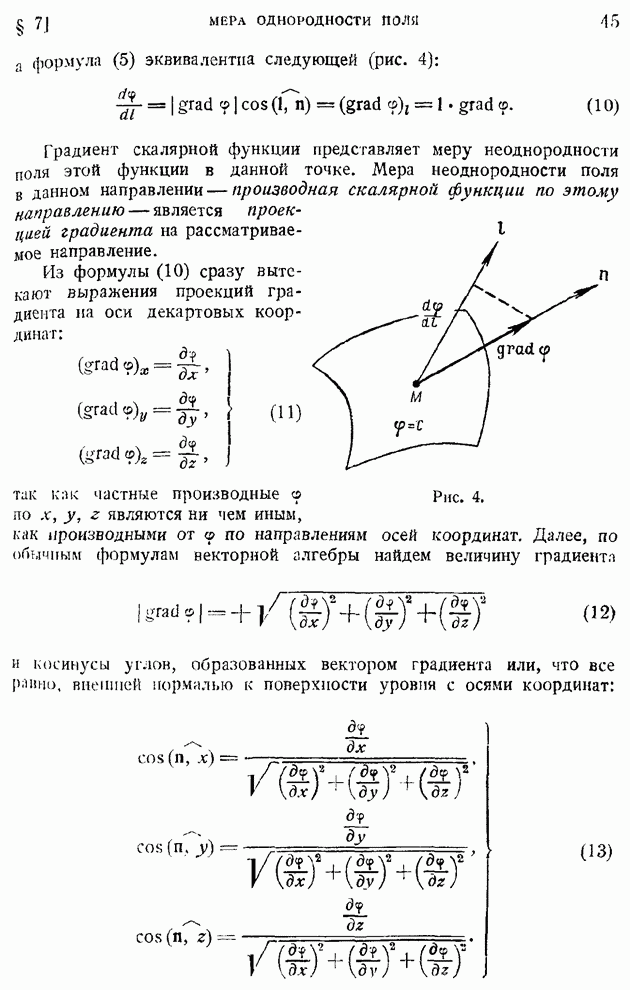
- § 7. Мера однородности поля в данном направлении и в дайной точке. Градиевт скалярного поля и дифференциальный тензор векторного поля как меры неоднородности поля
- § 8. Задание движения сплошной среды. Поле скоростей. Линии тока и траектории
- § 9. Поле ускорений. Разложение ускорения частицы на локальную и конвективную составляющие
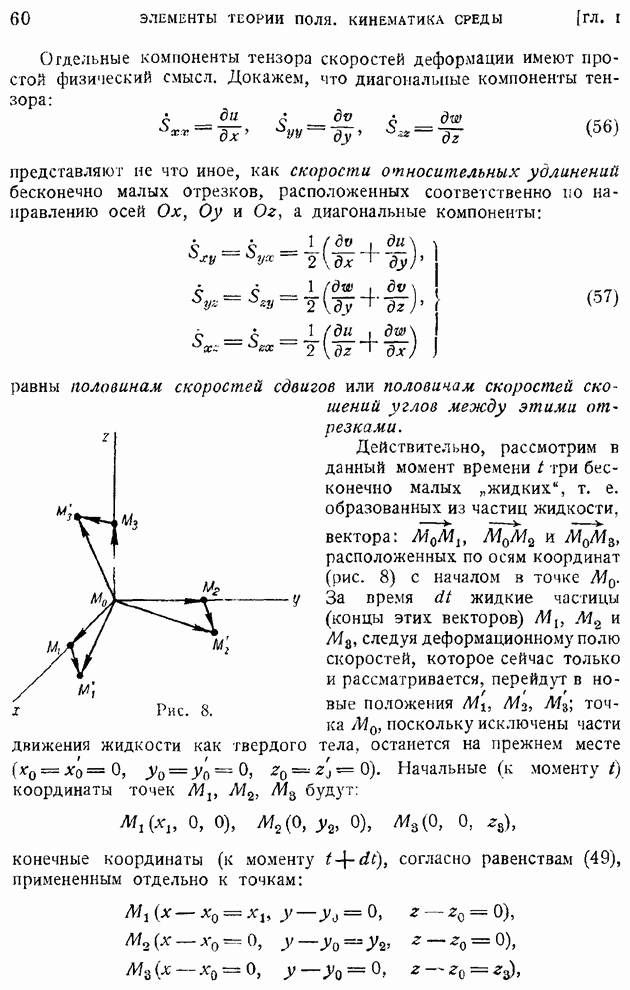
- § 10. Скоростное поле сплошной среды в окрестности данной точки. Угловая скорость и вихрь. Тензор скоростей деформаций и его компоненты
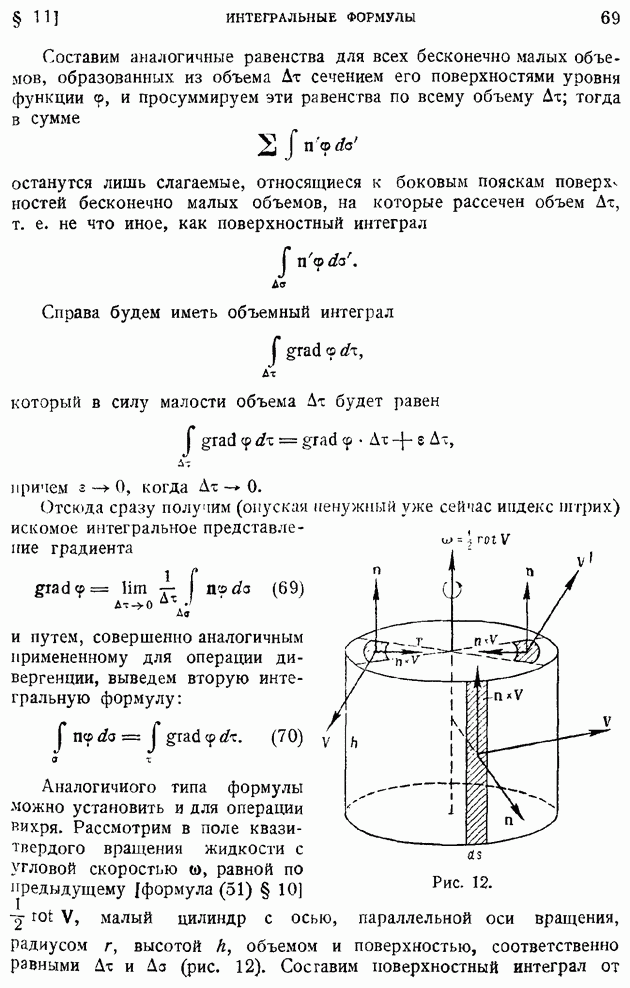
- § 11. Скорость объемного расширения жидкости. Интегральные представления дифференциальных операторов поля. Основные интегральные формулы
- § 12. Вихревые линии и трубки. Вторая теорема Гельмгольца. Интенсивность вихревой трубки
- § 13. Выражение интенсивности вихревой трубки через циркуляцию вектора по контуру, охватывающему трубку. Теорема об изменении циркуляции скорости во времени
- ГЛАВА II. ОСНОВНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ И РАВНОВЕСИЯ СПЛОШНОЙ СРЕДЫ
- § 14. Распределение массы в сплошной среде. Плотность и удельный вес. Напряжения. Тензор напряженности и его симметричность
- § 15. Общие уравнения динамики сплошной среды. Уравнение неразрывности. Уравнения динамики в напряжениях
- § 16. Тепловые явления в жидкостях и газах. Закон сохранения энергии и уравнение баланса энергии
- § 17. Общие уравнения равновесного состояния жидкости и газа. Равновесие воздуха в атмосфере. Приближенные барометрические формулы. Стандартная атмосфера
- § 18. Равновесие несжимаемой жидкости. Уравнение поверхности раздела. Равновесие вращающейся жидкости
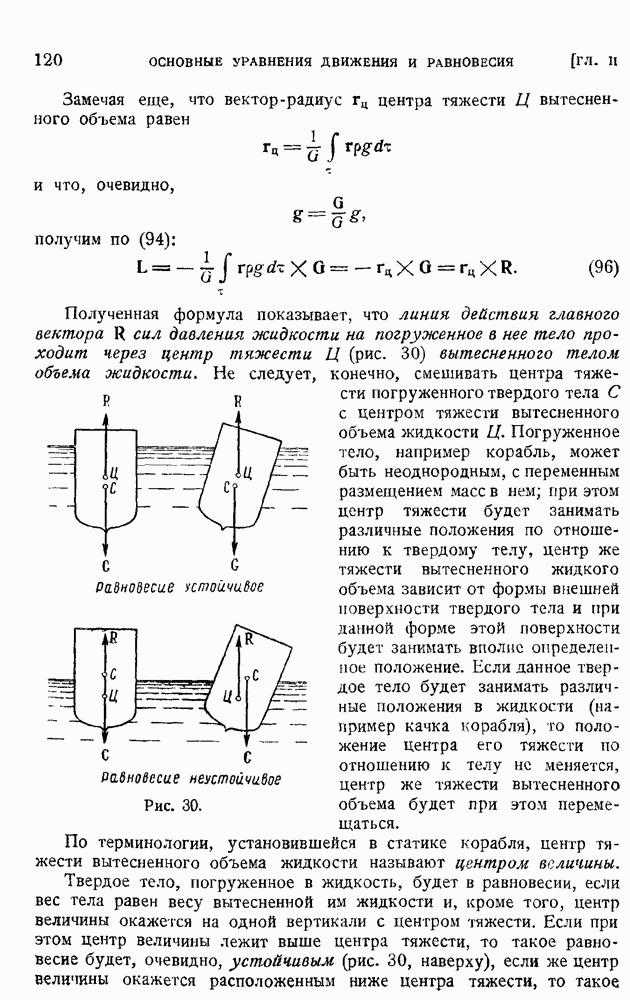
- § 19. Давление тяжелой несжимаемой жидкости на поверхность тела. Сила и момент, приложенные к телу, плавающему в тяжелой жидкости. Случай вращающейся жидкости
- ГЛАВА III. ДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ И ГАЗА. ОСНОВНЫЕ УРАВНЕНИЯ И ОБЩИЕ ТЕОРЕМЫ
- § 20. Идеальная жидкость. Основные уравнения движения
- § 21. Закон сохранения энергии в движущейся идеальной жидкости. Адиабатическое движение. Сохранение энтропии
- § 22. Эйлерово представление конвективного изменения объемного интеграла. Перенос величины сквозь контрольную поверхность
- § 23. Эйлерова форма законов сохранения массы и энергии, теоремы количеств движения и момента количеств движения при стационарном движении идеальной жидкости
- § 24. Теорема об изменении кинетической энергии. Работа и мощность внутренних сил. Эйлерова форма уравнения изменения кинетической энергии
- § 25. Теорема Бернулли о сохранении полной механической энергии при стационарном баротропном движении идеальной жидкости и газа
- ГЛАВА IV. ОДНОМЕРНЫЙ ПОТОК ИДЕАЛЬНОЙ ЖИДКОСТИ
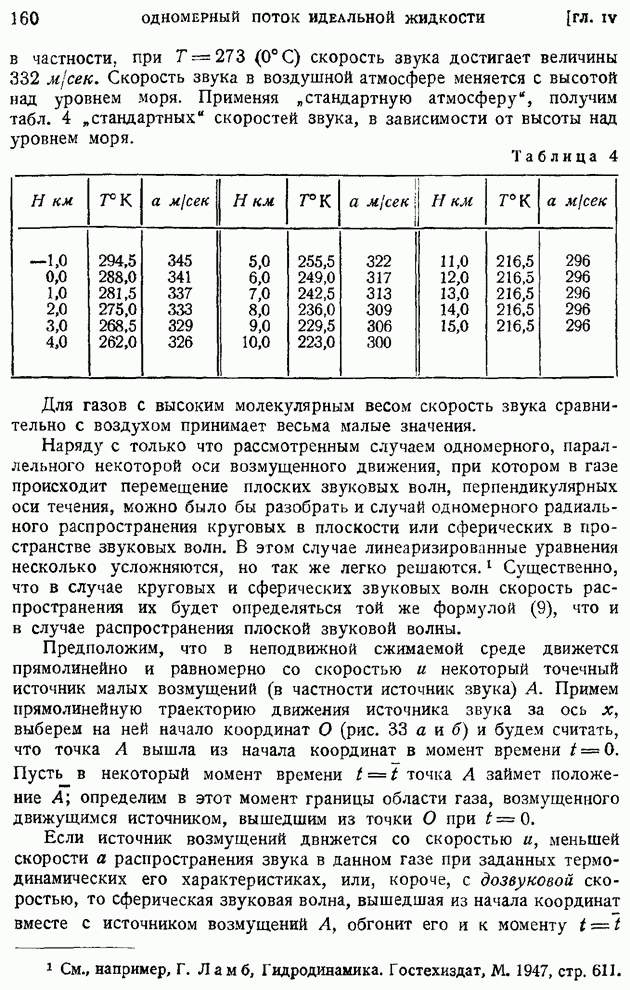
- § 26. Одномерное течение идеальной сжимаемой жидкости. Линеаризированные уравнения. Скорость распространения малых возмущений в жидкости или газе
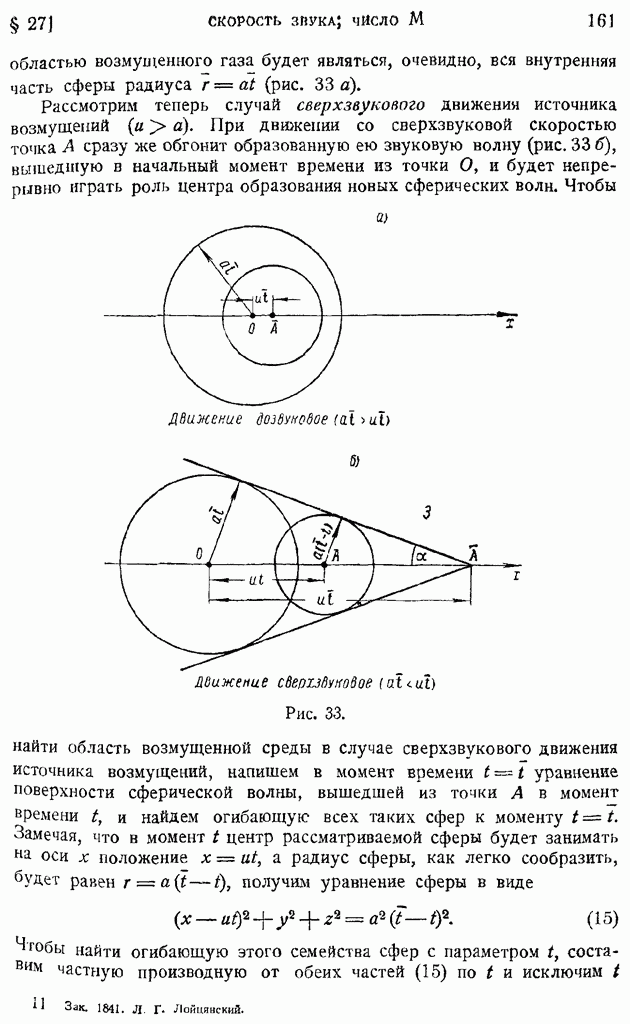
- § 27. Изотермическая и адиабатическая скорости звука. «Конус возмущений» при сверхзвуковом движении источника возмущения. Число M и его связь с углом конуса возмущений
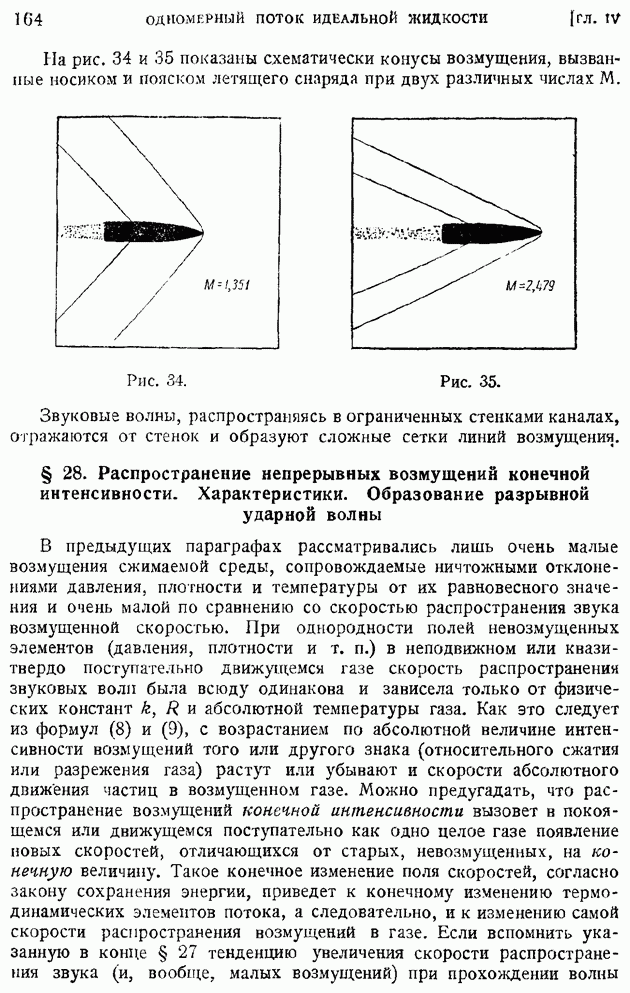
- § 28. Распространение непрерывных возмущений конечной интенсивности. Характеристики. Образование разрывной ударной волны
- § 29. Стоячая ударная волна или скачок уплотнения. Ударная адиабата
- § 30. Критические величины в одномерном потоке газа. Связь между скоростями до и после скачка. Изменение давления, плотности и температуры в скачке уплотнения
- § 31. Скорость распространения ударной волны. Спутное движение газа за ударной волной
- § 32. Влияние интенсивности скачка уплотнения на сжатие газа. Измерение скоростей и давлений в до- и сверхзвуковых потоках
- § 33. Одномерное движение газа по трубе переменного сечения. Истечение из резервуара большой емкости сквозь сходящееся сопло
- § 34. Одномерное течение в сопле Лаваля. Движение газа с притоком тепла
- ГЛАВА V. БЕЗВИХРЕВОЕ ДВИЖЕНИЕ ЖИДКОСТИ. ПЛОСКОЕ ДВИЖЕНИЕ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 35. Сохранение циркуляции скорости в потоке идеальной жидкости. Теорема Кельвина и Лаграижа. Безвихревое движение. Потенциал скоростей
- § 36. Интеграл Лагранжа — Коши уравнений безвихревого движения. Теорема Бернулли. Некоторые общие свойства безвихревого движения идеальной несжимаемой жидкости в односвязной области
- § 37. Плоское безвихревое движение несжимаемой жидкости. Потенциал скоростей и функция тока. Применение функций комплексного переменного. Комплексный потенциал и сопряженная скорость
- § 38. Построение полей течения по заданной характеристической Функции. Простейшие плоские потоки и их наложение
- § 39. Бесциркуляционное и циркуляционное обтекания круглого цилиндра
- § 40. Применение криволинейных координат. Бесциркуляционное и циркуляционное обтекания эллиптического цилиндра и пластинки. Задача Жуковского об обтекании решетки пластин.
- § 41. Плоское движение с отрывом струй. Разрывное обтекание пластинки и протекание жидкости сквозь отверстие
- § 42. Прямая задача в теории плоского движения идеальной несжимаемой жидкости. Применение метода конформных отображений. Гипотеза Чаплыгина о безотрывном обтекании задней кромки профиля. Формула циркуляции
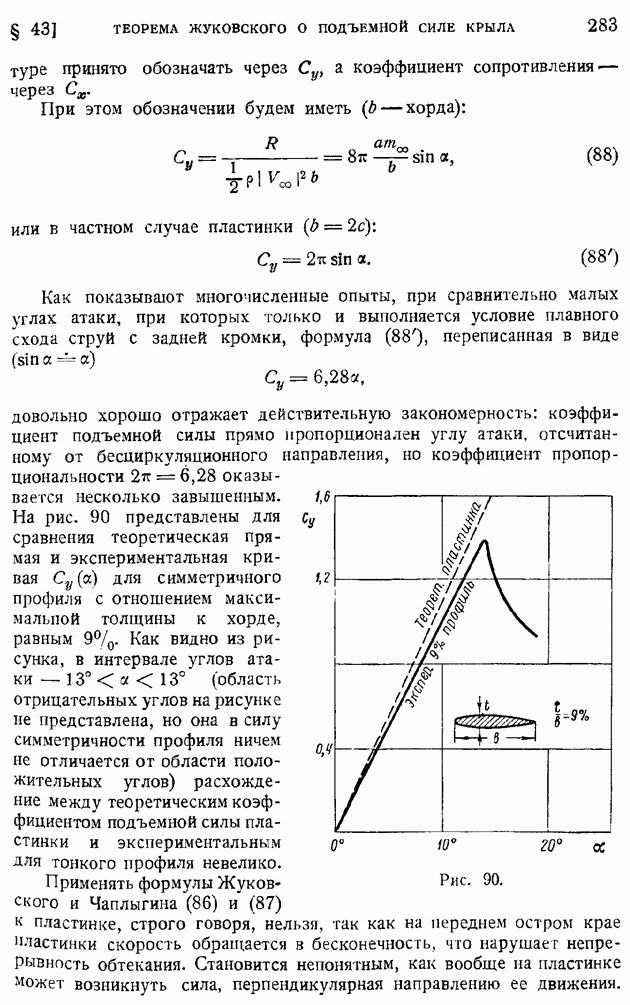
- § 43. Теорема Жуковского о подъемной силе крыла. Зависимость подъемной силы от угла атаки. Коэффициент подъемной силы
- § 44. Применение метода комплексных переменных к выводу теоремы Жуковского. Формулы Чаплыгина для главного вектора и момента сил давления потока на крыло
- § 45. Выражение главного момента сил давления потока через коэффициенты конформного отображения. Фокус крыла. Независимость от угла атаки момента относительно фокуса. Парабола устойчивости
- § 46. Частные случаи конформного отображения крылового профиля на круг. Преобразование Жуковского-Чаплыгина. Теоретические крыловые профили
- § 47. Задача об обтекании слабо изогнутой дужки произвольной формы (теория тонкого крыла)
- § 48. Определение обтекания крылового профиля произвольной формы
- § 49. Обобщение теоремы Жуковского на случай плоской решетки с бесчисленным множеством профилей
- ГЛАВА VI. ПЛОСКОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ СЖИМАЕМОГО ГАЗА
- § 50. Основные уравнения плоского стационарного безвихревого движения сжимаемого газа. Линеаризированные уравнения
- 51. Линеаризированный до- и сверхзвуковой газовый поток вдоль волнистой стенки
- § 52. Тонкое крыло в линеаризированном до- и сверхзвуковом потоках. Влияние сжимаемости газа на коэффициент подъемной силы в дозвуковом потоке. Коэффициенты подъемной силы и волнового сопротивления при сверхзвуковом потоке
- § 53. Нелинеаризированные уравнения движения идеального сжимаемого газа. Переход в плоскость годографа. Уравнения Чаплыгина
- § 54. Метод С. А. Христиановича. Приближенные формулы учета влияния сжимаемости на распределение давления
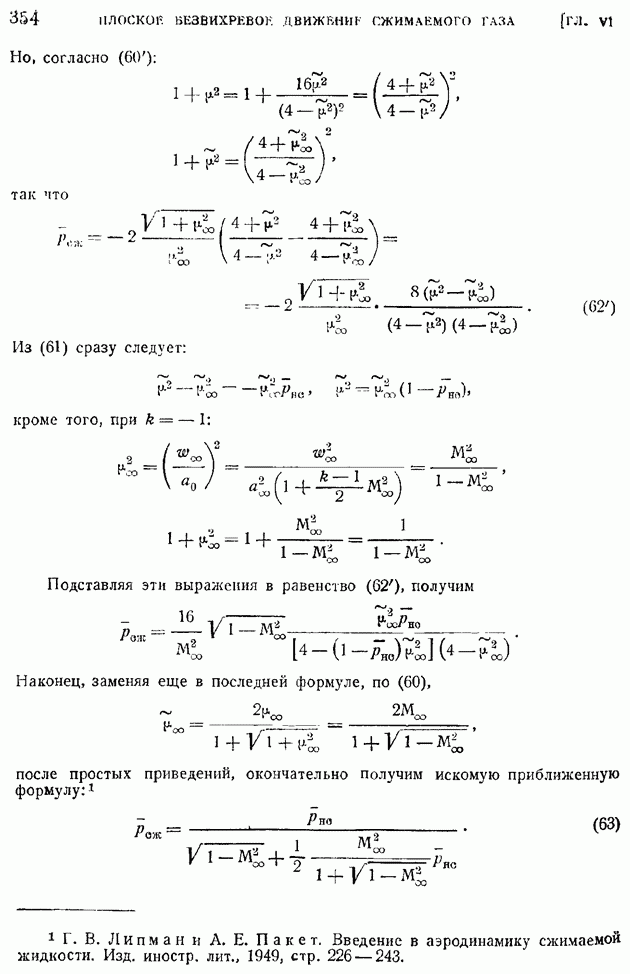
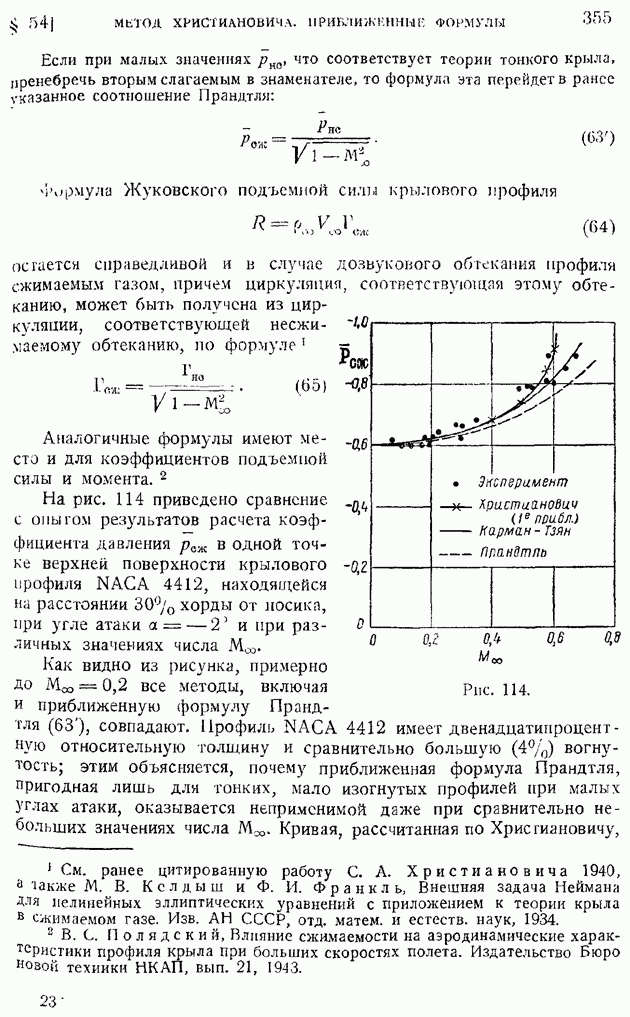
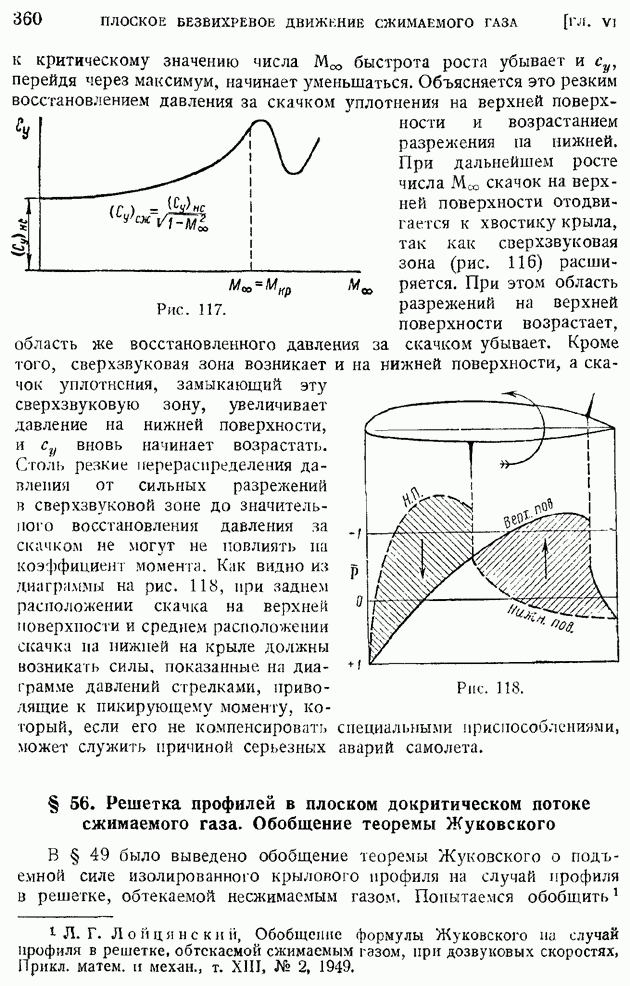
- § 55. Критическое число M и его определение по заданному распределению давления в несжимаемом обтекании. Поведение коэффициента подъемной силы и момента при около- и закритических значениях числа M
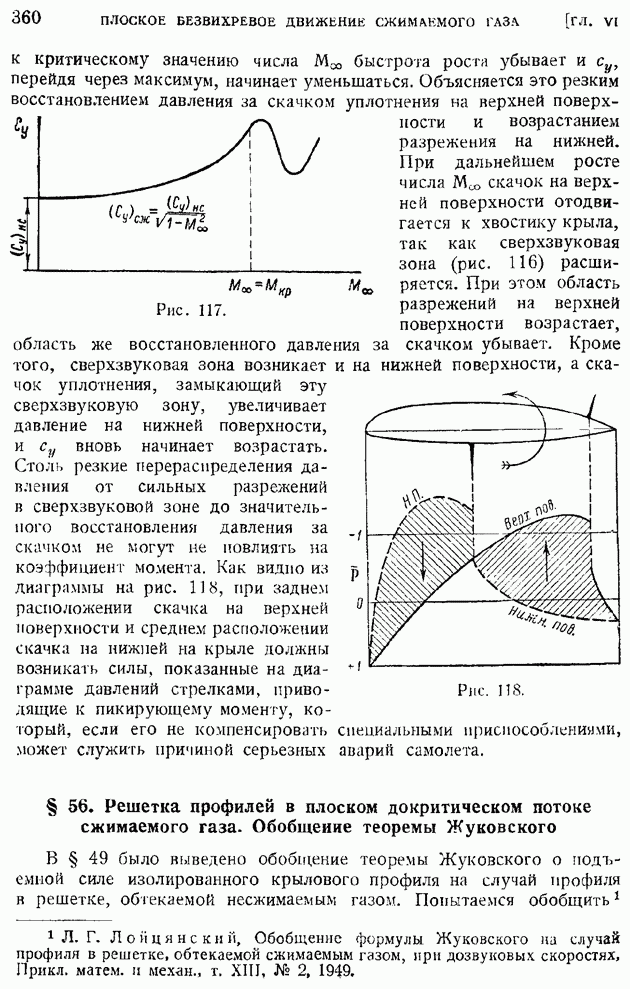
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
- § 57. Нелинеаризированный сверхзвуковой поток. «Характеристики» уравнений плоского сверхзвукового потока. Линин возмущения и их основные свойства
- § 58. Обтекание выпуклого угла сверхзвуковым потоком. Влияние угла поворота струи на ее газодинамические элементы
- § 59. Сверхзвуковой поток внутри тупого угла. Косой скачок уплотнения. Связь между газодинамическими элементами до и за косым скачком
- ГЛАВА VII. ПРОСТРАНСТВЕННОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ
- § 60. Ортогональные криволинейные координаты в пространстве. Основные дифференциальные операторы поля в криволинейных координатах
- § 61. Потенциал скоростей. Поле источника и диполя. Непрерывное распределение источников и диполей. Ньютонов потенциал. Потенциал простого и двойного слоев
- § 62. Поле скоростей вокруг заданной системы вихрей. Формула Био — Савара. Потенциал скоростей замкнутой вихревой нити. Аналогия с потенциалом двойного слоя
- § 63. Функция тока и ее связь с векторным потенциалом скоростей. Функции тока простейших течений
- § 64. Обтекание сферы. Давление однородного стационарного потока идеальной несжимаемой жидкости на погруженное в нее тело. Парадокс Даламбера
- § 65. Общие уравнения осесимметричного движения. Применение цилиндрических координат. Течение сквозь каналы
- § 66. Осесимметричное продольное обтекание тел вращения. Случай эллипсоида вращения
- § 67. Поперечное обтекание тел вращения. Пример эллипсоида вращения
- § 68. Продольное и поперечное обтекание тел вращения большого удлинения. Приближенные выражения граничных условий. Применение тригонометрических сумм для определения коэффициентов …
- § 69. Метод «особенностей». Применение непрерывно распределенных источников (стоков) и диполей для решения задачи о продольном и поперечном обтекании тел вращения
- § 70. Общий случай движения твердого тела сквозь несжимаемую идеальную жидкость. Определение потенциала скоростей. Главный вектор и главный момент сил давления потока на тело
- § 71. Коэффициенты «присоединенных масс». Свойство симметрии. «Присоединенная» кинетическая энергия. Определение «присоединенных масс» поступательно движущегося цилиндра, шара и эллипсоида
- § 72. Элементы теории крыла конечного размаха. Вихревая система крыла. Гипотеза плоских сечеиий. Геометрические и действительные углы атаки. Подъемная сила и «индуктивное сопротивление»
- § 73. Основные формулы теории «несущей линии». «Индуктивная скорость» и «индуктивный угол». Прямая задача определения подъемной силы и индуктивного сопротивления по заданному распределению циркуляции
- § 74. Крыло с минимальным индуктивным сопротивлением. Эллиптическое распределение циркуляции. Связь между коэффициентами индуктивного сопротивления и подъемной силы. Основное уравнение теории крыла и понятие о его интегрировании
- ГЛАВА VIII. ДИНАМИКА ВЯЗКОЙ ЖИДКОСТИ И ГАЗА
- § 75. Внутреннее трение и теплопроводность в жидкостях и газах. Законы Ньютона и Фурье. Влияние температуры на коэффициенты вязкости и теплопроводности. Число «сигма»
- § 76. Обобщение закона Ньютона на случай произвольного движения среды. Закон линейной связи между тензорами напряжений и скоростей деформации
- § 77. Общие уравнения движения вязкой жидкости. Динамические уравнения и уравнение баланса энергии. Граничные условия движения жидкости с треннем и теплопроводностью
- § 78. Понятие о подобии гидродинамических явлений. Безразмерные уравнения движения вязкой жидкости и газа. Условия подобия
- § 79. Ламинарное движение вязкой несжимаемой жидкости по цилиндрической трубе
- § 80. Обтекание шара при очень малых значениях числа Рейнольдса. Формула сопротивления шара по Стоксу и ее обобщения
- § 81. Вихревые линии в идеальной и вязкой жидкости. Сохраняемость вихревых линий при отсутствии внутреннего трения. Диффузия вихря в вязкой жидкости
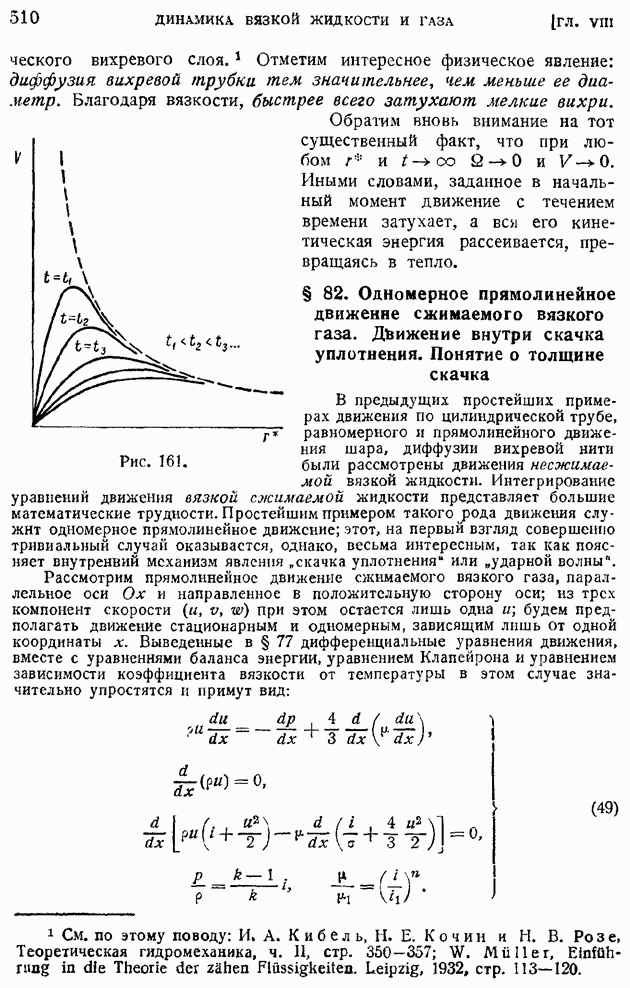
- § 82. Одномерное прямолинейное движение сжимаемого вязкого газа. Движение внутри скачка уплотнения. Понятие о толщине скачка
- § 83. Работа внутренних сил и диссипация механической энергии в движущейся вязкой среде
- § 84. Обтекание тел жидкостью и газом при больших значениях числа Рейнольдса. Основные уравнения теории ламинарного пограничного слоя
- § 85. Ламинарный пограничный слой на пластинке, продольно обтекаемой несжимаемой жидкостью. Неизотермическое движение
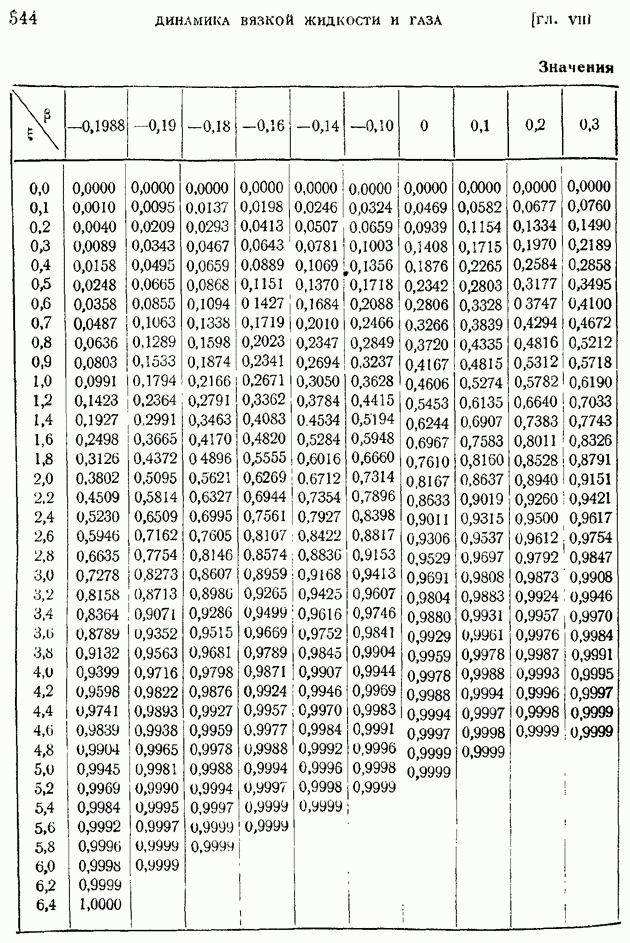
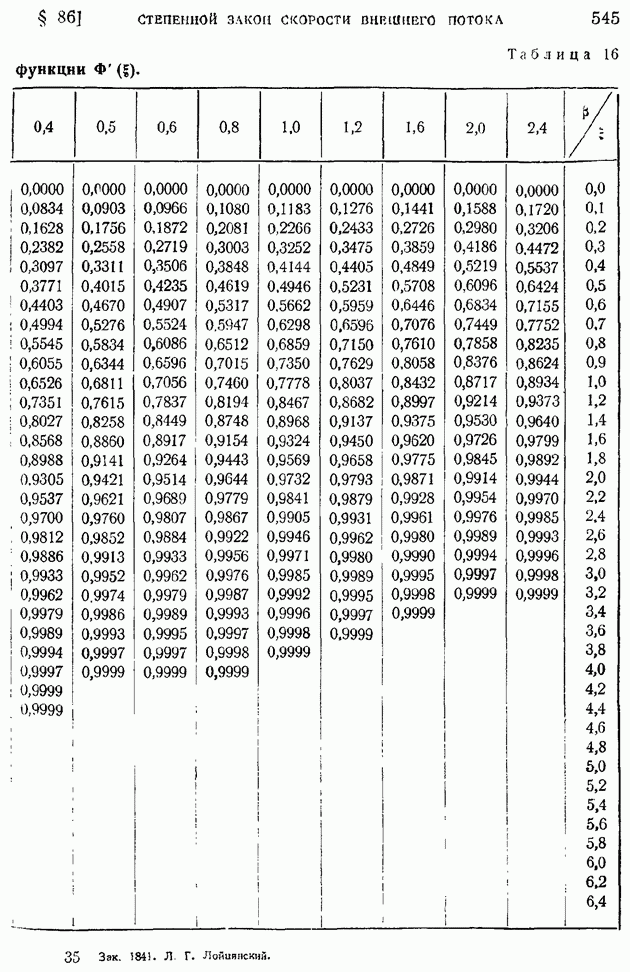
- § 86. Ламинарный пограничный слой при степенном задании скорости внешнего потока
- § 87. Ламинарный пограничный слой в общем случае задания скорости внешнего потока. Применение уравнения импульсов для приближенного расчета ламинарного пограничного слоя
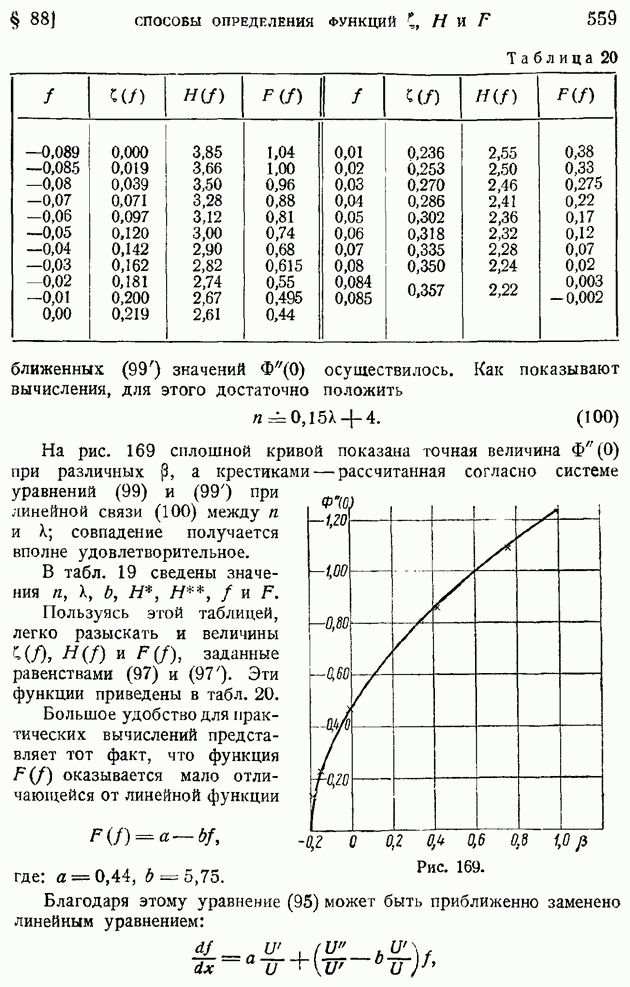
- § 88. Способы определения функций … Приближенный метод расчета ламинарного пограничного слоя
- § 89. Ламинарный пограничный слой на пластинке, продольно обтекаемой сжимаемым газом при больших скоростях. Случай линейной зависимости коэффициента вязкости от температуры (n = 1)
- § 90. Ламинарный пограничный слой на пластинке при любом законе связи между вязкостью и температурой и при числе … Обтекание крылового профиля потоком больших скоростей
- ГЛАВА IX. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ
- § 91. Переход ламинарного движения в турбулентное. Критическое рейнольдсово число
- § 92. Область и «точка» перехода. Явление «кризиса обтекания»
- § 93. Основные уравнения осреднеиного турбулентного движения. Тензор турбулентных напряжений
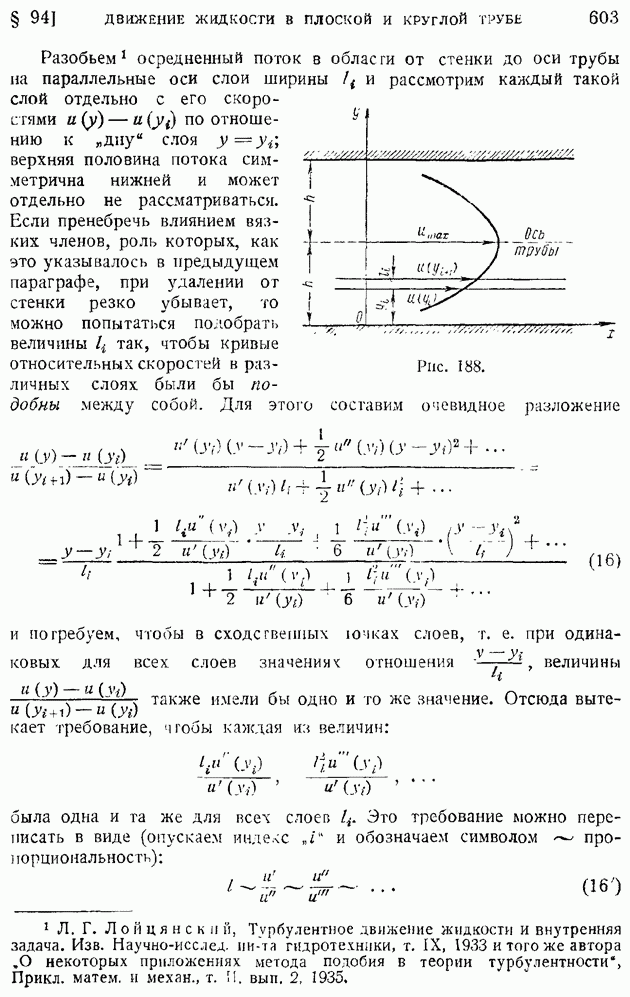
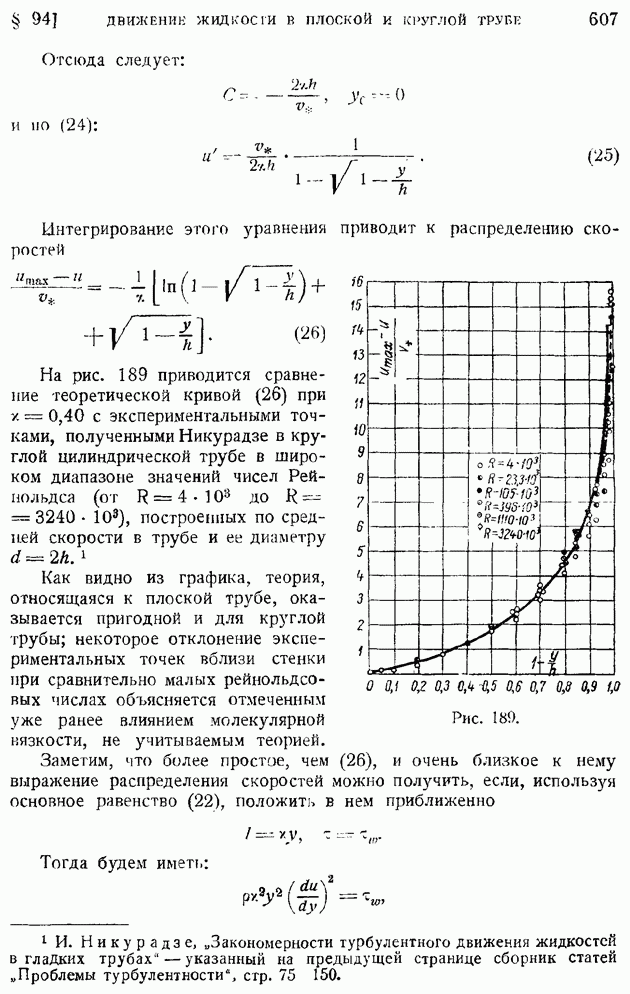
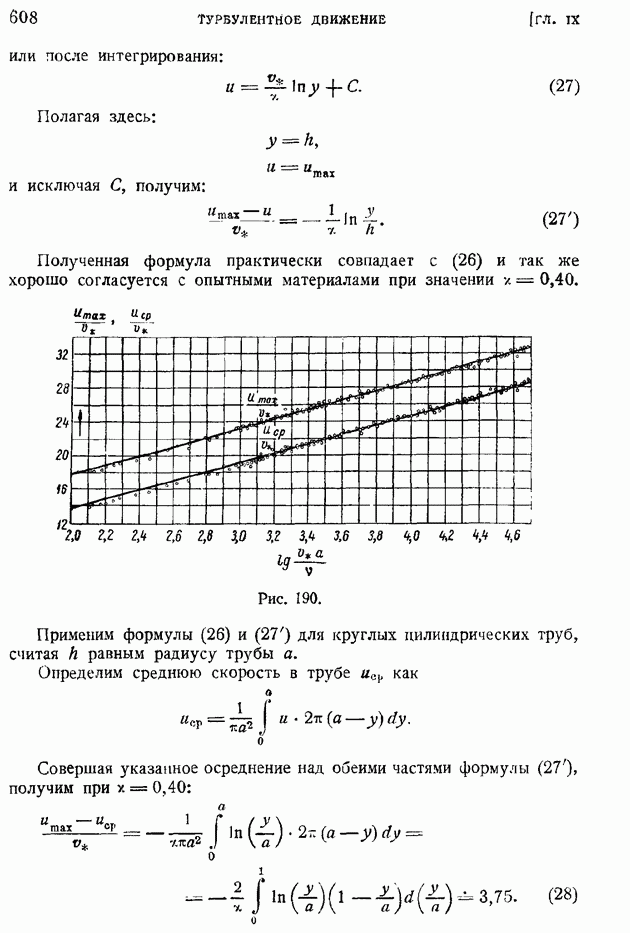
- § 94. Турбулентное движение жидкости в плоской и круглой трубе. Логарифмические формулы скоростей
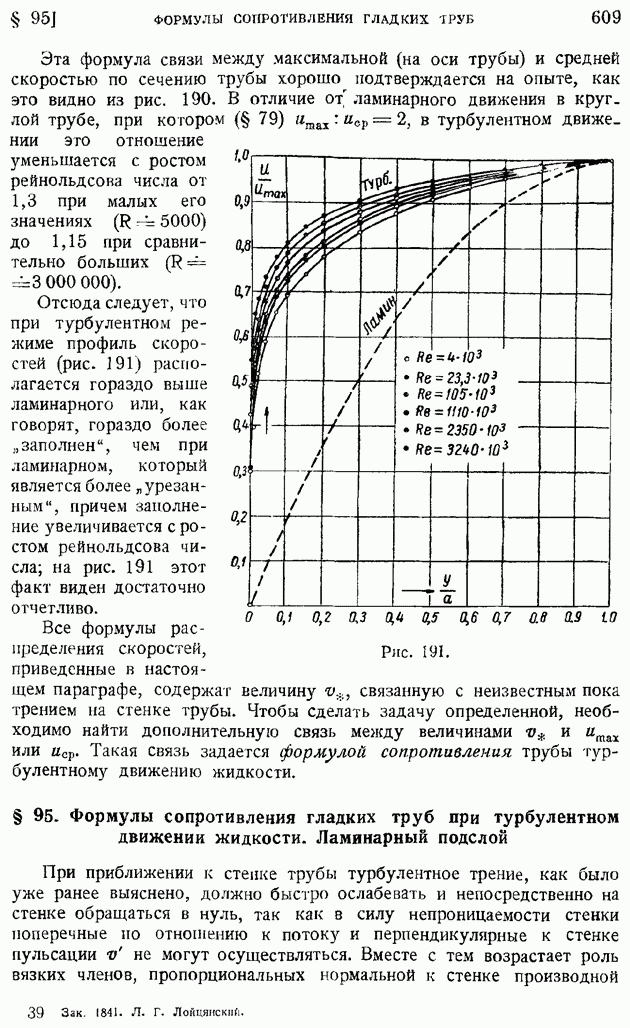
- § 95. Формулы сопротивления гладких труб при турбулентном движении жидкости. Ламинарный подслой
- § 96. Влияние шероховатости стенок трубы на ее сопротивление. Предельные режимы течения. Режим установившейся шероховатости
- § 97. Турбулентный пограничный слой на продольно обтекаемой пластине. Сопротивление пластины
- § 98. Турбулентный пограничный слой на крыловом профиле при малом продольном перепаде давлений
- § 99. Турбулентный пограничный слой на крыловом профиле при значительных продольных перепадах давления
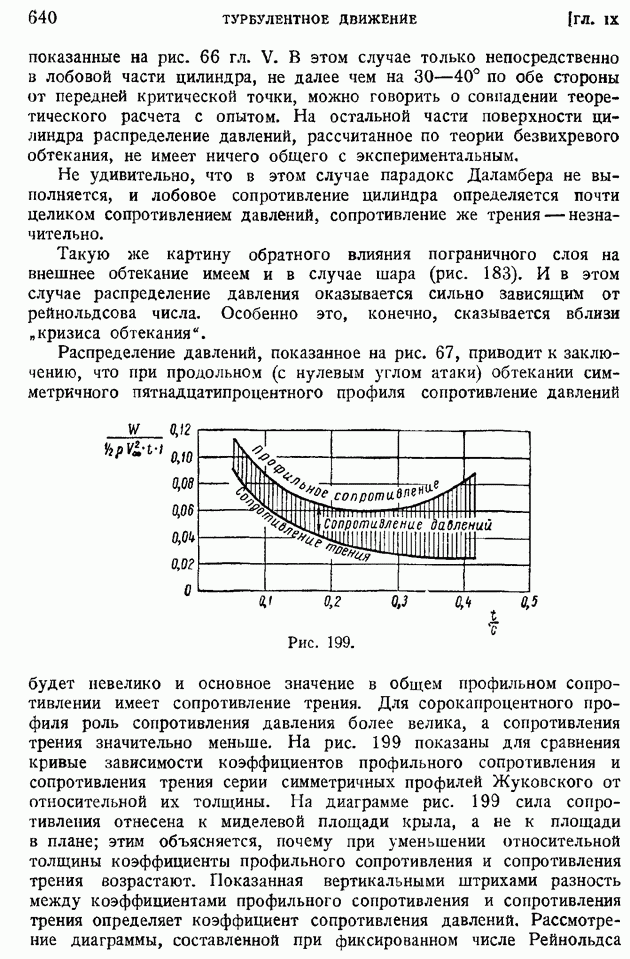
- § 100. Профильное сопротивление крыла. Разложение профильного сопротивления на сопротивление трения и сопротивление давлений. Обратное влияние пограничного слоя на распределение давлений по поверхности обтекаемого профиля
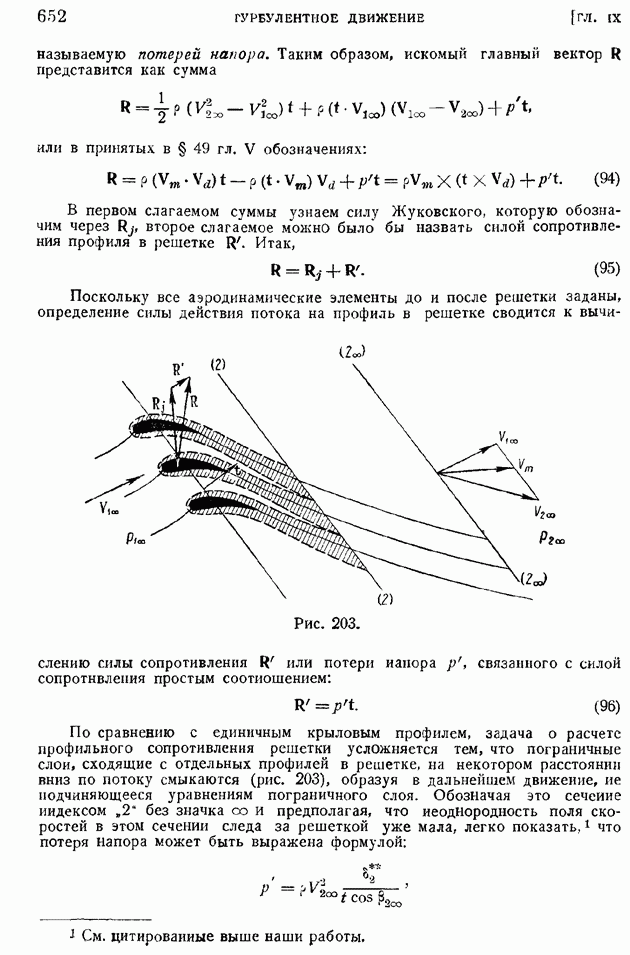
- § 101. Приближенные формулы профильного сопротивления крыла и крылового профиля в решетке
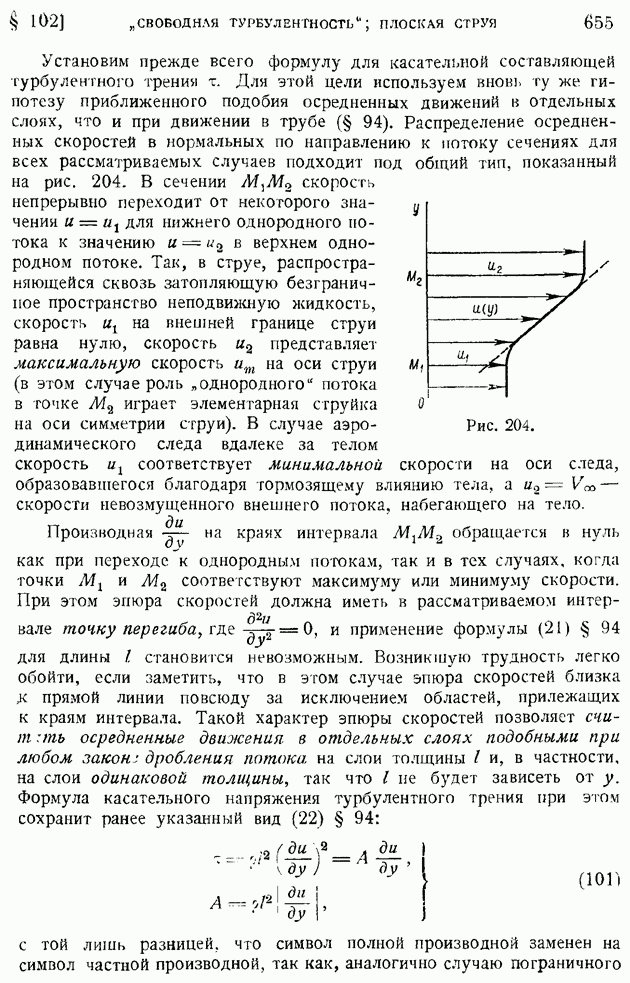
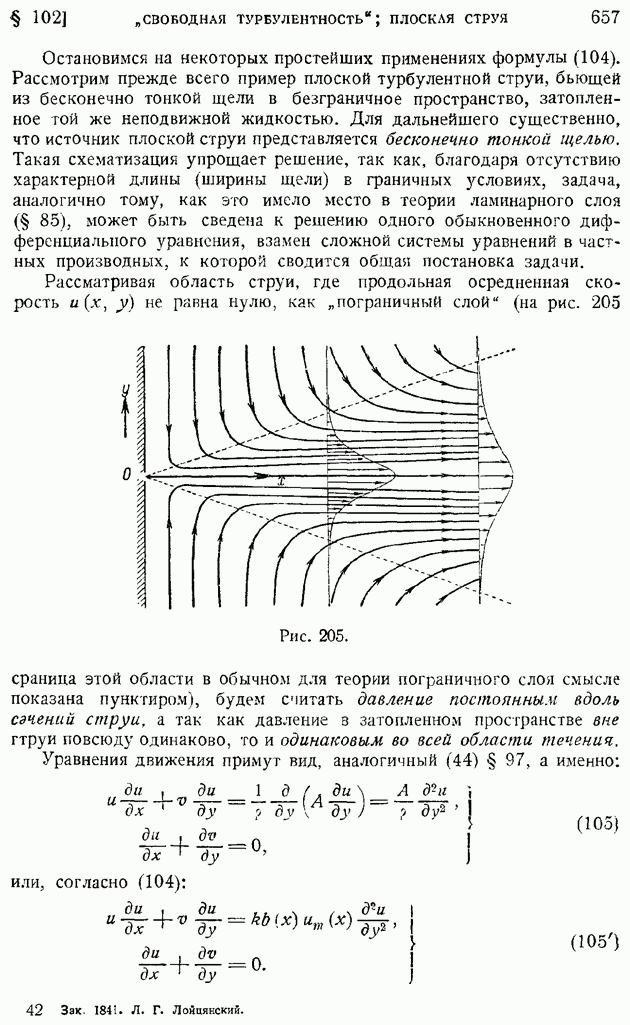
- § 102. Основные закономерности «свободной турбулентности». Плоская турбулентная струя в пространстве, заполненном той же жидкостью
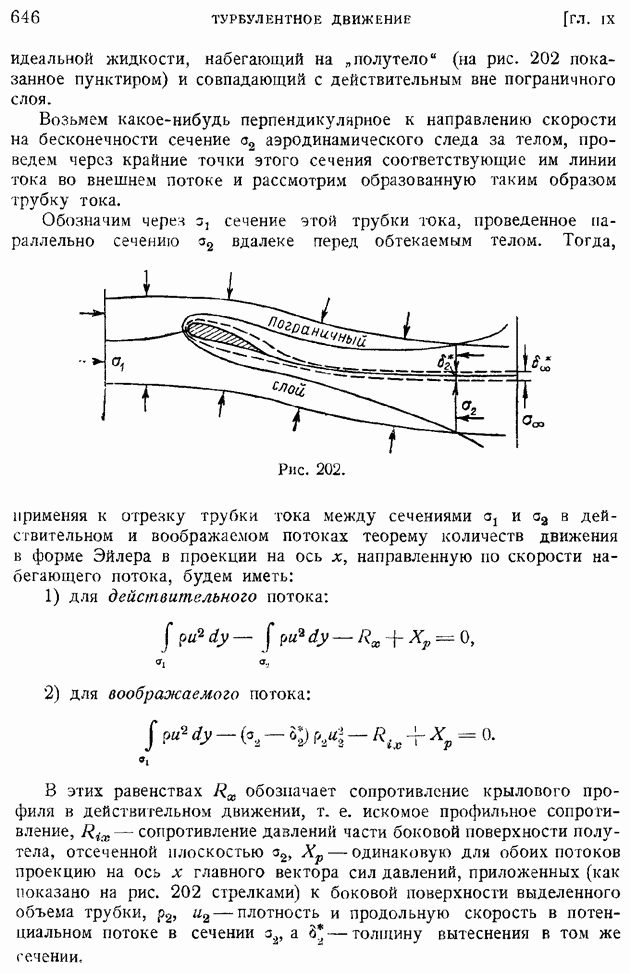
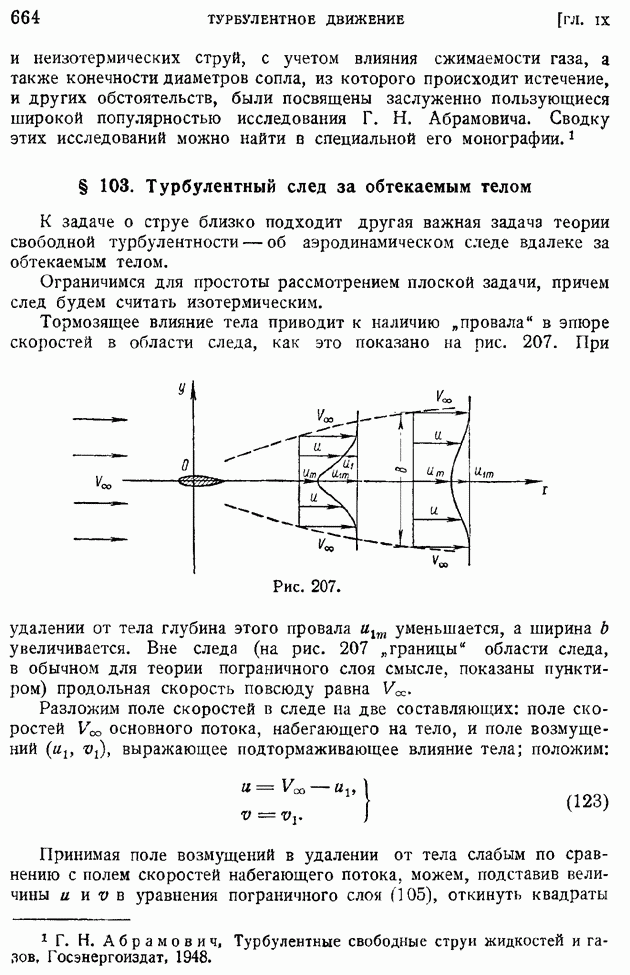
- § 103. Турбулентный след за обтекаемым телом
- § 104. Рассеяние турбулентных возмущений в жидкости. Случай изотропной и однородной турбулентности. Закон сохранения момента возмущений