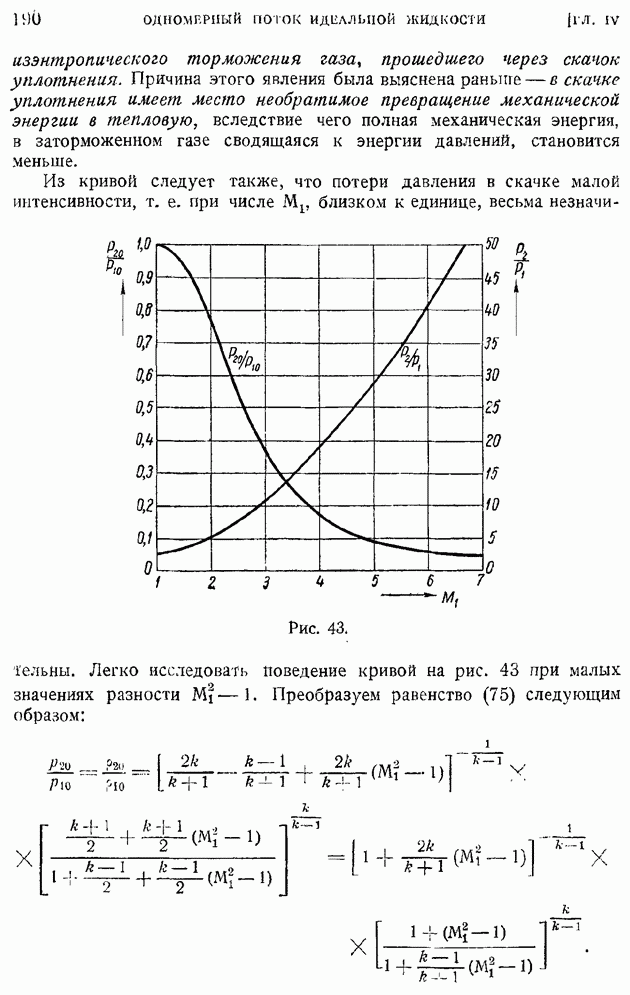
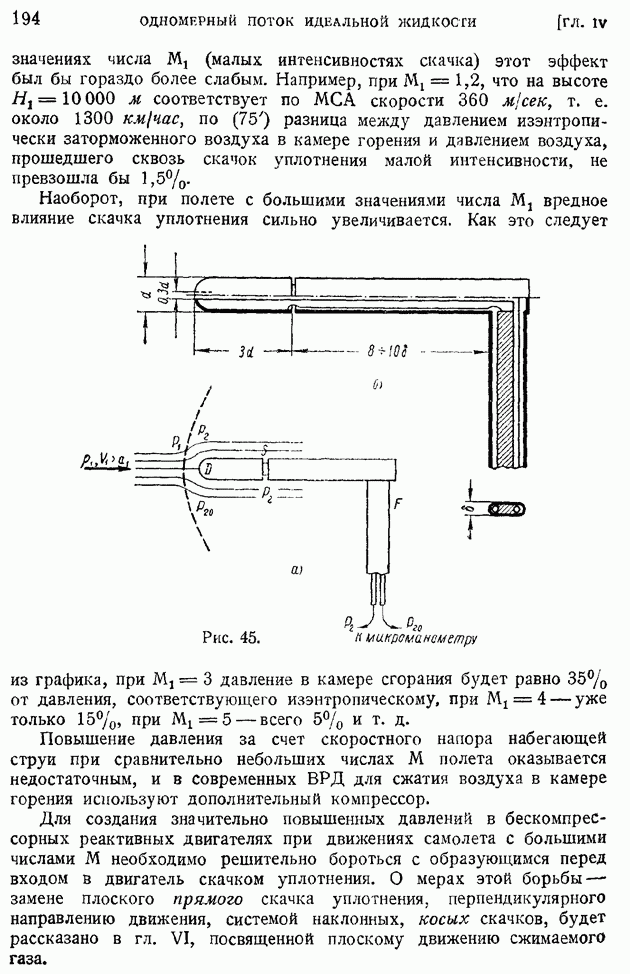
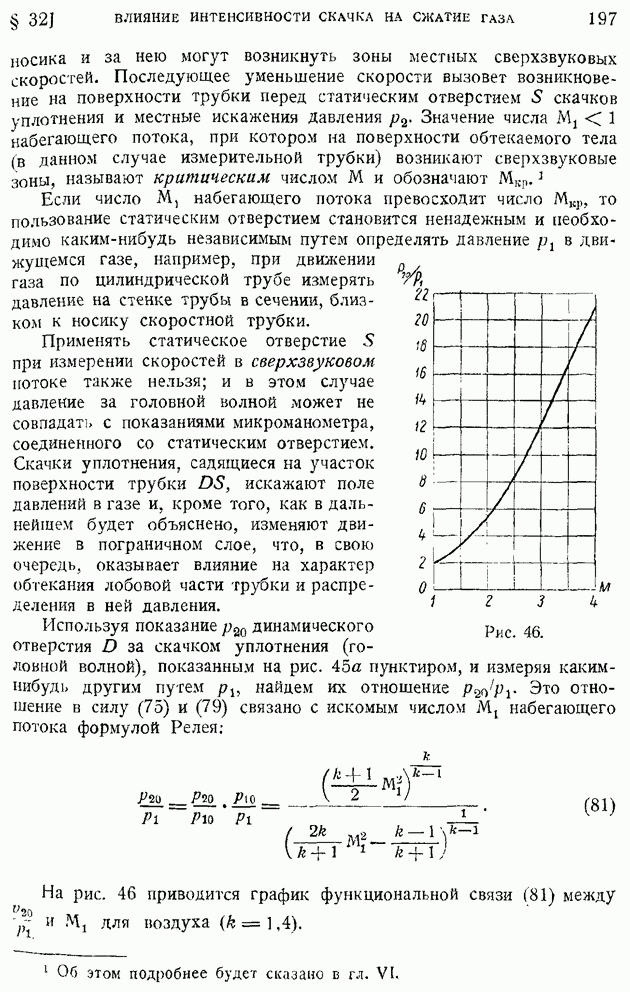
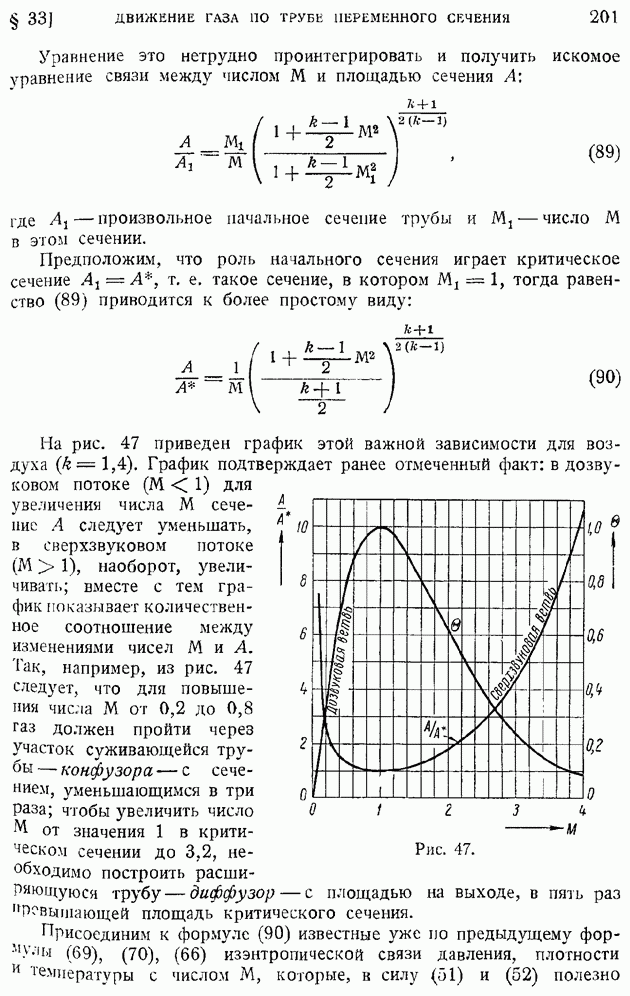
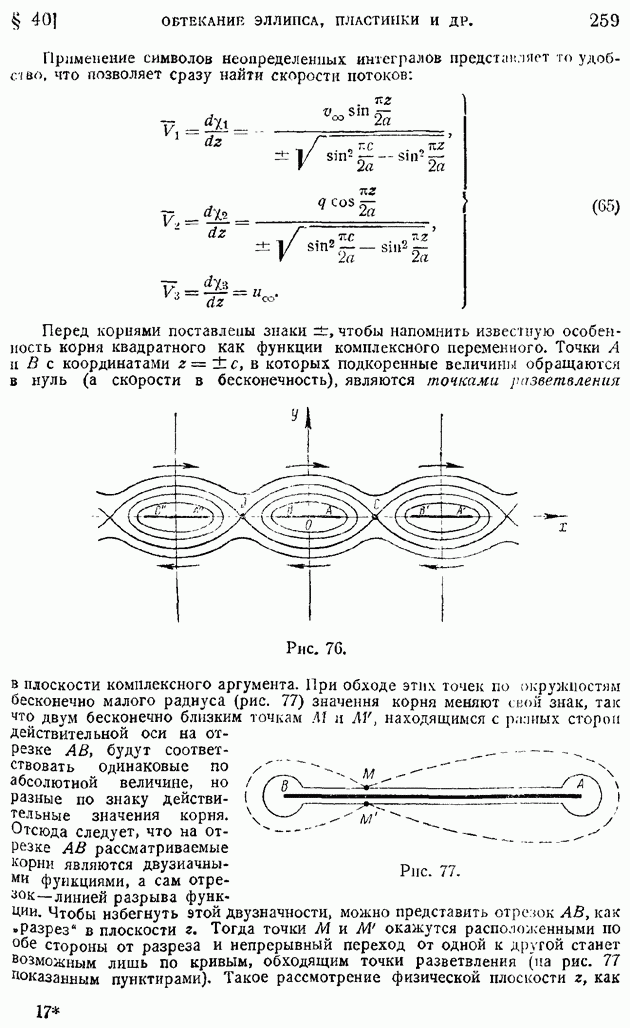
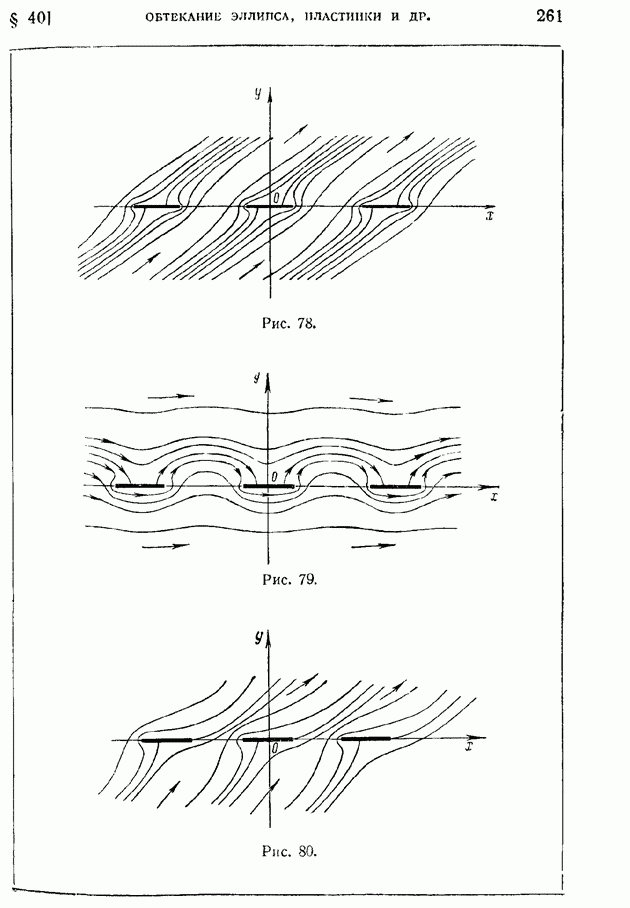
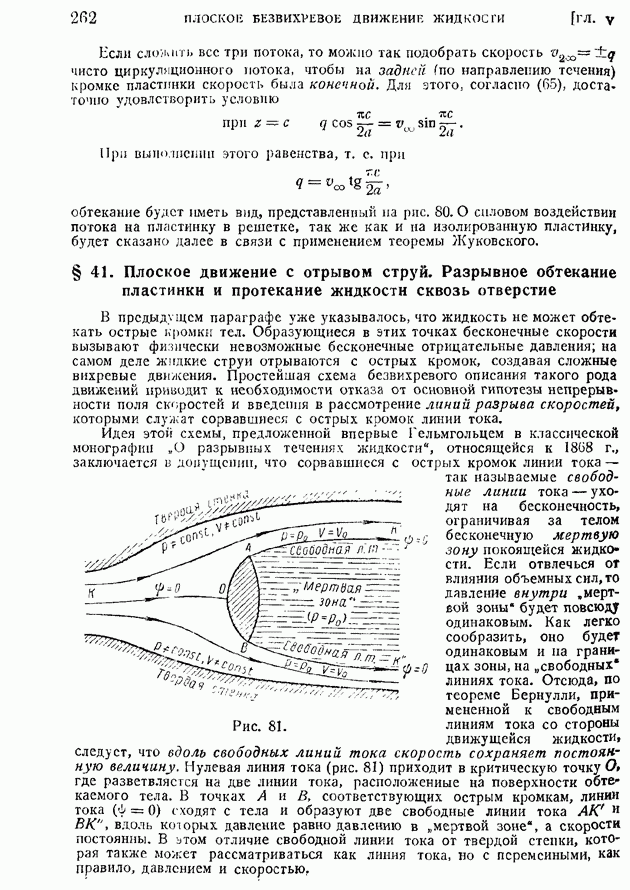
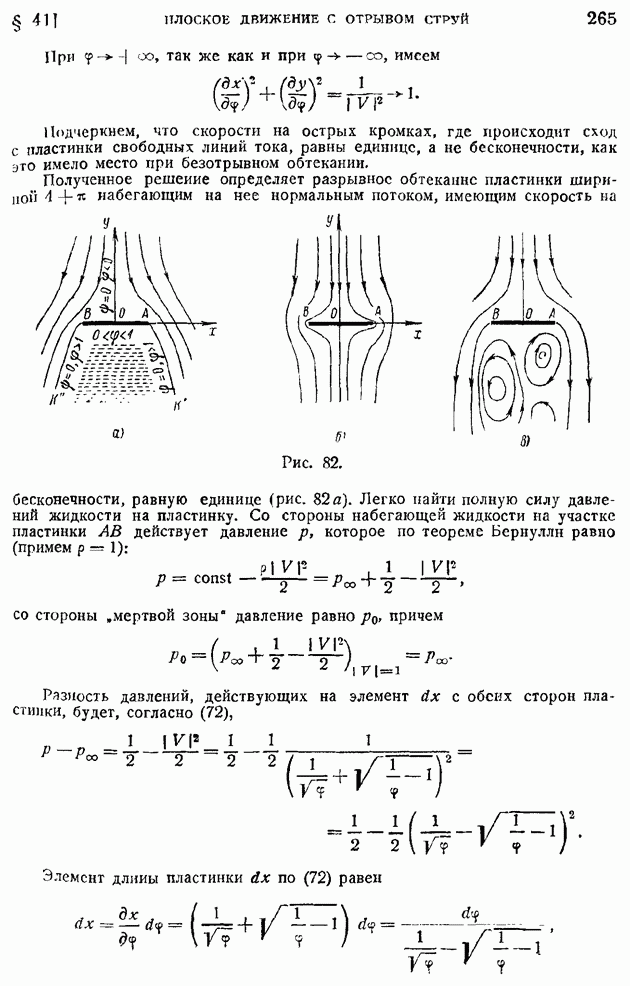
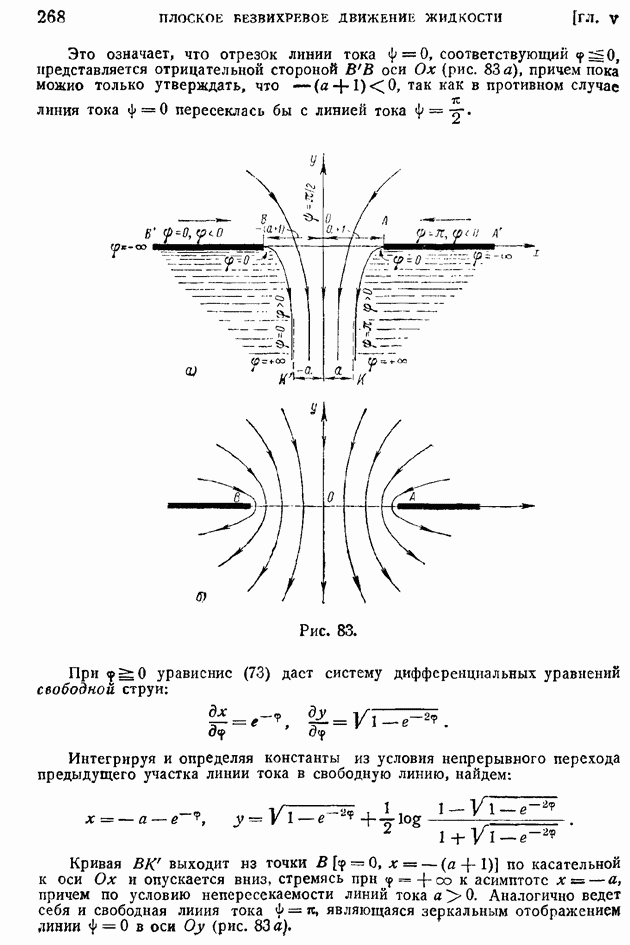
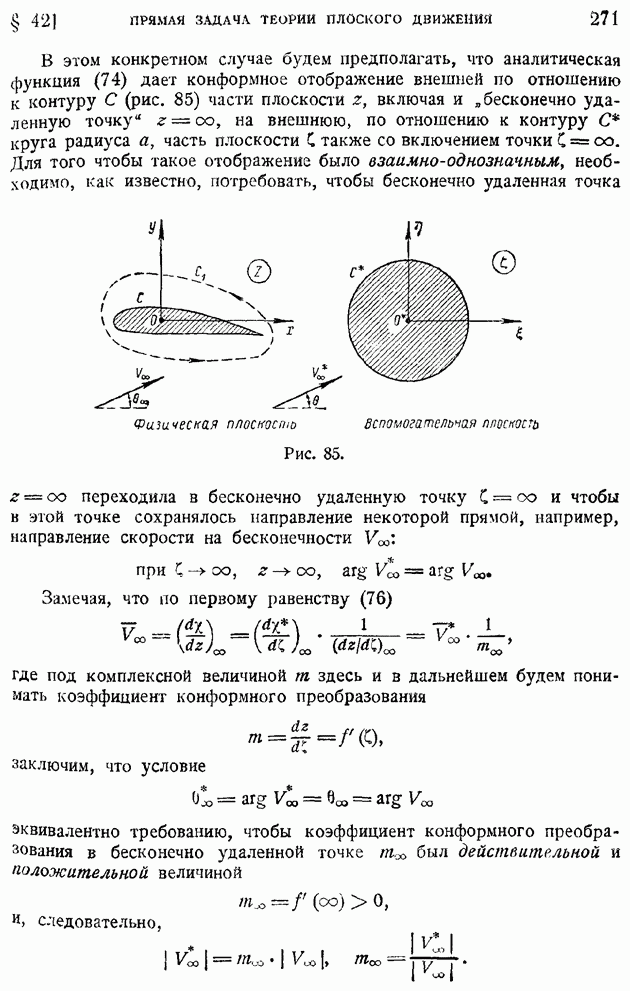
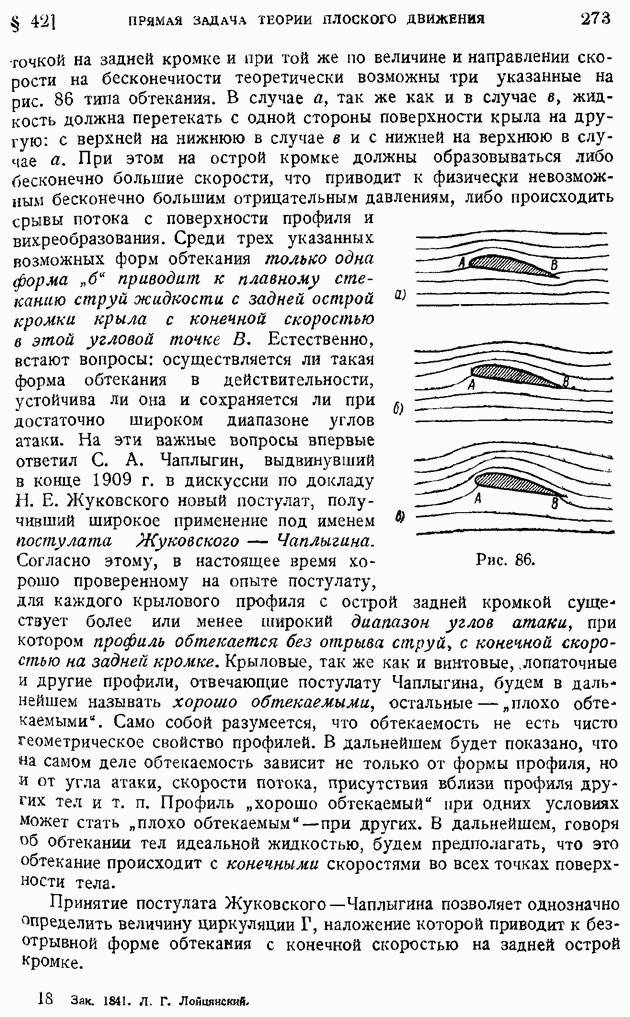
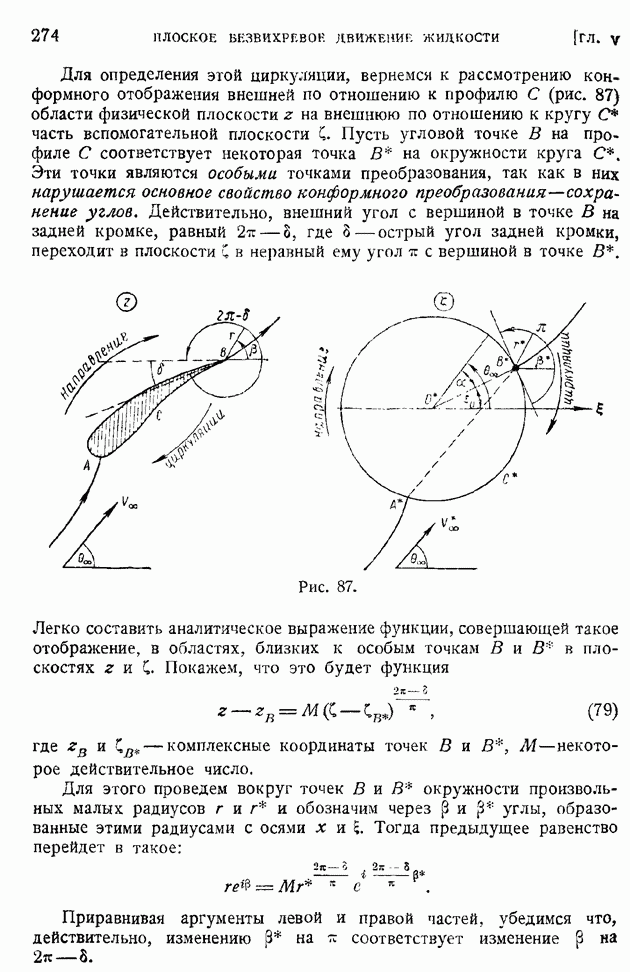
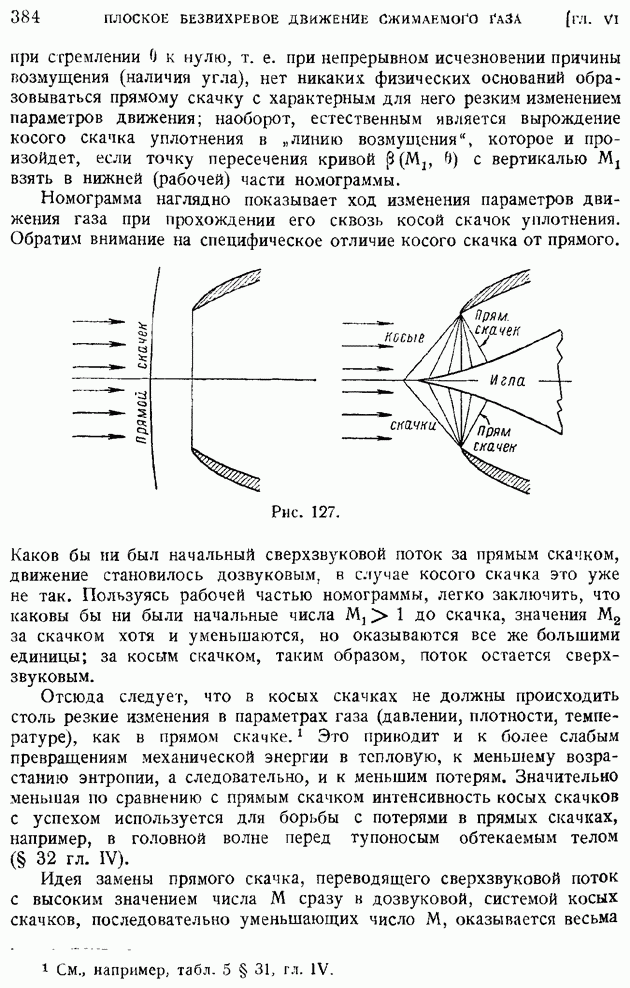
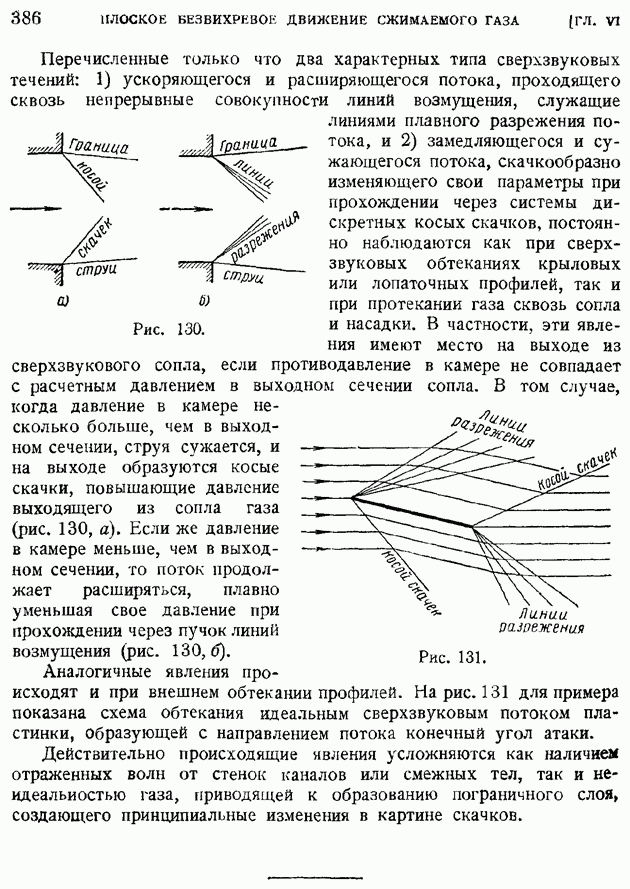
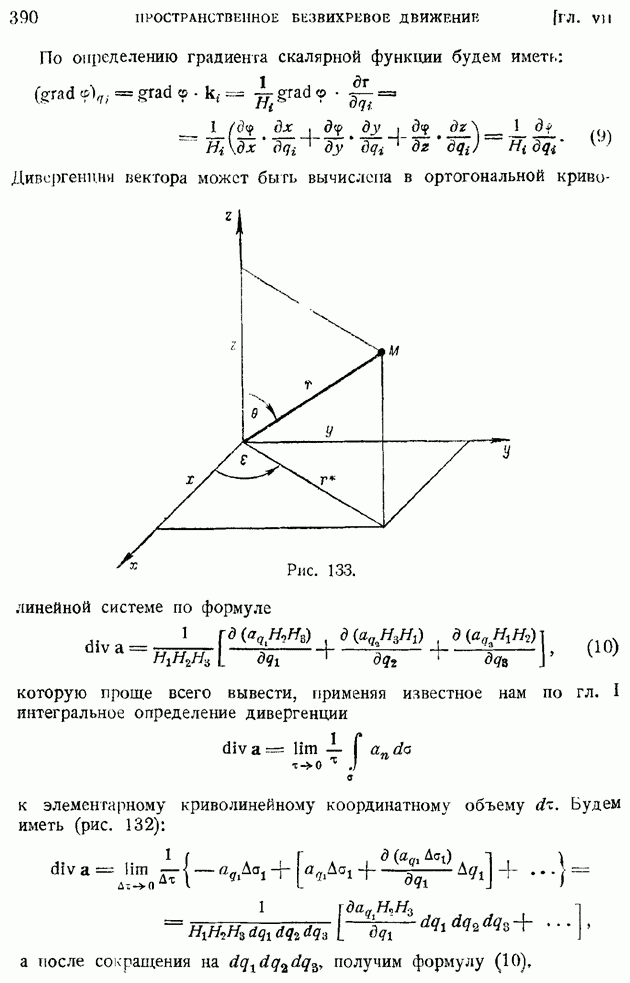
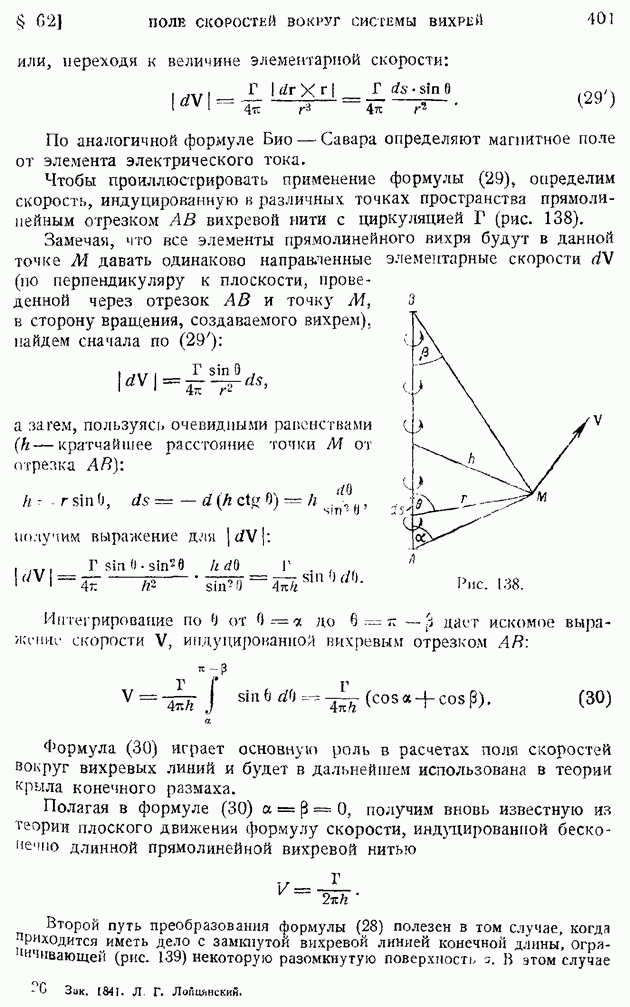
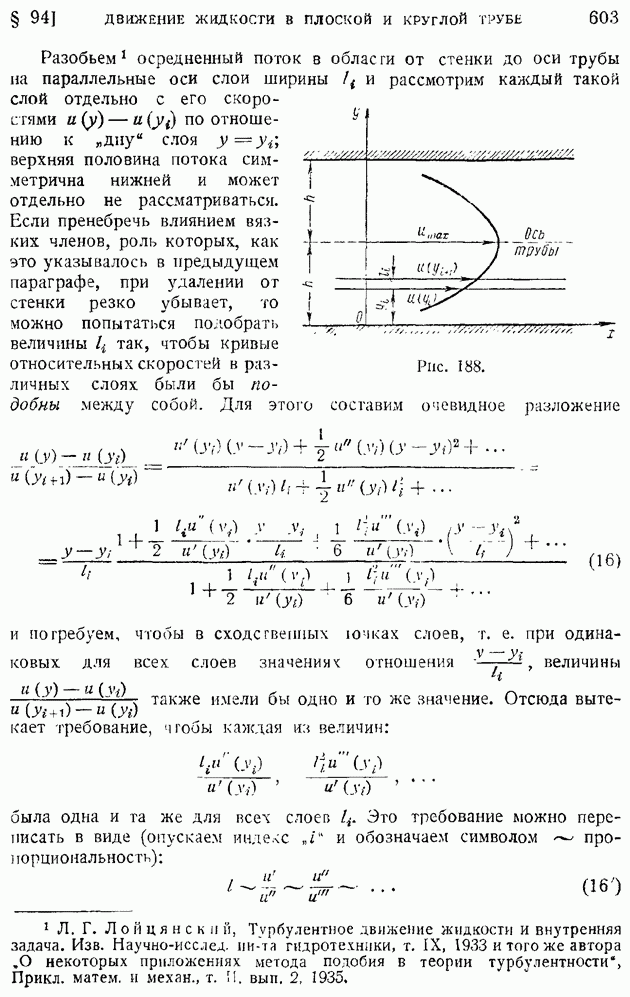
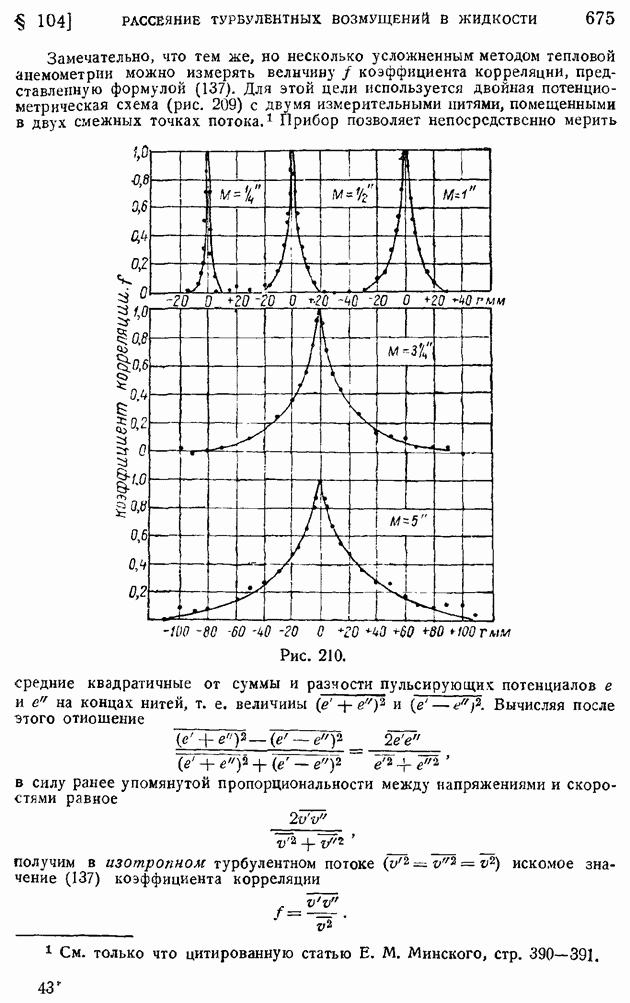
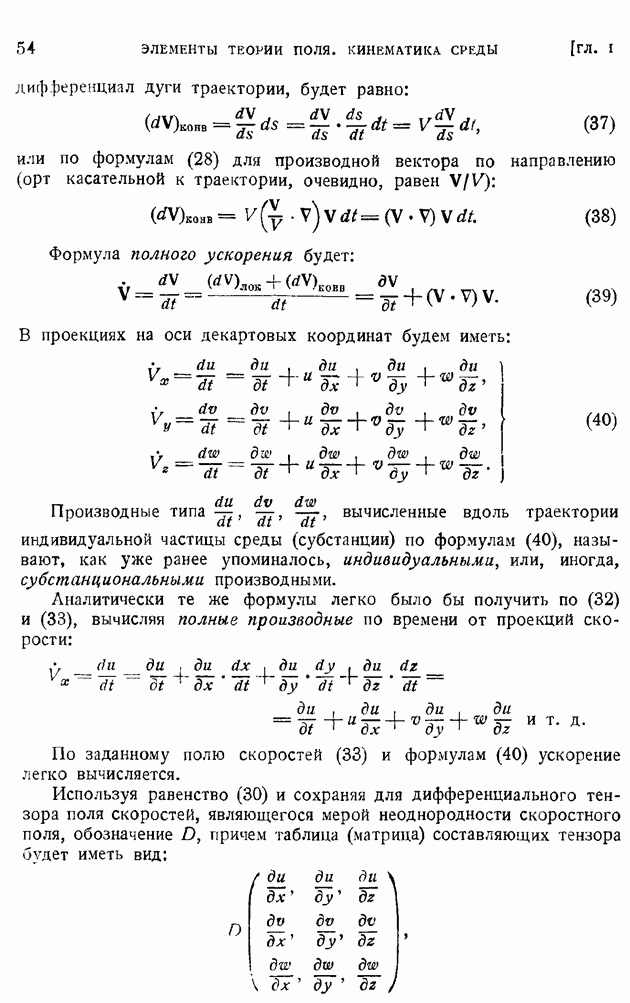| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 89. Ламинарный пограничный слой на пластинке, продольно обтекаемой сжимаемым газом при больших скоростях. Случай линейной зависимости коэффициента вязкости от температуры (n = 1)
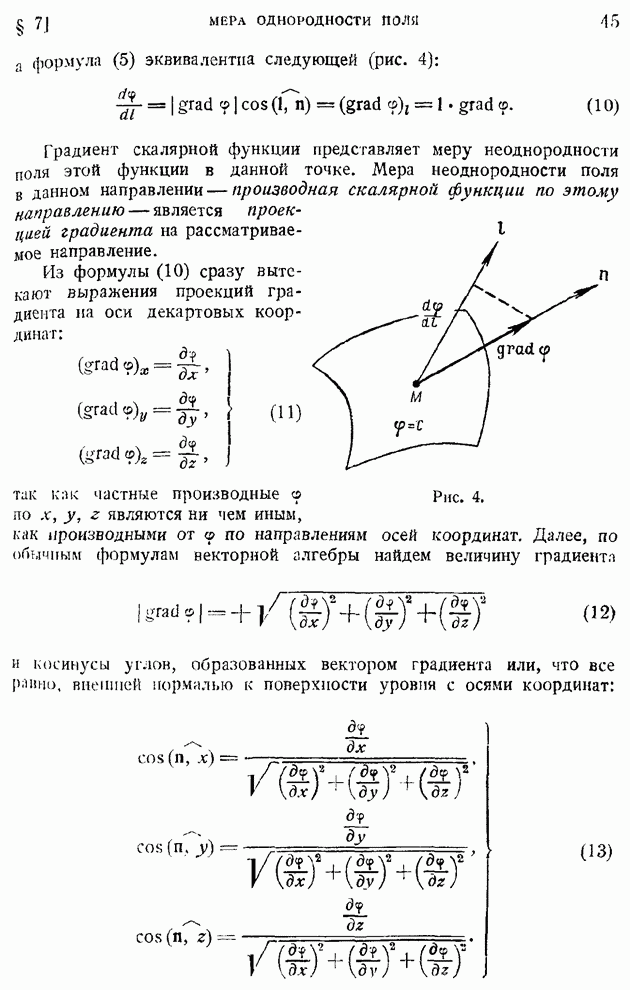
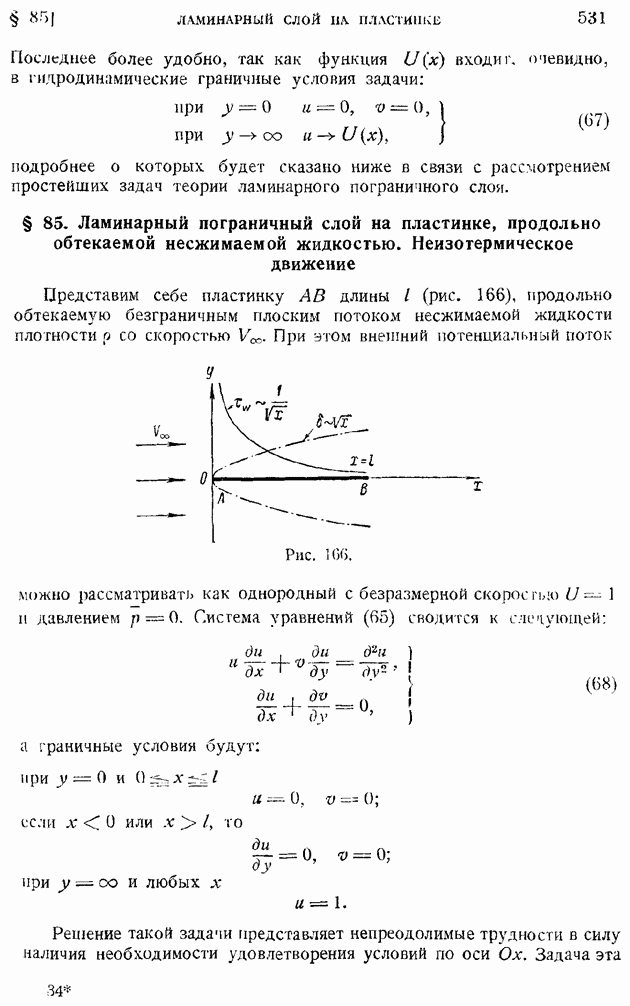
В качестве простейшего примера применения уравнений (63) рассмотрим продольное обтекание пластинки. В этом случае  следовательно, в принятых безразмерных величинах система (63) может быть переписана в виде:
следовательно, в принятых безразмерных величинах система (63) может быть переписана в виде:

или, производя очевидное сокращение в третьем равенстве при помощи первого:

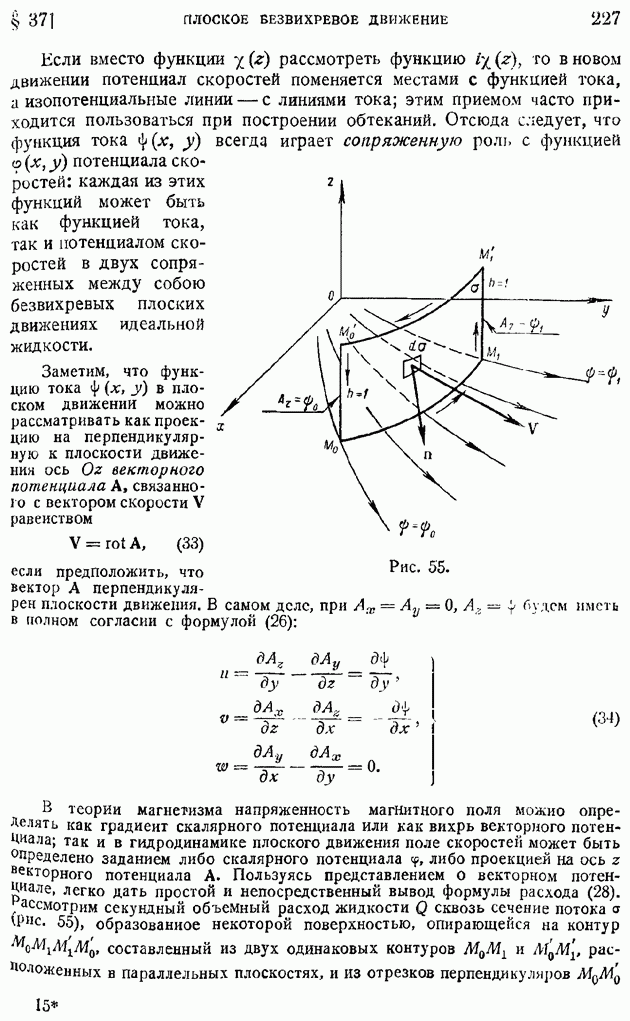
А. А. Дородницын указал общее преобразование координат, позволяющее придавать уравнениям пограничного слоя в сжимаемом газе форму, напоминающую уравнения пограничного слоя в несжимаемой жидкости. Преобразование это определяется системой равенств в размерных величинах

где  и
и  - давление и плотность в адиабатически и изэнтропически заторможенном внешнем потоке.
- давление и плотность в адиабатически и изэнтропически заторможенном внешнем потоке.
Используя в (105) вместо  величины
величины  будем иметь в случае пластинки
будем иметь в случае пластинки  в принятых ранее безразмерных величинах:
в принятых ранее безразмерных величинах:

Формулы перехода от дифференцирования по х, у к дифференцированию по  будут:
будут:

так как  является функцией не только у, но и х.
является функцией не только у, но и х.
Первое равенство системы (104) преобразуется к виду:

и, после сокращения на  и принятия в расчет последних двух равенств системы, дает:
и принятия в расчет последних двух равенств системы, дает:

Из второго равенства (уравнения неразрывности) вытекает наличие функции тока  причем:
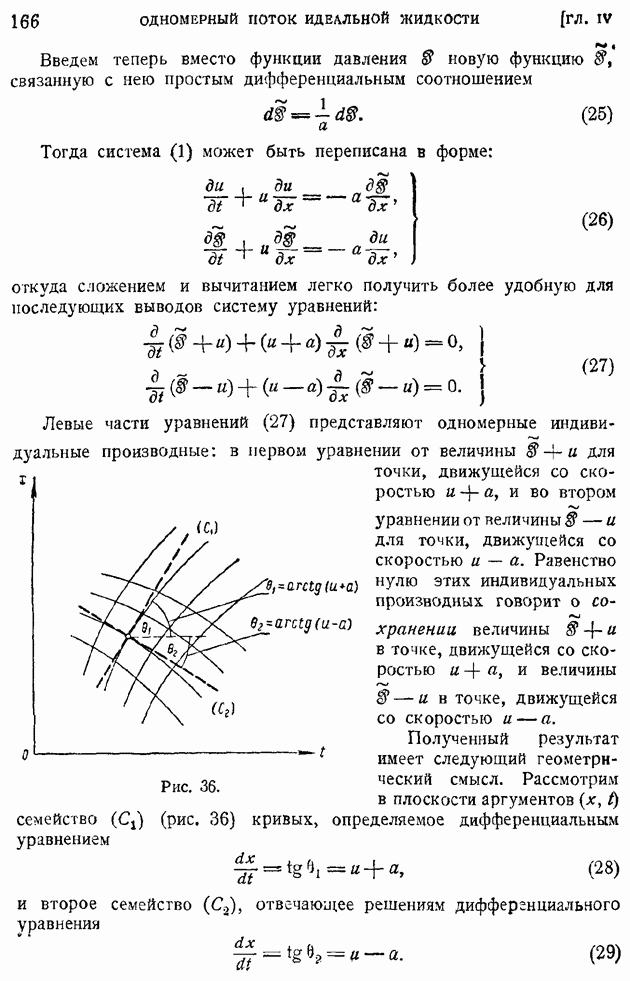
причем:

Отсюда можно заключить о справедливости соотношений:

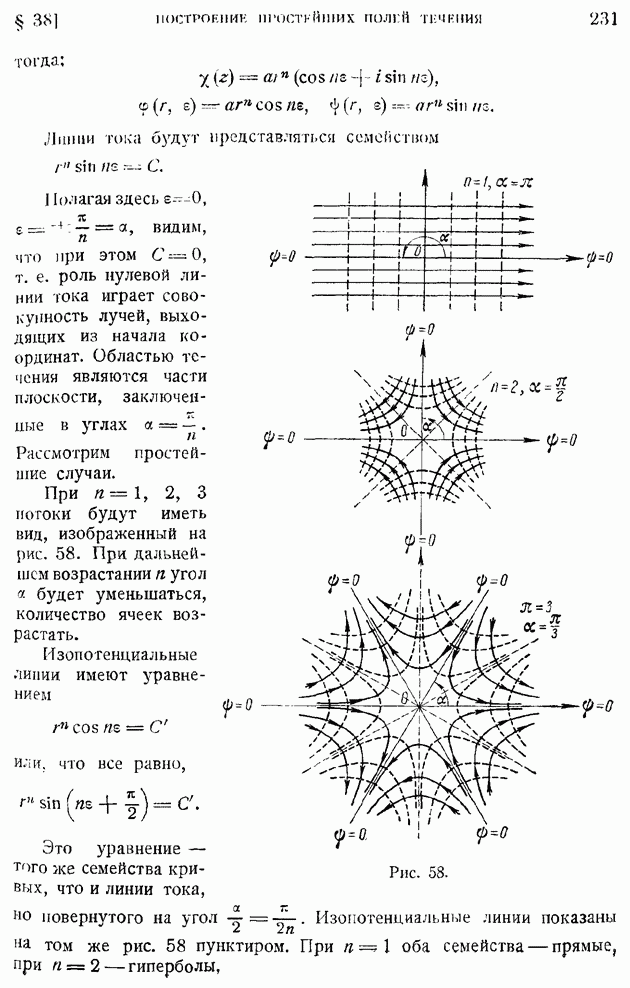
Сравнивая с уравнением (107), видим, что, если ввести обозначение

то уравнения (107) и (108) приведутся к виду:

Аналогичному преобразованию подвергнем и третье уравнение системы (104) — уравнение энергий; будем иметь:

или, сокращая обе части на  и используя обозначение (109) и последние два соотношения в системе (104):
и используя обозначение (109) и последние два соотношения в системе (104):

Принимая во внимание общие соображения об упрощении граничных условий путем перехода от пластинки  к бесконечной плоскости
к бесконечной плоскости  приведенные подробно в начале § 85 при изложении задачи о пограничном слое на пластинке в потоке несжимаемой жидкости, будем искать выражение для продольной скорости
приведенные подробно в начале § 85 при изложении задачи о пограничном слое на пластинке в потоке несжимаемой жидкости, будем искать выражение для продольной скорости  и теплосодержания
и теплосодержания  в функции от одного аргумента С, представляющего комплекс
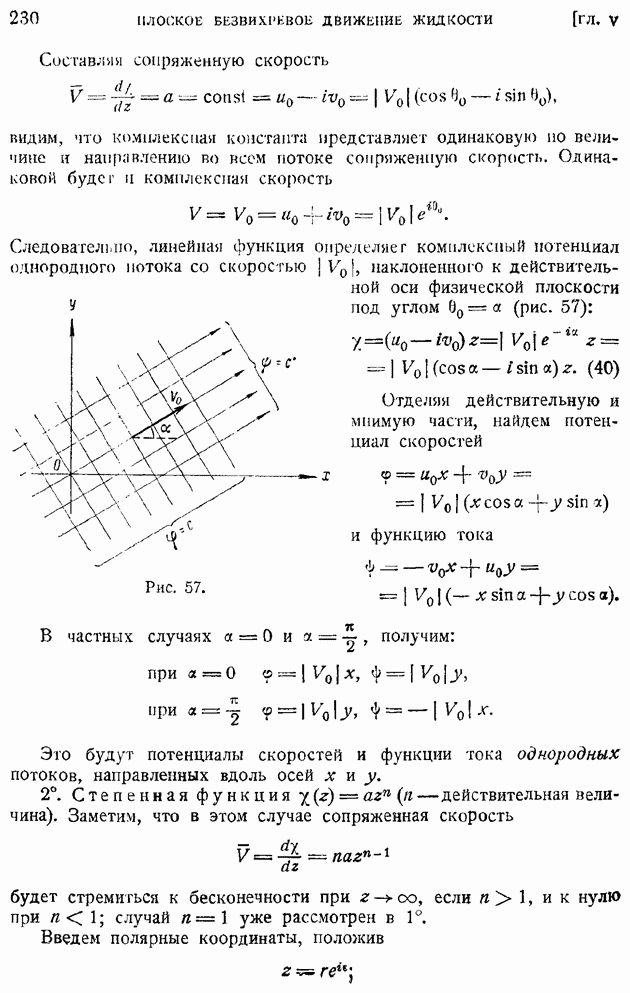
в функции от одного аргумента С, представляющего комплекс

Тогда, согласно второму равенству системы (110), получим:

Введем для краткости обозначение

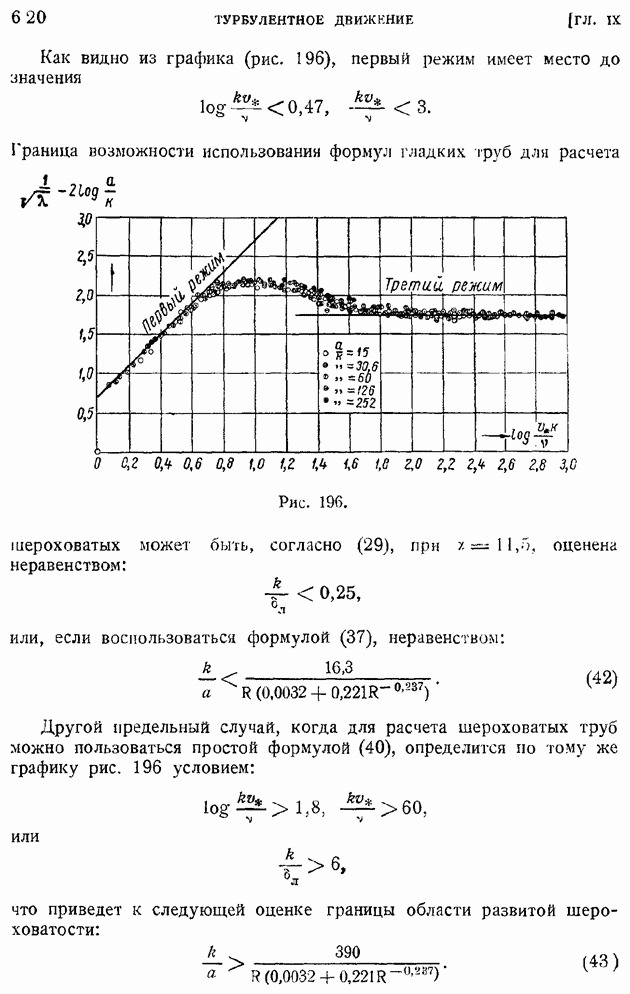
тогда, как и в § 85, будем иметь следующие выражения функции тока  скоростей
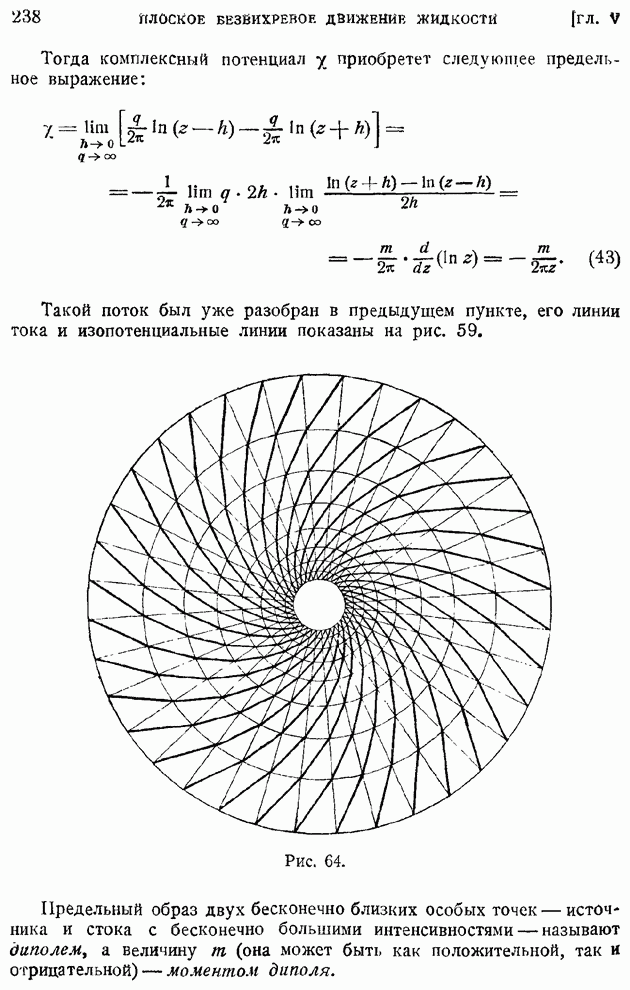
скоростей  , а также производных (обозначаемых в дальнейшем штрихом) от скорости и и теплосодержания
, а также производных (обозначаемых в дальнейшем штрихом) от скорости и и теплосодержания  по
по 

Подставляя эти выражения в первое из уравнений (110) и в уравнение (111), получим следующие два уравнения; служащие для определения неизвестных функций 

Граничные условия для  будут те же, что и в случае несжимаемой жидкости:
будут те же, что и в случае несжимаемой жидкости:

Граничные условия для безразмерного теплосодержания  могут быть разнообразны. Если задана постоянная вдоль всей пластинки безразмерная температура
могут быть разнообразны. Если задана постоянная вдоль всей пластинки безразмерная температура  то граничные условия запишутся в виде:
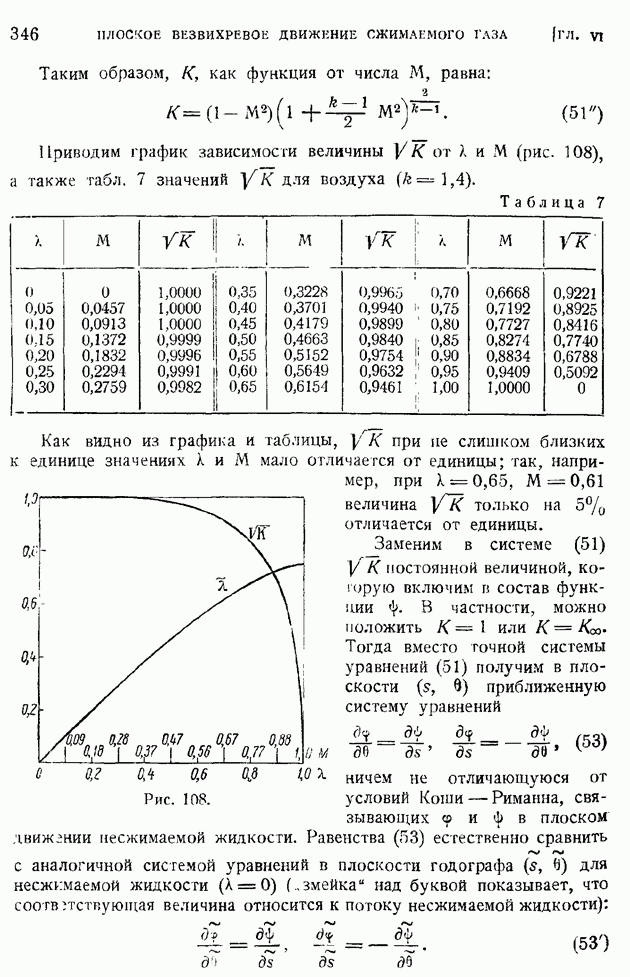
то граничные условия запишутся в виде:

Если на пластинке отсутствует теплоотдача, то граничные условия сведутся к следующим равенствам:

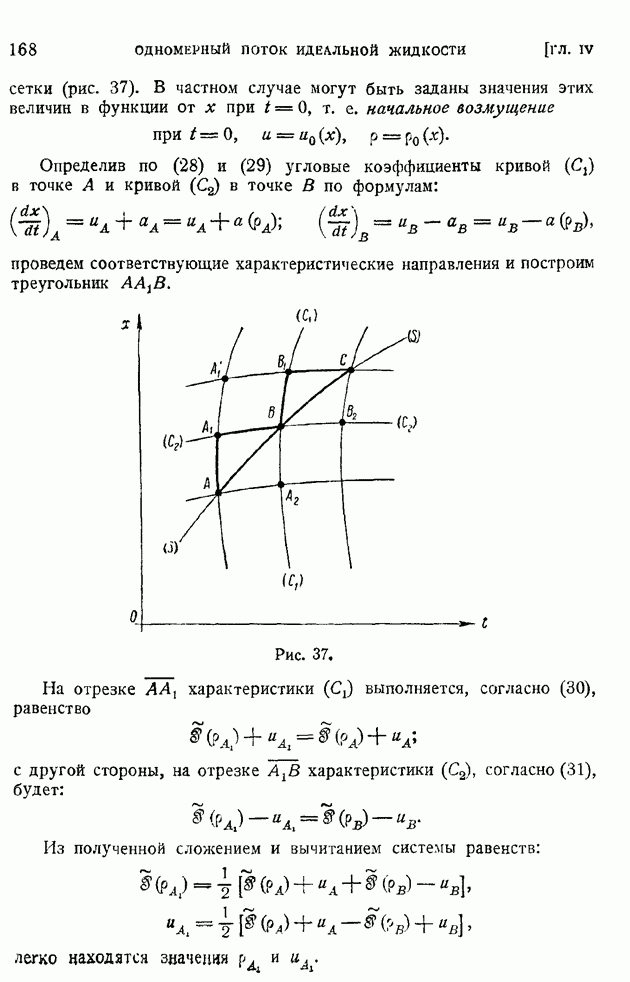
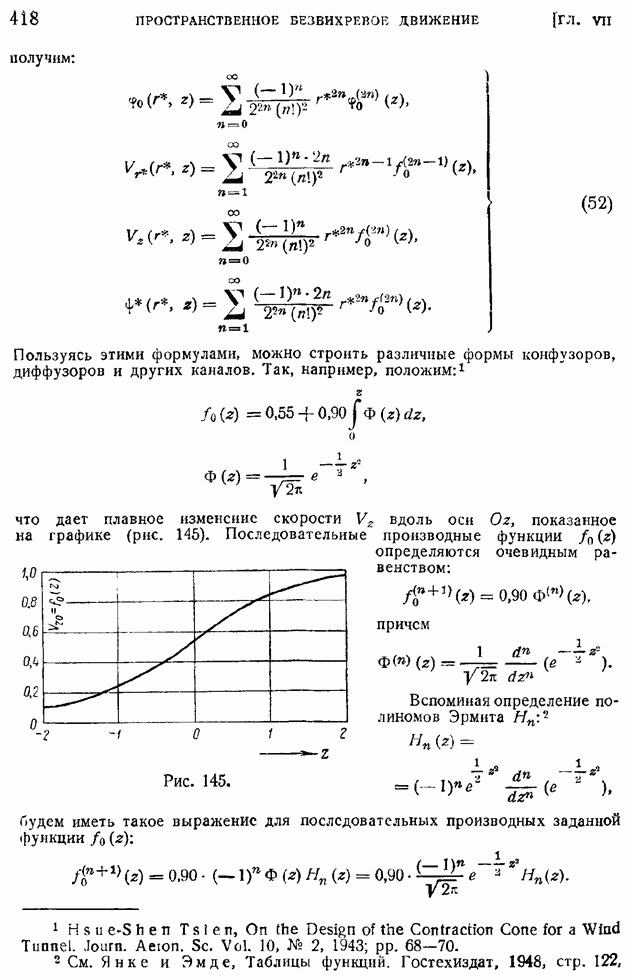
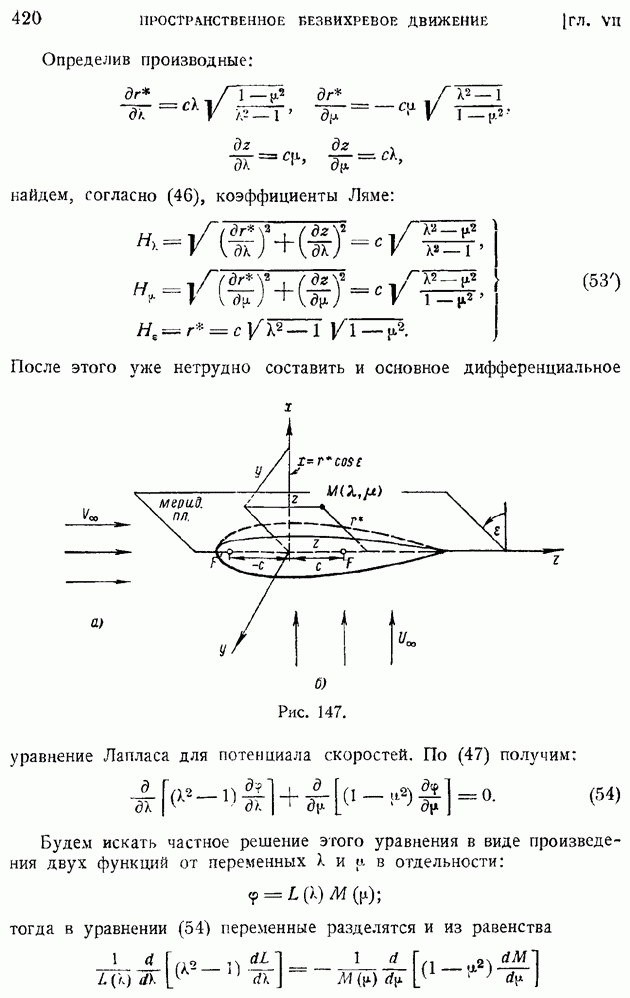
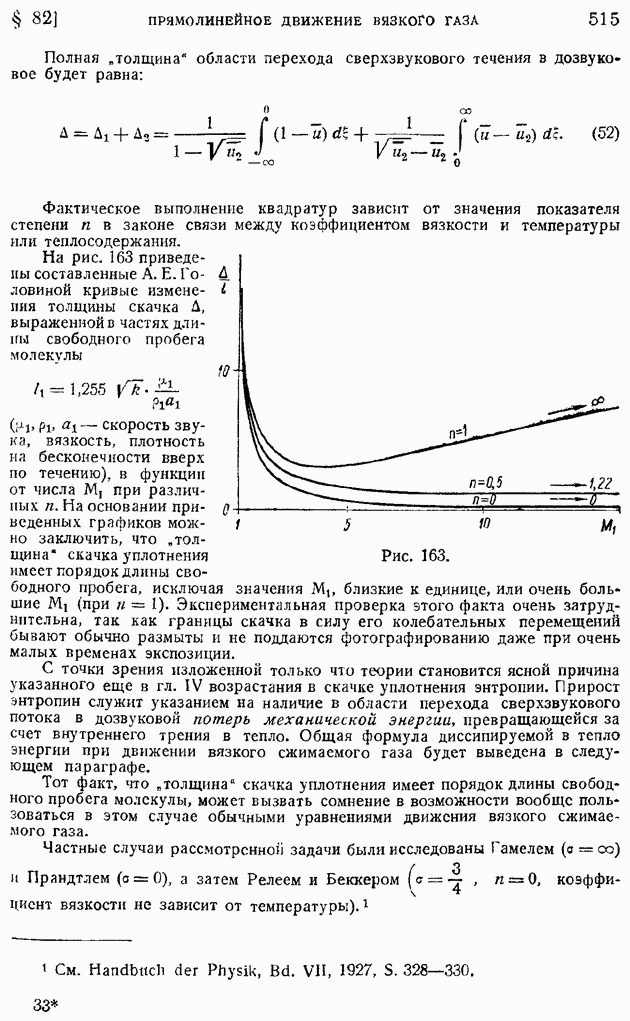
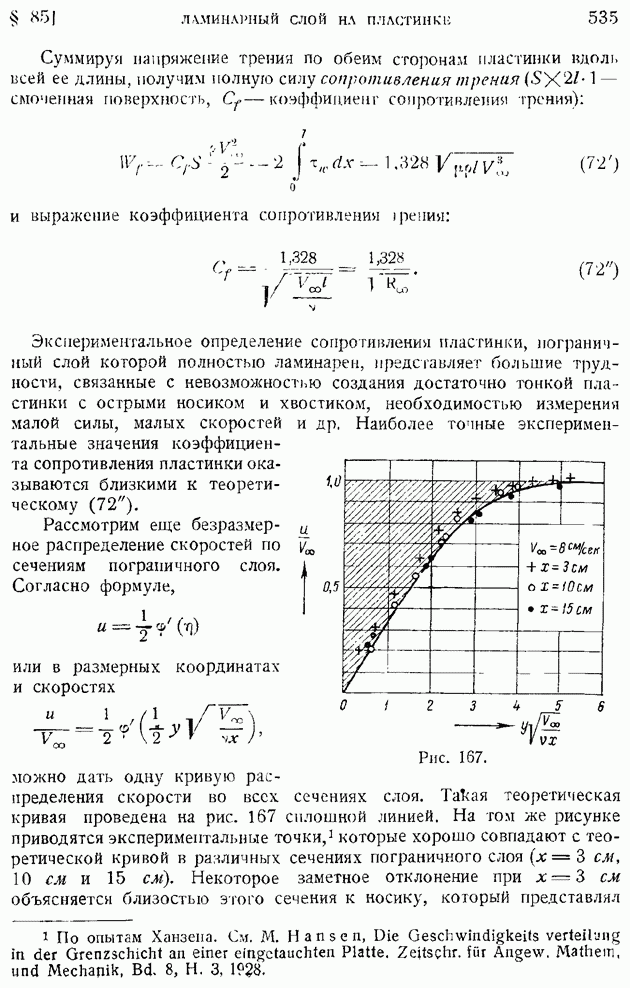
Интегрирование уравнений (113) в общем случае представляет большие затруднения, так как приходится производить численное интегрирование уравнений с несколькими характерными параметрами: 
Рассмотрим простейший случай, когда связь между коэффициентом вязкости и температурой линейна  В этом случае вместо (113) получим систему уравнений:
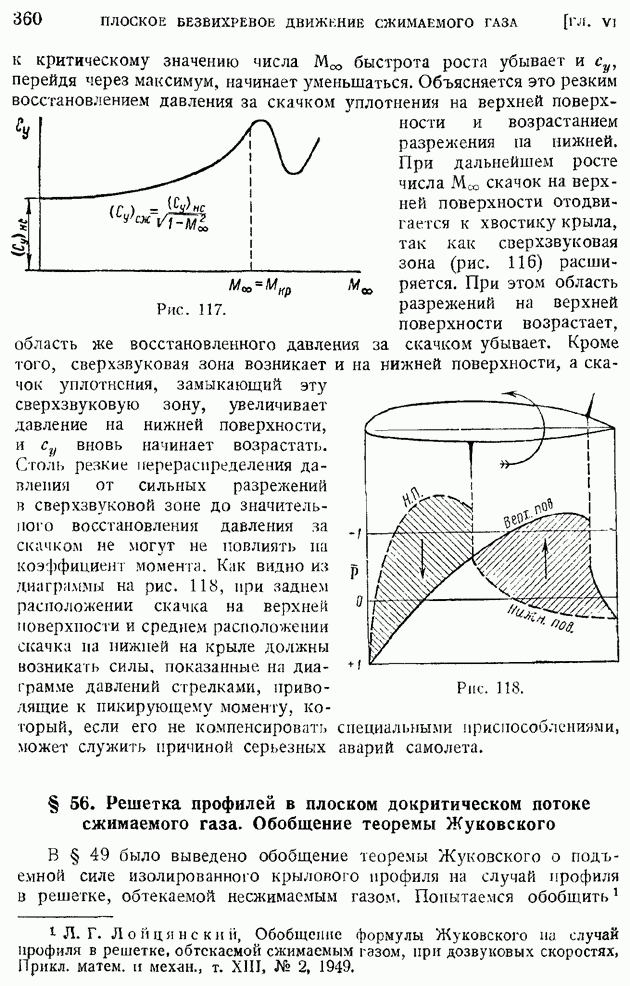
В этом случае вместо (113) получим систему уравнений:

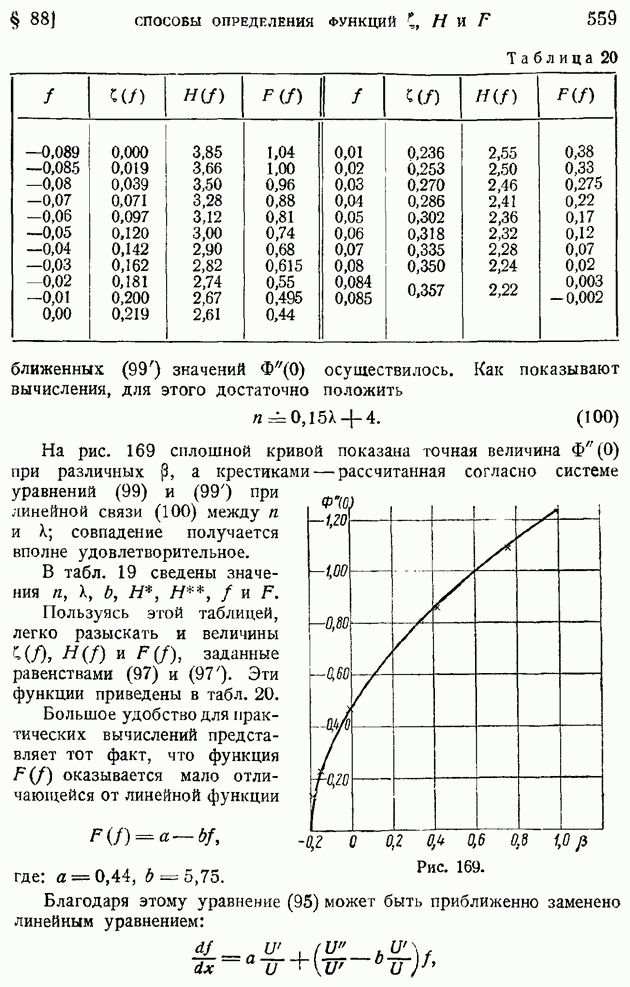
Первое из этих уравнений, разрешаемое при граничных условиях (114), ничем формально не отличается от соответствующего уравнения (71) и граничных условий (71) задачи о пограничном слое на пластинке в несжимаемой жидкости, гак что для определения функции  можно пользоваться приведенной ранее табл. 14. Но тогда, интегрируя второе уравнение системы (117), подобно тому как это было сделано в конце § 85, найдем значение
можно пользоваться приведенной ранее табл. 14. Но тогда, интегрируя второе уравнение системы (117), подобно тому как это было сделано в конце § 85, найдем значение  в форме:
в форме:

где введено обозначение

а произвольные постоянные интегрирования  должны быть определены из начальных условий (115) или (116). Полагая
должны быть определены из начальных условий (115) или (116). Полагая 
найдем значение постоянной  полагая
полагая  получим
получим

Обозначим теперь через  значения теплосодержания и температуры пластинки в условиях (116) отсутствия теплоотдачи, т. е. тогда, когда пластинка играет роль измерителя температуры потока — пластинчатого термометра. Условие отсутствия теплоотдачи будет:
значения теплосодержания и температуры пластинки в условиях (116) отсутствия теплоотдачи, т. е. тогда, когда пластинка играет роль измерителя температуры потока — пластинчатого термометра. Условие отсутствия теплоотдачи будет:

Дифференцируя (118) и замечая, что но (119) будет  найдем в этом частном случае
найдем в этом частном случае  т. е. по (120) при
т. е. по (120) при  получим
получим

или, переходя к размерным температурам:

где

Тогда постоянную С в общем случае наличия теплоотдачи с поверхности пластинки можно представить, согласно (120) и (121), в следующем виде:

Проанализируем полученные результаты. Прежде всего  убедиться, что при Мгао соотношение (118) в переменной С совпадет с ранее выведенной формулой (74) для несжимаемой жидкости в переменной
убедиться, что при Мгао соотношение (118) в переменной С совпадет с ранее выведенной формулой (74) для несжимаемой жидкости в переменной  принятой в § 85; полученное таким путем равенство
принятой в § 85; полученное таким путем равенство

дает распределение температур в пограничном слое на пластинке, обтекаемой несжимаемой жидкостью при учете линейного закона связи между коэффициентом вязкости и температурой.
Возвращаясь к случаю газа, движущегося с большими скоростями, когда влиянием сжимаемости (числа  ) пренебрегать нельзя, будем предполагать, что функция
) пренебрегать нельзя, будем предполагать, что функция  затабулирована для различных а. Для дальнейшего особенно важно знать величины
затабулирована для различных а. Для дальнейшего особенно важно знать величины  приводим их значения при нескольких
приводим их значения при нескольких  :
:

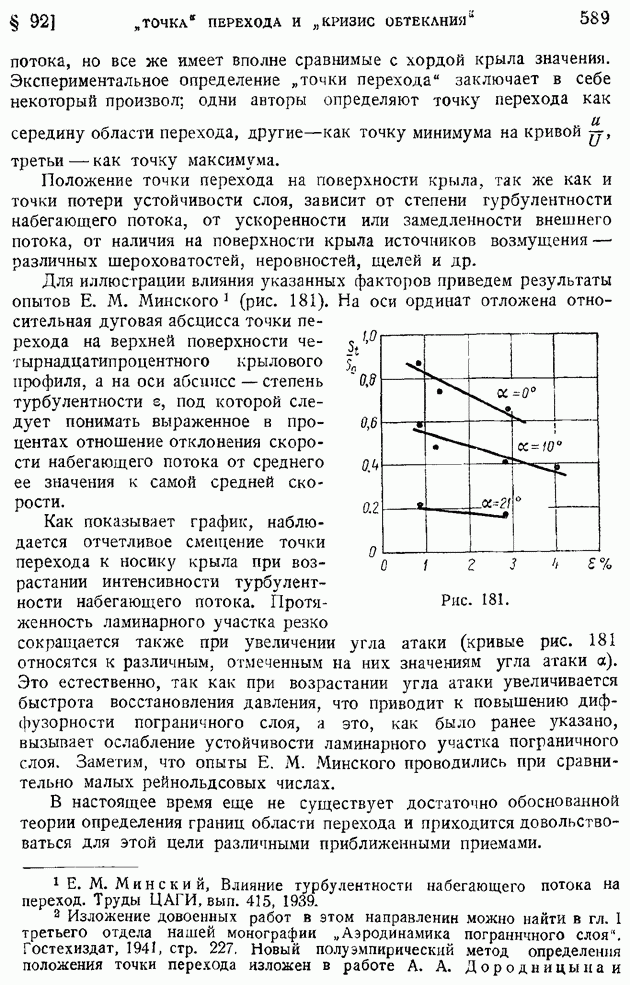
Обращаясь теперь к формуле (122), видим, что она представляет для случая  решение задачи об измерении температуры газового потока
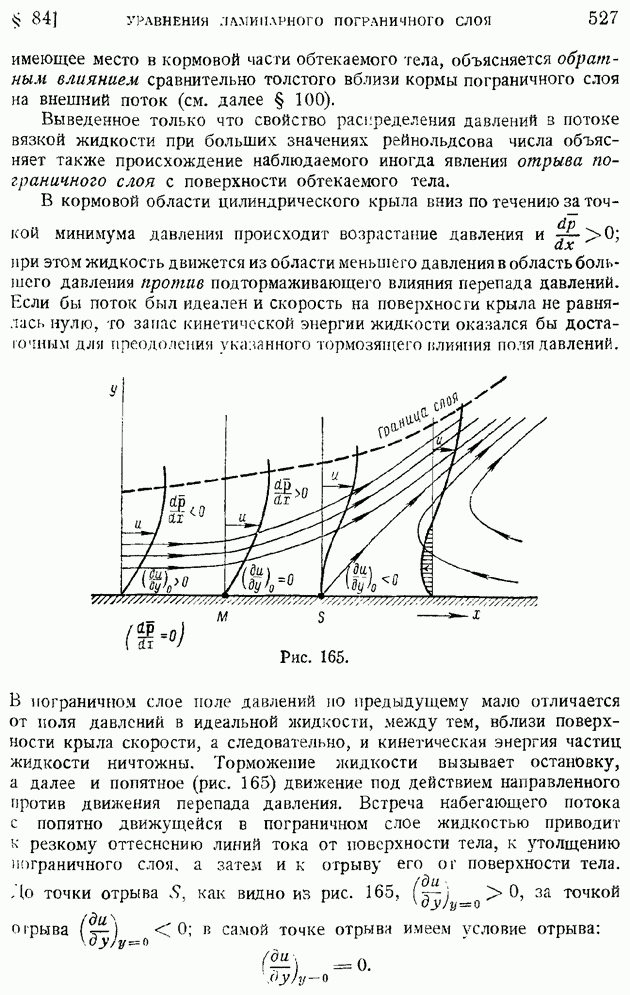
решение задачи об измерении температуры газового потока  при помощи непосредственного замера температуры
при помощи непосредственного замера температуры  поверхности продольно обтекаемой этим газом пластинки, при условии, что тепло от пластинки не отводится (нет теплоотвода через державку и проволочки измерительной термопары). Как наглядно показывает формула (122), такой пластинчатый термометр будет вместо температуры потока
поверхности продольно обтекаемой этим газом пластинки, при условии, что тепло от пластинки не отводится (нет теплоотвода через державку и проволочки измерительной термопары). Как наглядно показывает формула (122), такой пластинчатый термометр будет вместо температуры потока  показывать тем большую температуру
показывать тем большую температуру  чем больше число
чем больше число  Это и естественно, так как пластинка тормозит поток и, вследствие перехода энергии потока в тепло, должна дополнительно нагреваться. Конечно, это торможение будет не изэнтроническим, так как связано с переходом механической энергии в тепловую и повышением энтропии. Однако, как это сразу следует из формулы (122), при
Это и естественно, так как пластинка тормозит поток и, вследствие перехода энергии потока в тепло, должна дополнительно нагреваться. Конечно, это торможение будет не изэнтроническим, так как связано с переходом механической энергии в тепловую и повышением энтропии. Однако, как это сразу следует из формулы (122), при  термометр будет показывать температуру адиабатического и изэитропического торможения
термометр будет показывать температуру адиабатического и изэитропического торможения

при других значениях а это уже не так:

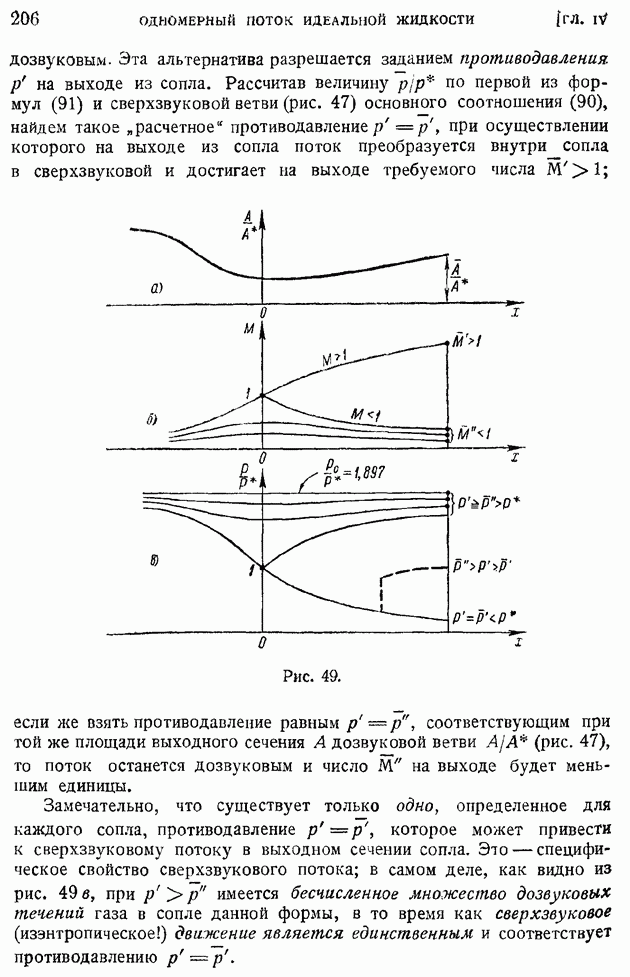
Формула (122) может служить для вычисления поправок на указания пластинчатого термометра в газе с заданным числом а, отличным от единицы.
Температуру, определенную по формуле (122), будет также иметь поверхность самолета или снаряда в установившемся их движении. При больших значениях  эти температуры достигали бы катастрофических для металла и материалов значений; для борьбы с этим необходимо применять охлаждение поверхностей изнутри. Имеющее место при высоких температурах влияние лучеиспускания также способствует понижению поверхностной температуры.
эти температуры достигали бы катастрофических для металла и материалов значений; для борьбы с этим необходимо применять охлаждение поверхностей изнутри. Имеющее место при высоких температурах влияние лучеиспускания также способствует понижению поверхностной температуры.
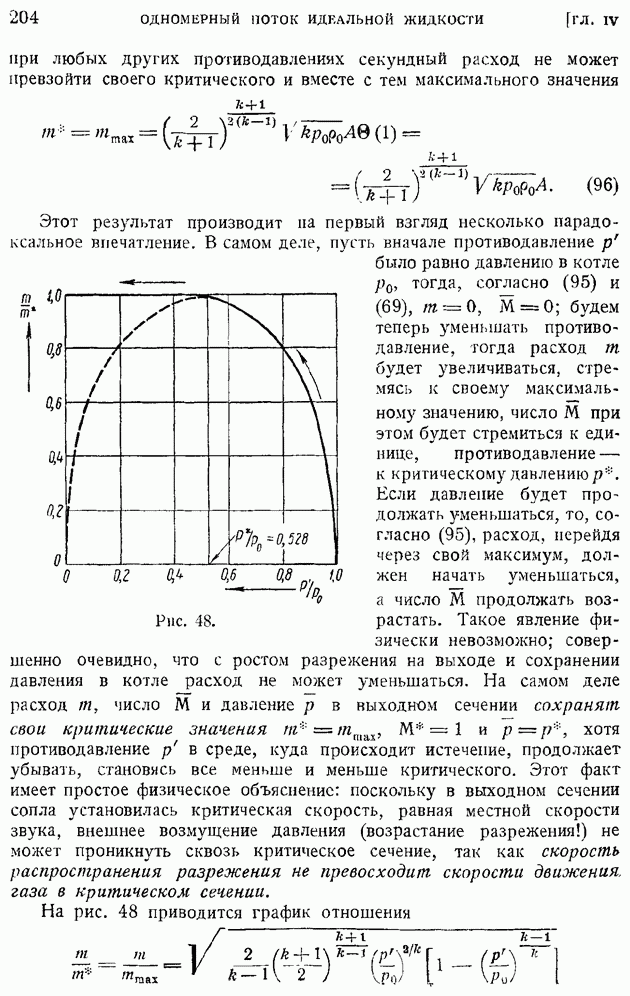
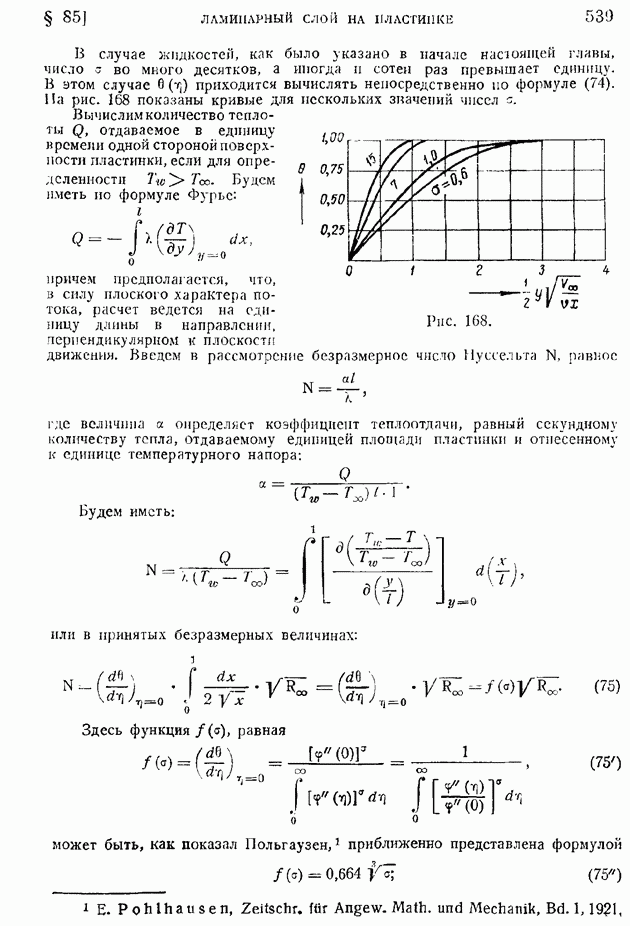
Для того чтобы определить коэффициент теплоотдачи пластинки, имеющей температуру  вычислим размерную производную от температуры по нормали к пластинке на поверхности пластинки. Имеем, переходя к размерным величинам:
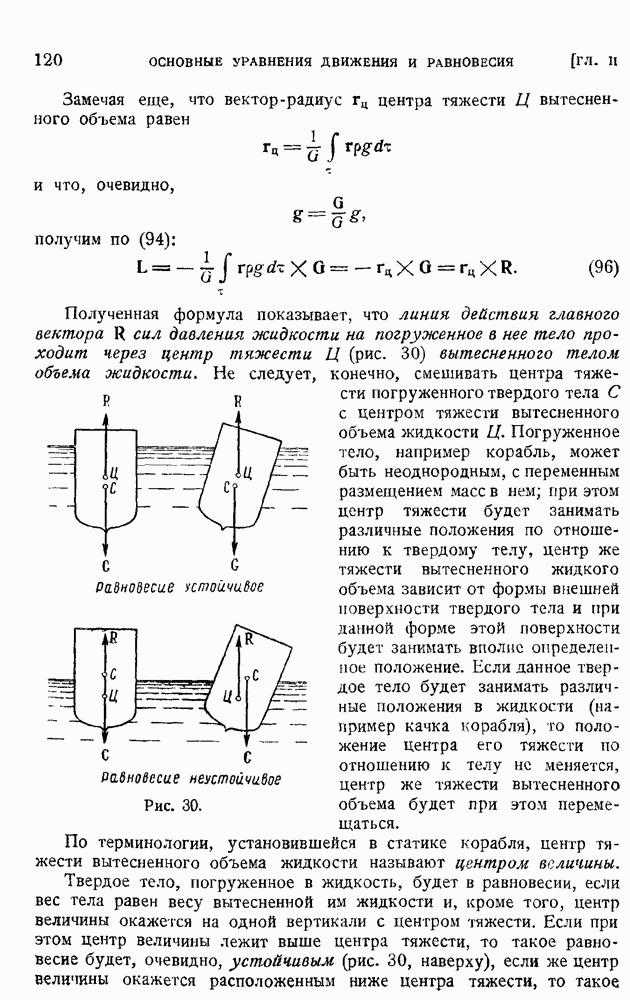
вычислим размерную производную от температуры по нормали к пластинке на поверхности пластинки. Имеем, переходя к размерным величинам:

откуда следует:

Но по (118)

кроме того, к случае пластинки, по формуле Клапейрона:

Используя ранее выведенное значение С (124) и исключая  или
или  получим:
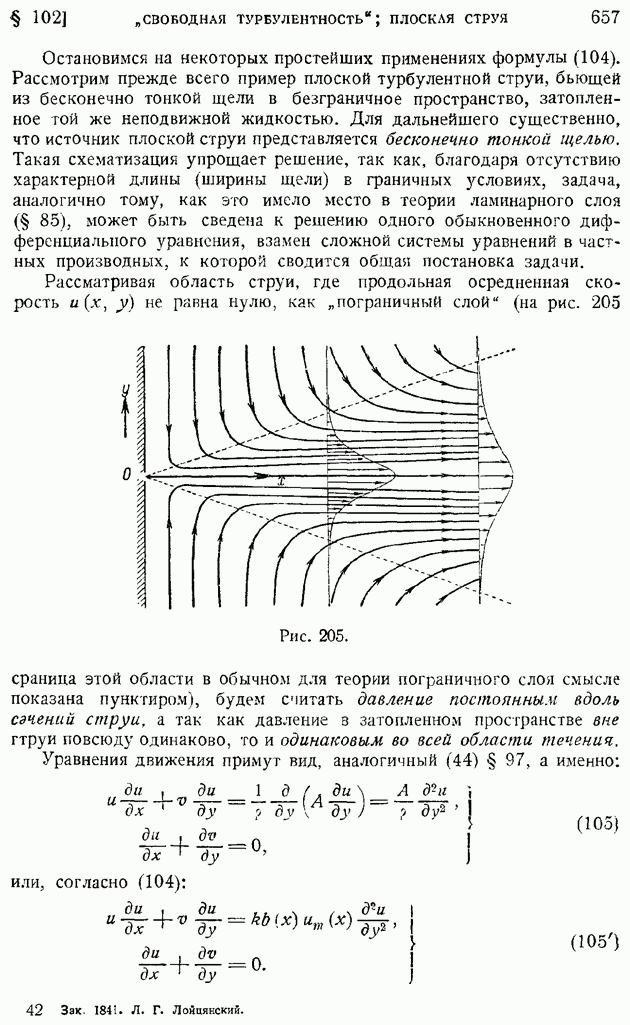
получим:

отсюда уже нетрудно  том или другом виде рассчитать теплоотдачу.
том или другом виде рассчитать теплоотдачу.
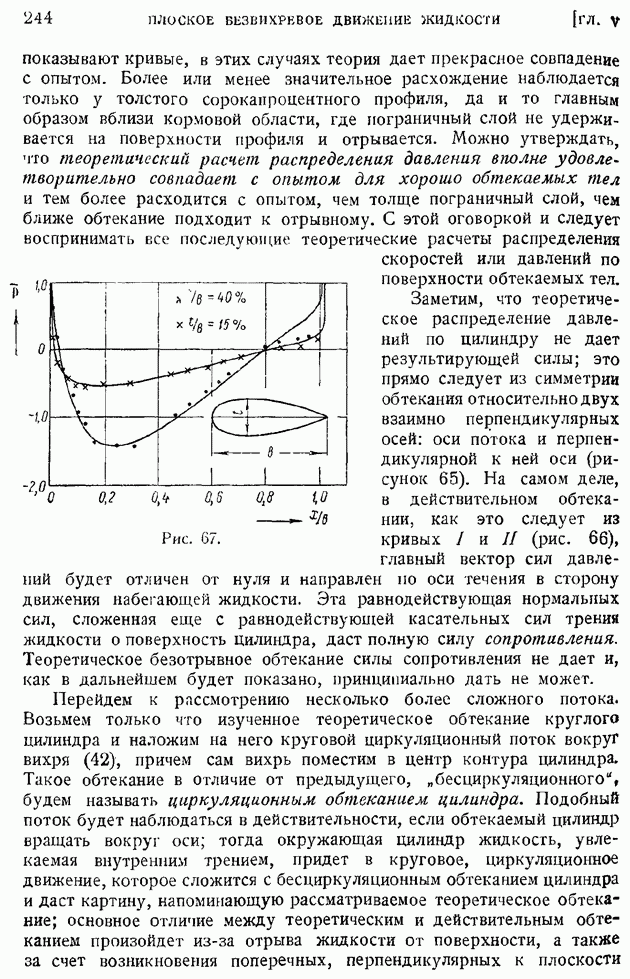
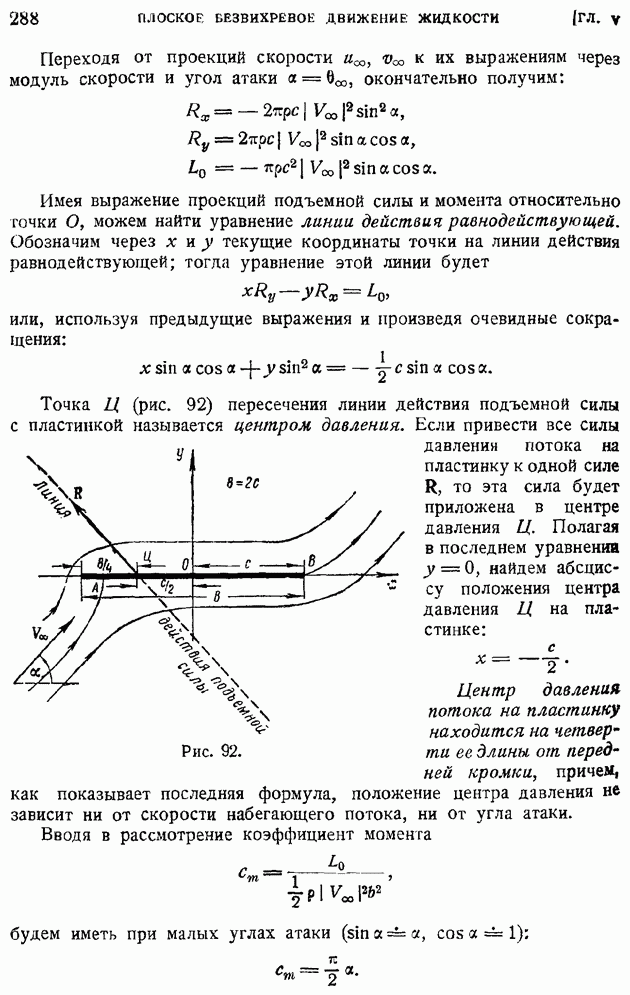
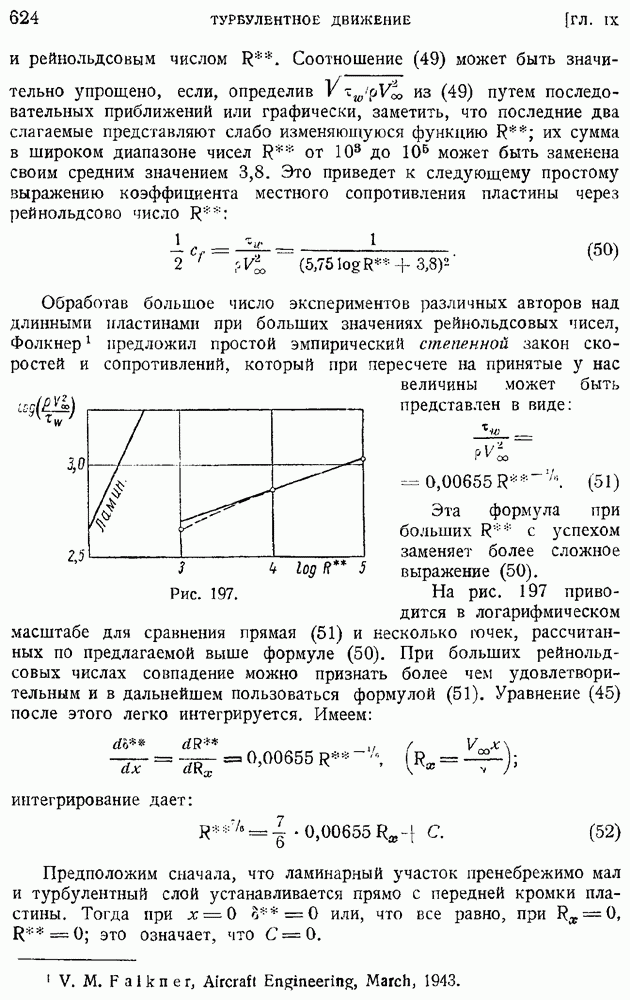
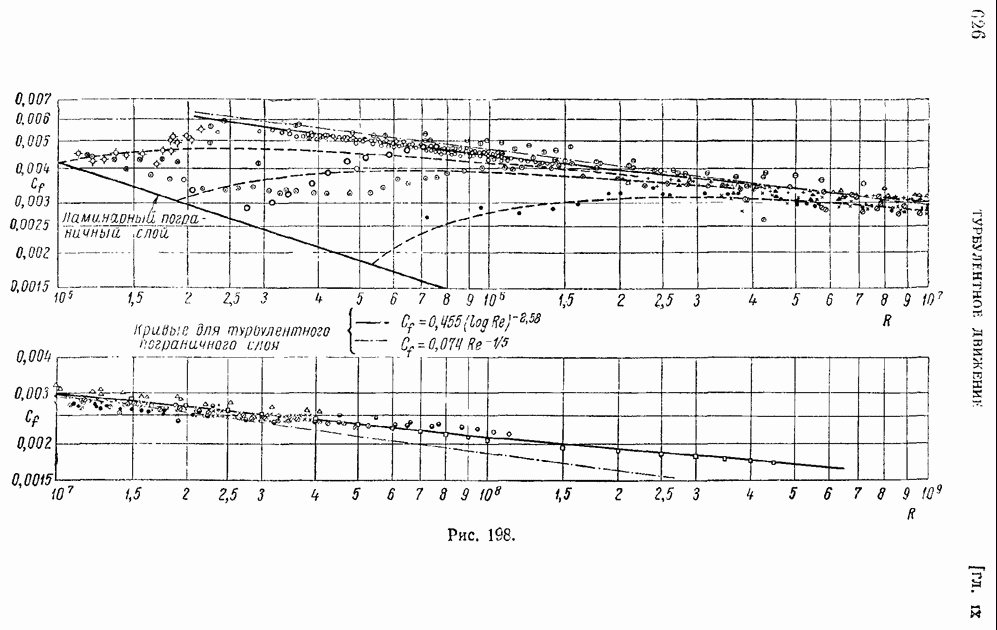
Обращаясь к вопросу о сопротивлении пластинки, найдем сначала напряжение трения  Имеем, переходя к размерным величинам:
Имеем, переходя к размерным величинам:

откуда следует:

причем  имеет то же значение, что в несжимаемом газе, и равно по предыдущему (§ 85)
имеет то же значение, что в несжимаемом газе, и равно по предыдущему (§ 85)  Итак, если при
Итак, если при  константы
константы  в формуле коэффициента местного трения определены
в формуле коэффициента местного трения определены
для набегающего потока, то коэффициент, местного трения остается тем же, что и в случае несжимаемой жидкости:

Как можно заключить из проведенных выкладок, для вычисления коэффициента сопротивления и теплоотдачи нет необходимости иметь явные формулы связи между новым переменным С и обычным  так как в окончательные выражении входят лишь значения величин при
так как в окончательные выражении входят лишь значения величин при  или
или 
Несколько сложнее решается вопрос о распределении скоростей и температур в сечениях пограничного слоя, так как полученные распределения скоростей  и температур
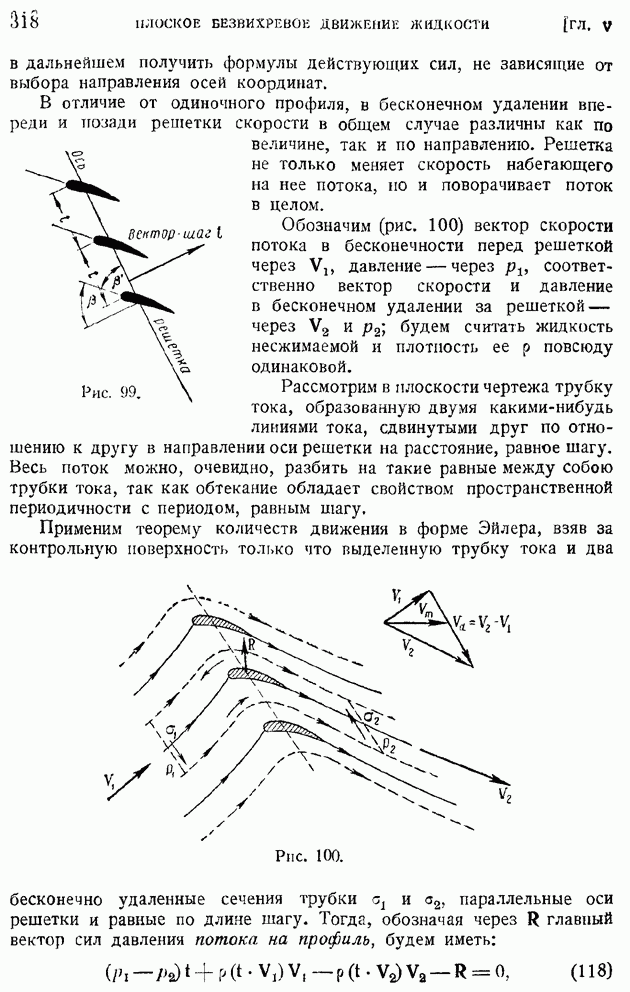
и температур  отнесены к переменному С, выражающемуся через обычные размерные координаты по формуле:
отнесены к переменному С, выражающемуся через обычные размерные координаты по формуле:

в свою очередь зависящей от распределения температур. Дифференцируя по у, получим:

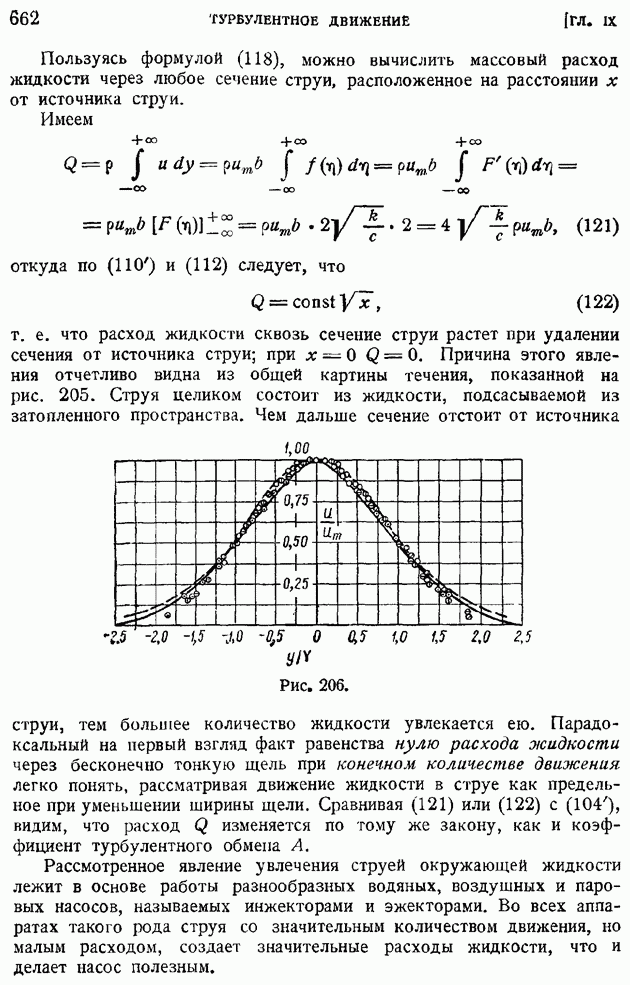
Связь между  определится интегральным соотношением:
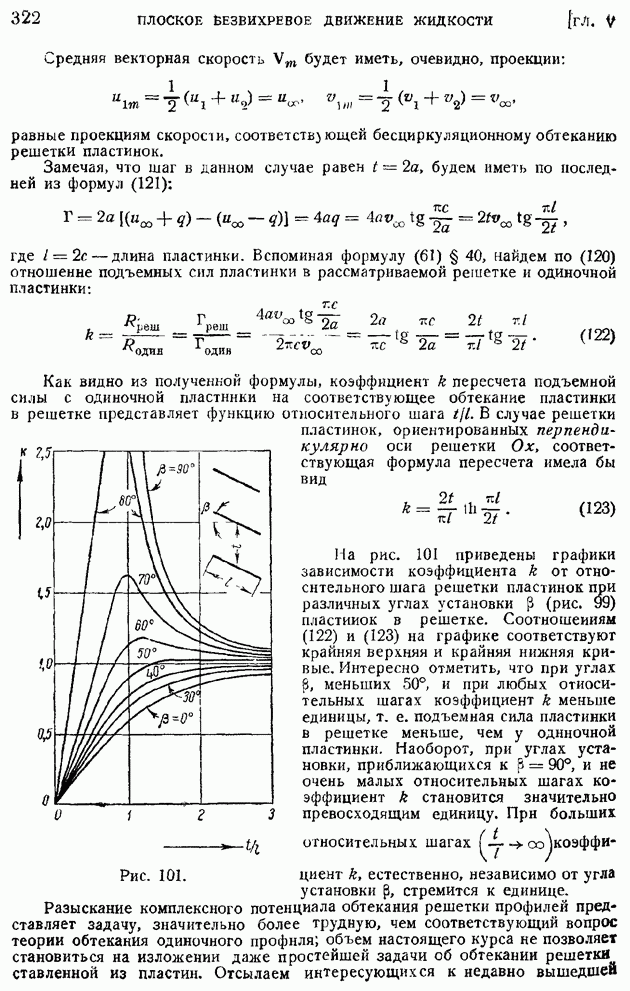
определится интегральным соотношением:

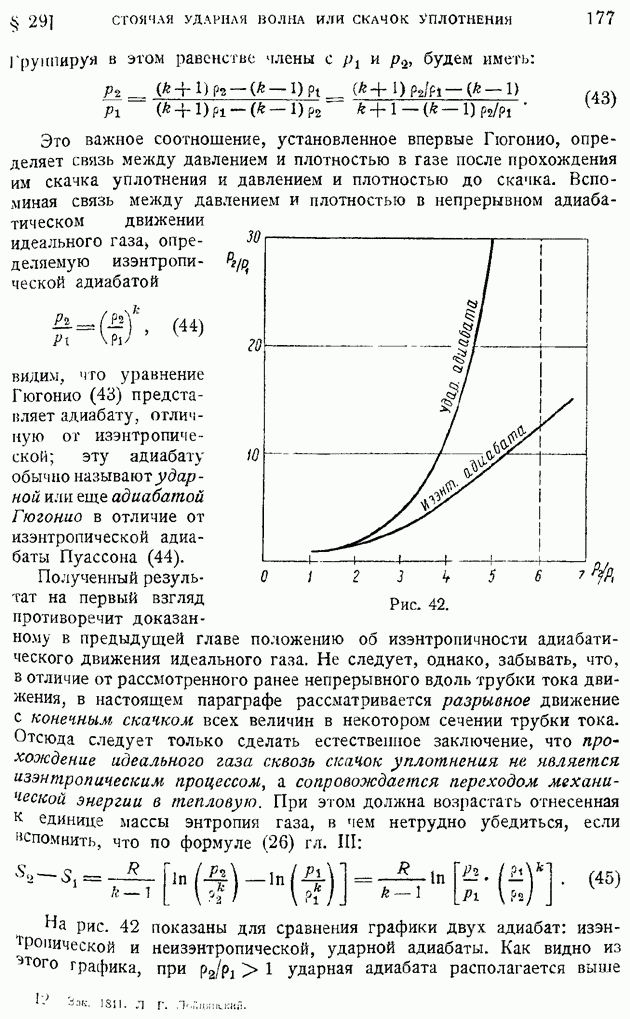
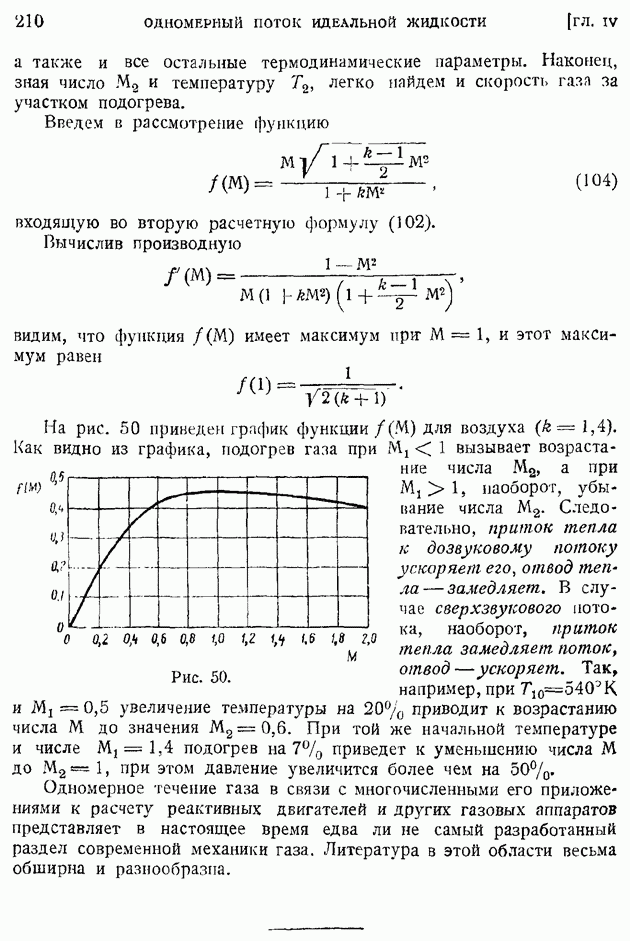
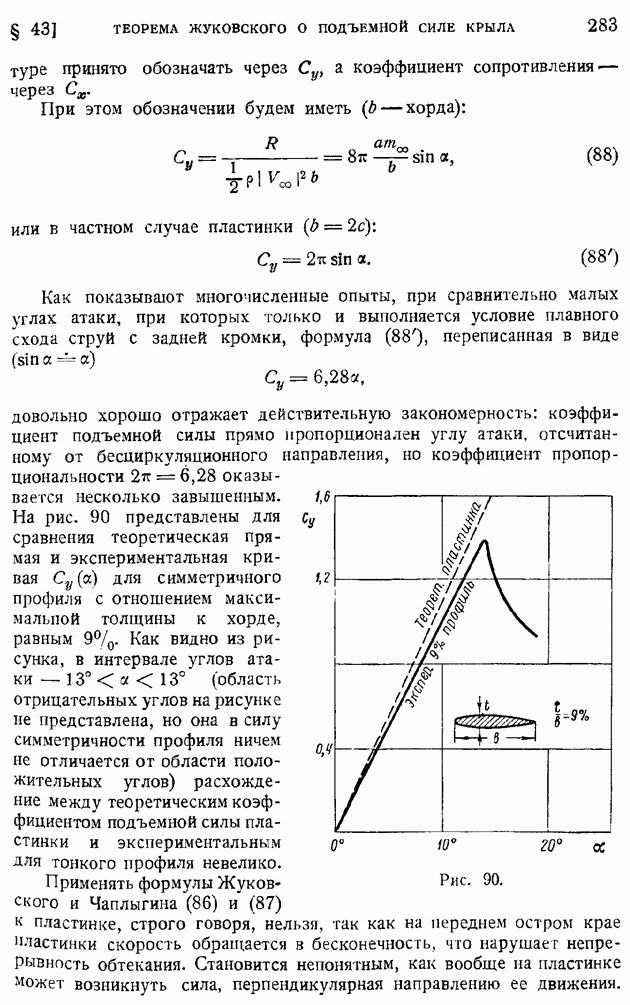
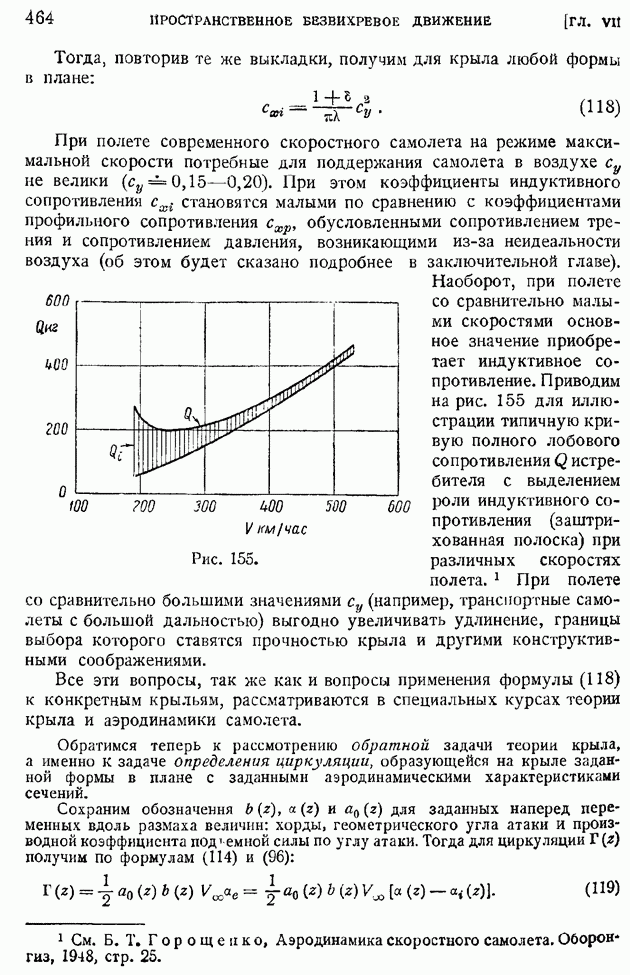
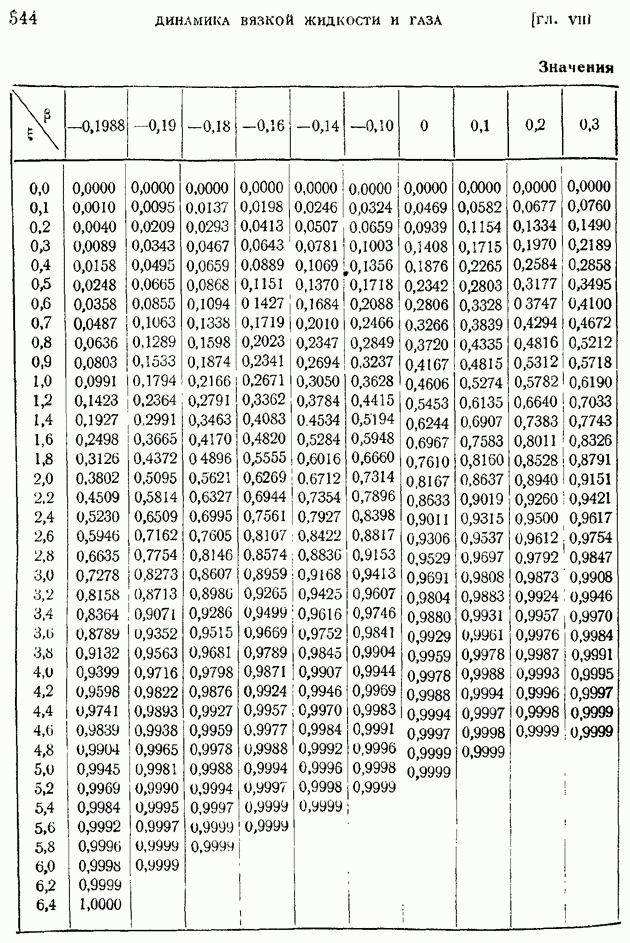
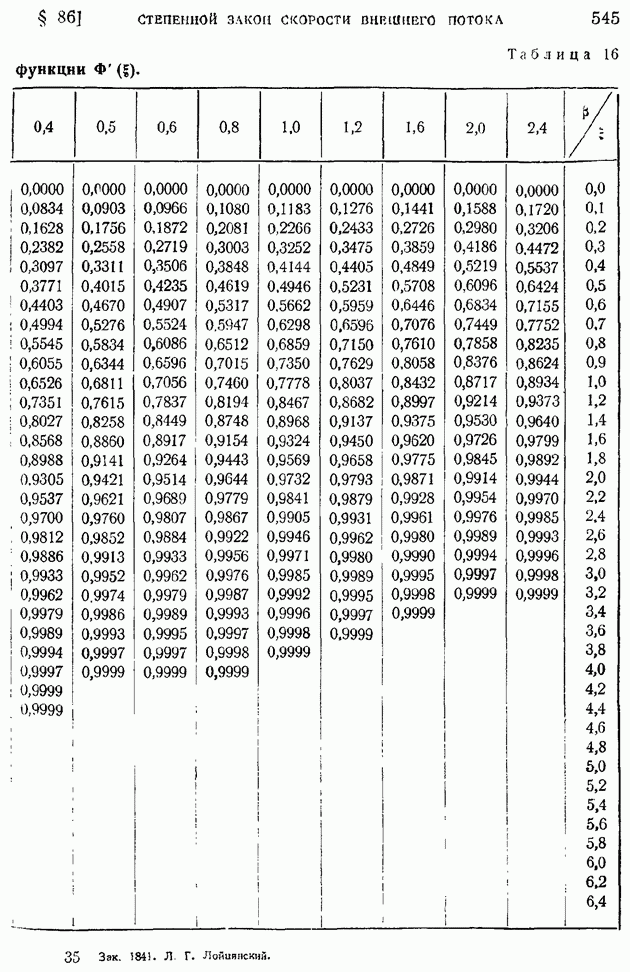
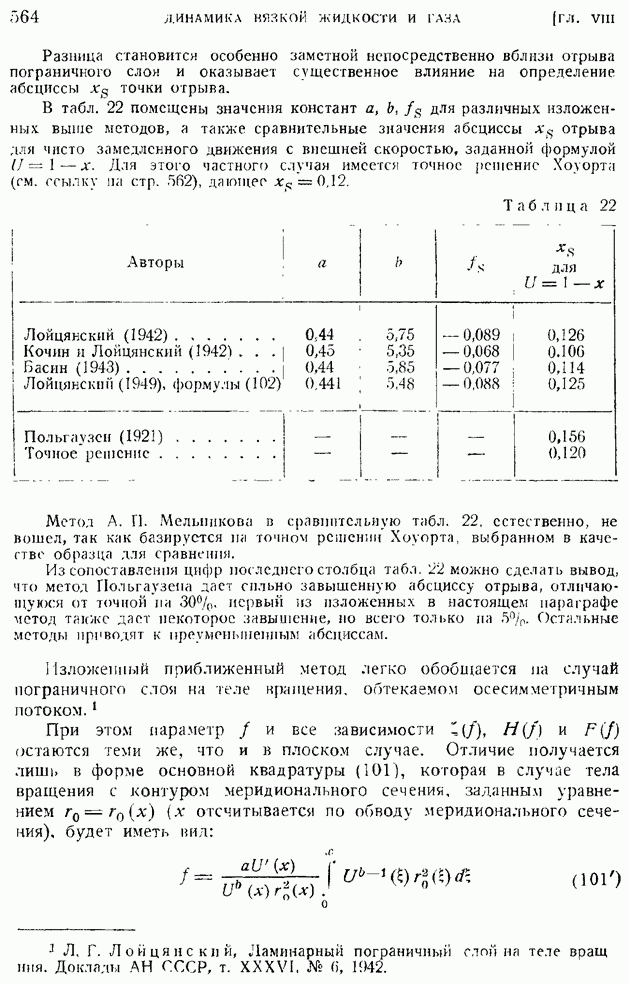
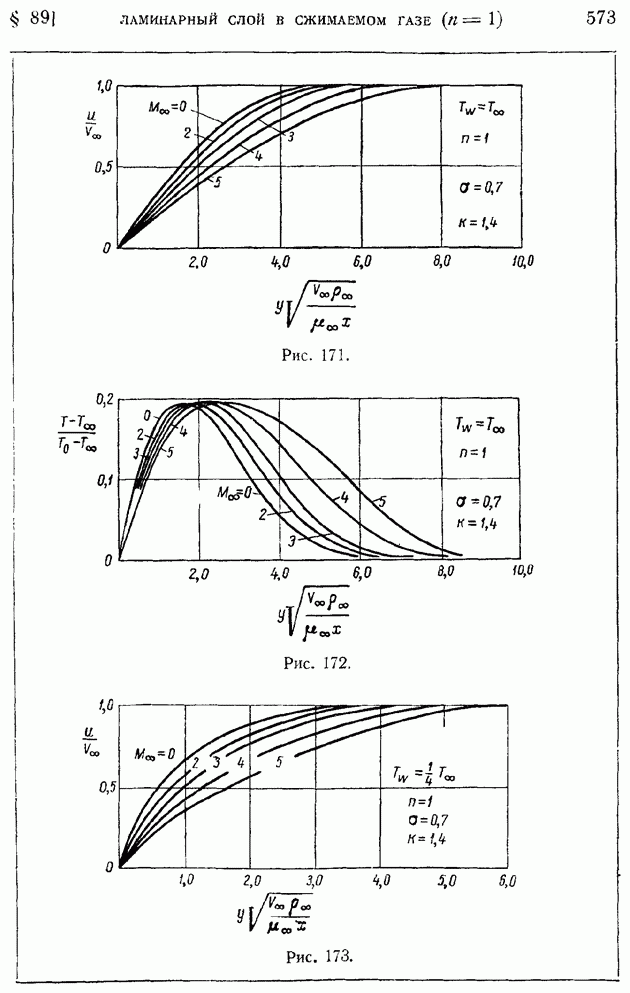
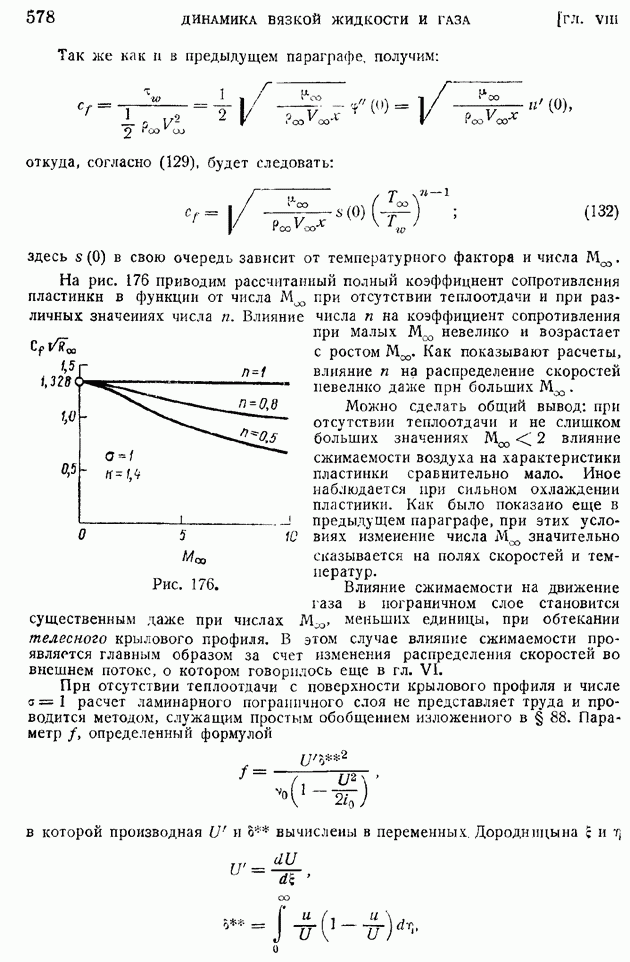
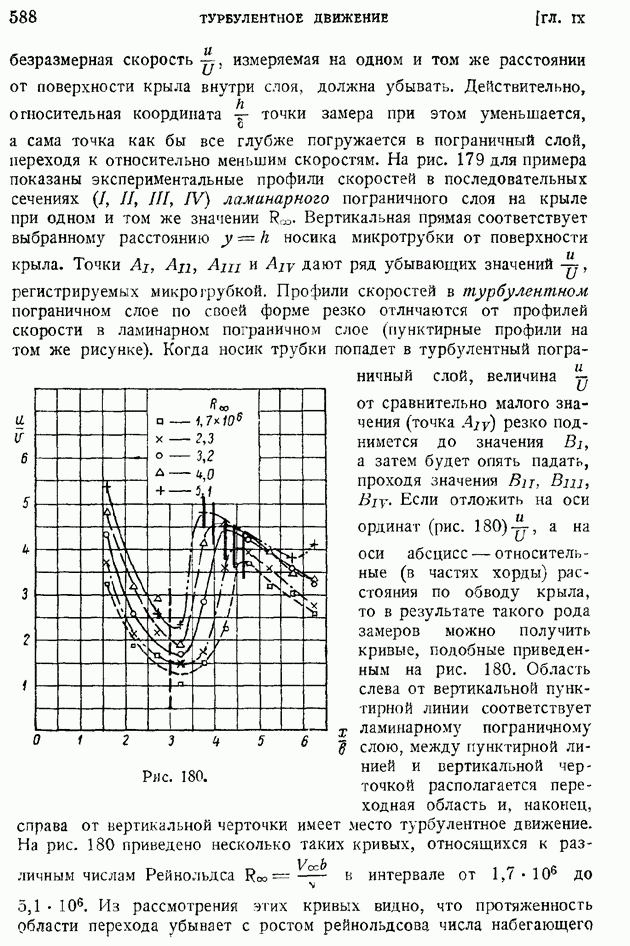
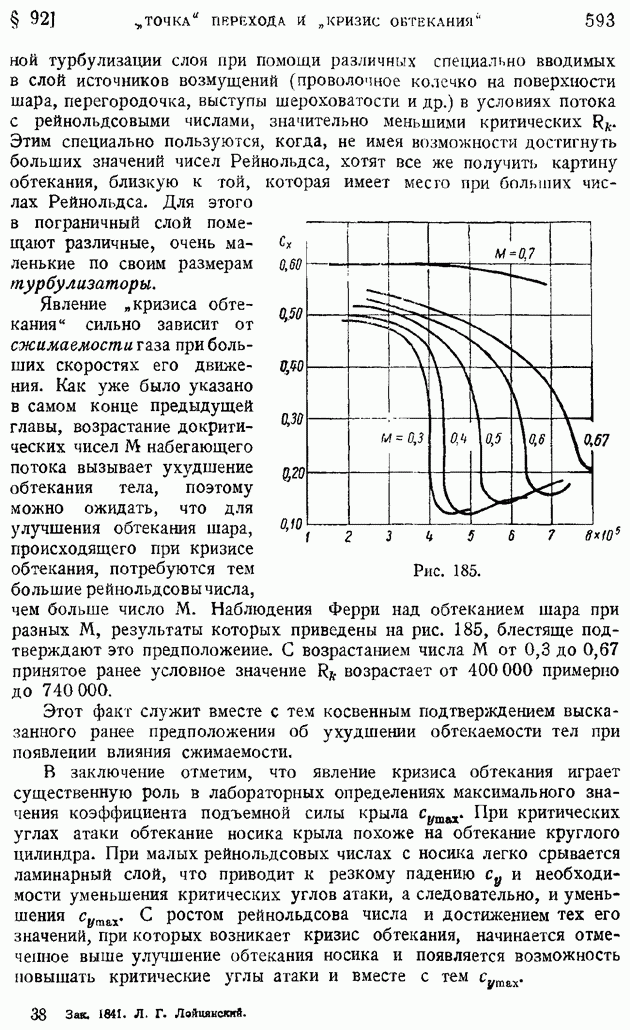
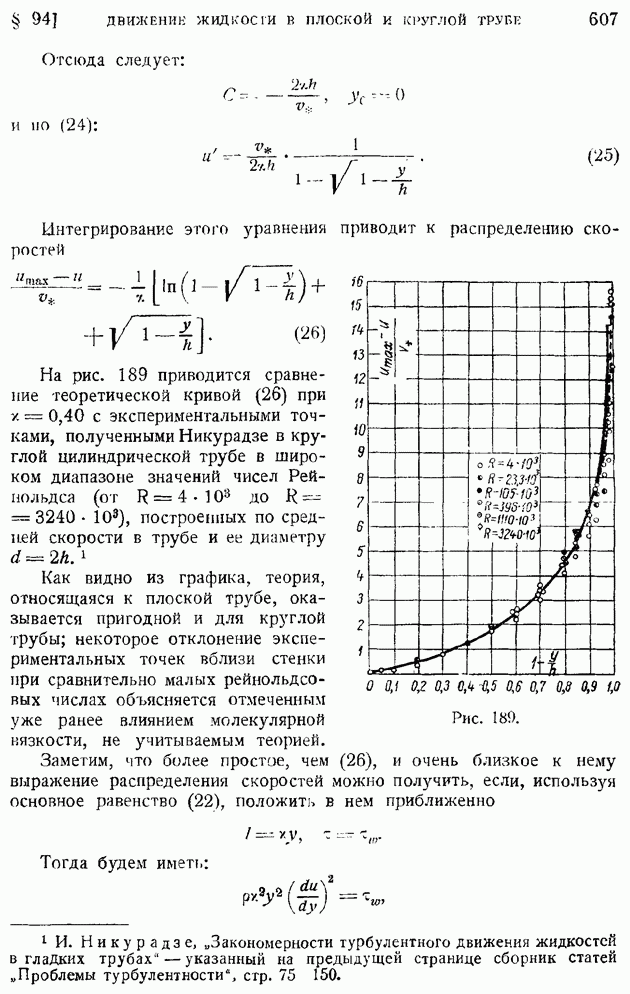
На рис. 171 и 172 1 приводим графики влияния числа  на профили скоростей и температур при
на профили скоростей и температур при  для пластинки, температура которой путем охлаждения поддерживается равной температуре набегающего потока. На обеих кривых обращает на себя внимание факт возрастания с числом
для пластинки, температура которой путем охлаждения поддерживается равной температуре набегающего потока. На обеих кривых обращает на себя внимание факт возрастания с числом  толщины пограничного слоя
толщины пограничного слоя

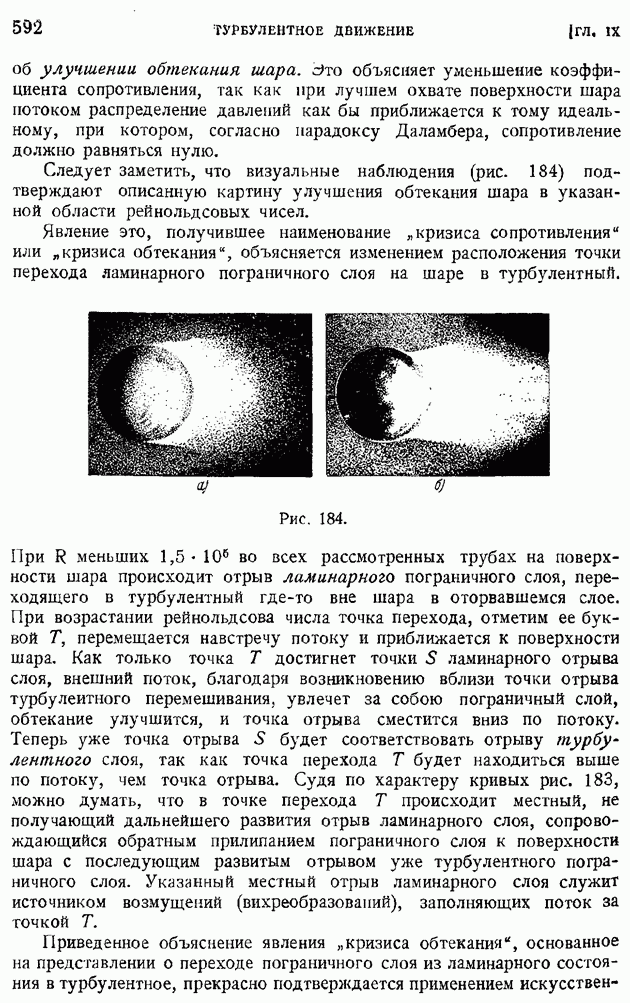
(кликните для просмотра скана)
(скоростного и температурного). Профиль скоростей с ростом числа  урезывается, становится более пологим.
урезывается, становится более пологим.

Рис. 174.
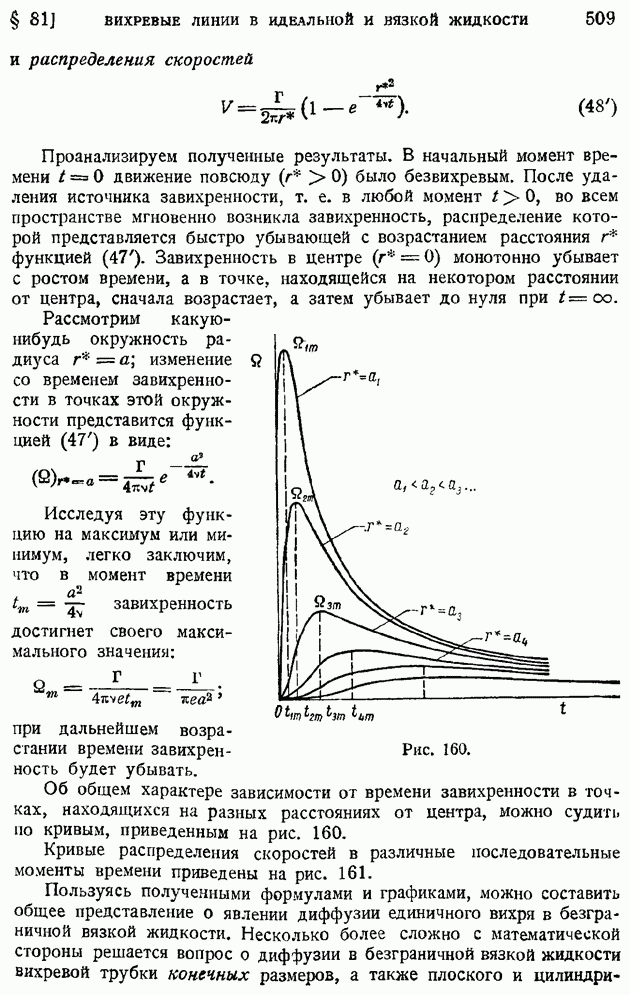
Температура при удалении от источника охлаждения стенки — сначала возрастает, а затем возвращается к прежнему значению, причем максимум отношения

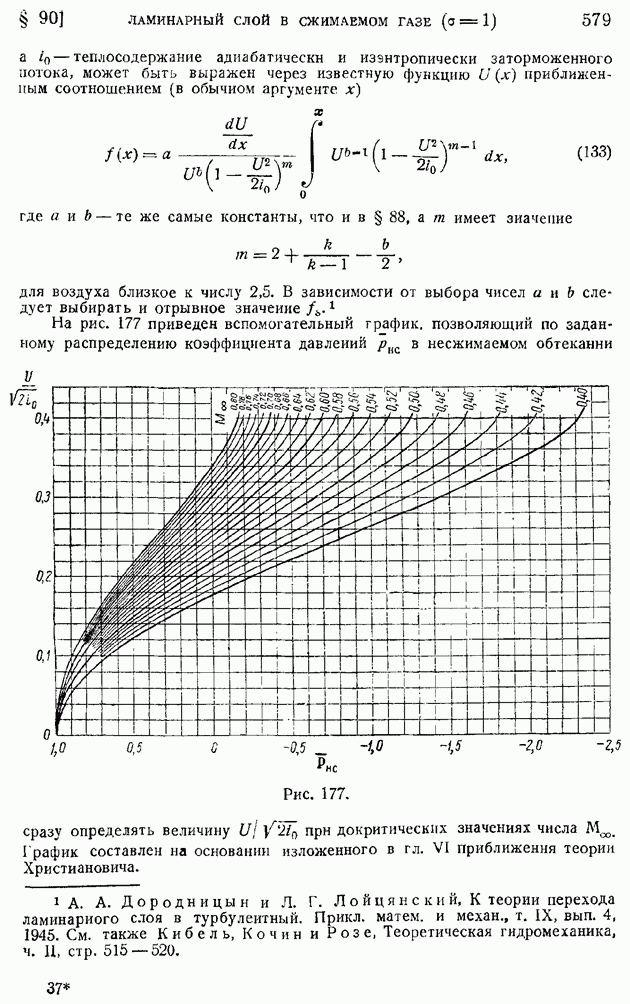
где  температура адиабатически и изэнтропически заторможенного газа, следуя расширению пограничного слоя, отодвигается от стенки, но сохраняет неизменной свою величину.
температура адиабатически и изэнтропически заторможенного газа, следуя расширению пограничного слоя, отодвигается от стенки, но сохраняет неизменной свою величину.
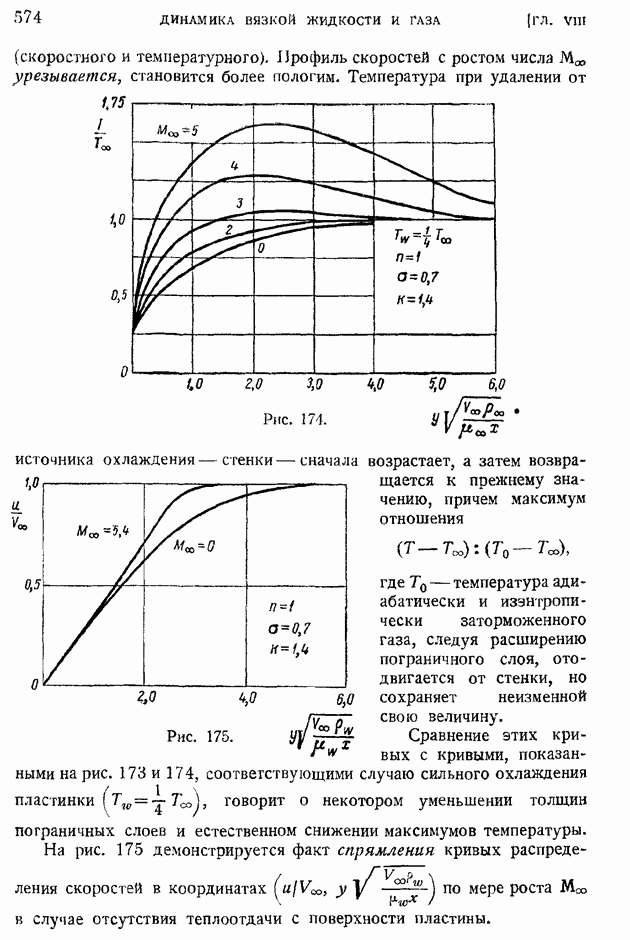
Сравнение этих кривых с кривыми, показанными на рис. 173 и 174, соответствующими случаю сильного охлаждения пластинки  говорит о некотором уменьшении толщин пограничных слоев и естественном снижении максимумов температуры.
говорит о некотором уменьшении толщин пограничных слоев и естественном снижении максимумов температуры.
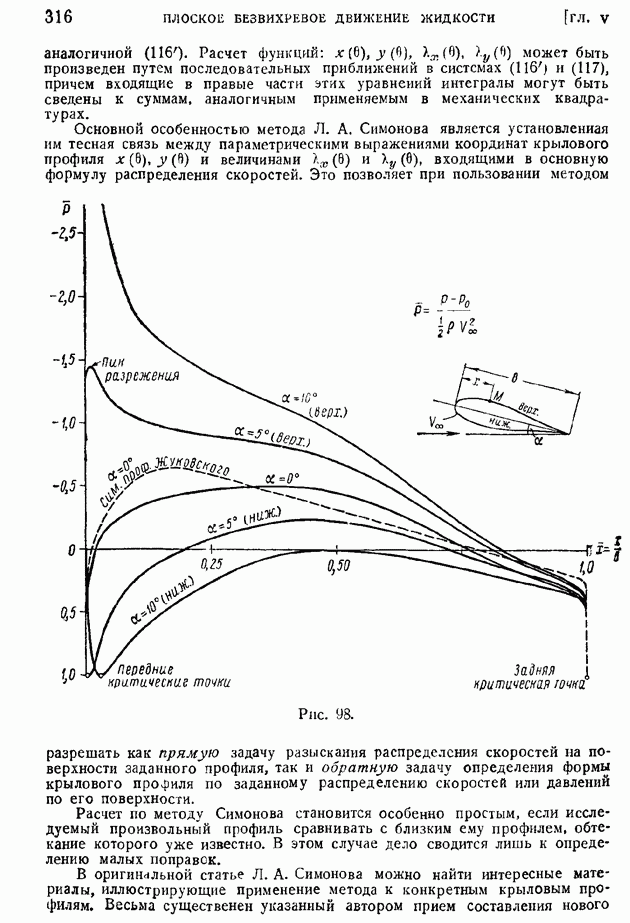
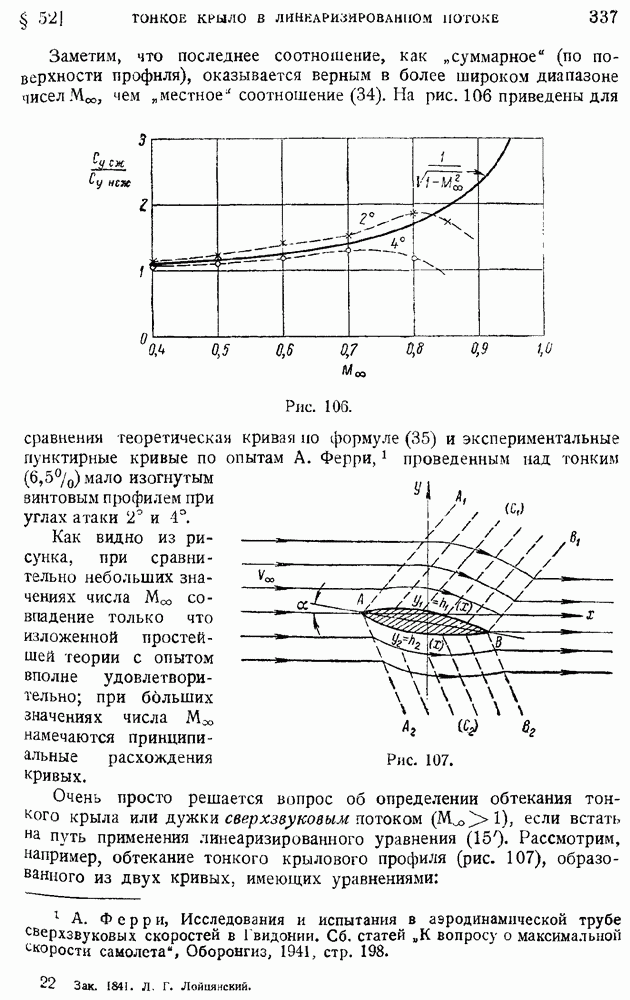
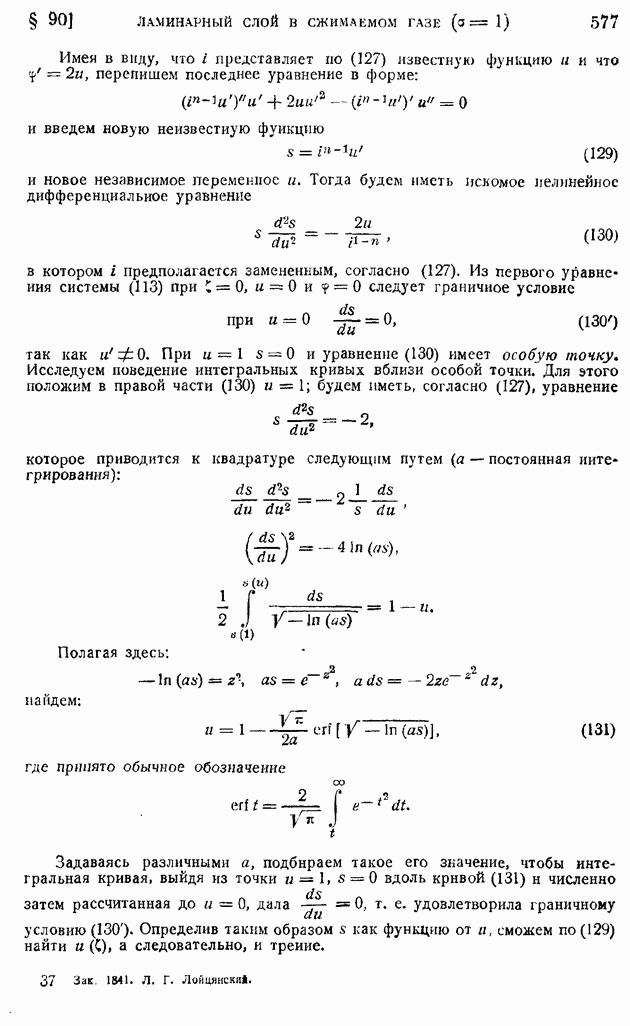
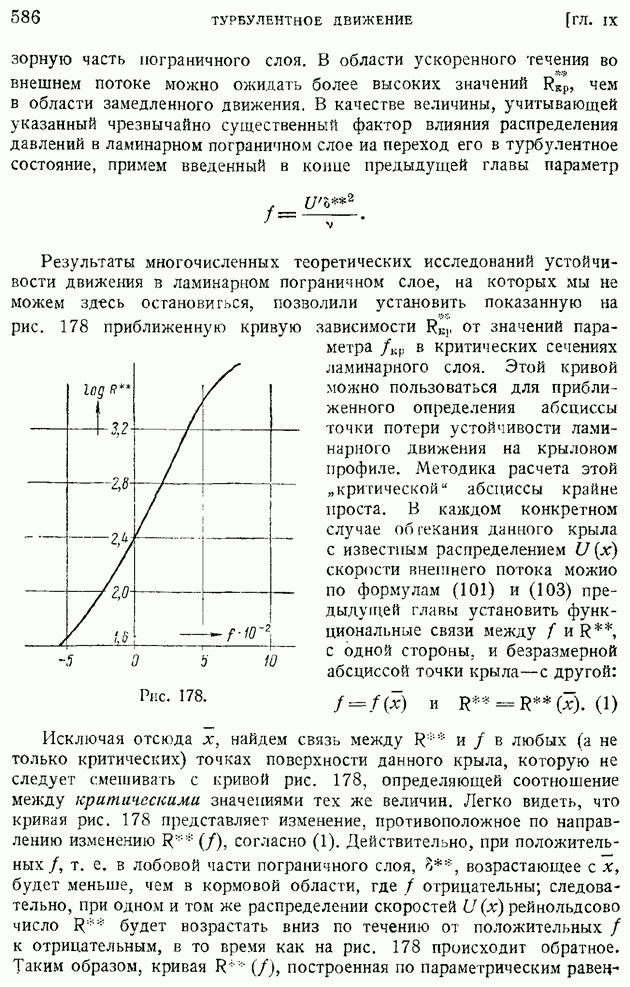
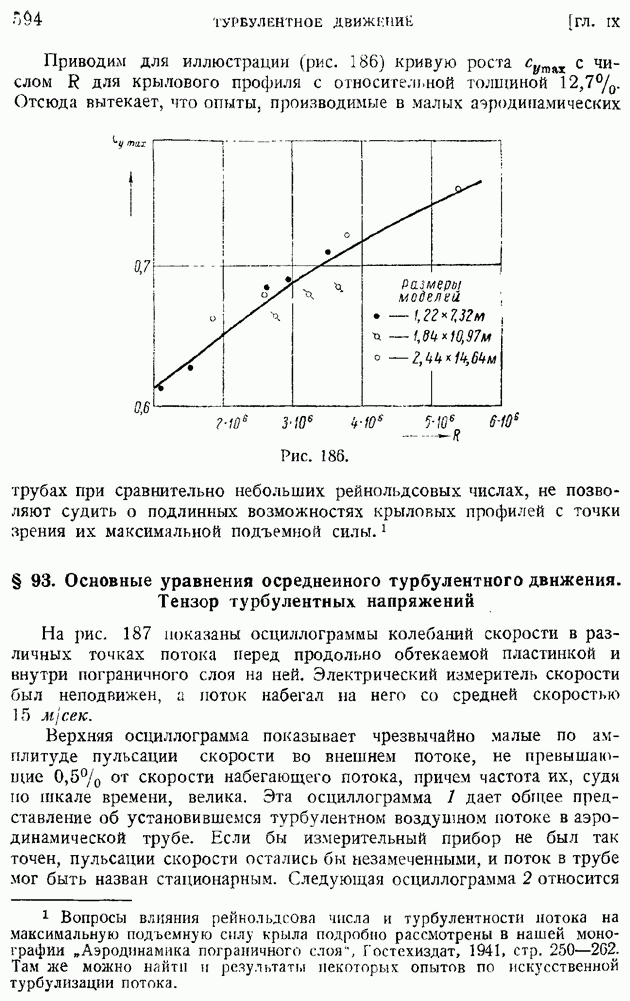
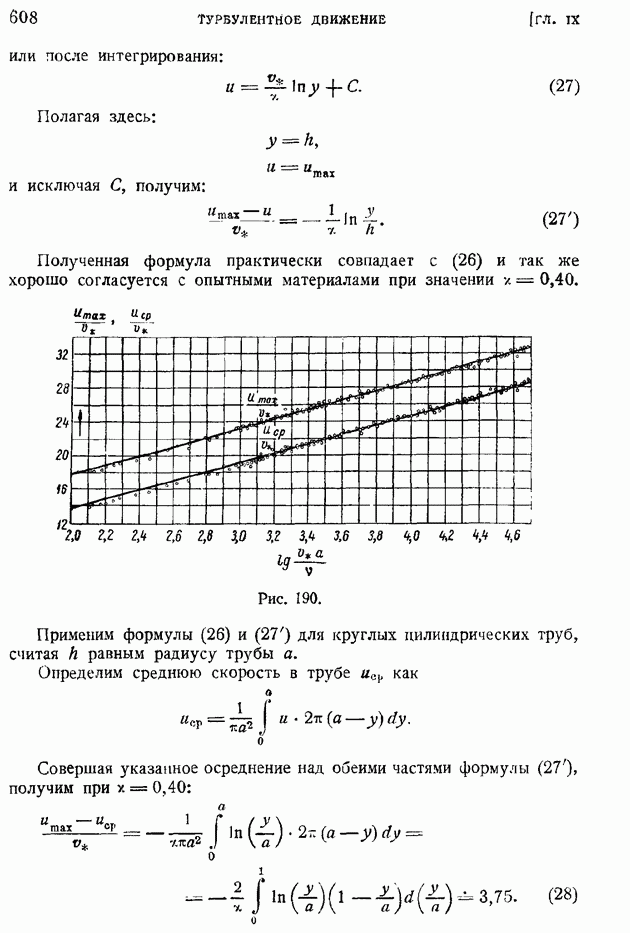
На рис. 175 демонстрируется факт спрямления кривых распределения скоростей в координатах  по мере роста
по мере роста  в случае отсутствия теплоотдачи с поверхности пластины.
в случае отсутствия теплоотдачи с поверхности пластины.

Рис. 175.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Предмет механики жидкости и газа. Основные свойства «макромодели» жидкости и газа: сплошность и подвижность
- § 2. Основные методы механики жидкости и газа. Области применения и главнейшие задачи
- § 3. Краткий очерк исторического развития механики жидкости и газа. От гидромеханики древних до установления воззрений ньютонианской эпохи
- § 4. Эпоха Эйлера и Бернулли. Гидроаэродинамика в XIX в.
- § 5. Современный этап развития механики жидкости и газа
- ГЛАВА I. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
- § 6. Поле физической величины. Скалярное и векторное поля. Поверхности уровня. Векторные линин и трубки
- § 7. Мера однородности поля в данном направлении и в дайной точке. Градиевт скалярного поля и дифференциальный тензор векторного поля как меры неоднородности поля
- § 8. Задание движения сплошной среды. Поле скоростей. Линии тока и траектории
- § 9. Поле ускорений. Разложение ускорения частицы на локальную и конвективную составляющие
- § 10. Скоростное поле сплошной среды в окрестности данной точки. Угловая скорость и вихрь. Тензор скоростей деформаций и его компоненты
- § 11. Скорость объемного расширения жидкости. Интегральные представления дифференциальных операторов поля. Основные интегральные формулы
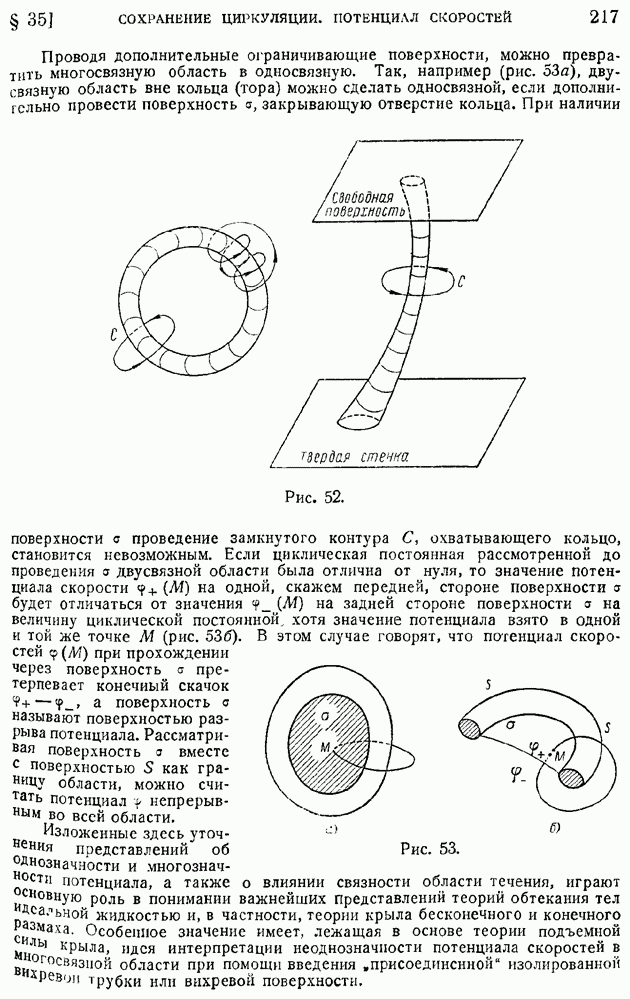
- § 12. Вихревые линии и трубки. Вторая теорема Гельмгольца. Интенсивность вихревой трубки
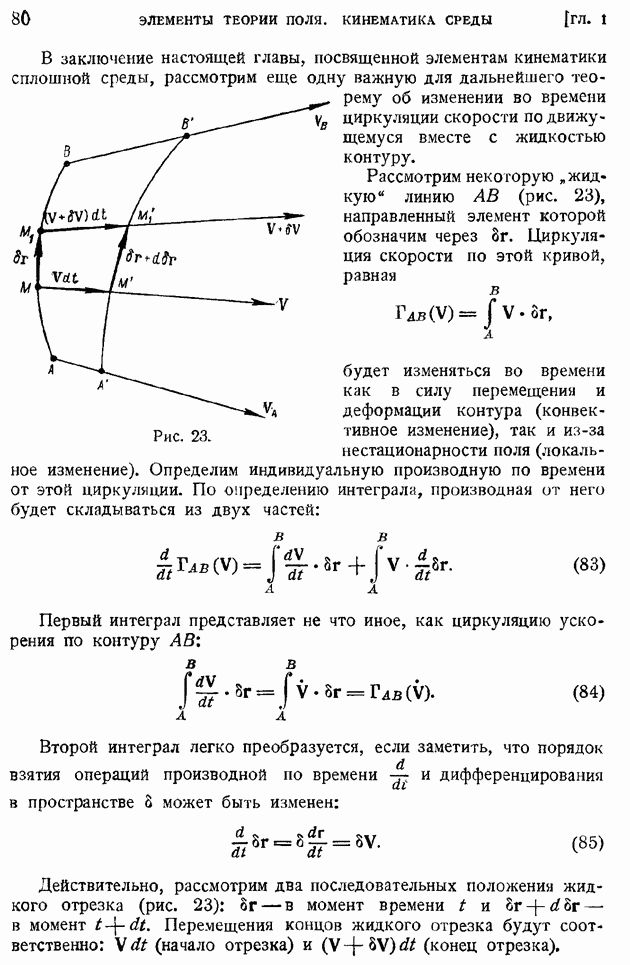
- § 13. Выражение интенсивности вихревой трубки через циркуляцию вектора по контуру, охватывающему трубку. Теорема об изменении циркуляции скорости во времени
- ГЛАВА II. ОСНОВНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ И РАВНОВЕСИЯ СПЛОШНОЙ СРЕДЫ
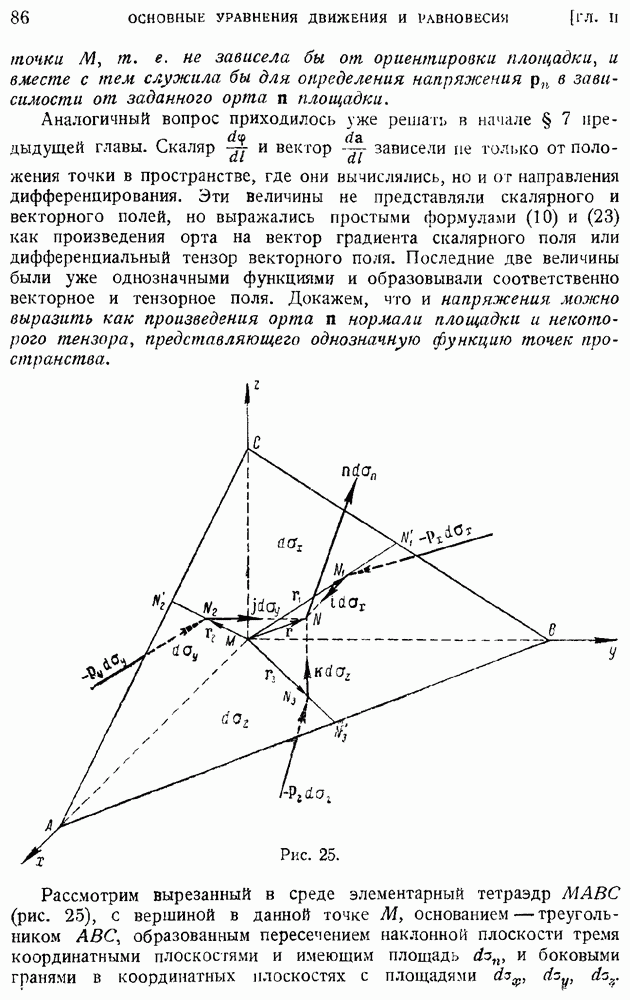
- § 14. Распределение массы в сплошной среде. Плотность и удельный вес. Напряжения. Тензор напряженности и его симметричность
- § 15. Общие уравнения динамики сплошной среды. Уравнение неразрывности. Уравнения динамики в напряжениях
- § 16. Тепловые явления в жидкостях и газах. Закон сохранения энергии и уравнение баланса энергии
- § 17. Общие уравнения равновесного состояния жидкости и газа. Равновесие воздуха в атмосфере. Приближенные барометрические формулы. Стандартная атмосфера
- § 18. Равновесие несжимаемой жидкости. Уравнение поверхности раздела. Равновесие вращающейся жидкости
- § 19. Давление тяжелой несжимаемой жидкости на поверхность тела. Сила и момент, приложенные к телу, плавающему в тяжелой жидкости. Случай вращающейся жидкости
- ГЛАВА III. ДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ И ГАЗА. ОСНОВНЫЕ УРАВНЕНИЯ И ОБЩИЕ ТЕОРЕМЫ
- § 20. Идеальная жидкость. Основные уравнения движения
- § 21. Закон сохранения энергии в движущейся идеальной жидкости. Адиабатическое движение. Сохранение энтропии
- § 22. Эйлерово представление конвективного изменения объемного интеграла. Перенос величины сквозь контрольную поверхность
- § 23. Эйлерова форма законов сохранения массы и энергии, теоремы количеств движения и момента количеств движения при стационарном движении идеальной жидкости
- § 24. Теорема об изменении кинетической энергии. Работа и мощность внутренних сил. Эйлерова форма уравнения изменения кинетической энергии
- § 25. Теорема Бернулли о сохранении полной механической энергии при стационарном баротропном движении идеальной жидкости и газа
- ГЛАВА IV. ОДНОМЕРНЫЙ ПОТОК ИДЕАЛЬНОЙ ЖИДКОСТИ
- § 26. Одномерное течение идеальной сжимаемой жидкости. Линеаризированные уравнения. Скорость распространения малых возмущений в жидкости или газе
- § 27. Изотермическая и адиабатическая скорости звука. «Конус возмущений» при сверхзвуковом движении источника возмущения. Число M и его связь с углом конуса возмущений
- § 28. Распространение непрерывных возмущений конечной интенсивности. Характеристики. Образование разрывной ударной волны
- § 29. Стоячая ударная волна или скачок уплотнения. Ударная адиабата
- § 30. Критические величины в одномерном потоке газа. Связь между скоростями до и после скачка. Изменение давления, плотности и температуры в скачке уплотнения
- § 31. Скорость распространения ударной волны. Спутное движение газа за ударной волной
- § 32. Влияние интенсивности скачка уплотнения на сжатие газа. Измерение скоростей и давлений в до- и сверхзвуковых потоках
- § 33. Одномерное движение газа по трубе переменного сечения. Истечение из резервуара большой емкости сквозь сходящееся сопло
- § 34. Одномерное течение в сопле Лаваля. Движение газа с притоком тепла
- ГЛАВА V. БЕЗВИХРЕВОЕ ДВИЖЕНИЕ ЖИДКОСТИ. ПЛОСКОЕ ДВИЖЕНИЕ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 35. Сохранение циркуляции скорости в потоке идеальной жидкости. Теорема Кельвина и Лаграижа. Безвихревое движение. Потенциал скоростей
- § 36. Интеграл Лагранжа — Коши уравнений безвихревого движения. Теорема Бернулли. Некоторые общие свойства безвихревого движения идеальной несжимаемой жидкости в односвязной области
- § 37. Плоское безвихревое движение несжимаемой жидкости. Потенциал скоростей и функция тока. Применение функций комплексного переменного. Комплексный потенциал и сопряженная скорость
- § 38. Построение полей течения по заданной характеристической Функции. Простейшие плоские потоки и их наложение
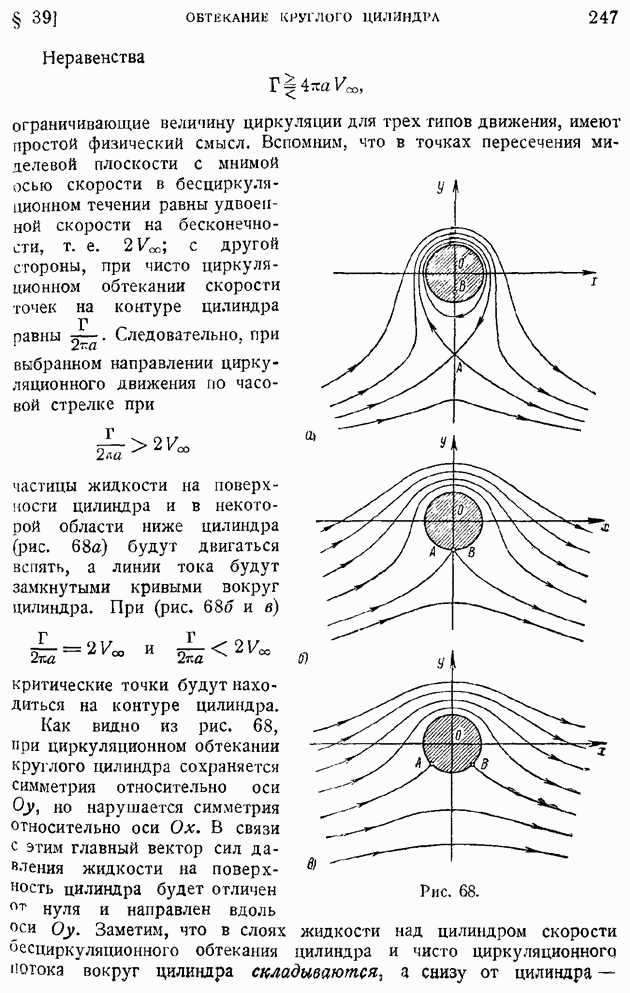
- § 39. Бесциркуляционное и циркуляционное обтекания круглого цилиндра
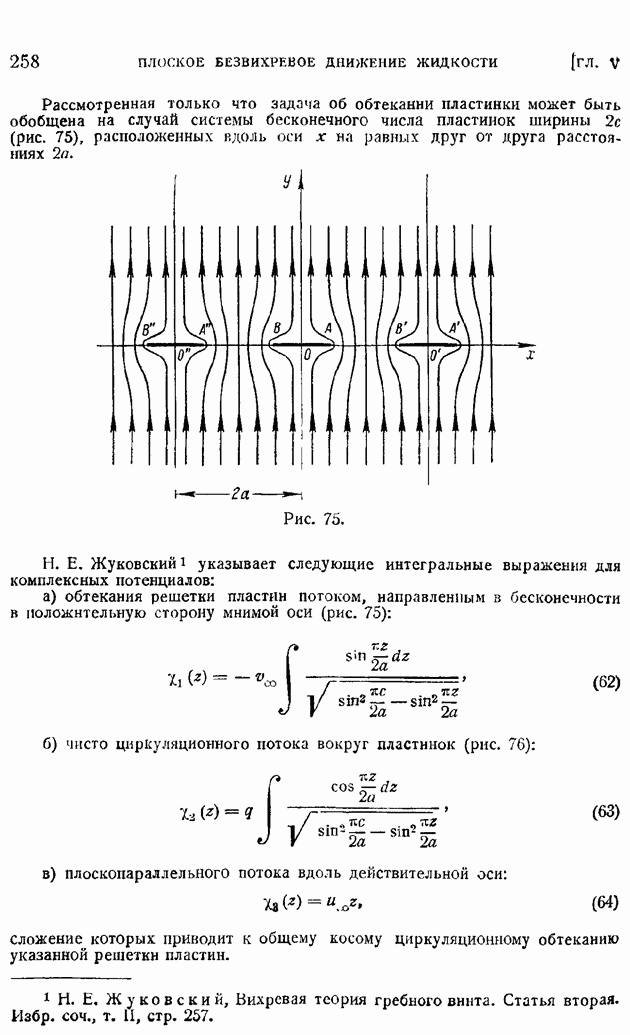
- § 40. Применение криволинейных координат. Бесциркуляционное и циркуляционное обтекания эллиптического цилиндра и пластинки. Задача Жуковского об обтекании решетки пластин.
- § 41. Плоское движение с отрывом струй. Разрывное обтекание пластинки и протекание жидкости сквозь отверстие
- § 42. Прямая задача в теории плоского движения идеальной несжимаемой жидкости. Применение метода конформных отображений. Гипотеза Чаплыгина о безотрывном обтекании задней кромки профиля. Формула циркуляции
- § 43. Теорема Жуковского о подъемной силе крыла. Зависимость подъемной силы от угла атаки. Коэффициент подъемной силы
- § 44. Применение метода комплексных переменных к выводу теоремы Жуковского. Формулы Чаплыгина для главного вектора и момента сил давления потока на крыло
- § 45. Выражение главного момента сил давления потока через коэффициенты конформного отображения. Фокус крыла. Независимость от угла атаки момента относительно фокуса. Парабола устойчивости
- § 46. Частные случаи конформного отображения крылового профиля на круг. Преобразование Жуковского-Чаплыгина. Теоретические крыловые профили
- § 47. Задача об обтекании слабо изогнутой дужки произвольной формы (теория тонкого крыла)
- § 48. Определение обтекания крылового профиля произвольной формы
- § 49. Обобщение теоремы Жуковского на случай плоской решетки с бесчисленным множеством профилей
- ГЛАВА VI. ПЛОСКОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ СЖИМАЕМОГО ГАЗА
- § 50. Основные уравнения плоского стационарного безвихревого движения сжимаемого газа. Линеаризированные уравнения
- 51. Линеаризированный до- и сверхзвуковой газовый поток вдоль волнистой стенки
- § 52. Тонкое крыло в линеаризированном до- и сверхзвуковом потоках. Влияние сжимаемости газа на коэффициент подъемной силы в дозвуковом потоке. Коэффициенты подъемной силы и волнового сопротивления при сверхзвуковом потоке
- § 53. Нелинеаризированные уравнения движения идеального сжимаемого газа. Переход в плоскость годографа. Уравнения Чаплыгина
- § 54. Метод С. А. Христиановича. Приближенные формулы учета влияния сжимаемости на распределение давления
- § 55. Критическое число M и его определение по заданному распределению давления в несжимаемом обтекании. Поведение коэффициента подъемной силы и момента при около- и закритических значениях числа M
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
- § 57. Нелинеаризированный сверхзвуковой поток. «Характеристики» уравнений плоского сверхзвукового потока. Линин возмущения и их основные свойства
- § 58. Обтекание выпуклого угла сверхзвуковым потоком. Влияние угла поворота струи на ее газодинамические элементы
- § 59. Сверхзвуковой поток внутри тупого угла. Косой скачок уплотнения. Связь между газодинамическими элементами до и за косым скачком
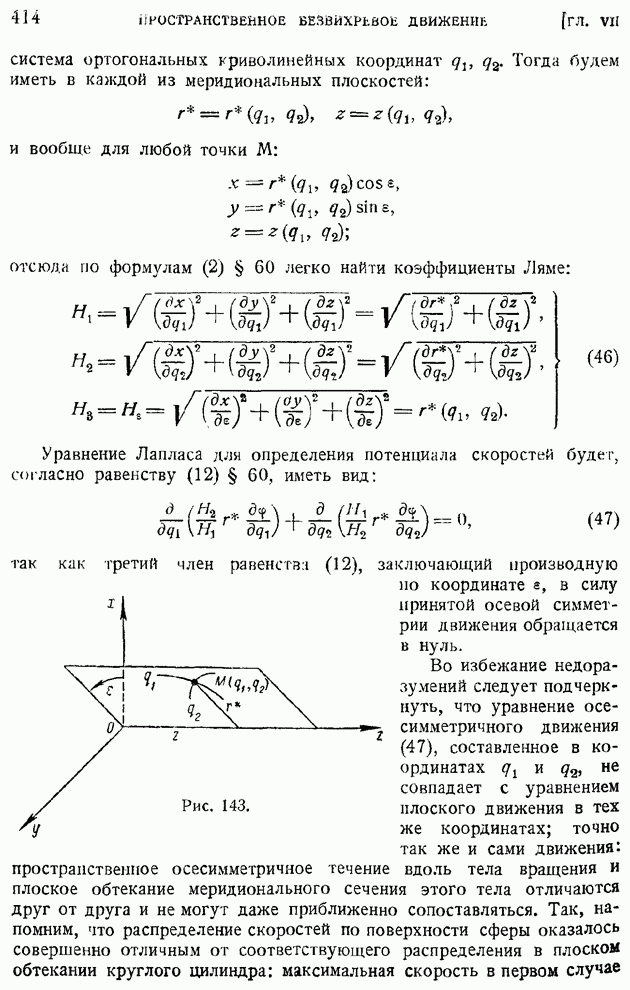
- ГЛАВА VII. ПРОСТРАНСТВЕННОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ
- § 60. Ортогональные криволинейные координаты в пространстве. Основные дифференциальные операторы поля в криволинейных координатах
- § 61. Потенциал скоростей. Поле источника и диполя. Непрерывное распределение источников и диполей. Ньютонов потенциал. Потенциал простого и двойного слоев
- § 62. Поле скоростей вокруг заданной системы вихрей. Формула Био — Савара. Потенциал скоростей замкнутой вихревой нити. Аналогия с потенциалом двойного слоя
- § 63. Функция тока и ее связь с векторным потенциалом скоростей. Функции тока простейших течений
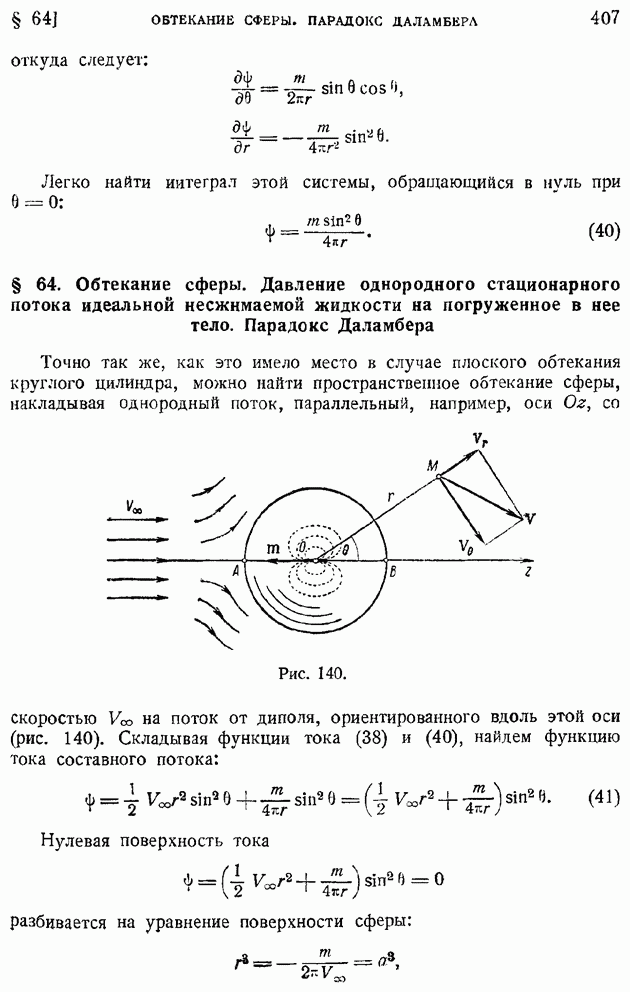
- § 64. Обтекание сферы. Давление однородного стационарного потока идеальной несжимаемой жидкости на погруженное в нее тело. Парадокс Даламбера
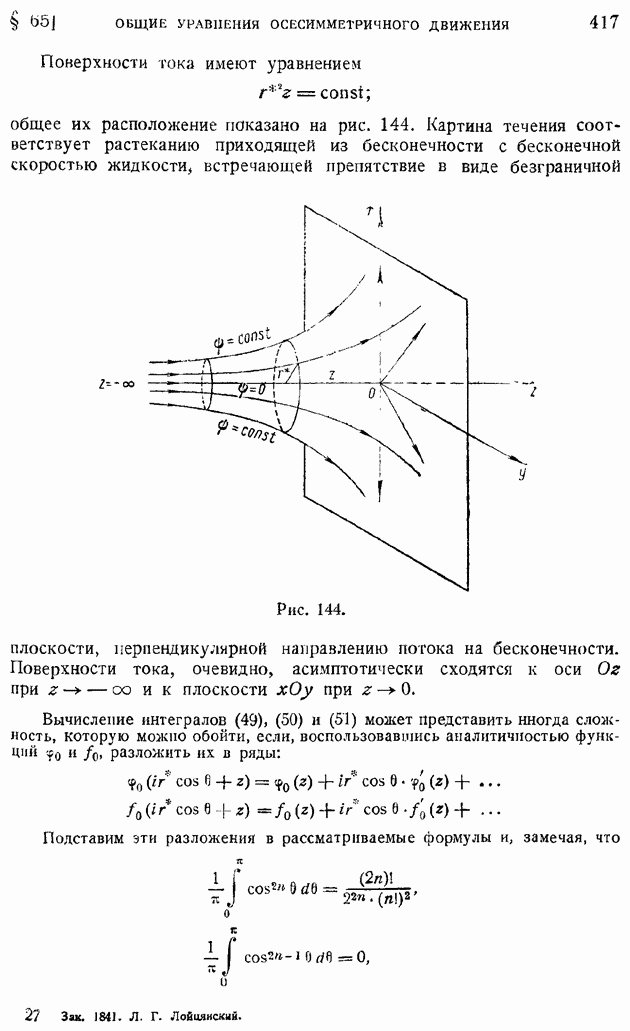
- § 65. Общие уравнения осесимметричного движения. Применение цилиндрических координат. Течение сквозь каналы
- § 66. Осесимметричное продольное обтекание тел вращения. Случай эллипсоида вращения
- § 67. Поперечное обтекание тел вращения. Пример эллипсоида вращения
- § 68. Продольное и поперечное обтекание тел вращения большого удлинения. Приближенные выражения граничных условий. Применение тригонометрических сумм для определения коэффициентов …
- § 69. Метод «особенностей». Применение непрерывно распределенных источников (стоков) и диполей для решения задачи о продольном и поперечном обтекании тел вращения
- § 70. Общий случай движения твердого тела сквозь несжимаемую идеальную жидкость. Определение потенциала скоростей. Главный вектор и главный момент сил давления потока на тело
- § 71. Коэффициенты «присоединенных масс». Свойство симметрии. «Присоединенная» кинетическая энергия. Определение «присоединенных масс» поступательно движущегося цилиндра, шара и эллипсоида
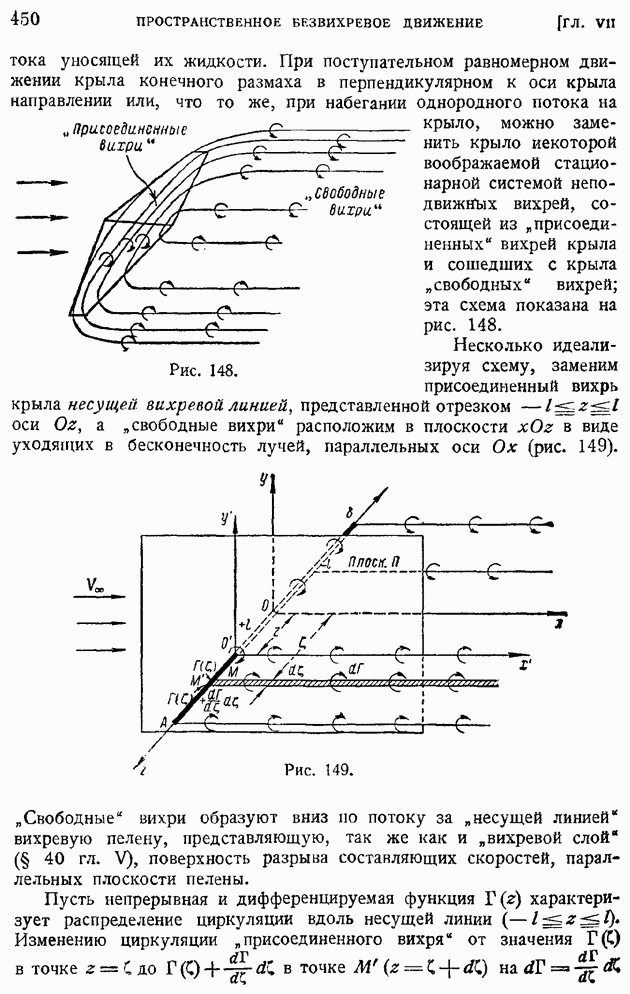
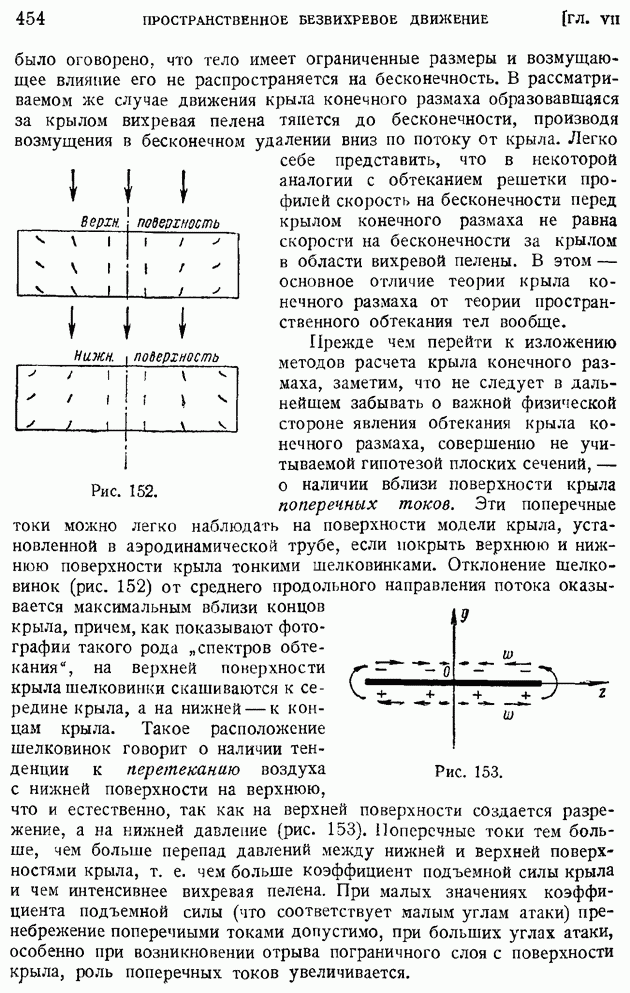
- § 72. Элементы теории крыла конечного размаха. Вихревая система крыла. Гипотеза плоских сечеиий. Геометрические и действительные углы атаки. Подъемная сила и «индуктивное сопротивление»
- § 73. Основные формулы теории «несущей линии». «Индуктивная скорость» и «индуктивный угол». Прямая задача определения подъемной силы и индуктивного сопротивления по заданному распределению циркуляции
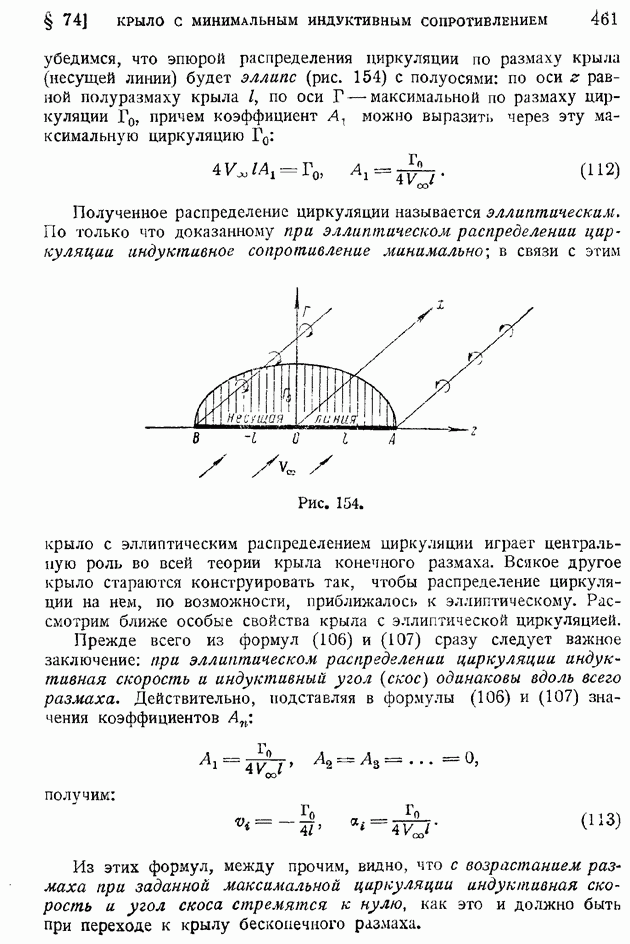
- § 74. Крыло с минимальным индуктивным сопротивлением. Эллиптическое распределение циркуляции. Связь между коэффициентами индуктивного сопротивления и подъемной силы. Основное уравнение теории крыла и понятие о его интегрировании
- ГЛАВА VIII. ДИНАМИКА ВЯЗКОЙ ЖИДКОСТИ И ГАЗА
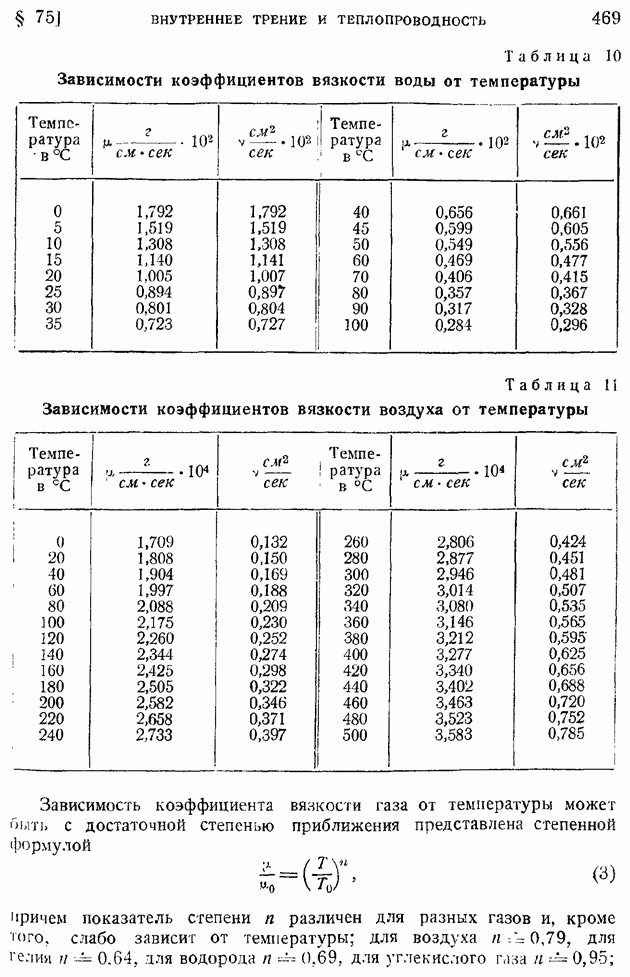
- § 75. Внутреннее трение и теплопроводность в жидкостях и газах. Законы Ньютона и Фурье. Влияние температуры на коэффициенты вязкости и теплопроводности. Число «сигма»
- § 76. Обобщение закона Ньютона на случай произвольного движения среды. Закон линейной связи между тензорами напряжений и скоростей деформации
- § 77. Общие уравнения движения вязкой жидкости. Динамические уравнения и уравнение баланса энергии. Граничные условия движения жидкости с треннем и теплопроводностью
- § 78. Понятие о подобии гидродинамических явлений. Безразмерные уравнения движения вязкой жидкости и газа. Условия подобия
- § 79. Ламинарное движение вязкой несжимаемой жидкости по цилиндрической трубе
- § 80. Обтекание шара при очень малых значениях числа Рейнольдса. Формула сопротивления шара по Стоксу и ее обобщения
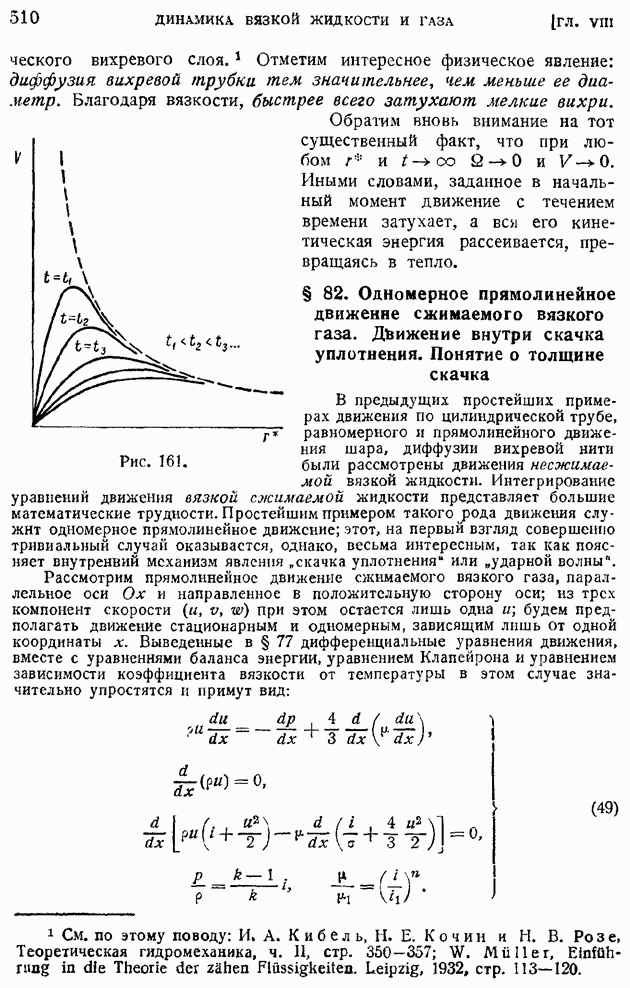
- § 81. Вихревые линии в идеальной и вязкой жидкости. Сохраняемость вихревых линий при отсутствии внутреннего трения. Диффузия вихря в вязкой жидкости
- § 82. Одномерное прямолинейное движение сжимаемого вязкого газа. Движение внутри скачка уплотнения. Понятие о толщине скачка
- § 83. Работа внутренних сил и диссипация механической энергии в движущейся вязкой среде
- § 84. Обтекание тел жидкостью и газом при больших значениях числа Рейнольдса. Основные уравнения теории ламинарного пограничного слоя
- § 85. Ламинарный пограничный слой на пластинке, продольно обтекаемой несжимаемой жидкостью. Неизотермическое движение
- § 86. Ламинарный пограничный слой при степенном задании скорости внешнего потока
- § 87. Ламинарный пограничный слой в общем случае задания скорости внешнего потока. Применение уравнения импульсов для приближенного расчета ламинарного пограничного слоя
- § 88. Способы определения функций … Приближенный метод расчета ламинарного пограничного слоя
- § 89. Ламинарный пограничный слой на пластинке, продольно обтекаемой сжимаемым газом при больших скоростях. Случай линейной зависимости коэффициента вязкости от температуры (n = 1)
- § 90. Ламинарный пограничный слой на пластинке при любом законе связи между вязкостью и температурой и при числе … Обтекание крылового профиля потоком больших скоростей
- ГЛАВА IX. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ
- § 91. Переход ламинарного движения в турбулентное. Критическое рейнольдсово число
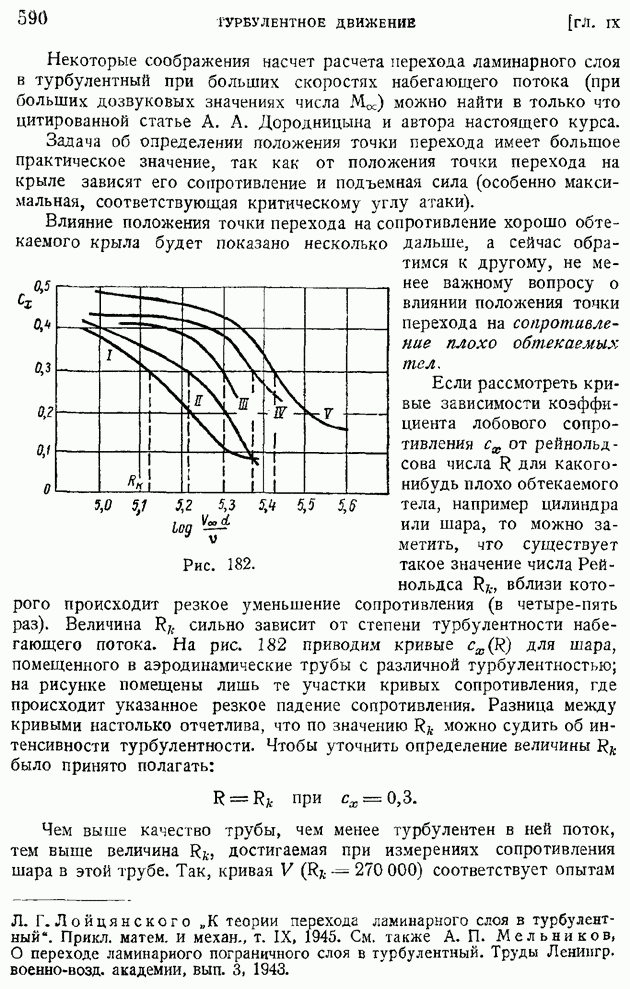
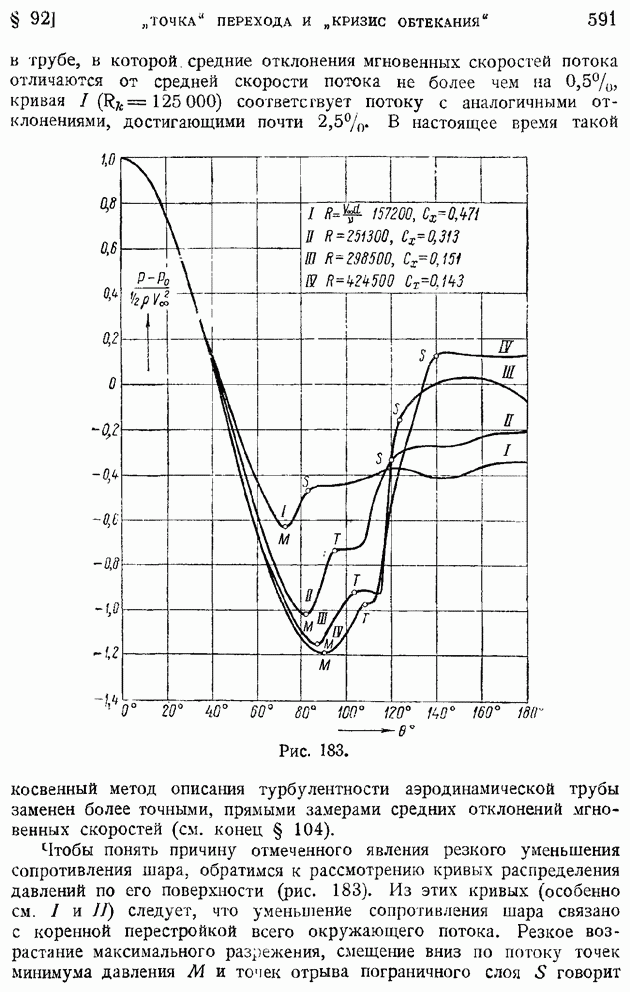
- § 92. Область и «точка» перехода. Явление «кризиса обтекания»
- § 93. Основные уравнения осреднеиного турбулентного движения. Тензор турбулентных напряжений
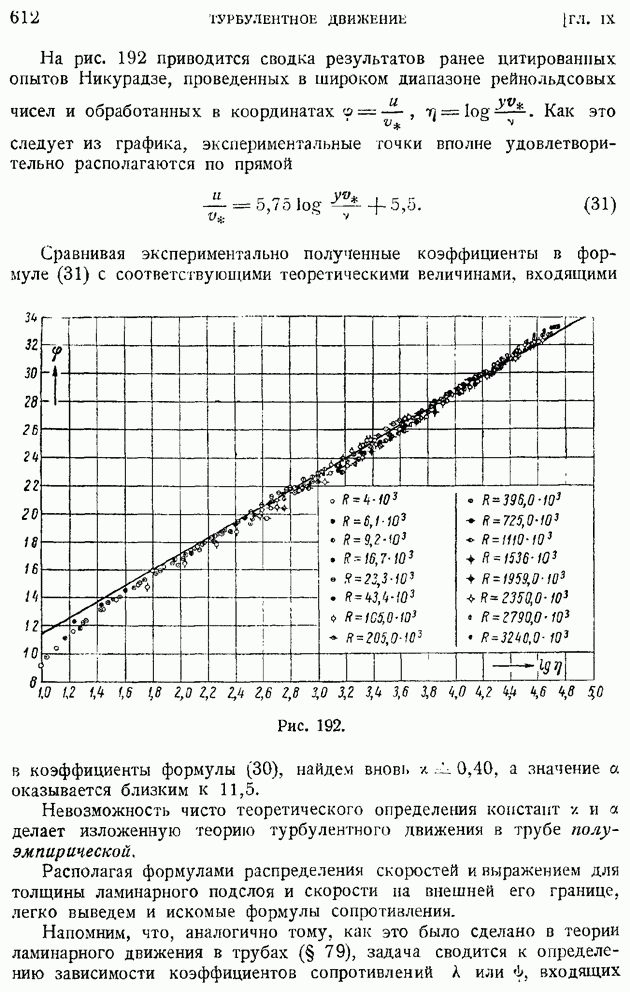
- § 94. Турбулентное движение жидкости в плоской и круглой трубе. Логарифмические формулы скоростей
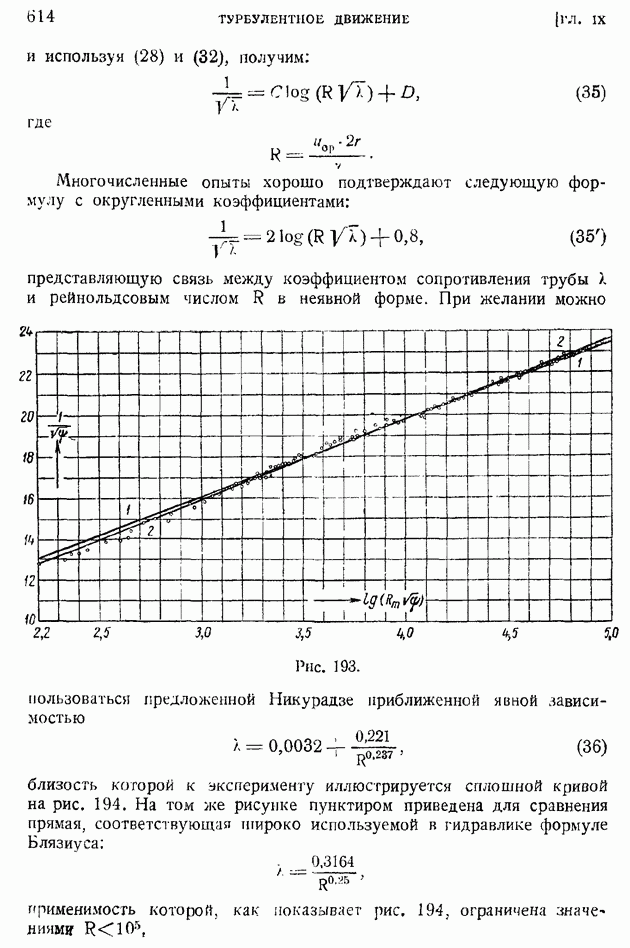
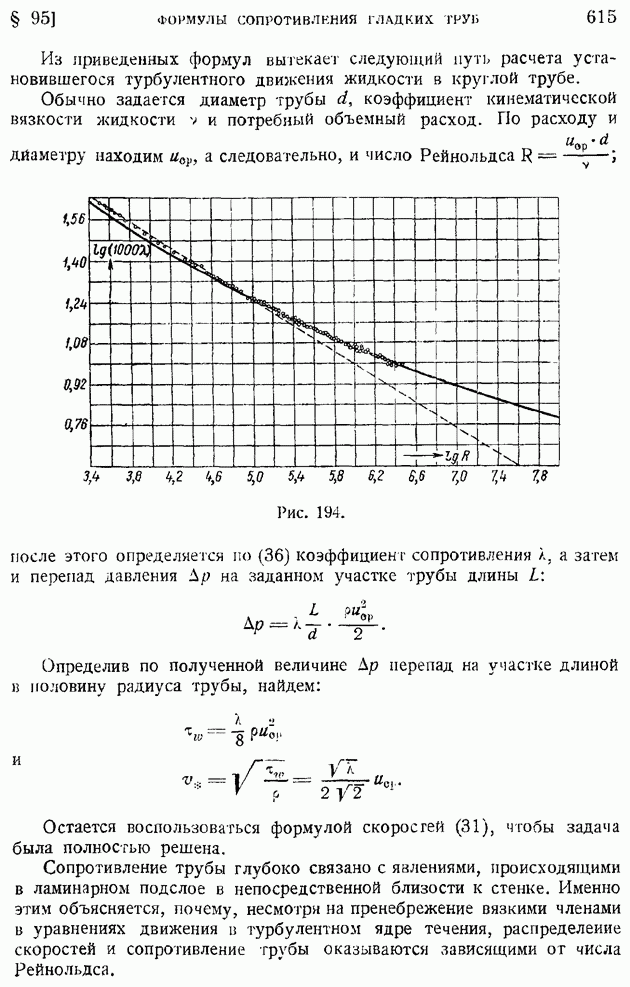
- § 95. Формулы сопротивления гладких труб при турбулентном движении жидкости. Ламинарный подслой
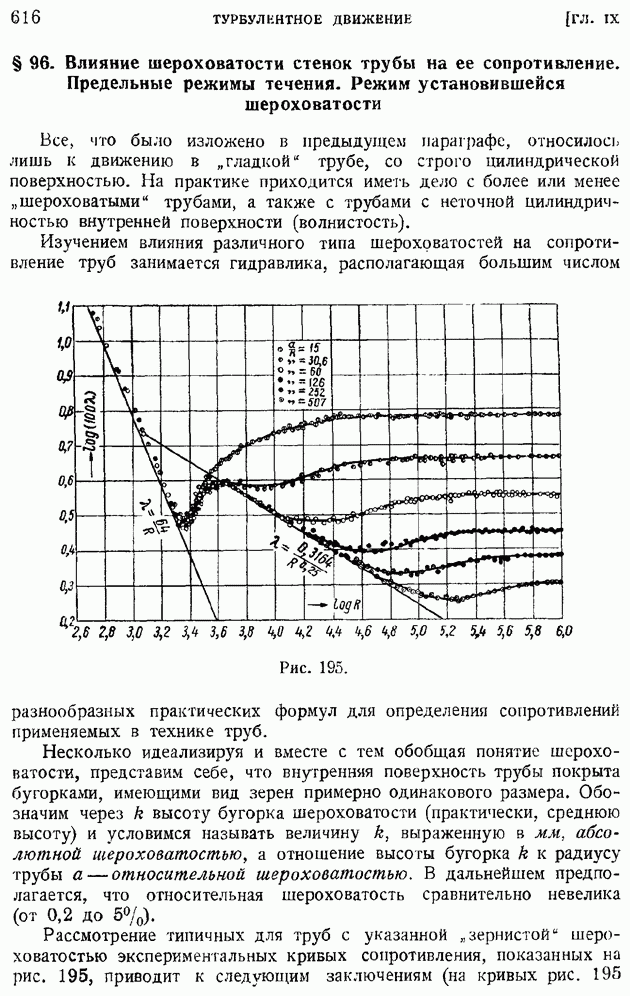
- § 96. Влияние шероховатости стенок трубы на ее сопротивление. Предельные режимы течения. Режим установившейся шероховатости
- § 97. Турбулентный пограничный слой на продольно обтекаемой пластине. Сопротивление пластины
- § 98. Турбулентный пограничный слой на крыловом профиле при малом продольном перепаде давлений
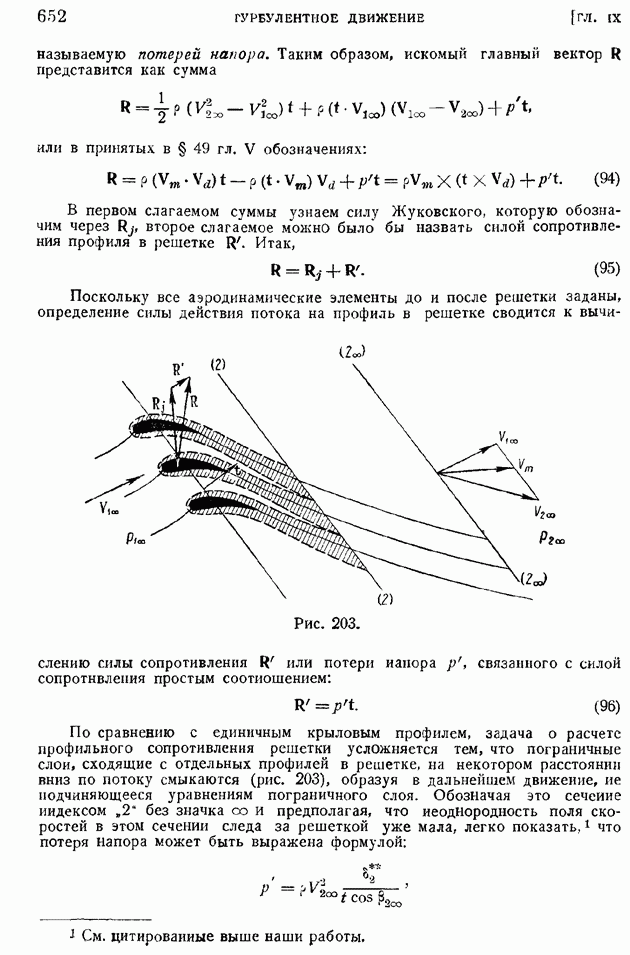
- § 99. Турбулентный пограничный слой на крыловом профиле при значительных продольных перепадах давления
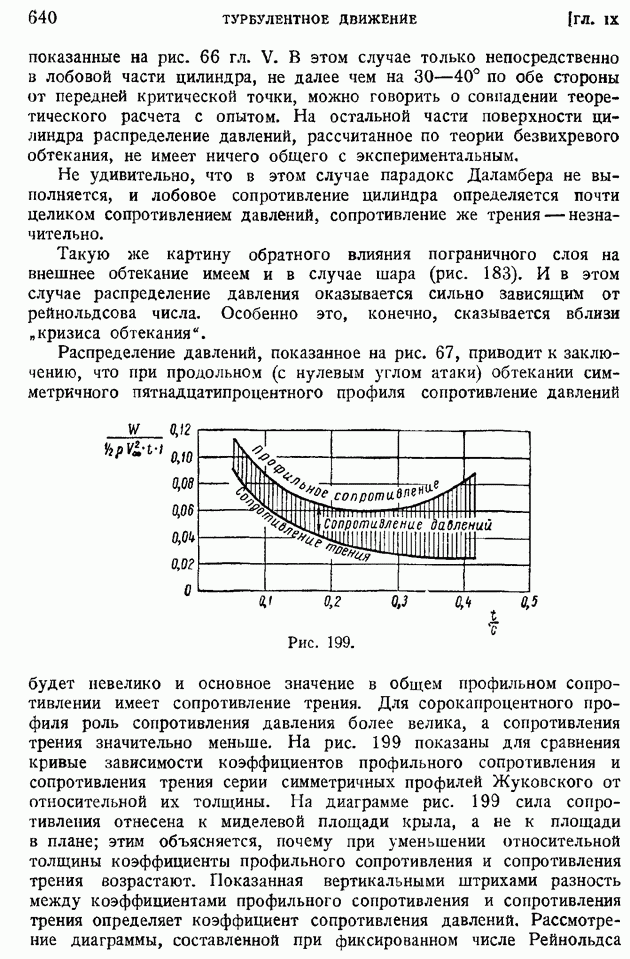
- § 100. Профильное сопротивление крыла. Разложение профильного сопротивления на сопротивление трения и сопротивление давлений. Обратное влияние пограничного слоя на распределение давлений по поверхности обтекаемого профиля
- § 101. Приближенные формулы профильного сопротивления крыла и крылового профиля в решетке
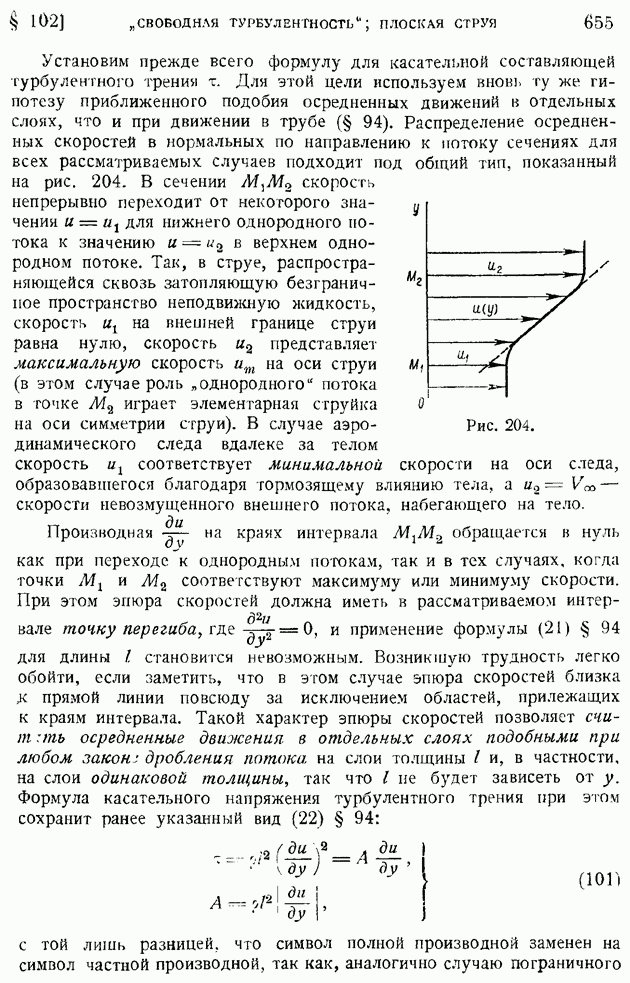
- § 102. Основные закономерности «свободной турбулентности». Плоская турбулентная струя в пространстве, заполненном той же жидкостью
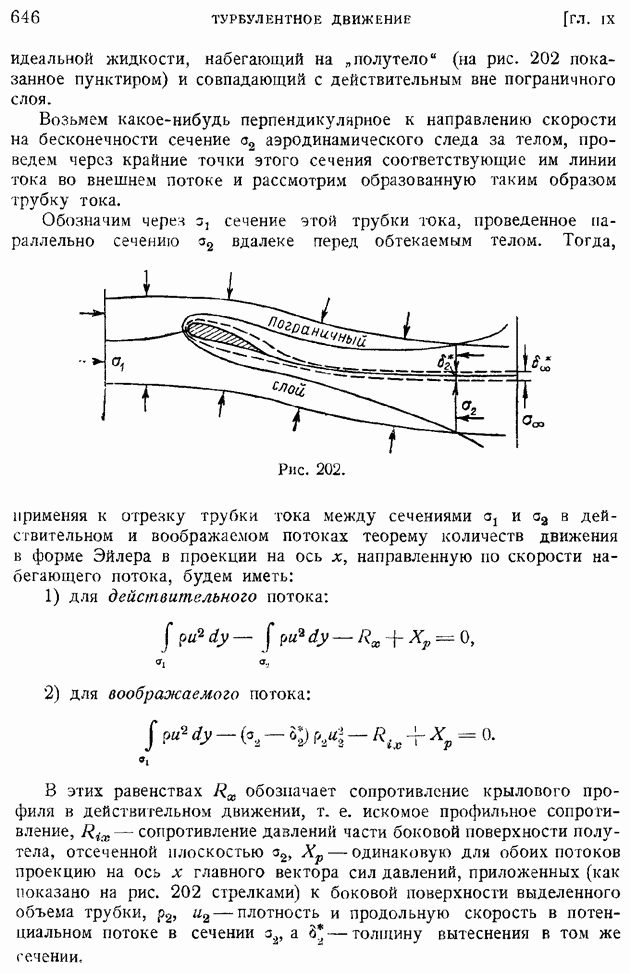
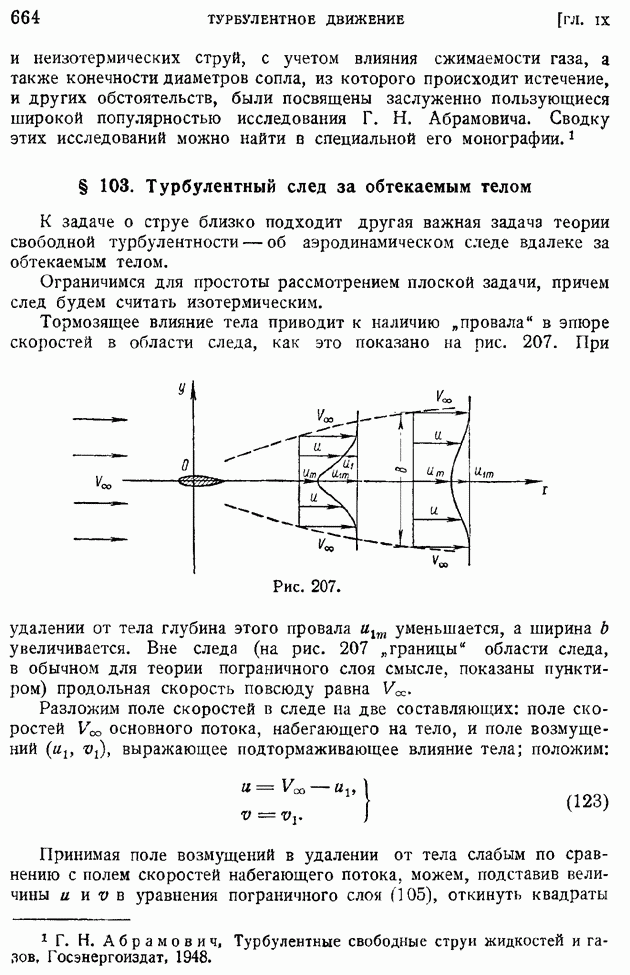
- § 103. Турбулентный след за обтекаемым телом
- § 104. Рассеяние турбулентных возмущений в жидкости. Случай изотропной и однородной турбулентности. Закон сохранения момента возмущений