| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА V. БЕЗВИХРЕВОЕ ДВИЖЕНИЕ ЖИДКОСТИ. ПЛОСКОЕ ДВИЖЕНИЕ НЕСЖИМАЕМОЙ ЖИДКОСТИ
§ 35. Сохранение циркуляции скорости в потоке идеальной жидкости. Теорема Кельвина и Лаграижа. Безвихревое движение. Потенциал скоростей
Рассмотрев в предыдущей главе одномерное движение в идеальной жидкости, перейдем теперь к следующим в порядке сложности классам движений — двух- и трехмерным. Таковы, прежде всего, плоское движение жидкости, затем осесимметричное и, наконец, общее пространственное движение. Исследование этих случаев представляет, по сравнению с одномерным потоком, большие математические трудности. Чтобы сделать решение возможным для интересующих практику конкретных задач, необходимо принять некоторые дополнительные упрощающие допущения об общем характере движения. В обосновании выбора этих допущений основную роль играют следующие две общие теоремы динамики идеальной жидкости.
Теорема Кельвина о сохранении циркуляции скорости: при баротропном движении идеального газа под действием потенциального поля объемных сил циркуляция скорости по любому замкнутому жидкому контуру сохраняет свое значение.
Эта теорема легко доказывается при помощи изложенной в конце § 13 кинематической теоремы Кельвина об изменении во времени циркуляции скорости. Согласно этой теореме, индивидуальная производная по времени от циркуляции скорости равна циркуляции ускорения:

Подставим в правую часть выражение ускорения по основному Уравнению Эйлера (5) гл. III, которое в случае потенциальных объемах сил и баротропности движения может быть переписано в виде

тогда получим

так как скалярное произведение градиента от некоторой функции на ориентированный в пространстве элемент дуги кривой есть не что иное как полный дифференциал этой функции, взятый вдоль дуги кривой.
При однозначности функций  контурный интеграл по замкнутому контуру от полного дифференциала равен нулю, так что
контурный интеграл по замкнутому контуру от полного дифференциала равен нулю, так что

и, следовательно,

что и доказывает теорему Кельвина. Вспоминая, что циркуляция скорости по замкнутому контуру равна суммарной интенсивности вихревых трубок, опоясанных этим контуром, можем на основании теоремы Кельвина заключить, что при принятых оговорках о баротропности движения и потенциальности объемных сил сохраняются и интенсивности вихревых трубок:

Предположим теперь, что в данный момент времени во всех точках некоторого жидкого объема отсутствует завихренность  т. е. жидкость в этом объеме движется без вращения, совершая лишь поступательное и деформационное движение; тогда, согласно (1), и в любой другой момент времени
т. е. жидкость в этом объеме движется без вращения, совершая лишь поступательное и деформационное движение; тогда, согласно (1), и в любой другой момент времени

В силу произвольности выбора величины и ориентации поверхности с из равенства (2) вытекает, что в любой момент времени в рассматриваемом движущемся объеме жидкости или газа будет выполняться условие отсутствия завихренности

Это чрезвычайно важное следствие теоремы Кельвина приводит ко второй теореме — теореме Лагранжа о сохранении безвихревого движения: если во всех точках некоторой баротропно движущейся под действием объемных сил с однозначным потенциалом идеальной жидкости вихрь скорости в данный момент равен нулю, то и в любой другой момент движение будет безвихревым.
Предположим, например, что твердое тело совершает движение сквозь неподвижную идеальную жидкую или газообразную среду.
или, что все равно, среда обтекает неподвижное тело, причем в том и другом случае вдалеке от тела поток не возмущен и поле скоростей однородно (жидкость покоится или движется как одно целое со скоростью, равной скорости движения тела по отношению к неподвижной среде). При этом вдалеке от тела вихрь скорости равен нулю и, следовательно, по теореме Лагранжа, при баротропности движения и потенциальности объемных сил не завихренные частицы идеальной жидкости не могут приобрести завихренность в процессе обтекания тела. Несмотря на наличие возмущающего поток тела, движение повсюду будет безвихревым.
Из теоремы Лагранжа следует, что в идеальной жидкости, находящейся под действием объемных сил с однозначным потенциалом и движущейся баротропно, не может быть вихрей, так как нет условий для их образования. Можно сказать и наоборот, что, если вихри путем нарушения ранее перечисленных условий были созданы в идеальной жидкости, то они уже не смогут исчезнуть, и движение сохранит свою вихревую структуру. В действительности приходится постоянно наблюдать как образование, так и исчезновение вихревых движений.. Главной причиной этих явлений служит неидеальность жидкости, наличие в ней внутреннего трения. Как уже ранее упоминалось, в практически интересующих нас случаях внутреннее трение играет роль лишь в тонком пограничном слое на поверхности обтекаемого тела и в "аэродинамическом следе" тела, т. е. в жидкости, которая прошла сквозь область пограничного слоя и образовала течение за кормой обтекаемого тела. Здесь, в тонком пограничном слое и образуется завихренность жидкости. Иногда в следе за телом завихренность быстро угасает, и поток в достаточном удалении за телом становится вновь безвихревым. В других случаях сошедший с поверхности тела слой завихренной жидкости распадается на отдельные вихри, которые сносятся уходящим потоком и сохраняются даже на сравнительно больших расстояниях от тела. Таковы, например, отдельные вихри, наблюдаемые в виде воронок в реках за мостовыми "быками", или пыльные смерчи, возникающие в ветреную погоду. Внутреннее трение не является единственной причиной возникновения вихрей. Так, в свободной атмосфере вдалеке от твердых поверхностей возникают непосредственно в воздухе грандиозные вихри — циклоны и антициклоны. Причиной этих вихреобразований служит отклонение движения воздуха от баротропности: плотность воздушных слоев зависит не только от Давления, но и от температуры, определяемой солнечной радиацией,  количества водяных паров и других причин.
количества водяных паров и других причин.
Несмотря на наличие всех этих факторов, нарушающих существование безвихревого движения, схема безвихревого движения во многих фактических случаях дает близкую к действительности картину. Эта схема и положена в основу настоящей главы. Итак, сделаем допущение отсутствии завихренности потока и обратимся к рассмотрению основных свойств безвихревого потока.
В силу равенства (3) во всей области безвихревого потока существует некоторая функция координат  при стационарном движении или функция координат и времени
при стационарном движении или функция координат и времени  при не стационарном движении — такая, что
при не стационарном движении — такая, что

или в проекциях на оси прямоугольной декартовой системы координат:

Функцию о назовем потенциалом скоростей и будем предполагать, что она непрерывна вместе со своими первыми двумя производными по времени и координатам.
Потенциал скоростей или, как иногда говорят, потенциал скоростного поля, так же как и потенциал силового поля, определяется с точностью до аддитивной постоянной, как это видно из равенств (4) или (5).

Рис. 51.
Равным значениям потенциала скоростей в различных точках пространства соответствуют поверхности уровня потенциала или изопотенциальные поверхности. Уравнение семейства изопотенциальных поверхностей будет

причем время  рассматривается как параметр в случае нестационарного движения и отсутствует при стационарном движении. Из определения потенциала скоростей (4) следует, что линии, нормальные к изопотенциальным поверхностям скоростного поля, являются линиями тока и, обратно, при выполнении условия (4) линиям тока соответствуют нормальные поверхности — изопопенциальные поверхности.
рассматривается как параметр в случае нестационарного движения и отсутствует при стационарном движении. Из определения потенциала скоростей (4) следует, что линии, нормальные к изопотенциальным поверхностям скоростного поля, являются линиями тока и, обратно, при выполнении условия (4) линиям тока соответствуют нормальные поверхности — изопопенциальные поверхности.
Имея заданным потенциальное скоростное поле, легко найти его потенциал, проинтегрировав уравнения в полных дифференциалах (4) или (5).
В самом деле, рассмотрим в данный момент времени в односвязной области течения кривую линию С (рис. 51), выходящую из точки  и оканчивающуюся в некоторой точке
и оканчивающуюся в некоторой точке  Умножив скалярно
Умножив скалярно
обе части равенства (4) на ориентированный элемент дуги  кривой С и проинтегрировав по этой кривой от точки
кривой С и проинтегрировав по этой кривой от точки  до
до  будем иметь
будем иметь

откуда сразу следует выражение для потенциала в любой точке  через потенциал в некоторой начальной точке
через потенциал в некоторой начальной точке  и заданные значения вектора скорости V или его проекций
и заданные значения вектора скорости V или его проекций 

Если течение во всей области безвихревое, то, замкнув (на рисунке пунктиром) кривую С при помощи кривой С так, чтобы точка  совпала с
совпала с  получим, согласно (7):
получим, согласно (7):

так как циркуляция скорости по замкнутому контуру  равная сумме интенсивностей опоясанных контуром вихревых трубок, в рассматриваемом скоростном поле, где нет вихрей, обращается в нуль. Отсюда вытекают два важные следствия:
равная сумме интенсивностей опоясанных контуром вихревых трубок, в рассматриваемом скоростном поле, где нет вихрей, обращается в нуль. Отсюда вытекают два важные следствия:
1°. Если в области течения нет вихрей (даже отдельных, изолированных вихревых нитей), то, согласно (8), потенциал скоростей представляет однозначную функцию координат;
2°. Интеграл в выражении (7) не зависит от формы кривой интегрирования С, так как в силу равенства нулю интеграла по замкнутому контуру, состоящему (рис. 51) из участка  представленного на рисунке сплошной кривой, и
представленного на рисунке сплошной кривой, и  нанесенного пунктиром, следует:
нанесенного пунктиром, следует:

Иное получится, если в безвихревом движении имеется изолированная вихревая трубка (рис. 51). Производя в этом случае интегрирование по контуру С, вновь получим равенство (8); но другой результат будет иметь место, если вместо контура С взять контур  охватывающий вихревую трубку. Интеграл, стоящий в правой части равенства (7), вычисленный по замкнутому контуру
охватывающий вихревую трубку. Интеграл, стоящий в правой части равенства (7), вычисленный по замкнутому контуру  (замыкание показано на рисунке пунктиром), как это следует из теоремы Стокса (§ 13), будет равен интенсивности вихревой трубки
(замыкание показано на рисунке пунктиром), как это следует из теоремы Стокса (§ 13), будет равен интенсивности вихревой трубки

и, согласно (7), потенциал в точке  после обхода вихревой трубки окажется равным
после обхода вихревой трубки окажется равным

Выйдя из точки  и взяв за контур интегрирования петлеобразную кривую (не показанную на рисунке), несколько раз опоясывающую вихревую трубку, вернемся в точку
и взяв за контур интегрирования петлеобразную кривую (не показанную на рисунке), несколько раз опоясывающую вихревую трубку, вернемся в точку  со значением потенциала, отличающимся от первоначального на величину, кратную интенсивности Г:
со значением потенциала, отличающимся от первоначального на величину, кратную интенсивности Г:

Таким образом, если в области безвихревого движения жидкости имеется отдельная вихревая трубка, то потенциал скоростей, выраженный через скорости по формуле (7), определяется, как многозначная функция, точек поля. Значение потенциала скоростей в точке  будет зависеть от формы кривой, вдоль которой производится интегрирование:
будет зависеть от формы кривой, вдоль которой производится интегрирование:

К вопросу о многозначности потенциала в безвихревом движении с изолированными трубками можно подойти и иначе. Выделим из области течения жидкости чисто безвихревую часть, рассматривая боковые поверхности изолированных трубок как границы течения, например, как твердые стенки. При таком рассмотрении движения в жидкости уже не будет изолированных вихревых трубок, но зато сама область течения станет многосвязной. Действительно, как уже упоминалось в следствиях второй теоремы Гельмгольца (§ 12), вихревые трубки не могут заканчиваться в самой жидкости: они образуют либо замкнутые трубки — вихревые кольца, либо опираются на граничные поверхности (твердые стенки, свободные поверхности раздела). Во всех этих случаях замкнутый контур, опоясывающий трубку, оставаясь в области безвихревого течения, не. может быть непрерывным преобразованием сведен в точку (рис. 52); это и доказывает, что область чисто безвихревого движения при наличии изолированных вихревых трубок не односвязна. Для многосвязиых областей в ранее проформулированную (§ 13) теорему Стокса должно быть внесено исправление. Как видно из только что приведенного на примере вихревых трубок рассуждения, циркуляция скорости по замкнутому контуру, опоясывающему кольцевую или трубчатую поверхность, нарушающую односвязность области течения, может быть отлична от нуля. Эта циркуляция, очевидно, зависит лишь от того, сколько раз контур охватывает трубчатую поверхность, и не зависит от формы контура интегрирования. Значения циркуляций при однократном охвате поверхностей, нарушающих связность области, называют циклическими постоянными миогосвязной области. В частном случае нарушения связности области поверхностями вихревых трубок циклические постоянные оказываются совпадающими с интенсивностями вихревых трубок.
В общем случае при наличии отдельных вихревых трубок в безвихревом потоке жидкости в многосвязпой области теорема Стокса должна быть сформулирована так: циркуляция скорости по замкнутому контуру, проведенному произвольным образом в многосвязной области, отличается от суммы интенсивностей опоясанных контуром вихревых трубок на  целых кратных циклических постоянных области.
целых кратных циклических постоянных области.
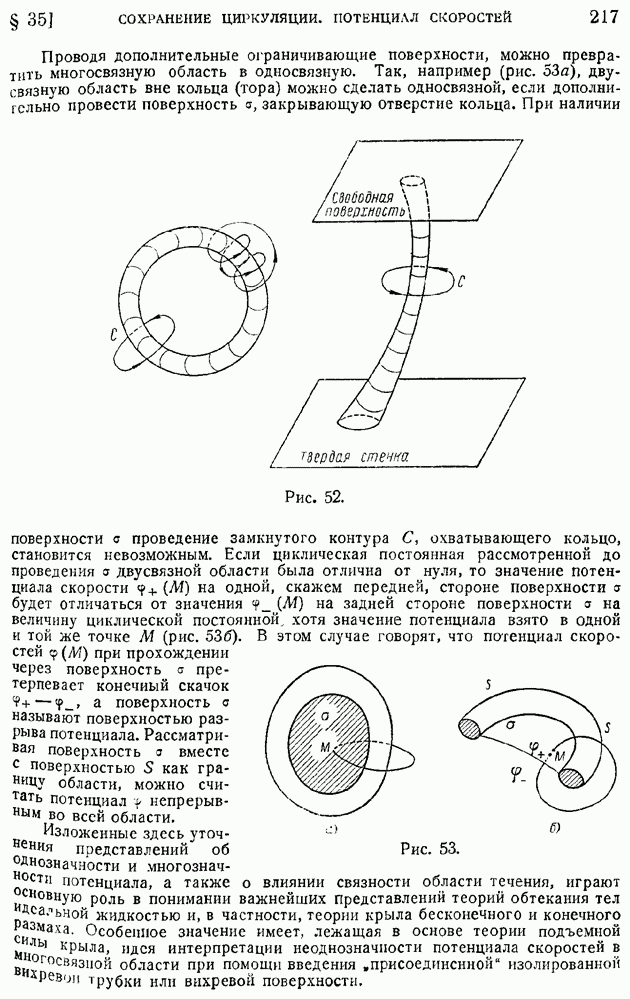
Проводя дополнительные ограничивающие поверхности, можно превратить многосвязную область в односвязную. Так, например (рис. 53а), двусвязную область вне кольца (тора) можно сделать односвязной, если дополнительно провести поверхность а, закрывающую отверстие кольца.

Рис. 52.
При наличии поверхности о проведение замкнутого контура С, охватывающего кольцо, становится невозможным. Если циклическая постоянная рассмотренной до проведения а двусвязной области была отлична от нуля, то значение потенциала скорости  на одной, скажем передней, стороне поверхности а будет отличаться от значения
на одной, скажем передней, стороне поверхности а будет отличаться от значения  на задней стороне поверхности а на величину циклической постоянной хотя значение потенциала взято в одной и той же точке
на задней стороне поверхности а на величину циклической постоянной хотя значение потенциала взято в одной и той же точке  (рис. 536). В этом случае говорят, что потенциал скоростей
(рис. 536). В этом случае говорят, что потенциал скоростей  при прохождении через поверхность а претерпевает конечный скачок
при прохождении через поверхность а претерпевает конечный скачок  а поверхность о называют поверхностью разрыва потенциала. Рассматривая поверхность а вместе с поверхностью
а поверхность о называют поверхностью разрыва потенциала. Рассматривая поверхность а вместе с поверхностью  как границу области, можно считать потенциал у непрерывным во всей области.
как границу области, можно считать потенциал у непрерывным во всей области.
Изложенные здесь уточнения представлений об однозначности и многозначности потенциала, а также о влиянии связности области течения, играют сновную роль в понимании важнейших представлений теорий обтекания тел идеальной жидкостью и, в частности, теории крыла бесконечного и конечного Размаха. Особенное значение имеет, лежащая в основе теории подъемной  крыла, идея интерпретации неоднозначности потенциала скоростей в огосвязиой области при помощи введения присоединенной изолированной вихревой трубки или вихревой поверхности.
крыла, идея интерпретации неоднозначности потенциала скоростей в огосвязиой области при помощи введения присоединенной изолированной вихревой трубки или вихревой поверхности.

Рис. 53.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Предмет механики жидкости и газа. Основные свойства «макромодели» жидкости и газа: сплошность и подвижность
- § 2. Основные методы механики жидкости и газа. Области применения и главнейшие задачи
- § 3. Краткий очерк исторического развития механики жидкости и газа. От гидромеханики древних до установления воззрений ньютонианской эпохи
- § 4. Эпоха Эйлера и Бернулли. Гидроаэродинамика в XIX в.
- § 5. Современный этап развития механики жидкости и газа
- ГЛАВА I. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
- § 6. Поле физической величины. Скалярное и векторное поля. Поверхности уровня. Векторные линин и трубки
- § 7. Мера однородности поля в данном направлении и в дайной точке. Градиевт скалярного поля и дифференциальный тензор векторного поля как меры неоднородности поля
- § 8. Задание движения сплошной среды. Поле скоростей. Линии тока и траектории
- § 9. Поле ускорений. Разложение ускорения частицы на локальную и конвективную составляющие
- § 10. Скоростное поле сплошной среды в окрестности данной точки. Угловая скорость и вихрь. Тензор скоростей деформаций и его компоненты
- § 11. Скорость объемного расширения жидкости. Интегральные представления дифференциальных операторов поля. Основные интегральные формулы
- § 12. Вихревые линии и трубки. Вторая теорема Гельмгольца. Интенсивность вихревой трубки
- § 13. Выражение интенсивности вихревой трубки через циркуляцию вектора по контуру, охватывающему трубку. Теорема об изменении циркуляции скорости во времени
- ГЛАВА II. ОСНОВНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ И РАВНОВЕСИЯ СПЛОШНОЙ СРЕДЫ
- § 14. Распределение массы в сплошной среде. Плотность и удельный вес. Напряжения. Тензор напряженности и его симметричность
- § 15. Общие уравнения динамики сплошной среды. Уравнение неразрывности. Уравнения динамики в напряжениях
- § 16. Тепловые явления в жидкостях и газах. Закон сохранения энергии и уравнение баланса энергии
- § 17. Общие уравнения равновесного состояния жидкости и газа. Равновесие воздуха в атмосфере. Приближенные барометрические формулы. Стандартная атмосфера
- § 18. Равновесие несжимаемой жидкости. Уравнение поверхности раздела. Равновесие вращающейся жидкости
- § 19. Давление тяжелой несжимаемой жидкости на поверхность тела. Сила и момент, приложенные к телу, плавающему в тяжелой жидкости. Случай вращающейся жидкости
- ГЛАВА III. ДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ И ГАЗА. ОСНОВНЫЕ УРАВНЕНИЯ И ОБЩИЕ ТЕОРЕМЫ
- § 20. Идеальная жидкость. Основные уравнения движения
- § 21. Закон сохранения энергии в движущейся идеальной жидкости. Адиабатическое движение. Сохранение энтропии
- § 22. Эйлерово представление конвективного изменения объемного интеграла. Перенос величины сквозь контрольную поверхность
- § 23. Эйлерова форма законов сохранения массы и энергии, теоремы количеств движения и момента количеств движения при стационарном движении идеальной жидкости
- § 24. Теорема об изменении кинетической энергии. Работа и мощность внутренних сил. Эйлерова форма уравнения изменения кинетической энергии
- § 25. Теорема Бернулли о сохранении полной механической энергии при стационарном баротропном движении идеальной жидкости и газа
- ГЛАВА IV. ОДНОМЕРНЫЙ ПОТОК ИДЕАЛЬНОЙ ЖИДКОСТИ
- § 26. Одномерное течение идеальной сжимаемой жидкости. Линеаризированные уравнения. Скорость распространения малых возмущений в жидкости или газе
- § 27. Изотермическая и адиабатическая скорости звука. «Конус возмущений» при сверхзвуковом движении источника возмущения. Число M и его связь с углом конуса возмущений
- § 28. Распространение непрерывных возмущений конечной интенсивности. Характеристики. Образование разрывной ударной волны
- § 29. Стоячая ударная волна или скачок уплотнения. Ударная адиабата
- § 30. Критические величины в одномерном потоке газа. Связь между скоростями до и после скачка. Изменение давления, плотности и температуры в скачке уплотнения
- § 31. Скорость распространения ударной волны. Спутное движение газа за ударной волной
- § 32. Влияние интенсивности скачка уплотнения на сжатие газа. Измерение скоростей и давлений в до- и сверхзвуковых потоках
- § 33. Одномерное движение газа по трубе переменного сечения. Истечение из резервуара большой емкости сквозь сходящееся сопло
- § 34. Одномерное течение в сопле Лаваля. Движение газа с притоком тепла
- ГЛАВА V. БЕЗВИХРЕВОЕ ДВИЖЕНИЕ ЖИДКОСТИ. ПЛОСКОЕ ДВИЖЕНИЕ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 35. Сохранение циркуляции скорости в потоке идеальной жидкости. Теорема Кельвина и Лаграижа. Безвихревое движение. Потенциал скоростей
- § 36. Интеграл Лагранжа — Коши уравнений безвихревого движения. Теорема Бернулли. Некоторые общие свойства безвихревого движения идеальной несжимаемой жидкости в односвязной области
- § 37. Плоское безвихревое движение несжимаемой жидкости. Потенциал скоростей и функция тока. Применение функций комплексного переменного. Комплексный потенциал и сопряженная скорость
- § 38. Построение полей течения по заданной характеристической Функции. Простейшие плоские потоки и их наложение
- § 39. Бесциркуляционное и циркуляционное обтекания круглого цилиндра
- § 40. Применение криволинейных координат. Бесциркуляционное и циркуляционное обтекания эллиптического цилиндра и пластинки. Задача Жуковского об обтекании решетки пластин.
- § 41. Плоское движение с отрывом струй. Разрывное обтекание пластинки и протекание жидкости сквозь отверстие
- § 42. Прямая задача в теории плоского движения идеальной несжимаемой жидкости. Применение метода конформных отображений. Гипотеза Чаплыгина о безотрывном обтекании задней кромки профиля. Формула циркуляции
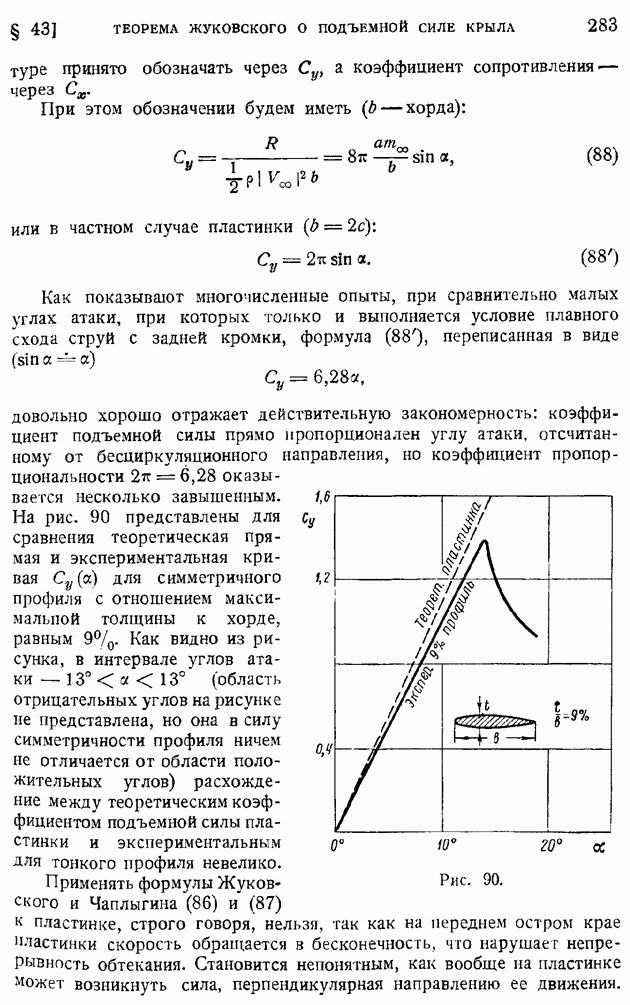
- § 43. Теорема Жуковского о подъемной силе крыла. Зависимость подъемной силы от угла атаки. Коэффициент подъемной силы
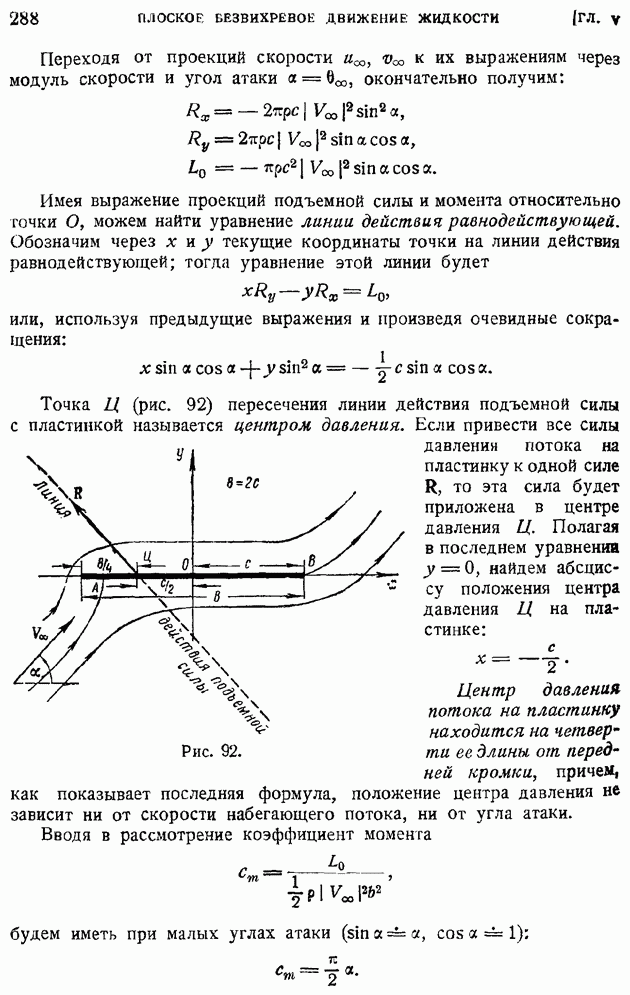
- § 44. Применение метода комплексных переменных к выводу теоремы Жуковского. Формулы Чаплыгина для главного вектора и момента сил давления потока на крыло
- § 45. Выражение главного момента сил давления потока через коэффициенты конформного отображения. Фокус крыла. Независимость от угла атаки момента относительно фокуса. Парабола устойчивости
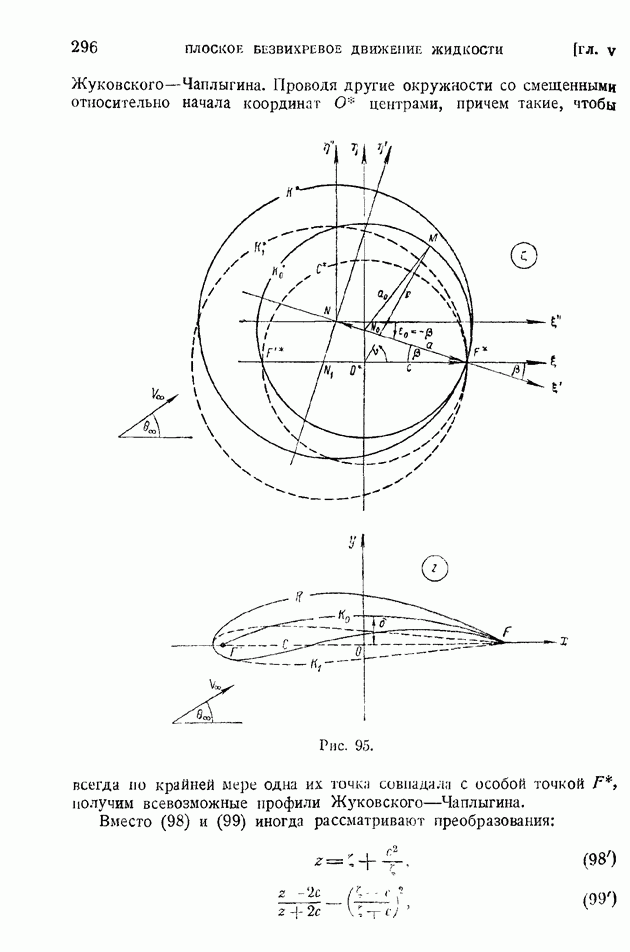
- § 46. Частные случаи конформного отображения крылового профиля на круг. Преобразование Жуковского-Чаплыгина. Теоретические крыловые профили
- § 47. Задача об обтекании слабо изогнутой дужки произвольной формы (теория тонкого крыла)
- § 48. Определение обтекания крылового профиля произвольной формы
- § 49. Обобщение теоремы Жуковского на случай плоской решетки с бесчисленным множеством профилей
- ГЛАВА VI. ПЛОСКОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ СЖИМАЕМОГО ГАЗА
- § 50. Основные уравнения плоского стационарного безвихревого движения сжимаемого газа. Линеаризированные уравнения
- 51. Линеаризированный до- и сверхзвуковой газовый поток вдоль волнистой стенки
- § 52. Тонкое крыло в линеаризированном до- и сверхзвуковом потоках. Влияние сжимаемости газа на коэффициент подъемной силы в дозвуковом потоке. Коэффициенты подъемной силы и волнового сопротивления при сверхзвуковом потоке
- § 53. Нелинеаризированные уравнения движения идеального сжимаемого газа. Переход в плоскость годографа. Уравнения Чаплыгина
- § 54. Метод С. А. Христиановича. Приближенные формулы учета влияния сжимаемости на распределение давления
- § 55. Критическое число M и его определение по заданному распределению давления в несжимаемом обтекании. Поведение коэффициента подъемной силы и момента при около- и закритических значениях числа M
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
- § 57. Нелинеаризированный сверхзвуковой поток. «Характеристики» уравнений плоского сверхзвукового потока. Линин возмущения и их основные свойства
- § 58. Обтекание выпуклого угла сверхзвуковым потоком. Влияние угла поворота струи на ее газодинамические элементы
- § 59. Сверхзвуковой поток внутри тупого угла. Косой скачок уплотнения. Связь между газодинамическими элементами до и за косым скачком
- ГЛАВА VII. ПРОСТРАНСТВЕННОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ
- § 60. Ортогональные криволинейные координаты в пространстве. Основные дифференциальные операторы поля в криволинейных координатах
- § 61. Потенциал скоростей. Поле источника и диполя. Непрерывное распределение источников и диполей. Ньютонов потенциал. Потенциал простого и двойного слоев
- § 62. Поле скоростей вокруг заданной системы вихрей. Формула Био — Савара. Потенциал скоростей замкнутой вихревой нити. Аналогия с потенциалом двойного слоя
- § 63. Функция тока и ее связь с векторным потенциалом скоростей. Функции тока простейших течений
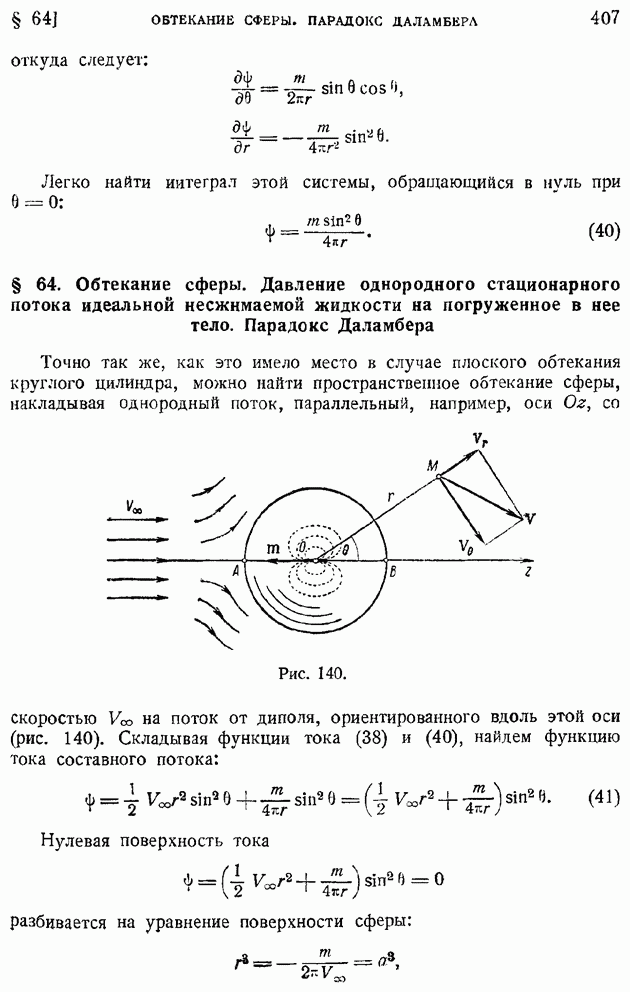
- § 64. Обтекание сферы. Давление однородного стационарного потока идеальной несжимаемой жидкости на погруженное в нее тело. Парадокс Даламбера
- § 65. Общие уравнения осесимметричного движения. Применение цилиндрических координат. Течение сквозь каналы
- § 66. Осесимметричное продольное обтекание тел вращения. Случай эллипсоида вращения
- § 67. Поперечное обтекание тел вращения. Пример эллипсоида вращения
- § 68. Продольное и поперечное обтекание тел вращения большого удлинения. Приближенные выражения граничных условий. Применение тригонометрических сумм для определения коэффициентов …
- § 69. Метод «особенностей». Применение непрерывно распределенных источников (стоков) и диполей для решения задачи о продольном и поперечном обтекании тел вращения
- § 70. Общий случай движения твердого тела сквозь несжимаемую идеальную жидкость. Определение потенциала скоростей. Главный вектор и главный момент сил давления потока на тело
- § 71. Коэффициенты «присоединенных масс». Свойство симметрии. «Присоединенная» кинетическая энергия. Определение «присоединенных масс» поступательно движущегося цилиндра, шара и эллипсоида
- § 72. Элементы теории крыла конечного размаха. Вихревая система крыла. Гипотеза плоских сечеиий. Геометрические и действительные углы атаки. Подъемная сила и «индуктивное сопротивление»
- § 73. Основные формулы теории «несущей линии». «Индуктивная скорость» и «индуктивный угол». Прямая задача определения подъемной силы и индуктивного сопротивления по заданному распределению циркуляции
- § 74. Крыло с минимальным индуктивным сопротивлением. Эллиптическое распределение циркуляции. Связь между коэффициентами индуктивного сопротивления и подъемной силы. Основное уравнение теории крыла и понятие о его интегрировании
- ГЛАВА VIII. ДИНАМИКА ВЯЗКОЙ ЖИДКОСТИ И ГАЗА
- § 75. Внутреннее трение и теплопроводность в жидкостях и газах. Законы Ньютона и Фурье. Влияние температуры на коэффициенты вязкости и теплопроводности. Число «сигма»
- § 76. Обобщение закона Ньютона на случай произвольного движения среды. Закон линейной связи между тензорами напряжений и скоростей деформации
- § 77. Общие уравнения движения вязкой жидкости. Динамические уравнения и уравнение баланса энергии. Граничные условия движения жидкости с треннем и теплопроводностью
- § 78. Понятие о подобии гидродинамических явлений. Безразмерные уравнения движения вязкой жидкости и газа. Условия подобия
- § 79. Ламинарное движение вязкой несжимаемой жидкости по цилиндрической трубе
- § 80. Обтекание шара при очень малых значениях числа Рейнольдса. Формула сопротивления шара по Стоксу и ее обобщения
- § 81. Вихревые линии в идеальной и вязкой жидкости. Сохраняемость вихревых линий при отсутствии внутреннего трения. Диффузия вихря в вязкой жидкости
- § 82. Одномерное прямолинейное движение сжимаемого вязкого газа. Движение внутри скачка уплотнения. Понятие о толщине скачка
- § 83. Работа внутренних сил и диссипация механической энергии в движущейся вязкой среде
- § 84. Обтекание тел жидкостью и газом при больших значениях числа Рейнольдса. Основные уравнения теории ламинарного пограничного слоя
- § 85. Ламинарный пограничный слой на пластинке, продольно обтекаемой несжимаемой жидкостью. Неизотермическое движение
- § 86. Ламинарный пограничный слой при степенном задании скорости внешнего потока
- § 87. Ламинарный пограничный слой в общем случае задания скорости внешнего потока. Применение уравнения импульсов для приближенного расчета ламинарного пограничного слоя
- § 88. Способы определения функций … Приближенный метод расчета ламинарного пограничного слоя
- § 89. Ламинарный пограничный слой на пластинке, продольно обтекаемой сжимаемым газом при больших скоростях. Случай линейной зависимости коэффициента вязкости от температуры (n = 1)
- § 90. Ламинарный пограничный слой на пластинке при любом законе связи между вязкостью и температурой и при числе … Обтекание крылового профиля потоком больших скоростей
- ГЛАВА IX. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ
- § 91. Переход ламинарного движения в турбулентное. Критическое рейнольдсово число
- § 92. Область и «точка» перехода. Явление «кризиса обтекания»
- § 93. Основные уравнения осреднеиного турбулентного движения. Тензор турбулентных напряжений
- § 94. Турбулентное движение жидкости в плоской и круглой трубе. Логарифмические формулы скоростей
- § 95. Формулы сопротивления гладких труб при турбулентном движении жидкости. Ламинарный подслой
- § 96. Влияние шероховатости стенок трубы на ее сопротивление. Предельные режимы течения. Режим установившейся шероховатости
- § 97. Турбулентный пограничный слой на продольно обтекаемой пластине. Сопротивление пластины
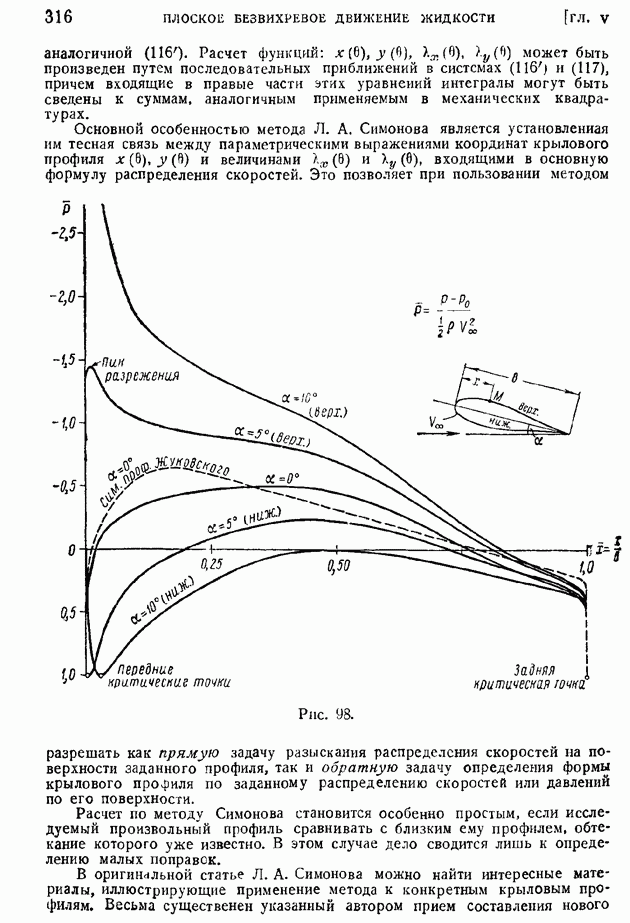
- § 98. Турбулентный пограничный слой на крыловом профиле при малом продольном перепаде давлений
- § 99. Турбулентный пограничный слой на крыловом профиле при значительных продольных перепадах давления
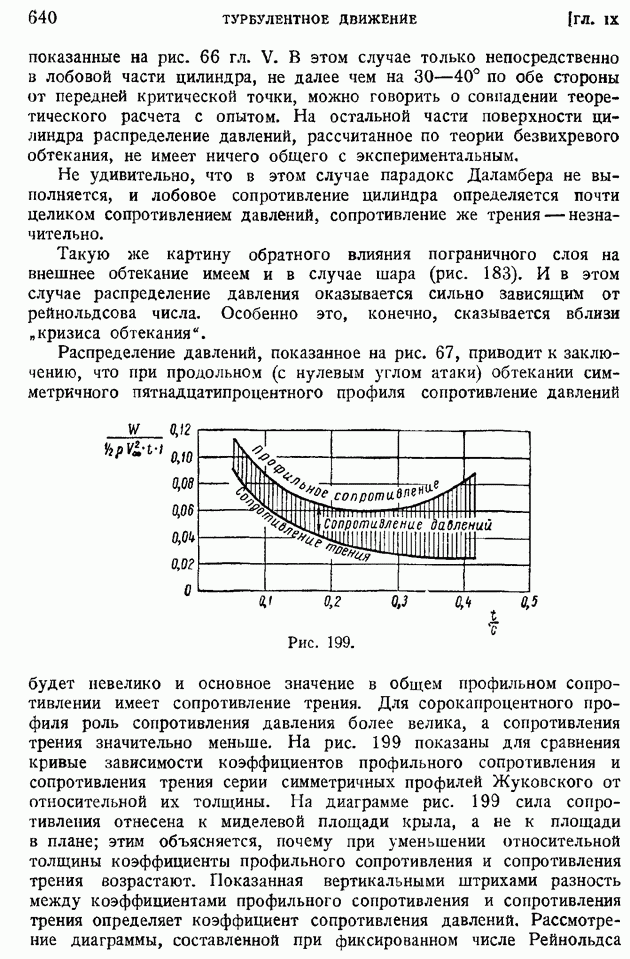
- § 100. Профильное сопротивление крыла. Разложение профильного сопротивления на сопротивление трения и сопротивление давлений. Обратное влияние пограничного слоя на распределение давлений по поверхности обтекаемого профиля
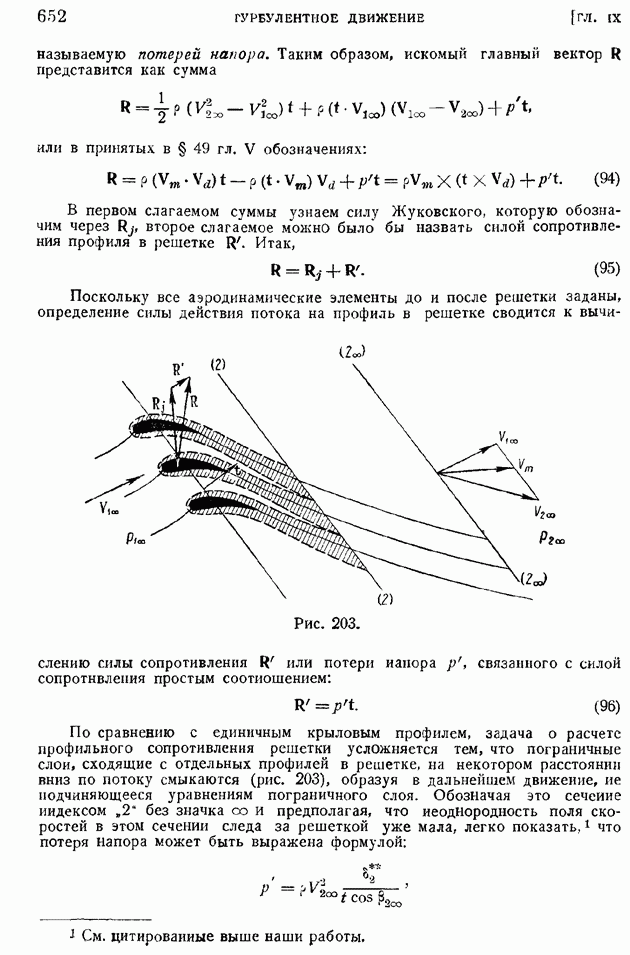
- § 101. Приближенные формулы профильного сопротивления крыла и крылового профиля в решетке
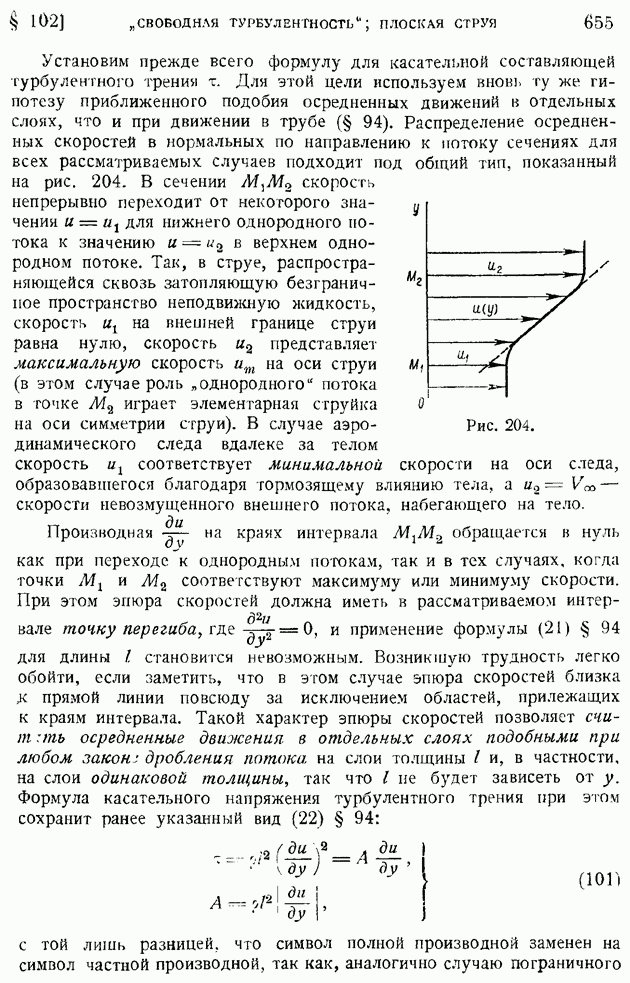
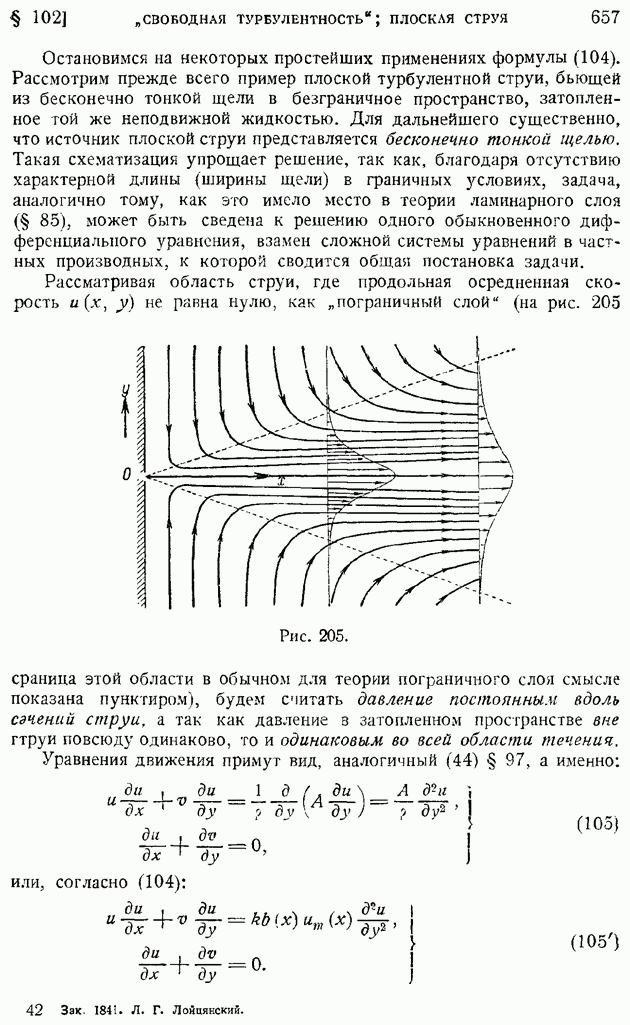
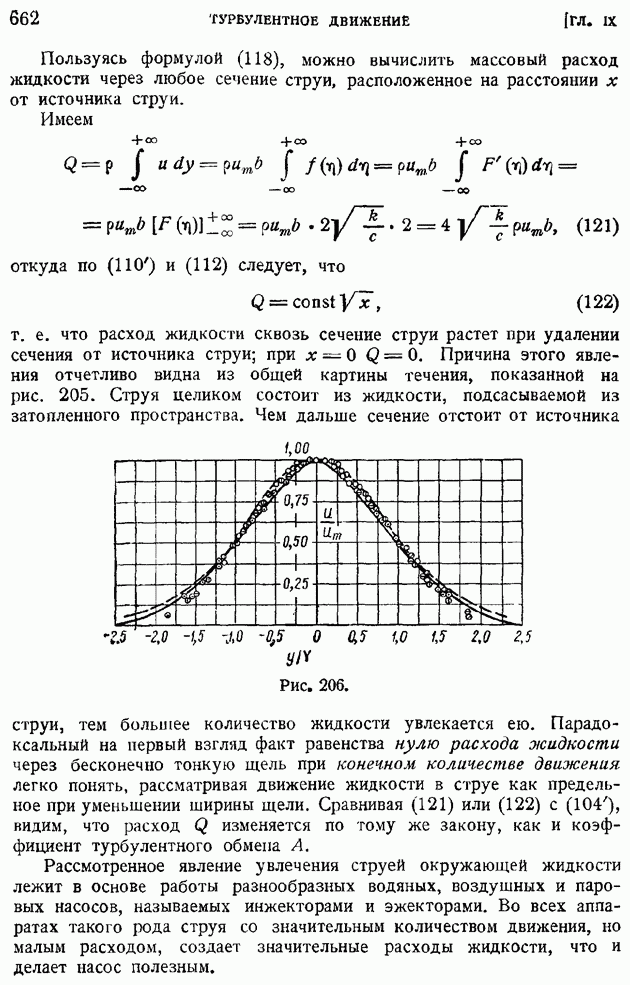
- § 102. Основные закономерности «свободной турбулентности». Плоская турбулентная струя в пространстве, заполненном той же жидкостью
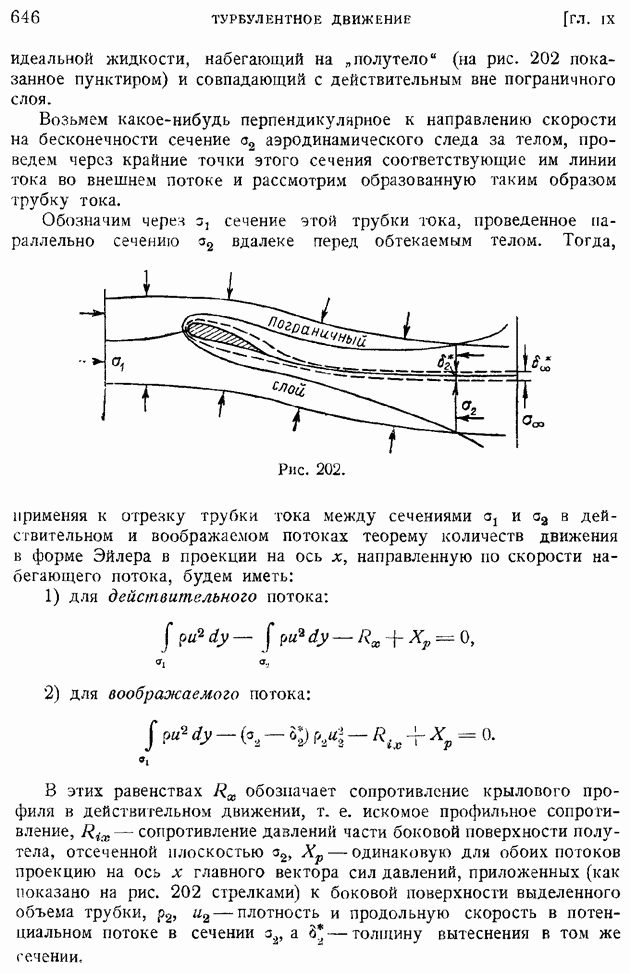
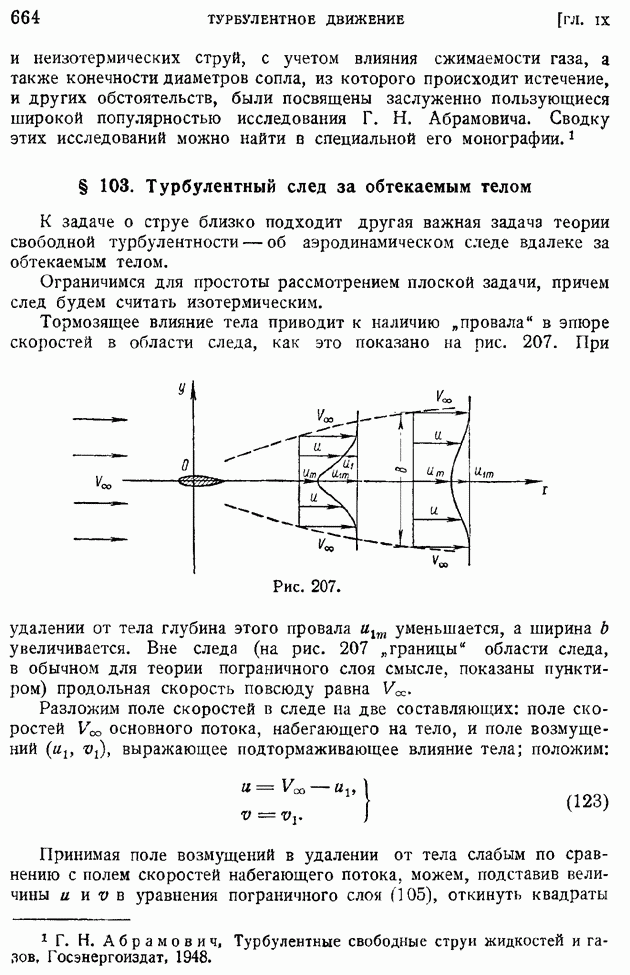
- § 103. Турбулентный след за обтекаемым телом
- § 104. Рассеяние турбулентных возмущений в жидкости. Случай изотропной и однородной турбулентности. Закон сохранения момента возмущений