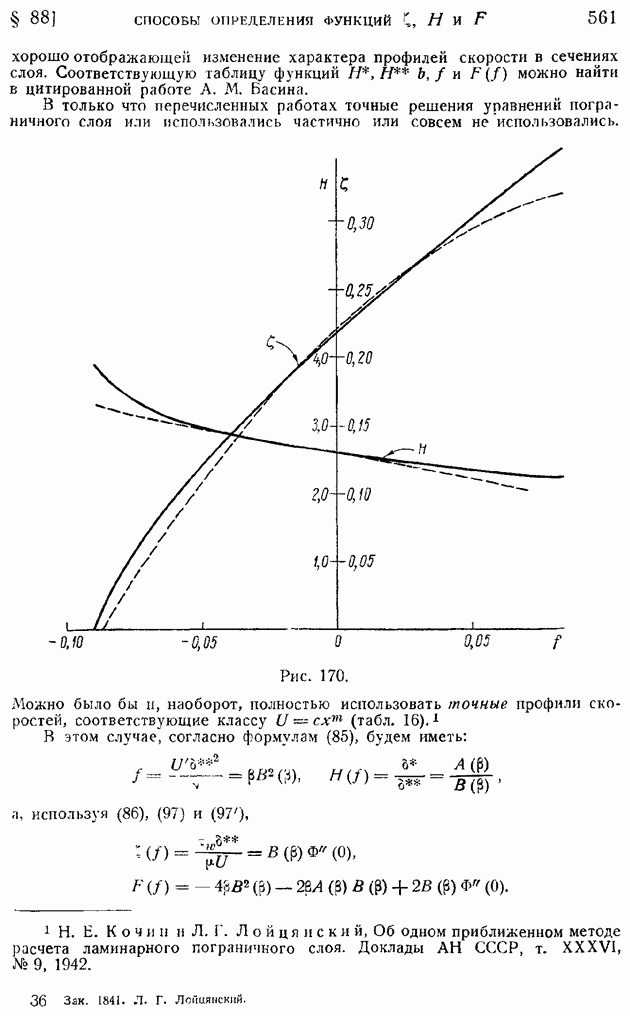| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 32. Влияние интенсивности скачка уплотнения на сжатие газа. Измерение скоростей и давлений в до- и сверхзвуковых потоках
Рассмотрим одномерное стационарное адиабатическое течение идеального газа и предположим, что где-то вдоль трубки тока или струи газа происходит изэнтропическое (без скачка уплотнения или других причин для превращения механической энергии в тепловую) торможение газа, приводящее газ к покою. Установим простые формулы связи параметров изэнтропически заторможенного газа  с текущими их значениями
с текущими их значениями  а в сечениях рассматриваемой трубки тока.
а в сечениях рассматриваемой трубки тока.
Возьмем основную формулу закона сохранения энергии 

и определим константу из условия: при  тогда получим:
тогда получим:

или, замечая, что но (17) гл. III и по определению местной адиабатической скорости звука

найдем искомое выражение температуры изэнтропически заторможенного газа:

а следовательно, и соответствующую скорость звука

Из уравнения изэнтронической адиабаты и уравнения Клапейрона

сразу следует:

откуда, используя (66), найдем выражения остальных параметров изэнтропически заторможенного газа:

Формулы (66), (69) и (70) являются основными во всех расчетах одномерных течений газа.
Из формулы (70) следует,  при значениях числа
при значениях числа  меньших единицы, имеет место разложение в ряд:
меньших единицы, имеет место разложение в ряд:

Отсюда можно сделать вывод, что, полагая в модели несжимаемой жидкости  делают тем меньшую ошибку, чем меньше число
делают тем меньшую ошибку, чем меньше число  в движущемся газе. Так, например, для того чтобы ошибка не превосходила
в движущемся газе. Так, например, для того чтобы ошибка не превосходила  число
число  должно быть меньше 0,14, а это соответствует в случае воздуха при нормальных условиях верхней границе допустимых скоростей
должно быть меньше 0,14, а это соответствует в случае воздуха при нормальных условиях верхней границе допустимых скоростей  Следует заметить, что даже при скорости в
Следует заметить, что даже при скорости в  ошибка не превосходит
ошибка не превосходит 
Легко также видеть, что при малых значениях числа  формула (69) "ерсходит в обычную формулу Бернулли (58) гл. III для несжимаемого
формула (69) "ерсходит в обычную формулу Бернулли (58) гл. III для несжимаемого
газа. Действительно, разлагая при малых  правую часть (69) в ряд, получим:
правую часть (69) в ряд, получим:

или, замечая еще, что по определению числа  и адиабатической скорости звука
и адиабатической скорости звука

получим

При  будем иметь формулу (58) гл. III для несжимаемой жидкости:
будем иметь формулу (58) гл. III для несжимаемой жидкости:

Ошибка, которую при этом делают, принимая газ несжимаемым, имеет порядок  т. е. в два раза меньше ошибки в изменении плотности. Так, применяя теорему Бернулли для несжимаемой жидкости в случае воздуха, движущегося при нормальных условиях со скоростью
т. е. в два раза меньше ошибки в изменении плотности. Так, применяя теорему Бернулли для несжимаемой жидкости в случае воздуха, движущегося при нормальных условиях со скоростью  сделаем ошибку порядка
сделаем ошибку порядка  Как известно, в капельных жидкостях скорость звука больше, чем в газах. В воде, например, скорость звука достигает значения 1500 мсек, т. е. почти в 5 раз превышает скорость звука в воздухе. Таким образом, воду можно рассматривать как несжимаемую жидкость при скоростях, доходящих до
Как известно, в капельных жидкостях скорость звука больше, чем в газах. В воде, например, скорость звука достигает значения 1500 мсек, т. е. почти в 5 раз превышает скорость звука в воздухе. Таким образом, воду можно рассматривать как несжимаемую жидкость при скоростях, доходящих до  такие скорости на практике еще не наблюдаются.
такие скорости на практике еще не наблюдаются.
При переходе от сверхзвуковых скоростей  к дозвуковым
к дозвуковым  как было ранее показано, газ проходит через скачок уплотнения. В этом случае величины
как было ранее показано, газ проходит через скачок уплотнения. В этом случае величины  для заторможенного газа уже не могут вычисляться по указанным только что формулам (69), (70) и (66), так как процесс в целом не изэнтропичен; расчет приходится вести иначе.
для заторможенного газа уже не могут вычисляться по указанным только что формулам (69), (70) и (66), так как процесс в целом не изэнтропичен; расчет приходится вести иначе.
Следуя принятым ранее обозначениям, будем считать, что газ до скачка имел параметры  после скачка —
после скачка —  соответствующие значения параметров изэнтропически заторможенного газа до и после скачка обозначим через
соответствующие значения параметров изэнтропически заторможенного газа до и после скачка обозначим через 
Как было показано в § 30:

следовательно, по (68):

С другой стороны, из первых двух равенств системы (59) легко вывести следующие соотношения:

Замечая, что по формуле Клапейрона

разделим почленно обе части равенств (72) и (73) друг на друга и получим:

Чтобы получить искомые отношения давлений и плотностей изэнтропически заторможенного газа за и перед скачком уплотнения, остается подставить выражения (72) и (74) в равенство (71); тогда будем иметь:

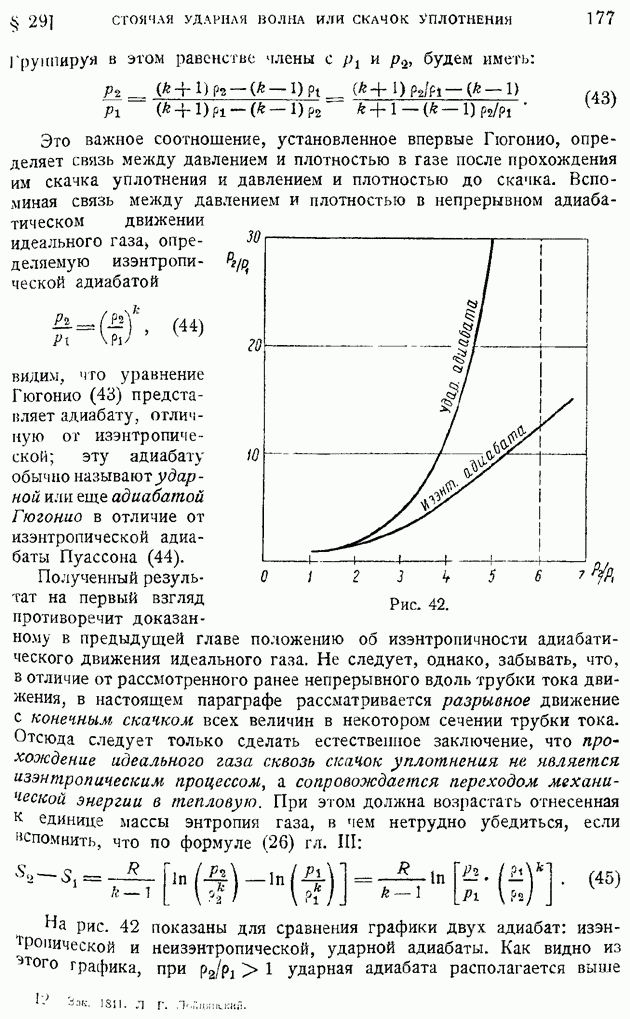
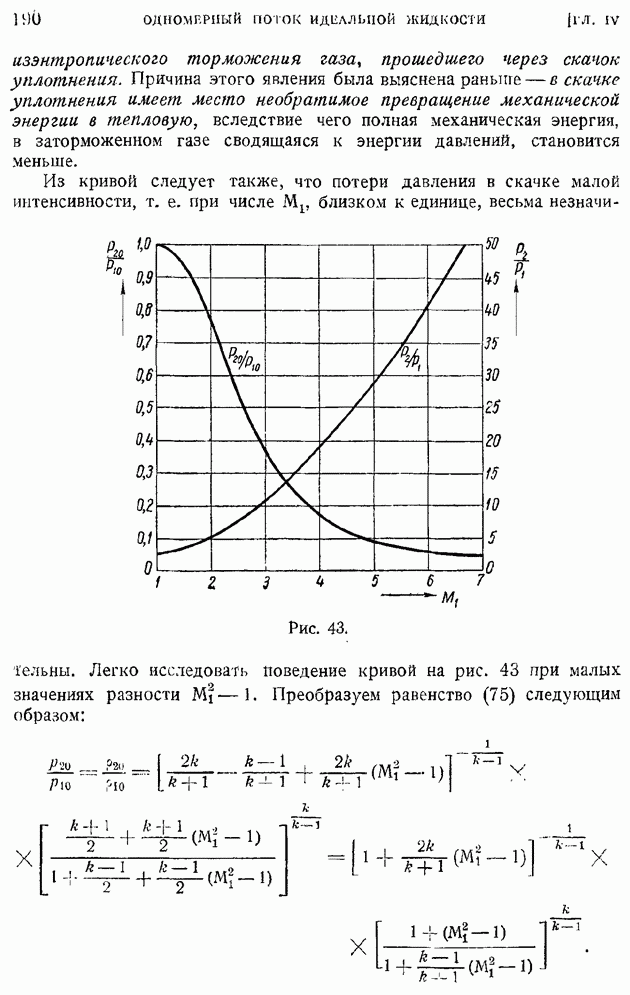
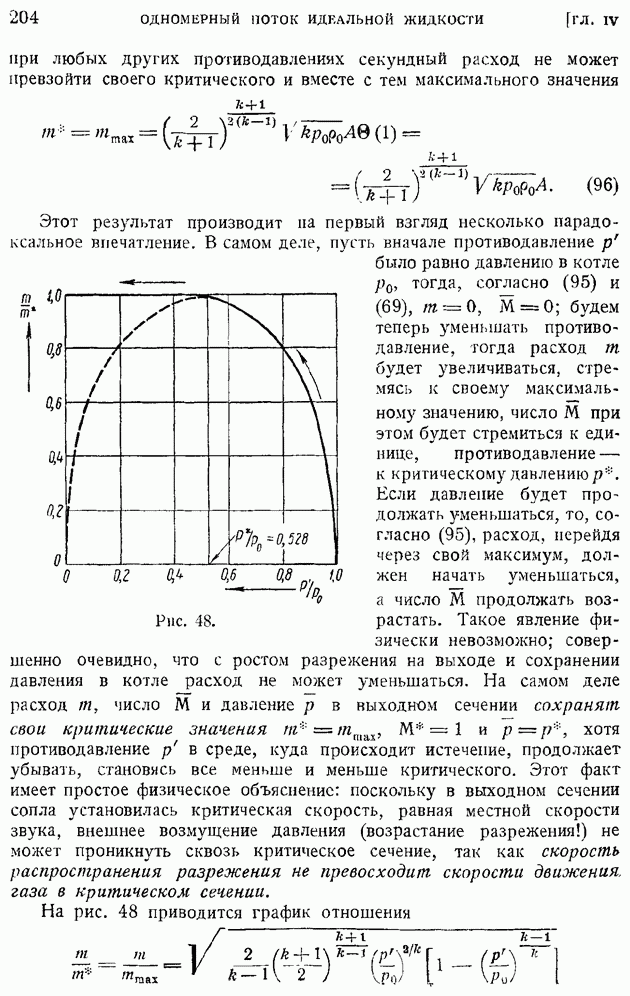
На рис. 43 представлен график этого соотношения для воздуха  том же Графике показано сжатие воздуха в скачке
том же Графике показано сжатие воздуха в скачке  разных
разных  Как видно из графика, чем больше число
Как видно из графика, чем больше число  набегающего воздуха, тем меньшее давление можно получить за счет
набегающего воздуха, тем меньшее давление можно получить за счет
изэнтропического торможения газа, прошедшего через скачок уплотнения. Причина этого явления была выяснена раньнге — в скачке уплотнения имеет место необратимое превращение механической энергии в тепловую, вследствие чего полная механическая энергия, в заторможенном газе сводящаяся к энергии давлений, становится меньше.
Из кривой следует также, что потери давления в скачке малой интенсивности, т. е. при числе  близком к единице, весьма незначительны.
близком к единице, весьма незначительны.

Рис. 43.
Легко исследовать поведение кривой на рис. 43 при малых значениях разности  Преобразуем равенство (75) следующим образом:
Преобразуем равенство (75) следующим образом:

Произведя разложение по стеиеням малой величины  убедимся, что коэффициенты при
убедимся, что коэффициенты при  обращаются в нуль, а разложение величины будет иметь вид:
обращаются в нуль, а разложение величины будет иметь вид:

Из последнего разложения видно, что скачки малой интенсивности не приводят к заметной потере давлений, так как при  близком к единице,
близком к единице,  совпадет с
совпадет с  с точностью до очень малой величины
с точностью до очень малой величины

Так, для воздуха  эта величина имеет порядок
эта величина имеет порядок  например, при превышении скорости звука на
например, при превышении скорости звука на  будет равна 0,0015.
будет равна 0,0015.
Можно показать, что такова же величина приращения в скачке уплотнения энтропии, являющейся мерой превращения механической энергии в тепло (потерь механической энергии). С этой целью применим равенство (45) к параметрам изэнтропически заторможенного газа, что допустимо, так как изэнтропическое торможение не должно повлиять на приращение энтропии в скачке; тогда получим:

но, по предыдущему,  следовательно, по (75):
следовательно, по (75):

Отсюда следует важный общий вывод: скашси малой интенсивности приводят к ничтожным изменениям, энтропии, так что с достаточной степенью приближения околозвуковые явления можно рассматривать как изэнтропические.
Из равенства (74) легко найти также соотношение между числами  до и за скачком уплотнения. Заметив, что
до и за скачком уплотнения. Заметив, что  связаны простыми соотношениями (66) с температурами
связаны простыми соотношениями (66) с температурами  изэнтропически заторможенного газа, причем, как было еще показано в § 30, получим:
изэнтропически заторможенного газа, причем, как было еще показано в § 30, получим:

откуда следует

Из последней формулы видно, как убывает число  за скачком с возрастанием числа
за скачком с возрастанием числа  перед скачком. Чем больше интенсивность скачка, т. е. чем больше отношение сверхзвуковой скорости газа перед скачком к местной скорости звука, тем меньше отношение дозвуковой скорости за скачком к своей скорости звука. Но не следует думать, что дозвуковое значение числа
перед скачком. Чем больше интенсивность скачка, т. е. чем больше отношение сверхзвуковой скорости газа перед скачком к местной скорости звука, тем меньше отношение дозвуковой скорости за скачком к своей скорости звука. Но не следует думать, что дозвуковое значение числа  за скачком будет беспредельно убывать с ростом интенсивности скачка
за скачком будет беспредельно убывать с ростом интенсивности скачка  Как показывает формула (77), при беспредельном росте
Как показывает формула (77), при беспредельном росте  величина
величина  остается больше величины
остается больше величины

для воздуха  равной 0,378.
равной 0,378.
Приводим табл. 6 значений  и отношения давлений
и отношения давлений  за и перед скачком в интервале наиболее употребительных значений чисел
за и перед скачком в интервале наиболее употребительных значений чисел  для воздуха.
для воздуха.
Таблица 6 (см. скан)
Рассмотрим в качестве примера простейшую схему воздушно-реактивного двигателя  без компрессора (рис. 44), установленного на самолете, который летит на высоте
без компрессора (рис. 44), установленного на самолете, который летит на высоте  со сверхзвуковой скоростью
со сверхзвуковой скоростью  скорость звука на высоте
скорость звука на высоте  Обозначим давление воздуха на высоте
Обозначим давление воздуха на высоте  через
через  давление в камере горения
давление в камере горения  будет значительно превышать давление
будет значительно превышать давление  так как в камере горения скорость сравнительно невелика. Пренебрегая этой скоростью, можем считать
так как в камере горения скорость сравнительно невелика. Пренебрегая этой скоростью, можем считать  Для улучшения сгорания горючего и повышения к. п. д. двигателя важно иметь в камере горения, по возможности, более высокое давление. Подсчитаем это давление сначала в предположении изэнтропичности процесса входа внешнего воздуха внутрь
Для улучшения сгорания горючего и повышения к. п. д. двигателя важно иметь в камере горения, по возможности, более высокое давление. Подсчитаем это давление сначала в предположении изэнтропичности процесса входа внешнего воздуха внутрь 
Будем иметь:

или для воздуха:

Нсли число  полета равно
полета равно  то
то

Па высоте  по таблице международной стандартной атмосферы
по таблице международной стандартной атмосферы  находим
находим  следовательно,
следовательно,

т. е., несмотря на большую высоту и разреженность атмосферы, за счет скоростного папора набегающего воздуха в камере горения должно было бы наблюдаться сжатие воздуха  и давление в
и давление в 

Рис. 44.
На самом деле торможение воздуха от сверхзвуковой скорости  при
при  по
по  равной
равной  сек, или
сек, или  до почти нулевой скорости в камере горения вызовет появление скачка уплотнения, показанного на рис. 44 жирным пунктиром. Этот скачок всегда садится впереди тупоносого тела, движущегося со сверхзвуковой скоростью, и называется головной волной. Участок головной волны перед входом в ВРД можно рассматривать приближенно как плоский скачок уплотнения в одномерном течении и определять
до почти нулевой скорости в камере горения вызовет появление скачка уплотнения, показанного на рис. 44 жирным пунктиром. Этот скачок всегда садится впереди тупоносого тела, движущегося со сверхзвуковой скоростью, и называется головной волной. Участок головной волны перед входом в ВРД можно рассматривать приближенно как плоский скачок уплотнения в одномерном течении и определять  по заданному
по заданному  при помощи графика рис. 43. Давление в изэнтропически заторможенном газе
при помощи графика рис. 43. Давление в изэнтропически заторможенном газе  определится опять по формуле
определится опять по формуле

давление в камере горения при  будет по графику равно:
будет по графику равно:

 на 25% меньше, чем то давление
на 25% меньше, чем то давление  которое установилось бы при изэнтропическом (бесскачковом) торможении. При меньших
которое установилось бы при изэнтропическом (бесскачковом) торможении. При меньших
значениях числа  (малых интенсивностях скачка) этот эффект был бы гораздо более слабым. Например, при
(малых интенсивностях скачка) этот эффект был бы гораздо более слабым. Например, при  что на высоте
что на высоте  соответствует по
соответствует по  скорости
скорости  около
около  по (75) разница между давлением изэнтропически заторможенного воздуха в камере горения и давлением воздуха, прошедшего сквозь скачок уплотнения малой интенсивности, не превзошла бы 1,5%.
по (75) разница между давлением изэнтропически заторможенного воздуха в камере горения и давлением воздуха, прошедшего сквозь скачок уплотнения малой интенсивности, не превзошла бы 1,5%.
Наоборот, при полете с большими значениями числа  вредное влияние скачка уплотнения сильно увеличивается.
вредное влияние скачка уплотнения сильно увеличивается.

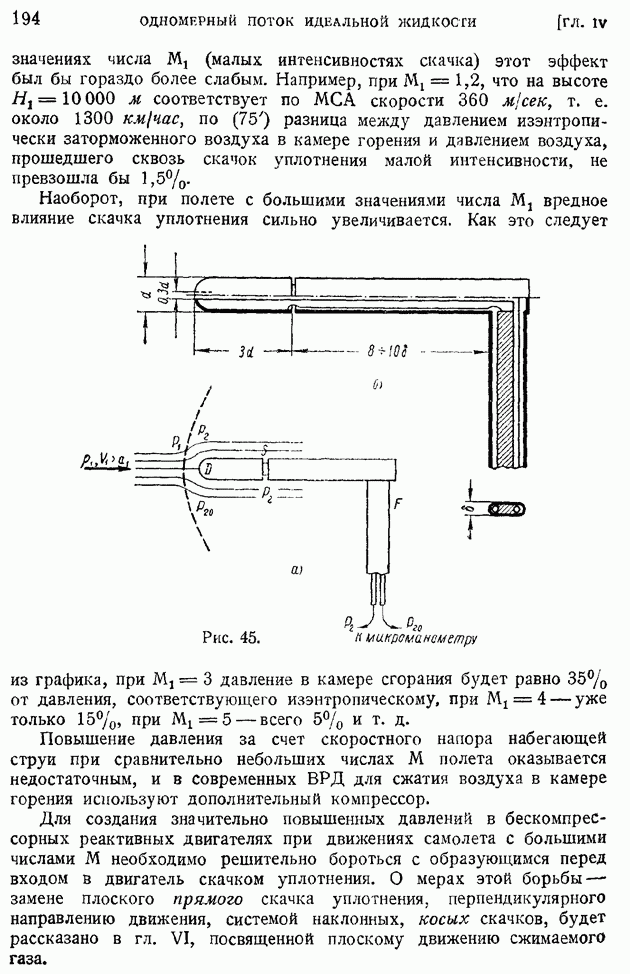
Рис. 45.
Как это следует из графика, при  давление в камере сгорания будет равно 35% от давления, соответствующего изэнтропическому, при
давление в камере сгорания будет равно 35% от давления, соответствующего изэнтропическому, при  уже только 15%, при
уже только 15%, при  всего 5% и т. д.
всего 5% и т. д.
Повышение давления за счет скоростного напора набегающей струи при сравнительно небольших числах  полета оказывается недостаточным, и в современных ВРД для сжатия воздуха в камере горения используют дополнительный компрессор.
полета оказывается недостаточным, и в современных ВРД для сжатия воздуха в камере горения используют дополнительный компрессор.
Для создания значительно повышенных давлений в бескомпрессорных реактивных двигателях при движениях самолета с большими числами  необходимо решительно бороться с образующимся перед входом в двигатель скачком уплотнения. О мерах этой борьбы — замене плоского прямого скачка уплотнения, перпендикулярного направлению движения, системой наклонных, косых скачков, будет рассказано в гл. VI, посвященной плоскому движению сжимаемого газа.
необходимо решительно бороться с образующимся перед входом в двигатель скачком уплотнения. О мерах этой борьбы — замене плоского прямого скачка уплотнения, перпендикулярного направлению движения, системой наклонных, косых скачков, будет рассказано в гл. VI, посвященной плоскому движению сжимаемого газа.
Для измерения скоростей движения газа или движения тела по отношению к газу применяют особые измерительные трубки (их называют обычно скоростными трубками), основная идея работы которых заключается в следующем. Газ набегает на носик трубки, где имеется так называемое динамическое отверстие  и обтекает боковую поверхность трубки, с расположенным на ней статическим отверстием (щелью) При надлежащей конструкции трубки — достаточном удалении ножки трубки
и обтекает боковую поверхность трубки, с расположенным на ней статическим отверстием (щелью) При надлежащей конструкции трубки — достаточном удалении ножки трубки  от статического отверстия 5 и статического отверстия 5 от носика трубки D (обычно принятые размеры показаны на рис. 45 б) можно считать, что вблизи отверстия
от статического отверстия 5 и статического отверстия 5 от носика трубки D (обычно принятые размеры показаны на рис. 45 б) можно считать, что вблизи отверстия  давление равно (рис. 45 а) давлению заторможенной жидкости или газа
давление равно (рис. 45 а) давлению заторможенной жидкости или газа  а вблизи статической щели — давлению проходящего мимо трубки газа. Последнее обстоятельство может вызвать недоумение, так как в реальной жидкости или газе существует трение, приводящее скорость частиц на стенке к нулю, т. е. также тормозящее газ. Однако это торможение совершенно иное, чем торможение набегающего потока в лобовой точке
а вблизи статической щели — давлению проходящего мимо трубки газа. Последнее обстоятельство может вызвать недоумение, так как в реальной жидкости или газе существует трение, приводящее скорость частиц на стенке к нулю, т. е. также тормозящее газ. Однако это торможение совершенно иное, чем торможение набегающего потока в лобовой точке  измерительной трубки. В конце курса при изложении теории вязкого движения жидкости к пограничном слое на поверхности обтекаемого тела будет показано, что при этом неизэнтропическом торможении давление в любой точке поверхности совпадает с давлением в жидкости или газе в сечении пограничного слоя, проведенном через эту точку. Таким образом, действительно, если щель
измерительной трубки. В конце курса при изложении теории вязкого движения жидкости к пограничном слое на поверхности обтекаемого тела будет показано, что при этом неизэнтропическом торможении давление в любой точке поверхности совпадает с давлением в жидкости или газе в сечении пограничного слоя, проведенном через эту точку. Таким образом, действительно, если щель  располагается заподлицо к стенкам трубки достаточно аккуратно для того, чтобы жидкость проходила мимо щели, не подвергаясь подпору со стороны выступающих стенок этой щели, то давление в щели будет равно давлению в невозмущенной трубкой жидкости вдалеке от трубки.
располагается заподлицо к стенкам трубки достаточно аккуратно для того, чтобы жидкость проходила мимо щели, не подвергаясь подпору со стороны выступающих стенок этой щели, то давление в щели будет равно давлению в невозмущенной трубкой жидкости вдалеке от трубки.
Условимся в дальнейшем обозначать через  давление, плотность, скорость звука и скорость набегающего на трубку потока.
давление, плотность, скорость звука и скорость набегающего на трубку потока.
Если жидкость или газ движутся со столь малыми скоростями, точнее говоря, с малыми значениями числа  что можно их движение рассматривать как несжимаемое, то по теореме Бернулли для несжимаемой жидкости, выражаемой равенством (58) гл. III, можно написать
что можно их движение рассматривать как несжимаемое, то по теореме Бернулли для несжимаемой жидкости, выражаемой равенством (58) гл. III, можно написать

 откуда сразу следует
откуда сразу следует

или, опуская индекс  так как скорость, плотность и давление в этом случае повсюду вдалеке от трубки одинаковы, и заменяя еще плотность
так как скорость, плотность и давление в этом случае повсюду вдалеке от трубки одинаковы, и заменяя еще плотность  на удельный вес
на удельный вес  будем окончательно иметь основную формулу теории скоростной трубки:
будем окончательно иметь основную формулу теории скоростной трубки:

Измеряя разность давлений  при помощи дифференциального манометра и зная удельный вес движущейся среды, можно найти и ее скорость. На самом деле, при неточностях изготовления отдельных измерительных трубок величины
при помощи дифференциального манометра и зная удельный вес движущейся среды, можно найти и ее скорость. На самом деле, при неточностях изготовления отдельных измерительных трубок величины  могут несколько отличаться от действительных своих значений; для учета этих поправок на практике в формулу (78) вводят некоторый дополнительный, близкий к единице коэффициент, который определяют тарировкой, сравнивая в воздушной струе аэродинамической трубы данную трубку с некоторой образцовой.
могут несколько отличаться от действительных своих значений; для учета этих поправок на практике в формулу (78) вводят некоторый дополнительный, близкий к единице коэффициент, который определяют тарировкой, сравнивая в воздушной струе аэродинамической трубы данную трубку с некоторой образцовой.
Предположим теперь, что газ движется с большими, но дозвуковыми скоростями  В этом случае "головной волны" перед трубкой нет, и если нет скачков уплотнения на участке поверхности трубки
В этом случае "головной волны" перед трубкой нет, и если нет скачков уплотнения на участке поверхности трубки  (смысл этой оговорки станет далее понятным), то можно применять формулы изэнтропичеекого движения. Таким образом найдем:
(смысл этой оговорки станет далее понятным), то можно применять формулы изэнтропичеекого движения. Таким образом найдем:

Регистрируя микроманометром отдельно давление  в динамическом и давление
в динамическом и давление  в статическом отверстии, определим число
в статическом отверстии, определим число  движущегося газа, а Зная температуру газа, найдем скорость звука а, в движущемся газе, а следовательно, и саму скорость
движущегося газа, а Зная температуру газа, найдем скорость звука а, в движущемся газе, а следовательно, и саму скорость  Измерение температуры можно производить, например, термопарой или другим термометрическим элементом, помещенным в такое место скоростной трубки или специального измерителя, где скорость равна нулю и можно быть уверенным, что измеряется температура изэнтропически заторможенного газа
Измерение температуры можно производить, например, термопарой или другим термометрическим элементом, помещенным в такое место скоростной трубки или специального измерителя, где скорость равна нулю и можно быть уверенным, что измеряется температура изэнтропически заторможенного газа  Таким местом является точка в лобовой части обтекаемого тела (например точка
Таким местом является точка в лобовой части обтекаемого тела (например точка  на скоростной трубке), где поток разветвляется, — так называемая критическая точка потока. Замеряя непосредственно
на скоростной трубке), где поток разветвляется, — так называемая критическая точка потока. Замеряя непосредственно  найдем
найдем  по ранее выведенной формуле:
по ранее выведенной формуле:

Определив  по формуле (79) и
по формуле (79) и  непосредственным замером, получим по
непосредственным замером, получим по  а следовательно, и скорость звука
а следовательно, и скорость звука

и искомую скорость

Показание давления  в динамическом отверстии
в динамическом отверстии  можно считать надежным, что же касается работы статического отверстия, то относительно него следует сделать оговорку. При достаточно больших, но меньших единицы значениях числа
можно считать надежным, что же касается работы статического отверстия, то относительно него следует сделать оговорку. При достаточно больших, но меньших единицы значениях числа  на сферической поверхности
на сферической поверхности
носика и за нею могут возникнуть зоны местных сверхзвуковых скоростей. Последующее уменьшение скорости вызовет возникновение на поверхности трубки перед статическим отверстием 5 скачков уплотнения и местные искажения Давления  Значение числа
Значение числа  набегающего потока, при котором на поверхности обтекаемого тела (в данном случае измерительной трубки) возникают сверхзвуковые зоны, называют критическим числом
набегающего потока, при котором на поверхности обтекаемого тела (в данном случае измерительной трубки) возникают сверхзвуковые зоны, называют критическим числом  и обозначают
и обозначают 
Если число  набегающего потока превосходит число
набегающего потока превосходит число  то пользование статическим отверстием становится ненадежным и необходимо каким-нибудь независимым путем определять давление
то пользование статическим отверстием становится ненадежным и необходимо каким-нибудь независимым путем определять давление  в движущемся газе, например, при движении газа по цилиндрической трубе измерять давление на стенке трубы в сечении, близком к носику скоростной трубки.
в движущемся газе, например, при движении газа по цилиндрической трубе измерять давление на стенке трубы в сечении, близком к носику скоростной трубки.

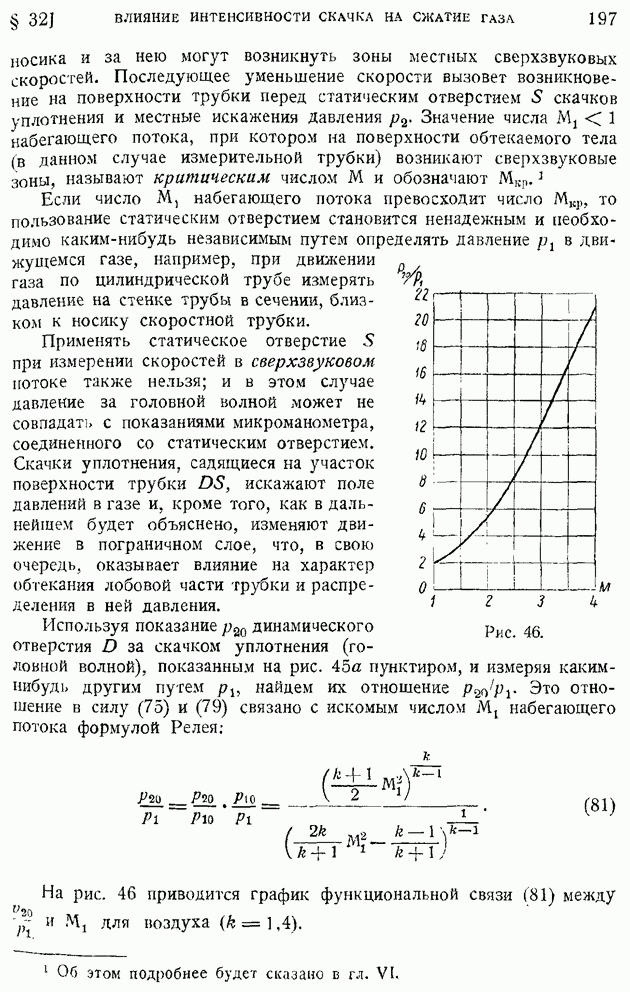
Рис. 46.
Применять статическое отверстие 5 при измерении скоростей в сверхзвуковом потоке также нельзя; и в этом случае давление за головной волной может не совпадать с показаниями микроманометра, соединенного со статическим отверстием. Скачки уплотнения, садящиеся на участок поверхности трубки  искажают поле давлений в газе и, кроме того, как в дальнейшем будет объяснено, изменяют движение в пограничном слое, что, в свою очередь, оказывает влияние на характер обтекания лобовой части трубки и распределения в ней давления.
искажают поле давлений в газе и, кроме того, как в дальнейшем будет объяснено, изменяют движение в пограничном слое, что, в свою очередь, оказывает влияние на характер обтекания лобовой части трубки и распределения в ней давления.
Используя показание  динамического отверстия
динамического отверстия  за скачком уплотнения (головной волной), показанным на рис. 45а пунктиром, и измеряя каким-нибудь другим путем
за скачком уплотнения (головной волной), показанным на рис. 45а пунктиром, и измеряя каким-нибудь другим путем  найдем их отношение
найдем их отношение  Это отношение в силу (75) и (79) связано с искомым числом
Это отношение в силу (75) и (79) связано с искомым числом  набегающего потока формулой Релея:
набегающего потока формулой Релея:

На рис. 46 приводится график функциональной связи (81) между  для воздуха
для воздуха 
Определив величину  по показанию динамического отверстия измерительной трубки, а
по показанию динамического отверстия измерительной трубки, а  например, при помощи отверстия в стенке канала, по которому движется газ, найдем отношение
например, при помощи отверстия в стенке канала, по которому движется газ, найдем отношение  а по графику рис. 46 — и искомое значение
а по графику рис. 46 — и искомое значение 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Предмет механики жидкости и газа. Основные свойства «макромодели» жидкости и газа: сплошность и подвижность
- § 2. Основные методы механики жидкости и газа. Области применения и главнейшие задачи
- § 3. Краткий очерк исторического развития механики жидкости и газа. От гидромеханики древних до установления воззрений ньютонианской эпохи
- § 4. Эпоха Эйлера и Бернулли. Гидроаэродинамика в XIX в.
- § 5. Современный этап развития механики жидкости и газа
- ГЛАВА I. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
- § 6. Поле физической величины. Скалярное и векторное поля. Поверхности уровня. Векторные линин и трубки
- § 7. Мера однородности поля в данном направлении и в дайной точке. Градиевт скалярного поля и дифференциальный тензор векторного поля как меры неоднородности поля
- § 8. Задание движения сплошной среды. Поле скоростей. Линии тока и траектории
- § 9. Поле ускорений. Разложение ускорения частицы на локальную и конвективную составляющие
- § 10. Скоростное поле сплошной среды в окрестности данной точки. Угловая скорость и вихрь. Тензор скоростей деформаций и его компоненты
- § 11. Скорость объемного расширения жидкости. Интегральные представления дифференциальных операторов поля. Основные интегральные формулы
- § 12. Вихревые линии и трубки. Вторая теорема Гельмгольца. Интенсивность вихревой трубки
- § 13. Выражение интенсивности вихревой трубки через циркуляцию вектора по контуру, охватывающему трубку. Теорема об изменении циркуляции скорости во времени
- ГЛАВА II. ОСНОВНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ И РАВНОВЕСИЯ СПЛОШНОЙ СРЕДЫ
- § 14. Распределение массы в сплошной среде. Плотность и удельный вес. Напряжения. Тензор напряженности и его симметричность
- § 15. Общие уравнения динамики сплошной среды. Уравнение неразрывности. Уравнения динамики в напряжениях
- § 16. Тепловые явления в жидкостях и газах. Закон сохранения энергии и уравнение баланса энергии
- § 17. Общие уравнения равновесного состояния жидкости и газа. Равновесие воздуха в атмосфере. Приближенные барометрические формулы. Стандартная атмосфера
- § 18. Равновесие несжимаемой жидкости. Уравнение поверхности раздела. Равновесие вращающейся жидкости
- § 19. Давление тяжелой несжимаемой жидкости на поверхность тела. Сила и момент, приложенные к телу, плавающему в тяжелой жидкости. Случай вращающейся жидкости
- ГЛАВА III. ДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ И ГАЗА. ОСНОВНЫЕ УРАВНЕНИЯ И ОБЩИЕ ТЕОРЕМЫ
- § 20. Идеальная жидкость. Основные уравнения движения
- § 21. Закон сохранения энергии в движущейся идеальной жидкости. Адиабатическое движение. Сохранение энтропии
- § 22. Эйлерово представление конвективного изменения объемного интеграла. Перенос величины сквозь контрольную поверхность
- § 23. Эйлерова форма законов сохранения массы и энергии, теоремы количеств движения и момента количеств движения при стационарном движении идеальной жидкости
- § 24. Теорема об изменении кинетической энергии. Работа и мощность внутренних сил. Эйлерова форма уравнения изменения кинетической энергии
- § 25. Теорема Бернулли о сохранении полной механической энергии при стационарном баротропном движении идеальной жидкости и газа
- ГЛАВА IV. ОДНОМЕРНЫЙ ПОТОК ИДЕАЛЬНОЙ ЖИДКОСТИ
- § 26. Одномерное течение идеальной сжимаемой жидкости. Линеаризированные уравнения. Скорость распространения малых возмущений в жидкости или газе
- § 27. Изотермическая и адиабатическая скорости звука. «Конус возмущений» при сверхзвуковом движении источника возмущения. Число M и его связь с углом конуса возмущений
- § 28. Распространение непрерывных возмущений конечной интенсивности. Характеристики. Образование разрывной ударной волны
- § 29. Стоячая ударная волна или скачок уплотнения. Ударная адиабата
- § 30. Критические величины в одномерном потоке газа. Связь между скоростями до и после скачка. Изменение давления, плотности и температуры в скачке уплотнения
- § 31. Скорость распространения ударной волны. Спутное движение газа за ударной волной
- § 32. Влияние интенсивности скачка уплотнения на сжатие газа. Измерение скоростей и давлений в до- и сверхзвуковых потоках
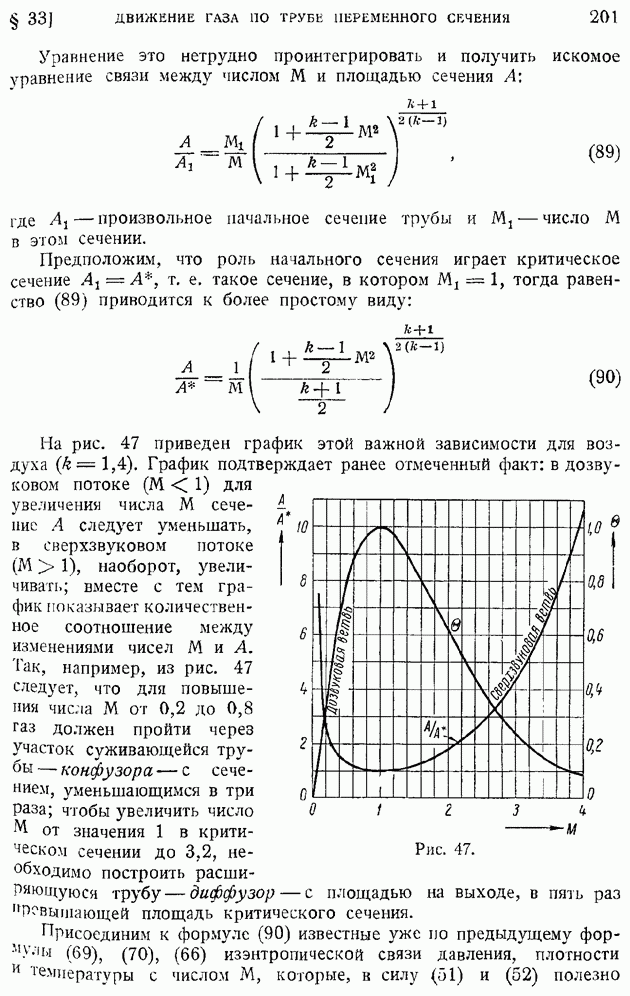
- § 33. Одномерное движение газа по трубе переменного сечения. Истечение из резервуара большой емкости сквозь сходящееся сопло
- § 34. Одномерное течение в сопле Лаваля. Движение газа с притоком тепла
- ГЛАВА V. БЕЗВИХРЕВОЕ ДВИЖЕНИЕ ЖИДКОСТИ. ПЛОСКОЕ ДВИЖЕНИЕ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 35. Сохранение циркуляции скорости в потоке идеальной жидкости. Теорема Кельвина и Лаграижа. Безвихревое движение. Потенциал скоростей
- § 36. Интеграл Лагранжа — Коши уравнений безвихревого движения. Теорема Бернулли. Некоторые общие свойства безвихревого движения идеальной несжимаемой жидкости в односвязной области
- § 37. Плоское безвихревое движение несжимаемой жидкости. Потенциал скоростей и функция тока. Применение функций комплексного переменного. Комплексный потенциал и сопряженная скорость
- § 38. Построение полей течения по заданной характеристической Функции. Простейшие плоские потоки и их наложение
- § 39. Бесциркуляционное и циркуляционное обтекания круглого цилиндра
- § 40. Применение криволинейных координат. Бесциркуляционное и циркуляционное обтекания эллиптического цилиндра и пластинки. Задача Жуковского об обтекании решетки пластин.
- § 41. Плоское движение с отрывом струй. Разрывное обтекание пластинки и протекание жидкости сквозь отверстие
- § 42. Прямая задача в теории плоского движения идеальной несжимаемой жидкости. Применение метода конформных отображений. Гипотеза Чаплыгина о безотрывном обтекании задней кромки профиля. Формула циркуляции
- § 43. Теорема Жуковского о подъемной силе крыла. Зависимость подъемной силы от угла атаки. Коэффициент подъемной силы
- § 44. Применение метода комплексных переменных к выводу теоремы Жуковского. Формулы Чаплыгина для главного вектора и момента сил давления потока на крыло
- § 45. Выражение главного момента сил давления потока через коэффициенты конформного отображения. Фокус крыла. Независимость от угла атаки момента относительно фокуса. Парабола устойчивости
- § 46. Частные случаи конформного отображения крылового профиля на круг. Преобразование Жуковского-Чаплыгина. Теоретические крыловые профили
- § 47. Задача об обтекании слабо изогнутой дужки произвольной формы (теория тонкого крыла)
- § 48. Определение обтекания крылового профиля произвольной формы
- § 49. Обобщение теоремы Жуковского на случай плоской решетки с бесчисленным множеством профилей
- ГЛАВА VI. ПЛОСКОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ СЖИМАЕМОГО ГАЗА
- § 50. Основные уравнения плоского стационарного безвихревого движения сжимаемого газа. Линеаризированные уравнения
- 51. Линеаризированный до- и сверхзвуковой газовый поток вдоль волнистой стенки
- § 52. Тонкое крыло в линеаризированном до- и сверхзвуковом потоках. Влияние сжимаемости газа на коэффициент подъемной силы в дозвуковом потоке. Коэффициенты подъемной силы и волнового сопротивления при сверхзвуковом потоке
- § 53. Нелинеаризированные уравнения движения идеального сжимаемого газа. Переход в плоскость годографа. Уравнения Чаплыгина
- § 54. Метод С. А. Христиановича. Приближенные формулы учета влияния сжимаемости на распределение давления
- § 55. Критическое число M и его определение по заданному распределению давления в несжимаемом обтекании. Поведение коэффициента подъемной силы и момента при около- и закритических значениях числа M
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
- § 57. Нелинеаризированный сверхзвуковой поток. «Характеристики» уравнений плоского сверхзвукового потока. Линин возмущения и их основные свойства
- § 58. Обтекание выпуклого угла сверхзвуковым потоком. Влияние угла поворота струи на ее газодинамические элементы
- § 59. Сверхзвуковой поток внутри тупого угла. Косой скачок уплотнения. Связь между газодинамическими элементами до и за косым скачком
- ГЛАВА VII. ПРОСТРАНСТВЕННОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ
- § 60. Ортогональные криволинейные координаты в пространстве. Основные дифференциальные операторы поля в криволинейных координатах
- § 61. Потенциал скоростей. Поле источника и диполя. Непрерывное распределение источников и диполей. Ньютонов потенциал. Потенциал простого и двойного слоев
- § 62. Поле скоростей вокруг заданной системы вихрей. Формула Био — Савара. Потенциал скоростей замкнутой вихревой нити. Аналогия с потенциалом двойного слоя
- § 63. Функция тока и ее связь с векторным потенциалом скоростей. Функции тока простейших течений
- § 64. Обтекание сферы. Давление однородного стационарного потока идеальной несжимаемой жидкости на погруженное в нее тело. Парадокс Даламбера
- § 65. Общие уравнения осесимметричного движения. Применение цилиндрических координат. Течение сквозь каналы
- § 66. Осесимметричное продольное обтекание тел вращения. Случай эллипсоида вращения
- § 67. Поперечное обтекание тел вращения. Пример эллипсоида вращения
- § 68. Продольное и поперечное обтекание тел вращения большого удлинения. Приближенные выражения граничных условий. Применение тригонометрических сумм для определения коэффициентов …
- § 69. Метод «особенностей». Применение непрерывно распределенных источников (стоков) и диполей для решения задачи о продольном и поперечном обтекании тел вращения
- § 70. Общий случай движения твердого тела сквозь несжимаемую идеальную жидкость. Определение потенциала скоростей. Главный вектор и главный момент сил давления потока на тело
- § 71. Коэффициенты «присоединенных масс». Свойство симметрии. «Присоединенная» кинетическая энергия. Определение «присоединенных масс» поступательно движущегося цилиндра, шара и эллипсоида
- § 72. Элементы теории крыла конечного размаха. Вихревая система крыла. Гипотеза плоских сечеиий. Геометрические и действительные углы атаки. Подъемная сила и «индуктивное сопротивление»
- § 73. Основные формулы теории «несущей линии». «Индуктивная скорость» и «индуктивный угол». Прямая задача определения подъемной силы и индуктивного сопротивления по заданному распределению циркуляции
- § 74. Крыло с минимальным индуктивным сопротивлением. Эллиптическое распределение циркуляции. Связь между коэффициентами индуктивного сопротивления и подъемной силы. Основное уравнение теории крыла и понятие о его интегрировании
- ГЛАВА VIII. ДИНАМИКА ВЯЗКОЙ ЖИДКОСТИ И ГАЗА
- § 75. Внутреннее трение и теплопроводность в жидкостях и газах. Законы Ньютона и Фурье. Влияние температуры на коэффициенты вязкости и теплопроводности. Число «сигма»
- § 76. Обобщение закона Ньютона на случай произвольного движения среды. Закон линейной связи между тензорами напряжений и скоростей деформации
- § 77. Общие уравнения движения вязкой жидкости. Динамические уравнения и уравнение баланса энергии. Граничные условия движения жидкости с треннем и теплопроводностью
- § 78. Понятие о подобии гидродинамических явлений. Безразмерные уравнения движения вязкой жидкости и газа. Условия подобия
- § 79. Ламинарное движение вязкой несжимаемой жидкости по цилиндрической трубе
- § 80. Обтекание шара при очень малых значениях числа Рейнольдса. Формула сопротивления шара по Стоксу и ее обобщения
- § 81. Вихревые линии в идеальной и вязкой жидкости. Сохраняемость вихревых линий при отсутствии внутреннего трения. Диффузия вихря в вязкой жидкости
- § 82. Одномерное прямолинейное движение сжимаемого вязкого газа. Движение внутри скачка уплотнения. Понятие о толщине скачка
- § 83. Работа внутренних сил и диссипация механической энергии в движущейся вязкой среде
- § 84. Обтекание тел жидкостью и газом при больших значениях числа Рейнольдса. Основные уравнения теории ламинарного пограничного слоя
- § 85. Ламинарный пограничный слой на пластинке, продольно обтекаемой несжимаемой жидкостью. Неизотермическое движение
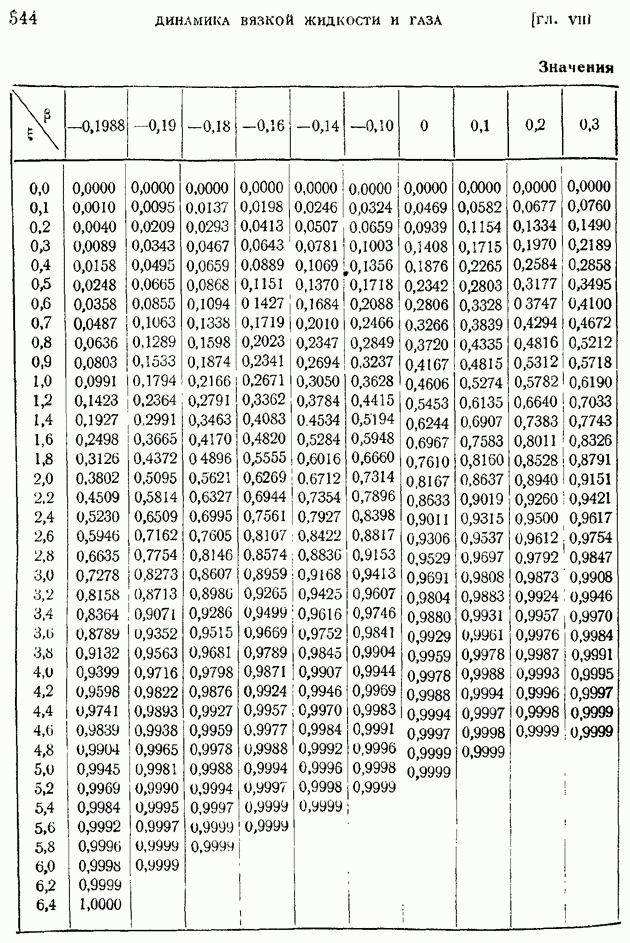
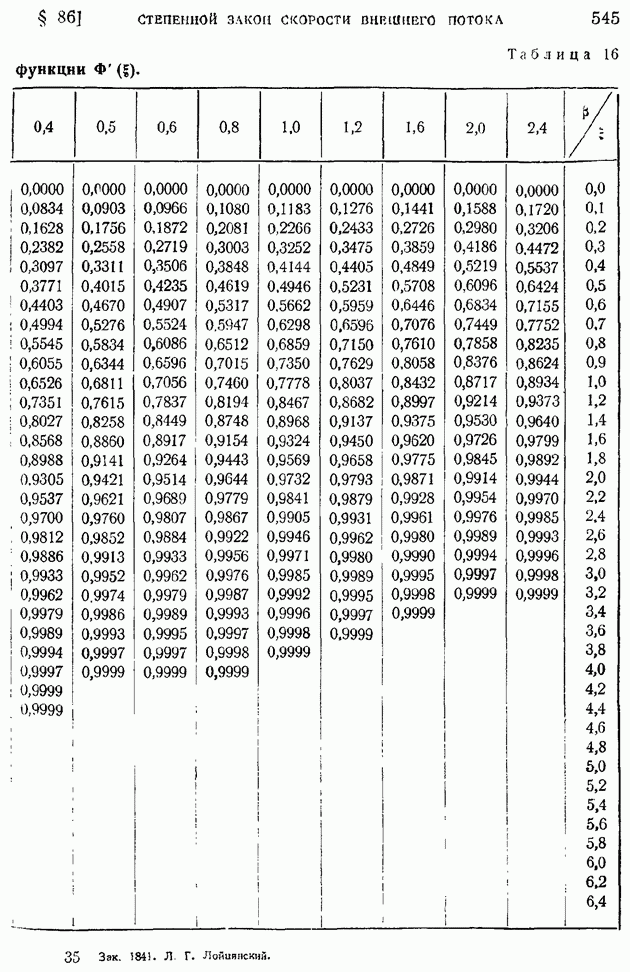
- § 86. Ламинарный пограничный слой при степенном задании скорости внешнего потока
- § 87. Ламинарный пограничный слой в общем случае задания скорости внешнего потока. Применение уравнения импульсов для приближенного расчета ламинарного пограничного слоя
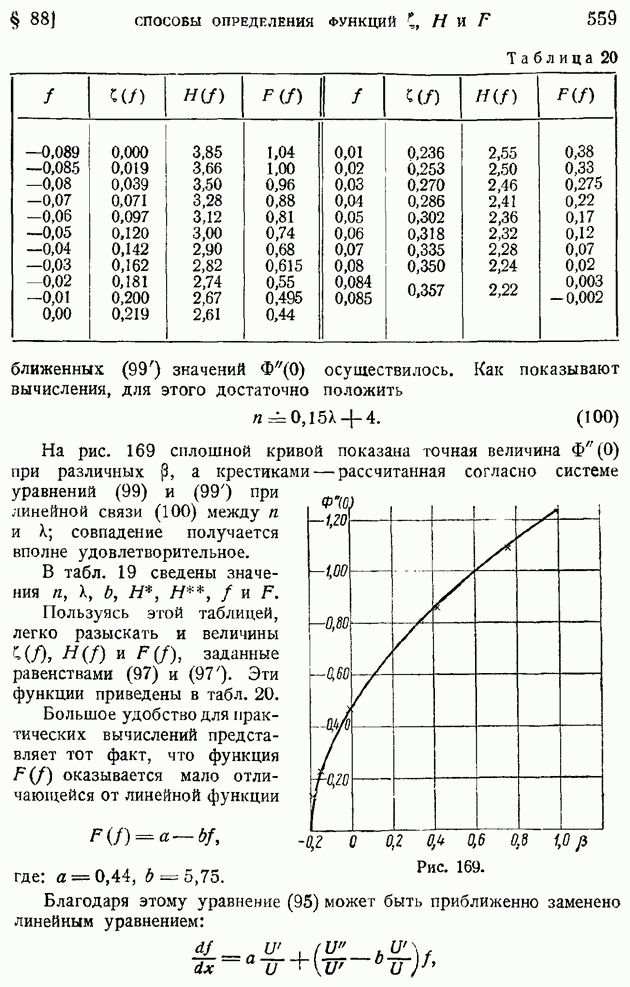
- § 88. Способы определения функций … Приближенный метод расчета ламинарного пограничного слоя
- § 89. Ламинарный пограничный слой на пластинке, продольно обтекаемой сжимаемым газом при больших скоростях. Случай линейной зависимости коэффициента вязкости от температуры (n = 1)
- § 90. Ламинарный пограничный слой на пластинке при любом законе связи между вязкостью и температурой и при числе … Обтекание крылового профиля потоком больших скоростей
- ГЛАВА IX. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ
- § 91. Переход ламинарного движения в турбулентное. Критическое рейнольдсово число
- § 92. Область и «точка» перехода. Явление «кризиса обтекания»
- § 93. Основные уравнения осреднеиного турбулентного движения. Тензор турбулентных напряжений
- § 94. Турбулентное движение жидкости в плоской и круглой трубе. Логарифмические формулы скоростей
- § 95. Формулы сопротивления гладких труб при турбулентном движении жидкости. Ламинарный подслой
- § 96. Влияние шероховатости стенок трубы на ее сопротивление. Предельные режимы течения. Режим установившейся шероховатости
- § 97. Турбулентный пограничный слой на продольно обтекаемой пластине. Сопротивление пластины
- § 98. Турбулентный пограничный слой на крыловом профиле при малом продольном перепаде давлений
- § 99. Турбулентный пограничный слой на крыловом профиле при значительных продольных перепадах давления
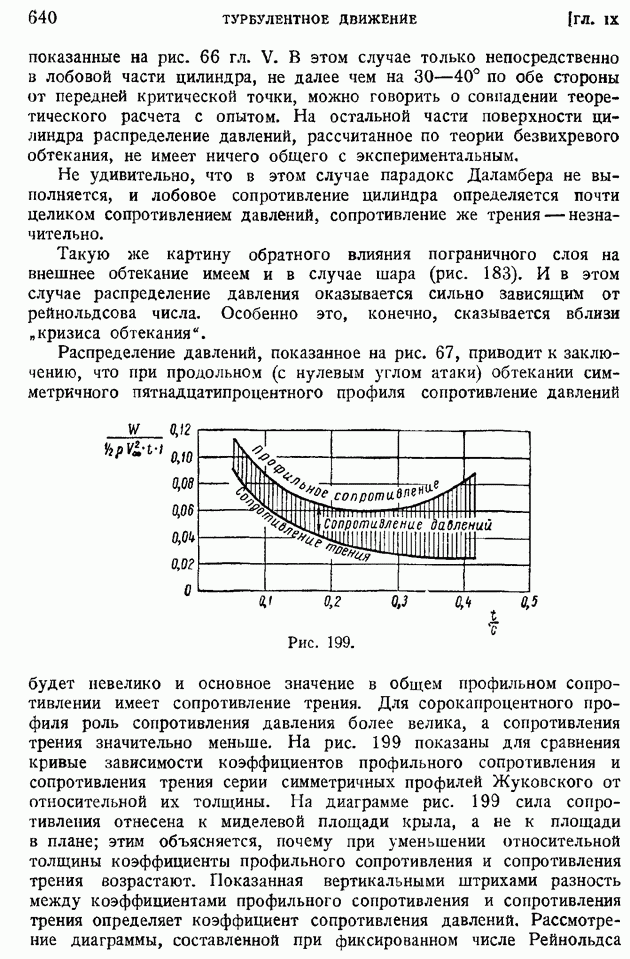
- § 100. Профильное сопротивление крыла. Разложение профильного сопротивления на сопротивление трения и сопротивление давлений. Обратное влияние пограничного слоя на распределение давлений по поверхности обтекаемого профиля
- § 101. Приближенные формулы профильного сопротивления крыла и крылового профиля в решетке
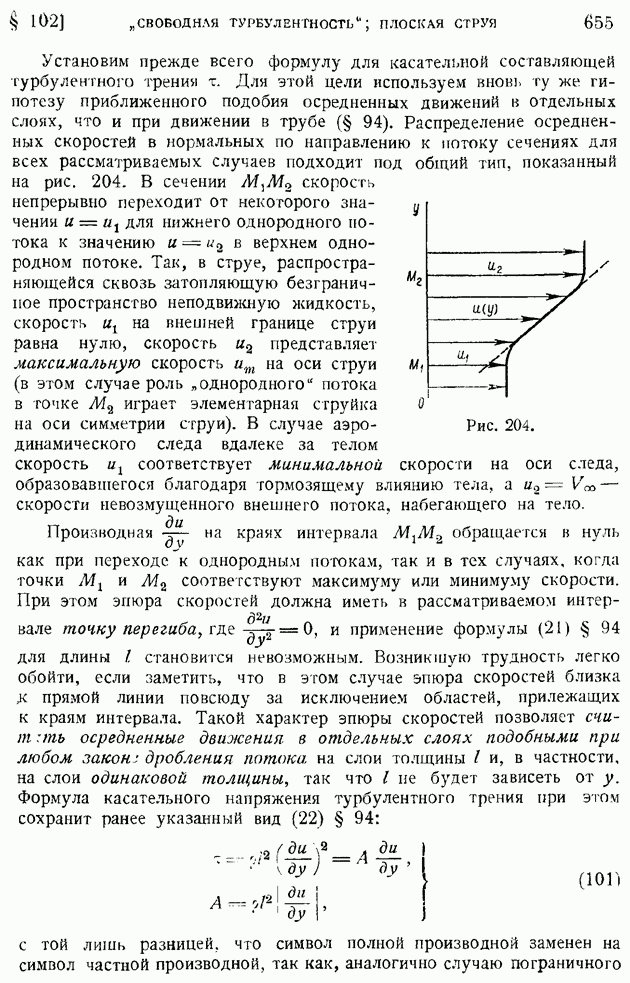
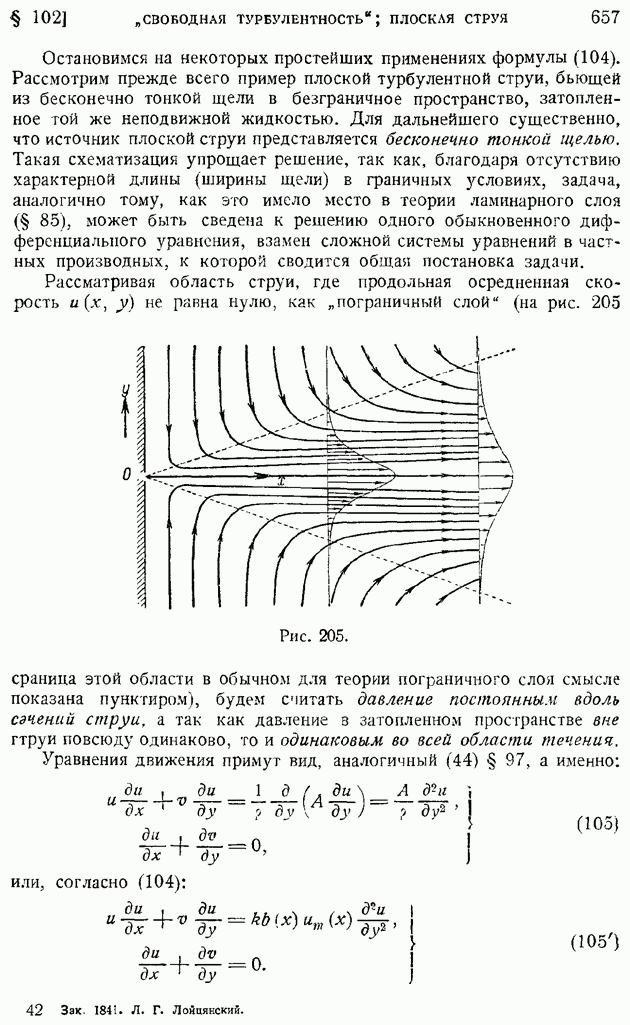
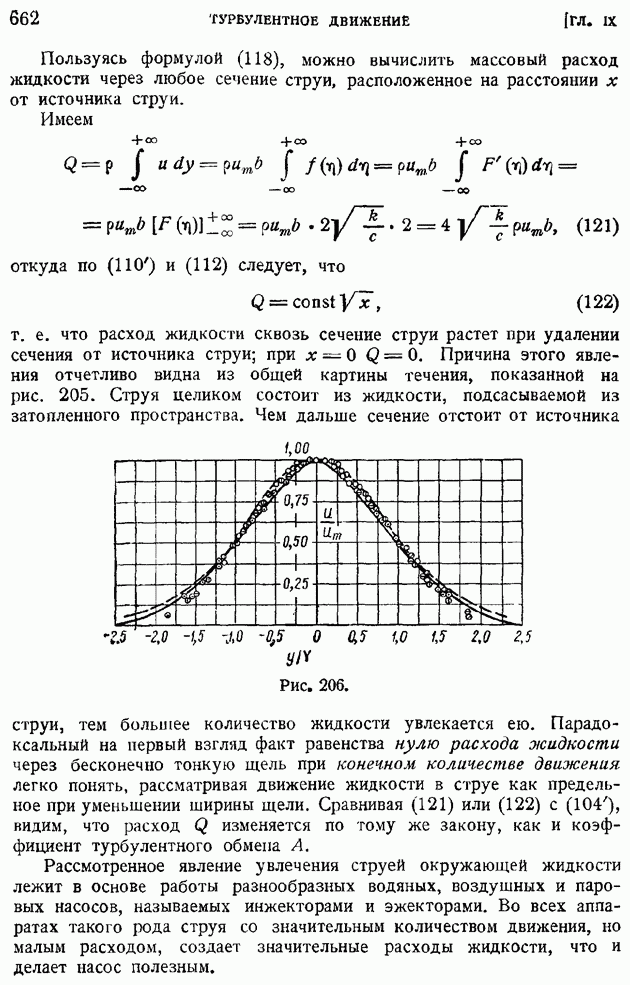
- § 102. Основные закономерности «свободной турбулентности». Плоская турбулентная струя в пространстве, заполненном той же жидкостью
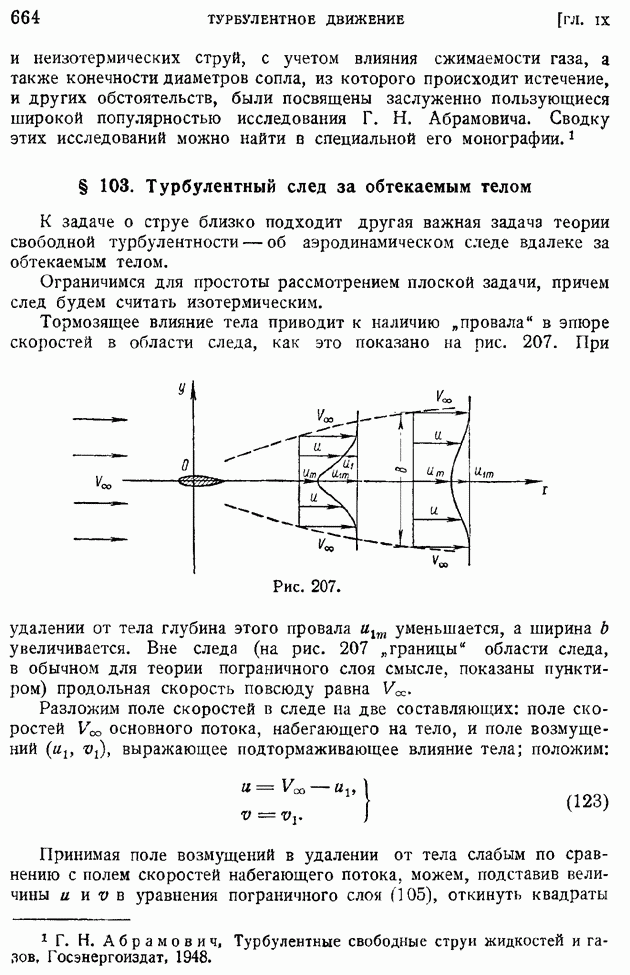
- § 103. Турбулентный след за обтекаемым телом
- § 104. Рассеяние турбулентных возмущений в жидкости. Случай изотропной и однородной турбулентности. Закон сохранения момента возмущений