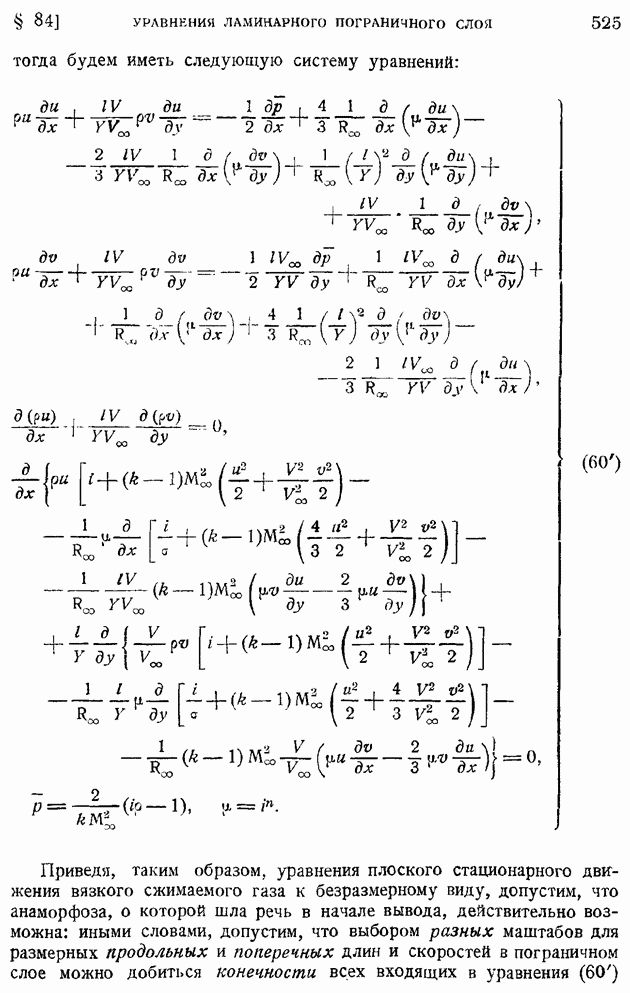| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. Эпоха Эйлера и Бернулли. Гидроаэродинамика в XIX в.
Фундаментальные открытия Галилея, Гюйгенса и Ньютона, приведшие к небывалому расцвету общей механики в конце XVII в., подготовили все предпосылки к мощному скачку в развитии механики жидкости и газа. Особенное значение имело установление Ньютоном основных законов и уравнений динамики. Отныне и гидродинамика начинает переходить от рпссмотрения отдельных, подчас не связанных
между собою, задач к систематическому изложению своих специфических законов и методов, что превращает ее в самостоятельный раздел механики.
Честь создания теоретической гидродинамики, как специальной науки с широкими задачами и строгими методами их разрешения, принадлежит Российской Академии наук в лице ее двух академиков — Леонарда Эйлера (1707—1783) и Даниила Бернулли (1700—1783). За краткостью очерка остановимся лишь на самых главных достижениях этих двух основоположников механики жидкости.
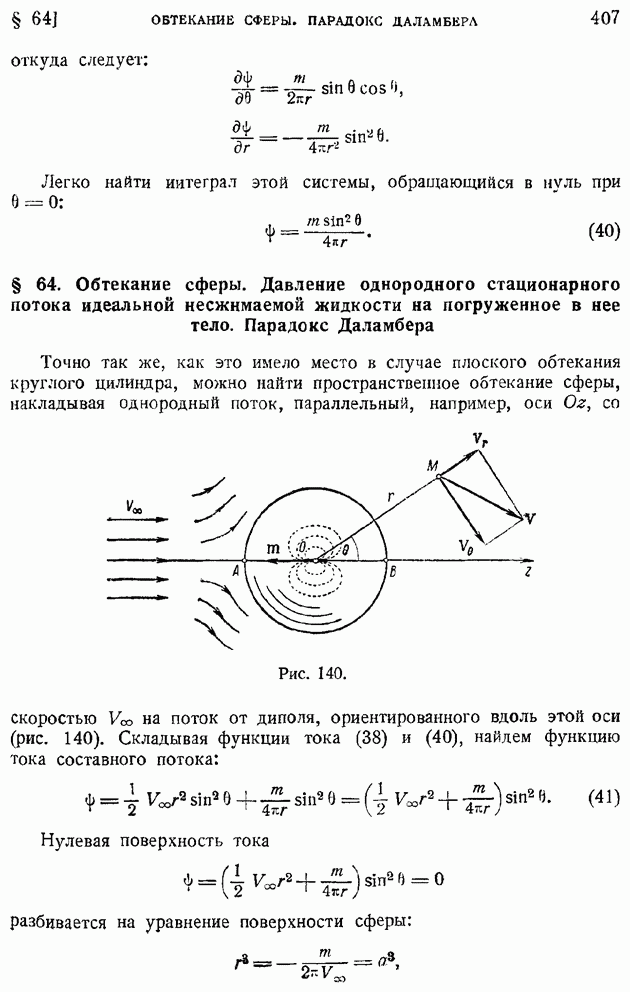
В своем трактате "Общие принципы движения жидкостей" (1755) Эйлер первый вывел основную систему уравнений движения идеальной жидкости, положив начало аналитической механике сплошной среды. Эйлеру гидродинамика обязана введением понятия давления и противопоставлением этого понятия ньютонианским "ударам" частиц жидкости о поверхность тела. Следует заметить, что и в настоящее время часто приходится встречаться с неправильными воззрениями на этот счет; стоит поэтому вспомнить слова Эйлера относительно того, что жидкость "до достижения тела изменяет свое направление и скорость так, что, подходя к телу, протекает мимо него вдоль его поверхности и не прилагает к телу никакой другой силы, кроме давления, соответствующего отдельным точкам соприкосновения" (курсив наш). Эйлеру принадлежит первый вывод уравнения сплошности жидкости (в частном случае движения жидкости по трубе этот закон был дан задолго до Эйлера в 1628 г. Кастелли — учеником Галилея), своеобразная и ныне общепринятая формулировка теоремы об изменении количества движения применительно к жидким и газообразным средам, вывод знаменитого «турбинного уравнения", создание теории реактивного колеса Сегнера и мн. др. Велика роль Эйлера в продолжающейся дискуссии о происхождении сопротивления. Эйлер совершенно отчетливо показывает значение понятия давления и разъясняет парадокс Даламбера о равенстве нулю равнодействующей сил давления идеальной жидкости на плавно обтекаемое тело, подчеркивая отличие действительной жидкости
Леонард Эйлер (1707— 1783)
с внутренним трением в ней от идеальной. "Если некоторые люди увлекутся и будут думать, — говорит Эйлер, — что можно продвигать тела через жидкость, не встречая сопротивления, так как сила, с которою жидкость действует на переднюю часть тела, будет уничтожаться действием такой же силы на зяднюю часть, что не имеет места при течении действительных жидкостей, то такой вывод будет неправилен" (курсив наш). В ряде своих работ Эйлер отмечает влияние трения в действительных жидкостях на создание сопротивления — взгляд, который лег в основу позднейших работ XIX в. и полностью оправдан современной механикой жидкости и газа.
Роль Эйлера как основоположника теоретической гидродинамики, предопределившего своими исследованиями развитие гидродинамики более чем на столетие вперед, в настоящее время общепризнана. Можно с удовлетворением отметить, что этот мощный скачок, подготовленный накопленными теоретическими и экспериментальными достижениями ньютоновского и посленьютоновского периодов, был осуществлен выдающимся ученым, вся жизнь и научная деятельность которого была тесно связана с Российской Академией наук, ныне Академией наук СССР. Приехав в Россию в двадцатилетнем возрасте, швейцарец Эйлер отдал Петербургской Академии всю силу молодого таланта, способствуя гениальными исследованиями поднятию научного авторитета тогда еще молодой Академии своей второй родины. В мрачную эпоху "бироновщины", когда Академия засорилась чужестранными авантюристами и лжеучеными, с которыми смело боролся М. В. Ломоносов, Эйлер решил временно уехать из России. Однако Эйлер не порывает с Петербургом, печатает в академических изданиях свои фундаментальные сочинения по основам гидродинамики, по теории реактивного сегнерова колеса и др., помогает М. В. Ломоносову, другом и защитником которого он всегда был, бороться с иностранной кликой и, наконец, в 1761 г. возвращается в Петербург, где продолжает плодотворно работать до самой смерти.
Забегая несколько вперед, отметим, что второй мощный скачок в развитии механики жидкости и газа, приведший к созданию теоретической аэродинамики, был столетие спустя произведен великими нашими соотечественниками Н. Е. Жуковским и С. А. Чаплыгиным.
Рядом с Эйлером должно быть поставлено имя другого выдающегося механика, петербургского академика Даниила Бернулли, выходца из Голландии, сына знаменитого математика Иоганна Бернулли.
Наибольшее значение для развития механики жидкости и газа имел замечательный трактат Бернулли "Гидродинамика" — "академический труд, выполненный автором во время работы в Петербурге", как
значится на титульном листе этой книги, опубликованной в 1738 г. С выходом этого трактата связано, между прочим, появление термина гидродинамика".
Основываясь на законе сохранения "живой силы", открытом для частного случая колебания маятника еще Гюйгенсом и получившем широкое распространение в первой половине XVIII в., Бернулли излагает в "Гидродинамике" свою знаменитую теорему, устанавливающую общую связь между давлением, высотой и скоростью движения жидкости. Теорема эта, частный случай которой был указан Торичелли (1608—1647) в 1644 г., в настоящее время является фундаментальной теоремой гидродинамики, обобщенной в XIX в. на случай сжимаемого газа.
Согласно теореме Бернулли, в тех точках потока, где понижается скорость, должно возрастать давление — результат, который вначале казался парадоксальным. Действительно, в это же время в связи как с ньютоновскими воззрениями на давление жидкости на обтекаемое тело, так и с исследованиями самого Бернулли о давлении жидкости на преграду, прочно установился как будто противоположный взгляд о возрастании давления жидкости с возрастанием ее скорости. Эйлер, которому, кстати говоря, мы обязаны современной формулировкой теоремы Бернулли (напоминаем, что Эйлер первый ввел в гидродинамику четкое понятие давления), пояснил кажущуюся парадоксальность теоремы Бернулли следующими словами: "вся сложность понимания этого предложения устраняется, если считать, что здесь сравнение производится не между скоростями двух разных течений, а между разными скоростями вдоль данной струи, которая обтекает поверхность тела" (курсив наш) — пояснение, заслуживающее быть приведенным в любом современном руководстве по гидродинамике.
Великий русский ученый М. В. Ломоносов (1711—1765), современник Эйлера и Бернулли, еще в сороковых годах XVIII столетия Сложил основы учения об упругости газов и теплоте, высказав
глубокие мысли о физической структуре газа и кинетической природа происходящих в нем процессов. Вместе с тем М. В. Ломоносов много сделал для развития изучения верхних слоев атмосферы, не только самолично изобретая необходимые приборы (например, анемометр), но и создавая смелые проекты летательных аппаратов для исследования атмосферы.
В развитии аналитической механики жидкости и газа большую роль сыграл также Даламбер (1717 — 1783), применивший к сплошным средам свой знаменитый общий принцип, и поныне носящий его имя. "Парадокс" Далгмбера, о котором уже неоднократно была речь выше, появился в свет в 1744 г. в "Трактате о равновесии и движении жидкости". Сам Даламбер не дал удовлетворительного объяснения обнаруженному им факту отсутствия сопротивления тел при теоретическом его определении. "Странный парадокс, объяснение которого предоставляю математикам", — пишет Даламбер.
Даламбер возглавлял обширные экспериментальные исследования сопротивления тел, предпринятые им в связи с задачей о сопротивлении кораблей в каналах. Эти опыты подтвердили квадратичную зависимость сопротивления от скорости движения тела, пропорциональность сопротивления тела площади его миделевого сечения, мялое влияние вязкости жидкости на сопротивление при больших скоростях и мн. др.
Работы Эйлера, Бернулли и Далаыбера завершили большой этап развития гидродинамики идеальной жидкости, приведший к почти законченному формированию этого основного раздела механики жидкости и газа. Лагранж (1736—1813) в своих гидродинамических работах усовершенствовал методы Эйлера и Даламбер  дальнейшее развитие аналитическим методам гидродинамики.
дальнейшее развитие аналитическим методам гидродинамики.
Следующий этап истории механики жидкости и газа, относящийся уже главным образом к XIX в., знаменуется, с одной стороны, дальнейшей математической разработкой гидродинамики идеальной жидкости, в частности, решением таких задач ее, как плоское и пространственное безвихревое движение, струйное разрывное движение, вихревое движение, волновое движение тяжелой жидкости, с другой — зарождением двух новых разделов, имеющих особое значение для современной гидроаэродинамики: динамики вязкой жидкости и газовой динамики.
Простейшим и наиболее глубоко и всесторонне изученным случаем интегрирования уравнений Эйлера для несжимаемой жидкости является так называемое безвихревое движение с потенциалом скоростей. Понятие потенциала скоростей было введено самим Эйлером. Лагранж в 1781 г. первый нашел те динамические условия, при выполнении которых будет существовать безвихревое движение с потенциалом скоростей. Теорема Лагранжа, лежащая в основе всей теории безвихревого течения и оправдывающая практическое применение теории, Гагранжа в 1815 г. более строго доказана Коши (1789—1857),
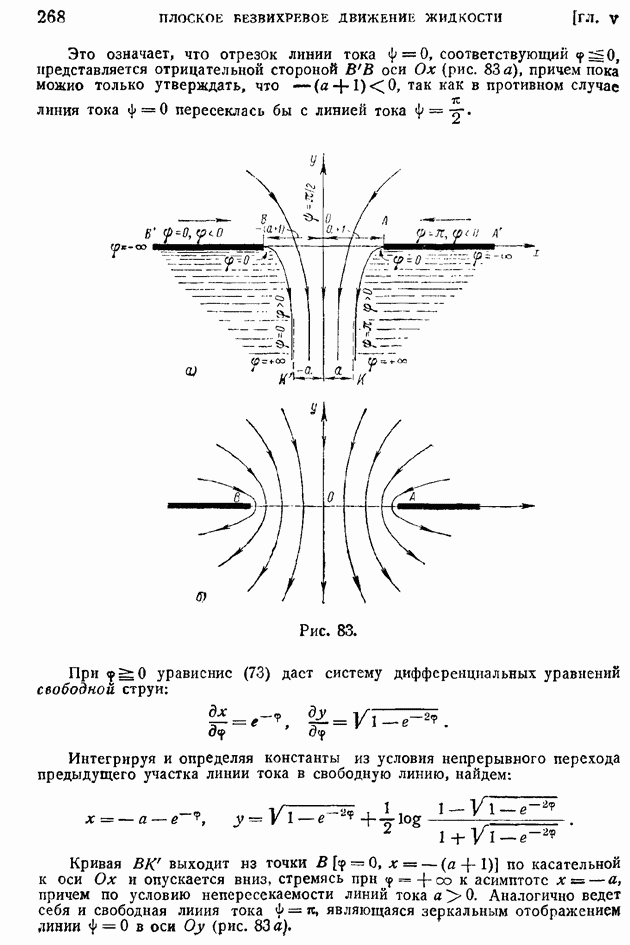
Наибольший интерес представляет плоское безвихревое движение, для которого, кроме потенциала скоростей, существует еще функция тока, введенная впервые Лагранжем в 1781 г.; кинематическая интерпретация функции тока, связанная с понятием линии тока, была дани значительно позднее (в 1864 г.) Рэнкиным. Наличие этих двух функций — потенциала скоростей и функции тока, удовлетворяющих в отдельности уравнениям Лапласа, позволило свести решение гидродинамической задачи к разысканию одной комплексной функции — комплексного потенциала. Подробное изложение этого метода, весьма близкого к современному, можно найти в двадцать первой лекции классических "Лекций по математической физике" (ч. 1, Механика) Кирхгоффа (1876). Отдельные задачи плоского безвихревого потока решались и ранее самим Кирхгоффом в 1845 г. и Гельмгольцем в 1868 г. Заметим, что с математической стороны эти задачи эквивалентны аналогичным задачам электростатики. Наряду с плоским стационарным безвихревым движением были изучена некоторые простейшие задачи нестационарного двюкения (Рэлей в 1878 г., Лэмб в 1875 г. и др.). Особенно больших успехов метод комплексной переменной достиг в теории обтекания тел со срывом струй, созданной трудами Гельмгольца, Кирхгоффа и Жуковского. Подлинного своего расцвета плоская задача безвихревого стационарного и нестационарного движения достигла в первую четверть нашего столетия в замечательных работах ученых московской школы, о чем еще будет речь впереди.
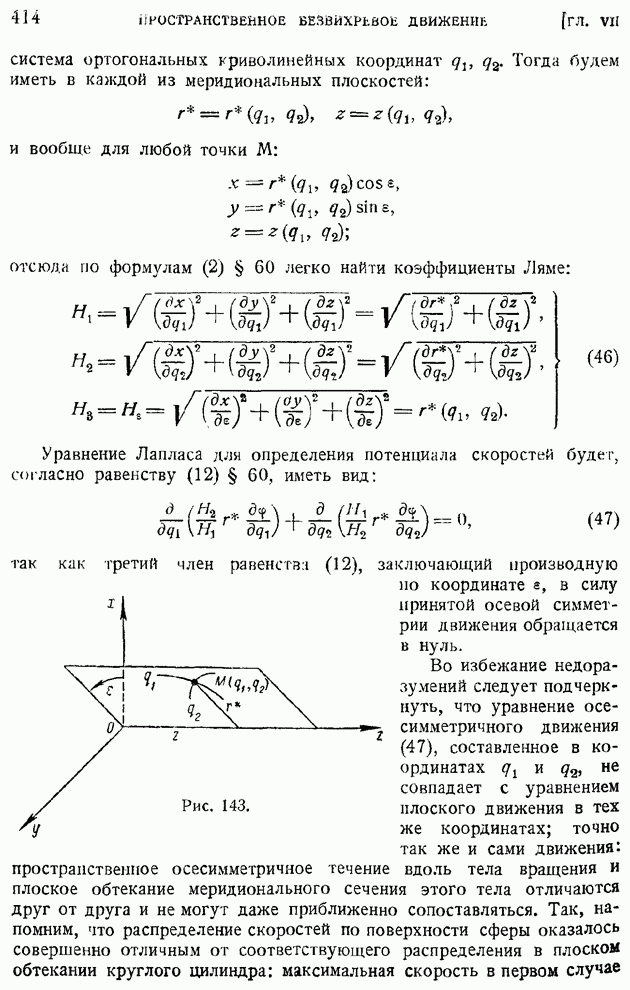
Пространственная задача о движении несжимаемой жидкости с потенциалом скоростей исследовалась параллельно с плоской. Отсутствие в пространстве комплексного переменного привело к необходимости непосредственного решения уравнения Лапласа при заданных граничных, а в случае нестационарного движения, и начальных условиях. Пространственная задача развивалась в тесном контакте с близкими ей задачами теории потенциала. Первая задача о пространственном безвихревом обтекании тела (шара) была разрешена Пуассоном в 1828 г. и затем обобщена и уточнена Стоксом в 1843 г. и Лежен — Дирихле в 1852 г. Безвихревое течение несжимаемой жидкости в эллипсоидальном сосуде и обтекание эллипсоида при поступательном и вращательном его движении было изучено в период 1843-1883 гг. целым рядом ученых, в числе которых можно отметить Клебша, Бельтрами, Грина и др.
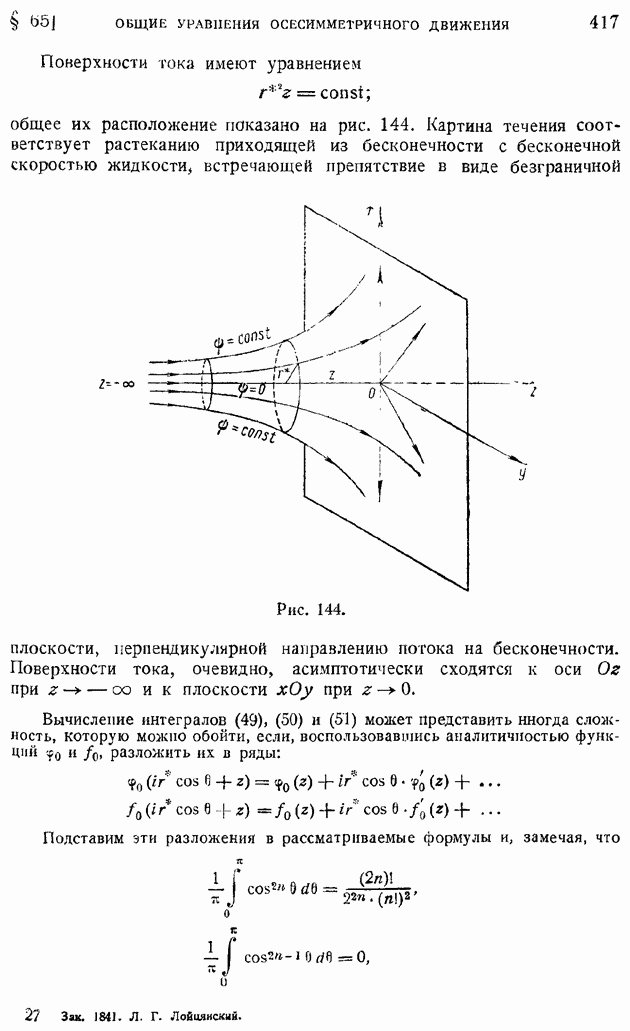
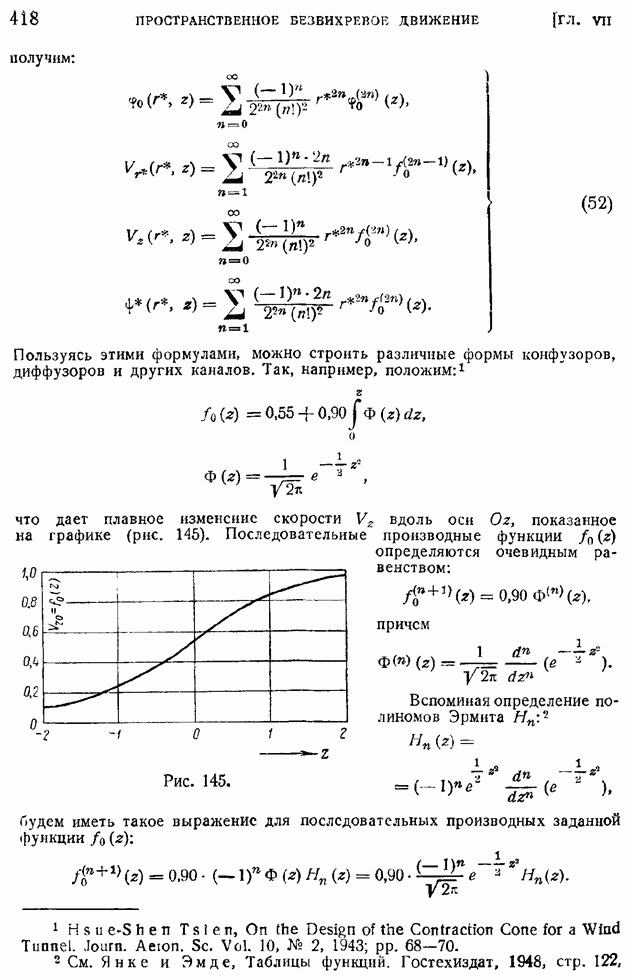
Продольное обтекание осесимметричных тел, для которого, как показал Стоке еще в 1842 г., существует функция тока, допускает приближенное исследование простым методом наложения однородного поступательного потока на систему источников, стоков или диполей; метод этот, иногда называемый "методом особенностей", был предложен впервые Рэнкиным в 1868 г. и получил широкое распространение.
Общая теория движения твердого тела в жидкости была дана кирхгоффом в 1869 г. и изложена в его ранее уже упомянутых
"Лекциях". Теория эта является одним из наиболее изящных разделов аналитической механики.
Фундаментальные результаты в этой области принадлежат русским ученым, в числе которых такие всемирно известные имена, как Н. Е. Жуковский и С. А. Чаплыгин, А. М. Ляпунов и В. А. Стеклов; С. А. Чаплыгин дал движению твердого тела в жидкости геометрическую интерпретацию, не уступающую по глубине и наглядности классической интерпретации Пуансо движения твердого тела по инерции в пустоте.
В разработке теории движения твердого тела в жидкости принимали участие крупнейшие зарубежные ученые XIX в.: Томсон и Тэт, Максвелл, Клебш и др.
Два новых существенных раздела гидродинамики идеальной жидкости: волновое и вихревое движения — были созданы в рассматриваемый период времени. Теория волнового движения развивалась главным образом в связи с вопросами качки волнового сопротивления корабля, а также теории приливных волн в каналах и реках.
Первые исследования, связанные с приближенной теорией "длинных" волн на поверхности тяжелой жидкости, принадлежат Лагранжу и относятся к 1781 г.; имя Лагранжа носит основное дифференциальное уравнение распространения волн и первая формула скорости их распространения. Классическим мемуаром, содержащим строгую теорию волн малой амплитуды, является появившийся в 1815 г. мемуар Коши. Среди лиц, способствовавших развитию теории волн малой амплитуды, мы находим имена Лапласа, Пуассона, Эри, Стокса, Рэнкина и др. Теорию волнового сопротивления дал Митчелл и, независимо от него, несколько позднее — Н. Е. Жуковский.
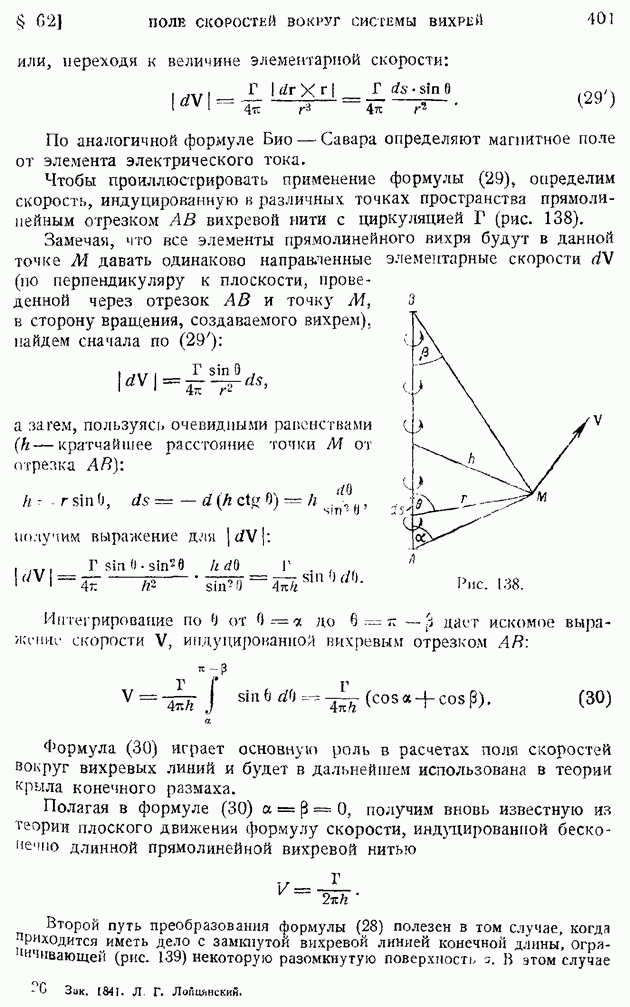
Во второй половине XIX в. появилось учение о вихревом движении жидкости, создателем которого справедливо считают Гельмгольца, указавшего в 1858 г. основные свойства вихрей в идеальной жидкости. Само понятие вихря и его интерпретация, как угловой скорости вращения жидкого элемента в целом, были даны раньше: Коши в 1815 г. и Стоксом в 1847 г.; возможность движения без потенциала скоростей была указана Эйлером еще в 1775 г. Теория вихрей имеет обширную литературу, в которой тесно переплетаются вопросы гидродинамики с аналогиями в области электричества и магнетизма. Магнитные линии вокруг электрического проводника эквивалентны линиям тока вокруг вихревой нити (теорема Био - Савара служит основой как для расчета движения жидкости вокруг вихревых линий, так и для расчета магнитного поля вокруг электрического тока). Теория вихрей сыграла большую роль в развитии динамики атмосферы, теории крыла самолета, теории пропеллера и корабельного винта и др. Об этих приложениях, получивших особенное развитие в работах русских ученых (Н.Е. Жуковского - по вихревой теории винта и А. А. Фридмана — по вихрям в атмосфере), будет упомянуто в следующем параграфе.
Особенно принципиальное значение для развития всей современной гидроаэродинамики имело возникновение в начале XIX в. механики вязкой жидкости и сжимаемого газа.
Теория движения вязкой жидкости в форме, весьма близкой к современной, была опубликована в 1845 г. Стоксом (1819—1903), который, выделив из общего перемещения элемента жидкости деформационную часть, указал простую линейную зависимость возникающих в жидкости напряжений от скоростей деформаций, т. е. дал обобщение ранее уже упомянутого закона Ньютона. До Стокса, основываясь на некоторых специальных молекулярных гипотезах относительно свойств реальных газов, уравнения движения вязкого газа выводили: в 1826 г. Навье (1785—1836), в 1831 г. Пуассон (1781 — 1846) и в 1843 г. Сен-Венан (1797—1886).
Развитие механики вязкой жидкости отвечало практическим запросам со стороны энергично развивавшихся в XIX в. гидравлики и гидротехники, учения о тревии в машинах, физики и химии нефтяных и других смазочных веществ. Первые опыты, показавшие преобладающее влияние сил вязкости на сопротивление при малых скоростях, принадлежали Кулону (1801), Дюбуа (1779) и Дюшемену (1829).
Основное значение имели теоретические и экспериментальные исследования сопротивления в трубах и каналах при движении в них воды и других вязких жидкостей. Теоретическое решение эгой задачи было дано самим Стоксом в 1846 г. и Степаном в 1862 г. Обстоятельные экспериментальные исследования движения вязкой жидкости в трубах очень малого диаметра были проведены Ж. Пуазейлем в 1840-1842 гг. и О. Рейнольдсом в период 1876 - 1883 гг. Более ранние опыты были проведены Хагеном и опубликованы в 1839 г. Ко времени работ Пуазейля и Рейнольдса относится открытие двух различных режимов движения вязкой жидкости в трубах — ламинарного и турбулентного, Работы Рейнольдса послужили началом создания теории турбулентного движения, применение которой в вопросах гидравлики, гидротехники, метеорологии, теории сопротивления и теплопередачи оказалось весьма обширным и плодотворным.
Изучение движения вязкой жидкости между двумя вращающимися цилиндрами привело в 1883 г. знаменитого русского инженера Н. П. Петрова к созданию гидродинамической теории трения обильно смазанных подшипников. Строгое решение той же задачи было указано Н. Е. Жуковским в работах, опубликованных в 1886 и 1887 гг. Уточнение и обобщение этой теории трения было проведено в работах Рейнольдса, Зоммерфельда, Митчелла и др.
Рассмотрение движения вязкой жидкости по капиллярным трубкам легло в основу создания теории фильтрации жидкости сквозь песчаные грунты и трещиноватые породы. Первые шаги в этом направлении были сделаны французским гидравликом Дарси в 1856 г., показавшим пропорциональность скорости фильтрации потере напора. Практические задачи о фильтрационных движениях воды в грунтах под
гидротехническими сооружениями, нефти сквозь почву и другие составили предмет огромного числа исследований; особенно надо отмстить замечательные работы Н. Е. Жуковского в 1889 и 1890 гг., а также теорию плоского фильтрационного движения академика Н. Н. Павловского, опубликованную в 1921 г.
О дальнейшем развитии этого направления в советских работах речь будет еще впереди.
Параллельно с развитием гидродинамики вязкой жидкости протекало и создание динамики сжимаемого газа. Первоначальные исследования в этой области были тесно связаны с зарождением двух основных разделов физики: термодинамики и акустики; первый из них развивался в связи с появлением паровой техники, второй стимулировался главным образом теорией музыкальных инструментов и физиологией слуха.
Первое теоретическое определение скорости звука — скорости распространения упругих волн малой амплитуды — дал Ньютон, показавший, что скорость распространения звука в воздухе, если рассматривать этот процесс как изотермический, пропорциональна корню квадратному из отношения давления воздуха к его плотности. На самом деле, как показал значительно позднее Лаплас, процесс распространения звуковых колебаний приближается к адиабатическому, что привело Лапласа к формуле, применяемой и в настоящее время. Формула эта, данная Лапласом в первом десятилетии прошлого века, отличается от формулы Ньютона коэффициентом под знаком корня, равным отношению теплоемкостей при постоянном давлении и постоянном объеме.
Основная система дифференциальных уравнений динамики сжимаемого газа появилась примерно в середине прошлого века, после того как к системе уравнений Эйлера и уравнения неразрывности было присоединено уравнение баланса энергий, выведенное из первого начала термодинамики, а также уравнение состояния газа. Несмотря на строгую математическую постановку задачи и наличие к тому времени развитых методов решения дифференциальных уравнений, решение уравнений газодинамики представило, даже при простейших предположениях об отсутствии вихрей, об адиабатичности потока и др., непреодолимые трудности. И в настоящее время имеется лишь небольшое число случаев точного решения задач газодинамики, зато значительную разработку получили приближенные методы, принадлежащие, главным образом, советским ученым.
Принципиальные особенности движения газа со сверхзвуковыми скоростями были отмечены впервые в середине прошлого века Допплером.
Выдающийся геометр Риманн (1826—1866) в классическом мемуаре, относящемся к 1860 г., теоретически доказал возможность возникновения поверхностей разрыва в газовом потоке, вначале непрерывном; эти разрывы были названы ударными волнами.
Наибольшее развитие, в связи с задачами, вставшими перед создателями паровых турбин, получила газовая гидравлика, предметом изучения которой явились одномерные течения сжимаемого газа с большими до- и сверхзвуковыми скоростями по трубам и соплам, вопросы истечения газа из резервуаров и тому подобные явления. Это направление механики сжимаемого газа нашло опору в общих теоремах: количеств движения, теореме Бернулли, баланса энергии, а также в основных закономерностях термодинамики газа. Наиболее популярным и важным результатом этого направления следует признать классическую формулу Сен-Венана и Ванцеля (1839), связывающую скорость адиабатического истечения газа с давлением и плотностью газа в резервуаре и с противодавлением.
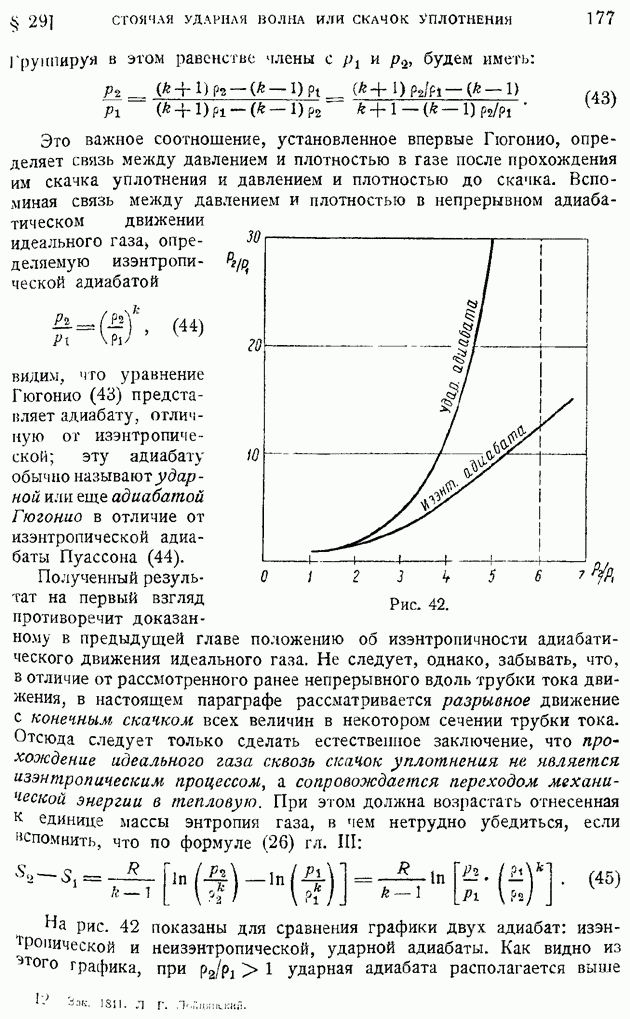
Элементарная газогидравлическая теория скачка уплотнения, установившая связь между давлением и плотностью до и после скачка, была дана Рэнкиным в 1870 г. и Гюгонио в 1887 г.; явление образования скачков уплотнения в сопле Лаваля было обнаружено и изучено Стодола.
Полного своего расцвета газовая динамика достигла лишь в первой половине нашего века в связи с вставшими перед нею запросами авиации, турбостроения и техники реактивного движения. Об этом этапе развития газовой динамики и особенно большом значении советских исследователей в этом направлении будет сказано в следующем параграфе.
Конец XIX в. ознаменовался высоким подъемом всеобщего интереса к воздухоплаванию. Не преследуя в настоящем курсе цель изложена специальных вопросов аэромеханики самолета, мы не будем останавливаться и на истории авиации, неразрывно связанной с историей развития аэродинамики. Упомянем лишь, что в первых рядах борцов за создание авиации, наряду с Жуковским и Лилиенталем, должны быть поставлены имена Д. И. Менделеева (1834—1907) и К. Э. Циолковского (1857 — 1935).
Широко известна роль Д. И. Менделеева в развитии учения о газах при больших и малых давлениях, его теоретические и экспериментальные заслуги в области метеорологии высоких слоев атмосферы. Д. И. Менделееву принадлежит опубликованная в 1880 г. фундаментальная монография "О сопротивлении жидкостей и воздухоплавании", в которой не только дается систематическое и критическое изложение существовавших к тому времени работ по теории сопротивления, что и приводятся оригинальные идеи Менделеева в этом направлении, в частности, указывается на важное значение вязкости жидкости при определении сопротивления трения хорошо обтекаемого тела. Н. Е. Жуковский высоко ценил эту книгу.
Д. И. Менделеев, всегда служивший образцом ученого, тесно связывающего все свои открытия с запросами народного хозяйства своей родины, не отрывал научные интересы в области аэродинамики от задач воздухоплавания и не только сам лично создавал проекты
новых летательных аппаратов, но и всемерно помогал изобретателям, работавшим в том же направлении. Так, в 1877 г. Д. И. Менделеев помог известному конструктору первого самолета А. Ф. Можайскому, в 1890 г. представил Русскому техническому обществу проект цельнометаллического дирижабля К. Э. Циолковского.
Выдающийся русский ученый и изобретатель К. Э. Циолковский, создал в 1896 г. первую аэродинамическую трубу, на которой проводил опыты по определению сопротивления тел. Ему принадлежит целый ряд смелых технических идей: возможность завоевания мирового пространства при помощи ракет, первые проекты ракетопланов, проекты цельнометаллических дирижаблей и др. К. Э. Циолковский установил первые формулы реактивного движения снаряда с переменной массой.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Предмет механики жидкости и газа. Основные свойства «макромодели» жидкости и газа: сплошность и подвижность
- § 2. Основные методы механики жидкости и газа. Области применения и главнейшие задачи
- § 3. Краткий очерк исторического развития механики жидкости и газа. От гидромеханики древних до установления воззрений ньютонианской эпохи
- § 4. Эпоха Эйлера и Бернулли. Гидроаэродинамика в XIX в.
- § 5. Современный этап развития механики жидкости и газа
- ГЛАВА I. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
- § 6. Поле физической величины. Скалярное и векторное поля. Поверхности уровня. Векторные линин и трубки
- § 7. Мера однородности поля в данном направлении и в дайной точке. Градиевт скалярного поля и дифференциальный тензор векторного поля как меры неоднородности поля
- § 8. Задание движения сплошной среды. Поле скоростей. Линии тока и траектории
- § 9. Поле ускорений. Разложение ускорения частицы на локальную и конвективную составляющие
- § 10. Скоростное поле сплошной среды в окрестности данной точки. Угловая скорость и вихрь. Тензор скоростей деформаций и его компоненты
- § 11. Скорость объемного расширения жидкости. Интегральные представления дифференциальных операторов поля. Основные интегральные формулы
- § 12. Вихревые линии и трубки. Вторая теорема Гельмгольца. Интенсивность вихревой трубки
- § 13. Выражение интенсивности вихревой трубки через циркуляцию вектора по контуру, охватывающему трубку. Теорема об изменении циркуляции скорости во времени
- ГЛАВА II. ОСНОВНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ И РАВНОВЕСИЯ СПЛОШНОЙ СРЕДЫ
- § 14. Распределение массы в сплошной среде. Плотность и удельный вес. Напряжения. Тензор напряженности и его симметричность
- § 15. Общие уравнения динамики сплошной среды. Уравнение неразрывности. Уравнения динамики в напряжениях
- § 16. Тепловые явления в жидкостях и газах. Закон сохранения энергии и уравнение баланса энергии
- § 17. Общие уравнения равновесного состояния жидкости и газа. Равновесие воздуха в атмосфере. Приближенные барометрические формулы. Стандартная атмосфера
- § 18. Равновесие несжимаемой жидкости. Уравнение поверхности раздела. Равновесие вращающейся жидкости
- § 19. Давление тяжелой несжимаемой жидкости на поверхность тела. Сила и момент, приложенные к телу, плавающему в тяжелой жидкости. Случай вращающейся жидкости
- ГЛАВА III. ДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ И ГАЗА. ОСНОВНЫЕ УРАВНЕНИЯ И ОБЩИЕ ТЕОРЕМЫ
- § 20. Идеальная жидкость. Основные уравнения движения
- § 21. Закон сохранения энергии в движущейся идеальной жидкости. Адиабатическое движение. Сохранение энтропии
- § 22. Эйлерово представление конвективного изменения объемного интеграла. Перенос величины сквозь контрольную поверхность
- § 23. Эйлерова форма законов сохранения массы и энергии, теоремы количеств движения и момента количеств движения при стационарном движении идеальной жидкости
- § 24. Теорема об изменении кинетической энергии. Работа и мощность внутренних сил. Эйлерова форма уравнения изменения кинетической энергии
- § 25. Теорема Бернулли о сохранении полной механической энергии при стационарном баротропном движении идеальной жидкости и газа
- ГЛАВА IV. ОДНОМЕРНЫЙ ПОТОК ИДЕАЛЬНОЙ ЖИДКОСТИ
- § 26. Одномерное течение идеальной сжимаемой жидкости. Линеаризированные уравнения. Скорость распространения малых возмущений в жидкости или газе
- § 27. Изотермическая и адиабатическая скорости звука. «Конус возмущений» при сверхзвуковом движении источника возмущения. Число M и его связь с углом конуса возмущений
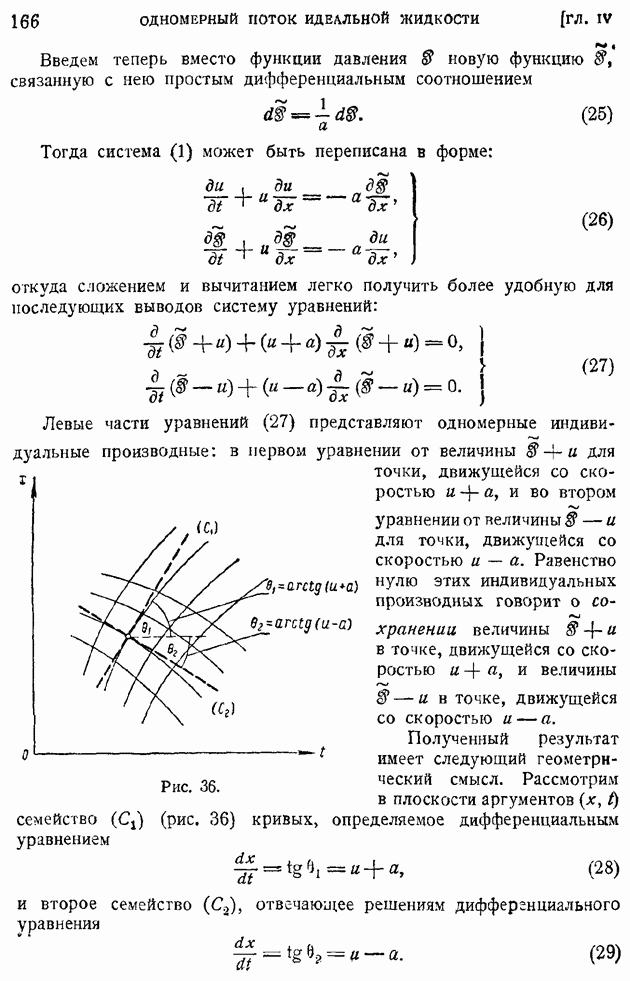
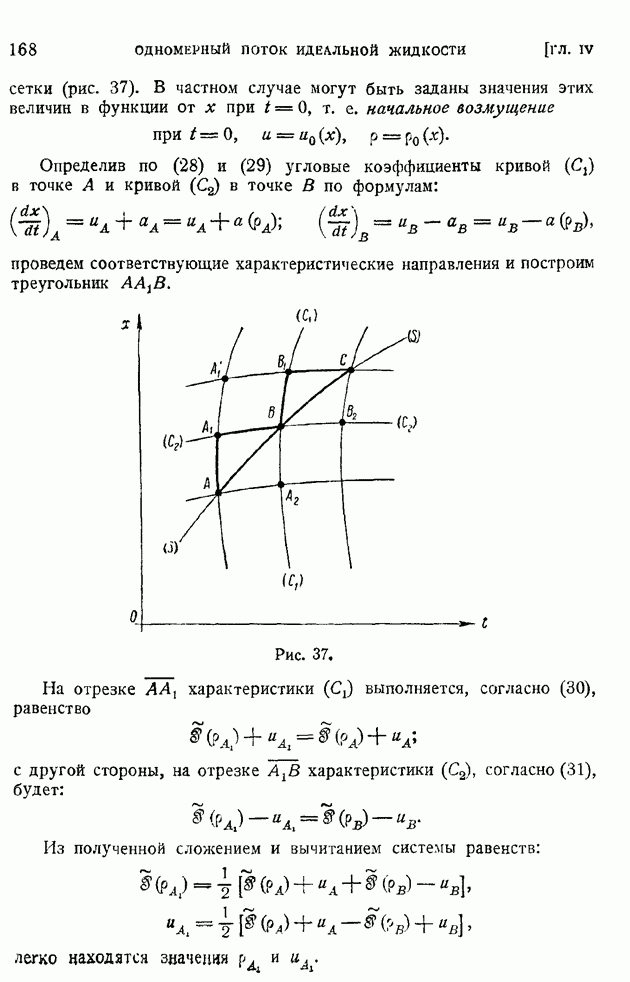
- § 28. Распространение непрерывных возмущений конечной интенсивности. Характеристики. Образование разрывной ударной волны
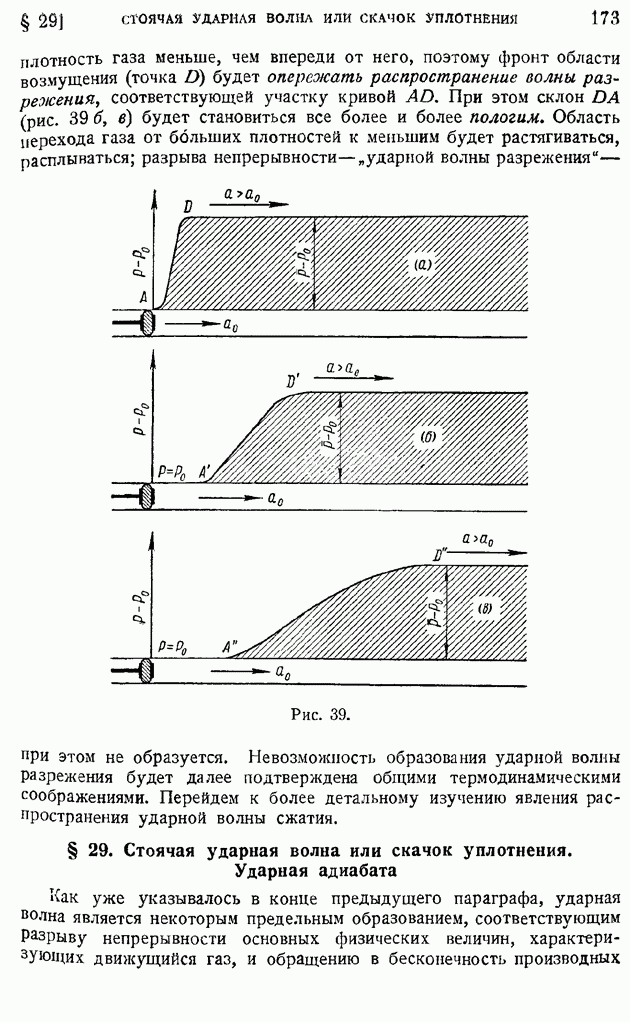
- § 29. Стоячая ударная волна или скачок уплотнения. Ударная адиабата
- § 30. Критические величины в одномерном потоке газа. Связь между скоростями до и после скачка. Изменение давления, плотности и температуры в скачке уплотнения
- § 31. Скорость распространения ударной волны. Спутное движение газа за ударной волной
- § 32. Влияние интенсивности скачка уплотнения на сжатие газа. Измерение скоростей и давлений в до- и сверхзвуковых потоках
- § 33. Одномерное движение газа по трубе переменного сечения. Истечение из резервуара большой емкости сквозь сходящееся сопло
- § 34. Одномерное течение в сопле Лаваля. Движение газа с притоком тепла
- ГЛАВА V. БЕЗВИХРЕВОЕ ДВИЖЕНИЕ ЖИДКОСТИ. ПЛОСКОЕ ДВИЖЕНИЕ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 35. Сохранение циркуляции скорости в потоке идеальной жидкости. Теорема Кельвина и Лаграижа. Безвихревое движение. Потенциал скоростей
- § 36. Интеграл Лагранжа — Коши уравнений безвихревого движения. Теорема Бернулли. Некоторые общие свойства безвихревого движения идеальной несжимаемой жидкости в односвязной области
- § 37. Плоское безвихревое движение несжимаемой жидкости. Потенциал скоростей и функция тока. Применение функций комплексного переменного. Комплексный потенциал и сопряженная скорость
- § 38. Построение полей течения по заданной характеристической Функции. Простейшие плоские потоки и их наложение
- § 39. Бесциркуляционное и циркуляционное обтекания круглого цилиндра
- § 40. Применение криволинейных координат. Бесциркуляционное и циркуляционное обтекания эллиптического цилиндра и пластинки. Задача Жуковского об обтекании решетки пластин.
- § 41. Плоское движение с отрывом струй. Разрывное обтекание пластинки и протекание жидкости сквозь отверстие
- § 42. Прямая задача в теории плоского движения идеальной несжимаемой жидкости. Применение метода конформных отображений. Гипотеза Чаплыгина о безотрывном обтекании задней кромки профиля. Формула циркуляции
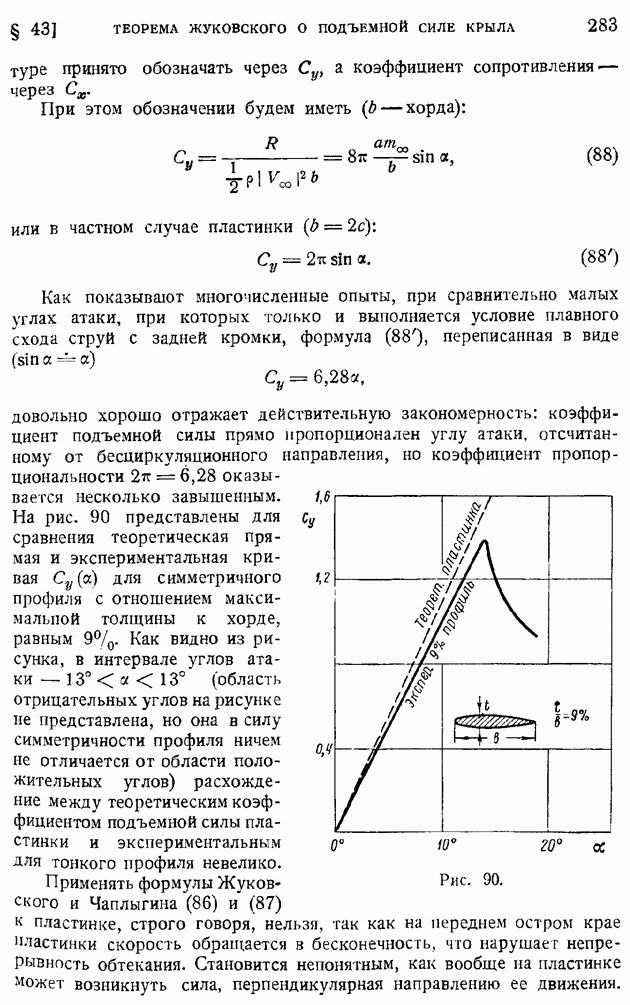
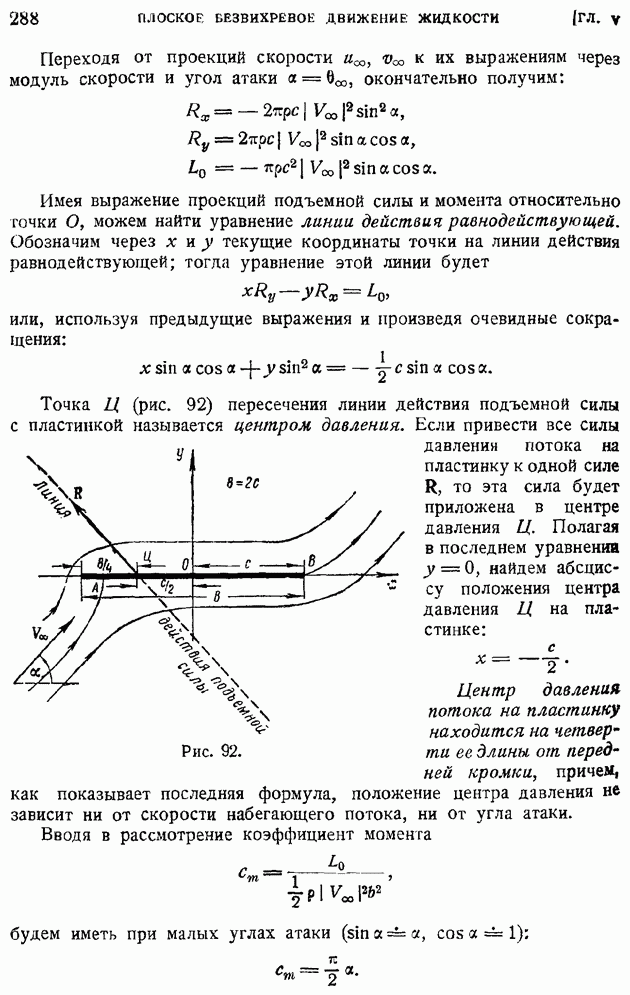
- § 43. Теорема Жуковского о подъемной силе крыла. Зависимость подъемной силы от угла атаки. Коэффициент подъемной силы
- § 44. Применение метода комплексных переменных к выводу теоремы Жуковского. Формулы Чаплыгина для главного вектора и момента сил давления потока на крыло
- § 45. Выражение главного момента сил давления потока через коэффициенты конформного отображения. Фокус крыла. Независимость от угла атаки момента относительно фокуса. Парабола устойчивости
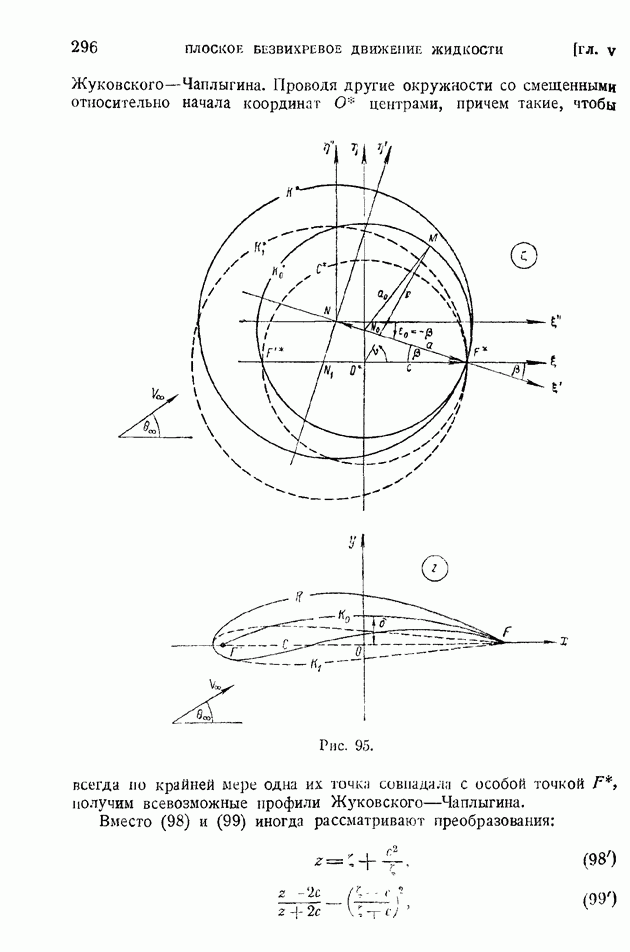
- § 46. Частные случаи конформного отображения крылового профиля на круг. Преобразование Жуковского-Чаплыгина. Теоретические крыловые профили
- § 47. Задача об обтекании слабо изогнутой дужки произвольной формы (теория тонкого крыла)
- § 48. Определение обтекания крылового профиля произвольной формы
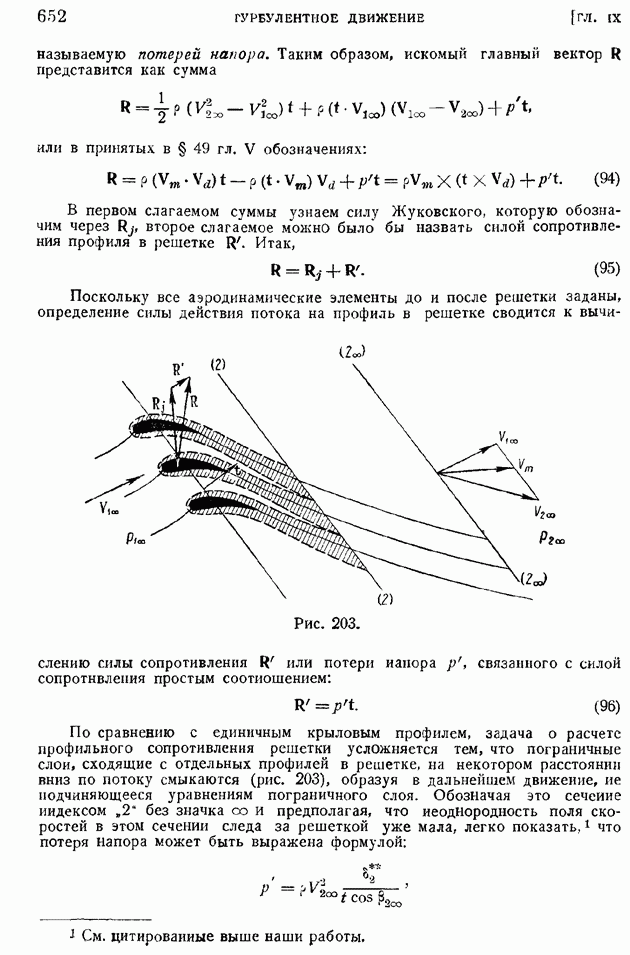
- § 49. Обобщение теоремы Жуковского на случай плоской решетки с бесчисленным множеством профилей
- ГЛАВА VI. ПЛОСКОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ СЖИМАЕМОГО ГАЗА
- § 50. Основные уравнения плоского стационарного безвихревого движения сжимаемого газа. Линеаризированные уравнения
- 51. Линеаризированный до- и сверхзвуковой газовый поток вдоль волнистой стенки
- § 52. Тонкое крыло в линеаризированном до- и сверхзвуковом потоках. Влияние сжимаемости газа на коэффициент подъемной силы в дозвуковом потоке. Коэффициенты подъемной силы и волнового сопротивления при сверхзвуковом потоке
- § 53. Нелинеаризированные уравнения движения идеального сжимаемого газа. Переход в плоскость годографа. Уравнения Чаплыгина
- § 54. Метод С. А. Христиановича. Приближенные формулы учета влияния сжимаемости на распределение давления
- § 55. Критическое число M и его определение по заданному распределению давления в несжимаемом обтекании. Поведение коэффициента подъемной силы и момента при около- и закритических значениях числа M
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
- § 57. Нелинеаризированный сверхзвуковой поток. «Характеристики» уравнений плоского сверхзвукового потока. Линин возмущения и их основные свойства
- § 58. Обтекание выпуклого угла сверхзвуковым потоком. Влияние угла поворота струи на ее газодинамические элементы
- § 59. Сверхзвуковой поток внутри тупого угла. Косой скачок уплотнения. Связь между газодинамическими элементами до и за косым скачком
- ГЛАВА VII. ПРОСТРАНСТВЕННОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ
- § 60. Ортогональные криволинейные координаты в пространстве. Основные дифференциальные операторы поля в криволинейных координатах
- § 61. Потенциал скоростей. Поле источника и диполя. Непрерывное распределение источников и диполей. Ньютонов потенциал. Потенциал простого и двойного слоев
- § 62. Поле скоростей вокруг заданной системы вихрей. Формула Био — Савара. Потенциал скоростей замкнутой вихревой нити. Аналогия с потенциалом двойного слоя
- § 63. Функция тока и ее связь с векторным потенциалом скоростей. Функции тока простейших течений
- § 64. Обтекание сферы. Давление однородного стационарного потока идеальной несжимаемой жидкости на погруженное в нее тело. Парадокс Даламбера
- § 65. Общие уравнения осесимметричного движения. Применение цилиндрических координат. Течение сквозь каналы
- § 66. Осесимметричное продольное обтекание тел вращения. Случай эллипсоида вращения
- § 67. Поперечное обтекание тел вращения. Пример эллипсоида вращения
- § 68. Продольное и поперечное обтекание тел вращения большого удлинения. Приближенные выражения граничных условий. Применение тригонометрических сумм для определения коэффициентов …
- § 69. Метод «особенностей». Применение непрерывно распределенных источников (стоков) и диполей для решения задачи о продольном и поперечном обтекании тел вращения
- § 70. Общий случай движения твердого тела сквозь несжимаемую идеальную жидкость. Определение потенциала скоростей. Главный вектор и главный момент сил давления потока на тело
- § 71. Коэффициенты «присоединенных масс». Свойство симметрии. «Присоединенная» кинетическая энергия. Определение «присоединенных масс» поступательно движущегося цилиндра, шара и эллипсоида
- § 72. Элементы теории крыла конечного размаха. Вихревая система крыла. Гипотеза плоских сечеиий. Геометрические и действительные углы атаки. Подъемная сила и «индуктивное сопротивление»
- § 73. Основные формулы теории «несущей линии». «Индуктивная скорость» и «индуктивный угол». Прямая задача определения подъемной силы и индуктивного сопротивления по заданному распределению циркуляции
- § 74. Крыло с минимальным индуктивным сопротивлением. Эллиптическое распределение циркуляции. Связь между коэффициентами индуктивного сопротивления и подъемной силы. Основное уравнение теории крыла и понятие о его интегрировании
- ГЛАВА VIII. ДИНАМИКА ВЯЗКОЙ ЖИДКОСТИ И ГАЗА
- § 75. Внутреннее трение и теплопроводность в жидкостях и газах. Законы Ньютона и Фурье. Влияние температуры на коэффициенты вязкости и теплопроводности. Число «сигма»
- § 76. Обобщение закона Ньютона на случай произвольного движения среды. Закон линейной связи между тензорами напряжений и скоростей деформации
- § 77. Общие уравнения движения вязкой жидкости. Динамические уравнения и уравнение баланса энергии. Граничные условия движения жидкости с треннем и теплопроводностью
- § 78. Понятие о подобии гидродинамических явлений. Безразмерные уравнения движения вязкой жидкости и газа. Условия подобия
- § 79. Ламинарное движение вязкой несжимаемой жидкости по цилиндрической трубе
- § 80. Обтекание шара при очень малых значениях числа Рейнольдса. Формула сопротивления шара по Стоксу и ее обобщения
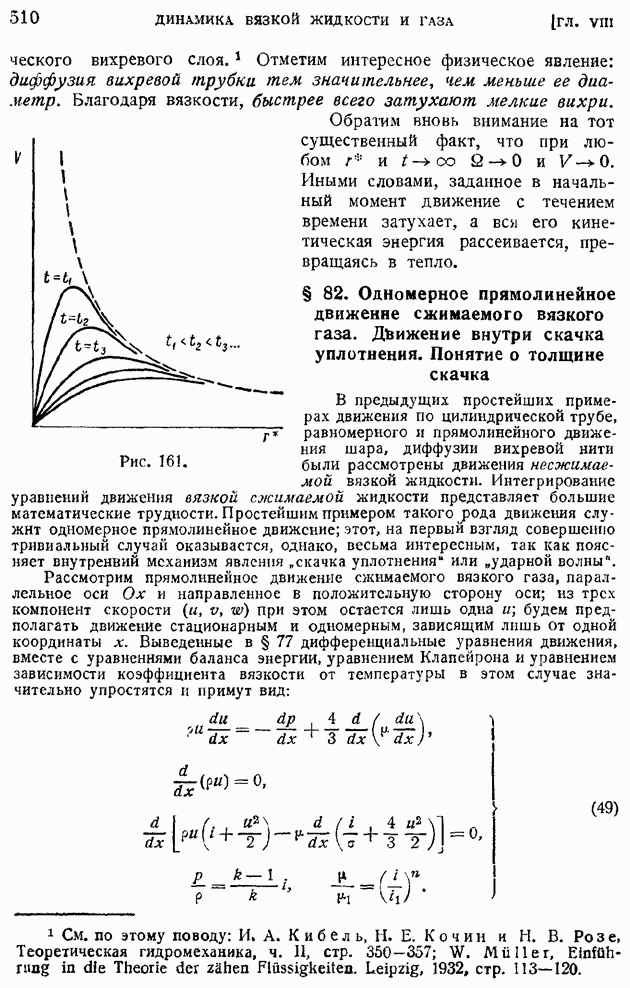
- § 81. Вихревые линии в идеальной и вязкой жидкости. Сохраняемость вихревых линий при отсутствии внутреннего трения. Диффузия вихря в вязкой жидкости
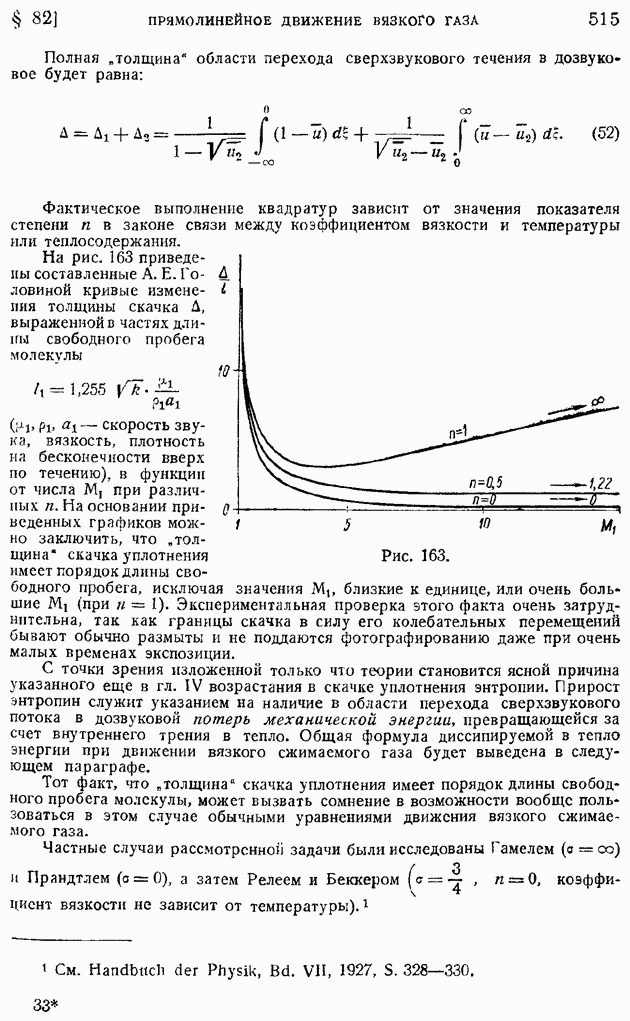
- § 82. Одномерное прямолинейное движение сжимаемого вязкого газа. Движение внутри скачка уплотнения. Понятие о толщине скачка
- § 83. Работа внутренних сил и диссипация механической энергии в движущейся вязкой среде
- § 84. Обтекание тел жидкостью и газом при больших значениях числа Рейнольдса. Основные уравнения теории ламинарного пограничного слоя
- § 85. Ламинарный пограничный слой на пластинке, продольно обтекаемой несжимаемой жидкостью. Неизотермическое движение
- § 86. Ламинарный пограничный слой при степенном задании скорости внешнего потока
- § 87. Ламинарный пограничный слой в общем случае задания скорости внешнего потока. Применение уравнения импульсов для приближенного расчета ламинарного пограничного слоя
- § 88. Способы определения функций … Приближенный метод расчета ламинарного пограничного слоя
- § 89. Ламинарный пограничный слой на пластинке, продольно обтекаемой сжимаемым газом при больших скоростях. Случай линейной зависимости коэффициента вязкости от температуры (n = 1)
- § 90. Ламинарный пограничный слой на пластинке при любом законе связи между вязкостью и температурой и при числе … Обтекание крылового профиля потоком больших скоростей
- ГЛАВА IX. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ
- § 91. Переход ламинарного движения в турбулентное. Критическое рейнольдсово число
- § 92. Область и «точка» перехода. Явление «кризиса обтекания»
- § 93. Основные уравнения осреднеиного турбулентного движения. Тензор турбулентных напряжений
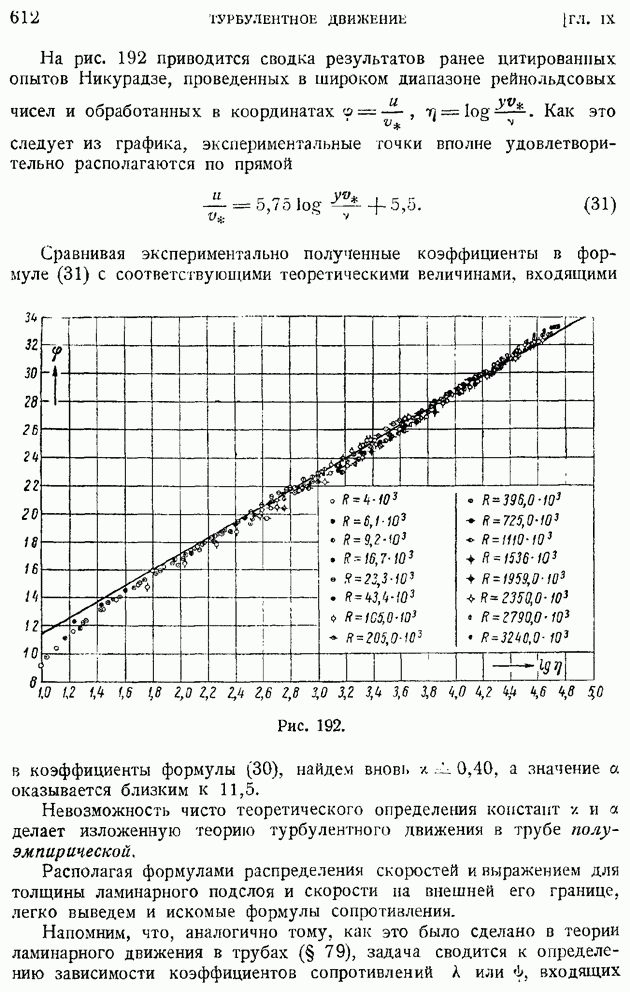
- § 94. Турбулентное движение жидкости в плоской и круглой трубе. Логарифмические формулы скоростей
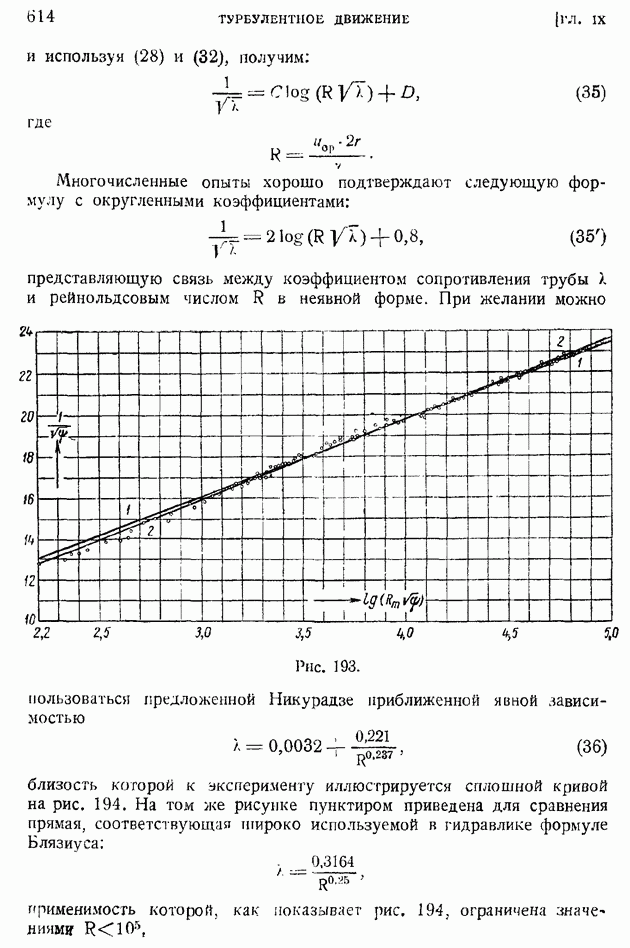
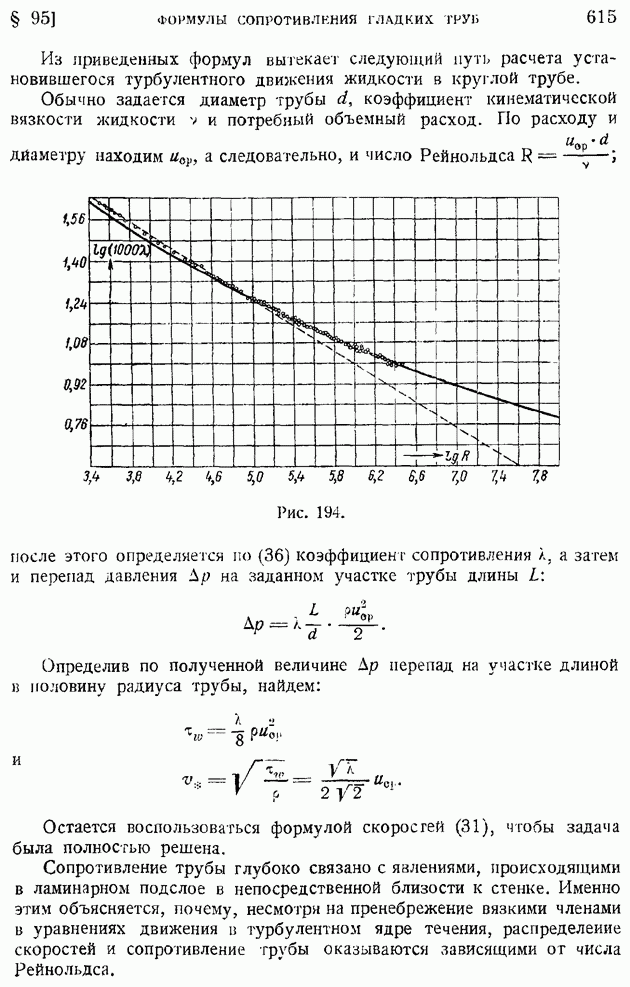
- § 95. Формулы сопротивления гладких труб при турбулентном движении жидкости. Ламинарный подслой
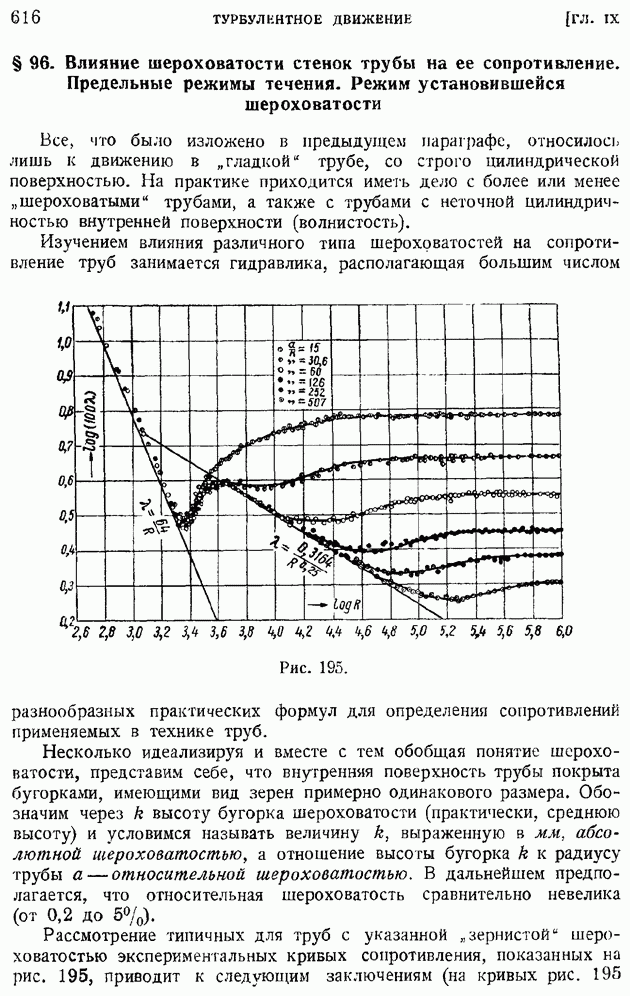
- § 96. Влияние шероховатости стенок трубы на ее сопротивление. Предельные режимы течения. Режим установившейся шероховатости
- § 97. Турбулентный пограничный слой на продольно обтекаемой пластине. Сопротивление пластины
- § 98. Турбулентный пограничный слой на крыловом профиле при малом продольном перепаде давлений
- § 99. Турбулентный пограничный слой на крыловом профиле при значительных продольных перепадах давления
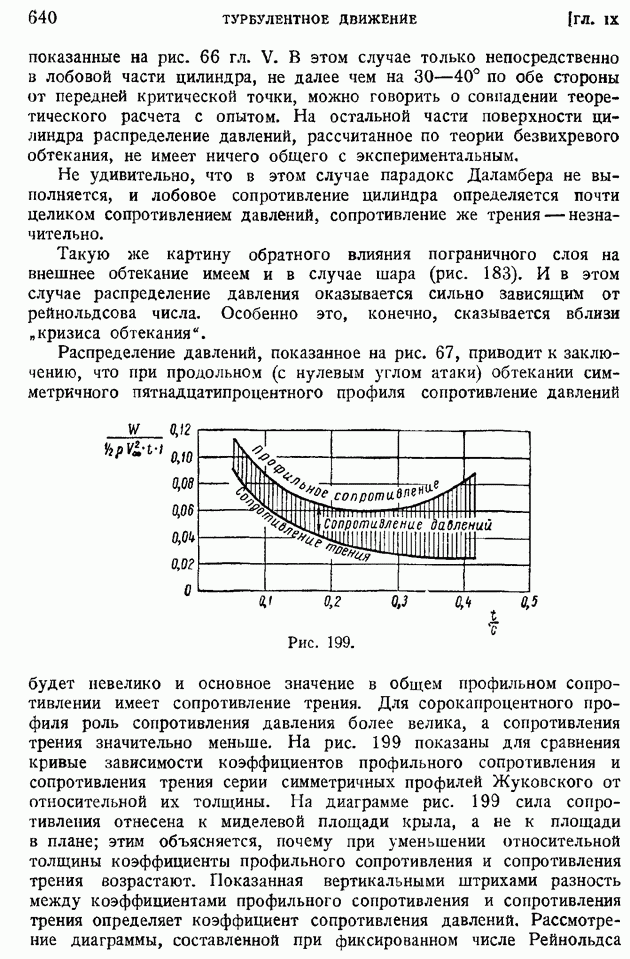
- § 100. Профильное сопротивление крыла. Разложение профильного сопротивления на сопротивление трения и сопротивление давлений. Обратное влияние пограничного слоя на распределение давлений по поверхности обтекаемого профиля
- § 101. Приближенные формулы профильного сопротивления крыла и крылового профиля в решетке
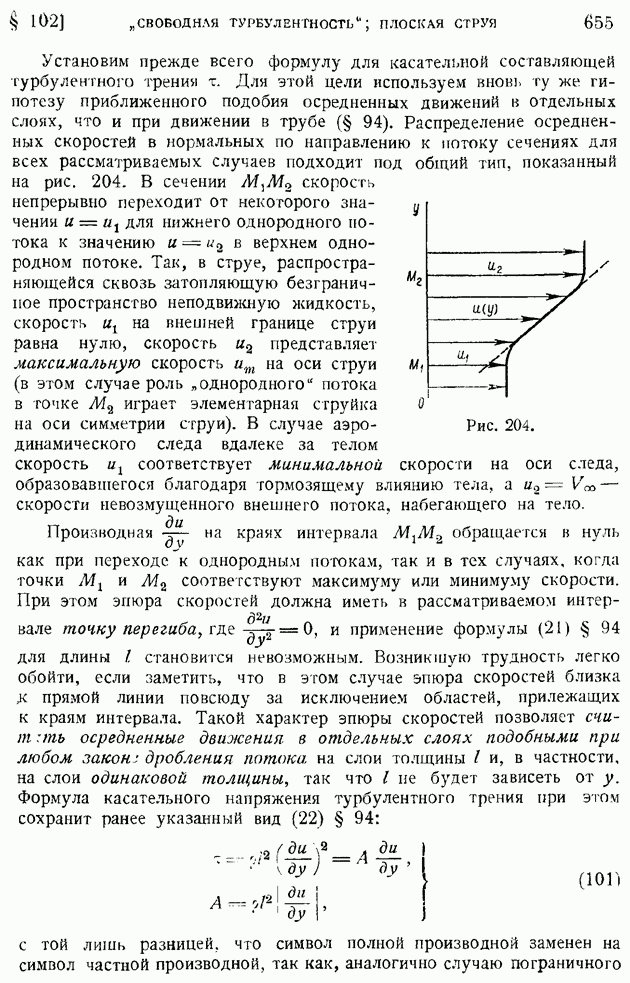
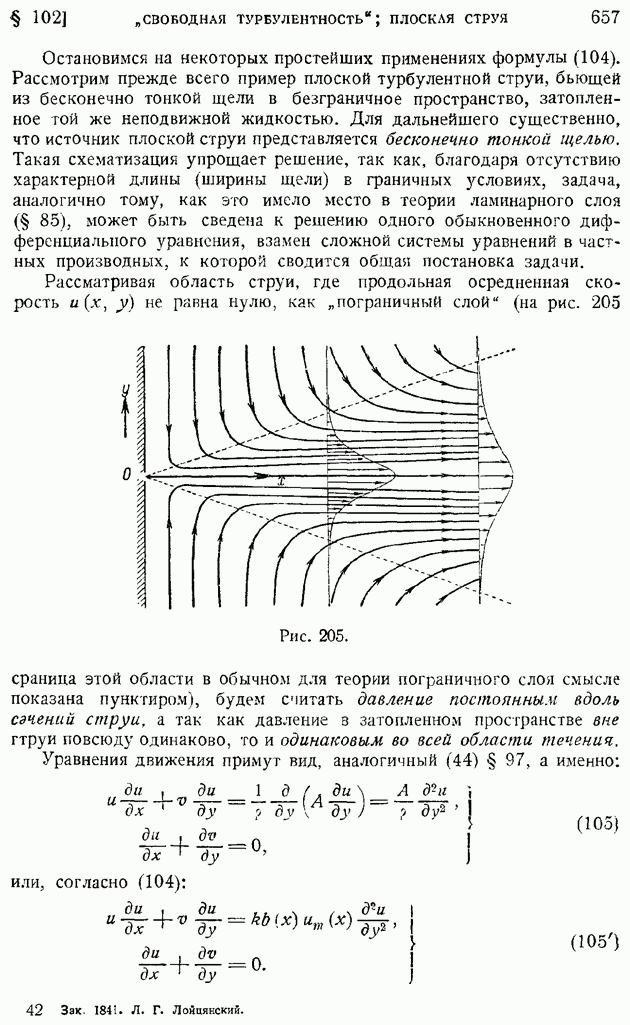
- § 102. Основные закономерности «свободной турбулентности». Плоская турбулентная струя в пространстве, заполненном той же жидкостью
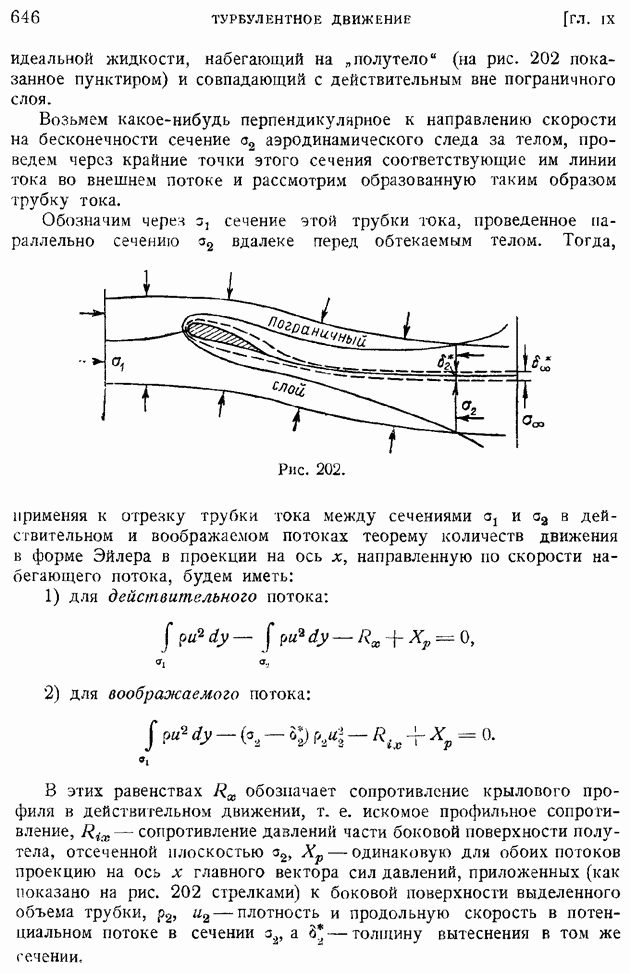
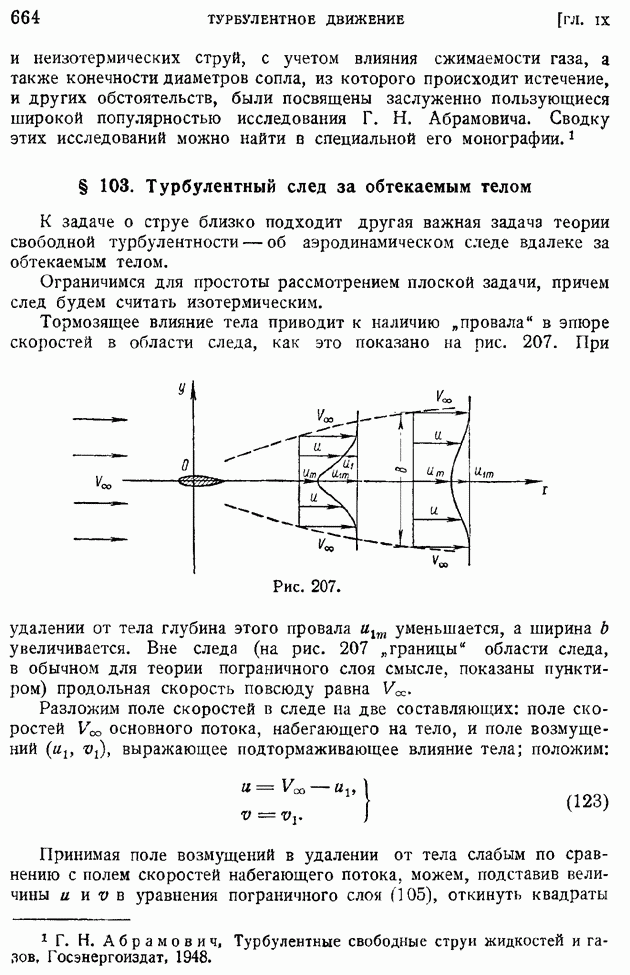
- § 103. Турбулентный след за обтекаемым телом
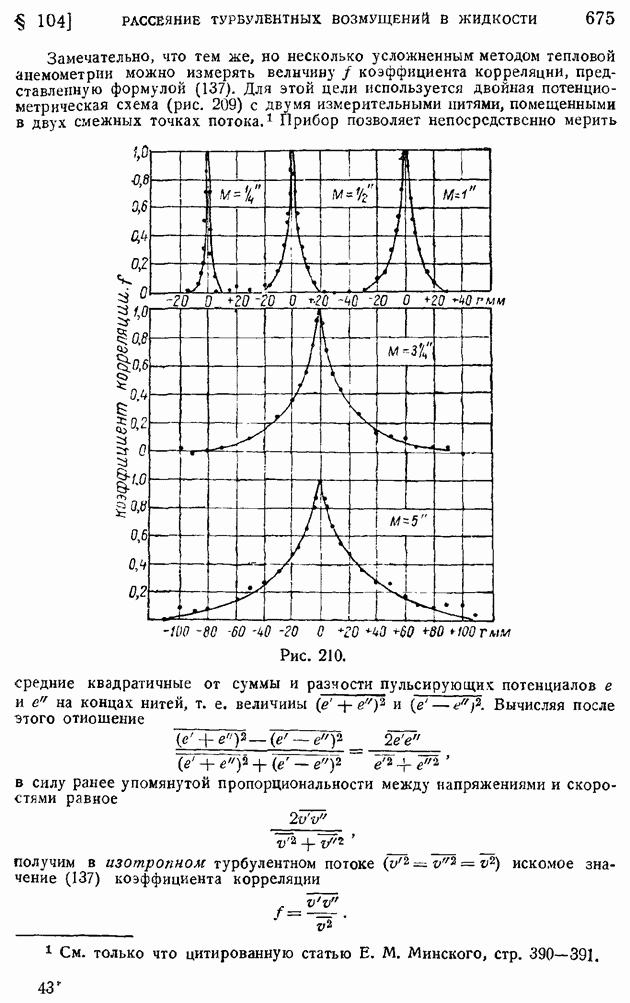
- § 104. Рассеяние турбулентных возмущений в жидкости. Случай изотропной и однородной турбулентности. Закон сохранения момента возмущений