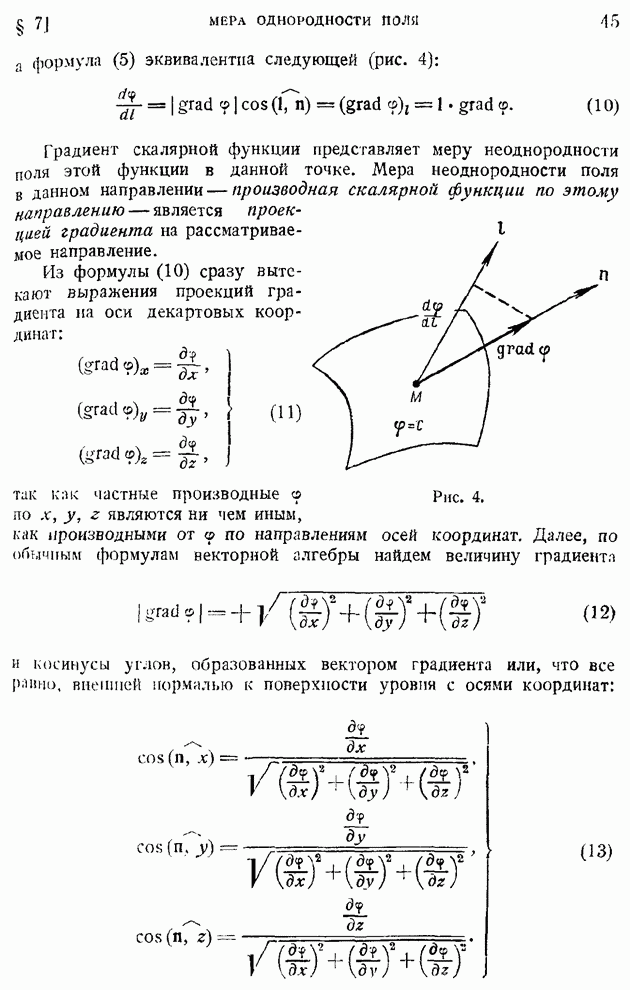
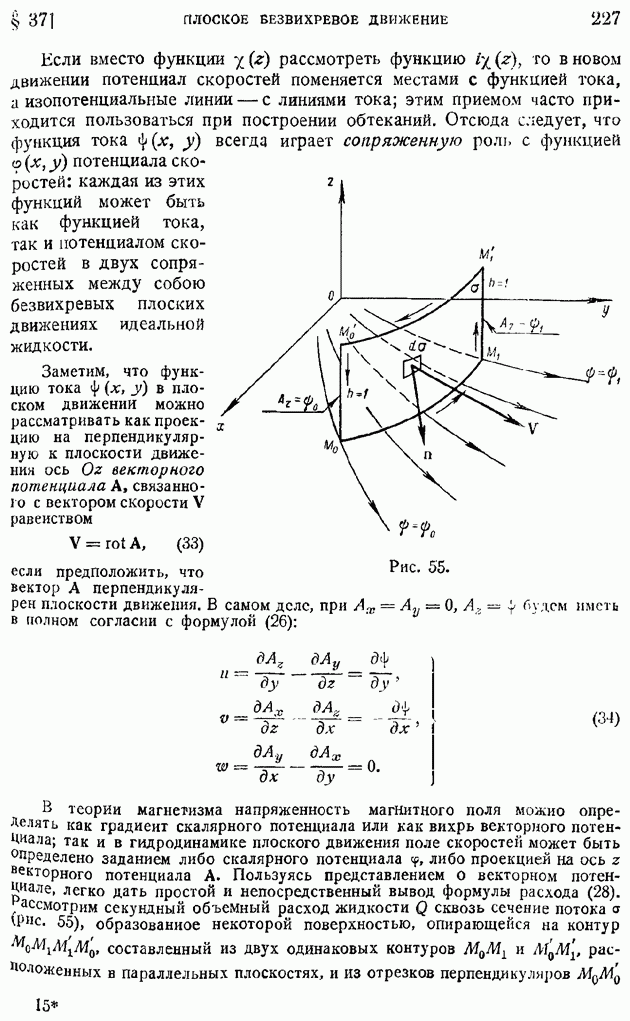
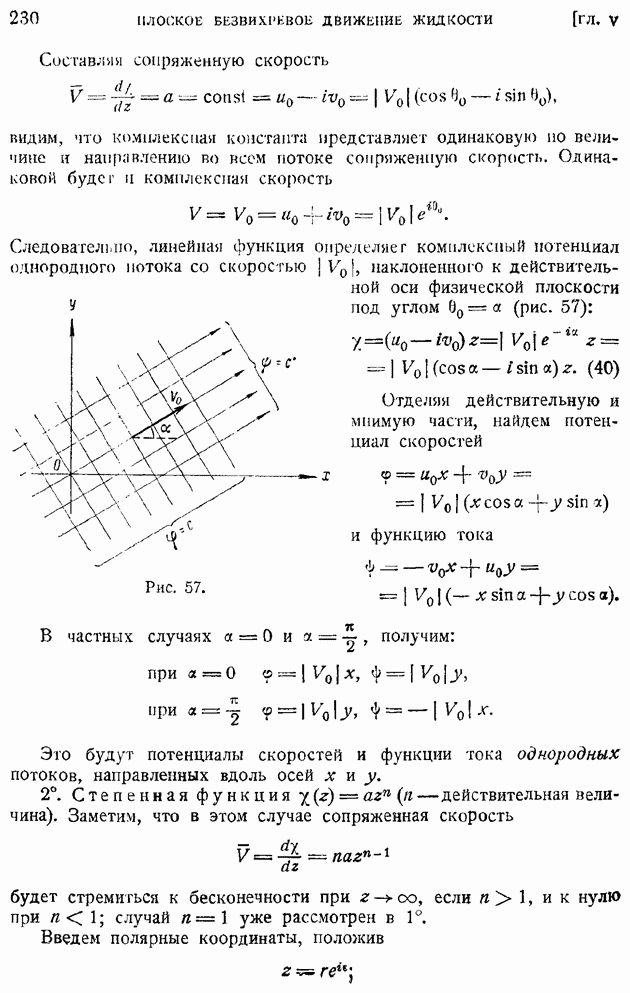
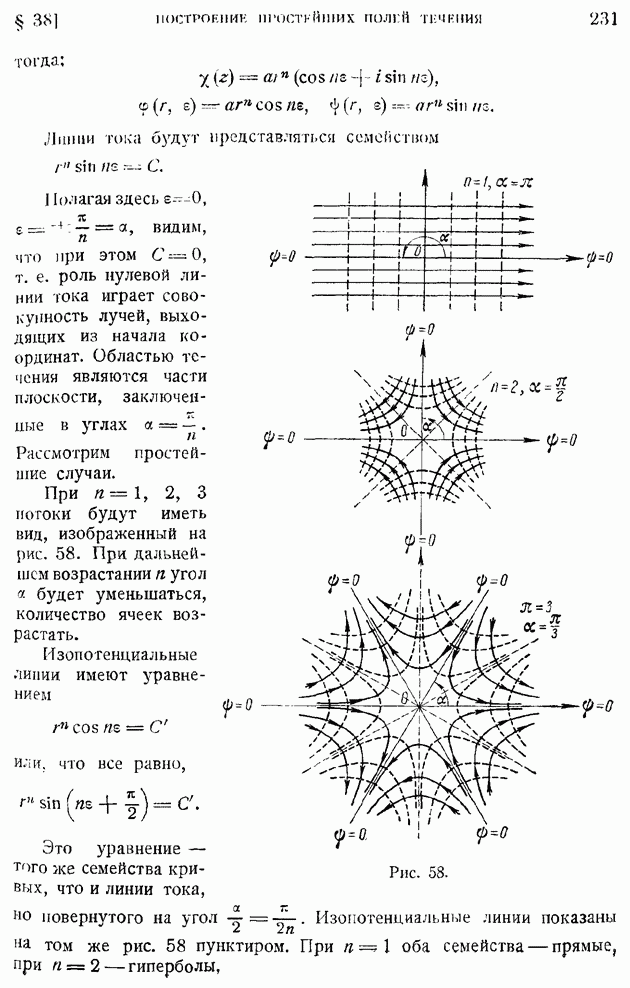
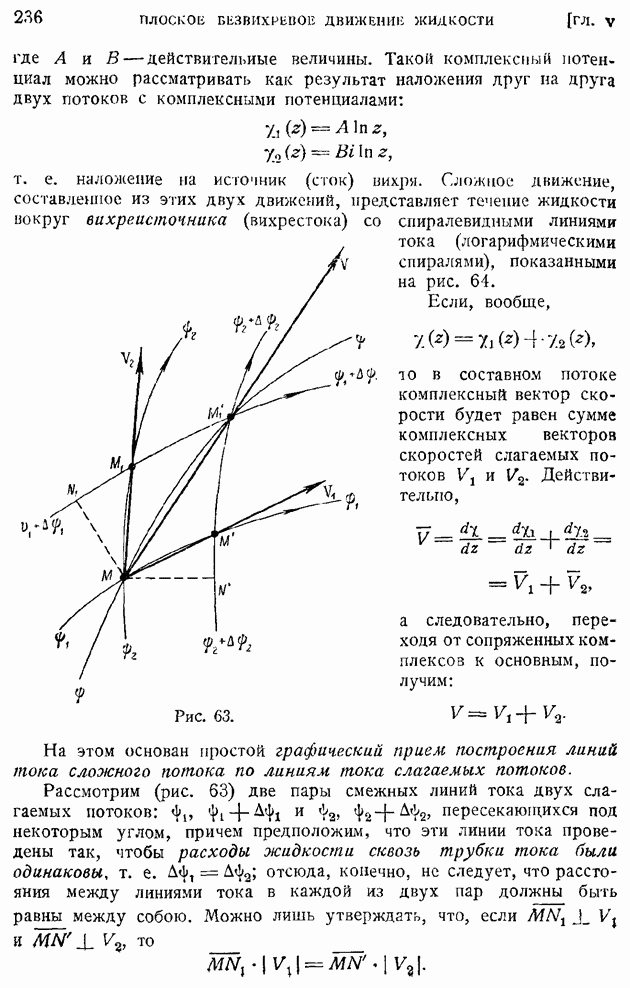
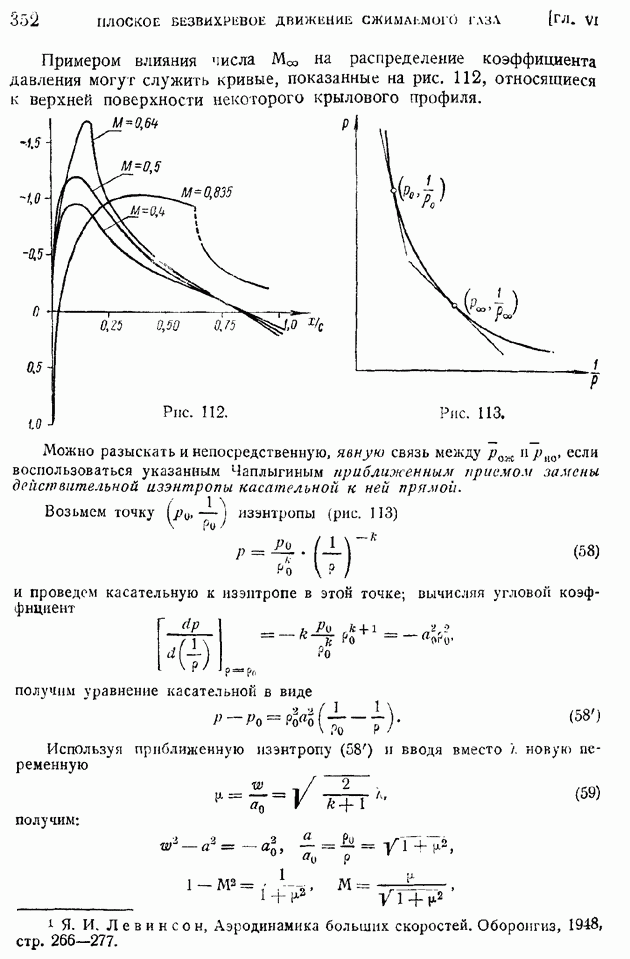
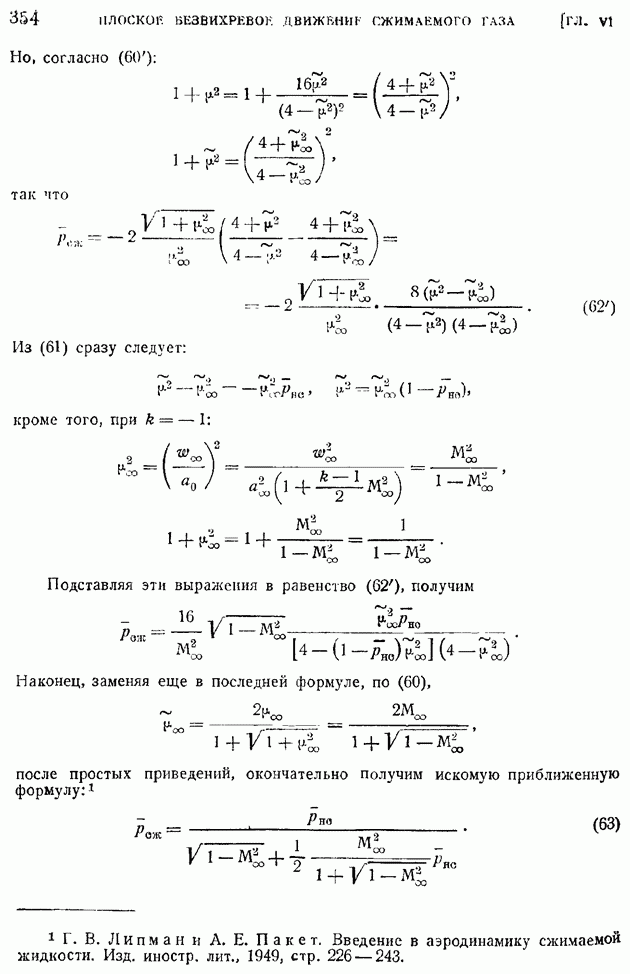
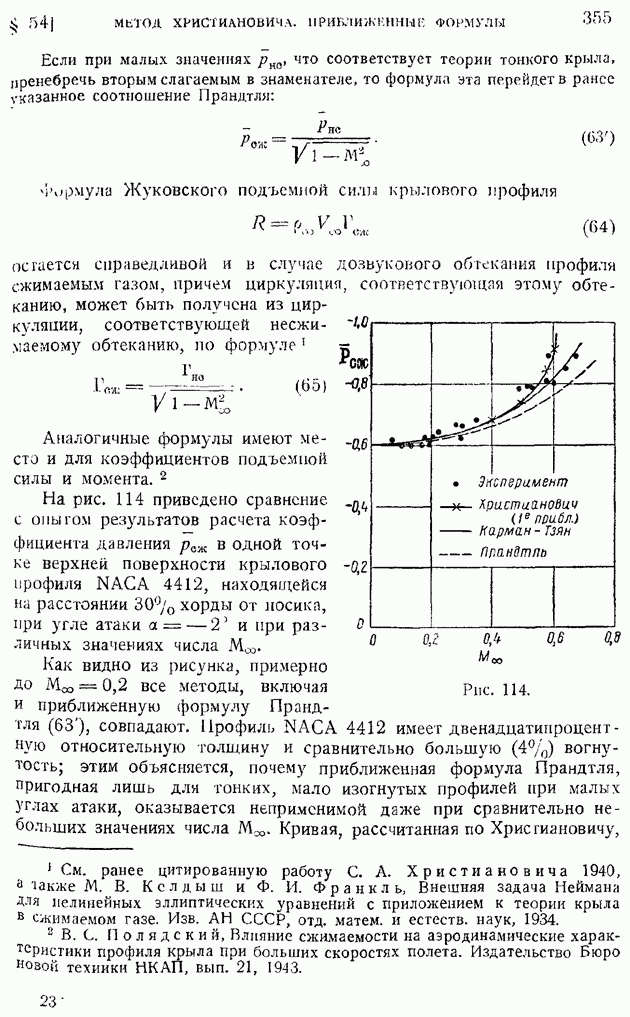
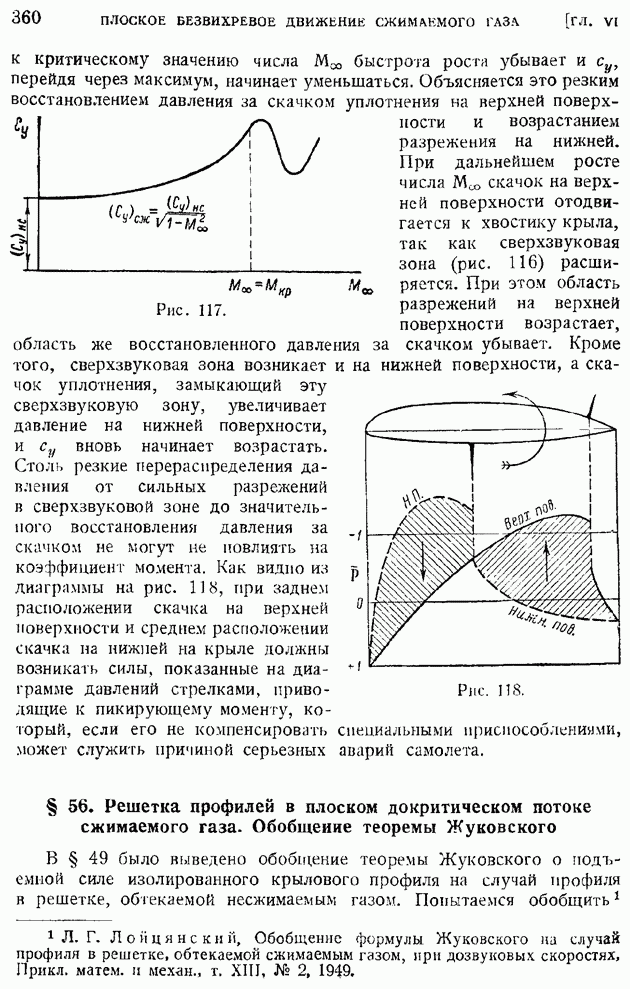
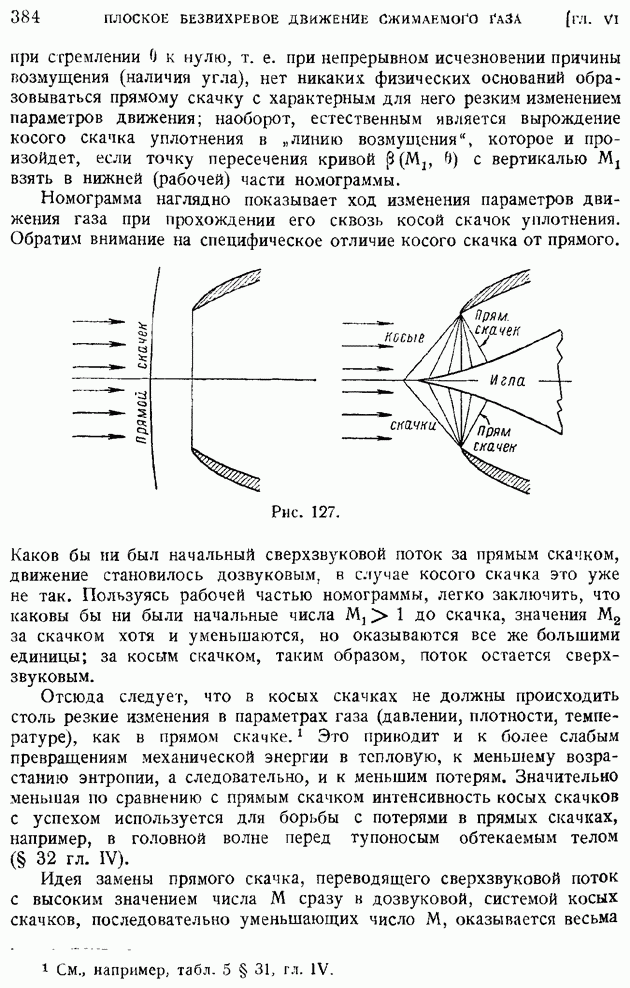
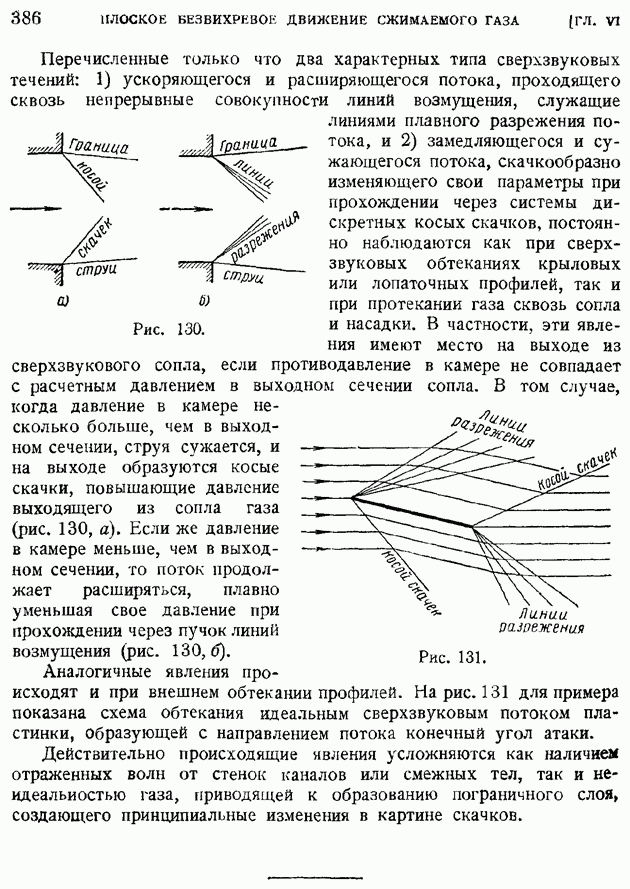
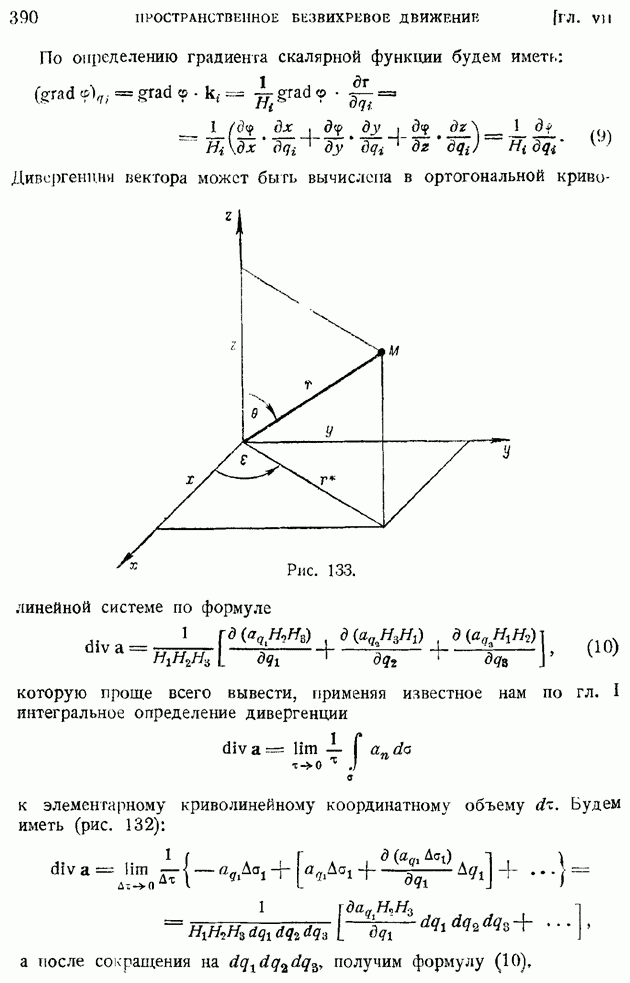
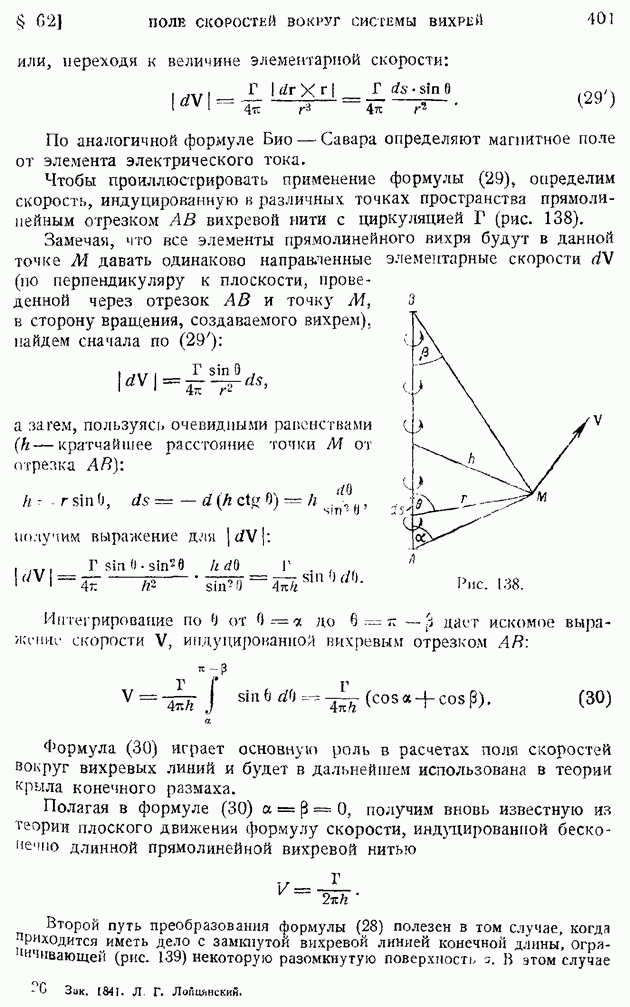
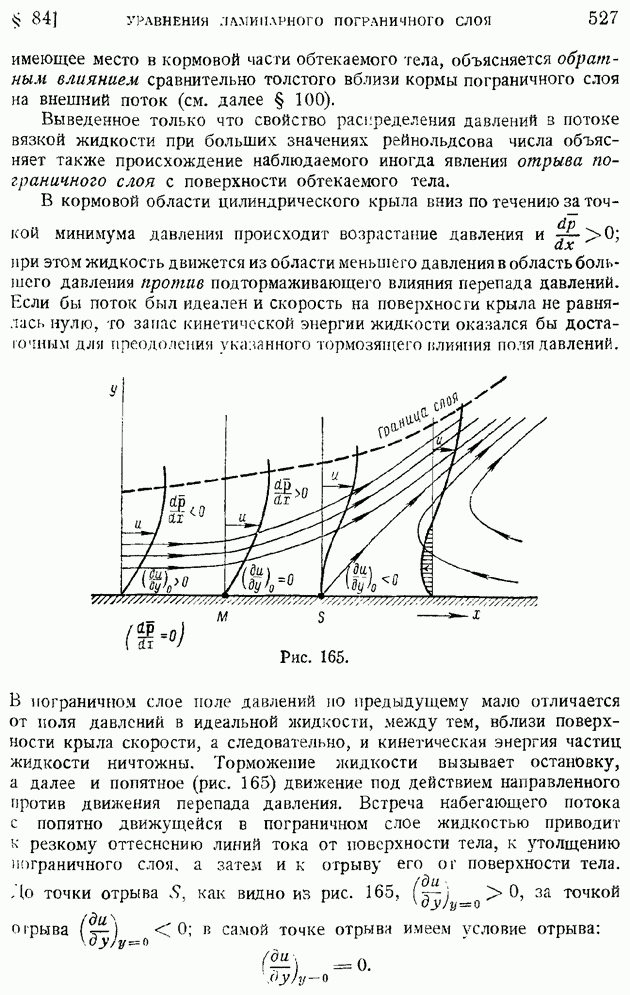
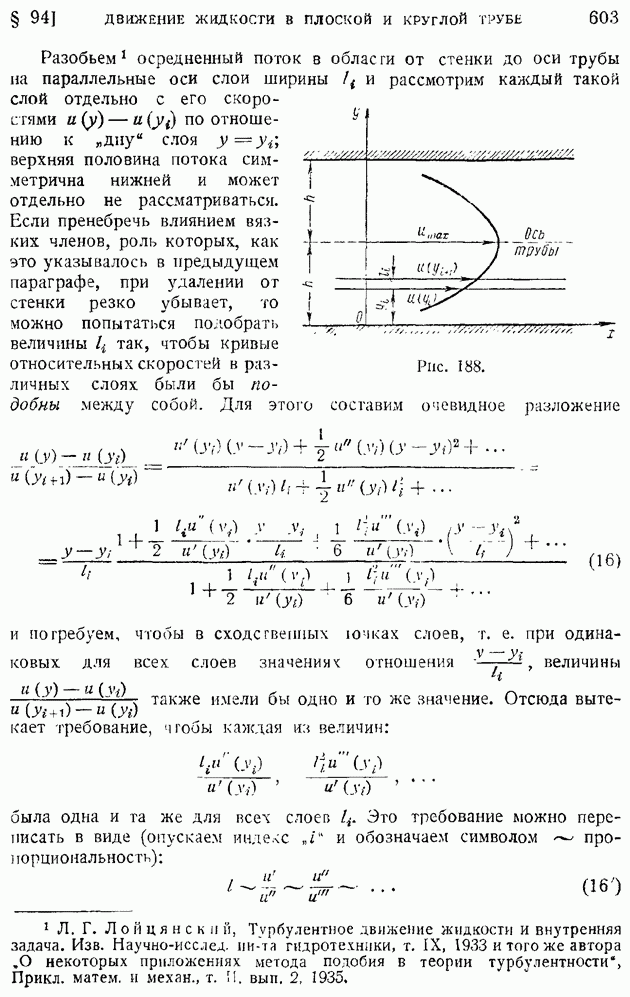
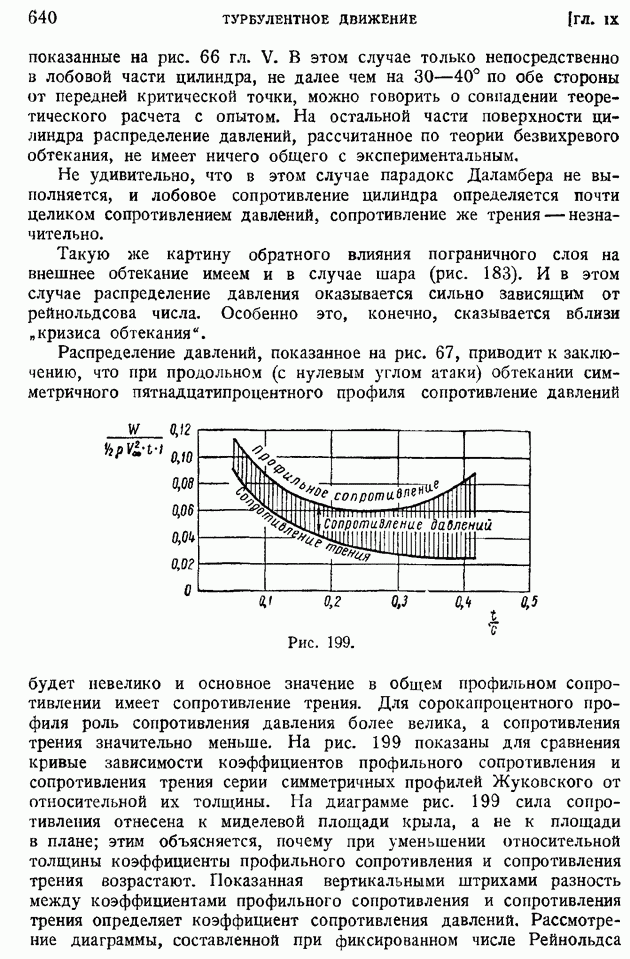
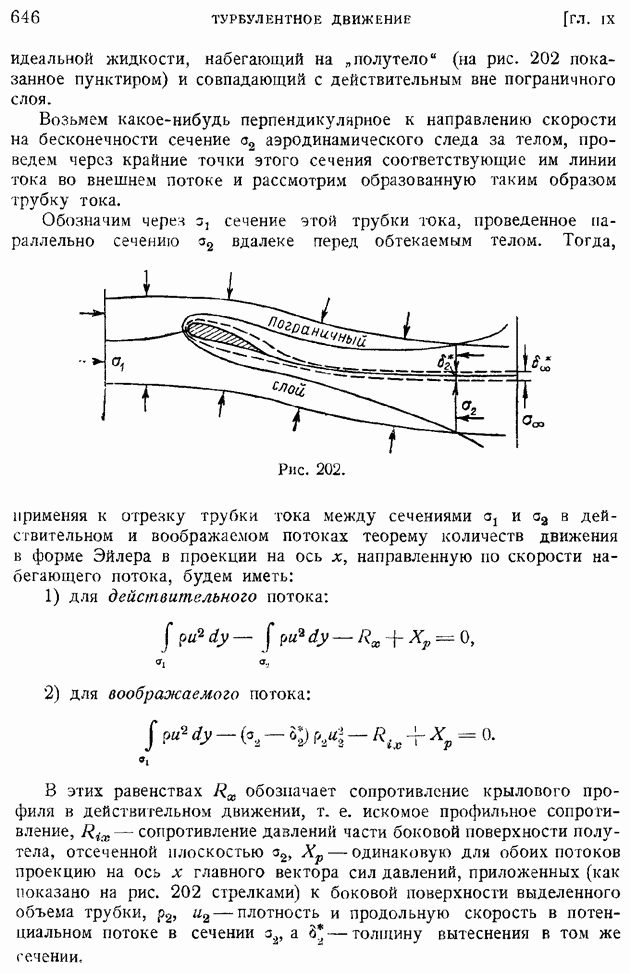
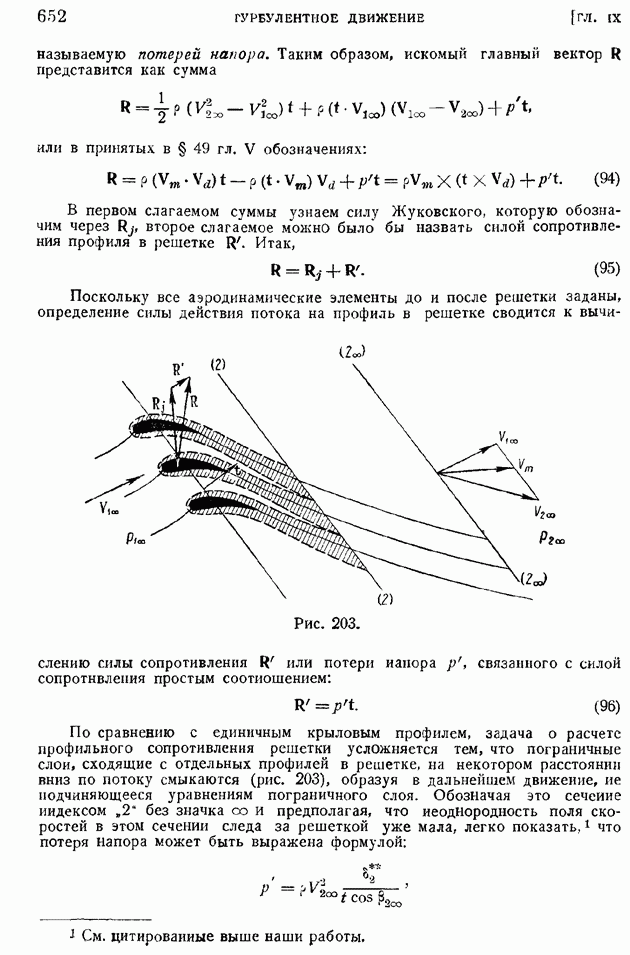
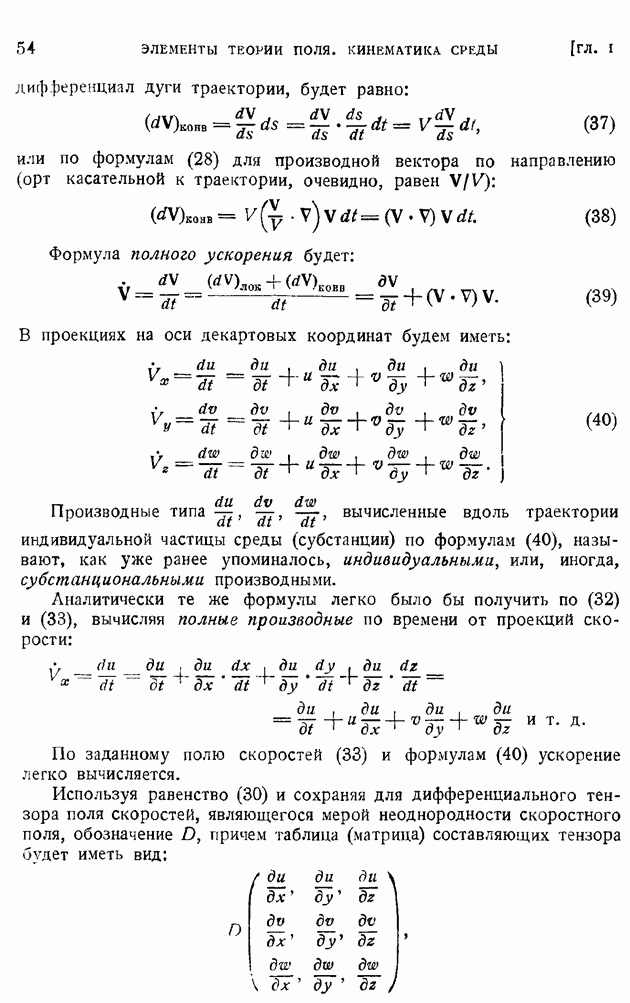| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
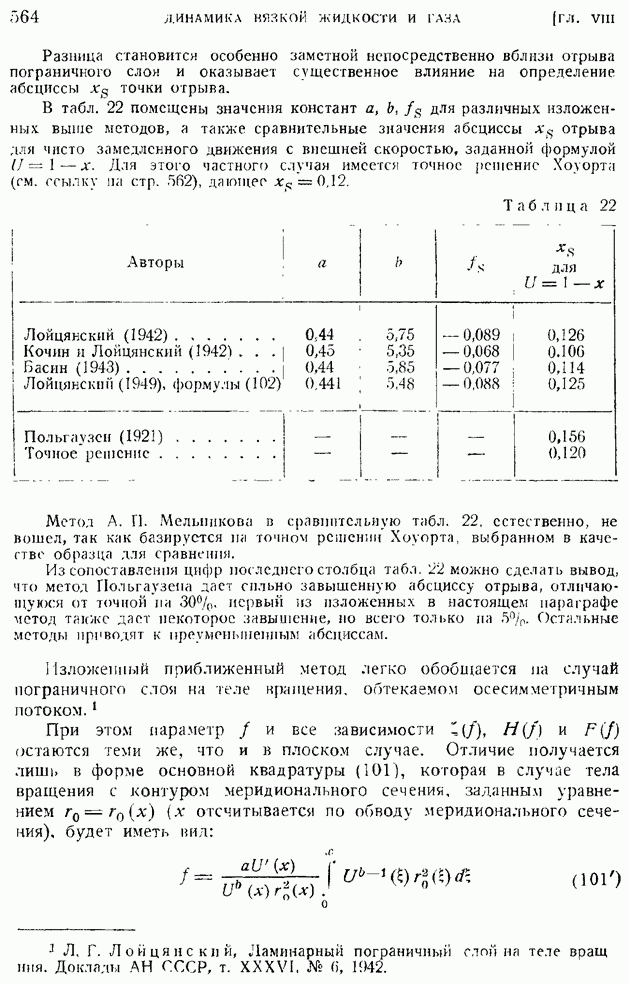
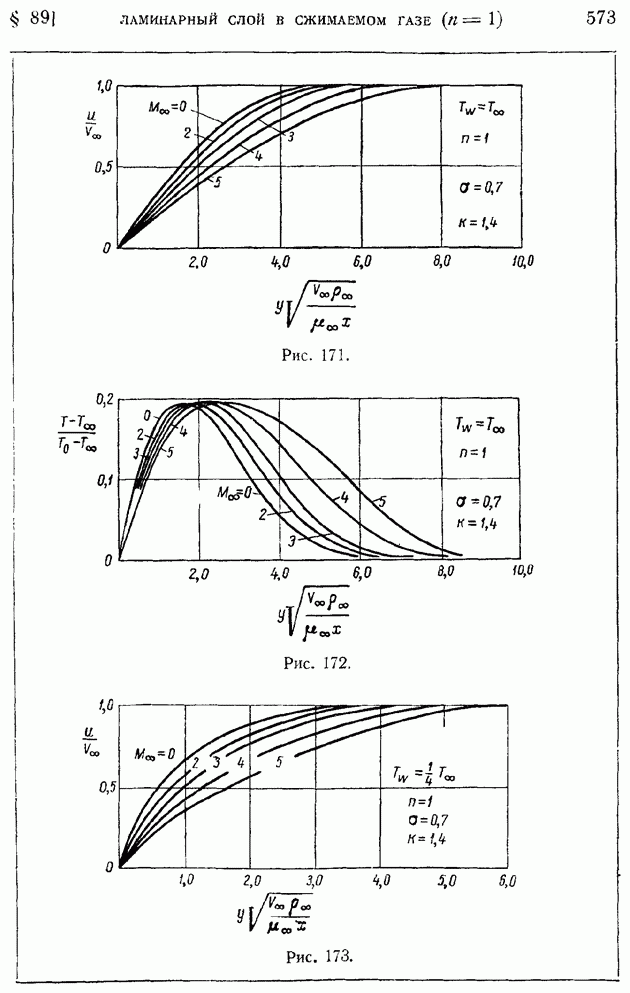
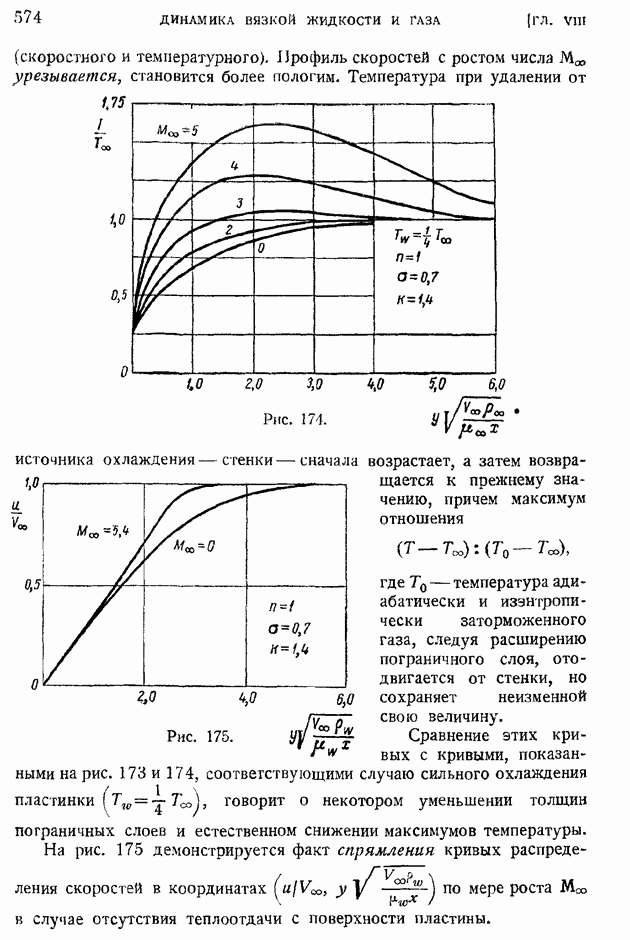
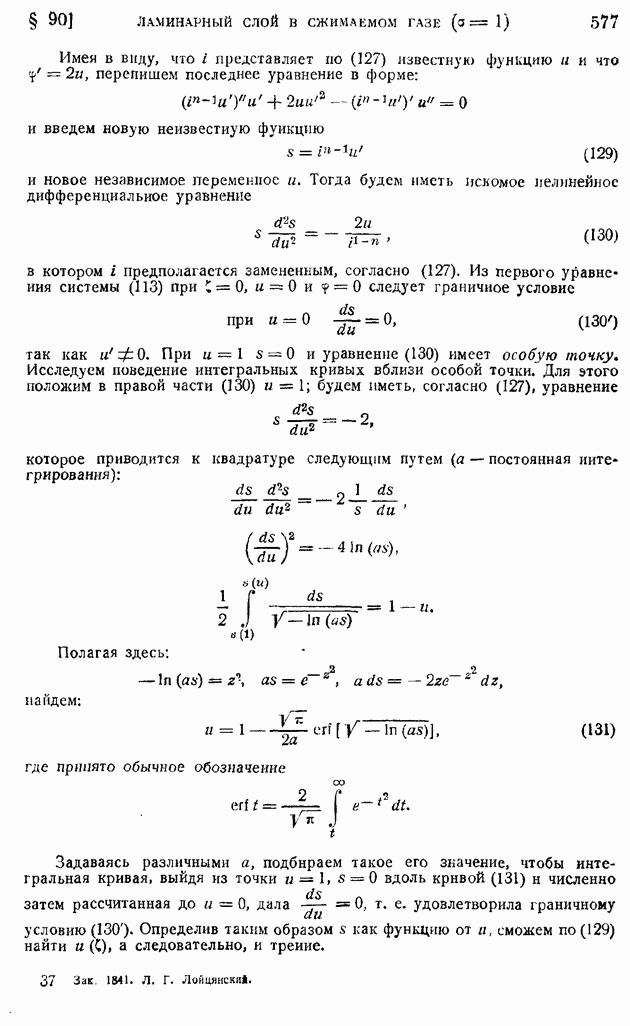
§ 102. Основные закономерности «свободной турбулентности». Плоская турбулентная струя в пространстве, заполненном той же жидкостью
Своеобразным аналогом пограничного слоя служат движения жидкости в струях, в следе за телом и, вообще, движения вблизи границы раздела двух потоков, имеющих различные скорости. Так же как и пограничный слой, эти области характеризуются сосредоточенным действием внутреннего трения — ламинарного или турбулентного, в зависимости от того, какова общая структура потока. Вместе с тем обращает на себя внимание и некоторое отличие задач этого рода от задач пограничного слоя, заключающееся в отсутствии влияния твердой стенки, непроницаемой для жидкости и тормозящей ее движение силами вязкости. Такого рода движения, происходящие в значительном удалении от поверхности твердых тел, называют свободными.
Для ламинарных движений своеобразие "свободных" движений сводится лишь к отсутствию характерного для твердой стенки граничного условия равенства нулю скорости жидкости на обтекаемой поверхности. В случае же турбулентного движения, как сейчас будет показано, специфическая форма эпюры скоростей позволяет упростить основную закономерность трения.
Рассматриваемые в настоящем и следующем параграфах случаи турбулентной струи и турбулентного следа за телом являются иллюстрациями общих методов теории свободной турбулентности. В задачи этой теории входит, наряду с перечисленными выше, изучение турбулентных движений в свободной атмосфере, воздушных и морских течений, различных вентиляционных потоков и др.
Механизм "свободных" турбулентных движений полностью сводится к чисто турбулентному перемешиванию; влияние обычной "молекулярной" вязкости при этом совершенно пренебрежимо, так что рассматриваемые ниже движения оказываются независимыми от рейнольдсова числа, в каком бы прямом или косвенном виде оно ни составлялось.
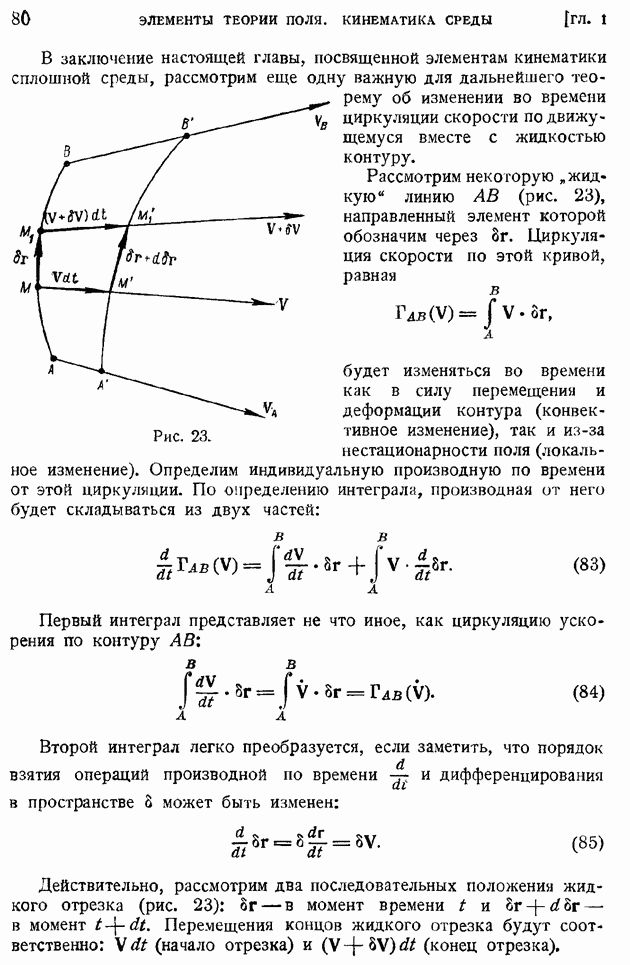
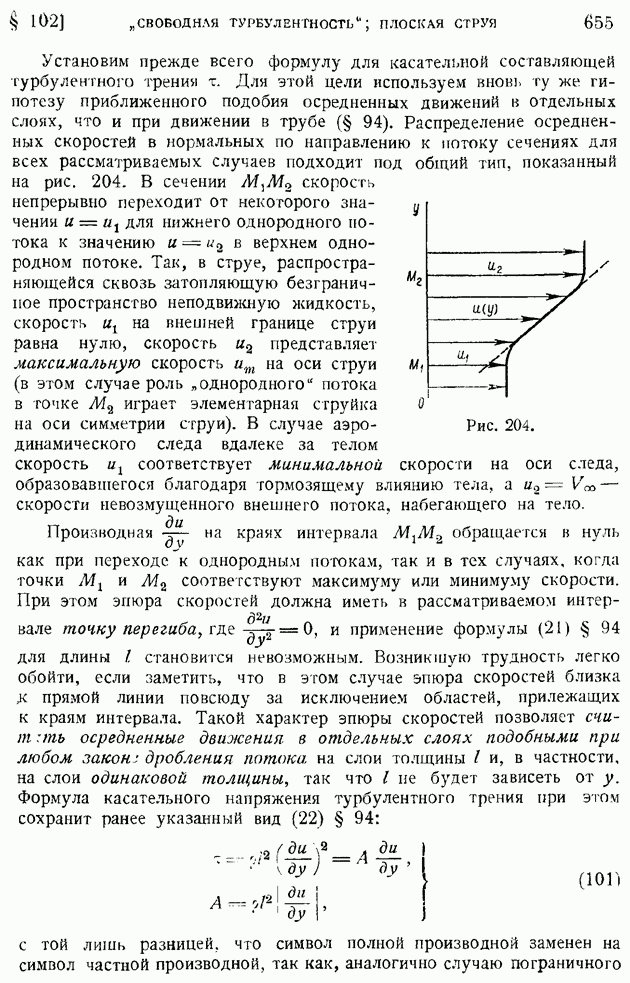
Установим прежде всего формулу для касательной составляющей турбулентного трения  Для этой цели используем вновь ту же гипотезу приближенного подобия осредненных движений в отдельных слоях, что и при движении в трубе (§ 94). Распределение осредненных скоростей в нормальных по направлению к потоку сечениях для всех рассматриваемых случаев подходит под общий тип, показанный на рис. 204. В сечении
Для этой цели используем вновь ту же гипотезу приближенного подобия осредненных движений в отдельных слоях, что и при движении в трубе (§ 94). Распределение осредненных скоростей в нормальных по направлению к потоку сечениях для всех рассматриваемых случаев подходит под общий тип, показанный на рис. 204. В сечении  скорость непрерывно переходит от некоторого значения
скорость непрерывно переходит от некоторого значения  для нижнего однородного потока к значению
для нижнего однородного потока к значению  в верхнем однородном потоке. Так, в струе, распространяющейся сквозь затопляющую безграничное пространство неподвижную жидкость, скорость
в верхнем однородном потоке. Так, в струе, распространяющейся сквозь затопляющую безграничное пространство неподвижную жидкость, скорость  на внешней границе струи равна нулю, скорость
на внешней границе струи равна нулю, скорость  представляет максимальную скорость
представляет максимальную скорость  на оси струи (в этом случае роль "однородного" потока в точке
на оси струи (в этом случае роль "однородного" потока в точке  играет элементарная струйка на оси симметрии струи). В случае аэродинамического следа вдалеке за телом скорость
играет элементарная струйка на оси симметрии струи). В случае аэродинамического следа вдалеке за телом скорость  соответствует минимальной скорости на оси следа, образовавшегося благодаря тормозящему влиянию тела, а
соответствует минимальной скорости на оси следа, образовавшегося благодаря тормозящему влиянию тела, а  скорости невозмущенного внешнего потока, набегающего на тело.
скорости невозмущенного внешнего потока, набегающего на тело.

Рис. 204.
Производная  на краях интервала
на краях интервала  обращается в нуль как при переходе к однородным потокам, так и в тех случаях, когда точки
обращается в нуль как при переходе к однородным потокам, так и в тех случаях, когда точки  соответствуют максимуму или минимуму скорости. При этом эпюра скоростей должна иметь в рассматриваемом интервале точку перегиба, где 0, и применение формулы (21) § 94 для длины I становится невозможным. Возникшую трудность легко обойти, если заметить, что в этом случае эпюра скоростей близка
соответствуют максимуму или минимуму скорости. При этом эпюра скоростей должна иметь в рассматриваемом интервале точку перегиба, где 0, и применение формулы (21) § 94 для длины I становится невозможным. Возникшую трудность легко обойти, если заметить, что в этом случае эпюра скоростей близка  прямой линии повсюду за исключением областей, прилежащих к краям интервала. Такой характер эпюры скоростей позволяет считать осредненные движения в отдельных слоях подобными при любом закон: дробления потока на слои толщины
прямой линии повсюду за исключением областей, прилежащих к краям интервала. Такой характер эпюры скоростей позволяет считать осредненные движения в отдельных слоях подобными при любом закон: дробления потока на слои толщины  в частности, на слои одинаковой толщины, так что I не будет зависеть от у. Формула касательного напряжения турбулентного трения при этом сохранит ранее указанный вид (22) § 94:
в частности, на слои одинаковой толщины, так что I не будет зависеть от у. Формула касательного напряжения турбулентного трения при этом сохранит ранее указанный вид (22) § 94:

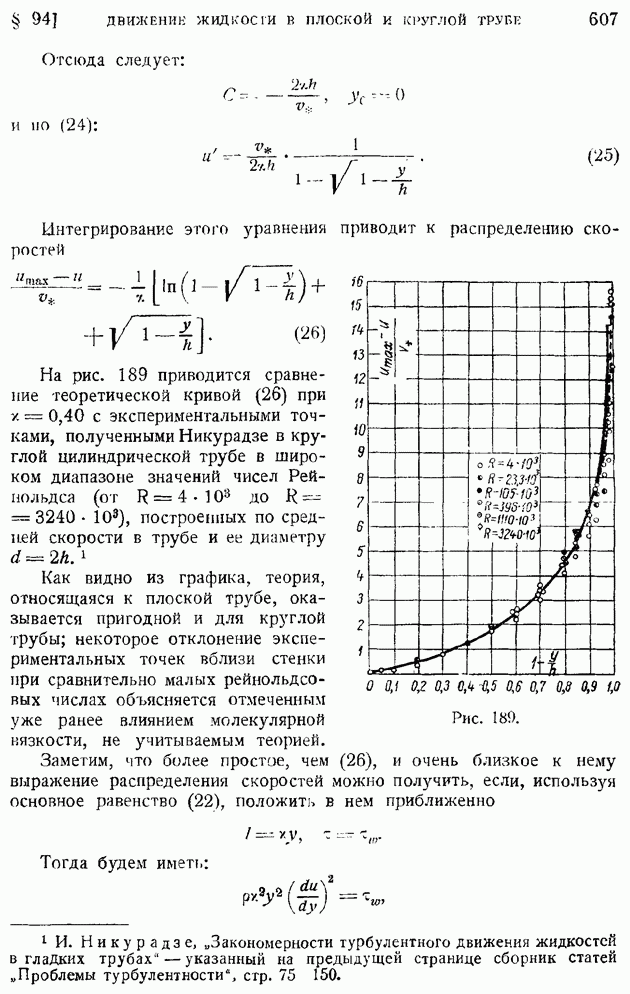
с той лишь разницей, что символ полной производной заменен на символ частной производной, так как, аналогично случаю пограничного
слоя, вдоль струи (при изменении абсциссы  поле скоростей деформируется. Пользуясь близостью эпюры скоростей к прямой линии, можем в выражении (101) коэффициента турбулентного обмена А произвести приближенную замену
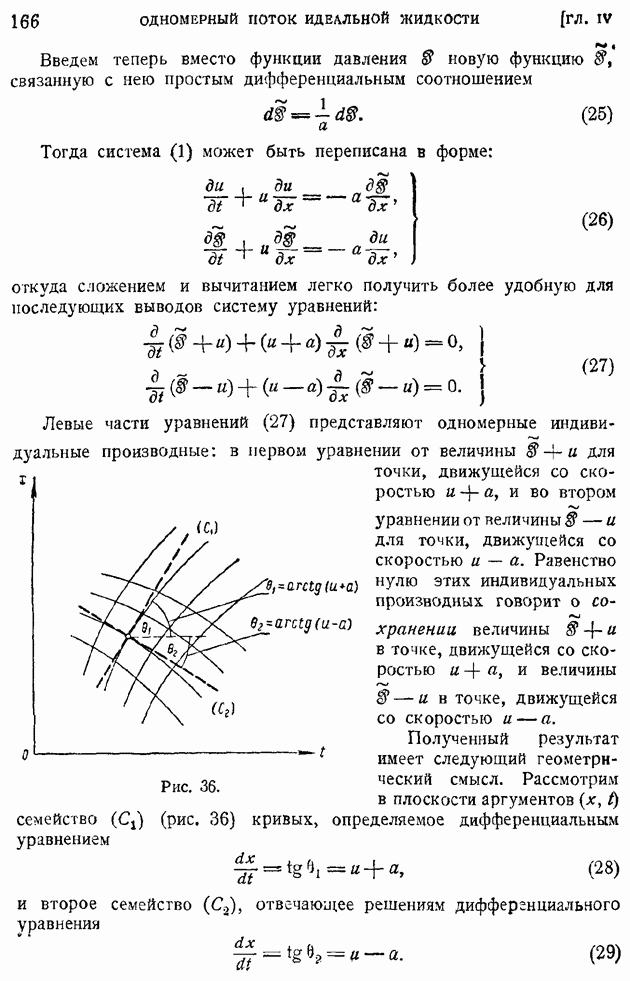
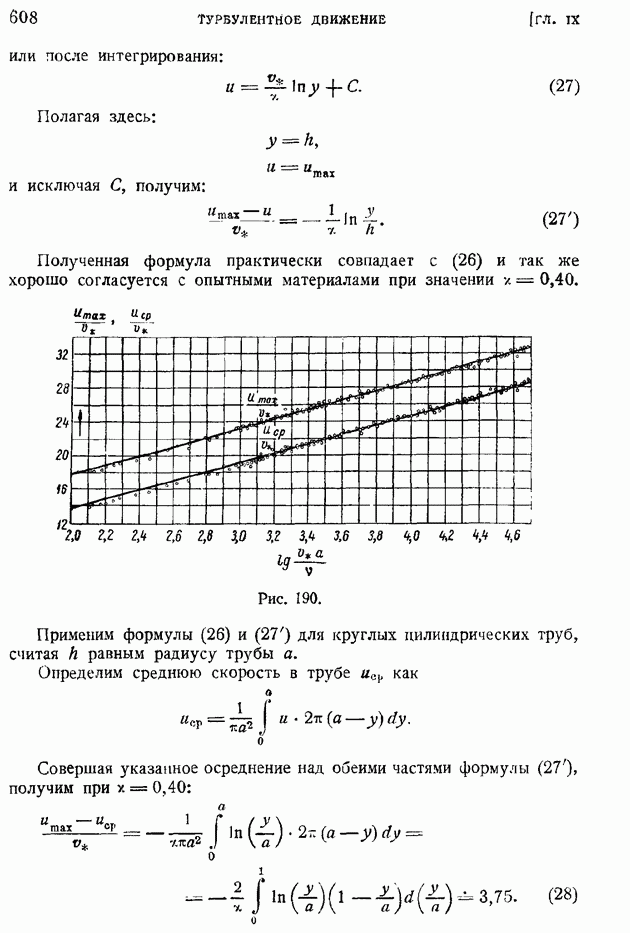
поле скоростей деформируется. Пользуясь близостью эпюры скоростей к прямой линии, можем в выражении (101) коэффициента турбулентного обмена А произвести приближенную замену

и положить

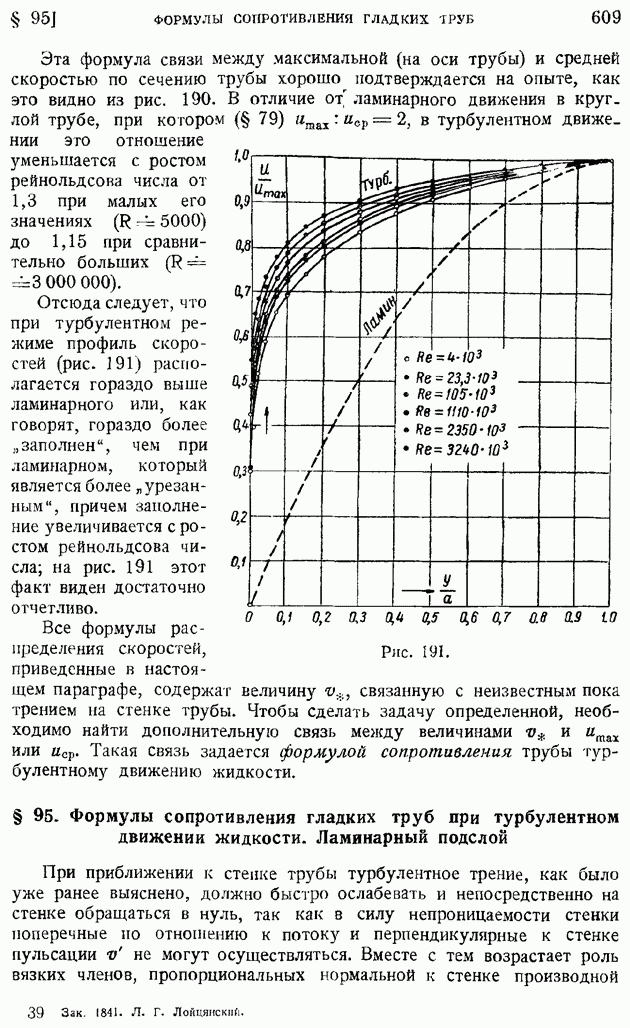
где  ширина области турбулентного перемешивания. Возникающая при этом на краях области ошибка несущественна, так как в выражении турбулентного трения (101) величина А умножается на обращающуюся на краях области в нуль. Таким образом, коэффициент, турбулентного обмена в задачах свободной турбулентности может бить принят постоянным по сечению, т. е. не зависящим от у (но, вообще говоря, зависящим от х, т. е. переменным вдоль течения). Принимая постоянную по сечению толщину слоев I пропорциональной размеру области обмена
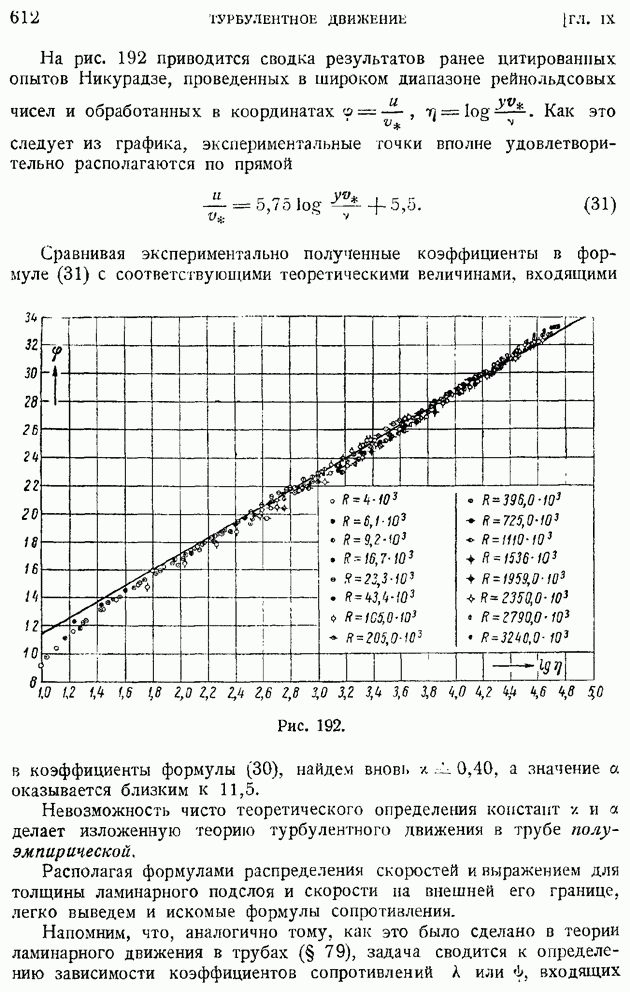
ширина области турбулентного перемешивания. Возникающая при этом на краях области ошибка несущественна, так как в выражении турбулентного трения (101) величина А умножается на обращающуюся на краях области в нуль. Таким образом, коэффициент, турбулентного обмена в задачах свободной турбулентности может бить принят постоянным по сечению, т. е. не зависящим от у (но, вообще говоря, зависящим от х, т. е. переменным вдоль течения). Принимая постоянную по сечению толщину слоев I пропорциональной размеру области обмена  окончательно получим следующую общую для большинства задач теории "свободной турбулентности" формулу коэффициента турбулентного обмена:
окончательно получим следующую общую для большинства задач теории "свободной турбулентности" формулу коэффициента турбулентного обмена:

где  некоторый одинаковый для всех рассматриваемых движений постоянный коэффициент пропорциональности; величины
некоторый одинаковый для всех рассматриваемых движений постоянный коэффициент пропорциональности; величины  меняются в общем случае от сечения к сечению и представляют неизвестные функции координаты х, отсчнтываемой вдоль по течению.
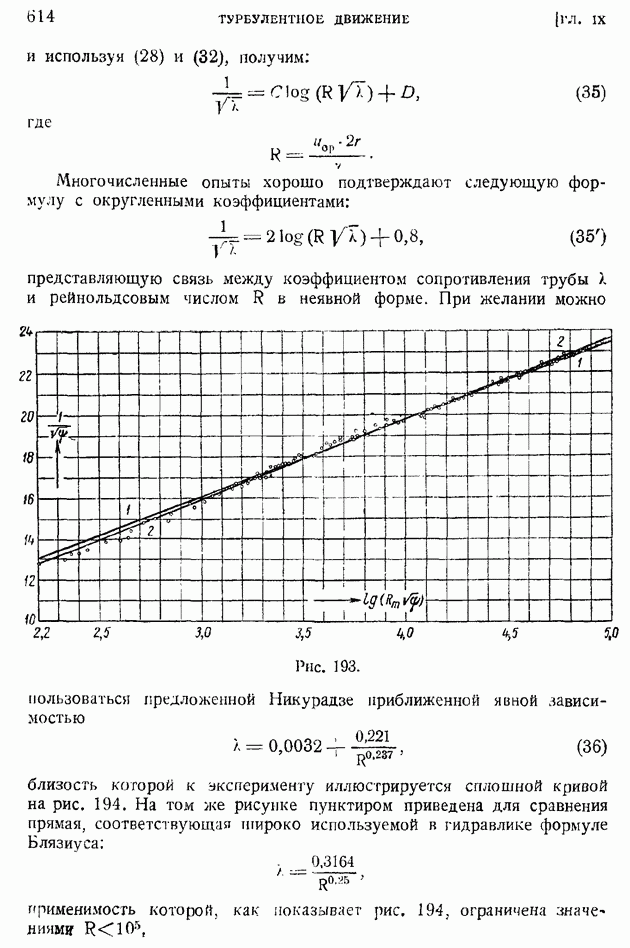
меняются в общем случае от сечения к сечению и представляют неизвестные функции координаты х, отсчнтываемой вдоль по течению.
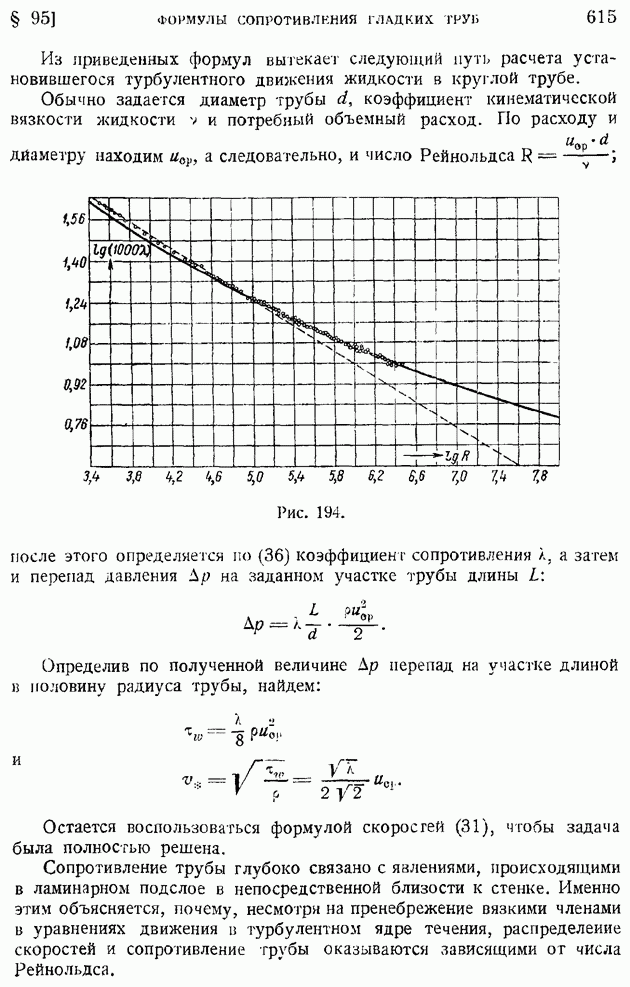
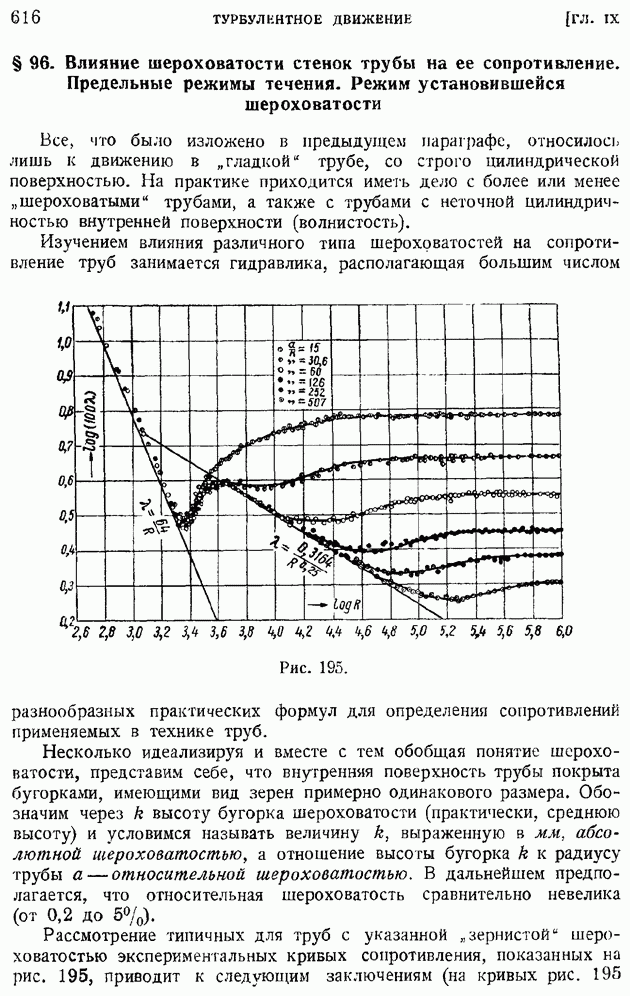
Гипотеза постоянства коэффициента турбулентного перемешивания неоднократно применялась в задачах турбулентного движения в свободной атмосфере, в океанах и реках. Для случая турбулентного движения жидкости в аэродинамическом и тепловом следе та же гипотеза была отчетливо сформулирована еще в 1938 г. Б. Я. Трубчиковым, принявшим А за постоянную величину, не зависящую ни от ни от у. Как далее будет показано, такое допущение действительно верно для турбулентного следа, но непригодно, например, для струи. Формула, аналогичная (104), была предложена в 1942 г. Л. Прандглем, исходившим из соображений, отличных от использованной нами гипотезы подобия. Первые применения новой формулы Прандтля были выполнены Гертлером.
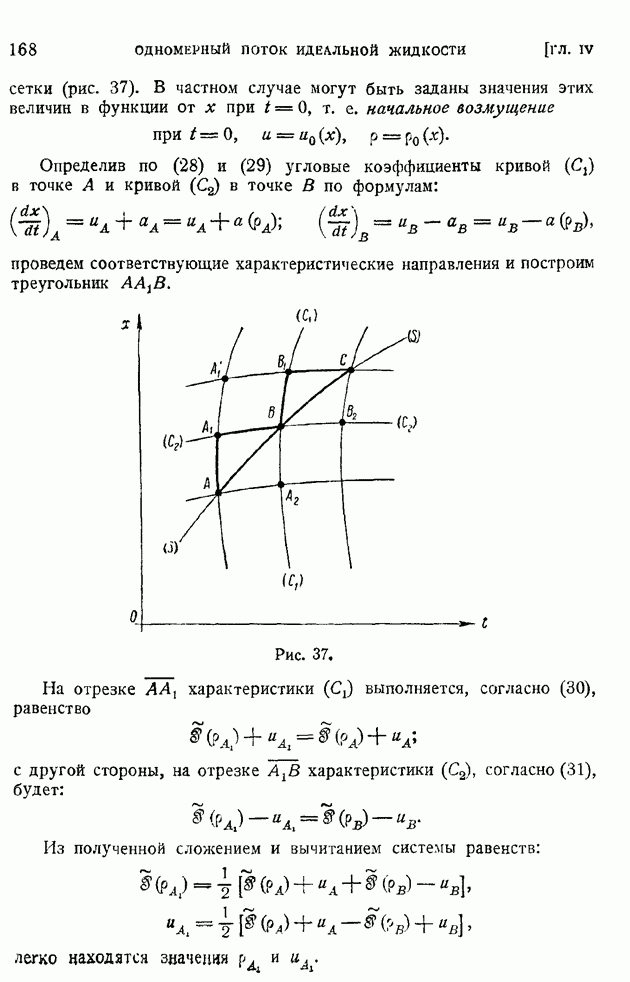
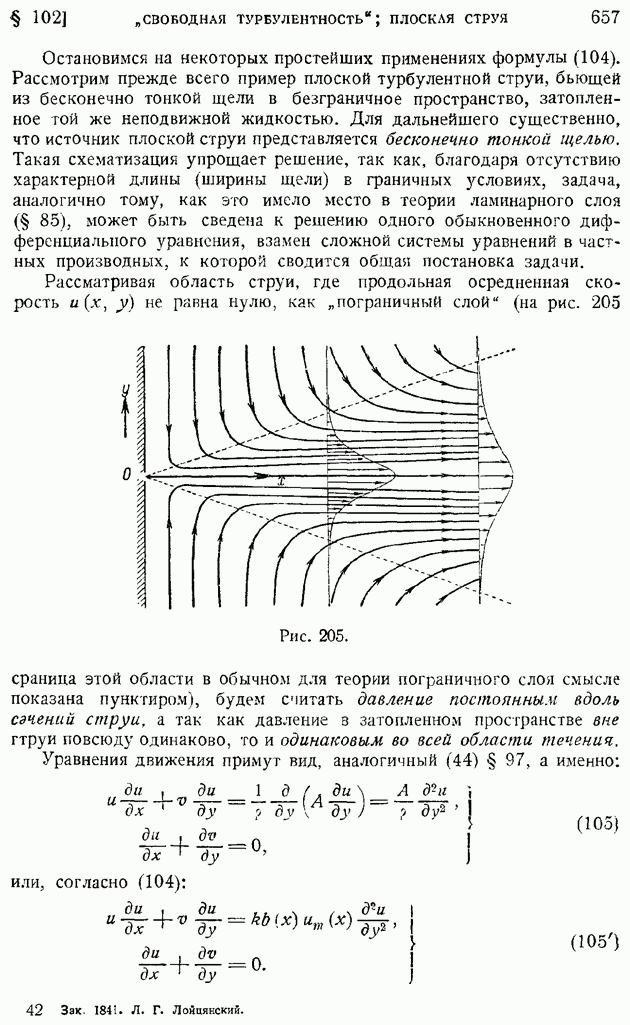
Остановимся на некоторых простейших применениях формулы (104). Рассмотрим прежде всего пример плоской турбулентной струи, бьющей из бесконечно тонкой щели в безграничное пространство, затопленное той же неподвижной жидкостью. Для дальнейшего существенно, что источник плоской струи представляется бесконечно тонкой щелью. Такая схематизация упрощает решение, так как, благодаря отсутствию характерной длины (ширины щели) в граничных условиях, задача, аналогично тому, как это имело место в теории ламинарного слоя (§ 85), может быть сведена к решению одного обыкновенного дифференциального уравнения, взамен сложной системы уравнений в частных производных, к которой сводится общая постановка задачи.

Рис. 205.
Рассматривая область струи, где продольная осредненная скорость и(х, у) не равна нулю, как "пограничный слой" (на рис. 205 граница этой области в обычном для теории пограничного слоя смысле показана пунктиром), будем считать давление постоянным вдоль сэчений струи, а так как давление в затопленном пространстве вне гтруи повсюду одинаково, то и одинаковым во всей области течения.
Уравнения движения примут вид, аналогичный (44) § 97, а именно:

или, согласно (104):

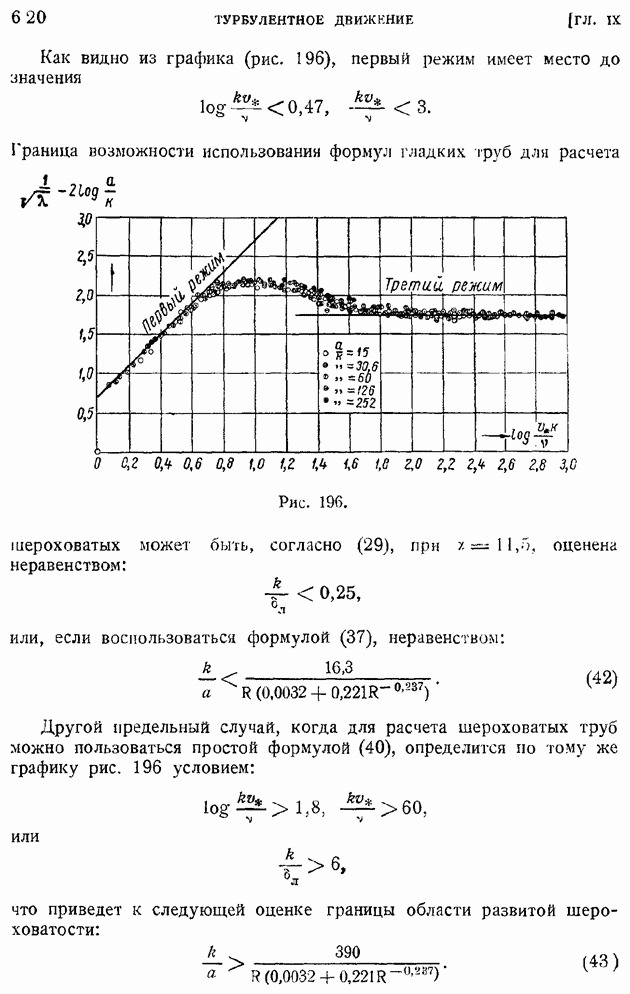
Задача представляется вначале неопределенной, поскольку наперед неизвестны законы изменения ширины струи  и максимальной скорости на оси струи
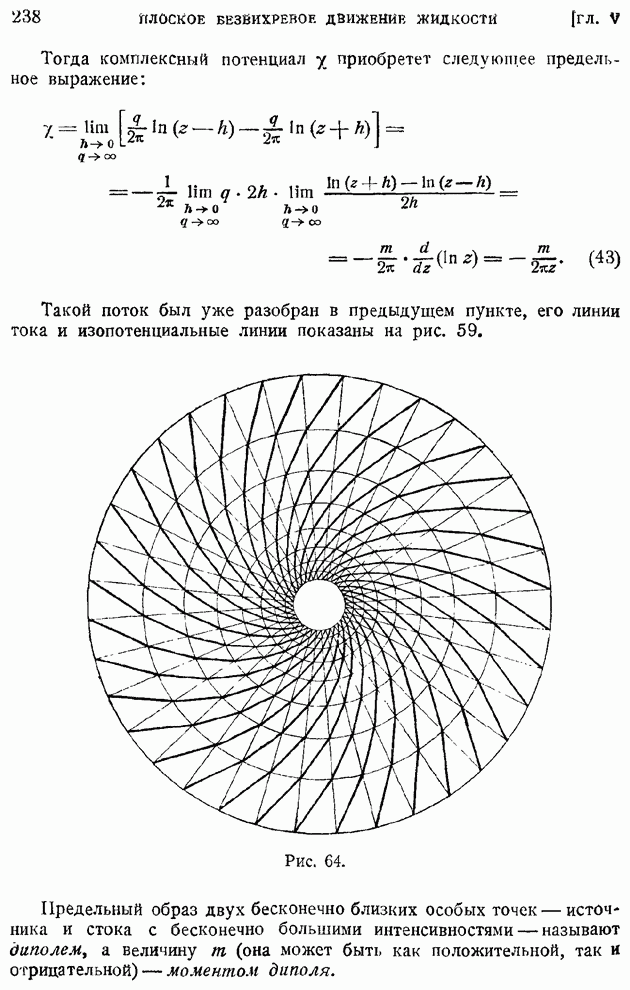
и максимальной скорости на оси струи  Эта неопределенность исчезает, если выражение продольной скорости искать в форме семейства подобных между собою кривых
Эта неопределенность исчезает, если выражение продольной скорости искать в форме семейства подобных между собою кривых

где под  понимается некоторая условная (в том же смысле, как "толщина" пограничного слоя) ширина струи, а
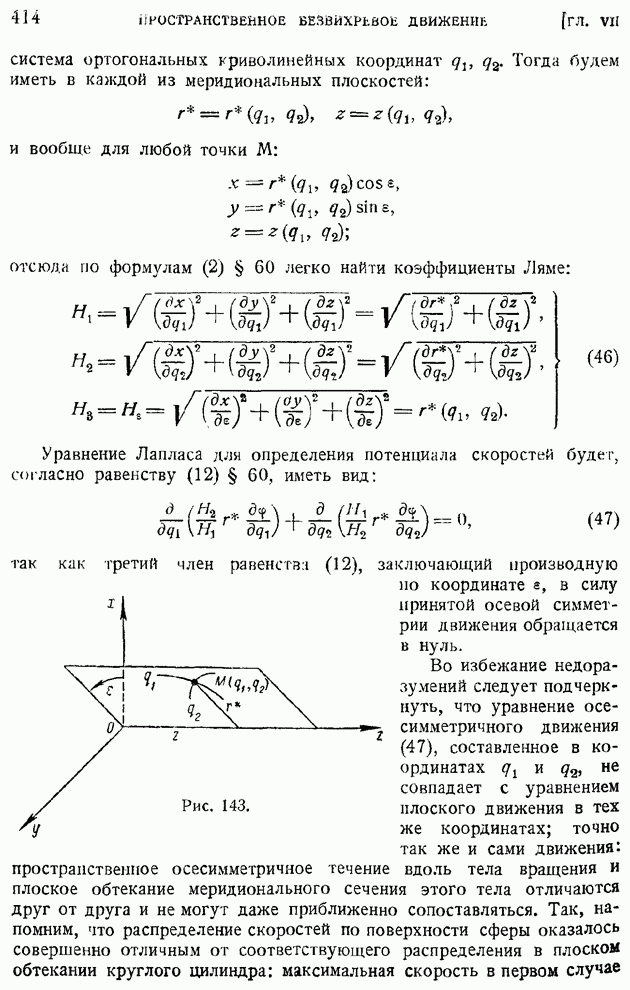
понимается некоторая условная (в том же смысле, как "толщина" пограничного слоя) ширина струи, а  новый аргумент. Пользуясь выражением (106), вычисляем (штрих означает дифференцирование по
новый аргумент. Пользуясь выражением (106), вычисляем (штрих означает дифференцирование по 

Подставим эти выражения в первое уравнение (105), тогда после простых приведений получим:

Введем в рассмотрение функцию  положив
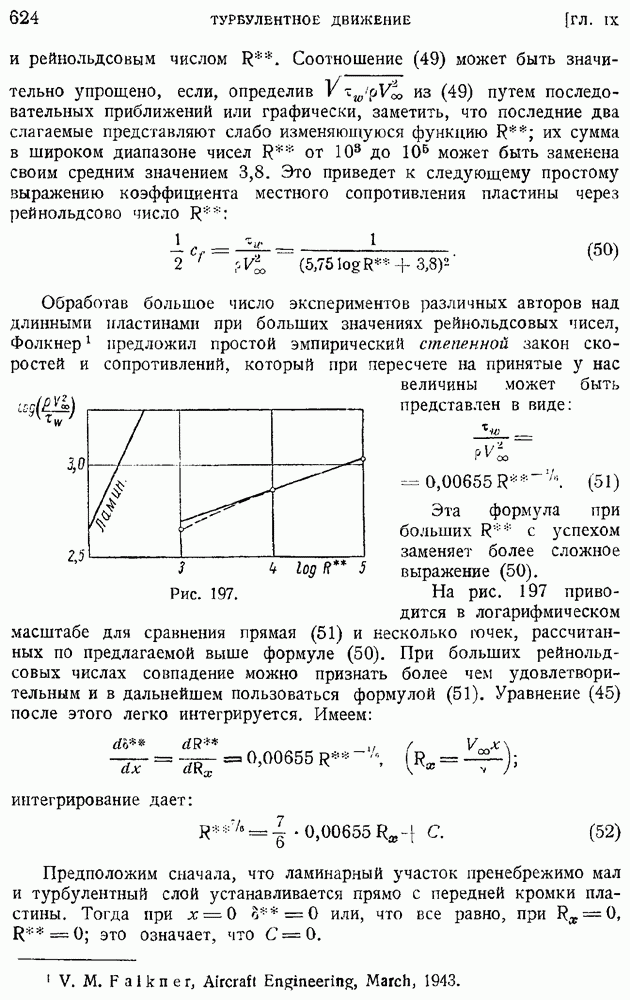
положив

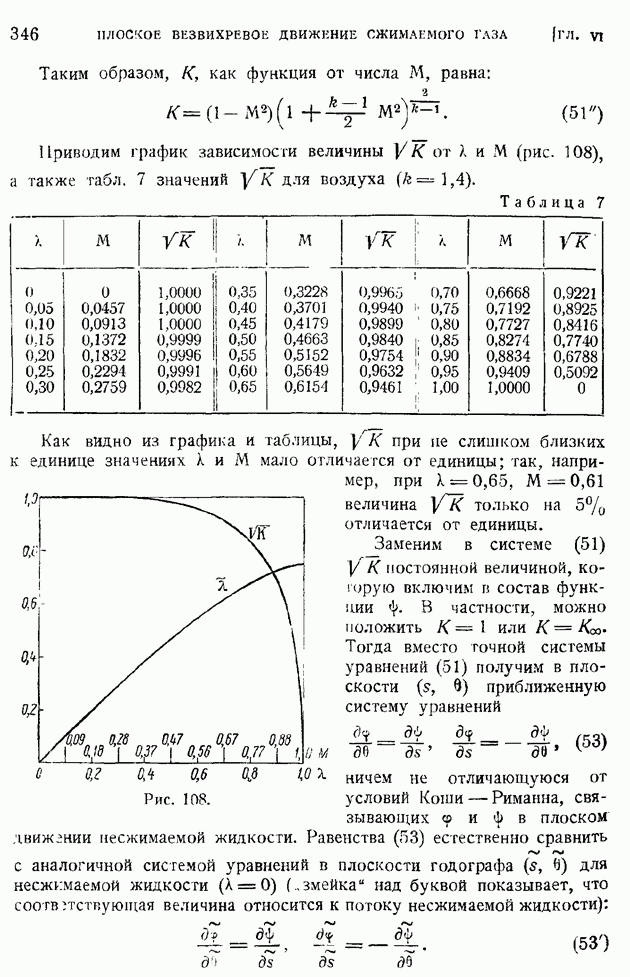
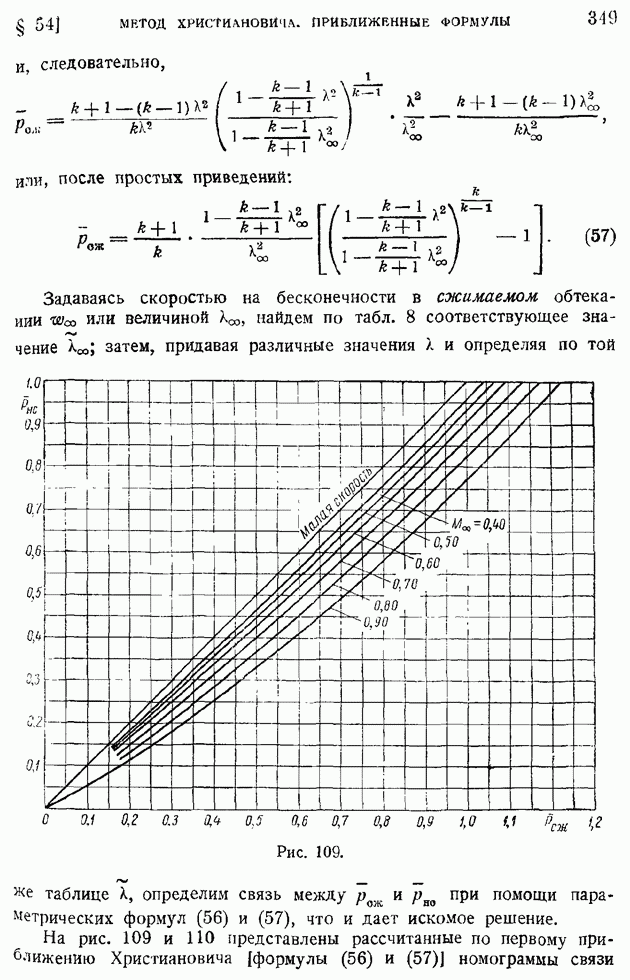
Функция  связана простым соотношением с функцией тока
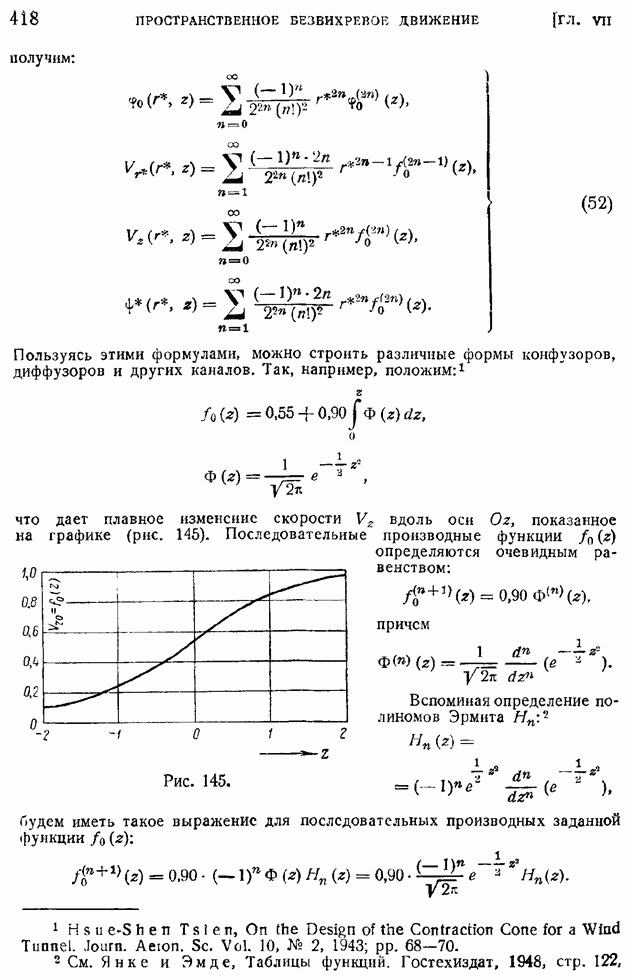
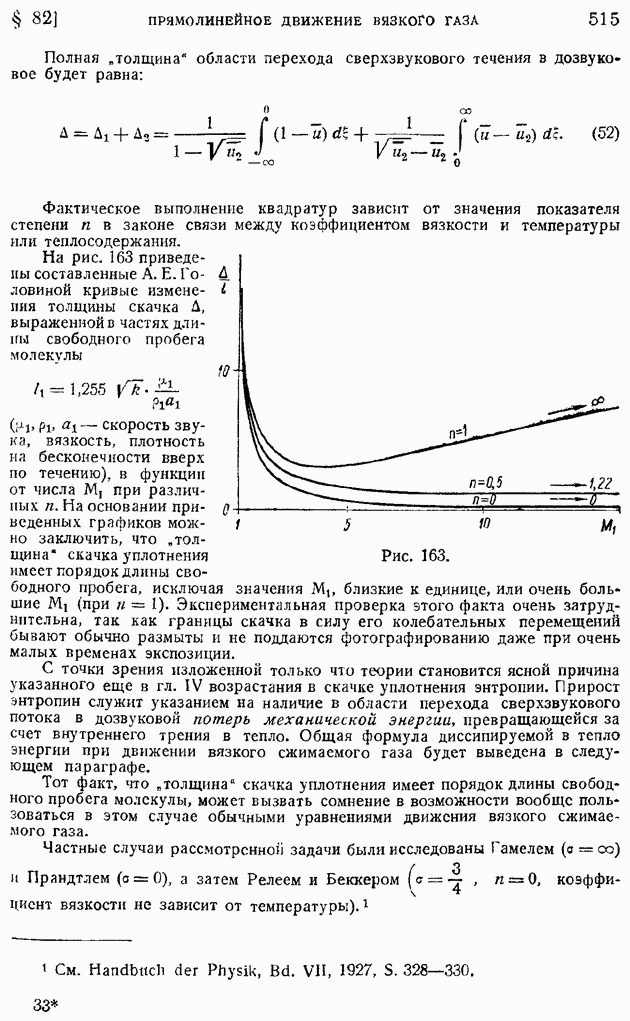
связана простым соотношением с функцией тока  Действительно, по определению функции тока, если принять
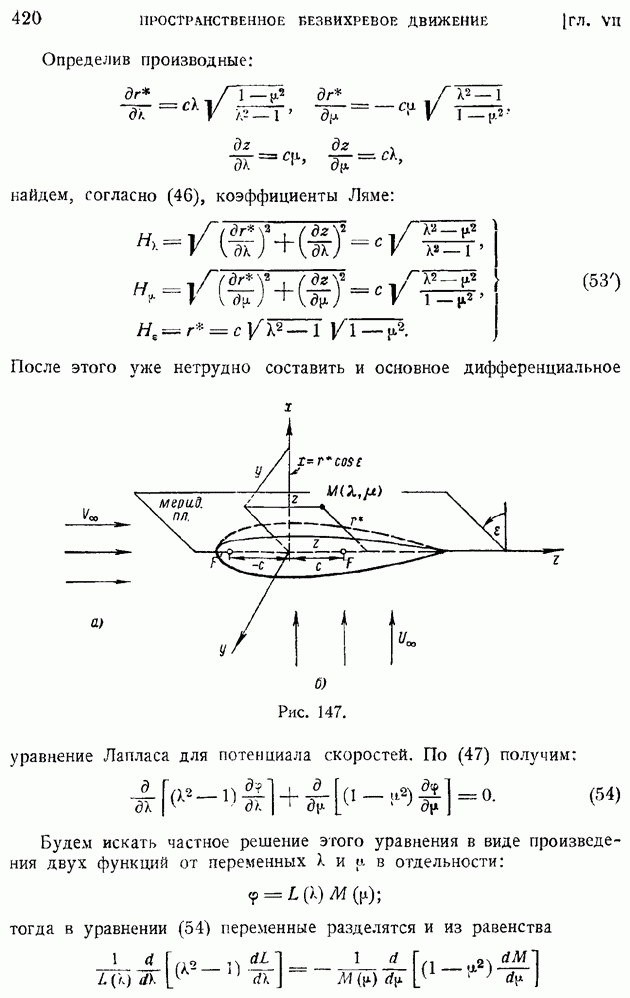
Действительно, по определению функции тока, если принять 

Будем иметь:

так что уравнение (107) может быть переписано в виде

Замечая, что, в силу одинаковости давления во всей области течения, проекция на ось  вектора количества движения, протекающего сквозь любое сечение струи, должна быть одна и та же, получим
вектора количества движения, протекающего сквозь любое сечение струи, должна быть одна и та же, получим

где  представляет заданное количество движения струи при выходе ее из щели, или интенсивность струи. Подставляя сюда значение и из формулы (106), найдем:
представляет заданное количество движения струи при выходе ее из щели, или интенсивность струи. Подставляя сюда значение и из формулы (106), найдем:

или

Дифференцируя обе части этого равенства по х, получим:

в силу чего уравнение (109) перепишется окончательно в виде:

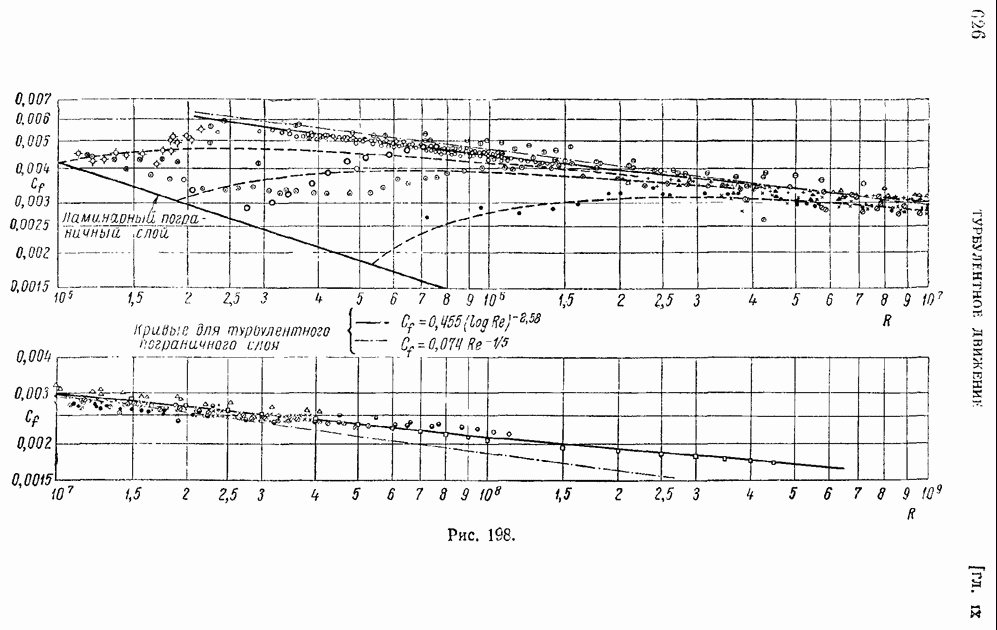
Из условия независимости аргументов  следует, что
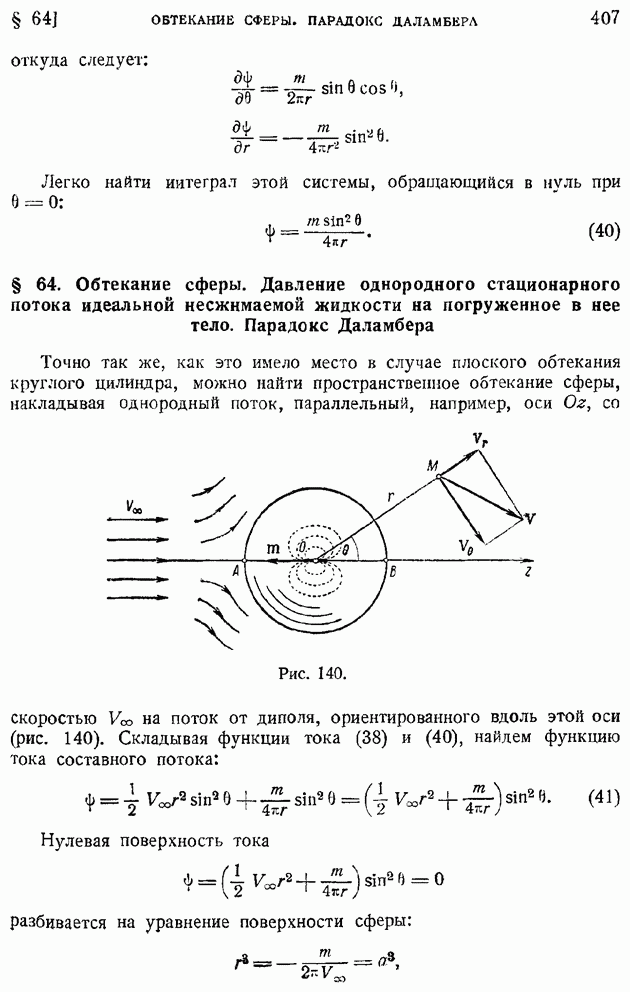
следует, что

где с — некоторая не зависящая от граничных условий константа, характеризующая турбулентный характер струи. Как показывает последнее равенство, "ширина" струи возрастает пропорционально расстоянию от источника, а границами струи служат прямолинейные лучи, выходящие из источника (на рис. 205 они показаны пунктиром).
Из равенства (110) можно найти закон убывания максимальной скорости на оси при удалении от источника струи:

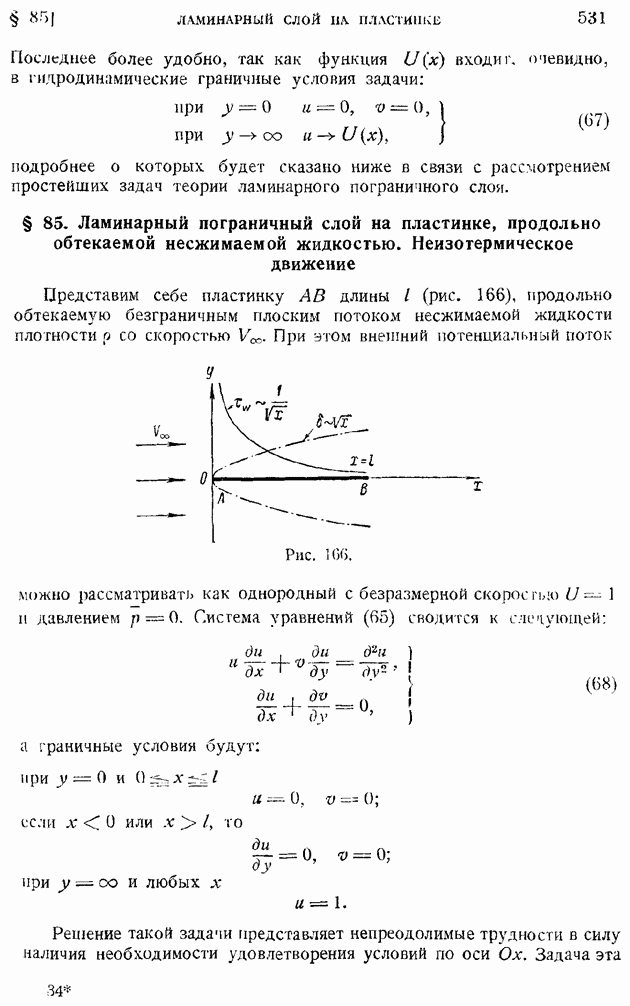
Найдя закон (112) изменения ширины струи  и (113) — осевой скорости
и (113) — осевой скорости  можем определить и закон изменения коэффициента турбулентного трения А. Имеем по (104) и только что указанным равенствам:
можем определить и закон изменения коэффициента турбулентного трения А. Имеем по (104) и только что указанным равенствам:

Коэффициент турбулентного обмена, не изменяясь по сечению струи, возрастает пропорционально корню квадратному из расстояния сечения до источника струи.
Основное дифференциальное уравнение (111) приводится к виду:

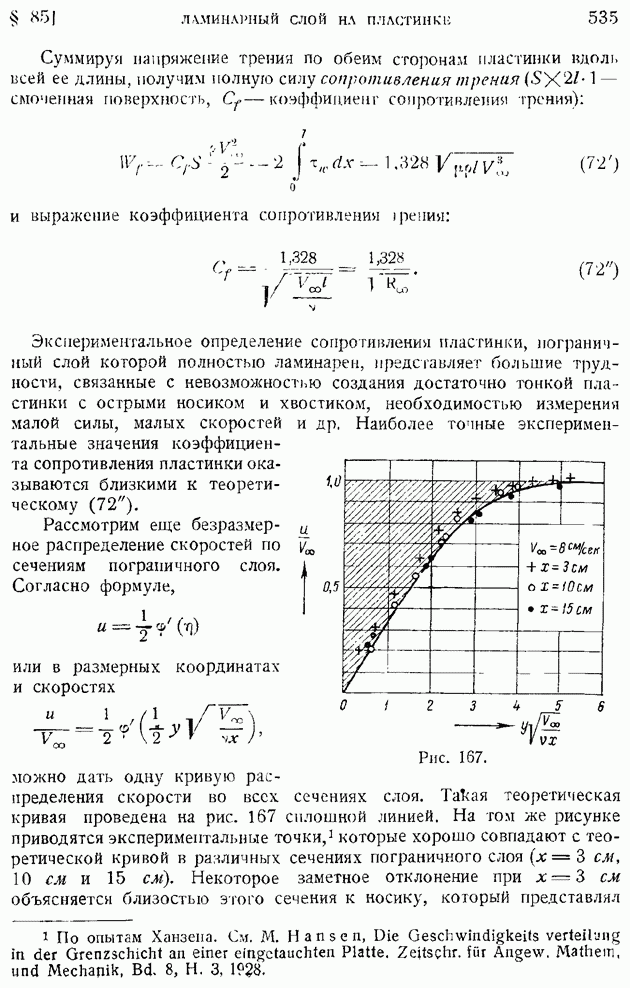
и легко может быть непосредственно два раза проинтегрировано. Действительно, имеем:

и, следовательно,

Постоянные интегрирования  найдем из очевидных граничных условий:
найдем из очевидных граничных условий:

выражающих: что ось струи принята за нулевую линию тока, что в силу симметрии производная обращается на оси в нуль и что вдоль оси  Уравнение (115) при этом переходит в легко интегрируемое уравнение
Уравнение (115) при этом переходит в легко интегрируемое уравнение

которое, при принятых граничных условиях (116), имеет решение:

Отсюда получаем

или, переходя к гиперболическим функциям,

Отсюда находим продольную составляющую скорости и:

и поперечную составляющую 

Чтобы сравнить теоретические формулы с опытными материалами, обозначим через У такое значение при котором  и тогда из равенства
и тогда из равенства

будет следовать:

При этом равенство (118) может быть переписано в виде:

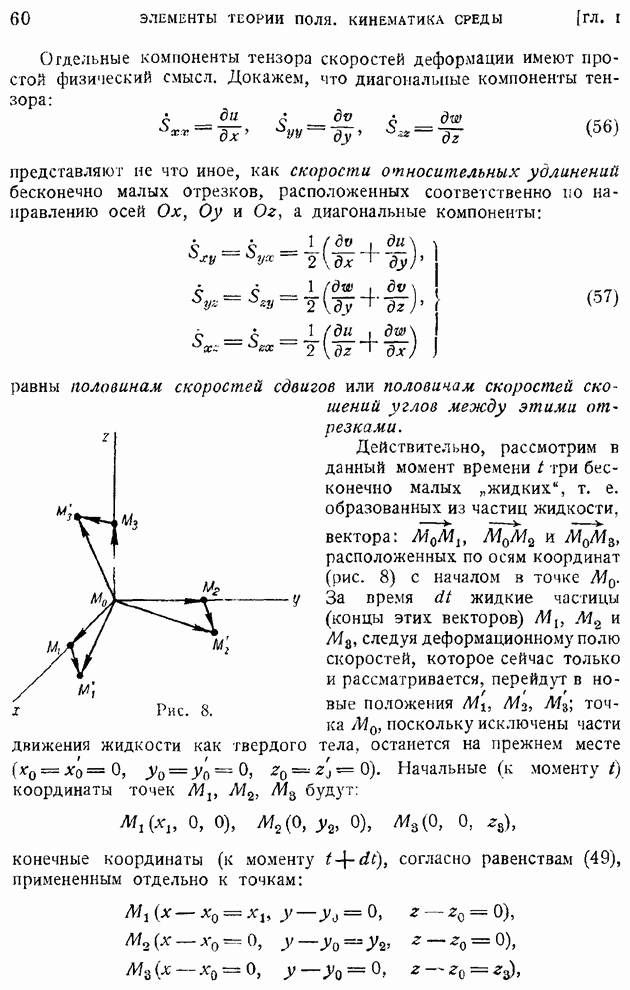
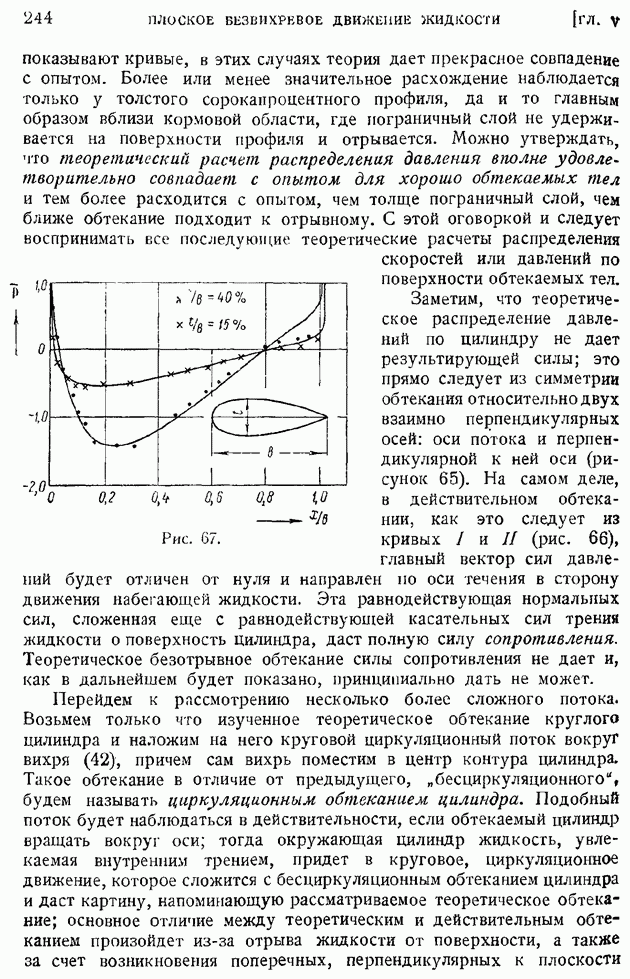
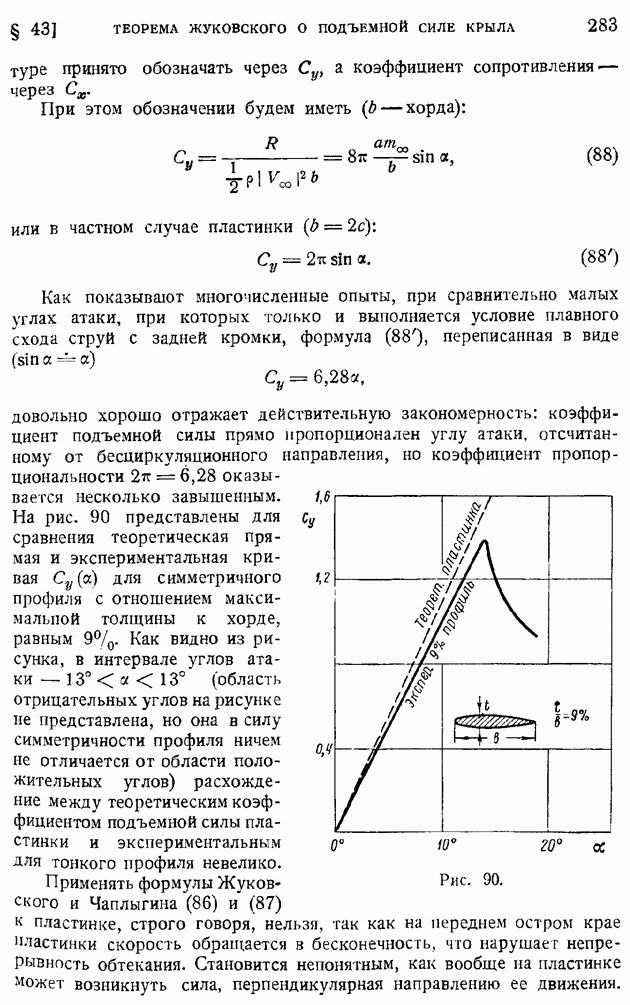
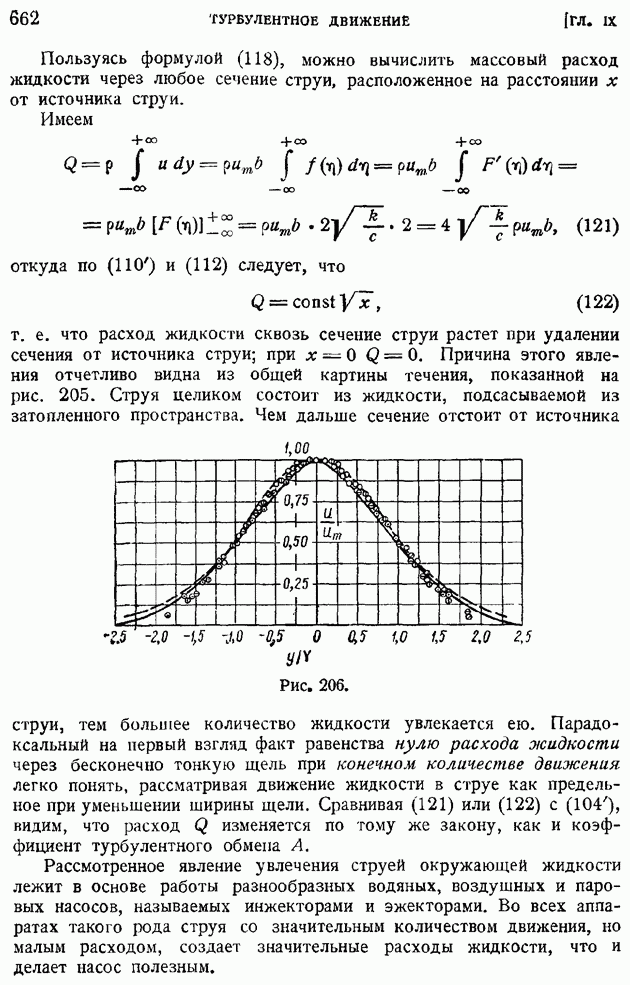
На рис. 206 соответствующая кривая показана пунктиром. Совпадение этой теоретической кривой с опытными точками вполне удовлетворительное. При таком сравнении неизвестные константы  входят в определение величины У.
входят в определение величины У.
Пользуясь формулой (118), можно вычислить массовый расход жидкости через любое сечение струи, расположенное на расстоянии х от источника струи. Имеем

откуда по (110) и (112) следует, что

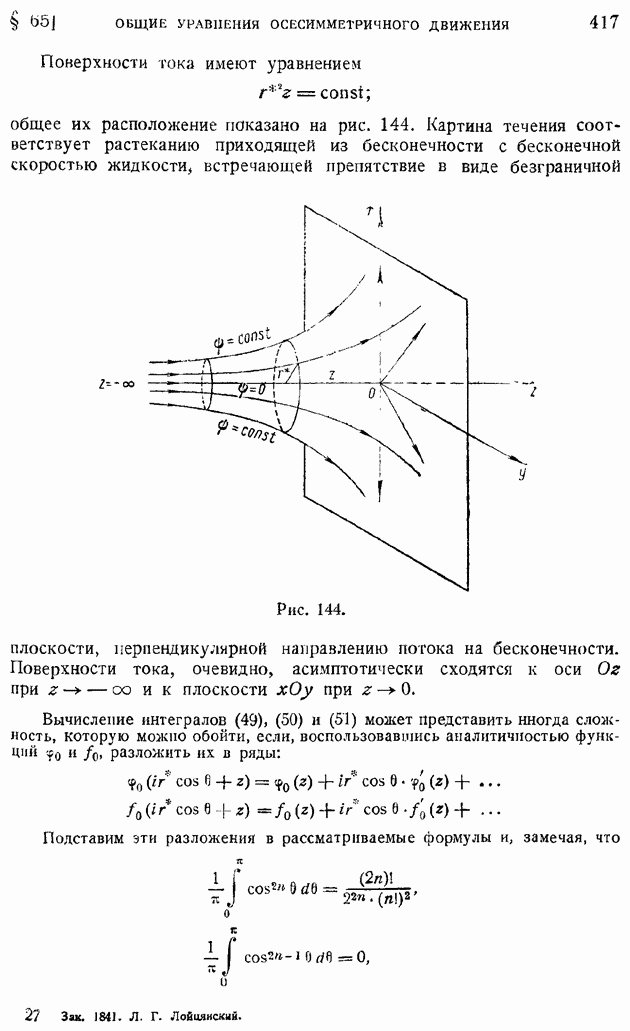
т. е. что расход жидкости сквозь сечение струи растет при удалении сечения от источника струи; при  Причина этого явления отчетливо видна из общей картины течения, показанной на рис. 205. Струя целиком состоит из жидкости, подсасываемой из затопленного пространства. Чем дальше сечение отстоит от источника струи, тем большее количество жидкости увлекается ею.
Причина этого явления отчетливо видна из общей картины течения, показанной на рис. 205. Струя целиком состоит из жидкости, подсасываемой из затопленного пространства. Чем дальше сечение отстоит от источника струи, тем большее количество жидкости увлекается ею.

Рис. 206.
Парадоксальный на первый взгляд факт равенства нулю расхода жидкости через бесконечно тонкую щель при конечном количестве движения легко понять, рассматривая движение жидкости в струе как предельное при уменьшении ширины щели. Сравнивая (121) или (122) с (104), видим, что расход  изменяется по тому же закону, как и коэффициент турбулентного обмена А.
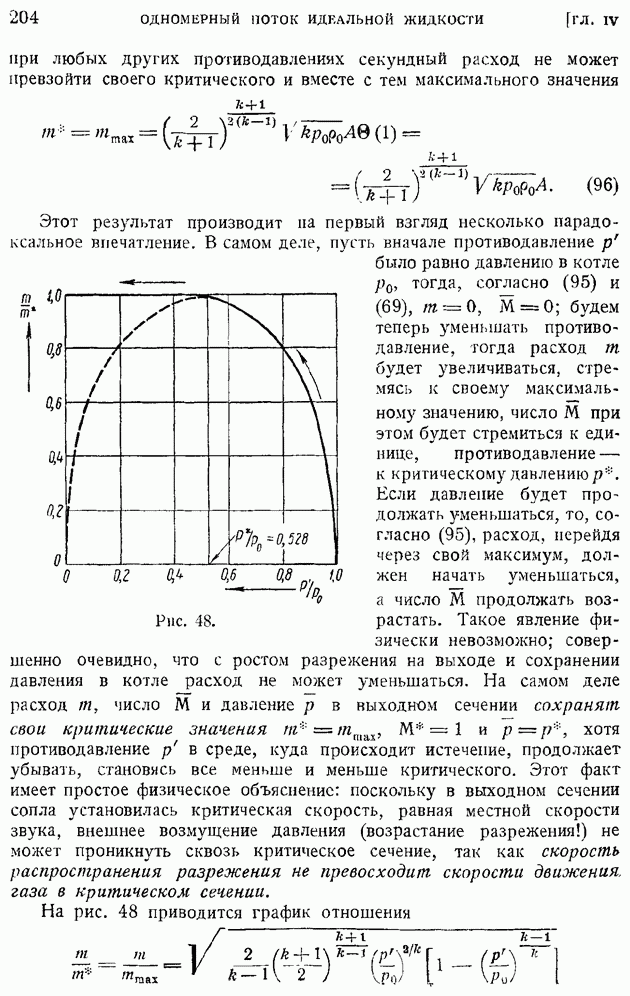
изменяется по тому же закону, как и коэффициент турбулентного обмена А.
Рассмотренное явление увлечения струей окружающей жидкости лежит в основе работы разнообразных водяных, воздушных и паровых насосов, называемых инжекторами и эжекторами. Во всех аппаратах такого рода струя со значительным количеством движения, но малым расходом, создает значительные расходы жидкости, что и делает насос полезным.
Для расчета плоской струи необходимо задать какие-то характерные для струи параметры. Это могут быть: сохраняющееся вдоль всей струи ее количество движения  расход или осевая скорость в некотором фиксированном сечении струи и др.
расход или осевая скорость в некотором фиксированном сечении струи и др.
Заметим, что рассмотренное решение, как это следует из ранее приведенных рассуждений, содержит произвольную постоянную с, существенно зависящую от турбулентности струи и являющуюся экспериментальной константой данной струи. От этой константы зависит угол расширения струи, который будет тем больше, чем интенсивнее турбулентность в струе.
Изложенный метод решения задачи не единственный. Можно было бы воспользоваться и непосредственно формулой (22) § 94, не опираясь на приближенное постоянство коэффициента турбулентного обмена. Такое решение задачи о плоской турбулентной струе оказывается более сложным, так как приводит к дифференциальному уравнению, требующему численного интегрирования. Результат такого решения, выполненного в свое время Толлмином, приведен в виде сплошной кривой на том же рис. 206. Можно заметить, что изложенное ранее решение (пунктирная кривая) ближе к экспериментальным данным в средней части струи, чем кривая Толлмина; по краям струи, наоборот, кривая Толлмина оказывается более близкой к опытам.
Мы не излагали решения задачи о ламинарной струе, так как это движение не представляет практического интереса. Решение задачи о ламинарной струе имеет много общего с только что изложенным решением задачи о турбулентной струе, так как и в том и в другом случае предполагается, что коэффициент внутреннего трения (молекулярной или турбулентной вязкости) постоянен по сечению струи. Однако не следует забывать, что в ламинарной струе коэффициент вязкости постоянен во всей области течения, а не только по сечению струи. Кроме того, наличие влияния вязкости изменяет вид основного аргумента  и форму границы струи. Подробное изложение задачи о ламинарной струе можно найти на стр. 124—134 нашей монографии "Аэродинамика пограничного слоя".
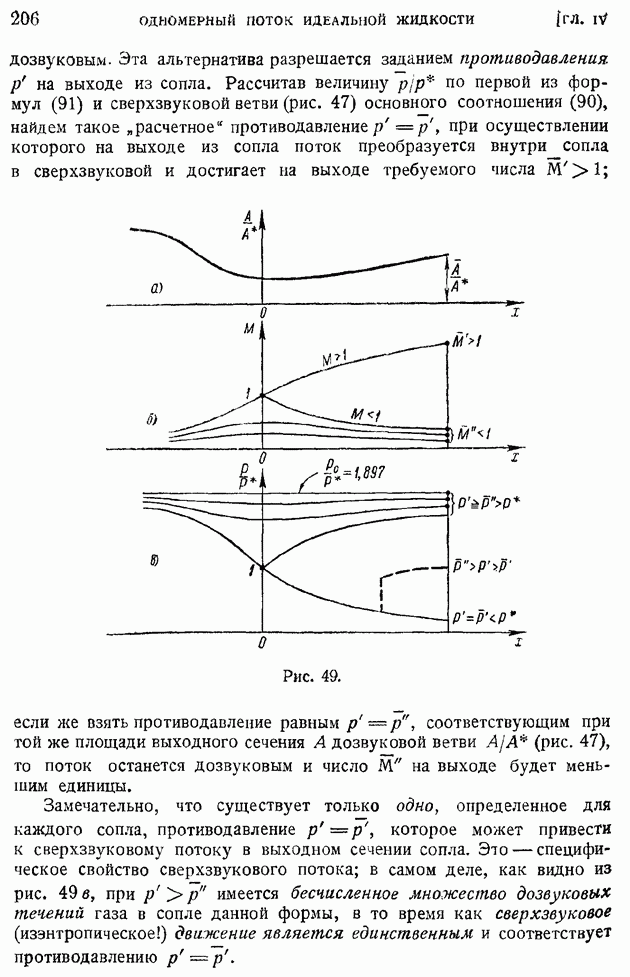
и форму границы струи. Подробное изложение задачи о ламинарной струе можно найти на стр. 124—134 нашей монографии "Аэродинамика пограничного слоя".
Не имея возможности останавливаться на изложении других задач о струях (осесимметричная струя, пограничный слой на границе двух движущихся жидкостей и др.), заметим, что все они могут быть разрешены теми же приближенными методами, что и задача о плоской струе.
Чрезвычайно важному вопросу об обобщении теории струй на случай практически используемых в технике как изотермических, так
и неизотермических струй, с учетом влияния сжимаемости газа, а также конечности диаметров сопла, из которого происходит истечение, и других обстоятельств, были посвящены заслуженно пользующиеся широкой популярностью исследования Г. Н. Абрамовича. Сводку этих исследований можно найти в специальной его монографии.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Предмет механики жидкости и газа. Основные свойства «макромодели» жидкости и газа: сплошность и подвижность
- § 2. Основные методы механики жидкости и газа. Области применения и главнейшие задачи
- § 3. Краткий очерк исторического развития механики жидкости и газа. От гидромеханики древних до установления воззрений ньютонианской эпохи
- § 4. Эпоха Эйлера и Бернулли. Гидроаэродинамика в XIX в.
- § 5. Современный этап развития механики жидкости и газа
- ГЛАВА I. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
- § 6. Поле физической величины. Скалярное и векторное поля. Поверхности уровня. Векторные линин и трубки
- § 7. Мера однородности поля в данном направлении и в дайной точке. Градиевт скалярного поля и дифференциальный тензор векторного поля как меры неоднородности поля
- § 8. Задание движения сплошной среды. Поле скоростей. Линии тока и траектории
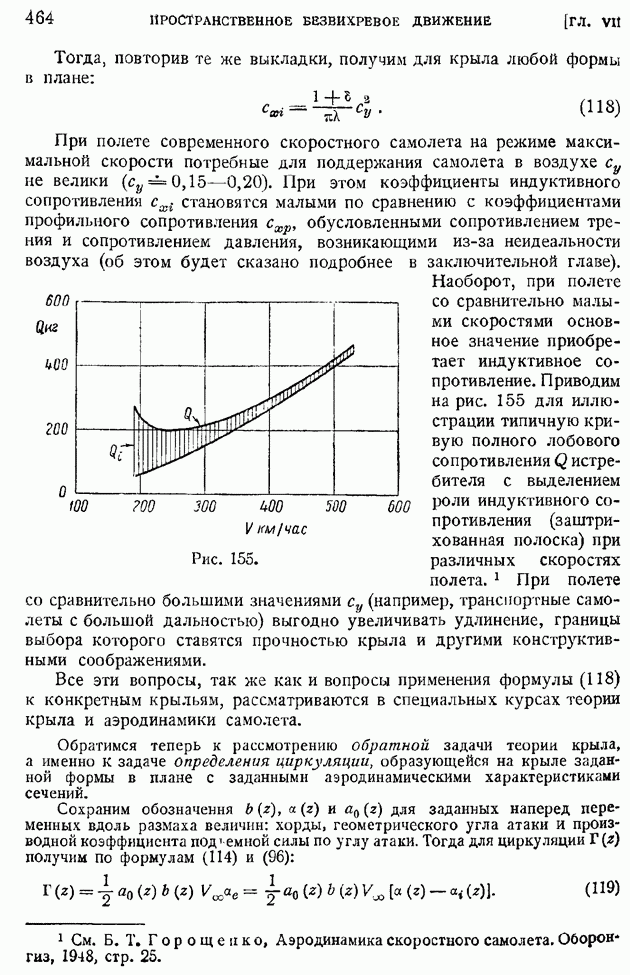
- § 9. Поле ускорений. Разложение ускорения частицы на локальную и конвективную составляющие
- § 10. Скоростное поле сплошной среды в окрестности данной точки. Угловая скорость и вихрь. Тензор скоростей деформаций и его компоненты
- § 11. Скорость объемного расширения жидкости. Интегральные представления дифференциальных операторов поля. Основные интегральные формулы
- § 12. Вихревые линии и трубки. Вторая теорема Гельмгольца. Интенсивность вихревой трубки
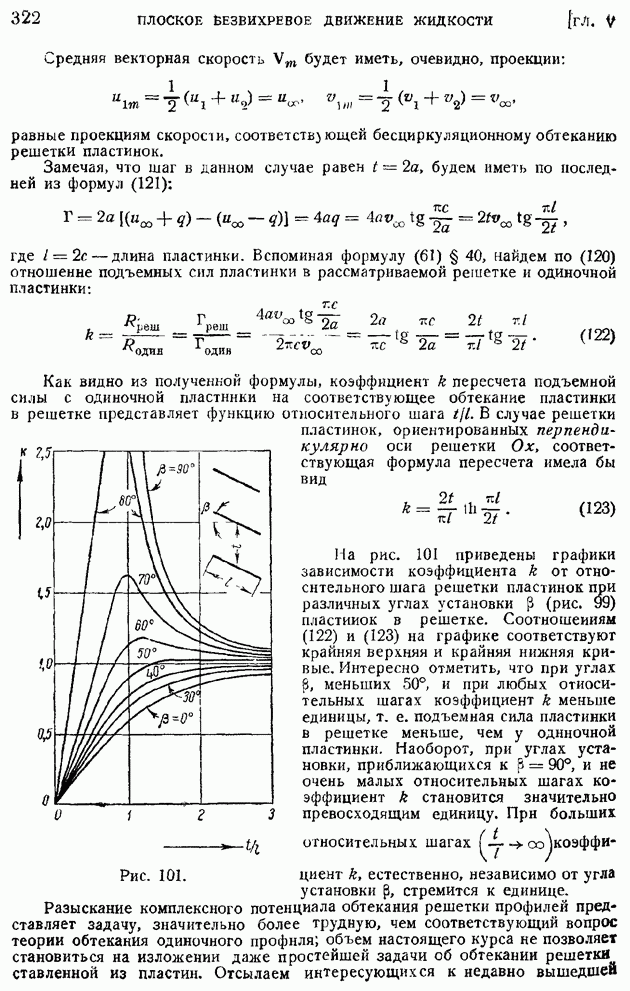
- § 13. Выражение интенсивности вихревой трубки через циркуляцию вектора по контуру, охватывающему трубку. Теорема об изменении циркуляции скорости во времени
- ГЛАВА II. ОСНОВНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ И РАВНОВЕСИЯ СПЛОШНОЙ СРЕДЫ
- § 14. Распределение массы в сплошной среде. Плотность и удельный вес. Напряжения. Тензор напряженности и его симметричность
- § 15. Общие уравнения динамики сплошной среды. Уравнение неразрывности. Уравнения динамики в напряжениях
- § 16. Тепловые явления в жидкостях и газах. Закон сохранения энергии и уравнение баланса энергии
- § 17. Общие уравнения равновесного состояния жидкости и газа. Равновесие воздуха в атмосфере. Приближенные барометрические формулы. Стандартная атмосфера
- § 18. Равновесие несжимаемой жидкости. Уравнение поверхности раздела. Равновесие вращающейся жидкости
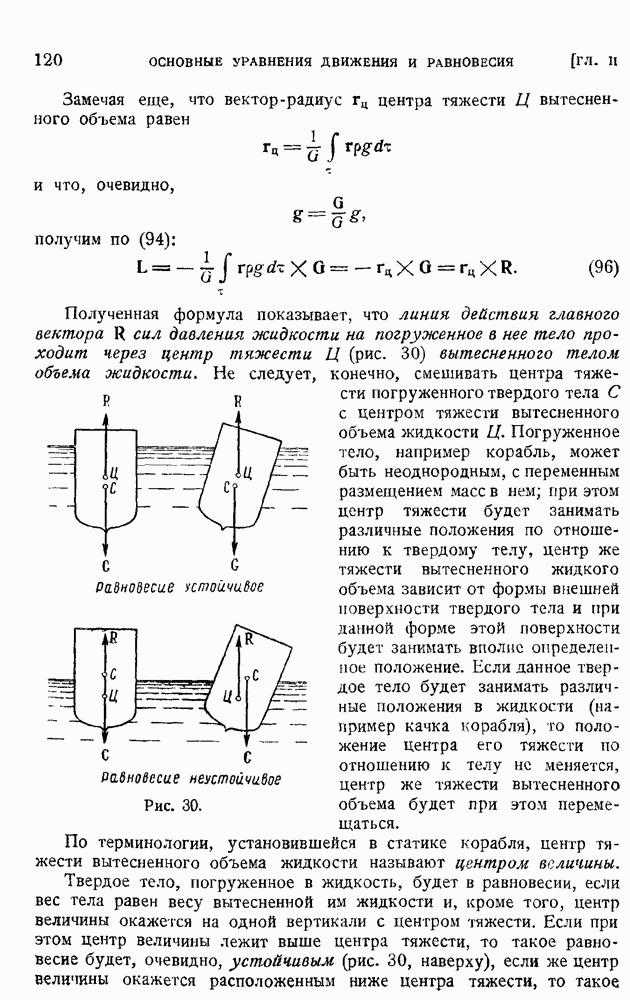
- § 19. Давление тяжелой несжимаемой жидкости на поверхность тела. Сила и момент, приложенные к телу, плавающему в тяжелой жидкости. Случай вращающейся жидкости
- ГЛАВА III. ДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ И ГАЗА. ОСНОВНЫЕ УРАВНЕНИЯ И ОБЩИЕ ТЕОРЕМЫ
- § 20. Идеальная жидкость. Основные уравнения движения
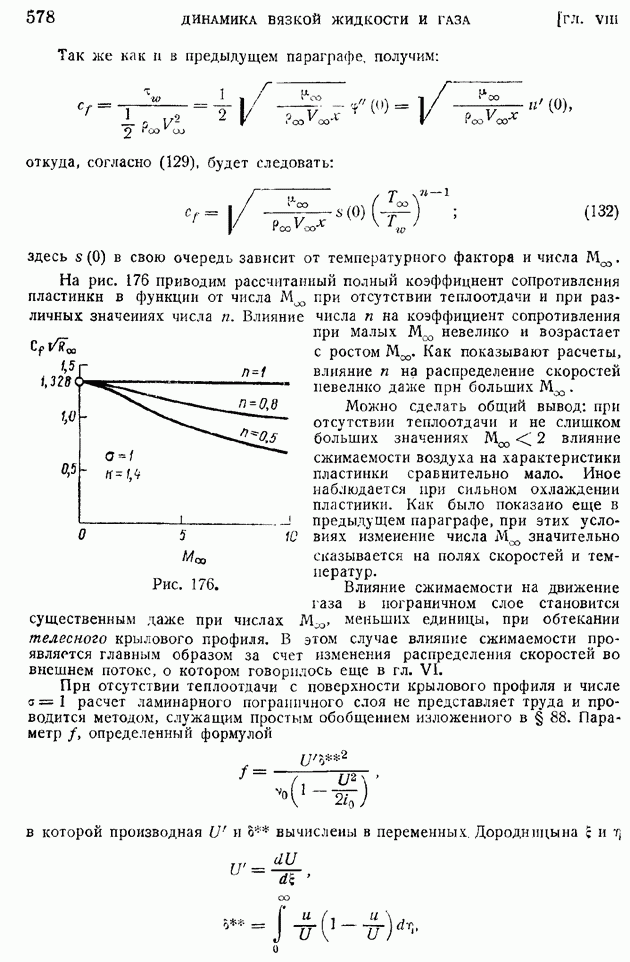
- § 21. Закон сохранения энергии в движущейся идеальной жидкости. Адиабатическое движение. Сохранение энтропии
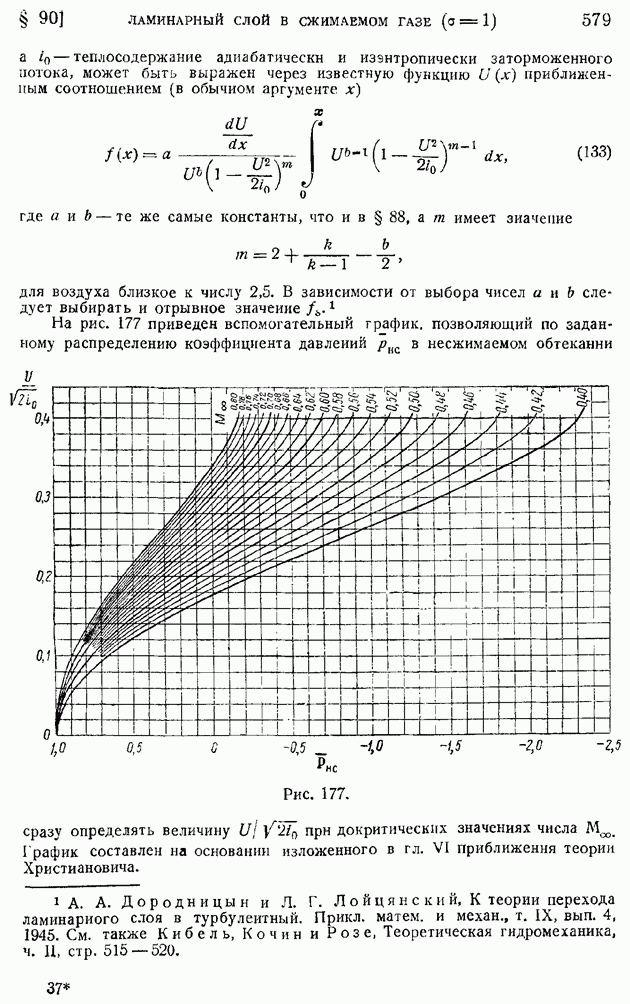
- § 22. Эйлерово представление конвективного изменения объемного интеграла. Перенос величины сквозь контрольную поверхность
- § 23. Эйлерова форма законов сохранения массы и энергии, теоремы количеств движения и момента количеств движения при стационарном движении идеальной жидкости
- § 24. Теорема об изменении кинетической энергии. Работа и мощность внутренних сил. Эйлерова форма уравнения изменения кинетической энергии
- § 25. Теорема Бернулли о сохранении полной механической энергии при стационарном баротропном движении идеальной жидкости и газа
- ГЛАВА IV. ОДНОМЕРНЫЙ ПОТОК ИДЕАЛЬНОЙ ЖИДКОСТИ
- § 26. Одномерное течение идеальной сжимаемой жидкости. Линеаризированные уравнения. Скорость распространения малых возмущений в жидкости или газе
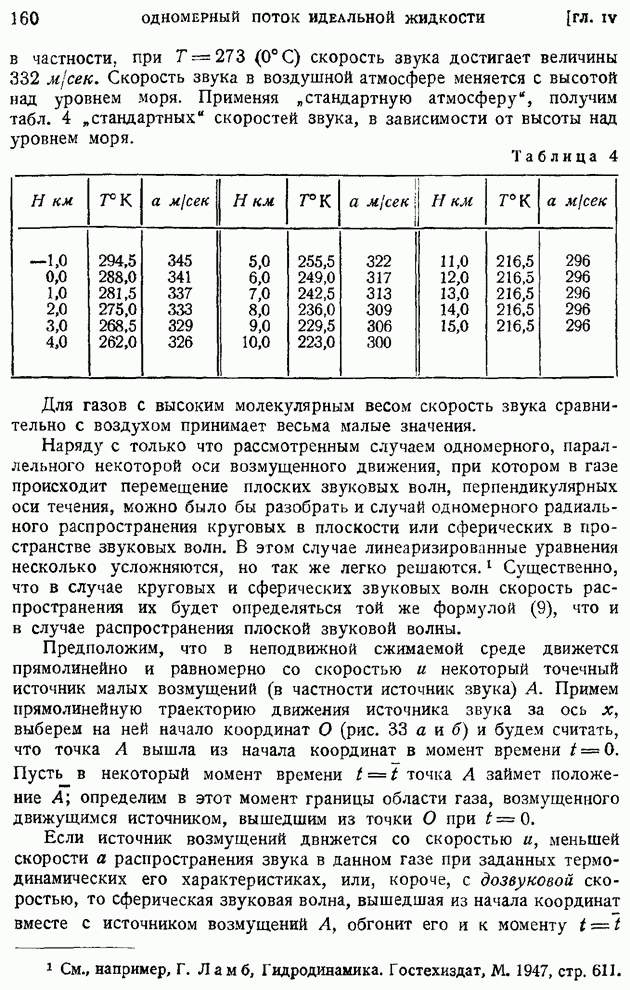
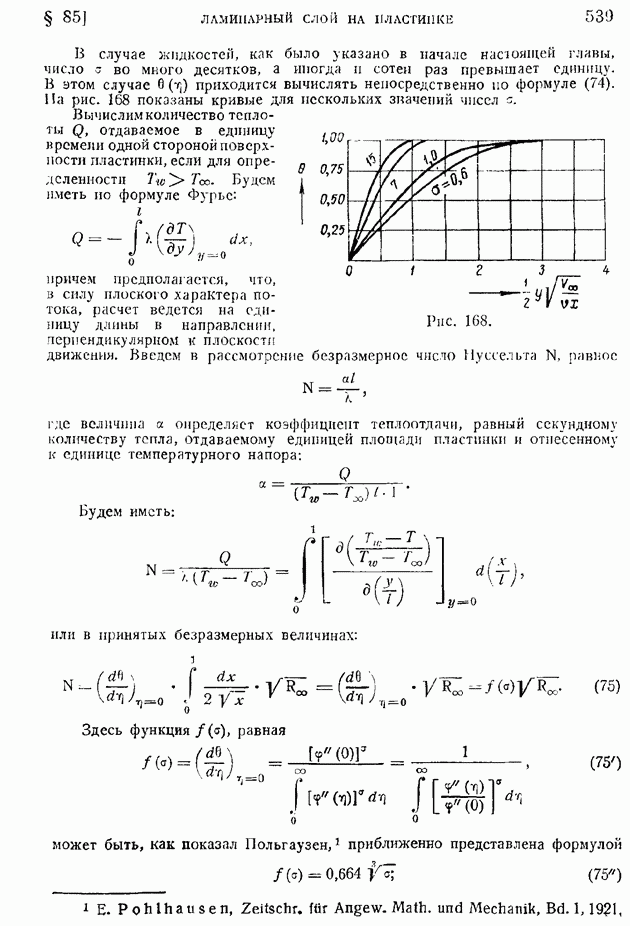
- § 27. Изотермическая и адиабатическая скорости звука. «Конус возмущений» при сверхзвуковом движении источника возмущения. Число M и его связь с углом конуса возмущений
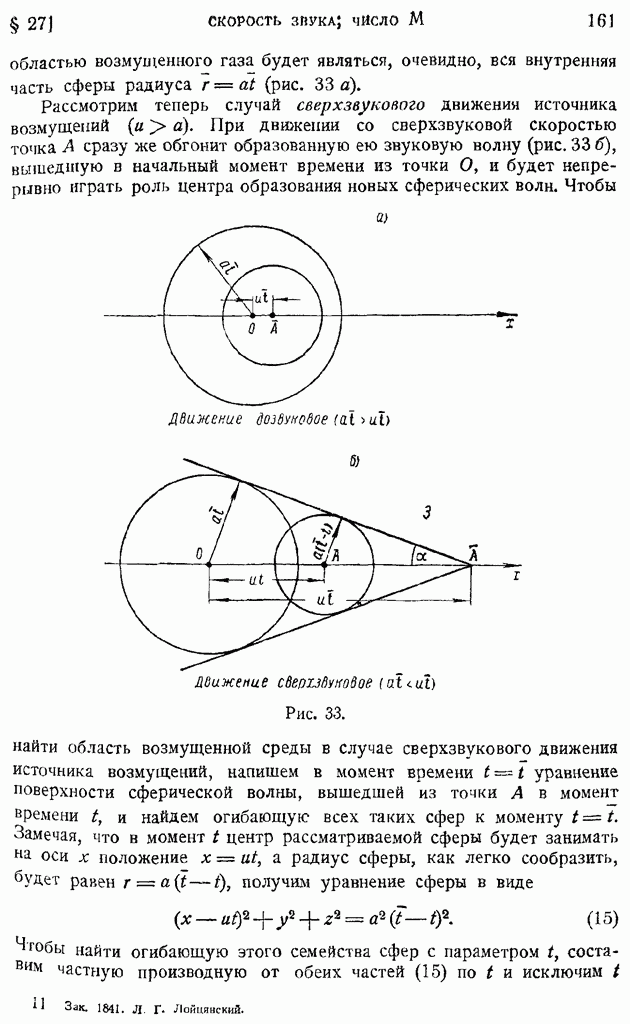
- § 28. Распространение непрерывных возмущений конечной интенсивности. Характеристики. Образование разрывной ударной волны
- § 29. Стоячая ударная волна или скачок уплотнения. Ударная адиабата
- § 30. Критические величины в одномерном потоке газа. Связь между скоростями до и после скачка. Изменение давления, плотности и температуры в скачке уплотнения
- § 31. Скорость распространения ударной волны. Спутное движение газа за ударной волной
- § 32. Влияние интенсивности скачка уплотнения на сжатие газа. Измерение скоростей и давлений в до- и сверхзвуковых потоках
- § 33. Одномерное движение газа по трубе переменного сечения. Истечение из резервуара большой емкости сквозь сходящееся сопло
- § 34. Одномерное течение в сопле Лаваля. Движение газа с притоком тепла
- ГЛАВА V. БЕЗВИХРЕВОЕ ДВИЖЕНИЕ ЖИДКОСТИ. ПЛОСКОЕ ДВИЖЕНИЕ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 35. Сохранение циркуляции скорости в потоке идеальной жидкости. Теорема Кельвина и Лаграижа. Безвихревое движение. Потенциал скоростей
- § 36. Интеграл Лагранжа — Коши уравнений безвихревого движения. Теорема Бернулли. Некоторые общие свойства безвихревого движения идеальной несжимаемой жидкости в односвязной области
- § 37. Плоское безвихревое движение несжимаемой жидкости. Потенциал скоростей и функция тока. Применение функций комплексного переменного. Комплексный потенциал и сопряженная скорость
- § 38. Построение полей течения по заданной характеристической Функции. Простейшие плоские потоки и их наложение
- § 39. Бесциркуляционное и циркуляционное обтекания круглого цилиндра
- § 40. Применение криволинейных координат. Бесциркуляционное и циркуляционное обтекания эллиптического цилиндра и пластинки. Задача Жуковского об обтекании решетки пластин.
- § 41. Плоское движение с отрывом струй. Разрывное обтекание пластинки и протекание жидкости сквозь отверстие
- § 42. Прямая задача в теории плоского движения идеальной несжимаемой жидкости. Применение метода конформных отображений. Гипотеза Чаплыгина о безотрывном обтекании задней кромки профиля. Формула циркуляции
- § 43. Теорема Жуковского о подъемной силе крыла. Зависимость подъемной силы от угла атаки. Коэффициент подъемной силы
- § 44. Применение метода комплексных переменных к выводу теоремы Жуковского. Формулы Чаплыгина для главного вектора и момента сил давления потока на крыло
- § 45. Выражение главного момента сил давления потока через коэффициенты конформного отображения. Фокус крыла. Независимость от угла атаки момента относительно фокуса. Парабола устойчивости
- § 46. Частные случаи конформного отображения крылового профиля на круг. Преобразование Жуковского-Чаплыгина. Теоретические крыловые профили
- § 47. Задача об обтекании слабо изогнутой дужки произвольной формы (теория тонкого крыла)
- § 48. Определение обтекания крылового профиля произвольной формы
- § 49. Обобщение теоремы Жуковского на случай плоской решетки с бесчисленным множеством профилей
- ГЛАВА VI. ПЛОСКОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ СЖИМАЕМОГО ГАЗА
- § 50. Основные уравнения плоского стационарного безвихревого движения сжимаемого газа. Линеаризированные уравнения
- 51. Линеаризированный до- и сверхзвуковой газовый поток вдоль волнистой стенки
- § 52. Тонкое крыло в линеаризированном до- и сверхзвуковом потоках. Влияние сжимаемости газа на коэффициент подъемной силы в дозвуковом потоке. Коэффициенты подъемной силы и волнового сопротивления при сверхзвуковом потоке
- § 53. Нелинеаризированные уравнения движения идеального сжимаемого газа. Переход в плоскость годографа. Уравнения Чаплыгина
- § 54. Метод С. А. Христиановича. Приближенные формулы учета влияния сжимаемости на распределение давления
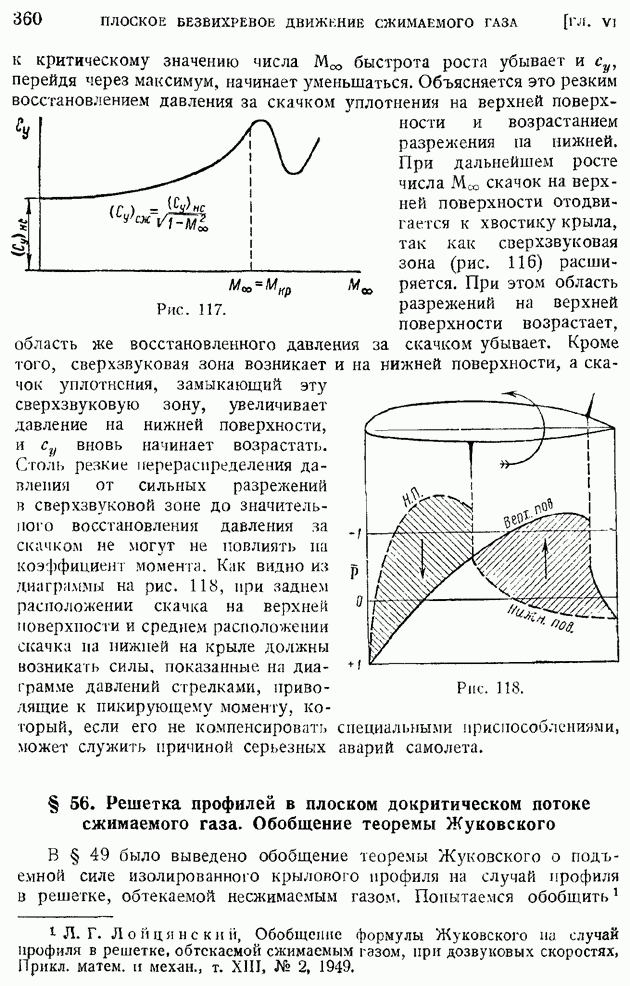
- § 55. Критическое число M и его определение по заданному распределению давления в несжимаемом обтекании. Поведение коэффициента подъемной силы и момента при около- и закритических значениях числа M
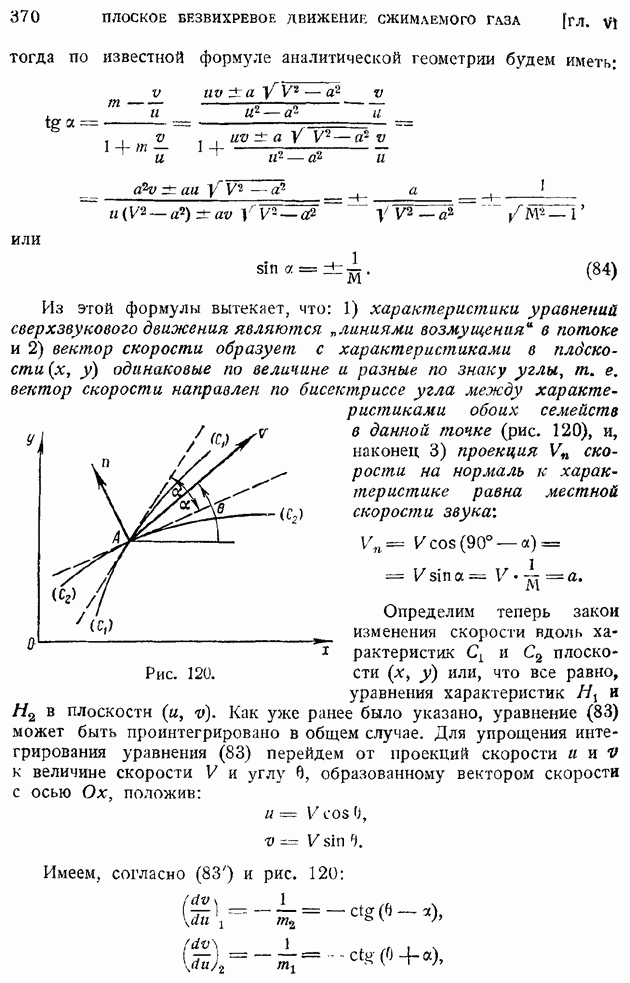
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
- § 57. Нелинеаризированный сверхзвуковой поток. «Характеристики» уравнений плоского сверхзвукового потока. Линин возмущения и их основные свойства
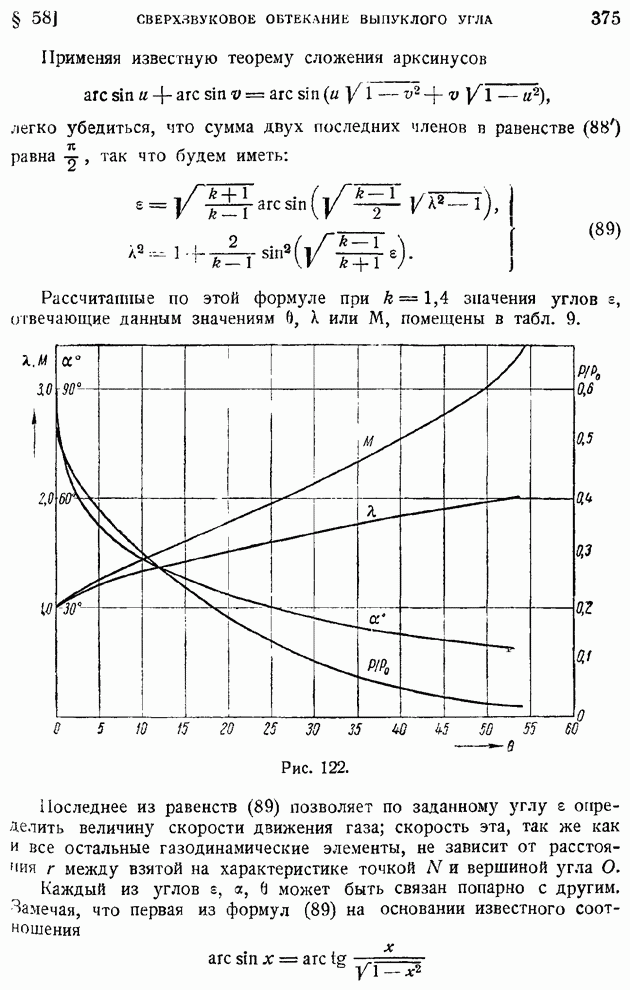
- § 58. Обтекание выпуклого угла сверхзвуковым потоком. Влияние угла поворота струи на ее газодинамические элементы
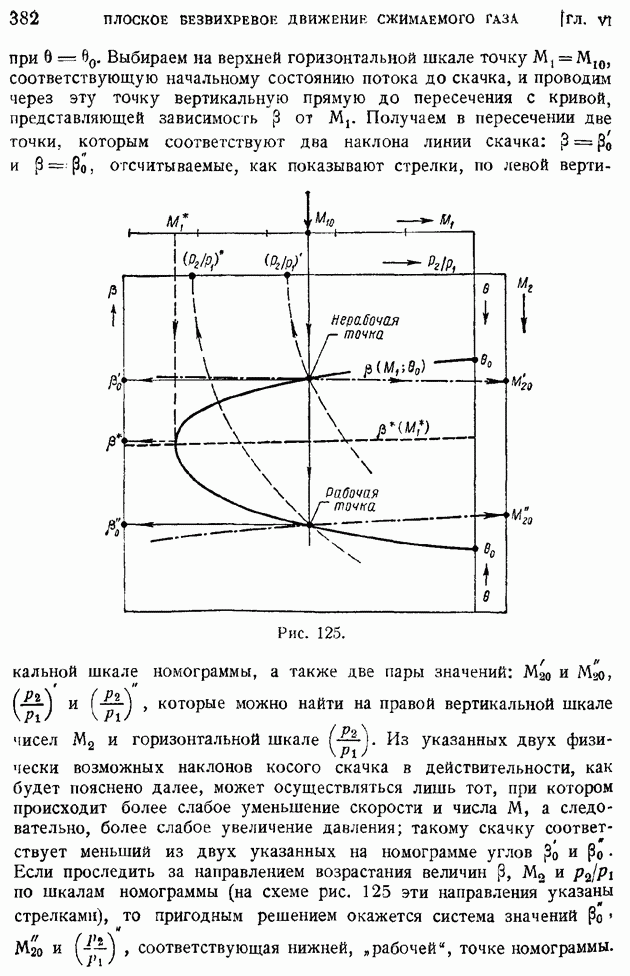
- § 59. Сверхзвуковой поток внутри тупого угла. Косой скачок уплотнения. Связь между газодинамическими элементами до и за косым скачком
- ГЛАВА VII. ПРОСТРАНСТВЕННОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ
- § 60. Ортогональные криволинейные координаты в пространстве. Основные дифференциальные операторы поля в криволинейных координатах
- § 61. Потенциал скоростей. Поле источника и диполя. Непрерывное распределение источников и диполей. Ньютонов потенциал. Потенциал простого и двойного слоев
- § 62. Поле скоростей вокруг заданной системы вихрей. Формула Био — Савара. Потенциал скоростей замкнутой вихревой нити. Аналогия с потенциалом двойного слоя
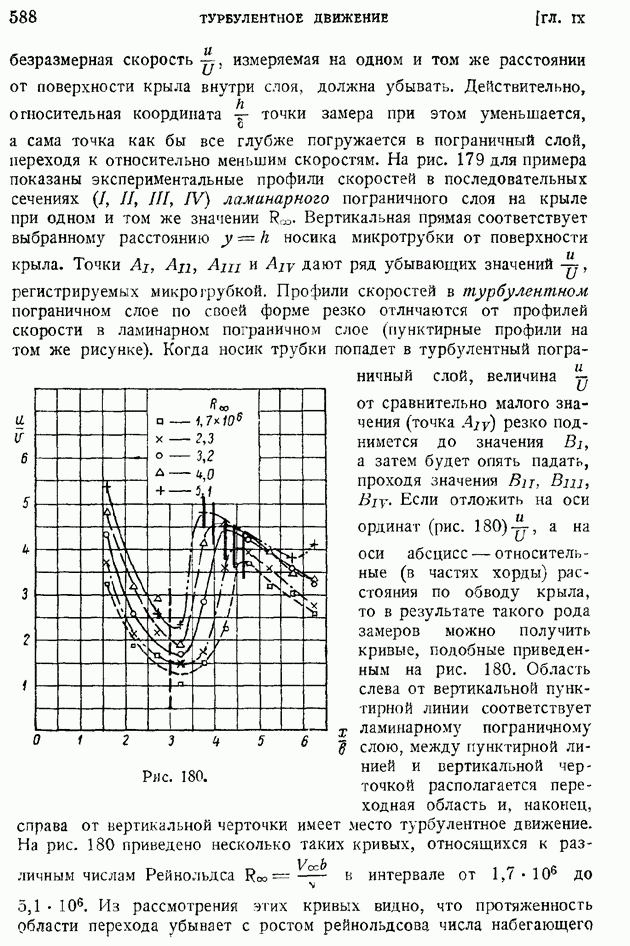
- § 63. Функция тока и ее связь с векторным потенциалом скоростей. Функции тока простейших течений
- § 64. Обтекание сферы. Давление однородного стационарного потока идеальной несжимаемой жидкости на погруженное в нее тело. Парадокс Даламбера
- § 65. Общие уравнения осесимметричного движения. Применение цилиндрических координат. Течение сквозь каналы
- § 66. Осесимметричное продольное обтекание тел вращения. Случай эллипсоида вращения
- § 67. Поперечное обтекание тел вращения. Пример эллипсоида вращения
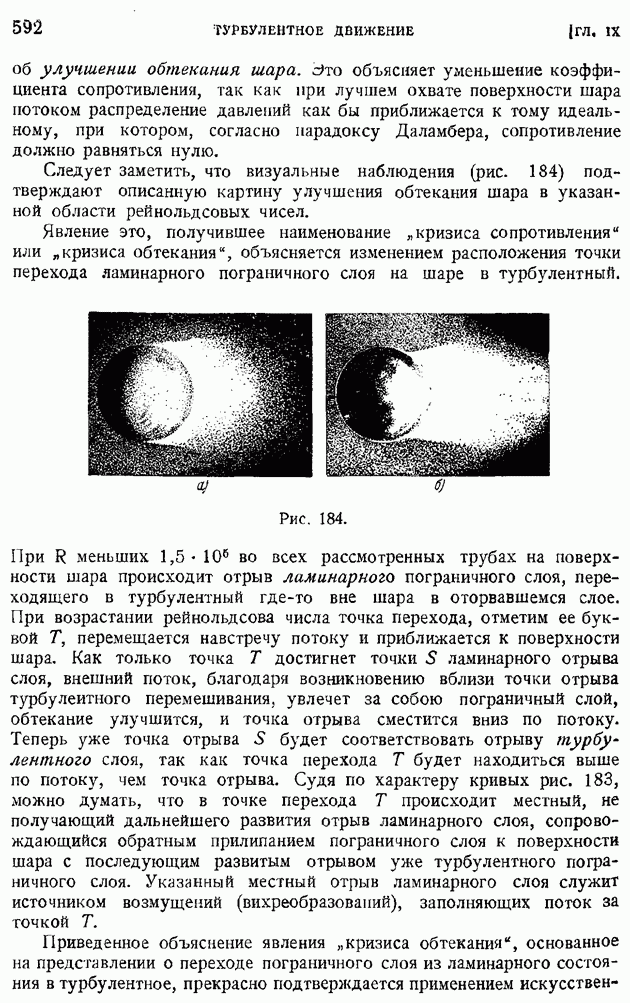
- § 68. Продольное и поперечное обтекание тел вращения большого удлинения. Приближенные выражения граничных условий. Применение тригонометрических сумм для определения коэффициентов …
- § 69. Метод «особенностей». Применение непрерывно распределенных источников (стоков) и диполей для решения задачи о продольном и поперечном обтекании тел вращения
- § 70. Общий случай движения твердого тела сквозь несжимаемую идеальную жидкость. Определение потенциала скоростей. Главный вектор и главный момент сил давления потока на тело
- § 71. Коэффициенты «присоединенных масс». Свойство симметрии. «Присоединенная» кинетическая энергия. Определение «присоединенных масс» поступательно движущегося цилиндра, шара и эллипсоида
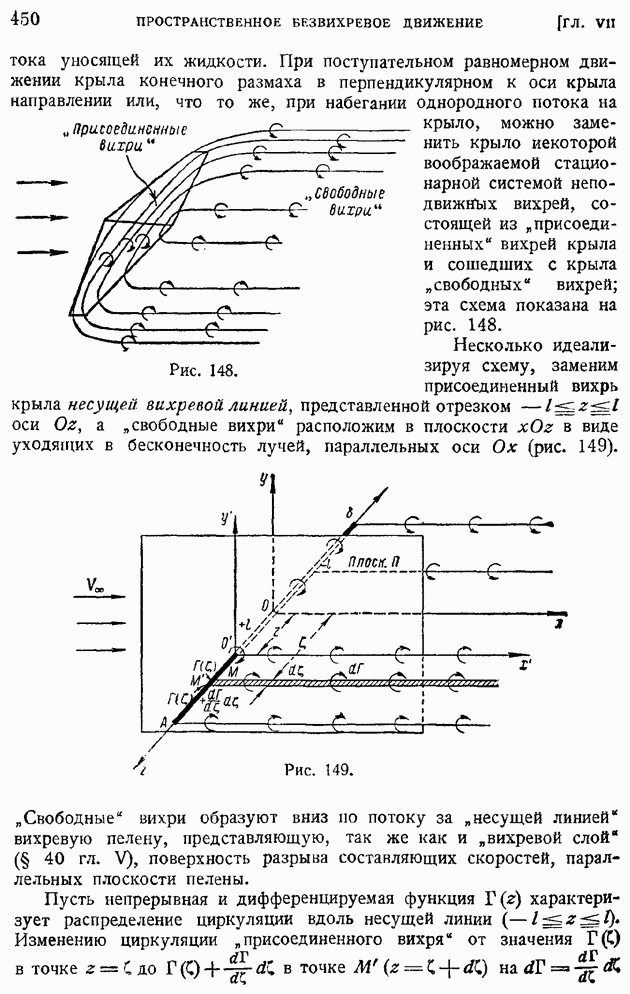
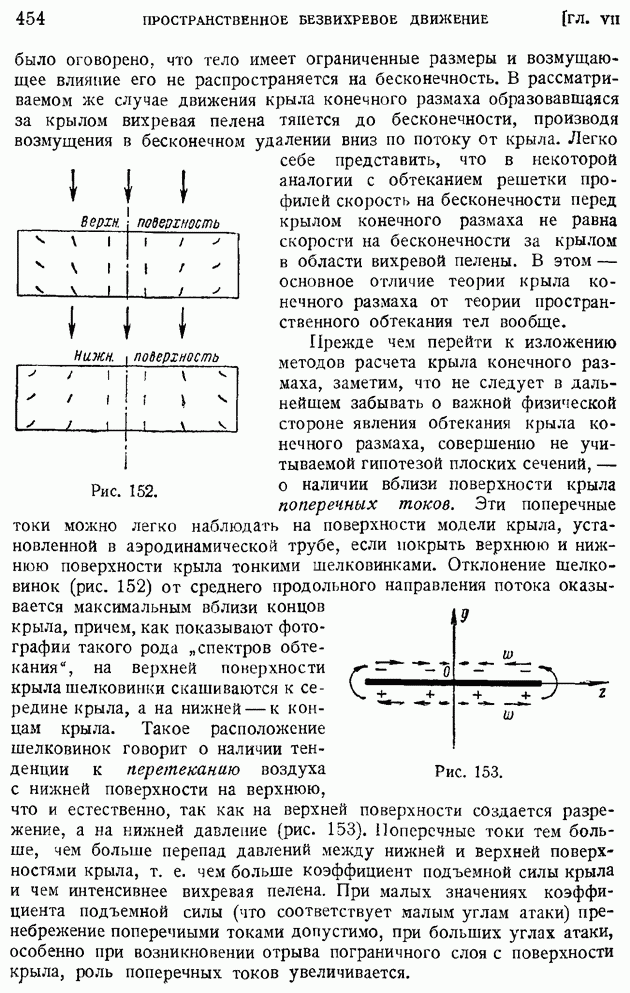
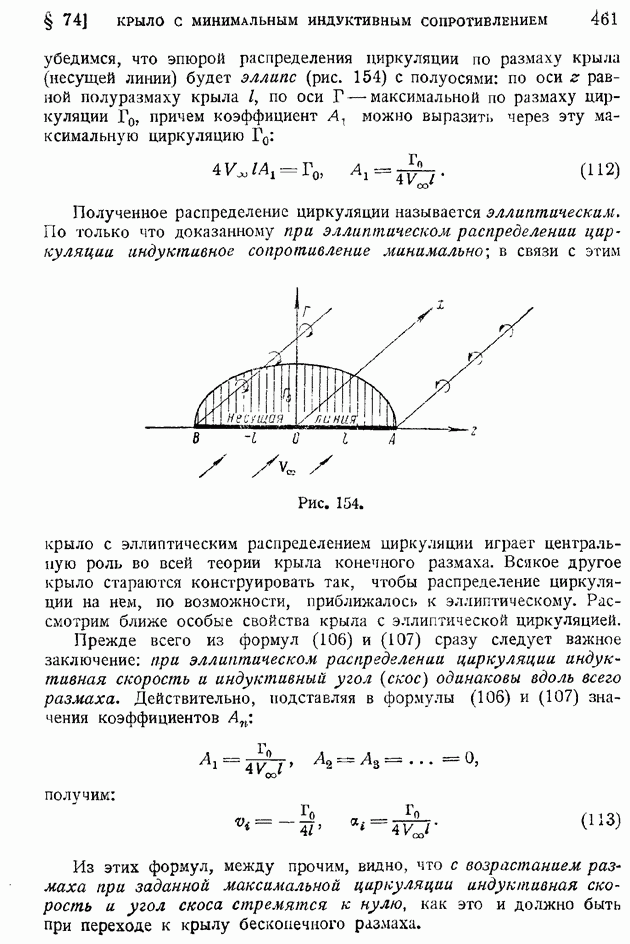
- § 72. Элементы теории крыла конечного размаха. Вихревая система крыла. Гипотеза плоских сечеиий. Геометрические и действительные углы атаки. Подъемная сила и «индуктивное сопротивление»
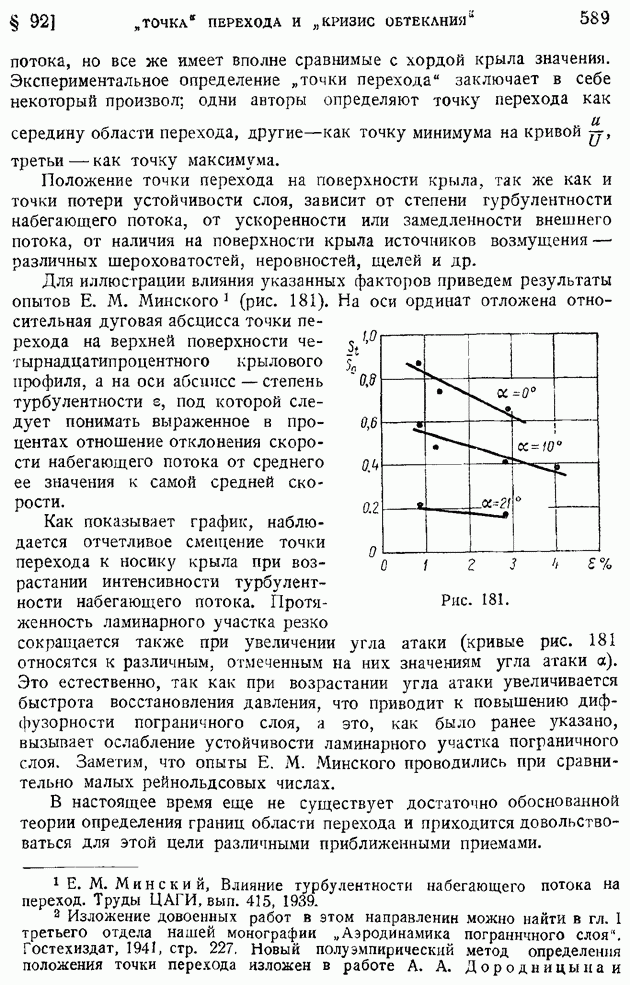
- § 73. Основные формулы теории «несущей линии». «Индуктивная скорость» и «индуктивный угол». Прямая задача определения подъемной силы и индуктивного сопротивления по заданному распределению циркуляции
- § 74. Крыло с минимальным индуктивным сопротивлением. Эллиптическое распределение циркуляции. Связь между коэффициентами индуктивного сопротивления и подъемной силы. Основное уравнение теории крыла и понятие о его интегрировании
- ГЛАВА VIII. ДИНАМИКА ВЯЗКОЙ ЖИДКОСТИ И ГАЗА
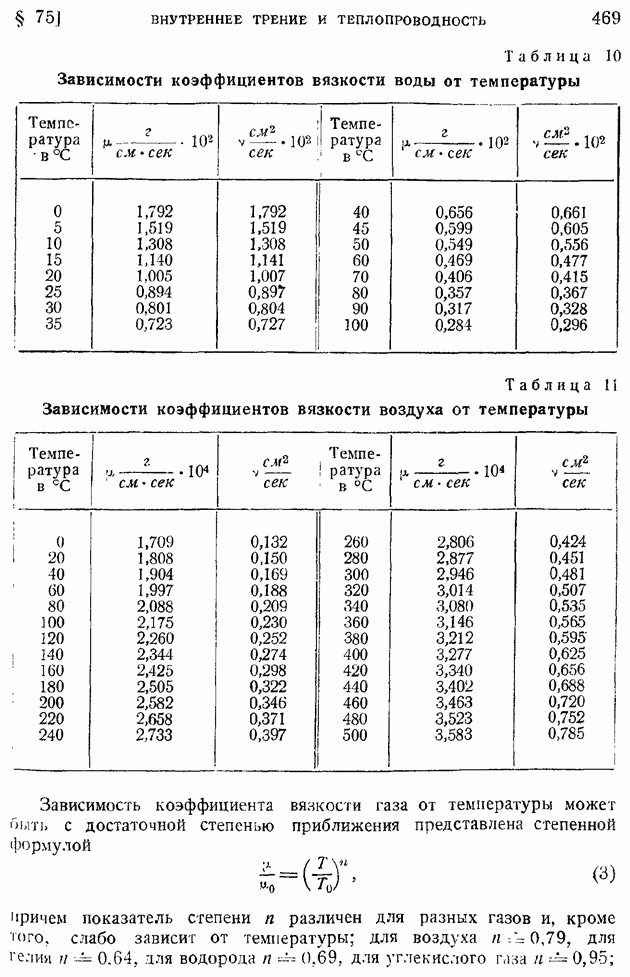
- § 75. Внутреннее трение и теплопроводность в жидкостях и газах. Законы Ньютона и Фурье. Влияние температуры на коэффициенты вязкости и теплопроводности. Число «сигма»
- § 76. Обобщение закона Ньютона на случай произвольного движения среды. Закон линейной связи между тензорами напряжений и скоростей деформации
- § 77. Общие уравнения движения вязкой жидкости. Динамические уравнения и уравнение баланса энергии. Граничные условия движения жидкости с треннем и теплопроводностью
- § 78. Понятие о подобии гидродинамических явлений. Безразмерные уравнения движения вязкой жидкости и газа. Условия подобия
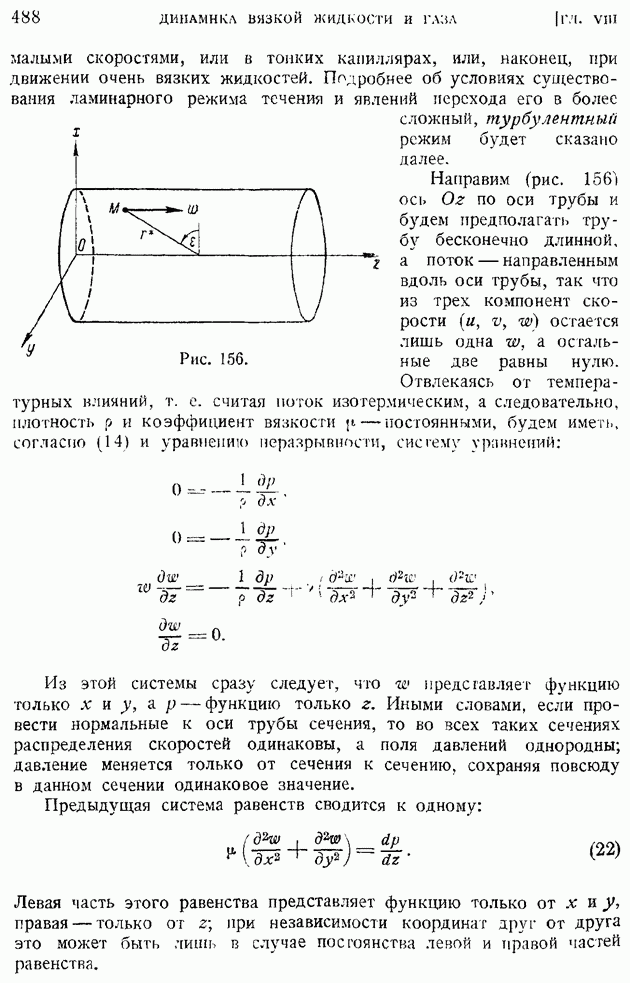
- § 79. Ламинарное движение вязкой несжимаемой жидкости по цилиндрической трубе
- § 80. Обтекание шара при очень малых значениях числа Рейнольдса. Формула сопротивления шара по Стоксу и ее обобщения
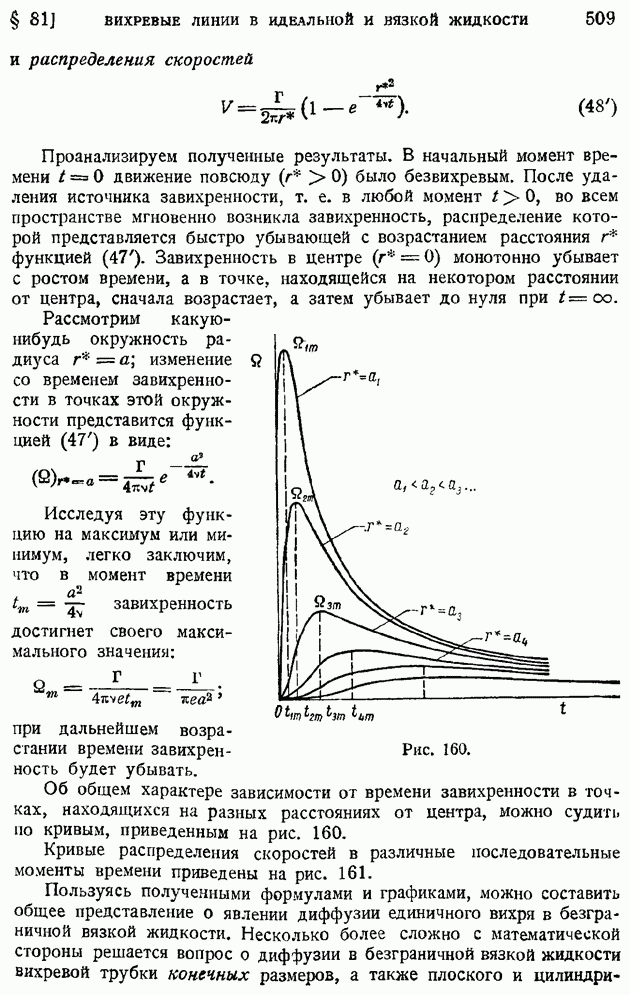
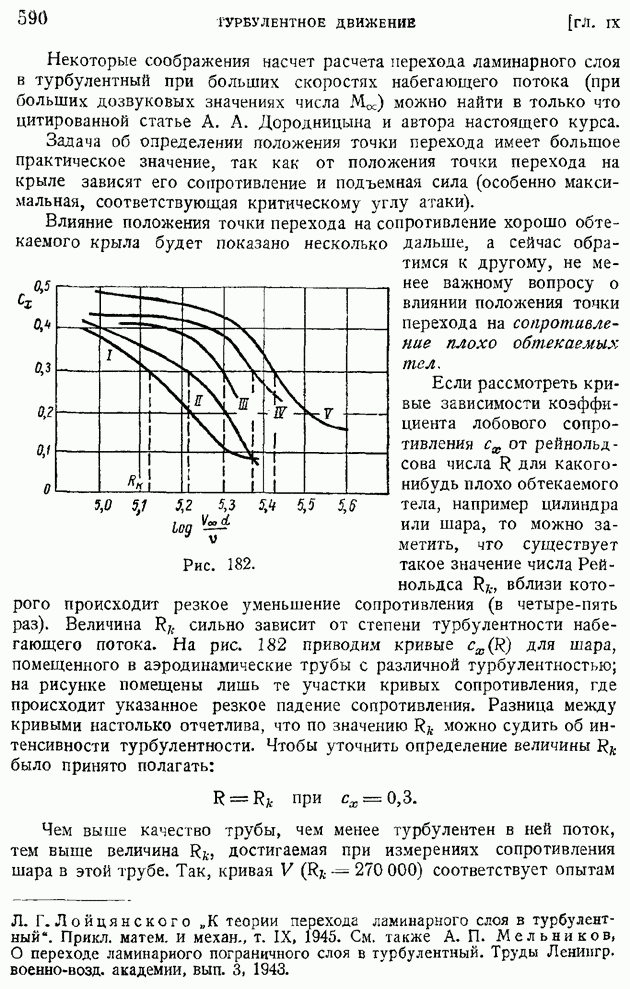
- § 81. Вихревые линии в идеальной и вязкой жидкости. Сохраняемость вихревых линий при отсутствии внутреннего трения. Диффузия вихря в вязкой жидкости
- § 82. Одномерное прямолинейное движение сжимаемого вязкого газа. Движение внутри скачка уплотнения. Понятие о толщине скачка
- § 83. Работа внутренних сил и диссипация механической энергии в движущейся вязкой среде
- § 84. Обтекание тел жидкостью и газом при больших значениях числа Рейнольдса. Основные уравнения теории ламинарного пограничного слоя
- § 85. Ламинарный пограничный слой на пластинке, продольно обтекаемой несжимаемой жидкостью. Неизотермическое движение
- § 86. Ламинарный пограничный слой при степенном задании скорости внешнего потока
- § 87. Ламинарный пограничный слой в общем случае задания скорости внешнего потока. Применение уравнения импульсов для приближенного расчета ламинарного пограничного слоя
- § 88. Способы определения функций … Приближенный метод расчета ламинарного пограничного слоя
- § 89. Ламинарный пограничный слой на пластинке, продольно обтекаемой сжимаемым газом при больших скоростях. Случай линейной зависимости коэффициента вязкости от температуры (n = 1)
- § 90. Ламинарный пограничный слой на пластинке при любом законе связи между вязкостью и температурой и при числе … Обтекание крылового профиля потоком больших скоростей
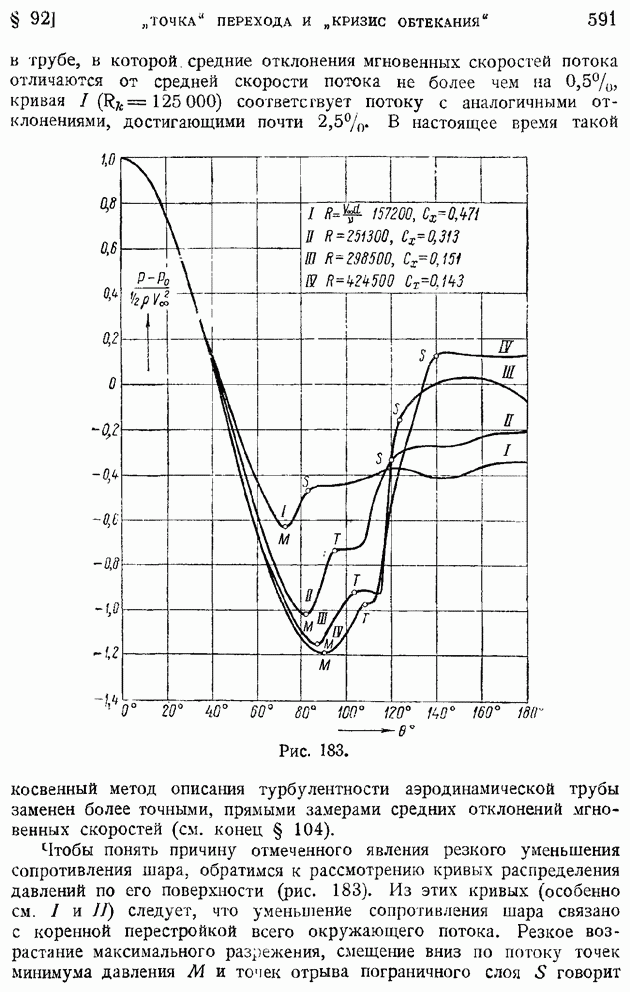
- ГЛАВА IX. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ
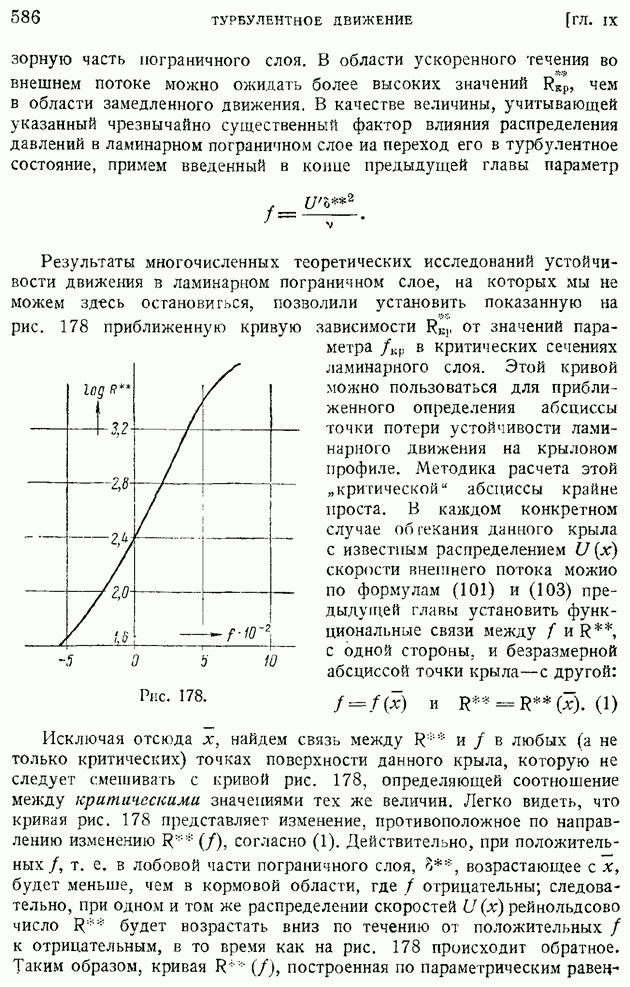
- § 91. Переход ламинарного движения в турбулентное. Критическое рейнольдсово число
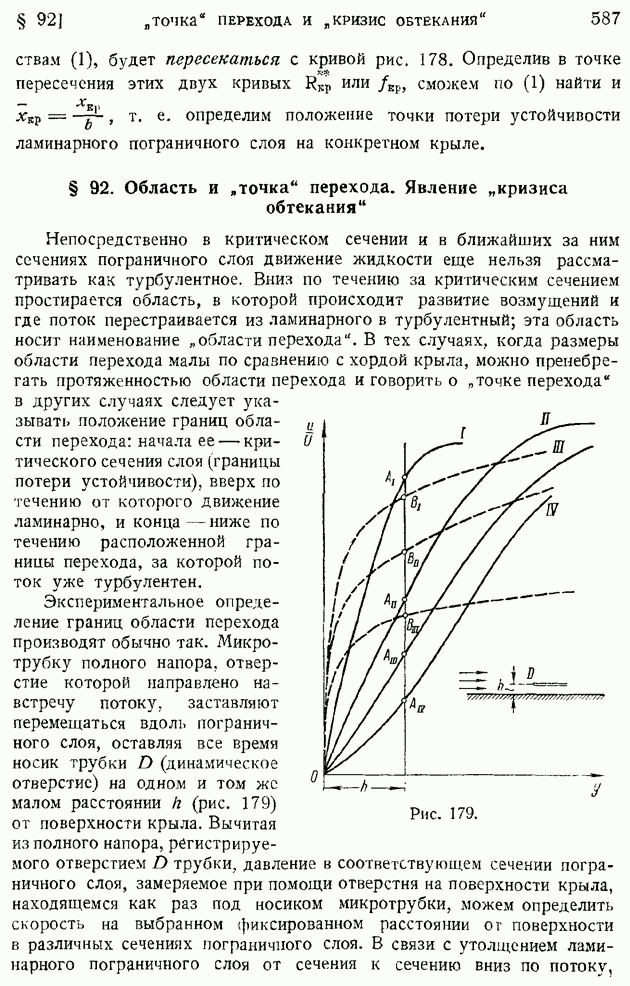
- § 92. Область и «точка» перехода. Явление «кризиса обтекания»
- § 93. Основные уравнения осреднеиного турбулентного движения. Тензор турбулентных напряжений
- § 94. Турбулентное движение жидкости в плоской и круглой трубе. Логарифмические формулы скоростей
- § 95. Формулы сопротивления гладких труб при турбулентном движении жидкости. Ламинарный подслой
- § 96. Влияние шероховатости стенок трубы на ее сопротивление. Предельные режимы течения. Режим установившейся шероховатости
- § 97. Турбулентный пограничный слой на продольно обтекаемой пластине. Сопротивление пластины
- § 98. Турбулентный пограничный слой на крыловом профиле при малом продольном перепаде давлений
- § 99. Турбулентный пограничный слой на крыловом профиле при значительных продольных перепадах давления
- § 100. Профильное сопротивление крыла. Разложение профильного сопротивления на сопротивление трения и сопротивление давлений. Обратное влияние пограничного слоя на распределение давлений по поверхности обтекаемого профиля
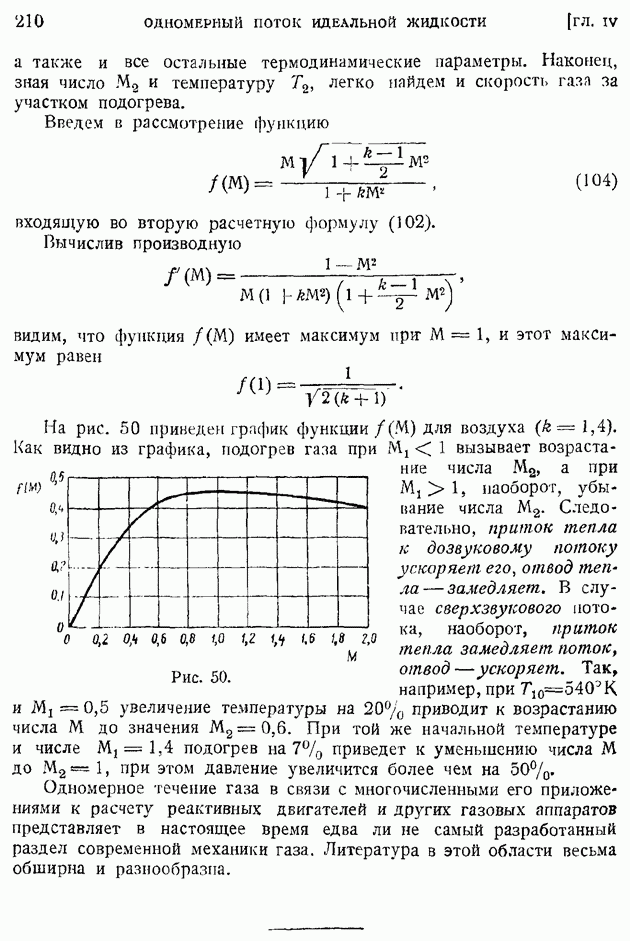
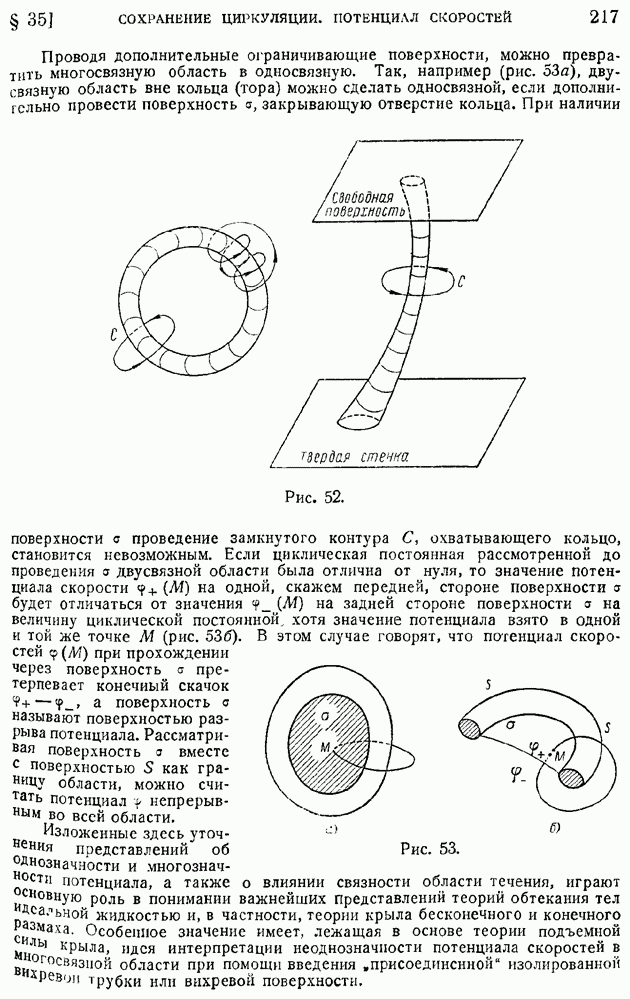
- § 101. Приближенные формулы профильного сопротивления крыла и крылового профиля в решетке
- § 102. Основные закономерности «свободной турбулентности». Плоская турбулентная струя в пространстве, заполненном той же жидкостью
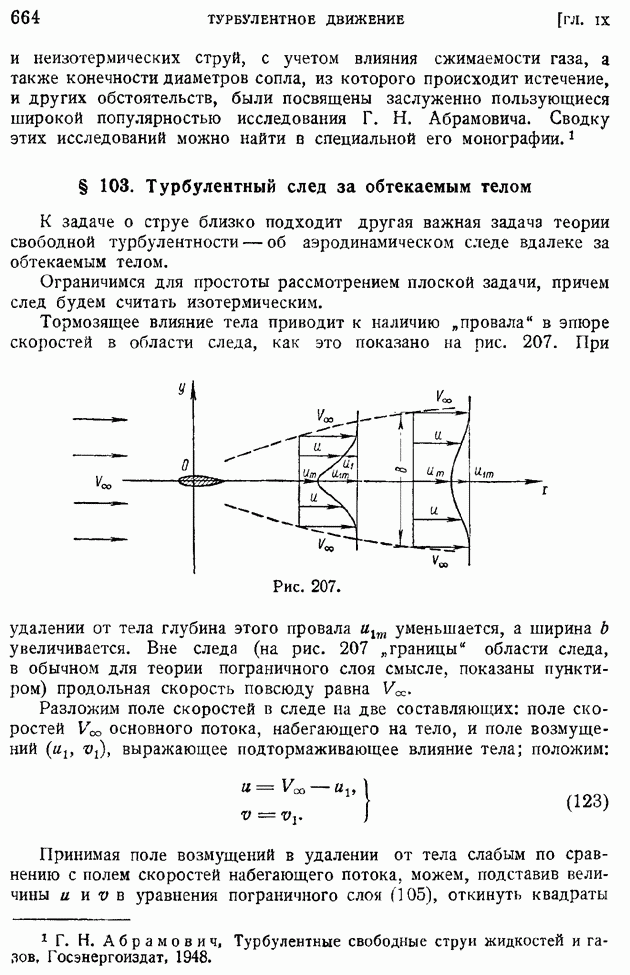
- § 103. Турбулентный след за обтекаемым телом
- § 104. Рассеяние турбулентных возмущений в жидкости. Случай изотропной и однородной турбулентности. Закон сохранения момента возмущений