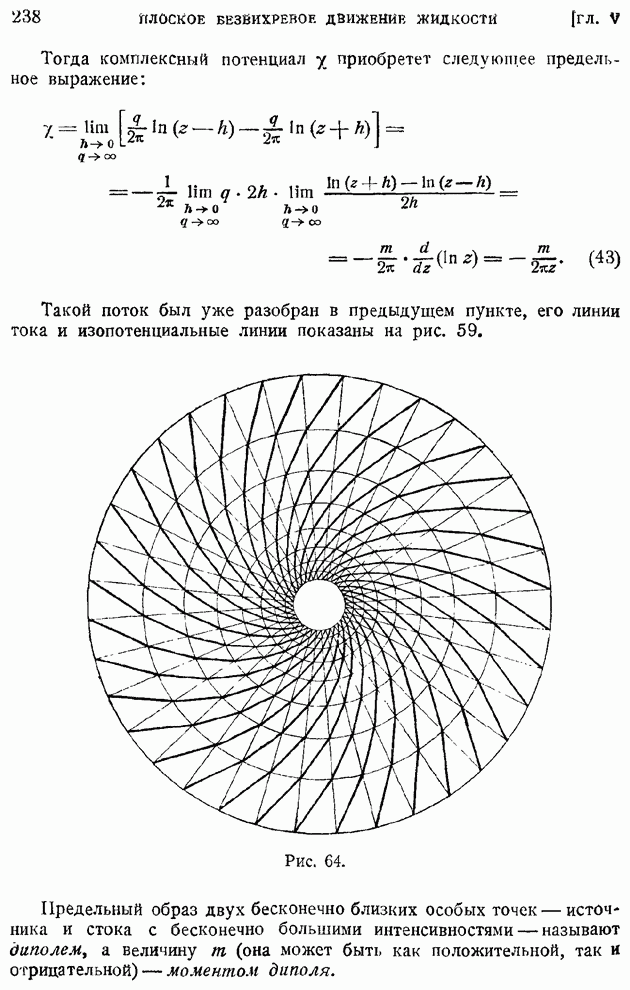
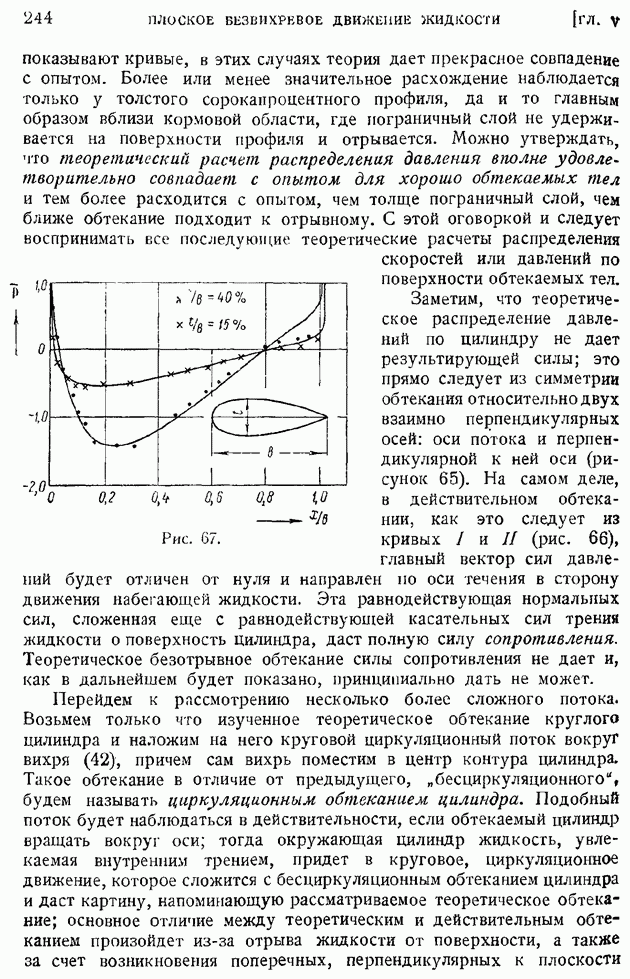
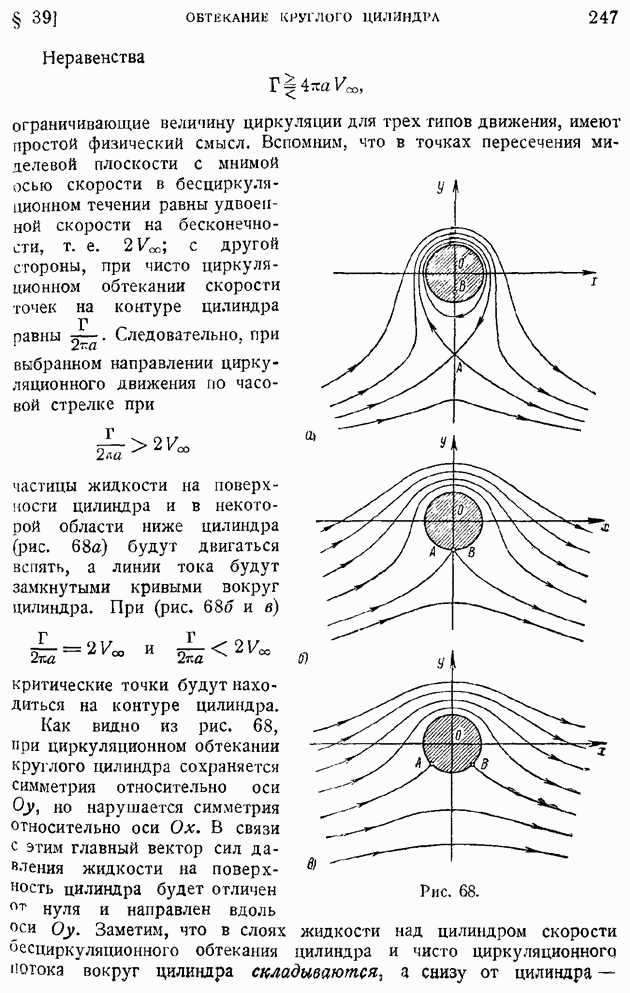
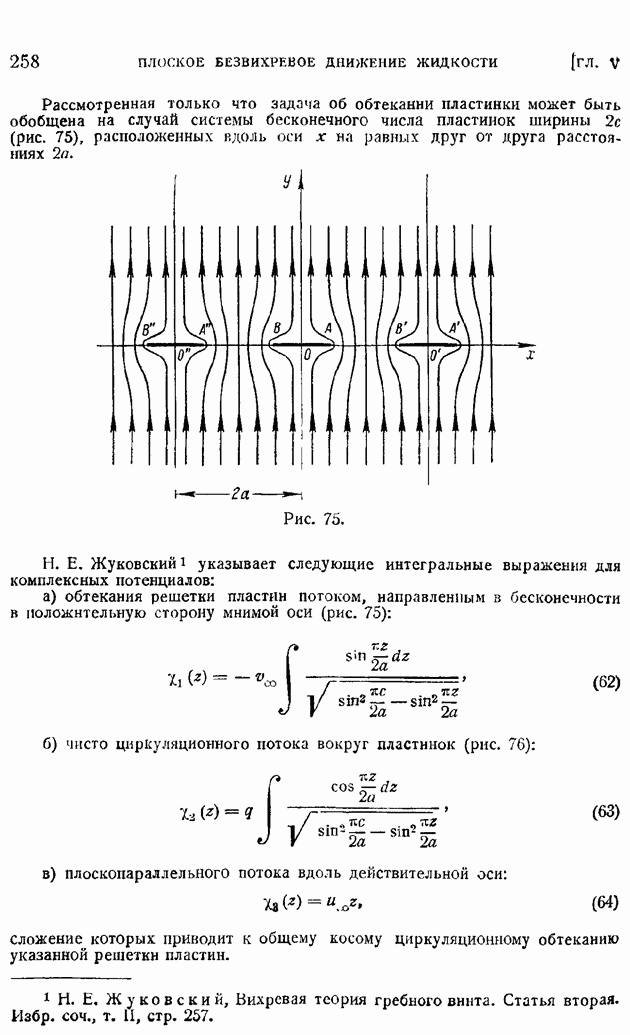
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
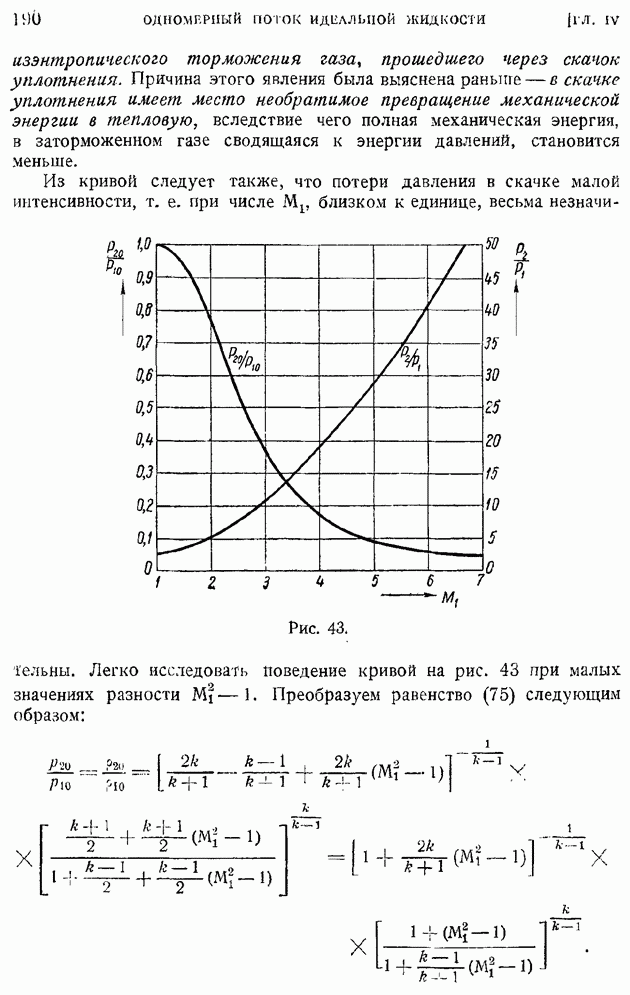
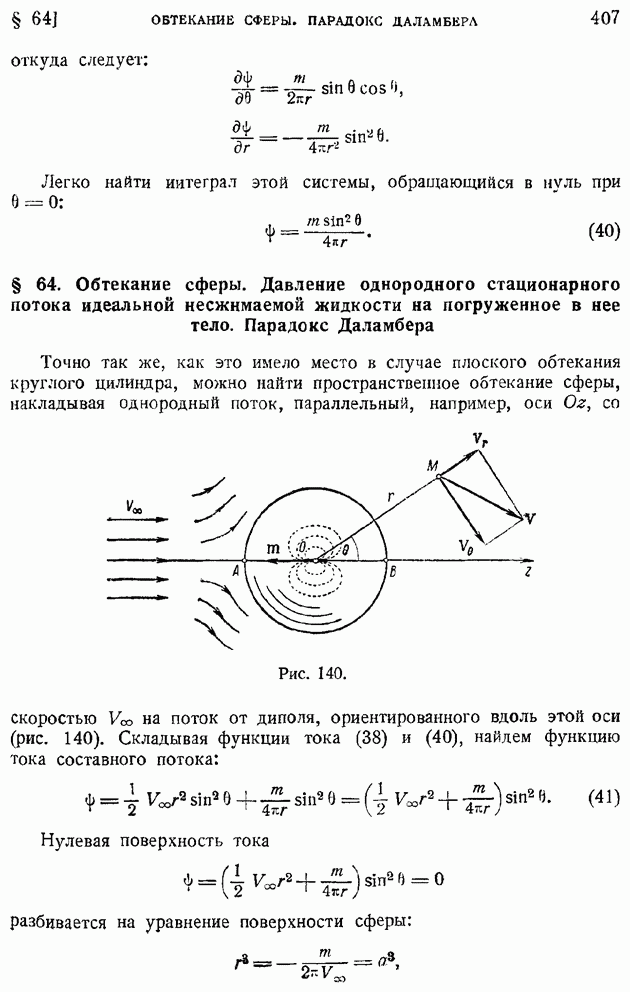
§ 34. Одномерное течение в сопле Лаваля. Движение газа с притоком тепла
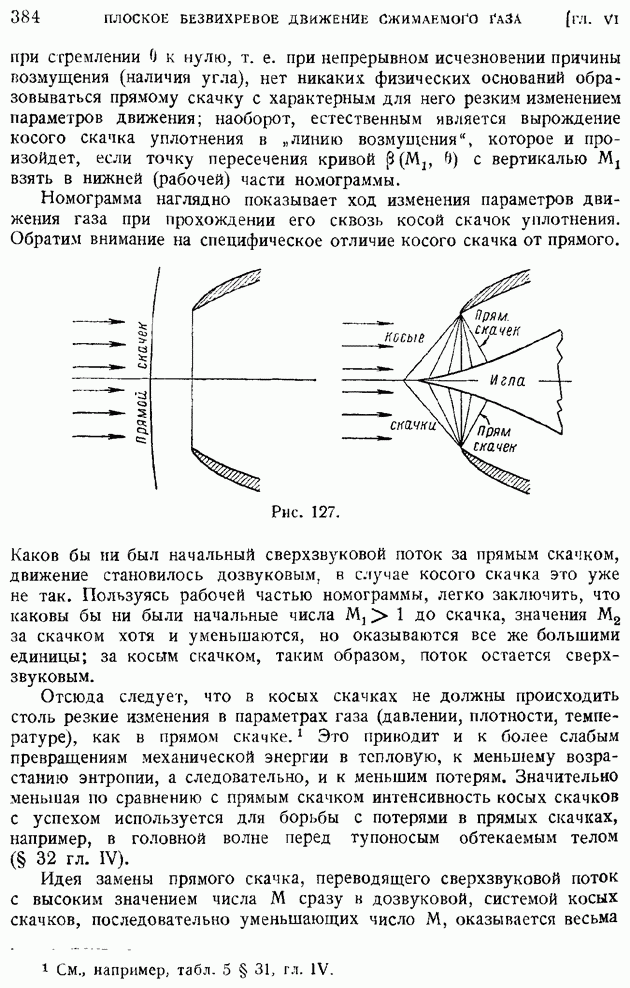
Явление истечения газа в среду с заданным противодавлением  протекает несколько иначе, если сопло имеет как начальную суживающуюся (конфузорную), так и выходную расширяющуюся (диффузорную) части. В этом случае, при достаточно малом противодавлении, в сечении, отграничивающем конфузорную часть от диффузорной. скорость газа достигнет своего критического значения, равного местной скорости звука, и при дальнейшем расширении газа в диффузорной части сопла образуется сверхзвуковой поток. Такого рода сопла называют соплами Лаваля.
протекает несколько иначе, если сопло имеет как начальную суживающуюся (конфузорную), так и выходную расширяющуюся (диффузорную) части. В этом случае, при достаточно малом противодавлении, в сечении, отграничивающем конфузорную часть от диффузорной. скорость газа достигнет своего критического значения, равного местной скорости звука, и при дальнейшем расширении газа в диффузорной части сопла образуется сверхзвуковой поток. Такого рода сопла называют соплами Лаваля.
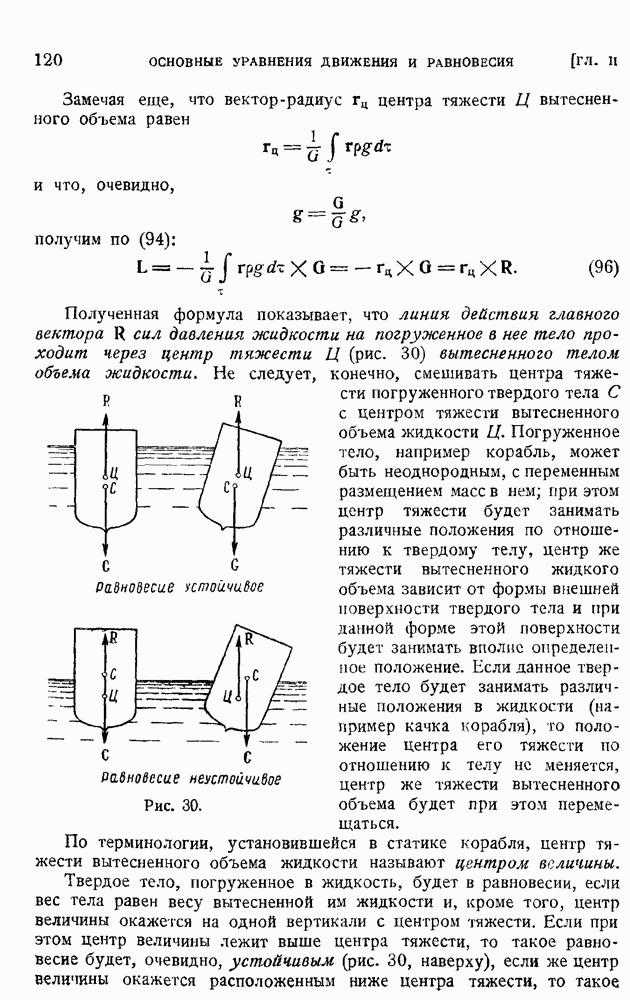
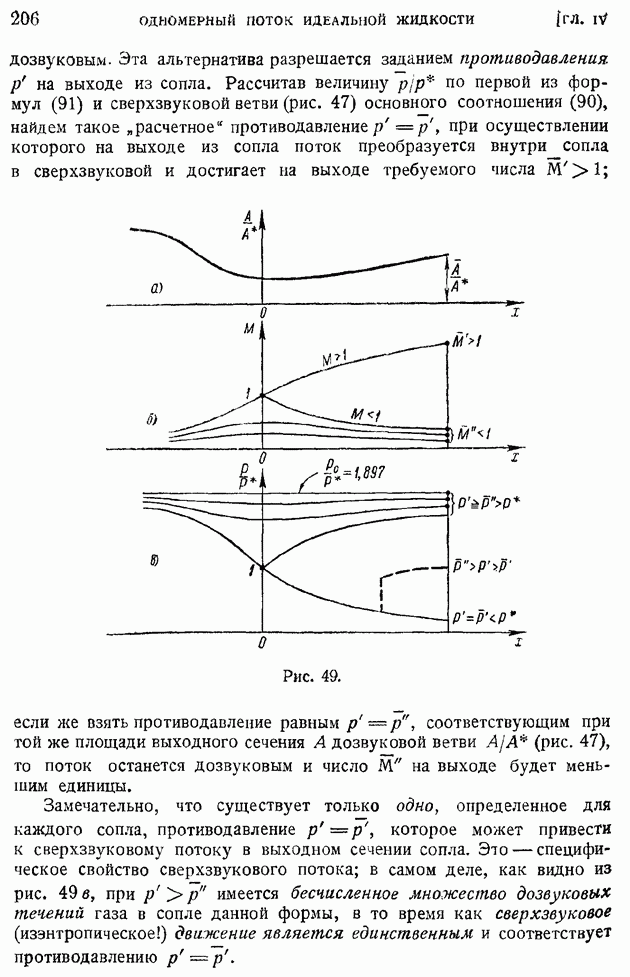
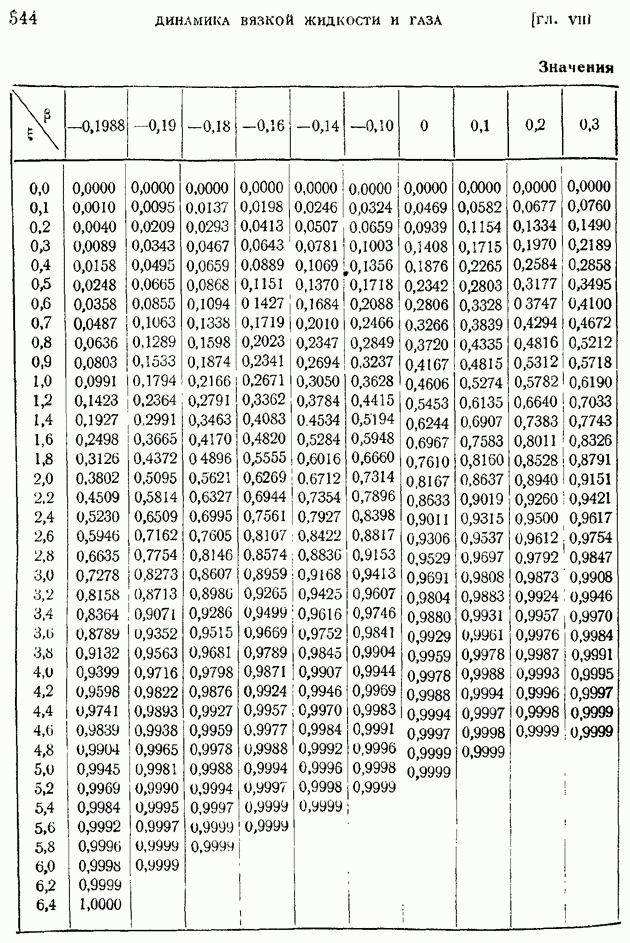
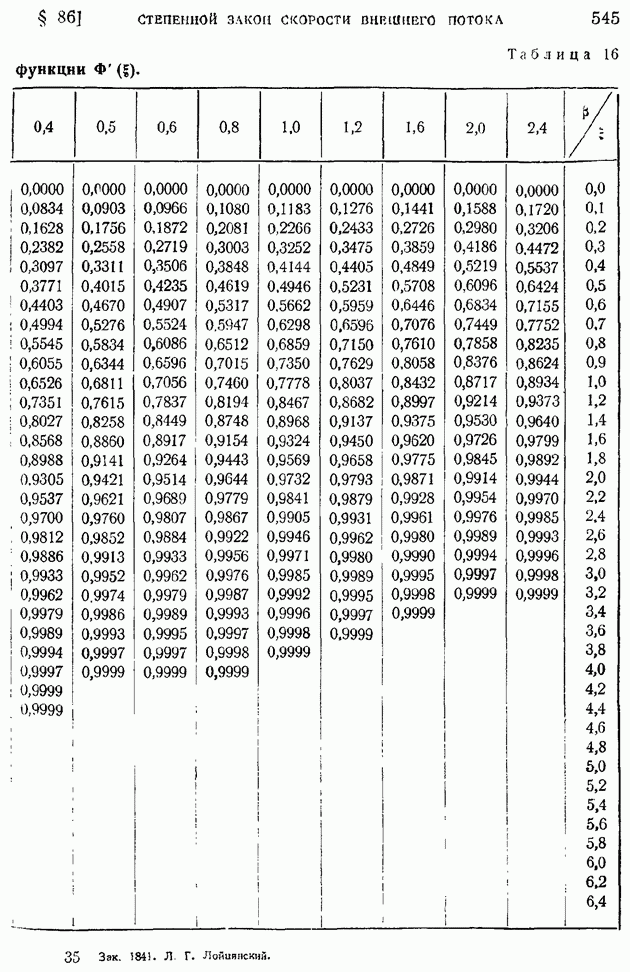
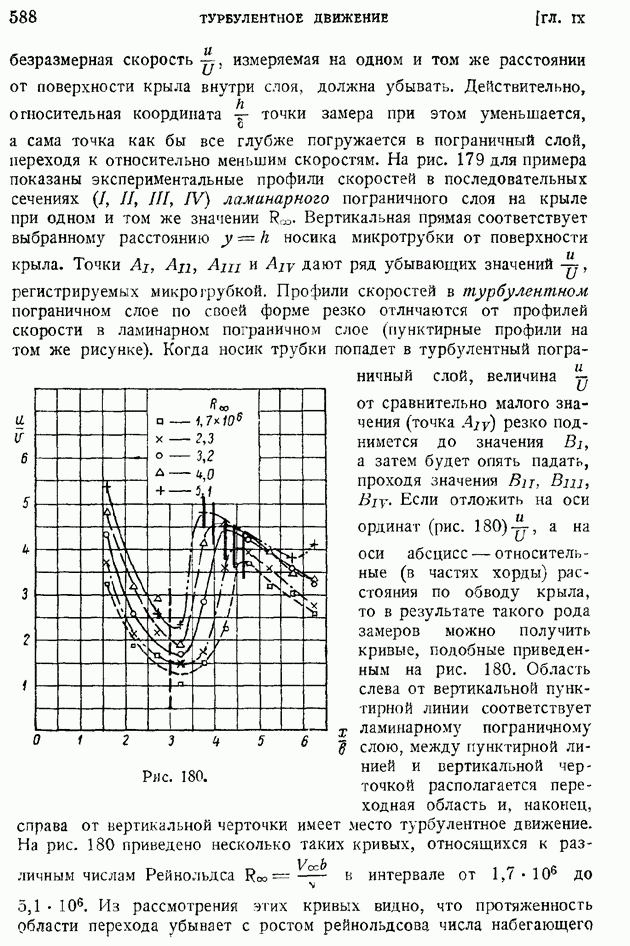
Рассмотрим одномерное адиабатическое и изэнтропическое течение газа в сопле Лаваля. Ход изменения площади А вдоль оси сопла задан верхней кривой а на рис. 49, соответствующее изменение числа  кривых
кривых  того же рисунка и, наконец, кривые давления, отнесенного к критическому его значению, — в нижней части графика в.
того же рисунка и, наконец, кривые давления, отнесенного к критическому его значению, — в нижней части графика в.
Кривые хода  построены по ранее выведенным формулам
построены по ранее выведенным формулам  и изэнтропического течения.
и изэнтропического течения.
Из хода кривых на рис. 49 можно сделать основные качественные выводы о явлениях, происходящих в сопле Лаваля. Если в наиболее узком сечении сопла  число
число  достигло значения
достигло значения  то дальнейшее развитие потока может идти по кривым как
то дальнейшее развитие потока может идти по кривым как  так и
так и  т. е. поток может или стать сверхзвуковым или остаться
т. е. поток может или стать сверхзвуковым или остаться
дозвуковым. Эта альтернатива разрешается заданием противодавления  на выходе из сопла. Рассчитав величину
на выходе из сопла. Рассчитав величину  по первой из формул (91) и сверхзвуковой ветви (рис. 47) основного соотношения (90), найдем такое "расчетное" противодавление
по первой из формул (91) и сверхзвуковой ветви (рис. 47) основного соотношения (90), найдем такое "расчетное" противодавление  при осуществлении которого на выходе из сопла поток преобразуется внутри сопла в сверхзвуковой и достигает на выходе требуемого числа
при осуществлении которого на выходе из сопла поток преобразуется внутри сопла в сверхзвуковой и достигает на выходе требуемого числа  если же взять противодавление равным
если же взять противодавление равным  соответствующим при той же площади выходного сечения А дозвуковой ветви
соответствующим при той же площади выходного сечения А дозвуковой ветви  (рис. 47), то поток останется дозвуковым и число
(рис. 47), то поток останется дозвуковым и число  на выходе будет меньшим единицы.
на выходе будет меньшим единицы.

Рис. 49.
Замечательно, что существует только одно, определенное для каждого сопла, противодавление которое может привести к сверхзвуковому потоку в выходном сечении сопла. Это — специфическое свойство сверхзвукового потока; в самом деле, как видно из рис. 49 в, при  имеется бесчисленное множество дозвуковых течений газа в сопле данной формы, в то время как сверхзвуковое (изэнтропическое!) движение является единственным и соответствует противодавлению
имеется бесчисленное множество дозвуковых течений газа в сопле данной формы, в то время как сверхзвуковое (изэнтропическое!) движение является единственным и соответствует противодавлению 
Естественно возникает вопрос, что же будет с газом, если на выходе из сопла создать противодавление  лежащее между расчетными значениями
лежащее между расчетными значениями  На этот вопрос может быть один лишь ответ: движение газа не будет изэнтропическим. Как показано на графике рис. 49 в пунктиром, в этом случае в расширяющейся части сопла появится скачок уплотнения или система скачков, что приведет к неизэнтропическому процессу. Если, наконец, взять
На этот вопрос может быть один лишь ответ: движение газа не будет изэнтропическим. Как показано на графике рис. 49 в пунктиром, в этом случае в расширяющейся части сопла появится скачок уплотнения или система скачков, что приведет к неизэнтропическому процессу. Если, наконец, взять  то в выходном сечении трубы давление примет свое расчетное значение
то в выходном сечении трубы давление примет свое расчетное значение  и уже затем сложным неизэнтропическим путем (система скачков уплотнения, нарушающая одномерность потока) снизится до выходного противодавления
и уже затем сложным неизэнтропическим путем (система скачков уплотнения, нарушающая одномерность потока) снизится до выходного противодавления 
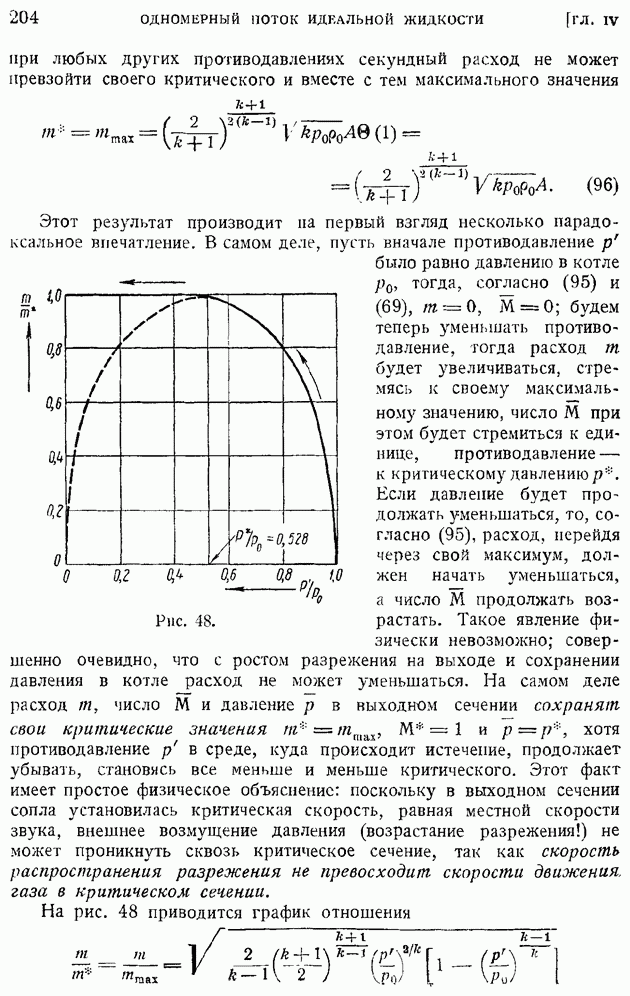
Секундный массовый расход  через сопло Лаваля, так же как и в случае чисто конфузорного сопла, не может превзойти своего максимального значения, равного тому расходу, который пройдет сквозь сопло, если в наиболее узком его сечении, на границе между конфузорной и диффузорной частями, будет достигнута местная скорость звука. Но в отличие от конфузорного сопла скорость на выходе из сопла Лаваля превосходит соответствующую выходу скорость звука и может быть подбором длины сопла сделана тем больше, чем меньше противодавление. Можно условно рассчитать такое "идеальное" сопло Лаваля, что оно будет работать на расчетном режиме
через сопло Лаваля, так же как и в случае чисто конфузорного сопла, не может превзойти своего максимального значения, равного тому расходу, который пройдет сквозь сопло, если в наиболее узком его сечении, на границе между конфузорной и диффузорной частями, будет достигнута местная скорость звука. Но в отличие от конфузорного сопла скорость на выходе из сопла Лаваля превосходит соответствующую выходу скорость звука и может быть подбором длины сопла сделана тем больше, чем меньше противодавление. Можно условно рассчитать такое "идеальное" сопло Лаваля, что оно будет работать на расчетном режиме  т. е. в полный вакуум. Найдем выходную скорость такого истечения. Согласно формуле Сен-Венана и Ванцеля (67) гл. III, скорость истечения возрастает с уменьшением давления, и при
т. е. в полный вакуум. Найдем выходную скорость такого истечения. Согласно формуле Сен-Венана и Ванцеля (67) гл. III, скорость истечения возрастает с уменьшением давления, и при  скорость истечения примет свое максимальное значение
скорость истечения примет свое максимальное значение

зависящее лишь от начальных параметров газа в котле, из которого происходит истечение. Вспоминая определения адиабатической скорости звука в неподвижном газе и критической скорости, получим вместо (97) следующие равенства:

Из которых следует, что максимально возможная скорость истечения, так же как и критическая скорость, зависят только от природы газа и его температуры в котле, т. е. температуры изэнтропически заторможенного газа.
Для воздуха  при
при 
При рассматриваемом "расчетном" истечении в вакуум давление, плотность и температура в выходном сечении равны нулю, равна нулю 1 скорость звука в этом сечении, так что 
Все изложенное, конечно, верно лишь для идеального газа, лишенного внутреннего трения, и в случае полной адиабатичности процесса, т. е. отсутствия притока или отвода тепла в сопле. На самом деле явление движения газа в сопле неизмеримо сложнее.
Во-первых, даже и для идеального газа, лишенного внутреннего трения, движение в сопле не одномерно, а представляет на самом деле сложное до- и сверхзвуковое пространственное течение.
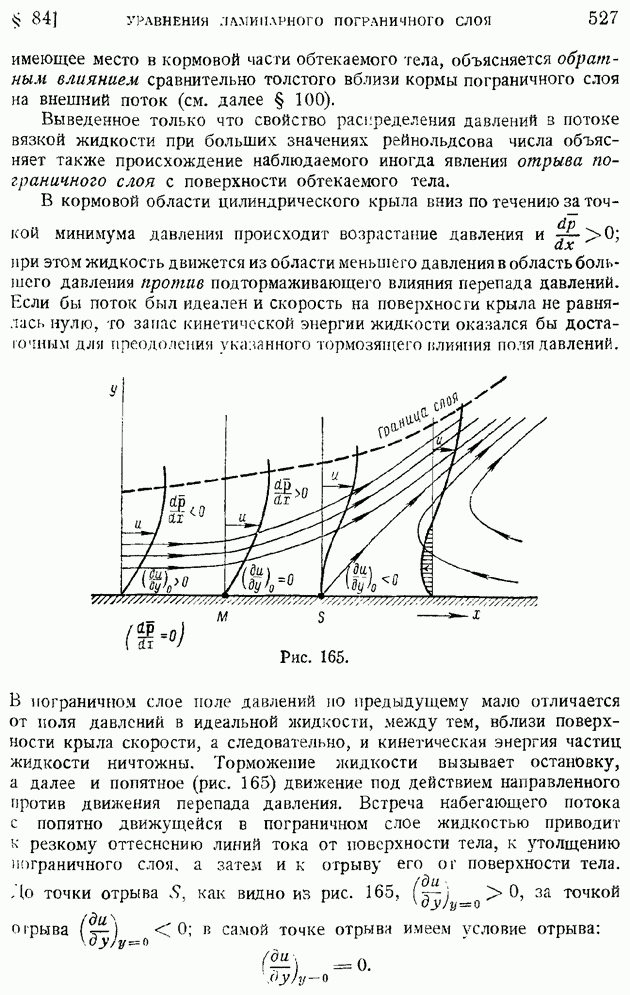
Во-вторых, при наличии трения частицы газа, движущиеся около стенок сопла, имеют меньшие скорости, чем частицы, удаленные от стенок; образующийся вблизи стенок сопла пограничный слой утолщается вниз по потоку, а иногда даже отрывается от стенок, искажая тем самым всю картину потока и делая невозможным применение гидравлической схемы одномерного потока; возникающие в потоке скачки уплотнения нызываюг появление отрывов пограничного слоя и, наоборот, пограничный слой стимулирует зарождение скачков уплотнения. Это взаимное влияние вязкости и сжимаемости газа также искажает изэнтропичность и превращает расчетный режим в нерасчетный.
И, наконец, в-третьих, существенной причиной нарушения адиабатичности потока является теплопередача через стенки сопла, что также сильно усложняет расчеты. Вот почему даже в настоящее время, когда многие из только что перечисленных обстоятельств хорошо изучены, все же практически после расчета вновь спроектированного сопла приходится его дополнительно исследовать на опытной установке в лаборатории. Рассчитанное сопло может не дать желательного увеличения числа  на выходе, кроме того, за счет неизэнтропичности движения газа возникают дополнительные потери механической энергии, коэффициент полезного действия при этом падает, что для непрерывно действующих установок большой мощности, конечно, недопустимо.
на выходе, кроме того, за счет неизэнтропичности движения газа возникают дополнительные потери механической энергии, коэффициент полезного действия при этом падает, что для непрерывно действующих установок большой мощности, конечно, недопустимо.
Оставляя пока в стороне вопросы, связанные с внутренним трением в газе и образованием пограничного слоя на стенках сопла (об этом будет еще идти речь в заключительных главах), остановимся вкратце на оценке влияния внешнего подогрева или охлаждения потока в соплс.
Рассмотрим опять одномерный стационарный поток идеального газа, адиабатичность которого нарушается тем, что на некотором весьма коротком участке к газу подводится извне тепло. Это вызывает изменение температуры газа  или температуры изэнгропически заторможенного газа
или температуры изэнгропически заторможенного газа  до участка подогрева на величину
до участка подогрева на величину  соответственно,
соответственно,  причем за участком подогрева вновь устанавливается адиабатическое течение с температурами
причем за участком подогрева вновь устанавливается адиабатическое течение с температурами  и
и 
Отвлекаясь от эффекта переменности сечения трубы на участке подогрева, определим изменение числа  на этом участке, после чего уже нетрудно будет найти по обычным изэнтропическим формулам и изменения всех остальных величин.
на этом участке, после чего уже нетрудно будет найти по обычным изэнтропическим формулам и изменения всех остальных величин.
Основные уравнения поставленной задачи легко получить, если написать, что приток тепла не мог нарушить баланса массы и количества движения, т. е. при прохождении газом участка подогрева остаются в силе следующие два равенства:

Припоминая известные уже формулы связи адиабатической скорости звука с температурой, давлением и плотностью газа, а также определение числа  будем иметь:
будем иметь:

Отсюда, деля одно равенство на другое, получим искомую связь числа  с обычной температурой
с обычной температурой  или температурой изэнтропически заторможенного газа
или температурой изэнтропически заторможенного газа 

Применим эти равенства к двум сечениям потока, ограничивающим участок подогрева, тогда будем иметь:

Зная отношения:

и число  до прохождения участка подогрева, по формулам (102) найдем
до прохождения участка подогрева, по формулам (102) найдем  а уже затем по второй из формул (100) — и отношение Давлений
а уже затем по второй из формул (100) — и отношение Давлений

а также и все остальные термодинамические параметры. Наконец, зная число  и температуру
и температуру  легко найдем и скорость газа за участком подогрева.
легко найдем и скорость газа за участком подогрева.
Введем в рассмотрение функцию

входящую во вторую расчетную формулу (102). Вычислив производную

видим, что функция  имеет максимум при
имеет максимум при  и этот максимум равен
и этот максимум равен

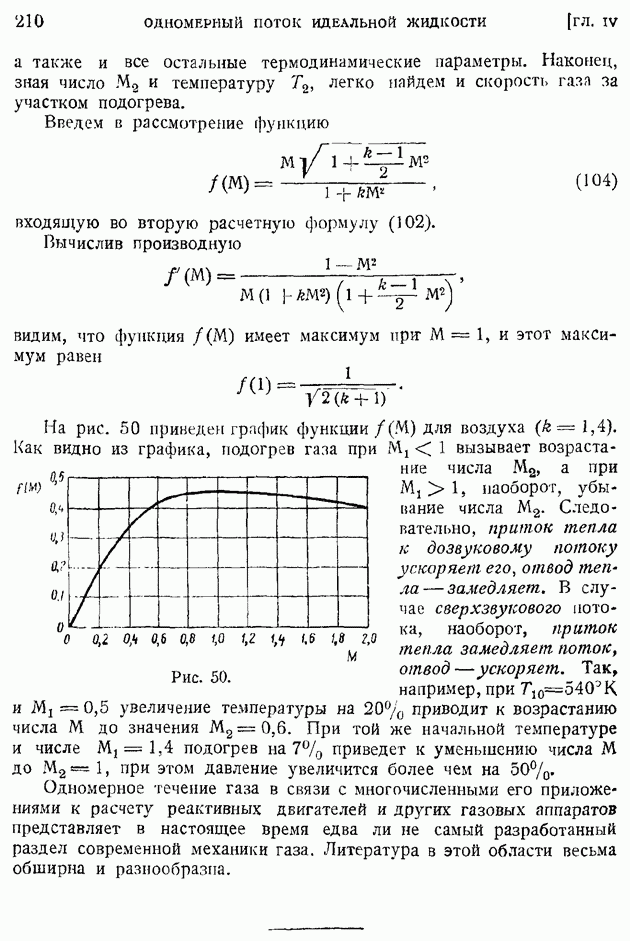
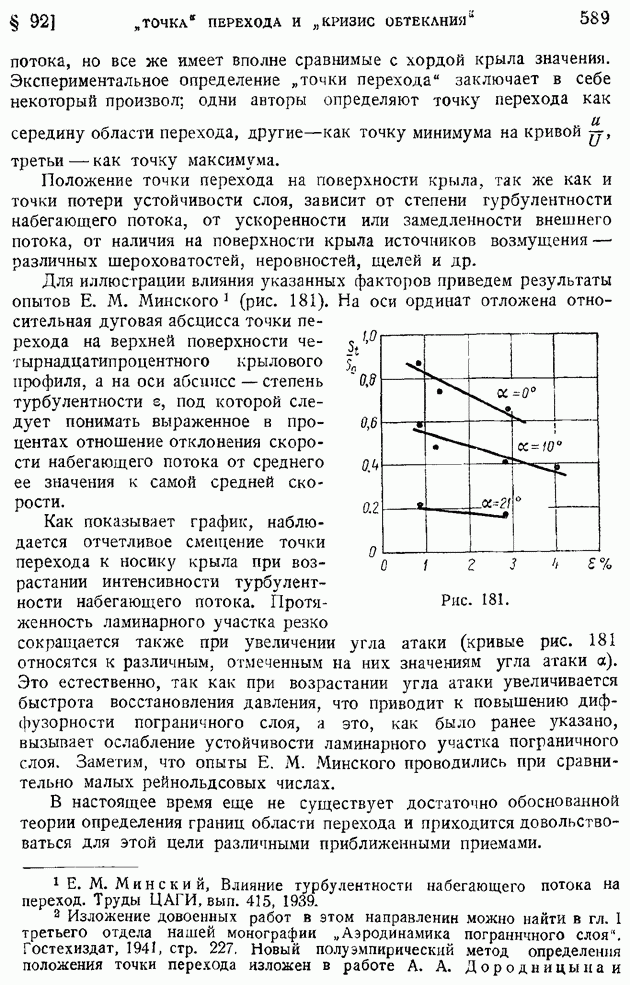
На рис. 50 приведен график функции  для воздуха
для воздуха  Как видно из графика, подогрев газа при
Как видно из графика, подогрев газа при  вызывает возрастание числа
вызывает возрастание числа  а при
а при  наоборот, убывание числа
наоборот, убывание числа  Следовательно, приток тепла к дозвуковому потоку ускоряет его, отвод тепла — замедляет. В случае сверхзвукового потока, наоборот, приток тепла замедляет поток, отвод — ускоряет. Так, например, при
Следовательно, приток тепла к дозвуковому потоку ускоряет его, отвод тепла — замедляет. В случае сверхзвукового потока, наоборот, приток тепла замедляет поток, отвод — ускоряет. Так, например, при  увеличение температуры на 20% приводит к возрастанию числа
увеличение температуры на 20% приводит к возрастанию числа  до значения
до значения  При той же начальной температуре и числе
При той же начальной температуре и числе  подогрев на 7% приведет к уменьшению числа
подогрев на 7% приведет к уменьшению числа  до
до  при этом давление увеличится более чем на 50%.
при этом давление увеличится более чем на 50%.

Рис. 50.
Одномерное течение газа в связи с многочисленными его приложениями к расчету реактивных двигателей и других газовых аппаратов представляет в настоящее время едва ли не самый разработанный раздел современной механики газа. Литература в этой области весьма обширна и разнообразна.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Предмет механики жидкости и газа. Основные свойства «макромодели» жидкости и газа: сплошность и подвижность
- § 2. Основные методы механики жидкости и газа. Области применения и главнейшие задачи
- § 3. Краткий очерк исторического развития механики жидкости и газа. От гидромеханики древних до установления воззрений ньютонианской эпохи
- § 4. Эпоха Эйлера и Бернулли. Гидроаэродинамика в XIX в.
- § 5. Современный этап развития механики жидкости и газа
- ГЛАВА I. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
- § 6. Поле физической величины. Скалярное и векторное поля. Поверхности уровня. Векторные линин и трубки
- § 7. Мера однородности поля в данном направлении и в дайной точке. Градиевт скалярного поля и дифференциальный тензор векторного поля как меры неоднородности поля
- § 8. Задание движения сплошной среды. Поле скоростей. Линии тока и траектории
- § 9. Поле ускорений. Разложение ускорения частицы на локальную и конвективную составляющие
- § 10. Скоростное поле сплошной среды в окрестности данной точки. Угловая скорость и вихрь. Тензор скоростей деформаций и его компоненты
- § 11. Скорость объемного расширения жидкости. Интегральные представления дифференциальных операторов поля. Основные интегральные формулы
- § 12. Вихревые линии и трубки. Вторая теорема Гельмгольца. Интенсивность вихревой трубки
- § 13. Выражение интенсивности вихревой трубки через циркуляцию вектора по контуру, охватывающему трубку. Теорема об изменении циркуляции скорости во времени
- ГЛАВА II. ОСНОВНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ И РАВНОВЕСИЯ СПЛОШНОЙ СРЕДЫ
- § 14. Распределение массы в сплошной среде. Плотность и удельный вес. Напряжения. Тензор напряженности и его симметричность
- § 15. Общие уравнения динамики сплошной среды. Уравнение неразрывности. Уравнения динамики в напряжениях
- § 16. Тепловые явления в жидкостях и газах. Закон сохранения энергии и уравнение баланса энергии
- § 17. Общие уравнения равновесного состояния жидкости и газа. Равновесие воздуха в атмосфере. Приближенные барометрические формулы. Стандартная атмосфера
- § 18. Равновесие несжимаемой жидкости. Уравнение поверхности раздела. Равновесие вращающейся жидкости
- § 19. Давление тяжелой несжимаемой жидкости на поверхность тела. Сила и момент, приложенные к телу, плавающему в тяжелой жидкости. Случай вращающейся жидкости
- ГЛАВА III. ДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ И ГАЗА. ОСНОВНЫЕ УРАВНЕНИЯ И ОБЩИЕ ТЕОРЕМЫ
- § 20. Идеальная жидкость. Основные уравнения движения
- § 21. Закон сохранения энергии в движущейся идеальной жидкости. Адиабатическое движение. Сохранение энтропии
- § 22. Эйлерово представление конвективного изменения объемного интеграла. Перенос величины сквозь контрольную поверхность
- § 23. Эйлерова форма законов сохранения массы и энергии, теоремы количеств движения и момента количеств движения при стационарном движении идеальной жидкости
- § 24. Теорема об изменении кинетической энергии. Работа и мощность внутренних сил. Эйлерова форма уравнения изменения кинетической энергии
- § 25. Теорема Бернулли о сохранении полной механической энергии при стационарном баротропном движении идеальной жидкости и газа
- ГЛАВА IV. ОДНОМЕРНЫЙ ПОТОК ИДЕАЛЬНОЙ ЖИДКОСТИ
- § 26. Одномерное течение идеальной сжимаемой жидкости. Линеаризированные уравнения. Скорость распространения малых возмущений в жидкости или газе
- § 27. Изотермическая и адиабатическая скорости звука. «Конус возмущений» при сверхзвуковом движении источника возмущения. Число M и его связь с углом конуса возмущений
- § 28. Распространение непрерывных возмущений конечной интенсивности. Характеристики. Образование разрывной ударной волны
- § 29. Стоячая ударная волна или скачок уплотнения. Ударная адиабата
- § 30. Критические величины в одномерном потоке газа. Связь между скоростями до и после скачка. Изменение давления, плотности и температуры в скачке уплотнения
- § 31. Скорость распространения ударной волны. Спутное движение газа за ударной волной
- § 32. Влияние интенсивности скачка уплотнения на сжатие газа. Измерение скоростей и давлений в до- и сверхзвуковых потоках
- § 33. Одномерное движение газа по трубе переменного сечения. Истечение из резервуара большой емкости сквозь сходящееся сопло
- § 34. Одномерное течение в сопле Лаваля. Движение газа с притоком тепла
- ГЛАВА V. БЕЗВИХРЕВОЕ ДВИЖЕНИЕ ЖИДКОСТИ. ПЛОСКОЕ ДВИЖЕНИЕ НЕСЖИМАЕМОЙ ЖИДКОСТИ
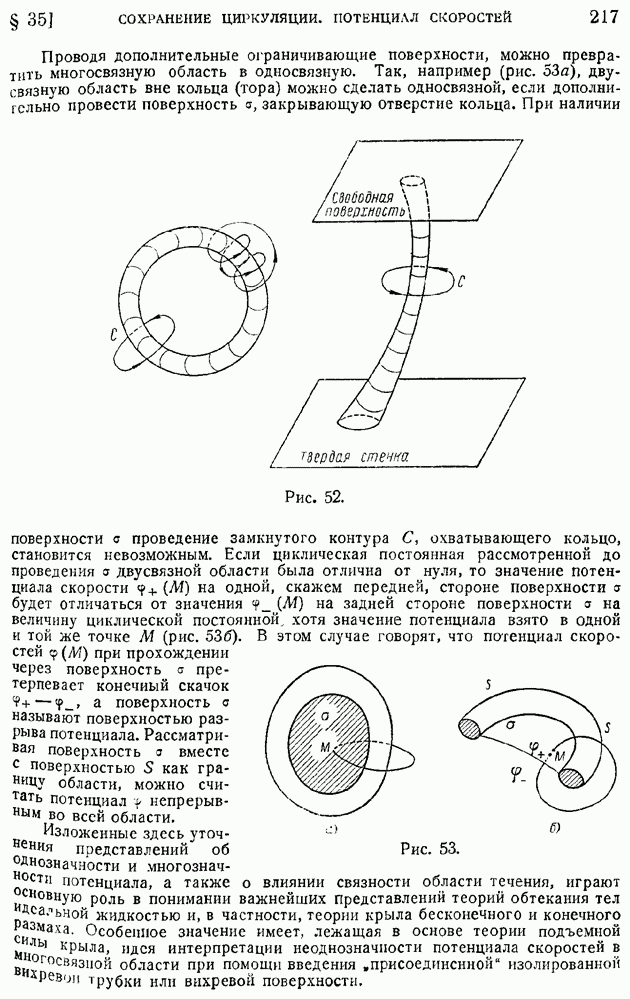
- § 35. Сохранение циркуляции скорости в потоке идеальной жидкости. Теорема Кельвина и Лаграижа. Безвихревое движение. Потенциал скоростей
- § 36. Интеграл Лагранжа — Коши уравнений безвихревого движения. Теорема Бернулли. Некоторые общие свойства безвихревого движения идеальной несжимаемой жидкости в односвязной области
- § 37. Плоское безвихревое движение несжимаемой жидкости. Потенциал скоростей и функция тока. Применение функций комплексного переменного. Комплексный потенциал и сопряженная скорость
- § 38. Построение полей течения по заданной характеристической Функции. Простейшие плоские потоки и их наложение
- § 39. Бесциркуляционное и циркуляционное обтекания круглого цилиндра
- § 40. Применение криволинейных координат. Бесциркуляционное и циркуляционное обтекания эллиптического цилиндра и пластинки. Задача Жуковского об обтекании решетки пластин.
- § 41. Плоское движение с отрывом струй. Разрывное обтекание пластинки и протекание жидкости сквозь отверстие
- § 42. Прямая задача в теории плоского движения идеальной несжимаемой жидкости. Применение метода конформных отображений. Гипотеза Чаплыгина о безотрывном обтекании задней кромки профиля. Формула циркуляции
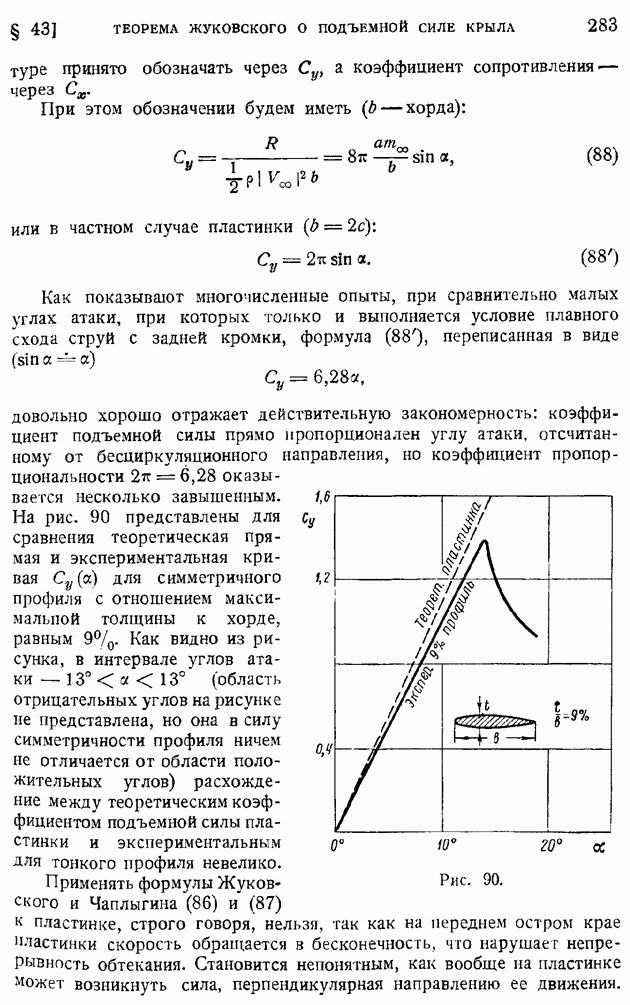
- § 43. Теорема Жуковского о подъемной силе крыла. Зависимость подъемной силы от угла атаки. Коэффициент подъемной силы
- § 44. Применение метода комплексных переменных к выводу теоремы Жуковского. Формулы Чаплыгина для главного вектора и момента сил давления потока на крыло
- § 45. Выражение главного момента сил давления потока через коэффициенты конформного отображения. Фокус крыла. Независимость от угла атаки момента относительно фокуса. Парабола устойчивости
- § 46. Частные случаи конформного отображения крылового профиля на круг. Преобразование Жуковского-Чаплыгина. Теоретические крыловые профили
- § 47. Задача об обтекании слабо изогнутой дужки произвольной формы (теория тонкого крыла)
- § 48. Определение обтекания крылового профиля произвольной формы
- § 49. Обобщение теоремы Жуковского на случай плоской решетки с бесчисленным множеством профилей
- ГЛАВА VI. ПЛОСКОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ СЖИМАЕМОГО ГАЗА
- § 50. Основные уравнения плоского стационарного безвихревого движения сжимаемого газа. Линеаризированные уравнения
- 51. Линеаризированный до- и сверхзвуковой газовый поток вдоль волнистой стенки
- § 52. Тонкое крыло в линеаризированном до- и сверхзвуковом потоках. Влияние сжимаемости газа на коэффициент подъемной силы в дозвуковом потоке. Коэффициенты подъемной силы и волнового сопротивления при сверхзвуковом потоке
- § 53. Нелинеаризированные уравнения движения идеального сжимаемого газа. Переход в плоскость годографа. Уравнения Чаплыгина
- § 54. Метод С. А. Христиановича. Приближенные формулы учета влияния сжимаемости на распределение давления
- § 55. Критическое число M и его определение по заданному распределению давления в несжимаемом обтекании. Поведение коэффициента подъемной силы и момента при около- и закритических значениях числа M
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
- § 57. Нелинеаризированный сверхзвуковой поток. «Характеристики» уравнений плоского сверхзвукового потока. Линин возмущения и их основные свойства
- § 58. Обтекание выпуклого угла сверхзвуковым потоком. Влияние угла поворота струи на ее газодинамические элементы
- § 59. Сверхзвуковой поток внутри тупого угла. Косой скачок уплотнения. Связь между газодинамическими элементами до и за косым скачком
- ГЛАВА VII. ПРОСТРАНСТВЕННОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ
- § 60. Ортогональные криволинейные координаты в пространстве. Основные дифференциальные операторы поля в криволинейных координатах
- § 61. Потенциал скоростей. Поле источника и диполя. Непрерывное распределение источников и диполей. Ньютонов потенциал. Потенциал простого и двойного слоев
- § 62. Поле скоростей вокруг заданной системы вихрей. Формула Био — Савара. Потенциал скоростей замкнутой вихревой нити. Аналогия с потенциалом двойного слоя
- § 63. Функция тока и ее связь с векторным потенциалом скоростей. Функции тока простейших течений
- § 64. Обтекание сферы. Давление однородного стационарного потока идеальной несжимаемой жидкости на погруженное в нее тело. Парадокс Даламбера
- § 65. Общие уравнения осесимметричного движения. Применение цилиндрических координат. Течение сквозь каналы
- § 66. Осесимметричное продольное обтекание тел вращения. Случай эллипсоида вращения
- § 67. Поперечное обтекание тел вращения. Пример эллипсоида вращения
- § 68. Продольное и поперечное обтекание тел вращения большого удлинения. Приближенные выражения граничных условий. Применение тригонометрических сумм для определения коэффициентов …
- § 69. Метод «особенностей». Применение непрерывно распределенных источников (стоков) и диполей для решения задачи о продольном и поперечном обтекании тел вращения
- § 70. Общий случай движения твердого тела сквозь несжимаемую идеальную жидкость. Определение потенциала скоростей. Главный вектор и главный момент сил давления потока на тело
- § 71. Коэффициенты «присоединенных масс». Свойство симметрии. «Присоединенная» кинетическая энергия. Определение «присоединенных масс» поступательно движущегося цилиндра, шара и эллипсоида
- § 72. Элементы теории крыла конечного размаха. Вихревая система крыла. Гипотеза плоских сечеиий. Геометрические и действительные углы атаки. Подъемная сила и «индуктивное сопротивление»
- § 73. Основные формулы теории «несущей линии». «Индуктивная скорость» и «индуктивный угол». Прямая задача определения подъемной силы и индуктивного сопротивления по заданному распределению циркуляции
- § 74. Крыло с минимальным индуктивным сопротивлением. Эллиптическое распределение циркуляции. Связь между коэффициентами индуктивного сопротивления и подъемной силы. Основное уравнение теории крыла и понятие о его интегрировании
- ГЛАВА VIII. ДИНАМИКА ВЯЗКОЙ ЖИДКОСТИ И ГАЗА
- § 75. Внутреннее трение и теплопроводность в жидкостях и газах. Законы Ньютона и Фурье. Влияние температуры на коэффициенты вязкости и теплопроводности. Число «сигма»
- § 76. Обобщение закона Ньютона на случай произвольного движения среды. Закон линейной связи между тензорами напряжений и скоростей деформации
- § 77. Общие уравнения движения вязкой жидкости. Динамические уравнения и уравнение баланса энергии. Граничные условия движения жидкости с треннем и теплопроводностью
- § 78. Понятие о подобии гидродинамических явлений. Безразмерные уравнения движения вязкой жидкости и газа. Условия подобия
- § 79. Ламинарное движение вязкой несжимаемой жидкости по цилиндрической трубе
- § 80. Обтекание шара при очень малых значениях числа Рейнольдса. Формула сопротивления шара по Стоксу и ее обобщения
- § 81. Вихревые линии в идеальной и вязкой жидкости. Сохраняемость вихревых линий при отсутствии внутреннего трения. Диффузия вихря в вязкой жидкости
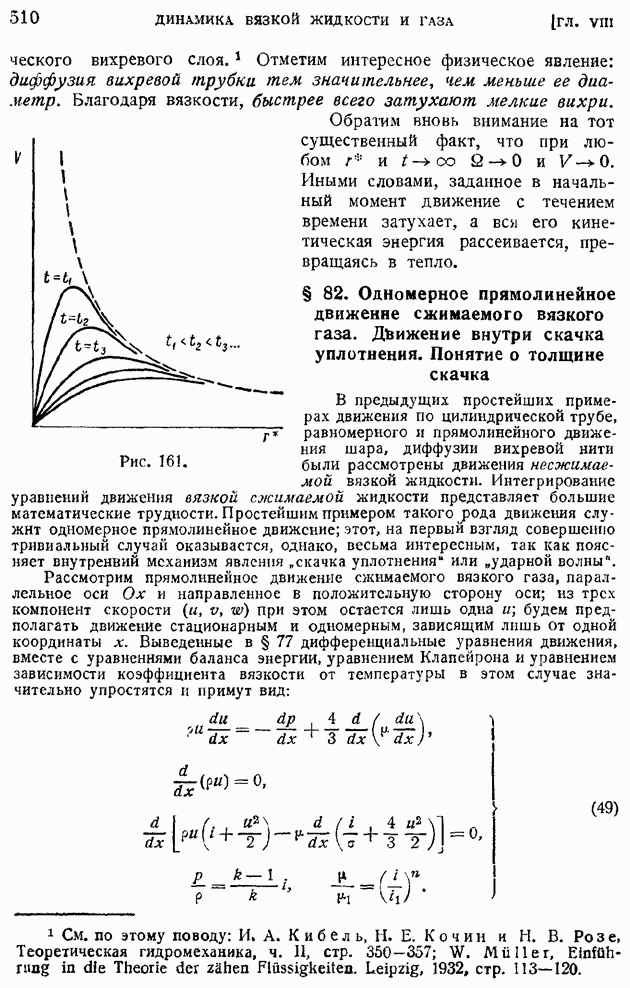
- § 82. Одномерное прямолинейное движение сжимаемого вязкого газа. Движение внутри скачка уплотнения. Понятие о толщине скачка
- § 83. Работа внутренних сил и диссипация механической энергии в движущейся вязкой среде
- § 84. Обтекание тел жидкостью и газом при больших значениях числа Рейнольдса. Основные уравнения теории ламинарного пограничного слоя
- § 85. Ламинарный пограничный слой на пластинке, продольно обтекаемой несжимаемой жидкостью. Неизотермическое движение
- § 86. Ламинарный пограничный слой при степенном задании скорости внешнего потока
- § 87. Ламинарный пограничный слой в общем случае задания скорости внешнего потока. Применение уравнения импульсов для приближенного расчета ламинарного пограничного слоя
- § 88. Способы определения функций … Приближенный метод расчета ламинарного пограничного слоя
- § 89. Ламинарный пограничный слой на пластинке, продольно обтекаемой сжимаемым газом при больших скоростях. Случай линейной зависимости коэффициента вязкости от температуры (n = 1)
- § 90. Ламинарный пограничный слой на пластинке при любом законе связи между вязкостью и температурой и при числе … Обтекание крылового профиля потоком больших скоростей
- ГЛАВА IX. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ
- § 91. Переход ламинарного движения в турбулентное. Критическое рейнольдсово число
- § 92. Область и «точка» перехода. Явление «кризиса обтекания»
- § 93. Основные уравнения осреднеиного турбулентного движения. Тензор турбулентных напряжений
- § 94. Турбулентное движение жидкости в плоской и круглой трубе. Логарифмические формулы скоростей
- § 95. Формулы сопротивления гладких труб при турбулентном движении жидкости. Ламинарный подслой
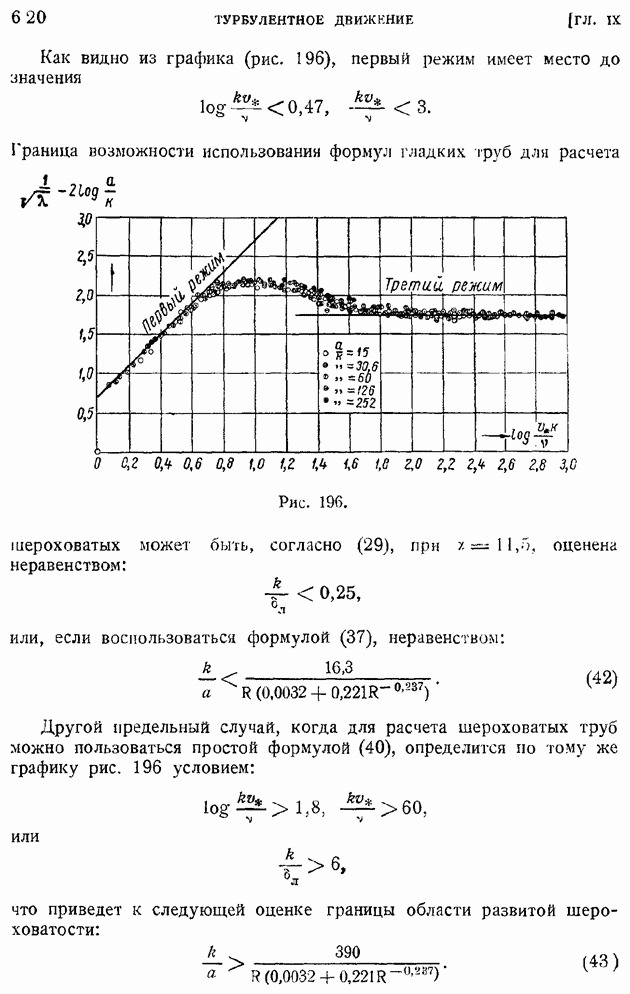
- § 96. Влияние шероховатости стенок трубы на ее сопротивление. Предельные режимы течения. Режим установившейся шероховатости
- § 97. Турбулентный пограничный слой на продольно обтекаемой пластине. Сопротивление пластины
- § 98. Турбулентный пограничный слой на крыловом профиле при малом продольном перепаде давлений
- § 99. Турбулентный пограничный слой на крыловом профиле при значительных продольных перепадах давления
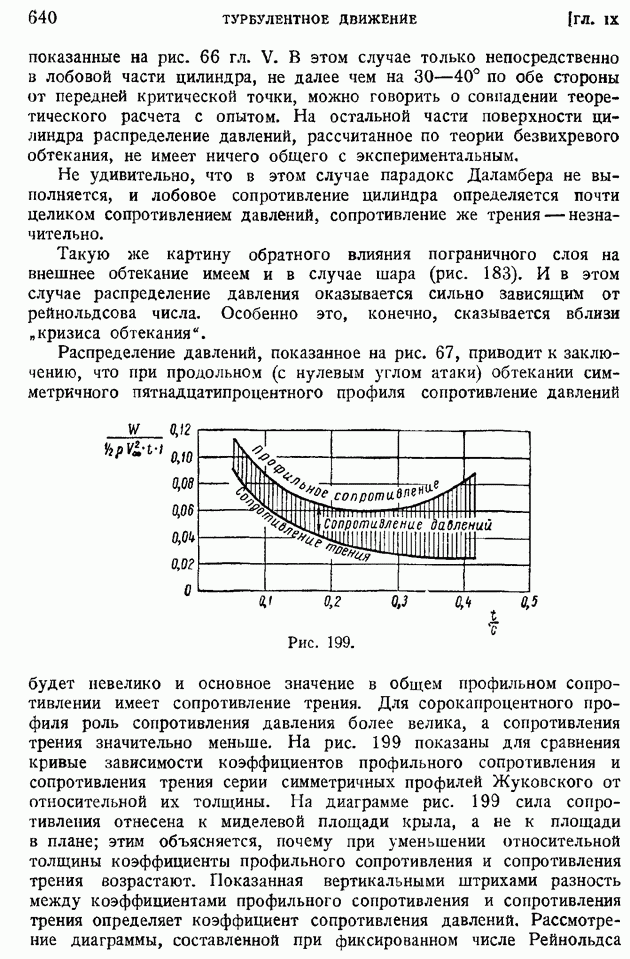
- § 100. Профильное сопротивление крыла. Разложение профильного сопротивления на сопротивление трения и сопротивление давлений. Обратное влияние пограничного слоя на распределение давлений по поверхности обтекаемого профиля
- § 101. Приближенные формулы профильного сопротивления крыла и крылового профиля в решетке
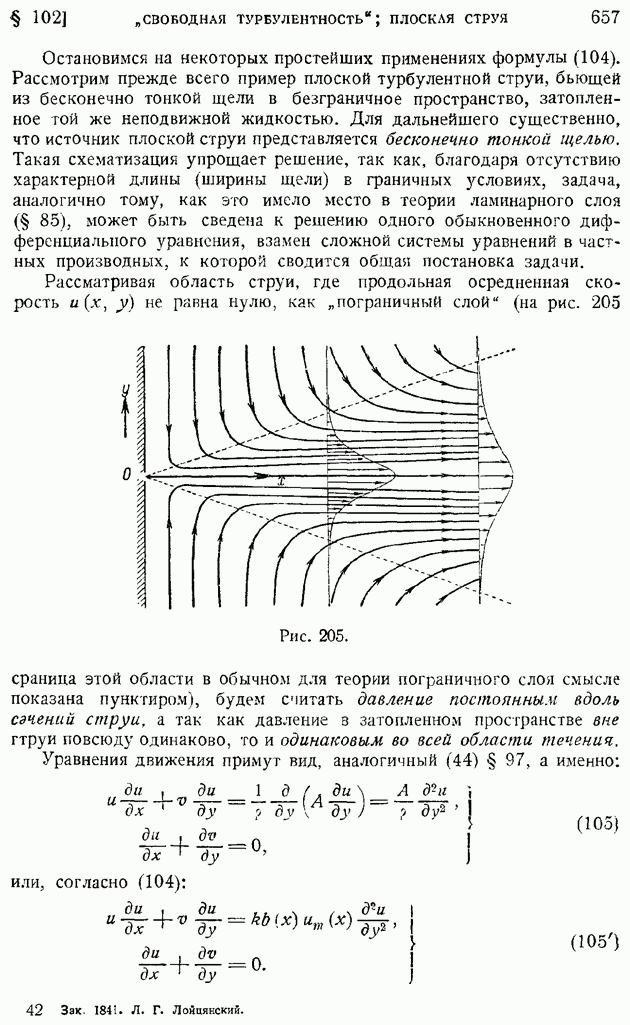
- § 102. Основные закономерности «свободной турбулентности». Плоская турбулентная струя в пространстве, заполненном той же жидкостью
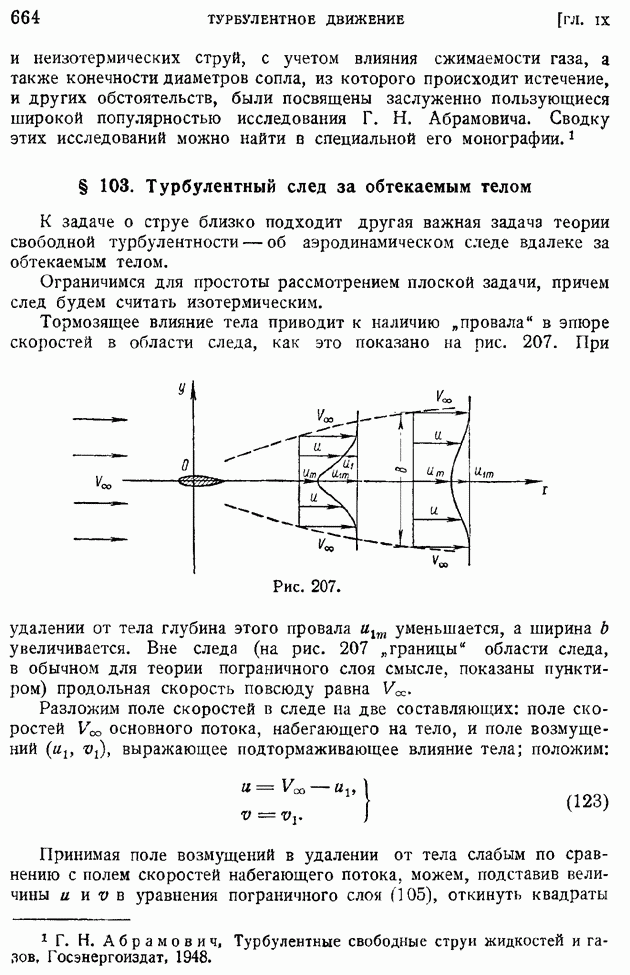
- § 103. Турбулентный след за обтекаемым телом
- § 104. Рассеяние турбулентных возмущений в жидкости. Случай изотропной и однородной турбулентности. Закон сохранения момента возмущений