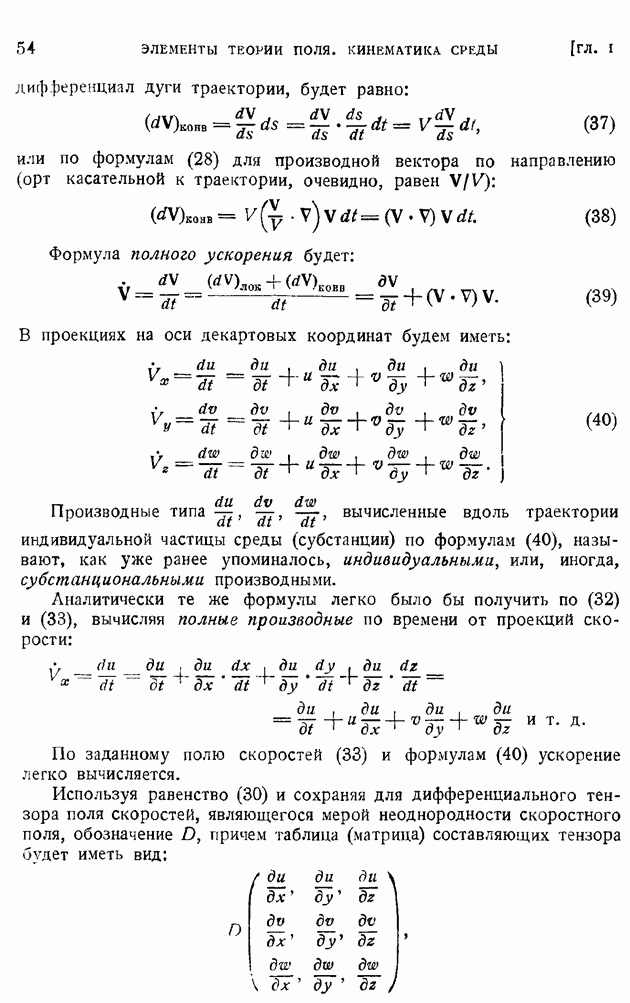| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
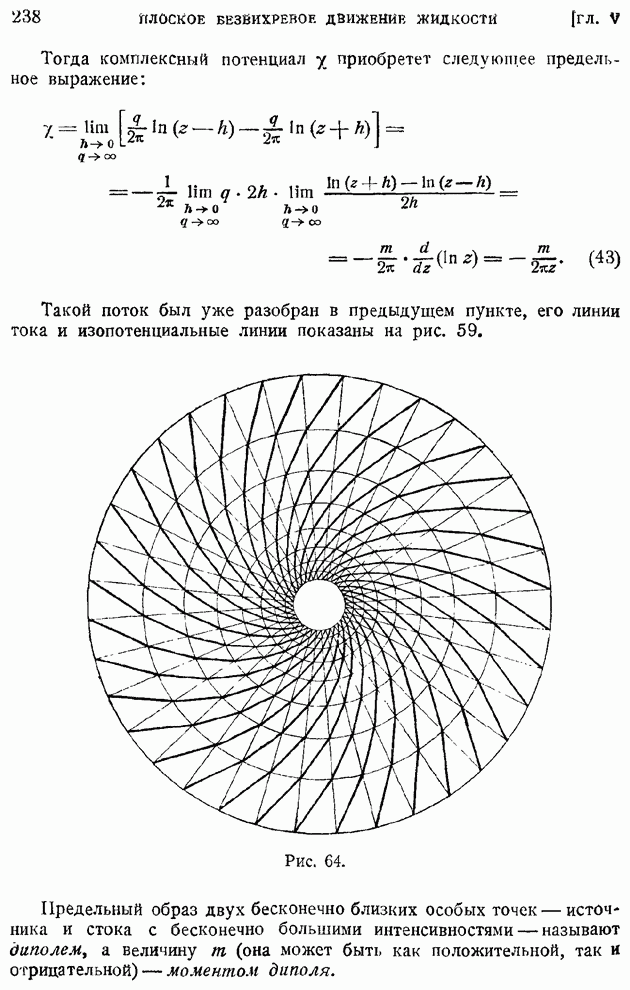
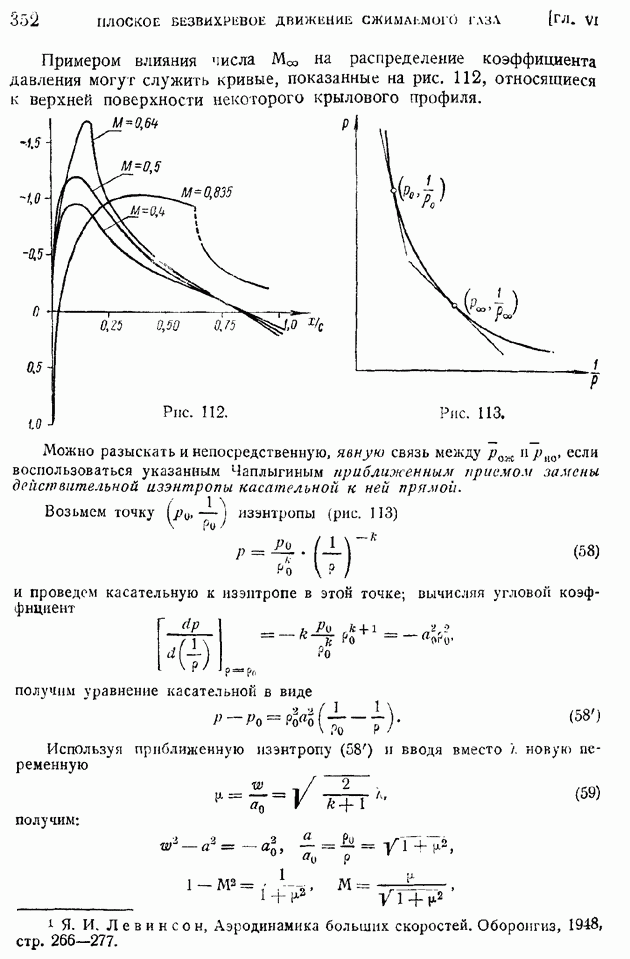
§ 59. Сверхзвуковой поток внутри тупого угла. Косой скачок уплотнения. Связь между газодинамическими элементами до и за косым скачком
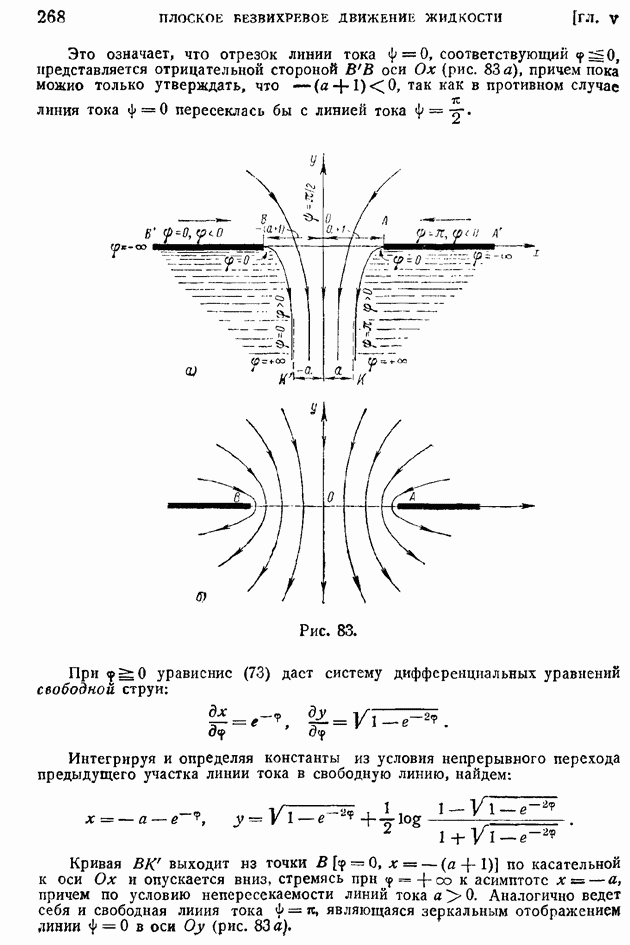
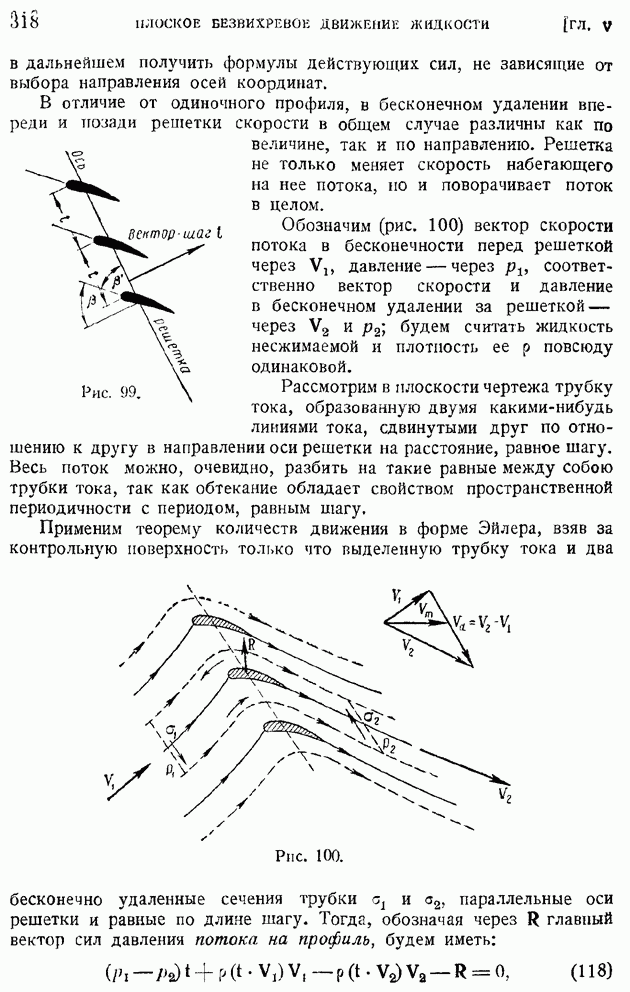
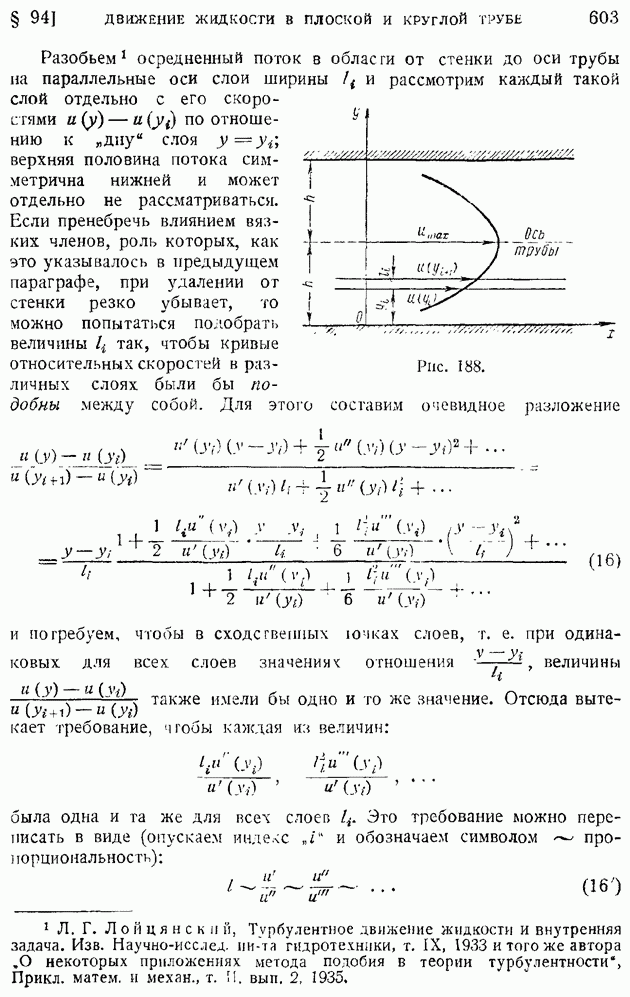
Рассмотрим сверхзвуковое обтекание внутренней части тупого угла (рис. 123). В отличие от предыдущего случая после прохождения вершины угла О скорость потока должна уменьшиться, поэтому будем предполагать, что на участке слева от линии возмущения  поток был сверхзвуковым, число
поток был сверхзвуковым, число  было больше единицы, а угол
было больше единицы, а угол
 меньше прямого. Так как при повороте потока скорость его и число
меньше прямого. Так как при повороте потока скорость его и число  уменьшаются, то угол возмущения
уменьшаются, то угол возмущения  должен увеличиться, что в связи с поворотом потока в целом навстречу линии
должен увеличиться, что в связи с поворотом потока в целом навстречу линии  должно было бы привести к физически нелепому выводу — линия возмущения
должно было бы привести к физически нелепому выводу — линия возмущения  оказалась бы лежащей выше по потоку, чем линия
оказалась бы лежащей выше по потоку, чем линия  Отсюда следует, что непрерывное сверхзвуковое движение внутри тупого угла невозможно. Если угол 9 поворота потока представляет конечную величину, то внутри тупого угла образуется линия разрыва, аналогичная ранее уже рассмотренному скачку уплотнения; но в отличие от прямого, перпендикулярного направлению движения потока скачка, в этом случае возникает косой скачок, образующий с направлением набегающего потока острый угол (рис. 124). Угол этот, как будет сейчас показано, зависит от начальных параметров движения до скачка и подлежит определению.
Отсюда следует, что непрерывное сверхзвуковое движение внутри тупого угла невозможно. Если угол 9 поворота потока представляет конечную величину, то внутри тупого угла образуется линия разрыва, аналогичная ранее уже рассмотренному скачку уплотнения; но в отличие от прямого, перпендикулярного направлению движения потока скачка, в этом случае возникает косой скачок, образующий с направлением набегающего потока острый угол (рис. 124). Угол этот, как будет сейчас показано, зависит от начальных параметров движения до скачка и подлежит определению.

Рис. 123.

Рис. 124.
Анализ прохождения газа сквозь косой скачок уплотнения ничем на будет отличаться от соответствующего анализа в случае прямого скачка. Подобно тому, как это делалось в гл. IV, применим для установления связи между элементами движения до и за скачком три основных уравнения механики: закон сохранения массы, энергии и закон изменения количества движения.
Условимся обозначать в дальнейшем индексом  все величины до скачка, индексом
все величины до скачка, индексом  -после скачка; кроме того, применим индекс
-после скачка; кроме того, применим индекс  для обозначения составляющей скорости в плоскости скачка и индекс
для обозначения составляющей скорости в плоскости скачка и индекс  для нормальной составляющей скорости.
для нормальной составляющей скорости.
Выбирая контрольную поверхность так, как показано на рис. 124, будем иметь:
а) согласно закону сохранения массы:

б) по закону количеств движения в проекции на касательную к поверхности раздела:

в) по тому же закону в проекции на нормаль к поверхности раздела:

г) на основании закона сохранения энергии:

Из уравнений пп. "а" и "б" сразу вытекает основное для теории коссго скачка равенство

утверждающее, что при прохождении газа сквозь косой скачок уплотнения составляющая скорости, касательная к поверхности скачка, сохраняется; скачкообразно изменяется лишь нормальная составляющая.
Переписывая уравнение энергии  в виде
в виде

и сравнивая последнее уравнение, а также уравнения пп. "а" и "в" с соответствующими уравнениями теории прямого скачка, убеждаемся, что уравнения косого скачка совпадают с уравнениями прямого скачка, составленными для нормальной скорости.
Отсюда можно заключить прежде всего, что между отношениями давлений  и плотностей
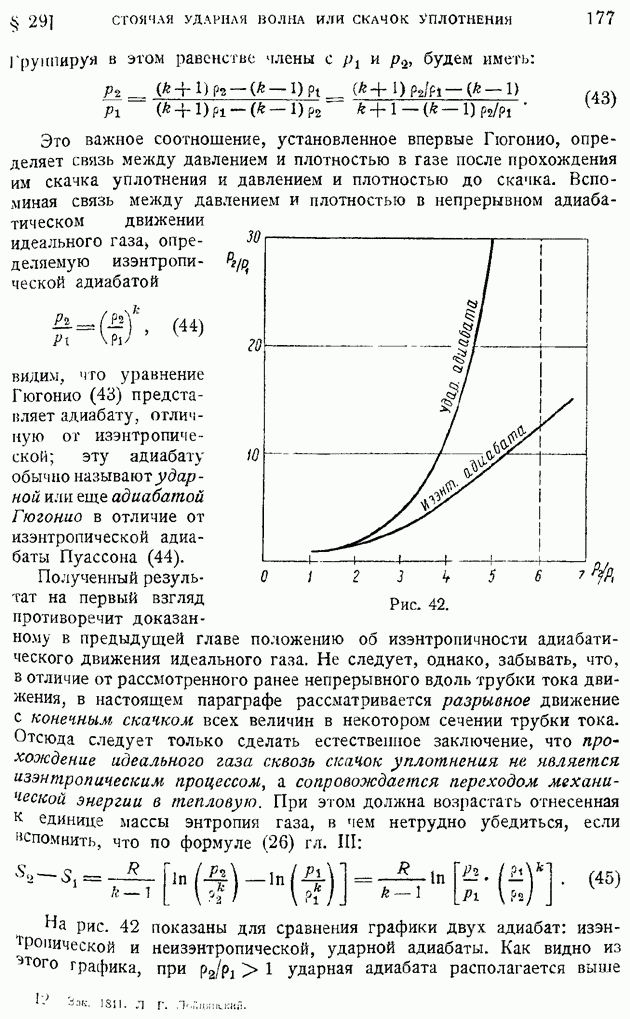
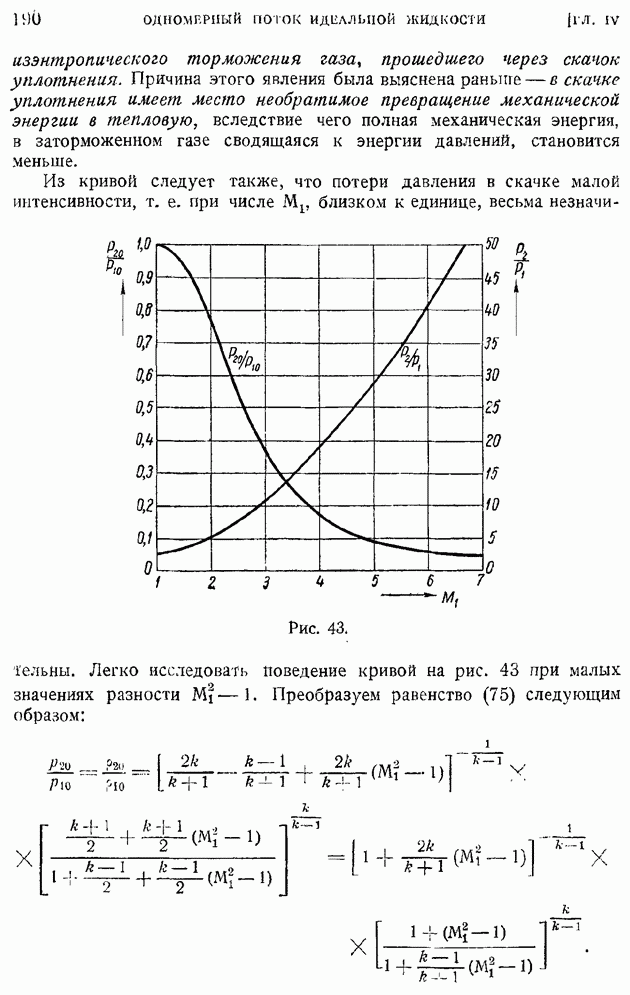
и плотностей  до и после скачка будет существовать та же связь, что и при прямом скачке, это — известная уже нам ударная (неизэнтропическая) адиабата, определяемая равенством (43) § 29 гл. IV и показанная на рис. 42.
до и после скачка будет существовать та же связь, что и при прямом скачке, это — известная уже нам ударная (неизэнтропическая) адиабата, определяемая равенством (43) § 29 гл. IV и показанная на рис. 42.
Приводя поток перед и за косым скачком уплотнения каким-нибудь адиабатическим и изэнтропическим процессом к покою (индекс  получим на основании уравнения п. "г":
получим на основании уравнения п. "г":

отсюда сразу следует также, что:

Итак, при прохождении газа сквозь косой скачок уплотнения сохраняются температура и скорость звука в адиабатически и изэнтропически заторможенном газе, а также критические значения температуры а скорости звука. Переписывая уравнение Бернулли

в виде

заключаем, что, как ранее было уже указано, для расчета косого скачка можно с успехом использовать формулы расчета прямого скачка, если только за скорость принять нормальную составляющую аействительной скорости  а за критическую скорость величину
а за критическую скорость величину

так же как и истинная критическая скорость сохраняющуюся, согласно (93) и (94), при переходе газа сквозь косой скачок уплотнения. При этом вместо известного соотношения для прямого скачка [формула (54) гл. IV]

получим обобщение этого соотношения на случай косого скачка:

Замечая, что, согласно рис. 124:

получим  :
:

откуда

Перейдем еще обычным образом от к  тогда будем иметь:
тогда будем иметь:

Это соотношение является основным для теории расчета косого скачка. Задаваясь числом  и углом
и углом  поворота потока, по (98) найдем угол
поворота потока, по (98) найдем угол  скачка с начальным направлением потока. Заменяя в формуле прямого скачка (72) гл. IV число
скачка с начальным направлением потока. Заменяя в формуле прямого скачка (72) гл. IV число  на
на  , соответствующее нормальной составляющей скорости, получим отношение давлений в потоке за и перед косым скачком:
, соответствующее нормальной составляющей скорости, получим отношение давлений в потоке за и перед косым скачком:

Перейдем к давлениям  адиабатически и изэнтропически заторможенного газа до и за скачком. В полном согласии с ранее выведенной для прямого скачка формулой (75) и заменяя в ней
адиабатически и изэнтропически заторможенного газа до и за скачком. В полном согласии с ранее выведенной для прямого скачка формулой (75) и заменяя в ней  на
на  получим:
получим:

Напомним, что натуральный логарифм этого отношения пропорционален возрастанию энтропии газа при прохождении его сквозь скачок уплотнения.
Аналогичным путем выведем выражение числа  за скачком через число
за скачком через число  до скачка и угол
до скачка и угол 

Пользование формулами (98), (99) и (101) требует сложных вычислений, для избежания которых предложены различные графические приемы. Рекомендуем номограмму, позволяющую по заданному числу  до скачка и углу поворота струи
до скачка и углу поворота струи  определять угол
определять угол  скачка с начальным направлением потока и величины
скачка с начальным направлением потока и величины  и — в потоке за скачком. Поясним пользование номограммой на схеме (рис. 125), где жирной линией показана одна из кривых зависимости
и — в потоке за скачком. Поясним пользование номограммой на схеме (рис. 125), где жирной линией показана одна из кривых зависимости  от
от 
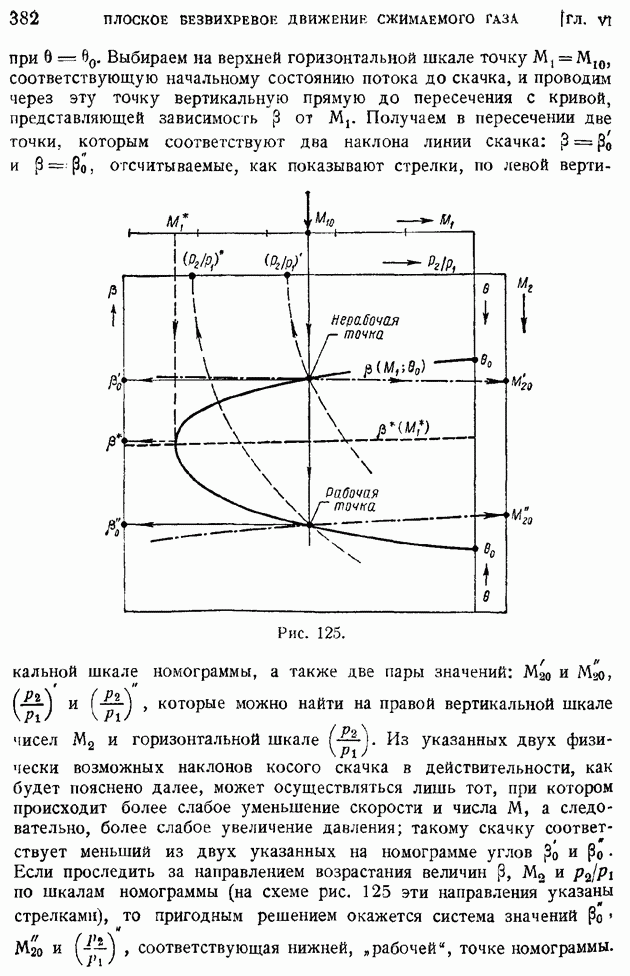
при  Выбираем на верхней горизонтальной шкале точку
Выбираем на верхней горизонтальной шкале точку  соответствующую начальному состоянию потока до скачка, и проводим через эту точку вертикальную прямую до пересечения с кривой, представляющей зависимость
соответствующую начальному состоянию потока до скачка, и проводим через эту точку вертикальную прямую до пересечения с кривой, представляющей зависимость  от
от  Получаем в пересечении две точки, которым соответствуют два наклона линии скачка:
Получаем в пересечении две точки, которым соответствуют два наклона линии скачка:  отсчитываемые, как показывают стрелки, по левой вертикальной шкале номограммы, а также две пары значений:
отсчитываемые, как показывают стрелки, по левой вертикальной шкале номограммы, а также две пары значений:  которые можно найти на правой вертикальной шкале чисел
которые можно найти на правой вертикальной шкале чисел  и горизонтальной шкале
и горизонтальной шкале 

Рис. 125.
Из указанных двух физически возможных наклонов косого скачка в действительности, как будет пояснено далее, может осуществляться лишь тот, при котором происходит более слабое уменьшение скорости и числа  а следовательно, более слабое увеличение давления; такому скачку соответствует меньший из двух указанных на номограмме углов
а следовательно, более слабое увеличение давления; такому скачку соответствует меньший из двух указанных на номограмме углов  Если проследить за направлением возрастания величин
Если проследить за направлением возрастания величин  по шкалам номограммы (на схеме рис. 125 эти направления указаны стрелками), то пригодным решением окажется система значений
по шкалам номограммы (на схеме рис. 125 эти направления указаны стрелками), то пригодным решением окажется система значений  соответствующая нижней, "рабочей", точке номограммы.
соответствующая нижней, "рабочей", точке номограммы.
Рассматривая номограмму более подробно, заметим, что не при всяком начальном значении числа  можно найти величину угла
можно найти величину угла  скачка с начальным направлением потока. Каждому значению угла отклонения потока
скачка с начальным направлением потока. Каждому значению угла отклонения потока  соответствует некоторое значение
соответствует некоторое значение  при котором вертикаль
при котором вертикаль  пересечет кривую
пересечет кривую  только в одной точке
только в одной точке  При заданном
При заданном  получить косой скачок вообще нельзя. Этот факт можно проинтерпретировать и несколько иначе: при любом заданном числе
получить косой скачок вообще нельзя. Этот факт можно проинтерпретировать и несколько иначе: при любом заданном числе  набегающего потока можно указать такое максимальное значение
набегающего потока можно указать такое максимальное значение  угла отклонения потока, что при
угла отклонения потока, что при  построить косой скачок нельзя. В этом случае явление усложняется тем, что скачок перемещается вверх по потоку, отходит от вершины угла, образуя так называемую головную волну, о которой уже была речь в гл. IV. Схема такой волны на примере обтекания клина показана на рис. 126. При
построить косой скачок нельзя. В этом случае явление усложняется тем, что скачок перемещается вверх по потоку, отходит от вершины угла, образуя так называемую головную волну, о которой уже была речь в гл. IV. Схема такой волны на примере обтекания клина показана на рис. 126. При  обтекание остроносого профиля становится аналогичным обтеканию тупоносого.
обтекание остроносого профиля становится аналогичным обтеканию тупоносого.

Рис. 126.
Если угол поворота потока  устремить к нулю, то семейство кривых
устремить к нулю, то семейство кривых  показанных на номограмме жирными линиями, сведется к нижней кривой
показанных на номограмме жирными линиями, сведется к нижней кривой  Как это следует из уравнения (98), будем иметь при
Как это следует из уравнения (98), будем иметь при 

т. е. в этом случае косой скачок превращается в "линию возмущения". Обращаясь теперь вновь к вопросу о двузначности решения задачи о наклоне косого скачка, можем сказать, что в действительности осуществляется тот из двух возможных скачков уплотнения, который ближе к "линии возмущения".
Соединим между собою на номограмме вершины кривых  соответствующие значениям
соответствующие значениям  тогда между этой кривой
тогда между этой кривой  (на номограмме и схеме рис. 125 показанной жирным пунктиром) и линией
(на номограмме и схеме рис. 125 показанной жирным пунктиром) и линией  окажется заключенной вся рабочая часть номограммы.
окажется заключенной вся рабочая часть номограммы.
Возьмем точку пересечения кривой  с вертикалью
с вертикалью  и верхней части номограммы и, не уменьшая числа
и верхней части номограммы и, не уменьшая числа  устремим
устремим  к нулю; тогда
к нулю; тогда  станет равным 90°, а косой скачок — прямым. Но
станет равным 90°, а косой скачок — прямым. Но
при стремлении  к нулю, т. е. при непрерывном исчезновении причины возмущения (наличия угла), нет никаких физических оснований образовываться прямому скачку с характерным для него резким изменением параметров движения; наоборот, естественным является вырождение косого скачка уплотнения в "линию возмущения", которое и произойдет, если точку пересечения кривой
к нулю, т. е. при непрерывном исчезновении причины возмущения (наличия угла), нет никаких физических оснований образовываться прямому скачку с характерным для него резким изменением параметров движения; наоборот, естественным является вырождение косого скачка уплотнения в "линию возмущения", которое и произойдет, если точку пересечения кривой  с вертикалью
с вертикалью  взять в нижней (рабочей) части номограммы.
взять в нижней (рабочей) части номограммы.
Номограмма наглядно показывает ход изменения параметров движения газа при прохождении его сквозь косой скачок уплотнения. Обратим внимание на специфическое отличие косого скачка от прямого.

Рис. 127.
Каков бы ни был начальный сверхзвуковой поток за прямым скачком, движение становилось дозвуковым, в случае косого скачка это уже не так. Пользуясь рабочей частью номограммы, легко заключить, что каковы бы ни были начальные числа  до скачка, значения
до скачка, значения  за скачком хотя и уменьшаются, но оказываются все же большими единицы; за косым скачком, таким образом, поток остается сверхзвуковым.
за скачком хотя и уменьшаются, но оказываются все же большими единицы; за косым скачком, таким образом, поток остается сверхзвуковым.
Отсюда следует, что в косых скачках не должны происходить столь резкие изменения в параметрах газа (давлении, плотности, температуре), как в прямом скачке. Это приводит и к более слабым превращениям механической энергии в тепловую, к меньшему возрастанию энтропии, а следовательно, и к меньшим потерям. Значительно меньшая по сравнению с прямым скачком интенсивность косых скачков с успехом используется для борьбы с потерями в прямых скачках, например, в головной волне перед тупоносым обтекаемым телом (§ 32 гл. IV).
Идея замены прямого скачка, переводящего сверхзвуковой поток с высоким значением числа  сразу в дозвуковой, системой косых скачков, последовательно уменьшающих число
сразу в дозвуковой, системой косых скачков, последовательно уменьшающих число  оказывается весьма
оказывается весьма
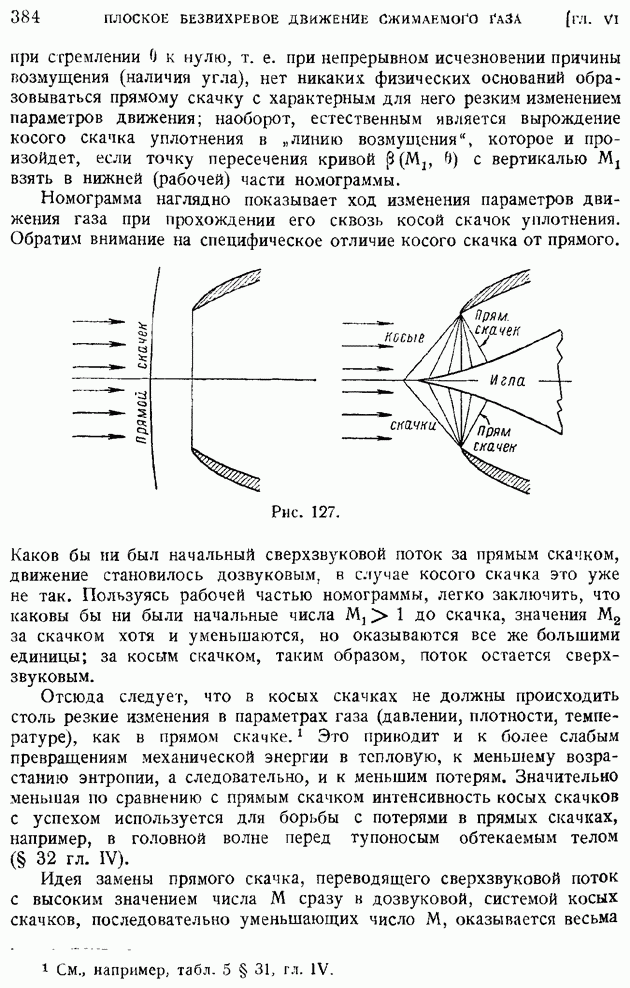
полезной для практики. Так, например, для того, чтобы ослабить вредное влияние головной волны, образующейся на входе в реактивный двигатель самолета (вспомнить рис. 44) и уменьшающей естественное и полезное сжатие воздуха в камере горения, конструкцию входа изменяют. Помещая на входе в двигатель (рис. 127) "иглу", вызывают появление системы косых скачков, которые способствуют менее резкому, чем при одном прямом скачке, переходу набегающего потока от сверхзвукового к дозвуковому движению. Указанные на рисунке четыре косых скачка переводят сверхзвуковой поток со значительным числом  постепенно в сверхзвуковой поток с числом
постепенно в сверхзвуковой поток с числом  близким к единице, а уже после этого прямой скачок малой мощности совершает с ничтожными потерями окончательное превращение набегающего потока в дозвуковой. При такой конструкции входа в реактивный двигатель потери напора значительно уменьшаются.
близким к единице, а уже после этого прямой скачок малой мощности совершает с ничтожными потерями окончательное превращение набегающего потока в дозвуковой. При такой конструкции входа в реактивный двигатель потери напора значительно уменьшаются.

Рис. 128.
Изложенная в настоящем и предыдущем параграфах теория сверхзвукового течения внутри и вне вершины угла может быть положена в основу описания сверхзвукового движения газа около выпуклой или вогнутой поверхности. Действительно, заменяя непрерывную плавную поверхность (в плоском движении — линию) ломаной с достаточно малыми гранями, можно для каждого такого угла построить системы "линий возмущений" и таким образом установить течение в целом. На рис. 128 показано построение расширяющегося потока около выпуклой стенки, на рис. 129 — около вогнутой стенки. В первом случае поток ускоряется, местное число  растет, и "линии возмущения" расходятся веером, так как с ростом вниз но течению числа
растет, и "линии возмущения" расходятся веером, так как с ростом вниз но течению числа  углы линий возмущения с линиями тока убывают. Во втором случае, наоборот, поток замедляется, число
углы линий возмущения с линиями тока убывают. Во втором случае, наоборот, поток замедляется, число  убывает, и углы линий возмущения с направлением потока возрастают; это приводит к взаимному пересечению линий возмущения и к образованию огибающей их в некотором удалении от поверхности тела; эта огибающая представляет криволинейный скачок уплотнения, показанный жирной линией на рис. 129.
убывает, и углы линий возмущения с направлением потока возрастают; это приводит к взаимному пересечению линий возмущения и к образованию огибающей их в некотором удалении от поверхности тела; эта огибающая представляет криволинейный скачок уплотнения, показанный жирной линией на рис. 129.
Рис. 129. (см. скан)
Перечисленные только что два характерных типа сверхзвуковых течений: 1) ускоряющегося и расширяющегося потока, проходящего сквозь непрерывные совокупности линий возмущения, служащие линиями плавного разрежения потока, и 2) замедляющегося и сужающегося потока, скачкообразно изменяющего свои параметры при прохождении через системы дискретных косых скачков, постоянно наблюдаются как при сверхзвуковых обтеканиях крыловых или лопаточных профилей, так и при протекании газа сквозь сопла и насадки.

Рис. 130.
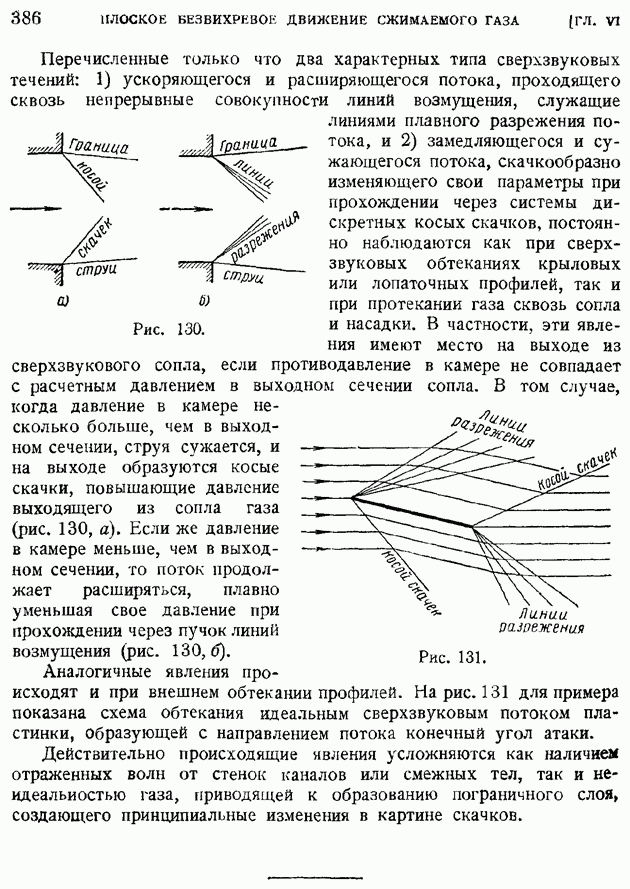
В частности, эти явления имеют место на выходе из сверхзвукового сопла, если противодавление в камере не совпадает с расчетным давлением в выходном сечении сопла. В том случае, когда давление в камере несколько больше, чем в выходном сечении, струя сужается, и на выходе образуются косые скачки, повышающие давление выходящего из сопла газа (рис. 130, а). Если же давление в камере меньше, чем в выходном сечении, то поток продолжает расширяться, плавно уменьшая свое давление при прохождении через пучок линий возмущения (рис. 130,б).
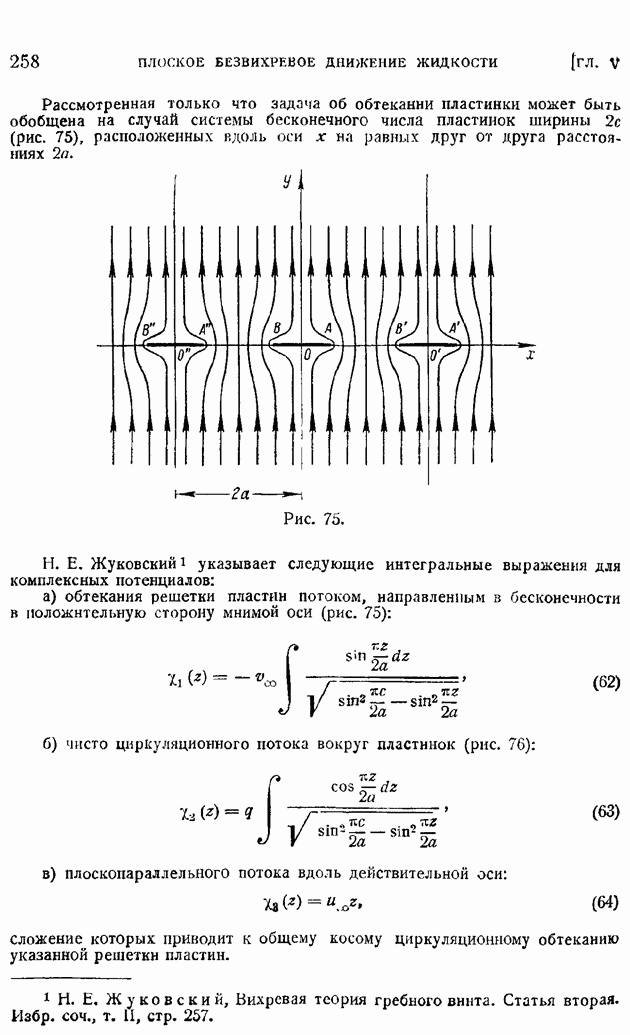
Аналогичные явления происходят и при внешнем обтекании профилей. На рис. 131 для примера показана схема обтекания идеальным сверхзвуковым потоком пластинки, образующей с направлением потока конечный угол атаки.
Действительно происходящие явления усложняются как наличием отраженных волн от стенок каналов или смежных тел, так и неидеальиостью газа, приводящей к образованию пограничного слоя, создающего принципиальные изменения в картине скачков.

Рис. 131.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Предмет механики жидкости и газа. Основные свойства «макромодели» жидкости и газа: сплошность и подвижность
- § 2. Основные методы механики жидкости и газа. Области применения и главнейшие задачи
- § 3. Краткий очерк исторического развития механики жидкости и газа. От гидромеханики древних до установления воззрений ньютонианской эпохи
- § 4. Эпоха Эйлера и Бернулли. Гидроаэродинамика в XIX в.
- § 5. Современный этап развития механики жидкости и газа
- ГЛАВА I. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
- § 6. Поле физической величины. Скалярное и векторное поля. Поверхности уровня. Векторные линин и трубки
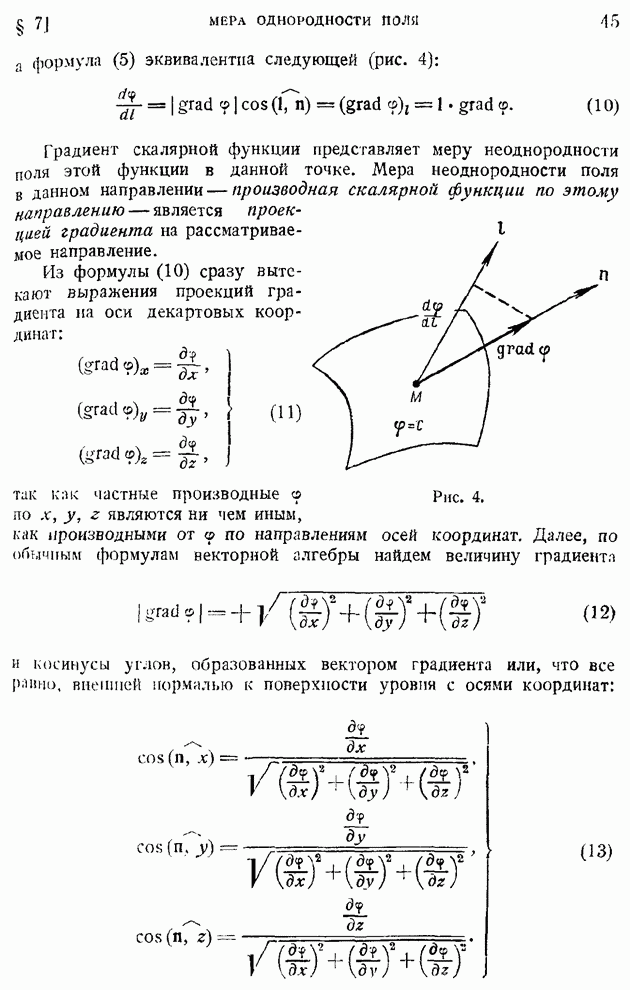
- § 7. Мера однородности поля в данном направлении и в дайной точке. Градиевт скалярного поля и дифференциальный тензор векторного поля как меры неоднородности поля
- § 8. Задание движения сплошной среды. Поле скоростей. Линии тока и траектории
- § 9. Поле ускорений. Разложение ускорения частицы на локальную и конвективную составляющие
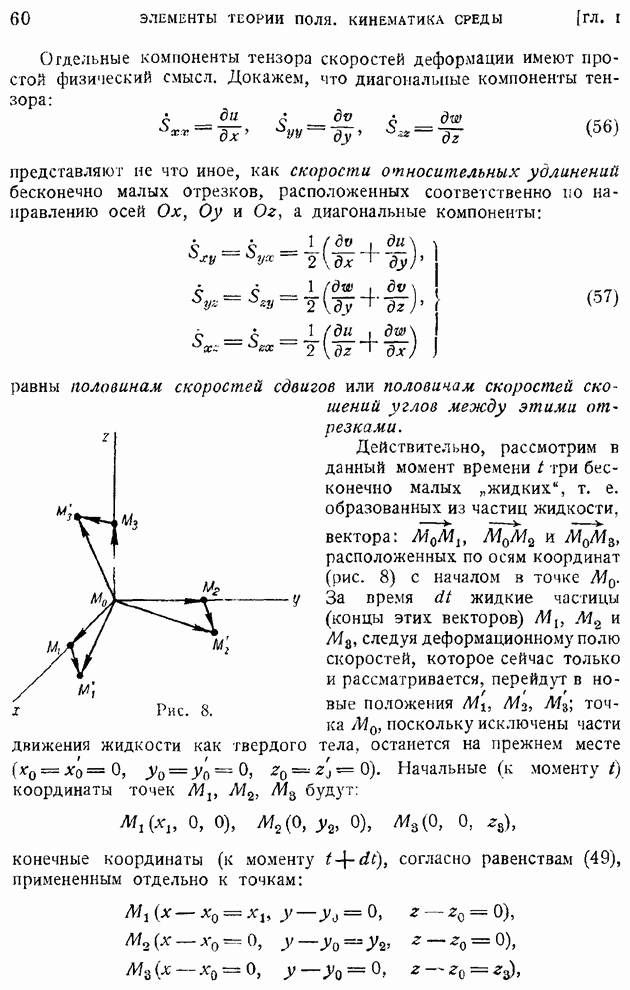
- § 10. Скоростное поле сплошной среды в окрестности данной точки. Угловая скорость и вихрь. Тензор скоростей деформаций и его компоненты
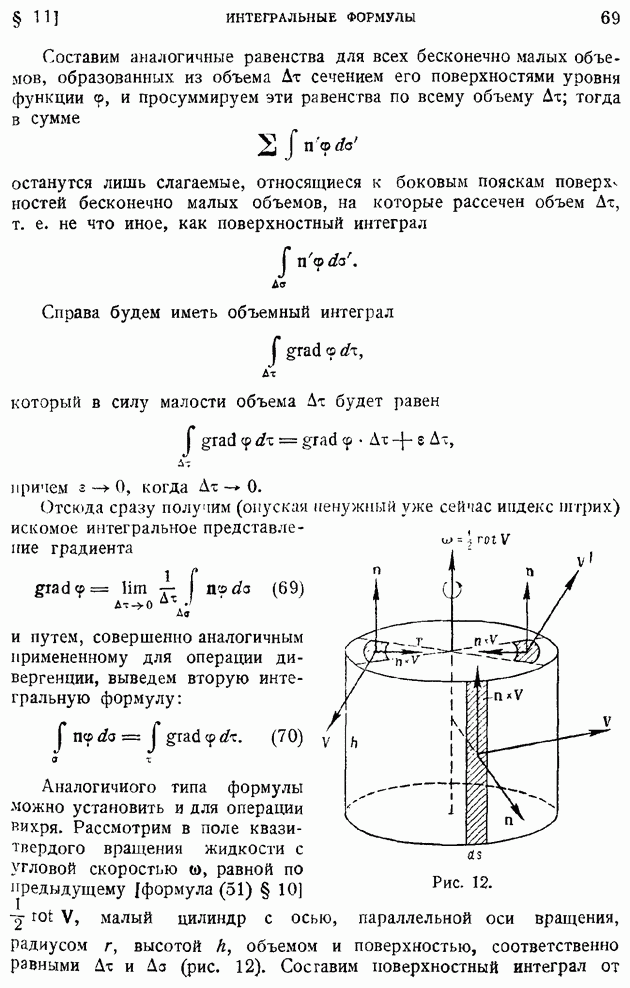
- § 11. Скорость объемного расширения жидкости. Интегральные представления дифференциальных операторов поля. Основные интегральные формулы
- § 12. Вихревые линии и трубки. Вторая теорема Гельмгольца. Интенсивность вихревой трубки
- § 13. Выражение интенсивности вихревой трубки через циркуляцию вектора по контуру, охватывающему трубку. Теорема об изменении циркуляции скорости во времени
- ГЛАВА II. ОСНОВНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ И РАВНОВЕСИЯ СПЛОШНОЙ СРЕДЫ
- § 14. Распределение массы в сплошной среде. Плотность и удельный вес. Напряжения. Тензор напряженности и его симметричность
- § 15. Общие уравнения динамики сплошной среды. Уравнение неразрывности. Уравнения динамики в напряжениях
- § 16. Тепловые явления в жидкостях и газах. Закон сохранения энергии и уравнение баланса энергии
- § 17. Общие уравнения равновесного состояния жидкости и газа. Равновесие воздуха в атмосфере. Приближенные барометрические формулы. Стандартная атмосфера
- § 18. Равновесие несжимаемой жидкости. Уравнение поверхности раздела. Равновесие вращающейся жидкости
- § 19. Давление тяжелой несжимаемой жидкости на поверхность тела. Сила и момент, приложенные к телу, плавающему в тяжелой жидкости. Случай вращающейся жидкости
- ГЛАВА III. ДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ И ГАЗА. ОСНОВНЫЕ УРАВНЕНИЯ И ОБЩИЕ ТЕОРЕМЫ
- § 20. Идеальная жидкость. Основные уравнения движения
- § 21. Закон сохранения энергии в движущейся идеальной жидкости. Адиабатическое движение. Сохранение энтропии
- § 22. Эйлерово представление конвективного изменения объемного интеграла. Перенос величины сквозь контрольную поверхность
- § 23. Эйлерова форма законов сохранения массы и энергии, теоремы количеств движения и момента количеств движения при стационарном движении идеальной жидкости
- § 24. Теорема об изменении кинетической энергии. Работа и мощность внутренних сил. Эйлерова форма уравнения изменения кинетической энергии
- § 25. Теорема Бернулли о сохранении полной механической энергии при стационарном баротропном движении идеальной жидкости и газа
- ГЛАВА IV. ОДНОМЕРНЫЙ ПОТОК ИДЕАЛЬНОЙ ЖИДКОСТИ
- § 26. Одномерное течение идеальной сжимаемой жидкости. Линеаризированные уравнения. Скорость распространения малых возмущений в жидкости или газе
- § 27. Изотермическая и адиабатическая скорости звука. «Конус возмущений» при сверхзвуковом движении источника возмущения. Число M и его связь с углом конуса возмущений
- § 28. Распространение непрерывных возмущений конечной интенсивности. Характеристики. Образование разрывной ударной волны
- § 29. Стоячая ударная волна или скачок уплотнения. Ударная адиабата
- § 30. Критические величины в одномерном потоке газа. Связь между скоростями до и после скачка. Изменение давления, плотности и температуры в скачке уплотнения
- § 31. Скорость распространения ударной волны. Спутное движение газа за ударной волной
- § 32. Влияние интенсивности скачка уплотнения на сжатие газа. Измерение скоростей и давлений в до- и сверхзвуковых потоках
- § 33. Одномерное движение газа по трубе переменного сечения. Истечение из резервуара большой емкости сквозь сходящееся сопло
- § 34. Одномерное течение в сопле Лаваля. Движение газа с притоком тепла
- ГЛАВА V. БЕЗВИХРЕВОЕ ДВИЖЕНИЕ ЖИДКОСТИ. ПЛОСКОЕ ДВИЖЕНИЕ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 35. Сохранение циркуляции скорости в потоке идеальной жидкости. Теорема Кельвина и Лаграижа. Безвихревое движение. Потенциал скоростей
- § 36. Интеграл Лагранжа — Коши уравнений безвихревого движения. Теорема Бернулли. Некоторые общие свойства безвихревого движения идеальной несжимаемой жидкости в односвязной области
- § 37. Плоское безвихревое движение несжимаемой жидкости. Потенциал скоростей и функция тока. Применение функций комплексного переменного. Комплексный потенциал и сопряженная скорость
- § 38. Построение полей течения по заданной характеристической Функции. Простейшие плоские потоки и их наложение
- § 39. Бесциркуляционное и циркуляционное обтекания круглого цилиндра
- § 40. Применение криволинейных координат. Бесциркуляционное и циркуляционное обтекания эллиптического цилиндра и пластинки. Задача Жуковского об обтекании решетки пластин.
- § 41. Плоское движение с отрывом струй. Разрывное обтекание пластинки и протекание жидкости сквозь отверстие
- § 42. Прямая задача в теории плоского движения идеальной несжимаемой жидкости. Применение метода конформных отображений. Гипотеза Чаплыгина о безотрывном обтекании задней кромки профиля. Формула циркуляции
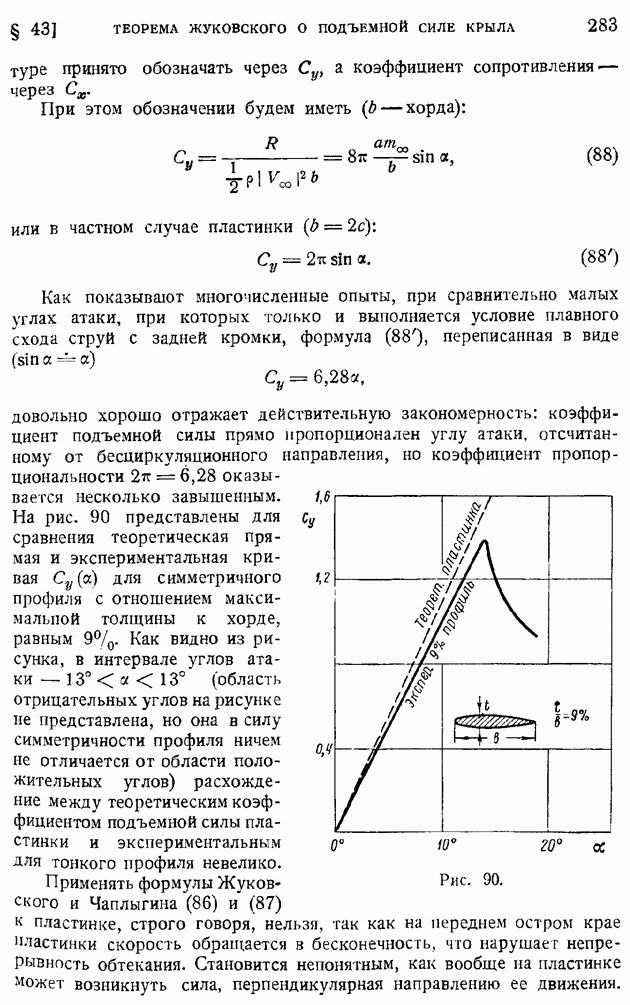
- § 43. Теорема Жуковского о подъемной силе крыла. Зависимость подъемной силы от угла атаки. Коэффициент подъемной силы
- § 44. Применение метода комплексных переменных к выводу теоремы Жуковского. Формулы Чаплыгина для главного вектора и момента сил давления потока на крыло
- § 45. Выражение главного момента сил давления потока через коэффициенты конформного отображения. Фокус крыла. Независимость от угла атаки момента относительно фокуса. Парабола устойчивости
- § 46. Частные случаи конформного отображения крылового профиля на круг. Преобразование Жуковского-Чаплыгина. Теоретические крыловые профили
- § 47. Задача об обтекании слабо изогнутой дужки произвольной формы (теория тонкого крыла)
- § 48. Определение обтекания крылового профиля произвольной формы
- § 49. Обобщение теоремы Жуковского на случай плоской решетки с бесчисленным множеством профилей
- ГЛАВА VI. ПЛОСКОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ СЖИМАЕМОГО ГАЗА
- § 50. Основные уравнения плоского стационарного безвихревого движения сжимаемого газа. Линеаризированные уравнения
- 51. Линеаризированный до- и сверхзвуковой газовый поток вдоль волнистой стенки
- § 52. Тонкое крыло в линеаризированном до- и сверхзвуковом потоках. Влияние сжимаемости газа на коэффициент подъемной силы в дозвуковом потоке. Коэффициенты подъемной силы и волнового сопротивления при сверхзвуковом потоке
- § 53. Нелинеаризированные уравнения движения идеального сжимаемого газа. Переход в плоскость годографа. Уравнения Чаплыгина
- § 54. Метод С. А. Христиановича. Приближенные формулы учета влияния сжимаемости на распределение давления
- § 55. Критическое число M и его определение по заданному распределению давления в несжимаемом обтекании. Поведение коэффициента подъемной силы и момента при около- и закритических значениях числа M
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
- § 57. Нелинеаризированный сверхзвуковой поток. «Характеристики» уравнений плоского сверхзвукового потока. Линин возмущения и их основные свойства
- § 58. Обтекание выпуклого угла сверхзвуковым потоком. Влияние угла поворота струи на ее газодинамические элементы
- § 59. Сверхзвуковой поток внутри тупого угла. Косой скачок уплотнения. Связь между газодинамическими элементами до и за косым скачком
- ГЛАВА VII. ПРОСТРАНСТВЕННОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ
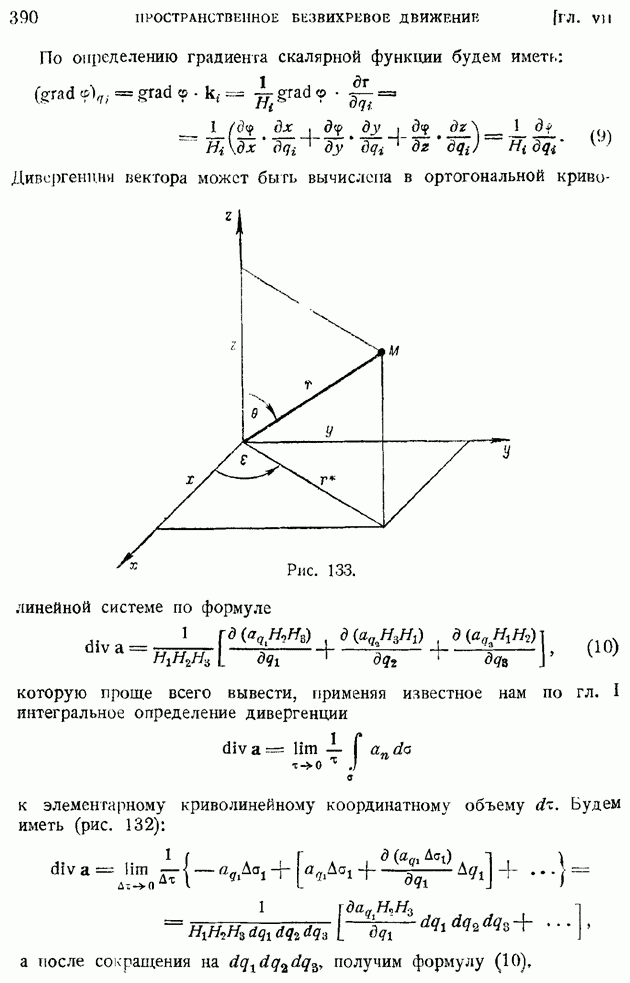
- § 60. Ортогональные криволинейные координаты в пространстве. Основные дифференциальные операторы поля в криволинейных координатах
- § 61. Потенциал скоростей. Поле источника и диполя. Непрерывное распределение источников и диполей. Ньютонов потенциал. Потенциал простого и двойного слоев
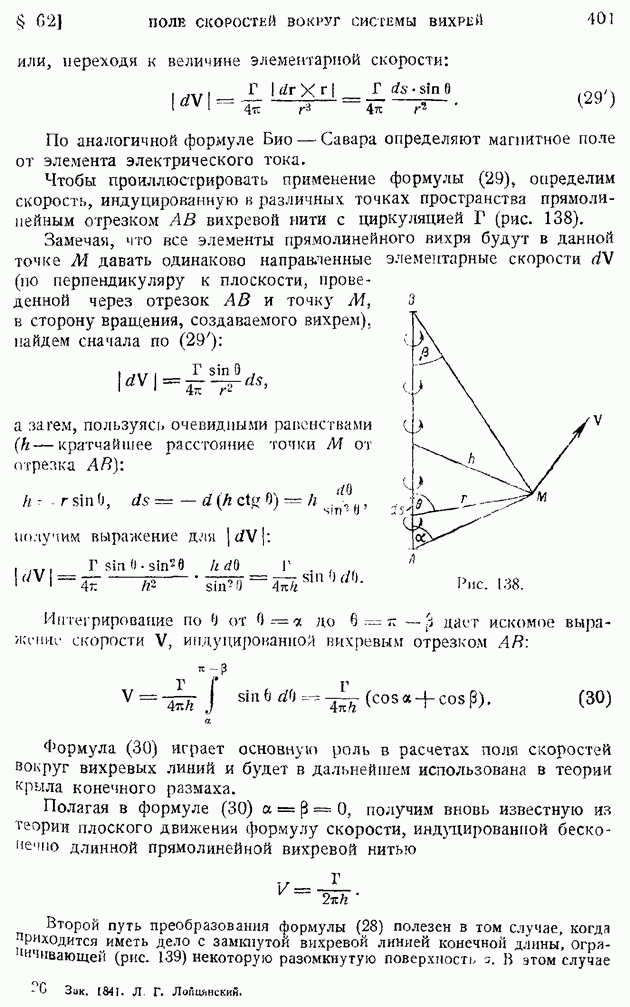
- § 62. Поле скоростей вокруг заданной системы вихрей. Формула Био — Савара. Потенциал скоростей замкнутой вихревой нити. Аналогия с потенциалом двойного слоя
- § 63. Функция тока и ее связь с векторным потенциалом скоростей. Функции тока простейших течений
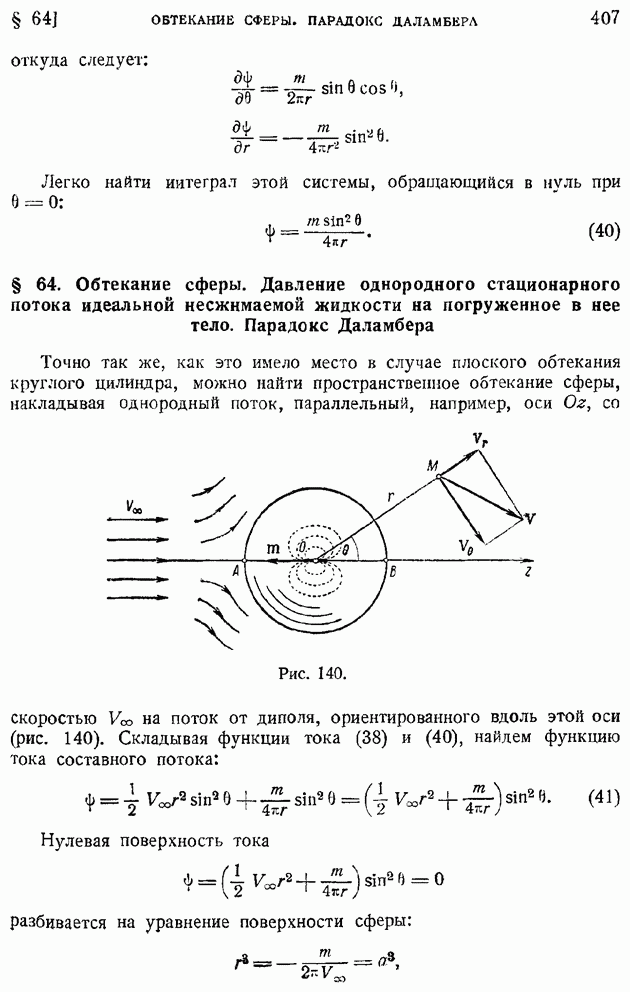
- § 64. Обтекание сферы. Давление однородного стационарного потока идеальной несжимаемой жидкости на погруженное в нее тело. Парадокс Даламбера
- § 65. Общие уравнения осесимметричного движения. Применение цилиндрических координат. Течение сквозь каналы
- § 66. Осесимметричное продольное обтекание тел вращения. Случай эллипсоида вращения
- § 67. Поперечное обтекание тел вращения. Пример эллипсоида вращения
- § 68. Продольное и поперечное обтекание тел вращения большого удлинения. Приближенные выражения граничных условий. Применение тригонометрических сумм для определения коэффициентов …
- § 69. Метод «особенностей». Применение непрерывно распределенных источников (стоков) и диполей для решения задачи о продольном и поперечном обтекании тел вращения
- § 70. Общий случай движения твердого тела сквозь несжимаемую идеальную жидкость. Определение потенциала скоростей. Главный вектор и главный момент сил давления потока на тело
- § 71. Коэффициенты «присоединенных масс». Свойство симметрии. «Присоединенная» кинетическая энергия. Определение «присоединенных масс» поступательно движущегося цилиндра, шара и эллипсоида
- § 72. Элементы теории крыла конечного размаха. Вихревая система крыла. Гипотеза плоских сечеиий. Геометрические и действительные углы атаки. Подъемная сила и «индуктивное сопротивление»
- § 73. Основные формулы теории «несущей линии». «Индуктивная скорость» и «индуктивный угол». Прямая задача определения подъемной силы и индуктивного сопротивления по заданному распределению циркуляции
- § 74. Крыло с минимальным индуктивным сопротивлением. Эллиптическое распределение циркуляции. Связь между коэффициентами индуктивного сопротивления и подъемной силы. Основное уравнение теории крыла и понятие о его интегрировании
- ГЛАВА VIII. ДИНАМИКА ВЯЗКОЙ ЖИДКОСТИ И ГАЗА
- § 75. Внутреннее трение и теплопроводность в жидкостях и газах. Законы Ньютона и Фурье. Влияние температуры на коэффициенты вязкости и теплопроводности. Число «сигма»
- § 76. Обобщение закона Ньютона на случай произвольного движения среды. Закон линейной связи между тензорами напряжений и скоростей деформации
- § 77. Общие уравнения движения вязкой жидкости. Динамические уравнения и уравнение баланса энергии. Граничные условия движения жидкости с треннем и теплопроводностью
- § 78. Понятие о подобии гидродинамических явлений. Безразмерные уравнения движения вязкой жидкости и газа. Условия подобия
- § 79. Ламинарное движение вязкой несжимаемой жидкости по цилиндрической трубе
- § 80. Обтекание шара при очень малых значениях числа Рейнольдса. Формула сопротивления шара по Стоксу и ее обобщения
- § 81. Вихревые линии в идеальной и вязкой жидкости. Сохраняемость вихревых линий при отсутствии внутреннего трения. Диффузия вихря в вязкой жидкости
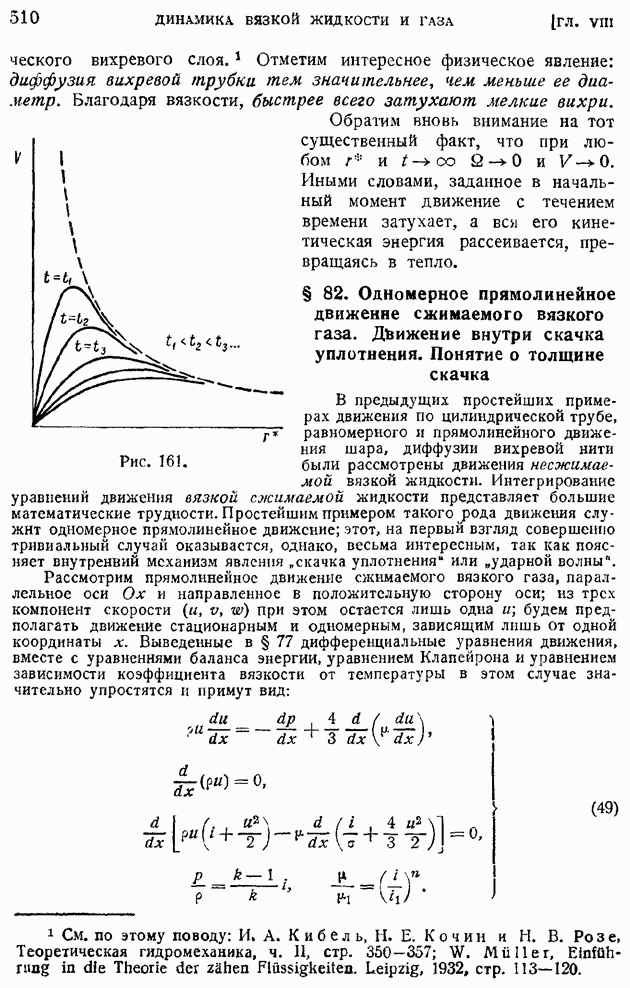
- § 82. Одномерное прямолинейное движение сжимаемого вязкого газа. Движение внутри скачка уплотнения. Понятие о толщине скачка
- § 83. Работа внутренних сил и диссипация механической энергии в движущейся вязкой среде
- § 84. Обтекание тел жидкостью и газом при больших значениях числа Рейнольдса. Основные уравнения теории ламинарного пограничного слоя
- § 85. Ламинарный пограничный слой на пластинке, продольно обтекаемой несжимаемой жидкостью. Неизотермическое движение
- § 86. Ламинарный пограничный слой при степенном задании скорости внешнего потока
- § 87. Ламинарный пограничный слой в общем случае задания скорости внешнего потока. Применение уравнения импульсов для приближенного расчета ламинарного пограничного слоя
- § 88. Способы определения функций … Приближенный метод расчета ламинарного пограничного слоя
- § 89. Ламинарный пограничный слой на пластинке, продольно обтекаемой сжимаемым газом при больших скоростях. Случай линейной зависимости коэффициента вязкости от температуры (n = 1)
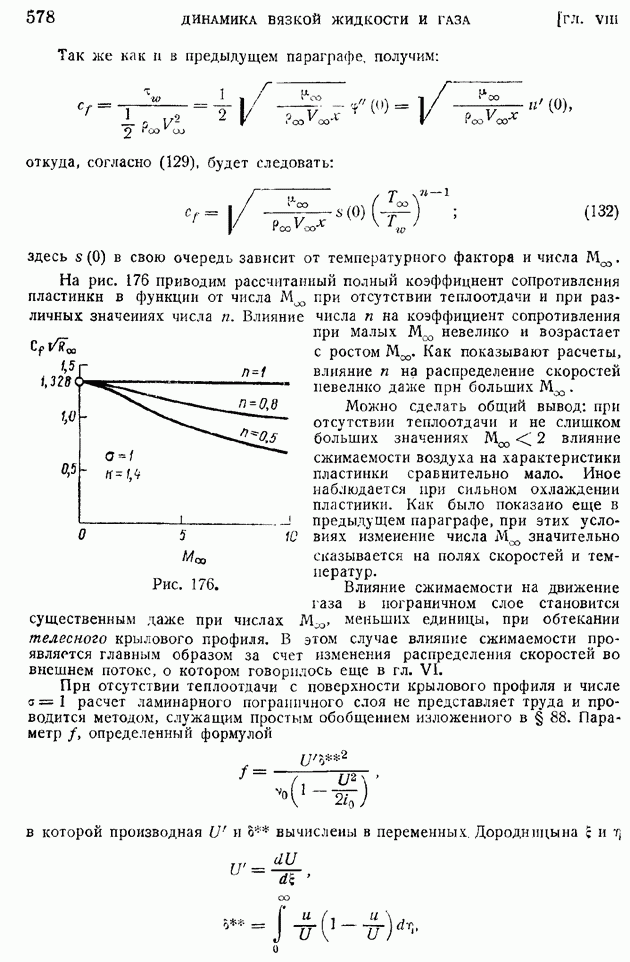
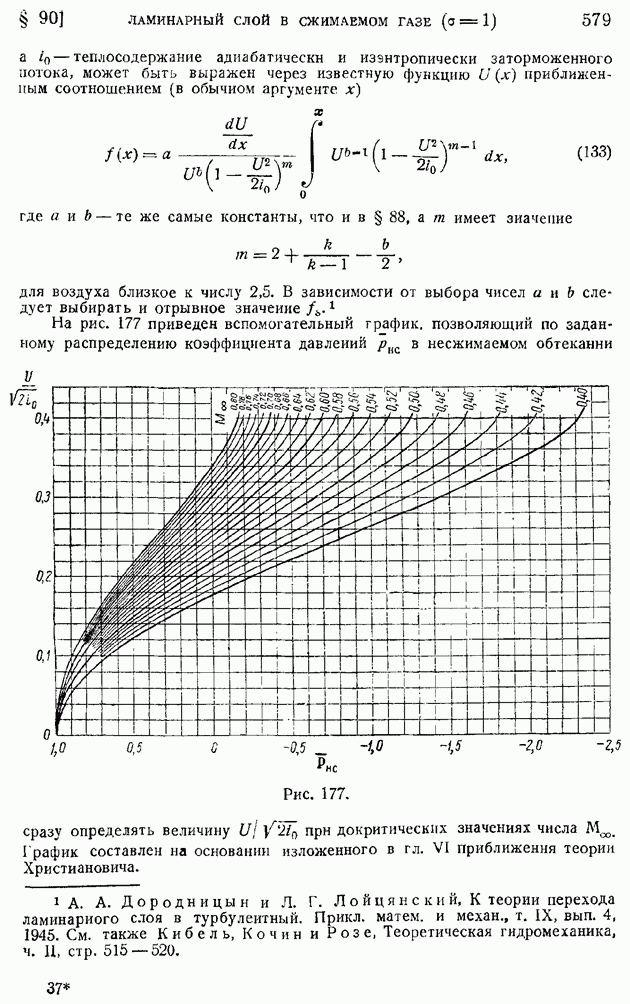
- § 90. Ламинарный пограничный слой на пластинке при любом законе связи между вязкостью и температурой и при числе … Обтекание крылового профиля потоком больших скоростей
- ГЛАВА IX. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ
- § 91. Переход ламинарного движения в турбулентное. Критическое рейнольдсово число
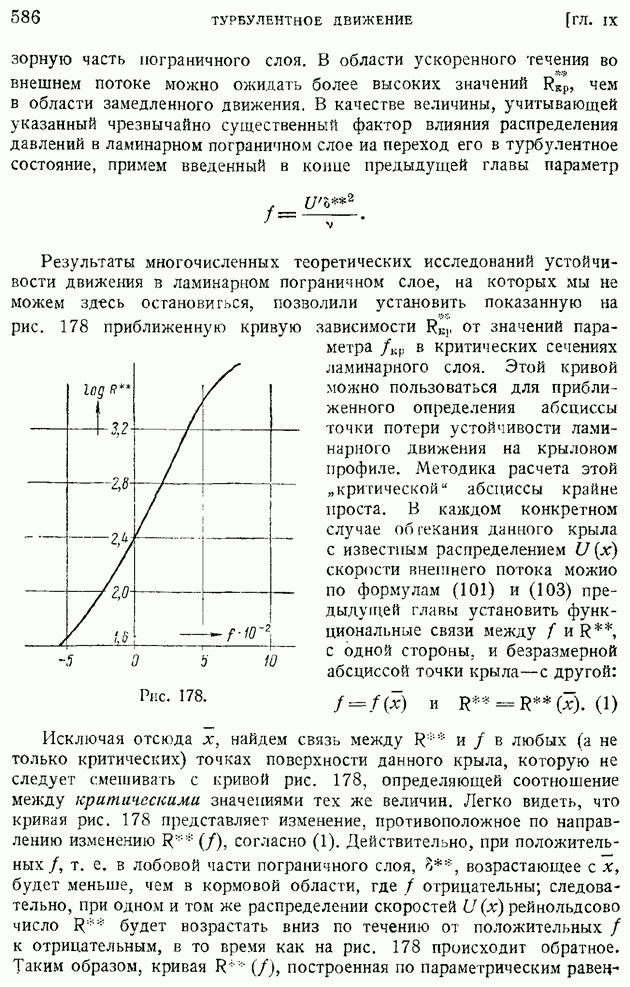
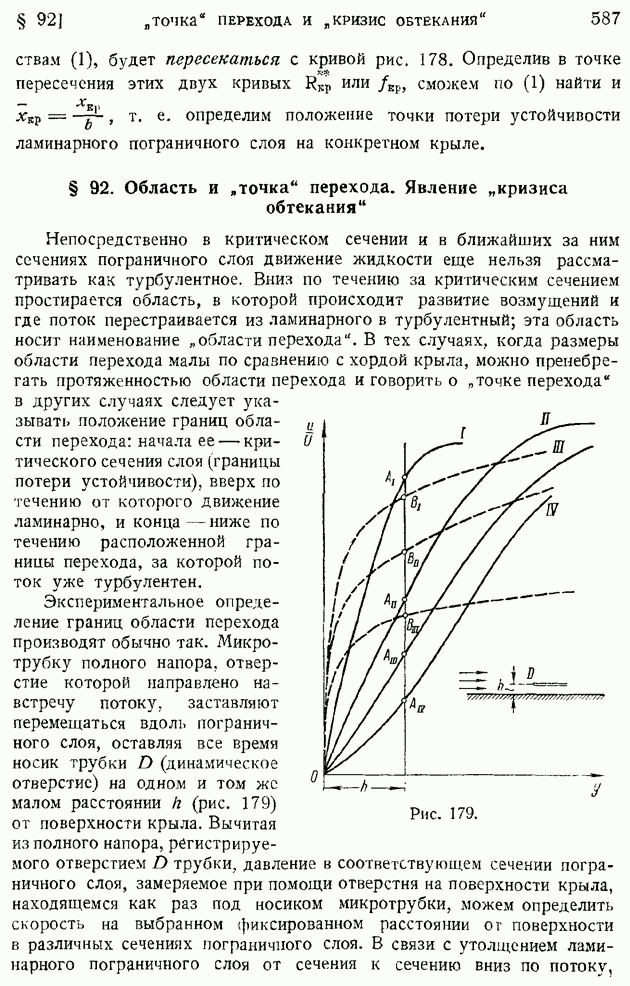
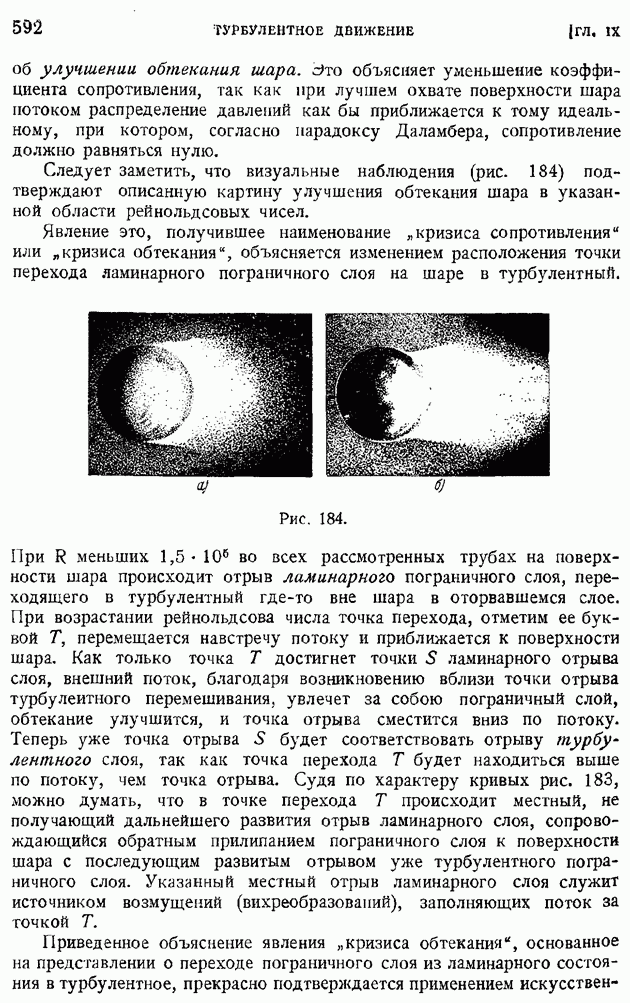
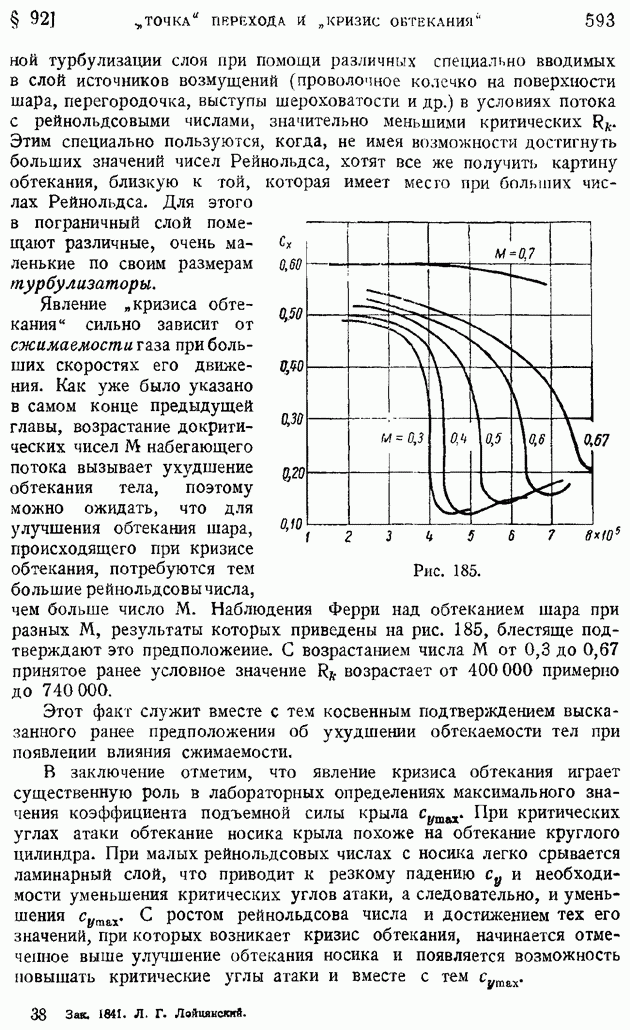
- § 92. Область и «точка» перехода. Явление «кризиса обтекания»
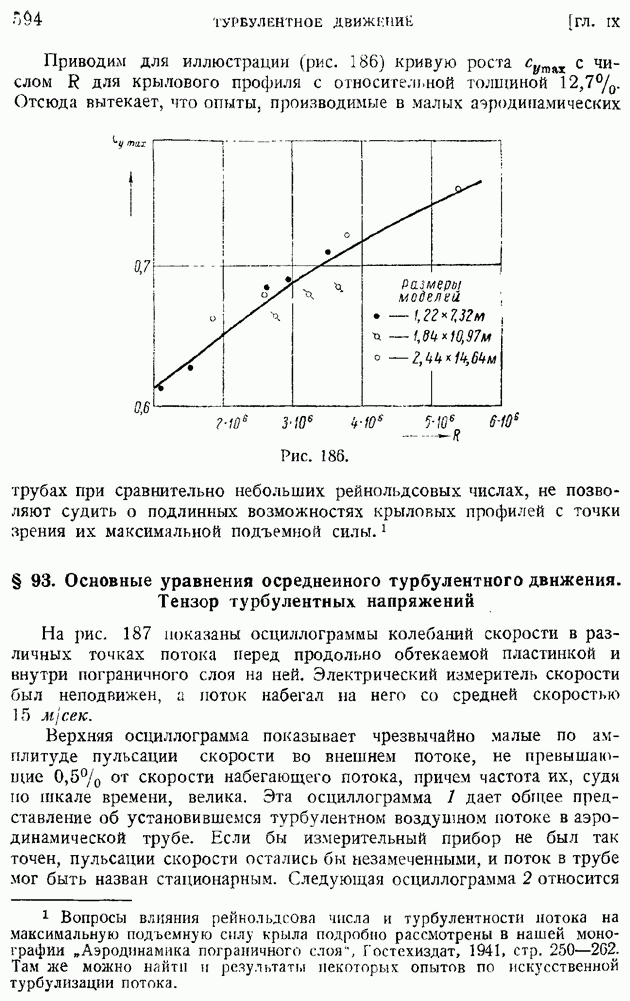
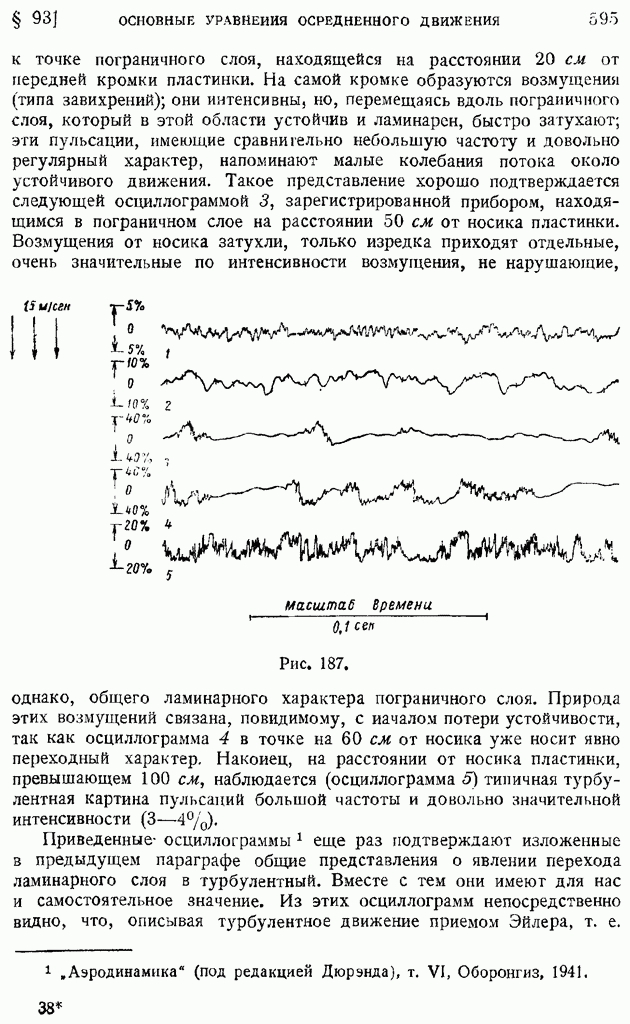
- § 93. Основные уравнения осреднеиного турбулентного движения. Тензор турбулентных напряжений
- § 94. Турбулентное движение жидкости в плоской и круглой трубе. Логарифмические формулы скоростей
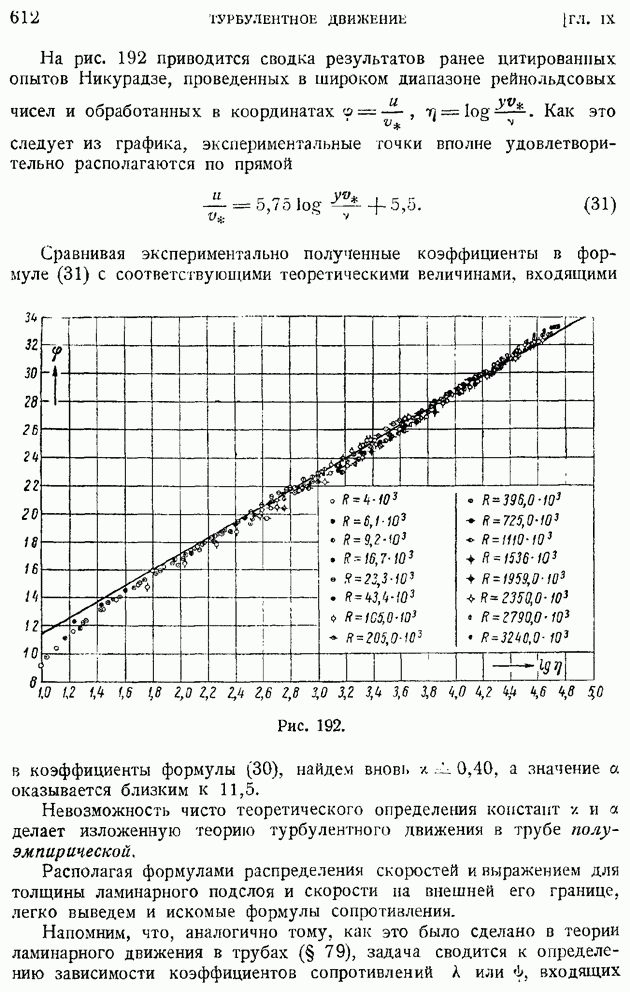
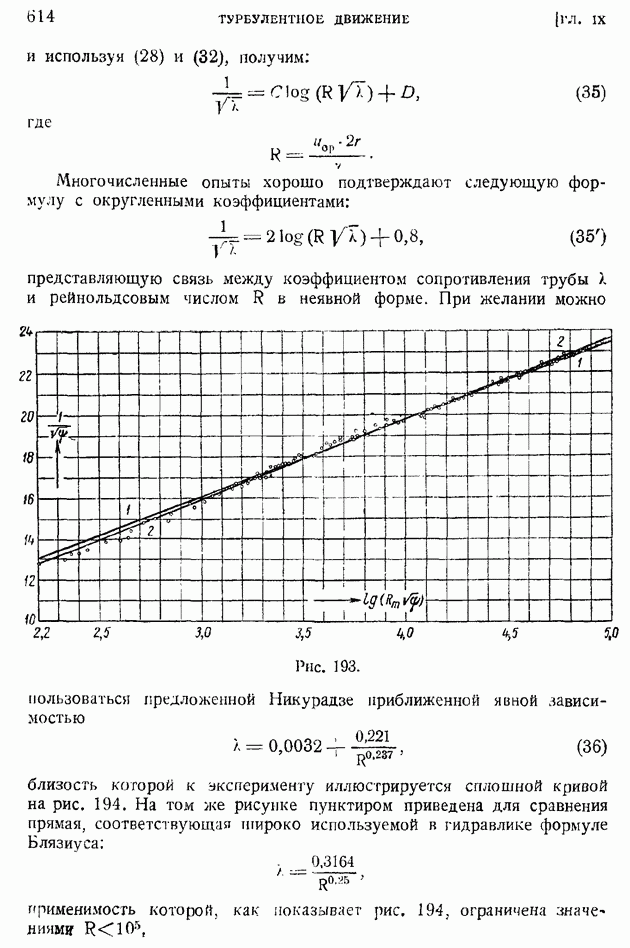
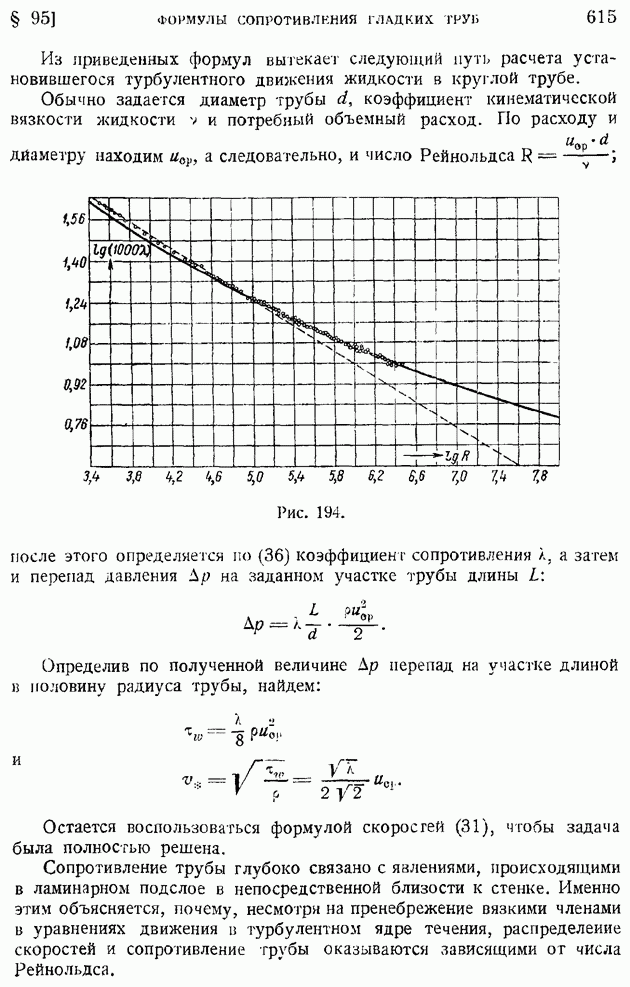
- § 95. Формулы сопротивления гладких труб при турбулентном движении жидкости. Ламинарный подслой
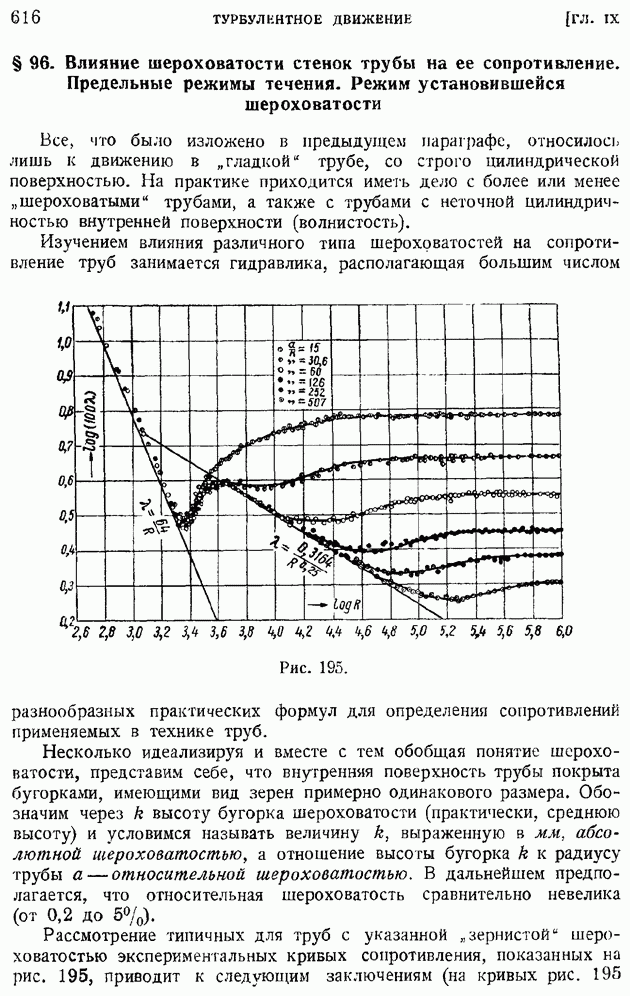
- § 96. Влияние шероховатости стенок трубы на ее сопротивление. Предельные режимы течения. Режим установившейся шероховатости
- § 97. Турбулентный пограничный слой на продольно обтекаемой пластине. Сопротивление пластины
- § 98. Турбулентный пограничный слой на крыловом профиле при малом продольном перепаде давлений
- § 99. Турбулентный пограничный слой на крыловом профиле при значительных продольных перепадах давления
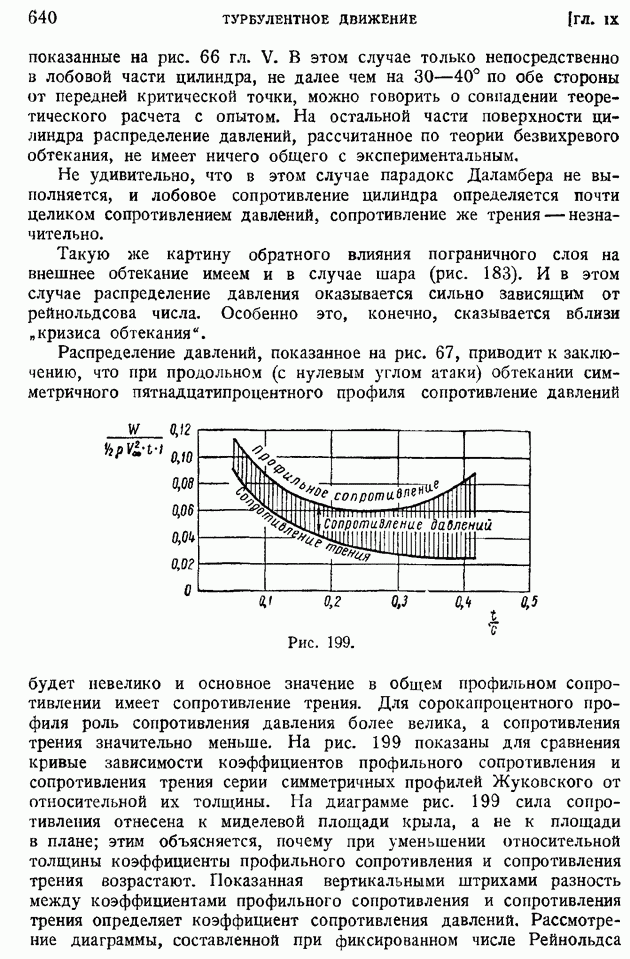
- § 100. Профильное сопротивление крыла. Разложение профильного сопротивления на сопротивление трения и сопротивление давлений. Обратное влияние пограничного слоя на распределение давлений по поверхности обтекаемого профиля
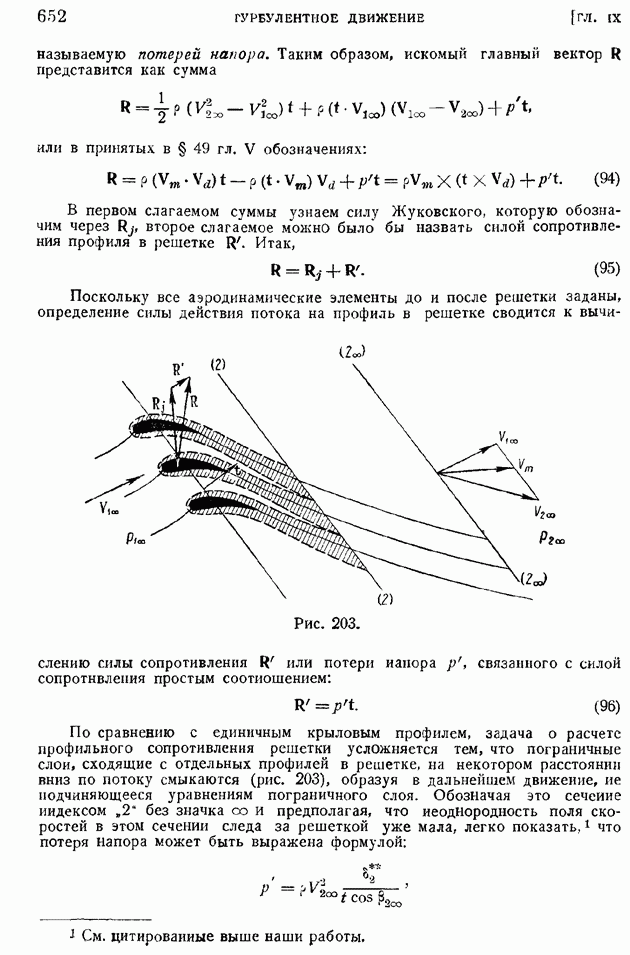
- § 101. Приближенные формулы профильного сопротивления крыла и крылового профиля в решетке
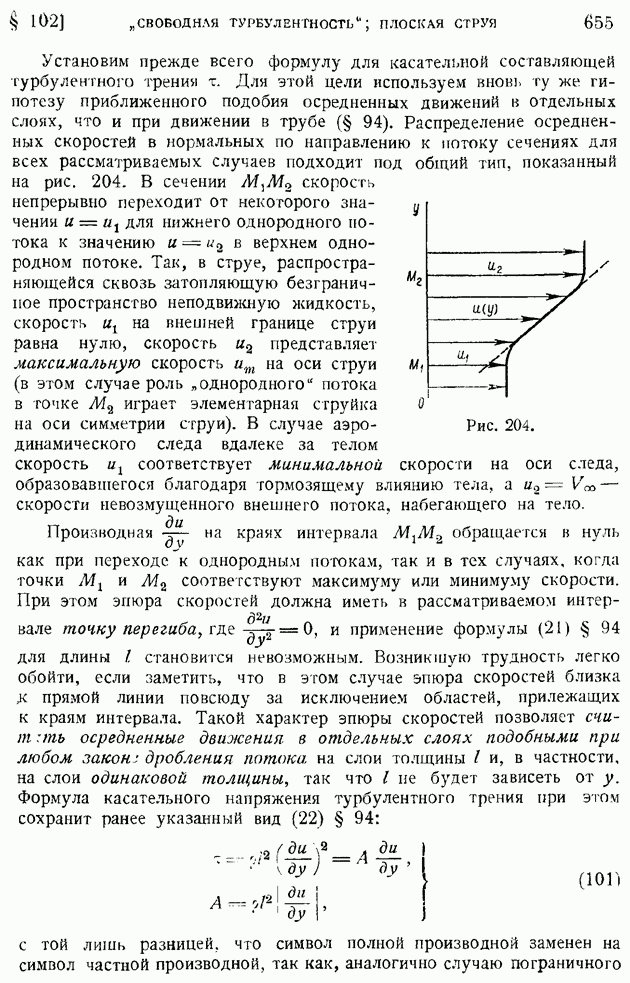
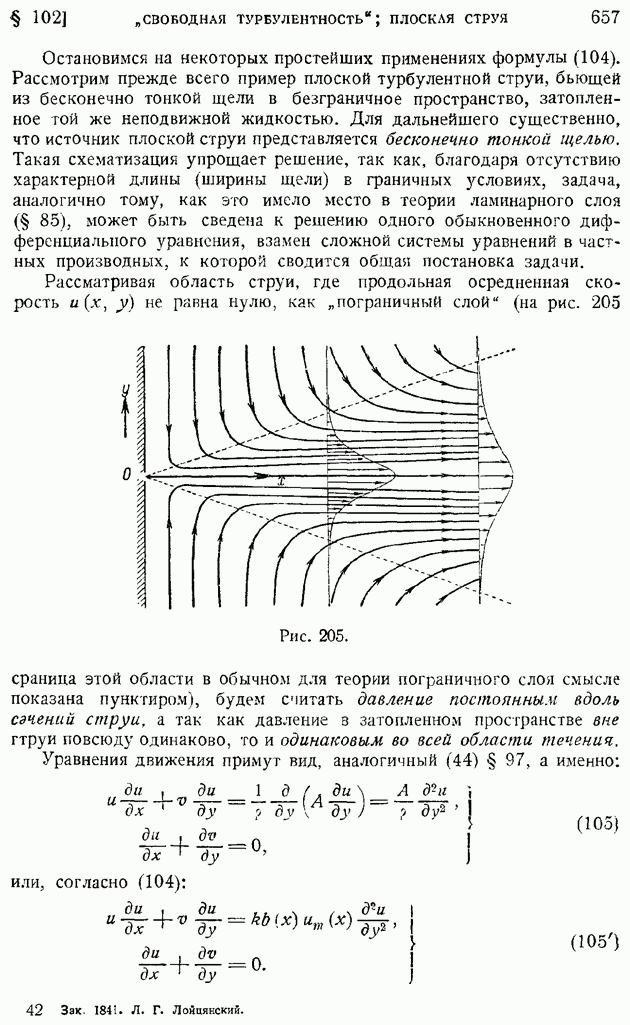
- § 102. Основные закономерности «свободной турбулентности». Плоская турбулентная струя в пространстве, заполненном той же жидкостью
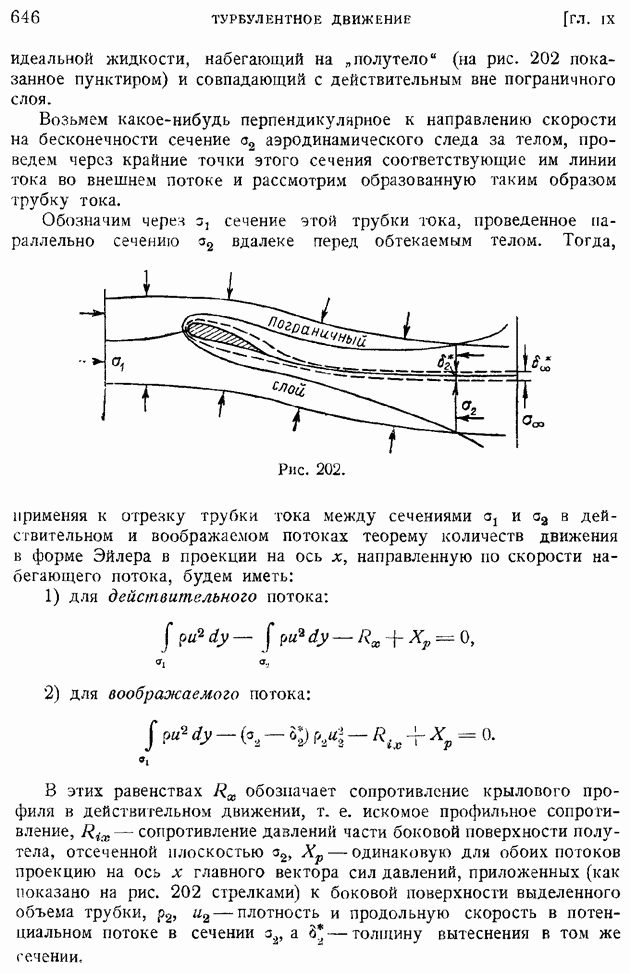
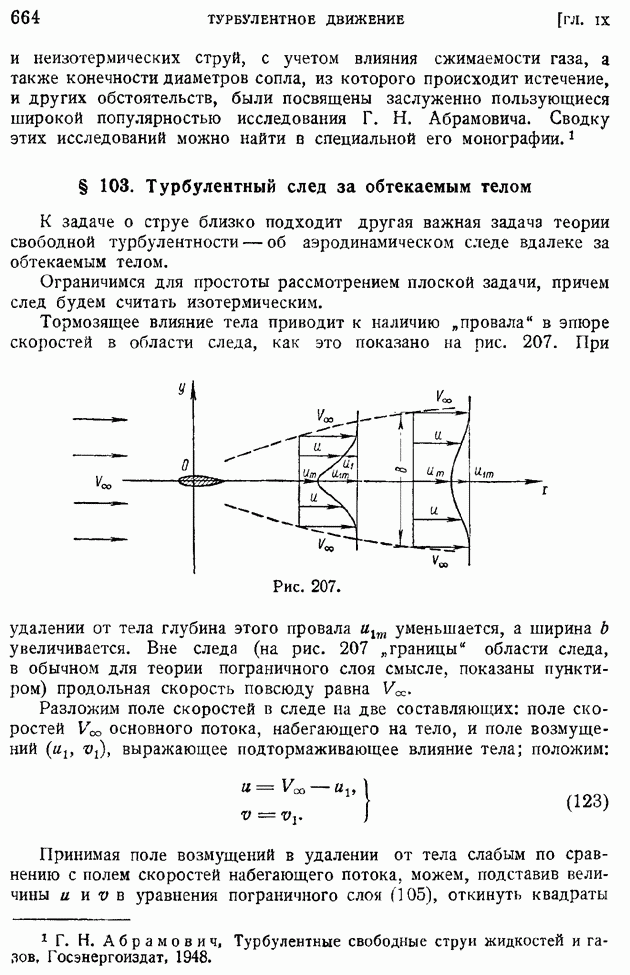
- § 103. Турбулентный след за обтекаемым телом
- § 104. Рассеяние турбулентных возмущений в жидкости. Случай изотропной и однородной турбулентности. Закон сохранения момента возмущений