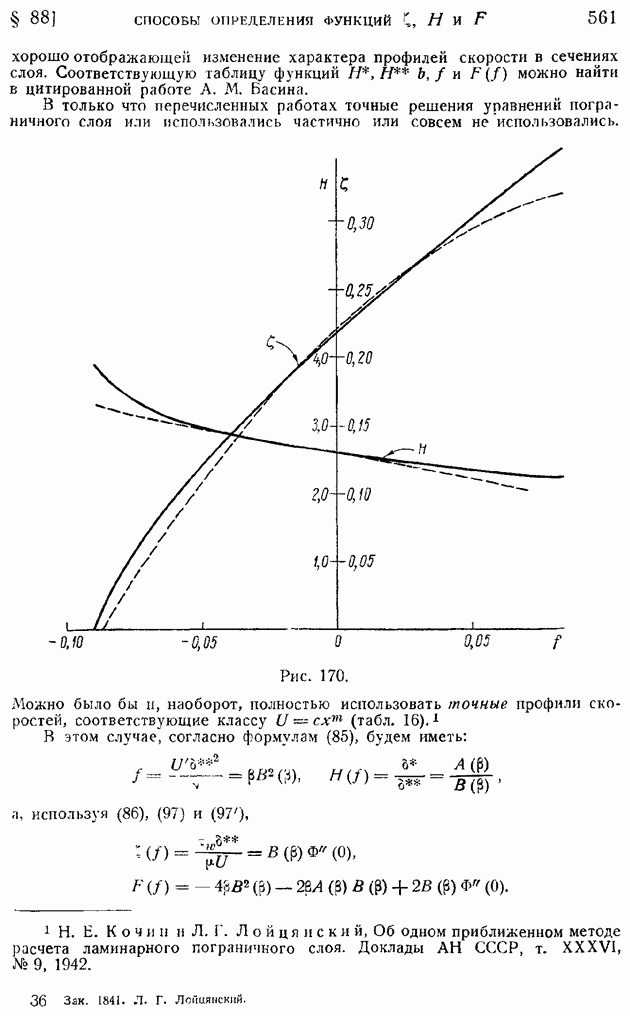| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 48. Определение обтекания крылового профиля произвольной формы
В современных расчетах крыльев и винтов самолета, лопаток рабочих колес и направляющих аппаратов турбомашнн, вентиляторов и др. приходится определять обтекания разнообразного типа профилей, значительно отличающихся от "теоретических" профилей и имеющих настолько большую относительную толщину и вогнутость, что уже нельзя применять изложенную в предыдущем параграфе теорию тонкой слабо изогнутой дужки. Для решения этих задач встал вопрос о создании практического метода расчета обтекаиия крылового профиля произвольной заданной формы; основной целью такого расчета является определение распределения скоростей и давлений по поверхности профиля, причем технические требования к точности расчета оказываются по необходимости весьма высокими.
В настоящее время существует большое число методов такого расчета: одни методы используют идею приближенного конформного отображения заданного профиля на контур, обтекание которого заранее хорошо известно, другие сводят задачу к определению такой интеиснвностн размещаемого на
поверхности крыла вихревого слоя, чтобы в результате наложения плоско-параллельного набегающего потока на течение, индуцированное слоем, получилось обтекание заданного профиля. Последний путь крайне сложен, так как приводит к необходимости приближенного решения интегральных уравнений и тем самым к большому числу трудоемких вычислений. Наиболее оправдавшим себя, без сомнения, является первый путь, основанный на использовании конформных отображений. У нас в Союзе широко используются удачно доведенные до практических вычислительных приемов методы Я. М. Серебрнйского, С. Г. Нужина и Л. А. Симонова. За границей принят метод Теодорсена и его модификации.
Отсылая за деталями отдельных методов к цитируемым работам, остановимся здесь на основной идее применения метода конформных отображений и общем характере вычислительного анализа, приводящего к решению поставленной задачи. Начнем с метода Я. М. Серебрийского. Как уже было выяснено в § 46, формула конформного отображения Жуковского — Чаплыгина (98) преобразует систему софокусных эллипсов, стягивающихся к отрезку  (рис. 94) физической плоскости
(рис. 94) физической плоскости  в систему кругов с общим центром в начале координат во вспомогательной плоскости С. Далее было показано, что в плоскости
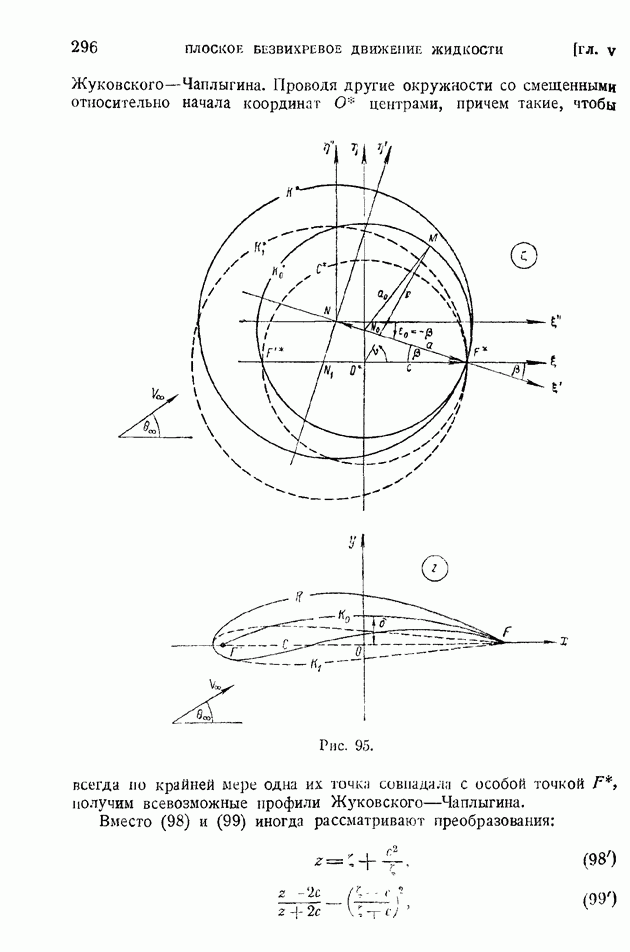
в систему кругов с общим центром в начале координат во вспомогательной плоскости С. Далее было показано, что в плоскости  существуют такие крыловые профили с нулевым углом на задней кромке (профили Жуковского — Чаплыгина), которые при выполнении того же конформного отображения (98) преобразуются в плоскости С в круги со смещенными относительно начала координат центрами (рис. 95). Если вместо отображения (98) взять обобщенное отображение (100), то аналогичному преобразованию в круг будут подвергаться и крыловые профили — обобщенные профили Жуковского-Чаплыгина, - заканчивающиеся острым углом, отличным от нуля (рис. 96).
существуют такие крыловые профили с нулевым углом на задней кромке (профили Жуковского — Чаплыгина), которые при выполнении того же конформного отображения (98) преобразуются в плоскости С в круги со смещенными относительно начала координат центрами (рис. 95). Если вместо отображения (98) взять обобщенное отображение (100), то аналогичному преобразованию в круг будут подвергаться и крыловые профили — обобщенные профили Жуковского-Чаплыгина, - заканчивающиеся острым углом, отличным от нуля (рис. 96).
Возьмем теперь крыловой профиль "произвольной" формы. Наметим среднюю линию ("скелет") этого профиля и определим его относительную вогнутость и толщину; после этого совместим, насколько это окажется возможным, профиль произвольной формы с подходящим к нему по вогнутости и толщине обычным или обобщенным профилем Жуковского-Чаплыгина. Из непрерывности отображающей функции (98) или (100) следует, что профили, близкие друг к другу в физической плоскости  окажутся близкими и во вспомогательной плоскости Но один из этих профилей — профиль Жуковского — Чаплыгина — отображается на круг со смещенным центром, следовательно, второй — профиль произвольной формы — отобразится на некоторый близкий к кругу контур, который в дальнейшем изложении будем называть почти кругом. Для того чтобы "почти-круг" был по возможности близок к точному кругу, следует особо внимательно отнестись к вопросу о расположении передней и задней кромок относительно фокусов
окажутся близкими и во вспомогательной плоскости Но один из этих профилей — профиль Жуковского — Чаплыгина — отображается на круг со смещенным центром, следовательно, второй — профиль произвольной формы — отобразится на некоторый близкий к кругу контур, который в дальнейшем изложении будем называть почти кругом. Для того чтобы "почти-круг" был по возможности близок к точному кругу, следует особо внимательно отнестись к вопросу о расположении передней и задней кромок относительно фокусов  эллипсов в плоскости
эллипсов в плоскости 
Так, при пользовании обобщенным преобразованием (100), если за  взят угол на задней кромке исследуемого профиля, то заднюю кромку профиля следует помещать точно в один из фокусов. При использовании обычного преобразования (98) это можно делать только в том случае, когда угол на
взят угол на задней кромке исследуемого профиля, то заднюю кромку профиля следует помещать точно в один из фокусов. При использовании обычного преобразования (98) это можно делать только в том случае, когда угол на
задней кромке очень близок к нулю; в противном случае следует угол на задней кромке исследуемого профиля закруглить и помещать фокус на половине расстояния от закругленной кромкн до центра ее кривизны.
Что касается расположения передней закругленной кромки (носка профиля), то при пользовании преобразованием (98) можно сохранить ту же рекомендацию, что и для задней кромкн. Основанием для этой рекомендации служит известное геометрическое свойство носка достаточно тонкого эллипса: фокус такого эллипса близок к середине радиуса кривизны носка. При использовании обобщенного преобразования (100) фокус рекомендуется размещать между только что указанной точкой и носком профиля.
При выполнении этих требований "почти-круг" будет представлять кривую, весьма близкую к кругу.
Произведя указанное размещение исследуемого профиля по отношению к точкам  особым точкам преобразований 98) и (100), перейдем к самим преобразованиям. Будем для общности пользоваться преобразованием (100)
особым точкам преобразований 98) и (100), перейдем к самим преобразованиям. Будем для общности пользоваться преобразованием (100)

имея в виду, что при  преобразование (100) переходит в обычное преобразование Жуковского — Чаплыгина (99).
преобразование (100) переходит в обычное преобразование Жуковского — Чаплыгина (99).
Я. М. Серебрийскнй использует более простое преобразование (99), однако с точки зрения выгодного для дальнейших расчетов максимального приближения "почтн-круга" к кругу можно рекомендовать для профилей с конечным углом на задней кромке применение преобразования  учитывающего наличие этого угла.
учитывающего наличие этого угла.

Рис. 97.
Обозначим (рис. 97) через  декартовы координаты точек
декартовы координаты точек  на профиле К в плоскости 2, церсз
на профиле К в плоскости 2, церсз  декартовы и через
декартовы и через  полярные координаты соответствующих точек
полярные координаты соответствующих точек  "почти-круга" К в плоскости
"почти-круга" К в плоскости  и через а — радиус близкого к "почти-кругу" точного круга
и через а — радиус близкого к "почти-кругу" точного круга  в плоскости
в плоскости  на рис. 97, совмещенной с плоскостью С. Наиболее трудоемкими в смысле вычислений операциями являются: определение уравнения .почти-круга в полярных координатах и представление логарифма отношения радиуса-вектора
на рис. 97, совмещенной с плоскостью С. Наиболее трудоемкими в смысле вычислений операциями являются: определение уравнения .почти-круга в полярных координатах и представление логарифма отношения радиуса-вектора  к радиусу круга а в виде ряда Фурье
к радиусу круга а в виде ряда Фурье

Для этой цели следовало бы применять математические механизмы: конформный трансформатор для преобразования заданного профиля в "почти-круг" и гармонический анализатор для определения коэффициентов Фурье  Механизмы, осуществляющие конформные преобразования (99) и (100), уже давно изобретены советскими учеными, но еще не внедрены в аэродинамическую практику.
Механизмы, осуществляющие конформные преобразования (99) и (100), уже давно изобретены советскими учеными, но еще не внедрены в аэродинамическую практику.
Аналитическое установление связи (110) между  представляет каких-либо трудностей, но требует кропотливых вычислений.
представляет каких-либо трудностей, но требует кропотливых вычислений.
Перепишем соотношение (100) в виде (опускаем индекс, нуль)

и будем считать, что координаты заданного профиля х, у выражены в частях длины  , а радиус-вектор
, а радиус-вектор  в частях длины
в частях длины  . Сохраняя обозначение
. Сохраняя обозначение  , у для этих безразмерных величин, будем иметь:
, у для этих безразмерных величин, будем иметь:

положим:

тогда будем иметь расчетные формулы:

где

Задаваясь парами значений координат профиля  последовательно вычисляем
последовательно вычисляем  а затем
а затем  При
При  в случае обычного преобразования Жуковского — Чаплыгина, формулы упрощаются. По вычисленным значениям
в случае обычного преобразования Жуковского — Чаплыгина, формулы упрощаются. По вычисленным значениям  строим график
строим график  Для обработки полученной кривой к виду (110) можно применять любые известные приемы гармонического анализа. В ранее цитированной работе
Для обработки полученной кривой к виду (110) можно применять любые известные приемы гармонического анализа. В ранее цитированной работе  Серебрийского излагаются остроумные приемы, позволяющие легко получать тригонометрические представления резких местных отклонений на кривой вблизи точки
Серебрийского излагаются остроумные приемы, позволяющие легко получать тригонометрические представления резких местных отклонений на кривой вблизи точки  при помощи комплексов вида
при помощи комплексов вида

названных автором "горками". Применение широко затабулированных автором "горок" сильно сокращает объем вычислений, необходимых для определения коэффициентов 
Опуская изложение практических деталей вычислительного характера — их можно найти в раиее цитированной работе  Серебрийского, — будем считать, что ряд (110) уже составлен и коэффициенты его
Серебрийского, — будем считать, что ряд (110) уже составлен и коэффициенты его  определены. Обратимся к установлению приближенных формул конформного отображения области вне "почти-круга"
определены. Обратимся к установлению приближенных формул конформного отображения области вне "почти-круга"  в плоскости комплексного переменного С на область вне круга
в плоскости комплексного переменного С на область вне круга  в плоскости
в плоскости  Введем обозначения:
Введем обозначения:

где  являются полярными координатами точек плоскости С, а величины
являются полярными координатами точек плоскости С, а величины  соответственно полярными координатами точек плоскости
соответственно полярными координатами точек плоскости  в последнем случае радиус-вектор выражен как произведение радиуса круга а на переменный коэффициент X, причем окружности
в последнем случае радиус-вектор выражен как произведение радиуса круга а на переменный коэффициент X, причем окружности  соответствует значение
соответствует значение 
Следуя  Серебрийскому, будем искать функцию, отображающую внешнюю по отношению к "почти-кругу" К часть плоскости С на внешнюю по отношению к кругу
Серебрийскому, будем искать функцию, отображающую внешнюю по отношению к "почти-кругу" К часть плоскости С на внешнюю по отношению к кругу  часть плоскости
часть плоскости  в виде
в виде

где при  коэффициенты
коэффициенты  являются комплексными величинами, а
являются комплексными величинами, а  представляет действительную величину. Тогда, согласно (111). найдем
представляет действительную величину. Тогда, согласно (111). найдем

или, полагая

и сравнивая в (112) действительные и мнимые части, будем иметь:

Как уже ранее указывалось, при достаточно тщательном расположении преобразуемого крылового контура К относительно точек  и удачном
и удачном
подборе угла  а следовательно, и
а следовательно, и  , контур "почти-круга" К будет мало отличаться от контура круга
, контур "почти-круга" К будет мало отличаться от контура круга  соответствующие точки будут близки друг к другу и, как показал
соответствующие точки будут близки друг к другу и, как показал  Серебрийский, можно с достаточной для практики точностью пренебречь в перлом приближении разницей между полярными углами
Серебрийский, можно с достаточной для практики точностью пренебречь в перлом приближении разницей между полярными углами  и в соответствующих точек в плоскостях
и в соответствующих точек в плоскостях  . При желании метод позволяет получить следующие приближения, учитывающие разннцу между углами
. При желании метод позволяет получить следующие приближения, учитывающие разннцу между углами  .
.
Замечая, что для точек, лежащих на контурах  будет:
будет:  перепишем в принятом приближении
перепишем в принятом приближении  первое равенство предыдущей системы в виде
первое равенство предыдущей системы в виде

Это равенство полностью совпадает с ранее установленным разложением (110). Таким образом, искомые коэффициенты  входящие в преобразование (112) через комплексные коэффициенты
входящие в преобразование (112) через комплексные коэффициенты  оказываются уже известными. После этого не трудно по
оказываются уже известными. После этого не трудно по  вычислить комплексные коэффициенты
вычислить комплексные коэффициенты  тем самым полностью определить основное преобразование (112) и решить поставленную задачу. Опыт многочисленных расчетов показал, что для употребительных на практике крыловых профилей изложенное первое приближение оказывается вполне достаточным.
тем самым полностью определить основное преобразование (112) и решить поставленную задачу. Опыт многочисленных расчетов показал, что для употребительных на практике крыловых профилей изложенное первое приближение оказывается вполне достаточным.
Совокупность равенств (100) и (112) дает преобразование части плоскости  вне крылового контура К на внешнюю по отношению к окружности круга
вне крылового контура К на внешнюю по отношению к окружности круга  часть плоскости
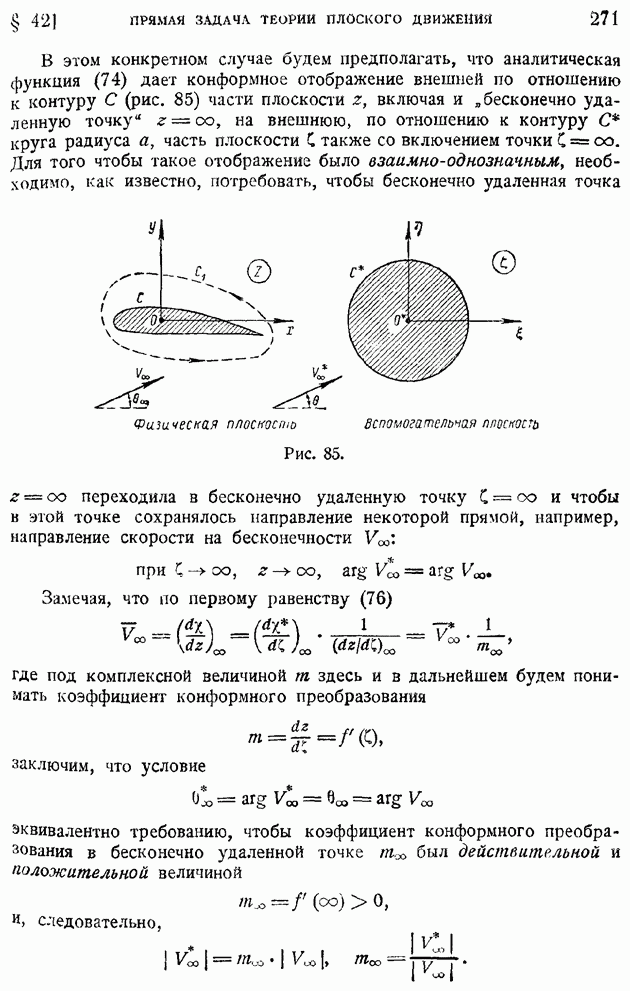
часть плоскости  т. е. как раз то основное конформное преобразование (74), о котором говорилось в § 42 (вспомнить рис. 85).
т. е. как раз то основное конформное преобразование (74), о котором говорилось в § 42 (вспомнить рис. 85).
Желая найти распределение скоростей по поверхности крылового профиля К или вне его, используем комплексный потенциал  обтекания кругового контура
обтекания кругового контура  с наложенной на него циркуляцией. Будем иметь
с наложенной на него циркуляцией. Будем иметь

Величину наложенной циркуляции определим, пользуясь постулатом Чаплыгина о плавном обтекании задней кромки крыла, представленным формулой (80), Заметим, что последние два сомножителя в только что составленном выражении комплексной скорости имеют чисто геометрический характер и не зависят от кинематических условий обтекания — скорости и угла атаки. Это делает простым пересчет распределений скоростей с одного угла атаки на другой, если комплексные величины и — для заданной формы крылового профиля уже определены. Расчет поля скоростей вокруг профиля представляет особые вычислительные трудности, удачно обойденные  Серебрийским путем применения специальных приемов.
Серебрийским путем применения специальных приемов.
В методе  Нужина промежуточное отображение на "почти-круг" отсутствует и решение задачи сводится к непосредственному отображению области, внешней по отношению к крыловому контуру К, на область вне круга
Нужина промежуточное отображение на "почти-круг" отсутствует и решение задачи сводится к непосредственному отображению области, внешней по отношению к крыловому контуру К, на область вне круга  (см. рис. 97).
(см. рис. 97).
Для этого между физической плоскостью течения z и вспомогательной плоскостью  устанавливается соответствие в форме ряда Лорана
устанавливается соответствие в форме ряда Лорана

с неизвестными комплексными коэффициентами 
Полагая в  и выделяя в нем действительную и мнимую части, получим систему двух действительных равенств:
и выделяя в нем действительную и мнимую части, получим систему двух действительных равенств:

представляющих параметрическое уравнение крылового контура, выраженное через параметр  — угол в плоскости
— угол в плоскости  между радиусами-векторами точек на круге
между радиусами-векторами точек на круге  соответствующих точкам на контуре К, и действительной осью.
соответствующих точкам на контуре К, и действительной осью.
Разобьем координаты  и
и  на полусуммы и полуразности их значений на круге
на полусуммы и полуразности их значений на круге  в точках с угловыми координатами
в точках с угловыми координатами  и
и  положив
положив

Входящие сюда иовыс коэффициенты Фурье:

могуг быть определены по обычным формулам:

Неизвестные коэффициенты  определяются следующим процессом последовательных приближений. За нулевое приближение принимается:
определяются следующим процессом последовательных приближений. За нулевое приближение принимается:

что соответствует отображению на круг пластинки. Затем, задаваясь последовательными значениями  и соответствующими значениями
и соответствующими значениями  определяют по чертежу крылового профиля величины ординат
определяют по чертежу крылового профиля величины ординат  а также
а также  и
и  проведенных через выбранные абсциссы. Пользуясь интегральными выражениями коэффициентов Фурье (115), по найденным значениям
проведенных через выбранные абсциссы. Пользуясь интегральными выражениями коэффициентов Фурье (115), по найденным значениям 
определяют новые значения коэффициентов  и в первом приближении. Эти значения коэффициентов позволяют найти новые функции
и в первом приближении. Эти значения коэффициентов позволяют найти новые функции  а это в свою очередь по предыдущему приведет к уточненным значениям ординат и т. д.
а это в свою очередь по предыдущему приведет к уточненным значениям ординат и т. д.
Не останавливаясь на весьма интересных деталях метода С. Г. Нужина, облегчающих проведение выкладок и делающих  наглядными, заметим, что автору метода удалось провести доказательство сходимости процесса последовательных приближений, что выгодно характеризует метод с теоретической стороны.
наглядными, заметим, что автору метода удалось провести доказательство сходимости процесса последовательных приближений, что выгодно характеризует метод с теоретической стороны.
Можно заметить, что наибольшие вычислительные трудности в обоих только что рассмотренных методах связаны с необходимостью определения коэффициентов ряда Фурье, выражающего логарифм отношения радиуса-вектора точек "почти-круга" к радиусу круга через угол в промежуточной плоскости в методе Серебрийского, или координаты крылового профиля в физической плоскости в функции от полярного угла в вспомогательной плоскости в методе Нужина. В первом из указанных методов для этой цели с успехом используется способ "горок", во втором приходится непосредственно вычислять квадратуры (115),
В методе Л. А. Симонова основную роль играет преобразование внешней по отношению к контуру крыла К части плоскости z на часть плоскости  вне круга
вне круга  аналогичное (113), с той лишь разницей, что при
аналогичное (113), с той лишь разницей, что при  в первой степени сохраняется комплексный коэффициент. Замечая, что из первых членов разложения (113) можно выделить группу, представляющую отображение некоторой "эквивалентной" пластинки, имеющей одинаковую с рассматриваемым крыловым контуром подъемную силу, Л. А. Симонов интерпретнрует указанный комплексный коэффициент, как одну четверть комплексного вектора, совпадающего по величине и направлению с эквивалентной пластинкой. Ряд (113) может быть представлен при этом в виде
в первой степени сохраняется комплексный коэффициент. Замечая, что из первых членов разложения (113) можно выделить группу, представляющую отображение некоторой "эквивалентной" пластинки, имеющей одинаковую с рассматриваемым крыловым контуром подъемную силу, Л. А. Симонов интерпретнрует указанный комплексный коэффициент, как одну четверть комплексного вектора, совпадающего по величине и направлению с эквивалентной пластинкой. Ряд (113) может быть представлен при этом в виде  проекции эквивалентной пластинки)
проекции эквивалентной пластинки)

Отделение действительной и мнимой частей приводит к рядам, аналогичным (113), которые, пользуясь известными формулами теории функции комплексного переменного, удается представить в интегральной форме:

Определенные в точках крылового контура производные  удовлетворяют системе равенств:
удовлетворяют системе равенств:

аналогичной (116). Расчет функций:  может быть произведен путем последовательных приближений в системах (116) и (117), причем входящие в правые части этих уравнений интегралы могут быть сведены к суммам, аналогичным применяемым в механических квадратурах.
может быть произведен путем последовательных приближений в системах (116) и (117), причем входящие в правые части этих уравнений интегралы могут быть сведены к суммам, аналогичным применяемым в механических квадратурах.
Основной особенностью метода Л. А. Симонова является установленная им тесная связь между параметрическими выражениями координат крылового профиля  и величинами (6) и (6), входящими в основную формулу распределения скоростей.
и величинами (6) и (6), входящими в основную формулу распределения скоростей.

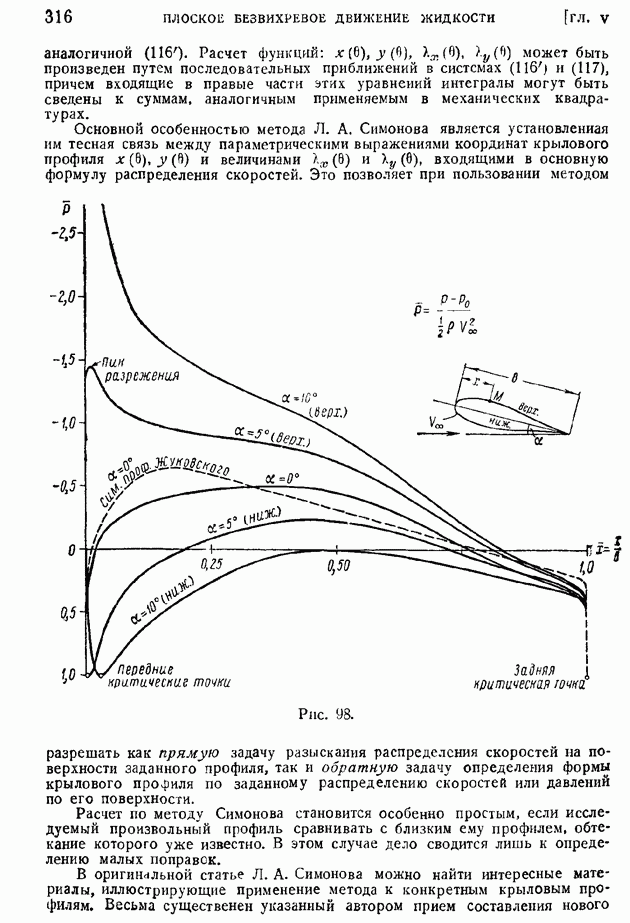
Рис. 98.
Это позволяет при пользовании методом разрешать как прямую задачу разыскания распределения скоростей на поверхности заданного профиля, так и обратную задачу определения формы крылового профиля по заданному распределению скоростей или давлений по его поверхности.
Расчет по методу Симонова становится особенно простым, если исследуемый произвольный профиль сравнивать с близким ему профилем, обтекание которого уже известно. В этом случае дело сводится лишь к определению малых поправок.
В оригиильной статье Л. А. Симонова можно найти интересные материалы, иллюстрирующие применение метода к конкретным крыловым профилям. Весьма существенен указанный автором прием составления нового
профиля путем сложения комплексных координат или пропорциональных  величин двух известных профилей, и определения скоростей по поверхности такого составного профиля.
величин двух известных профилей, и определения скоростей по поверхности такого составного профиля.
На рис. 98 сплошными кривыми представлены рассчитанные по методу Серебрийского распределения давления по верхней и нижней поверхностям некоторого симметричного профиля, имеющего сравнительно с профилем Жуковского смещенное назад мнделево сечение (место максимальной толщины).
По оси ординат отложена уже знакомая нам безразмерная величина разности давлений в данной точке поверхности профиля и на бесконечности, отнесенная к скоростному напору набегающего потока

по оси абсцисс — безразмерная координата, равная отношению абсциссы точки на профиле, отсчитываемой по оси симметрии профиля от носика, к длине профиля.
Как видно  графика, смещение назад места максимальной толщины симметричного профиля приводит при нулевом угле атаки к более плавному распределению давлений по поверхности профиля, чем у симметричного профиля Жуковского (на рис. 98 — пунктир) той же относительной толщины. В дальнейшем будет показано, что при прочих равных условиях, в частности, при том же коэффициенте подъемной силы, плавность распределения является положительным признаком крылового профиля с точки зрения его сопротивления и поведения при больших скоростях. Далее из графиков видно, как меняется распределение давления при возрастании угла атакн, как возникает пик разрежения
графика, смещение назад места максимальной толщины симметричного профиля приводит при нулевом угле атаки к более плавному распределению давлений по поверхности профиля, чем у симметричного профиля Жуковского (на рис. 98 — пунктир) той же относительной толщины. В дальнейшем будет показано, что при прочих равных условиях, в частности, при том же коэффициенте подъемной силы, плавность распределения является положительным признаком крылового профиля с точки зрения его сопротивления и поведения при больших скоростях. Далее из графиков видно, как меняется распределение давления при возрастании угла атакн, как возникает пик разрежения  на верхней поверхности и насколько он быстро развивается (на рис. 98 пик разрежения, при
на верхней поверхности и насколько он быстро развивается (на рис. 98 пик разрежения, при  равный
равный  не поместился на чертеже).
не поместился на чертеже).
Как можно заключить из предыдущего, задача об определении обтекания крылового профиля произвольной формы не представляет теоретических трудностей. Существующие в настоящее время работы посвящены, главным образом, улучшению вычислительных приемов.
Для той же цели может служить специальный электрический прибор, использующий для определения потенциала скоростей обтекания электрогидродинамическую аналогию (ЭГДА) между этим потенциалом и электрическим потенциалом, создаваемым в специальной электролитической ванне.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Предмет механики жидкости и газа. Основные свойства «макромодели» жидкости и газа: сплошность и подвижность
- § 2. Основные методы механики жидкости и газа. Области применения и главнейшие задачи
- § 3. Краткий очерк исторического развития механики жидкости и газа. От гидромеханики древних до установления воззрений ньютонианской эпохи
- § 4. Эпоха Эйлера и Бернулли. Гидроаэродинамика в XIX в.
- § 5. Современный этап развития механики жидкости и газа
- ГЛАВА I. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
- § 6. Поле физической величины. Скалярное и векторное поля. Поверхности уровня. Векторные линин и трубки
- § 7. Мера однородности поля в данном направлении и в дайной точке. Градиевт скалярного поля и дифференциальный тензор векторного поля как меры неоднородности поля
- § 8. Задание движения сплошной среды. Поле скоростей. Линии тока и траектории
- § 9. Поле ускорений. Разложение ускорения частицы на локальную и конвективную составляющие
- § 10. Скоростное поле сплошной среды в окрестности данной точки. Угловая скорость и вихрь. Тензор скоростей деформаций и его компоненты
- § 11. Скорость объемного расширения жидкости. Интегральные представления дифференциальных операторов поля. Основные интегральные формулы
- § 12. Вихревые линии и трубки. Вторая теорема Гельмгольца. Интенсивность вихревой трубки
- § 13. Выражение интенсивности вихревой трубки через циркуляцию вектора по контуру, охватывающему трубку. Теорема об изменении циркуляции скорости во времени
- ГЛАВА II. ОСНОВНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ И РАВНОВЕСИЯ СПЛОШНОЙ СРЕДЫ
- § 14. Распределение массы в сплошной среде. Плотность и удельный вес. Напряжения. Тензор напряженности и его симметричность
- § 15. Общие уравнения динамики сплошной среды. Уравнение неразрывности. Уравнения динамики в напряжениях
- § 16. Тепловые явления в жидкостях и газах. Закон сохранения энергии и уравнение баланса энергии
- § 17. Общие уравнения равновесного состояния жидкости и газа. Равновесие воздуха в атмосфере. Приближенные барометрические формулы. Стандартная атмосфера
- § 18. Равновесие несжимаемой жидкости. Уравнение поверхности раздела. Равновесие вращающейся жидкости
- § 19. Давление тяжелой несжимаемой жидкости на поверхность тела. Сила и момент, приложенные к телу, плавающему в тяжелой жидкости. Случай вращающейся жидкости
- ГЛАВА III. ДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ И ГАЗА. ОСНОВНЫЕ УРАВНЕНИЯ И ОБЩИЕ ТЕОРЕМЫ
- § 20. Идеальная жидкость. Основные уравнения движения
- § 21. Закон сохранения энергии в движущейся идеальной жидкости. Адиабатическое движение. Сохранение энтропии
- § 22. Эйлерово представление конвективного изменения объемного интеграла. Перенос величины сквозь контрольную поверхность
- § 23. Эйлерова форма законов сохранения массы и энергии, теоремы количеств движения и момента количеств движения при стационарном движении идеальной жидкости
- § 24. Теорема об изменении кинетической энергии. Работа и мощность внутренних сил. Эйлерова форма уравнения изменения кинетической энергии
- § 25. Теорема Бернулли о сохранении полной механической энергии при стационарном баротропном движении идеальной жидкости и газа
- ГЛАВА IV. ОДНОМЕРНЫЙ ПОТОК ИДЕАЛЬНОЙ ЖИДКОСТИ
- § 26. Одномерное течение идеальной сжимаемой жидкости. Линеаризированные уравнения. Скорость распространения малых возмущений в жидкости или газе
- § 27. Изотермическая и адиабатическая скорости звука. «Конус возмущений» при сверхзвуковом движении источника возмущения. Число M и его связь с углом конуса возмущений
- § 28. Распространение непрерывных возмущений конечной интенсивности. Характеристики. Образование разрывной ударной волны
- § 29. Стоячая ударная волна или скачок уплотнения. Ударная адиабата
- § 30. Критические величины в одномерном потоке газа. Связь между скоростями до и после скачка. Изменение давления, плотности и температуры в скачке уплотнения
- § 31. Скорость распространения ударной волны. Спутное движение газа за ударной волной
- § 32. Влияние интенсивности скачка уплотнения на сжатие газа. Измерение скоростей и давлений в до- и сверхзвуковых потоках
- § 33. Одномерное движение газа по трубе переменного сечения. Истечение из резервуара большой емкости сквозь сходящееся сопло
- § 34. Одномерное течение в сопле Лаваля. Движение газа с притоком тепла
- ГЛАВА V. БЕЗВИХРЕВОЕ ДВИЖЕНИЕ ЖИДКОСТИ. ПЛОСКОЕ ДВИЖЕНИЕ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 35. Сохранение циркуляции скорости в потоке идеальной жидкости. Теорема Кельвина и Лаграижа. Безвихревое движение. Потенциал скоростей
- § 36. Интеграл Лагранжа — Коши уравнений безвихревого движения. Теорема Бернулли. Некоторые общие свойства безвихревого движения идеальной несжимаемой жидкости в односвязной области
- § 37. Плоское безвихревое движение несжимаемой жидкости. Потенциал скоростей и функция тока. Применение функций комплексного переменного. Комплексный потенциал и сопряженная скорость
- § 38. Построение полей течения по заданной характеристической Функции. Простейшие плоские потоки и их наложение
- § 39. Бесциркуляционное и циркуляционное обтекания круглого цилиндра
- § 40. Применение криволинейных координат. Бесциркуляционное и циркуляционное обтекания эллиптического цилиндра и пластинки. Задача Жуковского об обтекании решетки пластин.
- § 41. Плоское движение с отрывом струй. Разрывное обтекание пластинки и протекание жидкости сквозь отверстие
- § 42. Прямая задача в теории плоского движения идеальной несжимаемой жидкости. Применение метода конформных отображений. Гипотеза Чаплыгина о безотрывном обтекании задней кромки профиля. Формула циркуляции
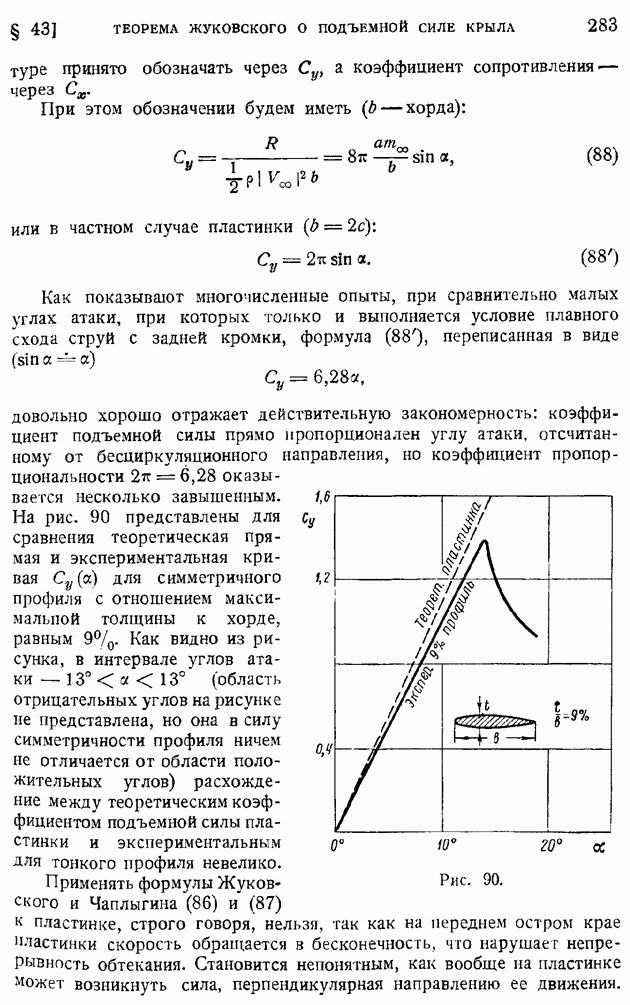
- § 43. Теорема Жуковского о подъемной силе крыла. Зависимость подъемной силы от угла атаки. Коэффициент подъемной силы
- § 44. Применение метода комплексных переменных к выводу теоремы Жуковского. Формулы Чаплыгина для главного вектора и момента сил давления потока на крыло
- § 45. Выражение главного момента сил давления потока через коэффициенты конформного отображения. Фокус крыла. Независимость от угла атаки момента относительно фокуса. Парабола устойчивости
- § 46. Частные случаи конформного отображения крылового профиля на круг. Преобразование Жуковского-Чаплыгина. Теоретические крыловые профили
- § 47. Задача об обтекании слабо изогнутой дужки произвольной формы (теория тонкого крыла)
- § 48. Определение обтекания крылового профиля произвольной формы
- § 49. Обобщение теоремы Жуковского на случай плоской решетки с бесчисленным множеством профилей
- ГЛАВА VI. ПЛОСКОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ СЖИМАЕМОГО ГАЗА
- § 50. Основные уравнения плоского стационарного безвихревого движения сжимаемого газа. Линеаризированные уравнения
- 51. Линеаризированный до- и сверхзвуковой газовый поток вдоль волнистой стенки
- § 52. Тонкое крыло в линеаризированном до- и сверхзвуковом потоках. Влияние сжимаемости газа на коэффициент подъемной силы в дозвуковом потоке. Коэффициенты подъемной силы и волнового сопротивления при сверхзвуковом потоке
- § 53. Нелинеаризированные уравнения движения идеального сжимаемого газа. Переход в плоскость годографа. Уравнения Чаплыгина
- § 54. Метод С. А. Христиановича. Приближенные формулы учета влияния сжимаемости на распределение давления
- § 55. Критическое число M и его определение по заданному распределению давления в несжимаемом обтекании. Поведение коэффициента подъемной силы и момента при около- и закритических значениях числа M
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
- § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского
- § 57. Нелинеаризированный сверхзвуковой поток. «Характеристики» уравнений плоского сверхзвукового потока. Линин возмущения и их основные свойства
- § 58. Обтекание выпуклого угла сверхзвуковым потоком. Влияние угла поворота струи на ее газодинамические элементы
- § 59. Сверхзвуковой поток внутри тупого угла. Косой скачок уплотнения. Связь между газодинамическими элементами до и за косым скачком
- ГЛАВА VII. ПРОСТРАНСТВЕННОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ
- § 60. Ортогональные криволинейные координаты в пространстве. Основные дифференциальные операторы поля в криволинейных координатах
- § 61. Потенциал скоростей. Поле источника и диполя. Непрерывное распределение источников и диполей. Ньютонов потенциал. Потенциал простого и двойного слоев
- § 62. Поле скоростей вокруг заданной системы вихрей. Формула Био — Савара. Потенциал скоростей замкнутой вихревой нити. Аналогия с потенциалом двойного слоя
- § 63. Функция тока и ее связь с векторным потенциалом скоростей. Функции тока простейших течений
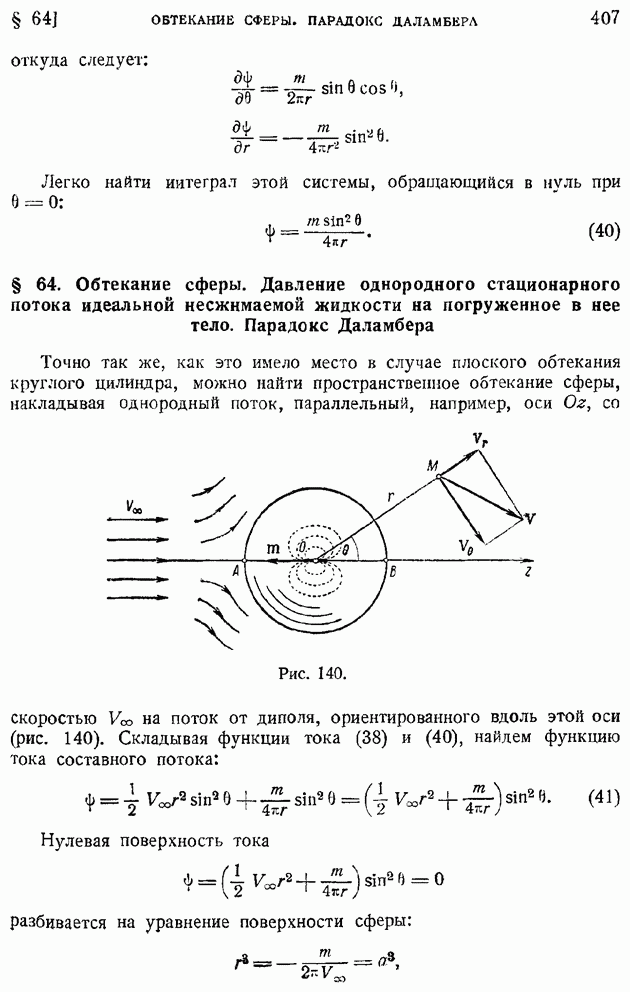
- § 64. Обтекание сферы. Давление однородного стационарного потока идеальной несжимаемой жидкости на погруженное в нее тело. Парадокс Даламбера
- § 65. Общие уравнения осесимметричного движения. Применение цилиндрических координат. Течение сквозь каналы
- § 66. Осесимметричное продольное обтекание тел вращения. Случай эллипсоида вращения
- § 67. Поперечное обтекание тел вращения. Пример эллипсоида вращения
- § 68. Продольное и поперечное обтекание тел вращения большого удлинения. Приближенные выражения граничных условий. Применение тригонометрических сумм для определения коэффициентов …
- § 69. Метод «особенностей». Применение непрерывно распределенных источников (стоков) и диполей для решения задачи о продольном и поперечном обтекании тел вращения
- § 70. Общий случай движения твердого тела сквозь несжимаемую идеальную жидкость. Определение потенциала скоростей. Главный вектор и главный момент сил давления потока на тело
- § 71. Коэффициенты «присоединенных масс». Свойство симметрии. «Присоединенная» кинетическая энергия. Определение «присоединенных масс» поступательно движущегося цилиндра, шара и эллипсоида
- § 72. Элементы теории крыла конечного размаха. Вихревая система крыла. Гипотеза плоских сечеиий. Геометрические и действительные углы атаки. Подъемная сила и «индуктивное сопротивление»
- § 73. Основные формулы теории «несущей линии». «Индуктивная скорость» и «индуктивный угол». Прямая задача определения подъемной силы и индуктивного сопротивления по заданному распределению циркуляции
- § 74. Крыло с минимальным индуктивным сопротивлением. Эллиптическое распределение циркуляции. Связь между коэффициентами индуктивного сопротивления и подъемной силы. Основное уравнение теории крыла и понятие о его интегрировании
- ГЛАВА VIII. ДИНАМИКА ВЯЗКОЙ ЖИДКОСТИ И ГАЗА
- § 75. Внутреннее трение и теплопроводность в жидкостях и газах. Законы Ньютона и Фурье. Влияние температуры на коэффициенты вязкости и теплопроводности. Число «сигма»
- § 76. Обобщение закона Ньютона на случай произвольного движения среды. Закон линейной связи между тензорами напряжений и скоростей деформации
- § 77. Общие уравнения движения вязкой жидкости. Динамические уравнения и уравнение баланса энергии. Граничные условия движения жидкости с треннем и теплопроводностью
- § 78. Понятие о подобии гидродинамических явлений. Безразмерные уравнения движения вязкой жидкости и газа. Условия подобия
- § 79. Ламинарное движение вязкой несжимаемой жидкости по цилиндрической трубе
- § 80. Обтекание шара при очень малых значениях числа Рейнольдса. Формула сопротивления шара по Стоксу и ее обобщения
- § 81. Вихревые линии в идеальной и вязкой жидкости. Сохраняемость вихревых линий при отсутствии внутреннего трения. Диффузия вихря в вязкой жидкости
- § 82. Одномерное прямолинейное движение сжимаемого вязкого газа. Движение внутри скачка уплотнения. Понятие о толщине скачка
- § 83. Работа внутренних сил и диссипация механической энергии в движущейся вязкой среде
- § 84. Обтекание тел жидкостью и газом при больших значениях числа Рейнольдса. Основные уравнения теории ламинарного пограничного слоя
- § 85. Ламинарный пограничный слой на пластинке, продольно обтекаемой несжимаемой жидкостью. Неизотермическое движение
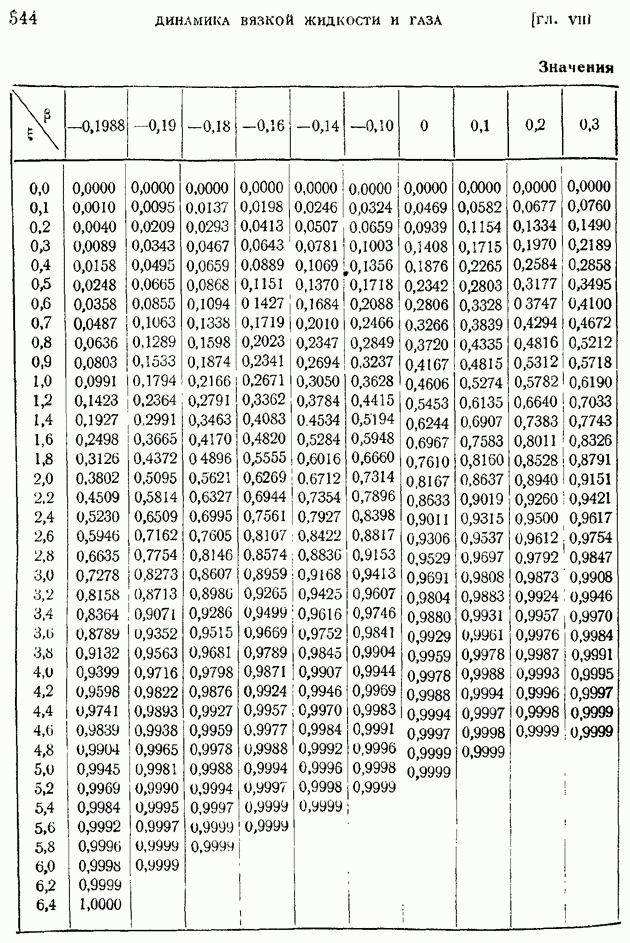
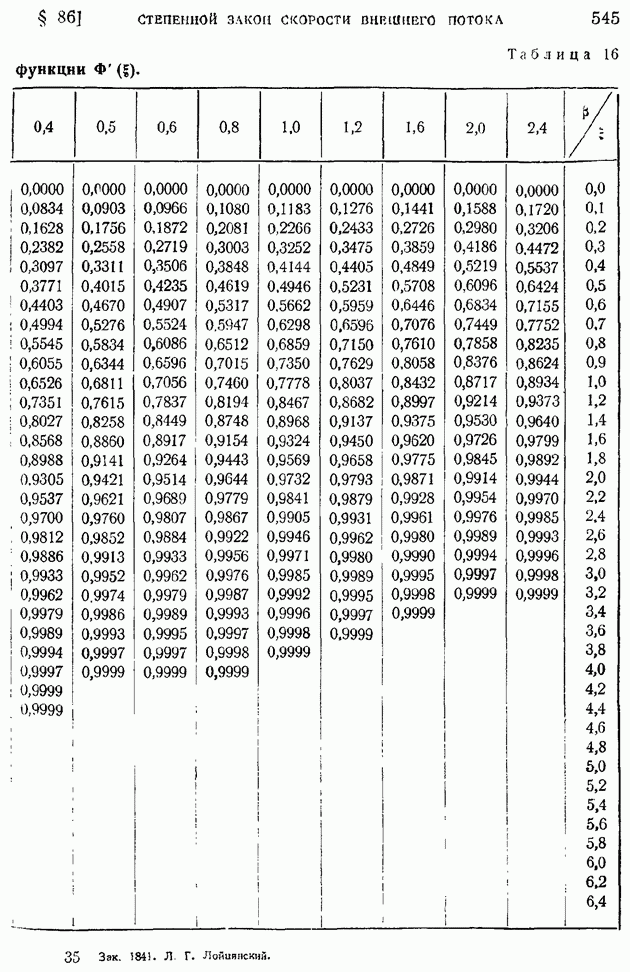
- § 86. Ламинарный пограничный слой при степенном задании скорости внешнего потока
- § 87. Ламинарный пограничный слой в общем случае задания скорости внешнего потока. Применение уравнения импульсов для приближенного расчета ламинарного пограничного слоя
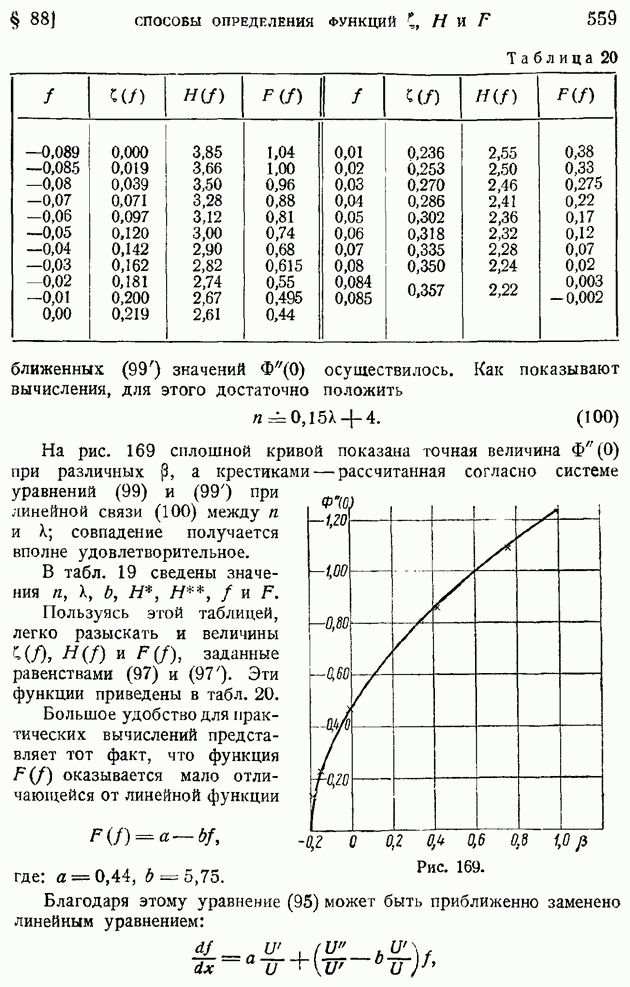
- § 88. Способы определения функций … Приближенный метод расчета ламинарного пограничного слоя
- § 89. Ламинарный пограничный слой на пластинке, продольно обтекаемой сжимаемым газом при больших скоростях. Случай линейной зависимости коэффициента вязкости от температуры (n = 1)
- § 90. Ламинарный пограничный слой на пластинке при любом законе связи между вязкостью и температурой и при числе … Обтекание крылового профиля потоком больших скоростей
- ГЛАВА IX. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ
- § 91. Переход ламинарного движения в турбулентное. Критическое рейнольдсово число
- § 92. Область и «точка» перехода. Явление «кризиса обтекания»
- § 93. Основные уравнения осреднеиного турбулентного движения. Тензор турбулентных напряжений
- § 94. Турбулентное движение жидкости в плоской и круглой трубе. Логарифмические формулы скоростей
- § 95. Формулы сопротивления гладких труб при турбулентном движении жидкости. Ламинарный подслой
- § 96. Влияние шероховатости стенок трубы на ее сопротивление. Предельные режимы течения. Режим установившейся шероховатости
- § 97. Турбулентный пограничный слой на продольно обтекаемой пластине. Сопротивление пластины
- § 98. Турбулентный пограничный слой на крыловом профиле при малом продольном перепаде давлений
- § 99. Турбулентный пограничный слой на крыловом профиле при значительных продольных перепадах давления
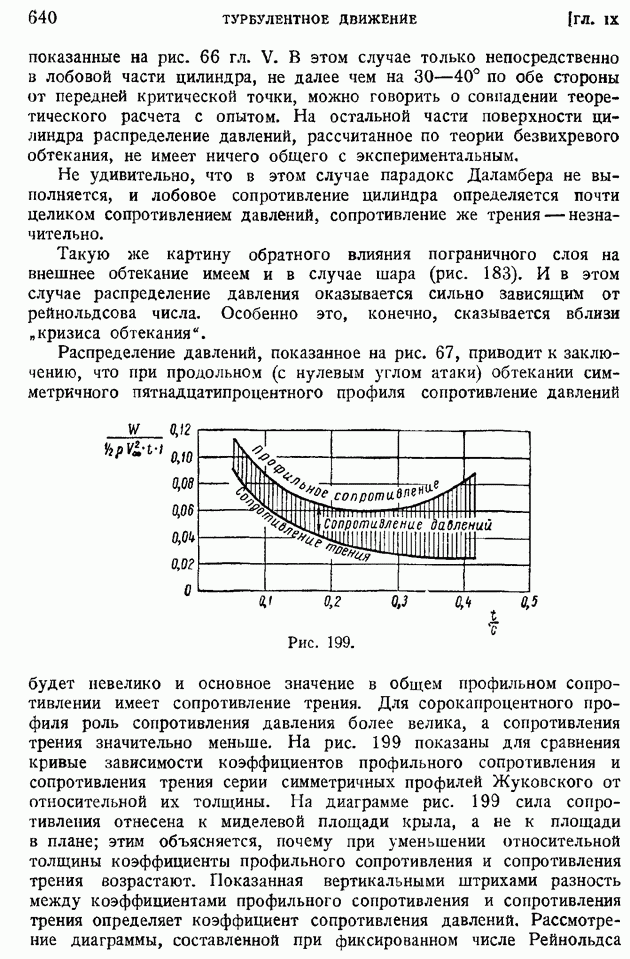
- § 100. Профильное сопротивление крыла. Разложение профильного сопротивления на сопротивление трения и сопротивление давлений. Обратное влияние пограничного слоя на распределение давлений по поверхности обтекаемого профиля
- § 101. Приближенные формулы профильного сопротивления крыла и крылового профиля в решетке
- § 102. Основные закономерности «свободной турбулентности». Плоская турбулентная струя в пространстве, заполненном той же жидкостью
- § 103. Турбулентный след за обтекаемым телом
- § 104. Рассеяние турбулентных возмущений в жидкости. Случай изотропной и однородной турбулентности. Закон сохранения момента возмущений