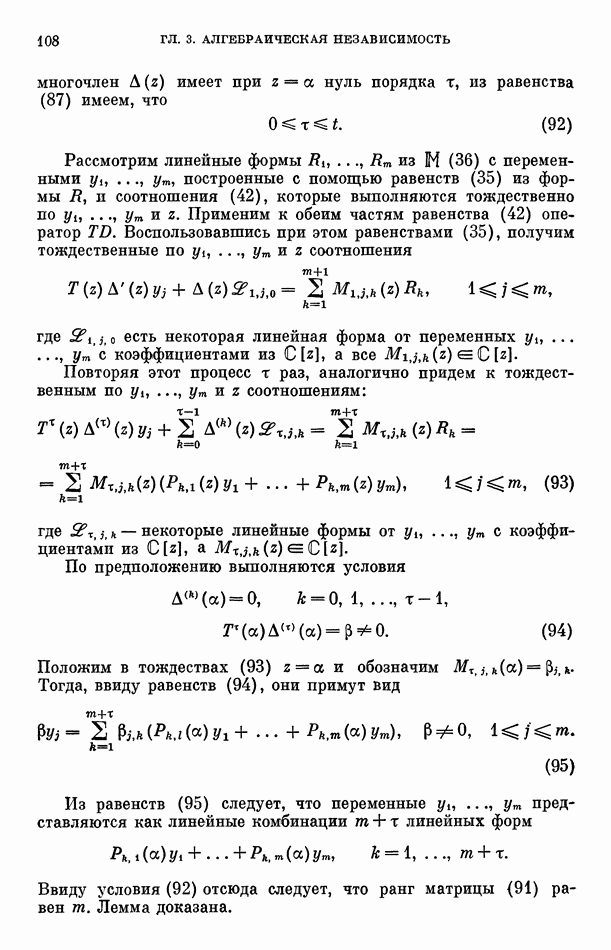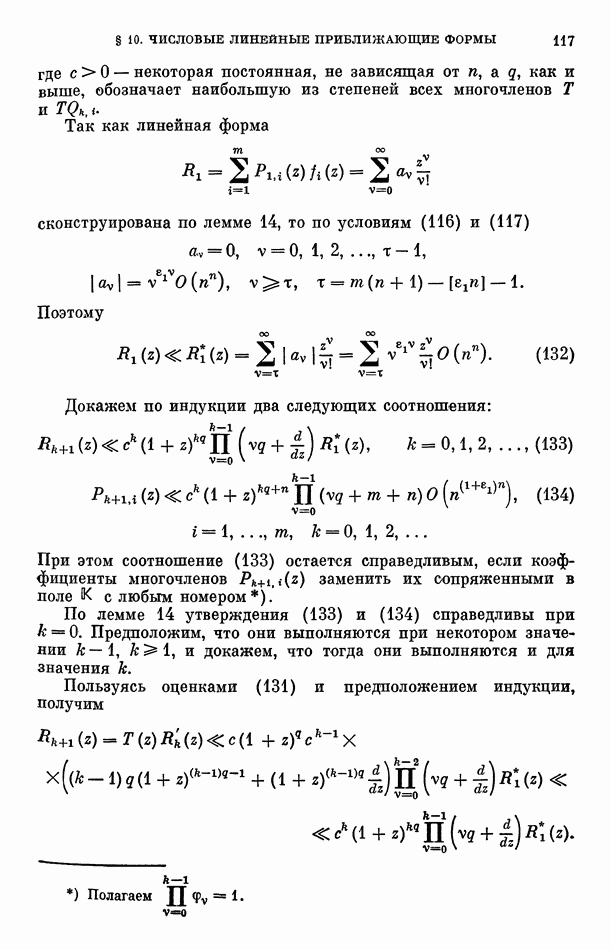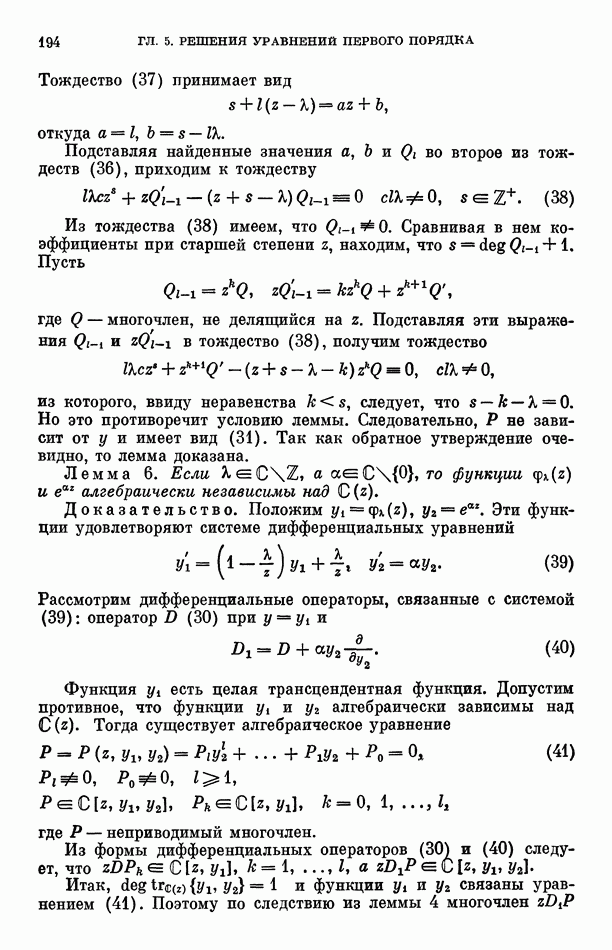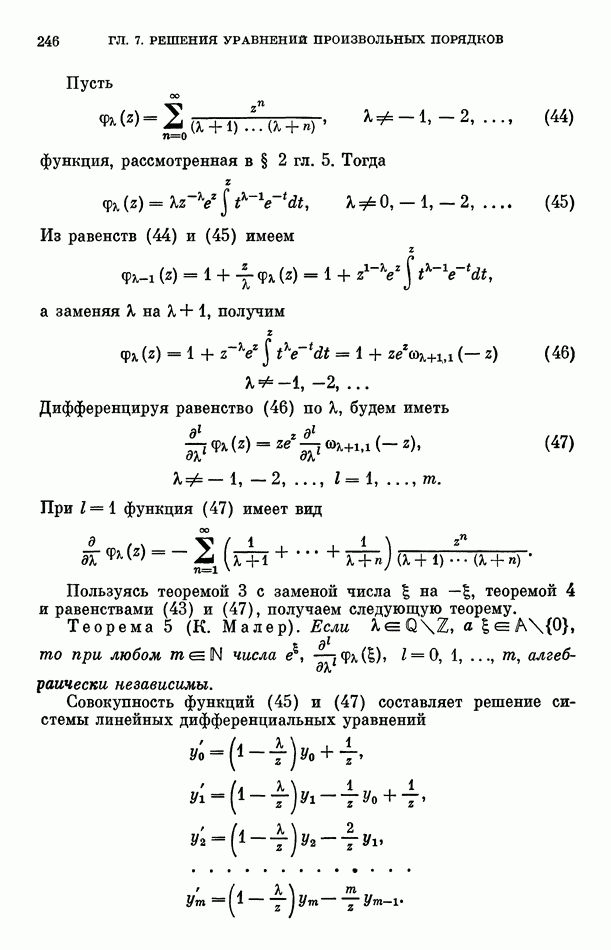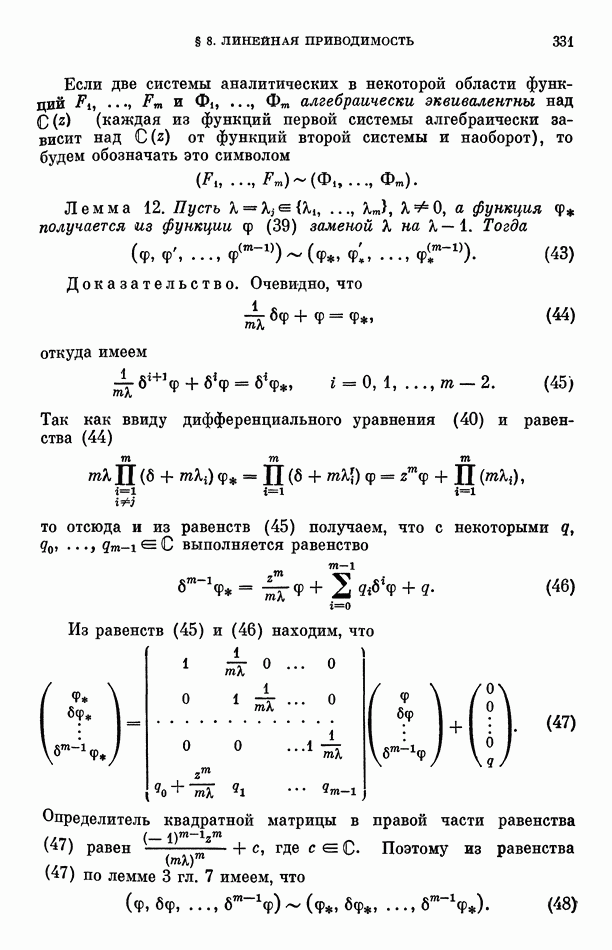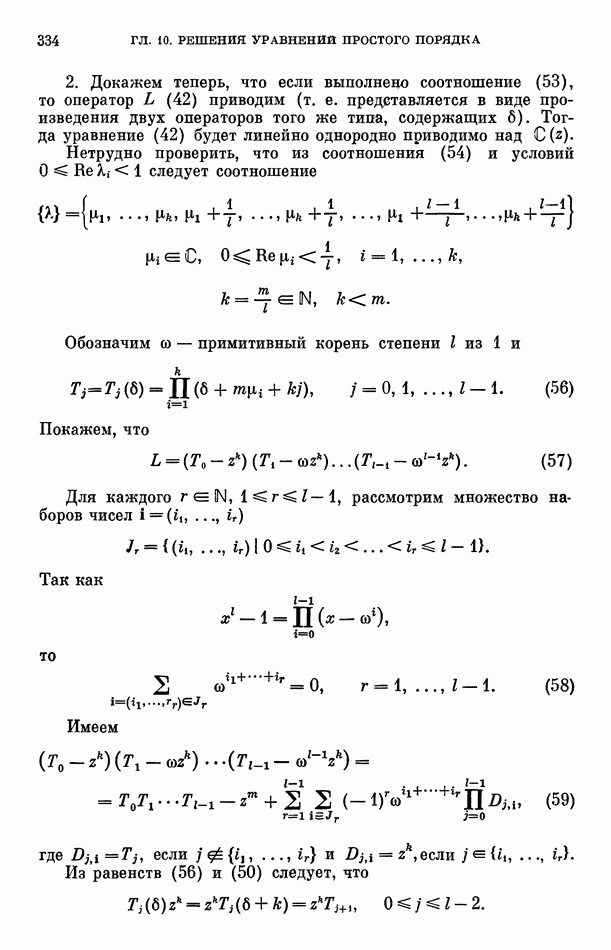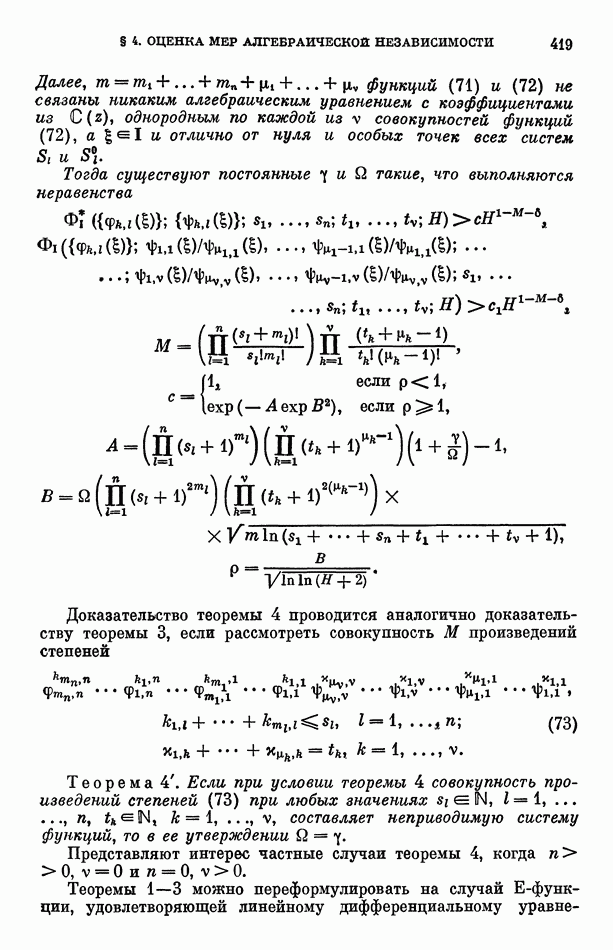| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 3. Оценка мер линейной независимости
В этом параграфе алгебраические поля  и сопряженные поля
и сопряженные поля  будут иметь тот же смысл, что и в гл. 11 и 12.
будут иметь тот же смысл, что и в гл. 11 и 12.
Как и в § 2 гл. 11,  будет обозначать произвольную линейную форму с коэффициентами из
будет обозначать произвольную линейную форму с коэффициентами из  с размером
с размером  линейные формы, получающиеся из формы
линейные формы, получающиеся из формы  после замены ее коэффициентов на сопряженные числа из поля
после замены ее коэффициентов на сопряженные числа из поля 
Обобщим теорему 1, доказанную в гл. 11.
Теорема 1. Пусть совокупность КЕ-функций  составляет решение системы линейных однородных дифференциальных уравнений (1) и линейно независима над
составляет решение системы линейных однородных дифференциальных уравнений (1) и линейно независима над 
Тогда существуют постоянные  такие, что при условии
такие, что при условии  выполняется неравенство
выполняется неравенство

а если  то неравенство
то неравенство

Следствие.  условиях теоремы 1 существуют постоянные
условиях теоремы 1 существуют постоянные  такие, что гари любом Я выполняется неравенство
такие, что гари любом Я выполняется неравенство

Теорема 1. Если при условиях теоремы 1 функции  образуют неприводимую систему функций, то в утверждении теоремы I и ее следствия
образуют неприводимую систему функций, то в утверждении теоремы I и ее следствия

где

Теорема 1 утверждает, что при условии неприводимости рассматриваемой совокупности функций все постоянные, входящие в утверждение теоремы 1 и ее следствия, эффективны.
Теорема 1 доказывается аналогично теореме 1 гл. И, только при этом вместо леммы 16 гл. 3 используется лемма 6.
Рассмотрим произвольную линейную форму  от чисел
от чисел  и сопряженные с ней линейные формы
и сопряженные с ней линейные формы  получающиеся из формы
получающиеся из формы  заменой ее коэффициентов, коэффициентов стеленных рядов функций
заменой ее коэффициентов, коэффициентов стеленных рядов функций  и числа
и числа  на сопряженные числа из полей
на сопряженные числа из полей  сопряженных для поля
сопряженных для поля 
По лемме 6 при  существуют
существуют  линейно независимых линейных форм (48) от чисел
линейно независимых линейных форм (48) от чисел  с коэффициентами из удовлетворяющие условиям (49) и (50). Среди этих форм можно выбрать
с коэффициентами из удовлетворяющие условиям (49) и (50). Среди этих форм можно выбрать  форму так, что вместе с формой
форму так, что вместе с формой  они будут линейно независимы. Пусть для определенности это будут формы
они будут линейно независимы. Пусть для определенности это будут формы  Рассмотрим сопряженные для них формы
Рассмотрим сопряженные для них формы 
Обозначим буквой А определитель линейных форм  определитель, получающийся из А заменой его элементов на сопряженные числа из поля Кол. Далее, обозначим символом алгебраическое дополнение элемента
определитель, получающийся из А заменой его элементов на сопряженные числа из поля Кол. Далее, обозначим символом алгебраическое дополнение элемента  строки и
строки и  столбца в А. Так
столбца в А. Так  и
и  то
то  Значит, при некотором значении
Значит, при некотором значении  выполняется неравенство (11.39). Из: равенств (11.34) и (11.38) при каждом
выполняется неравенство (11.39). Из: равенств (11.34) и (11.38) при каждом  имеем, что выполняется равенство (11.40). Выберем I так, чтобы
имеем, что выполняется равенство (11.40). Выберем I так, чтобы  что возможно, поскольку
что возможно, поскольку  Тогда из равенства (11.40) получаем неравенство (11.41).
Тогда из равенства (11.40) получаем неравенство (11.41).
Пользуясь неравенствами (49) и (50) и замечая, что неравенство (50) справедливо для всех форм  получаем
получаем

Из неравенств (11.39), (11.41), (53) -(55) находим, что

Выберем  наименьшим возможным так, чтобы выполнялось условие
наименьшим возможным так, чтобы выполнялось условие

Из неравенства (57) имеем, что  Логарифмируя это неравенство два раза, получим
Логарифмируя это неравенство два раза, получим

В § 1 указано, что  Поэтому существует постоянная;
Поэтому существует постоянная;  такая, что при
такая, что при

будут справедливы неравенства

Тогда из неравенств (58) следует, что условия, наложенные в лемме 6 на число  выполнены, а из неравенств (56) и (57) имеем
выполнены, а из неравенств (56) и (57) имеем

Ввиду выбора числа  выполняется неравенство
выполняется неравенство

откуда

Логарифмируя, получим

а тогда, используя неравенство (58), имеем

откуда, ввиду неравенств (57), (60) и (61), находим, что

и

Из неравенств (59), (61) и (62) получаем

а так как  и выполняются неравенства (58) и (63), то
и выполняются неравенства (58) и (63), то

Положим

Тогда при  из неравенства (65) следует неравенство (51).
из неравенства (65) следует неравенство (51).
При  неравенство (52) следует из неравенства (51), тгак как модули комплексно сопряженных чисел равны. Следствие и теорема 1 следуют из теоремы 1 и равенств (24) и (65) ввиду того, что при
неравенство (52) следует из неравенства (51), тгак как модули комплексно сопряженных чисел равны. Следствие и теорема 1 следуют из теоремы 1 и равенств (24) и (65) ввиду того, что при  имеет место неравенство
имеет место неравенство

Из теоремы 1 следует полезная для приложений к конкретным функциям формулируемая ниже теорема.
Теорема 2. Пусть совокупность КЕ-функций  составляет решение системы линейных дифференциальных уравнений (8) и линейно независима с числом 1 над
составляет решение системы линейных дифференциальных уравнений (8) и линейно независима с числом 1 над 
Тогда существуют постоянные у и  такие, что тгри условии
такие, что тгри условии  выполняется неравенство
выполняется неравенство

а если  то неравенство
то неравенство

Имеют место следствие из теоремы 2 и теорема 2, аналогичные следствию из теоремы 1 и теорем 1.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Приближение алгебраических чисел
- § 2. Классический метод Эрмита — Линдемана
- § 3. Методы, возникшие при решении седьмой проблемы Гильберта, и их дальнейшее развитие
- § 4. Метод Зигеля и его дальнейшее развитие
- Глава 1. ПРИБЛИЖЕНИЕ ДЕЙСТВИТЕЛЬНЫХ И АЛГЕБРАИЧЕСКИХ ЧИСЕЛ
- § 1. Приближение действительных чисел рациональными числами
- § 2. Совместные приближения
- § 3. Приближение алгебраических чисел рациональными числами
- § 4. Приближение алгебраических чисел алгебраическими числами
- § 5. Дальнейшие усиления и обобщения теоремы Лиувилля
- Замечания
- Глава 2. АРИФМЕТИЧЕСКИЕ СВОЙСТВА ЗНАЧЕНИЙ ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ В АЛГЕБРАИЧЕСКИХ ТОЧКАХ
- § 1. Трансцендентность числа e
- § 2. Трансцендентность числа «пи»
- § 3. Трансцендентность значений показательной функции в алгебраических точках
- § 4. Приближение функции e^z рациональными функциями
- § 5. Линейная приближающая форма для функции …
- § 6. Совокупность линейных приближающих форм
- § 7. Теорема Линдемана
- § 8. Линейные приближающие формы и разложение показательной функции в интерполяционный ряд Ньютона
- Замечания
- Глава 3. ТРАНСЦЕНДЕНТНОСТЬ И АЛГЕБРАИЧЕСКАЯ НЕЗАВИСИМОСТЬ ЗНАЧЕНИЙ Е-ФУНКЦИЙ, НЕ СВЯЗАННЫХ АЛГЕБРАИЧЕСКИМИ УРАВНЕНИЯМИ НАД ПОЛЕМ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
- § 1. Е-функции
- § 2. Первая основная теорема
- § 3. Некоторые свойства линейных и дробно-линейных форм
- § 4. Свойства линейных форм от функций, удовлетворяющих системе линейных однородных дифференциальных уравнений
- § 5. Порядок нуля линейной формы при z = 0
- § 6. Определитель системы линейных форм
- § 7. Переход к числовым линейно независимым линейным формам
- § 8. Вспомогательные предложения о решениях систем линейных однородных уравнений
- § 9. Функциональные линейные приближающие формы
- § 10. Числовые линейные приближающие формы
- § 11. Ранг совокупности чисел
- § 12. Доказательство первой основной теоремы
- § 13. Следствия из первой основной теоремы
- Замечания
- Глава 4. ТРАНСЦЕНДЕНТНОСТЬ И АЛГЕБРАИЧЕСКАЯ НЕЗАВИСИМОСТЬ ЗНАЧЕНИЙ Е-ФУНКЦИЙ, СВЯЗАННЫХ АЛГЕБРАИЧЕСКИМИ УРАВНЕНИЯМИ НАД ПОЛЕМ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
- § 2. Вспомогательные предложения
- § 3. Оценки размерностей векторных пространств, порожденных произведениями степеней элементов из расширения некоторого поля
- § 4. Третья основная теорема
- § 5. Трансцендентность значений Е-функций, связанных произвольными алгебраическими уравнениями над C(z)
- § 6. Алгебраическая независимость значений Е-функций, связанных произвольными алгебраическими уравнениями над C(z)
- § 7. Е-функции, связанные уравнениями специального вида
- § 8. Е-функции, связанные алгебраическими уравнениями с постоянными коэффициентами
- § 9. Е-функции, связанные одним алгебраическим уравнением вид C(z)
- § 10. Минимальные уравнения
- § 11. Размерности векторных пространств, порожденных произведениями степеней элементов из расширения некоторого поля
- § 12. Алгебраическая независимость значений IE-функций
- § 13. Алгебраическая независимость значений КЕ-функций
- Замечания
- Глава 5. ТРАНСЦЕНДЕНТНОСТЬ И АЛГЕБРАИЧЕСКАЯ НЕЗАВИСИМОСТЬ ЗНАЧЕНИЙ Е-ФУНКЦИЙ, УДОВЛЕТВОРЯЮЩИХ ЛИНЕЙНЫМ ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ ПЕРВОГО ПОРЯДКА
- § 1. Гипергеометрические Е-функции
- § 2. Простейшая гипергеометрическая Е-функция
- § 3. Совокупность решений линейных дифференциальных уравнений первого порядка
- § 4. Вспомогательные предложения
- § 5. Доказательства теорем
- Замечания
- Глава 6. АЛГЕБРАИЧЕСКАЯ НЕЗАВИСИМОСТЬ ЗНАЧЕНИИ Е-ФУНКЦИЙ, УДОВЛЕТВОРЯЮЩИХ ЛИНЕЙНЫМ ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ ВТОРОГО ПОРЯДКА
- § 1. Общая теорема об алгебраической независимости значений Е-функции и ее производной
- § 2. Функции K(z), связанные с функциями Бесселя
- § 3. Функции …
- § 4. Функции Куммера
- § 5. Решения линейных неоднородных дифференциальных уравнений
- Глава 7. РЕШЕНИЯ НЕКОТОРЫХ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПРОИЗВОЛЬНОГО ПОРЯДКА
- § 1. Решения неоднородных дифференциальных уравнений
- § 2. Решения однородных дифференциальных уравнений
- § 3. Следствия из теорем 1 и 2
- Глава 8. ИССЛЕДОВАНИЕ РЕШЕНИЙ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПРОИЗВОЛЬНОГО ПОРЯДКА АРИФМЕТИЧЕСКИМ МЕТОДОМ
- § 2. Вспомогательные предложения
- § 3. Доказательства теорем 1—5
- § 4. Доказательства теорем 6 и 7
- § 5. Дальнейшие результаты
- Глава 9. ТЕОРЕМА ЗИГЕЛЯ
- § 2. Вспомогательные предложения
- § 3. Некоторые свойства решений линейных однородных дифференциальных уравнений второго порядка
- § 4. Алгебраическая независимость решений совокупности линейных однородных дифференциальных уравнений второго порядка
- § 5. Доказательство теоремы Зигеля
- § 6. Решения линейных неоднородных дифференциальных уравнении
- § 7. Обобщение теоремы Зигеля
- Глава 10. РЕШЕНИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПРОСТОГО ПОРЯДКА p
- § 2. Однородный идеал J
- § 3. Алгебраические функции нескольких переменных
- § 4. Дифференциальный оператор G
- § 5. Дифференциальные операторы S и «дельта»
- § 6. Лемма о линейном приближении
- § 7. Завершение доказательства теоремы 7
- § 8. Линейная приводимость
- § 9. Доказательства теорем 6 и 5
- Замечания
- Глава 11. МЕРА АЛГЕБРАИЧЕСКОЙ НЕЗАВИСИМОСТИ ЗНАЧЕНИЙ IE-ФУНКЦИЙ
- § 2. Мера линейной независимости значений IE-функций
- § 3. Мера алгебраической независимости значений IE-функций, не связанных алгебраическими уравнениями над C(z)
- § 4. Вспомогательные предложения
- § 5. Мера алгебраической независимости значений IE-функций, связанных алгебраическими уравнениями над C(z)
- § 6. Некоторые применения общих теорем
- Глава 12. МЕРА АЛГЕБРАИЧЕСКОЙ НЕЗАВИСИМОСТИ ЗНАЧЕНИЙ КЕ-ФУНКЦИЙ
- § 2. Оценки мер значений Е-функций, не связанных алгебраическими уравнениями над C(z)
- § 3. Оценки мер значений Е-функций, связанных одним алгебраическим уравнением над C(z)
- § 4. Оценки мер значений Е-функций, связанных произвольными алгебраическими уравнениями над C(z)
- § 5. Алгебраическая независимость значений Е-функций в сопряженных полях
- § 6. Вспомогательная теорема
- § 7. Следствия из вспомогательной теоремы
- § 8. Некоторые применения общих теорем
- Глава 13. ЭФФЕКТИВНЫЕ ОЦЕНКИ МЕР
- § 2. Уточнение основных лемм метода
- § 3. Оценка мер линейной независимости
- § 4. Оценка мер алгебраической независимости
- § 5. Некоторые применения общих теорем
- ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
- СПИСОК ЛИТЕРАТУРЫ