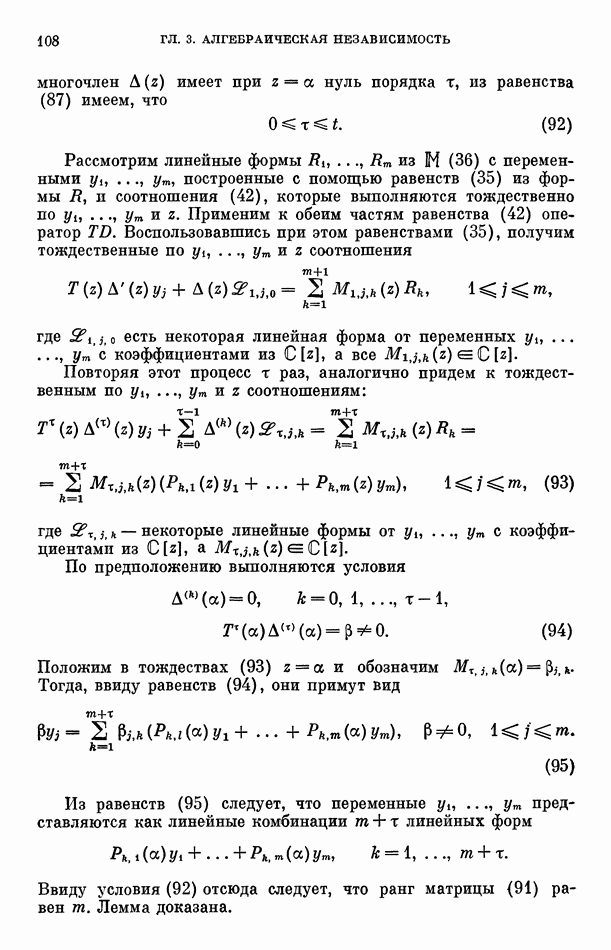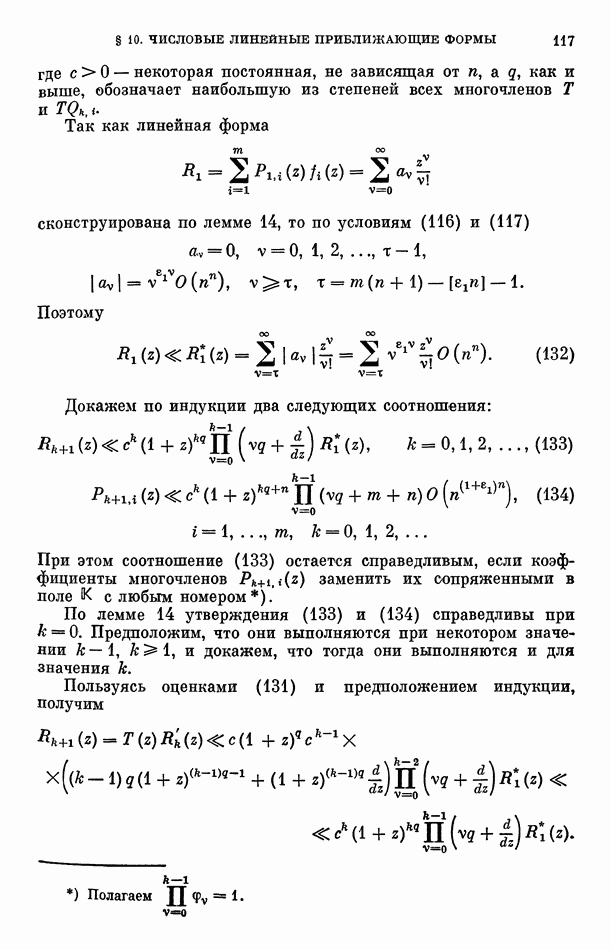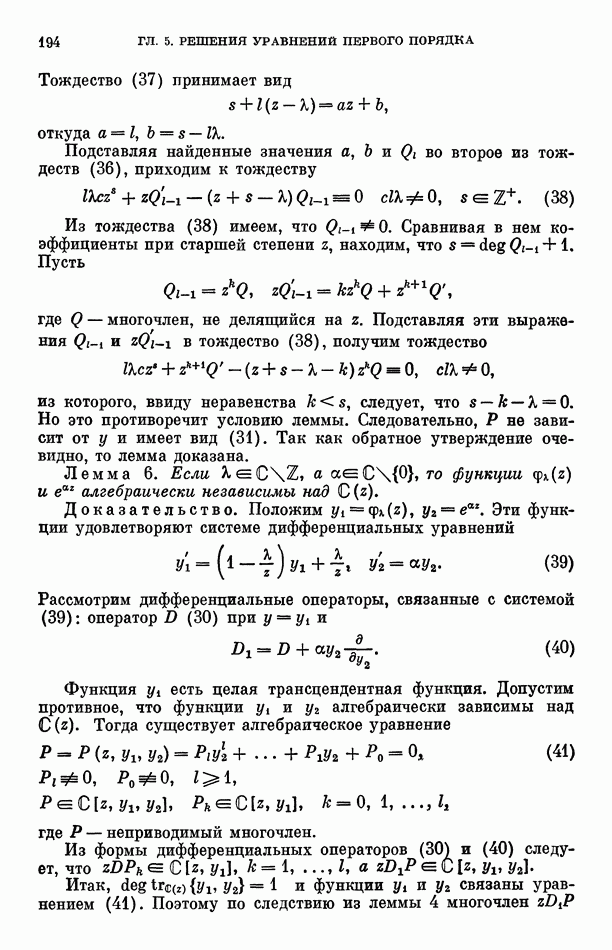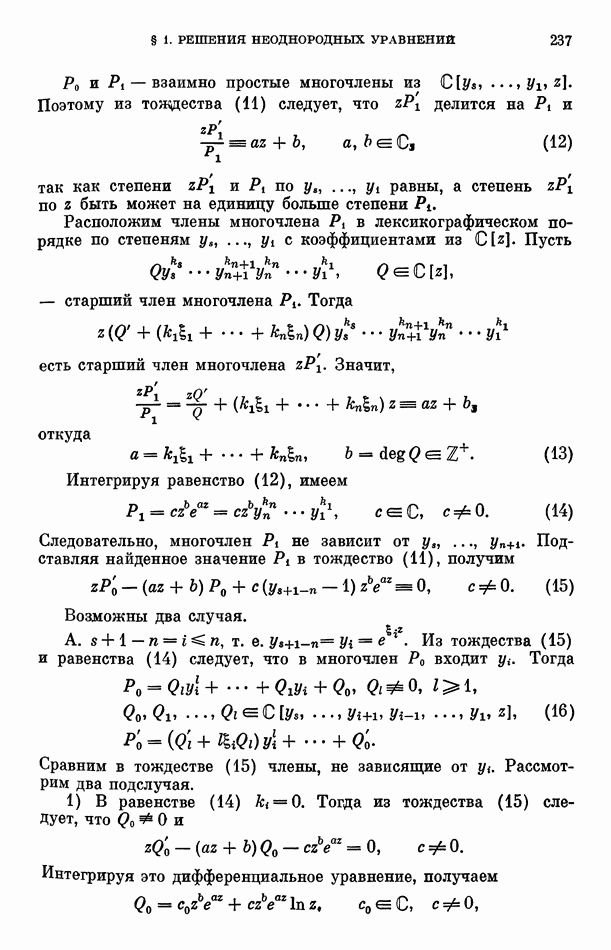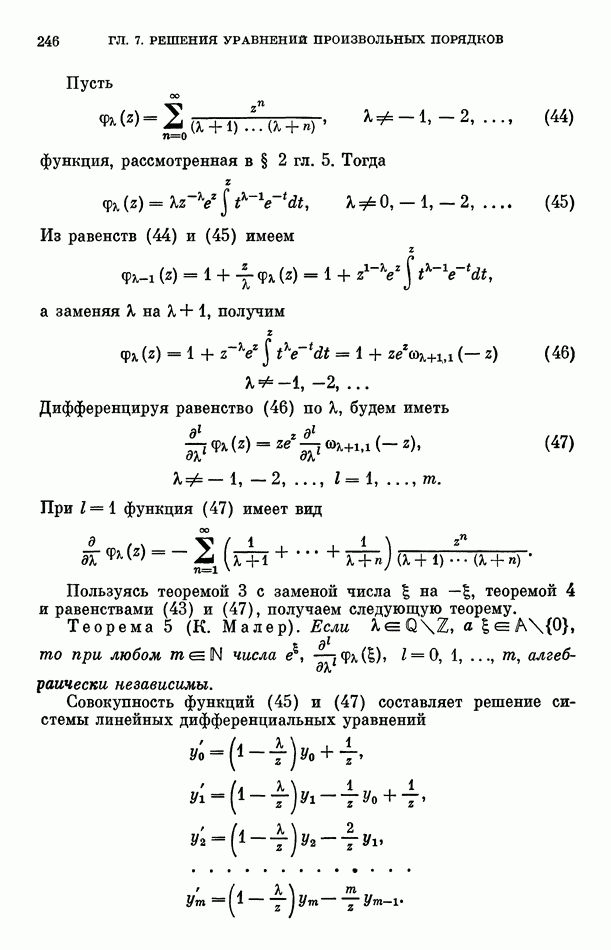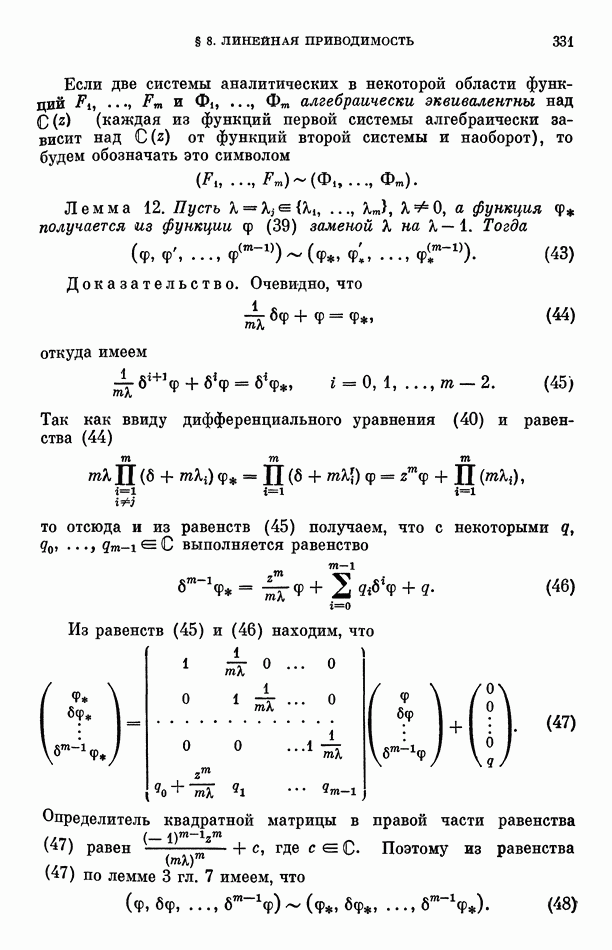| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 7. Теорема Линдемана
Теперь, пользуясь методом, изложенным в § 5 и 6, докажем теорему Линдемана. Предварительно установим одно вспомогательное предложение.
Пусть  Обозначим число различных систем
Обозначим число различных систем  из
из  неотрицательных целых чисел
неотрицательных целых чисел  удовлетворяющих условию
удовлетворяющих условию  число таких же систем, но удовлетворяющих условию
число таких же систем, но удовлетворяющих условию 
Лемма 7. При любых  выполняются равенства
выполняются равенства

Доказательство. Число решений уравнения  в целых неотрицательных числах
в целых неотрицательных числах  равно коэффициенту при
равно коэффициенту при  в ряде
в ряде

Но

откуда следует равенство (130).
Далее, заметим, что

Действительно, полагая в равенстве  последовательно
последовательно  и подсчитывая при этом каждый раз число различных систем
и подсчитывая при этом каждый раз число различных систем  получим, что
получим, что

Из равенств (130) и (132) следует равенство (131). Теорема Линдемана. Если  алгебраические числа линейно независимые над полем
алгебраические числа линейно независимые над полем  то числа
то числа  алгебраически независимы.
алгебраически независимы.
Доказательство. Допустим противное, что  алгебраически зависимы. Тогда существует многочлен
алгебраически зависимы. Тогда существует многочлен

такой, что

Пусть К обозначает алгебраическое поле, содержащее числя  и все коэффициенты многочлена
и все коэффициенты многочлена 
Положим  где
где  и рассмотрим совокупность
и рассмотрим совокупность  произведений степеней
произведений степеней

Перенумеруем ее произвольно и обозначим  Рассмотрим также совокупность
Рассмотрим также совокупность  произведений степеней
произведений степеней

Перенумеруем ее произвольно и обозначим  Тогда
Тогда

где  либо нули, либо коэффициенты многочлена
либо нули, либо коэффициенты многочлена 
Правые части равенств (137) как линейные формы от  с постоянными коэффициентами линейно независимы, поскольку
с постоянными коэффициентами линейно независимы, поскольку  являются многочленами от
являются многочленами от  не связанными никаким линейным однородным уравнением с постоянными коэффициентами.
не связанными никаким линейным однородным уравнением с постоянными коэффициентами.
Обозначим

где  набор показателей, соответствующий произведению
набор показателей, соответствующий произведению  Тогда
Тогда  являются различными числами поля К, поскольку числа
являются различными числами поля К, поскольку числа  линейно независимы над
линейно независимы над  а наборы
а наборы  соответствующие различным значениям
соответствующие различным значениям  различны.
различны.
Полагая  ввиду равенств (137) и (138) и уравнения (134), получим, что
ввиду равенств (137) и (138) и уравнения (134), получим, что

Теперь рассмотрим  приближающих линейных форм
приближающих линейных форм  от функций
от функций  введенных в § 6,
введенных в § 6,

Определитель  этой системы линейных форм в точке
этой системы линейных форм в точке  отличен от нуля. Поэтому числовые линейные формы от чисел
отличен от нуля. Поэтому числовые линейные формы от чисел  с коэффициентами из
с коэффициентами из  получающиеся из форм (140) при
получающиеся из форм (140) при  линейно независимы и из них можно выбрать
линейно независимы и из них можно выбрать  форм для
форм для  так, что последние будут линейно независимы вместе с формами (139).
так, что последние будут линейно независимы вместе с формами (139).
Обозначим

Тогда

где ввиду равенств 
Пусть  — определитель системы линейных форм (141),
— определитель системы линейных форм (141),  алгебраические дополнения элементов
алгебраические дополнения элементов
первого столбца в  Из равенств (141) имеем, что
Из равенств (141) имеем, что

Теперь воспользуемся свойствами линейных форм (128). Так как  равно
равно  или
или  то по условию (117) существует число
то по условию (117) существует число  такое, что числа
такое, что числа 
Следовательно,  откуда
откуда 

Кроме того, из неравенств (116) следует, что

а тогда

С другой стороны, по неравенству (114)

а пользуясь неравенствами (144), (146) и равенством (142), находим, что

Из оценок (145) и (147) имеем, что

Пусть  Сравнивая оценки (143) и (148), получим, что
Сравнивая оценки (143) и (148), получим, что  или
или

Но по лемме 7

а тогда неравенства (149) и (150) при достаточно большом  противоречивы. Полученное противоречие доказывает, что утверждение теоремы Линдемана справедливо.
противоречивы. Полученное противоречие доказывает, что утверждение теоремы Линдемана справедливо.
Заметим, что если числа  линейно зависимы над
линейно зависимы над  то числа
то числа  алгебраически зависимы.
алгебраически зависимы.
Действительно, пусть

Обозначим

Тогда

откуда следует рассматриваемое утверждение.
Теорему Линдемана можно переформулировать в следующей эквивалентной форме.
Теорема Линдемана. Если  различные алгебраические числа,
различные алгебраические числа,  алгебраические числа не все равные нулю, то
алгебраические числа не все равные нулю, то

Докажем эквивалентность двух приведенных формулировок теоремы Линдемана.
1. Если выполнена теорема в первой формулировке, то она верна и во второй формулировке.
Действительно, пусть среди чисел  ровно I линейно независимых над
ровно I линейно независимых над  Выберем среди них любые I линейно независимых чисел и обозначим их
Выберем среди них любые I линейно независимых чисел и обозначим их  Тогда
Тогда

Если  есть наименьший общий знаменатель всех чисел
есть наименьший общий знаменатель всех чисел  то положим
то положим

Рассмотрим рациональную функцию

с произвольными алгебраическими коэффициентами, не всеми равными нулю.  так как наборы показателей
так как наборы показателей  различны. Положим в равенстве
различны. Положим в равенстве 
Пользуясь утверждением теоремы в первой формулировке и равенством (152), получим, что

при любых  не всех равных нулю.
не всех равных нулю.
2. Если выполнена теорема во второй формулировке, то она справедлива и в первой формулировке.
В самом деле, в противном случае существует многочлен

такой, что

где суммирование распространяется на конечное число различных систем  Но равенство (154) противоречит теореме Линдемана во второй формулировке, поскольку в нем показатели
Но равенство (154) противоречит теореме Линдемана во второй формулировке, поскольку в нем показатели  различны, ввиду линейной независимости чисел
различны, ввиду линейной независимости чисел  над
над 
Это завершает доказательство эквивалентности двух формулировок теоремы Линдемана.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Приближение алгебраических чисел
- § 2. Классический метод Эрмита — Линдемана
- § 3. Методы, возникшие при решении седьмой проблемы Гильберта, и их дальнейшее развитие
- § 4. Метод Зигеля и его дальнейшее развитие
- Глава 1. ПРИБЛИЖЕНИЕ ДЕЙСТВИТЕЛЬНЫХ И АЛГЕБРАИЧЕСКИХ ЧИСЕЛ
- § 1. Приближение действительных чисел рациональными числами
- § 2. Совместные приближения
- § 3. Приближение алгебраических чисел рациональными числами
- § 4. Приближение алгебраических чисел алгебраическими числами
- § 5. Дальнейшие усиления и обобщения теоремы Лиувилля
- Замечания
- Глава 2. АРИФМЕТИЧЕСКИЕ СВОЙСТВА ЗНАЧЕНИЙ ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ В АЛГЕБРАИЧЕСКИХ ТОЧКАХ
- § 1. Трансцендентность числа e
- § 2. Трансцендентность числа «пи»
- § 3. Трансцендентность значений показательной функции в алгебраических точках
- § 4. Приближение функции e^z рациональными функциями
- § 5. Линейная приближающая форма для функции …
- § 6. Совокупность линейных приближающих форм
- § 7. Теорема Линдемана
- § 8. Линейные приближающие формы и разложение показательной функции в интерполяционный ряд Ньютона
- Замечания
- Глава 3. ТРАНСЦЕНДЕНТНОСТЬ И АЛГЕБРАИЧЕСКАЯ НЕЗАВИСИМОСТЬ ЗНАЧЕНИЙ Е-ФУНКЦИЙ, НЕ СВЯЗАННЫХ АЛГЕБРАИЧЕСКИМИ УРАВНЕНИЯМИ НАД ПОЛЕМ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
- § 1. Е-функции
- § 2. Первая основная теорема
- § 3. Некоторые свойства линейных и дробно-линейных форм
- § 4. Свойства линейных форм от функций, удовлетворяющих системе линейных однородных дифференциальных уравнений
- § 5. Порядок нуля линейной формы при z = 0
- § 6. Определитель системы линейных форм
- § 7. Переход к числовым линейно независимым линейным формам
- § 8. Вспомогательные предложения о решениях систем линейных однородных уравнений
- § 9. Функциональные линейные приближающие формы
- § 10. Числовые линейные приближающие формы
- § 11. Ранг совокупности чисел
- § 12. Доказательство первой основной теоремы
- § 13. Следствия из первой основной теоремы
- Замечания
- Глава 4. ТРАНСЦЕНДЕНТНОСТЬ И АЛГЕБРАИЧЕСКАЯ НЕЗАВИСИМОСТЬ ЗНАЧЕНИЙ Е-ФУНКЦИЙ, СВЯЗАННЫХ АЛГЕБРАИЧЕСКИМИ УРАВНЕНИЯМИ НАД ПОЛЕМ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
- § 2. Вспомогательные предложения
- § 3. Оценки размерностей векторных пространств, порожденных произведениями степеней элементов из расширения некоторого поля
- § 4. Третья основная теорема
- § 5. Трансцендентность значений Е-функций, связанных произвольными алгебраическими уравнениями над C(z)
- § 6. Алгебраическая независимость значений Е-функций, связанных произвольными алгебраическими уравнениями над C(z)
- § 7. Е-функции, связанные уравнениями специального вида
- § 8. Е-функции, связанные алгебраическими уравнениями с постоянными коэффициентами
- § 9. Е-функции, связанные одним алгебраическим уравнением вид C(z)
- § 10. Минимальные уравнения
- § 11. Размерности векторных пространств, порожденных произведениями степеней элементов из расширения некоторого поля
- § 12. Алгебраическая независимость значений IE-функций
- § 13. Алгебраическая независимость значений КЕ-функций
- Замечания
- Глава 5. ТРАНСЦЕНДЕНТНОСТЬ И АЛГЕБРАИЧЕСКАЯ НЕЗАВИСИМОСТЬ ЗНАЧЕНИЙ Е-ФУНКЦИЙ, УДОВЛЕТВОРЯЮЩИХ ЛИНЕЙНЫМ ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ ПЕРВОГО ПОРЯДКА
- § 1. Гипергеометрические Е-функции
- § 2. Простейшая гипергеометрическая Е-функция
- § 3. Совокупность решений линейных дифференциальных уравнений первого порядка
- § 4. Вспомогательные предложения
- § 5. Доказательства теорем
- Замечания
- Глава 6. АЛГЕБРАИЧЕСКАЯ НЕЗАВИСИМОСТЬ ЗНАЧЕНИИ Е-ФУНКЦИЙ, УДОВЛЕТВОРЯЮЩИХ ЛИНЕЙНЫМ ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ ВТОРОГО ПОРЯДКА
- § 1. Общая теорема об алгебраической независимости значений Е-функции и ее производной
- § 2. Функции K(z), связанные с функциями Бесселя
- § 3. Функции …
- § 4. Функции Куммера
- § 5. Решения линейных неоднородных дифференциальных уравнений
- Глава 7. РЕШЕНИЯ НЕКОТОРЫХ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПРОИЗВОЛЬНОГО ПОРЯДКА
- § 1. Решения неоднородных дифференциальных уравнений
- § 2. Решения однородных дифференциальных уравнений
- § 3. Следствия из теорем 1 и 2
- Глава 8. ИССЛЕДОВАНИЕ РЕШЕНИЙ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПРОИЗВОЛЬНОГО ПОРЯДКА АРИФМЕТИЧЕСКИМ МЕТОДОМ
- § 2. Вспомогательные предложения
- § 3. Доказательства теорем 1—5
- § 4. Доказательства теорем 6 и 7
- § 5. Дальнейшие результаты
- Глава 9. ТЕОРЕМА ЗИГЕЛЯ
- § 2. Вспомогательные предложения
- § 3. Некоторые свойства решений линейных однородных дифференциальных уравнений второго порядка
- § 4. Алгебраическая независимость решений совокупности линейных однородных дифференциальных уравнений второго порядка
- § 5. Доказательство теоремы Зигеля
- § 6. Решения линейных неоднородных дифференциальных уравнении
- § 7. Обобщение теоремы Зигеля
- Глава 10. РЕШЕНИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПРОСТОГО ПОРЯДКА p
- § 2. Однородный идеал J
- § 3. Алгебраические функции нескольких переменных
- § 4. Дифференциальный оператор G
- § 5. Дифференциальные операторы S и «дельта»
- § 6. Лемма о линейном приближении
- § 7. Завершение доказательства теоремы 7
- § 8. Линейная приводимость
- § 9. Доказательства теорем 6 и 5
- Замечания
- Глава 11. МЕРА АЛГЕБРАИЧЕСКОЙ НЕЗАВИСИМОСТИ ЗНАЧЕНИЙ IE-ФУНКЦИЙ
- § 2. Мера линейной независимости значений IE-функций
- § 3. Мера алгебраической независимости значений IE-функций, не связанных алгебраическими уравнениями над C(z)
- § 4. Вспомогательные предложения
- § 5. Мера алгебраической независимости значений IE-функций, связанных алгебраическими уравнениями над C(z)
- § 6. Некоторые применения общих теорем
- Глава 12. МЕРА АЛГЕБРАИЧЕСКОЙ НЕЗАВИСИМОСТИ ЗНАЧЕНИЙ КЕ-ФУНКЦИЙ
- § 2. Оценки мер значений Е-функций, не связанных алгебраическими уравнениями над C(z)
- § 3. Оценки мер значений Е-функций, связанных одним алгебраическим уравнением над C(z)
- § 4. Оценки мер значений Е-функций, связанных произвольными алгебраическими уравнениями над C(z)
- § 5. Алгебраическая независимость значений Е-функций в сопряженных полях
- § 6. Вспомогательная теорема
- § 7. Следствия из вспомогательной теоремы
- § 8. Некоторые применения общих теорем
- Глава 13. ЭФФЕКТИВНЫЕ ОЦЕНКИ МЕР
- § 2. Уточнение основных лемм метода
- § 3. Оценка мер линейной независимости
- § 4. Оценка мер алгебраической независимости
- § 5. Некоторые применения общих теорем
- ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
- СПИСОК ЛИТЕРАТУРЫ