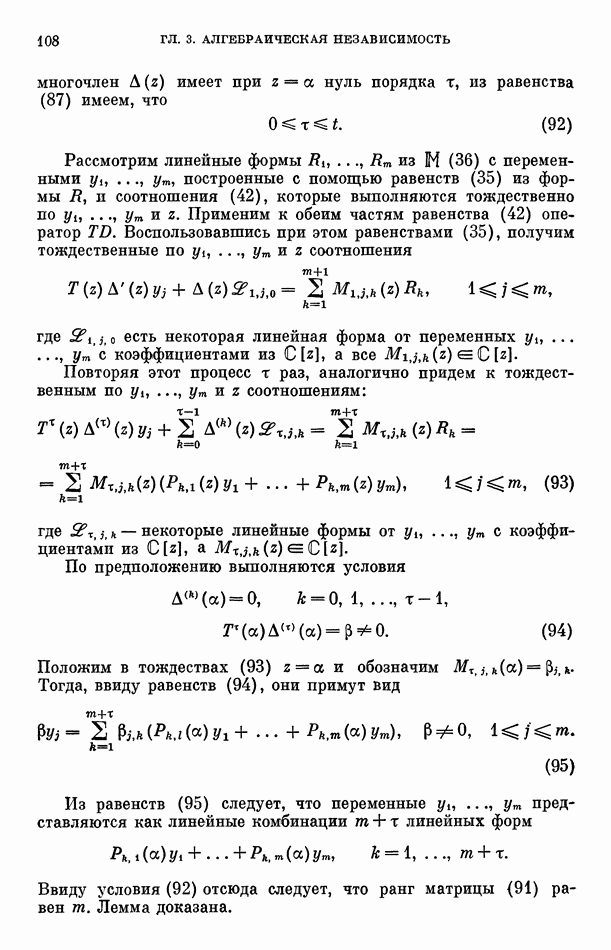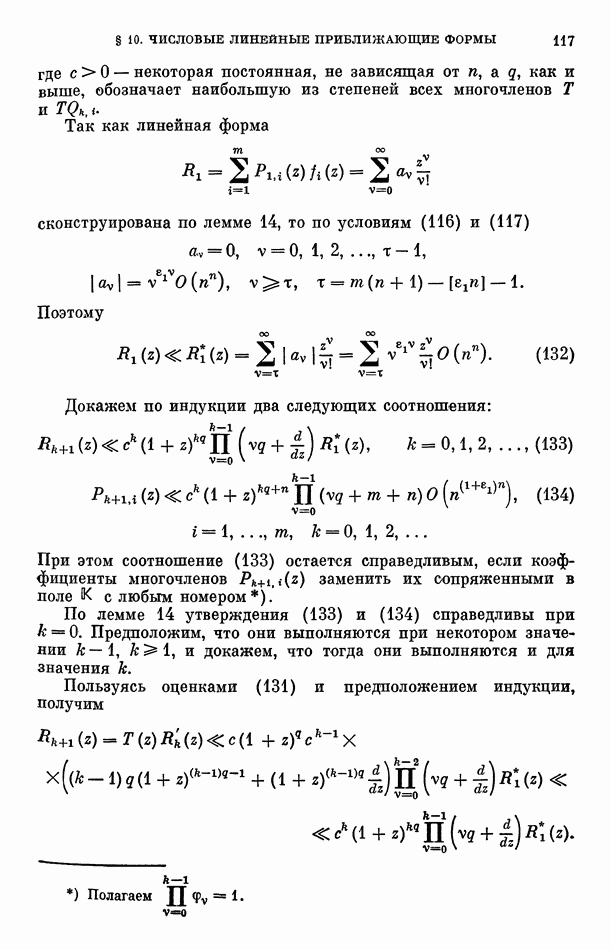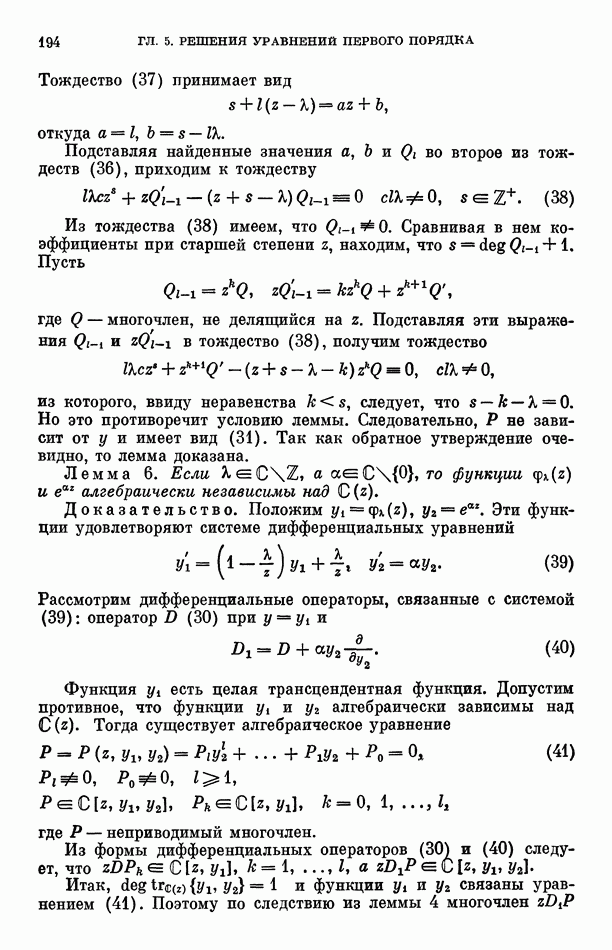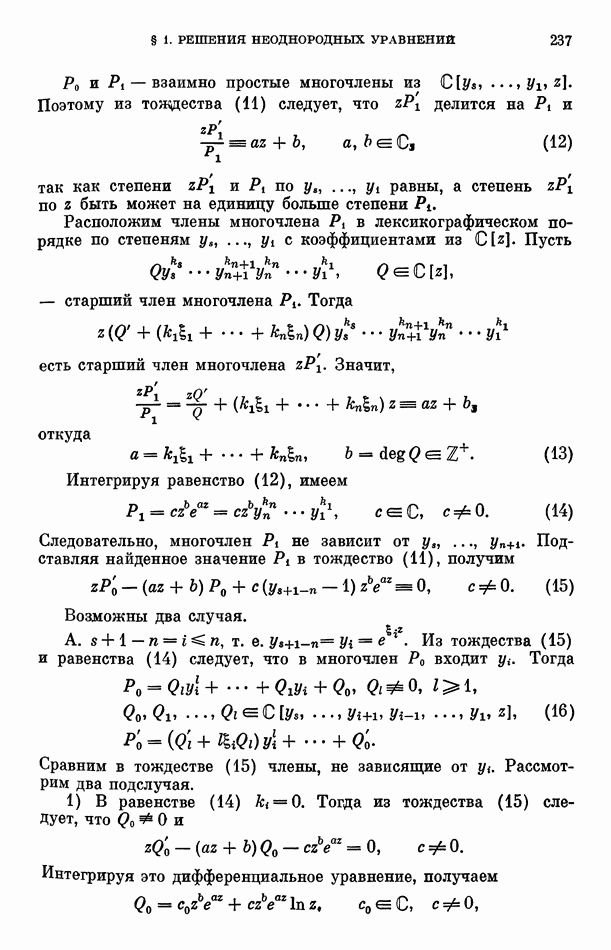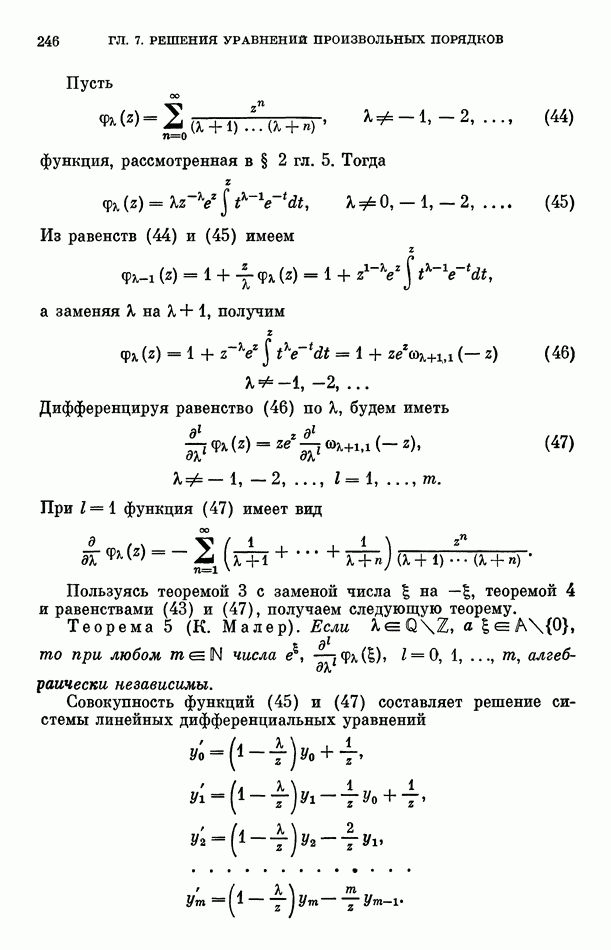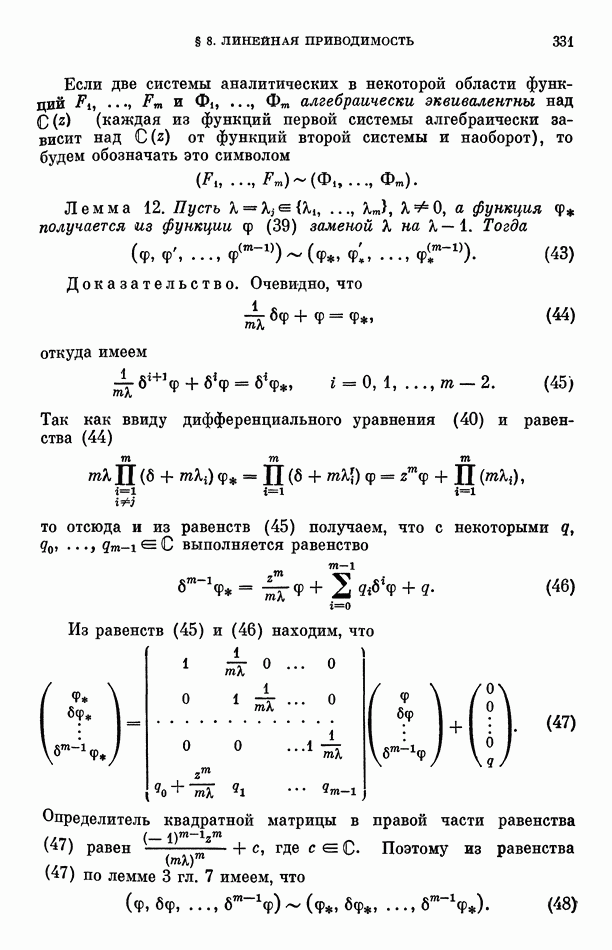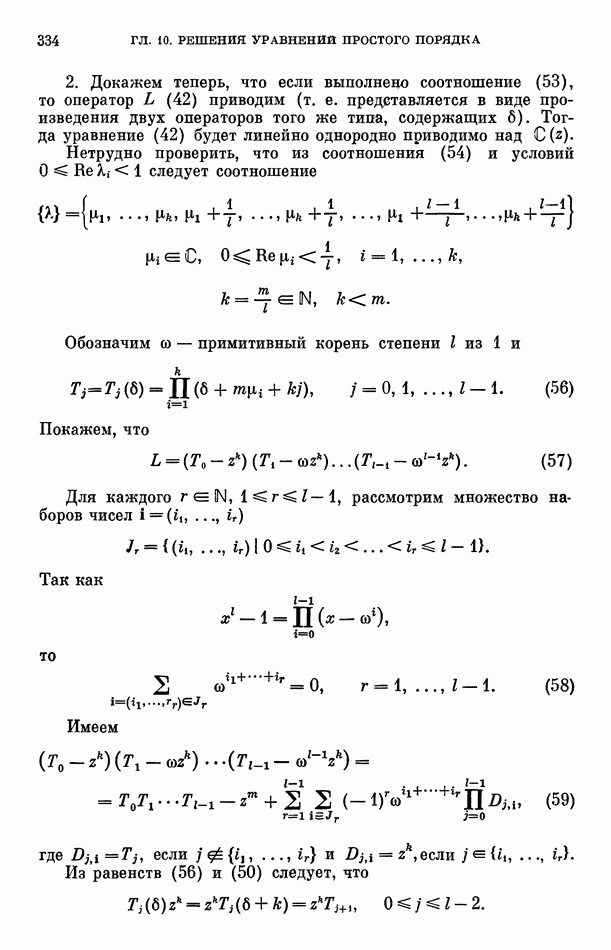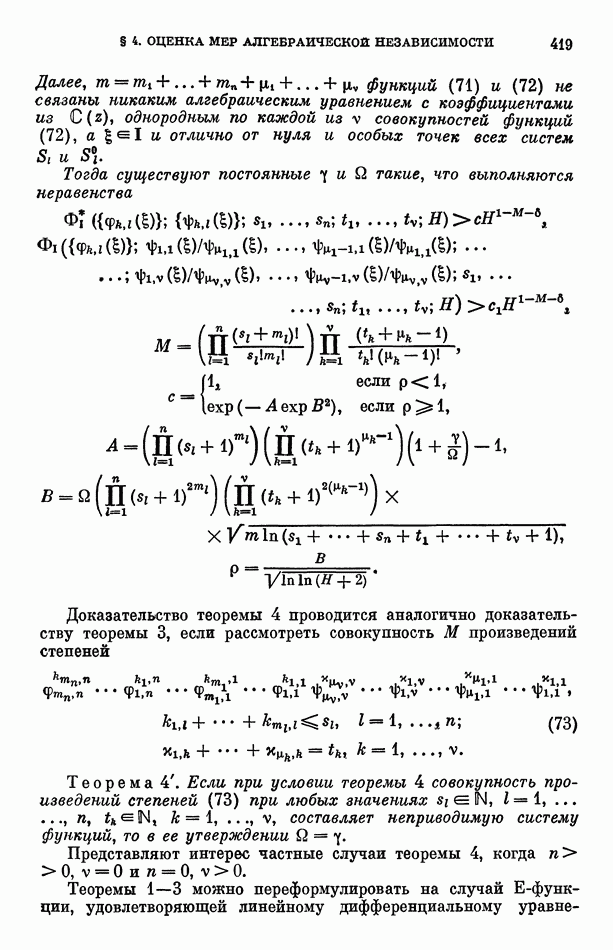| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 5. ТРАНСЦЕНДЕНТНОСТЬ И АЛГЕБРАИЧЕСКАЯ НЕЗАВИСИМОСТЬ ЗНАЧЕНИЙ Е-ФУНКЦИЙ, УДОВЛЕТВОРЯЮЩИХ ЛИНЕЙНЫМ ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ ПЕРВОГО ПОРЯДКА
§ 1. Гипергеометрические Е-функции
В гл. 3 и 4 были установлены общие теоремы о трансцендентности и алгебраической независимости значений Е-функций в алгебраических точках. Некоторые из них были применены к простейшим конкретным Е-функциям. В рассмотренных там случаях не требовалось доказывать, что исследуемые функции являются Е-функциями. Эти утверждения были очевидными следствиями из определения Е-функции. При применении общих теорем гл. 3 и 4 к более сложным Е-функциям необходимо доказывать, что они являются Е-функциями, удовлетворяющими линейным дифференциальным уравнениям с коэффициентами из 
До сих пор структура класса  всех Е-функций, удовлетворяющих линейным дифференциальным уравнениям с коэффициентами из
всех Е-функций, удовлетворяющих линейным дифференциальным уравнениям с коэффициентами из  не изучена. Эта проблема, по-видимому, является очень трудной. Можно указать только достаточно широкий подкласс класса
не изучена. Эта проблема, по-видимому, является очень трудной. Можно указать только достаточно широкий подкласс класса  который, быть может, совпадает со всем классом
который, быть может, совпадает со всем классом  Опишем этот подкласс Е-функций, включающий многие функции, применяемые в различных разделах математики и ее приложениях.
Опишем этот подкласс Е-функций, включающий многие функции, применяемые в различных разделах математики и ее приложениях.
Пусть  Положим
Положим

Если  то определим функцию
то определим функцию

Функции вида (1) называют обобщенными гипергеометрическими функциями, или, короче, гипергеометрическими функциями.
Лемма 1. Функция (1) является решением линейного дифференциального уравнения порядка 

Доказательство. Обозначим  Имеем
Имеем

Поэтому, применяя дифференциальный оператор  к функции (1), получим
к функции (1), получим

Из равенств (3) и (4) получаем дифференциальное уравнение

из которого следует дифференциальное уравнение (2).
Дифференциальное уравнение (2) имеет в конечной плоскости единственную особую точку 
Если хотя бы одно из чисел  равно 1, то правая часть уравнения (2) обращается в нуль и поэтому функция (1) является решением линейного однородного дифференциального Уравнения.
равно 1, то правая часть уравнения (2) обращается в нуль и поэтому функция (1) является решением линейного однородного дифференциального Уравнения.
Если же  то, заменяя
то, заменяя  на
на  положив
положив  по доказанному получим, что функция (1) удовлетворяет линейному однородному дифференциальному уравнению вида (2), но порядка
по доказанному получим, что функция (1) удовлетворяет линейному однородному дифференциальному уравнению вида (2), но порядка 
Заметим также, что если все  то в уравнении (2)
то в уравнении (2)

Обозначим

Тогда гипергеометрическая функция (1) примет вид

Лемма 2. Если

то существует постоянная  такая, что коэффициенты функции (7) удовлетворяют следующим условиям:
такая, что коэффициенты функции (7) удовлетворяют следующим условиям:

2°. Существует последовательность  такая, что
такая, что

Доказательство. Из равенства (6) имеем

Рассмотрим отношение

Пусть  Тогда при
Тогда при 

Пользуясь формулой Тейлора для функции  и известным равенством
и известным равенством

получим

Далее,

Из равенств (11) и (12) следует, что существует постоянная  такая, что выполняется оценка (8).
такая, что выполняется оценка (8).
Докажем теперь, что выполнено условие 2°. Так как  то, ввиду равенства (10), достаточно доказать, что общий наименьший знаменатель
то, ввиду равенства (10), достаточно доказать, что общий наименьший знаменатель  чисел
чисел

имеет величину  при
при  для любых
для любых  и
и 
Положим  и обозначим
и обозначим

Пусть  любой простой делитель числа
любой простой делитель числа  Тогда
Тогда  Если
Если  то, когда х пробегает I последовательных целых чисел,
то, когда х пробегает I последовательных целых чисел,  пробегает полную систему вычетов по модулю
пробегает полную систему вычетов по модулю  Поэтому если х пробегает
Поэтому если х пробегает  последовательных целых чисел, то одно и только одно из
последовательных целых чисел, то одно и только одно из  соответствующих целых чисел
соответствующих целых чисел  делится на
делится на  при каждом
при каждом  Отсюда следует, что из к множителей
Отсюда следует, что из к множителей

входящих в  по крайней мере
по крайней мере  и не более чем
и не более чем  делятся на
делятся на  Если же
Если же  то ни один из этих множителей не делится на
то ни один из этих множителей не делится на 
Допустим, что  делится на
делится на  но не делится на
но не делится на  Тогда
Тогда

Отсюда имеем, что

причем

Оценим теперь степень  числа
числа  на которую делится числитель
на которую делится числитель 
Если  то, рассуждая, как и выше, получим оценки, аналогичные оценкам (14), из которых убеждаемся, что
то, рассуждая, как и выше, получим оценки, аналогичные оценкам (14), из которых убеждаемся, что

Последнее будет верно и для простых делителей числа  так как в
так как в  входит множитель
входит множитель
Проведя сокращение в числителе и знаменателе дроби  обозначим
обозначим  показатель, с которым простое число
показатель, с которым простое число  входит в разложение на простые множители точного знаменателя дроби
входит в разложение на простые множители точного знаменателя дроби  Тогда из оценок (14) и (15) находим, что
Тогда из оценок (14) и (15) находим, что

Поэтому для общего наименьшего знаменателя  дробей
дробей  отличающихся от
отличающихся от  множителем
множителем  выполняется оценка
выполняется оценка

где  число простых чисел не превосходящих
число простых чисел не превосходящих  Пользуясь простейшей оценкой
Пользуясь простейшей оценкой

получаем  Отсюда ввиду равенства (10) имеем оценку (9) с некоторой постоянной с. Выбирая в установленных неравенствах (8) и (9) в качестве постоянной с наибольшую, получим утверждение леммы 2.
Отсюда ввиду равенства (10) имеем оценку (9) с некоторой постоянной с. Выбирая в установленных неравенствах (8) и (9) в качестве постоянной с наибольшую, получим утверждение леммы 2.
Так как  при любом
при любом  то из лемм 1 и 2 имеем следующее утверждение.
то из лемм 1 и 2 имеем следующее утверждение.
Лемма 3. Любая гипергеометрическая функция (1) с рациональными значениями параметров  и
и  принадлежит классу
принадлежит классу  т. е. является Е-функцией, удовлетворяющей линейному дифференциальному уравнению с коэффициентами из
т. е. является Е-функцией, удовлетворяющей линейному дифференциальному уравнению с коэффициентами из  (и даже из
(и даже из  ).
).
Функции (1) с рациональными значениями параметров а и  будем называть гипергеометрическими Е-функциями.
будем называть гипергеометрическими Е-функциями.
Из лемм 1—3, леммы 9 гл. 4 и свойств Е-функций, изложенных в § 1 гл. 3, получаем следующее утверждение: любой многочлен с алгебраическими коэффициентами от z и конечного числа гипергеометрических Е-функций, а также функций, получающихся из последних заменой z на  при А, является Е-функцией из класса
при А, является Е-функцией из класса 
В 1949 г. К. Зигель [73:4] поставил проблему: представляется ли произвольная Е-функция из класса Е в виде подобного
многочлена? Эта проблема является очень трудной. До сих пор в направлении ее решения не получено никаких результатов.
Следующий пример показывает, что даже значительно упрощенная задача до сих пор не поддается решению.
Легко показать, что Е-функция, удовлетворяющая линейному однородному дифференциальному уравнению первого порядка с коэффициентами из  является произведением многочлена с алгебраическими коэффициентами на функцию
является произведением многочлена с алгебраическими коэффициентами на функцию  где
где  Но какой вид может иметь Е-функция, удовлетворяющая линейному неоднородному дифференциальному уравнению того же типа, до сих пор не известно.
Но какой вид может иметь Е-функция, удовлетворяющая линейному неоднородному дифференциальному уравнению того же типа, до сих пор не известно.
Вопрос о том, может ли гипергеометрическая функция (1) с алгебраическими параметрами а и  быть Е-функцией, был предметом исследования. Оказалось, что за исключением мало интересного случая, функция (1) будет Е-функцией только при рациональных значениях всех ее параметров
быть Е-функцией, был предметом исследования. Оказалось, что за исключением мало интересного случая, функция (1) будет Е-функцией только при рациональных значениях всех ее параметров  Сформулируем, не приводя доказательства, окончательный результат.
Сформулируем, не приводя доказательства, окончательный результат.
Будем говорить, что две системы алгебраических чисел  удовлетворяют условию
удовлетворяют условию  если либо все числа
если либо все числа  либо существует такое разбиение всех тех из них, которые не являются рациональными, на пары
либо существует такое разбиение всех тех из них, которые не являются рациональными, на пары  при
при  что все разности
что все разности 
В 1978 г. А. И. Галочкин [3:11] доказал: Для того чтобы гипергеометрическая функция (1) с комплексными параметрами  отличными от чисел
отличными от чисел  и такими, что
и такими, что  при
при  была Е-функцией, необходимо и достаточно, чтобы числа
была Е-функцией, необходимо и достаточно, чтобы числа  и чтобы системы чисел
и чтобы системы чисел  удовлетворяли условию
удовлетворяли условию 
Из этого результата следует, что при  гипергеометрическая функция (1) является Е-функцией тогда и только тогда, когда
гипергеометрическая функция (1) является Е-функцией тогда и только тогда, когда 
Гипергеометрические функции с иррациональными алгебраическими параметрами не являются Е-функциями (за исключением указанного выше случая) ввиду того, что общее наименьшее кратное знаменателей первых  коэффициентов их степенных рядов растет значительно быстрее, чем у Е-функций.
коэффициентов их степенных рядов растет значительно быстрее, чем у Е-функций.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Приближение алгебраических чисел
- § 2. Классический метод Эрмита — Линдемана
- § 3. Методы, возникшие при решении седьмой проблемы Гильберта, и их дальнейшее развитие
- § 4. Метод Зигеля и его дальнейшее развитие
- Глава 1. ПРИБЛИЖЕНИЕ ДЕЙСТВИТЕЛЬНЫХ И АЛГЕБРАИЧЕСКИХ ЧИСЕЛ
- § 1. Приближение действительных чисел рациональными числами
- § 2. Совместные приближения
- § 3. Приближение алгебраических чисел рациональными числами
- § 4. Приближение алгебраических чисел алгебраическими числами
- § 5. Дальнейшие усиления и обобщения теоремы Лиувилля
- Замечания
- Глава 2. АРИФМЕТИЧЕСКИЕ СВОЙСТВА ЗНАЧЕНИЙ ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ В АЛГЕБРАИЧЕСКИХ ТОЧКАХ
- § 1. Трансцендентность числа e
- § 2. Трансцендентность числа «пи»
- § 3. Трансцендентность значений показательной функции в алгебраических точках
- § 4. Приближение функции e^z рациональными функциями
- § 5. Линейная приближающая форма для функции …
- § 6. Совокупность линейных приближающих форм
- § 7. Теорема Линдемана
- § 8. Линейные приближающие формы и разложение показательной функции в интерполяционный ряд Ньютона
- Замечания
- Глава 3. ТРАНСЦЕНДЕНТНОСТЬ И АЛГЕБРАИЧЕСКАЯ НЕЗАВИСИМОСТЬ ЗНАЧЕНИЙ Е-ФУНКЦИЙ, НЕ СВЯЗАННЫХ АЛГЕБРАИЧЕСКИМИ УРАВНЕНИЯМИ НАД ПОЛЕМ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
- § 1. Е-функции
- § 2. Первая основная теорема
- § 3. Некоторые свойства линейных и дробно-линейных форм
- § 4. Свойства линейных форм от функций, удовлетворяющих системе линейных однородных дифференциальных уравнений
- § 5. Порядок нуля линейной формы при z = 0
- § 6. Определитель системы линейных форм
- § 7. Переход к числовым линейно независимым линейным формам
- § 8. Вспомогательные предложения о решениях систем линейных однородных уравнений
- § 9. Функциональные линейные приближающие формы
- § 10. Числовые линейные приближающие формы
- § 11. Ранг совокупности чисел
- § 12. Доказательство первой основной теоремы
- § 13. Следствия из первой основной теоремы
- Замечания
- Глава 4. ТРАНСЦЕНДЕНТНОСТЬ И АЛГЕБРАИЧЕСКАЯ НЕЗАВИСИМОСТЬ ЗНАЧЕНИЙ Е-ФУНКЦИЙ, СВЯЗАННЫХ АЛГЕБРАИЧЕСКИМИ УРАВНЕНИЯМИ НАД ПОЛЕМ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
- § 2. Вспомогательные предложения
- § 3. Оценки размерностей векторных пространств, порожденных произведениями степеней элементов из расширения некоторого поля
- § 4. Третья основная теорема
- § 5. Трансцендентность значений Е-функций, связанных произвольными алгебраическими уравнениями над C(z)
- § 6. Алгебраическая независимость значений Е-функций, связанных произвольными алгебраическими уравнениями над C(z)
- § 7. Е-функции, связанные уравнениями специального вида
- § 8. Е-функции, связанные алгебраическими уравнениями с постоянными коэффициентами
- § 9. Е-функции, связанные одним алгебраическим уравнением вид C(z)
- § 10. Минимальные уравнения
- § 11. Размерности векторных пространств, порожденных произведениями степеней элементов из расширения некоторого поля
- § 12. Алгебраическая независимость значений IE-функций
- § 13. Алгебраическая независимость значений КЕ-функций
- Замечания
- Глава 5. ТРАНСЦЕНДЕНТНОСТЬ И АЛГЕБРАИЧЕСКАЯ НЕЗАВИСИМОСТЬ ЗНАЧЕНИЙ Е-ФУНКЦИЙ, УДОВЛЕТВОРЯЮЩИХ ЛИНЕЙНЫМ ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ ПЕРВОГО ПОРЯДКА
- § 1. Гипергеометрические Е-функции
- § 2. Простейшая гипергеометрическая Е-функция
- § 3. Совокупность решений линейных дифференциальных уравнений первого порядка
- § 4. Вспомогательные предложения
- § 5. Доказательства теорем
- Замечания
- Глава 6. АЛГЕБРАИЧЕСКАЯ НЕЗАВИСИМОСТЬ ЗНАЧЕНИИ Е-ФУНКЦИЙ, УДОВЛЕТВОРЯЮЩИХ ЛИНЕЙНЫМ ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ ВТОРОГО ПОРЯДКА
- § 1. Общая теорема об алгебраической независимости значений Е-функции и ее производной
- § 2. Функции K(z), связанные с функциями Бесселя
- § 3. Функции …
- § 4. Функции Куммера
- § 5. Решения линейных неоднородных дифференциальных уравнений
- Глава 7. РЕШЕНИЯ НЕКОТОРЫХ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПРОИЗВОЛЬНОГО ПОРЯДКА
- § 1. Решения неоднородных дифференциальных уравнений
- § 2. Решения однородных дифференциальных уравнений
- § 3. Следствия из теорем 1 и 2
- Глава 8. ИССЛЕДОВАНИЕ РЕШЕНИЙ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПРОИЗВОЛЬНОГО ПОРЯДКА АРИФМЕТИЧЕСКИМ МЕТОДОМ
- § 2. Вспомогательные предложения
- § 3. Доказательства теорем 1—5
- § 4. Доказательства теорем 6 и 7
- § 5. Дальнейшие результаты
- Глава 9. ТЕОРЕМА ЗИГЕЛЯ
- § 2. Вспомогательные предложения
- § 3. Некоторые свойства решений линейных однородных дифференциальных уравнений второго порядка
- § 4. Алгебраическая независимость решений совокупности линейных однородных дифференциальных уравнений второго порядка
- § 5. Доказательство теоремы Зигеля
- § 6. Решения линейных неоднородных дифференциальных уравнении
- § 7. Обобщение теоремы Зигеля
- Глава 10. РЕШЕНИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПРОСТОГО ПОРЯДКА p
- § 2. Однородный идеал J
- § 3. Алгебраические функции нескольких переменных
- § 4. Дифференциальный оператор G
- § 5. Дифференциальные операторы S и «дельта»
- § 6. Лемма о линейном приближении
- § 7. Завершение доказательства теоремы 7
- § 8. Линейная приводимость
- § 9. Доказательства теорем 6 и 5
- Замечания
- Глава 11. МЕРА АЛГЕБРАИЧЕСКОЙ НЕЗАВИСИМОСТИ ЗНАЧЕНИЙ IE-ФУНКЦИЙ
- § 2. Мера линейной независимости значений IE-функций
- § 3. Мера алгебраической независимости значений IE-функций, не связанных алгебраическими уравнениями над C(z)
- § 4. Вспомогательные предложения
- § 5. Мера алгебраической независимости значений IE-функций, связанных алгебраическими уравнениями над C(z)
- § 6. Некоторые применения общих теорем
- Глава 12. МЕРА АЛГЕБРАИЧЕСКОЙ НЕЗАВИСИМОСТИ ЗНАЧЕНИЙ КЕ-ФУНКЦИЙ
- § 2. Оценки мер значений Е-функций, не связанных алгебраическими уравнениями над C(z)
- § 3. Оценки мер значений Е-функций, связанных одним алгебраическим уравнением над C(z)
- § 4. Оценки мер значений Е-функций, связанных произвольными алгебраическими уравнениями над C(z)
- § 5. Алгебраическая независимость значений Е-функций в сопряженных полях
- § 6. Вспомогательная теорема
- § 7. Следствия из вспомогательной теоремы
- § 8. Некоторые применения общих теорем
- Глава 13. ЭФФЕКТИВНЫЕ ОЦЕНКИ МЕР
- § 2. Уточнение основных лемм метода
- § 3. Оценка мер линейной независимости
- § 4. Оценка мер алгебраической независимости
- § 5. Некоторые применения общих теорем
- ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
- СПИСОК ЛИТЕРАТУРЫ