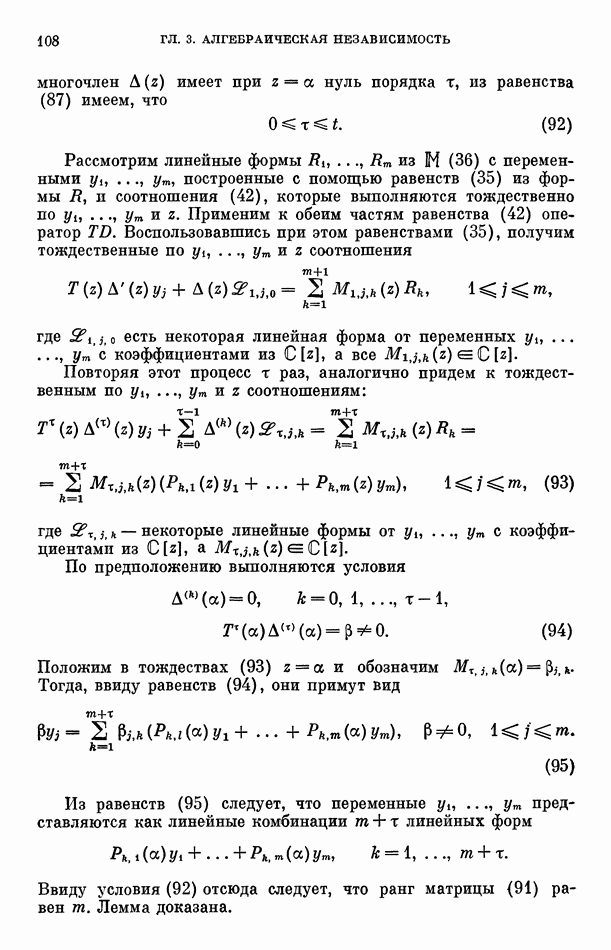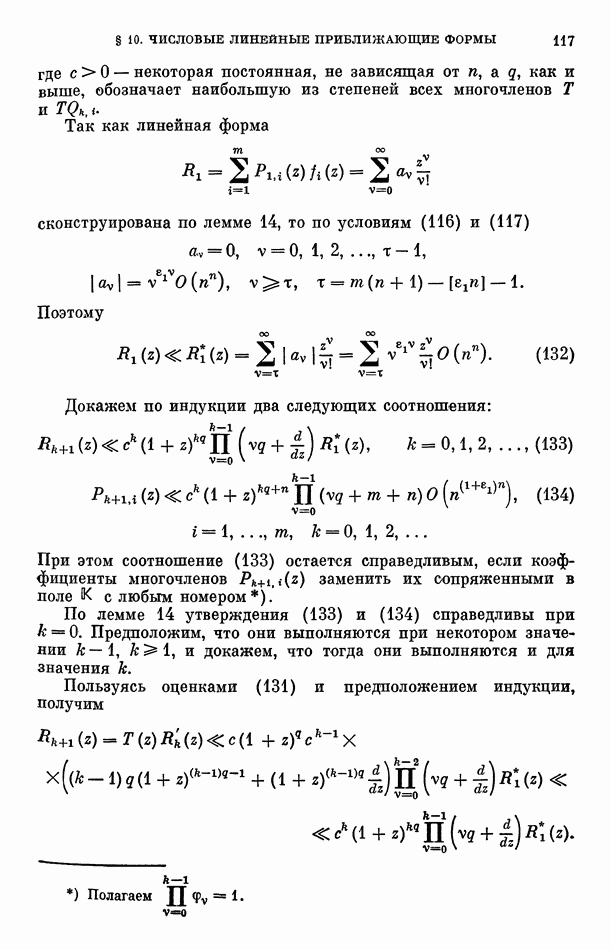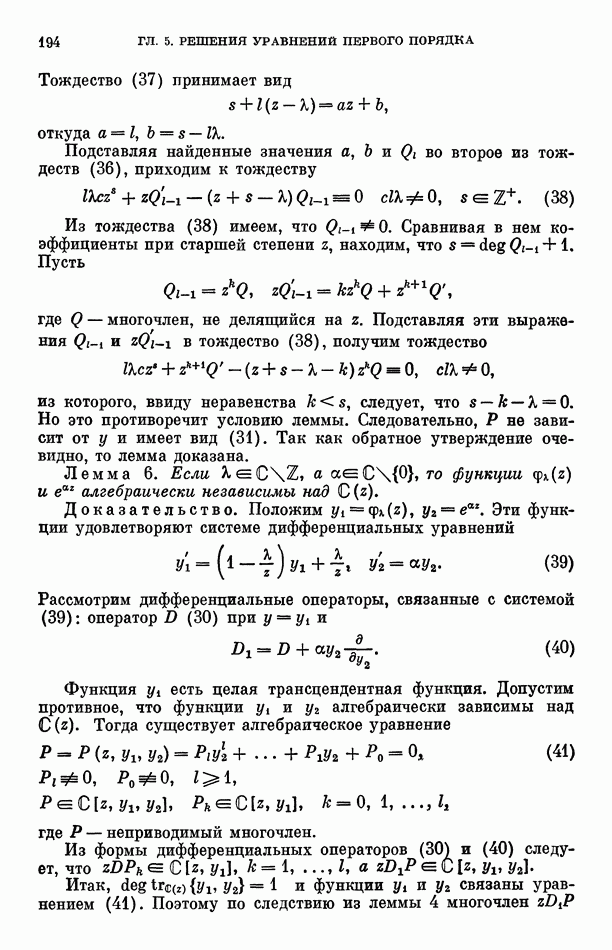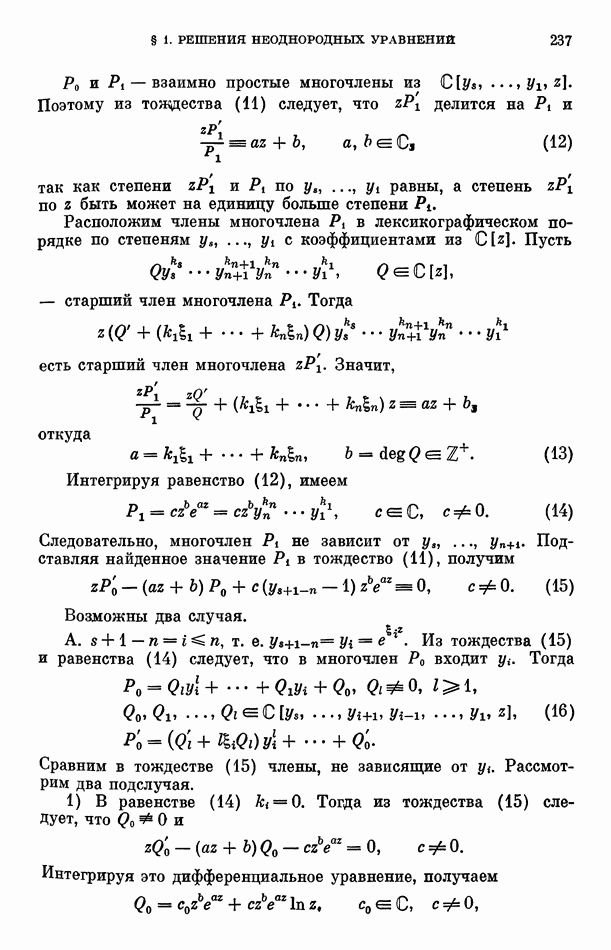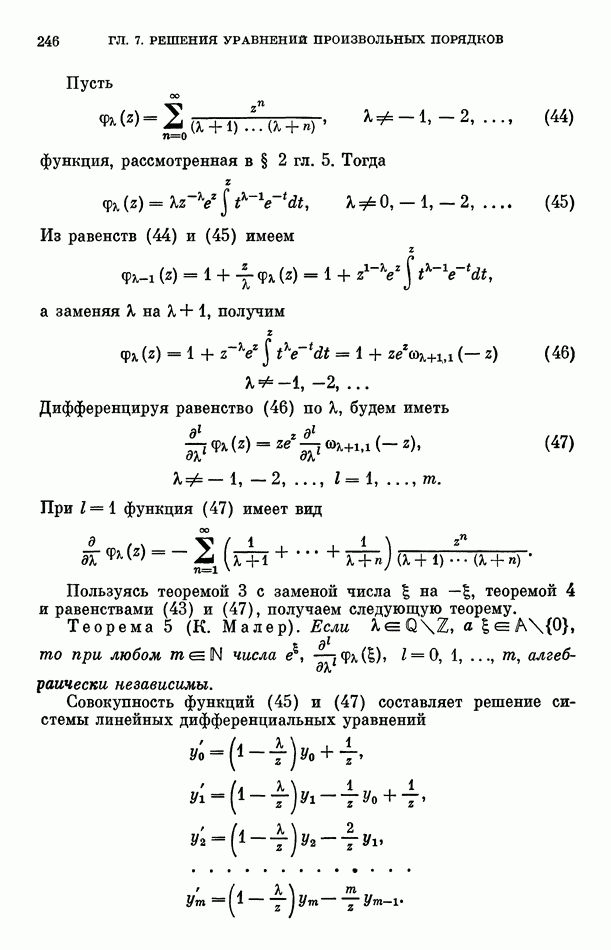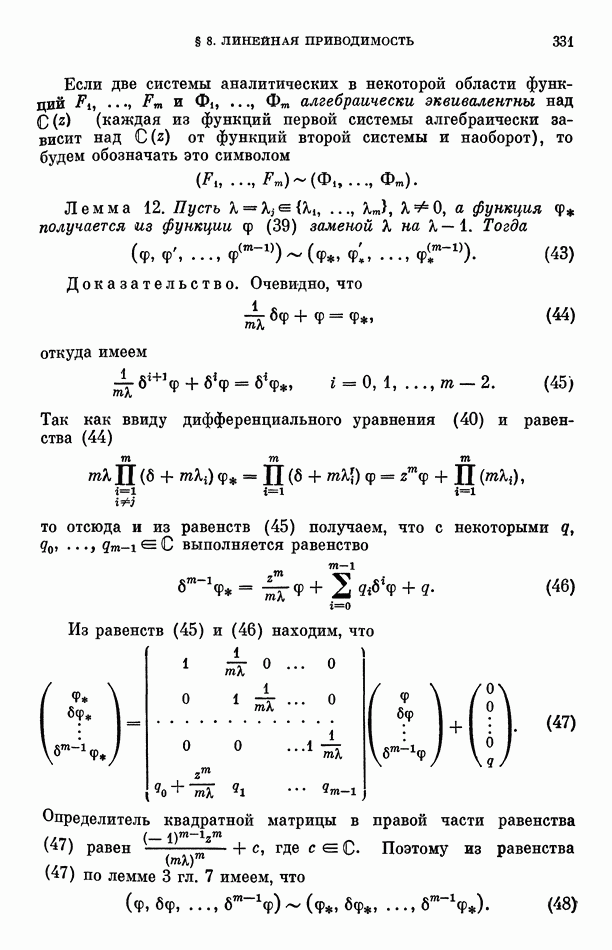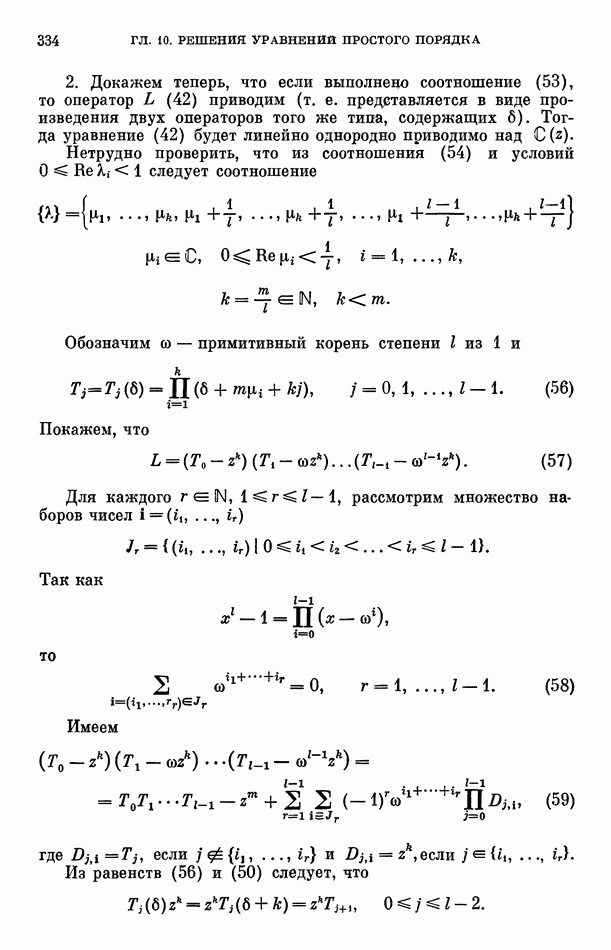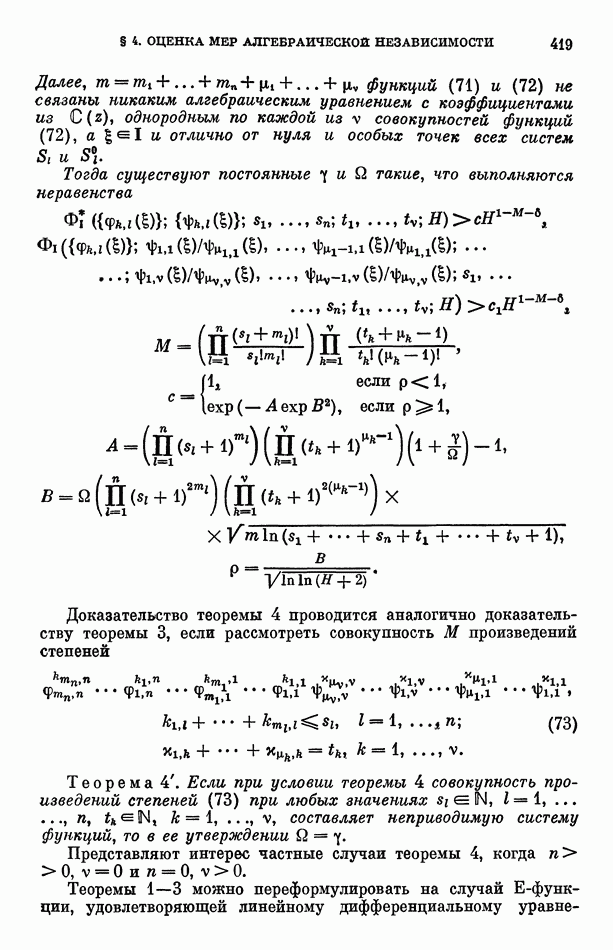| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 5. Дифференциальные операторы S и «дельта»
На четвертом этапе доказательства теоремы строится некоторый простой идеал  кольца
кольца  и изучаются его свойства.
и изучаются его свойства.
Так как  то существуют элементы
то существуют элементы  такие, что
такие, что

При этом для  имеем
имеем  Следовательно, среди
Следовательно, среди  имеется не менее чем к алгебраически независимых над
имеется не менее чем к алгебраически независимых над  элементов. В частности, не все эти элементы равны нулю.
элементов. В частности, не все эти элементы равны нулю.
Лемма 7. Пусть  простой идеал кольца
простой идеал кольца  состоящий из всех многочленов, обращающихся в нуль при подстановке в них вместо
состоящий из всех многочленов, обращающихся в нуль при подстановке в них вместо  и
и

— дифференциальный оператор, действующий в кольце  определены в формулировке теоремы).
определены в формулировке теоремы).
Тогда  однородный идеал,
однородный идеал, 
Доказательство. Обозначим  — совокупность многочленов
— совокупность многочленов  кольца
кольца  для каждого из которых существует многочлен
для каждого из которых существует многочлен  с условием
с условием  где нормирование
где нормирование  определено перед формулировкой леммы 2. Напомним, что значение
определено перед формулировкой леммы 2. Напомним, что значение  на элементах кольца
на элементах кольца  определены в доказательстве леммы 2. Докажем, что
определены в доказательстве леммы 2. Докажем, что  однородный идеал кольца
однородный идеал кольца 
Если  то с некоторыми
то с некоторыми  имеем
имеем  Для
Для  находим
находим  Если
Если  то с некоторым
то с некоторым  имеем
имеем

Так как  то
то  Следовательно,
Следовательно,  идеал.
идеал.
Пусть  где — однородная компонента
где — однородная компонента  степени
степени  Если
Если  и такой, что
и такой, что  где
где  однородная компонента
однородная компонента  степени
степени  то
то  так как
так как  однородный идеал. Поскольку и
однородный идеал. Поскольку и  являются однородными многочленами разных степеней, то
являются однородными многочленами разных степеней, то  следовательно,
следовательно,  Итак,
Итак,  есть однородный идеал.
есть однородный идеал.
Пусть  и такой, что
и такой, что  Легко видеть, что
Легко видеть, что  Из этих неравенств следует, что
Из этих неравенств следует, что  Так как
Так как  и
и  то
то  Поэтому
Поэтому 
Далее, так как  то
то  значит,
значит,  Поскольку
Поскольку  находим, что
находим, что  т. е.
т. е.  есть нуль идеала «90 и поэтому «
есть нуль идеала «90 и поэтому «
Точно так же, как и в доказательстве леммы 1, отсюда следует, что идеал  однороден,
однороден,  более того, что идеал
более того, что идеал  минимален во множестве простых идеалов, содержащих
минимален во множестве простых идеалов, содержащих 
Напомним некоторые факты, необходимые для завершения доказательства леммы.
Каждому идеалу кольца  соответствует однозначно определенное множество простых идеалов
соответствует однозначно определенное множество простых идеалов 
называемых ассоциированными с  , такое, что пересечение
, такое, что пересечение  есть в точности совокупность многочленов
есть в точности совокупность многочленов  удовлетворяющих с некоторым числом
удовлетворяющих с некоторым числом  условию
условию  Все простые идеалы минимальные во множестве простых идеалов, содержащих
Все простые идеалы минимальные во множестве простых идеалов, содержащих  , находятся среди
, находятся среди 
Продолжим теперь доказательство леммы, считая, что  простые идеалы, ассоциированные с
простые идеалы, ассоциированные с  . Так как идеал
. Так как идеал  минимален во множестве простых идеалов, содержащих
минимален во множестве простых идеалов, содержащих  то
то  , и, значит, существуют многочлены
, и, значит, существуют многочлены  такие, что
такие, что  . Пусть
. Пусть  Тогда
Тогда  значит, с некоторым
значит, с некоторым  имеем
имеем  где
где  Из включения
Из включения  следует, что
следует, что  Поскольку отсюда следует, что
Поскольку отсюда следует, что  и так как
и так как  а идеал
а идеал  прост, то
прост, то  Этим доказано, что а вместе с тем завершено доказательство леммы.
Этим доказано, что а вместе с тем завершено доказательство леммы.
Из включения  аналогично лемме 4, следует, что на поле
аналогично лемме 4, следует, что на поле  можно определить дифференциальный оператор
можно определить дифференциальный оператор  для которого
для которого

Так как  есть алгебраическое расширение, то оператор
есть алгебраическое расширение, то оператор  подобно
подобно  единственным образом может быть продолжен на поле
единственным образом может быть продолжен на поле 
Лемма 8. Пусть  ненулевые элементы поля
ненулевые элементы поля  для которых существует связывающее их однородное алгебраическое уравнение с коэффициентами из С, и выполняются условия
для которых существует связывающее их однородное алгебраическое уравнение с коэффициентами из С, и выполняются условия

Тогда найдутся целые числа  в совокупности отличные от нуля такие, что
в совокупности отличные от нуля такие, что 
Доказательство. Пусть

— однородное уравнение, связывающее элементы  Применяя к этому уравнению
Применяя к этому уравнению  раз дифференциальный оператор
раз дифференциальный оператор  получим
получим

Рассмотрим равенства (23) при  как систему линейных однородных уравнений относительно произведений
как систему линейных однородных уравнений относительно произведений  Так как не все эти произведения равны нулю, то определитель рассматриваемой системы должен равняться нулю. Но этот определитель есть определитель Вандермонда, составленный из чисел
Так как не все эти произведения равны нулю, то определитель рассматриваемой системы должен равняться нулю. Но этот определитель есть определитель Вандермонда, составленный из чисел  при
при  Поэтому найдутся два различных набора чисел из
Поэтому найдутся два различных набора чисел из  таких, что
таких, что

Отсюда следует утверждение леммы.
Лемма 9. Идеал рассмотренный в лемме 7, имеет базис, состоящий из  линейных форм от переменных
линейных форм от переменных  Корни характеристического уравнения матрицы А, определенной в формулировке теоремы 7, можно занумеровать так, что
Корни характеристического уравнения матрицы А, определенной в формулировке теоремы 7, можно занумеровать так, что  где линейные формы удовлетворяют равенствам
где линейные формы удовлетворяют равенствам

Доказательство. Будем использовать здесь и ниже обозначения  для векторов с координатами
для векторов с координатами  Дифференциальный оператор
Дифференциальный оператор  можно рассматривать как линейное преобразование, действующее на пространстве линейных форм с коэффициентами из С от переменных
можно рассматривать как линейное преобразование, действующее на пространстве линейных форм с коэффициентами из С от переменных  Матрица этого преобразования в координатах
Матрица этого преобразования в координатах  есть
есть  и по условию теоремы 7 имеет различные характеристические корни
и по условию теоремы 7 имеет различные характеристические корни  Значит, существуют линейные формы
Значит, существуют линейные формы  такие, что
такие, что

Кроме того, можно утверждать, что формы  линейно независимы над С (так как
линейно независимы над С (так как 
Следовательно, наибольшее число алгебраически независимых над С среди элементов  равно
равно  и идеал алгебраических уравнений между
и идеал алгебраических уравнений между  с коэффициентами из С однороден (см. лемму 7).
с коэффициентами из С однороден (см. лемму 7).
Перенумеруем корни характеристического уравнения матрицы А так, чтобы алгебраически независимыми над С были элементы  Из леммы 8, ввиду условия теоремы, следует теперь, что
Из леммы 8, ввиду условия теоремы, следует теперь, что  т. е. формы
т. е. формы  принадлежат идеалу
принадлежат идеалу  Идеал
Идеал  прост и, поскольку формы
прост и, поскольку формы  линейно независимы над С, имеет
линейно независимы над С, имеет
размерность, равную  Значит,
Значит,  Лемма доказана.
Лемма доказана.
Лемма 10. Пусть  а элемент
а элемент  и такой, что алгебраичен над полем
и такой, что алгебраичен над полем 
Тогда если для некоторого  выполняется равенство
выполняется равенство  то
то 
Доказательство. Из условия леммы следует, что элементы  связаны однородным алгебраическим уравнением с коэффициентами из С. Утверждение леммы следует теперь из леммы 8 ввиду условия теоремы 7 и того, что элементы
связаны однородным алгебраическим уравнением с коэффициентами из С. Утверждение леммы следует теперь из леммы 8 ввиду условия теоремы 7 и того, что элементы  алгебраически независимы над С и, значит, отличны от нуля.
алгебраически независимы над С и, значит, отличны от нуля.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Приближение алгебраических чисел
- § 2. Классический метод Эрмита — Линдемана
- § 3. Методы, возникшие при решении седьмой проблемы Гильберта, и их дальнейшее развитие
- § 4. Метод Зигеля и его дальнейшее развитие
- Глава 1. ПРИБЛИЖЕНИЕ ДЕЙСТВИТЕЛЬНЫХ И АЛГЕБРАИЧЕСКИХ ЧИСЕЛ
- § 1. Приближение действительных чисел рациональными числами
- § 2. Совместные приближения
- § 3. Приближение алгебраических чисел рациональными числами
- § 4. Приближение алгебраических чисел алгебраическими числами
- § 5. Дальнейшие усиления и обобщения теоремы Лиувилля
- Замечания
- Глава 2. АРИФМЕТИЧЕСКИЕ СВОЙСТВА ЗНАЧЕНИЙ ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ В АЛГЕБРАИЧЕСКИХ ТОЧКАХ
- § 1. Трансцендентность числа e
- § 2. Трансцендентность числа «пи»
- § 3. Трансцендентность значений показательной функции в алгебраических точках
- § 4. Приближение функции e^z рациональными функциями
- § 5. Линейная приближающая форма для функции …
- § 6. Совокупность линейных приближающих форм
- § 7. Теорема Линдемана
- § 8. Линейные приближающие формы и разложение показательной функции в интерполяционный ряд Ньютона
- Замечания
- Глава 3. ТРАНСЦЕНДЕНТНОСТЬ И АЛГЕБРАИЧЕСКАЯ НЕЗАВИСИМОСТЬ ЗНАЧЕНИЙ Е-ФУНКЦИЙ, НЕ СВЯЗАННЫХ АЛГЕБРАИЧЕСКИМИ УРАВНЕНИЯМИ НАД ПОЛЕМ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
- § 1. Е-функции
- § 2. Первая основная теорема
- § 3. Некоторые свойства линейных и дробно-линейных форм
- § 4. Свойства линейных форм от функций, удовлетворяющих системе линейных однородных дифференциальных уравнений
- § 5. Порядок нуля линейной формы при z = 0
- § 6. Определитель системы линейных форм
- § 7. Переход к числовым линейно независимым линейным формам
- § 8. Вспомогательные предложения о решениях систем линейных однородных уравнений
- § 9. Функциональные линейные приближающие формы
- § 10. Числовые линейные приближающие формы
- § 11. Ранг совокупности чисел
- § 12. Доказательство первой основной теоремы
- § 13. Следствия из первой основной теоремы
- Замечания
- Глава 4. ТРАНСЦЕНДЕНТНОСТЬ И АЛГЕБРАИЧЕСКАЯ НЕЗАВИСИМОСТЬ ЗНАЧЕНИЙ Е-ФУНКЦИЙ, СВЯЗАННЫХ АЛГЕБРАИЧЕСКИМИ УРАВНЕНИЯМИ НАД ПОЛЕМ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
- § 2. Вспомогательные предложения
- § 3. Оценки размерностей векторных пространств, порожденных произведениями степеней элементов из расширения некоторого поля
- § 4. Третья основная теорема
- § 5. Трансцендентность значений Е-функций, связанных произвольными алгебраическими уравнениями над C(z)
- § 6. Алгебраическая независимость значений Е-функций, связанных произвольными алгебраическими уравнениями над C(z)
- § 7. Е-функции, связанные уравнениями специального вида
- § 8. Е-функции, связанные алгебраическими уравнениями с постоянными коэффициентами
- § 9. Е-функции, связанные одним алгебраическим уравнением вид C(z)
- § 10. Минимальные уравнения
- § 11. Размерности векторных пространств, порожденных произведениями степеней элементов из расширения некоторого поля
- § 12. Алгебраическая независимость значений IE-функций
- § 13. Алгебраическая независимость значений КЕ-функций
- Замечания
- Глава 5. ТРАНСЦЕНДЕНТНОСТЬ И АЛГЕБРАИЧЕСКАЯ НЕЗАВИСИМОСТЬ ЗНАЧЕНИЙ Е-ФУНКЦИЙ, УДОВЛЕТВОРЯЮЩИХ ЛИНЕЙНЫМ ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ ПЕРВОГО ПОРЯДКА
- § 1. Гипергеометрические Е-функции
- § 2. Простейшая гипергеометрическая Е-функция
- § 3. Совокупность решений линейных дифференциальных уравнений первого порядка
- § 4. Вспомогательные предложения
- § 5. Доказательства теорем
- Замечания
- Глава 6. АЛГЕБРАИЧЕСКАЯ НЕЗАВИСИМОСТЬ ЗНАЧЕНИИ Е-ФУНКЦИЙ, УДОВЛЕТВОРЯЮЩИХ ЛИНЕЙНЫМ ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ ВТОРОГО ПОРЯДКА
- § 1. Общая теорема об алгебраической независимости значений Е-функции и ее производной
- § 2. Функции K(z), связанные с функциями Бесселя
- § 3. Функции …
- § 4. Функции Куммера
- § 5. Решения линейных неоднородных дифференциальных уравнений
- Глава 7. РЕШЕНИЯ НЕКОТОРЫХ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПРОИЗВОЛЬНОГО ПОРЯДКА
- § 1. Решения неоднородных дифференциальных уравнений
- § 2. Решения однородных дифференциальных уравнений
- § 3. Следствия из теорем 1 и 2
- Глава 8. ИССЛЕДОВАНИЕ РЕШЕНИЙ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПРОИЗВОЛЬНОГО ПОРЯДКА АРИФМЕТИЧЕСКИМ МЕТОДОМ
- § 2. Вспомогательные предложения
- § 3. Доказательства теорем 1—5
- § 4. Доказательства теорем 6 и 7
- § 5. Дальнейшие результаты
- Глава 9. ТЕОРЕМА ЗИГЕЛЯ
- § 2. Вспомогательные предложения
- § 3. Некоторые свойства решений линейных однородных дифференциальных уравнений второго порядка
- § 4. Алгебраическая независимость решений совокупности линейных однородных дифференциальных уравнений второго порядка
- § 5. Доказательство теоремы Зигеля
- § 6. Решения линейных неоднородных дифференциальных уравнении
- § 7. Обобщение теоремы Зигеля
- Глава 10. РЕШЕНИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПРОСТОГО ПОРЯДКА p
- § 2. Однородный идеал J
- § 3. Алгебраические функции нескольких переменных
- § 4. Дифференциальный оператор G
- § 5. Дифференциальные операторы S и «дельта»
- § 6. Лемма о линейном приближении
- § 7. Завершение доказательства теоремы 7
- § 8. Линейная приводимость
- § 9. Доказательства теорем 6 и 5
- Замечания
- Глава 11. МЕРА АЛГЕБРАИЧЕСКОЙ НЕЗАВИСИМОСТИ ЗНАЧЕНИЙ IE-ФУНКЦИЙ
- § 2. Мера линейной независимости значений IE-функций
- § 3. Мера алгебраической независимости значений IE-функций, не связанных алгебраическими уравнениями над C(z)
- § 4. Вспомогательные предложения
- § 5. Мера алгебраической независимости значений IE-функций, связанных алгебраическими уравнениями над C(z)
- § 6. Некоторые применения общих теорем
- Глава 12. МЕРА АЛГЕБРАИЧЕСКОЙ НЕЗАВИСИМОСТИ ЗНАЧЕНИЙ КЕ-ФУНКЦИЙ
- § 2. Оценки мер значений Е-функций, не связанных алгебраическими уравнениями над C(z)
- § 3. Оценки мер значений Е-функций, связанных одним алгебраическим уравнением над C(z)
- § 4. Оценки мер значений Е-функций, связанных произвольными алгебраическими уравнениями над C(z)
- § 5. Алгебраическая независимость значений Е-функций в сопряженных полях
- § 6. Вспомогательная теорема
- § 7. Следствия из вспомогательной теоремы
- § 8. Некоторые применения общих теорем
- Глава 13. ЭФФЕКТИВНЫЕ ОЦЕНКИ МЕР
- § 2. Уточнение основных лемм метода
- § 3. Оценка мер линейной независимости
- § 4. Оценка мер алгебраической независимости
- § 5. Некоторые применения общих теорем
- ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
- СПИСОК ЛИТЕРАТУРЫ