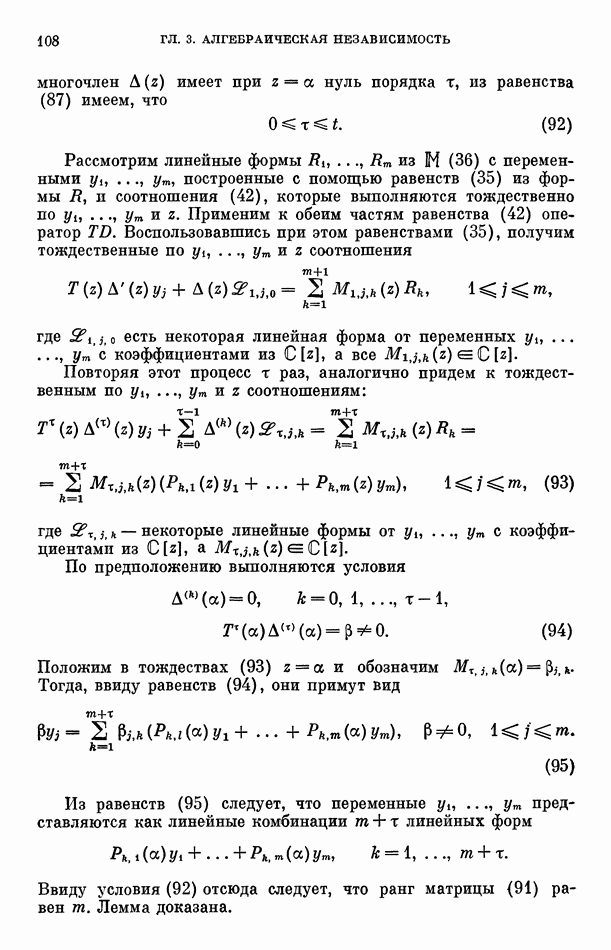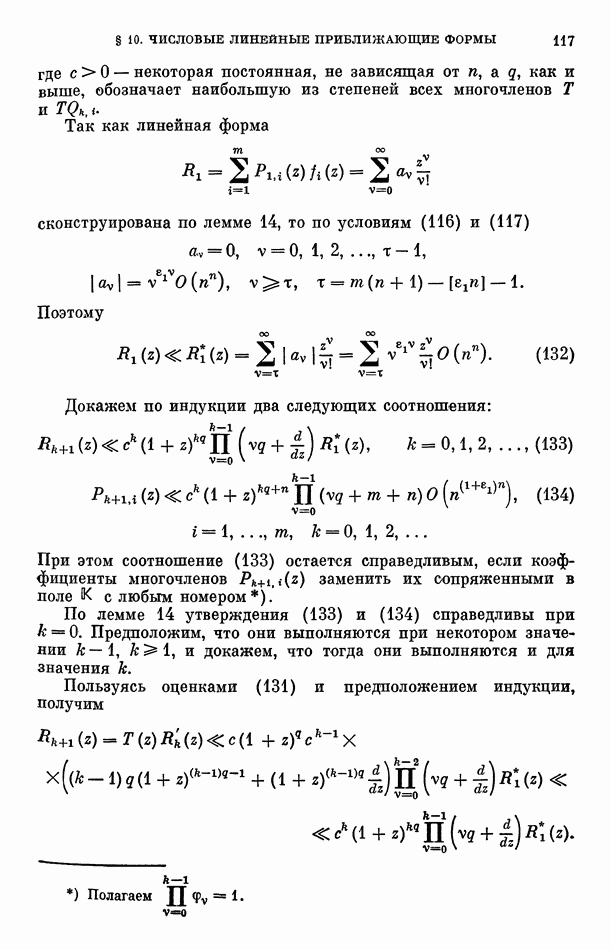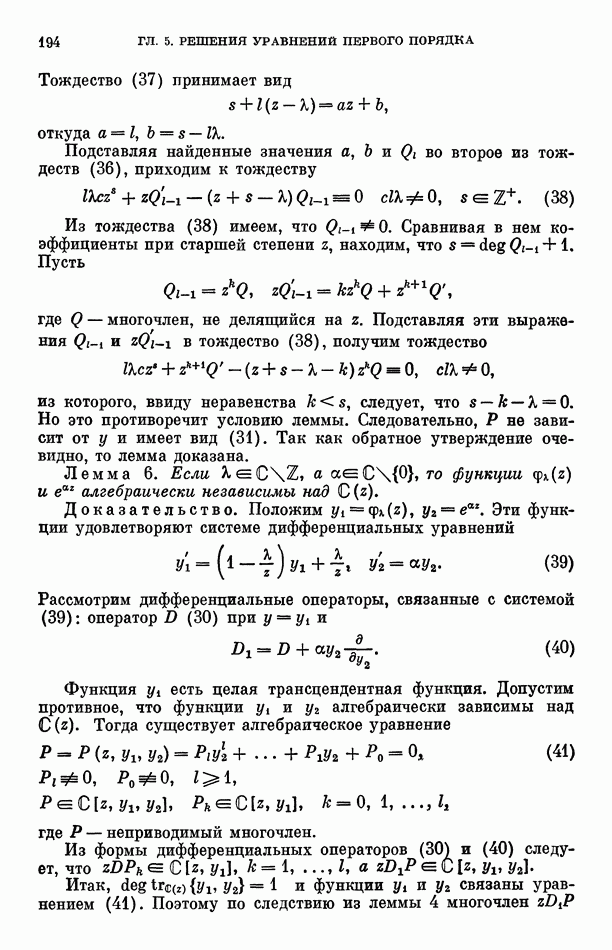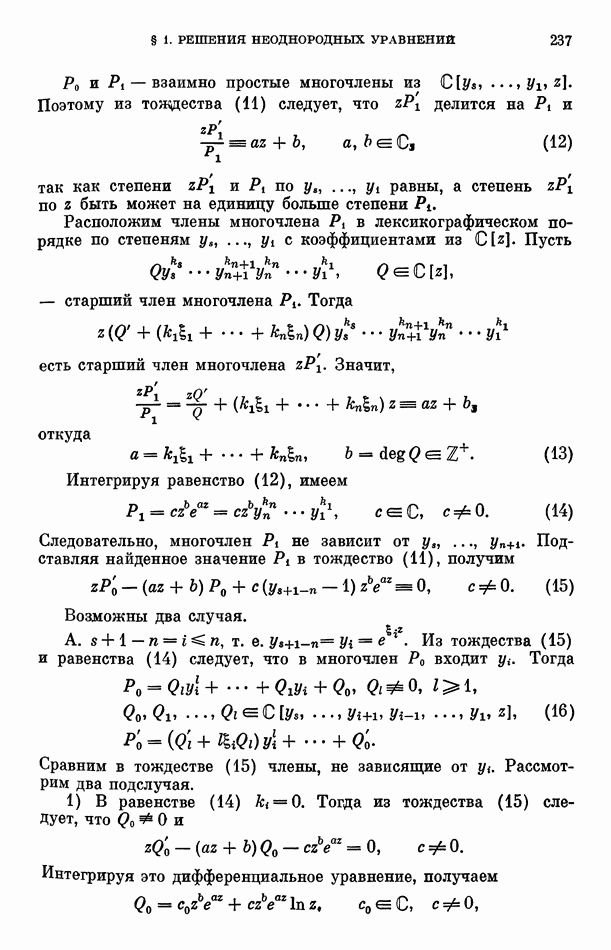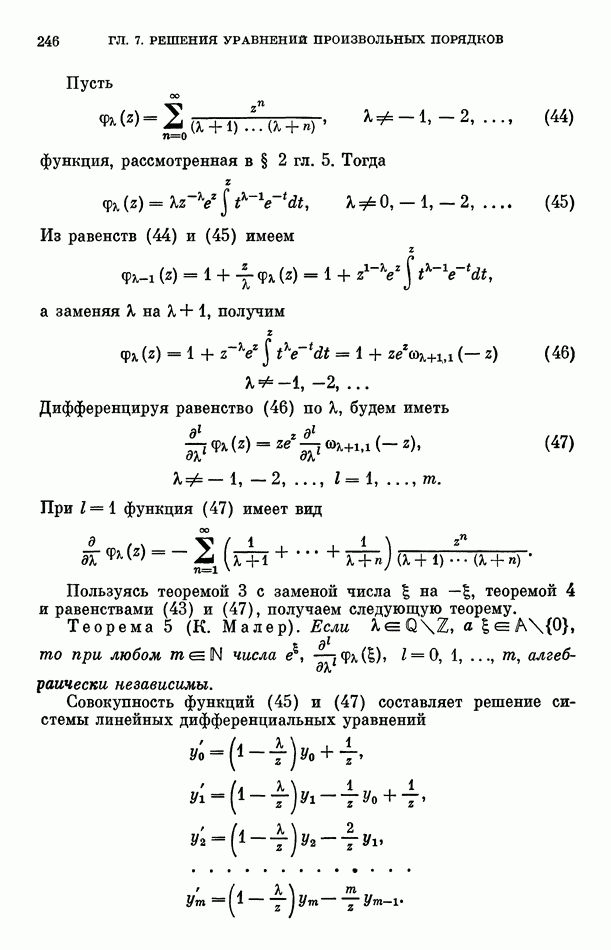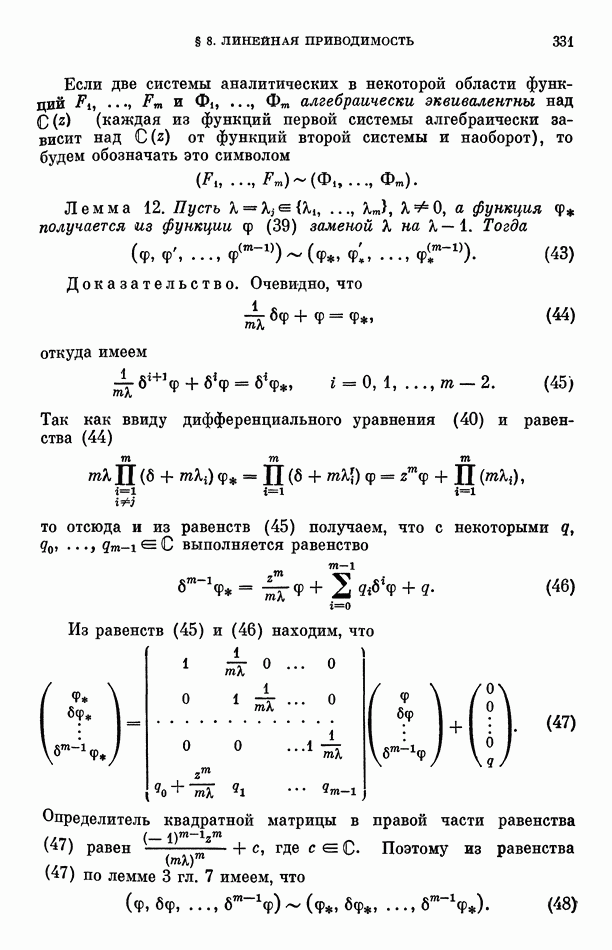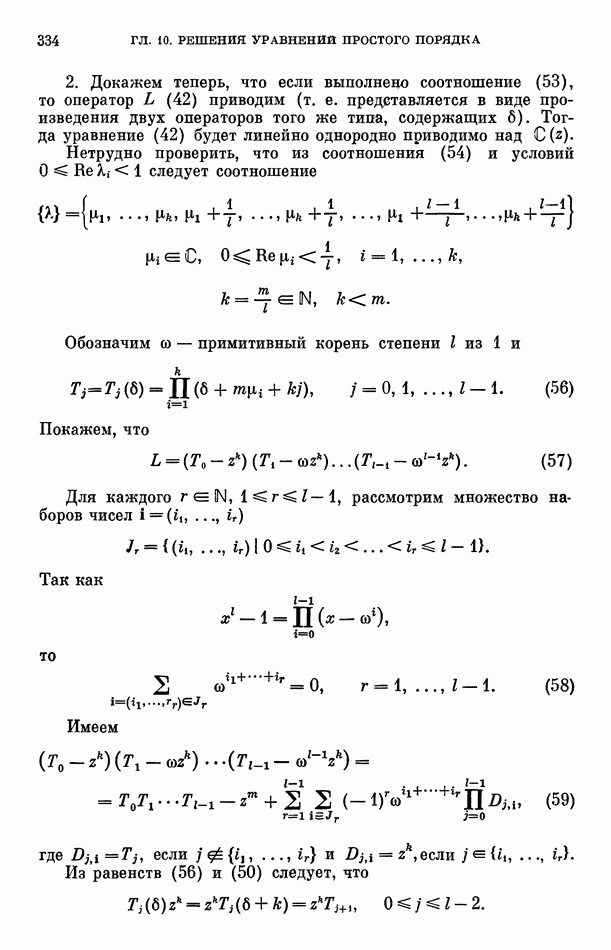| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. Трансцендентность значений показательной функции в алгебраических точках
Теорема 6. (Ф. Линдеман) Если  алгебраическое число,
алгебраическое число,  то число
то число  трансцендентно.
трансцендентно.
Эта теорема может быть доказана с помощью тождества Эрмита, аналогично тому, как была доказана теорема 5, с некоторыми усложнениями в преобразованиях. Приводимое ниже доказательство основано на другой идее, ведущей свое начало от работы А. О. Гельфонда [5: 1, 2], в которой было дано частичное решение седьмой проблемы Гильберта.
В этом доказательстве с помощью разложения функции  в интерполяционный ряд Ньютона строится последовательность многочленов
в интерполяционный ряд Ньютона строится последовательность многочленов  с целыми коэффициентами такая, что
с целыми коэффициентами такая, что  достаточно быстро убывает с ростом
достаточно быстро убывает с ростом  Если допустить, что
Если допустить, что  алгебраические числа и воспользоваться оценкой снизу многочлена с целыми коэффициентами от двух алгебраических чисел (теорема И гл. 1), то получается оценка снизу для
алгебраические числа и воспользоваться оценкой снизу многочлена с целыми коэффициентами от двух алгебраических чисел (теорема И гл. 1), то получается оценка снизу для  противоречащая установленной оценке сверху. Отсюда следует, что число
противоречащая установленной оценке сверху. Отсюда следует, что число  не может быть алгебраическим.
не может быть алгебраическим.
Прежде чем доказывать теорему 6 рассмотрим разложение в интерполяционный ряд функции 
Пусть функция  является аналитической в области
является аналитической в области  фиксированный набор точек из
фиксированный набор точек из  среди которых могут быть и совпадающие.
среди которых могут быть и совпадающие.
Определим

Пусть  При каждом
При каждом  выполняется очевид ное тождество
выполняется очевид ное тождество

Умножая его обе части на  имеем
имеем

Складывая почленно все последние тождества и пользуясь тем, что  получаем тождество
получаем тождество

или

Пусть С — простой замкнутый контур целиком лежащий в  вместе с ограниченной им областью, которая содержит все точки
вместе с ограниченной им областью, которая содержит все точки  Умножая обе части тождества (46) на
Умножая обе части тождества (46) на  и интегрируя по контуру С в положительном направлении, пользуясь при этом формулой Коши, получим
и интегрируя по контуру С в положительном направлении, пользуясь при этом формулой Коши, получим

Обозначим

Из равенств (47), (48) и (49) следует, что

Равенство (50) называется интерполяционной формулой Ньютона для функции  с узлами интерполяции
с узлами интерполяции 
Пусть теперь дана бесконечная последовательность  точек из области
точек из области  Предположим, что
Предположим, что  для всех z из области
для всех z из области  где
где  Тогда
Тогда

Ряд (51) называется интерполяционным рядом Ньютона для функции  в области
в области  с узлами интерполяции
с узлами интерполяции 
Если все узлы интерполяции совпадают, то ряд Ньютона переходит в ряд Тейлора.
Пусть  натуральное число. Выберем за узлы интерполяции бесконечную периодическую последовательность
натуральное число. Выберем за узлы интерполяции бесконечную периодическую последовательность

с периодом  где
где

Разложим функцию  где
где  комплексное число,
комплексное число,  в ряд Ньютона с узлами интерполяции (52).
в ряд Ньютона с узлами интерполяции (52).
Пусть  любое число такое, что
любое число такое, что  Рассмотрим и оценим остаточный член (49) формулы Ньютона для функции
Рассмотрим и оценим остаточный член (49) формулы Ньютона для функции  при
при 

где С — окружность 
Так как из условия (53) следует, что  то
то

и

для всех z таких, что 
Далее, поскольку  то на окружности
то на окружности  имеем
имеем

и

Пользуясь неравенствами (55), (56) и  так как
так как  получим оценку для интеграла (54)
получим оценку для интеграла (54)

Числа  фиксированы. Поэтому из неравенства (57) имеем, что
фиксированы. Поэтому из неравенства (57) имеем, что

для всех z таких, что 
Число  может быть выбрано сколь угодно большим. Поэтому условие (58) выполняется при любом комплексном
может быть выбрано сколь угодно большим. Поэтому условие (58) выполняется при любом комплексном  Следовательно, при любом комплексном z функция
Следовательно, при любом комплексном z функция  представляется в виде суммы ряда Ньютона (51) с узлами интерполяции (52), удовлетворяющими условиям (53).
представляется в виде суммы ряда Ньютона (51) с узлами интерполяции (52), удовлетворяющими условиям (53).
Итак,

где

Выбирая за контур С окружность  где
где  аналогично тому, как в случае оценки интеграла (54), получим оценку сверху для
аналогично тому, как в случае оценки интеграла (54), получим оценку сверху для 

где число  зависит только от
зависит только от 
Для доказательства теоремы 6 будет необходима оценка  снизу. Для этого докажем одно вспомогательное предложение
снизу. Для этого докажем одно вспомогательное предложение
Условие (53), определяющее последовательность узлов интерполяции (52), позволяет представить  следующим образом:
следующим образом:

где целые числа  зависящие от
зависящие от  удовлетворяют условиям
удовлетворяют условиям

Поэтому равенства (60) примут вид

Пусть  общее наименьшее кратное чисел
общее наименьшее кратное чисел 

Лемма 3. Пусть  определено равенством (64), а число
определено равенством (64), а число  равенством (65).
равенством (65).
Тогда существует многочлен

такой, что

и

Доказательство. По теореме Коши из равенства (64) имеем

где  окружность
окружность  с обходом в положительном направлении.
с обходом в положительном направлении.
Разложим функцию  в ряд Тейлора по степеням
в ряд Тейлора по степеням  к).
к).

Тогда

где  - целая функция, имеющая в точке
- целая функция, имеющая в точке  нуль порядка
нуль порядка  Поэтому по теореме Коши
Поэтому по теореме Коши

и

Обозначим при каждом 

Докажем, что все числа 
Число  равно вычету в точке
равно вычету в точке  подынтегральной функции в интеграле (72), т. е. коэффициенту при
подынтегральной функции в интеграле (72), т. е. коэффициенту при  в разложении этой функции в ряд Лорана по степеням
в разложении этой функции в ряд Лорана по степеням  . Найдем это разложение.
. Найдем это разложение.
Пусть  Рассмотрим функцию
Рассмотрим функцию

Положим

и разложим функцию (73) в ряд по степеням и. Получим

Ряд (75) абсолютно сходится в круге 
Так как  общее наименьшее кратное чисел
общее наименьшее кратное чисел  то все числа
то все числа  являются целыми и поэтому
являются целыми и поэтому 
Функция

является произведением  сомножителей вида
сомножителей вида  среди которых имеются и равные.
среди которых имеются и равные.
Перемножая ряды вида (75), соответствующие всем таким функциям  ввиду равенства (74), получим
ввиду равенства (74), получим

где все  По теореме о перемножении рядов ряды в равенстве (76) сходятся, соответственно, в кругах
По теореме о перемножении рядов ряды в равенстве (76) сходятся, соответственно, в кругах 
По теореме о вычетах из равенств (72) и (76) находим, что

Из равенств (77) имеем, что 
Из равенств (70), (71) и (72) получаем

откуда, ввиду равенств (77), следует, что существует многочлен  степени которого по х и у удовлетворяют неравенствам (67), и такой, что выполняется равенство (69).
степени которого по х и у удовлетворяют неравенствам (67), и такой, что выполняется равенство (69).
Оценим числа  пользуясь представлением (72). Если
пользуясь представлением (72). Если  то
то  а при
а при  к имеем, что
к имеем, что  Поэтому
Поэтому

Из равенств (69) и (78) и неравенств (79) получаем, что высота многочлена  удовлетворяет неравенству (68).
удовлетворяет неравенству (68).
Доказательство теоремы 6. Допустим противное, что  являются алгебраическими числами,
являются алгебраическими числами,  Пусть
Пусть  степень алгебраического поля, которому принадлежат
степень алгебраического поля, которому принадлежат 
Рассмотрим разложение (59) функции  в интерполяционный ряд Ньютона с узлами интерполяции (52), удовлетворяющими условиям (53), положив
в интерполяционный ряд Ньютона с узлами интерполяции (52), удовлетворяющими условиям (53), положив 
По доказанному для коэффициентов  этого разложения имеет место оценка сверху (61), а по лемме 3 выполняется равенство (69), где
этого разложения имеет место оценка сверху (61), а по лемме 3 выполняется равенство (69), где  а степени по х и у и высота
а степени по х и у и высота  удовлетворяют неравенствам (67) и (68).
удовлетворяют неравенствам (67) и (68).
Пусть  обозначают положительные постоянные, зависящие только от чисел
обозначают положительные постоянные, зависящие только от чисел 
По теореме 11 гл. 1 ввиду предположения, что  либо выполняется равенство
либо выполняется равенство  либо
либо

где  как это следует из неравенств (67) и (68).
как это следует из неравенств (67) и (68).
Так как  а из неравенства (65) следует, что
а из неравенства (65) следует, что  из неравенства (80) получаем оценку
из неравенства (80) получаем оценку

Из равенства (69) и неравенства (61) имеем, что

Неравенства (81) и (82) при достаточно большом  противоречивы. Следовательно, существует число
противоречивы. Следовательно, существует число  такое, что
такое, что  при всех
при всех  а функция
а функция  должна быть многочленом, что невозможно. Полученное противоречие доказывает утверждение теоремы 6.
должна быть многочленом, что невозможно. Полученное противоречие доказывает утверждение теоремы 6.
Теорема Линдемана о линейной независимости над полем алгебраических чисел значений в алгебраических точках показательной функции будет доказана другим методом с помощью построения системы линейных форм с коэффициентами из  от рассматриваемой совокупности показательных функций. Как будет показано, он тесно связан с методом, изложенным в § 3. Ознакомление с этим новым методом будет полезно для читателя, так как в дальнейшем он будет существенно обобщен и применен к более широкому классу функций. Его изложение начнем с простейшего случая — приближения показательной функции рациональными функциями.
от рассматриваемой совокупности показательных функций. Как будет показано, он тесно связан с методом, изложенным в § 3. Ознакомление с этим новым методом будет полезно для читателя, так как в дальнейшем он будет существенно обобщен и применен к более широкому классу функций. Его изложение начнем с простейшего случая — приближения показательной функции рациональными функциями.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Приближение алгебраических чисел
- § 2. Классический метод Эрмита — Линдемана
- § 3. Методы, возникшие при решении седьмой проблемы Гильберта, и их дальнейшее развитие
- § 4. Метод Зигеля и его дальнейшее развитие
- Глава 1. ПРИБЛИЖЕНИЕ ДЕЙСТВИТЕЛЬНЫХ И АЛГЕБРАИЧЕСКИХ ЧИСЕЛ
- § 1. Приближение действительных чисел рациональными числами
- § 2. Совместные приближения
- § 3. Приближение алгебраических чисел рациональными числами
- § 4. Приближение алгебраических чисел алгебраическими числами
- § 5. Дальнейшие усиления и обобщения теоремы Лиувилля
- Замечания
- Глава 2. АРИФМЕТИЧЕСКИЕ СВОЙСТВА ЗНАЧЕНИЙ ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ В АЛГЕБРАИЧЕСКИХ ТОЧКАХ
- § 1. Трансцендентность числа e
- § 2. Трансцендентность числа «пи»
- § 3. Трансцендентность значений показательной функции в алгебраических точках
- § 4. Приближение функции e^z рациональными функциями
- § 5. Линейная приближающая форма для функции …
- § 6. Совокупность линейных приближающих форм
- § 7. Теорема Линдемана
- § 8. Линейные приближающие формы и разложение показательной функции в интерполяционный ряд Ньютона
- Замечания
- Глава 3. ТРАНСЦЕНДЕНТНОСТЬ И АЛГЕБРАИЧЕСКАЯ НЕЗАВИСИМОСТЬ ЗНАЧЕНИЙ Е-ФУНКЦИЙ, НЕ СВЯЗАННЫХ АЛГЕБРАИЧЕСКИМИ УРАВНЕНИЯМИ НАД ПОЛЕМ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
- § 1. Е-функции
- § 2. Первая основная теорема
- § 3. Некоторые свойства линейных и дробно-линейных форм
- § 4. Свойства линейных форм от функций, удовлетворяющих системе линейных однородных дифференциальных уравнений
- § 5. Порядок нуля линейной формы при z = 0
- § 6. Определитель системы линейных форм
- § 7. Переход к числовым линейно независимым линейным формам
- § 8. Вспомогательные предложения о решениях систем линейных однородных уравнений
- § 9. Функциональные линейные приближающие формы
- § 10. Числовые линейные приближающие формы
- § 11. Ранг совокупности чисел
- § 12. Доказательство первой основной теоремы
- § 13. Следствия из первой основной теоремы
- Замечания
- Глава 4. ТРАНСЦЕНДЕНТНОСТЬ И АЛГЕБРАИЧЕСКАЯ НЕЗАВИСИМОСТЬ ЗНАЧЕНИЙ Е-ФУНКЦИЙ, СВЯЗАННЫХ АЛГЕБРАИЧЕСКИМИ УРАВНЕНИЯМИ НАД ПОЛЕМ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
- § 2. Вспомогательные предложения
- § 3. Оценки размерностей векторных пространств, порожденных произведениями степеней элементов из расширения некоторого поля
- § 4. Третья основная теорема
- § 5. Трансцендентность значений Е-функций, связанных произвольными алгебраическими уравнениями над C(z)
- § 6. Алгебраическая независимость значений Е-функций, связанных произвольными алгебраическими уравнениями над C(z)
- § 7. Е-функции, связанные уравнениями специального вида
- § 8. Е-функции, связанные алгебраическими уравнениями с постоянными коэффициентами
- § 9. Е-функции, связанные одним алгебраическим уравнением вид C(z)
- § 10. Минимальные уравнения
- § 11. Размерности векторных пространств, порожденных произведениями степеней элементов из расширения некоторого поля
- § 12. Алгебраическая независимость значений IE-функций
- § 13. Алгебраическая независимость значений КЕ-функций
- Замечания
- Глава 5. ТРАНСЦЕНДЕНТНОСТЬ И АЛГЕБРАИЧЕСКАЯ НЕЗАВИСИМОСТЬ ЗНАЧЕНИЙ Е-ФУНКЦИЙ, УДОВЛЕТВОРЯЮЩИХ ЛИНЕЙНЫМ ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ ПЕРВОГО ПОРЯДКА
- § 1. Гипергеометрические Е-функции
- § 2. Простейшая гипергеометрическая Е-функция
- § 3. Совокупность решений линейных дифференциальных уравнений первого порядка
- § 4. Вспомогательные предложения
- § 5. Доказательства теорем
- Замечания
- Глава 6. АЛГЕБРАИЧЕСКАЯ НЕЗАВИСИМОСТЬ ЗНАЧЕНИИ Е-ФУНКЦИЙ, УДОВЛЕТВОРЯЮЩИХ ЛИНЕЙНЫМ ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ ВТОРОГО ПОРЯДКА
- § 1. Общая теорема об алгебраической независимости значений Е-функции и ее производной
- § 2. Функции K(z), связанные с функциями Бесселя
- § 3. Функции …
- § 4. Функции Куммера
- § 5. Решения линейных неоднородных дифференциальных уравнений
- Глава 7. РЕШЕНИЯ НЕКОТОРЫХ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПРОИЗВОЛЬНОГО ПОРЯДКА
- § 1. Решения неоднородных дифференциальных уравнений
- § 2. Решения однородных дифференциальных уравнений
- § 3. Следствия из теорем 1 и 2
- Глава 8. ИССЛЕДОВАНИЕ РЕШЕНИЙ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПРОИЗВОЛЬНОГО ПОРЯДКА АРИФМЕТИЧЕСКИМ МЕТОДОМ
- § 2. Вспомогательные предложения
- § 3. Доказательства теорем 1—5
- § 4. Доказательства теорем 6 и 7
- § 5. Дальнейшие результаты
- Глава 9. ТЕОРЕМА ЗИГЕЛЯ
- § 2. Вспомогательные предложения
- § 3. Некоторые свойства решений линейных однородных дифференциальных уравнений второго порядка
- § 4. Алгебраическая независимость решений совокупности линейных однородных дифференциальных уравнений второго порядка
- § 5. Доказательство теоремы Зигеля
- § 6. Решения линейных неоднородных дифференциальных уравнении
- § 7. Обобщение теоремы Зигеля
- Глава 10. РЕШЕНИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПРОСТОГО ПОРЯДКА p
- § 2. Однородный идеал J
- § 3. Алгебраические функции нескольких переменных
- § 4. Дифференциальный оператор G
- § 5. Дифференциальные операторы S и «дельта»
- § 6. Лемма о линейном приближении
- § 7. Завершение доказательства теоремы 7
- § 8. Линейная приводимость
- § 9. Доказательства теорем 6 и 5
- Замечания
- Глава 11. МЕРА АЛГЕБРАИЧЕСКОЙ НЕЗАВИСИМОСТИ ЗНАЧЕНИЙ IE-ФУНКЦИЙ
- § 2. Мера линейной независимости значений IE-функций
- § 3. Мера алгебраической независимости значений IE-функций, не связанных алгебраическими уравнениями над C(z)
- § 4. Вспомогательные предложения
- § 5. Мера алгебраической независимости значений IE-функций, связанных алгебраическими уравнениями над C(z)
- § 6. Некоторые применения общих теорем
- Глава 12. МЕРА АЛГЕБРАИЧЕСКОЙ НЕЗАВИСИМОСТИ ЗНАЧЕНИЙ КЕ-ФУНКЦИЙ
- § 2. Оценки мер значений Е-функций, не связанных алгебраическими уравнениями над C(z)
- § 3. Оценки мер значений Е-функций, связанных одним алгебраическим уравнением над C(z)
- § 4. Оценки мер значений Е-функций, связанных произвольными алгебраическими уравнениями над C(z)
- § 5. Алгебраическая независимость значений Е-функций в сопряженных полях
- § 6. Вспомогательная теорема
- § 7. Следствия из вспомогательной теоремы
- § 8. Некоторые применения общих теорем
- Глава 13. ЭФФЕКТИВНЫЕ ОЦЕНКИ МЕР
- § 2. Уточнение основных лемм метода
- § 3. Оценка мер линейной независимости
- § 4. Оценка мер алгебраической независимости
- § 5. Некоторые применения общих теорем
- ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
- СПИСОК ЛИТЕРАТУРЫ