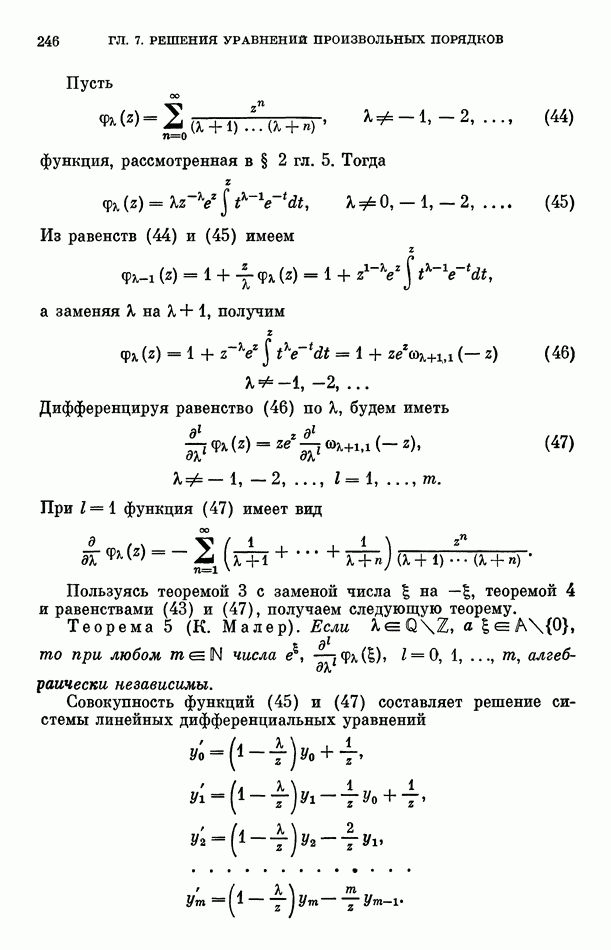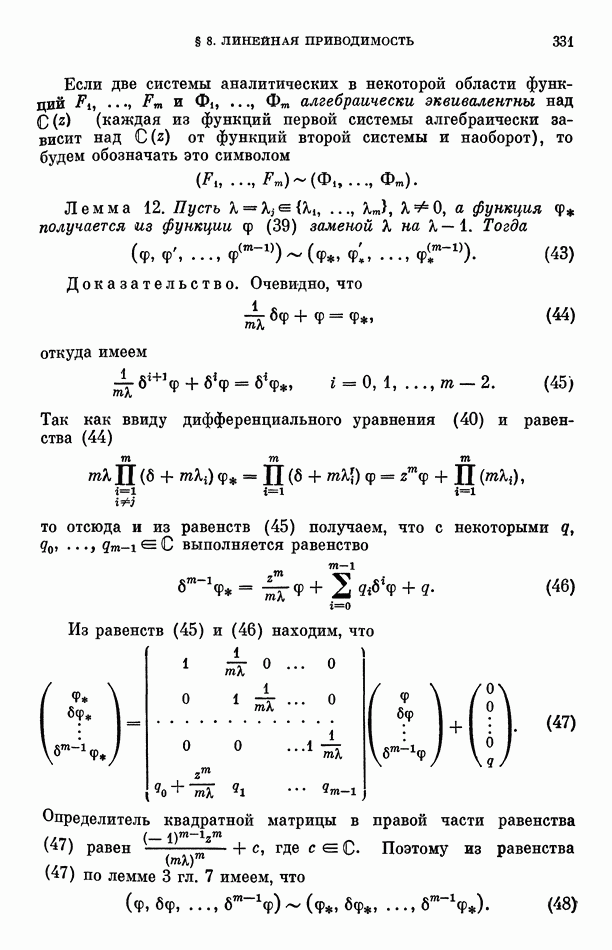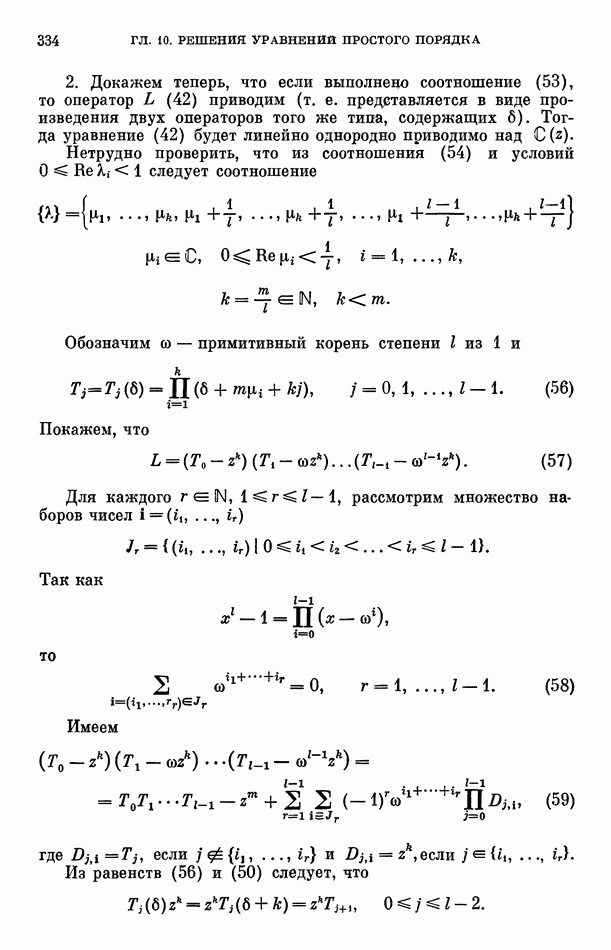| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 6. Решения линейных неоднородных дифференциальных уравнении
Метод, изложенный в § 2—5, а также некоторые другие методы доказательства алгебраической независимости решений линейных дифференциальных уравнений, не позволяют вести непосредственно исследование алгебраической независимости решений неоднородных дифференциальных уравнений.
В гл. 6 (теоремы 6 и 7) было показано, что если рассматриваемые функции, удовлетворяющие линейному неоднородному дифференциальному уравнению или системе линейных
неоднородных дифференциальных уравнений, связаны не более чем одним алгебраическим уравнением над полем  то исследование алгебраической независимости этих функций сводится к исследованию алгебраической независимости решений соответствующего однородного дифференциального уравнения или соответствующей однородной системы дифференциальных уравнений. Там же были приведены примеры приложения этих теорем к конкретным Е-функциям.
то исследование алгебраической независимости этих функций сводится к исследованию алгебраической независимости решений соответствующего однородного дифференциального уравнения или соответствующей однородной системы дифференциальных уравнений. Там же были приведены примеры приложения этих теорем к конкретным Е-функциям.
В § 6 будет показано, что указанный переход от исследования неоднородных дифференциальных уравнений к однородным возможен при наличии любого числа алгебраических уравнений, связывающих рассматриваемые функции над  Этот переход был обоснован Ю. В. Нестеренко в 1969 г. в работе
Этот переход был обоснован Ю. В. Нестеренко в 1969 г. в работе  Все доказываемые в § 7 теоремы содержатся в этой работе.
Все доказываемые в § 7 теоремы содержатся в этой работе.
По-прежнему  будет обозначать поле аналитических функций от z, замкнутое относительно операции дифференцирования и содержащее поле С.
будет обозначать поле аналитических функций от z, замкнутое относительно операции дифференцирования и содержащее поле С.
Теорема 2. Пусть совокупность аналитических функций

составляет решение системы линейных дифференциальных уравнений

а любое нетривиальное решение соответствующей однородной системы дифференциальных уравнений

состоит из функций алгебраически независимых над 
Тогда функции (55) или алгебраически независимы над полем  или все принадлежат
или все принадлежат 
Доказательство. Предположим, что функции (55) алгебраически зависимы над  Для каждого многочлена
Для каждого многочлена  будем обозначать
будем обозначать  сумму членов старшей степени, входящих в
сумму членов старшей степени, входящих в  Пусть
Пусть  идеал в кольце
идеал в кольце  состоящий из всех многочленов
состоящий из всех многочленов  таких, что
таких, что  — идеал, порожденный всеми многочленами
— идеал, порожденный всеми многочленами  такими, что
такими, что  а
а

и

— дифференциальные операторы, связанные с системами дифференциальных уравнений (56) и (57), действующие в кольце 
Из равенства (15) следует, что  Пусть Так как
Пусть Так как  то
то  а так как
а так как  равно либо 0, либо
равно либо 0, либо  то
то  Отсюда следует, что
Отсюда следует, что  Предположим, что 9° имеет нетривиальный нуль. Тогда, пользуясь утверждением 2° леммы 3, получим противоречие с условием теоремы. Следовательно, идеал
Предположим, что 9° имеет нетривиальный нуль. Тогда, пользуясь утверждением 2° леммы 3, получим противоречие с условием теоремы. Следовательно, идеал  имеет единственный нуль (
имеет единственный нуль ( . Тогда по теореме Гильберта о нулях с некоторым целым
. Тогда по теореме Гильберта о нулях с некоторым целым  для каждого
для каждого  имеем
имеем 
Пусть  образуют базис идеала 9°. Такие многочлены найдутся, так как
образуют базис идеала 9°. Такие многочлены найдутся, так как  порожден многочленами
порожден многочленами  Тогда существуют однородные многочлены
Тогда существуют однородные многочлены  для которых
для которых

Обозначим

Так как  »
»  то и, значит
то и, значит  а поскольку
а поскольку  то
то  является линейной комбинацией произведений степеней
является линейной комбинацией произведений степеней

с показателями, удовлетворяющими неравенствам к  и коэффициентами из
и коэффициентами из  Отсюда же следует, что линейное пространство над
Отсюда же следует, что линейное пространство над  порожденное всевозможными произведениями степеней (58) с
порожденное всевозможными произведениями степеней (58) с  конечномерно и, значит, все функции (55) алгебраичны над
конечномерно и, значит, все функции (55) алгебраичны над 
Пусть  совокупность функций, сопряженных с функциями (55) над
совокупность функций, сопряженных с функциями (55) над  По лемме 2 функции
По лемме 2 функции  также составляют решение системы дифференциальных уравнений (55). Тогда функции
также составляют решение системы дифференциальных уравнений (55). Тогда функции  образуют решение системы однородных дифференциальных уравнений (57), состоящее из функций алгебраических над полем
образуют решение системы однородных дифференциальных уравнений (57), состоящее из функций алгебраических над полем  По условию теоремы это возможно только, если
По условию теоремы это возможно только, если  Следовательно, все совокупности функций, сопряженные для функций (55) над полем
Следовательно, все совокупности функций, сопряженные для функций (55) над полем  совпадают с функциями (55). Это означает, что
совпадают с функциями (55). Это означает, что  Теорема доказана.
Теорема доказана.
Заметим, что при условиях теоремы 2 могут иметь место обе рассмотренные в ней ситуации. Например, уравнение 
 имеет как рациональное решение
имеет как рациональное решение  так и трансцендентное
так и трансцендентное 
Докажем теперь более общую теорему о решениях совокупности неоднородных систем дифференциальных уравнений.
Рассмотрим совокупность  систем линейных дифференциальных уравнений
систем линейных дифференциальных уравнений

и совокупность соответствующих однородных систем дифференциальных уравнений

Теорема 3. Пусть для любого набора нетривиальных решений систем  совокупность
совокупность  функций, входящих в него, алгебраически независима над полем
функций, входящих в него, алгебраически независима над полем  , а
, а

— совокупность решений систем (59) такая, что при каждом  хотя бы одна из функций (60) не принадлежит
хотя бы одна из функций (60) не принадлежит  .
.
Тогда функции (60) алгебраически независимы над полем  .
.
Доказательство. Проведем его индукцией по  числу систем (59). При
числу систем (59). При  утверждение теоремы 3 следует из теоремы 2. Допустим, что теорема справедлива, когда число систем (59) меньше
утверждение теоремы 3 следует из теоремы 2. Допустим, что теорема справедлива, когда число систем (59) меньше  Докажем, что тогда она выполняется и для
Докажем, что тогда она выполняется и для  систем (59).
систем (59).
Пусть I обозначает число неоднородных систем среди систем (59). Если  то утверждение теоремы имеет место. Предположим, что теорема доказана для всех наборов по
то утверждение теоремы имеет место. Предположим, что теорема доказана для всех наборов по  систем, в которых число неоднородных систем меньше
систем, в которых число неоднородных систем меньше  Если
Если  то, не уменьшая общности доказательства, можно считать, что система
то, не уменьшая общности доказательства, можно считать, что система  однородна.
однородна.
Обозначим  поле, полученное присоединим к полю
поле, полученное присоединим к полю  функций
функций  Поле
Поле  замкнуто относительно операции дифференцирования. Любой набор нетривиальных решений систем
замкнуто относительно операции дифференцирования. Любой набор нетривиальных решений систем  состоит из функций алгебраически независимых над
состоит из функций алгебраически независимых над  При
При  это следует из выбора системы
это следует из выбора системы  и условия теоремы. При
и условия теоремы. При  из предположения относительно
из предположения относительно 
Предположим, что найдется такое  например
например  что все Функции соответствующего решения принадлежат
что все Функции соответствующего решения принадлежат  :
:

Обозначим  дифференциальные операторы, соответствующие системам
дифференциальные операторы, соответствующие системам  и в дальнейшем, для краткости, коэффициенты системы
и в дальнейшем, для краткости, коэффициенты системы  вместо
вместо  будем обозначать
будем обозначать  Итак, существуют рациональные функции
Итак, существуют рациональные функции  , такие, что
, такие, что

Оператор  можно продолжить с кольца
можно продолжить с кольца  на поле рациональных функций
на поле рациональных функций  по правилу
по правилу

Тогда для  имеем
имеем

В частности,

Поскольку по теореме 2 функции  алгебраически независимы над
алгебраически независимы над  то
то

Если  рациональная функция, то степенью
рациональная функция, то степенью  будем называть разность степеней многочленов
будем называть разность степеней многочленов 
Пусть  наибольшая из степеней функций
наибольшая из степеней функций  если степень
если степень  меньше
меньше  и равно отношению суммы однородных членов старшей степени числителя и знаменателя
и равно отношению суммы однородных членов старшей степени числителя и знаменателя  если степень
если степень  равна
равна 
Предположим, что  Тогда, сравнивая в равенствах (62) слева и справа члены степени
Тогда, сравнивая в равенствах (62) слева и справа члены степени  получим
получим

Пусть  нетривиальное решение системы
нетривиальное решение системы  Обозначим
Обозначим

Среди функций  хоть одна отлична от нуля, так как не все
хоть одна отлична от нуля, так как не все  равны
равны  алгебраически независимы над
алгебраически независимы над  Из равенств (63) следует, что
Из равенств (63) следует, что  есть решение
есть решение  но тогда равенство (64) противоречит условию теоремы. Следовательно,
но тогда равенство (64) противоречит условию теоремы. Следовательно,  и из равенств (62) имеем
и из равенств (62) имеем

В равенствах 
Пусть  где
где  — наименьший общий знаменатель всех рациональных функций
— наименьший общий знаменатель всех рациональных функций  Покажем, что
Покажем, что  . При
. При  очевидно, это имеет место. Пусть
очевидно, это имеет место. Пусть  Тогда, подставляя в равенства
Тогда, подставляя в равенства  и пользуясь равенством (61), получаем равенство
и пользуясь равенством (61), получаем равенство

Отсюда, так как В — наименьший общий знаменатель, получаем, что В делит  значит, однородный главный идеал
значит, однородный главный идеал  замкнут относительно применения оператора
замкнут относительно применения оператора  Если предположить, что
Если предположить, что  то тогда, так как
то тогда, так как  будет иметь нетривиальный нуль. Пользуясь леммой 3 придем к противоречию с условием теоремы. Следовательно,
будет иметь нетривиальный нуль. Пользуясь леммой 3 придем к противоречию с условием теоремы. Следовательно,  т. е.
т. е.  .
.
А так как все  имеют степень 0, то и все
имеют степень 0, то и все  Отсюда имеем, что и из равенств (65) следует, что
Отсюда имеем, что и из равенств (65) следует, что  есть решение
есть решение 
Обозначим  Так как
Так как  Поскольку
Поскольку  являются решениями
являются решениями  то
то  есть решение
есть решение  Но по доказанному выше нетривиальные решения систем
Но по доказанному выше нетривиальные решения систем  алгебраически независимы над
алгебраически независимы над  Поэтому
Поэтому  значит,
значит, 
Полученное утверждение противоречит условию теоремы и показывает, что для каждого  не все функции
не все функции  принадлежат
принадлежат  Пользуясь предположением индукции, получаем, что
Пользуясь предположением индукции, получаем, что  функций
функций  алгебраически независимы над
алгебраически независимы над  Это доказывает теорему, так как функции
Это доказывает теорему, так как функции  по теореме 2 алгебраически независимы над 2.
по теореме 2 алгебраически независимы над 2.
Теорема 3 может быть переформулирована на случай решений нескольких линейных дифференциальных уравнений. Теорема 4. Пусть дифференциальные уравнения

таковы, что для любых нетривиальных решений  однородных дифференциальных уравнений, соответствующих уравнениям (66), функции
однородных дифференциальных уравнений, соответствующих уравнениям (66), функции

алгебраически независимы над  решения уравнений (66) такие, что
решения уравнений (66) такие, что 
Тогда функции

алгебраически независимы над 
Применим полученные результаты к конкретным функциям. Рассмотрим гипергеометрическую функцию

удовлетворяющую линейному неоднородному дифференциальному уравнению

Теорема 5. Пусть  и удовлетворяют условиям
и удовлетворяют условиям

а алгебраические числа  таковы,
таковы,  числа
числа  отличны друг от друга и от нуля.
отличны друг от друга и от нуля.
Тогда  чисел
чисел

алгебраически независимы.
Для доказательства теоремы 5 установим следующую лемму. Лемма 8. Пусть числа  удовлетворяют условиям теоремы 5, а комплексные числа
удовлетворяют условиям теоремы 5, а комплексные числа  таковы, что
таковы, что  отличны друг от друга и от нуля.
отличны друг от друга и от нуля.
Тогда  функций
функций

алгебраически независимы над 
Доказательство. Пусть  есть поле алгебраических функций от
есть поле алгебраических функций от  . Очевидно, достаточно доказать алгебраическую независимость функций (68) над полем
. Очевидно, достаточно доказать алгебраическую независимость функций (68) над полем 
Рассмотрим совокупность функций

Эти функции трансцендентны и являются решениями дифференциальных уравнений

Коэффициенты дифференциальных уравнений (70) принадлежат полю  а соответствующие им однородные дифференциальные уравнения того же типа, что и уравнения (43), полученные из уравнения Бесселя. Эти однородные уравнения удовлетворяют условиям леммы 6. Тогда из леммы 6 следует, что для дифференциальных уравнений (70) выполнены все условия теоремы 4, по которой функции (69) вместе с функциями
а соответствующие им однородные дифференциальные уравнения того же типа, что и уравнения (43), полученные из уравнения Бесселя. Эти однородные уравнения удовлетворяют условиям леммы 6. Тогда из леммы 6 следует, что для дифференциальных уравнений (70) выполнены все условия теоремы 4, по которой функции (69) вместе с функциями  алгебраически независимы над полем
алгебраически независимы над полем  Поскольку
Поскольку  то и функции (68) алгебраически независимы над
то и функции (68) алгебраически независимы над  Лемма доказана.
Лемма доказана.
Доказательство теоремы 5. Совокупность  -функций (68) составляет решение системы линейных дифференциальных уравнений
-функций (68) составляет решение системы линейных дифференциальных уравнений

и по лемме 8 алгебраически независима над  Поэтому Утверждение теоремы 5 следует из второй основной теоремы гл. 3.
Поэтому Утверждение теоремы 5 следует из второй основной теоремы гл. 3.
Заметим, что теорема 5 впервые была установлена
А. А. Шмелевым в 1969 г. [29 : 1]. Его доказательство алгебраической независимости соответствующих функций было довольно сложным. В нем использовался метод работы [28 : 9].
И. И. Белогривов в 1971 г. в статье [1:4] исследовал функции Куммера

рассмотренные в § 4 гл. 6. Он доказал следующую теорему, аналогичную теореме Зигеля.
Теорема 6. Пусть  удовлетворяют условиям
удовлетворяют условиям

а  алгебраические числа линейно независимые над
алгебраические числа линейно независимые над 
Тогда  чисел
чисел

алгебраически независимы.
Теорема 6 может быть доказана аналогично теореме Зигеля с помощью вспомогательных предложений 
Рассмотрим гипергеометрическую Е-функцию

являющуюся решением дифференциального уравнения

Используя алгебраическую независимость над  функций, составляющих решение совокупности дифференциальных уравнений, рассмотренных в теореме 6, с помощью теоремы 4 можно доказать теорему, аналогичную теореме 5.
функций, составляющих решение совокупности дифференциальных уравнений, рассмотренных в теореме 6, с помощью теоремы 4 можно доказать теорему, аналогичную теореме 5.
Теорема 7. Пусть  и удовлетворяют условиям:
и удовлетворяют условиям:

 алгебраические числа линейно независимые над
алгебраические числа линейно независимые над 
Тогда  чисел
чисел

алгебраически независимы.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Приближение алгебраических чисел
- § 2. Классический метод Эрмита — Линдемана
- § 3. Методы, возникшие при решении седьмой проблемы Гильберта, и их дальнейшее развитие
- § 4. Метод Зигеля и его дальнейшее развитие
- Глава 1. ПРИБЛИЖЕНИЕ ДЕЙСТВИТЕЛЬНЫХ И АЛГЕБРАИЧЕСКИХ ЧИСЕЛ
- § 1. Приближение действительных чисел рациональными числами
- § 2. Совместные приближения
- § 3. Приближение алгебраических чисел рациональными числами
- § 4. Приближение алгебраических чисел алгебраическими числами
- § 5. Дальнейшие усиления и обобщения теоремы Лиувилля
- Замечания
- Глава 2. АРИФМЕТИЧЕСКИЕ СВОЙСТВА ЗНАЧЕНИЙ ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ В АЛГЕБРАИЧЕСКИХ ТОЧКАХ
- § 1. Трансцендентность числа e
- § 2. Трансцендентность числа «пи»
- § 3. Трансцендентность значений показательной функции в алгебраических точках
- § 4. Приближение функции e^z рациональными функциями
- § 5. Линейная приближающая форма для функции …
- § 6. Совокупность линейных приближающих форм
- § 7. Теорема Линдемана
- § 8. Линейные приближающие формы и разложение показательной функции в интерполяционный ряд Ньютона
- Замечания
- Глава 3. ТРАНСЦЕНДЕНТНОСТЬ И АЛГЕБРАИЧЕСКАЯ НЕЗАВИСИМОСТЬ ЗНАЧЕНИЙ Е-ФУНКЦИЙ, НЕ СВЯЗАННЫХ АЛГЕБРАИЧЕСКИМИ УРАВНЕНИЯМИ НАД ПОЛЕМ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
- § 1. Е-функции
- § 2. Первая основная теорема
- § 3. Некоторые свойства линейных и дробно-линейных форм
- § 4. Свойства линейных форм от функций, удовлетворяющих системе линейных однородных дифференциальных уравнений
- § 5. Порядок нуля линейной формы при z = 0
- § 6. Определитель системы линейных форм
- § 7. Переход к числовым линейно независимым линейным формам
- § 8. Вспомогательные предложения о решениях систем линейных однородных уравнений
- § 9. Функциональные линейные приближающие формы
- § 10. Числовые линейные приближающие формы
- § 11. Ранг совокупности чисел
- § 12. Доказательство первой основной теоремы
- § 13. Следствия из первой основной теоремы
- Замечания
- Глава 4. ТРАНСЦЕНДЕНТНОСТЬ И АЛГЕБРАИЧЕСКАЯ НЕЗАВИСИМОСТЬ ЗНАЧЕНИЙ Е-ФУНКЦИЙ, СВЯЗАННЫХ АЛГЕБРАИЧЕСКИМИ УРАВНЕНИЯМИ НАД ПОЛЕМ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
- § 2. Вспомогательные предложения
- § 3. Оценки размерностей векторных пространств, порожденных произведениями степеней элементов из расширения некоторого поля
- § 4. Третья основная теорема
- § 5. Трансцендентность значений Е-функций, связанных произвольными алгебраическими уравнениями над C(z)
- § 6. Алгебраическая независимость значений Е-функций, связанных произвольными алгебраическими уравнениями над C(z)
- § 7. Е-функции, связанные уравнениями специального вида
- § 8. Е-функции, связанные алгебраическими уравнениями с постоянными коэффициентами
- § 9. Е-функции, связанные одним алгебраическим уравнением вид C(z)
- § 10. Минимальные уравнения
- § 11. Размерности векторных пространств, порожденных произведениями степеней элементов из расширения некоторого поля
- § 12. Алгебраическая независимость значений IE-функций
- § 13. Алгебраическая независимость значений КЕ-функций
- Замечания
- Глава 5. ТРАНСЦЕНДЕНТНОСТЬ И АЛГЕБРАИЧЕСКАЯ НЕЗАВИСИМОСТЬ ЗНАЧЕНИЙ Е-ФУНКЦИЙ, УДОВЛЕТВОРЯЮЩИХ ЛИНЕЙНЫМ ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ ПЕРВОГО ПОРЯДКА
- § 1. Гипергеометрические Е-функции
- § 2. Простейшая гипергеометрическая Е-функция
- § 3. Совокупность решений линейных дифференциальных уравнений первого порядка
- § 4. Вспомогательные предложения
- § 5. Доказательства теорем
- Замечания
- Глава 6. АЛГЕБРАИЧЕСКАЯ НЕЗАВИСИМОСТЬ ЗНАЧЕНИИ Е-ФУНКЦИЙ, УДОВЛЕТВОРЯЮЩИХ ЛИНЕЙНЫМ ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ ВТОРОГО ПОРЯДКА
- § 1. Общая теорема об алгебраической независимости значений Е-функции и ее производной
- § 2. Функции K(z), связанные с функциями Бесселя
- § 3. Функции …
- § 4. Функции Куммера
- § 5. Решения линейных неоднородных дифференциальных уравнений
- Глава 7. РЕШЕНИЯ НЕКОТОРЫХ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПРОИЗВОЛЬНОГО ПОРЯДКА
- § 1. Решения неоднородных дифференциальных уравнений
- § 2. Решения однородных дифференциальных уравнений
- § 3. Следствия из теорем 1 и 2
- Глава 8. ИССЛЕДОВАНИЕ РЕШЕНИЙ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПРОИЗВОЛЬНОГО ПОРЯДКА АРИФМЕТИЧЕСКИМ МЕТОДОМ
- § 2. Вспомогательные предложения
- § 3. Доказательства теорем 1—5
- § 4. Доказательства теорем 6 и 7
- § 5. Дальнейшие результаты
- Глава 9. ТЕОРЕМА ЗИГЕЛЯ
- § 2. Вспомогательные предложения
- § 3. Некоторые свойства решений линейных однородных дифференциальных уравнений второго порядка
- § 4. Алгебраическая независимость решений совокупности линейных однородных дифференциальных уравнений второго порядка
- § 5. Доказательство теоремы Зигеля
- § 6. Решения линейных неоднородных дифференциальных уравнении
- § 7. Обобщение теоремы Зигеля
- Глава 10. РЕШЕНИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПРОСТОГО ПОРЯДКА p
- § 2. Однородный идеал J
- § 3. Алгебраические функции нескольких переменных
- § 4. Дифференциальный оператор G
- § 5. Дифференциальные операторы S и «дельта»
- § 6. Лемма о линейном приближении
- § 7. Завершение доказательства теоремы 7
- § 8. Линейная приводимость
- § 9. Доказательства теорем 6 и 5
- Замечания
- Глава 11. МЕРА АЛГЕБРАИЧЕСКОЙ НЕЗАВИСИМОСТИ ЗНАЧЕНИЙ IE-ФУНКЦИЙ
- § 2. Мера линейной независимости значений IE-функций
- § 3. Мера алгебраической независимости значений IE-функций, не связанных алгебраическими уравнениями над C(z)
- § 4. Вспомогательные предложения
- § 5. Мера алгебраической независимости значений IE-функций, связанных алгебраическими уравнениями над C(z)
- § 6. Некоторые применения общих теорем
- Глава 12. МЕРА АЛГЕБРАИЧЕСКОЙ НЕЗАВИСИМОСТИ ЗНАЧЕНИЙ КЕ-ФУНКЦИЙ
- § 2. Оценки мер значений Е-функций, не связанных алгебраическими уравнениями над C(z)
- § 3. Оценки мер значений Е-функций, связанных одним алгебраическим уравнением над C(z)
- § 4. Оценки мер значений Е-функций, связанных произвольными алгебраическими уравнениями над C(z)
- § 5. Алгебраическая независимость значений Е-функций в сопряженных полях
- § 6. Вспомогательная теорема
- § 7. Следствия из вспомогательной теоремы
- § 8. Некоторые применения общих теорем
- Глава 13. ЭФФЕКТИВНЫЕ ОЦЕНКИ МЕР
- § 2. Уточнение основных лемм метода
- § 3. Оценка мер линейной независимости
- § 4. Оценка мер алгебраической независимости
- § 5. Некоторые применения общих теорем
- ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
- СПИСОК ЛИТЕРАТУРЫ