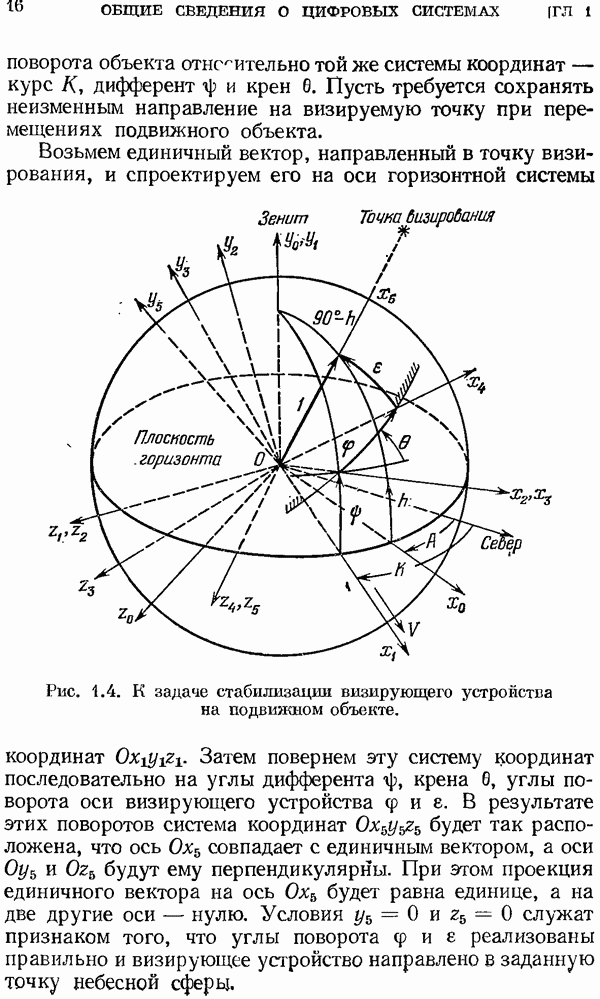
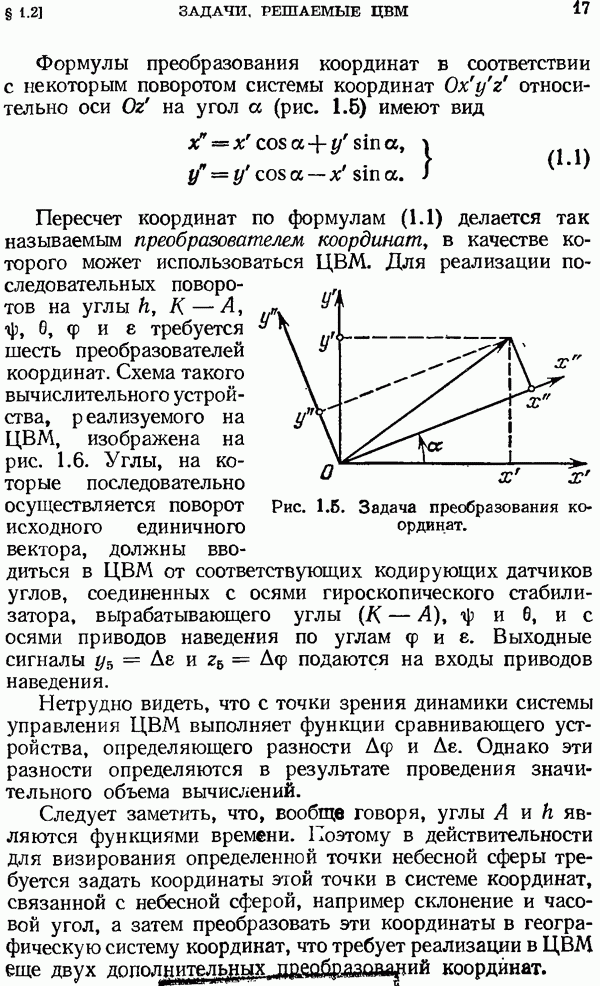
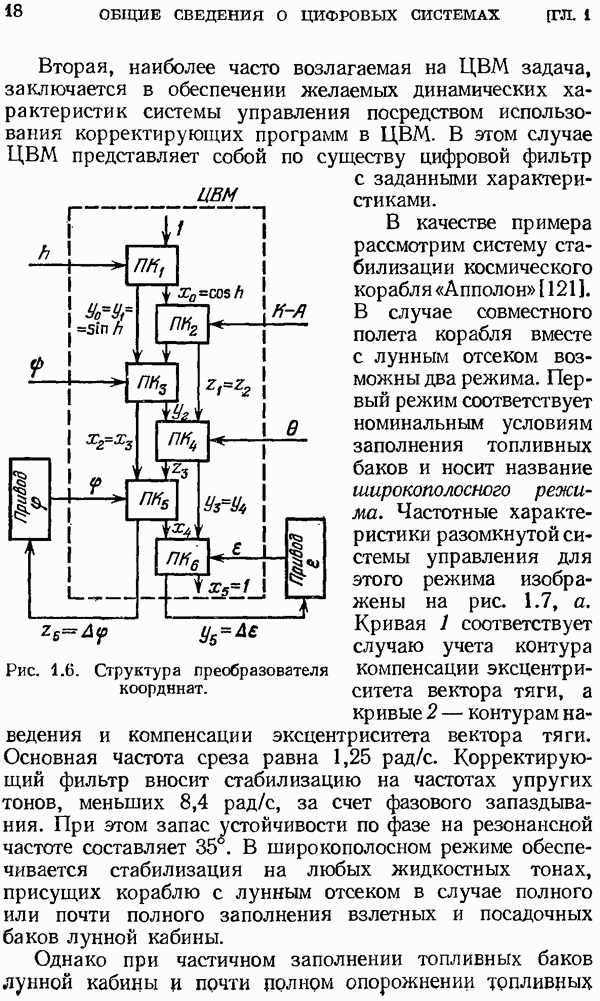
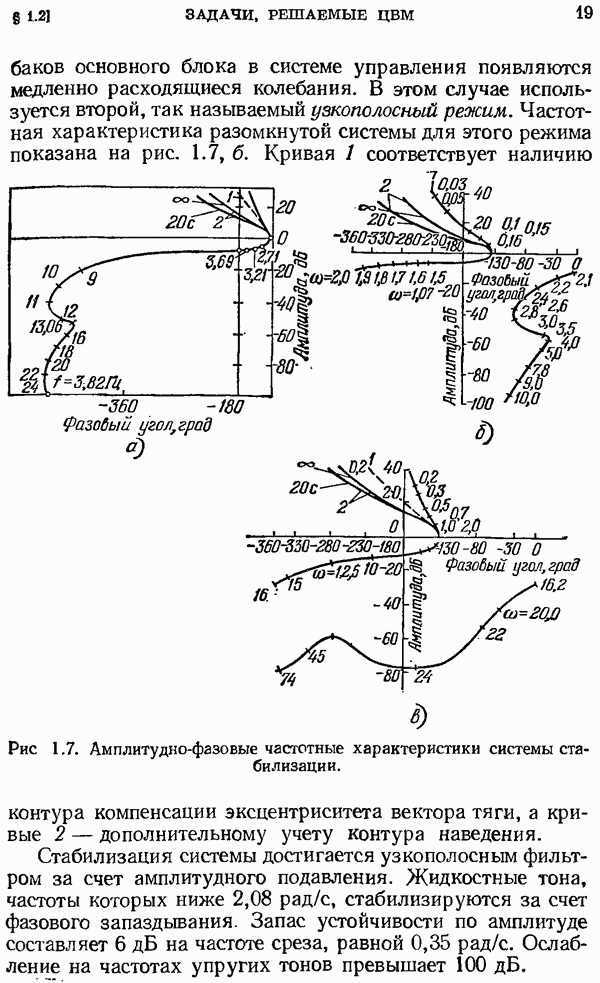
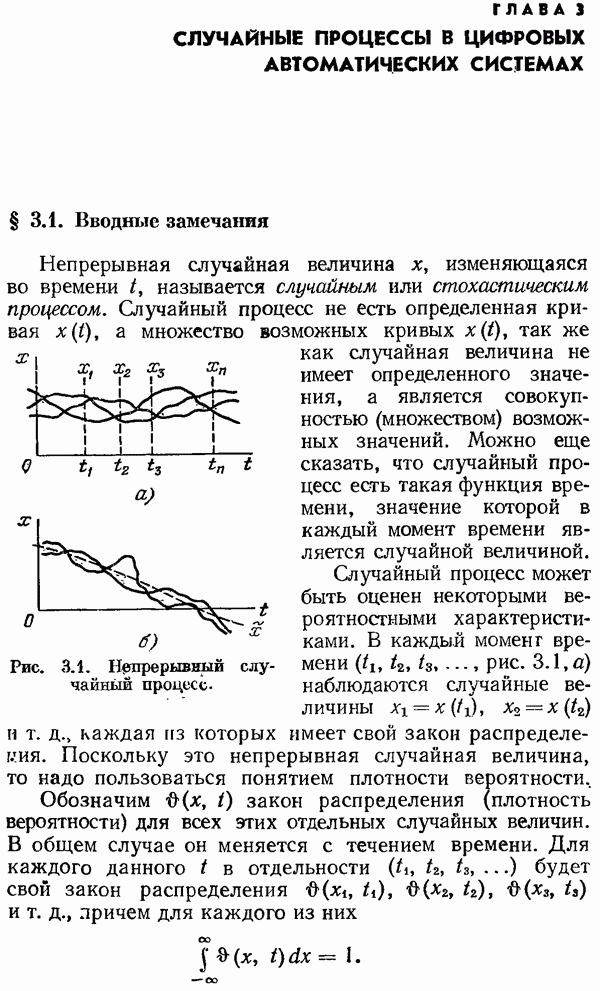
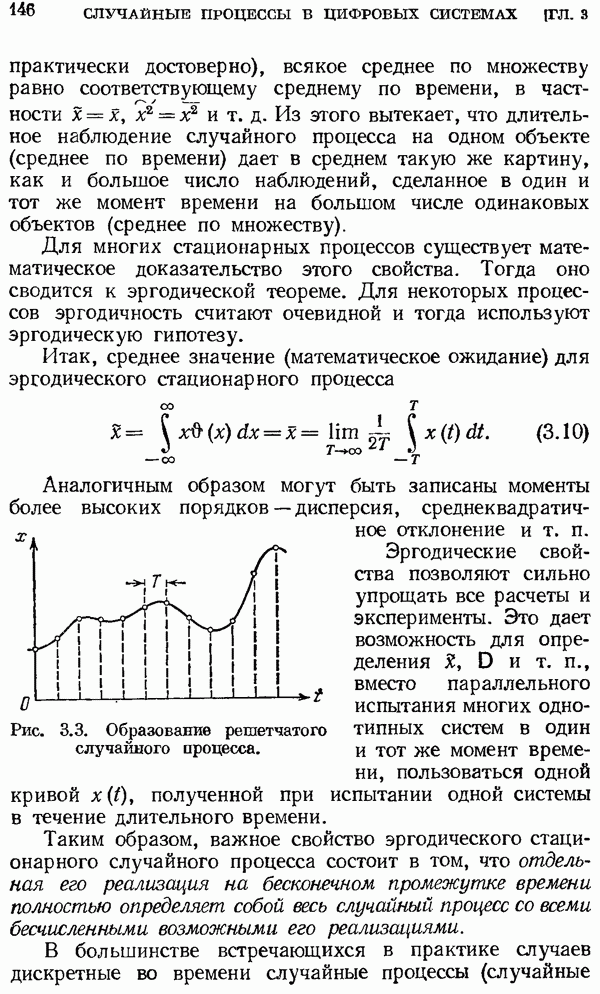
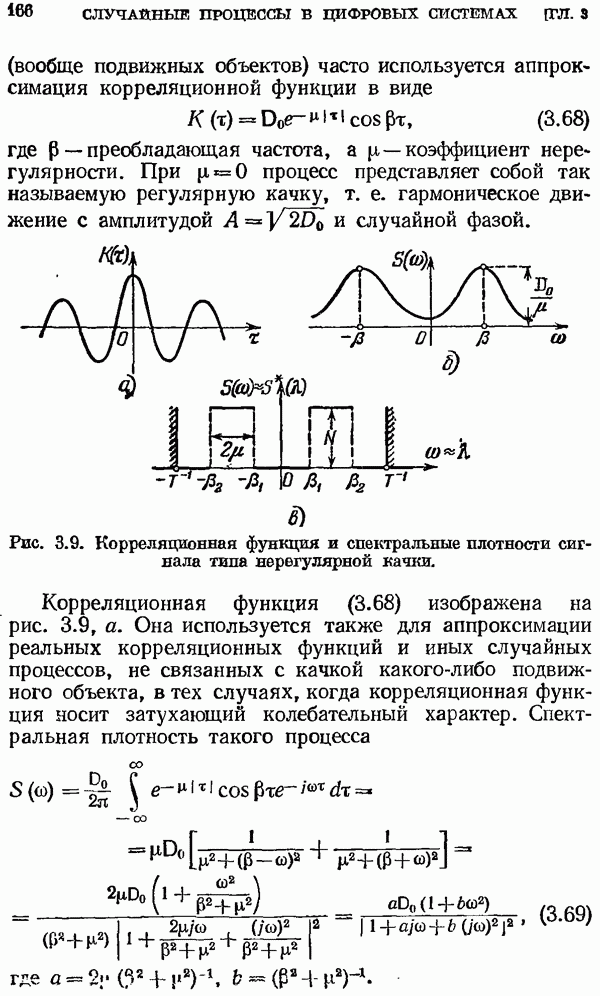
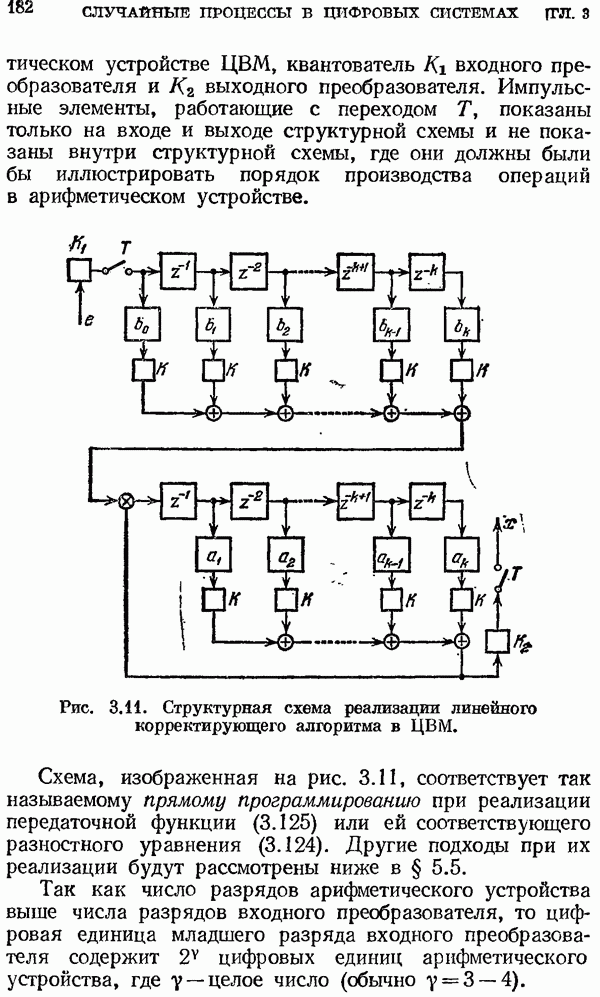
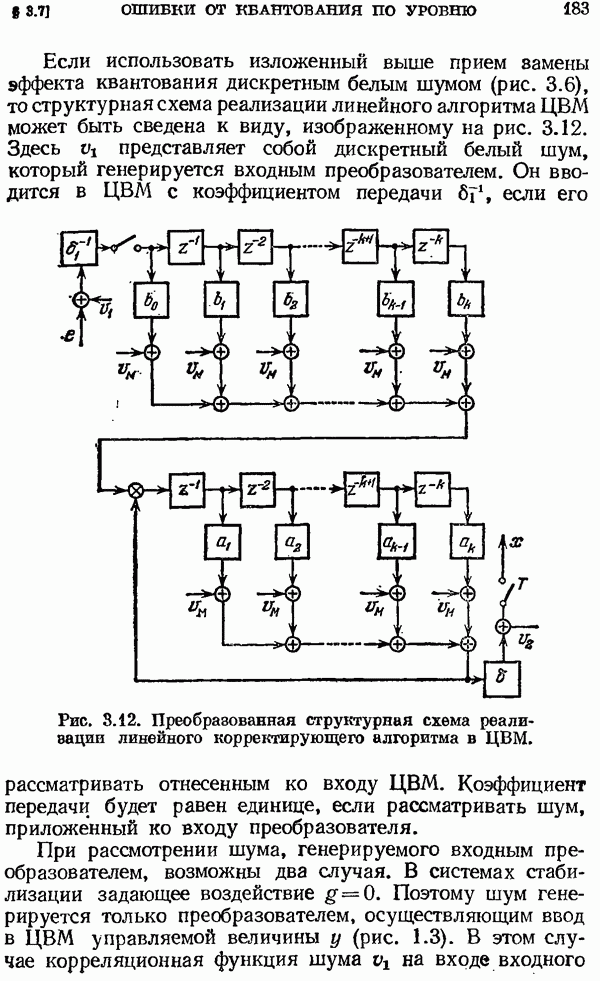
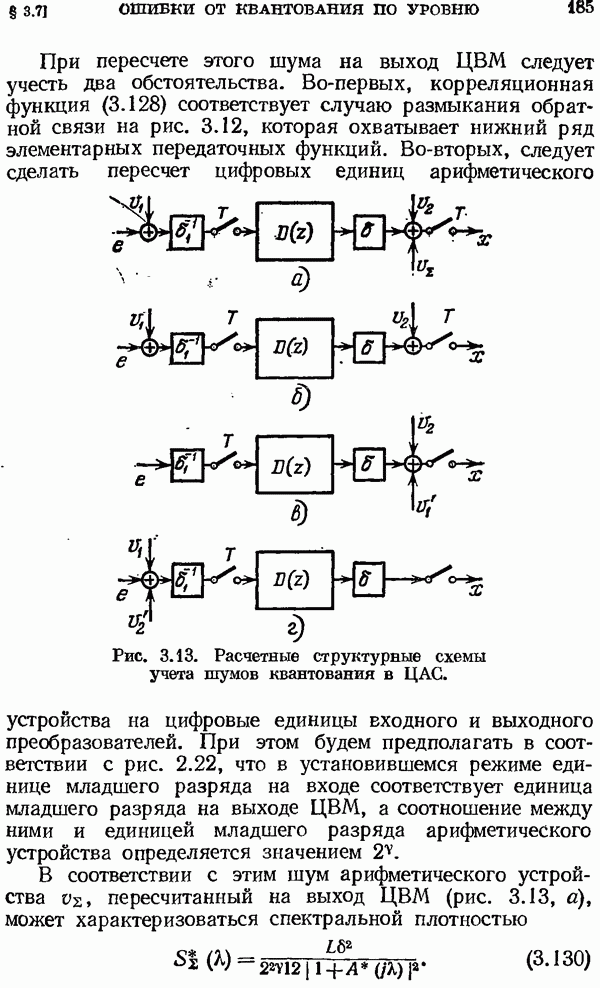
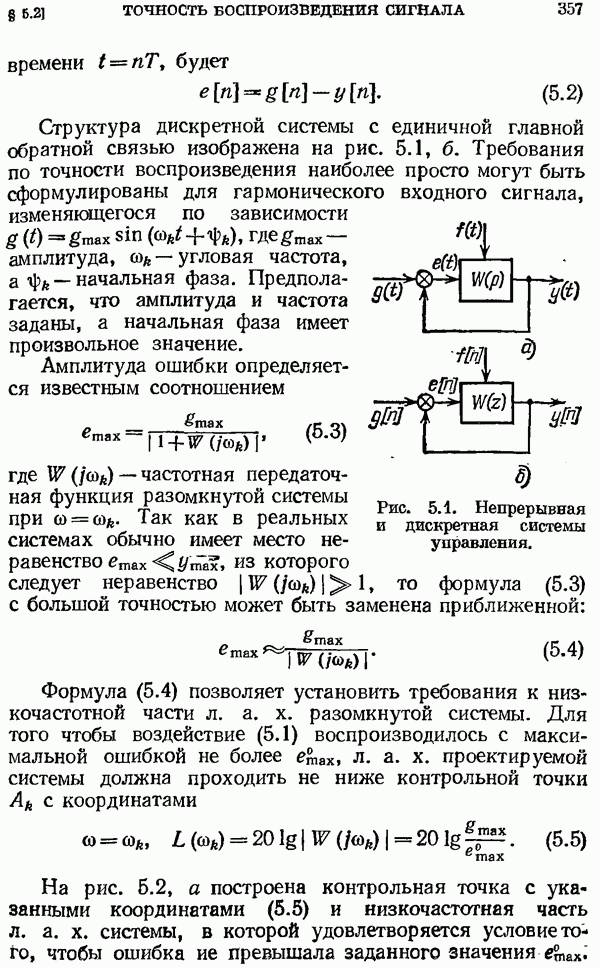
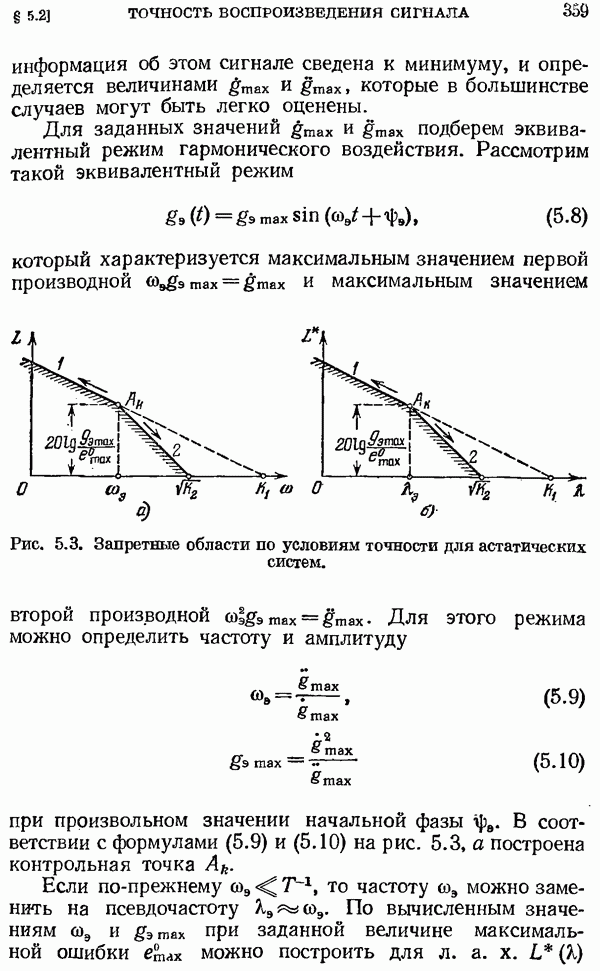
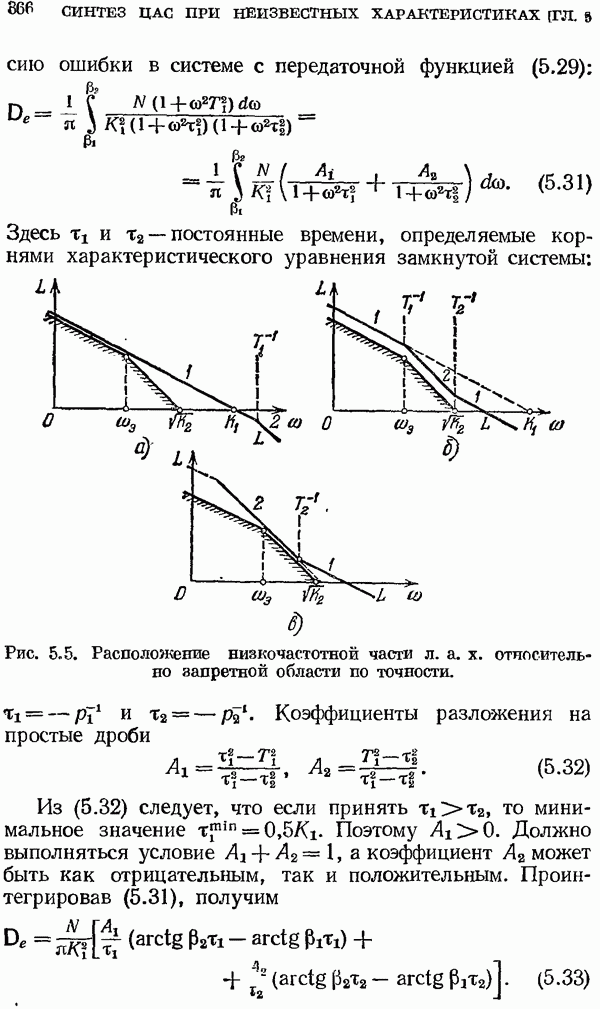
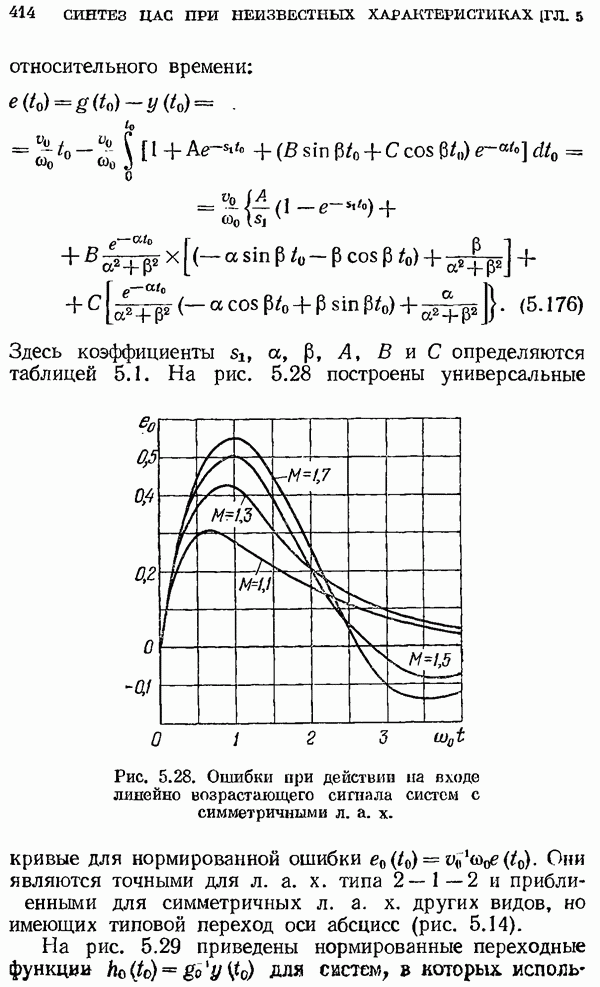
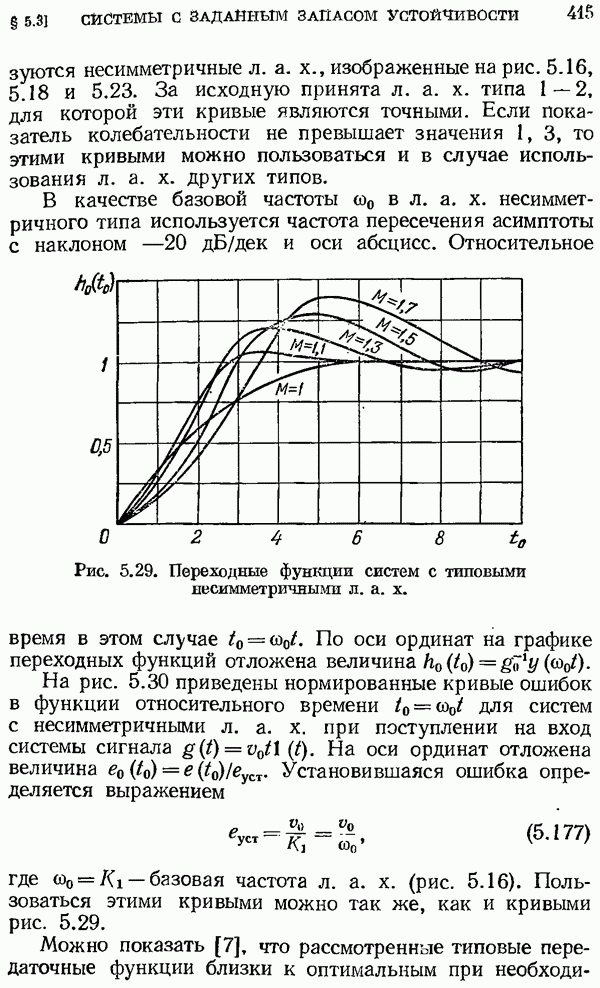
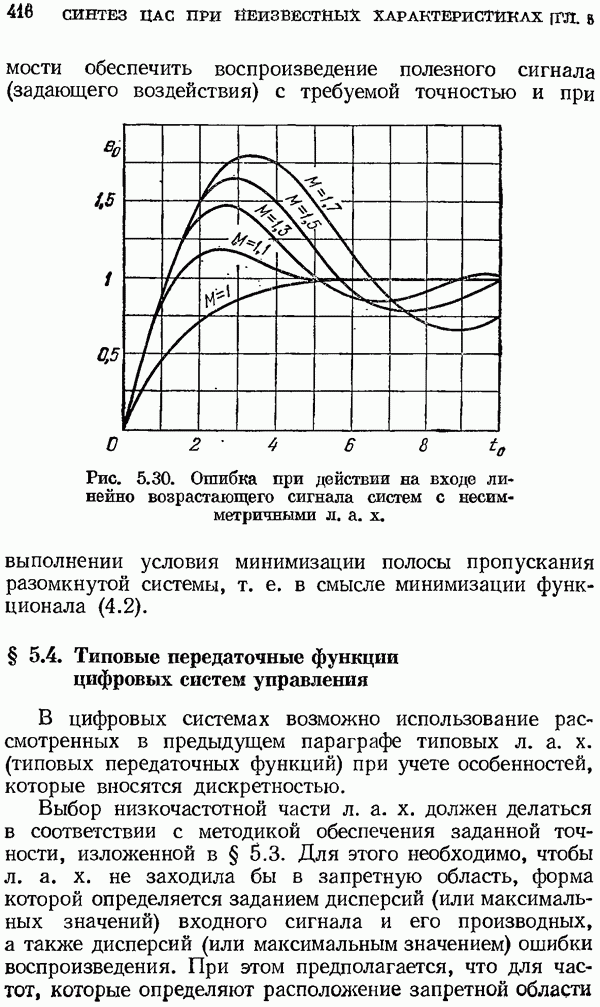
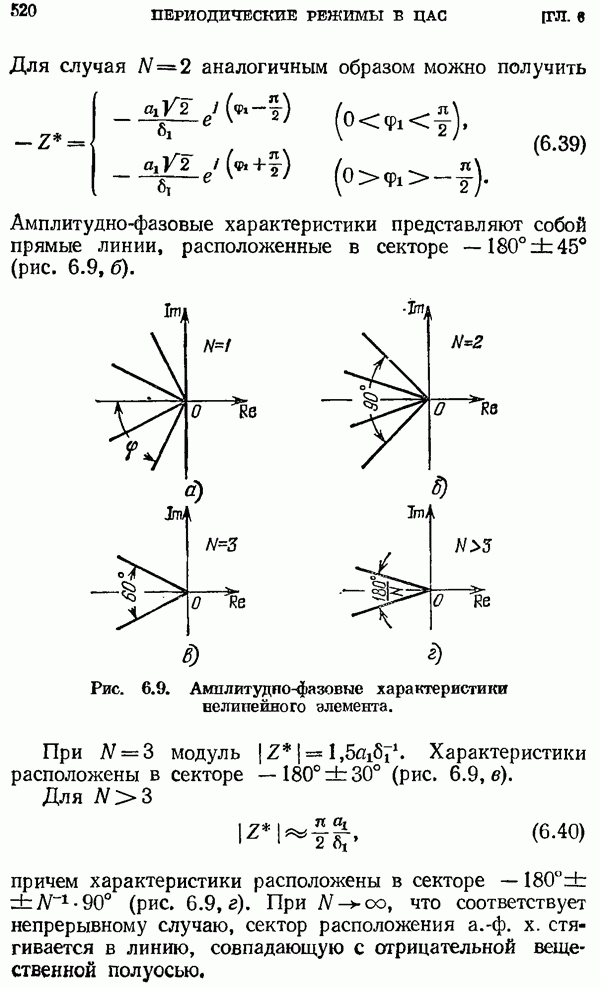
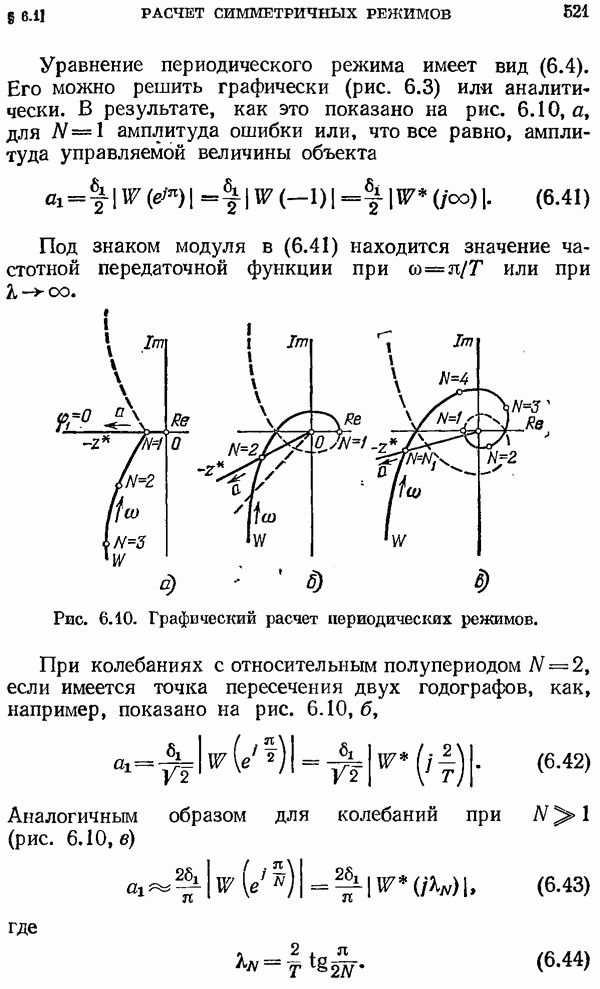
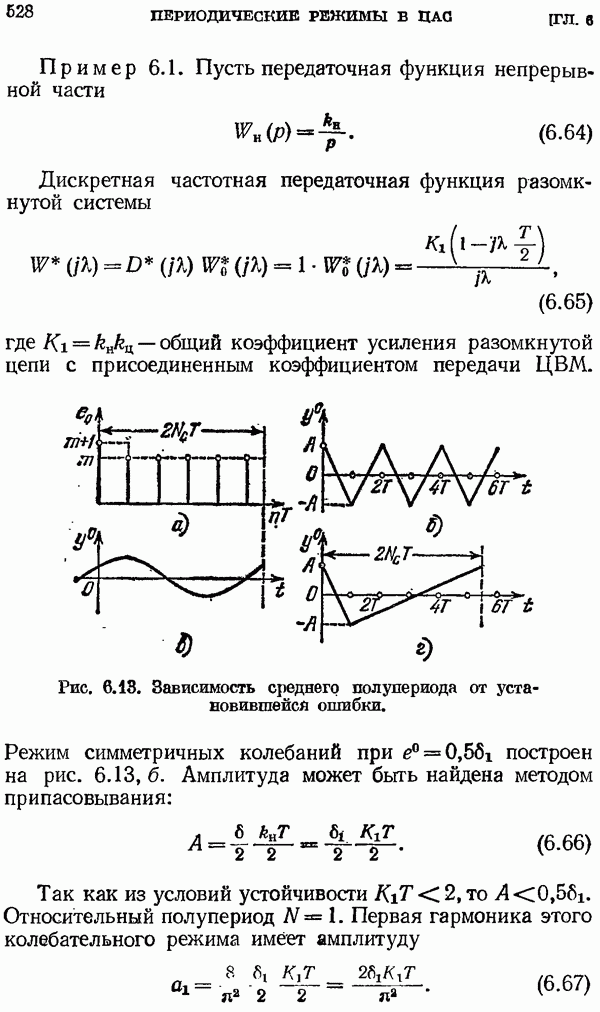
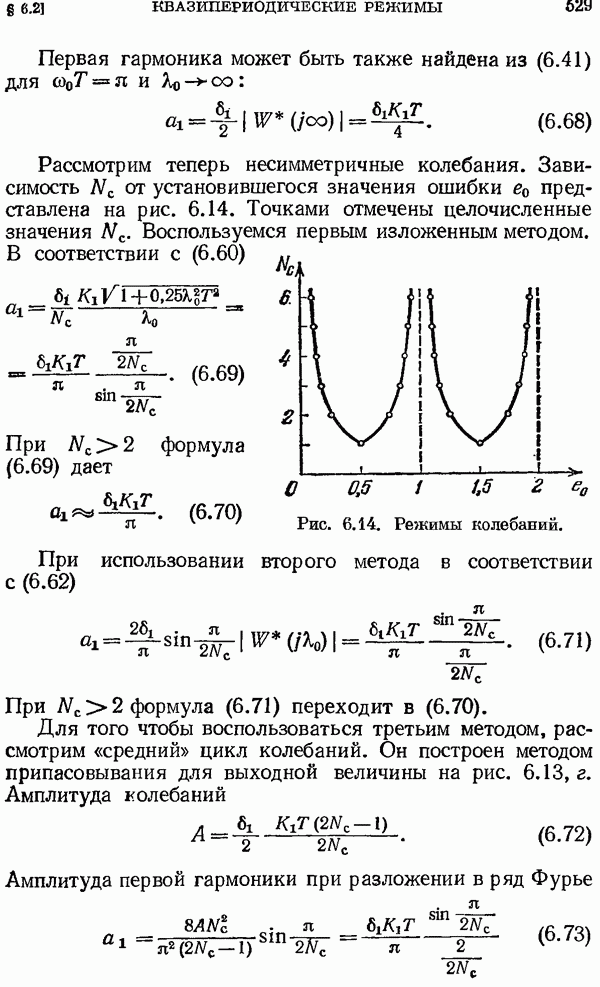
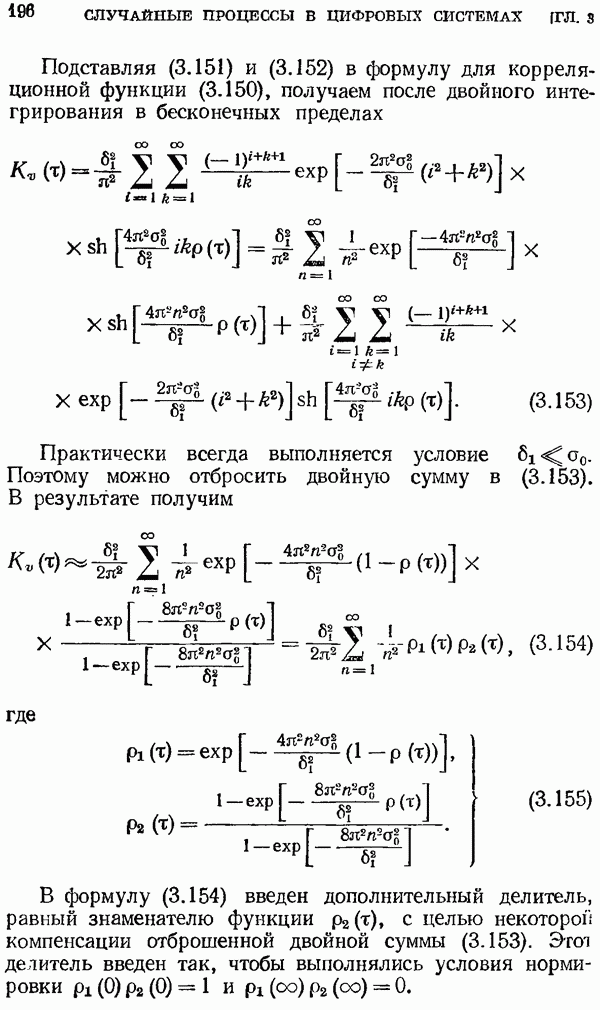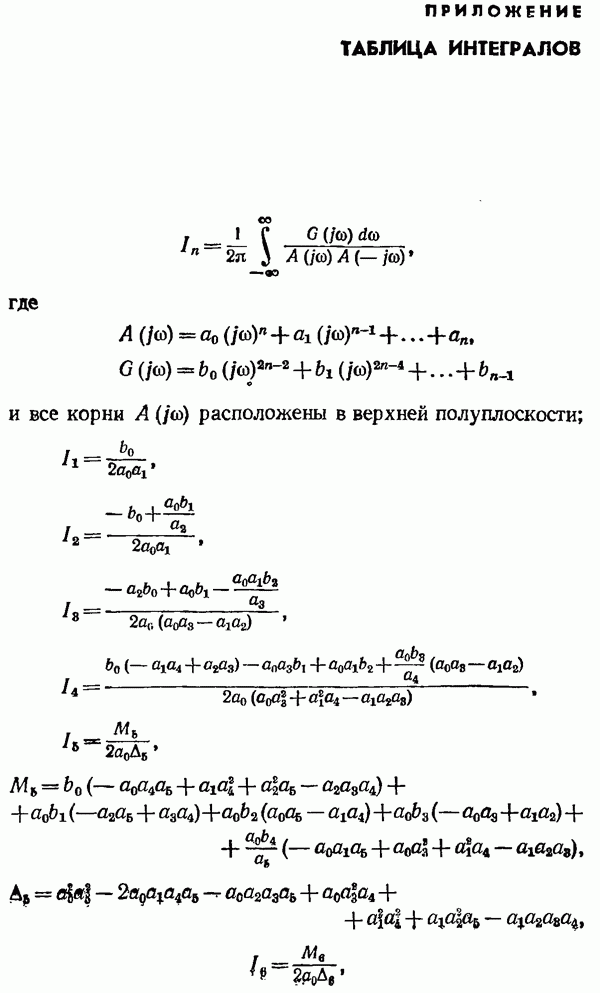| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
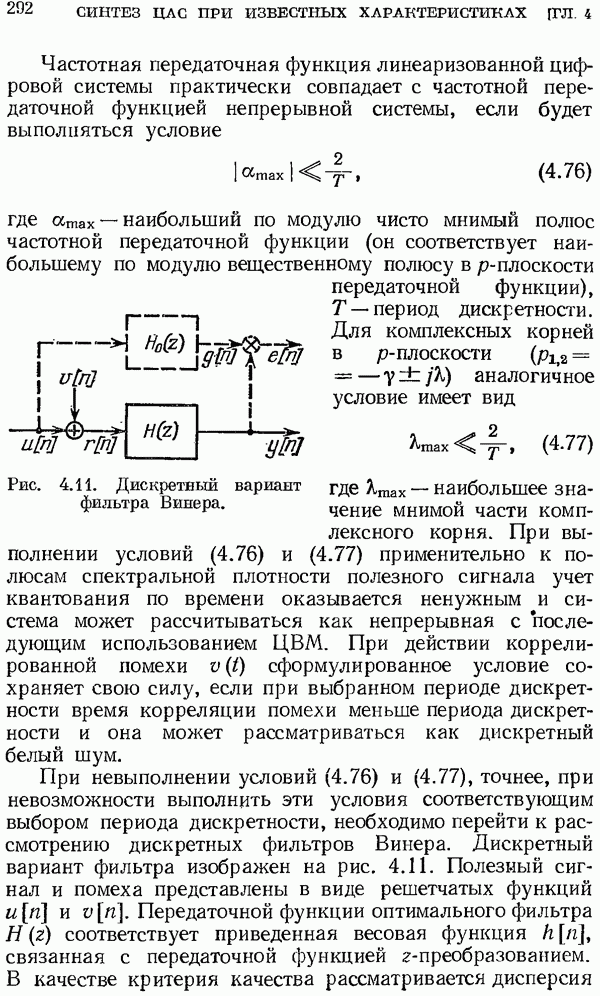
Использование z-преобразования.
Для исследования импульсных систем большое распространение получило так называемое z-преобразование, которое связано с дискретным преобразованием Лапласа и вытекает из него. Применительно к z-преобразованию ниже будут
рассмотрены основные свойства и теоремы дискретного преобразования Лапласа.
Под  -преобразованием понимается изображение несмещенной или смещенной решетчатых функций, определяемое формулами
-преобразованием понимается изображение несмещенной или смещенной решетчатых функций, определяемое формулами

В этих формулах введено новое обозначение  Из них следует, что
Из них следует, что  -преобразование практически совпадает с дискретным преобразованием Лапласа и отличается только аргументом изображения.
-преобразование практически совпадает с дискретным преобразованием Лапласа и отличается только аргументом изображения.
Таким образом, решетчатая функция времени (оригинал) заменяется ее изображением (г-преобразованием). Формулы преобразования (2.42) могут быть записаны в символической форме:

Формулы преобразования (2.43) могут быть записаны и для непрерывной производящей функции в виде

где 
Ряды (2.42) сходятся, и изображение решетчатой функции существует, если выполняется условие, сформулированное выше для дискретного преобразования Лапласа:  где с — абсцисса абсолютной сходимости.
где с — абсцисса абсолютной сходимости.
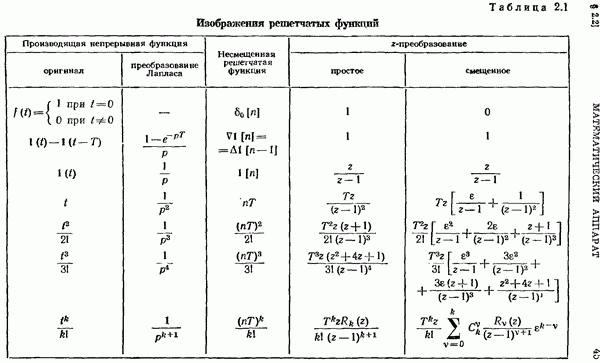
В таблице 2.1 приведены изображения некоторых решетчатых функций, а также производящих функций времени и их изображений Лапласа. В таблице введена единичная импульсная решетчатая функция

Эта функция играет в дискретных системах такую же важную роль, как  -функция (функция Дирака) в непрерывных системах.
-функция (функция Дирака) в непрерывных системах.

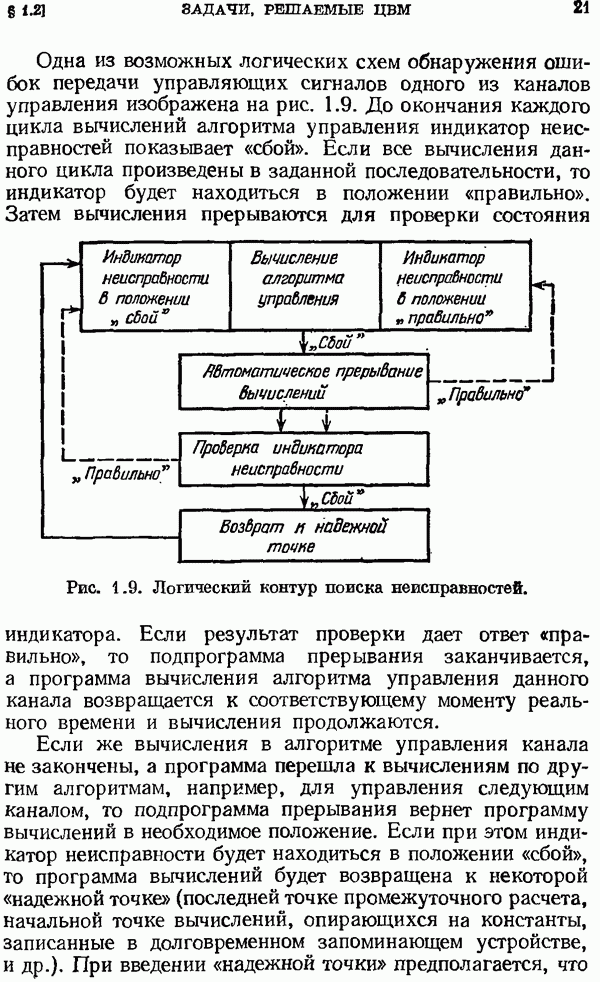
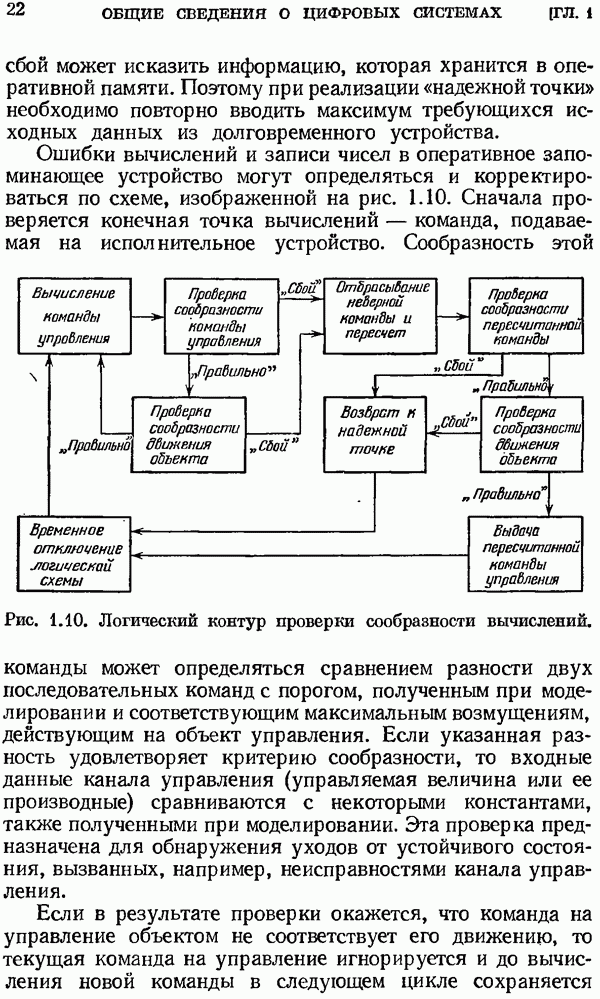
(кликните для просмотра скана)

(кликните для просмотра скана)

(кликните для просмотра скана)
Для всех непрерывных и решетчатых функций, приведенных в таблице 2.1, предполагается, что они тождественно равны нулю при  . В некоторых изображениях таблицы 2.1 использованы полиномы
. В некоторых изображениях таблицы 2.1 использованы полиномы  которые могут быть представлены в виде определителя
которые могут быть представлены в виде определителя

Некоторые частные значения этого полинома

Приведем основные правила и теоремы применительно к  -преобразованию. (Эти же правила и теоремы будут справедливыми и для дискретного преобразования Лапласа.) Рассмотрение проведем для несмещенных решетчатых функций, но полученные результаты можно распространить и на случай смещенных функций
-преобразованию. (Эти же правила и теоремы будут справедливыми и для дискретного преобразования Лапласа.) Рассмотрение проведем для несмещенных решетчатых функций, но полученные результаты можно распространить и на случай смещенных функций  кроме случаев, оговоренных особо.
кроме случаев, оговоренных особо.
1. Свойство линейности. Это свойство заключается в том, что изображение линейной комбинации решетчатых функций равно той же линейной комбинации их изображений. Пусть решетчатая функция определяется выражением

Тогда для ее изображения можно записать

2. Теорема запаздывания и упреждения. Рассмотрим решетчатую функцию  сдвинутую вправо (запаздывающую) на целое число тактов
сдвинутую вправо (запаздывающую) на целое число тактов  . Тогда из (2.42) следует, если обозначить
. Тогда из (2.42) следует, если обозначить 

Здесь  — изображение функции
— изображение функции  Если исходная решетчатая функция
Если исходная решетчатая функция  равна нулю при отрицательных значениях аргумента, то формула (2.50) упрощается:
равна нулю при отрицательных значениях аргумента, то формула (2.50) упрощается:

Если сдвиг функции  происходит влево (упреждение) и рассматривается функция
происходит влево (упреждение) и рассматривается функция  где
где  — целое положительное число, то, аналогично случаю запаздываний, можно показать, что
— целое положительное число, то, аналогично случаю запаздываний, можно показать, что

Второе слагаемое в правой части (2.52) обращается в нуль, если  при
при 
При запаздывании на не целое число периодов  приходится вводить смещенную решетчатую функцию. Пусть рассматривается функция
приходится вводить смещенную решетчатую функцию. Пусть рассматривается функция  где
где  целая,
целая,  — дробная часть запаздывания. Если смещение
— дробная часть запаздывания. Если смещение  удовлетворяет условию
удовлетворяет условию  при
при  то можно показать, что
то можно показать, что

Если

При использовании таблицы 2.1 для нахождения изображений следует в этом случае вместо  подставить
подставить
 или в
или в  в соответствии с формулами (2.53) и (2.54).
в соответствии с формулами (2.53) и (2.54).
3. Теорема об умножении оригинала на экспоненту (теорема смещения в области изображений). Умножим решетчатую функцию на экспоненту  Тогда из (2.42) следует:
Тогда из (2.42) следует:

Для смещенной решетчатой функции аналогичная формула имеет вид

4. Теорема об умножении оригинала на степенную функцию. Пусть решетчатой функции  соответствует изображение
соответствует изображение  Тогда можно показать, что
Тогда можно показать, что

Для смещенной решетчатой функции аналогичная зависимость имеет вид

5. Изображение разностей. Для первой прямой разности на основании (2.52)

Если  — целое число, то аналогичным образом
— целое число, то аналогичным образом

причем 
Если решетчатая функция  равна нулю в первых точках оси времени, т. е.
равна нулю в первых точках оси времени, т. е.  то формула (2.60) упрощается:
то формула (2.60) упрощается:

Для первой обратной разности можно аналогичным образом найти

Если для отрицательных аргументов решетчатая функция тождественно равна нулю, то формула (2.62) упрощается:

Для  обратной разности при
обратной разности при  для
для 

Полученные формулы изображений прямых и обратных разностей формально напоминают формулы для нахождения изображений производных непрерывных функций. Формула (2.64) аналогична случаю изображения производной  порядка непрерывной функции по начальным условиям слева при их нулевых значениях. Заметим, что при Т —0 (непрерывный случай) множитель в правой части стремится к пределу:
порядка непрерывной функции по начальным условиям слева при их нулевых значениях. Заметим, что при Т —0 (непрерывный случай) множитель в правой части стремится к пределу:

К этому же пределу стремится множитель  в (2.61). Это также иллюстрирует сходство формул изображений производных и разностей.
в (2.61). Это также иллюстрирует сходство формул изображений производных и разностей.
6. Изображение сумм. Рассмотрим вначале неполную сумму (2.26):

Составим первую прямую разность этой суммы

и возьмем  -преобразование от правой и левой частей
-преобразование от правой и левой частей

На основании (2.61) имеем, учитывая, что 

Отсюда можно найти изображение неполной суммы

Распространяя эту зависимость на случай  -кратного суммирования, можно записать
-кратного суммирования, можно записать

Для полной суммы (2.27) аналогичным образом можно найти первую обратную разность

и ее изображение из (2.63)

Отсюда изображение полной суммы

Для случая А-кратного суммирования

Из приведенного рассмотрения вытекает справедливость равенства

Таким образом, взятие прямой разности и взятие неполной суммы (или обратной разности и полной суммы) решетчатой функции являются обратными операциями. Роль оператора, аналогичного оператору  в непрерывных системах, в первом случае играет оператор
в непрерывных системах, в первом случае играет оператор  а во втором случае — оператор
а во втором случае — оператор  . В случае перехода к пределу при
. В случае перехода к пределу при  обе пары операций над решетчатыми функциями сливаются и превращаются в операции дифференцирования и интегрирования непрерывных функций.
обе пары операций над решетчатыми функциями сливаются и превращаются в операции дифференцирования и интегрирования непрерывных функций.
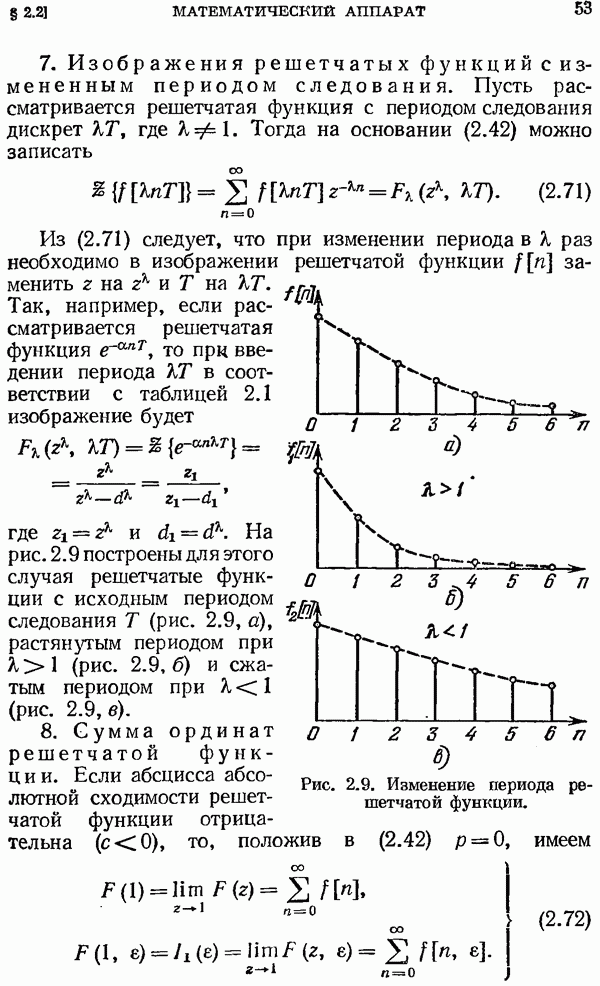
7. Изображения решетчатых функций с измененным периодом следования. Пусть рассматривается решетчатая функция с периодом следования дискрет  где
где  Тогда на основании (2.42) можно записать
Тогда на основании (2.42) можно записать

Из (2.71) следует, что при изменении периода в К раз необходимо в изображении решетчатой функции  заменить
заменить  на
на  и
и  на
на 
Так, например, если рассматривается решетчатая функция  то при введении периода
то при введении периода  в соответствии с таблицей 2.1 изображение будет
в соответствии с таблицей 2.1 изображение будет

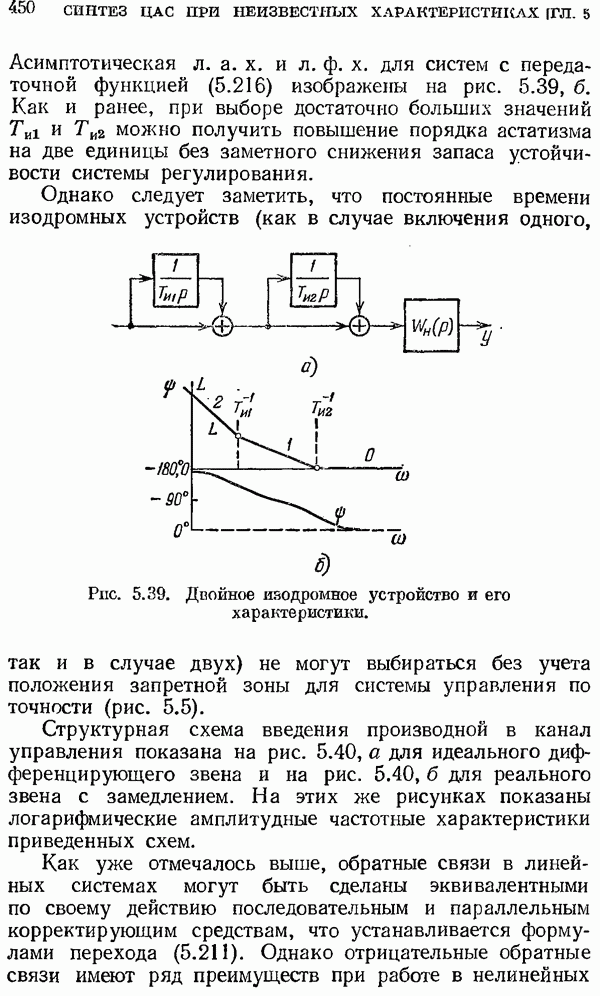
где  рис. 2.9 построены для этого случая решетчатые функции с исходным периодом следования Т (рис. 2.9, а), растянутым периодом при
рис. 2.9 построены для этого случая решетчатые функции с исходным периодом следования Т (рис. 2.9, а), растянутым периодом при  (рис. 2.9, б) и сжатым периодом при
(рис. 2.9, б) и сжатым периодом при  (рис. 2.9, в).
(рис. 2.9, в).

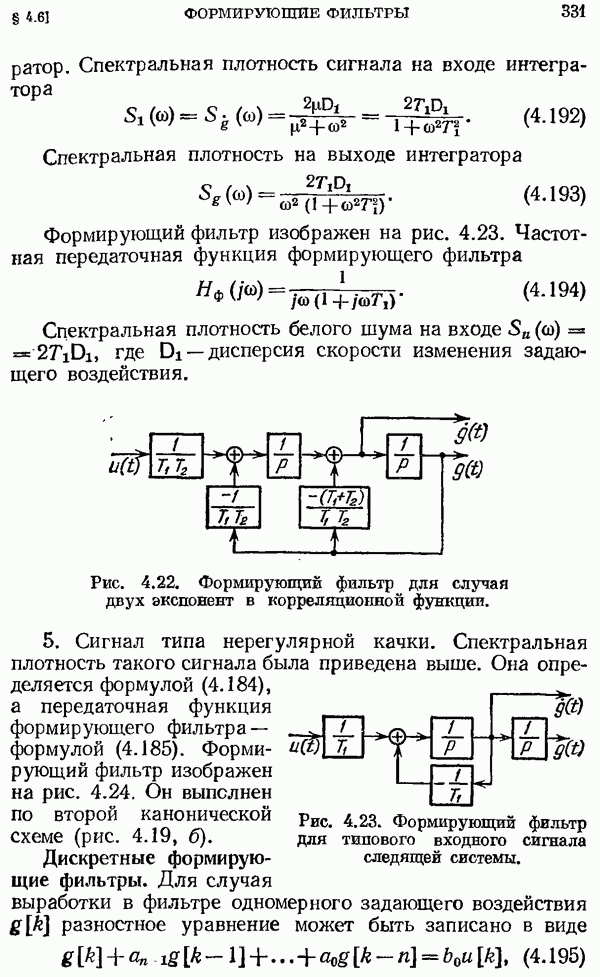
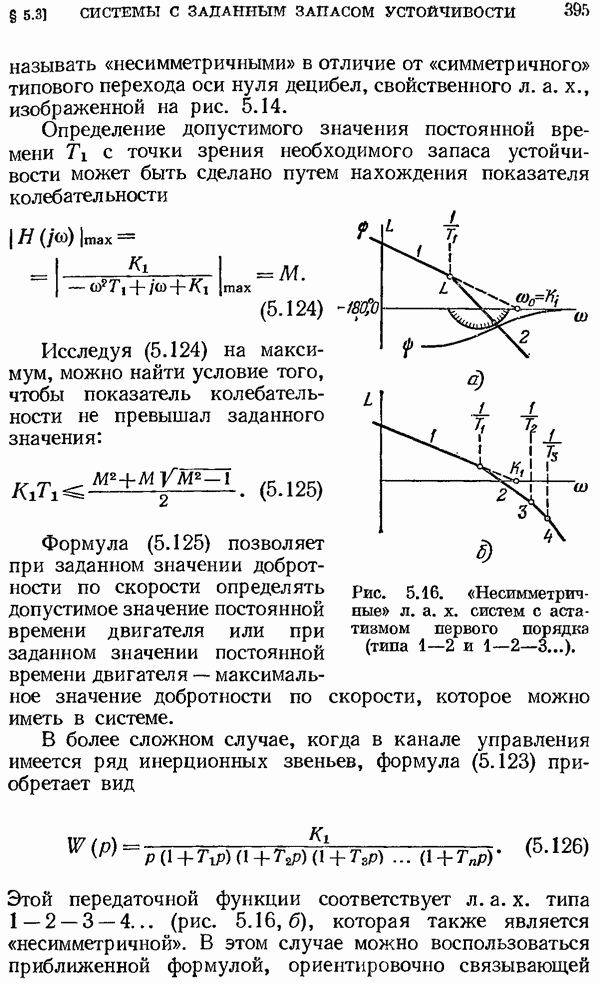
Рис. 2.9. Изменение периода решетчатой функции.
8. Сумма ординат решетчатой функции. Если абсцисса абсолютной сходимости решетчатой функции отрицательна  то, положив в
то, положив в  имеем
имеем

9. Конечное значение решетчатой функции. Составим первую прямую разность решетчатой функции  и на основании (2.49) найдем ее изображение
и на основании (2.49) найдем ее изображение

Далее на основании (2.72) найдем сумму ординат 

Кроме того, можно записать

Из двух последних выражений следует:

Если провести аналогичное рассмотрение с первой обратной разностью, то можно получить формулу для вычисления конечного значения решетчатой функции в другом виде:

10. Начальное значение решетчатой функции. Составим первую прямую разность

и на основании (2.50) найдем ее изображение

Рассмотрим теперь предел выражения

Тогда из последних двух формул можно найти

Зависимости (2.74) и (2.75) представляют собой аналоги соответствующих выражений для нахождения
конечного и начального значений непрерывной функции  по ее изображению Лапласа:
по ее изображению Лапласа:

11. Свертка решетчатых функций. Если

то можно показать, что

Эта формула аналогична соответствующему выражению для свертки двух непрерывных функций.
12. Формула обращения. Рассмотрим задачу нахождения решетчатой функции (оригинала) по ее изображению. Эту операцию запишем в символическом виде как обратное z-преобразование:

Заметим, что аргумент изображения обладает свойством

где  — произвольное целое число. Вследствие этого изображения
— произвольное целое число. Вследствие этого изображения  представляют собой периодические функции относительно мнимой части аргумента
представляют собой периодические функции относительно мнимой части аргумента  с периодом
с периодом  что дает основание рассматривать изображения только внутри интервала изменения
что дает основание рассматривать изображения только внутри интервала изменения 
Удобнее использовать интервал  с
с  так как он оказывается аналогичным интервалу частот —
так как он оказывается аналогичным интервалу частот —  , рассматриваемому обычно для непрерывных функций времени. Принятый интервал дает на комплексной плоскости
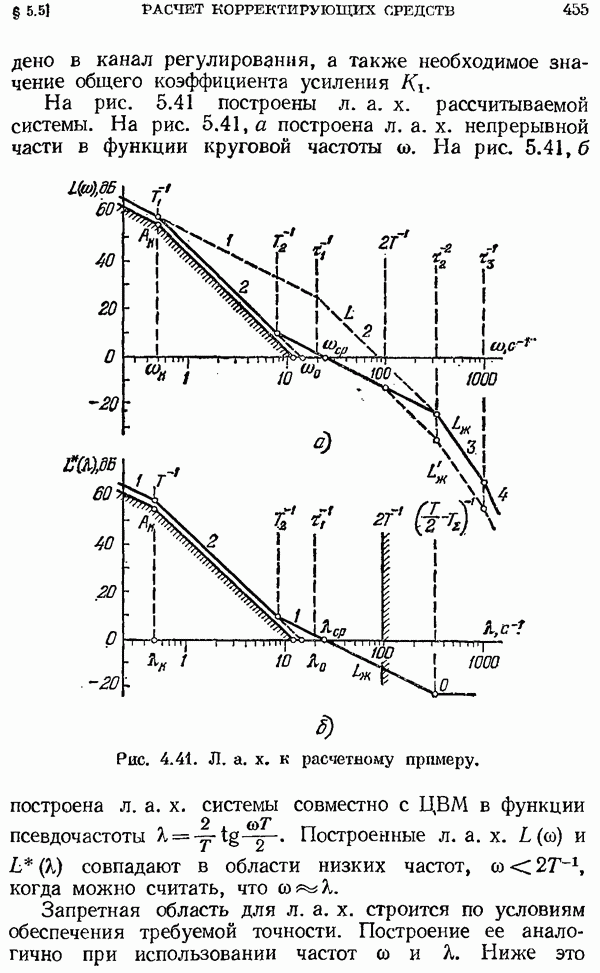
, рассматриваемому обычно для непрерывных функций времени. Принятый интервал дает на комплексной плоскости  область (рис. 2.10), в которой достаточно рассматривать изображение
область (рис. 2.10), в которой достаточно рассматривать изображение 
Изображение  может иметь в этой области особые точки типа полюсов
может иметь в этой области особые точки типа полюсов  . Полюсы
. Полюсы
могут быть или вещественными, или комплексно-сопряженными. В случае  достаточно рассматривать один из этих полюсов, соответствующий, например, положительной мнимой части (на верхней границе области).
достаточно рассматривать один из этих полюсов, соответствующий, например, положительной мнимой части (на верхней границе области).

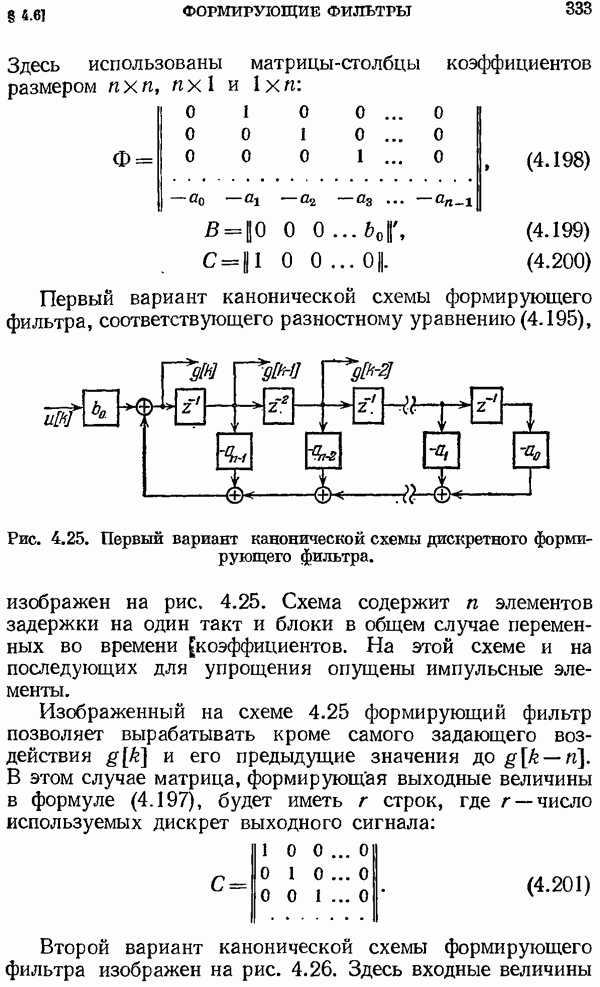
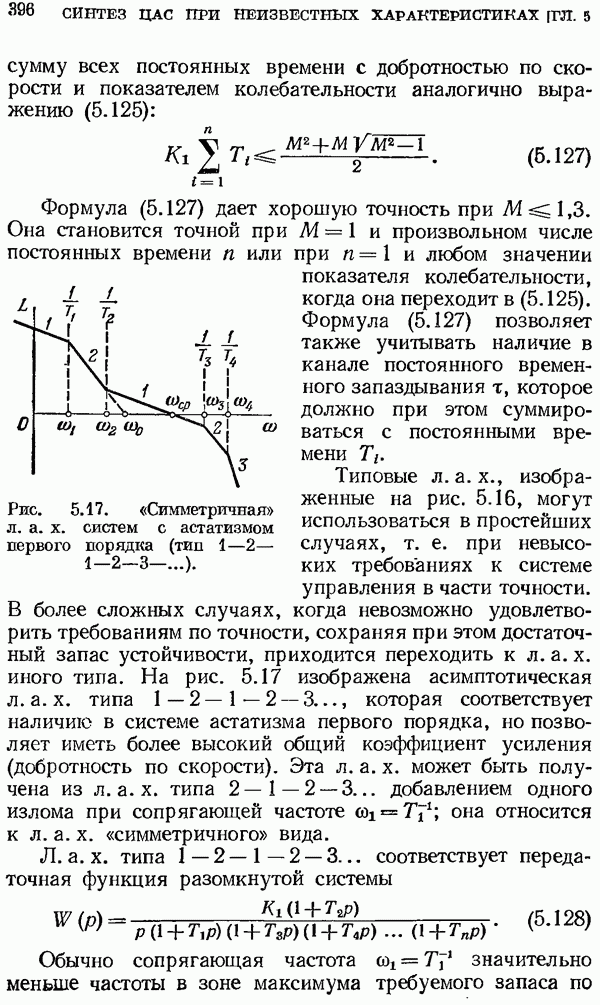
Рис. 2.10. Область интегрирования.
Рассмотрим выражение (2.42)

Умножим левую и правую его части на  где
где  — целое число, и проинтегрируем его вдоль линии
— целое число, и проинтегрируем его вдоль линии  (рис. 2.10) в пределах от
(рис. 2.10) в пределах от  до
до  где с — произвольная величина, большая, чем абсцисса абсолютной сходимости:
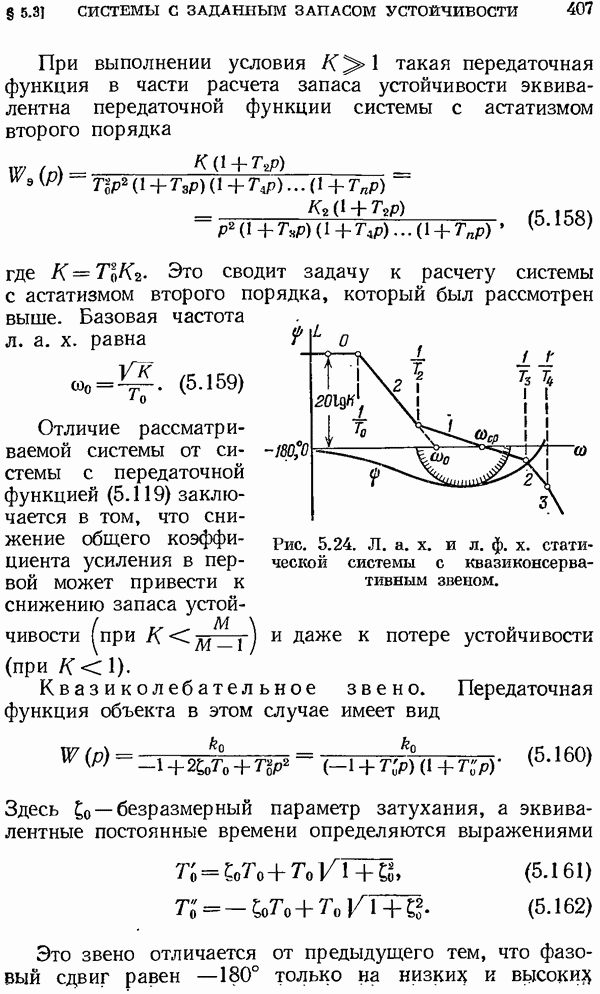
где с — произвольная величина, большая, чем абсцисса абсолютной сходимости:

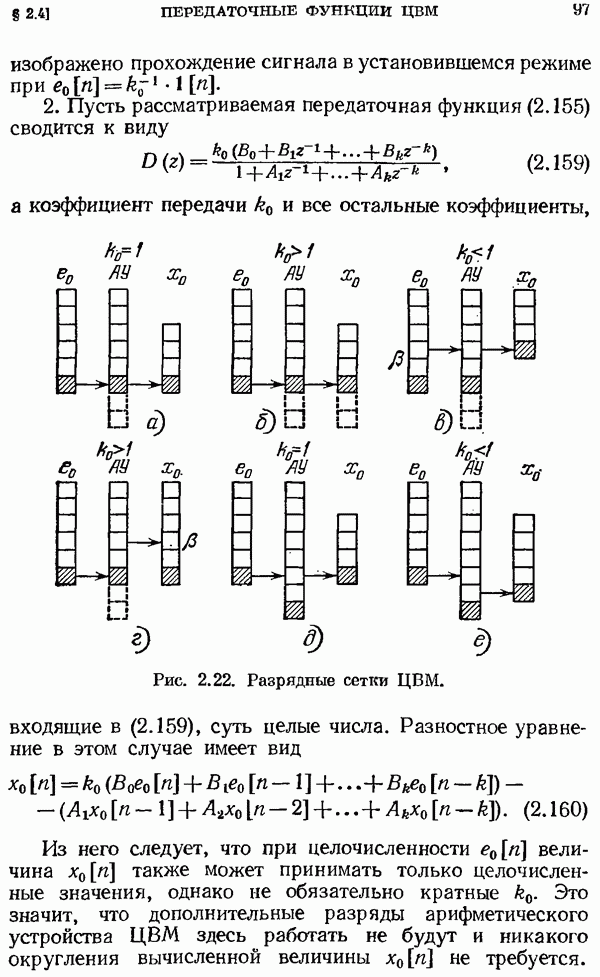
При этом все полюсы  будут лежать в рассматриваемой области на комплексной плоскости левее линии интегрирования
будут лежать в рассматриваемой области на комплексной плоскости левее линии интегрирования  Это и дает право изменить в (2.79) порядок операций интегрирования и суммирования.
Это и дает право изменить в (2.79) порядок операций интегрирования и суммирования.
Если 

Если 

Вследствие этого (2.79) можно представить в виде

Заменяя  на
на  получим окончательно формулу обращения
получим окончательно формулу обращения

Так как  то формула (2.80) может быть представлена в другом виде:
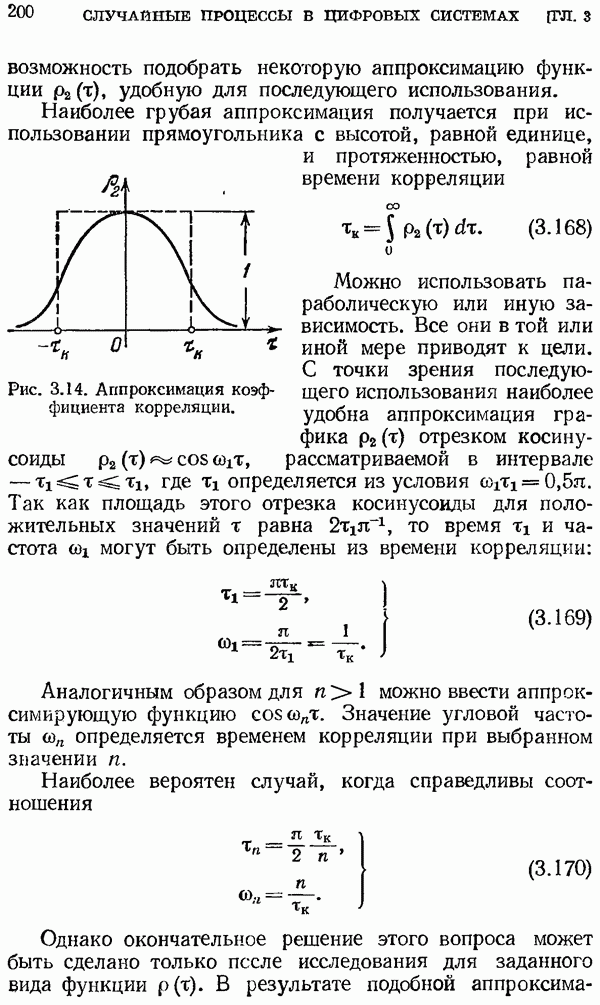
то формула (2.80) может быть представлена в другом виде:

Интегрирование ведется по окружности с центром в начале координат и радиусом  где
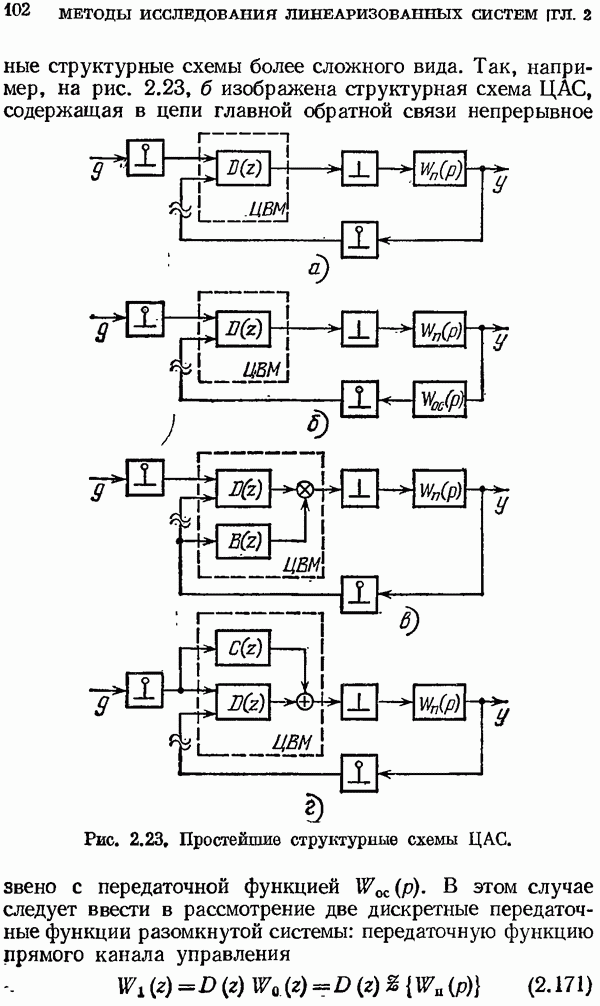
где 
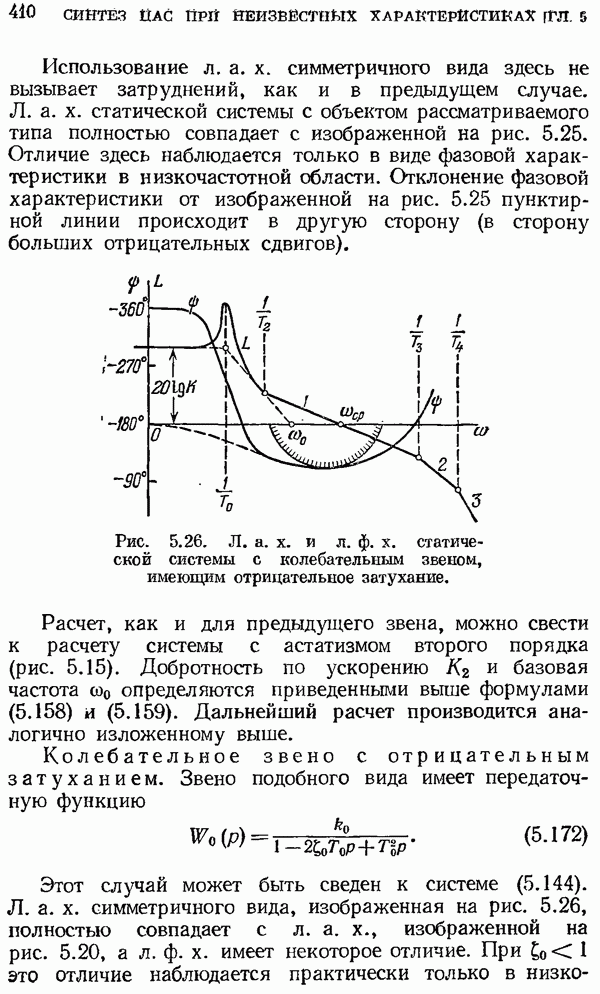
— полюсы функции 
В случае простых полюсов значение интегрального вычета в точке  может быть определено из выражения
может быть определено из выражения

В случае полюса кратности  значение интегрального вычета в точке
значение интегрального вычета в точке  определяется выражением
определяется выражением

Если функция  имеет нулевой полюс кратности
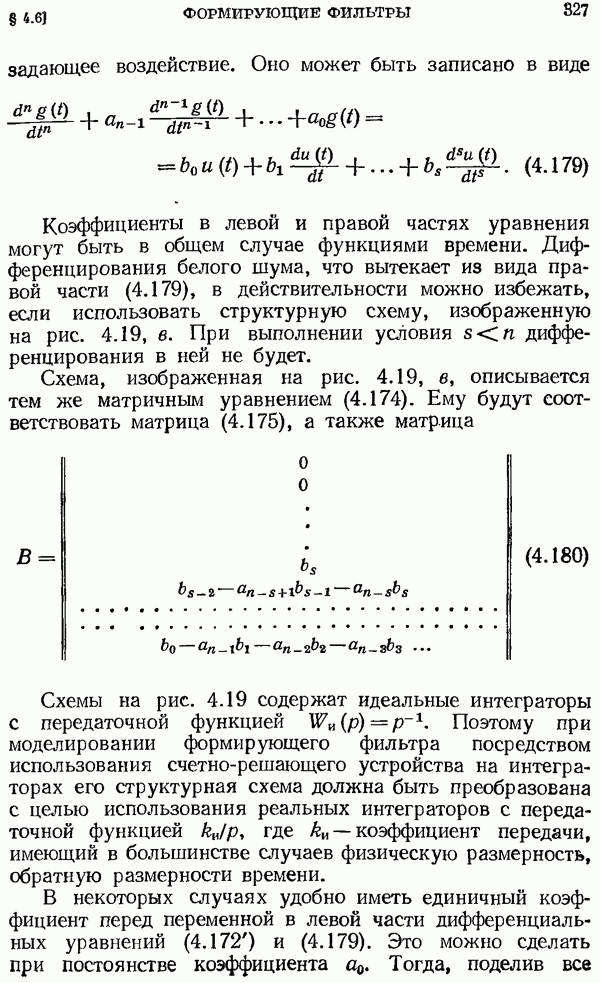
имеет нулевой полюс кратности  то для функции
то для функции  при
при  полюс будет иметь кратность
полюс будет иметь кратность  . В этом случае значение интегрального вычета в точке
. В этом случае значение интегрального вычета в точке  будет
будет

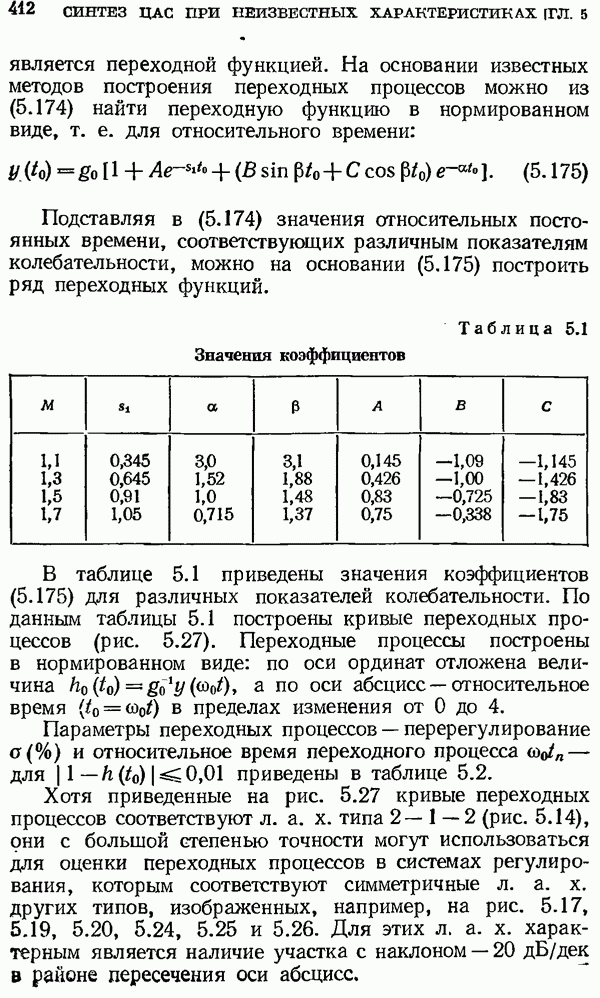
Аналогичные формулы обращения имеют место и для смещенной решетчатой функции:

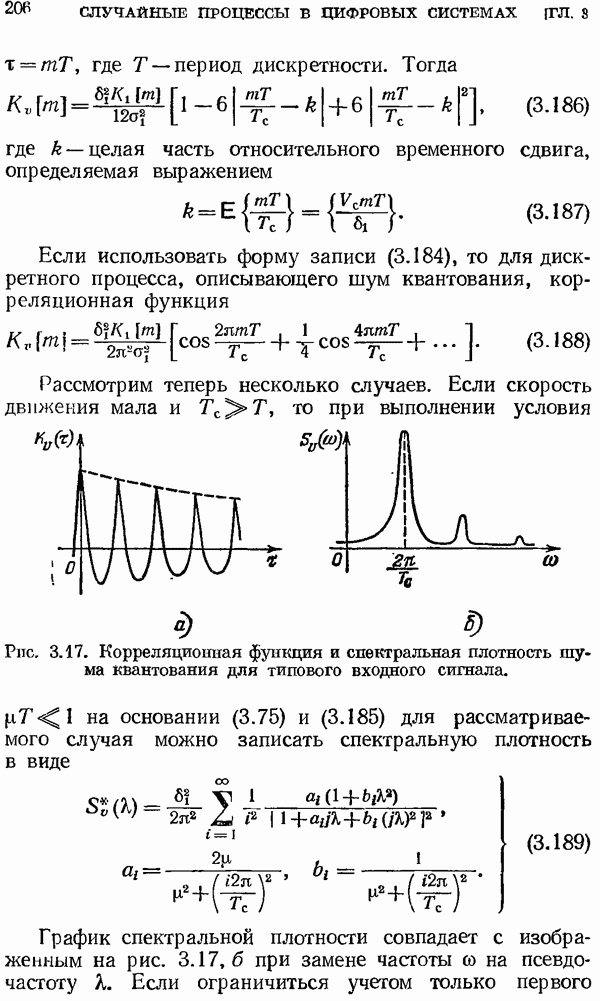
Полученные выражения (2.80), (2.81), (2.85) и (2.86) несколько сложны для практического использования. Поэтому для нахождения решетчатой функции по ее изображению обычно применяются другие методы, которые даны ниже.
13. Формулы разложения. Если изображение представляет собой простейшую табличную форму (см., например, таблицу 2.1), то переход к оригиналу не представляет трудностей. Сложная дробно-рациональная форма может быть представлена в виде суммы дробей первой степени. Рассмотрим некоторые употребительные разновидности формулы разложения.
а) Пусть изображение  представляет собой отношение двух многочленов:
представляет собой отношение двух многочленов:

причем будем предполагать, что степень числителя не выше, чем степень знаменателя, а корни знаменателя простые. Тогда изображение можно представить в виде суммы

где  производная
производная  по
по  — корни знаменателя. Элементарному слагаемому
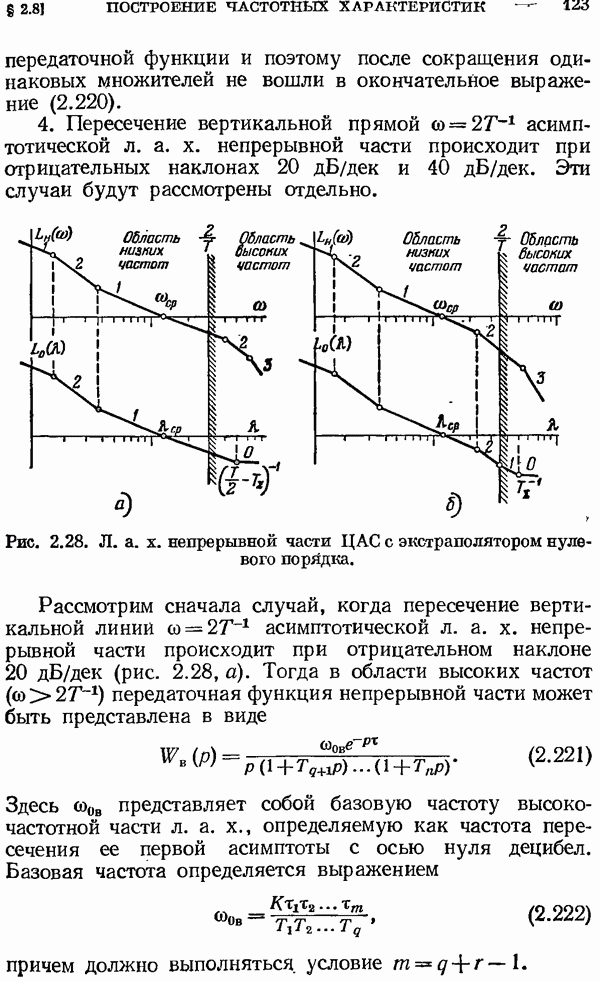
— корни знаменателя. Элементарному слагаемому  соответствует оригинал
соответствует оригинал  где
где  (см. таблицу 2.1). В таблице 2.1 единственный корень дроби первой степени обозначен
(см. таблицу 2.1). В таблице 2.1 единственный корень дроби первой степени обозначен 
Поэтому оригинал (2.87) можно записать следующим образом:

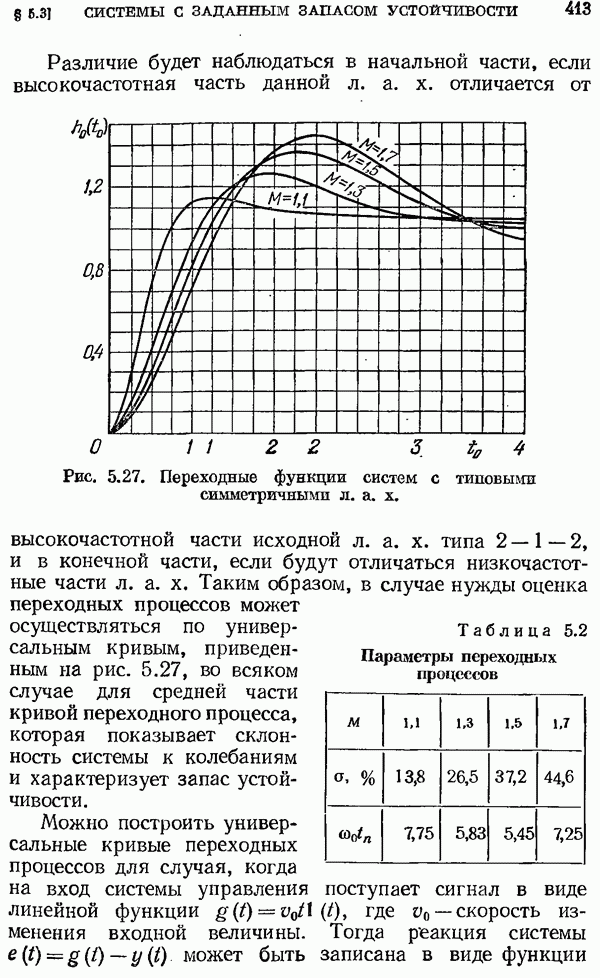
б) Пусть изображение  не имеет нулевого корня числителя, но степень числителя
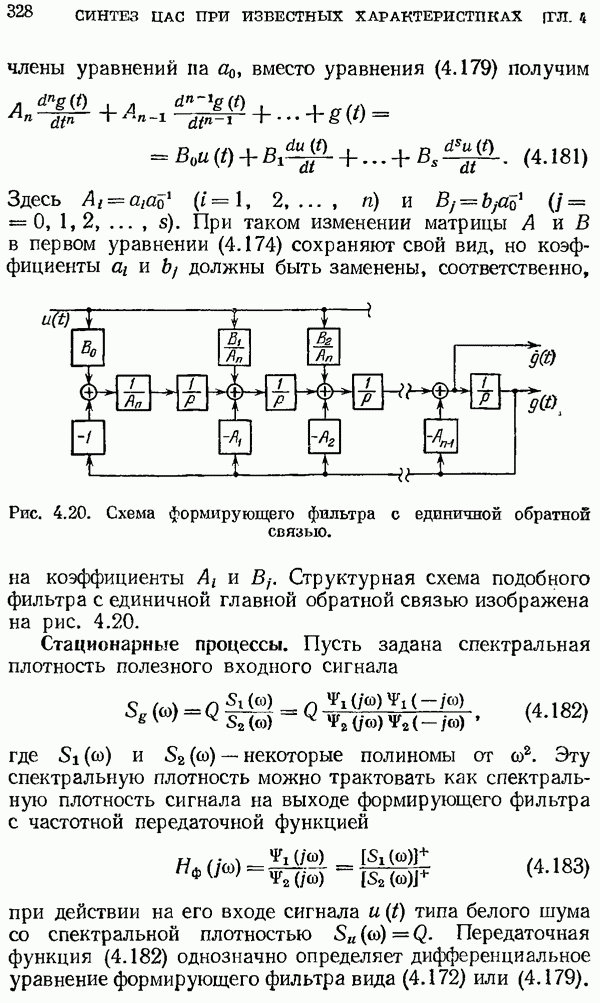
не имеет нулевого корня числителя, но степень числителя  меньше степени знаменателя. Тогда, как следует из (2.75), начальное значение решетчатой функции
меньше степени знаменателя. Тогда, как следует из (2.75), начальное значение решетчатой функции  Числитель и знаменатель
Числитель и знаменатель  можно умножить на
можно умножить на  Тогда, если корни знаменателя
Тогда, если корни знаменателя  простые, имеем
простые, имеем

Множитель  перед суммой в (2.89) означает запаздывание на один такт. Следовательно, чтобы получить исходную решетчатую функцию, следует в правой части (2.88) сделать сдвиг на один такт вправо, для чего нужно заменить
перед суммой в (2.89) означает запаздывание на один такт. Следовательно, чтобы получить исходную решетчатую функцию, следует в правой части (2.88) сделать сдвиг на один такт вправо, для чего нужно заменить  на
на  . В результате имеем
. В результате имеем

причем последнее выражение будет справедливым только для 
в) Пусть изображение  не имеет нулевого корня числителя
не имеет нулевого корня числителя  причем степень
причем степень  равна степени знаменателя
равна степени знаменателя  Тогда следует понизить степень числителя, поделив его на знаменатель, и представить
Тогда следует понизить степень числителя, поделив его на знаменатель, и представить  в виде суммы составляющей нулевого порядка и дробнорационального остатка
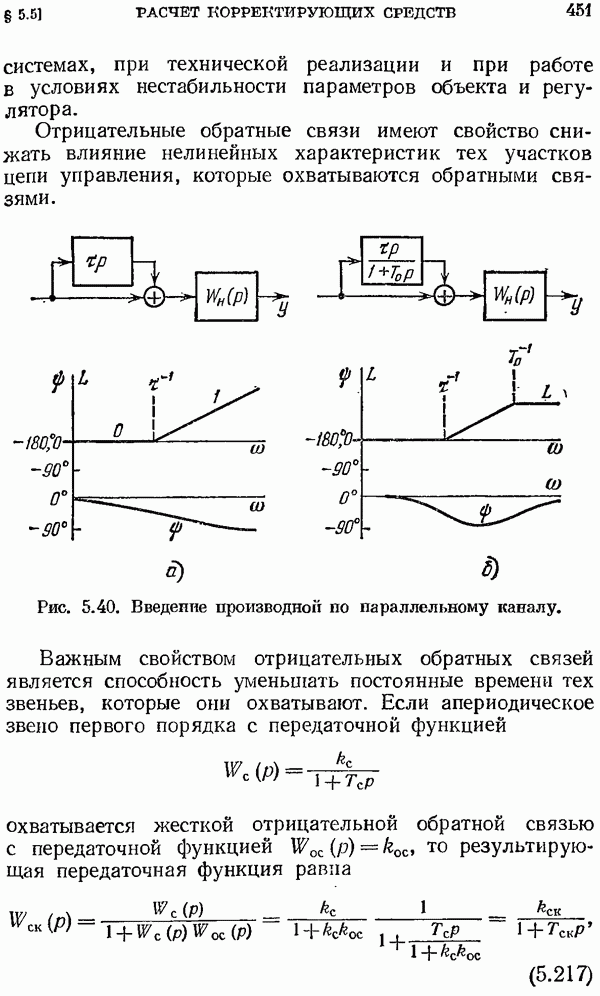
в виде суммы составляющей нулевого порядка и дробнорационального остатка  . В соответствии с (2.42) первая составляющая равна начальному значению решетчатой функции
. В соответствии с (2.42) первая составляющая равна начальному значению решетчатой функции  Поэтому
Поэтому

Переход от второй составляющей изображения к оригиналу может быть сделан по формуле (2.90), которая справедлива для 
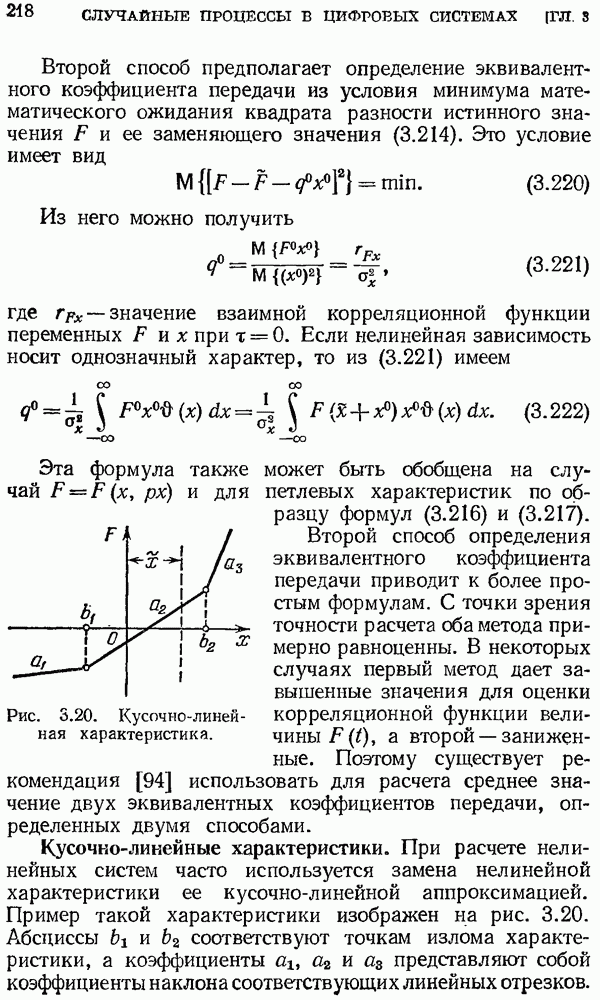
г) Если изображение  можно представить в виде некоторой дробно-рациональной функции
можно представить в виде некоторой дробно-рациональной функции  умноженной
умноженной
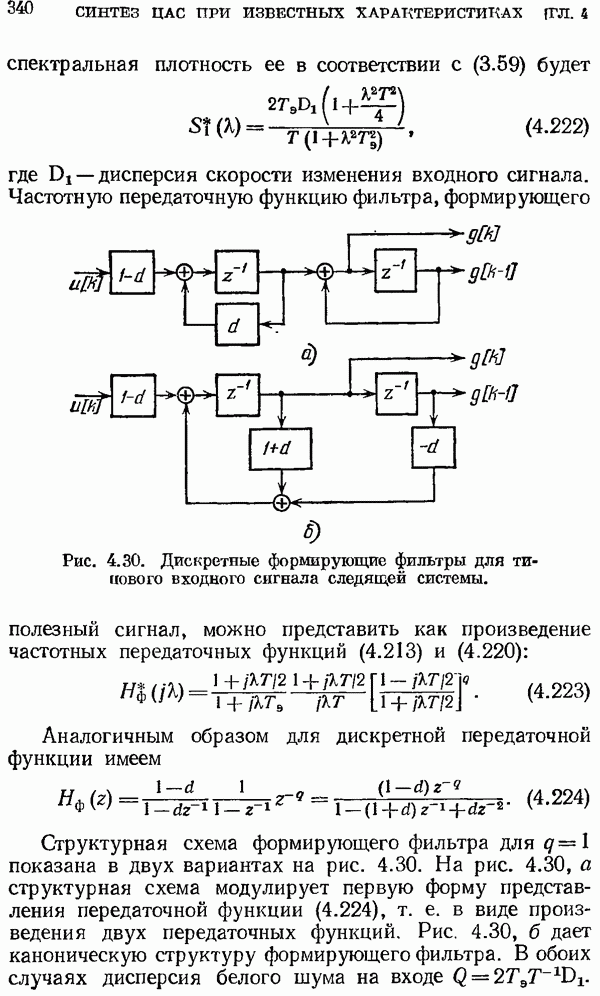
ной на изображение единичной ступенчатой решетчатой функции  которое равно
которое равно  т. е.
т. е.

то можно показать, что формула разложения приобретает вид

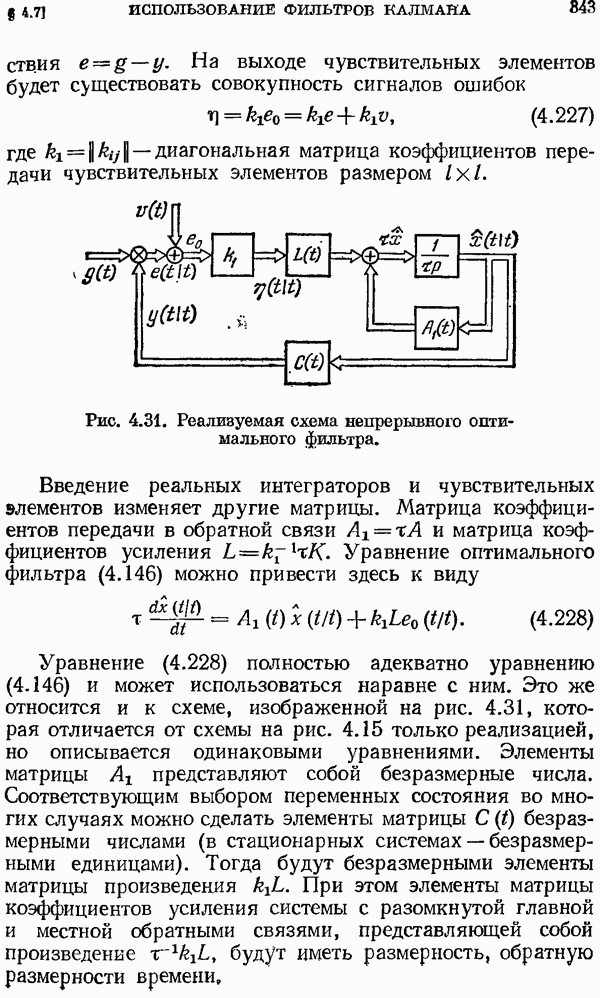
Последнее выражение представляет собой аналог известной формулы разложения Хевисайда, полученной им для непрерывных систем.
д) Пусть изображение  имеет нулевой полюс кратности
имеет нулевой полюс кратности  и простые остальные полюсы
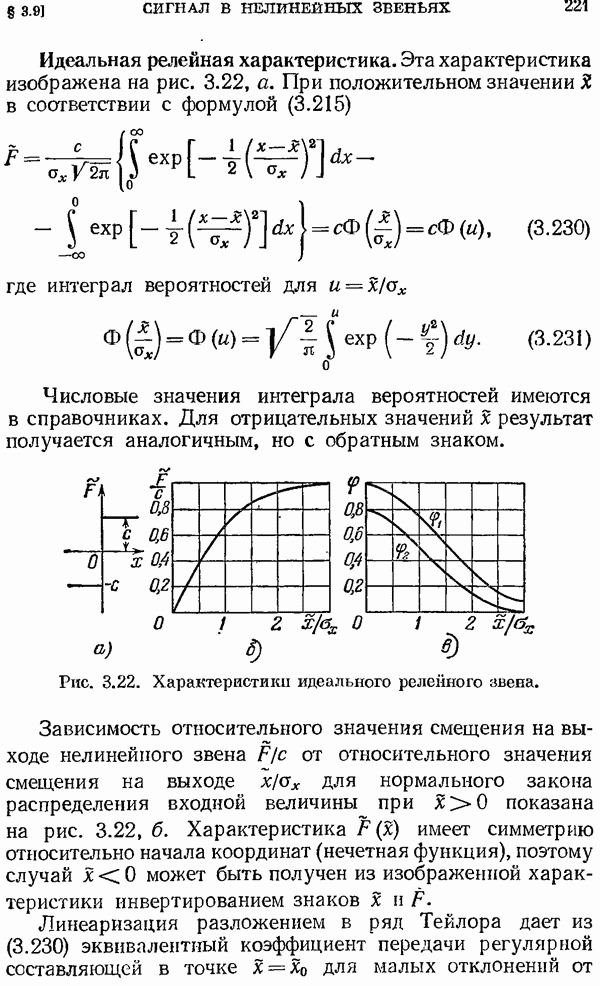
и простые остальные полюсы

причем степень числителя  меньше степени полинома
меньше степени полинома  Тогда на основании (2.84) и (2.90) можно найти оригинал в виде
Тогда на основании (2.84) и (2.90) можно найти оригинал в виде

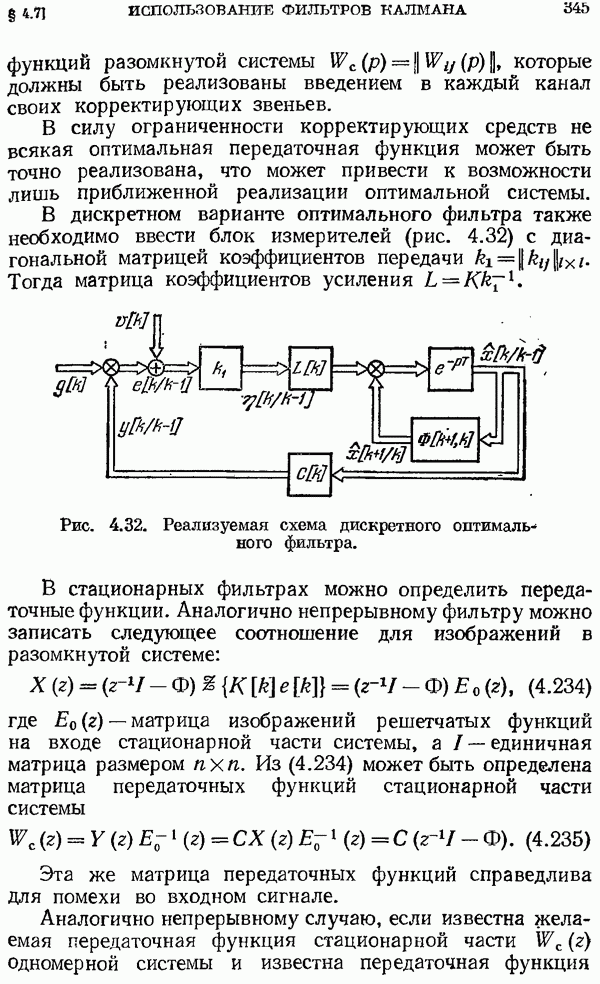
При равенстве степеней числителя и полинома  следует выделить делением
следует выделить делением  на
на  нулевую составляющую и остаток, после чего представить изображение в виде
нулевую составляющую и остаток, после чего представить изображение в виде

Здесь  — значение оригинала в момент
— значение оригинала в момент  Далее можно воспользоваться формулой (2.92), заменив в ней
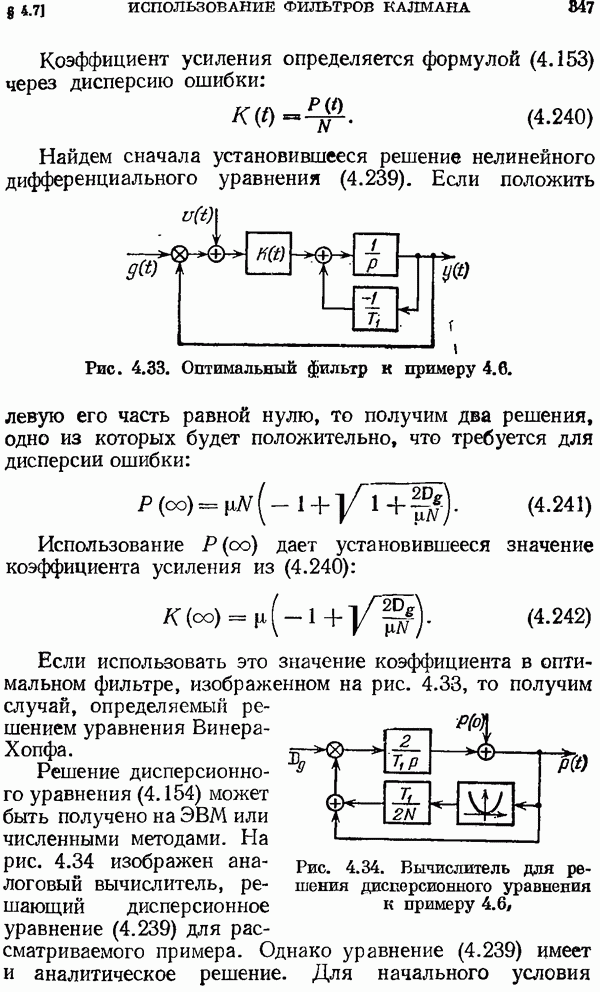
Далее можно воспользоваться формулой (2.92), заменив в ней  на
на 
е) Пусть изображение  имеет полюс
имеет полюс  кратности
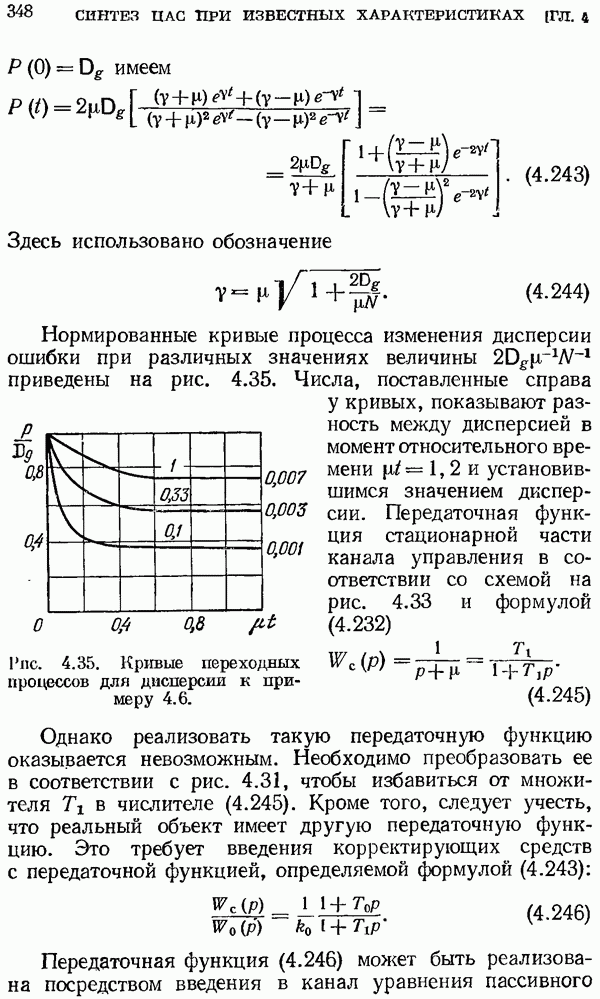
кратности  а все остальные полюсы простые:
а все остальные полюсы простые:

причем степень числителя меньше степени знаменателя. Тогда в соответствии с (2.83) и (2.90) оригинал будет

Эта формула справедлива для  При
При  значение оригинала
значение оригинала 
Для случая двойного корня  формула (2.93) приобретает вид
формула (2.93) приобретает вид

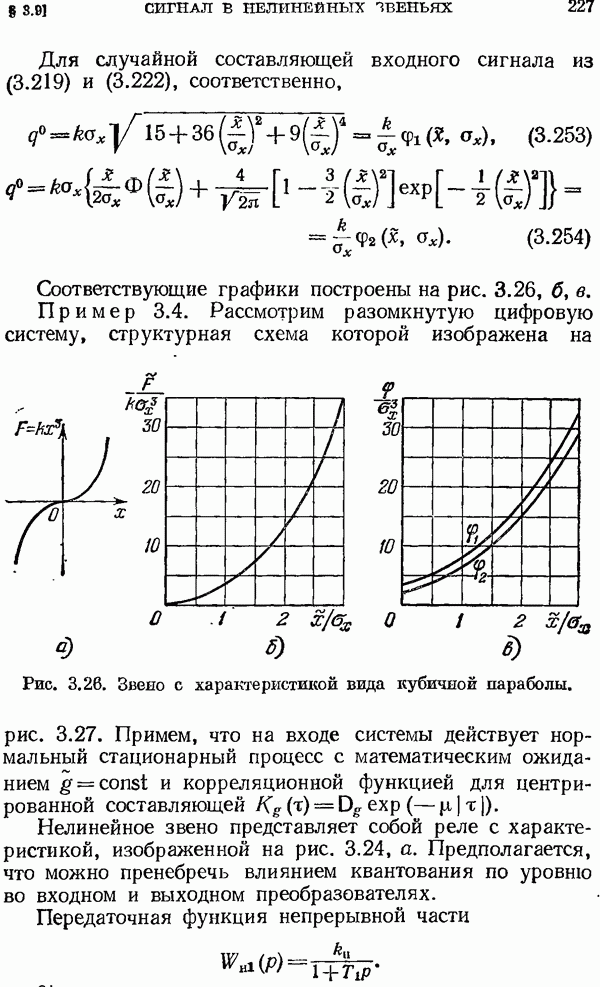
Так, например, если

то

что совпадает с таблицей 2.1.
В случае, когда степень числителя  равна степени знаменателя, следует, аналогично изложенному выше, выделить член нулевого порядка
равна степени знаменателя, следует, аналогично изложенному выше, выделить член нулевого порядка  делением числителя на знаменатель и рассматривать далее остаток от деления.
делением числителя на знаменатель и рассматривать далее остаток от деления.
14. Разложение в ряд Лорана. Из основного выражения для нахождения  -преобразования (2.42) следует:
-преобразования (2.42) следует:

Разложив любым способом изображение  в ряд Лорана (ряд по убывающим степеням z):
в ряд Лорана (ряд по убывающим степеням z):

и сравнивая два ряда между собой, можно установить, что 
Разложение в ряд можно делать любым способом, так как такое разложение единственно. Наиболее удобным
приемом для дробно-рациональных функций является деление числителя на знаменатель.
Применяя разложение в ряд Лорана, можно вычислить значения оригинала  или
или  в дискретных точках без нахождения полюсов изображения
в дискретных точках без нахождения полюсов изображения 
15. Решение разностных уравнений. Пусть имеется разностное уравнение в форме (2.29)

с начальными условиями  Найдем
Найдем  -преобразование от его левой и правой частей. В соответствии с формулой (2.52) для случая упреждения на
-преобразование от его левой и правой частей. В соответствии с формулой (2.52) для случая упреждения на  тактов
тактов

Аналогичные зависимости могут быть записаны для упреждения на  тактов. Поэтому при переходе в рассматриваемом разностном уравнении к изображениям можно получить
тактов. Поэтому при переходе в рассматриваемом разностном уравнении к изображениям можно получить

В правой части (2.95), кроме изображения  решетчатой функции
решетчатой функции  находятся члены, определяемые начальными условиями. Сумма их обозначения
находятся члены, определяемые начальными условиями. Сумма их обозначения 
Из (2.95) можно найти изображение  искомой решетчатой функции
искомой решетчатой функции

где  . Далее можно использовать изложенные выше приемы перехода к искомому оригиналу
. Далее можно использовать изложенные выше приемы перехода к искомому оригиналу 
Для решения рассматриваемого разностного уравнения необходимо, как следует из изложенного, знать начальные условия  Последние же зависят от вида действующей в правой части разностного уравнения решетчатой функции.
Последние же зависят от вида действующей в правой части разностного уравнения решетчатой функции.
Более удобны для решения разностные уравнения вида (2.33)

с начальными условиями 
Изображение решетчатой функции  запаздывающей на
запаздывающей на  тактов, в соответствии с (2.50) будет
тактов, в соответствии с (2.50) будет

Подобные зависимости могут быть записаны для запаздывания на  тактов.
тактов.
При переходе в рассматриваемом разностном уравнении к изображениям могут быть получены выражения, аналогичные (2.95) и (2.96). Переход к искомой решетчатой функции  осуществляется в соответствии с изложенными выше приемами.
осуществляется в соответствии с изложенными выше приемами.
Особый интерес представляет случай, когда до момента времени  искомая решетчатая функция тождественно равна нулю. Это эквивалентно случаю нулевых начальных условий слева (при
искомая решетчатая функция тождественно равна нулю. Это эквивалентно случаю нулевых начальных условий слева (при  при решении дифференциальных уравнений для непрерывных функций. Тогда в выражении для изображения (2.96) пропадает член в правой части, определяемый начальными условиями, и оно приобретает вид
при решении дифференциальных уравнений для непрерывных функций. Тогда в выражении для изображения (2.96) пропадает член в правой части, определяемый начальными условиями, и оно приобретает вид

Рассмотрим разностное уравнение вида (2.33),  записанное в более общем виде:
записанное в более общем виде:

Если ввести предположение, что решетчатая функция  тождественно равна нулю при
тождественно равна нулю при  , кроме того, функция
, кроме того, функция  в правой части (2.98) прикладывается в момент времени
в правой части (2.98) прикладывается в момент времени  то переход к изображениям дает
то переход к изображениям дает

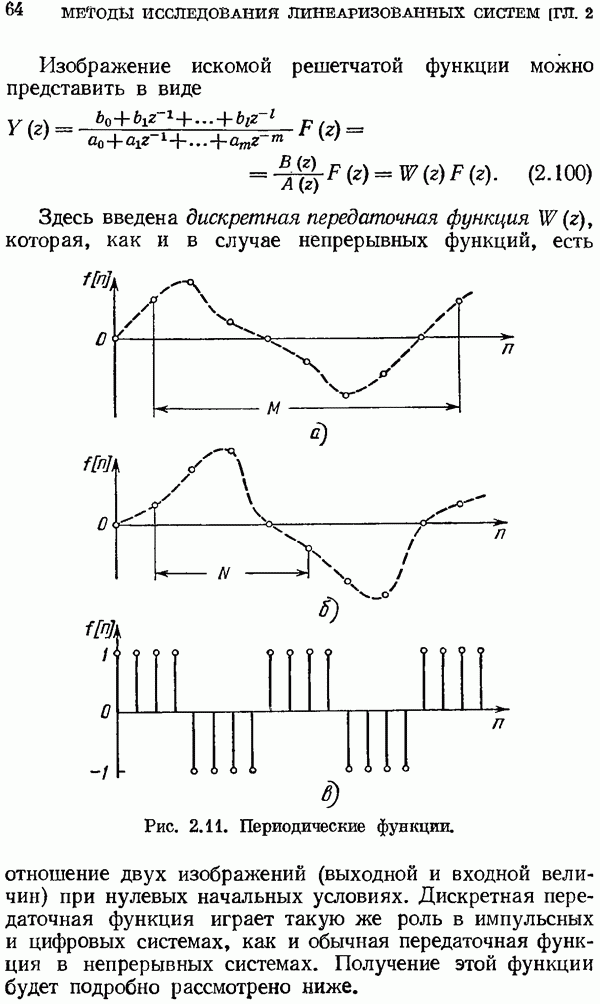
Изображение искомой решетчатой функции можно представить в виде

Здесь введена дискретная передаточная функция  которая, как и в случае непрерывных функций, есть отношение двух изображений (выходной и входной величин) при нулевых начальных условиях.
которая, как и в случае непрерывных функций, есть отношение двух изображений (выходной и входной величин) при нулевых начальных условиях.

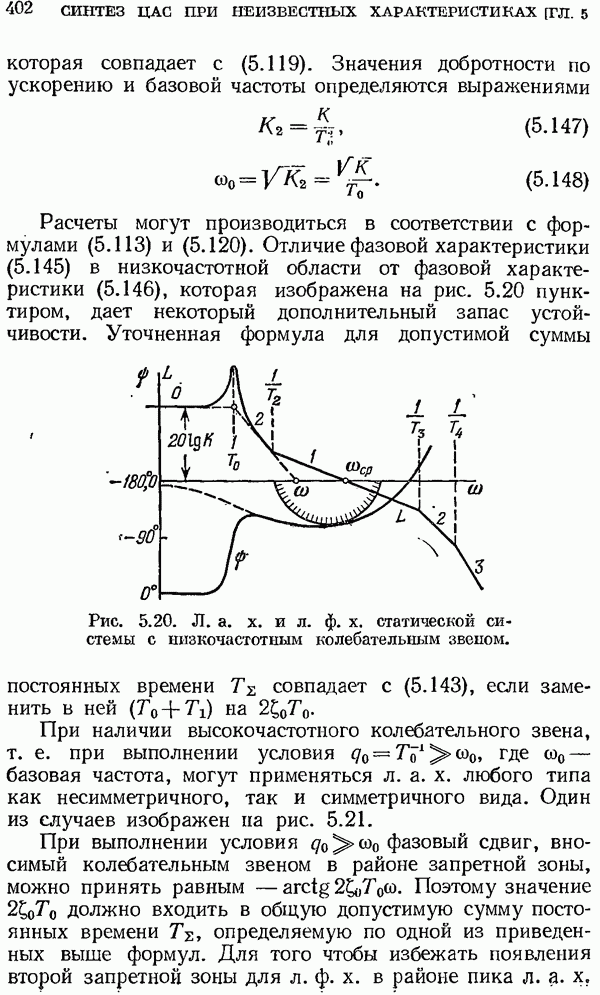
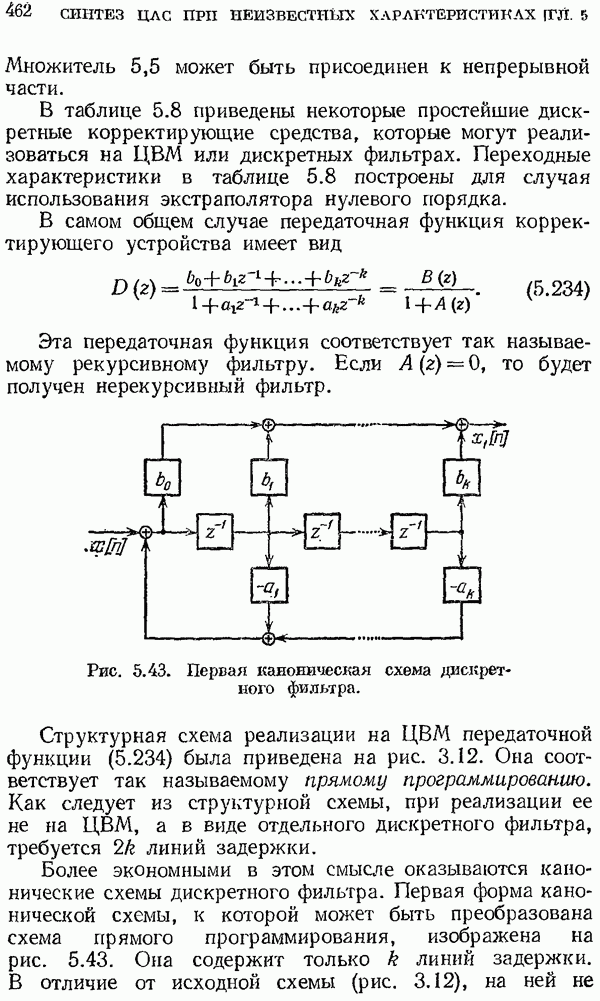
Рис. 2.11. Периодические функции.
Дискретная передаточная функция играет такую же роль в импульсных и цифровых системах, как и обычная передаточная функция в непрерывных системах. Получение этой функции будет подробно рассмотрено ниже.
16. Периодические решетчатые функции и их изображения. Введем в рассмотрение периодическую решетчатую функцию

где  и М — целые числа, причем М представляет собой относительный период (рис. 2.11, о). Первая гармоника имеет относительную угловую частоту
и М — целые числа, причем М представляет собой относительный период (рис. 2.11, о). Первая гармоника имеет относительную угловую частоту  Функция (2.101) может быть точно представлена в виде суммы конечного числа гармоник с частотами, кратными
Функция (2.101) может быть точно представлена в виде суммы конечного числа гармоник с частотами, кратными

Число гармоник равно целой части  Ряд (2.102) может быть представлен в комплексной форме:
Ряд (2.102) может быть представлен в комплексной форме:

где

Для  при
при 

Комплексные амплитуды могут находиться из формул:
при 

при 


и при

Для симметричной периодической функции (рис. 2.11, б), т. е. при выполнении условий  формула для комплексной амплитуды принимает вид
формула для комплексной амплитуды принимает вид

Из последнего выражения следует, что  при четном
при четном  т. е. четные гармоники отсутствуют. При
т. е. четные гармоники отсутствуют. При  нечетном
нечетном

Если  нечетно, то при
нечетно, то при 

Так как здесь присутствуют только нечетные гармоники, то тригонометрический ряд может быть записан в вещественной форме:

где  для четных
для четных  и
и  для нечетных
для нечетных  Для нахождения изображения периодической решетчатой функции (2.101) применим теорему сдвига (2.52):
Для нахождения изображения периодической решетчатой функции (2.101) применим теорему сдвига (2.52):

Отсюда следует:

Сумма в правой части (2.107) представляет собой изображение решетчатой функции на интервале  .
.
Для симметричной функции  аналогичным образом можно получить
аналогичным образом можно получить

Найдем, например, изображение симметричной периодической решетчатой функции, показанной на рис. 2.11, б,

Симметричная периодическая функция (2.108) всегда является центрированной, и для нее сумма ординат за период

Это не относится к несимметричной периодической функции (2.107), для которой сумма ординат за период может быть отличной от нуля, если эта функция содержит некоторую постоянную составляющую,

Несимметричная периодическая функция может быть центрирована выделением постоянной составляющей. Если (2.107) содержит постоянную составляющую, то уравнение  не должно иметь корня
не должно иметь корня  Действительно, при наличии такого корня формулу (2.107) можно
Действительно, при наличии такого корня формулу (2.107) можно
упростить:

где 
Если же  не содержит корня
не содержит корня  то в изображении периодической функции (2.107) можно выделить постоянную составляющую
то в изображении периодической функции (2.107) можно выделить постоянную составляющую

Второе слагаемое (2.109) представляет собой центрированный несимметричный периодический процесс. Полином  имеет наивысшую степень (М — 2). Коэффициент разложения
имеет наивысшую степень (М — 2). Коэффициент разложения 
Для получения изображения внутри периода центрированной решетчатой функции, изображение которой соответствует второму слагаемому формулы (2.109), последнее следует привести к виду (2.107):

Найдем, например, изображение периодической функции, представляющей собой единичную дискрету, повторяющуюся периодически через каждые М тактов. В соответствии с (2.107) изображение этого периодического процесса будет

Разложим  на слагаемые:
на слагаемые:

Центрированный процесс определяется вторым слагаемым последнего выражения:

По изображению  можно найти значения дискрет рассматриваемого центрированного процесса:
можно найти значения дискрет рассматриваемого центрированного процесса:  .
.
17. Площадь огибающей смещенной решетчатой функции. Площадь огибающей смещенной решетчатой функции, равная интегралу от производящей функции 

На основании (2.72) эта площадь 

Рассмотрим, например, площадь огибающей функции  основании таблицы 2.1 сумма дискрет этой функции
основании таблицы 2.1 сумма дискрет этой функции

Интегрируя последнее выражение по  имеем
имеем

18. Сумма квадратов дискрет решетчатой функции. Рассмотрим сумму квадратов дискрет
решетчатой функции и применим к ней формулу обращения (2.80):

Если абсцисса абсолютной сходимости отрицательна, то можно положить  Тогда
Тогда

где  — частотное изображение решетчатой функции, получаемое из
— частотное изображение решетчатой функции, получаемое из  -преобразования подстановкой
-преобразования подстановкой  Выражение (2.112) представляет собой дискретный аналог формулы Релея [8], записанной для функции времени
Выражение (2.112) представляет собой дискретный аналог формулы Релея [8], записанной для функции времени  отличной от нуля при
отличной от нуля при 

где  — частотное изображение (изображение Фурье) функции времени
— частотное изображение (изображение Фурье) функции времени 
Посредством подстановки, которая более подробно будет рассмотрена в § 2.5,

где К — абсолютная псевдочастота, или

формула (2.112) приводится к виду

где  — частотное изображение решетчатой функции
— частотное изображение решетчатой функции  Выражение (2.113) представляет собой другой вариант дискретного аналога формулы Релея.
Выражение (2.113) представляет собой другой вариант дискретного аналога формулы Релея.
Интегрирование выражения (2.113) в бесконечных пределах не представляет труда и может быть сделано с использованием известных таблиц интегралов (см. Приложение).
Найдем, например, сумму квадратов дискрет функции  Ее изображение в соответствии с таблицей 2.1
Ее изображение в соответствии с таблицей 2.1

Далее находим

Сумма квадратов дискрет, в соответствии с (2.113) и Приложением,

Если рассматривается смещенная функция  то, аналогично изложенному выше,
то, аналогично изложенному выше,

где  представляет собой z-преобразование решетчатой функции
представляет собой z-преобразование решетчатой функции  при замене
при замене  частотное изображение в функции псевдочастоты.
частотное изображение в функции псевдочастоты.
19. Площадь квадрата огибающей решетчатой функции. Площадь квадрата огибающей смещенной решетчатой функции равна интегралу от квадрата производящей функции:

где  определяется формулой (2.114).
определяется формулой (2.114).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ОБЩИЕ СВЕДЕНИЯ О ЦИФРОВЫХ СИСТЕМАХ УПРАВЛЕНИЯ
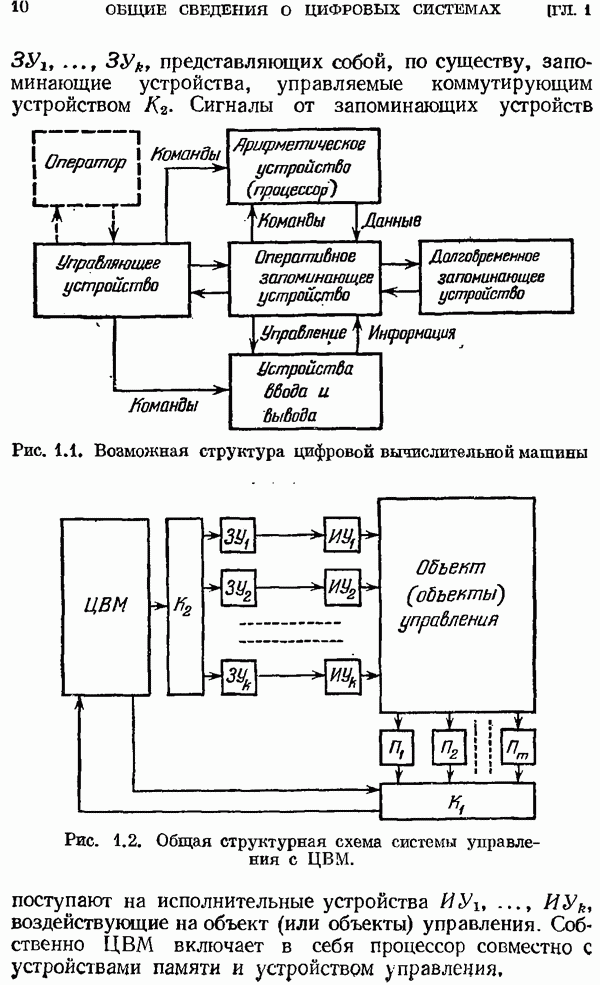
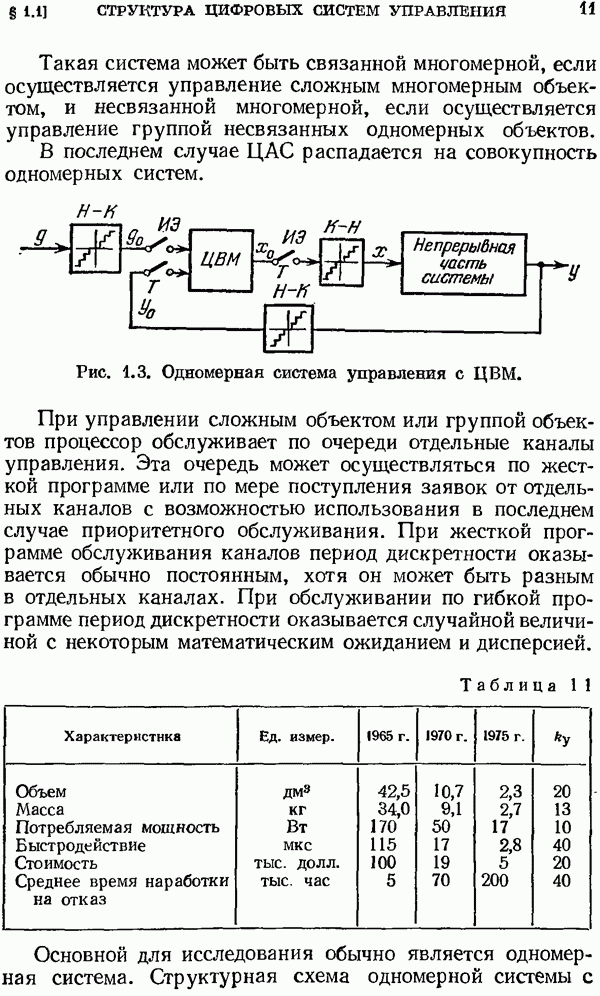
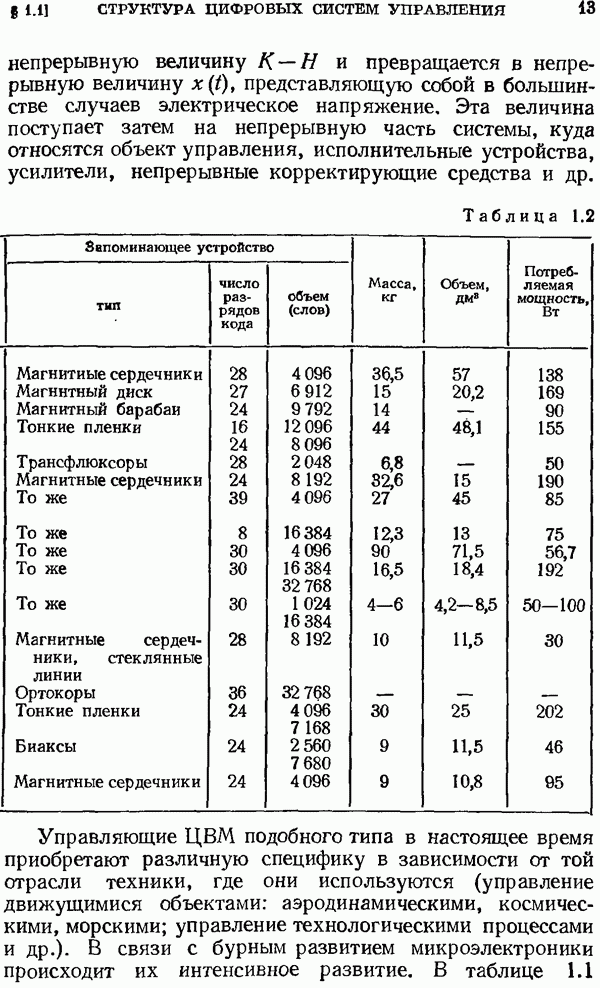
- § 1.1. Структура цифровых систем управления
- § 1.2. Задачи, решаемые ЦВМ в системах автоматического управления
- § 1.3. Методы исследования цифровых систем управления
- ГЛАВА 2. МЕТОДЫ ИССЛЕДОВАНИЯ ЛИНЕАРИЗОВАННЫХ СИСТЕМ
- § 2.2. Математический аппарат
- Решетчатые функции.
- Разностные уравнения.
- Дискретное преобразование Лапласа.
- Использование z-преобразования.
- § 2.3. Передаточные функции непрерывной части ЦАС
- Экстраполяторы нулевого порядка.
- Экстраполяторы первого порядка.
- Экстраполяторы более высоких порядков.
- Непрерывные экстраполяторы.
- Экстраполяторы со сложной формой выходного импульса.
- § 2.4. Передаточные функции ЦВМ
- § 2.5. Передаточные функции ЦАС
- Передаточные функции для возмущений.
- Частотные передаточные функции.
- § 2.6. Устойчивость и качество линеаризованных ЦАС
- § 2.7. Расчет вынужденных периодических режимов
- § 2.8. Построение логарифмических частотных характеристик
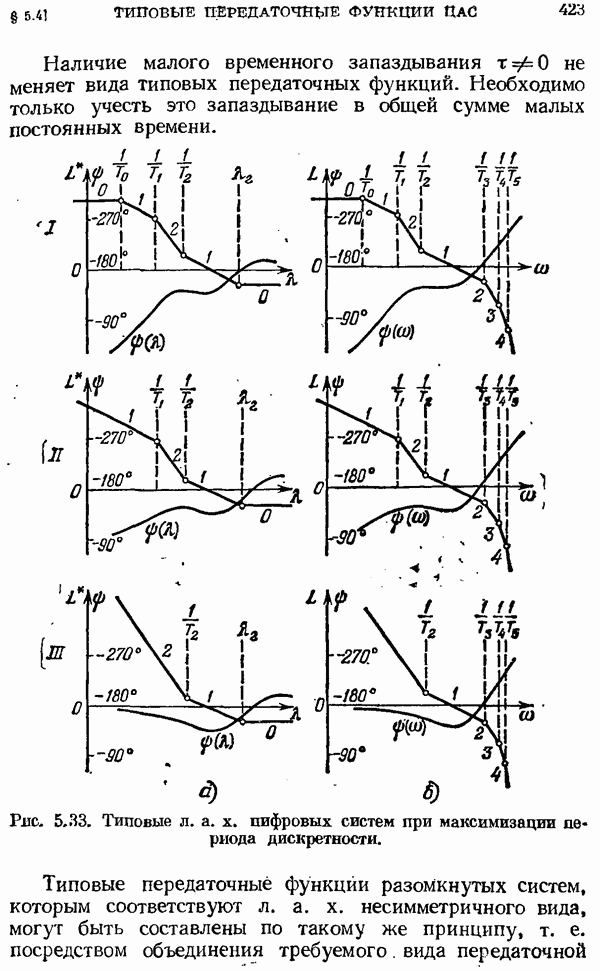
- Колебательные звенья.
- § 2.9. Передаточные функции многомерных ЦАС
- ГЛАВА 3. СЛУЧАЙНЫЕ ПРОЦЕССЫ В ЦИФРОВЫХ АВТОМАТИЧЕСКИХ СИСТЕМАХ
- § 3.2. Корреляционная функция
- Стационарные процессы.
- § 3.3. Спектральная плотность стационарных процессов
- § 3.4. Типовые решетчатые случайные стационарные процессы
- Процессы с корреляционной функцией экспоненциального вида.
- Процесс с равномерным спектром в ограниченной полосе частот.
- Нерегулярная качка.
- Гармонический сигнал.
- § 3.5. Прохождение случайного сигнала через линейную систему
- § 3.6. Расчет установившихся ошибок в линеаризованных ЦАС
- § 3.7. Приближенным расчет дополнительных ошибок ЦАС, вызванных квантованием по уровню
- Помехи на выходе ЦВМ.
- § 3.8. Корреляционные функции и спектральные плотности шумов квантования
- Взаимосвязь шума квантования и полезного сигнала.
- § 3.9. Прохождение случайного сигнала через нелинейные звенья в разомкнутых системах
- Кусочно-линейные характеристики.
- Характеристики с разрывом непрерывностей.
- Идеальная релейная характеристика.
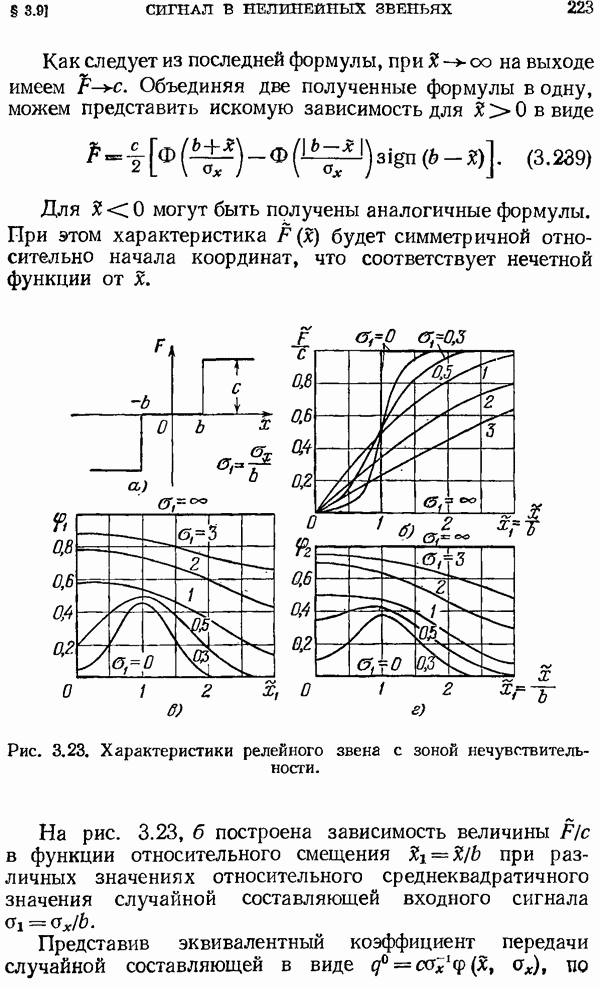
- Релейная характеристика с зоной нечувствительности.
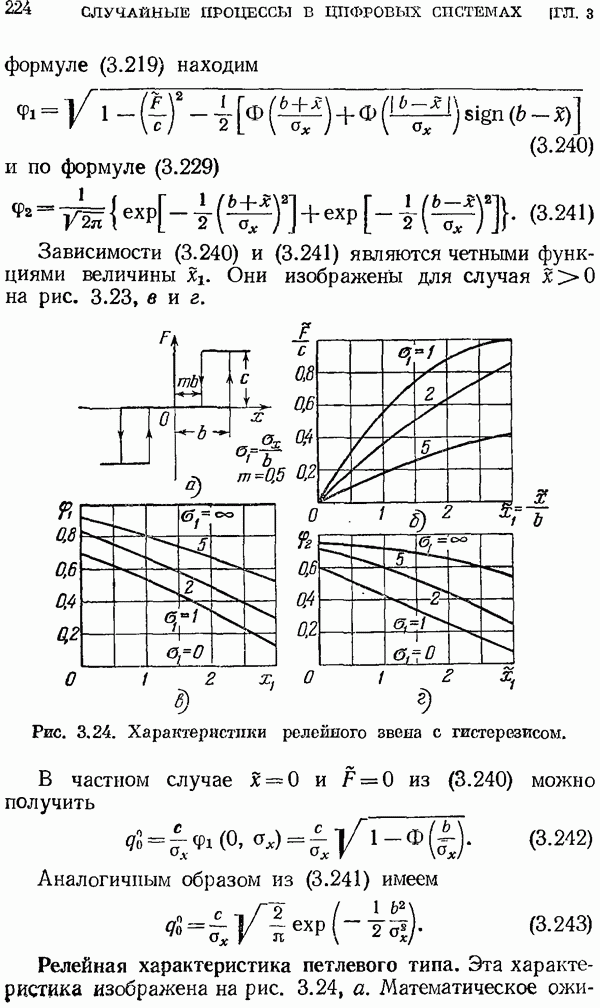
- Релейная характеристика петлевого типа.
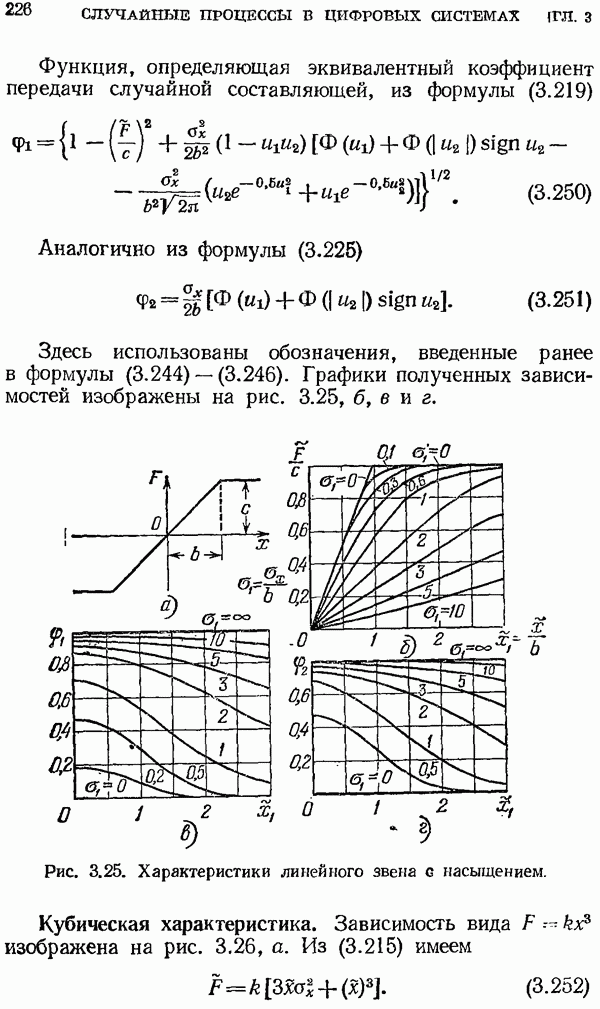
- Линейная характеристика с насыщением.
- Кубическая характеристика.
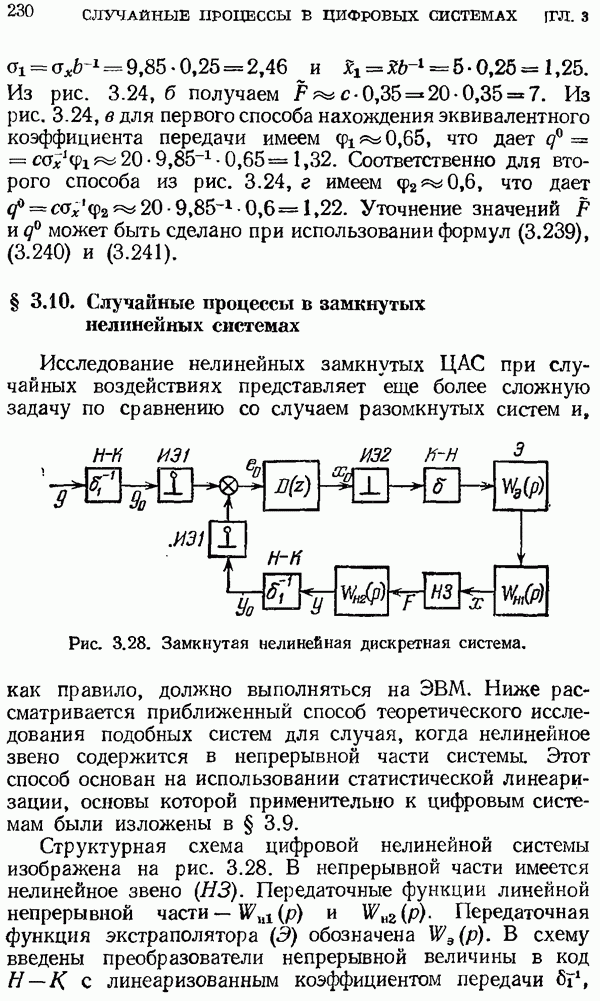
- § 3.10. Случайные процессы в замкнутых нелинейных системах
- § 3.11. Системы со случайным периодом дискретности
- ГЛАВА 4. ОПТИМАЛЬНЫЙ ДИНАМИЧЕСКИЙ СИНТЕЗ ЛИНЕАРИЗОВАННЫХ ЦАС ПРИ ИЗВЕСТНЫХ СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИКАХ ВХОДНЫХ ВОЗДЕЙСТВИЙ
- § 4.2. Критерии качества и методы синтеза
- Использование фильтров Винера.
- Использование фильтров Калмана.
- § 4.3. Основы теории фильтров Винера
- Системы с белым шумом на входе.
- Передаточная функция разомкнутой системы.
- Прогнозирование.
- § 4.4. Использование фильтров Винера в цифровых системах
- Системы с белым шумом на входе.
- Прогнозирование.
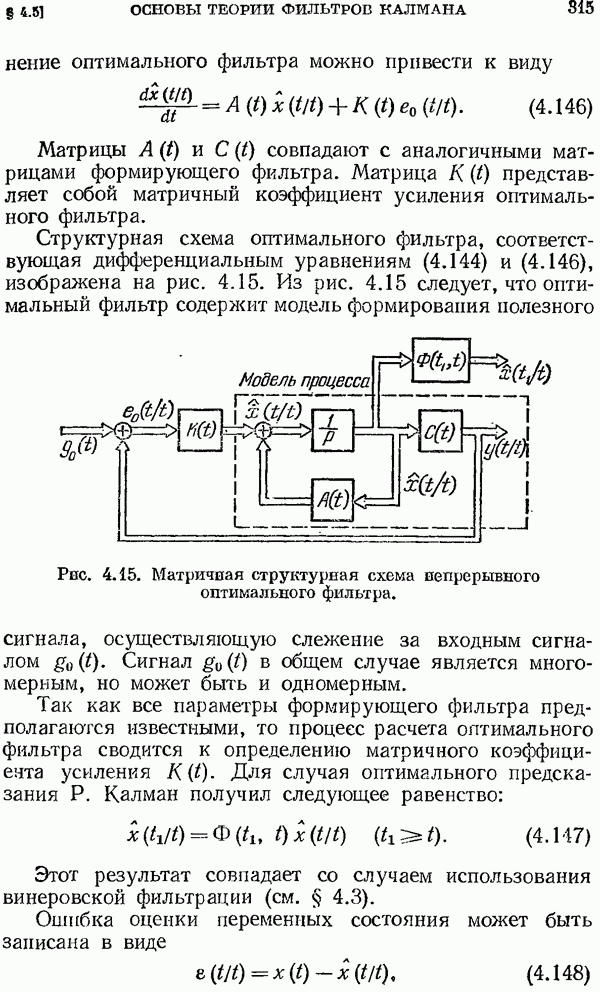
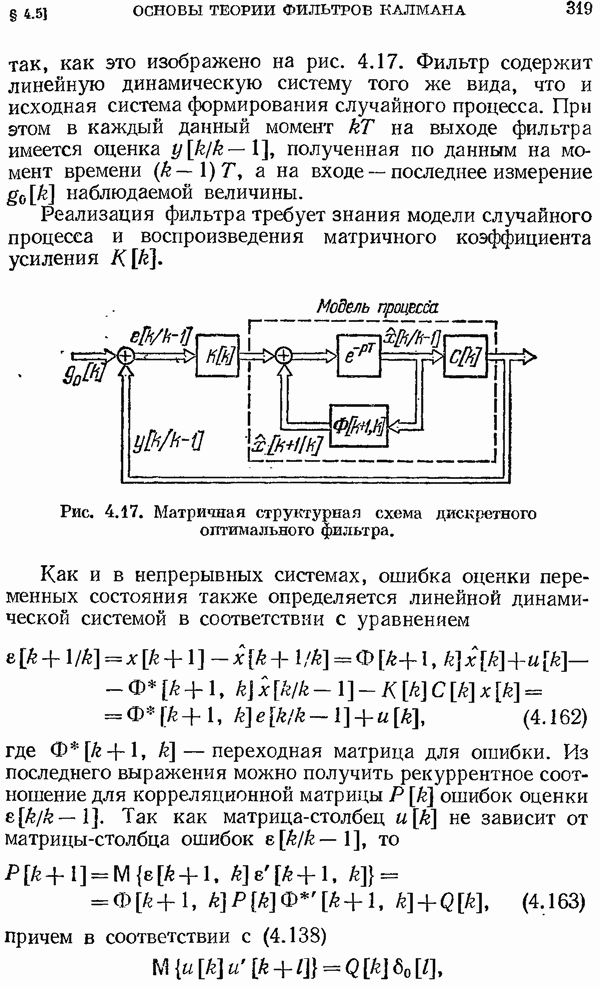
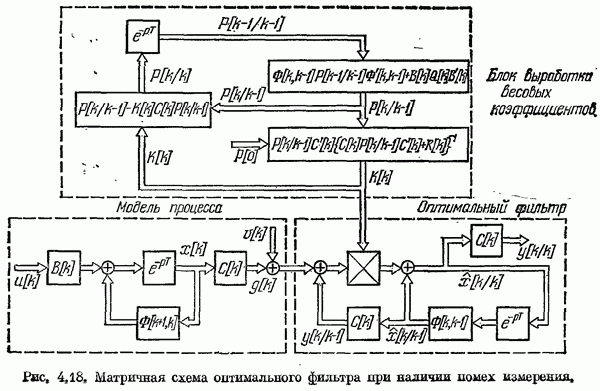
- § 4.5. Основы теории фильтров Калмана
- Алгоритм фильтра Калмана для непрерывных систем.
- Алгоритм фильтра Калмана для дискретных систем.
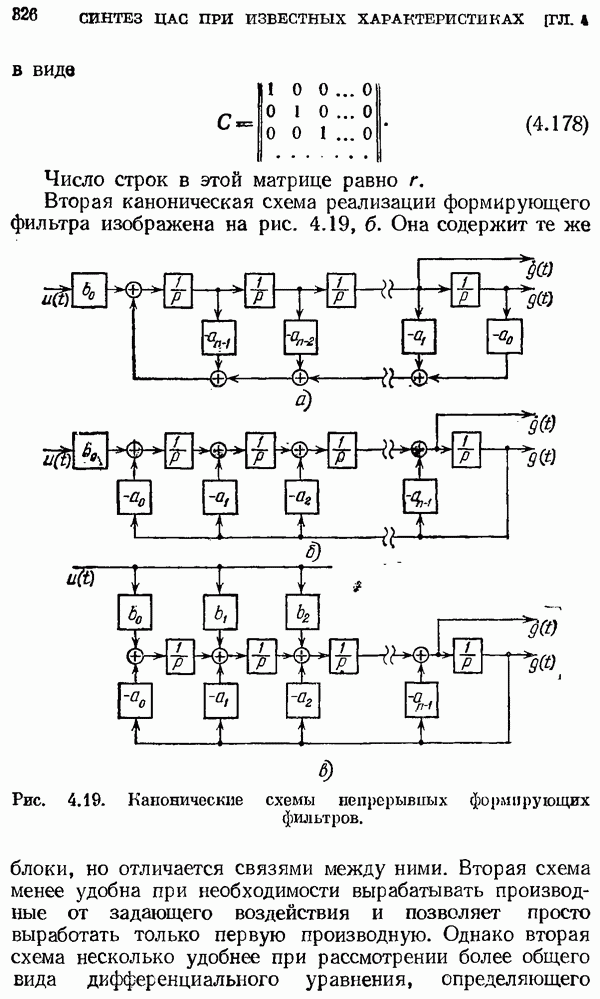
- § 4.6. Формирующие фильтры
- Стационарные процессы.
- Типовые стационарные процессы.
- Дискретные формирующие фильтры.
- Типовые дискретные стационарные процессы.
- § 4.7. Использование оптимальных фильтров Калмана в системах управления
- Стационарные системы.
- ГЛАВА 5. ДИНАМИЧЕСКИЙ СИНТЕЗ ЛИНЕАРИЗОВАННЫХ ЦАС ПРИ НЕИЗВЕСТНЫХ СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИКАХ ВХОДНЫХ ВОЗДЕЙСТВИИ
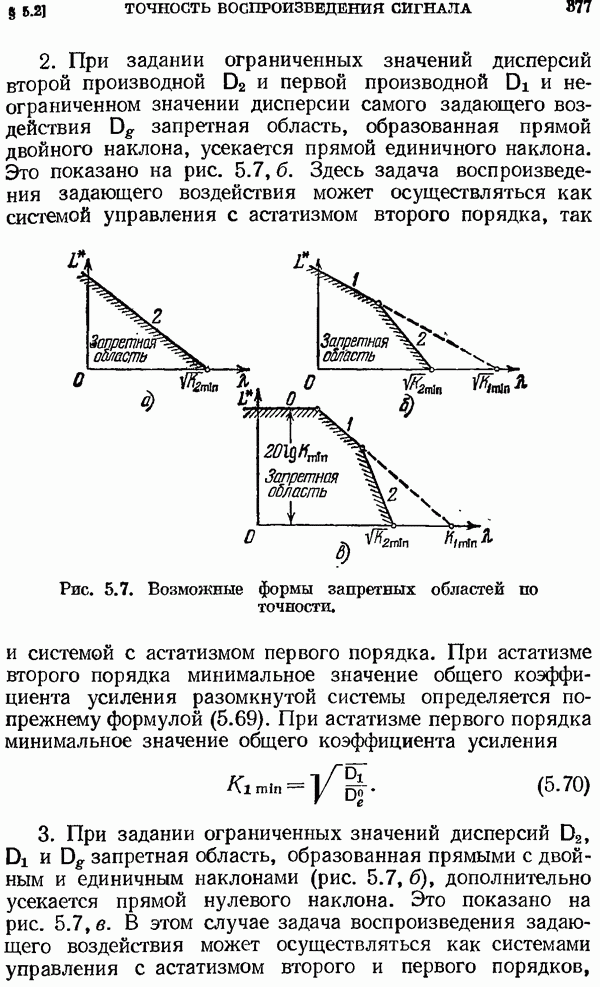
- § 5.2. Обеспечение требуемой точности воспроизведения полезного сигнала. Предельные фильтры
- Ограниченные значения скорости и ускорения входного сигнала.
- Типовые передаточные функции астатических систем.
- Ограниченное значение модуля входного воздействия.
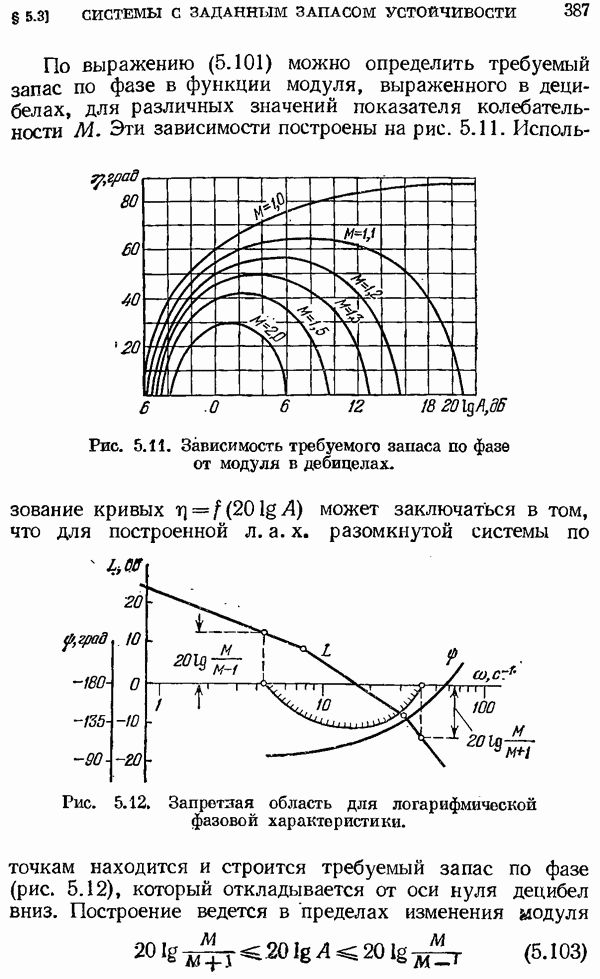
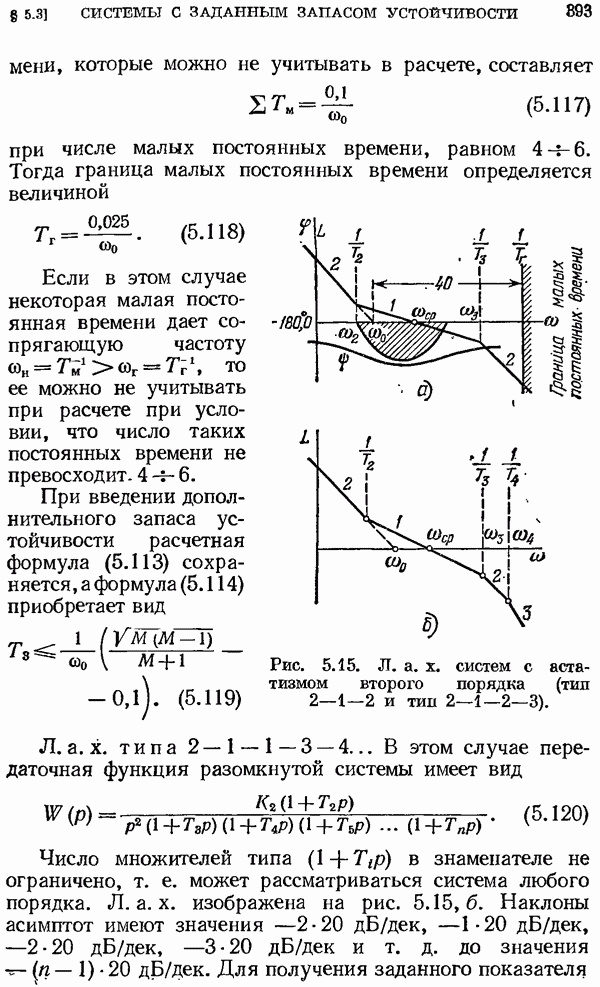
- § 5.3. Общие принципы построения систем управления с заданным запасом устойчивости
- Системы с астатизмом второго порядка.
- Системы с астатизмом первого порядка.
- Статические системы.
- Системы, содержащие неустойчивые звенья.
- Переходные процессы в системах с типовыми передаточными функциями.
- § 5.4. Типовые передаточные функции цифровых систем управления
- Типовые передаточные функции при использовании дискретной коррекции.
- Сглаживающие системы.
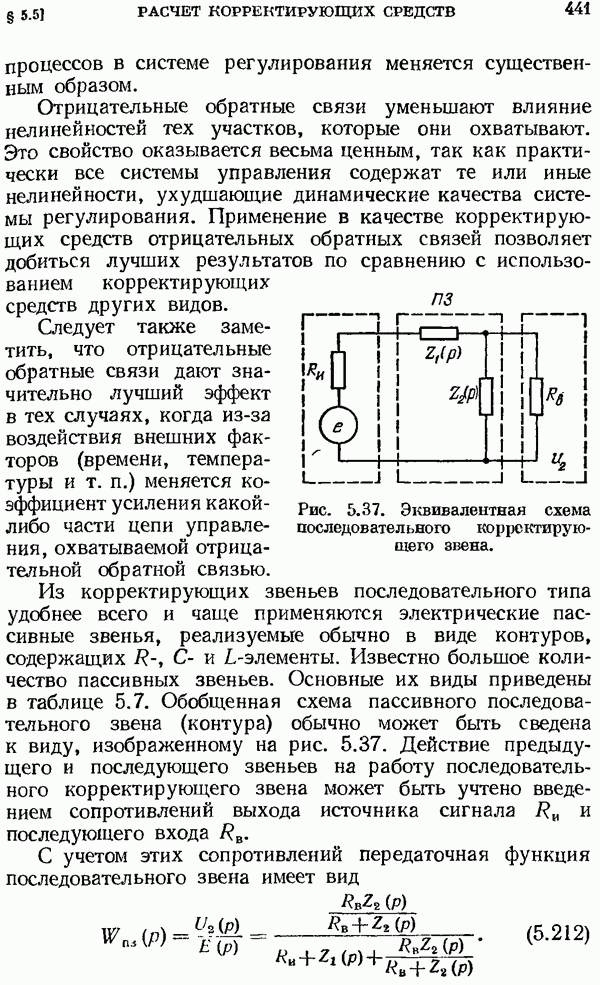
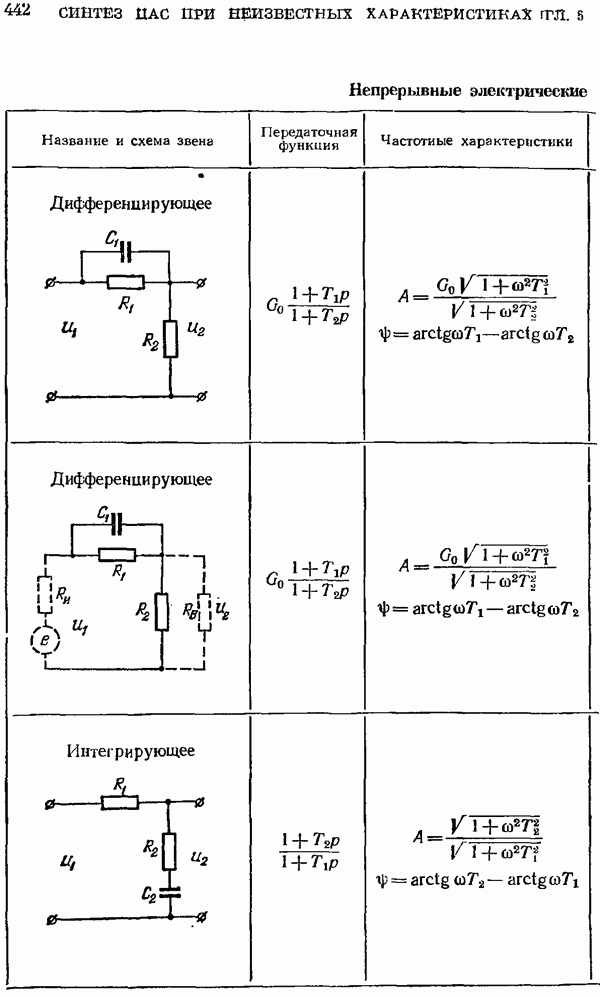
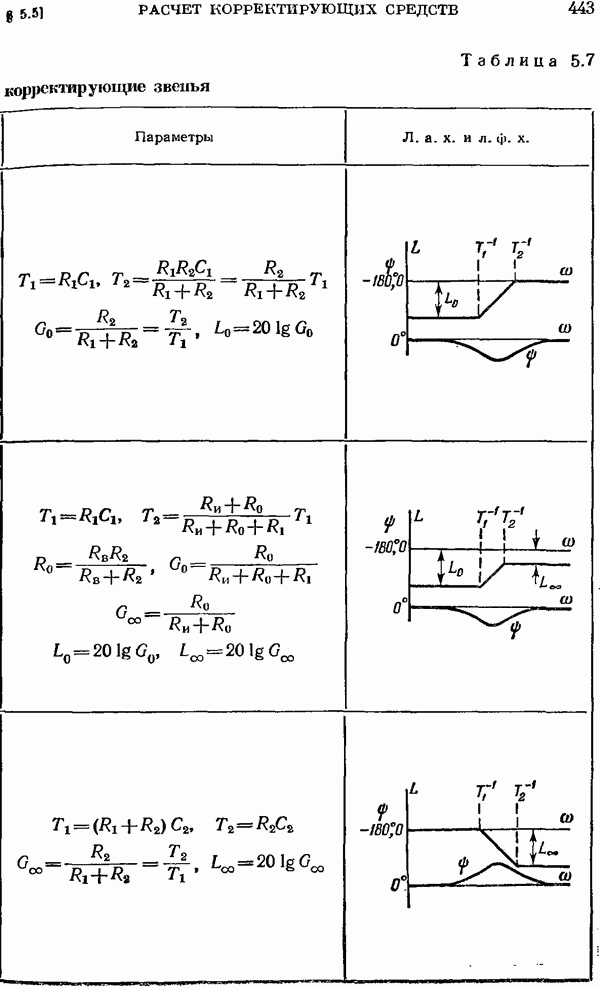
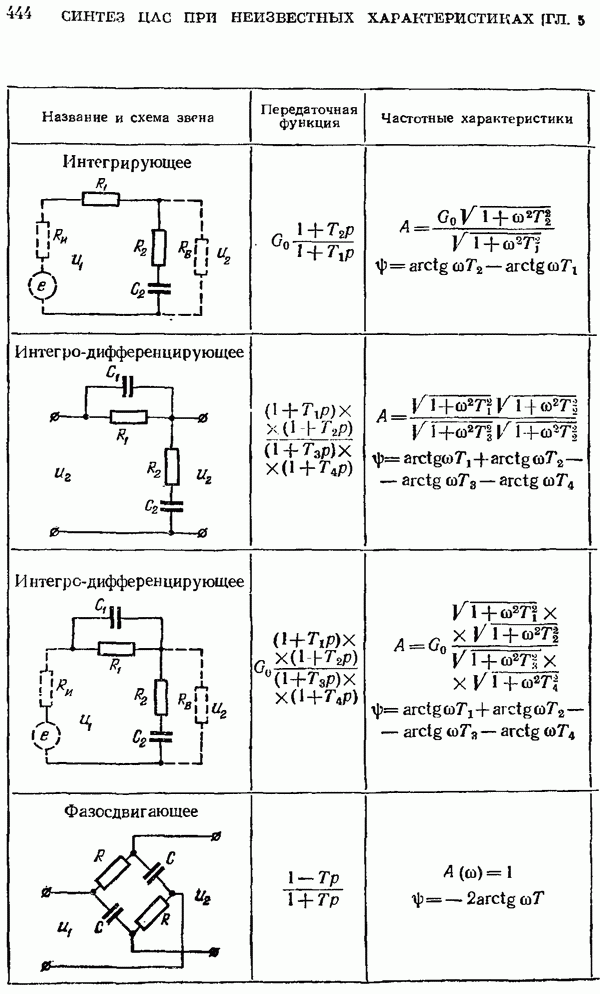
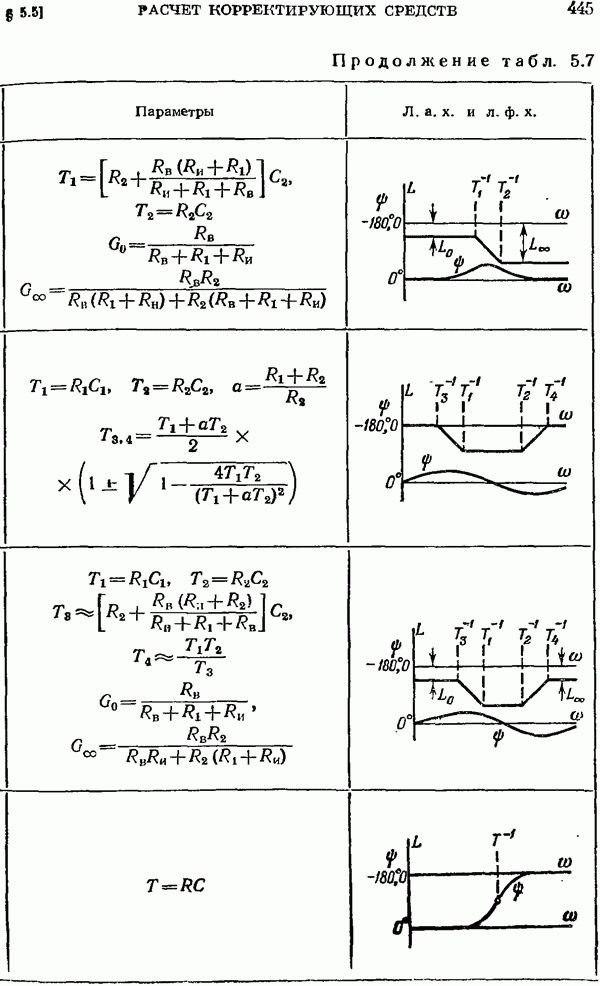
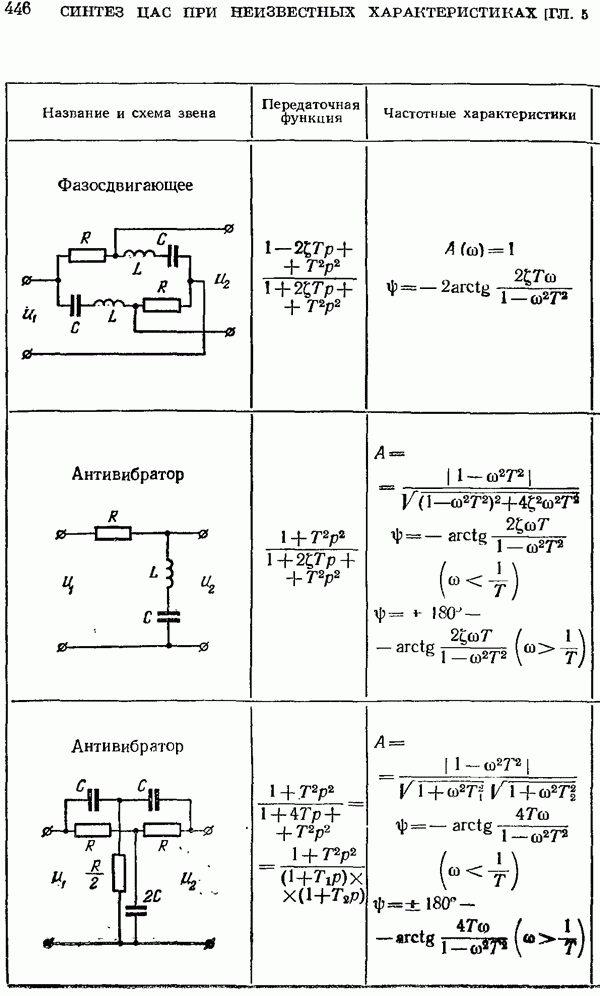
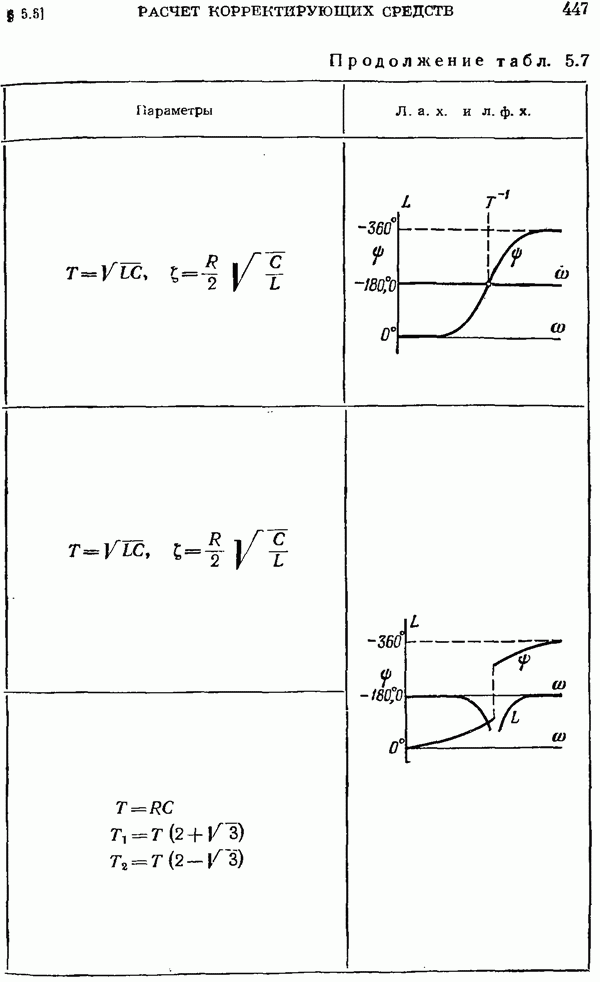
- § 5.5. Расчет корректирующих средств
- Непрерывные корректирующие средства.
- Расчет непрерывных корректирующих средств.
- Дискретные корректирующие средства.
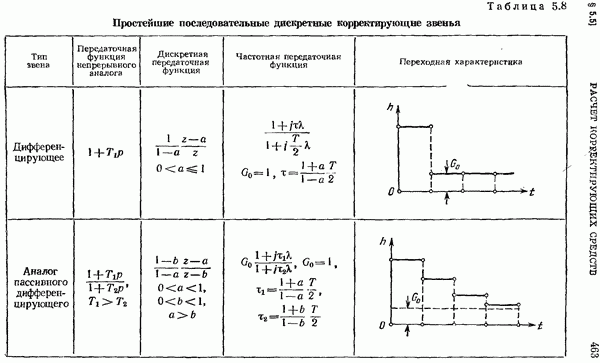
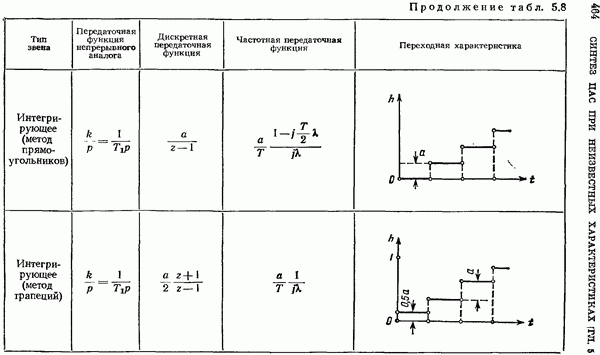
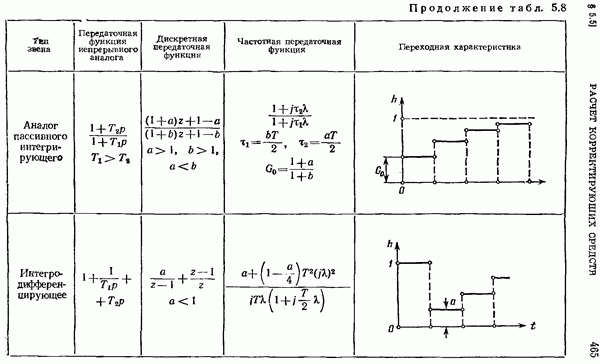
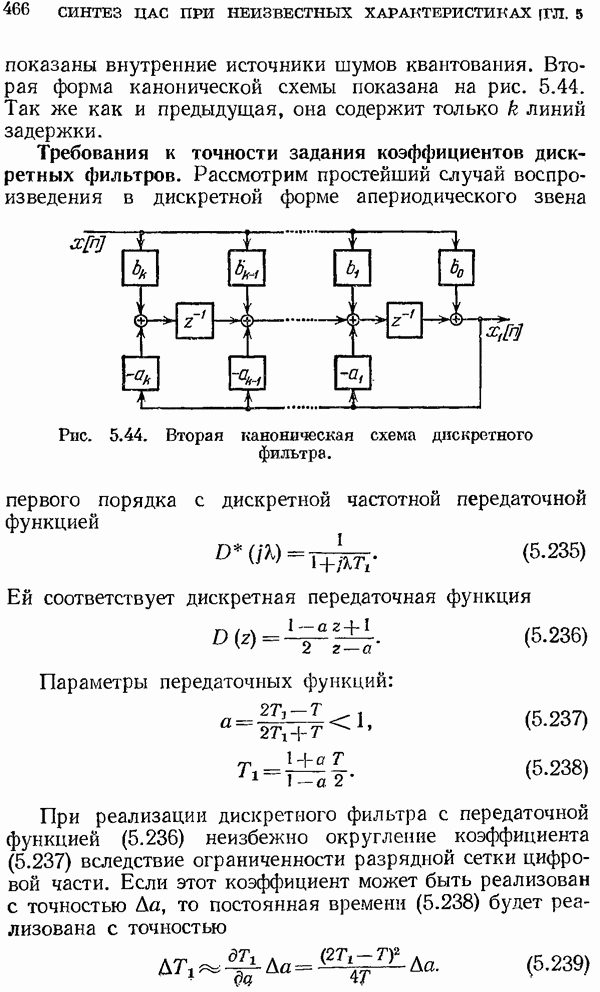
- Требования к точности задания коэффициентов дискретных фильтров.
- Корректирующие обратные связи.
- Псевдолинейные корректирующие устройства.
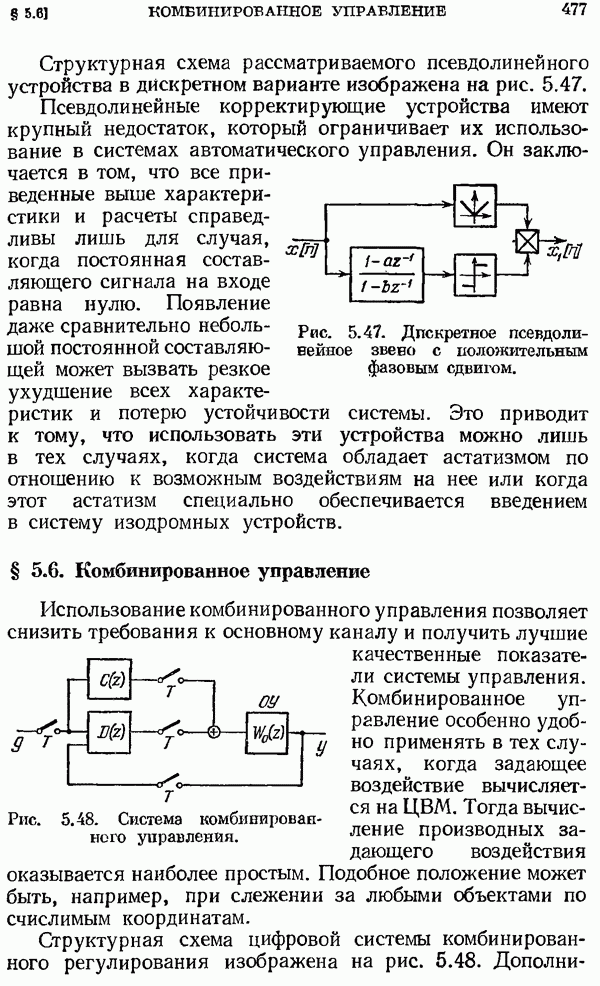
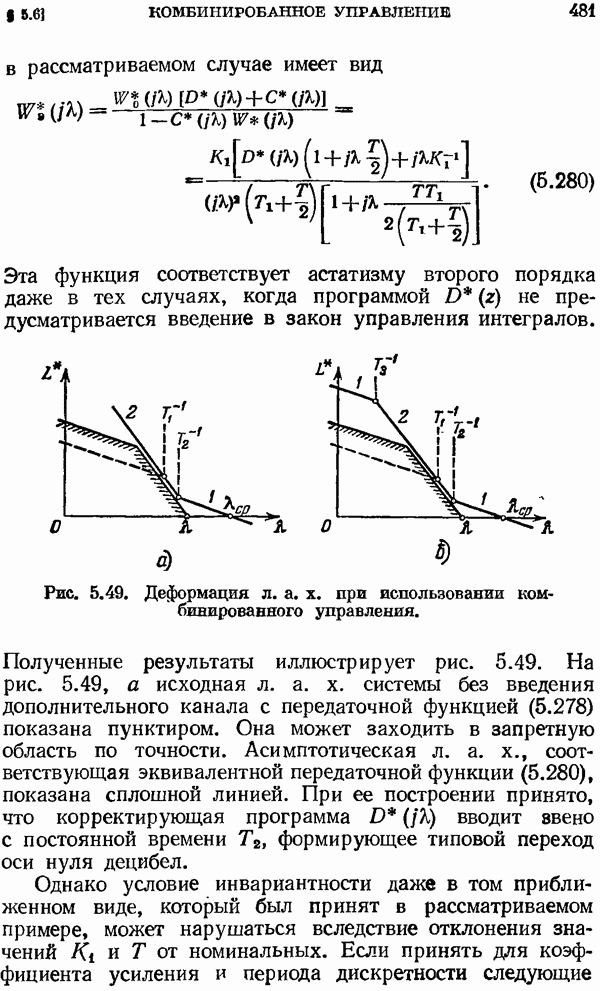
- § 5.6. Комбинированное управление
- Снижение требований к ЦВМ.
- Цифровое дифференцирование непрерывных сигналов.
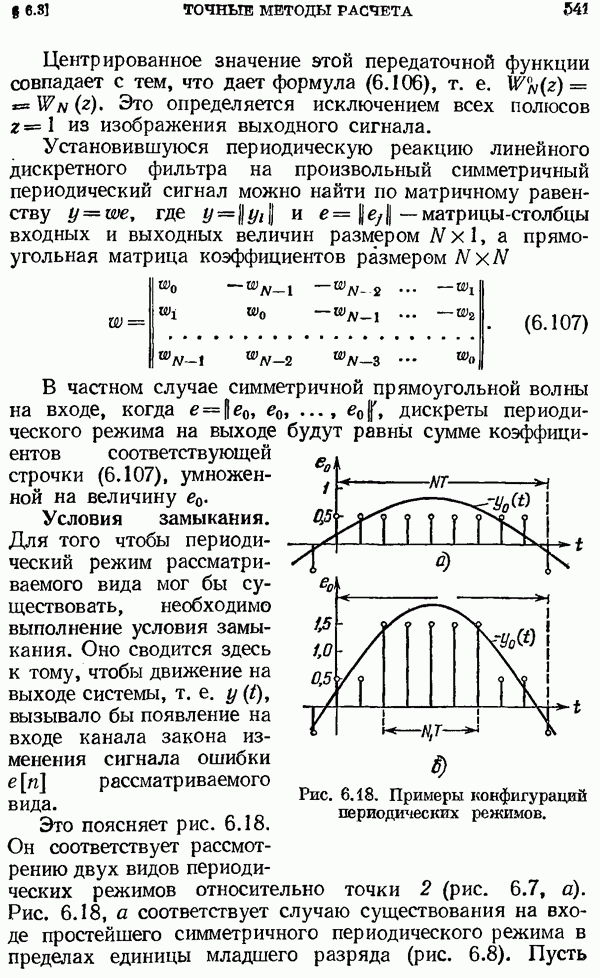
- ГЛАВА 6. ПЕРИОДИЧЕСКИЕ РЕЖИМЫ В ЦАС, ВЫЗВАННЫЕ КВАНТОВАНИЕМ ПО УРОВНЮ
- § 6.2. Квазипериодические режимы
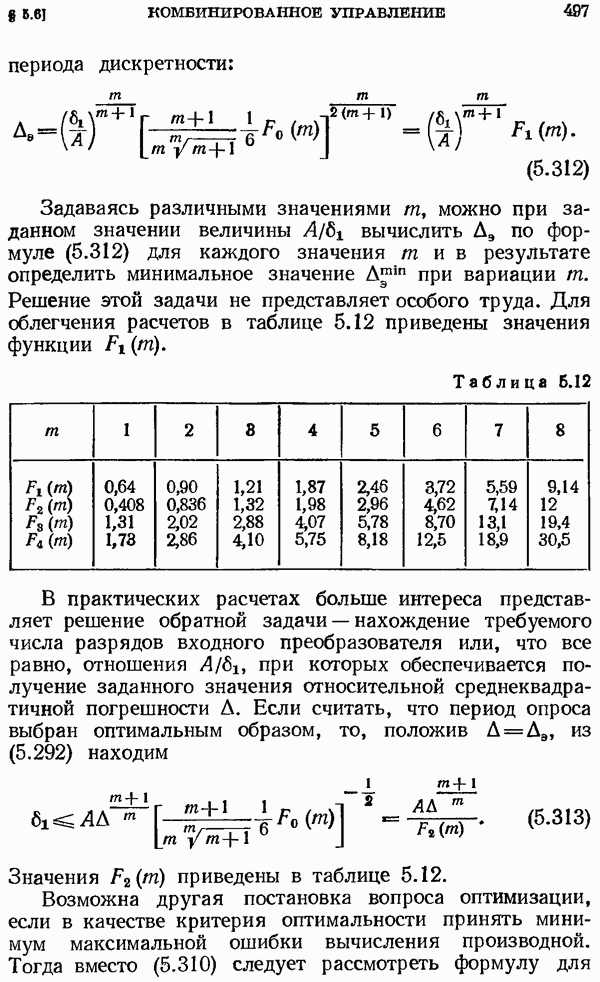
- § 6.3. Точные методы расчета периодических режимов в ЦАС
- Условия замыкания.
- Учет влияния второго квантующего элемента.
- § 6.4. Определение требований к входным и выходным преобразователям
- ПРИЛОЖЕНИЕ
- ТАБЛИЦА ИНТЕГРАЛОВ
- ЛИТЕРАТУРА