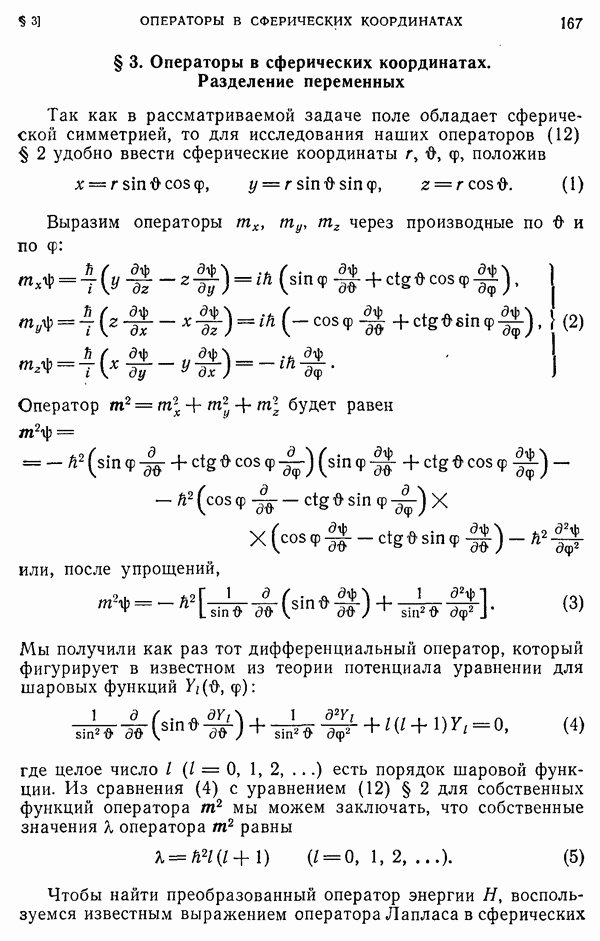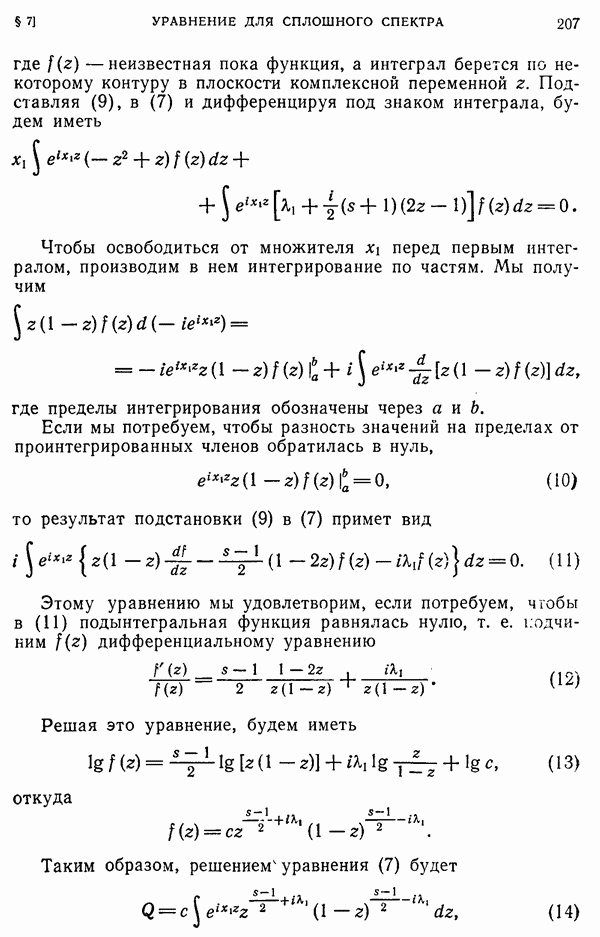| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Часть II. ТЕОРИЯ ШРЕДИНГЕРА
Глава I. ВОЛНОВОЕ УРАВНЕНИЕ ШРЕДИНГЕРА. ПРИМЕР ВИБРАТОРА
§ 1. Волновое уравнение и уравнения движения
Как мы знаем, волновое уравнение, дающее закон изменения функции во времени, должно иметь вид

где  оператор энергии. Вид оператора энергии будет, вообще говоря, различным для различных задач. В теории Шредингера рассматривается тот случай, когда количество движения электрона мало по сравнению с величиной
оператор энергии. Вид оператора энергии будет, вообще говоря, различным для различных задач. В теории Шредингера рассматривается тот случай, когда количество движения электрона мало по сравнению с величиной  где с — скорость света, так что поправкой на теорию относительности можно пренебречь и когда магнитное поле отсутствует, так что электрон движется в электрическом поле с потенциальной энергией
где с — скорость света, так что поправкой на теорию относительности можно пренебречь и когда магнитное поле отсутствует, так что электрон движется в электрическом поле с потенциальной энергией  Обобщение уравнения Шредингера на случай наличия магнитного поля мы рассмотрим в третьей части этой книги.
Обобщение уравнения Шредингера на случай наличия магнитного поля мы рассмотрим в третьей части этой книги.
В § 8 гл. III, ч. I мы написали, по аналогии с классической механикой, следующее выражение для оператора энергии:

Здесь первый член представляет кинетическую, а второй — потенциальную энергию электрона. Заменяя операторы  их выражениями, мы можем написать волновое уравнение в виде
их выражениями, мы можем написать волновое уравнение в виде

Рассмотрим уравнения движения, вытекающие из уравнения Шредингера. Найдем операторы для скорости и ускорения. Имеем, на основании (22) § 13 гл. III ч. I,

В выражении для  все члены, кроме
все члены, кроме  переместительны с х, поэтому
переместительны с х, поэтому

Но мы знаем, что

Поэтому

и аналогично

Таким образом, оператор для скорости равен деленному на  оператору для количества движения, как и следовало ожидать. Найдем теперь оператор для производной
оператору для количества движения, как и следовало ожидать. Найдем теперь оператор для производной  Мы имеем
Мы имеем

Единственный член в  , не коммутирующий с
, не коммутирующий с  есть
есть  так что
так что

Присоединяя сюда аналогичные соотношения для двух других составляющих, получим

Уравнения (4) и (5) совпадают по форме с соответствующими уравнениями классической механики. Припоминая связь между уравнениями движения и законом изменения математических ожиданий, мы можем также написать

и два аналогичных уравнения для координат  Эти уравнения носят название уравнений Эренфеста (Ehrenfest)!
Эти уравнения носят название уравнений Эренфеста (Ehrenfest)!
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- Часть I. ОСНОВАНИЯ КВАНТОВОЙ МЕХАНИКИ
- Глава I. ФИЗИЧЕСКИЕ И ТЕОРЕТИКО-ПОЗНАВАТЕЛЬНЫЕ ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ
- § 3. Область применимости классического способа описания явлений. Соотношения Гейзенберга и Бора
- § 4. Относительность к средствам наблюдения как основа квантового способа описания явлений
- § 5. Понятие потенциальной возможности в квантовой физике
- Глава II. МАТЕМАТИЧЕСКИЙ АППАРАТ КВАНТОВОЙ МЕХАНИКИ
- § 1. Квантовая механика и задачи на линейные операторы
- § 2. Понятие об операторе и примеры операторов
- § 3. Оператор, сопряженный к данному. Самосопряженность
- § 4. Произведение операторов. Правило умножения матриц
- § 5. Собственные значения и собственные функции операторов
- § 6. Интеграл Стильтьеса и оператор умножения на независимую переменную
- § 7. Ортогональность и нормировка собственных функций
- § 8. Разложение по собственным функциям. Замкнутость системы функций
- Глава III. ФИЗИЧЕСКОЕ ЗНАЧЕНИЕ ОПЕРАТОРОВ
- § 1. Толкование собственных значений оператора
- § 2. Скобки Пуассона
- § 3. Операторы для координат и моментов
- § 4. Собственные значения и собственные функции оператора количества движения
- § 5. Квантовое описание состояния системы
- § 6. Коммутативность операторов
- § 7. Момент количества движения
- § 8. Оператор энергии
- § 9. Каноническое преобразование
- § 10. Пример канонического преобразования
- § 11. Каноническое преобразование как оператор
- § 12. Унитарные инварианты
- § 13. Изменение состояния системы во времени. Операторы как функции от времени
- § 14. Гейзенберговы матрицы
- § 15. Полуклассическое приближение
- § 16. Связь канонического преобразования с касательным преобразованием классической механики
- Глава IV. ВЕРОЯТНОСТНОЕ ТОЛКОВАНИЕ КВАНТОВОЙ МЕХАНИКИ
- § 1. Математическое ожидание в теории вероятностей
- § 2. Математическое ожидание в квантовой механике
- § 3. Выражение для вероятностей
- § 4. Закон изменения математического ожидания во времени
- § 5. Соответствие между понятиями теории линейных операторов и теории квантов
- § 6. Понятие статистического коллектива в квантовой механике
- Часть II. ТЕОРИЯ ШРЕДИНГЕРА
- § 1. Волновое уравнение и уравнения движения
- § 2. Интегралы уравнений движения
- § 3. Уравнение Шредингера для гармонического вибратора
- § 4. Вибратор в одном измерении
- § 5. Полиномы Чебышева — Эрмита
- § 6. Каноническое преобразование на примере вибратора
- § 7. Неравенства Гейзенберга
- § 8. Зависимость матриц от времени. Сравнение с классической теорией
- § 9. Элементарный критерий применимости формул классической механики
- Глава II. ТЕОРИЯ ВОЗМУЩЕНИЙ
- § 2. Решение неоднородного уравнения
- § 3. Простые собственные значения
- § 4. Кратные собственные значения. Разложение по степеням малого параметра
- § 5. Собственные функции в нулевом приближении
- § 6. Первое и последующие приближения
- § 7. Случай близких собственных значений
- § 8. Ангармонический вибратор
- Глава III. ИЗЛУЧЕНИЕ, ТЕОРИЯ ДИСПЕРСИИ И ЗАКОН РАСПАДА
- § 2. Плотность и вектор тока
- § 3. Частоты и интенсивности
- § 4. Интенсивности в сплошном спектре
- § 5. Возмущение атома световой волной
- § 6. Формула дисперсии
- § 7. Прохождение частицы сквозь барьер потенциальной энергии
- § 8. Закон распада почти стационарного состояния
- Глава IV. ЭЛЕКТРОН В ПОЛЕ С ЦЕНТРАЛЬНОЙ СИММЕТРИЕЙ
- § 2. Интегралы площадей
- § 3. Операторы в сферических координатах. Разделение переменных
- § 4. Решение дифференциального уравнения для шаровых функций
- § 5. Некоторые свойства шаровых функций
- § 6. Нормированные шаровые функции
- § 7. Радиальные функции. Общее исследование
- § 8. Описание состояния валентного электрона. Квантовые числа
- § 9. Правило отбора
- Глава V. КУЛОНОВО ПОЛЕ
- § 2. Уравнение для радиальных функций водорода. Атомные единицы меры
- § 3. Решение одной вспомогательной задачи
- § 4. Некоторые свойства обобщенных полиномов Лагерра
- § 5. Собственные значения и собственные функции вспомогательной задачи
- § 6. Уровни энергии и радиальные функции точечного спектра для водорода
- § 7. Решение дифференциального уравне им для сплошного спектра в виде определенного интеграла
- § 8. Вывод асимптотического выражения
- § 9. Радиальные функции водорода для сплошного спектра
- § 10. Интенсивности в спектре водорода
- § 11. Явление Штарка. Общие замечания
- § 12. Уравнение Шредингера в параболических координатах
- § 13. Расщепление уровней энергии в электрическом поле
- § 14. Рассеяние а-частиц. Постановка задачи
- § 15. Решение уравнений
- § 16. Формула Резерфорда
- § 17. Теорема вириала в классической и квантовой механике
- § 18. Замечания о принципе наложения и о вероятностном толковании волновой функции
- Часть III. ТЕОРИЯ ПАУЛИ
- § 1. Момент количества движения электрона
- § 2. Операторы полного момента количества движения в сферических координатах
- § 3. Шаровые функции со спином
- § 4. Некоторые свойства шаровых функций со спином
- § 5. Волновое уравнение Паули
- § 6. Преобразование оператора P к цилиндрическим и сферическим координатам и выражение его через оператор M
- § 7. Электрон в магнитном поле
- Часть IV. МНОГОЭЛЕКТРОННАЯ ЗАДАЧА КВАНТОВОЙ МЕХАНИКИ И СТРОЕНИЕ АТОМА
- § 1. Свойства симметрии волновой функции
- § 2. Оператор энергии и его симметрия
- § 3. Метод согласованного поля
- § 4. Уравнение для валентного электрона и оператор квантового обмена
- § 5. Применение метода согласованного поля к теории строения атома
- § 6. Симметрия оператора энергии водородоподобного атома
- Часть V. ТЕОРИЯ ДИРАКА
- Глава I. ВОЛНОВОЕ УРАВНЕНИЕ ДИРАКА
- § 2. Классические уравнения движения
- § 3. Вывод волнового уравнения
- § 4. Матрицы Дирака
- § 5. Уравнение Дирака для свободного электрона
- § 6. Преобразование Лоренца
- § 7. Вид матрицы S для пространственного поворота осей и для преобразования Лоренца
- § 8. Вектор тока
- § 9. Уравнение Дирака при наличии поля. Уравнения движения
- § 10. Момент количества движения и вектор спина в теории Дирака
- § 11. Кинетическая энергия электрона
- § 12. Вторая внутренняя степень свободы электрона
- § 13. Уравнения второго порядка
- Глава II. ПРИМЕНЕНИЕ УРАВНЕНИЯ ДИРАКА К НЕКОТОРЫМ ФИЗИЧЕСКИМ ЗАДАЧАМ
- § 1. Свободный электрон
- § 2. Электрон в однородном магнитном поле
- § 3. Интегралы уравнений движения в задаче со сферической симметрией
- § 4. Обобщенные шаровые функции
- § 5. Уравнение для радиальных функций
- § 6. Сравнение с уравнением Шредингера
- § 7. Общее исследование уравнений для радиальных функций
- § 8. Квантовые числа
- § 9. Гейзенберговы матрицы и правило отбора
- § 10. Другой вывод правила отбора
- § 11. Атом водорода. Радиальные функции
- § 12. Тонкая структура водородных линий
- § 13. Явление Зеемана. Постановка задачи
- § 14. Вычисление матрицы возмущающей энергии
- § 15. Расщепление уровней в магнитном поле
- Глава III. О ТЕОРИИ ПОЗИТРОНОВ
- § 2. Основные идеи теории позитронов
- § 3. Модель позитронов как незаполненных состояний
- ПОСЛЕСЛОВИЕ