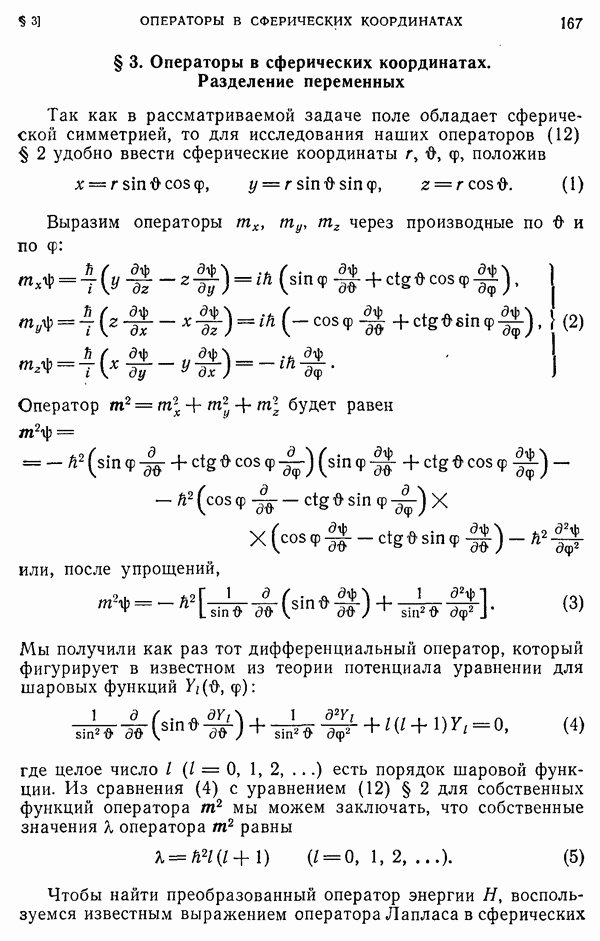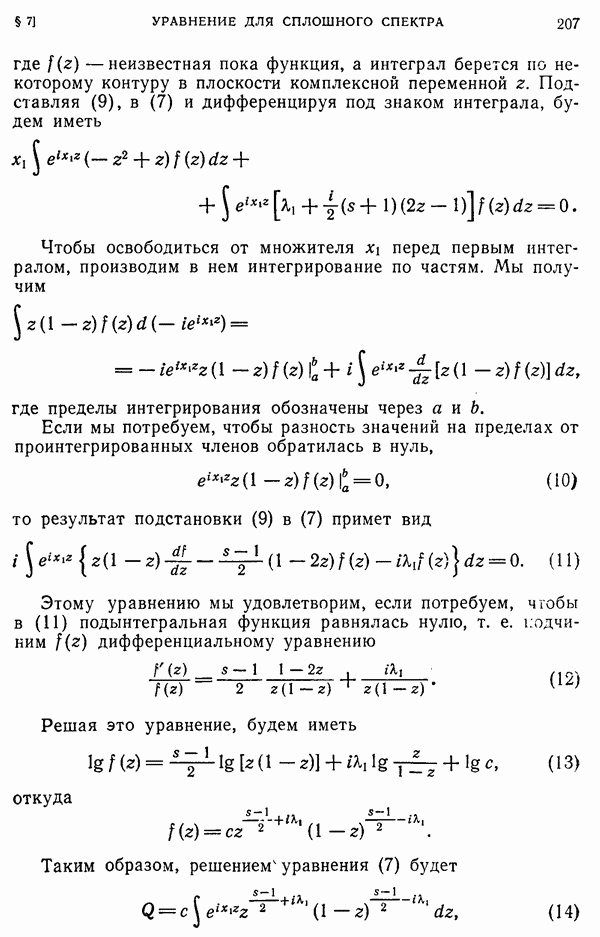| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Часть IV. МНОГОЭЛЕКТРОННАЯ ЗАДАЧА КВАНТОВОЙ МЕХАНИКИ И СТРОЕНИЕ АТОМА
§ 1. Свойства симметрии волновой функции
В предыдущих главах мы рассматривали волновую функцию, описывающую состояние одного электрона. Для стационарных состояний волновая функция должна удовлетворять уравнению Шредингера. В задаче об определении состояний системы  электронов волновая функция должна также удовлетворять некоторому условию симметрии (точнее, антисимметрии) относительно перестановки координат и спиновых переменных электронов. Условие это называется принципом Паули. Кроме того, во многих задачах можно считать заданным полный спин (собственный момент количества движения) системы электронов; в таком случае волновая функция должна удовлетворять еще одному дополнительному условию.
электронов волновая функция должна также удовлетворять некоторому условию симметрии (точнее, антисимметрии) относительно перестановки координат и спиновых переменных электронов. Условие это называется принципом Паули. Кроме того, во многих задачах можно считать заданным полный спин (собственный момент количества движения) системы электронов; в таком случае волновая функция должна удовлетворять еще одному дополнительному условию.
Как мы знаем, волновая функцияодного электрона зависит от трех пространственных координат х, у, z и от спиновой переменной  принимающей только два значения (например,
принимающей только два значения (например,  ). Обозначив буквой
). Обозначив буквой  совокупность трех пространственных координат, мы можем написать волновую функцию одного электрона в виде
совокупность трех пространственных координат, мы можем написать волновую функцию одного электрона в виде

Волновая функция системы  электронов будет зависеть от всех координат и всех спиновых переменных этих электронов. Мы будем иметь
электронов будет зависеть от всех координат и всех спиновых переменных этих электронов. Мы будем иметь

Часто бывает удобно обозначать одной буквой  совокупность всех переменных, относящихся к электрону номер
совокупность всех переменных, относящихся к электрону номер  (т. е. совокупность его пространственных координат и спиновой переменной). Волновую функцию системы
(т. е. совокупность его пространственных координат и спиновой переменной). Волновую функцию системы  электронов можно тогда писать в виде
электронов можно тогда писать в виде

Согласно принципу Паули, волновая функция должна быть антисимметрична относительно переменных  т. е. она
т. е. она
должна менять знак при перестановке любой пары этих переменных. Например,

Переходим теперь к формулировке требования, чтобы система  электронов имела определенный результирующий спин. Напомним сперва основные свойства спина, уже изученные нами в предыдущей главе.
электронов имела определенный результирующий спин. Напомним сперва основные свойства спина, уже изученные нами в предыдущей главе.
В случае одного электрона всякий оператор, действующий на спиновую переменную, может быть представлен как линейная комбинация трех операторов  определяемых равенствами
определяемых равенствами

Если рассматривать  как двухкомпонентную волновую функцию, первая компонента которой равна
как двухкомпонентную волновую функцию, первая компонента которой равна  а вторая
а вторая  то действие операторов
то действие операторов  будет то же, что и действие матриц Паули:
будет то же, что и действие матриц Паули:

Операторы

удовлетворяют перестановочным соотношениям

которые характеризуют свойства момента количества движения (выраженного в единицах  Поэтому их можно толковать как операторы для составляющих собственного момента количества движения электрона. В случае многих электронов можно определить аналогично (5) операторы
Поэтому их можно толковать как операторы для составляющих собственного момента количества движения электрона. В случае многих электронов можно определить аналогично (5) операторы  действующие на спиновую переменную электрона номер
действующие на спиновую переменную электрона номер  Мы будем иметь
Мы будем иметь

Операторы для составляющих спинового момента количества
движения системы электронов, выраженные в единицах  могут быть определены аналогично (7), а именно,
могут быть определены аналогично (7), а именно,

Эти операторы удовлетворяют тем же перестановочным соотношениям (8). Из перестановочных соотношений (8) можно вывести, что оператор

для квадрата собственного момента количества движения электронов будет коммутировать с каждым из операторов  и что его собственные значения будут равны
и что его собственные значения будут равны  , где
, где  есть половина целого неотрицательного числа. Если число
есть половина целого неотрицательного числа. Если число  электронов — четное, то
электронов — четное, то  есть целое положительное число или нуль. Если же
есть целое положительное число или нуль. Если же  нечетное, то
нечетное, то  есть полуцелое число (половина нечетного целого числа). В обоих случаях число
есть полуцелое число (половина нечетного целого числа). В обоих случаях число  будет неотрицательным целым числом. Это число
будет неотрицательным целым числом. Это число  можно толковать как число пар электронов с компенсированным спином.
можно толковать как число пар электронов с компенсированным спином.
При заданном  собственные значения каждого из операторов
собственные значения каждого из операторов  пробегают ряд чисел
пробегают ряд чисел

т. е. всего  значений.
значений.
Оператор  для
для  может быть представлен в виде
может быть представлен в виде

где символ  означает перестановку спиновых переменных
означает перестановку спиновых переменных 
Требование, чтобы система  электронов имела определенный результирующий спин, может быть теперь записано в виде уравнения
электронов имела определенный результирующий спин, может быть теперь записано в виде уравнения

Построим функцию, удовлетворяющую этому уравнению. Положим  и пусть
и пусть  есть совокупность
есть совокупность  различных чисел, взятых из ряда
различных чисел, взятых из ряда  Пусть, далее,
Пусть, далее,

есть функция от спиновых переменных, симметричная как
относительно аргументов  стоящих до вертикальной черты, так и относительно аргументов
стоящих до вертикальной черты, так и относительно аргументов  стоящих после черты. Введем совокупность
стоящих после черты. Введем совокупность  функций
функций

от координат всех электронов (эти функции уже не содержат спиновых переменных). Функции (16), так же как и функции (15), симметричны относительно значков  Составим теперь сумму
Составим теперь сумму

На основании формулы (13) можно показать, что функция (17) будет удовлетворять уравнению (14) со значением  равным
равным  если только координатные функции (16) связаны соотношениями
если только координатные функции (16) связаны соотношениями

где значок а пробегает все значения из ряда  за исключением значений
за исключением значений  Число соотношений (18) равно
Число соотношений (18) равно 
Для того чтобы полученная собственная функция оператора  представляла физически возможное состояние системы электронов с заданным спином, необходимо, чтобы она удовлетворяла также принципу Паули, т. е. была антисимметрична относительно переменных
представляла физически возможное состояние системы электронов с заданным спином, необходимо, чтобы она удовлетворяла также принципу Паули, т. е. была антисимметрична относительно переменных  Этого можно достигнуть, выразив по формуле
Этого можно достигнуть, выразив по формуле

все функции (16) через одну функцию

от координат электронов. В формуле (19) через  обозначены числа
обозначены числа  взятые в произвольном порядке, и через
взятые в произвольном порядке, и через  та перестановка
та перестановка

которая переводит 1 в  Символом
Символом  обозначено число, равное
обозначено число, равное  если перестановка
если перестановка  четная, и равное — 1, если она нечетная.
четная, и равное — 1, если она нечетная.
Функция (20) должна удовлетворять следующим условиям симметрии:
1)  антисимметрична относительно первых
антисимметрична относительно первых  аргументов (стоящих в (20) слева от черты), например,
аргументов (стоящих в (20) слева от черты), например,

2)  антисимметрична относительно последних
антисимметрична относительно последних  аргументов (стоящих справа от черты), например,
аргументов (стоящих справа от черты), например,

3)  обладает свойством циклической симметрии, которое выражается равенством
обладает свойством циклической симметрии, которое выражается равенством

Правая часть этого равенства состоит из  членов, в которых аргумент
членов, в которых аргумент  ставится последовательно на место каждого из
ставится последовательно на место каждого из  аргументов справа от черты.
аргументов справа от черты.
Свойство циклической симметрии является следствием соотношений (18). Каждое из этих соотношений приводит к одному из равенств вида (24). Проверить это можно непосредственным вычислением, учитывая свойства антисимметрии (22) и (23). Если обозначить через  циклическую перестановку аргументов
циклическую перестановку аргументов  т.е. такую перестановку, в которой каждый член цикла
т.е. такую перестановку, в которой каждый член цикла  заменяется следующим членом, а последний член — первым членом, то равенство (24) может быть записано в виде
заменяется следующим членом, а последний член — первым членом, то равенство (24) может быть записано в виде

при  четном и в виде
четном и в виде

при  нечетном.
нечетном.
В частном случае двух электронов состояние с нулевым спином  описывается симметричной функцией от
описывается симметричной функцией от
координат, а состояние со спином  антисимметричной функцией.
антисимметричной функцией.
Весьма важным примером функции от  аргументов
аргументов  удовлетворяющей трем сформулированным выше условиям симметрии, является произведение двух определителей
удовлетворяющей трем сформулированным выше условиям симметрии, является произведение двух определителей

где

Эти определители составлены из функций

зависящих от координат одного электрона, причем больший определитель содержит все  функций (29), а меньший - только первые k из них.
функций (29), а меньший - только первые k из них.
Предыдущие рассуждения позволили нам выразить волновую функцию (2), которая зависит кроме координат еще от всех спиновых переменных, через Шредингеровскую волновую функцию (20), зависящую только от одних координат. При этом как принцип Паули, так и уравнение (14) для спинового момента количества движения были учтены вполне строго.
Несмотря на то, что Шредингеровская волновая функция не зависит от спиновых переменных, значение результирующего спина отражается на ее свойствах, так как от него зависит ее симметрия.
Этим объясняется тот факт, который на первый взгляд кажется парадоксом: ни уравнение Шредингера, ни волновая функция спиновых переменных не содержат, между тем уровни энергии зависят от значения результирующего спина. Парадокс разъясняется тем, что на волновую функцию, соответствующую уровню с данным спином, дополнительно накладываются условия симметрии, различные для различных значений результирующего спина.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- Часть I. ОСНОВАНИЯ КВАНТОВОЙ МЕХАНИКИ
- Глава I. ФИЗИЧЕСКИЕ И ТЕОРЕТИКО-ПОЗНАВАТЕЛЬНЫЕ ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ
- § 3. Область применимости классического способа описания явлений. Соотношения Гейзенберга и Бора
- § 4. Относительность к средствам наблюдения как основа квантового способа описания явлений
- § 5. Понятие потенциальной возможности в квантовой физике
- Глава II. МАТЕМАТИЧЕСКИЙ АППАРАТ КВАНТОВОЙ МЕХАНИКИ
- § 1. Квантовая механика и задачи на линейные операторы
- § 2. Понятие об операторе и примеры операторов
- § 3. Оператор, сопряженный к данному. Самосопряженность
- § 4. Произведение операторов. Правило умножения матриц
- § 5. Собственные значения и собственные функции операторов
- § 6. Интеграл Стильтьеса и оператор умножения на независимую переменную
- § 7. Ортогональность и нормировка собственных функций
- § 8. Разложение по собственным функциям. Замкнутость системы функций
- Глава III. ФИЗИЧЕСКОЕ ЗНАЧЕНИЕ ОПЕРАТОРОВ
- § 1. Толкование собственных значений оператора
- § 2. Скобки Пуассона
- § 3. Операторы для координат и моментов
- § 4. Собственные значения и собственные функции оператора количества движения
- § 5. Квантовое описание состояния системы
- § 6. Коммутативность операторов
- § 7. Момент количества движения
- § 8. Оператор энергии
- § 9. Каноническое преобразование
- § 10. Пример канонического преобразования
- § 11. Каноническое преобразование как оператор
- § 12. Унитарные инварианты
- § 13. Изменение состояния системы во времени. Операторы как функции от времени
- § 14. Гейзенберговы матрицы
- § 15. Полуклассическое приближение
- § 16. Связь канонического преобразования с касательным преобразованием классической механики
- Глава IV. ВЕРОЯТНОСТНОЕ ТОЛКОВАНИЕ КВАНТОВОЙ МЕХАНИКИ
- § 1. Математическое ожидание в теории вероятностей
- § 2. Математическое ожидание в квантовой механике
- § 3. Выражение для вероятностей
- § 4. Закон изменения математического ожидания во времени
- § 5. Соответствие между понятиями теории линейных операторов и теории квантов
- § 6. Понятие статистического коллектива в квантовой механике
- Часть II. ТЕОРИЯ ШРЕДИНГЕРА
- § 1. Волновое уравнение и уравнения движения
- § 2. Интегралы уравнений движения
- § 3. Уравнение Шредингера для гармонического вибратора
- § 4. Вибратор в одном измерении
- § 5. Полиномы Чебышева — Эрмита
- § 6. Каноническое преобразование на примере вибратора
- § 7. Неравенства Гейзенберга
- § 8. Зависимость матриц от времени. Сравнение с классической теорией
- § 9. Элементарный критерий применимости формул классической механики
- Глава II. ТЕОРИЯ ВОЗМУЩЕНИЙ
- § 2. Решение неоднородного уравнения
- § 3. Простые собственные значения
- § 4. Кратные собственные значения. Разложение по степеням малого параметра
- § 5. Собственные функции в нулевом приближении
- § 6. Первое и последующие приближения
- § 7. Случай близких собственных значений
- § 8. Ангармонический вибратор
- Глава III. ИЗЛУЧЕНИЕ, ТЕОРИЯ ДИСПЕРСИИ И ЗАКОН РАСПАДА
- § 2. Плотность и вектор тока
- § 3. Частоты и интенсивности
- § 4. Интенсивности в сплошном спектре
- § 5. Возмущение атома световой волной
- § 6. Формула дисперсии
- § 7. Прохождение частицы сквозь барьер потенциальной энергии
- § 8. Закон распада почти стационарного состояния
- Глава IV. ЭЛЕКТРОН В ПОЛЕ С ЦЕНТРАЛЬНОЙ СИММЕТРИЕЙ
- § 2. Интегралы площадей
- § 3. Операторы в сферических координатах. Разделение переменных
- § 4. Решение дифференциального уравнения для шаровых функций
- § 5. Некоторые свойства шаровых функций
- § 6. Нормированные шаровые функции
- § 7. Радиальные функции. Общее исследование
- § 8. Описание состояния валентного электрона. Квантовые числа
- § 9. Правило отбора
- Глава V. КУЛОНОВО ПОЛЕ
- § 2. Уравнение для радиальных функций водорода. Атомные единицы меры
- § 3. Решение одной вспомогательной задачи
- § 4. Некоторые свойства обобщенных полиномов Лагерра
- § 5. Собственные значения и собственные функции вспомогательной задачи
- § 6. Уровни энергии и радиальные функции точечного спектра для водорода
- § 7. Решение дифференциального уравне им для сплошного спектра в виде определенного интеграла
- § 8. Вывод асимптотического выражения
- § 9. Радиальные функции водорода для сплошного спектра
- § 10. Интенсивности в спектре водорода
- § 11. Явление Штарка. Общие замечания
- § 12. Уравнение Шредингера в параболических координатах
- § 13. Расщепление уровней энергии в электрическом поле
- § 14. Рассеяние а-частиц. Постановка задачи
- § 15. Решение уравнений
- § 16. Формула Резерфорда
- § 17. Теорема вириала в классической и квантовой механике
- § 18. Замечания о принципе наложения и о вероятностном толковании волновой функции
- Часть III. ТЕОРИЯ ПАУЛИ
- § 1. Момент количества движения электрона
- § 2. Операторы полного момента количества движения в сферических координатах
- § 3. Шаровые функции со спином
- § 4. Некоторые свойства шаровых функций со спином
- § 5. Волновое уравнение Паули
- § 6. Преобразование оператора P к цилиндрическим и сферическим координатам и выражение его через оператор M
- § 7. Электрон в магнитном поле
- Часть IV. МНОГОЭЛЕКТРОННАЯ ЗАДАЧА КВАНТОВОЙ МЕХАНИКИ И СТРОЕНИЕ АТОМА
- § 1. Свойства симметрии волновой функции
- § 2. Оператор энергии и его симметрия
- § 3. Метод согласованного поля
- § 4. Уравнение для валентного электрона и оператор квантового обмена
- § 5. Применение метода согласованного поля к теории строения атома
- § 6. Симметрия оператора энергии водородоподобного атома
- Часть V. ТЕОРИЯ ДИРАКА
- Глава I. ВОЛНОВОЕ УРАВНЕНИЕ ДИРАКА
- § 2. Классические уравнения движения
- § 3. Вывод волнового уравнения
- § 4. Матрицы Дирака
- § 5. Уравнение Дирака для свободного электрона
- § 6. Преобразование Лоренца
- § 7. Вид матрицы S для пространственного поворота осей и для преобразования Лоренца
- § 8. Вектор тока
- § 9. Уравнение Дирака при наличии поля. Уравнения движения
- § 10. Момент количества движения и вектор спина в теории Дирака
- § 11. Кинетическая энергия электрона
- § 12. Вторая внутренняя степень свободы электрона
- § 13. Уравнения второго порядка
- Глава II. ПРИМЕНЕНИЕ УРАВНЕНИЯ ДИРАКА К НЕКОТОРЫМ ФИЗИЧЕСКИМ ЗАДАЧАМ
- § 1. Свободный электрон
- § 2. Электрон в однородном магнитном поле
- § 3. Интегралы уравнений движения в задаче со сферической симметрией
- § 4. Обобщенные шаровые функции
- § 5. Уравнение для радиальных функций
- § 6. Сравнение с уравнением Шредингера
- § 7. Общее исследование уравнений для радиальных функций
- § 8. Квантовые числа
- § 9. Гейзенберговы матрицы и правило отбора
- § 10. Другой вывод правила отбора
- § 11. Атом водорода. Радиальные функции
- § 12. Тонкая структура водородных линий
- § 13. Явление Зеемана. Постановка задачи
- § 14. Вычисление матрицы возмущающей энергии
- § 15. Расщепление уровней в магнитном поле
- Глава III. О ТЕОРИИ ПОЗИТРОНОВ
- § 2. Основные идеи теории позитронов
- § 3. Модель позитронов как незаполненных состояний
- ПОСЛЕСЛОВИЕ