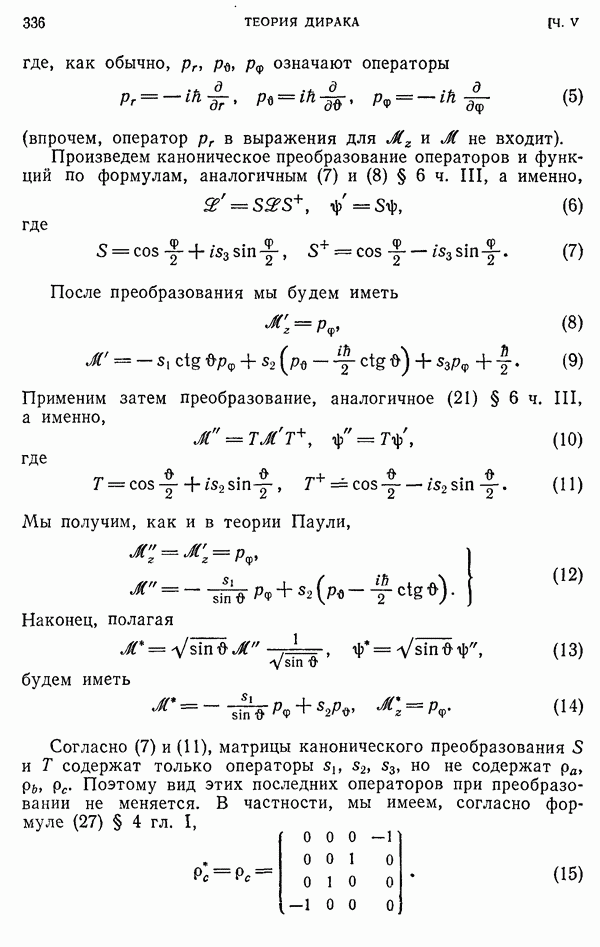| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 4. Обобщенные шаровые функции
Для нахождения общих собственных функций операторов  необходимо преобразовать их к сферическим координатам. Это преобразование мы будем сопровождать каноническим преобразованием четырехкомпонентной волновой функции, аналогичным тому, какое применялось в § 2 ч. III к двухкомпонентной волновой функции теории Паули.
необходимо преобразовать их к сферическим координатам. Это преобразование мы будем сопровождать каноническим преобразованием четырехкомпонентной волновой функции, аналогичным тому, какое применялось в § 2 ч. III к двухкомпонентной волновой функции теории Паули.
Четырехрядные матрицы  соответствующие нашему выбору матриц Дирака, мы будем обозначать через
соответствующие нашему выбору матриц Дирака, мы будем обозначать через  Согласно формулам (26) § 4 гл. I ч. V, мы имеем
Согласно формулам (26) § 4 гл. I ч. V, мы имеем

Чтобы выразить операторы  в сферических координатах, мы можем воспользоваться формулами, выведенными в § 2 ч. III на основе теории Паули, с той только разницей, что мы должны заменить фигурирующие в них матрицы а
в сферических координатах, мы можем воспользоваться формулами, выведенными в § 2 ч. III на основе теории Паули, с той только разницей, что мы должны заменить фигурирующие в них матрицы а  на
на  Выпишем главнейшие из этих формул вновь (в новых обозначениях).
Выпишем главнейшие из этих формул вновь (в новых обозначениях).
В сферических координатах  связанных с прямоугольными
связанных с прямоугольными  обычными соотношениями
обычными соотношениями

операторы  имеют вид
имеют вид

где, как обычно,  означают операторы
означают операторы

(впрочем, оператор  в выражения для
в выражения для  не входит).
не входит).
Произведем каноническое преобразование операторов и функций по формулам, аналогичным (7) и (8) § 6 ч. III, а именно,

где

После преобразования мы будем иметь

Применим затем преобразование, аналогичное (21) § 6 ч. III, а именно,

где

Мы получим, как и в теории Паули,

Наконец, полагая

будем иметь

Согласно (7) и (11), матрицы канонического преобразования  содержат только операторы
содержат только операторы  но не содержат
но не содержат  Поэтому вид этих последних операторов при преобразовании не меняется. В частности, мы имеем, согласно формуле (27) § 4 гл. I,
Поэтому вид этих последних операторов при преобразовании не меняется. В частности, мы имеем, согласно формуле (27) § 4 гл. I,

После умножения на  уравнение для собственных функций оператора
уравнение для собственных функций оператора  можно написать в виде
можно написать в виде

Соответствующая уравнению (16) система уравнений для четырех компонент функции  будет иметь вид
будет иметь вид

Если выразить операторы  через производные и изменить знак в обеих частях некоторых из этих уравнений, мы можем написать их в виде двух одинаковых систем уравнений для двух функций каждая, а именно,
через производные и изменить знак в обеих частях некоторых из этих уравнений, мы можем написать их в виде двух одинаковых систем уравнений для двух функций каждая, а именно,

и

Уравнения (18 отличаются от (18) только знаком при 
Такие уравнения уже встречались нам в теории Паули при рассмотрении шаровых функций со спином (§ 3 ч. III). Мы их писали там в виде

Решением наших уравнений (18) и (18 будут функции 

где функции  уже от
уже от  не зависят. Зависимость их от
не зависят. Зависимость их от  определяется уравнением для собственных функций оператора энергии.
определяется уравнением для собственных функций оператора энергии.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- Часть I. ОСНОВАНИЯ КВАНТОВОЙ МЕХАНИКИ
- Глава I. ФИЗИЧЕСКИЕ И ТЕОРЕТИКО-ПОЗНАВАТЕЛЬНЫЕ ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ
- § 3. Область применимости классического способа описания явлений. Соотношения Гейзенберга и Бора
- § 4. Относительность к средствам наблюдения как основа квантового способа описания явлений
- § 5. Понятие потенциальной возможности в квантовой физике
- Глава II. МАТЕМАТИЧЕСКИЙ АППАРАТ КВАНТОВОЙ МЕХАНИКИ
- § 1. Квантовая механика и задачи на линейные операторы
- § 2. Понятие об операторе и примеры операторов
- § 3. Оператор, сопряженный к данному. Самосопряженность
- § 4. Произведение операторов. Правило умножения матриц
- § 5. Собственные значения и собственные функции операторов
- § 6. Интеграл Стильтьеса и оператор умножения на независимую переменную
- § 7. Ортогональность и нормировка собственных функций
- § 8. Разложение по собственным функциям. Замкнутость системы функций
- Глава III. ФИЗИЧЕСКОЕ ЗНАЧЕНИЕ ОПЕРАТОРОВ
- § 1. Толкование собственных значений оператора
- § 2. Скобки Пуассона
- § 3. Операторы для координат и моментов
- § 4. Собственные значения и собственные функции оператора количества движения
- § 5. Квантовое описание состояния системы
- § 6. Коммутативность операторов
- § 7. Момент количества движения
- § 8. Оператор энергии
- § 9. Каноническое преобразование
- § 10. Пример канонического преобразования
- § 11. Каноническое преобразование как оператор
- § 12. Унитарные инварианты
- § 13. Изменение состояния системы во времени. Операторы как функции от времени
- § 14. Гейзенберговы матрицы
- § 15. Полуклассическое приближение
- § 16. Связь канонического преобразования с касательным преобразованием классической механики
- Глава IV. ВЕРОЯТНОСТНОЕ ТОЛКОВАНИЕ КВАНТОВОЙ МЕХАНИКИ
- § 1. Математическое ожидание в теории вероятностей
- § 2. Математическое ожидание в квантовой механике
- § 3. Выражение для вероятностей
- § 4. Закон изменения математического ожидания во времени
- § 5. Соответствие между понятиями теории линейных операторов и теории квантов
- § 6. Понятие статистического коллектива в квантовой механике
- Часть II. ТЕОРИЯ ШРЕДИНГЕРА
- § 1. Волновое уравнение и уравнения движения
- § 2. Интегралы уравнений движения
- § 3. Уравнение Шредингера для гармонического вибратора
- § 4. Вибратор в одном измерении
- § 5. Полиномы Чебышева — Эрмита
- § 6. Каноническое преобразование на примере вибратора
- § 7. Неравенства Гейзенберга
- § 8. Зависимость матриц от времени. Сравнение с классической теорией
- § 9. Элементарный критерий применимости формул классической механики
- Глава II. ТЕОРИЯ ВОЗМУЩЕНИЙ
- § 2. Решение неоднородного уравнения
- § 3. Простые собственные значения
- § 4. Кратные собственные значения. Разложение по степеням малого параметра
- § 5. Собственные функции в нулевом приближении
- § 6. Первое и последующие приближения
- § 7. Случай близких собственных значений
- § 8. Ангармонический вибратор
- Глава III. ИЗЛУЧЕНИЕ, ТЕОРИЯ ДИСПЕРСИИ И ЗАКОН РАСПАДА
- § 2. Плотность и вектор тока
- § 3. Частоты и интенсивности
- § 4. Интенсивности в сплошном спектре
- § 5. Возмущение атома световой волной
- § 6. Формула дисперсии
- § 7. Прохождение частицы сквозь барьер потенциальной энергии
- § 8. Закон распада почти стационарного состояния
- Глава IV. ЭЛЕКТРОН В ПОЛЕ С ЦЕНТРАЛЬНОЙ СИММЕТРИЕЙ
- § 2. Интегралы площадей
- § 3. Операторы в сферических координатах. Разделение переменных
- § 4. Решение дифференциального уравнения для шаровых функций
- § 5. Некоторые свойства шаровых функций
- § 6. Нормированные шаровые функции
- § 7. Радиальные функции. Общее исследование
- § 8. Описание состояния валентного электрона. Квантовые числа
- § 9. Правило отбора
- Глава V. КУЛОНОВО ПОЛЕ
- § 2. Уравнение для радиальных функций водорода. Атомные единицы меры
- § 3. Решение одной вспомогательной задачи
- § 4. Некоторые свойства обобщенных полиномов Лагерра
- § 5. Собственные значения и собственные функции вспомогательной задачи
- § 6. Уровни энергии и радиальные функции точечного спектра для водорода
- § 7. Решение дифференциального уравне им для сплошного спектра в виде определенного интеграла
- § 8. Вывод асимптотического выражения
- § 9. Радиальные функции водорода для сплошного спектра
- § 10. Интенсивности в спектре водорода
- § 11. Явление Штарка. Общие замечания
- § 12. Уравнение Шредингера в параболических координатах
- § 13. Расщепление уровней энергии в электрическом поле
- § 14. Рассеяние а-частиц. Постановка задачи
- § 15. Решение уравнений
- § 16. Формула Резерфорда
- § 17. Теорема вириала в классической и квантовой механике
- § 18. Замечания о принципе наложения и о вероятностном толковании волновой функции
- Часть III. ТЕОРИЯ ПАУЛИ
- § 1. Момент количества движения электрона
- § 2. Операторы полного момента количества движения в сферических координатах
- § 3. Шаровые функции со спином
- § 4. Некоторые свойства шаровых функций со спином
- § 5. Волновое уравнение Паули
- § 6. Преобразование оператора P к цилиндрическим и сферическим координатам и выражение его через оператор M
- § 7. Электрон в магнитном поле
- Часть IV. МНОГОЭЛЕКТРОННАЯ ЗАДАЧА КВАНТОВОЙ МЕХАНИКИ И СТРОЕНИЕ АТОМА
- § 1. Свойства симметрии волновой функции
- § 2. Оператор энергии и его симметрия
- § 3. Метод согласованного поля
- § 4. Уравнение для валентного электрона и оператор квантового обмена
- § 5. Применение метода согласованного поля к теории строения атома
- § 6. Симметрия оператора энергии водородоподобного атома
- Часть V. ТЕОРИЯ ДИРАКА
- Глава I. ВОЛНОВОЕ УРАВНЕНИЕ ДИРАКА
- § 2. Классические уравнения движения
- § 3. Вывод волнового уравнения
- § 4. Матрицы Дирака
- § 5. Уравнение Дирака для свободного электрона
- § 6. Преобразование Лоренца
- § 7. Вид матрицы S для пространственного поворота осей и для преобразования Лоренца
- § 8. Вектор тока
- § 9. Уравнение Дирака при наличии поля. Уравнения движения
- § 10. Момент количества движения и вектор спина в теории Дирака
- § 11. Кинетическая энергия электрона
- § 12. Вторая внутренняя степень свободы электрона
- § 13. Уравнения второго порядка
- Глава II. ПРИМЕНЕНИЕ УРАВНЕНИЯ ДИРАКА К НЕКОТОРЫМ ФИЗИЧЕСКИМ ЗАДАЧАМ
- § 1. Свободный электрон
- § 2. Электрон в однородном магнитном поле
- § 3. Интегралы уравнений движения в задаче со сферической симметрией
- § 4. Обобщенные шаровые функции
- § 5. Уравнение для радиальных функций
- § 6. Сравнение с уравнением Шредингера
- § 7. Общее исследование уравнений для радиальных функций
- § 8. Квантовые числа
- § 9. Гейзенберговы матрицы и правило отбора
- § 10. Другой вывод правила отбора
- § 11. Атом водорода. Радиальные функции
- § 12. Тонкая структура водородных линий
- § 13. Явление Зеемана. Постановка задачи
- § 14. Вычисление матрицы возмущающей энергии
- § 15. Расщепление уровней в магнитном поле
- Глава III. О ТЕОРИИ ПОЗИТРОНОВ
- § 2. Основные идеи теории позитронов
- § 3. Модель позитронов как незаполненных состояний
- ПОСЛЕСЛОВИЕ