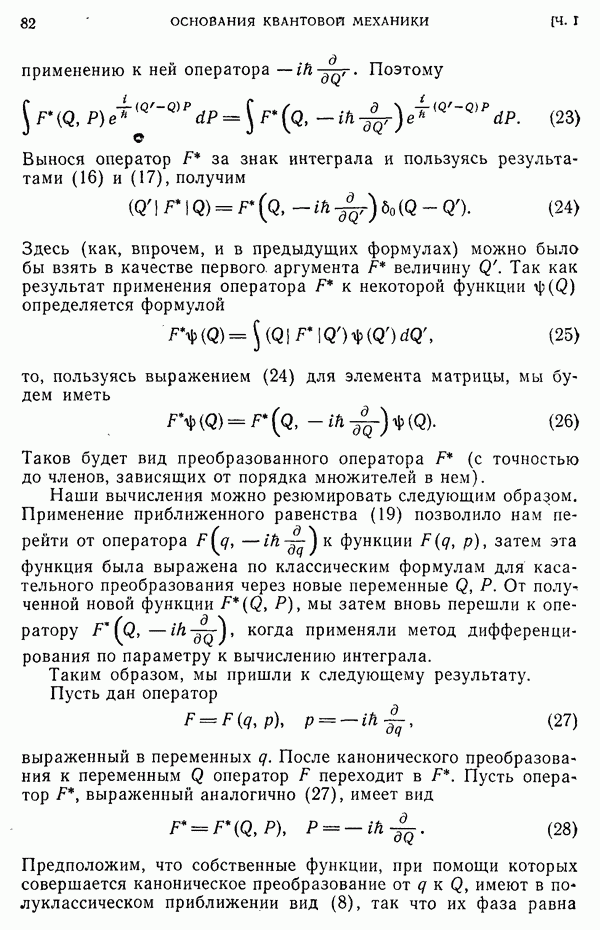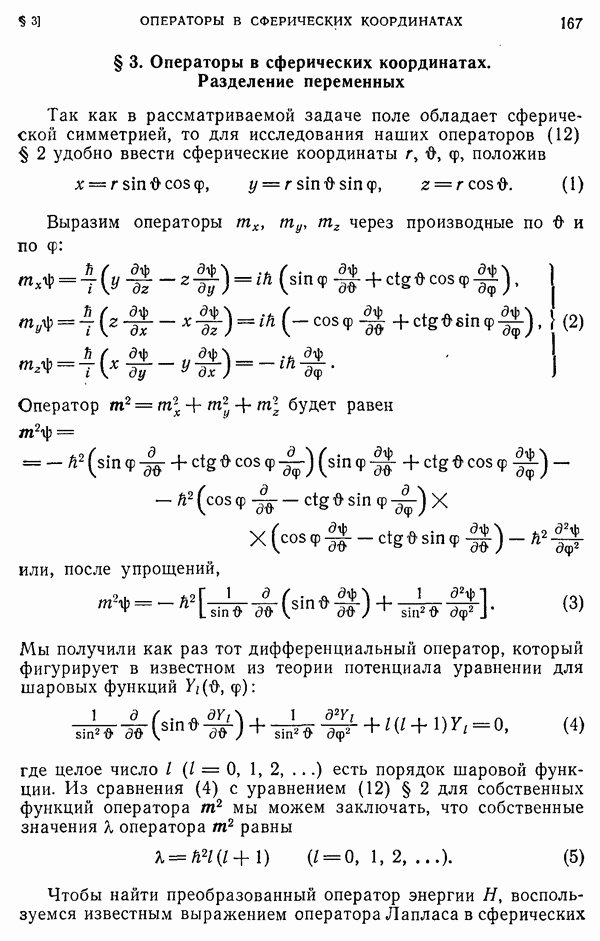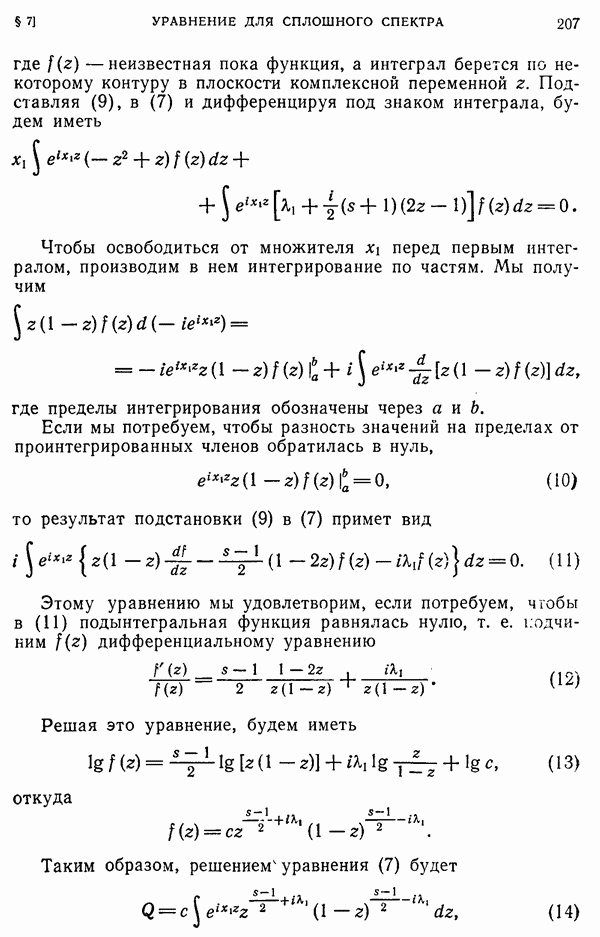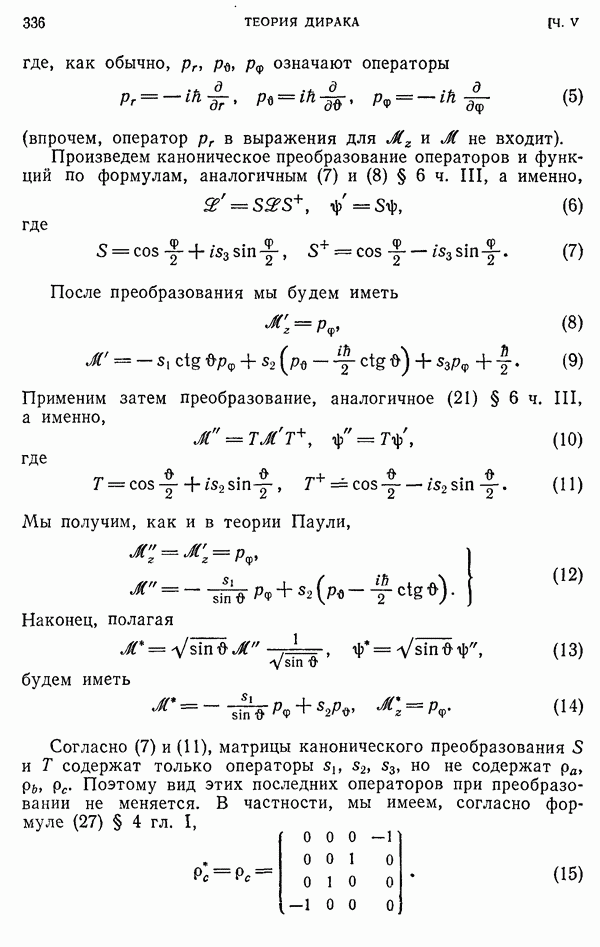| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Часть III. ТЕОРИЯ ПАУЛИ
§ 1. Момент количества движения электрона
В § 7 гл. II мы рассматривали операторы момента количества движения, составленные из операторов для координат и для количества движения по формулам

Эти операторы можно сопоставить моменту количества движения материальной точки с тремя степенями свободы, соответствующими движению в пространстве. Поведение электрона в магнитном поле, а также свойства систем, составленных из многих электронов (например, электронной оболочки атома), показали, что электрон обладает также некоторой внутренней степенью свободы, связанной с его собственным моментом количества движения, не зависящим от движения его в пространстве. Эту внутреннюю степень свободы (и соответствующий ей собственный момент количества движения электрона) принято называть английским словом («спин»).
Свойства собственного (спинового) момента количества движения электрона можно изучать исходя из перестановочных соотношений для обычного (орбитального) момента количества движения

если считать, что спиновый момент удовлетворяет тем же перестановочным соотношениям, и ввести гипотезу о том, что операторы для каждой из составляющих спинового момента электрона имеют два и только два собственных значения, которые отличаются лишь знаком.
Операторы для составляющих спинового момента можно положить равными

где  самосопряженные операторы, имеющие простые собственные значения, равные ±1. Множитель
самосопряженные операторы, имеющие простые собственные значения, равные ±1. Множитель  вытекает из требования, чтобы операторы (3) удовлетворяли соотношениям (2).
вытекает из требования, чтобы операторы (3) удовлетворяли соотношениям (2).
При вычислении спина в единицах  (а не
(а не  ) удобно пользоваться вместо
) удобно пользоваться вместо  операторами
операторами

Эти операторы будут применяться в части IV при рассмотрении многоэлектронной задачи.
Перестановочные соотношения для операторов  имеют вид
имеют вид

 Но мы имеем тождественно
Но мы имеем тождественно

и, вследствие предыдущих соотношений,

Согласно нашей гипотезе, собственные значения  равны ±1, так что
равны ±1, так что  имеет единственное собственное значение
имеет единственное собственное значение  и будет уже не оператором, а числом, коммутирующим с любым оператором, в том числе с оператором
и будет уже не оператором, а числом, коммутирующим с любым оператором, в том числе с оператором  Поэтому правая часть последнего уравнения равна нулю. Записывая это равенство вместе с двумя аналогичными равенствами, мы будем иметь
Поэтому правая часть последнего уравнения равна нулю. Записывая это равенство вместе с двумя аналогичными равенствами, мы будем иметь

Сопоставляя равенства (4) и (5), мы получаем

Кроме того, мы имеем

Величины  можно рассматривать либо как матрицы, состоящие из двух строк и столбцов, либо как операторы, действующие на функцию от некоторой новой (дополнительной к координатам) переменной
можно рассматривать либо как матрицы, состоящие из двух строк и столбцов, либо как операторы, действующие на функцию от некоторой новой (дополнительной к координатам) переменной  , принимающей только два значения, например значения
, принимающей только два значения, например значения  Обозначая эту функцию через
Обозначая эту функцию через  где
где  есть совокупность трех пространственных координат, мы можем удовлетворить соотношениям (6) и (7), положив, например,
есть совокупность трех пространственных координат, мы можем удовлетворить соотношениям (6) и (7), положив, например,

Если записать функцию  в виде столбика
в виде столбика

где  то предыдущие формулы напишутся
то предыдущие формулы напишутся

Таким образом, операторы  принимают форму матриц
принимают форму матриц

где

Эти матрицы носят название матриц Паули  Выбор матриц для операторов
Выбор матриц для операторов  определен лишь с точностью до канонического преобразования (соответствующего линейной подстановке над величинами
определен лишь с точностью до канонического преобразования (соответствующего линейной подстановке над величинами  Поэтому, если, как это принято в литературе, разуметь под
Поэтому, если, как это принято в литературе, разуметь под  численные матрицы (12), а сохранить за
численные матрицы (12), а сохранить за  физический смысл, вытекающий из формул (8), то равенства (11) не являются обязательными, но могут быть заменены другими эквивалентными равенствами.
физический смысл, вытекающий из формул (8), то равенства (11) не являются обязательными, но могут быть заменены другими эквивалентными равенствами.
Операторы  удовлетворяющие уравнениям (6) и (7), обладают векториальным характером в том смысле, что если мы введем три линейные комбинации
удовлетворяющие уравнениям (6) и (7), обладают векториальным характером в том смысле, что если мы введем три линейные комбинации

где  суть косинусы углов между двумя системами прямоугольных координат, то новые операторы
суть косинусы углов между двумя системами прямоугольных координат, то новые операторы  будут обладать такими же свойствами (6) и (7), как и старые
будут обладать такими же свойствами (6) и (7), как и старые  Отсюда следует, что если мы будем рассматривать эти величины как составляющие вектора, то проекции этого вектора на любое направление будут иметь собственные значения ±1. Заметим, что если мы, согласно (11), возьмем в качестве
Отсюда следует, что если мы будем рассматривать эти величины как составляющие вектора, то проекции этого вектора на любое направление будут иметь собственные значения ±1. Заметим, что если мы, согласно (11), возьмем в качестве  матрицы (12), то выражения (13) дают самый общий вид матриц с двумя строками и столбцами, удовлетворяющих условиям (6) и (7).
матрицы (12), то выражения (13) дают самый общий вид матриц с двумя строками и столбцами, удовлетворяющих условиям (6) и (7).
Три матрицы (12) вместе с единичной матрицей образуют полную систему в том смысле, что всякую матрицу с двумя строками и столбцами (т. е. с 4 элементами) можно выразить в виде линейных комбинаций этих четырех с численными коэффициентами. Если заданная матрица — самосопряженная, то эти коэффициенты будут вещественными.
Переходим к построению операторов для полного момента количества движения. Приняв для операторов спинового момента количества движения выражения (3), мы приходим к выводу, что операторы для полного момента количества движения электрона имеют вид

По общему свойству момента количества движения, операторы для результирующего момента количества движения удовлетворяют тем же перестановочным соотношениям, как и операторы для слагаемых, так что мы должны иметь, аналогично (2),

Равенства (15) можно проверить и непосредственно, используя
соотношения (2) и (4) для  и для
и для  и тот факт, что орбитальный и спиновый моменты количества движения между собой коммутируют.
и тот факт, что орбитальный и спиновый моменты количества движения между собой коммутируют.
Из составляющих орбитального и спинового момента количества движения можно построить такую билинейную комбинацию, которая коммутировала бы с каждой из составляющих полного момента количества движения. В самом деле, положим

или, что то же самое,

Мы имеем по свойству 

и по свойству 

Складывая эти два равенства, получаем в правой части нуль. Выражение в левой части и аналогичные выражения для составляющих по осям у и  можно записать в виде
можно записать в виде

Установим связь между оператором  и применяемым в теории Шредингера оператором для квадрата орбитального момента количества движения. Мы имеем
и применяемым в теории Шредингера оператором для квадрата орбитального момента количества движения. Мы имеем

С другой стороны, если мы возьмем сумму квадратов операторов (14) для составляющих полного момента количества движения и воспользуемся соотношением (18), мы получим

Таким образом, квадрат вектора  отличается от квадрата скаляра
отличается от квадрата скаляра  только слагаемым
только слагаемым  Мы будем называть оператор
Мы будем называть оператор  спиново-орбитальным скаляром момента количества движения.
спиново-орбитальным скаляром момента количества движения.
Правая часть (18) есть оператор, встречающийся в теории Шредингера и не содержащий матриц Паули. Его собственные значения равны  где
где  целое положительное число
целое положительное число
или нуль. Поэтому если мы обозначим собственные значения оператора  через
через  то будем иметь
то будем иметь

откуда при данном 

Но величина  не может равняться нулю. В самом деле, из формулы (19) следует, что математическое ожидание оператора
не может равняться нулю. В самом деле, из формулы (19) следует, что математическое ожидание оператора  в любом состоянии будет больше
в любом состоянии будет больше  Поэтому уравнение
Поэтому уравнение

для собственных функций оператора  не может иметь собственного значения, равного нулю. Это значит, что при
не может иметь собственного значения, равного нулю. Это значит, что при  единственное возможное значение
единственное возможное значение  есть 1, а при 1 существуют два значения
есть 1, а при 1 существуют два значения  даваемые формулой (21).
даваемые формулой (21).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- Часть I. ОСНОВАНИЯ КВАНТОВОЙ МЕХАНИКИ
- Глава I. ФИЗИЧЕСКИЕ И ТЕОРЕТИКО-ПОЗНАВАТЕЛЬНЫЕ ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ
- § 3. Область применимости классического способа описания явлений. Соотношения Гейзенберга и Бора
- § 4. Относительность к средствам наблюдения как основа квантового способа описания явлений
- § 5. Понятие потенциальной возможности в квантовой физике
- Глава II. МАТЕМАТИЧЕСКИЙ АППАРАТ КВАНТОВОЙ МЕХАНИКИ
- § 1. Квантовая механика и задачи на линейные операторы
- § 2. Понятие об операторе и примеры операторов
- § 3. Оператор, сопряженный к данному. Самосопряженность
- § 4. Произведение операторов. Правило умножения матриц
- § 5. Собственные значения и собственные функции операторов
- § 6. Интеграл Стильтьеса и оператор умножения на независимую переменную
- § 7. Ортогональность и нормировка собственных функций
- § 8. Разложение по собственным функциям. Замкнутость системы функций
- Глава III. ФИЗИЧЕСКОЕ ЗНАЧЕНИЕ ОПЕРАТОРОВ
- § 1. Толкование собственных значений оператора
- § 2. Скобки Пуассона
- § 3. Операторы для координат и моментов
- § 4. Собственные значения и собственные функции оператора количества движения
- § 5. Квантовое описание состояния системы
- § 6. Коммутативность операторов
- § 7. Момент количества движения
- § 8. Оператор энергии
- § 9. Каноническое преобразование
- § 10. Пример канонического преобразования
- § 11. Каноническое преобразование как оператор
- § 12. Унитарные инварианты
- § 13. Изменение состояния системы во времени. Операторы как функции от времени
- § 14. Гейзенберговы матрицы
- § 15. Полуклассическое приближение
- § 16. Связь канонического преобразования с касательным преобразованием классической механики
- Глава IV. ВЕРОЯТНОСТНОЕ ТОЛКОВАНИЕ КВАНТОВОЙ МЕХАНИКИ
- § 1. Математическое ожидание в теории вероятностей
- § 2. Математическое ожидание в квантовой механике
- § 3. Выражение для вероятностей
- § 4. Закон изменения математического ожидания во времени
- § 5. Соответствие между понятиями теории линейных операторов и теории квантов
- § 6. Понятие статистического коллектива в квантовой механике
- Часть II. ТЕОРИЯ ШРЕДИНГЕРА
- § 1. Волновое уравнение и уравнения движения
- § 2. Интегралы уравнений движения
- § 3. Уравнение Шредингера для гармонического вибратора
- § 4. Вибратор в одном измерении
- § 5. Полиномы Чебышева — Эрмита
- § 6. Каноническое преобразование на примере вибратора
- § 7. Неравенства Гейзенберга
- § 8. Зависимость матриц от времени. Сравнение с классической теорией
- § 9. Элементарный критерий применимости формул классической механики
- Глава II. ТЕОРИЯ ВОЗМУЩЕНИЙ
- § 2. Решение неоднородного уравнения
- § 3. Простые собственные значения
- § 4. Кратные собственные значения. Разложение по степеням малого параметра
- § 5. Собственные функции в нулевом приближении
- § 6. Первое и последующие приближения
- § 7. Случай близких собственных значений
- § 8. Ангармонический вибратор
- Глава III. ИЗЛУЧЕНИЕ, ТЕОРИЯ ДИСПЕРСИИ И ЗАКОН РАСПАДА
- § 2. Плотность и вектор тока
- § 3. Частоты и интенсивности
- § 4. Интенсивности в сплошном спектре
- § 5. Возмущение атома световой волной
- § 6. Формула дисперсии
- § 7. Прохождение частицы сквозь барьер потенциальной энергии
- § 8. Закон распада почти стационарного состояния
- Глава IV. ЭЛЕКТРОН В ПОЛЕ С ЦЕНТРАЛЬНОЙ СИММЕТРИЕЙ
- § 2. Интегралы площадей
- § 3. Операторы в сферических координатах. Разделение переменных
- § 4. Решение дифференциального уравнения для шаровых функций
- § 5. Некоторые свойства шаровых функций
- § 6. Нормированные шаровые функции
- § 7. Радиальные функции. Общее исследование
- § 8. Описание состояния валентного электрона. Квантовые числа
- § 9. Правило отбора
- Глава V. КУЛОНОВО ПОЛЕ
- § 2. Уравнение для радиальных функций водорода. Атомные единицы меры
- § 3. Решение одной вспомогательной задачи
- § 4. Некоторые свойства обобщенных полиномов Лагерра
- § 5. Собственные значения и собственные функции вспомогательной задачи
- § 6. Уровни энергии и радиальные функции точечного спектра для водорода
- § 7. Решение дифференциального уравне им для сплошного спектра в виде определенного интеграла
- § 8. Вывод асимптотического выражения
- § 9. Радиальные функции водорода для сплошного спектра
- § 10. Интенсивности в спектре водорода
- § 11. Явление Штарка. Общие замечания
- § 12. Уравнение Шредингера в параболических координатах
- § 13. Расщепление уровней энергии в электрическом поле
- § 14. Рассеяние а-частиц. Постановка задачи
- § 15. Решение уравнений
- § 16. Формула Резерфорда
- § 17. Теорема вириала в классической и квантовой механике
- § 18. Замечания о принципе наложения и о вероятностном толковании волновой функции
- Часть III. ТЕОРИЯ ПАУЛИ
- § 1. Момент количества движения электрона
- § 2. Операторы полного момента количества движения в сферических координатах
- § 3. Шаровые функции со спином
- § 4. Некоторые свойства шаровых функций со спином
- § 5. Волновое уравнение Паули
- § 6. Преобразование оператора P к цилиндрическим и сферическим координатам и выражение его через оператор M
- § 7. Электрон в магнитном поле
- Часть IV. МНОГОЭЛЕКТРОННАЯ ЗАДАЧА КВАНТОВОЙ МЕХАНИКИ И СТРОЕНИЕ АТОМА
- § 1. Свойства симметрии волновой функции
- § 2. Оператор энергии и его симметрия
- § 3. Метод согласованного поля
- § 4. Уравнение для валентного электрона и оператор квантового обмена
- § 5. Применение метода согласованного поля к теории строения атома
- § 6. Симметрия оператора энергии водородоподобного атома
- Часть V. ТЕОРИЯ ДИРАКА
- Глава I. ВОЛНОВОЕ УРАВНЕНИЕ ДИРАКА
- § 2. Классические уравнения движения
- § 3. Вывод волнового уравнения
- § 4. Матрицы Дирака
- § 5. Уравнение Дирака для свободного электрона
- § 6. Преобразование Лоренца
- § 7. Вид матрицы S для пространственного поворота осей и для преобразования Лоренца
- § 8. Вектор тока
- § 9. Уравнение Дирака при наличии поля. Уравнения движения
- § 10. Момент количества движения и вектор спина в теории Дирака
- § 11. Кинетическая энергия электрона
- § 12. Вторая внутренняя степень свободы электрона
- § 13. Уравнения второго порядка
- Глава II. ПРИМЕНЕНИЕ УРАВНЕНИЯ ДИРАКА К НЕКОТОРЫМ ФИЗИЧЕСКИМ ЗАДАЧАМ
- § 1. Свободный электрон
- § 2. Электрон в однородном магнитном поле
- § 3. Интегралы уравнений движения в задаче со сферической симметрией
- § 4. Обобщенные шаровые функции
- § 5. Уравнение для радиальных функций
- § 6. Сравнение с уравнением Шредингера
- § 7. Общее исследование уравнений для радиальных функций
- § 8. Квантовые числа
- § 9. Гейзенберговы матрицы и правило отбора
- § 10. Другой вывод правила отбора
- § 11. Атом водорода. Радиальные функции
- § 12. Тонкая структура водородных линий
- § 13. Явление Зеемана. Постановка задачи
- § 14. Вычисление матрицы возмущающей энергии
- § 15. Расщепление уровней в магнитном поле
- Глава III. О ТЕОРИИ ПОЗИТРОНОВ
- § 2. Основные идеи теории позитронов
- § 3. Модель позитронов как незаполненных состояний
- ПОСЛЕСЛОВИЕ