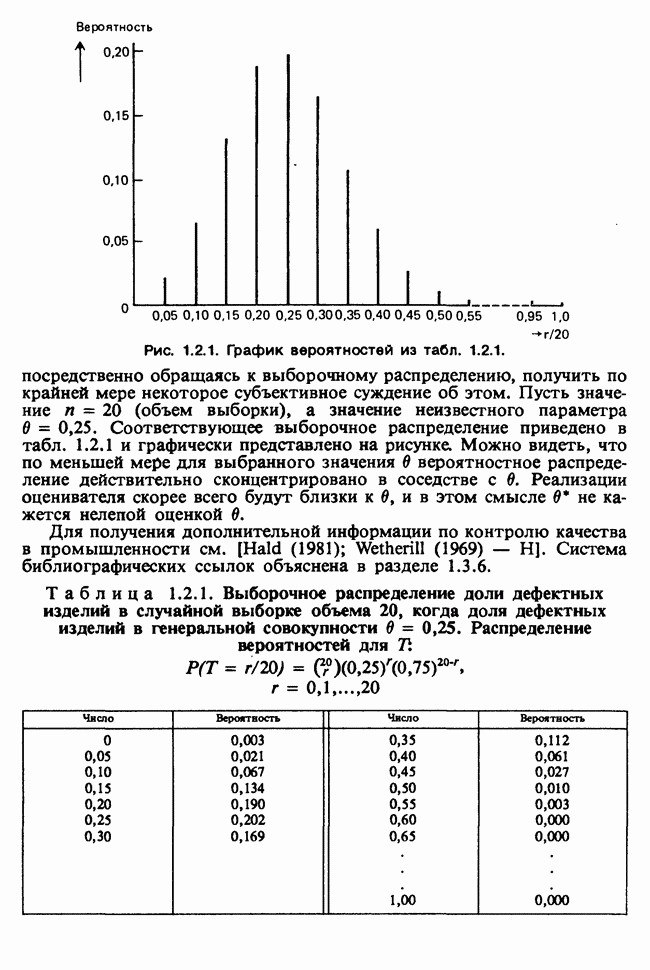
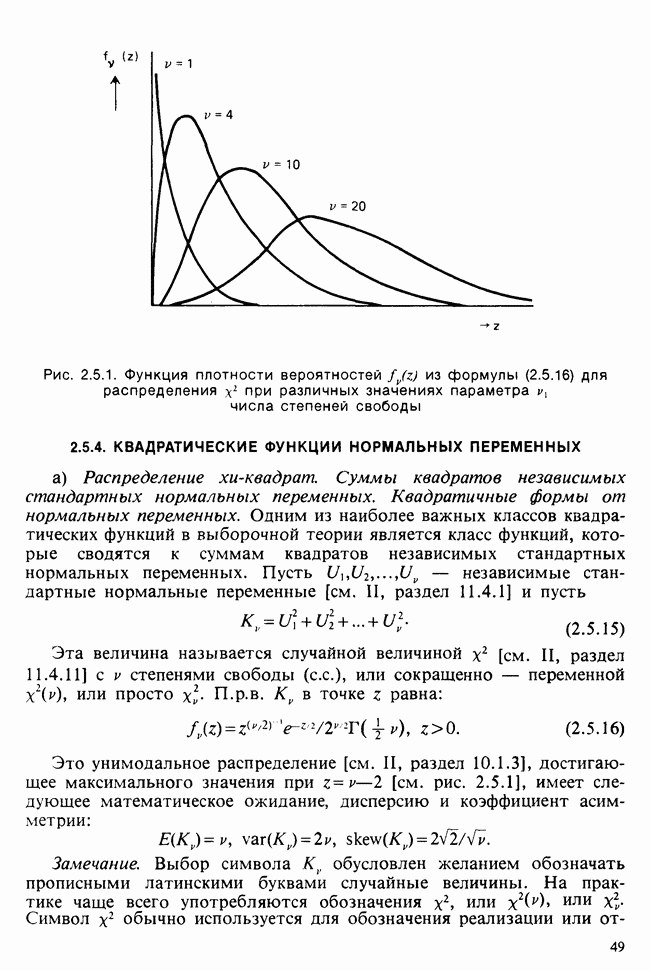
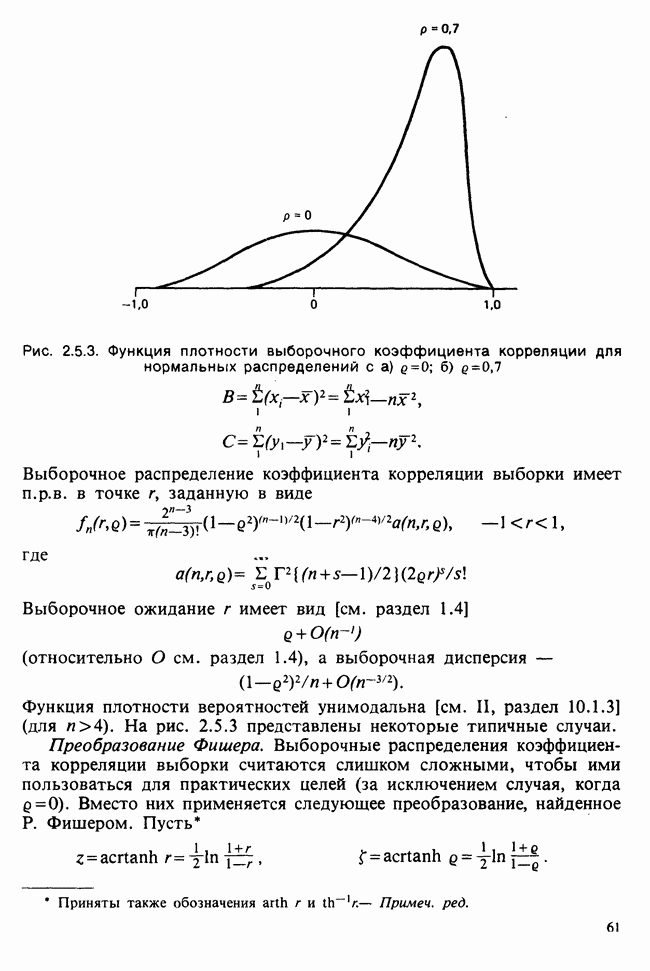
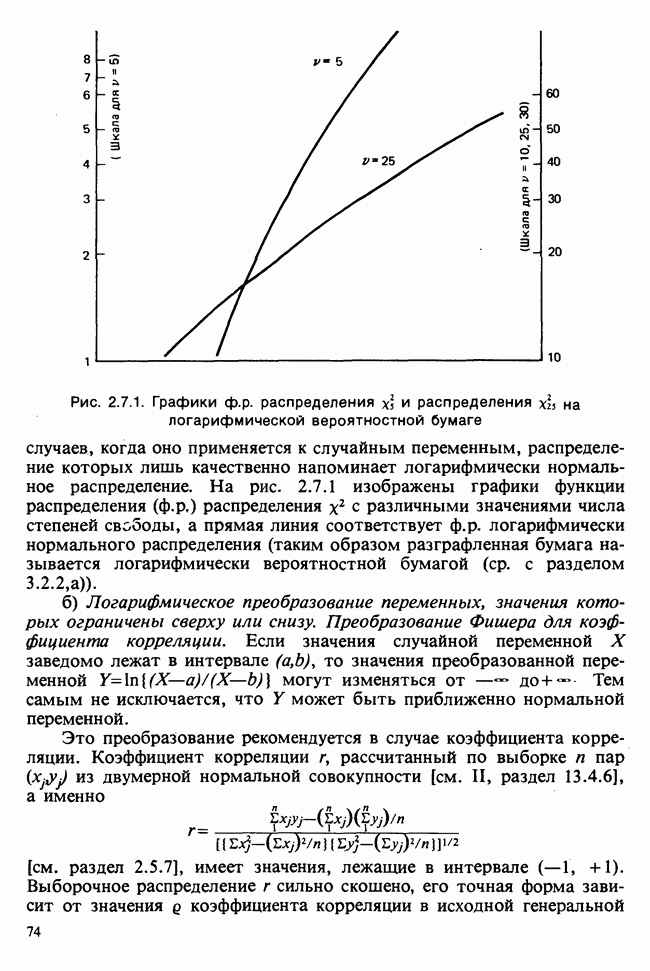
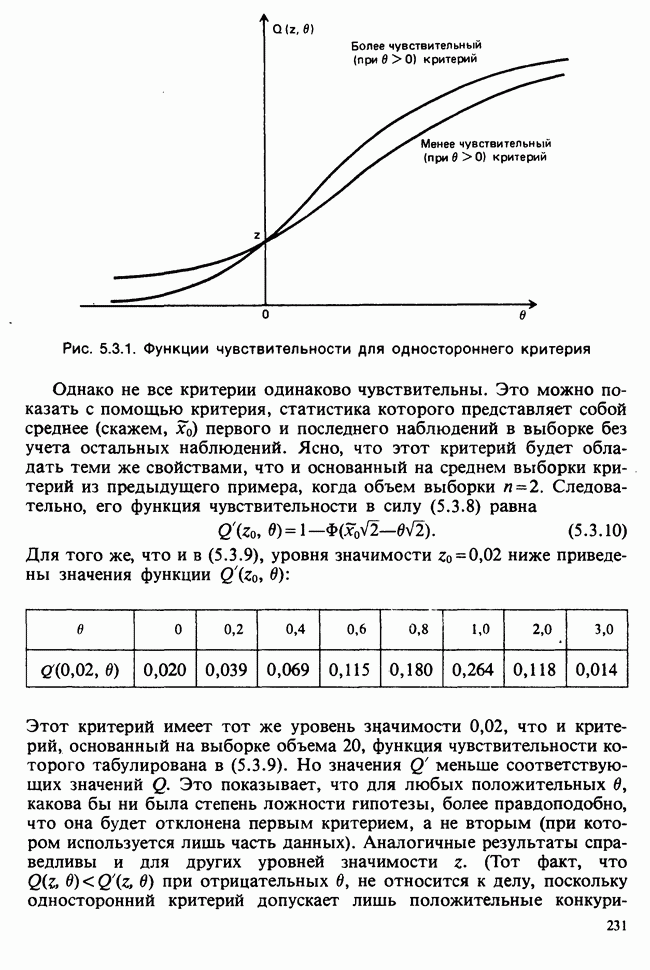
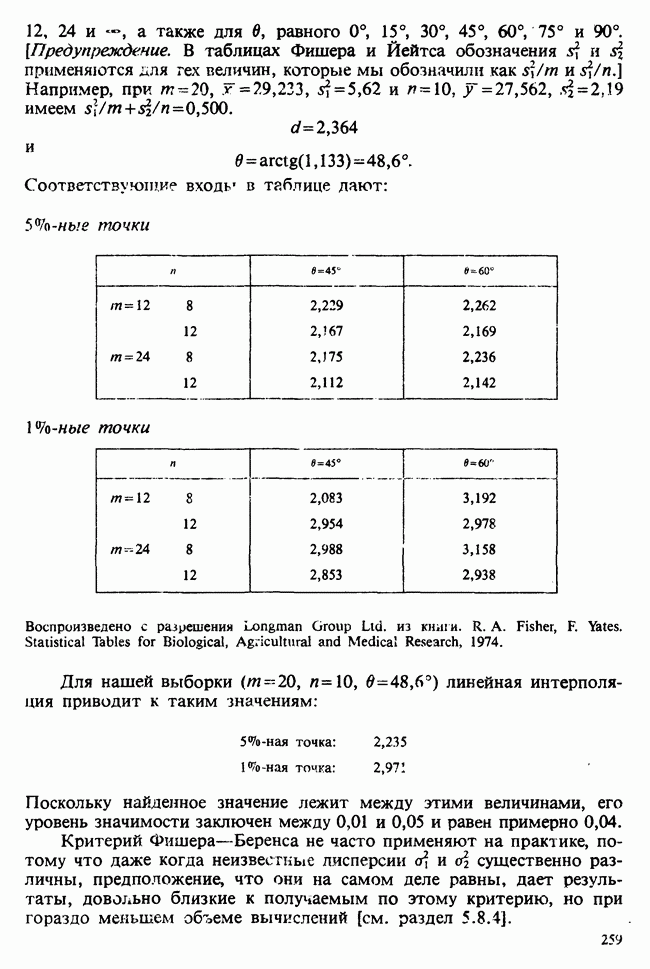
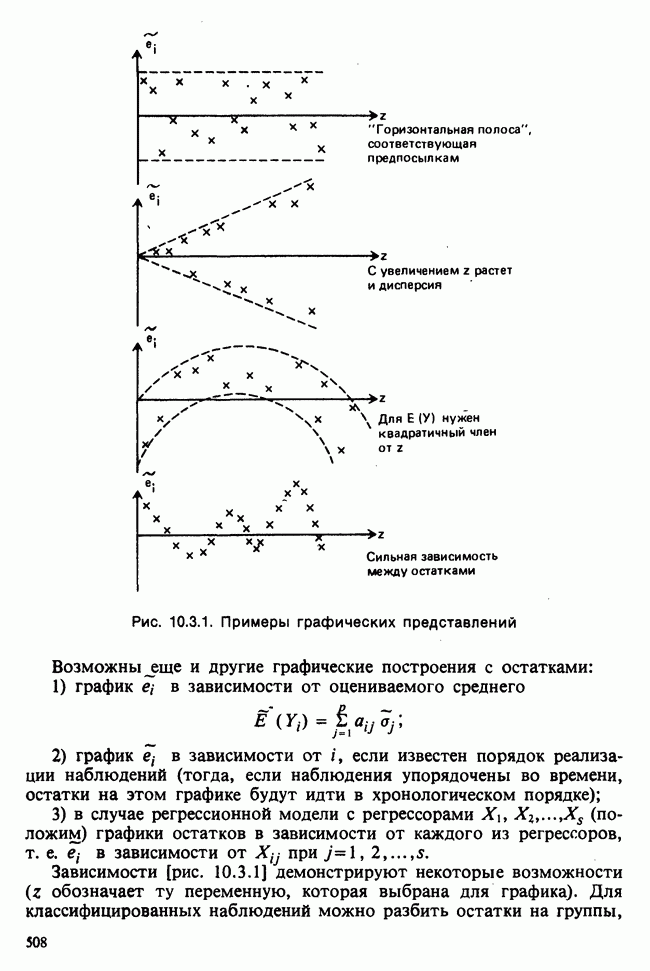
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2.5.8. НЕЗАВИСИМОСТЬ КВАДРАТИЧНЫХ ФОРМ. ТЕОРЕМА ФИШЕРА—КОКРЕНА. ТЕОРЕМА КРЕЙГА
При дисперсионном анализе, о котором говорилось в разделе 2.5.6 (а также в гл. 8 и 10), часто необходимо установить, будут ли определенные суммы квадратов взаимно независимыми. Главный критерий дает следующая теорема, известная как теорема Кокрена, или как теорема Фишера—Кокрена.
Теорема 2.5.3 (теорема Фишера—Кокрена). Пусть  — независимые стандартные нормальные величины. Пусть
— независимые стандартные нормальные величины. Пусть  — неотрицательные квадратичные формы от переменных
— неотрицательные квадратичные формы от переменных  с рангами
с рангами  соответственно [см. I, раздел 5.6], такие, что
соответственно [см. I, раздел 5.6], такие, что

 будут взаимно независимыми
будут взаимно независимыми  -переменными тогда и только тогда, когда
-переменными тогда и только тогда, когда

В этом случае  имеет
имеет  степеней свободы,
степеней свободы, 
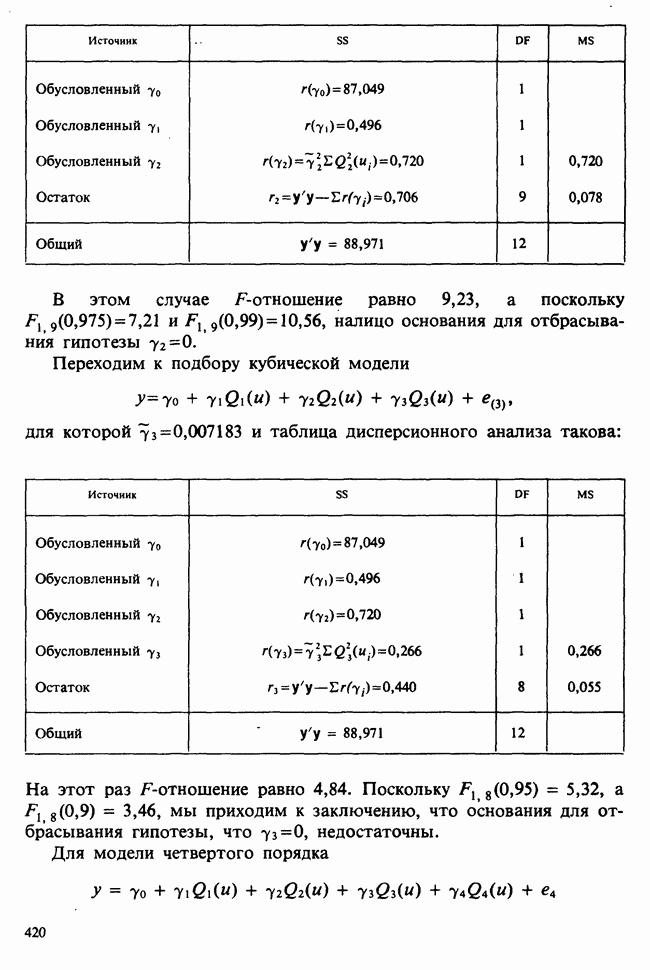
Далее приводятся две другие полезные теоремы.
Теорема 2.5.4. В обозначениях теоремы 2.5.3 предположим, что

где  переменная с
переменная с  — переменная с неотрицательными значениями. Тогда
— переменная с неотрицательными значениями. Тогда  имеет распределение
имеет распределение  и независима от
и независима от 
Теорема 2.5.5. В обозначениях теоремы 2.5.3 предположим, что  неотрицательные квадратичные формы от переменных
неотрицательные квадратичные формы от переменных  такие, что
такие, что

причем  и
и  распределены как
распределены как  соответственно. Тогда
соответственно. Тогда  распределена как
распределена как  и независима от
и независима от 
Пример 2.5.2. Ортогональное разложение  Рассмотрим следующее алгебраическое тождество для независимых стандартных нормальных переменных
Рассмотрим следующее алгебраическое тождество для независимых стандартных нормальных переменных 

Ясно, что квадратичные формы  неотрицательны. Очевидно, что ранг
неотрицательны. Очевидно, что ранг  равен 1, а ранг
равен 1, а ранг  Отсюда на основании теоремы 2.5.3 следует, что
Отсюда на основании теоремы 2.5.3 следует, что  и
и  — взаимно независимые
— взаимно независимые  -переменные
-переменные  соответственно. (Этот результат был установлен в примере 2.5.1.)
соответственно. (Этот результат был установлен в примере 2.5.1.)
Иначе говоря, можно утверждать (причем в более простой форме), что,  — нормальная переменная с параметрами
— нормальная переменная с параметрами  переменная
переменная  будет стандартной нормальной. Откуда получим, что
будет стандартной нормальной. Откуда получим, что  -
-  -переменная с 1 с.с. Применение результатов теоремы
-переменная с 1 с.с. Применение результатов теоремы
2.5.4 к указанному выше тождеству приводит к выводу, что  — переменная, имеющая распределение
— переменная, имеющая распределение  Соответствующий результат для н.о.р. нормальных случайных величин
Соответствующий результат для н.о.р. нормальных случайных величин  с параметрами
с параметрами  основан на тождестве
основан на тождестве

или, скажем,

Здесь  -переменная с
-переменная с  -переменная с
-переменная с  откуда, согласно теореме,
откуда, согласно теореме,  — переменная с распределением
— переменная с распределением  независимая от
независимая от  Этот результат важен для проверки значимости среднего выборки с помощью
Этот результат важен для проверки значимости среднего выборки с помощью  -критерия Стьюдента [см. раздел 5.8.2].
-критерия Стьюдента [см. раздел 5.8.2].
Пример 2.5.3. Сравнение двух средних. Тождество

требуется для применения критерия Стьюдента при сравнении средних  двух независимых выборок [см. раздел 5.8.4], скажем
двух независимых выборок [см. раздел 5.8.4], скажем  и
и  из нормальных генеральных совокупностей с одинаковой дисперсией
из нормальных генеральных совокупностей с одинаковой дисперсией  но, возможно, с неравными ожидаемыми значениями. В приведенном выше тождестве
но, возможно, с неравными ожидаемыми значениями. В приведенном выше тождестве

Записав тождество в виде

легко увидеть, что  суть
суть  -переменные с числом степеней свободы
-переменные с числом степеней свободы

Отсюда следует, что  не зависят друг от друга.
не зависят друг от друга.
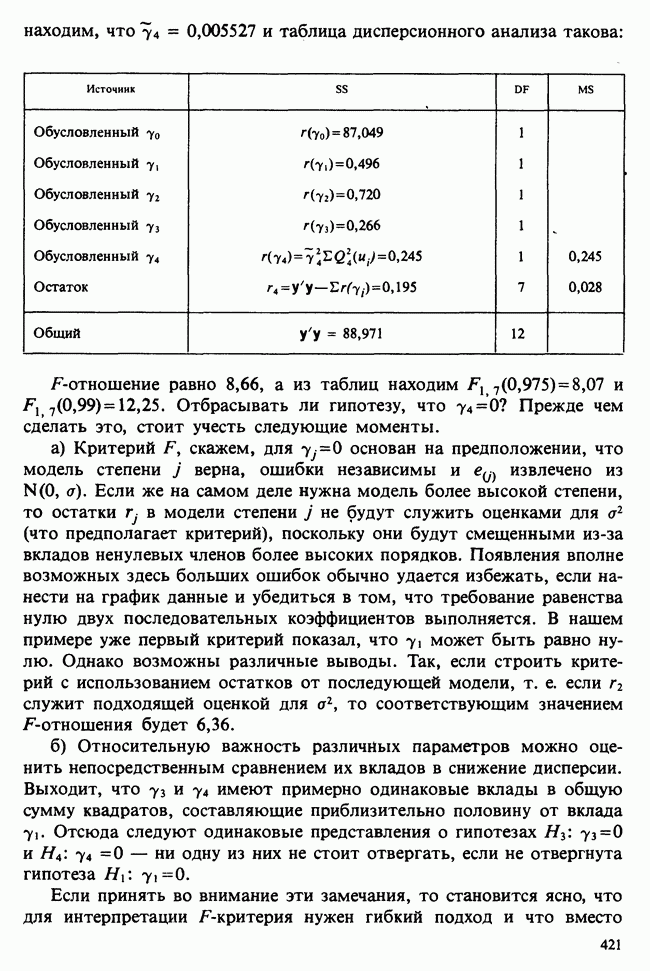
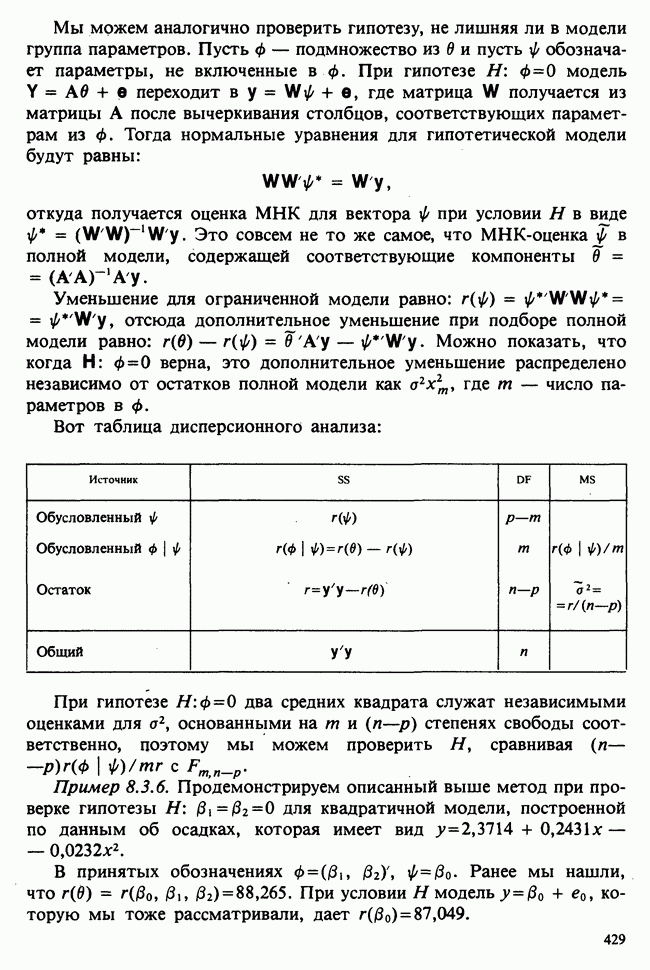
Приведенные выше теоремы полезны в случаях, когда квадратичная форма расщепляется на две или более квадратичные формы. Когда же этого нет, например, когда просто даются две квадратичные формы и возникает вопрос, являются ли они независимыми, главную роль может играть следующая теорема.
Теорема 2.5.6. Теорема Крейга. Пусть и  — квадратичные формы от независимых нормальных переменных
— квадратичные формы от независимых нормальных переменных  с параметрами
с параметрами  причем
причем  соответствует матрица
соответствует матрица  — матрица В. Случайные величины
— матрица В. Случайные величины  взаимно независимы тогда и только тогда, когда
взаимно независимы тогда и только тогда, когда 
Пример 2.5.4. Независимость  Пусть
Пусть  — случайная выборка из нормального распределения с параметрами (и,о). Установленную в примере 2.5.2 выборочную независимость
— случайная выборка из нормального распределения с параметрами (и,о). Установленную в примере 2.5.2 выборочную независимость  можно продемонстрировать с помощью теоремы 2.5.6: рассмотрим квадратичные формы
можно продемонстрировать с помощью теоремы 2.5.6: рассмотрим квадратичные формы  в которых, как обычно,
в которых, как обычно,  — случайная переменная, индуцированная
— случайная переменная, индуцированная  индуцированная х. Матрица А для
индуцированная х. Матрица А для  имеет вид
имеет вид  , а для
, а для  матрица
матрица  (I — единичная матрица,
(I — единичная матрица,  ). Тогда
). Тогда  (так как
(так как  ), откуда следует, что
), откуда следует, что  взаимно независимы. Предположим, что нас интересует, зависимы или нет линейная форма
взаимно независимы. Предположим, что нас интересует, зависимы или нет линейная форма  Построим квадратичную форму
Построим квадратичную форму  для которой матрица А равна
для которой матрица А равна  Как и раньше, матрица В для
Как и раньше, матрица В для  равна
равна  Тогда
Тогда  (где
(где  ).
).
Элемент  в этой матрице равен
в этой матрице равен  Он отличен от нуля для всех
Он отличен от нуля для всех  за исключением случая, когда
за исключением случая, когда  для всех
для всех  , т.е. когда
, т.е. когда 
пропорционально выборочному среднему X. Таким образом, X не просто независима от  (или линейная форма, пропорциональная X) оказывается единственной линейной формой от
(или линейная форма, пропорциональная X) оказывается единственной линейной формой от  которая не зависит от
которая не зависит от  Например, в выборке объема 3 сумма
Например, в выборке объема 3 сумма  независима от суммы квадратов выборки
независима от суммы квадратов выборки  однако линейная комбинация
однако линейная комбинация  этим свойством не обладает.
этим свойством не обладает.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- Глава I. ВВЕДЕНИЕ В СТАТИСТИКУ
- 1.1. СМЫСЛ ПОНЯТИЯ «СТАТИСТИКА»
- 1.2. ВЫБОРОЧНОЕ РАСПРЕДЕЛЕНИЕ, СТАТИСТИКА, ОЦЕНКА
- 1.3. ТЕМА ЭТОЙ КНИГИ
- 1.4. СОГЛАШЕНИЯ И ОБОЗНАЧЕНИЯ
- Глава 2. ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ
- 2.1. МОМЕНТЫ И ДРУГИЕ СТАТИСТИКИ
- 2.1.2. МОМЕНТЫ
- 2.2. ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ: ОПРЕДЕЛЕНИЯ И ПРИМЕРЫ
- 2.3. ВЫБОРОЧНЫЕ МОМЕНТЫ СТАТИСТИК
- 2.3.1. ПЕРВЫЕ ВЫБОРОЧНЫЕ МОМЕНТЫ СРЕДНЕГО ЗНАЧЕНИЯ ВЫБОРКИ
- 2.3.2. ПЕРВЫЕ ВЫБОРОЧНЫЕ МОМЕНТЫ ДИСПЕРСИИ ВЫБОРКИ
- 2.3.3. ВЫБОРОЧНАЯ КОВАРИАЦИЯ МЕЖДУ СРЕДНИМ ЗНАЧЕНИЕМ ВЫБОРКИ x И ДИСПЕРСИЕЙ ВЫБОРКИ v
- 2.3.4. ВЫБОРОЧНЫЕ МОМЕНТЫ ДЛЯ МОМЕНТОВ ВЫБОРКИ БОЛЕЕ ВЫСОКИХ ПОРЯДКОВ
- 2.3.5. ВЫБОРОЧНЫЕ МОМЕНТЫ СТАНДАРТНОГО ОТКЛОНЕНИЙ ВЫБОРКИ
- 2.3.6. ВЫБОРОЧНЫЕ МОМЕНТЫ КОЭФФИЦИЕНТА АСИММЕТРИИ ВЫБОРКИ
- 2.4. РАСПРЕДЕЛЕНИЯ СУММ НЕЗАВИСИМЫХ ОДИНАКОВО РАСПРЕДЕЛЕННЫХ ПЕРЕМЕННЫХ
- 2.5. ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ НОРМАЛЬНЫХ ПЕРЕМЕННЫХ
- 2.5.2. РЕЗУЛЬТАТ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ. СТАНДАРТИЗАЦИЯ
- 2.5.3. ЛИНЕЙНЫЕ ФУНКЦИИ НОРМАЛЬНЫХ ПЕРЕМЕННЫХ
- 2.5.4. КВАДРАТИЧЕСКИЕ ФУНКЦИИ НОРМАЛЬНЫХ ПЕРЕМЕННЫХ
- 2.5.5. РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА (t-распределение)
- 2.5.6. РАСПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ДИСПЕРСИЙ (F-распределение)
- 2.5.7. КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ ВЫБОРКИ
- 2.5.8. НЕЗАВИСИМОСТЬ КВАДРАТИЧНЫХ ФОРМ. ТЕОРЕМА ФИШЕРА—КОКРЕНА. ТЕОРЕМА КРЕЙГА
- 2.5.9. РАЗМАХ И СТЬЮДЕНТИЗИРОВАННЫЙ РАЗМАХ
- 2.6. АССИМПТОТИЧЕСКОЕ ВЫБОРОЧНОЕ РАСПРЕДЕЛЕНИЕ х И НЕЛИНЕЙНЫХ ФУНКЦИЙ ОТ х
- 2.7. ПРИБЛИЖЕНИЕ ВЫБОРОЧНЫХ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ И ДИСПЕРСИИ НЕЛИНЕЙНЫХ СТАТИСТИК. ПРЕОБРАЗОВАНИЯ, СТАБИЛИЗИРУЮЩИЕ ДИСПЕРСИЮ. НОРМАЛИЗУЮЩИЕ ПРЕОБРАЗОВАНИЯ
- 2.7.1. АППРОКСИМАЦИЯ
- 2.7.2. ПРЕОБРАЗОВАНИЯ, СТАБИЛИЗИРУЮЩИЕ ДИСПЕРСИЮ
- 2.7.3. НОРМАЛИЗУЮЩИЕ ПРЕОБРАЗОВАНИЯ
- 2.7.4. ПРЕОБРАЗОВАНИЯ, ВЫПРЯМЛЯЮЩИЕ ЗАВИСИМОСТЬ
- 2.7.5. ПРЕОБРАЗОВАНИЕ ВЫБОРОЧНОГО КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ ПРИ r=0 В СТЬЮДЕНТОВУ ВЕЛИЧИНУ
- 2.7.6. ПРЕОБРАЗОВАНИЕ РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ ПЕРЕМЕННОЙ В «хи-квадрат»-ПЕРЕМЕННУЮ
- 2.8. НЕЦЕНТРАЛЬНЫЕ ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ
- 2.8.1. НЕЦЕНТРАЛЬНОЕ РАСПРЕДЕЛЕНИЕ ХИ-КВАДРАТ
- 2.8.2. НЕЦЕНТРАЛЬНОЕ F-РАСПРЕДЕЛЕНИЕ
- 2.8.3. НЕЦЕНТРАЛЬНОЕ РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА
- 2.9. ПОЛИНОМИАЛЬНОЕ (МУЛЬТИНОМИАЛЬНОЕ) РАСПРЕДЕЛЕНИЕ В ТЕОРИИ ВЫБОРОЧНЫХ РАСПРЕДЕЛЕНИЙ
- 2.9.1. БИНОМИАЛЬНОЕ, ТРИНОМИАЛЬНОЕ И МУЛЬТИНОМИАЛЬНОЕ (ПОРЯДКА m) РАСПРЕДЕЛЕНИЯ
- 2.9.2. СВОЙСТВА ПОЛИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ
- 2.9.3. ПОЛИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ КАК УСЛОВНОЕ ОТ СОВМЕСТНОГО РАСПРЕДЕЛЕНИЯ НЕЗАВИСИМЫХ ПУАССОНОВСКИХ ПЕРЕМЕННЫХ
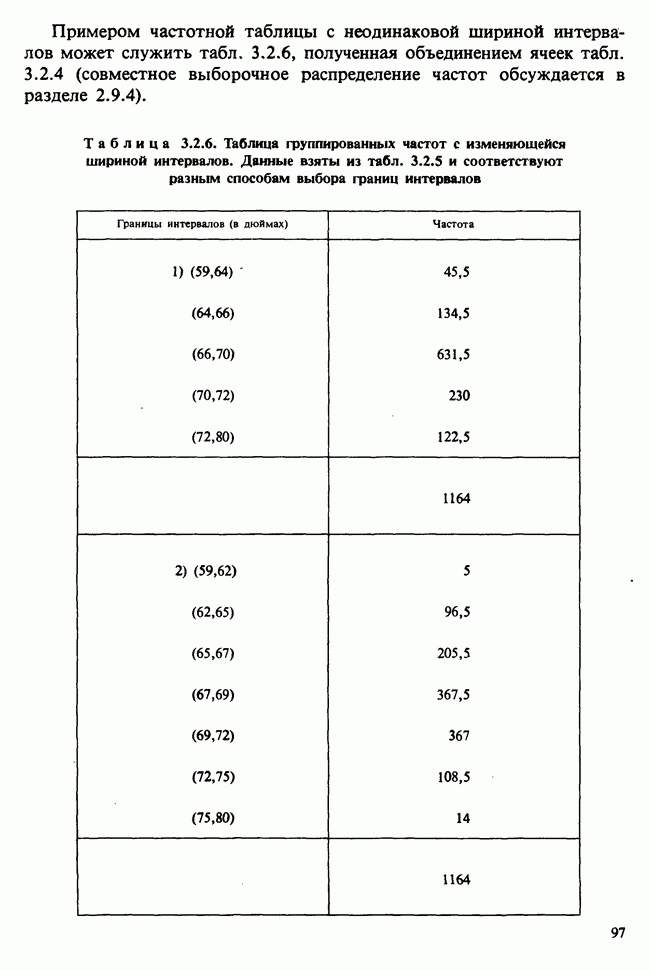
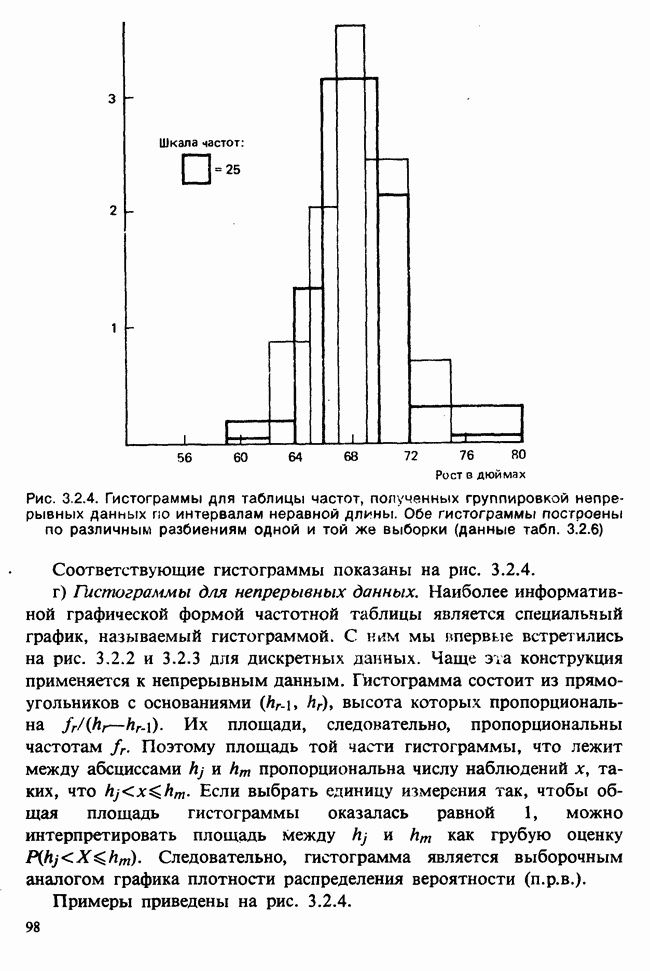
- 2.9.4. ТАБЛИЦЫ ЧАСТОТ
- 2.10. ЛИТЕРАТУРА ДЛЯ ДАЛЬНЕЙШЕГО ЧТЕНИЯ
- Глава 3. ОЦЕНИВАНИЕ. ВВОДНОЕ ОБОЗРЕНИЕ
- 3.1. ЗАДАЧА ОЦЕНИВАНИЯ
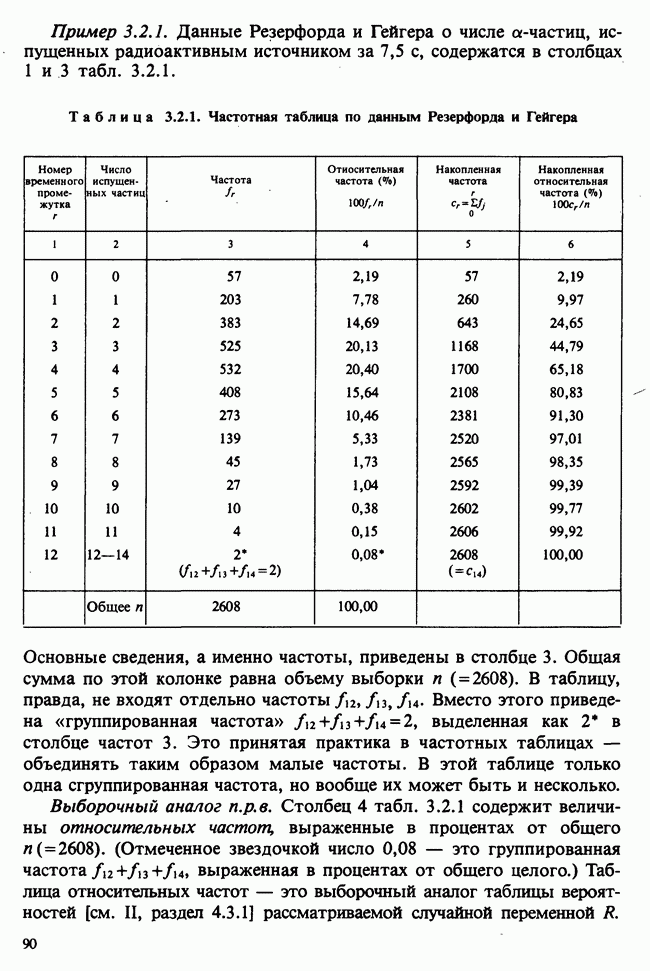
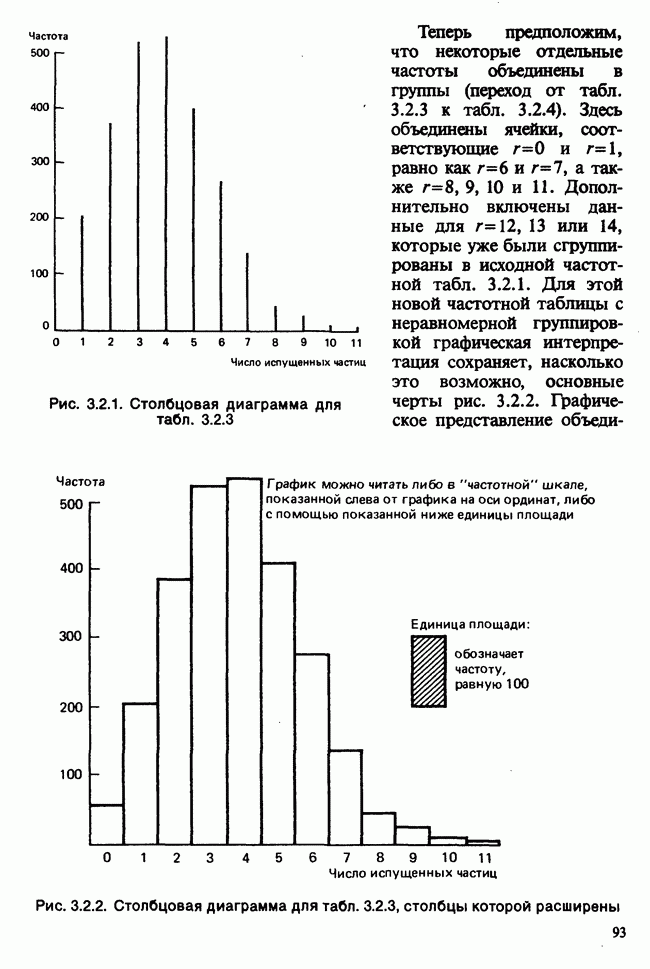
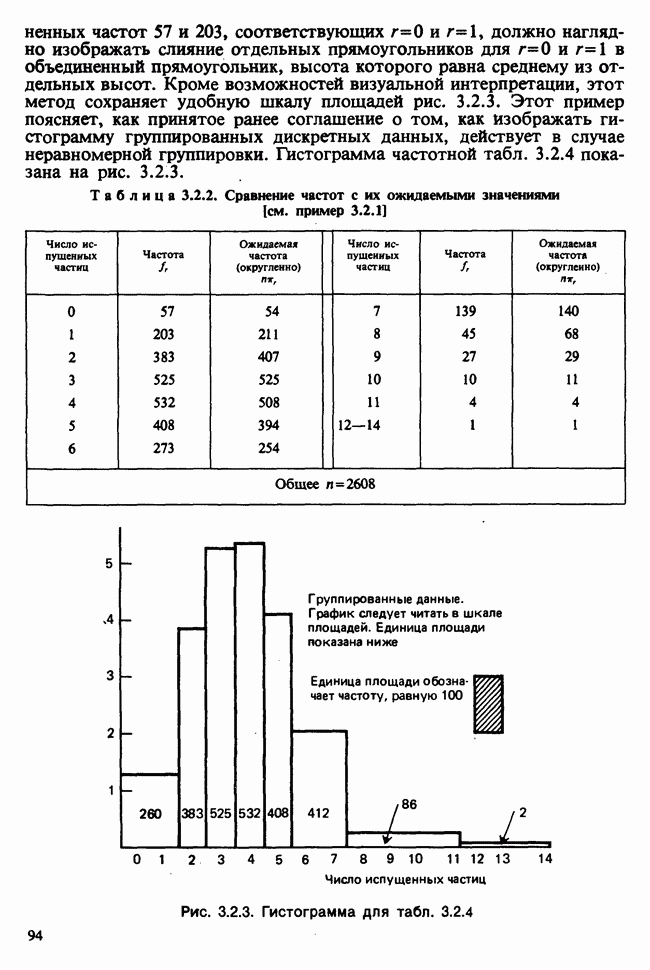
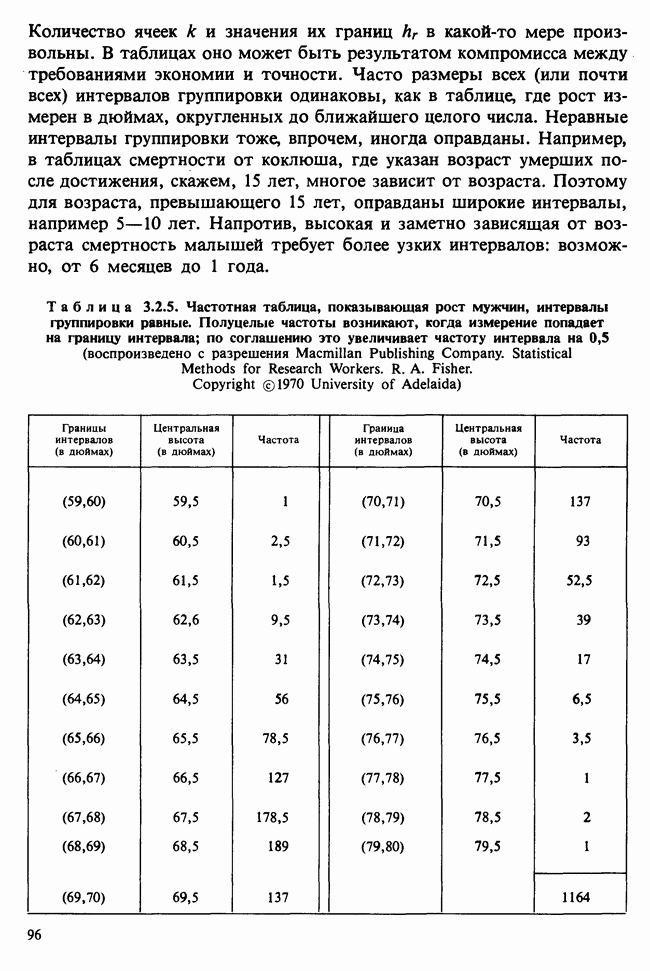
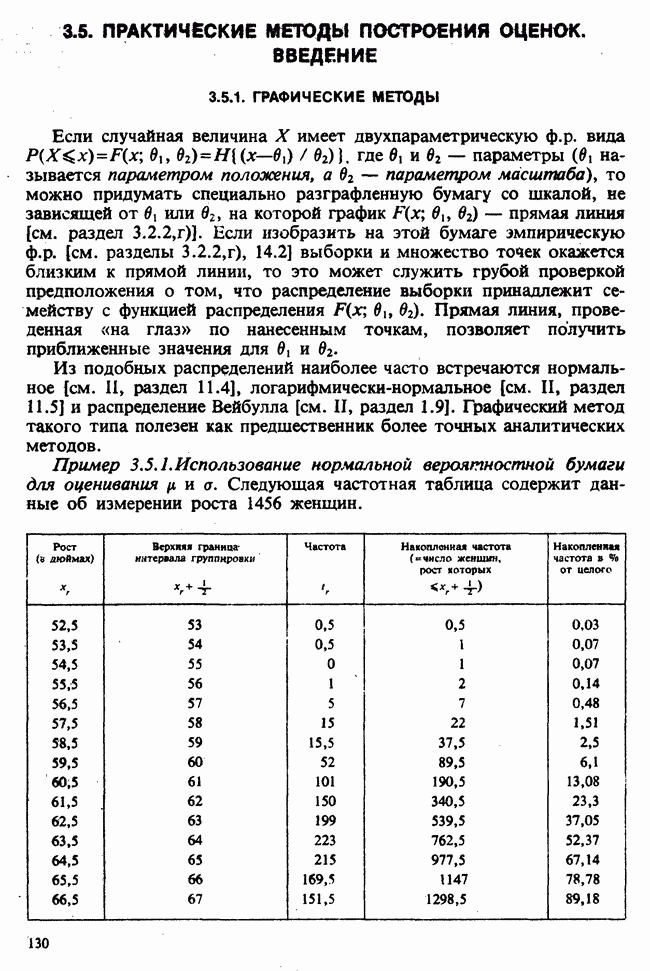
- 3.2. ИНТУИТИВНЫЕ ПРЕДСТАВЛЕНИЯ И ГРАФИЧЕСКИЙ МЕТОД
- 3.2.2. ЧАСТОТНЫЕ ТАБЛИЦЫ, ГИСТОГРАММЫ И ЭМПИРИЧЕСКАЯ ф.р.
- 3.3. НЕКОТОРЫЕ ОБЩИЕ КОНЦЕПЦИИ И КРИТЕРИИ ОЦЕНОК
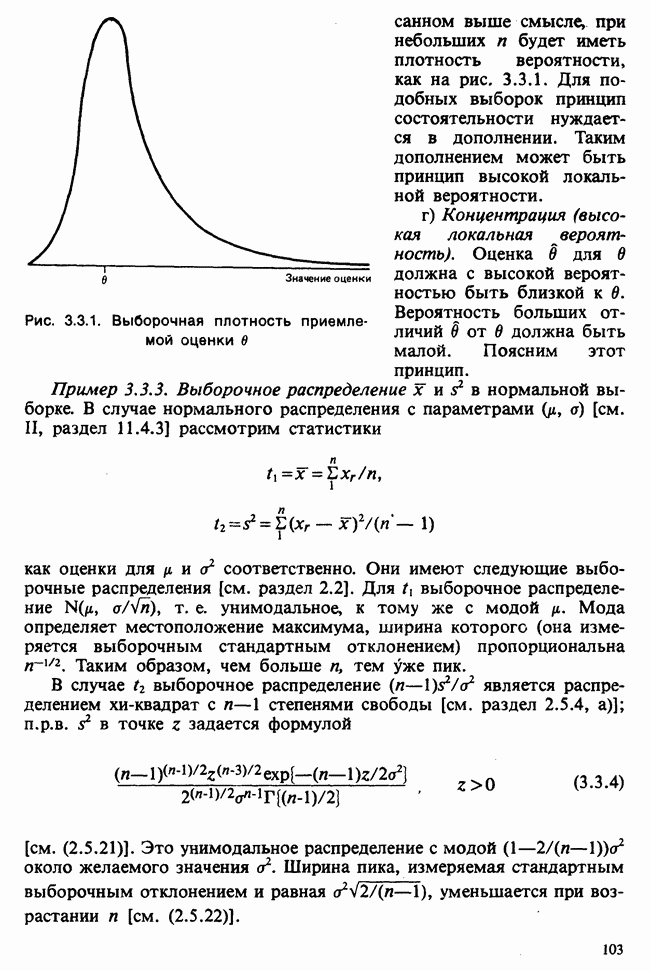
- 3.3.1. ВВЕДЕНИЕ. РАЗМЕРНОСТЬ, ЗАМЕНЯЕМОСТЬ, СОСТОЯТЕЛЬНОСТЬ, КОНЦЕНТРАЦИЯ
- 3.3.2. НЕСМЕЩЕННЫЕ ОЦЕНКИ И НЕСМЕЩЕННЫЕ ОЦЕНКИ С МИНИМАЛЬНОЙ ДИСПЕРСИЕЙ
- 3.3.3. ЭФФЕКТИВНОСТЬ. ГРАНИЦА КРАМЕРА—РАО
- 3.4. ДОСТАТОЧНОСТЬ
- 3.4.2. КРИТЕРИЙ ФАКТОРИЗАЦИИ И ЭКСПОНЕНЦИАЛЬНОЕ СЕМЕЙСТВО
- 3.4.3. ДОСТАТОЧНОСТЬ И НЕСМЕЩЕННАЯ МИНИМАЛЬНО ДИСПЕРСНАЯ ОЦЕНКА
- 3.4.4. ДОСТАТОЧНОСТЬ В СЛУЧАЕ МНОГИХ ПАРАМЕТРОВ
- 3.5. ПРАКТИЧЕСКИЕ МЕТОДЫ ПОСТРОЕНИЯ ОЦЕНОК. ВВЕДЕНИЕ
- 3.5.2. НЕСМЕЩЕННЫЕ ОЦЕНКИ С МИНИМАЛЬНОЙ ДИСПЕРСИЕЙ. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
- 3.5.3. МЕТОД МОМЕНТОВ
- 3.5.4. МЕТОД МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
- 3.5.5. НОРМАЛЬНЫЕ ЛИНЕЙНЫЕ МОДЕЛИ, В КОТОРЫХ ОЦЕНКИ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ И НАИМЕНЬШИХ КВАДРАТОВ СОВПАДАЮТ
- Глава 4. ИНТЕРВАЛЬНОЕ ОЦЕНИВАНИЕ
- 4.1.2. СТАНДАРТНОЕ ОТКЛОНЕНИЕ
- 4.1.3. ИНТЕРВАЛЫ ВЕРОЯТНОСТИ
- 4.2. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ И ДОВЕРИТЕЛЬНЫЕ ПРЕДЕЛЫ
- 4.3. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА С ПОМОЩЬЮ ОПОРНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
- 4.4. ИСТОЛКОВАНИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА КАК МЕРЫ ТОЧНОСТИ ОЦЕНКИ НЕИЗВЕСТНОГО ПАРАМЕТРА
- 4.5. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ ПРИ НЕСКОЛЬКИХ ПАРАМЕТРАХ
- 4.5.2. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ ДЛЯ ФУНКЦИЙ ДВУХ ПАРАМЕТРОВ, ВКЛЮЧАЮЩИХ ОТНОШЕНИЕ ПАРАМЕТРОВ И ИХ РАЗНОСТЬ (ТЕОРЕМА ФЕЛЛЕРА)
- 4.6. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ БЕЗ ИСПОЛЬЗОВАНИЯ ОПОРНОЙ ПЕРЕМЕННОЙ
- 4.7. ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ ДЛЯ ПАРАМЕТРОВ ДИСКРЕТНЫХ РАСПРЕДЕЛЕНИЙ
- 4.8. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ ДЛЯ КВАНТИЛЕЙ, НЕ ЗАВИСЯЩИЕ ОТ ИСХОДНОГО РАСПРЕДЕЛЕНИЯ (РАСПРЕДЕЛЕННЫЕ СВОБОДНО)
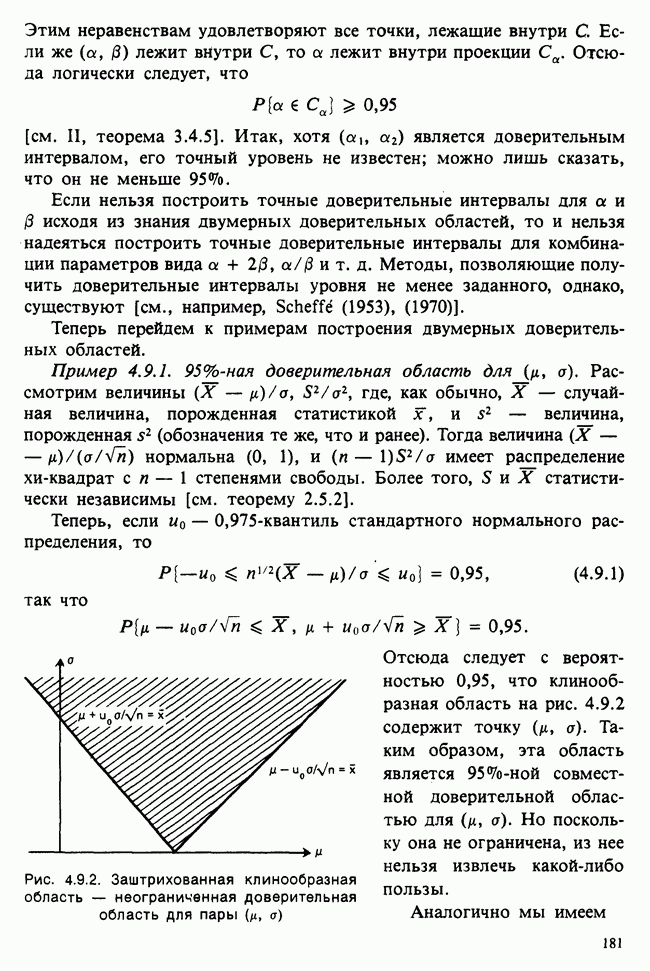
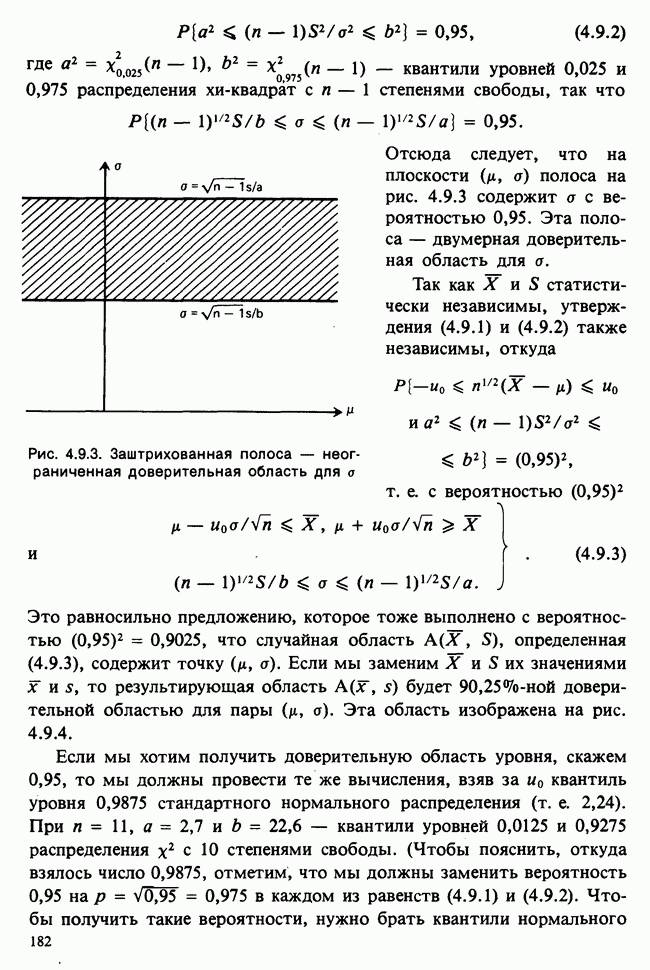
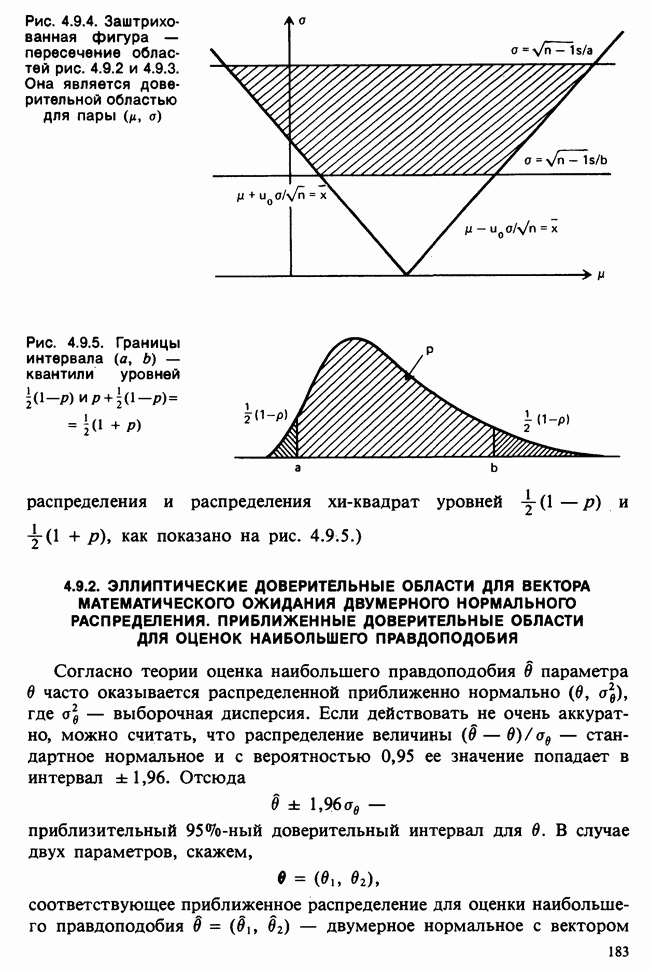
- 4.9. ДОВЕРИТЕЛЬНЫЕ ОБЛАСТИ ДЛЯ МНОГОМЕРНОГО ПАРАМЕТРА
- 4.9.2. ЭЛЛИПТИЧЕСКИЕ ДОВЕРИТЕЛЬНЫЕ ОБЛАСТИ ДЛЯ ВЕКТОРА МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ ДВУМЕРНОГО НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ. ПРИБЛИЖЕННЫЕ ДОВЕРИТЕЛЬНЫЕ ОБЛАСТИ ДЛЯ ОЦЕНОК НАИБОЛЬШЕГО ПРАВДОПОДОБИЯ
- 4.10. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ НА ОСНОВЕ БОЛЬШИХ ВЫБОРОК С ИСПОЛЬЗОВАНИЕМ ФУНКЦИИ ПРАВДОПОДОБИЯ
- 4.10.2. ПОСТРОЕНИЕ ПРИБЛИЖЕННЫХ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ С ПОМОЩЬЮ ПРОИЗВОДНОЙ ЛОГАРИФМИЧЕСКОЙ ФУНКЦИИ ПРАВДОПОДОБИЯ
- 4.10.3. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ С ПОМОЩЬЮ (ПРИБЛИЖЕННО) НОРМАЛИЗУЮЩЕГО ПРЕОБРАЗОВАНИЯ
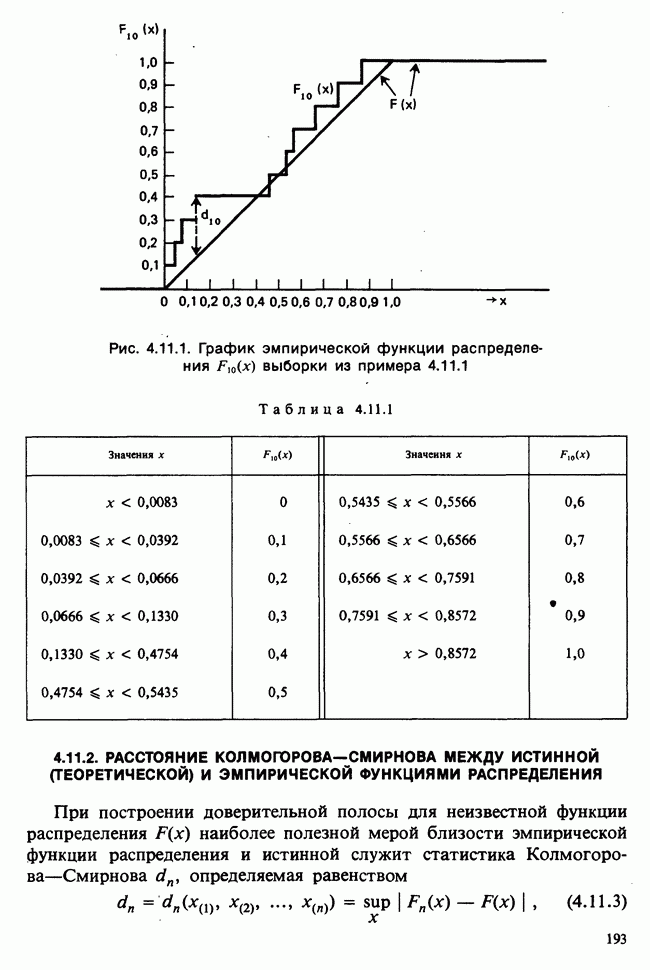
- 4.11. ДОВЕРИТЕЛЬНАЯ ПОЛОСА ДЛЯ НЕИЗВЕСТНОЙ НЕПРЕРЫВНОЙ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
- 4.11.2. РАССТОЯНИЕ КОЛМОГОРОВА—СМИРНОВА МЕЖДУ ИСТИННОЙ (ТЕОРЕТИЧЕСКОЙ) И ЭМПИРИЧЕСКОЙ ФУНКЦИЯМИ РАСПРЕДЕЛЕНИЯ
- 4.11.3. ВЫБОРОЧНОЕ РАСПРЕДЕЛЕНИЕ СТАТИСТИКИ КОЛМОГОРОВА—СМИРНОВА. ДОВЕРИТЕЛЬНЫЕ ПРЕДЕЛЫ ДЛЯ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
- 4.12. ТОЛЕРАНТНЫЕ ИНТЕРВАЛЫ
- 4.13. ИНТЕРВАЛЫ ПРАВДОПОДОБИЯ
- 4.13.2. ПРАВДОПОДОБНЫЕ ЗНАЧЕНИЯ И ИНТЕРВАЛЫ ПРАВДОПОДОБИЯ
- 4.13.3. СИТУАЦИЯ С ДВУМЯ ПАРАМЕТРАМИ
- 4.14. БАЙЕСОВСКИЕ ИНТЕРВАЛЫ
- Глава 5. СТАТИСТИЧЕСКИЕ КРИТЕРИИ
- 5.2.1. ДВУХСТОРОННИЙ БИНОМИАЛЬНЫЙ КРИТЕРИЙ. СОСТАВНЫЕ ЧАСТИ, ПРОЦЕДУРА И ИНТЕРПРЕТАЦИЯ
- 5.2.2. ТРАДИЦИОННАЯ ИНТЕРПРЕТАЦИЯ УРОВНЕЙ ЗНАЧИМОСТИ; ИСПОЛЬЗУЕМЫЕ НА ПРАКТИКЕ УРОВНИ ЗНАЧИМОСТИ; КРИТИЧЕСКАЯ ОБЛАСТЬ
- 5.2.3. ОДНОСТОРОННИЙ БИНОМИАЛЬНЫЙ КРИТЕРИЙ
- 5.2.4. КРИТЕРИИ О РАСПРЕДЕЛЕНИИ ПУАССОНА
- 5.2.5. КРИТЕРИИ ДЛЯ НЕПРЕРЫВНЫХ РАСПРЕДЕЛЕНИЙ
- 5.2.6. ВЫБОР СТАТИСТИКИ КРИТЕРИЯ
- 5.3. КРИТЕРИИ ДЛЯ ПРОВЕРКИ ГИПОТЕЗ
- 5.3.2. ФУНКЦИЯ ЧУВСТВИТЕЛЬНОСТИ ОДНОСТОРОННЕГО КРИТЕРИЯ ДЛЯ ВЫБОРКИ ИЗ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ, КОГДА ЗНАЧЕНИЕ «сигма» НЕИЗВЕСТНО
- 5.3.3. ФУНКЦИЯ ЧУВСТВИТЕЛЬНОСТИ ДВУХСТОРОННЕГО КРИТЕРИЯ
- 5.4. КРИТЕРИИ ДЛЯ СЛОЖНЫХ НУЛЕВЫХ ГИПОТЕЗ
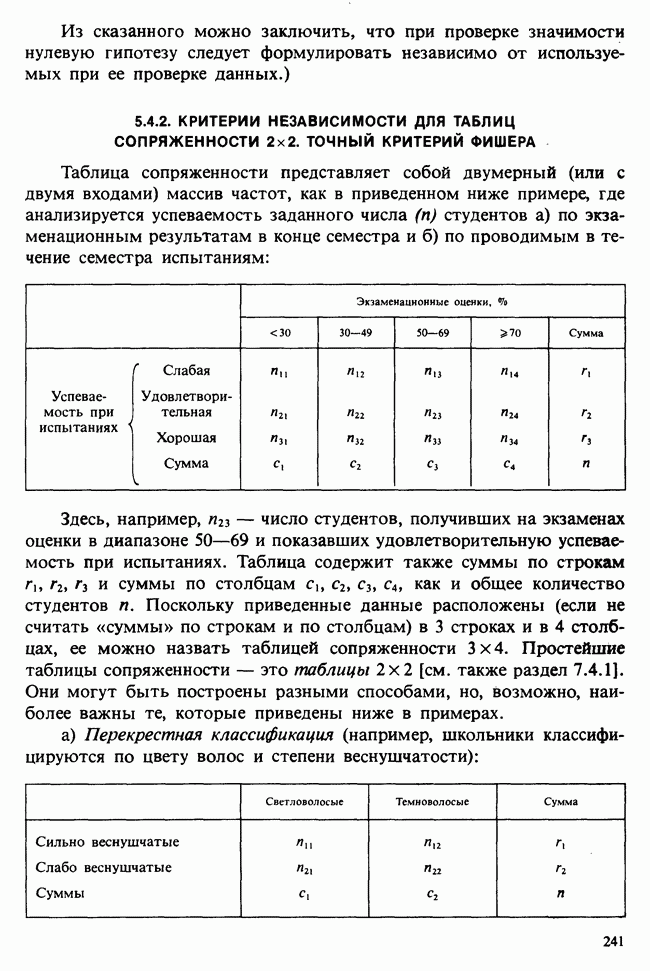
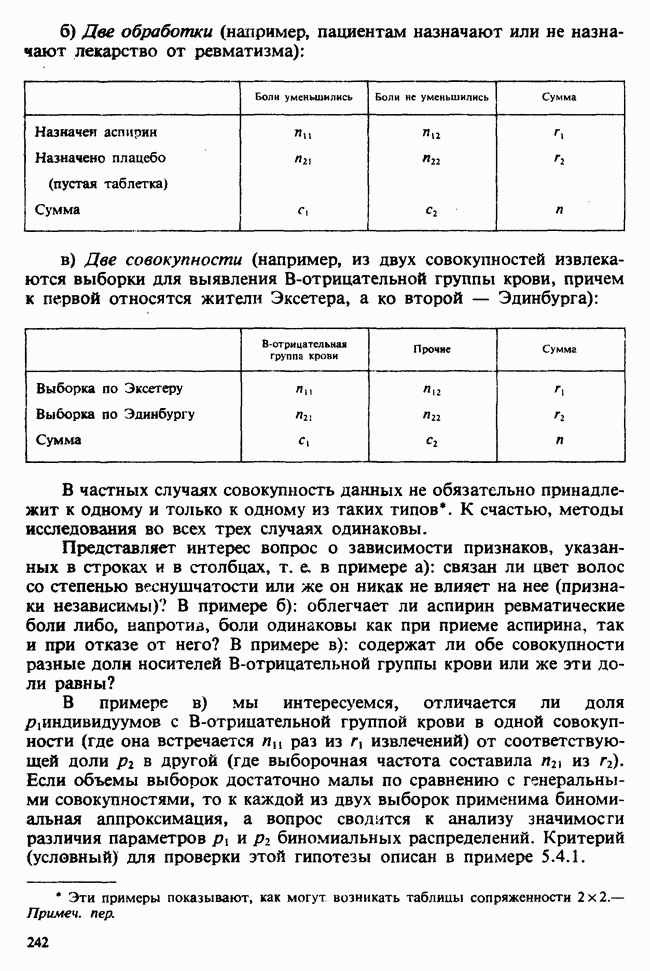
- 5.4.2. КРИТЕРИИ НЕЗАВИСИМОСТИ ДЛЯ ТАБЛИЦ СОПРЯЖЕННОСТИ 2×2. ТОЧНЫЙ КРИТЕРИЙ ФИШЕРА
- 5.5. КРИТЕРИИ, СОДЕРЖАЩИЕ БОЛЕЕ ОДНОГО ПАРАМЕТРА. ОБОБЩЕННЫЕ КРИТЕРИИ ОТНОШЕНИЯ ПРАВДОПОДОБИЯ
- 5.6. АППРОКСИМАЦИЯ УРОВНЯ ЗНАЧИМОСТИ КРИТЕРИЯ ОТНОШЕНИЯ ПРАВДОПОДОБИЯ ДЛЯ БОЛЬШИХ ВЫБОРОК
- 5.7. КРИТЕРИИ РАНДОМИЗАЦИИ
- 5.8. СТАНДАРТНЫЕ КРИТЕРИИ ДЛЯ МОДЕЛИ С НОРМАЛЬНЫМ РАСПРЕДЕЛЕНИЕМ
- 5.8.2. ЗНАЧИМОСТЬ СРЕДНЕГО, КОГДА ДИСПЕРСИЯ НЕИЗВЕСТНА. t-КРИТЕРИЙ СТЬЮДЕНТА
- 5.8.3. КРИТЕРИЙ ФИШЕРА-БЕРЕНСА ДЛЯ ПРОВЕРКИ ЗНАЧИМОСТИ РАЗЛИЧИЯ ДВУХ СРЕДНИХ
- 5.8.4. t-КРИТЕРИЙ ДЛЯ ПРОВЕРКИ ЗНАЧИМОСТИ РАЗЛИЧИЯ ДВУХ СРЕДНИХ (КОГДА ДИСПЕРСИИ РАВНЫ)
- 5.8.5. t-КРИТЕРИЙ ДЛЯ ПРОВЕРКИ ЗНАЧИМОСТИ КОЭФФИЦИЕНТА РЕГРЕССИИ В ПРОСТОЙ ЛИНЕЙНОЙ МОДЕЛИ
- 5.8.6. КРИТЕРИЙ РАВЕНСТВА ДВУХ ДИСПЕРСИЙ
- 5.8.7 ПРОВЕРКА РАВЕНСТВА НЕКОТОРЫХ СРЕДНИХ. ВВЕДЕНИЕ В ДИСПЕРСИОННЫЙ АНАЛИЗ
- 5.9. ПРОВЕРКА НОРМАЛЬНОСТИ
- 5.10. ПРОВЕРКА РАВЕНСТВА к ДИСПЕРСИЙ (КРИТЕРИЙ БАРТЛЕТТА)
- 5.11. СОЧЕТАНИЕ РЕЗУЛЬТАТОВ НЕСКОЛЬКИХ КРИТЕРИЕВ
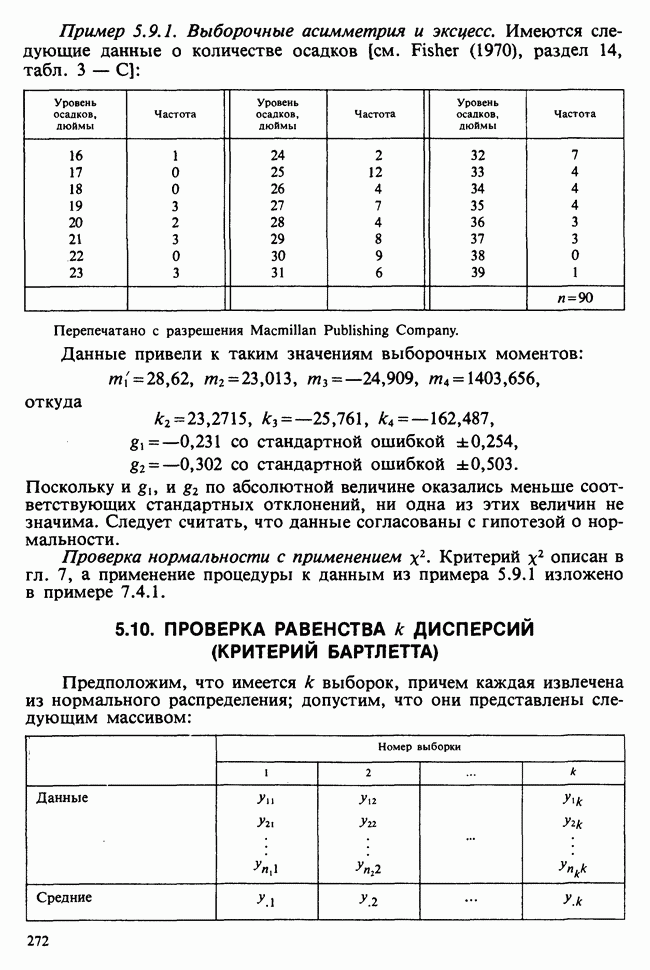
- 5.12. ТЕОРИЯ НЕЙМАНА—ПИРСОНА
- 5.12.2. ТЕОРИЯ НЕЙМАНА-ПИРСОНА ПРОВЕРКИ ГИПОТЕЗ
- Глава 6. МЕТОД МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
- 6.2. МЕТОД МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
- 6.2.2. ОЦЕНКА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
- 6.2.3. ОЦЕНКА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ: ИНТУИТИВНАЯ АРГУМЕНТАЦИЯ
- 6.2.4. ОЦЕНКА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ: ТИПЫ МАКСИМУМОВ
- 6.2.5. ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ МЕТОДА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ. СВОЙСТВА ФУНКЦИИ ПРАВДОПОДОБИЯ
- 6.2.6. ОЦЕНИВАНИЕ ФУНКЦИИ ПАРАМЕТРА «тетта». СВОЙСТВО ИНВАРИАНТНОСТИ
- 6.3. ПРИМЕРЫ ПРИМЕНЕНИЯ МЕТОДА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ В ОДНОПАРАМЕТРИЧЕСКОЙ СИТУАЦИИ
- 6.4. ПРИМЕРЫ О.М.П. В МНОГОПАРАМЕТРИЧЕСКИХ СЛУЧАЯХ
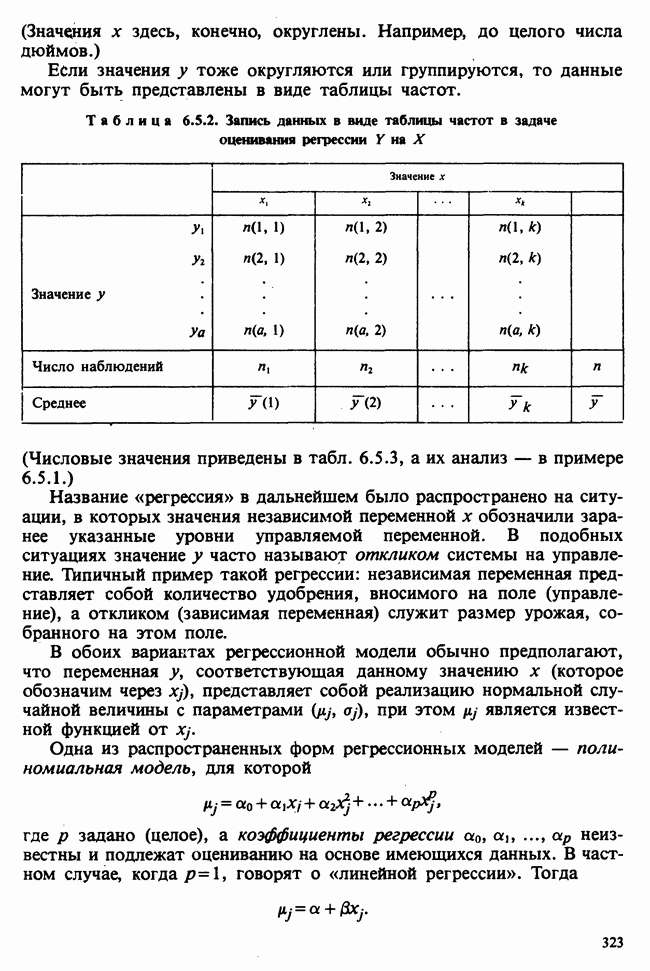
- 6.5. ОЦЕНКА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ КОЭФФИЦИЕНТОВ ЛИНЕЙНОЙ РЕГРЕССИИ
- 6.5.2. ОЦЕНКИ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ ДЛЯ ЛИНЕЙНОЙ РЕГРЕССИИ С ВЕСАМИ
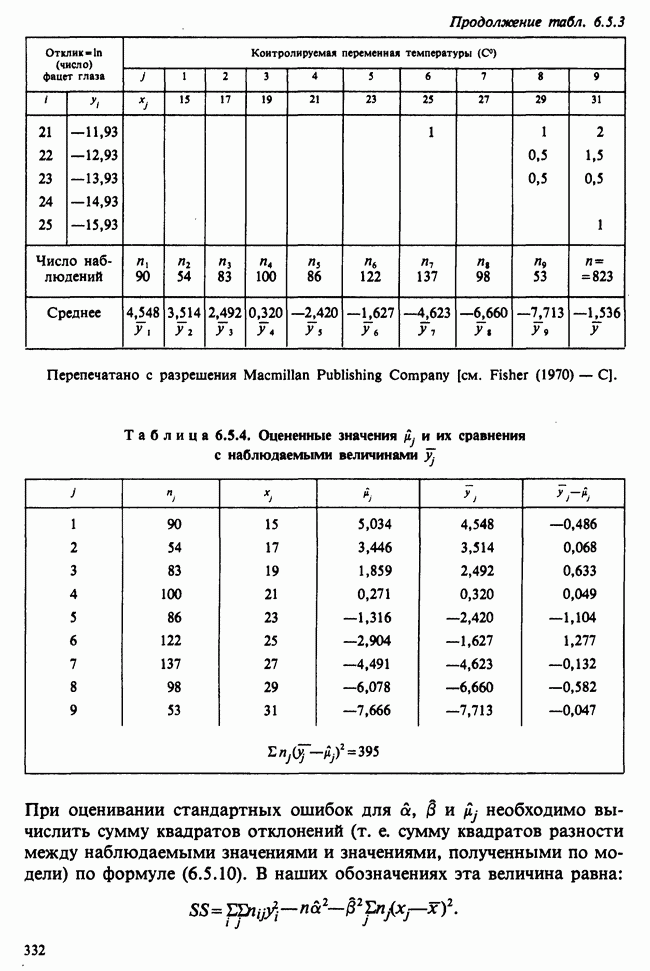
- 6.5.3. ЛИНЕЙНАЯ РЕГРЕССИЯ С ОДИНАКОВЫМИ ВЕСАМИ
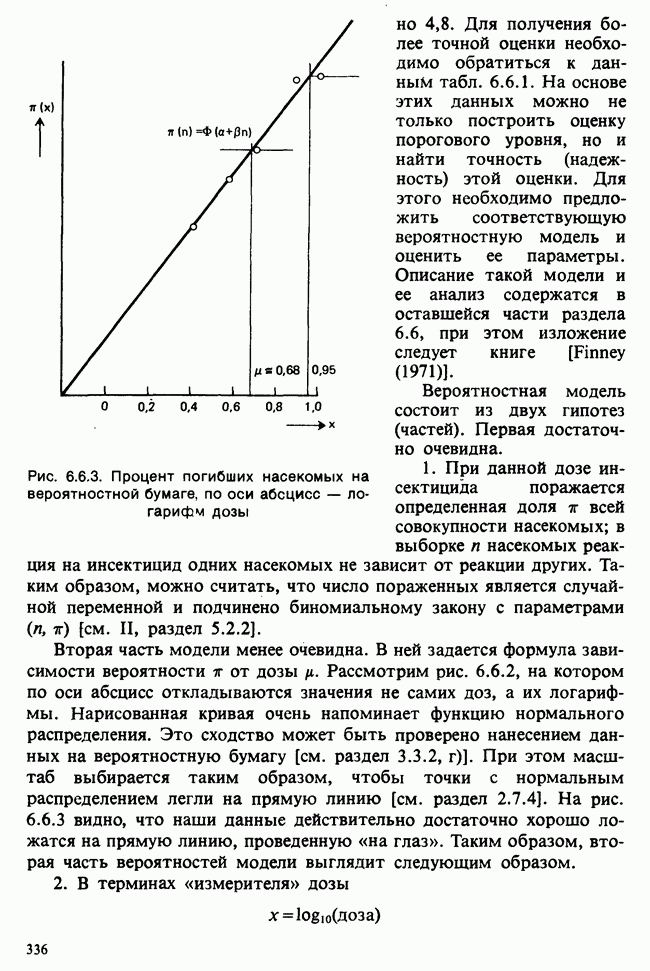
- 6.6. ОЦЕНИВАНИЕ ЗАВИСИМОСТИ ТОКСИЧНОСТИ ИНСЕКТИЦИДА ОТ УРОВНЯ ДОЗИРОВКИ
- 6.6.2. ВЕРОЯТНОСТНАЯ МОДЕЛЬ
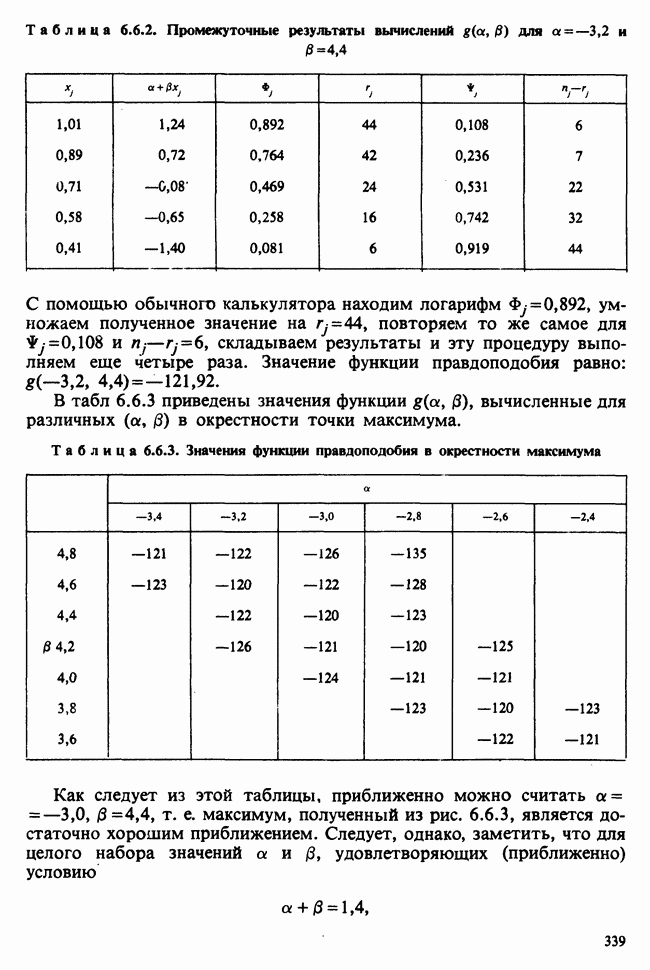
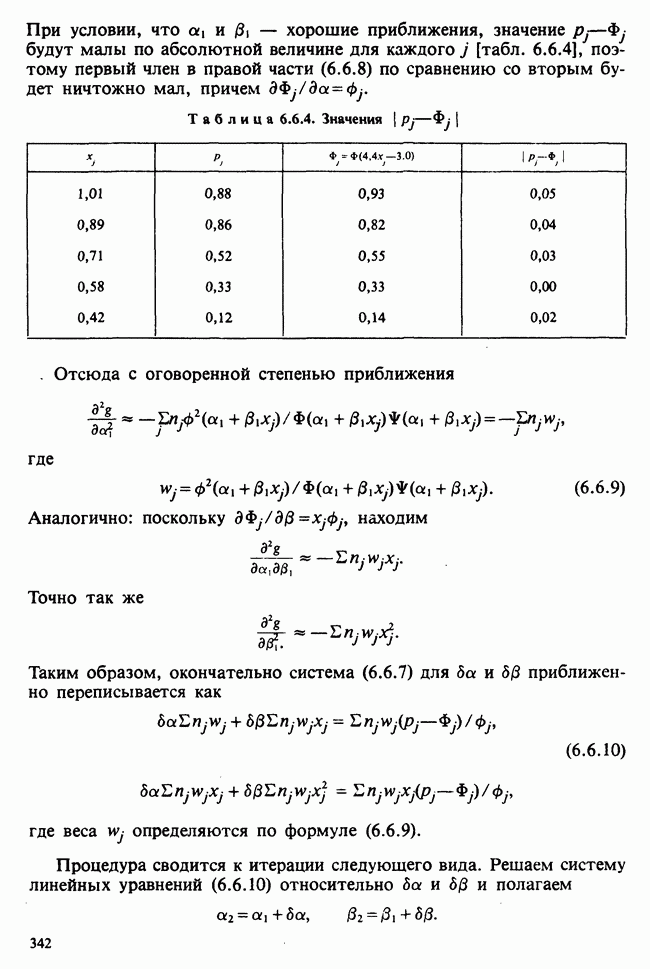
- 6.6.3. ИССЛЕДОВАНИЕ ПОВЕРХНОСТИ ФУНКЦИИ ПРАВДОПОДОБИЯ
- 6.6.4. ОЦЕНКА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
- 6.6.5. ТОЧНОСТЬ ОЦЕНОК
- 6.6.6. ДОЗА, НЕОБХОДИМАЯ ДЛЯ ЗАДАННОГО ЗНАЧЕНИЯ ОТКЛИКА
- 6.7. ОЦЕНКИ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ ПО ГРУППИРОВАННЫМ, ЦЕНЗУРИРОВАННЫМ И УСЕЧЕННЫМ ДАННЫМ
- 6.7.2. НЕПРЕРЫВНЫЕ ДАННЫЕ И ГРУППИРОВКА. ПОПРАВКА ШЕППАРДА
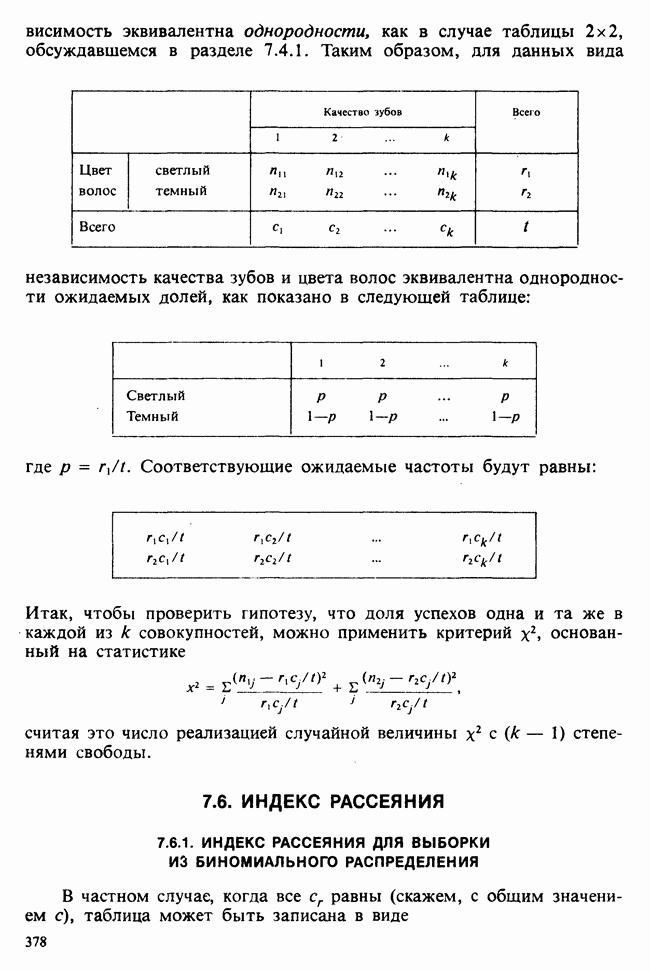
- ГЛАВА 7. СТАТИСТИКА ХИ-КВАДРАТ. КРИТЕРИИ СОГЛАСИЯ, НЕЗАВИСИМОСТИ И ОДНОРОДНОСТИ
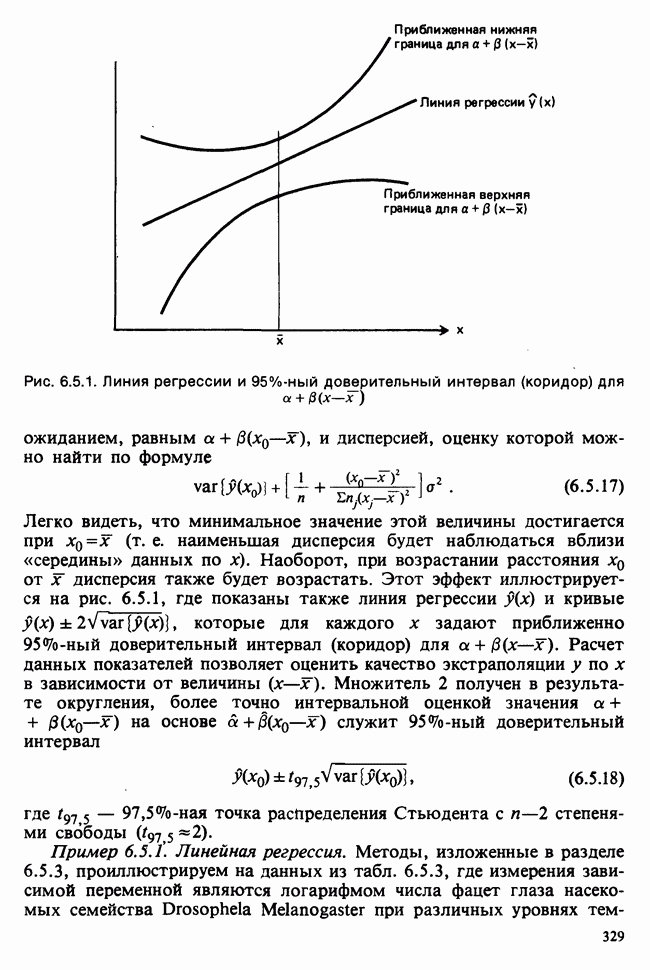
- 7.1.2. АДЕКВАТНОСТЬ ЛИНЕЙНОЙ РЕГРЕССИОННОЙ МОДЕЛИ
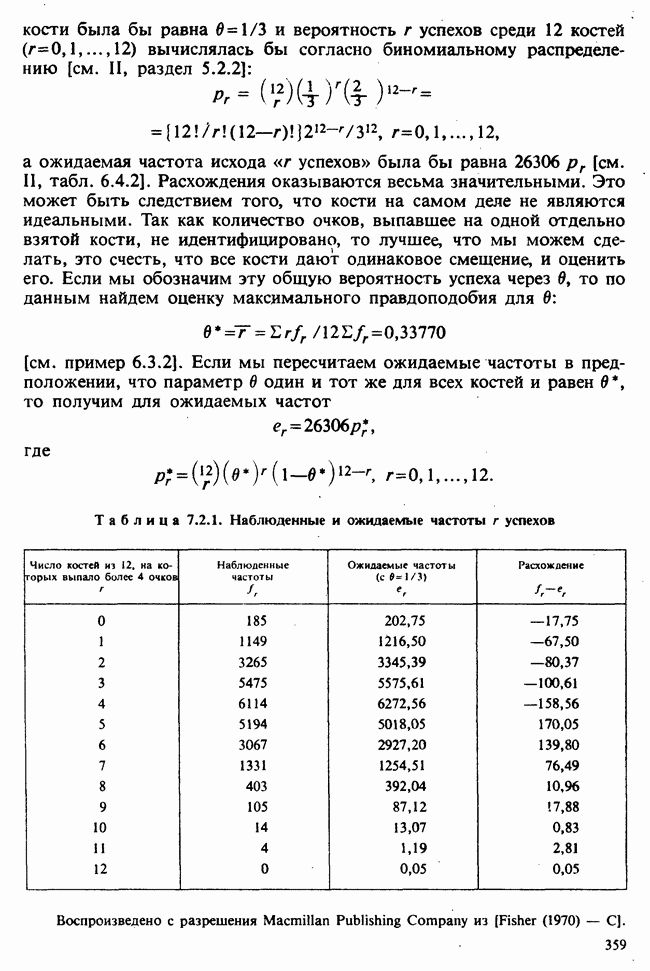
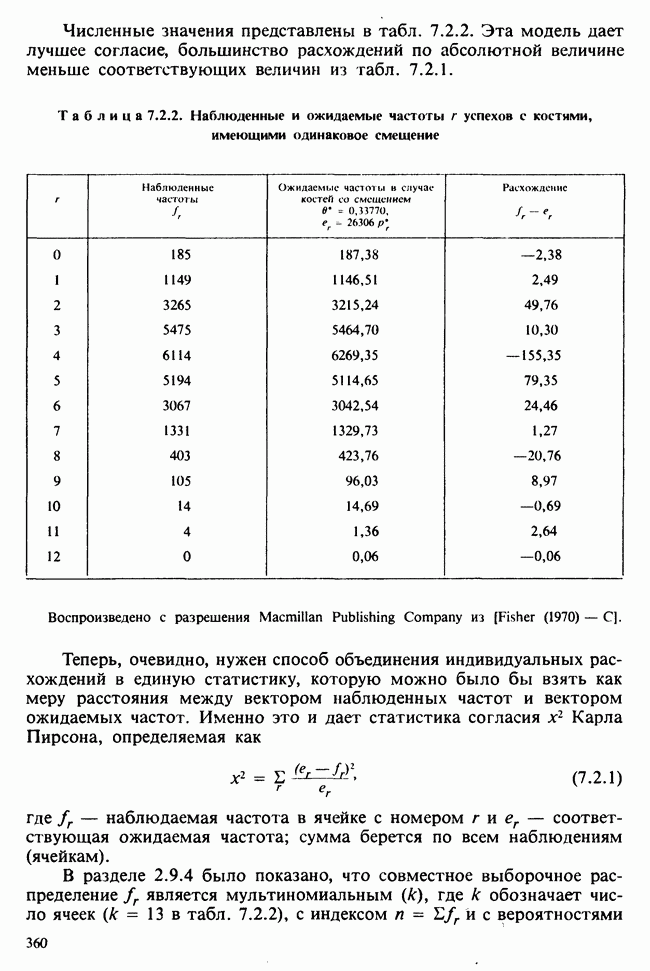
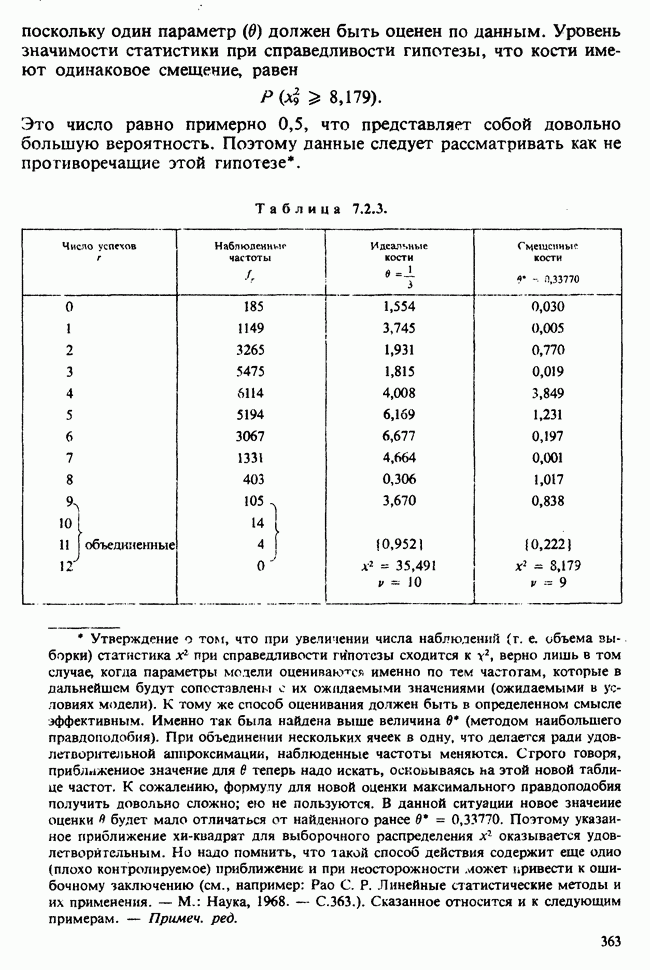
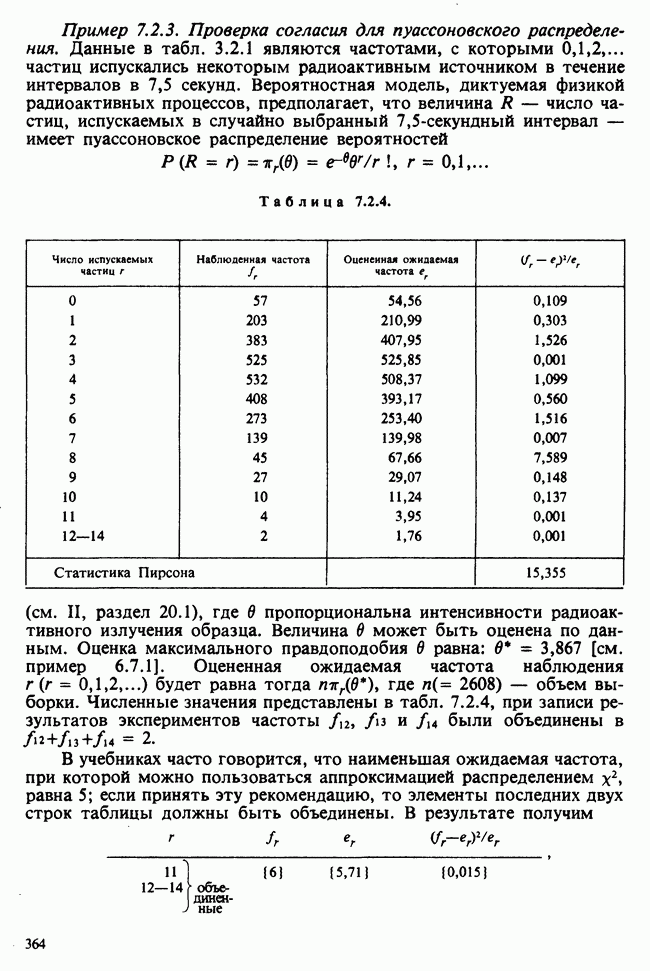
- 7.2. РАССТОЯНИЕ К. ПИРСОНА: КРИТЕРИЙ «хи-квадрат»
- 7.3. ОБЪЕДИНЕНИЕ ЯЧЕЕК С НИЗКИМИ ЧАСТОТАМИ. КРИТЕРИЙ У. КОКРЕНА
- 7.4. КРИТЕРИЙ «хи-квадрат» ДЛЯ НЕПРЕРЫВНЫХ РАСПРЕДЕЛЕНИЙ
- 7.5. ТАБЛИЦЫ ЧАСТОТ ПЕРЕКРЕСТНОЙ КЛАССИФИКАЦИИ (ТАБЛИЦЫ СОПРЯЖЕННОСТИ). КРИТЕРИИ НЕЗАВИСИМОСТИ
- 7.5.2. ТАБЛИЦЫ k x m
- 7.6. ИНДЕКС РАССЕЯНИЯ
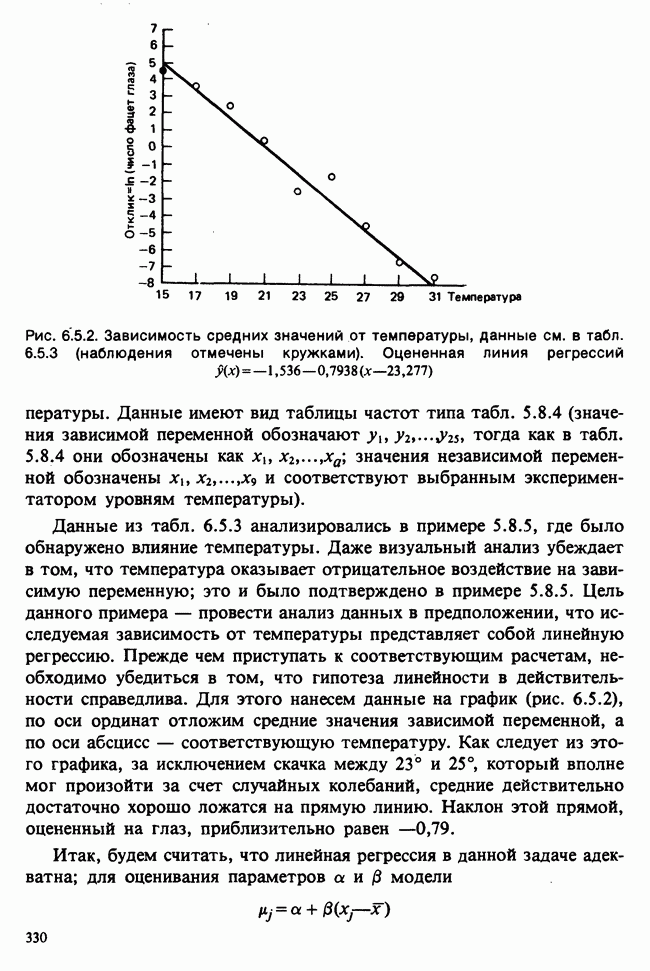
- 7.6.1. ИНДЕКС РАССЕЯНИЯ ДЛЯ ВЫБОРКИ ИЗ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ
- 7.6.2. ИНДЕКС РАССЕЯНИЯ ДЛЯ ПУАССОНОВСКИХ ВЫБОРОК
- Глава 8. ОЦЕНИВАНИЕ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ И ДИСПЕРСИОННЫЙ АНАЛИЗ
- 8.1. ОЦЕНИВАНИЕ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ ДЛЯ МОДЕЛЕЙ ОБЩЕГО ВИДА
- 8.2. ОЦЕНИВАНИЕ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ ДЛЯ ЛИНЕЙНЫХ МОДЕЛЕЙ ПОЛНОГО РАНГА. НОРМАЛЬНЫЕ УРАВНЕНИЯ. ТЕОРЕМА ГАУССА—МАРКОВА
- 8.2.1. ПРИМЕРЫ ОЦЕНИВАНИЯ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ
- 8.2.2. МАТРИЧНОЕ ПРЕДСТАВЛЕНИЕ ЛИНЕЙНЫХ МОДЕЛЕЙ
- 8.2.3. СВОЙСТВА ОЦЕНОК МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ
- 8.2.4. ОСТАТКИ
- 8.2.5. ОРТОГОНАЛЬНЫЕ ПЛАНЫ И ОРТОГОНАЛЬНЫЕ ПОЛИНОМЫ
- 8.2.6. МОДИФИКАЦИИ ДЛЯ НЕРАВНОТОЧНЫХ НАБЛЮДЕНИЙ; ВЗВЕШЕННЫЙ МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
- 8.2.7. МОДИФИКАЦИИ ДЛЯ НЕ НЕЗАВИСИМЫХ НАБЛЮДЕНИЙ
- 8.3. ДИСПЕРСИОННЫЙ АНАЛИЗ И ПРОВЕРКА ГИПОТЕЗ ДЛЯ ПЛАНОВ ПОЛНОГО РАНГА
- 8.3.2. ДОВЕРИТЕЛЬНЫЕ ОБЛАСТИ
- 8.2 3. ПРОВЕРКА ГИПОТЕЗ
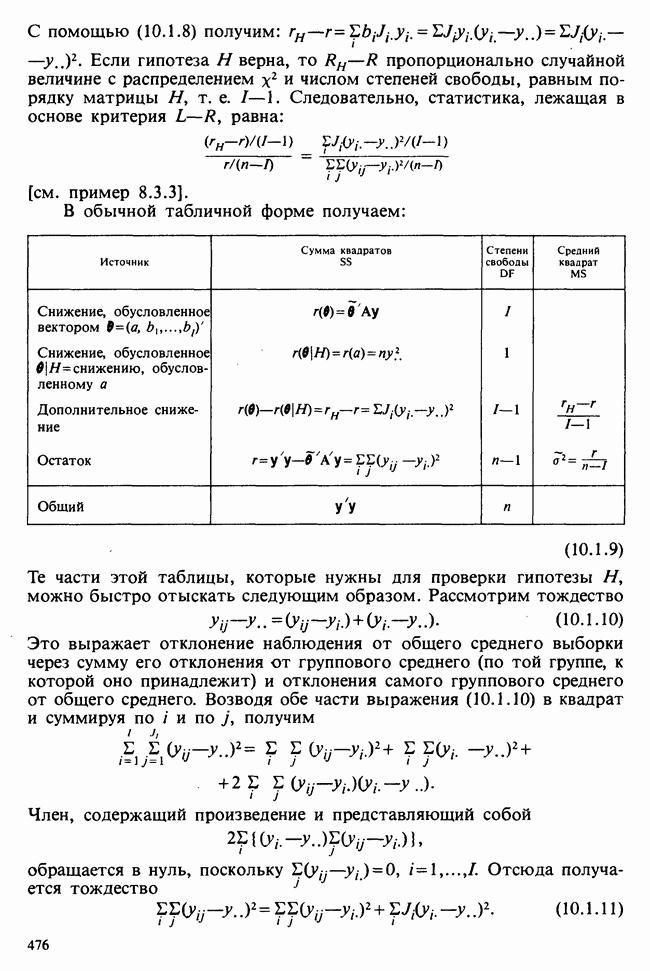
- 8.3.4. ОСНОВНЫЕ ТОЖДЕСТВА
- 8.3.5. ПРОВЕРКИ ГИПОТЕЗ В ОРТОГОНАЛЬНЫХ ПЛАНАХ
- 8.3.6. ПРОВЕРКА ГИПОТЕЗ ДЛЯ НЕ ОРТОГОНАЛЬНЫХ ПЛАНОВ
- 8.3.7 ГРУППОВАЯ ОРТОГОНАЛЬНОСТЬ
- 8.3.8. ОБЩИЕ ЛИНЕЙНЫЕ ГИПОТЕЗЫ
- Глава 9. ПЛАНИРОВАНИЕ СРАВНИТЕЛЬНЫХ ЭКСПЕРИМЕНТОВ
- 9.3. БОЛЕЕ СЛОЖНЫЙ ПРИМЕР: ЭКСПЕРИМЕНТ ДАРВИНА
- 9.4. ПОЛНОСТЬЮ РАНДОМИЗИРОВАННЫЕ БЛОЧНЫЕ ПЛАНЫ
- 9.5. ОБРАБОТКИ НА ОДНОМ И НА НЕСКОЛЬКИХ УРОВНЯХ
- 9.6. ПОТРЕБНОСТЬ В РАЗРАБОТКАХ ПО УМЕНЬШЕНИЮ РАЗМЕРОВ БЛОКОВ
- 9.7. СБАЛАНСИРОВАННЫЕ НЕПОЛНЫЕ БЛОКИ ДЛЯ СРАВНЕНИЯ ОДНОУРОВНЕВЫХ ОБРАБОТОК
- 9.8. ПОЛНЫЙ ФАКТОРНЫЙ ПЛАН
- 9.8.2. ГЛАВНЫЕ ЭФФЕКТЫ И ВЗАИМОДЕЙСТВИЯ: ТРИ ФАКТОРА НА ДВУХ УРОВНЯХ
- 9.8.3. ГЛАВНЫЕ ЭФФЕКТЫ И ВЗАИМОДЕЙСТВИЯ В ПЛАНЕ 2^j
- 9.9. НЕПОЛНЫЕ БЛОКИ: СМЕШИВАНИЕ
- 9.10. ЧАСТИЧНОЕ СМЕШИВАНИЕ
- 9.11. ФАКТОРЫ НА ТРЕХ И БОЛЕЕ УРОВНЯХ
- 9.11.2. ГРЕКО-ЛАТИНСКИЙ КВАДРАТ
- Глава 10. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ И АНАЛИЗ СТАТИСТИЧЕСКИХ ЭКСПЕРИМЕНТОВ: ВЫРОЖДЕННЫЕ МОДЕЛИ, МНОЖЕСТВЕННЫЕ КРИТЕРИИ
- 10.1.2. ОЦЕНИВАНИЕ. ФУНКЦИИ, ДОПУСКАЮЩИЕ ОЦЕНКУ
- 10.1.3. ПРОВЕРКА ГИПОТЕЗ
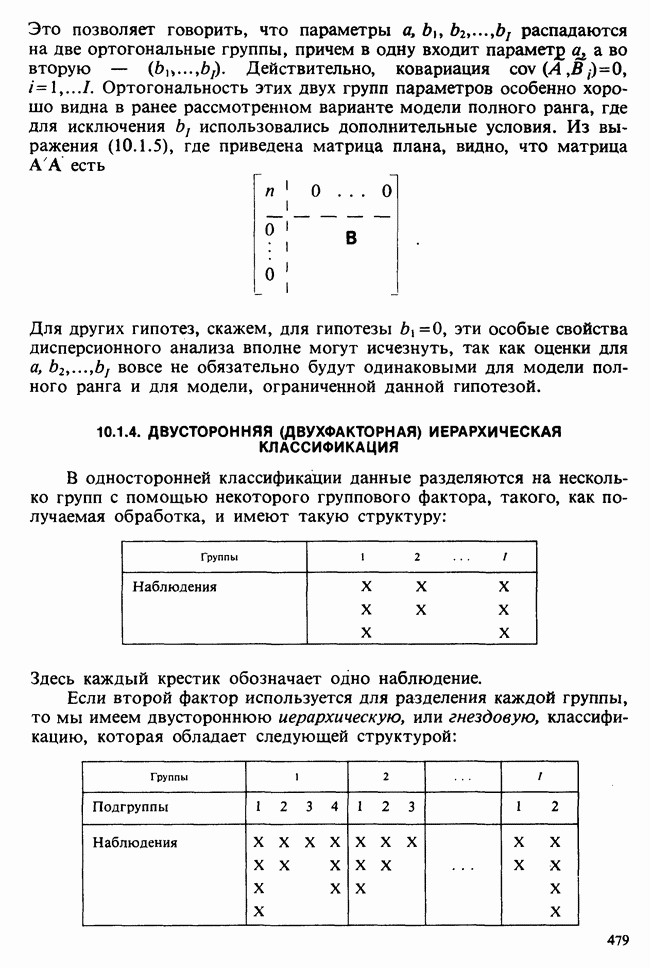
- 10.1.4. ДВУСТОРОННЯЯ (ДВУХФАКТОРНАЯ) ИЕРАРХИЧЕСКАЯ КЛАССИФИКАЦИЯ
- 10.1.5. ДВУСТОРОННЯЯ (ДВУХФАКТОРНАЯ) ПЕРЕКРЕСТНАЯ КЛАССИФИКАЦИЯ
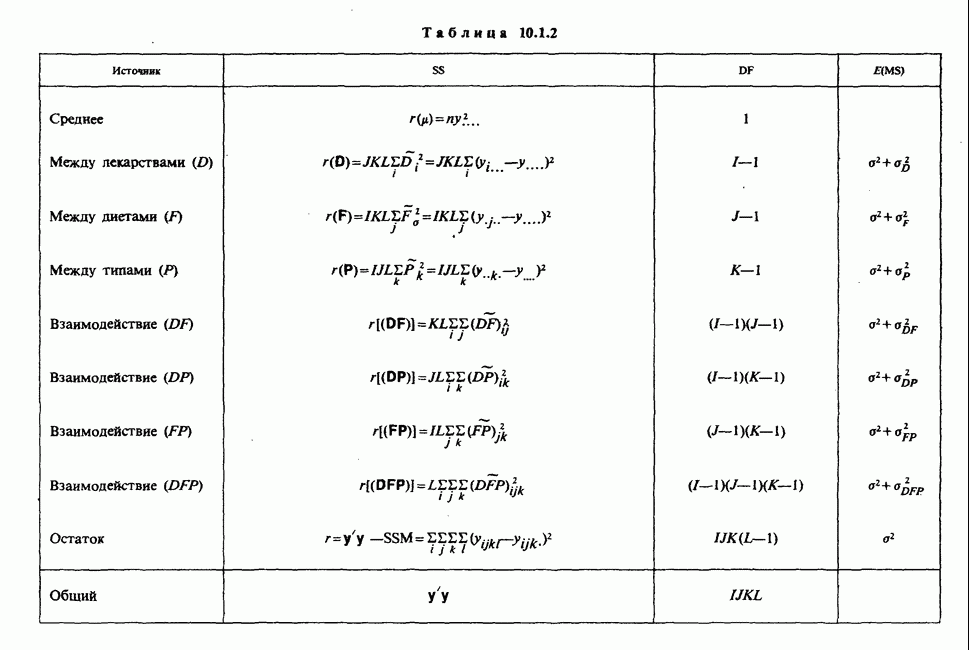
- 10.1.6. КЛАССИФИКАЦИИ БОЛЕЕ ВЫСОКОГО ПОРЯДКА
- 10.1.7. КОВАРИАЦИОННЫЙ АНАЛИЗ
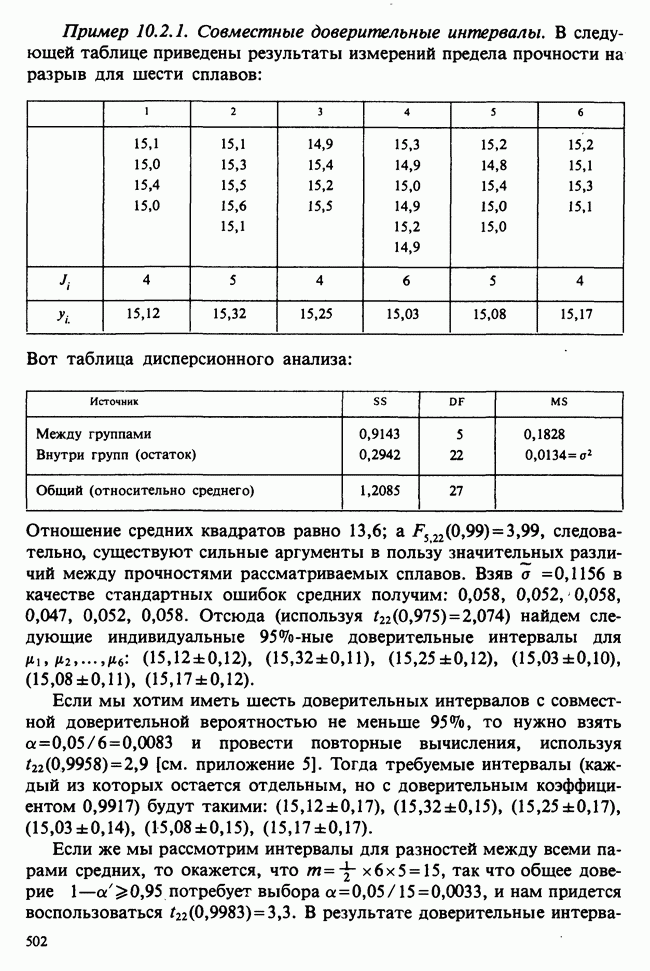
- 10.2. МНОЖЕСТВЕННЫЕ КРИТЕРИИ И СРАВНЕНИЯ
- 10.2.2. КОМБИНАЦИИ ПРОВЕРОК И ОБЩИЙ РАЗМЕР КРИТЕРИЯ
- 10.2.3. МНОЖЕСТВЕННЫЕ СРАВНЕНИЯ
- 10.3. ПРЕДПОЛОЖЕНИЯ ОТНОСИТЕЛЬНО ОШИБОК
- 10.3.2. АНАЛИЗ ОСТАТКОВ