| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
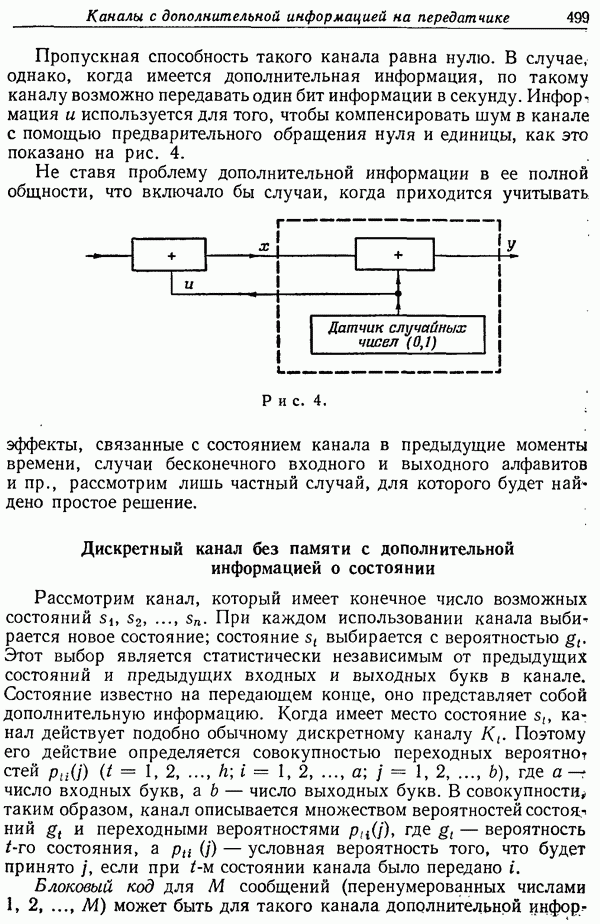
Пропускная способность канала при нулевой ошибке
Будем говорить, что в дискретном канале две входные буквы являются смежными, если существует некоторая выходная буква, которая может быть результатом передачи любой из них. Так  и
и  смежные, если существует некоторое
смежные, если существует некоторое  такое, что
такое, что  не
не
равны нулю. На рис. 1 буквы а и с являются смежными, тогда как  не являются смежными.
не являются смежными.
Если все входные буквы являются смежными друг с другом, то любой код, содержащий больше одного слова, имеет вероятность ошибки на приемном конце, отличную от нуля. Действительно, вероятность ошибки при декодировании слов удовлетворяет неравенству

где  — наименьшая (не равная нулю)
— наименьшая (не равная нулю)  вероятностей
вероятностей  — длина кода,
— длина кода,  число слов в коде. Для того чтобы доказать это, заметим, что любые два слова имеют некоторое общее возможное выходное слово, а именно то слово, которое состоит из последовательности выходных букв, совпадающих при побуквенном сопоставлении двух входных слов. Каждое из двух входных слов имеет вероятность произвести общее выходное слово, по крайней мере равную
число слов в коде. Для того чтобы доказать это, заметим, что любые два слова имеют некоторое общее возможное выходное слово, а именно то слово, которое состоит из последовательности выходных букв, совпадающих при побуквенном сопоставлении двух входных слов. Каждое из двух входных слов имеет вероятность произвести общее выходное слово, по крайней мере равную  При кодировании каждое из двух входных слов будет появляться в среднем
При кодировании каждое из двух входных слов будет появляться в среднем  долю раз и будет выдаваться общий выход в среднем
долю раз и будет выдаваться общий выход в среднем  долю раз. Этот выход может быть декодирован лишь единственным образом. Следовательно, по меньшей мере одна из этих ситуаций приводит к ошибке. Эта ошибка, равная
долю раз. Этот выход может быть декодирован лишь единственным образом. Следовательно, по меньшей мере одна из этих ситуаций приводит к ошибке. Эта ошибка, равная  приписывается данному слову и из оставшихся
приписывается данному слову и из оставшихся  кодовых слов выбирается другая пара. Ошибка величины
кодовых слов выбирается другая пара. Ошибка величины  приписывается подобным же образом одному из этих слов. Эти события оказываются непересекающимися. Продолжая этот процесс далее, получим для общей вероятности ошибки величину, по крайней мере равную
приписывается подобным же образом одному из этих слов. Эти события оказываются непересекающимися. Продолжая этот процесс далее, получим для общей вероятности ошибки величину, по крайней мере равную  .
.
Если условие, что каждая входная буква является смежной со всеми другими буквами, не выполняется, то возможно с положительной скоростью вести передачу при нулевой вероятности ошибки. Наименьшая верхняя граница всех скоростей, которые могут быть достигнуты при нулевой вероятности ошибки, будет называться пропускной способностью канала при нулевой ошибке и обозначаться через  Пусть
Пусть  — наибольшее число слов в коде длины
— наибольшее число слов в коде длины  никакие два слова которого не являются смежными; тогда
никакие два слова которого не являются смежными; тогда  есть верхняя граница чисел
есть верхняя граница чисел  когда значение
когда значение  пробегает по всем положительным целым числам.
пробегает по всем положительным целым числам.
Можно ожидать, что  будет равна
будет равна  т. е., что если выбрать наибольшее возможное множество несмежных букв и составить из них все возможные последовательности длины
т. е., что если выбрать наибольшее возможное множество несмежных букв и составить из них все возможные последовательности длины  то получится
то получится
наилучший код длины  свободный от ошибок. В общем случае это утверждение не верно, хотя оно и справедливо во многих случаях, особенно при малом числе входных букв. Первое отступление от этого правила происходит в случае пяти входных букв в канале, изображенном на рис. 2. В этом канале возможно выбрать по крайней мере две несмежные буквы, например 0 и 2. Используя составленные из них последовательности 00, 02, 20 и 22, получаем четыре слова в коде длины два. Возможно, однако, сконструировать код длины два из пяти попарно несмежных элементов 00, 12, 24, 31. 43.
свободный от ошибок. В общем случае это утверждение не верно, хотя оно и справедливо во многих случаях, особенно при малом числе входных букв. Первое отступление от этого правила происходит в случае пяти входных букв в канале, изображенном на рис. 2. В этом канале возможно выбрать по крайней мере две несмежные буквы, например 0 и 2. Используя составленные из них последовательности 00, 02, 20 и 22, получаем четыре слова в коде длины два. Возможно, однако, сконструировать код длины два из пяти попарно несмежных элементов 00, 12, 24, 31. 43.

Рис. 2.

Рис. 3.
Легко проверить, что никакие две из этих комбинаций не являются смежными. Таким образом,  для этого канала, самое меньшее, равна
для этого канала, самое меньшее, равна 
В настоящее время не найден метод определения  в случае произвольного дискретного канала. Отыскание этого метода предлагается в качестве интересной нерешенной задачи теории кодирования. Ниже будет получен ряд результатов, которые дают возможность определить
в случае произвольного дискретного канала. Отыскание этого метода предлагается в качестве интересной нерешенной задачи теории кодирования. Ниже будет получен ряд результатов, которые дают возможность определить  во многих частных случаях. Например, определим
во многих частных случаях. Например, определим  для всех каналов с пятью и меньшим числом входных букв. Единственное исключение составит канал, изображенный на рис. 2 (или каналы, эквивалентные ему по структуре смежности). Также получим некоторые общие неравенства, позволяющие в большинстве случаев весьма точно оценить
для всех каналов с пятью и меньшим числом входных букв. Единственное исключение составит канал, изображенный на рис. 2 (или каналы, эквивалентные ему по структуре смежности). Также получим некоторые общие неравенства, позволяющие в большинстве случаев весьма точно оценить 
Можно заметить прежде всего, что величина  зависит только от того, какие входные буквы смежны со всеми остальными входными буквами. Для произвольного канала определим следующим
зависит только от того, какие входные буквы смежны со всеми остальными входными буквами. Для произвольного канала определим следующим
образом матрицу смежности 

Предположим, что два канала имеют (может быть, после перенумерации входных букв одного из них) одну и ту же матрицу смежности. Тогда очевидно, что код, дающий нулевую ошибку в одном из каналов, будет кодом, дающим нулевую ошибку и для другого канала. Поэтому пропускная способность при нулевой ошибке  одного из каналов будет точно так же приложима и к другому каналу.
одного из каналов будет точно так же приложима и к другому каналу.
Структура смежности, отраженная в матрице смежности, может быть также представлена в виде линейного графа. Построим граф с вершинами по числу входных букв и соединим две различные вершины линией или ребром графа, если соответствующие им входные буквы являются смежными. На рис. 3 показаны два примера, соответствующие каналам, изображенным на рис. 1 и 2.
Теорема 1. Пропускная способность дискретного канала без памяти при нулевой ошибке  ограничена неравенствами
ограничена неравенствами

Здесь С — пропускная способность любого канала, имеющего переходные вероятности  и матрицу смежности
и матрицу смежности 
Оценка сверху совершенно очевидна. Пропускная способность при нулевой ошибке меньше или равна обычной пропускной способности любого канала с той же самой матрицей смежности, так как первая требует коды с нулевой вероятностью ошибки, тогда как вторая — только коды с вероятностью ошибки, стремящейся к нулю. Минимизируя пропускную способность варьированием  найдем наименьшую верхнюю границу, которую можно достичь на основании этих соображений. Так как пропускная способность является непрерывной функцией от
найдем наименьшую верхнюю границу, которую можно достичь на основании этих соображений. Так как пропускная способность является непрерывной функцией от  в замкнутой области, определяемой
в замкнутой области, определяемой  то можно писать
то можно писать  вместо наибольшей нижней грани.
вместо наибольшей нижней грани.
Стоит заметить, что хотя существует бесконечное число каналов с одной и той же матрицей смежности, при выполнении минимизации необходимо рассматривать только некоторый особый канал. Этот единственный особый канал получается следующим образом из матрицы смежности. Определим выходную букву  с отличными от
с отличными от
нуля  в случае, когда для пары
в случае, когда для пары  величина
величина  Далее, если существуют какие-либо входные буквы, скажем
Далее, если существуют какие-либо входные буквы, скажем  , не смежные друг с другом, определим выходную букву, например,
, не смежные друг с другом, определим выходную букву, например,  с отличными от нуля
с отличными от нуля  На графе смежности это соответствует полному подграфу с тремя вершинами. После этого подмножествам четырех букв, или полному подграфу с четырьмя вершинами, скажем
На графе смежности это соответствует полному подграфу с тремя вершинами. После этого подмножествам четырех букв, или полному подграфу с четырьмя вершинами, скажем  сопоставим выходную букву, которая будет связана с каждой из них, и т. д. Очевидно, что любой канал с той же самой матрицей смежности отличается от только что описанного числом выходных символов для некоторой пары, тройки и т. д. смежных входных букв. В случае если в канале имеется более чем один выходной символ для подмножества смежных входных букв, его пропускная способность лишь уменьшается при идентификации этих символов. Если некоторый канал не содержит символа, скажем для тройки смежных входных букв
сопоставим выходную букву, которая будет связана с каждой из них, и т. д. Очевидно, что любой канал с той же самой матрицей смежности отличается от только что описанного числом выходных символов для некоторой пары, тройки и т. д. смежных входных букв. В случае если в канале имеется более чем один выходной символ для подмножества смежных входных букв, его пропускная способность лишь уменьшается при идентификации этих символов. Если некоторый канал не содержит символа, скажем для тройки смежных входных букв  , то это будет специальный случай нашего канонического канала, в котором имеется выходная буква
, то это будет специальный случай нашего канонического канала, в котором имеется выходная буква  для этой тройки, в то время как
для этой тройки, в то время как  равны нулю.
равны нулю.
Докажем теперь справедливость оценки снизу. Воспользуемся методом построения случайных кодов, основанных на вероятностях  для букв. Последние будут выбраны так, чтобы минимизировать квадратичную форму
для букв. Последние будут выбраны так, чтобы минимизировать квадратичную форму  Построим ансамбль кодов, каждый из которых состоит из М слов, содержащих по
Построим ансамбль кодов, каждый из которых состоит из М слов, содержащих по  букв. Слова в коде выбираются следующим стохастическим методом. Любая буква
букв. Слова в коде выбираются следующим стохастическим методом. Любая буква  в любом слове выбирается независимо от всех остальных букв и с вероятностью
в любом слове выбирается независимо от всех остальных букв и с вероятностью  Вычислим теперь в этом ансамбле вероятность того, что какое-либо выбранное слово не является смежным ни с каким другим словом кода. Вероятность того, что первая буква первого слова не смежна с первой буквой второго слова, равна
Вычислим теперь в этом ансамбле вероятность того, что какое-либо выбранное слово не является смежным ни с каким другим словом кода. Вероятность того, что первая буква первого слова не смежна с первой буквой второго слова, равна  так как здесь случаи смежности суммируются с коэффициентом 1, а случаи несмежности с коэффициентом 0. Вероятность того, что два слова смежны по всем буквам и, следовательно, смежны как слова, равна
так как здесь случаи смежности суммируются с коэффициентом 1, а случаи несмежности с коэффициентом 0. Вероятность того, что два слова смежны по всем буквам и, следовательно, смежны как слова, равна  . Это значит, что вероятность несмежности равна
. Это значит, что вероятность несмежности равна  Вероятность того, что все
Вероятность того, что все  других слов в коде не смежны данному слову в силу их независимого выбора, равна
других слов в коде не смежны данному слову в силу их независимого выбора, равна

Согласно хорошо известному неравенству, эта вероятность больше, чем  что в свою очередь больше, чем
что в свою очередь больше, чем
 Если положить
Если положить  то, выбирая
то, выбирая  достаточно малым, получим скорость, сколь угодно близкую к
достаточно малым, получим скорость, сколь угодно близкую к  Далее, если
Далее, если  уже выбрано, можно, выбирая
уже выбрано, можно, выбирая  достаточно большим, сделать
достаточно большим, сделать  сколь угодно малым, например меньшим
сколь угодно малым, например меньшим  . В ансамбле кодов вероятность того, что какое-либо частное слово смежно с любым другим словом в собственном коде, теперь меньше
. В ансамбле кодов вероятность того, что какое-либо частное слово смежно с любым другим словом в собственном коде, теперь меньше  Это значит, что в ансамбле существуют коды, для которых отношение числа таких нежелательных слов к их общему числу в коде меньше или равно
Это значит, что в ансамбле существуют коды, для которых отношение числа таких нежелательных слов к их общему числу в коде меньше или равно  . В противном случае среднее по ансамблю было бы больше. Выберем такой код и вычеркнем из него слова, обладающие этим нежелательным свойством. Это уменьшит нашу скорость в худшем случае лишь на
. В противном случае среднее по ансамблю было бы больше. Выберем такой код и вычеркнем из него слова, обладающие этим нежелательным свойством. Это уменьшит нашу скорость в худшем случае лишь на  Так как
Так как  произвольно малы, получились свободные от ошибок коды для которых скорость сколь угодно близка к
произвольно малы, получились свободные от ошибок коды для которых скорость сколь угодно близка к  как и утверждается в теореме.
как и утверждается в теореме. 
В связи с оценкой сверху, данной в теореме 1, следующий далее результат полезен для вычисления минимальной С. Он интересен сам по себе и, кроме того, окажется полезным в дальнейшем при исследовании каналов, имеющих линию обратной связи.
Теорема 2. Для дискретного канала без памяти с переходными вероятностями  и вероятностями входных букв
и вероятностями входных букв  следующие три утверждения являются эквивалентными.
следующие три утверждения являются эквивалентными.
1) Скорость передачи

стационарна при вариации  всем не равным нулю
всем не равным нулю  связанным условием
связанным условием  и при вариации по таким
и при вариации по таким  для которых
для которых 
2) Взаимная информация между парой вход — выход  является постоянной
является постоянной  для всех пар
для всех пар  с неравными нулю вероятностями (т. е. для пар, у которых
с неравными нулю вероятностями (т. е. для пар, у которых 
3) Функция  является функцией
является функцией  для всех
для всех  для которых
для которых  а сумма
а сумма  есть постоянная, не
есть постоянная, не
зависящая от  где
где  множество входных букв, которые могут быть приняты как выходная буква
множество входных букв, которые могут быть приняты как выходная буква  с ненулевой вероятностью. При этом
с ненулевой вероятностью. При этом 
Величины  соответствующие максимуму и минимуму пропускной способности при вариации
соответствующие максимуму и минимуму пропускной способности при вариации  (при вариации, однако, предполагается, что все
(при вариации, однако, предполагается, что все  равные нулю, остаются равными нулю), удовлетворяют всем трем утверждениям теоремы.
равные нулю, остаются равными нулю), удовлетворяют всем трем утверждениям теоремы.
Сначала покажем, что эквивалентными являются утверждения 1) и 2), а затем покажем эквивалентность утверждений 2) и 3). В (конечной) области, определяемой соотношениями  функция
функция  является ограниченной и непрерывной функцией своих аргументов
является ограниченной и непрерывной функцией своих аргументов  Функция
Функция  обладает конечными частными производными по любой
обладает конечными частными производными по любой  . В самом деле, как легко подсчитать
. В самом деле, как легко подсчитать

Необходимое и достаточное условие того, что  постоянна при малых изменениях неотрицательной вероятности
постоянна при малых изменениях неотрицательной вероятности  подчиняющейся приведенным условиям, состоит в том, чтобы
подчиняющейся приведенным условиям, состоит в том, чтобы

при всех  и
и  для которых
для которых  не равны нулю. Это условие требует, чтобы
не равны нулю. Это условие требует, чтобы

Пусть  — вероятность выходной буквы У, тогда последнее равенство эквивалентно равенству
— вероятность выходной буквы У, тогда последнее равенство эквивалентно равенству

Иначе говоря,  не зависит от
не зависит от  и является функцией
и является функцией  тогда, когда
тогда, когда  Эту функцию от
Эту функцию от  обозначим через
обозначим через  Таким образом,
Таким образом,

если равенство  не имеет места.
не имеет места.
Взяв теперь частную производную  по
по  получим
получим

Для того чтобы функция была стационарной при условии  требуется, чтобы
требуется, чтобы  Таким образом,
Таким образом,

Так как для  имеем
имеем  то последнее равенство переходит в
то последнее равенство переходит в

Таким образом,  не зависит от
не зависит от  и может быть записано как а. Следовательно,
и может быть записано как а. Следовательно,

всегда, когда 
Обратный результат легко получается с помощью обращение приведенного выше доказательства. Если

то с помощью простой подстановки в формулу для  получим
получим  Следовательно,
Следовательно,  стационарно при вариации
стационарно при вариации  подчиняющихся условию
подчиняющихся условию  Далее,
Далее,  , следовательно, вариация
, следовательно, вариация  обращается в нуль при
обращается в нуль при 
Теперь докажем, что из 2) вытекает утверждение 3). Предположим, что  всегда, когда
всегда, когда  Тогда
Тогда  является функцией
является функцией  при тех же самых условиях. Также, если
при тех же самых условиях. Также, если  является условной вероятностью
является условной вероятностью  при заданном
при заданном  то
то

Чтобы доказать, что из утверждения 3) вытекает утверждение  предположим, что
предположим, что

когда  Тогда
Тогда

Суммируя теперь равенства  и используя предположение из утверждения 3), состоящее в том, что
и используя предположение из утверждения 3), состоящее в том, что  получим
получим

так что  равно
равно  и не зависит от
и не зависит от  Следовательно,
Следовательно, 
Последнее утверждение теоремы, касающееся минимальной и максимальной пропускной способности при вариации по  следует из того факта, что
следует из того факта, что  в этих точках должна быть неизменна при вариации по всем ненулевым
в этих точках должна быть неизменна при вариации по всем ненулевым  Поэтому соответствующие
Поэтому соответствующие  удовлетворяют утверждению 1) теоремы.
удовлетворяют утверждению 1) теоремы.
В простых каналах для оценки  обычно более удобно применить какой-нибудь специальный прием вместо данных в теореме 1 неравенств, которые включают в себя процесс максимизации и минимизации. Наиболее примитивная оценка снизу, как упоминалось ранее, получается просто с помощью отыскания логарифма максимального числа несмежных входных букв.
обычно более удобно применить какой-нибудь специальный прием вместо данных в теореме 1 неравенств, которые включают в себя процесс максимизации и минимизации. Наиболее примитивная оценка снизу, как упоминалось ранее, получается просто с помощью отыскания логарифма максимального числа несмежных входных букв.
Весьма полезный аппарат для определения  который применим во многих случаях, может быть описан, если использовать понятие отображения, понижающего смежность. Под этим понимается преобразование некоторых букв в другие буквы,
который применим во многих случаях, может быть описан, если использовать понятие отображения, понижающего смежность. Под этим понимается преобразование некоторых букв в другие буквы,  обладающее тем свойством, что если
обладающее тем свойством, что если  и
и  несмежны в канале (или на графе), то а
несмежны в канале (или на графе), то а  также не будут смежными. Если имеется код, дающий нулевую ошибку, то можно применить такое отображение буква за буквой ко всему этому коду и получить некоторый новый код, который будет также безошибочным, ибо отображение не добавит смежности между буквами.
также не будут смежными. Если имеется код, дающий нулевую ошибку, то можно применить такое отображение буква за буквой ко всему этому коду и получить некоторый новый код, который будет также безошибочным, ибо отображение не добавит смежности между буквами.
Теорема 3. Если все входные буквы  могут быть преобразованы при помощи отображения
могут быть преобразованы при помощи отображения  понижающего смежность, в подмножество попарно несмежных букв, то пропускная способность
понижающего смежность, в подмножество попарно несмежных букв, то пропускная способность  канала при нулевой ошибке равна логарифму числа букв этого подмножества.
канала при нулевой ошибке равна логарифму числа букв этого подмножества.
Это верно, во-первых, потому, что, если составить всевозможные последовательности из этих букв, получится код, дающий нулевую ошибку при этой скорости передачи. И, во-вторых, любой код для канала, дающий нулевую ошибку, может быть отображен в код, использующий только эти буквы и содержащий, следовательно, по меньшей мере  несмежных слов.
несмежных слов.
Пропускная способность при нулевой ошибке или, более точно, эквивалентные числа входных букв для всех графов смежности

(кликните для просмотра скана)
вплоть до графов, содержащих пять вершин, показаны на рис. 4. Все они легко могут быть найдены методом теоремы 3. Исключение составляет лишь ранее упоминавшийся канал, изображенный на рис. 2, относительно которого известно только то, что его пропускная способность при нулевой ошибке находится в пределах

Нами были рассмотрены все графы с шестью вершинами. Их пропускные способности также могут быть найдены с помощью этой теоремы, за исключением четырех случаев. Эти четыре случая можно изложить в терминах пропускной способности, соответствующей рис. 2, так что этот случай является единственной существенно не разрешенной проблемой вплоть до графов с семью вершинами. Графы с семью вершинами полностью исследованы не были, однако в этом случае возникает по меньшей мере одна новая ситуация, являющаяся аналогом изображенной на рис. 2, но с семью входными буквами.
В качестве примера, иллюстрирующего то, как методом отображения, понижающего смежность, были вычислены величины  несколько графов на рис. 4 снабжены обозначениями, указывающими на соответствующее отображение. Правило состоит в следующем. Все узлы графа, обозначенные через а, отображаются в узел а, а узел а отображается сам в себя. Все узлы, обозначенные через
несколько графов на рис. 4 снабжены обозначениями, указывающими на соответствующее отображение. Правило состоит в следующем. Все узлы графа, обозначенные через а, отображаются в узел а, а узел а отображается сам в себя. Все узлы, обозначенные через  отображаются в узел
отображаются в узел  Все узлы, обозначенные через
Все узлы, обозначенные через  отображаются в узел у. Легко проверить, что указанные отображения не создают никаких новых смежностей и что точки
отображаются в узел у. Легко проверить, что указанные отображения не создают никаких новых смежностей и что точки  и у не являются смежными.
и у не являются смежными.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- СИМВОЛИЧЕСКИЙ АНАЛИЗ РЕЛЕЙНЫХ И ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- 2. Параллельно-последовательные двухполюсные схемы. Основные определения и постулаты
- 3. Многополюсные и не параллельно-последовательные схемы
- Преобразование треугольника в звезду и звезды в ячейку
- Функция сопротивления не параллельно-последовательной схемы
- Системы уравнений
- Реле и переключатели специальных типов
- 4. Синтез схем
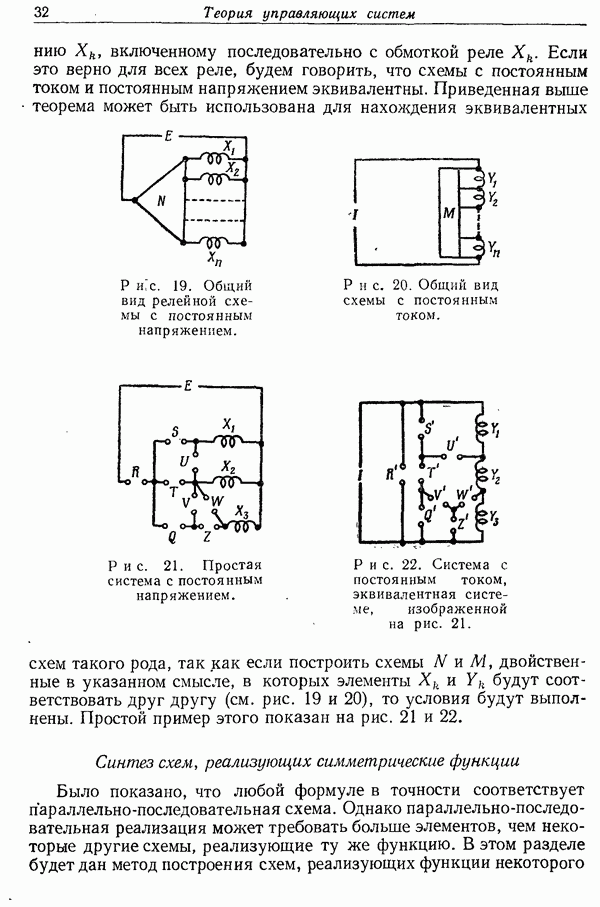
- Двойственные схемы
- Синтез схем, реализующих симметрические функции
- Составление уравнений по рабочим характеристикам
- 5. Примеры
- ЧИСЛО ДВУХПОЛЮСНЫХ ПАРАЛЛЕЛЬНО-ПОСЛЕДОВАТЕЛЬНЫХ СЕТЕЙ
- 1. Получение производящей функции
- 2. Численный подсчет
- 3. Асимптотическое поведение
- 4. Параллельно-последовательная реализация переключательных функций
- СИНТЕЗ ДВУХПОЛЮСНЫХ ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- 2. Основная теорема синтеза
- 3. Синтез схем для произвольных функций.
- Часть II. РАСПРЕДЕЛЕНИЕ НАГРУЗКИ МЕЖДУ РЕЛЕ
- 5. Разделительное дерево
- 6. Другие задачи распределения
- 7. Функция «мю»
- Часть III. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- 9. Частично симметрические функции
- ПРИМЕЧАНИЯ РЕДАКТОРА
- ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К ОБЪЕМУ ПАМЯТИ ТЕЛЕФОННОГО КОММУТАТОРА
- 2. Память, требуемая для S произвольных вызовов от N абонентов
- 3. Условие раздельной памяти
- 4. Связь с теорией информации
- НАДЕЖНЫЕ СХЕМЫ ИЗ НЕНАДЕЖНЫХ РЕЛЕ
- Идеализированные реле
- Общий метод повышения надежности
- Свойства функции h(p)
- Комбинация двух схем
- Оценки функции h'(p)
- Схемы заданной длины и ширины
- Оценки числа контактов в случае, когда реле уже достаточно надежны
- Сравнение с элементами фон Неймана
- Реле с неопределенным временем срабатывания
- Синтез надежных схем в целом
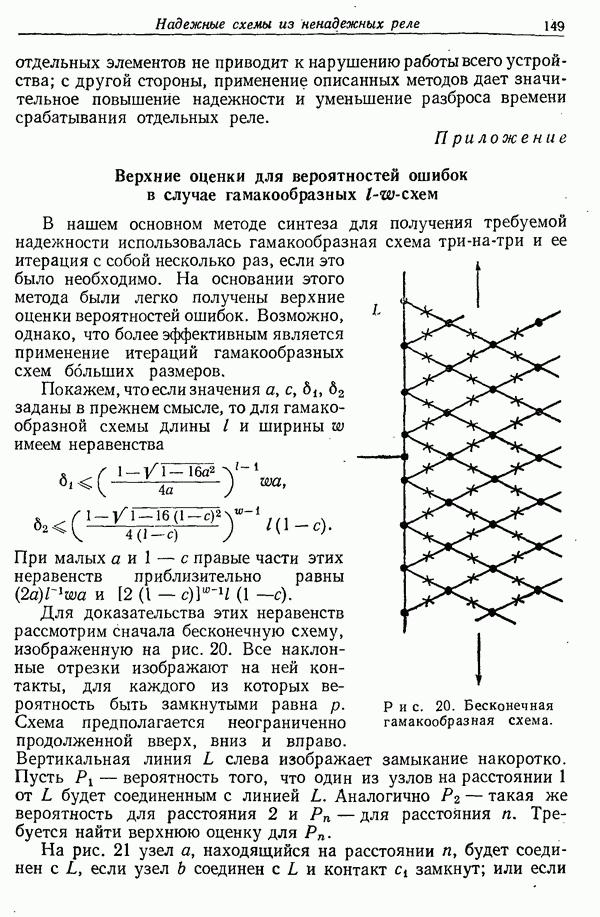
- Приложение. Верхние оценки для вероятностей ошибок в случае гамакообразных l-w-схем
- ИСПОЛЬЗОВАНИЕ МАШИНЫ ДЛЯ ПРОЕКТИРОВАНИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА И АВТОМАТЫ
- Машины Тьюринга
- Логические машины
- «Играющие машины»
- Обучаемые машины
- Самовоспроизводящиеся машины
- Обращение к читателю
- МАШИНА ДЛЯ ИГРЫ В ШАХМАТЫ
- СОСТАВЛЕНИЕ ПРОГРАММ ДЛЯ ИГРЫ В ШАХМАТЫ НА ВЫЧИСЛИТЕЛЬНОЙ МАШИНЕ
- 3. Приближенная оценочная функция
- 4. Стратегия, основанная на оценочной функции
- 5. Составление программы для универсальной вычислительной машины для реализации стратегии типа А
- 6. Улучшение стратегии
- 7. Изменения в игре и в стиле
- 8. Другой тип стратегии
- ПРИЛОЖЕНИЕ. ОЦЕНОЧНАЯ ФУНКЦИЯ ДЛЯ ШАХМАТ
- ИГРАЮЩИЕ МАШИНЫ
- СООБЩЕНИЕ О МАШИНЕ, РЕШАЮЩЕЙ ЛАБИРИНТНУЮ ЗАДАЧУ
- ВКЛАД ФОН НЕЙМАНА В ТЕОРИЮ АВТОМАТОВ
- МАТЕМАТИЧЕСКАЯ ТЕОРИЯ СВЯЗИ
- 1. ДИСКРЕТНЫЕ СИСТЕМЫ БЕЗ ШУМОВ
- 2. Дискретный источник сообщений
- 3. Последовательные приближения к английскому языку
- 4. Графическое представление марковского процесса
- 5. Эргодические и смешанные источники
- 6. Выбор, неопределенность и энтропия
- 7. Энтропия источника сообщений
- 8. Представление операций кодирования и декодирования
- 9. Основная теорема для канала без шума
- 10. Рассмотрение полученных результатов и примеры
- 11. Примеры
- II. ДИСКРЕТНЫЙ КАНАЛ С ШУМОМ
- 12. Надежность и пропускная способность канала
- 13. Основная теорема для дискретного канала с шумом
- 14. Рассмотрение полученных результатов
- 15. Пример дискретного канала и его пропускной способности
- 16. Пропускная способность канала в некоторых частных случаях
- 17. Пример эффективного кодирования
- III. ИНФОРМАЦИЯ ДЛЯ НЕПРЕРЫВНЫХ ВЕЛИЧИН
- 19. Ансамбли функций с ограниченной полосой частот
- 20. Энтропия непрерывного распределения
- 21. Энтропия ансамбля функций
- 22. Потеря энтропии в линейных фильтрах
- 23. Энтропия суммы двух ансамблей
- IV. НЕПРЕРЫВНЫЙ КАНАЛ
- 24. Пропускная способность непрерывного канала
- 25. Пропускная способность канала при ограничении средней мощности
- 26. Пропускная способность канала при ограничении пиковой мощности
- V. СКОРОСТЬ СОЗДАНИЯ СООБЩЕНИЙ ДЛЯ НЕПРЕРЫВНОГО ИСТОЧНИКА
- 28. Скорость создания сообщений источником при данной точности воспроизведения
- 29. Вычисление скорости создания сообщений
- Приложение 1. РОСТ ЧИСЛА БЛОКОВ СИМВОЛОВ ПРИ УСЛОВИЯХ, ОПИСЫВАЕМЫХ КОНЕЧНЫМ ЧИСЛОМ СОСТОЯНИЙ
- Приложение 2. ВЫВОД РАВЕНСТВА …
- Приложение 3. ТЕОРЕМА ОБ ЭРГОДИЧЕСКИХ ИСТОЧНИКАХ
- Приложение 4. МАКСИМИЗАЦИЯ СКОРОСТИ ДЛЯ СИСТЕМЫ ОГРАНИЧЕНИЯ
- Приложение 5
- Приложение 6
- Приложение 7
- ТЕОРИЯ СВЯЗИ В СЕКРЕТНЫХ СИСТЕМАХ
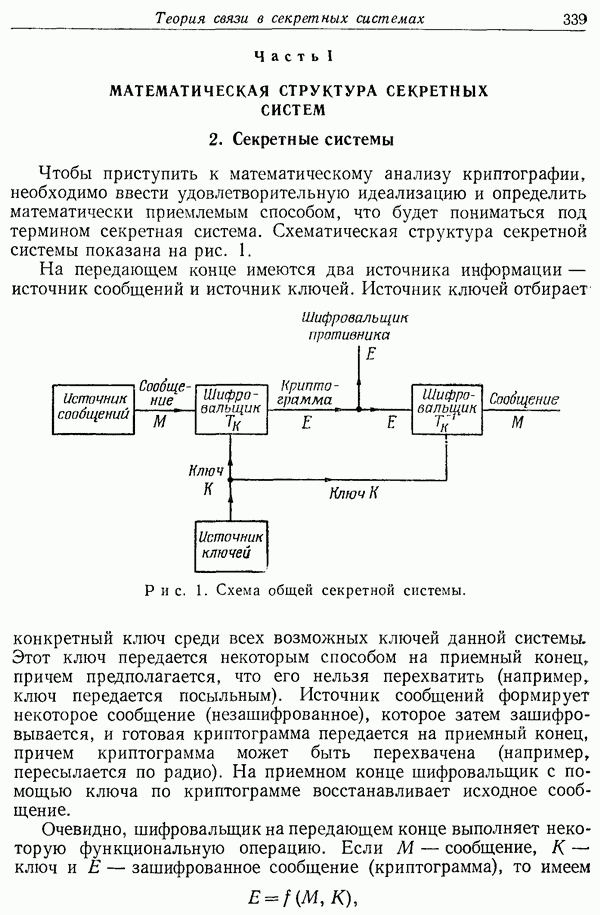
- Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ СИСТЕМ
- 3. Способы изображения систем
- 4. Примеры секретных систем
- 5. Оценка секретных систем
- 6. Алгебра секретных систем
- 7. Чистые и смешанные шифры
- 8. Подобные системы
- Часть II. ТЕОРЕТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 10. Совершенная секретность
- 11. Ненадежность
- 12. Свойства ненадежности
- 13. Ненадежность простой подстановки для языка с двухбуквенным алфавитом
- 14. Характеристика ненадежности для «случайного» шифра
- 15. Применение к стандартным шифрам
- 16. Правильность решения криптограммы
- 17. Идеальные секретные системы
- 18. Примеры идеальных секретных систем
- 19. Дополнительные замечания о ненадежности и избыточности
- 20. Распределение ненадежности
- Часть III. ПРАКТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 22. Общие замечания о решении криптограмм
- 23. Статистические методы
- 24. Метод вероятных слов
- 25. Перемешивание
- 26. Шифры типа …
- 27. Несовместимость требований к хорошим системам
- ПРИЛОЖЕНИЕ. Доказательство теоремы 3
- СОВРЕМЕННЫЕ ДОСТИЖЕНИЯ ТЕОРИИ СВЯЗИ
- Измерение информаций
- Кодирование информации
- Пропускная способность канала
- Идеальные и практические системы
- ПРИНЦИПЫ КОДОВО-ИМПУЛЬСНОЙ МОДУЛЯЦИИ
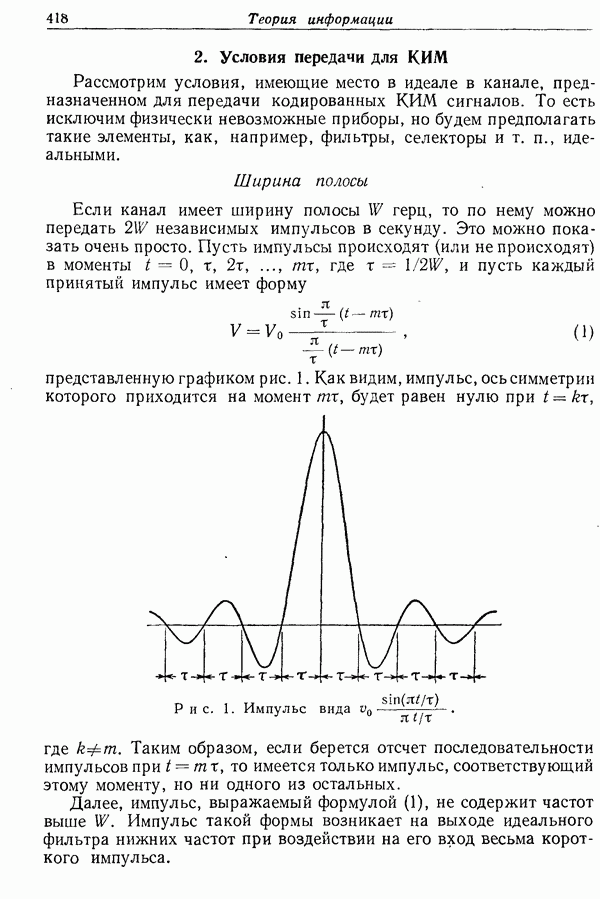
- 2. Условия передачи для КИМ
- 3. Действие системы КИМ
- 4. Сравнение КИМ и ЧМ
- 5. Заключение
- Приложение I
- Приложение II
- СВЯЗЬ ПРИ НАЛИЧИИ ШУМА
- 2. Теорема отсчетов
- 3. Геометрическое представление сигналов
- 4. Геометрическое представление сообщений
- 5. Геометрическое представление передатчика и приемника
- 6. Отображение пространства
- 7. Пропускная способность канала при наличии белого теплового шума
- 8. Обсуждение
- 9. Произвольный гауссовский шум
- 10. Пропускная способность канала при произвольном типе шума
- 11. Дискретные источники информации
- 12. Непрерывные источники информации
- НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ИНФОРМАЦИИ
- ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА С ШУМОМ ПРИ НУЛЕВОЙ ОШИБКЕ
- Пропускная способность канала при нулевой ошибке
- Пропускная способность для суммы и произведения каналов
- Каналы с обратной связью
- ГЕОМЕТРИЧЕСКИЙ ПОДХОД К ТЕОРИИ ПРОПУСКНОЙ СПОСОБНОСТИ. КАНАЛОВ СВЯЗИ
- КАНАЛЫ С ДОПОЛНИТЕЛЬНОЙ ИНФОРМАЦИЕЙ НА ПЕРЕДАТЧИКЕ
- Дискретный канал без памяти с дополнительной информацией о состоянии
- Приложение
- НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ТЕОРИИ КОДИРОВАНИЯ ДЛЯ КАНАЛОВ С ШУМАМИ
- Оценка вероятности ошибки в терминах производящей функции моментов
- Пропускная способность канала с конечным числом состояний, состояние которого вычислимо на обоих концах
- Пропускная способность канала с конечным числом состояний в случае, когда состояние вычислимо на передающем конце и не вычислимо на приемном конце
- ЗАМЕЧАНИЯ О ЧАСТИЧНОМ УПОРЯДОЧИВАНИИ КАНАЛОВ СВЯЗИ
- Дальнейшее обобщение и некоторые предположения
- ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ ОПТИМАЛЬНЫХ кодов В ГАУССОВСКОМ КАНАЛЕ
- 2. Сводка результатов
- 3. Нижняя граница, основанная на соображениях «сферической упаковки»
- 4. Верхняя граница, определяемая методом случайного кодирования
- 5. Формулы для скорости передачи R как функции угла конуса
- 6. Асимптотические формулы для …
- 7. Асимптотическое выражение для верхней границы при случайном кодировании
- 8. Жесткая верхняя граница
- 9. Жесткая нижняя граница
- 10. Поведение границ вблизи пропускной способности канала
- 11. Верхняя граница, полученная методом исчерпывания
- 12. Нижняя граница для гауссовского канала, получаемая исходя из минимального расстояния
- 13. Границы ошибок и другие условия, накладываемые на точки
- 14. Кривые для асимптотических границ
- ТЕОРЕМЫ КОДИРОВАНИЯ ДЛЯ ДИСКРЕТНОГО ИСТОЧНИКА ПРИ ЗАДАННОМ КРИТЕРИИ ТОЧНОСТИ
- Мера искажения отдельной буквы
- Несколько простых примеров
- Скорость при заданном искажении R(d)
- Выпуклость вниз кривой R(d)
- Нахождение R(d) в некоторых простых случаях
- Скорость передачи для произведения источников с мерой, являющейся суммой мер искажения
- Нижняя граница для искажения при заданной пропускной способности канала
- Теоремы кодирования при заданной мере искажения отдельной буквы
- Двойственность источника и канала
- Численные расчеты для некоторых простых каналов
- Обобщение на случаи непрерывных алфавитов
- Разностная мера искажения
- Определение меры локального искажения
- Функции Rn(d) и R(d) для меры локального искажения и эргодического источника
- Прямая теорема кодирования для меры локального искажения
- Обратная теорема кодирования
- Канал с памятью
- ДВУСТОРОННИЕ КАНАЛЫ СВЯЗИ
- 4. Средние взаимные скорости передачи информации
- 5. Распределение информации
- 6. Случайное кодирование для двусторонних каналов
- 7. Вероятность ошибки для ансамбля кодов
- 8. Выпуклая оболочка G как внутренняя граница области пропускной способности
- 9. Внешняя граница для области пропускной способности
- 10. Выпуклость вниз как функций от …
- 11. Приложения свойства выпуклости. Каналы с симметричной структурой
- 12. Характер области, выделяемой внешней границей
- 13. Пример, в котором внутренняя и внешняя границы различны
- 14. Достижимость внешней границы при зависимых источниках
- 15. Общий метод нахождения области пропускной способности двустороннего канала
- 16. Двусторонние каналы с памятью
- 17. Обобщение на каналы с Т концами
- БАНДВАГОН
- ПРЕДСКАЗАНИЕ И ЭНТРОПИЯ ПЕЧАТНОГО АНГЛИЙСКОГО ТЕКСТА
- 2. Вычисление энтропии по статистике английского языка
- 3. Предсказание английского текста
- 4. Идеальное N-граммное предсказывание
- 5. Граница для энтропии на основании частот предсказания
- 6. Результаты эксперимента для английского языка
- УПРОЩЕННЫЙ ВЫВОД ЛИНЕЙНОЙ ТЕОРИИ СГЛАЖИВАНИЯ И ПРЕДСКАЗАНИЯ ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ
- 3. Свойства линейных фильтров
- 4. Основное выражение для среднеквадратичной ошибки
- 5. Чистая проблема сглаживания
- 6. Проблема чистого предсказания
- 7. Предсказание при наличии шума
- 8. Обобщения
- 9. Обсуждение основных предположений
- МАТЕМАТИЧЕСКАЯ ТЕОРИЯ ДИФФЕРЕНЦИАЛЬНОГО АНАЛИЗАТОРА
- Основное условие разрешимости
- Реализация функций
- Системы уравнений
- Аппроксимация множителей с помощью передаточных чисел
- Автоматическое управление скоростью работы устройства
- О МАКСИМАЛЬНОМ ПОТОКЕ ЧЕРЕЗ СЕТЬ
- ТЕОРЕМА О РАСКРАСКЕ РЕБЕР ГРАФА
- УНИВЕРСАЛЬНАЯ МАШИНА ТЬЮРИНГА С ДВУМЯ ВНУТРЕННИМИ СОСТОЯНИЯМИ
- Невозможность создания универсальной машины Тьюринга с одним состоянием
- Моделирование машины Тьюринга с помощью только двух символов на ленте
- ВЫЧИСЛИМОСТЬ НА ВЕРОЯТНОСТНЫХ МАШИНАХ
- Приложение
- БИБЛИОГРАФИЯ РАБОТ ПО ШЕННОНОВСКОЙ ТЕОРИИ ОПТИМАЛЬНОГО КОДИРОВАНИЯ ИНФОРМАЦИИ