| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
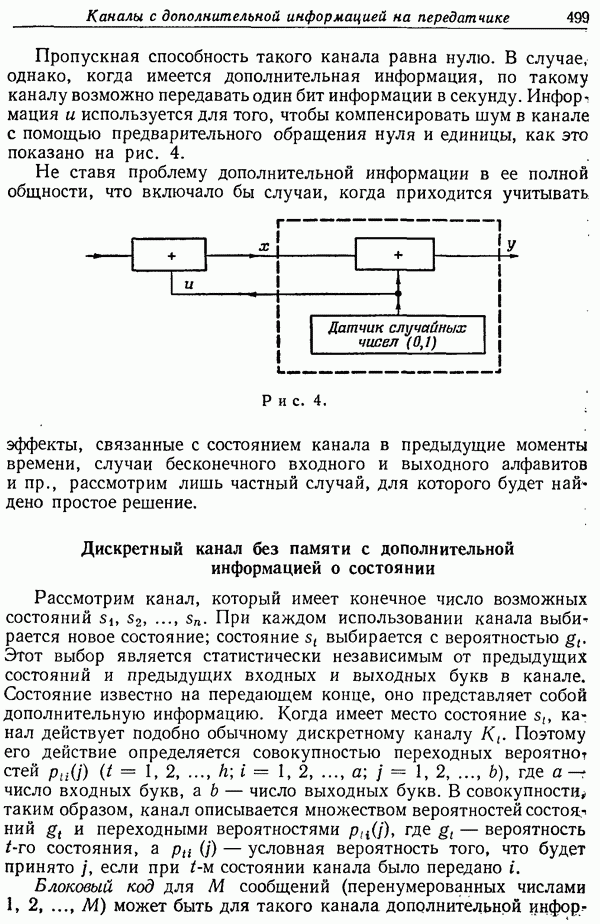
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Каналы с обратной связью
Рассмотрим теперь соответствующую задачу для каналов с полной обратной связью. Под этим будем понимать то, что существует «обратный» канал, безошибочно посылающий принятые на самом деле буквы из точки приема обратно на передающий конец. Предполагается, что эта информация принимается на передающем конце до того момента, когда должна быть передана следующая буква. Поэтому при желании она может быть использована при выборе следующей подлежащей передаче буквы.

Рис. 5.
Интересно, что в канале без памяти обычная пропускная способность в прямом направлении равняется одной и той же величине в присутствии и в отсутствии обратной связи. Это будет показано в теореме 6. Иначе обстоит дело с пропускной способностью при нулевой ошибке, которая в некоторых случаях может быть больше в присутствии обратной связи, чем при ее отсутствии. Например, в канале, изображенном на рис. 5,  . Однако, как будет показано на основании теоремы 7, пропускная способность при нулевой ошибке и обратной связи
. Однако, как будет показано на основании теоремы 7, пропускная способность при нулевой ошибке и обратной связи  .
.
Сначала определим код из блоков длины  для системы с обратной связью. Это означает, что на передающем конце имеется устройство с двумя входами или математически — функция двух аргументов. Один аргумент — это сообщение, которое должно быть послано, другой — принятые ранее слова, поступившие по каналу обратной связи. Значение функции представляет собой букву, которую следует передать. Таким образом, функция может быть представлена как
для системы с обратной связью. Это означает, что на передающем конце имеется устройство с двумя входами или математически — функция двух аргументов. Один аргумент — это сообщение, которое должно быть послано, другой — принятые ранее слова, поступившие по каналу обратной связи. Значение функции представляет собой букву, которую следует передать. Таким образом, функция может быть представлена как  , где
, где  есть
есть  буква, переданная в блоке,
буква, переданная в блоке,  -индекс, принимающий значения от 1 до М и выделяющий специфику переданного сообщения,
-индекс, принимающий значения от 1 до М и выделяющий специфику переданного сообщения,  принятое слово длины
принятое слово длины  Так
Так  изменяемся в пределах от 0 до
изменяемся в пределах от 0 до  это значит, что
это значит, что  принимает значения всех принятых слов этой длины.
принимает значения всех принятых слов этой длины.
Передача осуществляется следующим образом. Если подлежит передаче сообщение  то
то  вычисляется как
вычисляется как  где знак минус
где знак минус
означает «слово отсутствует», и посылается первая буква. Если канал обратной связи в качестве первой принятой буквы приносит, например, букву а, то следующей передаваемой буквой будет  . Если далее принимается
. Если далее принимается  то следующей переданной буквой будет
то следующей переданной буквой будет 
Теорема 6. Пропускная способность в прямом направлении дискретного канала без памяти при наличии обратной связи равна обычной пропускной способности С (в отсутствии обратной связи). Среднее приращение взаимной информации  принятой последовательности
принятой последовательности  относительно сообщения
относительно сообщения  на одну букву текста не превосходит С.
на одну букву текста не превосходит С.
Пусть  — последовательность, принятая к моменту окончания блока,
— последовательность, принятая к моменту окончания блока,  — сообщение, х — следующая переданная буква и у — следующая принятая буква. Все они являются случайными величинами, в том числе и х, которая является функцией от
— сообщение, х — следующая переданная буква и у — следующая принятая буква. Все они являются случайными величинами, в том числе и х, которая является функцией от  и
и  Эта функция фактически является функцией, которая определяется методом кодирования при наличии обратной связи, на основании которого следующая передаваемая буква х определяется сообщением
Эта функция фактически является функцией, которая определяется методом кодирования при наличии обратной связи, на основании которого следующая передаваемая буква х определяется сообщением  и информацией
и информацией  относительно ранее принятых сигналов, поступающей по каналу обратной связи. То, что канал является каналом без памяти, означает, что последующая операция не зависит от предыдущей и, в частности, что
относительно ранее принятых сигналов, поступающей по каналу обратной связи. То, что канал является каналом без памяти, означает, что последующая операция не зависит от предыдущей и, в частности, что 
Для среднего приращения взаимной информации, вызываемого парой  при условии, что было принято некоторое заданное
при условии, что было принято некоторое заданное  имеем (усредняя по сообщениям
имеем (усредняя по сообщениям  и последующим принятым буквам у при некотором заданном
и последующим принятым буквам у при некотором заданном 

Так как  вторая сумма может быть записана в виде
вторая сумма может быть записана в виде

Объединяя обе суммы, получим теперь, что

Помня, что х является функцией тип, представим суммирование по  как суммирование сначала по тем т., которые дают в результате одно и то же х (при заданном и), а затем по различным х. При первом суммировании величина
как суммирование сначала по тем т., которые дают в результате одно и то же х (при заданном и), а затем по различным х. При первом суммировании величина  является постоянной, равной
является постоянной, равной  а коэффициенты при логарифме дают в сумме
а коэффициенты при логарифме дают в сумме  . В результате можно написать
. В результате можно написать

Рассмотрим теперь скорость передачи в канале (в обычном смысле при отсутствии обратной связи) так, как будто бы значениям х приписаны вероятности  При этом вероятности
При этом вероятности  для пар х, у и вероятности
для пар х, у и вероятности  просто для у были бы равны
просто для у были бы равны

Скорость, следовательно, равнялась бы

Так как  где С — пропускная способность канала (С является максимально возможным значением
где С — пропускная способность канала (С является максимально возможным значением  по всем
по всем  заключаем, что
заключаем, что

Так как среднее изменение I на одну букву не превосходит С, среднее изменение на  букв не превосходит
букв не превосходит  Следовательно, в блоковом коде длины
Следовательно, в блоковом коде длины  при скорости на входе, равной
при скорости на входе, равной  ненадежность при окончании блока будет по крайней мере
ненадежность при окончании блока будет по крайней мере  т. е. точно такая же, как в случае канала без обратной связи. Иначе говоря, невозможно достигнуть нулевой ненадежности (или, что легко следует отсюда, нулевой вероятности ошибки) в случае, когда скорость превышает пропускную способность канала. Это, конечно, возможно сделать при скоростях, меньших С, ибо, наверняка, все, что может быть сделано без обратной связи, может быть сделано и с обратной связью.
т. е. точно такая же, как в случае канала без обратной связи. Иначе говоря, невозможно достигнуть нулевой ненадежности (или, что легко следует отсюда, нулевой вероятности ошибки) в случае, когда скорость превышает пропускную способность канала. Это, конечно, возможно сделать при скоростях, меньших С, ибо, наверняка, все, что может быть сделано без обратной связи, может быть сделано и с обратной связью.
Интересно, что первое утверждение теоремы 6 может быть легко обобщено на каналы с памятью при условии, что они имеют такую структуру, что внутреннее состояние канала может быть вычислено на передающем конце по начальному состоянию и последовательности посланных букв. Если этот случай не имеет места, заключение
теоремы не будет всегда справедливым, т. е. существуют каналы более сложной структуры, для которых при наличии обратной связи пропускная способность в прямом направлении превосходит ту, которая имеет место при отсутствии обратной связи. Здесь, однако, не будут приводиться подробности этих обобщений.
Обращаясь теперь вновь к задачам передачи с нулевой ошибкой, дадим определение пропускной способности при нулевой ошибке  для канала с обратной связью следующим очевидным образом: пропускная способность есть верхняя граница скоростей для блоковых кодов, которые не приводят к ошибкам. Следующая теорема решает задачу вычисления
для канала с обратной связью следующим очевидным образом: пропускная способность есть верхняя граница скоростей для блоковых кодов, которые не приводят к ошибкам. Следующая теорема решает задачу вычисления  для канала без памяти при наличии обратной связи и указывает, как быстро при увеличении длины блока
для канала без памяти при наличии обратной связи и указывает, как быстро при увеличении длины блока  можно достигнуть скорости
можно достигнуть скорости 
Теорема 7. Пропускная способность дискретного канала без памяти при нулевой ошибке и при наличии полной обратной связи, воспроизводящей принятые буквы на передающем конце, равна нулю, если все пары входных букв являются смежными. В противном случае  где
где

 — заданная вероятность входной буквы
— заданная вероятность входной буквы  — множество входных букв, переходящих в выходную букву 1 с положительной вероятностью. Для такого канала с обратной связью при передаче со скоростью
— множество входных букв, переходящих в выходную букву 1 с положительной вероятностью. Для такого канала с обратной связью при передаче со скоростью  где
где  — число входных букв, можно найти не дающий ошибок код из блоков длины
— число входных букв, можно найти не дающий ошибок код из блоков длины 
Появившаяся вэтой теоремевеличина  имеет следующий смысл. При любых заранее заданных вероятностях входных букв Р, для каждой выходной буквы
имеет следующий смысл. При любых заранее заданных вероятностях входных букв Р, для каждой выходной буквы  можно вычислить совокупную вероятность всех входных букв, переходящих (с положительной вероятностью) в букву
можно вычислить совокупную вероятность всех входных букв, переходящих (с положительной вероятностью) в букву  Это будет
Это будет  Выходные буквы, для которых сумма будет очень большой, являются «плохими» с той точки зрения, что, когда они приняты, существует большая неопределенность, относящаяся к переходам. Чтобы получить
Выходные буквы, для которых сумма будет очень большой, являются «плохими» с той точки зрения, что, когда они приняты, существует большая неопределенность, относящаяся к переходам. Чтобы получить  следует выбрать
следует выбрать  так, чтобы «худшее» в указанном смысле выходное слово было бы возможно «лучшим».
так, чтобы «худшее» в указанном смысле выходное слово было бы возможно «лучшим».
Покажем сначала, что  если все буквы являются взаимно смежными. В самом деле, какова бы ни была система кодирования, любые два сообщения, например
если все буквы являются взаимно смежными. В самом деле, какова бы ни была система кодирования, любые два сообщения, например  могут с положительной вероятностью дать при декодировании одну и ту же выходную последовательность. А именно первые переданные буквы,
могут с положительной вероятностью дать при декодировании одну и ту же выходную последовательность. А именно первые переданные буквы,
соответствующие  и
и  имеют общую возможную выходную букву. Предполагая, что такая буква появилась на выходе, обратимся к следующим передаваемым для
имеют общую возможную выходную букву. Предполагая, что такая буква появилась на выходе, обратимся к следующим передаваемым для  и
и  буквам в той же системе кодирования. Они также имеют общую возможную выходную букву. Продолжая этот процесс, установим некоторое выходное слово, которое может быть результатом приема любой из
буквам в той же системе кодирования. Они также имеют общую возможную выходную букву. Продолжая этот процесс, установим некоторое выходное слово, которое может быть результатом приема любой из  и
и  и поэтому сообщения не могут быть однозначно распознаны.
и поэтому сообщения не могут быть однозначно распознаны.
Рассмотрим теперь такой случай, при котором не все пары являются смежными. Сначала, введя в рассмотрение блоковый код длины  докажем, что при кодировании, не дающем ошибок, нельзя превзойти скорости
докажем, что при кодировании, не дающем ошибок, нельзя превзойти скорости  Для
Для  это утверждение, очевидно, справедливо. Пусть доказываемая по индукции гипотеза будет состоять в том, что не существует блокового кода длины
это утверждение, очевидно, справедливо. Пусть доказываемая по индукции гипотеза будет состоять в том, что не существует блокового кода длины  передающего со скоростью, превышающей
передающего со скоростью, превышающей  или, иначе говоря, нельзя однозначно различить более чем
или, иначе говоря, нельзя однозначно различить более чем  различных сообщений. Предположим теперь (в противоположность ожидаемому результату), что имеется блоковый код длины
различных сообщений. Предположим теперь (в противоположность ожидаемому результату), что имеется блоковый код длины  различающий М сообщений при
различающий М сообщений при  Первая передаваемая в коде буква делит эти М сообщений между входными буквами канала. Пусть — доля сообщений, приписанных к букве! (т. е. таких сообщений, для которых
Первая передаваемая в коде буква делит эти М сообщений между входными буквами канала. Пусть — доля сообщений, приписанных к букве! (т. е. таких сообщений, для которых  является первой передаваемой буквой). Эти
является первой передаваемой буквой). Эти  теперь подобны вероятностям, заданным для различных букв, и поэтому, согласно определению
теперь подобны вероятностям, заданным для различных букв, и поэтому, согласно определению  существует некоторая выходная буква, скажем буква
существует некоторая выходная буква, скажем буква  такая, что
такая, что  Рассмотр им множество сообщений, для которых первая передаваемая буква принадлежит
Рассмотр им множество сообщений, для которых первая передаваемая буква принадлежит  Число сообщений в этом множестве равно по меньшей мере
Число сообщений в этом множестве равно по меньшей мере  . Каждое из них может дать выходную букву
. Каждое из них может дать выходную букву  в качестве первой принимаемой буквы. Тогда, когда это случится, существуют еще
в качестве первой принимаемой буквы. Тогда, когда это случится, существуют еще  букв, подлежащих передачи, и так как
букв, подлежащих передачи, и так как  то имеем
то имеем  Таким образом, существует не дающий ошибок блоковый код длины
Таким образом, существует не дающий ошибок блоковый код длины  дающий скорость передачи, большую чем
дающий скорость передачи, большую чем  что противоречит предположению индукции. Отметим, что кодирующая функция для кода длины
что противоречит предположению индукции. Отметим, что кодирующая функция для кода длины  определяется формально из первоначальной кодирующей функции с помощью фиксирования
определяется формально из первоначальной кодирующей функции с помощью фиксирования  в качестве применяемой буквы.
в качестве применяемой буквы.
Теперь требуется показать, что при кодировании, не дающем ошибок, можно на самом деле достигнуть скорости, сколь угодно близкой к  Пусть
Пусть  — совокупность вероятностей, которые, будучи приписанными входным буквам, дадут
— совокупность вероятностей, которые, будучи приписанными входным буквам, дадут  для
для  Тогда общая схема кода будет заключаться в разделении М первоначальных сообщений на
Тогда общая схема кода будет заключаться в разделении М первоначальных сообщений на  различных групп в соответствии с первой передаваемой буквой. Число сообщений в этих группах будет приблизительно пропорционально
различных групп в соответствии с первой передаваемой буквой. Число сообщений в этих группах будет приблизительно пропорционально 
Первая передаваемая буква будет соответствовать группе, содержащей сообщение, которое должно быть передано. Какая бы буква ни была принята, число сообщений, совместимых с этой принятой буквой, будет приблизительно  Это подмножество возможных сообщений известно как на приемном, так и на передающем конце (после того, как принятая буква посылается обратно к передатчику).
Это подмножество возможных сообщений известно как на приемном, так и на передающем конце (после того, как принятая буква посылается обратно к передатчику).
Кодирующая система далее разделяет это подмножество сообщений на  групп, снова приблизительно пропорционально вероятностям
групп, снова приблизительно пропорционально вероятностям  Вторая передаваемая буква соответствует группе, содержащей существующее сообщение. Какая бы буква ни была принята, число сообщений, совместимых с обеими принятыми буквами, равняется теперь примерно
Вторая передаваемая буква соответствует группе, содержащей существующее сообщение. Какая бы буква ни была принята, число сообщений, совместимых с обеими принятыми буквами, равняется теперь примерно 
Этот процесс продолжается до тех пор, пока лишь незначительное число сообщений (меньшее  не станет совместимым со всеми принятыми буквами. Неопределенность между ними может быть снята, если использовать пары несмежных букв в простом двоичном коде. Код, построенный таким образом, будет кодом с нулевой ошибкой для рассматриваемого канала.
не станет совместимым со всеми принятыми буквами. Неопределенность между ними может быть снята, если использовать пары несмежных букв в простом двоичном коде. Код, построенный таким образом, будет кодом с нулевой ошибкой для рассматриваемого канала.
Теперь более тщательно оценим аппроксимацию, которая имеет место при подразделении сообщений на  групп. Покажем, что для любого М и любой совокупности
групп. Покажем, что для любого М и любой совокупности  можно разделить М сообщений на группы по
можно разделить М сообщений на группы по  сообщений, такие, что
сообщений, такие, что  всегда, когда
всегда, когда  и
и

Без ограничения общности предположим, что  не равны нулю. Выбираем
не равны нулю. Выбираем  так, чтобы это было наибольшее целое число, такое, что
так, чтобы это было наибольшее целое число, такое, что  Пусть
Пусть  Ясно, что
Ясно, что  Выберем далее
Выберем далее  так, чтобы это было наименьшее целое число, такое, что
так, чтобы это было наименьшее целое число, такое, что  Положим
Положим  Имеем
Имеем  Точно так же
Точно так же  так как
так как  противоположны по знаку и каждая из них по абсолютной величине меньше
противоположны по знаку и каждая из них по абсолютной величине меньше  Далее выберем
Далее выберем  так, чтобы
так, чтобы  было приблизительно, с точностью
было приблизительно, с точностью  равно
равно  Если
Если  то
то  выбирается меньшим или равным
выбирается меньшим или равным  Если
Если  то
то  выбирается большим или равным
выбирается большим или равным  Таким образом, снова
Таким образом, снова  Продолжая этот процесс до
Продолжая этот процесс до  включительно, получим приближения для
включительно, получим приближения для  обладающие тем свойством, что
обладающие тем свойством, что  , или
, или  Если теперь определить
Если теперь определить  как
как  это неравенство может
это неравенство может
быть записано в виде  Отсюда
Отсюда  Таким образом, так как все приближения
Таким образом, так как все приближения  лежали в пределах
лежали в пределах  от
от  , цель достигнута.
, цель достигнута.
Возвращаясь теперь к нашей основной задаче, отметим сначала, что если  то
то  и справедливость теоремы тривиальна. Предположим затем, что
и справедливость теоремы тривиальна. Предположим затем, что  Покажем, что
Покажем, что  Рассмотрим множество входных букв, которые имеют максимальное значение
Рассмотрим множество входных букв, которые имеют максимальное значение  Этот максимум, конечно, больше или равен среднему значению, равному
Этот максимум, конечно, больше или равен среднему значению, равному  Можно далее сделать так, чтобы по крайней мере одна из этих входных букв не была связанной с некоторой выходной буквой. Предположим, что этого сделать нельзя. Тогда либо не существует других входных букв, кроме этого множества, что противоречит предположению, что
Можно далее сделать так, чтобы по крайней мере одна из этих входных букв не была связанной с некоторой выходной буквой. Предположим, что этого сделать нельзя. Тогда либо не существует других входных букв, кроме этого множества, что противоречит предположению, что  либо существуют другие входные буквы с меньшими значениями
либо существуют другие входные буквы с меньшими значениями  . В этом случае уменьшение Р, для одной из входных букв в максимальном множестве и увеличение соответственно вероятности для какой-либо входной буквы, не связанной со всеми выходными буквами, не увеличит значения
. В этом случае уменьшение Р, для одной из входных букв в максимальном множестве и увеличение соответственно вероятности для какой-либо входной буквы, не связанной со всеми выходными буквами, не увеличит значения  (при любом
(при любом  и даст входную букву желаемого типа. Рассматривая выходные буквы, с которыми эта входная буква не связана, видим, что
и даст входную букву желаемого типа. Рассматривая выходные буквы, с которыми эта входная буква не связана, видим, что 
Предположим теперь, что передача начинается с М сообщений, подразделенных на группы, вероятности которых, согласно описанному ранее, приблизительно пропорциональны  Тогда, если некоторая буква является уже принятой, множество возможных сообщений (совместимых с этой принятой буквой) сводится к тем, которые объединены в группы, соответствующие буквам, соединенным с уже принятой буквой. Каждая выходная буква соединена не более чем с
Тогда, если некоторая буква является уже принятой, множество возможных сообщений (совместимых с этой принятой буквой) сводится к тем, которые объединены в группы, соответствующие буквам, соединенным с уже принятой буквой. Каждая выходная буква соединена не более чем с  входными буквами (в противном случае имелось бы равенство
входными буквами (в противном случае имелось бы равенство  Для любой из образованных групп ошибка в приближении Р. меньше или равна
Для любой из образованных групп ошибка в приближении Р. меньше или равна  Следовательно, общее относительное число сообщений во всех соединенных группах меньше или равно
Следовательно, общее относительное число сообщений во всех соединенных группах меньше или равно  для любой выходной буквы. Общее число возможных сообщений после приема первой буквы снижается поэтому от М до числа, меньшего или равного
для любой выходной буквы. Общее число возможных сообщений после приема первой буквы снижается поэтому от М до числа, меньшего или равного 
В системе кодирования, которая была использована, оставшееся возможное подмножество сообщений снова делится между входными буквами так, чтобы аппроксимировать точно таким же образом вероятности  Это подразделение может быть выполнено с использованием того же стандартного приема (в точности такого же, как описанный выше), как в точке приема, так и на передающем конце, в силу того, что обратная связь для обоих из них делает доступным требуемые данные, а именно первую принятую букву.
Это подразделение может быть выполнено с использованием того же стандартного приема (в точности такого же, как описанный выше), как в точке приема, так и на передающем конце, в силу того, что обратная связь для обоих из них делает доступным требуемые данные, а именно первую принятую букву.
Вторая передаваемая буква, полученная таким образом, в свою очередь сведет на приемном конце число возможных сообщений
к величине, не превышающей  Тот же самый процесс продолжается для каждой передаевамой буквы. Если оценка сверху числа возможных остающихся сообщений после
Тот же самый процесс продолжается для каждой передаевамой буквы. Если оценка сверху числа возможных остающихся сообщений после  букв есть М, то
букв есть М, то  Решением этого разностного уравнения является
Решением этого разностного уравнения является

Это легко может быть проверено подстановкой в разностное уравнение. Для того чтобы удовлетворить начальным условиям  , требуется, чтобы
, требуется, чтобы  Таким образом, решением оказывается выражение:
Таким образом, решением оказывается выражение:

так как выше было показано, что 
Если описанный процесс выполнить для  шагов, где
шагов, где  — наименьшее целое число не менее
— наименьшее целое число не менее  решение уравнения
решение уравнения  то число оставшихся сообщений, совместимых с принятой последовательностью, не будет превышать
то число оставшихся сообщений, совместимых с принятой последовательностью, не будет превышать  (так как
(так как  , в противном случае
, в противном случае  ). Теперь пары несмежных букв, существование которых предполагается в теореме, могут быть использованы для разрешения неопределенности по этим
). Теперь пары несмежных букв, существование которых предполагается в теореме, могут быть использованы для разрешения неопределенности по этим  (или меньшего числа) сообщений. Это потребует не более чем
(или меньшего числа) сообщений. Это потребует не более чем  дополнительных букв. Таким образом, в общем можно использовать не большую чем
дополнительных букв. Таким образом, в общем можно использовать не большую чем  длину блока. При такой длине блока передается одно сообщение, выбранное из
длину блока. При такой длине блока передается одно сообщение, выбранное из  возможных. Следовательно, скорость передачи при нулевой ошибке, которая будет достигнута, равна
возможных. Следовательно, скорость передачи при нулевой ошибке, которая будет достигнута, равна

Итак получено скольугодно близкое приближение к  при помощи кодов, не дающих ошибок.
при помощи кодов, не дающих ошибок.
В качестве примера к теореме 7 рассмотрим канал, изображенный на рис. 5. Требуется вычислить  Легко увидеть, что, составляя минимакс, входящий в формулировку теоремы 7, можно положить
Легко увидеть, что, составляя минимакс, входящий в формулировку теоремы 7, можно положить  так как, если бы они были неравными, максимум Для соответствующих трех выходных букв можно было бы снизить уравнением. Очевидно также, что тогда
так как, если бы они были неравными, максимум Для соответствующих трех выходных букв можно было бы снизить уравнением. Очевидно также, что тогда 
ибо в противном случае сдвиг вероятностей в ту или другую сторону привел бы к понижению максимума. Отсюда можно заключить, что  Окончательно пропускная способность канала с обратной связью при нулевой ошибке равна
Окончательно пропускная способность канала с обратной связью при нулевой ошибке равна 
Существует тесная связь между, минимаксным процессом теоремы 7 и процессом отыскания минимальной пропускной способности канала при вариациях переходных вероятностей  подобным тем, которые имели место в теореме 2. Там было отмечено, что при минимуме пропускной способности каждая выходная буква может получиться из входных букв, имеющих одну и ту же общую вероятность. Всамомделе, кажется весьма правдоподобным то, что вероятности входных букв, на которых достигается минимум пропускной способности, в точности совпадают с вероятностями, которые решают проблему минимакса в теореме 7, и если это так, то
подобным тем, которые имели место в теореме 2. Там было отмечено, что при минимуме пропускной способности каждая выходная буква может получиться из входных букв, имеющих одну и ту же общую вероятность. Всамомделе, кажется весьма правдоподобным то, что вероятности входных букв, на которых достигается минимум пропускной способности, в точности совпадают с вероятностями, которые решают проблему минимакса в теореме 7, и если это так, то 
Автор приносит благодарность Питеру Элайесу за первое указание на то, что линия обратной связи может увеличить пропускную способность при нулевой ошибке, а также за ряд советов, которые были полезными при доказательстве теоремы 7.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- СИМВОЛИЧЕСКИЙ АНАЛИЗ РЕЛЕЙНЫХ И ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- 2. Параллельно-последовательные двухполюсные схемы. Основные определения и постулаты
- 3. Многополюсные и не параллельно-последовательные схемы
- Преобразование треугольника в звезду и звезды в ячейку
- Функция сопротивления не параллельно-последовательной схемы
- Системы уравнений
- Реле и переключатели специальных типов
- 4. Синтез схем
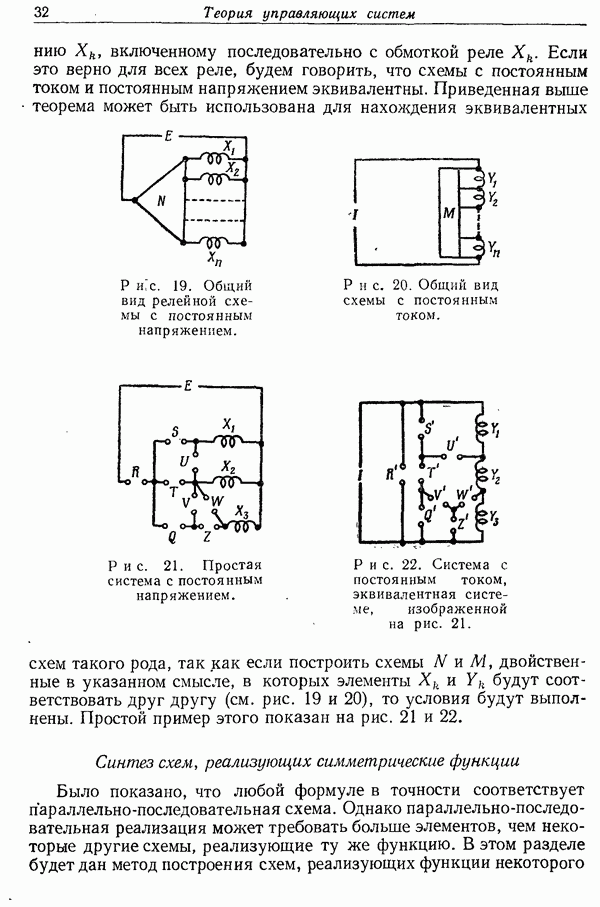
- Двойственные схемы
- Синтез схем, реализующих симметрические функции
- Составление уравнений по рабочим характеристикам
- 5. Примеры
- ЧИСЛО ДВУХПОЛЮСНЫХ ПАРАЛЛЕЛЬНО-ПОСЛЕДОВАТЕЛЬНЫХ СЕТЕЙ
- 1. Получение производящей функции
- 2. Численный подсчет
- 3. Асимптотическое поведение
- 4. Параллельно-последовательная реализация переключательных функций
- СИНТЕЗ ДВУХПОЛЮСНЫХ ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- 2. Основная теорема синтеза
- 3. Синтез схем для произвольных функций.
- Часть II. РАСПРЕДЕЛЕНИЕ НАГРУЗКИ МЕЖДУ РЕЛЕ
- 5. Разделительное дерево
- 6. Другие задачи распределения
- 7. Функция «мю»
- Часть III. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- 9. Частично симметрические функции
- ПРИМЕЧАНИЯ РЕДАКТОРА
- ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К ОБЪЕМУ ПАМЯТИ ТЕЛЕФОННОГО КОММУТАТОРА
- 2. Память, требуемая для S произвольных вызовов от N абонентов
- 3. Условие раздельной памяти
- 4. Связь с теорией информации
- НАДЕЖНЫЕ СХЕМЫ ИЗ НЕНАДЕЖНЫХ РЕЛЕ
- Идеализированные реле
- Общий метод повышения надежности
- Свойства функции h(p)
- Комбинация двух схем
- Оценки функции h'(p)
- Схемы заданной длины и ширины
- Оценки числа контактов в случае, когда реле уже достаточно надежны
- Сравнение с элементами фон Неймана
- Реле с неопределенным временем срабатывания
- Синтез надежных схем в целом
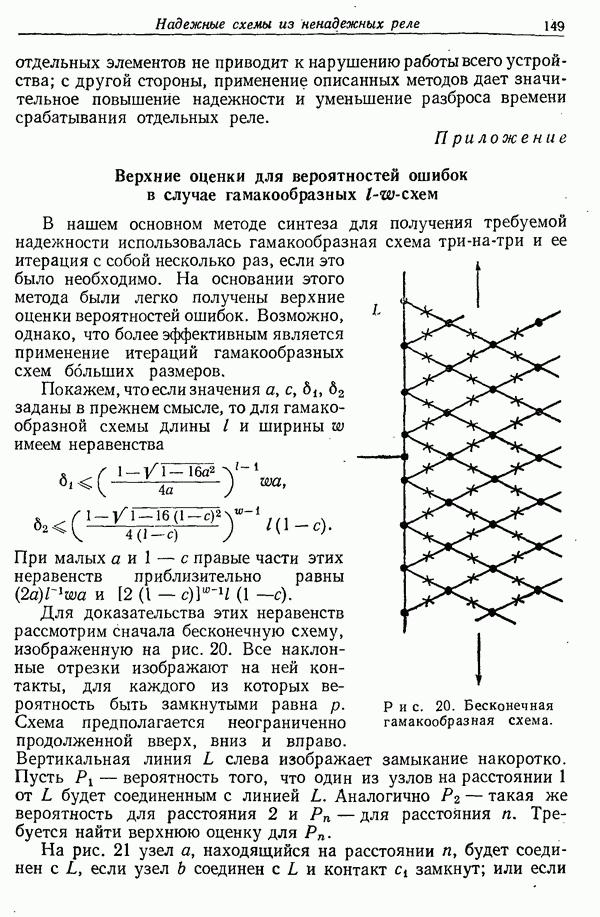
- Приложение. Верхние оценки для вероятностей ошибок в случае гамакообразных l-w-схем
- ИСПОЛЬЗОВАНИЕ МАШИНЫ ДЛЯ ПРОЕКТИРОВАНИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА И АВТОМАТЫ
- Машины Тьюринга
- Логические машины
- «Играющие машины»
- Обучаемые машины
- Самовоспроизводящиеся машины
- Обращение к читателю
- МАШИНА ДЛЯ ИГРЫ В ШАХМАТЫ
- СОСТАВЛЕНИЕ ПРОГРАММ ДЛЯ ИГРЫ В ШАХМАТЫ НА ВЫЧИСЛИТЕЛЬНОЙ МАШИНЕ
- 3. Приближенная оценочная функция
- 4. Стратегия, основанная на оценочной функции
- 5. Составление программы для универсальной вычислительной машины для реализации стратегии типа А
- 6. Улучшение стратегии
- 7. Изменения в игре и в стиле
- 8. Другой тип стратегии
- ПРИЛОЖЕНИЕ. ОЦЕНОЧНАЯ ФУНКЦИЯ ДЛЯ ШАХМАТ
- ИГРАЮЩИЕ МАШИНЫ
- СООБЩЕНИЕ О МАШИНЕ, РЕШАЮЩЕЙ ЛАБИРИНТНУЮ ЗАДАЧУ
- ВКЛАД ФОН НЕЙМАНА В ТЕОРИЮ АВТОМАТОВ
- МАТЕМАТИЧЕСКАЯ ТЕОРИЯ СВЯЗИ
- 1. ДИСКРЕТНЫЕ СИСТЕМЫ БЕЗ ШУМОВ
- 2. Дискретный источник сообщений
- 3. Последовательные приближения к английскому языку
- 4. Графическое представление марковского процесса
- 5. Эргодические и смешанные источники
- 6. Выбор, неопределенность и энтропия
- 7. Энтропия источника сообщений
- 8. Представление операций кодирования и декодирования
- 9. Основная теорема для канала без шума
- 10. Рассмотрение полученных результатов и примеры
- 11. Примеры
- II. ДИСКРЕТНЫЙ КАНАЛ С ШУМОМ
- 12. Надежность и пропускная способность канала
- 13. Основная теорема для дискретного канала с шумом
- 14. Рассмотрение полученных результатов
- 15. Пример дискретного канала и его пропускной способности
- 16. Пропускная способность канала в некоторых частных случаях
- 17. Пример эффективного кодирования
- III. ИНФОРМАЦИЯ ДЛЯ НЕПРЕРЫВНЫХ ВЕЛИЧИН
- 19. Ансамбли функций с ограниченной полосой частот
- 20. Энтропия непрерывного распределения
- 21. Энтропия ансамбля функций
- 22. Потеря энтропии в линейных фильтрах
- 23. Энтропия суммы двух ансамблей
- IV. НЕПРЕРЫВНЫЙ КАНАЛ
- 24. Пропускная способность непрерывного канала
- 25. Пропускная способность канала при ограничении средней мощности
- 26. Пропускная способность канала при ограничении пиковой мощности
- V. СКОРОСТЬ СОЗДАНИЯ СООБЩЕНИЙ ДЛЯ НЕПРЕРЫВНОГО ИСТОЧНИКА
- 28. Скорость создания сообщений источником при данной точности воспроизведения
- 29. Вычисление скорости создания сообщений
- Приложение 1. РОСТ ЧИСЛА БЛОКОВ СИМВОЛОВ ПРИ УСЛОВИЯХ, ОПИСЫВАЕМЫХ КОНЕЧНЫМ ЧИСЛОМ СОСТОЯНИЙ
- Приложение 2. ВЫВОД РАВЕНСТВА …
- Приложение 3. ТЕОРЕМА ОБ ЭРГОДИЧЕСКИХ ИСТОЧНИКАХ
- Приложение 4. МАКСИМИЗАЦИЯ СКОРОСТИ ДЛЯ СИСТЕМЫ ОГРАНИЧЕНИЯ
- Приложение 5
- Приложение 6
- Приложение 7
- ТЕОРИЯ СВЯЗИ В СЕКРЕТНЫХ СИСТЕМАХ
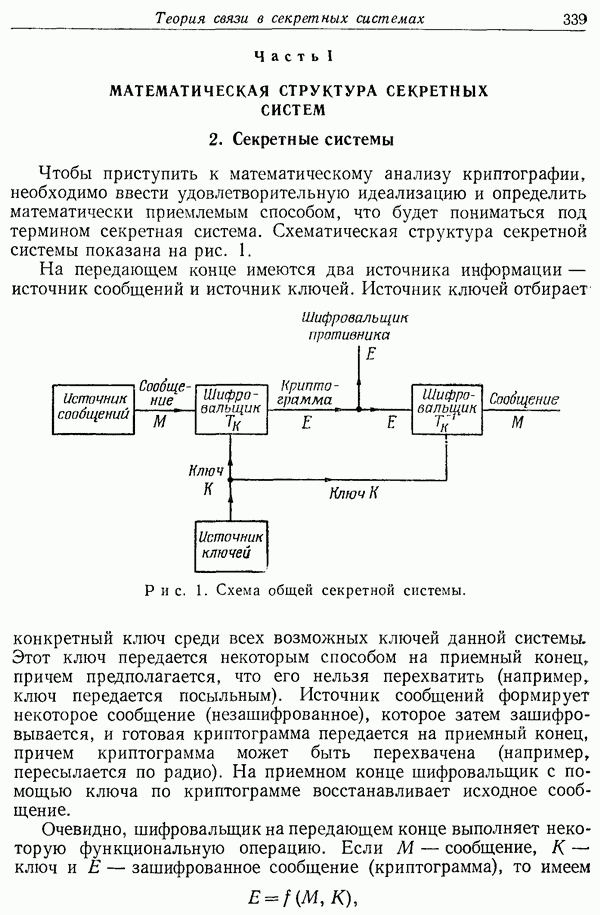
- Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ СИСТЕМ
- 3. Способы изображения систем
- 4. Примеры секретных систем
- 5. Оценка секретных систем
- 6. Алгебра секретных систем
- 7. Чистые и смешанные шифры
- 8. Подобные системы
- Часть II. ТЕОРЕТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 10. Совершенная секретность
- 11. Ненадежность
- 12. Свойства ненадежности
- 13. Ненадежность простой подстановки для языка с двухбуквенным алфавитом
- 14. Характеристика ненадежности для «случайного» шифра
- 15. Применение к стандартным шифрам
- 16. Правильность решения криптограммы
- 17. Идеальные секретные системы
- 18. Примеры идеальных секретных систем
- 19. Дополнительные замечания о ненадежности и избыточности
- 20. Распределение ненадежности
- Часть III. ПРАКТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 22. Общие замечания о решении криптограмм
- 23. Статистические методы
- 24. Метод вероятных слов
- 25. Перемешивание
- 26. Шифры типа …
- 27. Несовместимость требований к хорошим системам
- ПРИЛОЖЕНИЕ. Доказательство теоремы 3
- СОВРЕМЕННЫЕ ДОСТИЖЕНИЯ ТЕОРИИ СВЯЗИ
- Измерение информаций
- Кодирование информации
- Пропускная способность канала
- Идеальные и практические системы
- ПРИНЦИПЫ КОДОВО-ИМПУЛЬСНОЙ МОДУЛЯЦИИ
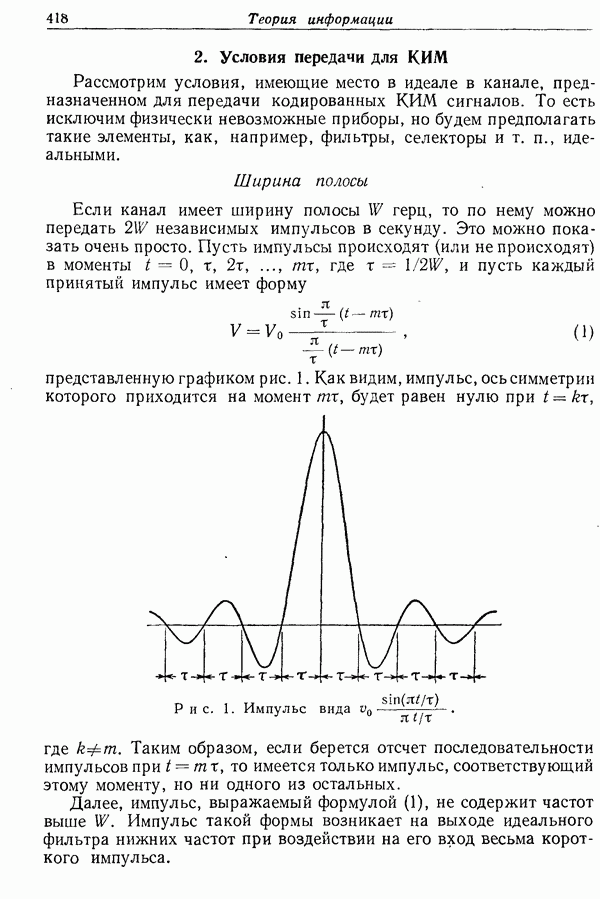
- 2. Условия передачи для КИМ
- 3. Действие системы КИМ
- 4. Сравнение КИМ и ЧМ
- 5. Заключение
- Приложение I
- Приложение II
- СВЯЗЬ ПРИ НАЛИЧИИ ШУМА
- 2. Теорема отсчетов
- 3. Геометрическое представление сигналов
- 4. Геометрическое представление сообщений
- 5. Геометрическое представление передатчика и приемника
- 6. Отображение пространства
- 7. Пропускная способность канала при наличии белого теплового шума
- 8. Обсуждение
- 9. Произвольный гауссовский шум
- 10. Пропускная способность канала при произвольном типе шума
- 11. Дискретные источники информации
- 12. Непрерывные источники информации
- НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ИНФОРМАЦИИ
- ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА С ШУМОМ ПРИ НУЛЕВОЙ ОШИБКЕ
- Пропускная способность канала при нулевой ошибке
- Пропускная способность для суммы и произведения каналов
- Каналы с обратной связью
- ГЕОМЕТРИЧЕСКИЙ ПОДХОД К ТЕОРИИ ПРОПУСКНОЙ СПОСОБНОСТИ. КАНАЛОВ СВЯЗИ
- КАНАЛЫ С ДОПОЛНИТЕЛЬНОЙ ИНФОРМАЦИЕЙ НА ПЕРЕДАТЧИКЕ
- Дискретный канал без памяти с дополнительной информацией о состоянии
- Приложение
- НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ТЕОРИИ КОДИРОВАНИЯ ДЛЯ КАНАЛОВ С ШУМАМИ
- Оценка вероятности ошибки в терминах производящей функции моментов
- Пропускная способность канала с конечным числом состояний, состояние которого вычислимо на обоих концах
- Пропускная способность канала с конечным числом состояний в случае, когда состояние вычислимо на передающем конце и не вычислимо на приемном конце
- ЗАМЕЧАНИЯ О ЧАСТИЧНОМ УПОРЯДОЧИВАНИИ КАНАЛОВ СВЯЗИ
- Дальнейшее обобщение и некоторые предположения
- ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ ОПТИМАЛЬНЫХ кодов В ГАУССОВСКОМ КАНАЛЕ
- 2. Сводка результатов
- 3. Нижняя граница, основанная на соображениях «сферической упаковки»
- 4. Верхняя граница, определяемая методом случайного кодирования
- 5. Формулы для скорости передачи R как функции угла конуса
- 6. Асимптотические формулы для …
- 7. Асимптотическое выражение для верхней границы при случайном кодировании
- 8. Жесткая верхняя граница
- 9. Жесткая нижняя граница
- 10. Поведение границ вблизи пропускной способности канала
- 11. Верхняя граница, полученная методом исчерпывания
- 12. Нижняя граница для гауссовского канала, получаемая исходя из минимального расстояния
- 13. Границы ошибок и другие условия, накладываемые на точки
- 14. Кривые для асимптотических границ
- ТЕОРЕМЫ КОДИРОВАНИЯ ДЛЯ ДИСКРЕТНОГО ИСТОЧНИКА ПРИ ЗАДАННОМ КРИТЕРИИ ТОЧНОСТИ
- Мера искажения отдельной буквы
- Несколько простых примеров
- Скорость при заданном искажении R(d)
- Выпуклость вниз кривой R(d)
- Нахождение R(d) в некоторых простых случаях
- Скорость передачи для произведения источников с мерой, являющейся суммой мер искажения
- Нижняя граница для искажения при заданной пропускной способности канала
- Теоремы кодирования при заданной мере искажения отдельной буквы
- Двойственность источника и канала
- Численные расчеты для некоторых простых каналов
- Обобщение на случаи непрерывных алфавитов
- Разностная мера искажения
- Определение меры локального искажения
- Функции Rn(d) и R(d) для меры локального искажения и эргодического источника
- Прямая теорема кодирования для меры локального искажения
- Обратная теорема кодирования
- Канал с памятью
- ДВУСТОРОННИЕ КАНАЛЫ СВЯЗИ
- 4. Средние взаимные скорости передачи информации
- 5. Распределение информации
- 6. Случайное кодирование для двусторонних каналов
- 7. Вероятность ошибки для ансамбля кодов
- 8. Выпуклая оболочка G как внутренняя граница области пропускной способности
- 9. Внешняя граница для области пропускной способности
- 10. Выпуклость вниз как функций от …
- 11. Приложения свойства выпуклости. Каналы с симметричной структурой
- 12. Характер области, выделяемой внешней границей
- 13. Пример, в котором внутренняя и внешняя границы различны
- 14. Достижимость внешней границы при зависимых источниках
- 15. Общий метод нахождения области пропускной способности двустороннего канала
- 16. Двусторонние каналы с памятью
- 17. Обобщение на каналы с Т концами
- БАНДВАГОН
- ПРЕДСКАЗАНИЕ И ЭНТРОПИЯ ПЕЧАТНОГО АНГЛИЙСКОГО ТЕКСТА
- 2. Вычисление энтропии по статистике английского языка
- 3. Предсказание английского текста
- 4. Идеальное N-граммное предсказывание
- 5. Граница для энтропии на основании частот предсказания
- 6. Результаты эксперимента для английского языка
- УПРОЩЕННЫЙ ВЫВОД ЛИНЕЙНОЙ ТЕОРИИ СГЛАЖИВАНИЯ И ПРЕДСКАЗАНИЯ ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ
- 3. Свойства линейных фильтров
- 4. Основное выражение для среднеквадратичной ошибки
- 5. Чистая проблема сглаживания
- 6. Проблема чистого предсказания
- 7. Предсказание при наличии шума
- 8. Обобщения
- 9. Обсуждение основных предположений
- МАТЕМАТИЧЕСКАЯ ТЕОРИЯ ДИФФЕРЕНЦИАЛЬНОГО АНАЛИЗАТОРА
- Основное условие разрешимости
- Реализация функций
- Системы уравнений
- Аппроксимация множителей с помощью передаточных чисел
- Автоматическое управление скоростью работы устройства
- О МАКСИМАЛЬНОМ ПОТОКЕ ЧЕРЕЗ СЕТЬ
- ТЕОРЕМА О РАСКРАСКЕ РЕБЕР ГРАФА
- УНИВЕРСАЛЬНАЯ МАШИНА ТЬЮРИНГА С ДВУМЯ ВНУТРЕННИМИ СОСТОЯНИЯМИ
- Невозможность создания универсальной машины Тьюринга с одним состоянием
- Моделирование машины Тьюринга с помощью только двух символов на ленте
- ВЫЧИСЛИМОСТЬ НА ВЕРОЯТНОСТНЫХ МАШИНАХ
- Приложение
- БИБЛИОГРАФИЯ РАБОТ ПО ШЕННОНОВСКОЙ ТЕОРИИ ОПТИМАЛЬНОГО КОДИРОВАНИЯ ИНФОРМАЦИИ