| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЕОМЕТРИЧЕСКИЙ ПОДХОД К ТЕОРИИ ПРОПУСКНОЙ СПОСОБНОСТИ. КАНАЛОВ СВЯЗИ
Методам вычисления скорости передачи информации  и пропускной способности С дискретного канала без памяти, может быть дано геометрическое толкование, которое приводит к новым результатам и новому пониманию свойств этих величин. Наши результаты обобщают интересную статью
и пропускной способности С дискретного канала без памяти, может быть дано геометрическое толкование, которое приводит к новым результатам и новому пониманию свойств этих величин. Наши результаты обобщают интересную статью  рога и в некоторой степени перекрываются с ней, хотя мы исходили из различных соображений. Метод нашего исследования совершенно иной, поскольку нами используется геометрический подход, основанный на результатах теории выпуклых тел в противоположность алгебраическому подходу, который использовал Мурога.
рога и в некоторой степени перекрываются с ней, хотя мы исходили из различных соображений. Метод нашего исследования совершенно иной, поскольку нами используется геометрический подход, основанный на результатах теории выпуклых тел в противоположность алгебраическому подходу, который использовал Мурога.
Пусть канал определен матрицей  вероятностей перехода от буквы
вероятностей перехода от буквы  на входе к букве
на входе к букве  на выходе
на выходе  Можно рассматривать каждую строку этой матрицы как вектор или точку в
Можно рассматривать каждую строку этой матрицы как вектор или точку в  -мерном равностороннем симплексе
-мерном равностороннем симплексе  -мерный аналог отрезка прямой, равностороннего треугольника, тетраэдра и т. д.]. Координатами точки являются ее расстояния от граней, в сумме равные единице
-мерный аналог отрезка прямой, равностороннего треугольника, тетраэдра и т. д.]. Координатами точки являются ее расстояния от граней, в сумме равные единице  Они известны под названием барицентрических координат и соответствуют, например, координатам, часто используемым химиками при описаниях сплавов в терминах долей различных компонент.
Они известны под названием барицентрических координат и соответствуют, например, координатам, часто используемым химиками при описаниях сплавов в терминах долей различных компонент.
Таким образом, с входом  связывается точка или вектор
связывается точка или вектор  Его компоненты равны вероятностям различных букв на выходе, если используются все входы. Если использованы все входы (с вероятностью
Его компоненты равны вероятностям различных букв на выходе, если используются все входы. Если использованы все входы (с вероятностью  для входа
для входа  ), то вероятности букв на выходе
), то вероятности букв на выходе
даются компонентами векторной суммы

Вектору или точке  симплекса соответствуют также вероятности букв на выходе. Тогда
симплекса соответствуют также вероятности букв на выходе. Тогда  компонента этого вектора равна
компонента этого вектора равна  Поскольку
Поскольку  неотрицательны и в сумме дают единицу, то точки
неотрицательны и в сумме дают единицу, то точки  лежат в выпуклой оболочке (или барицентрической оболочке) точек
лежат в выпуклой оболочке (или барицентрической оболочке) точек  Более того, любая точка в этой выпуклой оболочке может быть получена при подходящем выборе
Более того, любая точка в этой выпуклой оболочке может быть получена при подходящем выборе 
Теперь для удобства обозначений определим энтропию точки или вектора из симплекса как энтропию барицентрических координат точки, интерпретированных как вероятности. Таким образом, имеем

и

где  — энтропия распределения полученных символов.
— энтропия распределения полученных символов.
В этих обозначениях скорость передачи  для данной системы вероятностей на входе
для данной системы вероятностей на входе  задается формулой
задается формулой

Функция  где
где  — точка симплекса, является выпуклой кверху функцией. Так, если компоненты
— точка симплекса, является выпуклой кверху функцией. Так, если компоненты  равны
равны  то имеем
то имеем

Отсюда  является отрицательно определенной формой. Это справедливо для пространства всех неотрицательных
является отрицательно определенной формой. Это справедливо для пространства всех неотрицательных  и отсюда, конечно, и для подпространства, в котором
и отсюда, конечно, и для подпространства, в котором  Следовательно, скорость
Следовательно, скорость  о которой шла речь выше,
о которой шла речь выше, 
всегда неотрицательна. Н строго выпукла (без плоских участков), и  положительна, если только не равно
положительна, если только не равно  для всех тех
для всех тех  для которых
для которых 
Процесс вычисления  может быть легко изображен наглядно в случае двух или трех букв на выходе. Если на выходе имеется три буквы, то представим себе равносторонний треугольник на некоторой основной плоскости. Это будет симплекс, содержащий точки А и
может быть легко изображен наглядно в случае двух или трех букв на выходе. Если на выходе имеется три буквы, то представим себе равносторонний треугольник на некоторой основной плоскости. Это будет симплекс, содержащий точки А и  Сверху этот треугольник покрыт куполообразной поверхностью, как показано на рис. 1.
Сверху этот треугольник покрыт куполообразной поверхностью, как показано на рис. 1.

Рис. 1. Пропускная способность канала в случае трех букв на входе и на выходе.
Высота этой поверхности над любой точкой А равна  Если на входе имеются три буквы с соответствующими векторами
Если на входе имеются три буквы с соответствующими векторами  то они отвечают трем точкам в треугольнике и трем точкам на куполе, расположенным непосредственно над первыми тремя точками. Каждый выходной вектор
то они отвечают трем точкам в треугольнике и трем точкам на куполе, расположенным непосредственно над первыми тремя точками. Каждый выходной вектор  является точкой треугольника, находящегося на основной плоскости и определенного точками
является точкой треугольника, находящегося на основной плоскости и определенного точками 
Энтропия  равна высоте купола над точкой
равна высоте купола над точкой  а
а  равна высоте над точкой
равна высоте над точкой  плоскости, задаваемой тремя точками купола, расположенными над
плоскости, задаваемой тремя точками купола, расположенными над  Иными словами,
Иными словами,  равно вертикальному отрезку прямой, проходящей через
равно вертикальному отрезку прямой, проходящей через  который отсекается куполом и плоскостью, определяемой этими тремя точками.
который отсекается куполом и плоскостью, определяемой этими тремя точками.
Пропускная способность С равна максимуму  Следовательно, в этом частном случае она равна максимальному расстоянию в вертикальном направлении от купола до внутренней части треугольника, вершины которого расположены на куполе над точками
Следовательно, в этом частном случае она равна максимальному расстоянию в вертикальном направлении от купола до внутренней части треугольника, вершины которого расположены на куполе над точками  Этот максимум, очевидно, достигается в точке касания
Этот максимум, очевидно, достигается в точке касания
плоскости, касательной к куполу и параллельной плоскости того же треугольника при условии, что проекция точки касания на основную плоскость лежит внутри треугольника, заданного точками  . В противном случае максимум
. В противном случае максимум  достигается на одной из сторон этого треугольника.
достигается на одной из сторон этого треугольника.
Если бы имелось четыре буквы на входе, то они в зависимости от своего расположения определили бы треугольник или четырехугольник на основной плоскости, а точки, расположенные прямо над ними на куполе, определили бы, вообще говоря, тетраэдр.

Рис. 2. Пропускная способность канала для пяти входных букв и трех выходных букв.
Использование для букв на входе различных распределений вероятности приводит к различным точкам в тетраэдре и к различным значениям  вычитаемым при вычислении
вычитаемым при вычислении  Очевидно, что максимум
Очевидно, что максимум  был бы достигнут только при таком выборе вероятностей, когда эта вычитаемая часть лежит где-либо на нижней грани тетраэдра. Эти замечания применимы также в случае, когда имеется еще большее количество букв на входе. Если имеется а букв на входе, то они определяют многоугольник с а или меньшим числом сторон на основной плоскости, а точки на куполе, расположенные над вершинами этого многоугольника, образуют симплекс. Любая точка из выпуклой оболочки точек, полученная на куполе, достигается при подходящем выборе
был бы достигнут только при таком выборе вероятностей, когда эта вычитаемая часть лежит где-либо на нижней грани тетраэдра. Эти замечания применимы также в случае, когда имеется еще большее количество букв на входе. Если имеется а букв на входе, то они определяют многоугольник с а или меньшим числом сторон на основной плоскости, а точки на куполе, расположенные над вершинами этого многоугольника, образуют симплекс. Любая точка из выпуклой оболочки точек, полученная на куполе, достигается при подходящем выборе  ей соответствует некоторое значение вычитаемого в формуле для вычисления
ей соответствует некоторое значение вычитаемого в формуле для вычисления  Ясно, что для нахождения максимума
Ясно, что для нахождения максимума  и определения таким образом значения С необходимо рассмотреть только нижнюю часть поверхности выпуклой оболочки (см. рис. 2).
и определения таким образом значения С необходимо рассмотреть только нижнюю часть поверхности выпуклой оболочки (см. рис. 2).
Геометрически очевидно также, что из выпуклости книзу нижней части симплекса и строгой выпуклости кверху купола вытекает существование единственной точки, в которой достигается максимум  и значит, и С. Если бы имелись две такие точки, то значение
и значит, и С. Если бы имелись две такие точки, то значение  в середине отрезка, соединяющего эти две точки, давало бы еще лучшее значение. Это объясняется тем, что вдоль кривой на куполе, соединяющей проекции этих точек, поверхность купола выпукла вверх, а средняя точка нижней соединительной кривой (на нижней грани выпуклой оболочки) не может сдвинуться вверх. Далее, скорость
в середине отрезка, соединяющего эти две точки, давало бы еще лучшее значение. Это объясняется тем, что вдоль кривой на куполе, соединяющей проекции этих точек, поверхность купола выпукла вверх, а средняя точка нижней соединительной кривой (на нижней грани выпуклой оболочки) не может сдвинуться вверх. Далее, скорость  является строго выпуклой кверху функцией выходного вектора
является строго выпуклой кверху функцией выходного вектора  Оказывается справедливым также тот факт, что скорость
Оказывается справедливым также тот факт, что скорость  является выпуклой кверху функцией вектора входных вероятностей (этот вектор имеет а барицентрических координат
является выпуклой кверху функцией вектора входных вероятностей (этот вектор имеет а барицентрических координат  в противоположность
в противоположность  координатам других наших векторов). Это утверждение выполняется потому, что векторы
координатам других наших векторов). Это утверждение выполняется потому, что векторы  и
и  отвечающие вероятностям на входе
отвечающие вероятностям на входе  , даются формулами
, даются формулами

Точкой  отвечающей вектору
отвечающей вектору  (где
(где  положительны), является точка
положительны), является точка  , следовательно,
, следовательно,  что и требовалось установить. Равенство может встретиться в случае
что и требовалось установить. Равенство может встретиться в случае  так что в этом случае нельзя говорить о строго выпуклой функции.
так что в этом случае нельзя говорить о строго выпуклой функции.
Из этих последних замечаний вытекает также, что множество  векторов Р, для которых скорость
векторов Р, для которых скорость  равна пропускной способности С, образует выпуклое множество в своем
равна пропускной способности С, образует выпуклое множество в своем  -мерном симплексе. Если максимум достигается в двух различных точках, то он также достигается и во всех точках отрезка, соединяющего эти точки. Более того, любой локальный максимум
-мерном симплексе. Если максимум достигается в двух различных точках, то он также достигается и во всех точках отрезка, соединяющего эти точки. Более того, любой локальный максимум  является также абсолютным максимумом, равным С. Допустим, что это неверно, и соединим отрезком точки, соответствующие локальному и абсолютному максимумам. Значение
является также абсолютным максимумом, равным С. Допустим, что это неверно, и соединим отрезком точки, соответствующие локальному и абсолютному максимумам. Значение  должно в силу выпуклости лежать на этой линии или выше ее, но в силу свойств максимума оно должно лежать ниже ее в достаточной близости от локального максимума. Это противоречие доказывает наше утверждение.
должно в силу выпуклости лежать на этой линии или выше ее, но в силу свойств максимума оно должно лежать ниже ее в достаточной близости от локального максимума. Это противоречие доказывает наше утверждение.
Приведенные результаты для геометрической наглядности были описаны для случая трех букв на выходе, но они легко обобщаются на случай  букв на выходе, если использовать хорошо известные результаты теории выпуклых тел.
букв на выходе, если использовать хорошо известные результаты теории выпуклых тел.
Еще одно легко выводимое свойство канала состоит в том, что пропускная способность С может быть достигнута при использовании не более чем  букв на входе, гдед — ранг матрицы
букв на входе, гдед — ранг матрицы  Это объясняется тем, что
Это объясняется тем, что  равно размерности множества точек
равно размерности множества точек
 Любая точка на поверхности
Любая точка на поверхности  -мерного симплекса лежит на некоторой его грани. Эта грань может быть подразделена на
-мерного симплекса лежит на некоторой его грани. Эта грань может быть подразделена на  -мерные симплексы (если она сама еще не является симплексом). Значит, точка лежит в одном из них. Вершинами симплекса являются
-мерные симплексы (если она сама еще не является симплексом). Значит, точка лежит в одном из них. Вершинами симплекса являются  букв на входе, и рассматриваемая точка может быть выражена через них. Теперь легко получается результат Мурога, состоящий в том, что пропускная способность не превышает
букв на входе, и рассматриваемая точка может быть выражена через них. Теперь легко получается результат Мурога, состоящий в том, что пропускная способность не превышает  Действительно, если использованы только
Действительно, если использованы только  букв, то энтропия входа не может превысить
букв, то энтропия входа не может превысить  а ненадежность может только уменьшить её значение.
а ненадежность может только уменьшить её значение.
Геометрическая картина дает важную информацию относительно того, какие буквы на входе следует использовать для достижения пропускной способности канала. Если, скажем, вектор  соответствующий входной букве
соответствующий входной букве  лежит в выпуклой оболочке векторов, соответствующих остальным буквам, то его не нужно использовать.
лежит в выпуклой оболочке векторов, соответствующих остальным буквам, то его не нужно использовать.
Так, предположим, что  где
где  Тогда по свойству выпуклости
Тогда по свойству выпуклости  Если при использовании
Если при использовании  с вероятностями
с вероятностями  получаем скорость
получаем скорость

то скорость, большая или равная  может быть получена, если в этой формуле выразить
может быть получена, если в этой формуле выразить  через другие
через другие  эта операция не изменит первый член
эта операция не изменит первый член  и уменьшит или не изменит вычитаемую сумму.
и уменьшит или не изменит вычитаемую сумму.
В случае наличия только двух букв на выходе ситуация чрезвычайно проста. Каково бы ни было количество букв на входе, для достижения пропускной способности канала нужно использовать только две из них. Эти две буквы должны быть выбраны так, чтобы на них достигались максимум и минимум вероятностей перехода к одной из букв на выходе. Эти буквы, скажем  помещены в одномерном симплексе — отрезке единичной длины и проектируются кверху на кривую Я, как показано на рис. 3. Если провести секущую, то пропускная способность будет равна наибольшему расстоянию в вертикальном направлении от секущей до кривой. Вероятности и
помещены в одномерном симплексе — отрезке единичной длины и проектируются кверху на кривую Я, как показано на рис. 3. Если провести секущую, то пропускная способность будет равна наибольшему расстоянию в вертикальном направлении от секущей до кривой. Вероятности и  которые необходимы для достижения этой пропускной способности, пропорциональны расстояниям от этой точки до обоих концов секущей.
которые необходимы для достижения этой пропускной способности, пропорциональны расстояниям от этой точки до обоих концов секущей.
В случае трех букв на выходе концы всех векторов, соответствующих буквам на входе, могут быть изображены точками равностороннего треугольника. Можно рассмотреть многоугольник, ограничивающий эти точки (их выпуклую оболочку вычеркнуть), и точки, внутренние для этого многоугольника (включая и точки на контуре),
требуется рассмотреть нижнюю поверхность симплекса, определенного точками, расположенными на куполе (над оставшимися точками). Эта нижняя поверхность, вообще говоря, будет состоять из треугольников, и наша задача заключается в нахождении вершин, лежащих на этой нижней поверхности. Метод решения этой задачи состоит, например, в рассмотрении отрезка, соединяющего пару вершин, и в последующем выяснении, лежат ли выше или ниже этого отрезка другие отрезки, проекции которых на основную плоскость пересекают проекцию первого отрезка.

Рис. 3. Пропускная способность канала в случае двух букв на выходе.
Если нет отрезков, лежащих ниже первого, то этот отрезок является ребром нижней поверхности симплекса. Если же некоторый отрезок лежит ниже первого, то он может быть исследован аналогичным способом, и в конце концов будет найдено одно ребро. Это ребро делит проекцию на два меньших многоугольника, и каждый из этих многоугольников должен быть рассмотрен таким же способом. В конце концов начальный многоугольник будет разбит на систему многоугольников, соответствующих поверхности симплекса. Относительно каждого из этих многоугольников нужно затем проверить, лежит ли или нет в этом многоугольнике проекция точки касания плоскости, параллельной ему соответствующей грани, касательной к куполу. Это случится в точности в одном из многоугольников, и тем самым будет определена точка  в которой достигается максимум
в которой достигается максимум 
Теперь докажем другое свойство выпуклости для дискретных каналов: докажем, что пропускная способность канала с
переходными вероятностями  является выпуклой книзу функцией этих вероятностей. Это значит, что пропускная способность С удовлетворяет неравенству, аналогичному неравенству соответствующих переходных вероятностей:
является выпуклой книзу функцией этих вероятностей. Это значит, что пропускная способность С удовлетворяет неравенству, аналогичному неравенству соответствующих переходных вероятностей:

где  является пропускной способностью, отвечающей вероятностям
является пропускной способностью, отвечающей вероятностям  — пропускной способностью, отвечающей вероятностям
— пропускной способностью, отвечающей вероятностям 
Чтобы доказать это, допустим, что пропускная способность канала с переходными вероятностями  достигается, когда вероятности букв на входе равны
достигается, когда вероятности букв на входе равны  Рассмотрим следующий канал. Он имеет такое же число входных букв, как и данный канал, и удвоенное число выходных букв (которое разобьем на два равных множества
Рассмотрим следующий канал. Он имеет такое же число входных букв, как и данный канал, и удвоенное число выходных букв (которое разобьем на два равных множества  Каждой выходной букве соответствуют переходные вероятности
Каждой выходной букве соответствуют переходные вероятности  Таким образом, этот канал является каналом, который получился бы при делении пополам всех вероятностей в каналах, отвечающих переходным вероятностям
Таким образом, этот канал является каналом, который получился бы при делении пополам всех вероятностей в каналах, отвечающих переходным вероятностям  и при одновременном отождествлении соответствующих входных букв и оставлении выходных букв различными. Заметим, что если соответственные выходные буквы отождествлены, то канал сводится к каналу, отвечающему переходным вероятностям
и при одновременном отождествлении соответствующих входных букв и оставлении выходных букв различными. Заметим, что если соответственные выходные буквы отождествлены, то канал сводится к каналу, отвечающему переходным вероятностям  Заметим также, что без такого отождествления этот канал будет работать так же, как канал, который половину времени работает как канал с переходными вероятностями
Заметим также, что без такого отождествления этот канал будет работать так же, как канал, который половину времени работает как канал с переходными вероятностями  а половину времени как канал с переходными вероятностями
а половину времени как канал с переходными вероятностями  Отождествление некоторых выходов всегда уменьшает (или не изменяет) скорость передачи. Пусть этот канал используется с вероятностями
Отождествление некоторых выходов всегда уменьшает (или не изменяет) скорость передачи. Пусть этот канал используется с вероятностями  для входных символов. Тогда для скоростей передачи может быть написано такое неравенство
для входных символов. Тогда для скоростей передачи может быть написано такое неравенство

где  является условной энтропией х, когда у принадлежит группе
является условной энтропией х, когда у принадлежит группе  является условной энтропией х, когда у принадлежит группе
является условной энтропией х, когда у принадлежит группе  Разбивая
Разбивая  на две части, чтобы объединить их с
на две части, чтобы объединить их с  получаем
получаем

где  является скоростью передачи канала, отвечающего переходным вероятностям
является скоростью передачи канала, отвечающего переходным вероятностям  когда выходы имеют вероятностии
когда выходы имеют вероятностии 
является аналогичной величиной для канала, отвечающего переходным вероятностям  Эти скорости, конечно, меньше соответственно, чем
Эти скорости, конечно, меньше соответственно, чем  или
или  так как пропускные способности являются максимальными возможными скоростями. Отсюда получаем желаемый результат
так как пропускные способности являются максимальными возможными скоростями. Отсюда получаем желаемый результат

Различные результаты, полученные нами, могут быть объединены следующим образом.
Теорема. Конечный дискретный канал без памяти обладает следующими свойствами.
1. Скорость передачи  является строго выпуклой кверху функцией от вероятностей полученных букв
является строго выпуклой кверху функцией от вероятностей полученных букв 
2. Скорость  является выпуклой кверху функцией от вероятностей букв
является выпуклой кверху функцией от вероятностей букв  на входе.
на входе.
3. Область пространства вероятностей букв на входе, в которой достигается пропускная способность канала, является выпуклым множеством.
4. Не существует локального максимума  который не является абсолютным максимумом С.
который не является абсолютным максимумом С.
5. Любая буква на входе, внутренняя для выпуклого тела, определенного другими буквами на входе, может быть выкинута без снижения пропускной способности канала.
6. Для достижения пропускной способности канала нужно использовать только  (соответствующим образом выбранных) букв на входе, где
(соответствующим образом выбранных) букв на входе, где  равно рангу матрицы
равно рангу матрицы  Более того,
Более того,  (по данным
(по данным  рога).
рога).
7. Пропускная способность является выпуклой вниз функцией переходных вероятностей 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- СИМВОЛИЧЕСКИЙ АНАЛИЗ РЕЛЕЙНЫХ И ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- 2. Параллельно-последовательные двухполюсные схемы. Основные определения и постулаты
- 3. Многополюсные и не параллельно-последовательные схемы
- Преобразование треугольника в звезду и звезды в ячейку
- Функция сопротивления не параллельно-последовательной схемы
- Системы уравнений
- Реле и переключатели специальных типов
- 4. Синтез схем
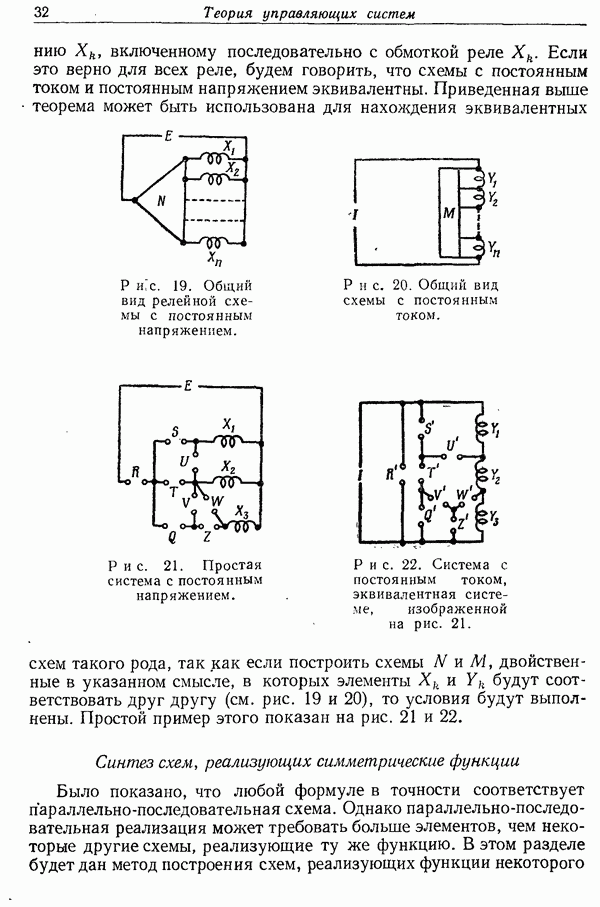
- Двойственные схемы
- Синтез схем, реализующих симметрические функции
- Составление уравнений по рабочим характеристикам
- 5. Примеры
- ЧИСЛО ДВУХПОЛЮСНЫХ ПАРАЛЛЕЛЬНО-ПОСЛЕДОВАТЕЛЬНЫХ СЕТЕЙ
- 1. Получение производящей функции
- 2. Численный подсчет
- 3. Асимптотическое поведение
- 4. Параллельно-последовательная реализация переключательных функций
- СИНТЕЗ ДВУХПОЛЮСНЫХ ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- 2. Основная теорема синтеза
- 3. Синтез схем для произвольных функций.
- Часть II. РАСПРЕДЕЛЕНИЕ НАГРУЗКИ МЕЖДУ РЕЛЕ
- 5. Разделительное дерево
- 6. Другие задачи распределения
- 7. Функция «мю»
- Часть III. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- 9. Частично симметрические функции
- ПРИМЕЧАНИЯ РЕДАКТОРА
- ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К ОБЪЕМУ ПАМЯТИ ТЕЛЕФОННОГО КОММУТАТОРА
- 2. Память, требуемая для S произвольных вызовов от N абонентов
- 3. Условие раздельной памяти
- 4. Связь с теорией информации
- НАДЕЖНЫЕ СХЕМЫ ИЗ НЕНАДЕЖНЫХ РЕЛЕ
- Идеализированные реле
- Общий метод повышения надежности
- Свойства функции h(p)
- Комбинация двух схем
- Оценки функции h'(p)
- Схемы заданной длины и ширины
- Оценки числа контактов в случае, когда реле уже достаточно надежны
- Сравнение с элементами фон Неймана
- Реле с неопределенным временем срабатывания
- Синтез надежных схем в целом
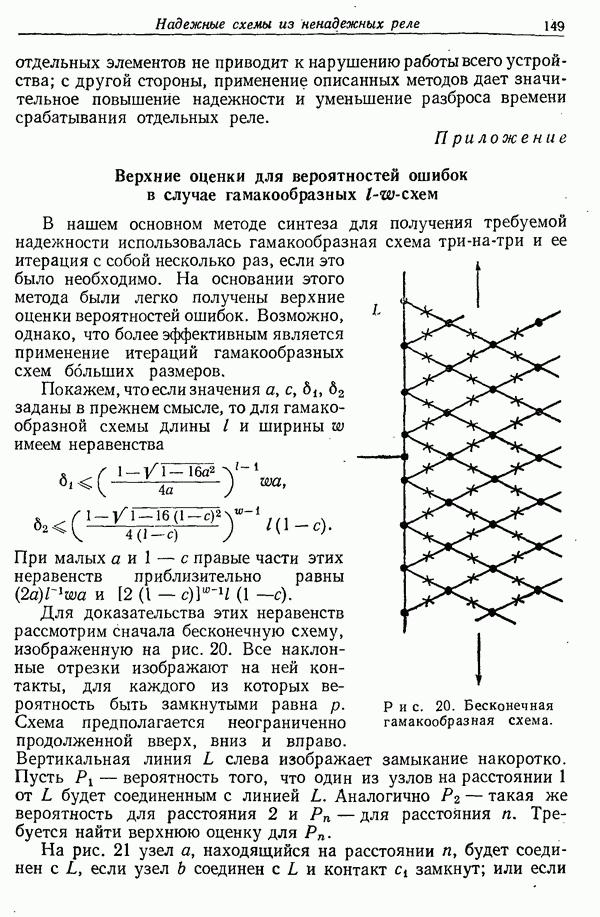
- Приложение. Верхние оценки для вероятностей ошибок в случае гамакообразных l-w-схем
- ИСПОЛЬЗОВАНИЕ МАШИНЫ ДЛЯ ПРОЕКТИРОВАНИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА И АВТОМАТЫ
- Машины Тьюринга
- Логические машины
- «Играющие машины»
- Обучаемые машины
- Самовоспроизводящиеся машины
- Обращение к читателю
- МАШИНА ДЛЯ ИГРЫ В ШАХМАТЫ
- СОСТАВЛЕНИЕ ПРОГРАММ ДЛЯ ИГРЫ В ШАХМАТЫ НА ВЫЧИСЛИТЕЛЬНОЙ МАШИНЕ
- 3. Приближенная оценочная функция
- 4. Стратегия, основанная на оценочной функции
- 5. Составление программы для универсальной вычислительной машины для реализации стратегии типа А
- 6. Улучшение стратегии
- 7. Изменения в игре и в стиле
- 8. Другой тип стратегии
- ПРИЛОЖЕНИЕ. ОЦЕНОЧНАЯ ФУНКЦИЯ ДЛЯ ШАХМАТ
- ИГРАЮЩИЕ МАШИНЫ
- СООБЩЕНИЕ О МАШИНЕ, РЕШАЮЩЕЙ ЛАБИРИНТНУЮ ЗАДАЧУ
- ВКЛАД ФОН НЕЙМАНА В ТЕОРИЮ АВТОМАТОВ
- МАТЕМАТИЧЕСКАЯ ТЕОРИЯ СВЯЗИ
- 1. ДИСКРЕТНЫЕ СИСТЕМЫ БЕЗ ШУМОВ
- 2. Дискретный источник сообщений
- 3. Последовательные приближения к английскому языку
- 4. Графическое представление марковского процесса
- 5. Эргодические и смешанные источники
- 6. Выбор, неопределенность и энтропия
- 7. Энтропия источника сообщений
- 8. Представление операций кодирования и декодирования
- 9. Основная теорема для канала без шума
- 10. Рассмотрение полученных результатов и примеры
- 11. Примеры
- II. ДИСКРЕТНЫЙ КАНАЛ С ШУМОМ
- 12. Надежность и пропускная способность канала
- 13. Основная теорема для дискретного канала с шумом
- 14. Рассмотрение полученных результатов
- 15. Пример дискретного канала и его пропускной способности
- 16. Пропускная способность канала в некоторых частных случаях
- 17. Пример эффективного кодирования
- III. ИНФОРМАЦИЯ ДЛЯ НЕПРЕРЫВНЫХ ВЕЛИЧИН
- 19. Ансамбли функций с ограниченной полосой частот
- 20. Энтропия непрерывного распределения
- 21. Энтропия ансамбля функций
- 22. Потеря энтропии в линейных фильтрах
- 23. Энтропия суммы двух ансамблей
- IV. НЕПРЕРЫВНЫЙ КАНАЛ
- 24. Пропускная способность непрерывного канала
- 25. Пропускная способность канала при ограничении средней мощности
- 26. Пропускная способность канала при ограничении пиковой мощности
- V. СКОРОСТЬ СОЗДАНИЯ СООБЩЕНИЙ ДЛЯ НЕПРЕРЫВНОГО ИСТОЧНИКА
- 28. Скорость создания сообщений источником при данной точности воспроизведения
- 29. Вычисление скорости создания сообщений
- Приложение 1. РОСТ ЧИСЛА БЛОКОВ СИМВОЛОВ ПРИ УСЛОВИЯХ, ОПИСЫВАЕМЫХ КОНЕЧНЫМ ЧИСЛОМ СОСТОЯНИЙ
- Приложение 2. ВЫВОД РАВЕНСТВА …
- Приложение 3. ТЕОРЕМА ОБ ЭРГОДИЧЕСКИХ ИСТОЧНИКАХ
- Приложение 4. МАКСИМИЗАЦИЯ СКОРОСТИ ДЛЯ СИСТЕМЫ ОГРАНИЧЕНИЯ
- Приложение 5
- Приложение 6
- Приложение 7
- ТЕОРИЯ СВЯЗИ В СЕКРЕТНЫХ СИСТЕМАХ
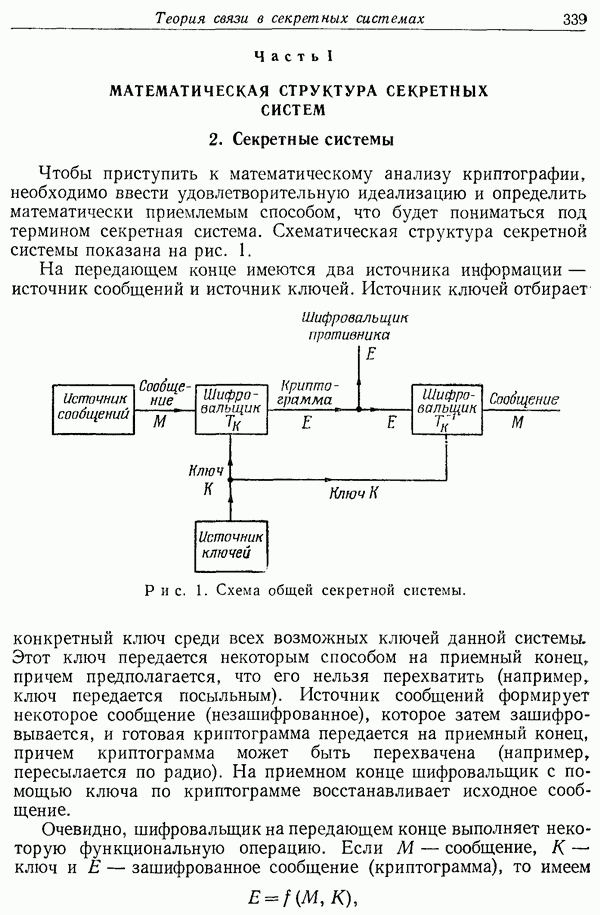
- Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ СИСТЕМ
- 3. Способы изображения систем
- 4. Примеры секретных систем
- 5. Оценка секретных систем
- 6. Алгебра секретных систем
- 7. Чистые и смешанные шифры
- 8. Подобные системы
- Часть II. ТЕОРЕТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 10. Совершенная секретность
- 11. Ненадежность
- 12. Свойства ненадежности
- 13. Ненадежность простой подстановки для языка с двухбуквенным алфавитом
- 14. Характеристика ненадежности для «случайного» шифра
- 15. Применение к стандартным шифрам
- 16. Правильность решения криптограммы
- 17. Идеальные секретные системы
- 18. Примеры идеальных секретных систем
- 19. Дополнительные замечания о ненадежности и избыточности
- 20. Распределение ненадежности
- Часть III. ПРАКТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 22. Общие замечания о решении криптограмм
- 23. Статистические методы
- 24. Метод вероятных слов
- 25. Перемешивание
- 26. Шифры типа …
- 27. Несовместимость требований к хорошим системам
- ПРИЛОЖЕНИЕ. Доказательство теоремы 3
- СОВРЕМЕННЫЕ ДОСТИЖЕНИЯ ТЕОРИИ СВЯЗИ
- Измерение информаций
- Кодирование информации
- Пропускная способность канала
- Идеальные и практические системы
- ПРИНЦИПЫ КОДОВО-ИМПУЛЬСНОЙ МОДУЛЯЦИИ
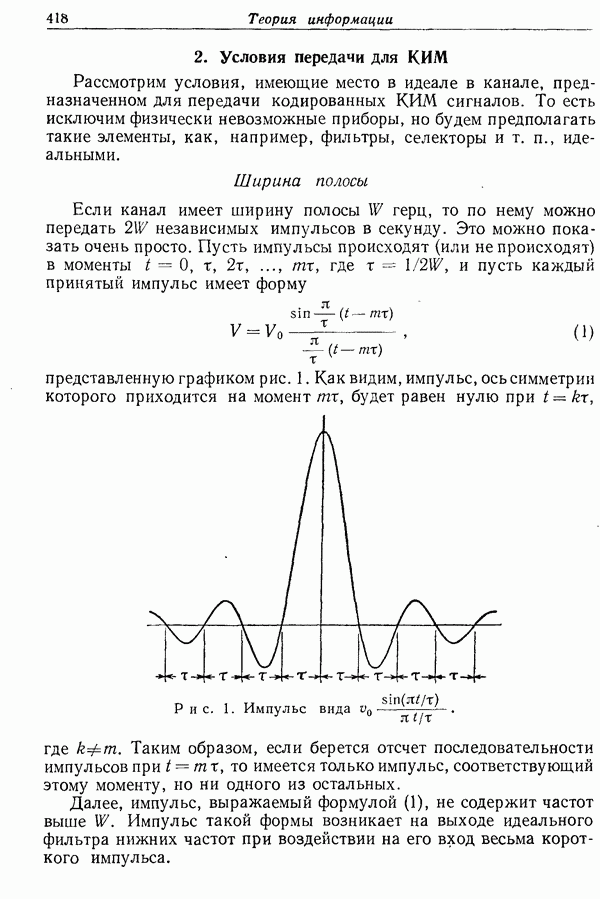
- 2. Условия передачи для КИМ
- 3. Действие системы КИМ
- 4. Сравнение КИМ и ЧМ
- 5. Заключение
- Приложение I
- Приложение II
- СВЯЗЬ ПРИ НАЛИЧИИ ШУМА
- 2. Теорема отсчетов
- 3. Геометрическое представление сигналов
- 4. Геометрическое представление сообщений
- 5. Геометрическое представление передатчика и приемника
- 6. Отображение пространства
- 7. Пропускная способность канала при наличии белого теплового шума
- 8. Обсуждение
- 9. Произвольный гауссовский шум
- 10. Пропускная способность канала при произвольном типе шума
- 11. Дискретные источники информации
- 12. Непрерывные источники информации
- НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ИНФОРМАЦИИ
- ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА С ШУМОМ ПРИ НУЛЕВОЙ ОШИБКЕ
- Пропускная способность канала при нулевой ошибке
- Пропускная способность для суммы и произведения каналов
- Каналы с обратной связью
- ГЕОМЕТРИЧЕСКИЙ ПОДХОД К ТЕОРИИ ПРОПУСКНОЙ СПОСОБНОСТИ. КАНАЛОВ СВЯЗИ
- КАНАЛЫ С ДОПОЛНИТЕЛЬНОЙ ИНФОРМАЦИЕЙ НА ПЕРЕДАТЧИКЕ
- Дискретный канал без памяти с дополнительной информацией о состоянии
- Приложение
- НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ТЕОРИИ КОДИРОВАНИЯ ДЛЯ КАНАЛОВ С ШУМАМИ
- Оценка вероятности ошибки в терминах производящей функции моментов
- Пропускная способность канала с конечным числом состояний, состояние которого вычислимо на обоих концах
- Пропускная способность канала с конечным числом состояний в случае, когда состояние вычислимо на передающем конце и не вычислимо на приемном конце
- ЗАМЕЧАНИЯ О ЧАСТИЧНОМ УПОРЯДОЧИВАНИИ КАНАЛОВ СВЯЗИ
- Дальнейшее обобщение и некоторые предположения
- ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ ОПТИМАЛЬНЫХ кодов В ГАУССОВСКОМ КАНАЛЕ
- 2. Сводка результатов
- 3. Нижняя граница, основанная на соображениях «сферической упаковки»
- 4. Верхняя граница, определяемая методом случайного кодирования
- 5. Формулы для скорости передачи R как функции угла конуса
- 6. Асимптотические формулы для …
- 7. Асимптотическое выражение для верхней границы при случайном кодировании
- 8. Жесткая верхняя граница
- 9. Жесткая нижняя граница
- 10. Поведение границ вблизи пропускной способности канала
- 11. Верхняя граница, полученная методом исчерпывания
- 12. Нижняя граница для гауссовского канала, получаемая исходя из минимального расстояния
- 13. Границы ошибок и другие условия, накладываемые на точки
- 14. Кривые для асимптотических границ
- ТЕОРЕМЫ КОДИРОВАНИЯ ДЛЯ ДИСКРЕТНОГО ИСТОЧНИКА ПРИ ЗАДАННОМ КРИТЕРИИ ТОЧНОСТИ
- Мера искажения отдельной буквы
- Несколько простых примеров
- Скорость при заданном искажении R(d)
- Выпуклость вниз кривой R(d)
- Нахождение R(d) в некоторых простых случаях
- Скорость передачи для произведения источников с мерой, являющейся суммой мер искажения
- Нижняя граница для искажения при заданной пропускной способности канала
- Теоремы кодирования при заданной мере искажения отдельной буквы
- Двойственность источника и канала
- Численные расчеты для некоторых простых каналов
- Обобщение на случаи непрерывных алфавитов
- Разностная мера искажения
- Определение меры локального искажения
- Функции Rn(d) и R(d) для меры локального искажения и эргодического источника
- Прямая теорема кодирования для меры локального искажения
- Обратная теорема кодирования
- Канал с памятью
- ДВУСТОРОННИЕ КАНАЛЫ СВЯЗИ
- 4. Средние взаимные скорости передачи информации
- 5. Распределение информации
- 6. Случайное кодирование для двусторонних каналов
- 7. Вероятность ошибки для ансамбля кодов
- 8. Выпуклая оболочка G как внутренняя граница области пропускной способности
- 9. Внешняя граница для области пропускной способности
- 10. Выпуклость вниз как функций от …
- 11. Приложения свойства выпуклости. Каналы с симметричной структурой
- 12. Характер области, выделяемой внешней границей
- 13. Пример, в котором внутренняя и внешняя границы различны
- 14. Достижимость внешней границы при зависимых источниках
- 15. Общий метод нахождения области пропускной способности двустороннего канала
- 16. Двусторонние каналы с памятью
- 17. Обобщение на каналы с Т концами
- БАНДВАГОН
- ПРЕДСКАЗАНИЕ И ЭНТРОПИЯ ПЕЧАТНОГО АНГЛИЙСКОГО ТЕКСТА
- 2. Вычисление энтропии по статистике английского языка
- 3. Предсказание английского текста
- 4. Идеальное N-граммное предсказывание
- 5. Граница для энтропии на основании частот предсказания
- 6. Результаты эксперимента для английского языка
- УПРОЩЕННЫЙ ВЫВОД ЛИНЕЙНОЙ ТЕОРИИ СГЛАЖИВАНИЯ И ПРЕДСКАЗАНИЯ ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ
- 3. Свойства линейных фильтров
- 4. Основное выражение для среднеквадратичной ошибки
- 5. Чистая проблема сглаживания
- 6. Проблема чистого предсказания
- 7. Предсказание при наличии шума
- 8. Обобщения
- 9. Обсуждение основных предположений
- МАТЕМАТИЧЕСКАЯ ТЕОРИЯ ДИФФЕРЕНЦИАЛЬНОГО АНАЛИЗАТОРА
- Основное условие разрешимости
- Реализация функций
- Системы уравнений
- Аппроксимация множителей с помощью передаточных чисел
- Автоматическое управление скоростью работы устройства
- О МАКСИМАЛЬНОМ ПОТОКЕ ЧЕРЕЗ СЕТЬ
- ТЕОРЕМА О РАСКРАСКЕ РЕБЕР ГРАФА
- УНИВЕРСАЛЬНАЯ МАШИНА ТЬЮРИНГА С ДВУМЯ ВНУТРЕННИМИ СОСТОЯНИЯМИ
- Невозможность создания универсальной машины Тьюринга с одним состоянием
- Моделирование машины Тьюринга с помощью только двух символов на ленте
- ВЫЧИСЛИМОСТЬ НА ВЕРОЯТНОСТНЫХ МАШИНАХ
- Приложение
- БИБЛИОГРАФИЯ РАБОТ ПО ШЕННОНОВСКОЙ ТЕОРИИ ОПТИМАЛЬНОГО КОДИРОВАНИЯ ИНФОРМАЦИИ