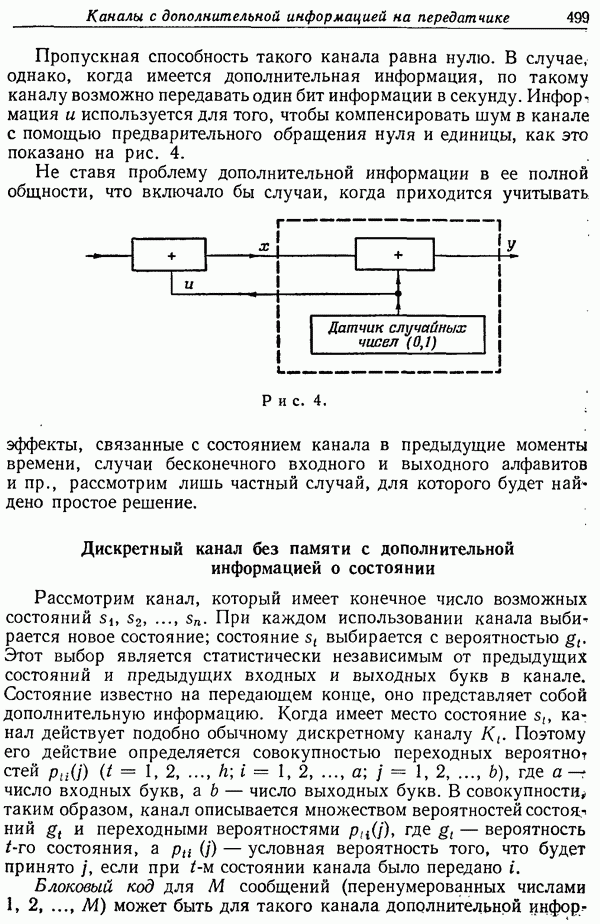
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ВЫЧИСЛИМОСТЬ НА ВЕРОЯТНОСТНЫХ МАШИНАХ
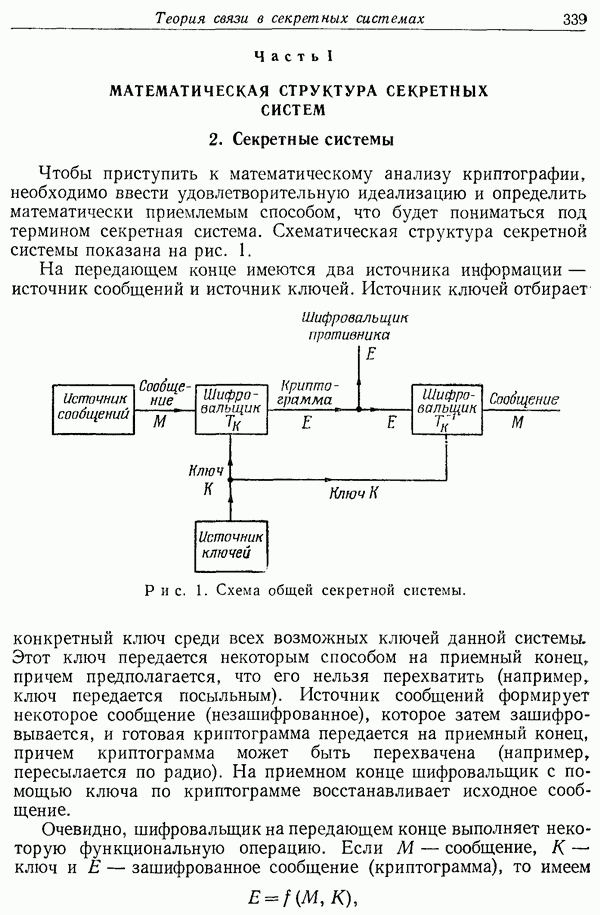
В статье рассматривается следующий вопрос: имеются ли задачи, которые может решать машина со случайным элементом, но не может решать детерминистская машина?
Конечно, в таком виде вопрос выглядит слишком неопределенным, чтобы быть доступным для математического анализа. В дальнейшем ограничим его в двояком отношении. Будет дано точное определение класса рассматриваемых машин и столь же точное определение выполняемых ими задач. Ясно, что наши выводы будут сильно зависеть от выбора этих двух определений, и поэтому их нельзя считать полным решением первоначального неформального вопроса. Читатель должен иметь в виду, что полученные нами результаты неприменимы вне области, обусловленной выбранными определениями. В частности, они указывают на возможность перечисления бесконечных множеств и вычисления бесконечных последовательностей, но не дают информации о типе вероятностных машин, предназначенных для решения конечных задач, например об относительной сложности и относительном быстродействии таких машин.
Подобные затруднения присутствуют неявно при всяком применении математики к некоторому поставленному неформально вопросу. Формулировка такого вопроса в точной математической форме неизбежно сосредоточивает внимание на некоторых его сторонах, в то время как другие стороны, одинаково и даже более важные в иной ситуации, могут оказаться совершенно неучтенными.
Основной текст настоящей статьи содержит определения, примеры и формулировки результатов. Доказательства перенесены в приложение, так как большей частью они представляют собой более или менее сложные построения, которые не являются абсолютно необходимыми для понимания работы.
Читатели, знакомые с теорией рекурсивных функций, без труда увидят, что наши теоремы принадлежат этой теории и легко могут быть переведены на ее язык. Ввиду этого доказательства получают двоякое значение. Если считать определенным интуитивное понятие эффективного процесса, то их можно рассматривать как полные доказательства. С другой стороны, их можно рассматривать как указания, исходя из которых, можно теоремы, сформулированные на языке теории рекурсивных функций, доказать формально средствами этой теории. Такие формальные доказательства не приводятся, чтобы не отвлекать читателя от содержания работы. Однако возможность формализации ясна всякому, кто знаком с теорией рекурсивных функций.
Вероятностные машины в сравнении с детерминистскими
Начнем с точного определения некоторого класса вычислительных машин. Эти машины имеют вход и выход. Входом является бесконечная последовательность двоичных знаков, которая может подаваться двумя различными способами: 1) как фиксированная последовательность (физически можно представить заранее подготовленную бесконечную ленту); 2) как выход двоичного случайного устройства (с вероятностью  появления 1). В последнем случае мы имеем вероятностную машину. Затем очертим точный класс задач, подлежащих решению на этих машинах, а именно перечисление с положительной вероятностью множеств выходных символов. После этого ключевой результат настоящей статьи — теорема 1— используется для получения подхода к ответу на наш вопрос. Ответ дается теоремой 2. Он гласит, что если случайное устройство имеет вероятность
появления 1). В последнем случае мы имеем вероятностную машину. Затем очертим точный класс задач, подлежащих решению на этих машинах, а именно перечисление с положительной вероятностью множеств выходных символов. После этого ключевой результат настоящей статьи — теорема 1— используется для получения подхода к ответу на наш вопрос. Ответ дается теоремой 2. Он гласит, что если случайное устройство имеет вероятность  где
где  — вычислимое действительное число (т. е. действительное число, для которого существует эффективный процесс нахождения любого знака в его двоичном разложении), то любое множество, перечислимое посредством вероятностной машины рассматриваемого типа, перечислимо посредством детерминистской машины. Это не справедливо, если
— вычислимое действительное число (т. е. действительное число, для которого существует эффективный процесс нахождения любого знака в его двоичном разложении), то любое множество, перечислимое посредством вероятностной машины рассматриваемого типа, перечислимо посредством детерминистской машины. Это не справедливо, если  — невычислимое действительное число. Аналогичные результаты получаются для случая, когда учитывается порядок следования выходных символов. Положение подытоживается теоремой 3.
— невычислимое действительное число. Аналогичные результаты получаются для случая, когда учитывается порядок следования выходных символов. Положение подытоживается теоремой 3.
Представим наши машины в виде объектов, которые воспринимают в качестве входа ленту с записанными на ней нулями и единицами и выдают в качестве выхода ленту, на которой они могут записывать конечную или счетную последовательность выходных
символов  символами могут быть конфигурации, образованные из некоторого конечного алфавита). Предполагается, что машина имеет некоторое начальное состояние, в которое она приводится перед началом любой операции (подобно тому, как счетно-клавишная машина гасится перед началом вычислений). Другое разумное требование к машине таково: должна существовать эффективная методика, позволяющая определить, какова будет последовательность выходных символов
символами могут быть конфигурации, образованные из некоторого конечного алфавита). Предполагается, что машина имеет некоторое начальное состояние, в которое она приводится перед началом любой операции (подобно тому, как счетно-клавишная машина гасится перед началом вычислений). Другое разумное требование к машине таково: должна существовать эффективная методика, позволяющая определить, какова будет последовательность выходных символов  если в начальном состоянии машине предъявлена входная последовательность нулей и единиц
если в начальном состоянии машине предъявлена входная последовательность нулей и единиц  Эту выходную последовательность обозначим через
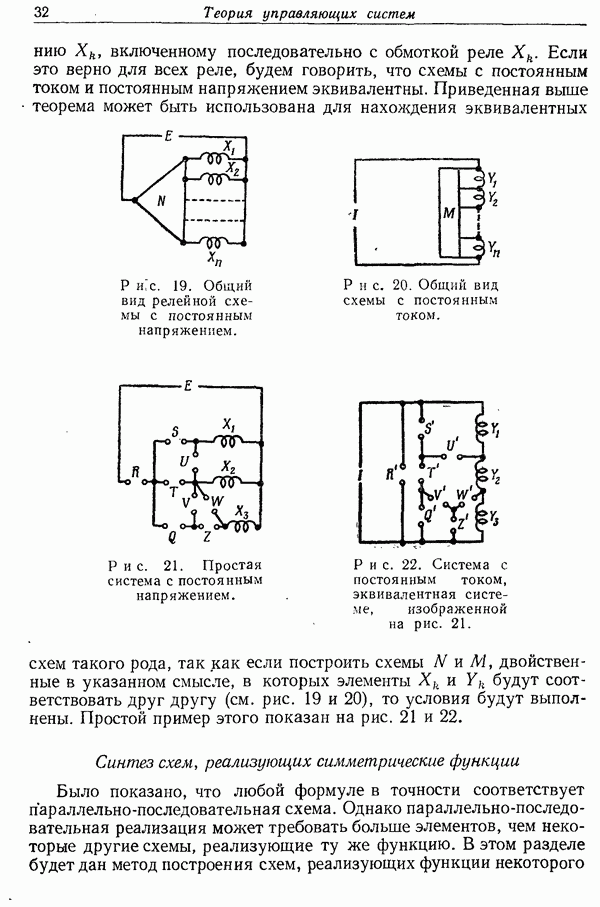
Эту выходную последовательность обозначим через  Так как нас интересует только зависимость между входом и выходом машин, то можно отвлечься от их внутреннего устройства и принять это требование за определение. (Хотя этим дано абстрактное определение, дальше будем говорить о конкретных машинах.)
Так как нас интересует только зависимость между входом и выходом машин, то можно отвлечься от их внутреннего устройства и принять это требование за определение. (Хотя этим дано абстрактное определение, дальше будем говорить о конкретных машинах.)
Определение. Машина есть функция, которая для каждого  ставит в соответствие каждой конечной последовательности из
ставит в соответствие каждой конечной последовательности из  нулей и единиц
нулей и единиц  некоторую конечную последовательность
некоторую конечную последовательность  состоящую из элементов заданного множества
состоящую из элементов заданного множества  причем выполняются условия:
причем выполняются условия:
1)  есть начальный отрезок в
есть начальный отрезок в

если  есть начальный отрезок в
есть начальный отрезок в

2) f — вычислимая функция, т. е. существует эффективный процесс, позволяющий определить  по заданной
по заданной 
Это определение распространяется на бесконечные последовательности следующим образом: если  то
то  есть последовательность с начальными отрезками
есть последовательность с начальными отрезками 
Неформально работу машины можно представить себе следующим образом. Получив на входе  она воспринимает
она воспринимает  и записывает последовательность символов
и записывает последовательность символов  на выходе; затем она воспринимает
на выходе; затем она воспринимает  и записывает символы на ленте после
и записывает символы на ленте после  производя
производя  затем она воспринимает
затем она воспринимает  и записывает символы на ленте после
и записывает символы на ленте после  производя
производя

и, наконец, останавливается.
Теперь дадим несколько конкретных примеров машин. Этим преследуется двоякая цель: проиллюстрировать наше понятие машины и подготовить материал для иллюстрации новых
понятий, вводимых далее. Пока можно при чтении пропустить ряд примеров.
Машина № 1. Выходными символами этой машины являются упорядоченные пары целых чисел  . Для каждого входного символа а машина записывает выходной символ
. Для каждого входного символа а машина записывает выходной символ  , если а был
, если а был  входным символом на входной ленте. Иными словами,
входным символом на входной ленте. Иными словами, 
Машина № 2. Пусть  — целочисленная положительная функция и пусть она вычислима, т. е. существует эффективный процесс для нахождения
— целочисленная положительная функция и пусть она вычислима, т. е. существует эффективный процесс для нахождения  по заданному
по заданному  Пусть машина записывает символ
Пусть машина записывает символ  после восприятия
после восприятия  входного символа. В этом случае
входного символа. В этом случае  и выход не зависит от входа. Эта машина и машина № 1 представляют крайние случаи. Машина № 2 забывает о входе, а № 1 по существу копирует вход на выходной ленте. Заметим, что объект № 2 не был бы машиной в смысле нашего определения, если бы функция
и выход не зависит от входа. Эта машина и машина № 1 представляют крайние случаи. Машина № 2 забывает о входе, а № 1 по существу копирует вход на выходной ленте. Заметим, что объект № 2 не был бы машиной в смысле нашего определения, если бы функция  не была вычислима, ибо в этом случае не существовало бы эффективного процесса, позволяющего определить выход по заданному входу.
не была вычислима, ибо в этом случае не существовало бы эффективного процесса, позволяющего определить выход по заданному входу.
Машина № 3. Пусть машина записывает символ 0, встретив первый нуль во входной последовательности. В остальное время она не записывает ничего. Тогда  если один из символов
если один из символов  является нулем. В противном случае машина не записывает ничего, и такая последовательность будет «пустой последовательностью»
является нулем. В противном случае машина не записывает ничего, и такая последовательность будет «пустой последовательностью» 
Машина № 4. Пусть  Машина просто копирует на выходной ленте первый входной символ, не записывая больше ничего.
Машина просто копирует на выходной ленте первый входной символ, не записывая больше ничего.
Машина № 5. Пусть машина записывает выходной символ  если максимальная длина групп единиц, воспринятых машиной, равна
если максимальная длина групп единиц, воспринятых машиной, равна  Например,
Например,  .
.
Машина № 6. Пусть  — вычислимая целочисленная положительная функция. Машина не записывает ничего, пока не встретит первой единицы на входе; если эта единица — первый входной символ, то машина вообще ничего не печатает; если же эта единица встретилась после
— вычислимая целочисленная положительная функция. Машина не записывает ничего, пока не встретит первой единицы на входе; если эта единица — первый входной символ, то машина вообще ничего не печатает; если же эта единица встретилась после  нулей, то записывается символ
нулей, то записывается символ  После следующего входного символа машина записывает символ
После следующего входного символа машина записывает символ  после следующего — символ
после следующего — символ  Пусть функция
Пусть функция  с фиксированным
с фиксированным  определяется соотношением
определяется соотношением  Тогда работа машины фактически состоит в вычислении функции
Тогда работа машины фактически состоит в вычислении функции  при поступлении в машину начальной группы нулей и следующей за ними единицы.
при поступлении в машину начальной группы нулей и следующей за ними единицы.
Машина № 7. Эта машина задается соотношением  где целое число
где целое число 
получается следующим образом. Возьмем первые  знаков в
знаков в  Пусть
Пусть  доля знаков, равных 1. Тогда
доля знаков, равных 1. Тогда  есть
есть  знак в двоичном разложении числа
знак в двоичном разложении числа  Число q есть наибольшее
Число q есть наибольшее  такое, что
такое, что  Аналогичная машина используется при доказательстве части теоремы 1.
Аналогичная машина используется при доказательстве части теоремы 1.
Хотя работа машины определена только для конечных входных последовательностей, тем не менее ясно, что сделала бы такая машина, получая бесконечную входную последовательность  и обладая бесконечной выходной лентой для записи. Работа машины определена тем фактом, что известен ее выход для всех конечных входных последовательностей. Таким образом, машина ставит в соответствие каждой бесконечной входной последовательности выходную последовательность, которая может быть или не быть бесконечной.
и обладая бесконечной выходной лентой для записи. Работа машины определена тем фактом, что известен ее выход для всех конечных входных последовательностей. Таким образом, машина ставит в соответствие каждой бесконечной входной последовательности выходную последовательность, которая может быть или не быть бесконечной.
Если вводить в машину № I бесконечную ленту, на которой записаны только единицы, то выходная последовательность будет  Для этой же ленты машина № 3 не даст никакого выхода [пустая последовательность
Для этой же ленты машина № 3 не даст никакого выхода [пустая последовательность  ], а машина № 4 даст выходную последовательность (1).
], а машина № 4 даст выходную последовательность (1).
Рассмотрим множество символов, появляющихся на выходной ленте машины, когда машина получает некоторую бесконечную входную последовательность А. (Если выходная последовательность есть ( то это множество состоит лишь из одного символа 1, а если наша выходная последовательность есть (
то это множество состоит лишь из одного символа 1, а если наша выходная последовательность есть ( то множество символов состоит из всех нечетных чисел.) Таким образом, машина ставит в соответствие каждой входной последовательности А некоторое множество выходных символов, которое она перечисляет. (Не будем здесь обращать внимание на порядок, в котором это множество перечисляется, а также на то, перечисляется ли оно с повторениями или без повторений. Это будет сделано позже, при рассмотрении вычисления последовательностей.)
то множество символов состоит из всех нечетных чисел.) Таким образом, машина ставит в соответствие каждой входной последовательности А некоторое множество выходных символов, которое она перечисляет. (Не будем здесь обращать внимание на порядок, в котором это множество перечисляется, а также на то, перечисляется ли оно с повторениями или без повторений. Это будет сделано позже, при рассмотрении вычисления последовательностей.)
Например, машина № 1 ставит в соответствие любой бесконечной входной последовательности  множество выходных символов, состоящее из всех
множество выходных символов, состоящее из всех  где
где  пробегает целые положительные числа. Машина № 2 ставит в соответствие любой входной последовательности множество всех
пробегает целые положительные числа. Машина № 2 ставит в соответствие любой входной последовательности множество всех  где
где  пробегает целые положительные числа. Машина № 3 ставит в соответствие входной последовательности, состоящей только из единиц, пустое множество. Такому же входу машина № 5 ставит в соответствие множество всех целых положительных чисел.
пробегает целые положительные числа. Машина № 3 ставит в соответствие входной последовательности, состоящей только из единиц, пустое множество. Такому же входу машина № 5 ставит в соответствие множество всех целых положительных чисел. 
Определение. Машина, получающая бесконечную входную последовательность  будет называться Л-машиной. Будем говорить, что она
будет называться Л-машиной. Будем говорить, что она  -перечисляет множество выходных символов, записываемых ею. Множество каких-либо
-перечисляет множество выходных символов, записываемых ею. Множество каких-либо
символов называется А-перечислимым, если существует Л-машина, которая А-перечисляет это множество.
А - перечислимые множества, где Л есть последовательность, состоящая только из единиц, обычно называются рекурсивно-перечислимыми множествами. Мы назовем их А-перечислимыми множествами. Л-машина будет называться  -машиной, если А состоит целиком из единиц.
-машиной, если А состоит целиком из единиц.
Каждой бесконечной последовательности  можно поставить в соответствие множество всех пар
можно поставить в соответствие множество всех пар  где
где  ость
ость  элемент в последовательности А, а
элемент в последовательности А, а  пробегает все целые положительные числа. Это множество обозначим через А. Последовательность А называется вычислимой, если существует эффективный процесс, с помощью которого можно определить
пробегает все целые положительные числа. Это множество обозначим через А. Последовательность А называется вычислимой, если существует эффективный процесс, с помощью которого можно определить  член в А для каждого
член в А для каждого  Три следующие леммы доказываются в приложении, хотя их доказательства почти очевидны.
Три следующие леммы доказываются в приложении, хотя их доказательства почти очевидны.
Лемма 1. Последовательность А вычислима тогда и только тогда, когда соответствующее множество А является  -перечислимым.
-перечислимым.
Лемма 2. Если А — вычислимая последовательность, то любое А-перечислимое множество  -перечислимо (и обратно).
-перечислимо (и обратно).
Лемма 3. Если А — невычислимая последовательность, то существуют множества А-перечислимые, но не  -перечислимые.
-перечислимые.
Лемма 3 и существование невычислимых последовательностей будут важны для нас позже.
Теперь желательно присоединить к машине случайное устройство, чтобы построить вероятностную машину. Если у нас есть устройство, записывающее нули и единицы на ленте, и если единицы появляются с вероятностью  нули — с вероятностью
нули — с вероятностью  причем каждая запись независима от предыдущих, то выход такого устройства можно использовать как входную ленту машины. Такая комбинация случайного устройства и машины будет называться
причем каждая запись независима от предыдущих, то выход такого устройства можно использовать как входную ленту машины. Такая комбинация случайного устройства и машины будет называться  -машиной.
-машиной.
Поставленный во введении вопрос о существовании вероятностных машин, более общих, чем детерминистские машины, можно теперь сузить до более частного вопроса: можно ли на  -машине сделать все, что делается на
-машине сделать все, что делается на  -машине? [В следующем разделе будет показано, что рассмотрение довольно узкого класса
-машине? [В следующем разделе будет показано, что рассмотрение довольно узкого класса  -машин вместо более широкого класса всех мыслимых вероятностных машин не вызывает большой потери общности, что широкий класс вероятностных машин эквивалентен (в определяемом далее смысле)
-машин вместо более широкого класса всех мыслимых вероятностных машин не вызывает большой потери общности, что широкий класс вероятностных машин эквивалентен (в определяемом далее смысле)  -машинам и что многие свойства машин широкого класса выводятся из свойств
-машинам и что многие свойства машин широкого класса выводятся из свойств 
Необходимо еще более ограничить наш вопрос, ибо ясно, что нельзя дать никакого точного ответа, пока нет точного определения выполняемой машинами задачи.
В настоящей статье задача, выполняемая машинами, состоит в перечислении множеств. Эта задача не так уж узка, как это может показаться с первого взгляда. Например, машина может вычислять функцию, перечисляя символы  или устанавливать истинность или ложность некоторого высказывания о целых положительных числах перечислением символов
или устанавливать истинность или ложность некоторого высказывания о целых положительных числах перечислением символов  истинно» и
истинно» и  ложно»; или же может вычислять двоичное разложение действительного числа перечислением символов
ложно»; или же может вычислять двоичное разложение действительного числа перечислением символов  знак числа
знак числа  равен а».
равен а».
Выше было определено, что понимается под  -перечислимым множеством символов. А именно некоторое множество
-перечислимым множеством символов. А именно некоторое множество  -пере-числимо, если существует машина, которая, получая на входе ленту с одними только единицами, производит в итоге это множество на выходе. Необходимо дать определение перечислимости для
-пере-числимо, если существует машина, которая, получая на входе ленту с одними только единицами, производит в итоге это множество на выходе. Необходимо дать определение перечислимости для  -машин, чтобы сравнить их с
-машин, чтобы сравнить их с  -машинами.
-машинами.
Будет предложено два определения: определение  -перечислимых множеств и определение сильно
-перечислимых множеств и определение сильно  -перечислимых множеств. Наш первоначальный неформальный вопрос будет сведен к двум точным вопросам: каждое ли
-перечислимых множеств. Наш первоначальный неформальный вопрос будет сведен к двум точным вопросам: каждое ли  -перечислимое множество
-перечислимое множество  -перечислимо? Каждое ли сильно
-перечислимо? Каждое ли сильно  -перечислимое множество
-перечислимое множество  -перечислимо?
-перечислимо?
Остается дать эти два определения. Каждому множеству возможных выходных символов данной  -машины можно приписать вероятность его появления в качестве полного выхода этой машины. Это есть вероятность того, что данное множество будет в точности множеством символов, которые появятся на выходной ленте машины, если машину привести в начальное положение, присоединить случайное устройство и пустить в работу. Указанная вероятность, конечно, равна нулю для большинства множеств. Дадим несколько примеров, ссылаясь на описанные выше машины. Предположим, что они присоединены к случайному устройству с
-машины можно приписать вероятность его появления в качестве полного выхода этой машины. Это есть вероятность того, что данное множество будет в точности множеством символов, которые появятся на выходной ленте машины, если машину привести в начальное положение, присоединить случайное устройство и пустить в работу. Указанная вероятность, конечно, равна нулю для большинства множеств. Дадим несколько примеров, ссылаясь на описанные выше машины. Предположим, что они присоединены к случайному устройству с  и стали поэтому
и стали поэтому  -машинами. Машина № 1 перечисляет любое множество с нулевой вероятностью. Следует отметить, что конечные множества появиться не могут, и по этой причине они имеют нулевую вероятность. Хотя некоторые бесконечные множества и могут быть выходом, однако это случается лишь с нулевой вероятностью. Не следует забывать о различии между появлением с нулевой вероятностью и невозможностью появления. Машина № 2 перечисляет множество всех
-машинами. Машина № 1 перечисляет любое множество с нулевой вероятностью. Следует отметить, что конечные множества появиться не могут, и по этой причине они имеют нулевую вероятность. Хотя некоторые бесконечные множества и могут быть выходом, однако это случается лишь с нулевой вероятностью. Не следует забывать о различии между появлением с нулевой вероятностью и невозможностью появления. Машина № 2 перечисляет множество всех  с вероятностью 1 (и притом с достоверностью). Выход машины № 3 есть множество, состоящее из единственного символа 0, с вероятностью 1, но без достоверности. Выход машины № 5 есть множество всех целых положительных чисел — с вероятностью 1, но без достоверности, ибо бесконечная последовательность нулей и единиц содержит произвольно длинные
с вероятностью 1 (и притом с достоверностью). Выход машины № 3 есть множество, состоящее из единственного символа 0, с вероятностью 1, но без достоверности. Выход машины № 5 есть множество всех целых положительных чисел — с вероятностью 1, но без достоверности, ибо бесконечная последовательность нулей и единиц содержит произвольно длинные
группы единиц с вероятностью 1, но без достоверности. Машина № 6 перечисляет с вероятностью  множество всех
множество всех  где
где  фиксировано, а
фиксировано, а  пробегает все целые положительные числа. Иными словами, машина вычисляет функцию
пробегает все целые положительные числа. Иными словами, машина вычисляет функцию  [определяемую соотношением
[определяемую соотношением  с вероятностью
с вероятностью  .
.
Определение. Для заданного  множество символов 5 будет называться сильно
множество символов 5 будет называться сильно  -перечислимым, если существует
-перечислимым, если существует  -машина, производящая (в любом порядке) это множество выходных символов с положительной вероятностью.
-машина, производящая (в любом порядке) это множество выходных символов с положительной вероятностью.
Предыдущие примеры показывают, что следующие множества сильно  -перечислимы: множество всех
-перечислимы: множество всех  — множество, состоящее только из 0; множество
— множество, состоящее только из 0; множество  целых положительных чисел; множество всех
целых положительных чисел; множество всех  с фиксированным
с фиксированным 
Ясно, как употребить  -машину для того, чтобы дать информацию о каком-нибудь сильно
-машину для того, чтобы дать информацию о каком-нибудь сильно  -перечислимом множестве
-перечислимом множестве  производимом ею с положительной вероятностью. Заставим
производимом ею с положительной вероятностью. Заставим  -машину работать, зная, что перечисляемое ею множество будет
-машину работать, зная, что перечисляемое ею множество будет  исходя из вероятности появления
исходя из вероятности появления  в качестве выхода. Поскольку
в качестве выхода. Поскольку  обладает положительной вероятностью,
обладает положительной вероятностью,  -машину можно использовать с некоторой степенью уверенности. Если же вероятность появления
-машину можно использовать с некоторой степенью уверенности. Если же вероятность появления  в качестве выхода равняется нулю, то нет уверенности в способности машины перечислить в точности
в качестве выхода равняется нулю, то нет уверенности в способности машины перечислить в точности  Однако даже машина, обладающая высокой вероятностью правильно записать любой отдельный выходной символ, может перечислять
Однако даже машина, обладающая высокой вероятностью правильно записать любой отдельный выходной символ, может перечислять  с нулевой вероятностью. Чтобы показать это, введем более слабое определение.
с нулевой вероятностью. Чтобы показать это, введем более слабое определение.
Существует определенная вероятность того, что данная  -машина М в конце концов запишет данный выходной символ. Пусть
-машина М в конце концов запишет данный выходной символ. Пусть  множество всех выходных символов, которые машина М в конце концов запишете вероятностью большей 1/2. Например, присоединим рассмотренные выше машины к случайному устройству с
множество всех выходных символов, которые машина М в конце концов запишете вероятностью большей 1/2. Например, присоединим рассмотренные выше машины к случайному устройству с  так что они станут
так что они станут  -машинами.
-машинами.  для машины № 2 есть множество всех
для машины № 2 есть множество всех  для машины № 3 — множество, состоящее только из 0; для машины № 4 — множество, состоящее только из 1; для машины № 5 — множество целых положительных чисел и для машины №
для машины № 3 — множество, состоящее только из 0; для машины № 4 — множество, состоящее только из 1; для машины № 5 — множество целых положительных чисел и для машины №  — пустое множество.
— пустое множество.
Если  -машина М начала работать, то она, наконец, запишет с вероятностью большей 1/2 любой данный элемент из
-машина М начала работать, то она, наконец, запишет с вероятностью большей 1/2 любой данный элемент из  и с вероятностью меньшей 1/2 любой данный элемент, не принадлежащий
и с вероятностью меньшей 1/2 любой данный элемент, не принадлежащий  Отсюда ясно, как употребить машину
Отсюда ясно, как употребить машину  чтобы получить информацию о
чтобы получить информацию о  Существует определенная степень уверенности в том, что любой элемент множества
Существует определенная степень уверенности в том, что любой элемент множества  в конце концов появится в качестве выходного символа и что любой элемент, не входящий в
в конце концов появится в качестве выходного символа и что любой элемент, не входящий в  не появится в качестве выходного символа. Однако само множество
не появится в качестве выходного символа. Однако само множество  может при этом иметь нулевую вероятность появления, и в таком случае нет уверенности в том, что машина
может при этом иметь нулевую вероятность появления, и в таком случае нет уверенности в том, что машина
перечислит в точности  что все это остается справедливым, если в определении
что все это остается справедливым, если в определении  взять вместо 1/2 большее число. Остаются справедливыми и все последующие результаты.)
взять вместо 1/2 большее число. Остаются справедливыми и все последующие результаты.)
Определение. Множество символов  называется
называется  -перечислимым, если существует такая машина М, что
-перечислимым, если существует такая машина М, что  есть в точности
есть в точности 
Условие  -перечислимости множества совсем слабое, предполагается, что нет более слабого определения, которое все же предусматривало бы существование
-перечислимости множества совсем слабое, предполагается, что нет более слабого определения, которое все же предусматривало бы существование  -машины, дающей некоторую информацию о каждом элементе множества. Следует заметить, что
-машины, дающей некоторую информацию о каждом элементе множества. Следует заметить, что  -машина
-машина  -перечисляет только одно множество, тогда как сильно
-перечисляет только одно множество, тогда как сильно  -перечислять она может несколько множеств или ни одного.
-перечислять она может несколько множеств или ни одного.
На первый взгляд понятие сильной  -перечислимости кажется намного сильнее понятия
-перечислимости кажется намного сильнее понятия  -перечислимости, и действительно покажем, что сильно
-перечислимости, и действительно покажем, что сильно  -перечислимое множество
-перечислимое множество  -перечислимо. Несколько более глубоким и, быть может, неожиданным является обратный результат, означающий фактическую эквивалентность этих двух понятий.
-перечислимо. Несколько более глубоким и, быть может, неожиданным является обратный результат, означающий фактическую эквивалентность этих двух понятий.
Чтобы сформулировать ключевой результат настоящей статьи и дать с его помощью ответ на два поставленных нами общих вопроса, требуется еще одно определение. Пусть  — действительное число,
— действительное число,  Тогда под
Тогда под  понимается бесконечная последовательность нулей и единиц
понимается бесконечная последовательность нулей и единиц  где
где  есть
есть  знак двоичного разложения действительного числа
знак двоичного разложения действительного числа  Так как
Так как  бесконечная последовательность нулей и единиц, то она может служить входом машин, и будет можно говорить об
бесконечная последовательность нулей и единиц, то она может служить входом машин, и будет можно говорить об  -машинах, А
-машинах, А  -перечислимости и т. д.
-перечислимости и т. д.
Теперь для любого числа  между 0 и 1 у нас есть три понятия:
между 0 и 1 у нас есть три понятия:  -перечислимости,
-перечислимости,  -перечислимости и сильной
-перечислимости и сильной  -перечислимости. Из них лишь первое понятие является строго детерминистским, тогда как остальные — вероятностными.
-перечислимости. Из них лишь первое понятие является строго детерминистским, тогда как остальные — вероятностными.
Основной результат формулируется следующим образом.
Теорема 1. Яусть  — множество символов,
— множество символов,  — действительное число,
— действительное число,  Три следующих предложения эквивалентны:
Три следующих предложения эквивалентны:
1)  является А
является А  -перечислимым;
-перечислимым;
2)  является
является  -перечислимым;
-перечислимым;
3)  является сильно
является сильно  -перечислимым.
-перечислимым.
Доказательство этой теоремы дано в приложении, но набросок доказательства приведем здесь, показав сначала, что эта теорема дает непосредственный ответ на наши два вопроса.
Пусть  — невычислимое действительное число между 0 и 1. Известно, что такие числа существуют и что в действительности почти все (в смысле меры Лебега) числа невычислимы.
— невычислимое действительное число между 0 и 1. Известно, что такие числа существуют и что в действительности почти все (в смысле меры Лебега) числа невычислимы.
Невычислимость  эквивалентна невычислимости
эквивалентна невычислимости  Тогда в силу леммы 3 существует множество
Тогда в силу леммы 3 существует множество  которое
которое  -перечислимо, но не
-перечислимо, но не  -перечислимо. В силу теоремы 1 это множество как
-перечислимо. В силу теоремы 1 это множество как  -перечислимо, так и сильно
-перечислимо, так и сильно  -перечислимо, но не
-перечислимо, но не  -перечислимо. Следовательно, если имеются случайные устройства, записывающие символ 1 с вероятностью, которая не является вычислимым действительным числом, то можно построить
-перечислимо. Следовательно, если имеются случайные устройства, записывающие символ 1 с вероятностью, которая не является вычислимым действительным числом, то можно построить  -машины, которые будут «перечислять» множества, не являющиеся
-машины, которые будут «перечислять» множества, не являющиеся  -перечислимыми.
-перечислимыми.
Положение совершенно меняется в случае, когда  есть вычислимое действительное число (в частности, когда оно равно 1/2). Это равносильно вычислимости последовательности
есть вычислимое действительное число (в частности, когда оно равно 1/2). Это равносильно вычислимости последовательности  Теорема 1 показывает, что любое
Теорема 1 показывает, что любое  -перечислимое или сильно
-перечислимое или сильно  -перечислимое множество должно быть А
-перечислимое множество должно быть А  -перечислимым. Так как А
-перечислимым. Так как А  -вычислимо, то по лемме 2 рассматриваемое множество должно быть
-вычислимо, то по лемме 2 рассматриваемое множество должно быть  -перечислимым. Следовательно,
-перечислимым. Следовательно,  -перечислимое или сильно
-перечислимое или сильно  -перечислимое множество должно быть
-перечислимое множество должно быть  -перечислимым. Отсюда вывод, что если в качестве
-перечислимым. Отсюда вывод, что если в качестве  брать только вычислимые действительные числа (в частности, 1/2), то машина со случайным устройством не сможет «перечислить» ничего сверх того, что перечисляет детерминистская машина.
брать только вычислимые действительные числа (в частности, 1/2), то машина со случайным устройством не сможет «перечислить» ничего сверх того, что перечисляет детерминистская машина.
Оба случая охватывает следующая теорема.
Теорема 2. Если  — вычислимое действительное число, то любое
— вычислимое действительное число, то любое  -перечислимое или сильно
-перечислимое или сильно  -перечислимое множество
-перечислимое множество  -перечислимо., Если
-перечислимо., Если  —невычислимое действительное число, то существуют
—невычислимое действительное число, то существуют  -перечислимые и сильно
-перечислимые и сильно  -перечислимые множества, не являющиеся 1-перечислимыми.
-перечислимые множества, не являющиеся 1-перечислимыми.
Дадим набросок доказательства теоремы 1. Доказательство состоит из вывода предложения 2 из предложения 3, вывода предложения 1 из предложения 2 и вывода предложения 3 из предложения 1. Эта цепочка заключений дает требуемую эквивалентность.
То, что 3 влечет 2, доказывается тем, что с помощью р-машины, у которой выход  появляется с положительной вероятностью, строится новая машина, у которой
появляется с положительной вероятностью, строится новая машина, у которой  появляется с вероятностью большей 1/2, а любой элемент, не входящий в
появляется с вероятностью большей 1/2, а любой элемент, не входящий в  появляется с вероятностью меньшей 1/2, так что
появляется с вероятностью меньшей 1/2, так что  перечислимо. Следовательно, всякое сильно
перечислимо. Следовательно, всякое сильно  -перечислимое множество
-перечислимое множество  -перечислимо.
-перечислимо.
То, что 2 влечет 1, доказывается следующим образом. Пусть дана  -машина М. Построим
-машина М. Построим  -машину, А
-машину, А  -перечисляющую множество
-перечисляющую множество  Предположим, что имеется бесконечная лента, на которой записано
Предположим, что имеется бесконечная лента, на которой записано  Используя все более длинные начальные отрезки бесконечной последовательности
Используя все более длинные начальные отрезки бесконечной последовательности  можно вычислить сколь угодно хорошие нижние границы для вероятности справедливости высказываний вида «за время, в течение которого
можно вычислить сколь угодно хорошие нижние границы для вероятности справедливости высказываний вида «за время, в течение которого
из случайного устройства появилось  входных символов, М запишет символ
входных символов, М запишет символ  Но машина М запишет
Но машина М запишет  с вероятностью большей 1/2 тогда
с вероятностью большей 1/2 тогда  и только тогда, когда существует такое
и только тогда, когда существует такое  что это высказывание справедливо с вероятностью большей 1/2. Это может случиться лишь тогда, когда одна из сколь угодно хороших нижних границ (вычислимых с использованием начальных отрезков последовательности
что это высказывание справедливо с вероятностью большей 1/2. Это может случиться лишь тогда, когда одна из сколь угодно хороших нижних границ (вычислимых с использованием начальных отрезков последовательности  для вероятности справедливости указанного высказывания большей 1/2. Можно вычислить последовательно (используя все более длинные начальные отрезки последовательности
для вероятности справедливости указанного высказывания большей 1/2. Можно вычислить последовательно (используя все более длинные начальные отрезки последовательности  все нижние границы этих вероятностей для каждого
все нижние границы этих вероятностей для каждого  и каждого
и каждого  После получения нижней границы большей 1/2 записывается соответствующий символ
После получения нижней границы большей 1/2 записывается соответствующий символ  Теперь видим, что перечисленное таким образом множество символов есть
Теперь видим, что перечисленное таким образом множество символов есть  и что перечисление произведено посредством процесса, действительно составляющего
и что перечисление произведено посредством процесса, действительно составляющего  -машину. Следовательно, всякое
-машину. Следовательно, всякое  -перечислимое множество
-перечислимое множество  -перечислимо.
-перечислимо.
То, что 1 влечет 3, доказывается следующим образом. Строится  -машина, вычисляющая с вероятностью большей 1/2 двоичное разложение действительного числа
-машина, вычисляющая с вероятностью большей 1/2 двоичное разложение действительного числа  или выход машины есть (с вероятностью большей 1/2) множество всех
или выход машины есть (с вероятностью большей 1/2) множество всех  где
где  есть
есть  знак в двоичном разложении числа
знак в двоичном разложении числа  Машина, делающая это, является видоизменением машины № 7. Если выход этой
Машина, делающая это, является видоизменением машины № 7. Если выход этой  -машины использовать как вход другой машины М, то выход последней будет с вероятностью большей 1/2 в точности таким, каким был бы выход машины М, имеющий в качестве входа последовательность
-машины использовать как вход другой машины М, то выход последней будет с вероятностью большей 1/2 в точности таким, каким был бы выход машины М, имеющий в качестве входа последовательность  Если
Если  есть любое
есть любое  -перечислимое множество и М — машина, А перечисляющая его, то построенная выше сложная машина есть
-перечислимое множество и М — машина, А перечисляющая его, то построенная выше сложная машина есть  -машина, сильно
-машина, сильно  -перечисляющая
-перечисляющая  Следовательно, любое
Следовательно, любое  -перечислимое множество сильно
-перечислимое множество сильно  -перечислимо. Это доказывает, что 1 влечет 3, и набросок доказательства теоремы 1 Тем самым закончен.
-перечислимо. Это доказывает, что 1 влечет 3, и набросок доказательства теоремы 1 Тем самым закончен.
Исследуем теперь, останутся ли результаты теми же, если учитывать не только совокупность выходных символов, но и порядок их следования. Будет показано, что такое положение можно свести к частному случаю уже полученных результатов.
Определение. Бесконечная последовательность символов  называется
называется  -вычислимой, если она появляется в данном порядке следования на выходе некоторой А-машины. Она называется
-вычислимой, если она появляется в данном порядке следования на выходе некоторой А-машины. Она называется  -вычислимой, если А состоит целиком из единиц.
-вычислимой, если А состоит целиком из единиц.  сильно
сильно  -вычислима, если существует
-вычислима, если существует  -машина, производящая
-машина, производящая  в данном порядке с положительной вероятностью.
в данном порядке с положительной вероятностью.  называется сильно
называется сильно  -вычислимой последовательностью, если существует
-вычислимой последовательностью, если существует  -машина, у которой
-машина, у которой  выходной символ есть
выходной символ есть  символ в
символ в  с вероятностью большей 1/2.
с вероятностью большей 1/2.
Будет показано, что для этих новых понятий справедлив точный аналог теоремы 2.
Пусть  — последовательность символов
— последовательность символов  Через
Через  обозначим множество всех пар
обозначим множество всех пар  где
где  пробегает все целые положительные числа. Следующие леммы, доказываемые в приложении, суть непосредственные следствия определений.
пробегает все целые положительные числа. Следующие леммы, доказываемые в приложении, суть непосредственные следствия определений.
Лемма 4. Последовательность  -вычислима тогда и только тогда, когда множество
-вычислима тогда и только тогда, когда множество  -перечислимо.
-перечислимо.
Лемма 5. Если  сильно
сильно  -вычислима, то
-вычислима, то  сильно
сильно  -перечислимо. Если
-перечислимо. Если  -вычислима, то
-вычислима, то  - перечислимо.
- перечислимо.
Из двух предыдущих лемм и теоремы 2 вытекает лемма 6.
Лемма  Пусть
Пусть  — вычислимое действительное число
— вычислимое действительное число  частности, 1/2). Тогда любая
частности, 1/2). Тогда любая  -вычислимая или сильно
-вычислимая или сильно  -вычислимая последовательность
-вычислимая последовательность  -вычислима.
-вычислима.
Доказательство. Пусть последовательность  будет
будет  -вычислима или сильно
-вычислима или сильно  -вычислима. Тогда
-вычислима. Тогда  -перечислимо или сильно
-перечислимо или сильно  -перечислимо по лемме 5. По теореме 2 множество
-перечислимо по лемме 5. По теореме 2 множество  будет
будет  -перечислимо. По лемме 4 последовательность
-перечислимо. По лемме 4 последовательность  должна быть
должна быть  -вычислимой.
-вычислимой.
Это охватывает случай, когда  — вычислимое действительное число. Если
— вычислимое действительное число. Если  невычислимо, то доказательство теоремы 1, данное в приложении, показывает, что существует
невычислимо, то доказательство теоремы 1, данное в приложении, показывает, что существует  -вычислимая и сильно
-вычислимая и сильно  -вычислимая, но не
-вычислимая, но не  -вычислимая последовательность (эта последовательность представляет собой двоичное разложение числа
-вычислимая последовательность (эта последовательность представляет собой двоичное разложение числа  Объединяя оба случая, получим следующий аналог теоремы 2 для понятий вычислимости.
Объединяя оба случая, получим следующий аналог теоремы 2 для понятий вычислимости.
Теорема 3. Если  есть вычислимое действительное число, то любая
есть вычислимое действительное число, то любая  -вычислимая или сильно
-вычислимая или сильно  -вычислимая последовательность
-вычислимая последовательность  -вычислима. Если
-вычислима. Если  — невычислимо, то существует
— невычислимо, то существует  -вычислимая и сильно
-вычислимая и сильно  -вычислимая последовательность, которая не
-вычислимая последовательность, которая не  -вычислима.
-вычислима.
Как частный случай этого находим, что  -машина не может записать с положительной вероятностью никакой невычислимой последовательности.
-машина не может записать с положительной вероятностью никакой невычислимой последовательности.
Более общий класс машин
В этом разделе обобщается результат, даваемый теоремой 2 для вычислимого числа  Определим широкий класс вероятностных машин — вычислимо стохастических машин (или в.с.-машин), не докрываемых нашими предыдущими определениями, и предложим
Определим широкий класс вероятностных машин — вычислимо стохастических машин (или в.с.-машин), не докрываемых нашими предыдущими определениями, и предложим
понятие эквивалентности для вероятностных машин. Покажем, что любая машина нового класса эквивалентна  -машине, и, как следствие теоремы 2, получим, что любое множество, перечислимое машиной этого класса, должно быть
-машине, и, как следствие теоремы 2, получим, что любое множество, перечислимое машиной этого класса, должно быть  -перечислимом. Далее, существует эффективный процесс, позволяющий по описанию машины этого класса найти описание эквивалентной ей
-перечислимом. Далее, существует эффективный процесс, позволяющий по описанию машины этого класса найти описание эквивалентной ей  -машины и описание
-машины и описание  -машины,
-машины,  -перечисляющей то же самое множество.
-перечисляющей то же самое множество.
Для простоты изложения рассмотрим в этом разделе только одно определение перечислимости, соответствующее  -перечислимости, и не дадим более сильного определения, соответствующего сильной
-перечислимости, и не дадим более сильного определения, соответствующего сильной  -перечислимости. Можно показать, что те же результаты справедливы и для сильного определения.
-перечислимости. Можно показать, что те же результаты справедливы и для сильного определения.
Сначала определим класс стохастических машин. Стохастическая машина есть объект со счетным числом состояний  выделенным начальным состоянием
выделенным начальным состоянием  и счетным набором выходных символов
и счетным набором выходных символов  При этом указано правило, дающее вероятность прихода машины в состояние
При этом указано правило, дающее вероятность прихода машины в состояние  и записи ею выходного символа
и записи ею выходного символа  если перед тем она прошла последовательно через состояния
если перед тем она прошла последовательно через состояния  Эту вероятность обозначим через
Эту вероятность обозначим через  не требуя, чтобы это правило давало эффективный метод для вычисления вероятностей Р.
не требуя, чтобы это правило давало эффективный метод для вычисления вероятностей Р.
Любой  -машине М можно поставить в соответствие стохастическую машину в указанном выше смысле. Состояния соответствующей стохастической машины суть конечные последовательности нулей и единиц
-машине М можно поставить в соответствие стохастическую машину в указанном выше смысле. Состояния соответствующей стохастической машины суть конечные последовательности нулей и единиц  а начальное состояние — «пустая» последовательность
а начальное состояние — «пустая» последовательность  (Фактически «состоянием»
(Фактически «состоянием»  -машины называют входную последовательность, воспринятую ею. Эти «состояния» могут не соответствовать возможным внутренним состояниям конкретной машины, но определяют их полностью.) Вероятность перехода из состояния
-машины называют входную последовательность, воспринятую ею. Эти «состояния» могут не соответствовать возможным внутренним состояниям конкретной машины, но определяют их полностью.) Вероятность перехода из состояния  есть
есть  а из состояния
а из состояния  есть
есть  Соответствующая стохастическая машина записывает по приходе в состояние
Соответствующая стохастическая машина записывает по приходе в состояние  то же, что и
то же, что и  -машина, принявшая
-машина, принявшая  входной символ
входной символ  после восприятия
после восприятия  Тем самым стохастическая машина полностью задана. Она будет в дальнейшем называться стохастической машиной, соответствующей
Тем самым стохастическая машина полностью задана. Она будет в дальнейшем называться стохастической машиной, соответствующей  -машине М. Таким образом,
-машине М. Таким образом,  -машины можно отождествить с частными случаями стохастических машин. Легко видеть, что если
-машины можно отождествить с частными случаями стохастических машин. Легко видеть, что если  — вычислимое число, то соответствующая стохастическая машина обладает следующим специальным свойством: функция Р вычислима, т. е. существует эффективный процесс, позволяющий по заданному целому положительному числу т. состояниям
— вычислимое число, то соответствующая стохастическая машина обладает следующим специальным свойством: функция Р вычислима, т. е. существует эффективный процесс, позволяющий по заданному целому положительному числу т. состояниям  и выходному символу
и выходному символу  вычислить первые
вычислить первые  знаков двоичного разложения
знаков двоичного разложения 
Назовем стохастические машины с таким свойством вычислимо стохастическими машинами (или в.с.-машинами). Непосредственным следствием этих определений является следующая лемма.
Лемма 7. Стохастическая машина, соответствующая  -машине, является в.с.-машиной тогда и только тогда, когда
-машине, является в.с.-машиной тогда и только тогда, когда  — вычислимое действительное число.
— вычислимое действительное число.
Остальную часть этого раздела посвятим тому, чтобы показать, что результат, сформулированный в теореме 2 для  -машин с вычислимым
-машин с вычислимым  также справедлив и для гораздо более широкого класса в.с.-машин. Таким образом, любое множество, перечислимое в.с.-машиной,
также справедлив и для гораздо более широкого класса в.с.-машин. Таким образом, любое множество, перечислимое в.с.-машиной,  -перечислимо.
-перечислимо.
Как для стохастических, так и для  -машин можно говорить о вероятности того, что машина в конце концов запишет выходные символы
-машин можно говорить о вероятности того, что машина в конце концов запишет выходные символы  (подобно тому, как раньше говорилось о вероятности того, что
(подобно тому, как раньше говорилось о вероятности того, что  -машина в конце концов запишет одиночный символ
-машина в конце концов запишет одиночный символ  Поскольку наши машины служат для перечисления множеств, то любые две машины, которые в конце концов сделают одно и то же с одной и той же вероятностью, можно считать тождественными с точки зрения окончательного выхода. Поэтому можно ввести следующее определение.
Поскольку наши машины служат для перечисления множеств, то любые две машины, которые в конце концов сделают одно и то же с одной и той же вероятностью, можно считать тождественными с точки зрения окончательного выхода. Поэтому можно ввести следующее определение.
Определение. Два объекта — стохастические машины или  -машины — будут называться эквивалентными, если для любого конечного множества символов
-машины — будут называться эквивалентными, если для любого конечного множества символов  они имеют одинаковую вероятность включения (в конце концов) этого множества в их выход. Если эти машины суть
они имеют одинаковую вероятность включения (в конце концов) этого множества в их выход. Если эти машины суть  то их эквивалентность будем обозначать так:
то их эквивалентность будем обозначать так: 
Например,  -машина и соответствующая ей стохастическая машина эквивалентны.
-машина и соответствующая ей стохастическая машина эквивалентны.
Вспомним, что  -машина названа
-машина названа  -перечисляющей некоторое множество символов, если каждый элемент этого множества появляется на выходе машины с вероятностью большей 1/2, а любой выходной символ, не принадлежащий данному множеству, появляется с вероятностью не большей 1/2. Определение можно непосредственно применить к стохастическим машинам и в.с.-машинам. Если М — стохастическая машина, то
-перечисляющей некоторое множество символов, если каждый элемент этого множества появляется на выходе машины с вероятностью большей 1/2, а любой выходной символ, не принадлежащий данному множеству, появляется с вероятностью не большей 1/2. Определение можно непосредственно применить к стохастическим машинам и в.с.-машинам. Если М — стохастическая машина, то  будет множеством всех выходных символов, появляющихся с вероятностью большей 1/2, в согласии с введенным выше обозначением для
будет множеством всех выходных символов, появляющихся с вероятностью большей 1/2, в согласии с введенным выше обозначением для  -машин.
-машин.
 есть множество символов, которое перечисляет машина М. Как непосредственное следствие из нашего определения эквивалентности получаем, что
есть множество символов, которое перечисляет машина М. Как непосредственное следствие из нашего определения эквивалентности получаем, что  влечет
влечет  Две эквивалентные машины перечисляют одно и то же множество.
Две эквивалентные машины перечисляют одно и то же множество.
Определение. Множество  в.
в.  -перечислимо, если существует такая в.с.-машина М, что
-перечислимо, если существует такая в.с.-машина М, что 
Теперь ответим на вопрос: каждое ли в.с.-перечислимое множество  -перечислимо? Ответ вытекает из следующего утверждения, доказанного в приложении.
-перечислимо? Ответ вытекает из следующего утверждения, доказанного в приложении.
Теорема 4. Каждая в.с.-машина эквивалентна  -машине.
-машине.
Следовательно, если М есть в.с.-машина, то множество  которое перечисляет машина М, перечислимо также некоторой
которое перечисляет машина М, перечислимо также некоторой  -машиной. По теореме 2 множество
-машиной. По теореме 2 множество  должно быть
должно быть  -перечислимым. Отсюда вытекает следующее утверждение.
-перечислимым. Отсюда вытекает следующее утверждение.
Теорема 5. Любое в.с.-перечислимое множество  -перечислимо.
-перечислимо.
Этот результат и был упомянут выше.
В действительности доказательство теоремы 4 дает больше, чем было высказано. Могло случиться, что доказательство только устанавливает существование  -машины, эквивалентной произвольной в.с.-машине, но не дает эффективных средств для ее нахождения. Однако это не так, и доказательство дает эффективный процесс.
-машины, эквивалентной произвольной в.с.-машине, но не дает эффективных средств для ее нахождения. Однако это не так, и доказательство дает эффективный процесс.
Теорема 4 (дополнение). Существует эффективный процесс, позволяющий по заданному описанию в.с.-машины получить описание эквивалентной ей  -машины.
-машины.
Следовательно, для заданного описания в.с.-машины  существует эффективный процесс, позволяющий найти такую
существует эффективный процесс, позволяющий найти такую  -машину
-машину  что
что  Но это еще не дает эффективного расширения теоремы 5, для которого необходимо следующее эффективное расширение части теоремы 1.
Но это еще не дает эффективного расширения теоремы 5, для которого необходимо следующее эффективное расширение части теоремы 1.
Теорема 1 (дополнение). Существует эффективный процесс, позволяющий по заданному описанию  -машины М (где
-машины М (где  вычислимое число) получить описание 1-машины, 1-перечисляющей то же самое
вычислимое число) получить описание 1-машины, 1-перечисляющей то же самое  которое
которое  -перечисляет машина М.
-перечисляет машина М.
Из объединения дополнений теорем 1 и 4 следует теорема 5.
Теорема 5 (дополнение). Существует эффективный процесс, позволяющий по заданному описанию в.с.-машины, в.с.-перечисляющей множество  получить описание
получить описание  -машины, которая
-машины, которая  -перечисляет
-перечисляет 
Результаты относительно вычислимости последовательностей, приведенные в конце предыдущего раздела, остаются справедливыми для в.с.-машин. Очевидным образом можно определить в.с.-вычислимые последовательности. Доказательства лемм 4, 5 и  в этом случае справедливы, откуда следует, что любая в.с.-вычислимая последовательность
в этом случае справедливы, откуда следует, что любая в.с.-вычислимая последовательность  -вычислима.
-вычислима.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- СИМВОЛИЧЕСКИЙ АНАЛИЗ РЕЛЕЙНЫХ И ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- 2. Параллельно-последовательные двухполюсные схемы. Основные определения и постулаты
- 3. Многополюсные и не параллельно-последовательные схемы
- Преобразование треугольника в звезду и звезды в ячейку
- Функция сопротивления не параллельно-последовательной схемы
- Системы уравнений
- Реле и переключатели специальных типов
- 4. Синтез схем
- Двойственные схемы
- Синтез схем, реализующих симметрические функции
- Составление уравнений по рабочим характеристикам
- 5. Примеры
- ЧИСЛО ДВУХПОЛЮСНЫХ ПАРАЛЛЕЛЬНО-ПОСЛЕДОВАТЕЛЬНЫХ СЕТЕЙ
- 1. Получение производящей функции
- 2. Численный подсчет
- 3. Асимптотическое поведение
- 4. Параллельно-последовательная реализация переключательных функций
- СИНТЕЗ ДВУХПОЛЮСНЫХ ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- 2. Основная теорема синтеза
- 3. Синтез схем для произвольных функций.
- Часть II. РАСПРЕДЕЛЕНИЕ НАГРУЗКИ МЕЖДУ РЕЛЕ
- 5. Разделительное дерево
- 6. Другие задачи распределения
- 7. Функция «мю»
- Часть III. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- 9. Частично симметрические функции
- ПРИМЕЧАНИЯ РЕДАКТОРА
- ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К ОБЪЕМУ ПАМЯТИ ТЕЛЕФОННОГО КОММУТАТОРА
- 2. Память, требуемая для S произвольных вызовов от N абонентов
- 3. Условие раздельной памяти
- 4. Связь с теорией информации
- НАДЕЖНЫЕ СХЕМЫ ИЗ НЕНАДЕЖНЫХ РЕЛЕ
- Идеализированные реле
- Общий метод повышения надежности
- Свойства функции h(p)
- Комбинация двух схем
- Оценки функции h'(p)
- Схемы заданной длины и ширины
- Оценки числа контактов в случае, когда реле уже достаточно надежны
- Сравнение с элементами фон Неймана
- Реле с неопределенным временем срабатывания
- Синтез надежных схем в целом
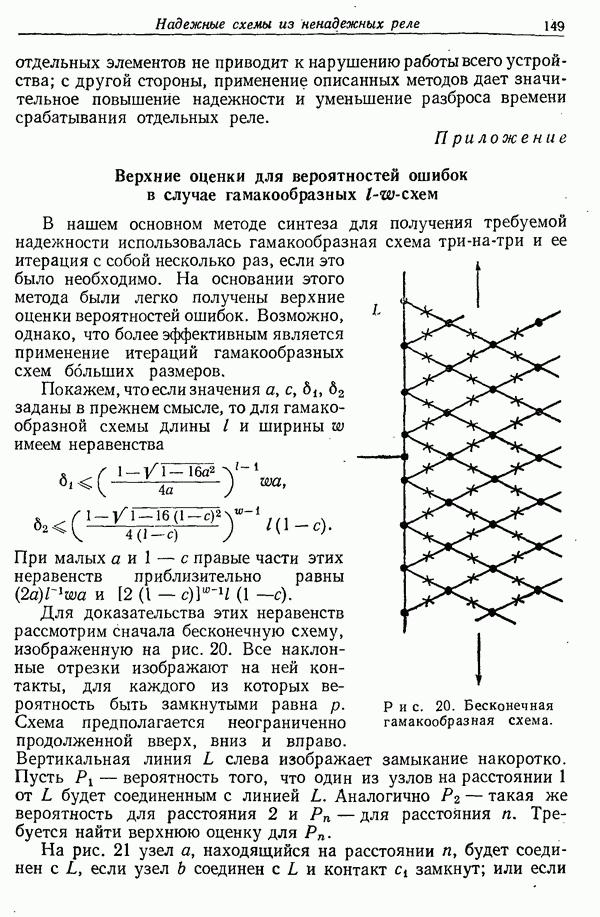
- Приложение. Верхние оценки для вероятностей ошибок в случае гамакообразных l-w-схем
- ИСПОЛЬЗОВАНИЕ МАШИНЫ ДЛЯ ПРОЕКТИРОВАНИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА И АВТОМАТЫ
- Машины Тьюринга
- Логические машины
- «Играющие машины»
- Обучаемые машины
- Самовоспроизводящиеся машины
- Обращение к читателю
- МАШИНА ДЛЯ ИГРЫ В ШАХМАТЫ
- СОСТАВЛЕНИЕ ПРОГРАММ ДЛЯ ИГРЫ В ШАХМАТЫ НА ВЫЧИСЛИТЕЛЬНОЙ МАШИНЕ
- 3. Приближенная оценочная функция
- 4. Стратегия, основанная на оценочной функции
- 5. Составление программы для универсальной вычислительной машины для реализации стратегии типа А
- 6. Улучшение стратегии
- 7. Изменения в игре и в стиле
- 8. Другой тип стратегии
- ПРИЛОЖЕНИЕ. ОЦЕНОЧНАЯ ФУНКЦИЯ ДЛЯ ШАХМАТ
- ИГРАЮЩИЕ МАШИНЫ
- СООБЩЕНИЕ О МАШИНЕ, РЕШАЮЩЕЙ ЛАБИРИНТНУЮ ЗАДАЧУ
- ВКЛАД ФОН НЕЙМАНА В ТЕОРИЮ АВТОМАТОВ
- МАТЕМАТИЧЕСКАЯ ТЕОРИЯ СВЯЗИ
- 1. ДИСКРЕТНЫЕ СИСТЕМЫ БЕЗ ШУМОВ
- 2. Дискретный источник сообщений
- 3. Последовательные приближения к английскому языку
- 4. Графическое представление марковского процесса
- 5. Эргодические и смешанные источники
- 6. Выбор, неопределенность и энтропия
- 7. Энтропия источника сообщений
- 8. Представление операций кодирования и декодирования
- 9. Основная теорема для канала без шума
- 10. Рассмотрение полученных результатов и примеры
- 11. Примеры
- II. ДИСКРЕТНЫЙ КАНАЛ С ШУМОМ
- 12. Надежность и пропускная способность канала
- 13. Основная теорема для дискретного канала с шумом
- 14. Рассмотрение полученных результатов
- 15. Пример дискретного канала и его пропускной способности
- 16. Пропускная способность канала в некоторых частных случаях
- 17. Пример эффективного кодирования
- III. ИНФОРМАЦИЯ ДЛЯ НЕПРЕРЫВНЫХ ВЕЛИЧИН
- 19. Ансамбли функций с ограниченной полосой частот
- 20. Энтропия непрерывного распределения
- 21. Энтропия ансамбля функций
- 22. Потеря энтропии в линейных фильтрах
- 23. Энтропия суммы двух ансамблей
- IV. НЕПРЕРЫВНЫЙ КАНАЛ
- 24. Пропускная способность непрерывного канала
- 25. Пропускная способность канала при ограничении средней мощности
- 26. Пропускная способность канала при ограничении пиковой мощности
- V. СКОРОСТЬ СОЗДАНИЯ СООБЩЕНИЙ ДЛЯ НЕПРЕРЫВНОГО ИСТОЧНИКА
- 28. Скорость создания сообщений источником при данной точности воспроизведения
- 29. Вычисление скорости создания сообщений
- Приложение 1. РОСТ ЧИСЛА БЛОКОВ СИМВОЛОВ ПРИ УСЛОВИЯХ, ОПИСЫВАЕМЫХ КОНЕЧНЫМ ЧИСЛОМ СОСТОЯНИЙ
- Приложение 2. ВЫВОД РАВЕНСТВА …
- Приложение 3. ТЕОРЕМА ОБ ЭРГОДИЧЕСКИХ ИСТОЧНИКАХ
- Приложение 4. МАКСИМИЗАЦИЯ СКОРОСТИ ДЛЯ СИСТЕМЫ ОГРАНИЧЕНИЯ
- Приложение 5
- Приложение 6
- Приложение 7
- ТЕОРИЯ СВЯЗИ В СЕКРЕТНЫХ СИСТЕМАХ
- Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ СИСТЕМ
- 3. Способы изображения систем
- 4. Примеры секретных систем
- 5. Оценка секретных систем
- 6. Алгебра секретных систем
- 7. Чистые и смешанные шифры
- 8. Подобные системы
- Часть II. ТЕОРЕТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 10. Совершенная секретность
- 11. Ненадежность
- 12. Свойства ненадежности
- 13. Ненадежность простой подстановки для языка с двухбуквенным алфавитом
- 14. Характеристика ненадежности для «случайного» шифра
- 15. Применение к стандартным шифрам
- 16. Правильность решения криптограммы
- 17. Идеальные секретные системы
- 18. Примеры идеальных секретных систем
- 19. Дополнительные замечания о ненадежности и избыточности
- 20. Распределение ненадежности
- Часть III. ПРАКТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 22. Общие замечания о решении криптограмм
- 23. Статистические методы
- 24. Метод вероятных слов
- 25. Перемешивание
- 26. Шифры типа …
- 27. Несовместимость требований к хорошим системам
- ПРИЛОЖЕНИЕ. Доказательство теоремы 3
- СОВРЕМЕННЫЕ ДОСТИЖЕНИЯ ТЕОРИИ СВЯЗИ
- Измерение информаций
- Кодирование информации
- Пропускная способность канала
- Идеальные и практические системы
- ПРИНЦИПЫ КОДОВО-ИМПУЛЬСНОЙ МОДУЛЯЦИИ
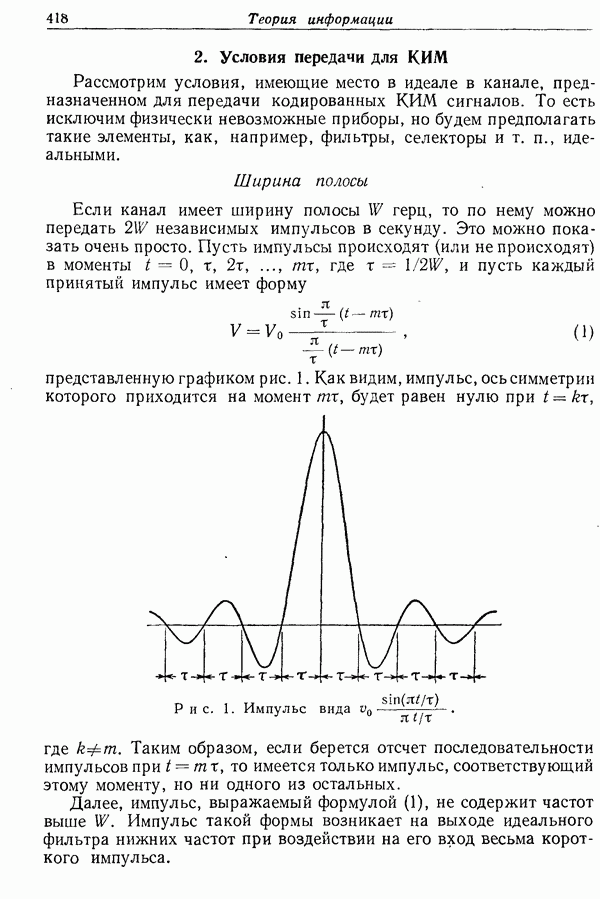
- 2. Условия передачи для КИМ
- 3. Действие системы КИМ
- 4. Сравнение КИМ и ЧМ
- 5. Заключение
- Приложение I
- Приложение II
- СВЯЗЬ ПРИ НАЛИЧИИ ШУМА
- 2. Теорема отсчетов
- 3. Геометрическое представление сигналов
- 4. Геометрическое представление сообщений
- 5. Геометрическое представление передатчика и приемника
- 6. Отображение пространства
- 7. Пропускная способность канала при наличии белого теплового шума
- 8. Обсуждение
- 9. Произвольный гауссовский шум
- 10. Пропускная способность канала при произвольном типе шума
- 11. Дискретные источники информации
- 12. Непрерывные источники информации
- НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ИНФОРМАЦИИ
- ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА С ШУМОМ ПРИ НУЛЕВОЙ ОШИБКЕ
- Пропускная способность канала при нулевой ошибке
- Пропускная способность для суммы и произведения каналов
- Каналы с обратной связью
- ГЕОМЕТРИЧЕСКИЙ ПОДХОД К ТЕОРИИ ПРОПУСКНОЙ СПОСОБНОСТИ. КАНАЛОВ СВЯЗИ
- КАНАЛЫ С ДОПОЛНИТЕЛЬНОЙ ИНФОРМАЦИЕЙ НА ПЕРЕДАТЧИКЕ
- Дискретный канал без памяти с дополнительной информацией о состоянии
- Приложение
- НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ТЕОРИИ КОДИРОВАНИЯ ДЛЯ КАНАЛОВ С ШУМАМИ
- Оценка вероятности ошибки в терминах производящей функции моментов
- Пропускная способность канала с конечным числом состояний, состояние которого вычислимо на обоих концах
- Пропускная способность канала с конечным числом состояний в случае, когда состояние вычислимо на передающем конце и не вычислимо на приемном конце
- ЗАМЕЧАНИЯ О ЧАСТИЧНОМ УПОРЯДОЧИВАНИИ КАНАЛОВ СВЯЗИ
- Дальнейшее обобщение и некоторые предположения
- ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ ОПТИМАЛЬНЫХ кодов В ГАУССОВСКОМ КАНАЛЕ
- 2. Сводка результатов
- 3. Нижняя граница, основанная на соображениях «сферической упаковки»
- 4. Верхняя граница, определяемая методом случайного кодирования
- 5. Формулы для скорости передачи R как функции угла конуса
- 6. Асимптотические формулы для …
- 7. Асимптотическое выражение для верхней границы при случайном кодировании
- 8. Жесткая верхняя граница
- 9. Жесткая нижняя граница
- 10. Поведение границ вблизи пропускной способности канала
- 11. Верхняя граница, полученная методом исчерпывания
- 12. Нижняя граница для гауссовского канала, получаемая исходя из минимального расстояния
- 13. Границы ошибок и другие условия, накладываемые на точки
- 14. Кривые для асимптотических границ
- ТЕОРЕМЫ КОДИРОВАНИЯ ДЛЯ ДИСКРЕТНОГО ИСТОЧНИКА ПРИ ЗАДАННОМ КРИТЕРИИ ТОЧНОСТИ
- Мера искажения отдельной буквы
- Несколько простых примеров
- Скорость при заданном искажении R(d)
- Выпуклость вниз кривой R(d)
- Нахождение R(d) в некоторых простых случаях
- Скорость передачи для произведения источников с мерой, являющейся суммой мер искажения
- Нижняя граница для искажения при заданной пропускной способности канала
- Теоремы кодирования при заданной мере искажения отдельной буквы
- Двойственность источника и канала
- Численные расчеты для некоторых простых каналов
- Обобщение на случаи непрерывных алфавитов
- Разностная мера искажения
- Определение меры локального искажения
- Функции Rn(d) и R(d) для меры локального искажения и эргодического источника
- Прямая теорема кодирования для меры локального искажения
- Обратная теорема кодирования
- Канал с памятью
- ДВУСТОРОННИЕ КАНАЛЫ СВЯЗИ
- 4. Средние взаимные скорости передачи информации
- 5. Распределение информации
- 6. Случайное кодирование для двусторонних каналов
- 7. Вероятность ошибки для ансамбля кодов
- 8. Выпуклая оболочка G как внутренняя граница области пропускной способности
- 9. Внешняя граница для области пропускной способности
- 10. Выпуклость вниз как функций от …
- 11. Приложения свойства выпуклости. Каналы с симметричной структурой
- 12. Характер области, выделяемой внешней границей
- 13. Пример, в котором внутренняя и внешняя границы различны
- 14. Достижимость внешней границы при зависимых источниках
- 15. Общий метод нахождения области пропускной способности двустороннего канала
- 16. Двусторонние каналы с памятью
- 17. Обобщение на каналы с Т концами
- БАНДВАГОН
- ПРЕДСКАЗАНИЕ И ЭНТРОПИЯ ПЕЧАТНОГО АНГЛИЙСКОГО ТЕКСТА
- 2. Вычисление энтропии по статистике английского языка
- 3. Предсказание английского текста
- 4. Идеальное N-граммное предсказывание
- 5. Граница для энтропии на основании частот предсказания
- 6. Результаты эксперимента для английского языка
- УПРОЩЕННЫЙ ВЫВОД ЛИНЕЙНОЙ ТЕОРИИ СГЛАЖИВАНИЯ И ПРЕДСКАЗАНИЯ ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ
- 3. Свойства линейных фильтров
- 4. Основное выражение для среднеквадратичной ошибки
- 5. Чистая проблема сглаживания
- 6. Проблема чистого предсказания
- 7. Предсказание при наличии шума
- 8. Обобщения
- 9. Обсуждение основных предположений
- МАТЕМАТИЧЕСКАЯ ТЕОРИЯ ДИФФЕРЕНЦИАЛЬНОГО АНАЛИЗАТОРА
- Основное условие разрешимости
- Реализация функций
- Системы уравнений
- Аппроксимация множителей с помощью передаточных чисел
- Автоматическое управление скоростью работы устройства
- О МАКСИМАЛЬНОМ ПОТОКЕ ЧЕРЕЗ СЕТЬ
- ТЕОРЕМА О РАСКРАСКЕ РЕБЕР ГРАФА
- УНИВЕРСАЛЬНАЯ МАШИНА ТЬЮРИНГА С ДВУМЯ ВНУТРЕННИМИ СОСТОЯНИЯМИ
- Невозможность создания универсальной машины Тьюринга с одним состоянием
- Моделирование машины Тьюринга с помощью только двух символов на ленте
- ВЫЧИСЛИМОСТЬ НА ВЕРОЯТНОСТНЫХ МАШИНАХ
- Приложение
- БИБЛИОГРАФИЯ РАБОТ ПО ШЕННОНОВСКОЙ ТЕОРИИ ОПТИМАЛЬНОГО КОДИРОВАНИЯ ИНФОРМАЦИИ