| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
СОСТАВЛЕНИЕ ПРОГРАММ ДЛЯ ИГРЫ В ШАХМАТЫ НА ВЫЧИСЛИТЕЛЬНОЙ МАШИНЕ
1. Введение
В статье рассматривается задача составления программы для игры в шахматы на современной универсальной вычислительной машине. Эта задача, не имея, возможно, практической ценности, представляет теоретический интерес. Можно надеяться, что ее удовлетворительное решение явится плацдармом для наступления на другие задачи сходной природы, но имеющие большее практическое значение. Вот некоторые возможности в этом направлении.
1) Конструирование фильтров, эквипотенциальных соединений и т. д.
2) Конструирование переключательных схем.
3) Управление распределением телефонных вызовов в зависимости от складывающихся обстоятельств, а не по фиксированной схеме.
4) Выполнение символических (не арифметических) математических операций.
5) Перевод с одного языка на другой.
6) Принятие решений командиром по упрощенным вариантам оперативной обстановки.
7) Оркестровка мелодий.
8) Выработка логических выводов.
Вероятно, разнообразные устройства различной природы для решения перечисленных задач будут созданы в ближайшем будущем. Техника, развитая для современных вычислительных машин, делает решение этих задач не только теоретически возможным, но в некоторых случаях позволяет серьезно рассматривать их с экономической точки зрения.
Универсальные машины имеют следующие преимущества перед обычными вычислительными машинами.
Во-первых, они могут выполнять операции не только над числами, но также над шахматными позициями, схемами, математическими выражениями, словами и т. д.
Во-вторых, сам вычислительный процесс включает некоторые общие принципы, своего рода разумный выбор, возможность изменения процесса решения на основе метода испытаний и ошибок, а не только на основе заранее заданных правил.
Наконец, решая указанные задачи, машины могут давать не только два ответа — правильный или неверный, — но непрерывный ряд ответов от лучшего к худшему. Например, машина, которая конструирует хорошие фильтры, а не обязательно наилучшие из всех возможных, может быть признана удовлетворительной. Машина для игры в шахматы наиболее соответствует первой попытке решения таких неарифметических задач, так как: 1) шахматная игра четко определяется, с одной стороны, допустимыми операциями (ходами), а с другой стороны, конечной целью (мат); 2) эта игра ни настолько проста, чтобы быть тривиальной, ни настолько трудна, чтобы нельзя было найти удовлетворительное решение;
3) считается, что обычно игра в шахматы требует «обдумывания» для достижения успеха; следовательно, решение этой задачи заставит нас либо допустить существование механического мышления, либо приведет к дальнейшему ограничению понятия «мышления»;
4) дискретная структура игры хорошо согласуется с цифровой природой современных вычислительных машин.
В настоящее время имеется значительная литература, описывающая машины для игры в шахматы. В конце XVIII и начале XIX века Маельзельский (Maelzels) шахматный автомат — устройство, изобретенное фон Кемпеленом (von Kempelen), широко демонстрировался в качестве машины, играющей в шахматы. В это время появилось большое количество статей, включая аналитический очерк Эдгара По (озаглавленный «Маельзельский шахматный игрок»), пытающихся объяснить принцип его работы. Большинство авторов совершенно правильно заключали, что автоматом управляет спрятанный шахматист. Однако аргументы, приводящие к такому заключению, часто были неверными. Эдгар По полагал, например, что можно построить машину, которая будет побеждать постоянно, либо машину, которая будет побеждать случайно, и отсюда выводит, что, поскольку автомат не является непобедимым, то, следовательно, он управляется человеком. Ясно, что такое рассуждение неправильно. Для полного знакомства с историей и принципом работы автомата читатель отсылается к серии статей Харкнеса и Беттела в журнале «Чесс ревью» (Chess Review) за 1947 год.
Более честная попытка сконструировать машину, играющую в шахматы, была сделана в 1914 году Торресом-и-Квеведо, который построил автомат для разыгрывания эндшпиля: король и ладья против короля. Машина играла за сторону, имеющую короля и ладью, и форсировала мат в несколько ходов независимо от игры противника. Так как для выбора правильного хода в таком окончании может быть дан точный ряд правил, то задача относительно проста, но идея такой машины была прогрессивна для своего времени.
Положение, которое будет развито в работе, состоит в том, что современные вычислительные машины могут быть успешно использованы для игры в шахматы. Для этого необходимо составить соответствующую программу. Хотя первое приближение, которое здесь дается, по нашему мнению, в основном полно, требуется сделать еще много как в экспериментальном, так и в теоретиче.ском отношении.
2. Общие положения
Шахматная позиция может быть определена следующими параметрами.
1) Описанием положения всех фигур на доске.
2) Указанием стороны, делающей ход в данной позиции.
3) Указанием того, ходили ли раньше короли и ладьи. Это важно, так как, например, после передвижения ладьи право на рокировку в соответствующую сторону теряется.
4) Указанием последнего сделанного хода; оно будет нужно, чтобы определить возможность взятия на проходе, так как эта привилегия после одного хода утрачивается.
5) Указанием числа ходов, выполненных после последнего движения пешкой или после последнего взятия. Это важно, так как в случае достижения этим числом 50 присуждается ничья. Для простоты будем пренебрегать правилом присуждения ничьей после троекратного повторения позиции.
В шахматах нет элементов случайности, кроме первоначального выбора, кому из игроков делать первый ход, в противоположность играм в карты, трик-трак и т. д. Далее, в шахматах каждый из партнеров имеет полную информацию о каждом ходе и о всех предыдущих ходах (в противоположность, например военным ситуациям). Из этих двух фактов вытекает, что любая шахматная позиция может быть:
1) либо выигрышной для белых (это означает, что белые могут выиграть, как бы ни защищались черные);
2) либо ничейной (белые могут добиться по крайней мере ничьей, как бы ни играли черные, но и черные могут добиться не более, чем ничьей, как бы ни играли белые);
3) выигрышной для черных (черные могут выиграть, как бы ни защищались белые).
Это утверждение является для практических целей аналогом теоремы существования. Неизвестно практического метода для определения того, к которой из этих трех категорий принадлежит любая выбранная позиция. Если такой метод появится, шахматы потеряют интерес как игра. Тогда можно будет определить, является ли начальная позиция выигрышной, проигрышной или ничейной для белых, и исход игры между противниками, знающими этот метод, будет полностью определен выбором того, кому первому ходить. Если исходить из того, что начальная позиция ничейная (что подсказывает опыт игр мастеров), каждая игра должна закончиться вничью.
Интересно, что небольшое изменение в шахматных правилах дает игру, для которой можно доказать, как теорему, что белые имеют по кралней мере ничью в начальной позиции. Действительно, предположим, что правила игры те же, что и в настоящие шахматы, но игрок может пропустить свою очередь хода. Тогда можно доказать как теорему, что белые при правильной игре добиваются по крайней мере ничьей.
В самом деле, в начальной позиции либо есть выигрышный ход, либо нет. Если есть — сделаем его. Если нет — передадим очередь хода противнику. Черные тогда будут находиться в том же самом положении, что и белые перед первым ходом вследствие зеркальной симметрии начальной позиции. Так как белые не имели в этой позиции выигрышного хода, теперь такого хода не имеют черные. Следовательно, черные могут самое большее добиться ничьей. Но тогда белые в любом случае имеют минимум ничью.
В некоторых играх существует простая оценочная функция  которая относится к позиции Р и величина которой определяет, к какой категории (выигрыш, проигрыш, ничья) принадлежит позиция Р. В игре Ним, например, она может быть определена записью числа спичек в каждой группе в двоичной системе. Эти числа подписываются друг под другом (как для сложения столбиком). Рассматриваются получившиеся столбцы. Если число единиц
которая относится к позиции Р и величина которой определяет, к какой категории (выигрыш, проигрыш, ничья) принадлежит позиция Р. В игре Ним, например, она может быть определена записью числа спичек в каждой группе в двоичной системе. Эти числа подписываются друг под другом (как для сложения столбиком). Рассматриваются получившиеся столбцы. Если число единиц
в каждом столбце четно, то позиция проигрышна для игрока, который должен делать очередной ход, и выигрышна в противном случае. Если для игры может быть найдена такая оценочная функция  то легко сконструировать машину, способную вести игру наилучшим образом. Она никогда не проиграет и не сведет в ничью выигрышную партию, никогда не проиграет ничейную партию и, если противник ошибется, воспользуется этим. Это можно сделать следующим образом: предположим, что
то легко сконструировать машину, способную вести игру наилучшим образом. Она никогда не проиграет и не сведет в ничью выигрышную партию, никогда не проиграет ничейную партию и, если противник ошибется, воспользуется этим. Это можно сделать следующим образом: предположим, что
 для выигрышной позиции,
для выигрышной позиции,
 для ничейной позиции,
для ничейной позиции,
 для проигрышной позиции.
для проигрышной позиции.
При своем ходе машина подсчитывает  для различных позиций, получающихся из данной каждым возможным ходом. Она выбирает ход (или один из нескольких ходов), дающий максимум величины
для различных позиций, получающихся из данной каждым возможным ходом. Она выбирает ход (или один из нескольких ходов), дающий максимум величины  В случае игры в Ним, где такая функция известна, машина, реализующая оптимальную игру, действительно построена.
В случае игры в Ним, где такая функция известна, машина, реализующая оптимальную игру, действительно построена.
В шахматах, в принципе, возможно играть абсолютно правильно или построить машину, которая будет это делать, следующим образом: в данной позиции рассматриваются все возможные ходы, затем все ходы за противника и т. д. до конца игры (в каждом варианте). Конец игры, согласно правилам, должен наступить через конечное число ходов (вспомните 50-ходовое правило ничьей). Каждый из вариантов заканчивается поражением, ничьей или выигрышем. Рассматривая варианты с конца, можно определить, имеется ли форсированная победа, позиция ничейная или проигрышная. Легко показать, однако, что даже при высоких скоростях, которыми обладают современные вычислительные машины, провести такое исследование практически невозможно.
В типовых шахматных позициях бывает около 30 возможных ходов. Это число остается примерно постоянным до тех пор, пока игра не приближается к концу, как показано на рис. 1. Этот график построен на основании данных, полученных де Гроотом, который определил среднее число допустимых ходов в позиции, обработав большое число партий шахматных мастеров. Таким образом, ход за белых и затем ответ за черных дает около 103 вариантов. Обычно шахматные партии длятся около 40 ходов до соглашения
между противниками. Такое определение окончания партии не подходит для наших целей, потому что машина должна вести вычисления до окончания по правилам, а не по соглашению. Однако даже в этом случае подсчет дает около 10120 вариантов, которые должны быть проверены в начальной позиции. Машина, работающая со скоростью одного варианта в микро-микро-секунду, потребует более  лет, чтобы выбрать первый ход!
лет, чтобы выбрать первый ход!

Рис. 1.
Другой (также практически невыполнимый) метод заключается в том, что надо иметь «словарь» всех возможных положений шахматных фигур на доске. Для каждой возможной позиции задается правильный ход (вычисленный указанным выше процессом или подсказанный шахматным мастером). При своем ходе машина просто смотрит на позицию и делает указанный ход. Число возможных позиций достигает порядка  или грубо
или грубо  , что, естественно, делает такой метод нереальным.
, что, естественно, делает такой метод нереальным.
Ясно, что задача состоит не в том, чтобы построить машину, играющую в шахматы идеально хорошо (что практически совершенно невозможно), и не в том, чтобы просто делать допустимые ходы (что тривиально). Надо научить ее играть искусно, может быть, сравнимо с хорошим шахматистом.
Шахматная стратегия может быть описана как правило для выбора хода в любой данной позиции. Если по этому правилу всегда выбирается один и тот же ход в одной и той же позиции, стратегия в теории игр называется «чистой». Если процесс выбора включает
случайные элементы и не всегда приводит к одному и тому же ходу в одной и той же позиции, то стратегия называется «смешанной».
Приведем простые примеры стратегий.
1. Перенумеруем все возможные ходы в позиции Р согласно некоторому определенному правилу. Будем всегда выбирать ход с номером 1. Это пример «чистой» стратегии.
2. Перенумеруем возможные ходы и будем выбирать номер хода случайным образом. Это пример «смешанной» стратегии.
Обе эти стратегии, конечно, очень бедны и не претендуют на выбор хороших ходов. Наша задача состоит в построении сравнительно хорошей стратегии для выбора очередного хода.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- СИМВОЛИЧЕСКИЙ АНАЛИЗ РЕЛЕЙНЫХ И ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- 2. Параллельно-последовательные двухполюсные схемы. Основные определения и постулаты
- 3. Многополюсные и не параллельно-последовательные схемы
- Преобразование треугольника в звезду и звезды в ячейку
- Функция сопротивления не параллельно-последовательной схемы
- Системы уравнений
- Реле и переключатели специальных типов
- 4. Синтез схем
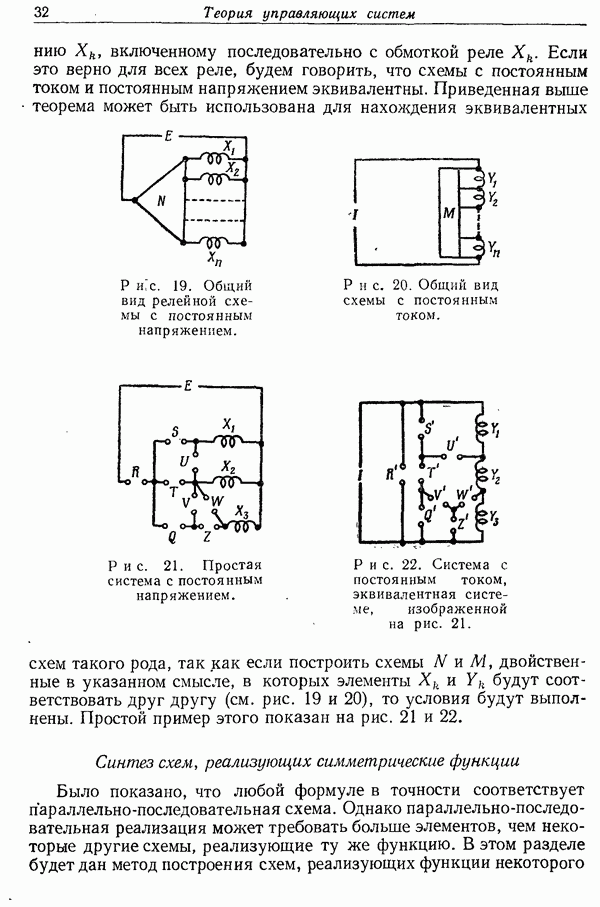
- Двойственные схемы
- Синтез схем, реализующих симметрические функции
- Составление уравнений по рабочим характеристикам
- 5. Примеры
- ЧИСЛО ДВУХПОЛЮСНЫХ ПАРАЛЛЕЛЬНО-ПОСЛЕДОВАТЕЛЬНЫХ СЕТЕЙ
- 1. Получение производящей функции
- 2. Численный подсчет
- 3. Асимптотическое поведение
- 4. Параллельно-последовательная реализация переключательных функций
- СИНТЕЗ ДВУХПОЛЮСНЫХ ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- 2. Основная теорема синтеза
- 3. Синтез схем для произвольных функций.
- Часть II. РАСПРЕДЕЛЕНИЕ НАГРУЗКИ МЕЖДУ РЕЛЕ
- 5. Разделительное дерево
- 6. Другие задачи распределения
- 7. Функция «мю»
- Часть III. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- 9. Частично симметрические функции
- ПРИМЕЧАНИЯ РЕДАКТОРА
- ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К ОБЪЕМУ ПАМЯТИ ТЕЛЕФОННОГО КОММУТАТОРА
- 2. Память, требуемая для S произвольных вызовов от N абонентов
- 3. Условие раздельной памяти
- 4. Связь с теорией информации
- НАДЕЖНЫЕ СХЕМЫ ИЗ НЕНАДЕЖНЫХ РЕЛЕ
- Идеализированные реле
- Общий метод повышения надежности
- Свойства функции h(p)
- Комбинация двух схем
- Оценки функции h'(p)
- Схемы заданной длины и ширины
- Оценки числа контактов в случае, когда реле уже достаточно надежны
- Сравнение с элементами фон Неймана
- Реле с неопределенным временем срабатывания
- Синтез надежных схем в целом
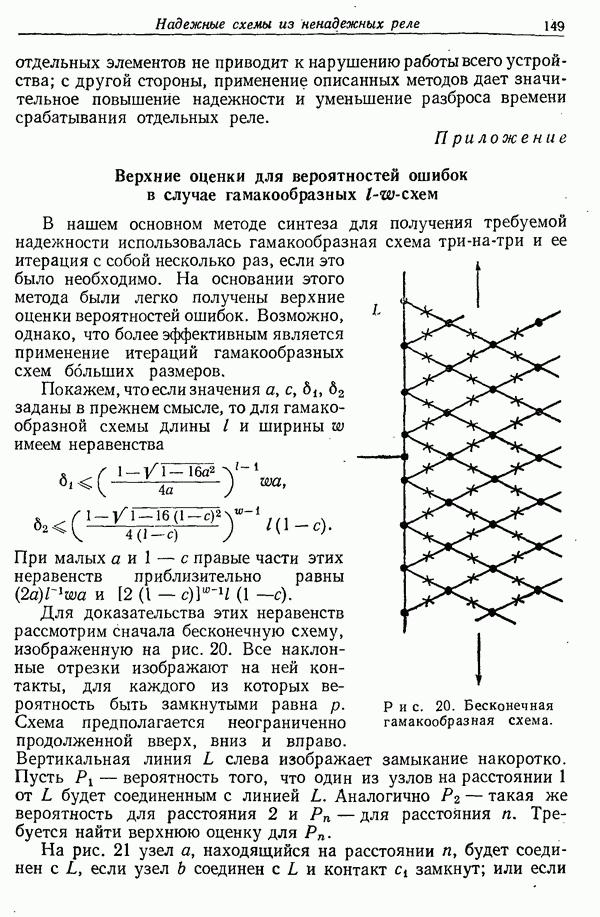
- Приложение. Верхние оценки для вероятностей ошибок в случае гамакообразных l-w-схем
- ИСПОЛЬЗОВАНИЕ МАШИНЫ ДЛЯ ПРОЕКТИРОВАНИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА И АВТОМАТЫ
- Машины Тьюринга
- Логические машины
- «Играющие машины»
- Обучаемые машины
- Самовоспроизводящиеся машины
- Обращение к читателю
- МАШИНА ДЛЯ ИГРЫ В ШАХМАТЫ
- СОСТАВЛЕНИЕ ПРОГРАММ ДЛЯ ИГРЫ В ШАХМАТЫ НА ВЫЧИСЛИТЕЛЬНОЙ МАШИНЕ
- 3. Приближенная оценочная функция
- 4. Стратегия, основанная на оценочной функции
- 5. Составление программы для универсальной вычислительной машины для реализации стратегии типа А
- 6. Улучшение стратегии
- 7. Изменения в игре и в стиле
- 8. Другой тип стратегии
- ПРИЛОЖЕНИЕ. ОЦЕНОЧНАЯ ФУНКЦИЯ ДЛЯ ШАХМАТ
- ИГРАЮЩИЕ МАШИНЫ
- СООБЩЕНИЕ О МАШИНЕ, РЕШАЮЩЕЙ ЛАБИРИНТНУЮ ЗАДАЧУ
- ВКЛАД ФОН НЕЙМАНА В ТЕОРИЮ АВТОМАТОВ
- МАТЕМАТИЧЕСКАЯ ТЕОРИЯ СВЯЗИ
- 1. ДИСКРЕТНЫЕ СИСТЕМЫ БЕЗ ШУМОВ
- 2. Дискретный источник сообщений
- 3. Последовательные приближения к английскому языку
- 4. Графическое представление марковского процесса
- 5. Эргодические и смешанные источники
- 6. Выбор, неопределенность и энтропия
- 7. Энтропия источника сообщений
- 8. Представление операций кодирования и декодирования
- 9. Основная теорема для канала без шума
- 10. Рассмотрение полученных результатов и примеры
- 11. Примеры
- II. ДИСКРЕТНЫЙ КАНАЛ С ШУМОМ
- 12. Надежность и пропускная способность канала
- 13. Основная теорема для дискретного канала с шумом
- 14. Рассмотрение полученных результатов
- 15. Пример дискретного канала и его пропускной способности
- 16. Пропускная способность канала в некоторых частных случаях
- 17. Пример эффективного кодирования
- III. ИНФОРМАЦИЯ ДЛЯ НЕПРЕРЫВНЫХ ВЕЛИЧИН
- 19. Ансамбли функций с ограниченной полосой частот
- 20. Энтропия непрерывного распределения
- 21. Энтропия ансамбля функций
- 22. Потеря энтропии в линейных фильтрах
- 23. Энтропия суммы двух ансамблей
- IV. НЕПРЕРЫВНЫЙ КАНАЛ
- 24. Пропускная способность непрерывного канала
- 25. Пропускная способность канала при ограничении средней мощности
- 26. Пропускная способность канала при ограничении пиковой мощности
- V. СКОРОСТЬ СОЗДАНИЯ СООБЩЕНИЙ ДЛЯ НЕПРЕРЫВНОГО ИСТОЧНИКА
- 28. Скорость создания сообщений источником при данной точности воспроизведения
- 29. Вычисление скорости создания сообщений
- Приложение 1. РОСТ ЧИСЛА БЛОКОВ СИМВОЛОВ ПРИ УСЛОВИЯХ, ОПИСЫВАЕМЫХ КОНЕЧНЫМ ЧИСЛОМ СОСТОЯНИЙ
- Приложение 2. ВЫВОД РАВЕНСТВА …
- Приложение 3. ТЕОРЕМА ОБ ЭРГОДИЧЕСКИХ ИСТОЧНИКАХ
- Приложение 4. МАКСИМИЗАЦИЯ СКОРОСТИ ДЛЯ СИСТЕМЫ ОГРАНИЧЕНИЯ
- Приложение 5
- Приложение 6
- Приложение 7
- ТЕОРИЯ СВЯЗИ В СЕКРЕТНЫХ СИСТЕМАХ
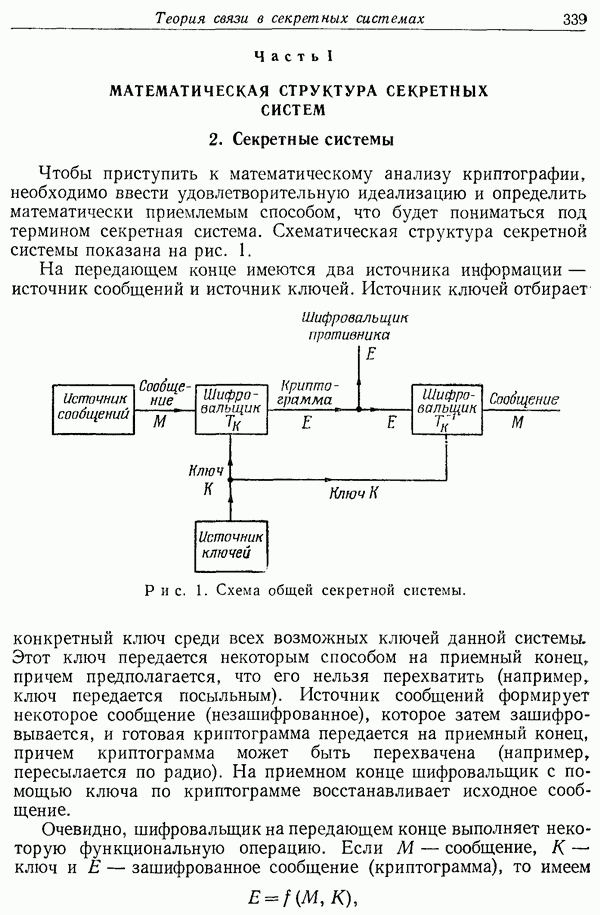
- Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ СИСТЕМ
- 3. Способы изображения систем
- 4. Примеры секретных систем
- 5. Оценка секретных систем
- 6. Алгебра секретных систем
- 7. Чистые и смешанные шифры
- 8. Подобные системы
- Часть II. ТЕОРЕТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 10. Совершенная секретность
- 11. Ненадежность
- 12. Свойства ненадежности
- 13. Ненадежность простой подстановки для языка с двухбуквенным алфавитом
- 14. Характеристика ненадежности для «случайного» шифра
- 15. Применение к стандартным шифрам
- 16. Правильность решения криптограммы
- 17. Идеальные секретные системы
- 18. Примеры идеальных секретных систем
- 19. Дополнительные замечания о ненадежности и избыточности
- 20. Распределение ненадежности
- Часть III. ПРАКТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 22. Общие замечания о решении криптограмм
- 23. Статистические методы
- 24. Метод вероятных слов
- 25. Перемешивание
- 26. Шифры типа …
- 27. Несовместимость требований к хорошим системам
- ПРИЛОЖЕНИЕ. Доказательство теоремы 3
- СОВРЕМЕННЫЕ ДОСТИЖЕНИЯ ТЕОРИИ СВЯЗИ
- Измерение информаций
- Кодирование информации
- Пропускная способность канала
- Идеальные и практические системы
- ПРИНЦИПЫ КОДОВО-ИМПУЛЬСНОЙ МОДУЛЯЦИИ
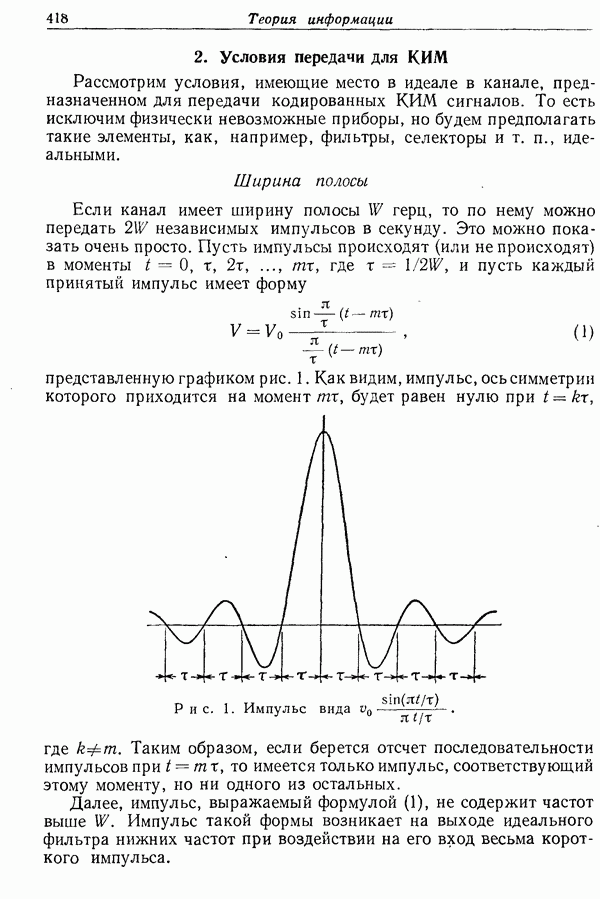
- 2. Условия передачи для КИМ
- 3. Действие системы КИМ
- 4. Сравнение КИМ и ЧМ
- 5. Заключение
- Приложение I
- Приложение II
- СВЯЗЬ ПРИ НАЛИЧИИ ШУМА
- 2. Теорема отсчетов
- 3. Геометрическое представление сигналов
- 4. Геометрическое представление сообщений
- 5. Геометрическое представление передатчика и приемника
- 6. Отображение пространства
- 7. Пропускная способность канала при наличии белого теплового шума
- 8. Обсуждение
- 9. Произвольный гауссовский шум
- 10. Пропускная способность канала при произвольном типе шума
- 11. Дискретные источники информации
- 12. Непрерывные источники информации
- НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ИНФОРМАЦИИ
- ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА С ШУМОМ ПРИ НУЛЕВОЙ ОШИБКЕ
- Пропускная способность канала при нулевой ошибке
- Пропускная способность для суммы и произведения каналов
- Каналы с обратной связью
- ГЕОМЕТРИЧЕСКИЙ ПОДХОД К ТЕОРИИ ПРОПУСКНОЙ СПОСОБНОСТИ. КАНАЛОВ СВЯЗИ
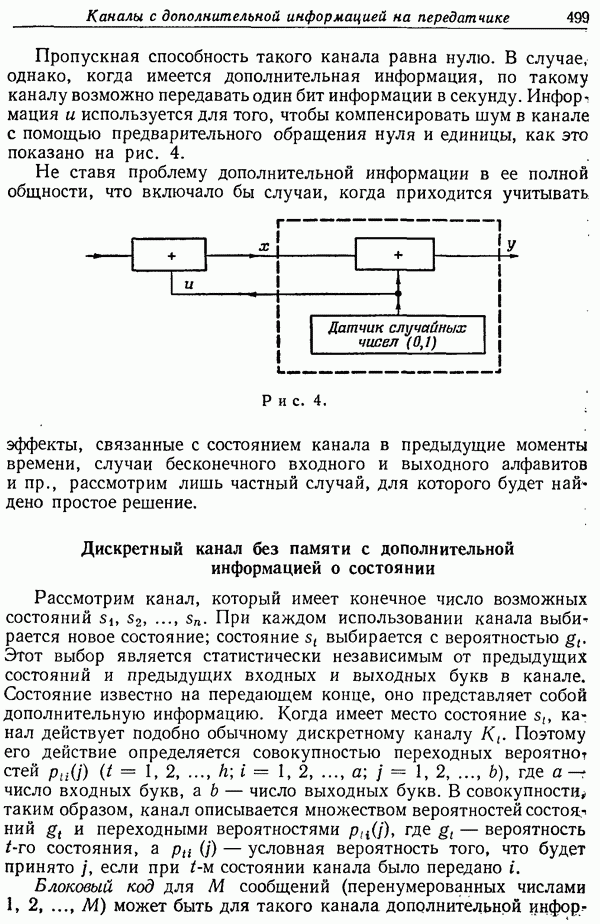
- КАНАЛЫ С ДОПОЛНИТЕЛЬНОЙ ИНФОРМАЦИЕЙ НА ПЕРЕДАТЧИКЕ
- Дискретный канал без памяти с дополнительной информацией о состоянии
- Приложение
- НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ТЕОРИИ КОДИРОВАНИЯ ДЛЯ КАНАЛОВ С ШУМАМИ
- Оценка вероятности ошибки в терминах производящей функции моментов
- Пропускная способность канала с конечным числом состояний, состояние которого вычислимо на обоих концах
- Пропускная способность канала с конечным числом состояний в случае, когда состояние вычислимо на передающем конце и не вычислимо на приемном конце
- ЗАМЕЧАНИЯ О ЧАСТИЧНОМ УПОРЯДОЧИВАНИИ КАНАЛОВ СВЯЗИ
- Дальнейшее обобщение и некоторые предположения
- ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ ОПТИМАЛЬНЫХ кодов В ГАУССОВСКОМ КАНАЛЕ
- 2. Сводка результатов
- 3. Нижняя граница, основанная на соображениях «сферической упаковки»
- 4. Верхняя граница, определяемая методом случайного кодирования
- 5. Формулы для скорости передачи R как функции угла конуса
- 6. Асимптотические формулы для …
- 7. Асимптотическое выражение для верхней границы при случайном кодировании
- 8. Жесткая верхняя граница
- 9. Жесткая нижняя граница
- 10. Поведение границ вблизи пропускной способности канала
- 11. Верхняя граница, полученная методом исчерпывания
- 12. Нижняя граница для гауссовского канала, получаемая исходя из минимального расстояния
- 13. Границы ошибок и другие условия, накладываемые на точки
- 14. Кривые для асимптотических границ
- ТЕОРЕМЫ КОДИРОВАНИЯ ДЛЯ ДИСКРЕТНОГО ИСТОЧНИКА ПРИ ЗАДАННОМ КРИТЕРИИ ТОЧНОСТИ
- Мера искажения отдельной буквы
- Несколько простых примеров
- Скорость при заданном искажении R(d)
- Выпуклость вниз кривой R(d)
- Нахождение R(d) в некоторых простых случаях
- Скорость передачи для произведения источников с мерой, являющейся суммой мер искажения
- Нижняя граница для искажения при заданной пропускной способности канала
- Теоремы кодирования при заданной мере искажения отдельной буквы
- Двойственность источника и канала
- Численные расчеты для некоторых простых каналов
- Обобщение на случаи непрерывных алфавитов
- Разностная мера искажения
- Определение меры локального искажения
- Функции Rn(d) и R(d) для меры локального искажения и эргодического источника
- Прямая теорема кодирования для меры локального искажения
- Обратная теорема кодирования
- Канал с памятью
- ДВУСТОРОННИЕ КАНАЛЫ СВЯЗИ
- 4. Средние взаимные скорости передачи информации
- 5. Распределение информации
- 6. Случайное кодирование для двусторонних каналов
- 7. Вероятность ошибки для ансамбля кодов
- 8. Выпуклая оболочка G как внутренняя граница области пропускной способности
- 9. Внешняя граница для области пропускной способности
- 10. Выпуклость вниз как функций от …
- 11. Приложения свойства выпуклости. Каналы с симметричной структурой
- 12. Характер области, выделяемой внешней границей
- 13. Пример, в котором внутренняя и внешняя границы различны
- 14. Достижимость внешней границы при зависимых источниках
- 15. Общий метод нахождения области пропускной способности двустороннего канала
- 16. Двусторонние каналы с памятью
- 17. Обобщение на каналы с Т концами
- БАНДВАГОН
- ПРЕДСКАЗАНИЕ И ЭНТРОПИЯ ПЕЧАТНОГО АНГЛИЙСКОГО ТЕКСТА
- 2. Вычисление энтропии по статистике английского языка
- 3. Предсказание английского текста
- 4. Идеальное N-граммное предсказывание
- 5. Граница для энтропии на основании частот предсказания
- 6. Результаты эксперимента для английского языка
- УПРОЩЕННЫЙ ВЫВОД ЛИНЕЙНОЙ ТЕОРИИ СГЛАЖИВАНИЯ И ПРЕДСКАЗАНИЯ ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ
- 3. Свойства линейных фильтров
- 4. Основное выражение для среднеквадратичной ошибки
- 5. Чистая проблема сглаживания
- 6. Проблема чистого предсказания
- 7. Предсказание при наличии шума
- 8. Обобщения
- 9. Обсуждение основных предположений
- МАТЕМАТИЧЕСКАЯ ТЕОРИЯ ДИФФЕРЕНЦИАЛЬНОГО АНАЛИЗАТОРА
- Основное условие разрешимости
- Реализация функций
- Системы уравнений
- Аппроксимация множителей с помощью передаточных чисел
- Автоматическое управление скоростью работы устройства
- О МАКСИМАЛЬНОМ ПОТОКЕ ЧЕРЕЗ СЕТЬ
- ТЕОРЕМА О РАСКРАСКЕ РЕБЕР ГРАФА
- УНИВЕРСАЛЬНАЯ МАШИНА ТЬЮРИНГА С ДВУМЯ ВНУТРЕННИМИ СОСТОЯНИЯМИ
- Невозможность создания универсальной машины Тьюринга с одним состоянием
- Моделирование машины Тьюринга с помощью только двух символов на ленте
- ВЫЧИСЛИМОСТЬ НА ВЕРОЯТНОСТНЫХ МАШИНАХ
- Приложение
- БИБЛИОГРАФИЯ РАБОТ ПО ШЕННОНОВСКОЙ ТЕОРИИ ОПТИМАЛЬНОГО КОДИРОВАНИЯ ИНФОРМАЦИИ