| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Параллельно-последовательные двухполюсные схемы. Основные определения и постулаты
Ограничим наше исследование схемами, содержащими только контакты реле и переключателей. Такие схемы между любыми двумя своими полюсами в каждый момент времени либо замкнуты (нулевое сопротивление), либо разомкнуты (бесконечное сопротивление). Сопоставим полюсам  символ
символ  или проще X.
или проще X.

Рис. 1. Символическое изображение функции сопротивления.

Рис. 2. Интерпретация сложения.

Рис. 3. Интерпретация умножения.
Эту переменную функцию времени будем называть двоичным сопротивлением двухполюсной схемы  Символом 0 (нуль) будем обозначать сопротивление замкнутой схемы, а символом 1 (единица) — сопротивление разомкнутой схемы. Следовательно, если схема
Символом 0 (нуль) будем обозначать сопротивление замкнутой схемы, а символом 1 (единица) — сопротивление разомкнутой схемы. Следовательно, если схема  разомкнута, то
разомкнута, то  а если замкнута, то
а если замкнута, то  Сопротивления
Сопротивления  называются равными, если схема
называются равными, если схема  разомкнута тогда и только тогда, когда схема
разомкнута тогда и только тогда, когда схема  разомкнута. Пусть теперь символ
разомкнута. Пусть теперь символ  (плюс) определяется в смысле последовательного соединения двухполюсных схем, при котором сопротивления
(плюс) определяется в смысле последовательного соединения двухполюсных схем, при котором сопротивления
складываются. Так  это сопротивление схемы
это сопротивление схемы  полученной в результате объединения полюсов бис схем
полученной в результате объединения полюсов бис схем  и
и  Аналогично произведение двух сопротивлений
Аналогично произведение двух сопротивлений  или короче
или короче  определяется как сопротивление схемы, образованной параллельным соединением схем
определяется как сопротивление схемы, образованной параллельным соединением схем  Контакты реле или переключателей изображаются в схемах, как показано на рис. 1, где буквы — это соответствующие функции сопротивления. На рис. 2 показана интерпретация сложения, а на рис. 3 — умножения. Такой выбор символики делает операции над сопротивлениями очень похожими на обычные алгебраические преобразования.
Контакты реле или переключателей изображаются в схемах, как показано на рис. 1, где буквы — это соответствующие функции сопротивления. На рис. 2 показана интерпретация сложения, а на рис. 3 — умножения. Такой выбор символики делает операции над сопротивлениями очень похожими на обычные алгебраические преобразования.
Очевидно, что при приведенных выше определениях справедливы следующие постулаты.
1.  Замкнутая схема, соединенная параллельно с замкнутой схемой, есть замкнутая схема.
Замкнутая схема, соединенная параллельно с замкнутой схемой, есть замкнутая схема.
 Разомкнутая схема, соединенная последовательно с разомкнутой схемой, есть разомкнутая схема.
Разомкнутая схема, соединенная последовательно с разомкнутой схемой, есть разомкнутая схема.
2.  Разомкнутая схема, соединенная последовательно с замкнутой схемой в любом порядке (т. е. разомкнутая схема справа или слева от замкнутой), есть разомкнутая схема.
Разомкнутая схема, соединенная последовательно с замкнутой схемой в любом порядке (т. е. разомкнутая схема справа или слева от замкнутой), есть разомкнутая схема.
 Замкнутая схема, соединенная параллельно с разомкнутой схемой (в любом порядке), есть замкнутая схема.
Замкнутая схема, соединенная параллельно с разомкнутой схемой (в любом порядке), есть замкнутая схема.
3.  Замкнутая схема, соединенная последовательно с замкнутой схемой, есть замкнутая схема.
Замкнутая схема, соединенная последовательно с замкнутой схемой, есть замкнутая схема.
 Разомкнутая схема, соединенная параллельно с разомкнутой схемой, есть разомкнутая схема.
Разомкнутая схема, соединенная параллельно с разомкнутой схемой, есть разомкнутая схема.
4. В каждый момент либо  либо
либо 
Этих постулатов достаточно, чтобы вывести все теоремы, которые будут использованы в связи со схемами, образованными только из последовательных и параллельных соединений. Постулаты расположены попарно, чтобы подчеркнуть двойственность между операциями сложения и умножения и константами 0 и 1. Так, если
в каком-нибудь постулате, относящемся к типу а, нули заменить на единицы, умножение на сложение и наоборот, то получится соответствующий постулат типа  Этот факт очень важен. Он дает для каждой теоремы двойственную; достаточно доказать одну, чтобы установить обе. Единственный из введенных нами постулатов, отличающийся от постулатов обычной алгебры, это
Этот факт очень важен. Он дает для каждой теоремы двойственную; достаточно доказать одну, чтобы установить обе. Единственный из введенных нами постулатов, отличающийся от постулатов обычной алгебры, это  Тем не менее он дает возможность существенно упростить операции над нашими символами.
Тем не менее он дает возможность существенно упростить операции над нашими символами.
Теоремы
Приведем ряд теорем о способах соединения сопротивлений. Так как любая из этих теорем может быть доказана очень простым способом, приведем один пример доказательства в качестве иллюстрации. Методом доказательства является метод «полной индукции», т. е. метод проверки теоремы для всех возможных случаев. Так как в силу постулата 4 каждое переменное может принимать только значения 0 и 1, это легко сделать. Некоторые теоремы могут быть доказаны более изящно сведением к предыдущим теоремам, но метод полной индукции настолько универсален, что, вероятно, ему следует отдать предпочтение.

Например, чтобы доказать теорему  , заметим, что X есть либо 0, либо 1. Если
, заметим, что X есть либо 0, либо 1. Если  теорема следует из постулата
теорема следует из постулата  если
если  она следует из постулата
она следует из постулата  Теорема
Теорема  теперь вытекает из
теперь вытекает из  по принципу двойственности в результате замены 0 на 1 и
по принципу двойственности в результате замены 0 на 1 и  на
на  .
.
В силу ассоциативных законов (2а) и (2b) в сумме или произведении нескольких членов скобки могут быть опущены. Символы  и П имеют те же значения, что и в обычной алгебре.
и П имеют те же значения, что и в обычной алгебре.
Дистрибутивный закон (3a) дает возможность «развернуть» умножение и «свернуть» сумму. Двойственная теорема  однако, в обычной алгебре неверна.
однако, в обычной алгебре неверна.
Определим теперь новую операцию, которую назовем отрицанием. Отрицание сопротивления X обозначается через X и определяется как переменная, равная 1, когда X равно 0, и равная 0, когда X равно 1. Если X — сопротивление замыкающего контакта реле, то X — сопротивление размыкающего контакта того же реле. Из определения отрицания сопротивления вытекают теоремы:

Аналогия с исчислением высказываний
Теперь можно доказать эквивалентность введенного исчисления некоторой элементарной части исчисления высказываний. Алгебра логики, введенная Джорджем Булем, является символическим методом вывода логических соотношений. Символы булевой алгебры допускают две логические интерпретации. При интерпретации в терминах классов переменные могут принимать не только два значения 0 и 1. Эта интерпретация называется алгеброй классов. Если, однако, символы рассматриваются как высказывания, то имеем исчисление высказываний, в котором переменные принимают только значения 0 и 1, как и рассмотренные выше функции сопротивления. Обычно обе интерпретации основываются на одном и том же множестве постулатов, за исключением того, что в случае
исчисления высказываний к постулатам 1—4 добавляется постулат эквивалентности, Е. В, Хантингтон дает следующую систему аксиом символической логики:
1. Класс К содержит по крайней мере два различных элемента;
2. Если  принадлежат классу К, то и а
принадлежат классу К, то и а  принадлежит классу К;
принадлежит классу К;

6.  , где
, где  определяется как
определяется как 
Если положить, что класс К состоит из двух элементов 0 и 1, то эти постулаты будут следствиями постулатов, приведенных во введении, и наоборот, приведенные там постулаты 1, 2, 3 могут быть выведены из постулатов Хантингтона. Если добавить постулат
4 и ограничиться исчислением высказываний, то становится очевидной полная аналогия между этой ветвью символической логики и исчислением переключательных схем. Обе интерпретации символов показаны в табл. I.
Благодаря этой аналогии любая теорема исчисления высказываний является также истинной теоремой, если ее интерпретировать в терминах релейных схем. Остальные теоремы данного раздела были установлены непосредственно на этой основе.
Теоремы де Моргана

выражают отрицание суммы или произведения в терминах отрицания слагаемых или сомножителей. Они могут быть проверены для двух членов подстановкой всех возможных значений, а затем методом индукции распространены на любое число  переменных.
переменных.
Функция нескольких переменных  — это выражение, образованное из переменных при помощи операций сложения, умножения и отрицания. Такая функция будет обозначаться через
— это выражение, образованное из переменных при помощи операций сложения, умножения и отрицания. Такая функция будет обозначаться через  Так, например, мы можем записать:
Так, например, мы можем записать:

Таблица I (см. скан) Аналогия между исчислением высказываний и символическим анализом релейных схем
В анализе бесконечно малых показано, что любую функцию (при условии, что она непрерывна и все ее производные непрерывны) можно разложить в ряд Тейлора. Некоторое подобное разложение возможно и в исчислении высказываний. Чтобы вывести разложение функции в ряд, рассмотрим сначала следующие равенства 

Они превращаются в тождества, если положить  или
или  . В этих равенствах функция
. В этих равенствах функция  называется разложенной по
называется разложенной по  Коэффициенты при
Коэффициенты при  в (10а) являются функциями от
в (10а) являются функциями от 
переменных и могут быть таким же образом разложены по любой из этих переменных. Аддитивные члены в  также могут быть разложены таким же образом. Разлагая по
также могут быть разложены таким же образом. Разлагая по  получим:
получим:

Повторяя разложение  раз, придем к полным разложениям в ряд, имеющим вид
раз, придем к полным разложениям в ряд, имеющим вид

Согласно  равна сумме произведений, полученных путем расстановки знаков отрицаний при
равна сумме произведений, полученных путем расстановки знаков отрицаний при  всеми возможными способами и умножения каждого произведения на коэффициент, равный значению функции, когда это произведение есть 1. Аналогично для
всеми возможными способами и умножения каждого произведения на коэффициент, равный значению функции, когда это произведение есть 1. Аналогично для 

Рис. 4, Разложение по одной переменной.
В качестве приложения такого разложения покажем, что, если требуется найти схему, реализующую данную функцию, можно всегда разложить эту функцию по формуле  или
или  так, что некоторая выделенная переменная встречается не более двух раз — один раз как замыкающий и один раз как размыкающий контакт. Это показано на рис. 4. Согласно формулам (11а) и (11b) другая переменная встречается не более четырех раз (два раза как замыкающий контакт и два раза — как размыкающий) и т. д.
так, что некоторая выделенная переменная встречается не более двух раз — один раз как замыкающий и один раз как размыкающий контакт. Это показано на рис. 4. Согласно формулам (11а) и (11b) другая переменная встречается не более четырех раз (два раза как замыкающий контакт и два раза — как размыкающий) и т. д.
Обобщение теоремы де Моргана представляется символически следующим уравнением:

Под этим подразумевается, что отрицание любой функции может быть получено заменой каждой переменной ее отрицанием и перестановкой символов  Явные и неявные скобки остаются, конечно, на тех же местах. Например, отрицание
Явные и неявные скобки остаются, конечно, на тех же местах. Например, отрицание  будет иметь вид
будет иметь вид  .
.
Приведем некоторые другие теоремы, используемые для упрощения формул:

Все эти теоремы могут быть доказаны методом полной индукции.
Любое выражение, образованное при помощи операций сложения, умножения и отрицания, является точным представлением схемы, содержащей только последовательные и параллельные соединения. Такая схема называется параллельно-последовательной. Каждая буква в выражении такого рода представляет замыкающий, размыкающий или переключающий контакт реле или переключателя. Поэтому, чтобы найти параллельно-последовательную схему, содержащую наименьшее число контактов, необходимо преобразовать выражение к форме, содержащей наименьшее число букв. Для этого вполне достаточно теорем, приведенных выше. Небольшой навык в оперировании символами — вот все, что требуется. К счастью, большинство из этих теорем в точности такие же, как в обычной алгебре. Автор считает, что особенно полезными для упрощения сложных выражений являются теоремы 3, 6, 9, 14, 15, 16а, 17 и 18.
Часто функция может быть записана различными способами, требующими одного и того же минимального числа элементов.
В таком случае может быть выбрана любая из схем или выбор может быть продиктован теми или иными соображениями.

Рис. 5. Схема, подлежащая упрощению.
В качестве примера упрощения формулы рассмотрим схему, изображенную на рис. 5. Функцией сопротивления  этой схемы будет:
этой схемы будет:

Эти преобразования были произведены с помощью формулы  где в качестве X последовательно бралось сначала
где в качестве X последовательно бралось сначала  затем X и
затем X и  Раскрывая скобки, получим
Раскрывая скобки, получим

Схема, соответствующая этой формуле, изображена на рис. 6. Следует обратить внимание на большое сокращение числа элементов.

Рис. 6. Упрощение схемы, изображенной на рис. 5.
При графическом представлении схем обмотки реле удобно обозначать той же буквой, что и сопротивление замыкающего контакта этого реле. Так, если обмотка реле соединена с источником питания схемой, функция сопротивления которой есть X, то само реле и любой его замыкающий контакт обозначается через X. Размыкающий контакт обозначается через X. При этом предполагается, что реле срабатывает мгновенно и что одновременно замыкающий контакт замыкается и размыкающий размыкается. Случай, когда имеется задержка во времени, будет рассмотрен ниже.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- СИМВОЛИЧЕСКИЙ АНАЛИЗ РЕЛЕЙНЫХ И ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- 2. Параллельно-последовательные двухполюсные схемы. Основные определения и постулаты
- 3. Многополюсные и не параллельно-последовательные схемы
- Преобразование треугольника в звезду и звезды в ячейку
- Функция сопротивления не параллельно-последовательной схемы
- Системы уравнений
- Реле и переключатели специальных типов
- 4. Синтез схем
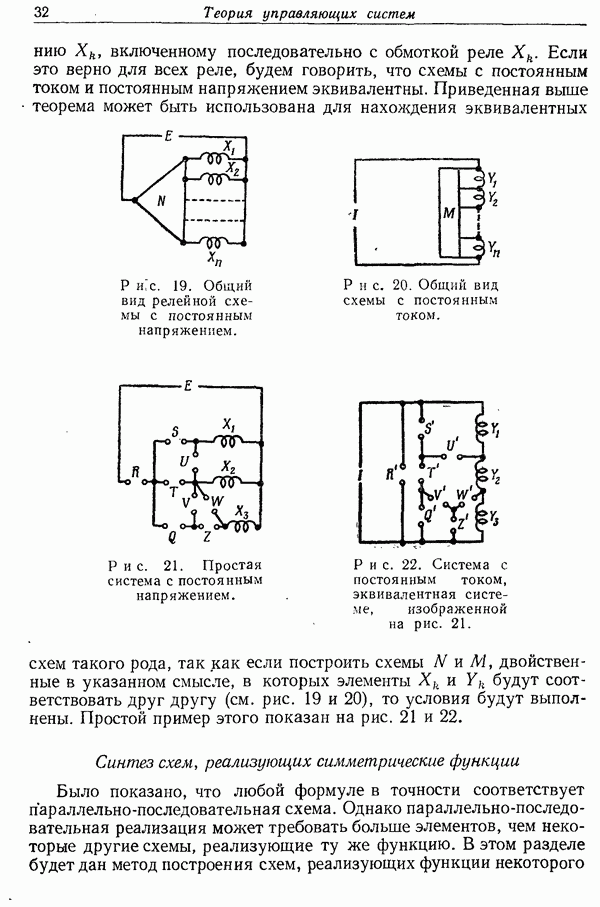
- Двойственные схемы
- Синтез схем, реализующих симметрические функции
- Составление уравнений по рабочим характеристикам
- 5. Примеры
- ЧИСЛО ДВУХПОЛЮСНЫХ ПАРАЛЛЕЛЬНО-ПОСЛЕДОВАТЕЛЬНЫХ СЕТЕЙ
- 1. Получение производящей функции
- 2. Численный подсчет
- 3. Асимптотическое поведение
- 4. Параллельно-последовательная реализация переключательных функций
- СИНТЕЗ ДВУХПОЛЮСНЫХ ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- 2. Основная теорема синтеза
- 3. Синтез схем для произвольных функций.
- Часть II. РАСПРЕДЕЛЕНИЕ НАГРУЗКИ МЕЖДУ РЕЛЕ
- 5. Разделительное дерево
- 6. Другие задачи распределения
- 7. Функция «мю»
- Часть III. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- 9. Частично симметрические функции
- ПРИМЕЧАНИЯ РЕДАКТОРА
- ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К ОБЪЕМУ ПАМЯТИ ТЕЛЕФОННОГО КОММУТАТОРА
- 2. Память, требуемая для S произвольных вызовов от N абонентов
- 3. Условие раздельной памяти
- 4. Связь с теорией информации
- НАДЕЖНЫЕ СХЕМЫ ИЗ НЕНАДЕЖНЫХ РЕЛЕ
- Идеализированные реле
- Общий метод повышения надежности
- Свойства функции h(p)
- Комбинация двух схем
- Оценки функции h'(p)
- Схемы заданной длины и ширины
- Оценки числа контактов в случае, когда реле уже достаточно надежны
- Сравнение с элементами фон Неймана
- Реле с неопределенным временем срабатывания
- Синтез надежных схем в целом
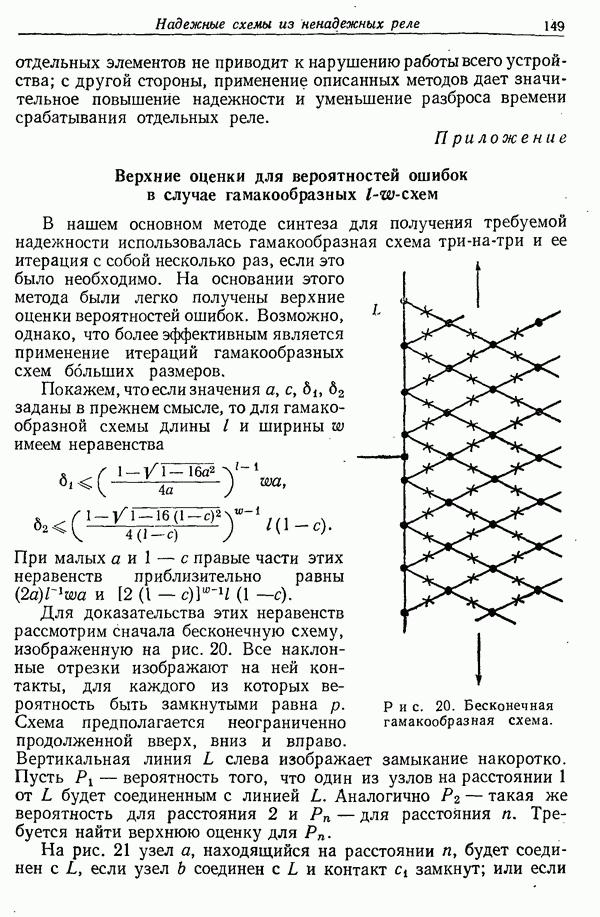
- Приложение. Верхние оценки для вероятностей ошибок в случае гамакообразных l-w-схем
- ИСПОЛЬЗОВАНИЕ МАШИНЫ ДЛЯ ПРОЕКТИРОВАНИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА И АВТОМАТЫ
- Машины Тьюринга
- Логические машины
- «Играющие машины»
- Обучаемые машины
- Самовоспроизводящиеся машины
- Обращение к читателю
- МАШИНА ДЛЯ ИГРЫ В ШАХМАТЫ
- СОСТАВЛЕНИЕ ПРОГРАММ ДЛЯ ИГРЫ В ШАХМАТЫ НА ВЫЧИСЛИТЕЛЬНОЙ МАШИНЕ
- 3. Приближенная оценочная функция
- 4. Стратегия, основанная на оценочной функции
- 5. Составление программы для универсальной вычислительной машины для реализации стратегии типа А
- 6. Улучшение стратегии
- 7. Изменения в игре и в стиле
- 8. Другой тип стратегии
- ПРИЛОЖЕНИЕ. ОЦЕНОЧНАЯ ФУНКЦИЯ ДЛЯ ШАХМАТ
- ИГРАЮЩИЕ МАШИНЫ
- СООБЩЕНИЕ О МАШИНЕ, РЕШАЮЩЕЙ ЛАБИРИНТНУЮ ЗАДАЧУ
- ВКЛАД ФОН НЕЙМАНА В ТЕОРИЮ АВТОМАТОВ
- МАТЕМАТИЧЕСКАЯ ТЕОРИЯ СВЯЗИ
- 1. ДИСКРЕТНЫЕ СИСТЕМЫ БЕЗ ШУМОВ
- 2. Дискретный источник сообщений
- 3. Последовательные приближения к английскому языку
- 4. Графическое представление марковского процесса
- 5. Эргодические и смешанные источники
- 6. Выбор, неопределенность и энтропия
- 7. Энтропия источника сообщений
- 8. Представление операций кодирования и декодирования
- 9. Основная теорема для канала без шума
- 10. Рассмотрение полученных результатов и примеры
- 11. Примеры
- II. ДИСКРЕТНЫЙ КАНАЛ С ШУМОМ
- 12. Надежность и пропускная способность канала
- 13. Основная теорема для дискретного канала с шумом
- 14. Рассмотрение полученных результатов
- 15. Пример дискретного канала и его пропускной способности
- 16. Пропускная способность канала в некоторых частных случаях
- 17. Пример эффективного кодирования
- III. ИНФОРМАЦИЯ ДЛЯ НЕПРЕРЫВНЫХ ВЕЛИЧИН
- 19. Ансамбли функций с ограниченной полосой частот
- 20. Энтропия непрерывного распределения
- 21. Энтропия ансамбля функций
- 22. Потеря энтропии в линейных фильтрах
- 23. Энтропия суммы двух ансамблей
- IV. НЕПРЕРЫВНЫЙ КАНАЛ
- 24. Пропускная способность непрерывного канала
- 25. Пропускная способность канала при ограничении средней мощности
- 26. Пропускная способность канала при ограничении пиковой мощности
- V. СКОРОСТЬ СОЗДАНИЯ СООБЩЕНИЙ ДЛЯ НЕПРЕРЫВНОГО ИСТОЧНИКА
- 28. Скорость создания сообщений источником при данной точности воспроизведения
- 29. Вычисление скорости создания сообщений
- Приложение 1. РОСТ ЧИСЛА БЛОКОВ СИМВОЛОВ ПРИ УСЛОВИЯХ, ОПИСЫВАЕМЫХ КОНЕЧНЫМ ЧИСЛОМ СОСТОЯНИЙ
- Приложение 2. ВЫВОД РАВЕНСТВА …
- Приложение 3. ТЕОРЕМА ОБ ЭРГОДИЧЕСКИХ ИСТОЧНИКАХ
- Приложение 4. МАКСИМИЗАЦИЯ СКОРОСТИ ДЛЯ СИСТЕМЫ ОГРАНИЧЕНИЯ
- Приложение 5
- Приложение 6
- Приложение 7
- ТЕОРИЯ СВЯЗИ В СЕКРЕТНЫХ СИСТЕМАХ
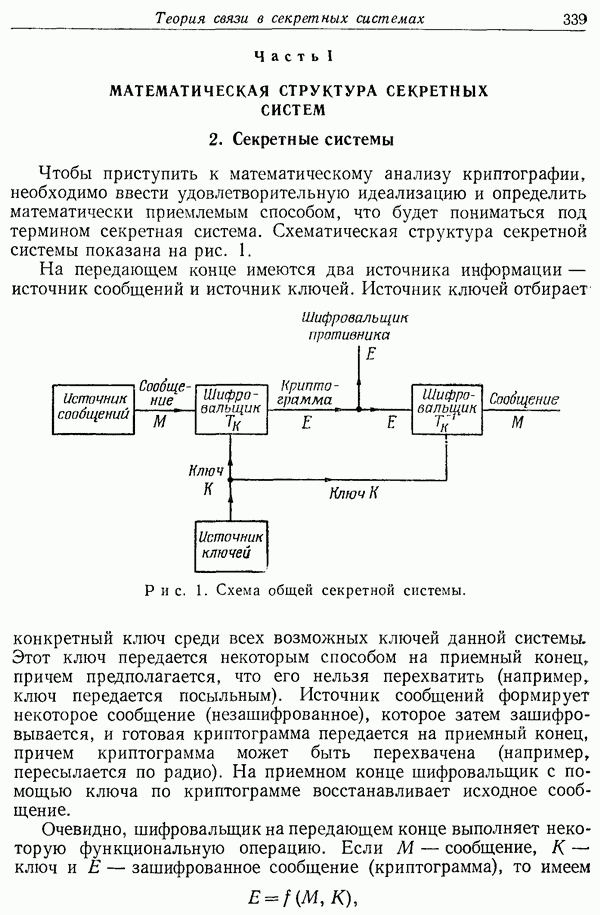
- Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ СИСТЕМ
- 3. Способы изображения систем
- 4. Примеры секретных систем
- 5. Оценка секретных систем
- 6. Алгебра секретных систем
- 7. Чистые и смешанные шифры
- 8. Подобные системы
- Часть II. ТЕОРЕТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 10. Совершенная секретность
- 11. Ненадежность
- 12. Свойства ненадежности
- 13. Ненадежность простой подстановки для языка с двухбуквенным алфавитом
- 14. Характеристика ненадежности для «случайного» шифра
- 15. Применение к стандартным шифрам
- 16. Правильность решения криптограммы
- 17. Идеальные секретные системы
- 18. Примеры идеальных секретных систем
- 19. Дополнительные замечания о ненадежности и избыточности
- 20. Распределение ненадежности
- Часть III. ПРАКТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 22. Общие замечания о решении криптограмм
- 23. Статистические методы
- 24. Метод вероятных слов
- 25. Перемешивание
- 26. Шифры типа …
- 27. Несовместимость требований к хорошим системам
- ПРИЛОЖЕНИЕ. Доказательство теоремы 3
- СОВРЕМЕННЫЕ ДОСТИЖЕНИЯ ТЕОРИИ СВЯЗИ
- Измерение информаций
- Кодирование информации
- Пропускная способность канала
- Идеальные и практические системы
- ПРИНЦИПЫ КОДОВО-ИМПУЛЬСНОЙ МОДУЛЯЦИИ
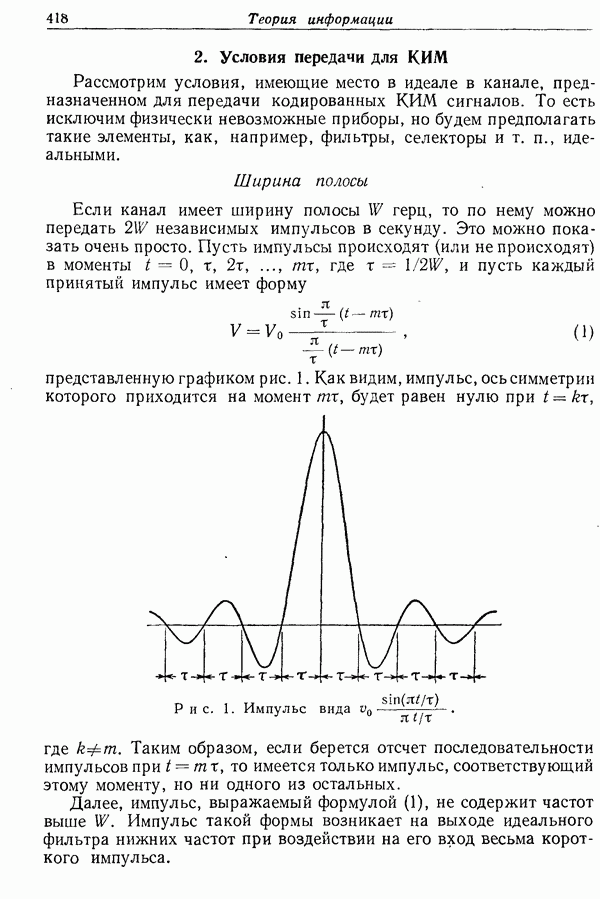
- 2. Условия передачи для КИМ
- 3. Действие системы КИМ
- 4. Сравнение КИМ и ЧМ
- 5. Заключение
- Приложение I
- Приложение II
- СВЯЗЬ ПРИ НАЛИЧИИ ШУМА
- 2. Теорема отсчетов
- 3. Геометрическое представление сигналов
- 4. Геометрическое представление сообщений
- 5. Геометрическое представление передатчика и приемника
- 6. Отображение пространства
- 7. Пропускная способность канала при наличии белого теплового шума
- 8. Обсуждение
- 9. Произвольный гауссовский шум
- 10. Пропускная способность канала при произвольном типе шума
- 11. Дискретные источники информации
- 12. Непрерывные источники информации
- НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ИНФОРМАЦИИ
- ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА С ШУМОМ ПРИ НУЛЕВОЙ ОШИБКЕ
- Пропускная способность канала при нулевой ошибке
- Пропускная способность для суммы и произведения каналов
- Каналы с обратной связью
- ГЕОМЕТРИЧЕСКИЙ ПОДХОД К ТЕОРИИ ПРОПУСКНОЙ СПОСОБНОСТИ. КАНАЛОВ СВЯЗИ
- КАНАЛЫ С ДОПОЛНИТЕЛЬНОЙ ИНФОРМАЦИЕЙ НА ПЕРЕДАТЧИКЕ
- Дискретный канал без памяти с дополнительной информацией о состоянии
- Приложение
- НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ТЕОРИИ КОДИРОВАНИЯ ДЛЯ КАНАЛОВ С ШУМАМИ
- Оценка вероятности ошибки в терминах производящей функции моментов
- Пропускная способность канала с конечным числом состояний, состояние которого вычислимо на обоих концах
- Пропускная способность канала с конечным числом состояний в случае, когда состояние вычислимо на передающем конце и не вычислимо на приемном конце
- ЗАМЕЧАНИЯ О ЧАСТИЧНОМ УПОРЯДОЧИВАНИИ КАНАЛОВ СВЯЗИ
- Дальнейшее обобщение и некоторые предположения
- ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ ОПТИМАЛЬНЫХ кодов В ГАУССОВСКОМ КАНАЛЕ
- 2. Сводка результатов
- 3. Нижняя граница, основанная на соображениях «сферической упаковки»
- 4. Верхняя граница, определяемая методом случайного кодирования
- 5. Формулы для скорости передачи R как функции угла конуса
- 6. Асимптотические формулы для …
- 7. Асимптотическое выражение для верхней границы при случайном кодировании
- 8. Жесткая верхняя граница
- 9. Жесткая нижняя граница
- 10. Поведение границ вблизи пропускной способности канала
- 11. Верхняя граница, полученная методом исчерпывания
- 12. Нижняя граница для гауссовского канала, получаемая исходя из минимального расстояния
- 13. Границы ошибок и другие условия, накладываемые на точки
- 14. Кривые для асимптотических границ
- ТЕОРЕМЫ КОДИРОВАНИЯ ДЛЯ ДИСКРЕТНОГО ИСТОЧНИКА ПРИ ЗАДАННОМ КРИТЕРИИ ТОЧНОСТИ
- Мера искажения отдельной буквы
- Несколько простых примеров
- Скорость при заданном искажении R(d)
- Выпуклость вниз кривой R(d)
- Нахождение R(d) в некоторых простых случаях
- Скорость передачи для произведения источников с мерой, являющейся суммой мер искажения
- Нижняя граница для искажения при заданной пропускной способности канала
- Теоремы кодирования при заданной мере искажения отдельной буквы
- Двойственность источника и канала
- Численные расчеты для некоторых простых каналов
- Обобщение на случаи непрерывных алфавитов
- Разностная мера искажения
- Определение меры локального искажения
- Функции Rn(d) и R(d) для меры локального искажения и эргодического источника
- Прямая теорема кодирования для меры локального искажения
- Обратная теорема кодирования
- Канал с памятью
- ДВУСТОРОННИЕ КАНАЛЫ СВЯЗИ
- 4. Средние взаимные скорости передачи информации
- 5. Распределение информации
- 6. Случайное кодирование для двусторонних каналов
- 7. Вероятность ошибки для ансамбля кодов
- 8. Выпуклая оболочка G как внутренняя граница области пропускной способности
- 9. Внешняя граница для области пропускной способности
- 10. Выпуклость вниз как функций от …
- 11. Приложения свойства выпуклости. Каналы с симметричной структурой
- 12. Характер области, выделяемой внешней границей
- 13. Пример, в котором внутренняя и внешняя границы различны
- 14. Достижимость внешней границы при зависимых источниках
- 15. Общий метод нахождения области пропускной способности двустороннего канала
- 16. Двусторонние каналы с памятью
- 17. Обобщение на каналы с Т концами
- БАНДВАГОН
- ПРЕДСКАЗАНИЕ И ЭНТРОПИЯ ПЕЧАТНОГО АНГЛИЙСКОГО ТЕКСТА
- 2. Вычисление энтропии по статистике английского языка
- 3. Предсказание английского текста
- 4. Идеальное N-граммное предсказывание
- 5. Граница для энтропии на основании частот предсказания
- 6. Результаты эксперимента для английского языка
- УПРОЩЕННЫЙ ВЫВОД ЛИНЕЙНОЙ ТЕОРИИ СГЛАЖИВАНИЯ И ПРЕДСКАЗАНИЯ ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ
- 3. Свойства линейных фильтров
- 4. Основное выражение для среднеквадратичной ошибки
- 5. Чистая проблема сглаживания
- 6. Проблема чистого предсказания
- 7. Предсказание при наличии шума
- 8. Обобщения
- 9. Обсуждение основных предположений
- МАТЕМАТИЧЕСКАЯ ТЕОРИЯ ДИФФЕРЕНЦИАЛЬНОГО АНАЛИЗАТОРА
- Основное условие разрешимости
- Реализация функций
- Системы уравнений
- Аппроксимация множителей с помощью передаточных чисел
- Автоматическое управление скоростью работы устройства
- О МАКСИМАЛЬНОМ ПОТОКЕ ЧЕРЕЗ СЕТЬ
- ТЕОРЕМА О РАСКРАСКЕ РЕБЕР ГРАФА
- УНИВЕРСАЛЬНАЯ МАШИНА ТЬЮРИНГА С ДВУМЯ ВНУТРЕННИМИ СОСТОЯНИЯМИ
- Невозможность создания универсальной машины Тьюринга с одним состоянием
- Моделирование машины Тьюринга с помощью только двух символов на ленте
- ВЫЧИСЛИМОСТЬ НА ВЕРОЯТНОСТНЫХ МАШИНАХ
- Приложение
- БИБЛИОГРАФИЯ РАБОТ ПО ШЕННОНОВСКОЙ ТЕОРИИ ОПТИМАЛЬНОГО КОДИРОВАНИЯ ИНФОРМАЦИИ