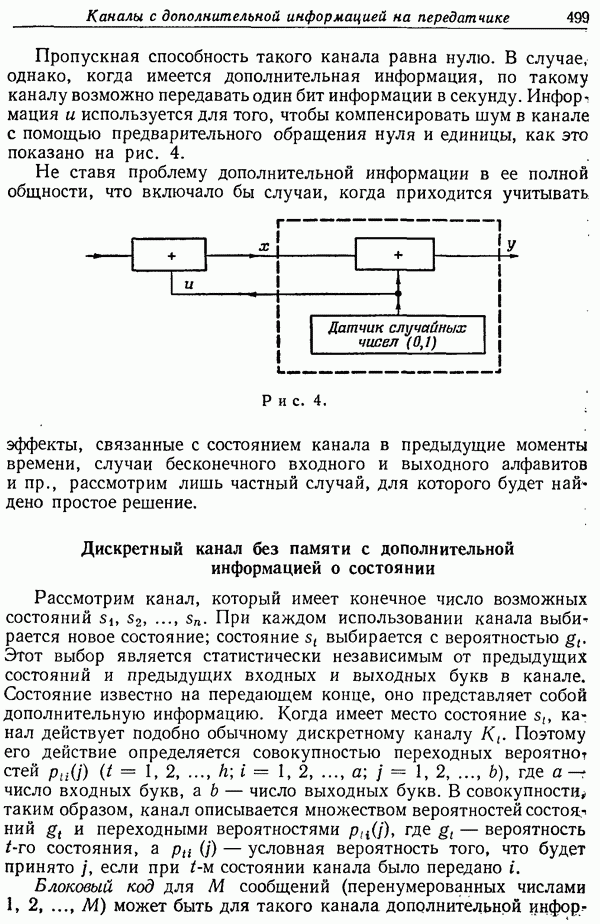
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. Синтез схем для произвольных функций.
а. Функции одной, двух и трех переменных.
Функции одной или двух переменных рассматриваются легко, так как число таких функций очень мало. Так, существуют лишь следующие функции одной переменной X:

и, очевидно, 
От двух переменных X и  существует 16 функций:
существует 16 функций:

так что 
Лекажем, что любая функция трех переменных  может быть реализована не более чем с 8 элементами и не более чем с 4 элементами на каждом реле. Любая функция трех переменных может быть разложена в следующее произведение:
может быть реализована не более чем с 8 элементами и не более чем с 4 элементами на каждом реле. Любая функция трех переменных может быть разложена в следующее произведение:

В терминах теоремы 1 полагаем

так что

Приведенные выше функции  реализуются схемой М рис. 7, и легко видеть, что
реализуются схемой М рис. 7, и легко видеть, что  . Теперь нужно построить другую схему
. Теперь нужно построить другую схему  имеющую в качестве
имеющую в качестве  функции
функции  . Каждая из них есть функция одной переменной
. Каждая из них есть функция одной переменной  и должна, следовательно, быть одной из четырех возможных функций одной переменной
и должна, следовательно, быть одной из четырех возможных функций одной переменной

Рассмотрим схему  на рис. 8. Если какие-либо V равны нулю, то присоединим соответствующие полюсы схемы М к полюсу схемы
на рис. 8. Если какие-либо V равны нулю, то присоединим соответствующие полюсы схемы М к полюсу схемы  отмеченному нулем; если какие-нибудь V равны
отмеченному нулем; если какие-нибудь V равны  присоединим соответствующие полюсы схемы М к полюсу схемы
присоединим соответствующие полюсы схемы М к полюсу схемы  отмеченному
отмеченному  и т. д. Полюсы, соответствующие 1, конечно, не соединены ни с чем.
и т. д. Полюсы, соответствующие 1, конечно, не соединены ни с чем.

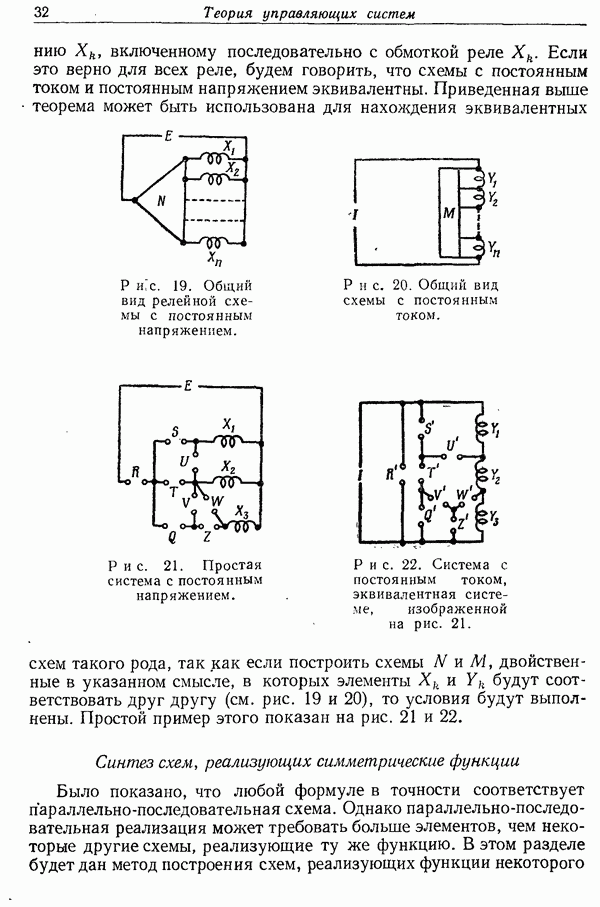
Рис. 7. Разделительное дерево с двумя ярусами.

Рис. 8. Схема, представляющая функции одной переменной.
Из теоремы 1 следует, что схема, построенная таким образом, будет реализовать функцию  Во многих случаях некоторые из элементов будут лишними: например, если одна из
Во многих случаях некоторые из элементов будут лишними: например, если одна из  равна 1, элемент схемы М, соединенный с полюсом
равна 1, элемент схемы М, соединенный с полюсом  может быть исключен. В худшем случае М содержит 6 элементов и
может быть исключен. В худшем случае М содержит 6 элементов и  содержит 2. Переменная X может встречаться дважды,
содержит 2. Переменная X может встречаться дважды,  — четырежды и
— четырежды и  — дважды. Конечно, совершенно несущественно, какие из переменных мы назовем
— дважды. Конечно, совершенно несущественно, какие из переменных мы назовем  или
или  Итак, доказано больше, чем было сформулировано выше, а именно следующая теорема.
Итак, доказано больше, чем было сформулировано выше, а именно следующая теорема.
Теорема 2. Любая функция трех переменных может быть реализована с использованием не более чем 2, 2 и 4 элементов соответственно для этих трех переменных, взятых в любом порядке. Таким образом,  Кроме того, так как замыкающие и размыкающие элементы содержатся в связных парах, то в терминах переключательных элементов может быть получено распределение 1, 1, 2.
Кроме того, так как замыкающие и размыкающие элементы содержатся в связных парах, то в терминах переключательных элементов может быть получено распределение 1, 1, 2.
Эта теорема дает лишь верхние оценки для  и
и  Возникает вопросотом, можно ли при помощи какого-либо другого метода синтеза снизить эти оценки, т. е. можно ли знак
Возникает вопросотом, можно ли при помощи какого-либо другого метода синтеза снизить эти оценки, т. е. можно ли знак  заменить знаком
заменить знаком  Можно показать изучением специальных случаев, что
Можно показать изучением специальных случаев, что  есть функция
есть функция

требующая в наиболее экономичной реализации 8 элементов.  однако, фактически равно 3.
однако, фактически равно 3.
Возможно, что вообще функция

требует  элементов, но это пока не доказано. Доказательство того, что некоторая функция не может быть реализована с малым числом элементов, отчасти похоже на доказательство существования трансцендентных чисел. Ниже будет показано, что почти все функции требуют для реализации большого числа элементов, однако трудно показать, что это справедливо для конкретной функции.
элементов, но это пока не доказано. Доказательство того, что некоторая функция не может быть реализована с малым числом элементов, отчасти похоже на доказательство существования трансцендентных чисел. Ниже будет показано, что почти все функции требуют для реализации большого числа элементов, однако трудно показать, что это справедливо для конкретной функции.
б. Функции четырех переменных.
При реализации функций четырех переменных тем же самым методом открываются два пути. Во-первых, можно разложить функцию следующим образом:

При таком разложении положим  и построим схему, изображенную на рис. 9.
и построим схему, изображенную на рис. 9.
 здесь та же, что на рис. 8. Рассуждая так же, как в случае трех переменных, можно убедиться в том, что
здесь та же, что на рис. 8. Рассуждая так же, как в случае трех переменных, можно убедиться в том, что 

Рис. 9. Разделительное деревос тремя ярусами. !
Используя несколько более сложный метод, можно, однако, снизить эту оценку. Пусть функция разложена следующим образом:

Можно использовать в качестве М схему типа, приведенного на рис. 7. Функции V теперь суть функции двух переменных  и
и  и могут быть любыми из следующих 16 функций:
и могут быть любыми из следующих 16 функций:

Мы разделили функции на 5 групп А, В, С, D и Е для дальнейших ссылок. Покажем, что любая функция четырех переменных может быть реализована не более чем с 14 элементами. Это означает, что мы должны построить схему  использующую не более чем 8 элементов (так как в схеме М использованы 6) для любого выбора четырех функций из перечисленных выше. Для доказательства рассмотрим несколько специальных случаев.
использующую не более чем 8 элементов (так как в схеме М использованы 6) для любого выбора четырех функций из перечисленных выше. Для доказательства рассмотрим несколько специальных случаев.
1. Если все 4 функции взяты из групп А, В, С и D, то N заведомо будет содержать не более 8 элементов, так как эти 4 функции содержат самое большее 8 символов переменных.
2. Предположим теперь, что в точности одна функция принадлежит группе Е; не нарушая общности, можно считать, что это  так как другая функция может быть получена из нее просто заменой У на У. Если одна или более из оставшихся функций
так как другая функция может быть получена из нее просто заменой У на У. Если одна или более из оставшихся функций
принадлежат группам А или В — ситуация удовлетворительна, для реализации этой функции не требуется дополнительных элементов. Очевидно, что для 0 и 1 элементов не нужно, а функция  или
или  может быть «извлечена» из схемы для
может быть «извлечена» из схемы для  если последнюю функцию представить в виде
если последнюю функцию представить в виде  Например,
Например,  можно получить при помощи схемы, изображенной на рис. 10. Оставшихся четырех элементов, несомненно, достаточно для реализации любых двух функций из групп А, В, С или D.
можно получить при помощи схемы, изображенной на рис. 10. Оставшихся четырех элементов, несомненно, достаточно для реализации любых двух функций из групп А, В, С или D.

Рис. 10. Упрощенная схема.

Рис. 11. Упрощенная схема.
3. Теперь, все еще предполагая, что имеем одну функцию,  из группы Е, допустим, что по крайней мере две оставшиеся функции принадлежат группе D. Используя подобный процесс «извлечения» [из схемы для YZ + YZ], можно сэкономить по одному элементу для реализации каждой из этих функций. Например, если эти функции суть
из группы Е, допустим, что по крайней мере две оставшиеся функции принадлежат группе D. Используя подобный процесс «извлечения» [из схемы для YZ + YZ], можно сэкономить по одному элементу для реализации каждой из этих функций. Например, если эти функции суть  то схема будет такой, как показано на рис. 11.
то схема будет такой, как показано на рис. 11.
4. При том же предположении наихудшим случаем является тот, когда две функции взяты из группы С и одна из D, или все три из С.
Этот последний случай удовлетворителен, так как по крайней мере одна из этих трех функций должна быть членом функции  и может быть «извлечена». Первый из названных случаев неудовлетворителен только тогда, когда две функции из группы С суть
и может быть «извлечена». Первый из названных случаев неудовлетворителен только тогда, когда две функции из группы С суть  и
и  . Легко видеть, что существенно различными являются только такие возможности для функций из группы
. Легко видеть, что существенно различными являются только такие возможности для функций из группы  То, что получающиеся здесь функции
То, что получающиеся здесь функции  могут быть реализованы с 14 контактами, может быть показано выписыванием типичных функций и упрощением их с помощью правил булевой алгебры.
могут быть реализованы с 14 контактами, может быть показано выписыванием типичных функций и упрощением их с помощью правил булевой алгебры.
5. Рассмотрим теперь случаи, где две функции принадлежат группе Е. Воспользовавшись схемой рис. 12, можно «извлечь» функции или части функций из А, В или D и увидеть, что трудными случаями являются лишь следующие.
а. Две функции принадлежат группе С. В этом случае или функция  симметрична относительно
симметрична относительно  и
и  или же обе эти функции могут быть получены из схемы для функции из группы Е, изображенной на рис. 12. Случай симметрии будет рассмотрен в последней части этой работы.
или же обе эти функции могут быть получены из схемы для функции из группы Е, изображенной на рис. 12. Случай симметрии будет рассмотрен в последней части этой работы.
б. Одна функция принадлежит группе С, другая — D, причем имеет место лишь один случай отсутствия симметрии. Предположим что эти четыре функции суть 

Рис. 12. Упрощенная схема.
Это приводит к нескольким типам функций  которые все могут быть упрощены с помощью алгебраических методов. Этим завершается доказательство теоремы, которая может быть сформулирована следующим образом:
которые все могут быть упрощены с помощью алгебраических методов. Этим завершается доказательство теоремы, которая может быть сформулирована следующим образом:
Теорема 3. Любая функция четырех переменных может быть реализована с использованием не более чем 14 элементов.
в. Функции более чем четырех переменных.
Любая функция пяти переменных может быть записана в виде

и, поскольку, как только что было показано, каждая из двух функций от четырех переменных может быть реализована с использованием 14 элементов,  можно реализовать с 30 элементами.
можно реализовать с 30 элементами.
Теперь рассмотрим функцию  от
от  переменных. Для
переменных. Для  получим наилучшую оценку путем разложения
получим наилучшую оценку путем разложения  по всем переменным, кроме двух
по всем переменным, кроме двух 

Функции V суть функции переменных  и могут быть получены из общей схемы
и могут быть получены из общей схемы  на рис. 13, в которой представлены все функции двух переменных.
на рис. 13, в которой представлены все функции двух переменных.

(кликните для просмотра скана)
Эта схема содержит 20 элементов, сгруппированных в 5 переключающих элементов для одной переменной и в 5 для другой. Схема М для (4), изображенная на рис. 14, требует в общем случае  элементов. Таким образом, доказана теорема:
элементов. Таким образом, доказана теорема:
Теорема 4. 
г. Верхние оценки для  при больших значениях
при больших значениях 
Конечно, не слишком часто приходится реализовывать функцию более чем 10 переменных, но представляет теоретический интерес определить поведение функции  при больших значениях
при больших значениях  настолько точно, насколько это возможно.
настолько точно, насколько это возможно.
Докажем сначала теорему, относящуюся к оценке числа элементов, требуемых для схемы, аналогичной схеме рис. 13, но обобщенной на случай  переменных.
переменных.
Теорема 5. Схема  реализующая все
реализующая все  функций
функций  переменных, может быть построена с использованием менее
переменных, может быть построена с использованием менее  элементов, т. е. не более двух элементов на функцию. Любая схема с этим свойством использует по крайней мере
элементов, т. е. не более двух элементов на функцию. Любая схема с этим свойством использует по крайней мере  элементов на функцию для любого
элементов на функцию для любого  при достаточно большом значении
при достаточно большом значении 

Рис. 15. Схема для всех функций от  переменных, построенная из схемы для всех функций от
переменных, построенная из схемы для всех функций от  переменных.
переменных.
Первая часть будет доказана по индукции. Очевидно, что это верно для  Предположим, что это верно для некоторого
Предположим, что это верно для некоторого  и схемы
и схемы  на рис. 15. Любая функция от
на рис. 15. Любая функция от  переменных может быть записана так:
переменных может быть записана так:

где  зависят только от
зависят только от  переменных. Легко видеть, что все функции
переменных. Легко видеть, что все функции  могут быть получены таким же образом, как
могут быть получены таким же образом, как  т. е. путем соединения соответствующих полюсов
т. е. путем соединения соответствующих полюсов  с полюсом
с полюсом  элементами
элементами  . Среди них будет
. Среди них будет  функций
функций  но они могут быть получены просто путем соединения с рассматриваемыми функциями
но они могут быть получены просто путем соединения с рассматриваемыми функциями  без каких-либо дополнительных элементов. Таким образом, во всей схеме используется меньше чем
без каких-либо дополнительных элементов. Таким образом, во всей схеме используется меньше чем

элементов, ибо по предположению схема  содержит меньше чем
содержит меньше чем  элементов, и первый член в этом выражении есть число дополнительных элементов.
элементов, и первый член в этом выражении есть число дополнительных элементов.
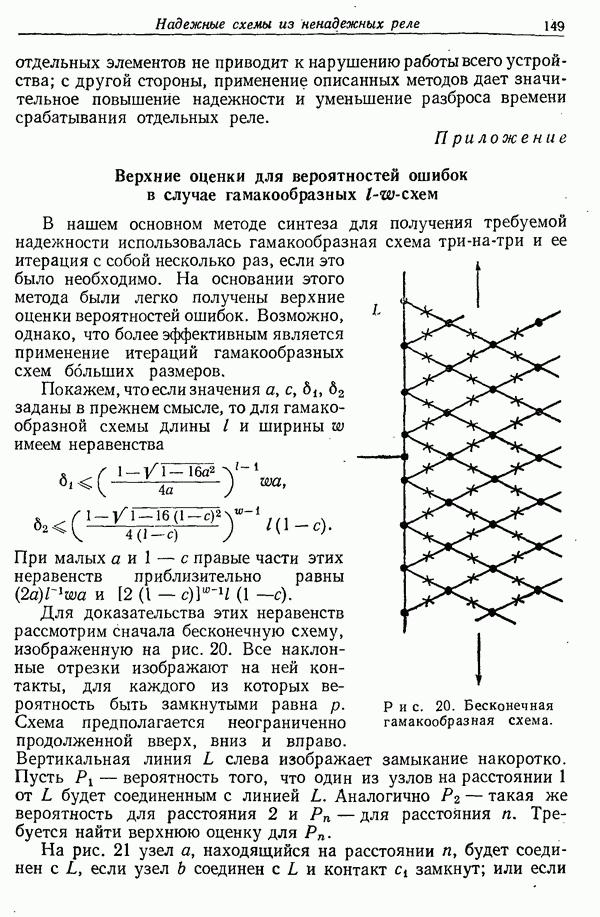
Второе утверждение теоремы 5 может быть доказано следующим образом. Пусть имеется схема (рис. 16), обладающая требуемым свойством.

Рис. 16. Схема для всех функций от  переменных.
переменных.

Рис. 17. Возможный вариант в схеме на рис. 16.
Полюсы могут быть разделены на три класса: те, которые имеют один или менее элементов, непосредственно с ними соединенных; имеющие два элемента, а также те, которые имеют три или более элементов. Первое множество состоит из 0,1 и функций типа

где X есть некоторая переменная или ее отрицание. Число таких функций не превосходит  для имеющихся
для имеющихся  способов выбора
способов выбора  различных функций
различных функций  от оставшихся
от оставшихся  переменных. Следовательно, доля полюсов этого класса стремится к нулю при
переменных. Следовательно, доля полюсов этого класса стремится к нулю при  Функции второго класса имеют вид
Функции второго класса имеют вид

В случае  функция может быть представлена в виде
функция может быть представлена в виде

и таких функций имеется не более чем  т. е. снова бесконечно малая доля. В случае
т. е. снова бесконечно малая доля. В случае  имеем положение, показанное на рис. 17, и соединение XX не может быть использовано для другого полюса, так как такая последовательная комбинация элементов всегда разомкнута. Внутренние концы этих элементов поэтому могут быть перемещены и присоединены к полюсам, соответствующим функциям, зависящим меньше чем от
имеем положение, показанное на рис. 17, и соединение XX не может быть использовано для другого полюса, так как такая последовательная комбинация элементов всегда разомкнута. Внутренние концы этих элементов поэтому могут быть перемещены и присоединены к полюсам, соответствующим функциям, зависящим меньше чем от  переменных, согласно равенству
переменных, согласно равенству

если они уже так не присоединены. Это означает, что полюсы второго класса соединены с бесконечно малой частью всех полюсов. Тогда можно относить два элемента к каждому из этих полюсов и по крайней мере 3/2 элемента каждому из полюсов третьей группы. Так как эти две группы исчерпывают все полюсы, за исключением доли, стремящейся к нулю при  то теорема доказана.
то теорема доказана.
Если при синтезе схем, реализующих функции  переменных, оборвать дерево на
переменных, оборвать дерево на  ярусе, то дерево будет содержать
ярусе, то дерево будет содержать  элемента, и можно найти схему
элемента, и можно найти схему  содержащую менее
содержащую менее  элементов, реализующую все функции оставшихся
элементов, реализующую все функции оставшихся  переменных. Следовательно,
переменных. Следовательно,

для любого целого  . Требуется найти целое число
. Требуется найти целое число  минимизирующее эту верхнюю оценку.
минимизирующее эту верхнюю оценку.
Считая, что  изменяется непрерывно, а
изменяется непрерывно, а  фиксировано, заключаем, что функция
фиксировано, заключаем, что функция

имеет только один минимум. Этот минимум должен, следовательно, находиться между и  где
где

т. е.

или

Заметим, что  не может быть целым числом, так как правая часть равенства есть степень двойки и второй член (в скобках) меньше половины первого. Следовательно, для того чтобы найти целое число М, обращающее
не может быть целым числом, так как правая часть равенства есть степень двойки и второй член (в скобках) меньше половины первого. Следовательно, для того чтобы найти целое число М, обращающее  в минимум, надо взять в
в минимум, надо взять в
качестве М наименьшее целое число, удовлетворяющее условию

Таким образом, М удовлетворяет неравенствам

Это дает

Наша верхняя оценка для  ведет себя подобно
ведет себя подобно  с пилообразными колебаниями при
с пилообразными колебаниями при  меняющимися между степенями двойки, вследствие того, что
меняющимися между степенями двойки, вследствие того, что  должно быть целым числом. Если определить
должно быть целым числом. Если определить  как
как

где М определено как точка минимума функции  [т. е. М удовлетворяет неравенству (5)], то
[т. е. М удовлетворяет неравенству (5)], то  меняется примерно так, как показано на рис. 18, где по оси абсцисс взята логарифмическая
меняется примерно так, как показано на рис. 18, где по оси абсцисс взята логарифмическая

Рис. 18. Поведение функции 
Шкала. Максимумы достигаются в точках, немного больших степеней двойки, причем все ближе и ближе к ним при  Пилообразный вид кривой становится все более и более точным. Резкое падение наступает при изменении одного значения М на следующее. Эти факты приводят к следующему результату.
Пилообразный вид кривой становится все более и более точным. Резкое падение наступает при изменении одного значения М на следующее. Эти факты приводят к следующему результату.
Теорема 6 а. Для всех 

б. Для почти всех 

в. Существует бесконечная последовательность  для которой
для которой

Строгое доказательство теоремы может быть получено без особых затруднений
д. Нижняя оценка для  при больших значениях
при больших значениях  До сих пор большая часть нашей работы относилась к определению верхней оценки для
До сих пор большая часть нашей работы относилась к определению верхней оценки для  Было показано, что для всех
Было показано, что для всех 

Теперь спрашивается, приближаются ли где-нибудь значения этой функции  к значениям функции
к значениям функции  или, быть может,
или, быть может,  можно мажорировать функцией с меньшим порядком роста, например пр. В течение некоторого времени считали, что на самом деле
можно мажорировать функцией с меньшим порядком роста, например пр. В течение некоторого времени считали, что на самом деле  может быть мажорирована функцией
может быть мажорирована функцией  для всех
для всех  что справедливо для первых нескольких значений: 1, 4, 8, 14. Покажем, что это весьма далеко от истины и что на самом деле — есть действительный порядок роста
что справедливо для первых нескольких значений: 1, 4, 8, 14. Покажем, что это весьма далеко от истины и что на самом деле — есть действительный порядок роста 

для всех  Дадим частичный ответ на следующий тесно связанный с этим вопрос, а именно: предположим, что «сложность» данной функции
Дадим частичный ответ на следующий тесно связанный с этим вопрос, а именно: предположим, что «сложность» данной функции  от
от  переменных будет определена как отношение числа элементов в наиболее экономичной ее реализации к
переменных будет определена как отношение числа элементов в наиболее экономичной ее реализации к  Тогда сложность любой функции заключена между 0 и 1. Возникает вопрос, каких функций больше — простых или сложных?
Тогда сложность любой функции заключена между 0 и 1. Возникает вопрос, каких функций больше — простых или сложных?
Теорема 7. Для всех достаточно больших  все функции
все функции  переменных, за исключением некоторой доли
переменных, за исключением некоторой доли  требуют по крайней мере
требуют по крайней мере  — элементов, где
— элементов, где  и
и  -произвольно малые положительные числа. Следовательно, для больших
-произвольно малые положительные числа. Следовательно, для больших 

и пснти все функции имеют сложность, большую  Для некоторой последовательности
Для некоторой последовательности  почти все функции имеют сложность, большую
почти все функции имеют сложность, большую  .
.
Доказательство этой теоремы довольно интересно; оно является чистым доказательством существования. Не будем показывать, что какая-то индивидуальная функция или множество функций требуют для своей реализации  элементов, но покажем, что невозможно все функции реализовать с меньшим числом элементов. Сделаем это, показав, что нельзя обойтись сетями 15 с менее чем
элементов, но покажем, что невозможно все функции реализовать с меньшим числом элементов. Сделаем это, показав, что нельзя обойтись сетями 15 с менее чем  — ребрами для того, чтобы представить все 22 функций
— ребрами для того, чтобы представить все 22 функций  переменных (учитывая, конечно, различные способы приписывания переменных ребрам каждой сети). Это оказывается возможным только из-за очень быстрого роста функции
переменных (учитывая, конечно, различные способы приписывания переменных ребрам каждой сети). Это оказывается возможным только из-за очень быстрого роста функции  Нам потребуется следующее утверждение:
Нам потребуется следующее утверждение:
Лемма. Число двухполюсных сетей не более чем с К ребрами меньше, чем 
Любая двухполюсная сеть с К или меньше ребрами может быть построена следующим образом: сначала расположим по порядку К ребер и два полюса 

Соединим прежде всего полюсы  вместе любым способом 16. Число различных способов соединения можно оценить сверху числом всех разбиений
вместе любым способом 16. Число различных способов соединения можно оценить сверху числом всех разбиений  элементов, которое в свою очередь меньше чем
элементов, которое в свою очередь меньше чем  что есть число способов, которыми можно расставить один или более знаков раздела между символами
что есть число способов, которыми можно расставить один или более знаков раздела между символами  Далее, предполагая, что
Далее, предполагая, что  соединены желаемым способом, можно соединить 1 или с одним из этих узлов или с дополнительным узлом, т. е. 1 имеет выбор самое большее из
соединены желаемым способом, можно соединить 1 или с одним из этих узлов или с дополнительным узлом, т. е. 1 имеет выбор самое большее из  узлов, 2 имеет выбор из
узлов, 2 имеет выбор из  Следовательно, число сетей заведомо меньше, чем
Следовательно, число сетей заведомо меньше, чем

и лемма легко проверяется для  .
.
Вернемся теперь к доказательству теоремы 7. Число функций  переменных, которые могут быть реализованы с
переменных, которые могут быть реализованы с  элементами, заведомо меньше, чем число сетей, которые можно построить
элементами, заведомо меньше, чем число сетей, которые можно построить
со столькими ребрами, умноженное на число способов приписывания переменных ребрам, т. е. меньше чем

Следовательно,

Выбирая  настолько большим, что
настолько большим, что  превосходит эти остальные члены в выражении для
превосходит эти остальные члены в выражении для  , приходим к неравенству
, приходим к неравенству

Однако имеется  функций
функций  переменных и
переменных и

Следовательно, почти все функции требуют больше чем  — элементов.
— элементов.
Далее, так как для всех  найдется по крайней мере одна функция, требующая больше чем (скажем)
найдется по крайней мере одна функция, требующая больше чем (скажем)  -элементов, и так как
-элементов, и так как  при
при  можно утверждать, что для всех
можно утверждать, что для всех 

для некоторой константы  ибо необходимо только выбрать А таким образом, чтобы оно было наименьшим числом в конечном множестве
ибо необходимо только выбрать А таким образом, чтобы оно было наименьшим числом в конечном множестве

Таким образом,  есть величина порядка
есть величина порядка  Остальные части теоремы 7 легко вытекают из уже доказанного.
Остальные части теоремы 7 легко вытекают из уже доказанного.
По мнению автора, почти все функции, имеют сложность, близкую к 1, т. е. большую  . Это может быть показано по крайней мере для бесконечной последовательности
. Это может быть показано по крайней мере для бесконечной последовательности  если утверждение леммы может быть усилено именно если будет показано, что число сетей с К ребрами для больших К меньше чем
если утверждение леммы может быть усилено именно если будет показано, что число сетей с К ребрами для больших К меньше чем 
Хотя при подсчете числа сетей с К ребрами были использованы различные методы, все они дают результат  Интересно показать, что для больших К число сетей больше, чем
Интересно показать, что для больших К число сетей больше, чем

Это можно сделать обращением вышеприведенных рассуждений. Пусть  — число сетей с К ребрами. Так как имеется
— число сетей с К ребрами. Так как имеется  функций
функций  переменных и каждая из них может быть реализована с
переменных и каждая из них может быть реализована с  элементами
элементами  достаточно велико), то
достаточно велико), то

для больших значений  Но, как нетрудно убедиться, предположение, что
Но, как нетрудно убедиться, предположение, что  противоречит этому неравенству. Аналогично для бесконечной последовательности К
противоречит этому неравенству. Аналогично для бесконечной последовательности К

Так как нет никаких очевидных соображений в пользу того, что  связано со степенями двойки, то, по-видимому, последнее неравенство верно для всех достаточно больших К.
связано со степенями двойки, то, по-видимому, последнее неравенство верно для всех достаточно больших К.
Теперь можно суммировать все доказанное относительно поведения  для больших
для больших  следующим образом:
следующим образом:  изменяется примерно как
изменяется примерно как  если положить
если положить

то  для больших значений
для больших значений  заключено между
заключено между  , а для некоторой бесконечной последовательности
, а для некоторой бесконечной последовательности 

Попутно было доказано, что описанный нами метод синтеза в некотором смысле не может быть существенно улучшен. Для параллельно-последовательных схем наилучшая известная оценка для  есть
есть

и почти все функции требуют для своей реализации  элементов. По сравнению с этим случаем имеем понижение порядка в бесконечное число раз: по крайней мере в
элементов. По сравнению с этим случаем имеем понижение порядка в бесконечное число раз: по крайней мере в  раз и, возможно, в
раз и, возможно, в  раз. Самое большее, что можно будет сделать в дальнейшем, — это разделить постоянный множитель на
раз. Самое большее, что можно будет сделать в дальнейшем, — это разделить постоянный множитель на  и для некоторых
и для некоторых  на
на  Возможность такого метода синтеза схем представляется, однако, маловероятной. Конечно, изложенное применимо только к совершенно общему методу синтеза, т. е. методу, применимому к любой функции. Многие специальные классы функций могут быть высоко экономично реализованы специальными методами.
Возможность такого метода синтеза схем представляется, однако, маловероятной. Конечно, изложенное применимо только к совершенно общему методу синтеза, т. е. методу, применимому к любой функции. Многие специальные классы функций могут быть высоко экономично реализованы специальными методами.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- СИМВОЛИЧЕСКИЙ АНАЛИЗ РЕЛЕЙНЫХ И ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- 2. Параллельно-последовательные двухполюсные схемы. Основные определения и постулаты
- 3. Многополюсные и не параллельно-последовательные схемы
- Преобразование треугольника в звезду и звезды в ячейку
- Функция сопротивления не параллельно-последовательной схемы
- Системы уравнений
- Реле и переключатели специальных типов
- 4. Синтез схем
- Двойственные схемы
- Синтез схем, реализующих симметрические функции
- Составление уравнений по рабочим характеристикам
- 5. Примеры
- ЧИСЛО ДВУХПОЛЮСНЫХ ПАРАЛЛЕЛЬНО-ПОСЛЕДОВАТЕЛЬНЫХ СЕТЕЙ
- 1. Получение производящей функции
- 2. Численный подсчет
- 3. Асимптотическое поведение
- 4. Параллельно-последовательная реализация переключательных функций
- СИНТЕЗ ДВУХПОЛЮСНЫХ ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- 2. Основная теорема синтеза
- 3. Синтез схем для произвольных функций.
- Часть II. РАСПРЕДЕЛЕНИЕ НАГРУЗКИ МЕЖДУ РЕЛЕ
- 5. Разделительное дерево
- 6. Другие задачи распределения
- 7. Функция «мю»
- Часть III. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- 9. Частично симметрические функции
- ПРИМЕЧАНИЯ РЕДАКТОРА
- ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К ОБЪЕМУ ПАМЯТИ ТЕЛЕФОННОГО КОММУТАТОРА
- 2. Память, требуемая для S произвольных вызовов от N абонентов
- 3. Условие раздельной памяти
- 4. Связь с теорией информации
- НАДЕЖНЫЕ СХЕМЫ ИЗ НЕНАДЕЖНЫХ РЕЛЕ
- Идеализированные реле
- Общий метод повышения надежности
- Свойства функции h(p)
- Комбинация двух схем
- Оценки функции h'(p)
- Схемы заданной длины и ширины
- Оценки числа контактов в случае, когда реле уже достаточно надежны
- Сравнение с элементами фон Неймана
- Реле с неопределенным временем срабатывания
- Синтез надежных схем в целом
- Приложение. Верхние оценки для вероятностей ошибок в случае гамакообразных l-w-схем
- ИСПОЛЬЗОВАНИЕ МАШИНЫ ДЛЯ ПРОЕКТИРОВАНИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА И АВТОМАТЫ
- Машины Тьюринга
- Логические машины
- «Играющие машины»
- Обучаемые машины
- Самовоспроизводящиеся машины
- Обращение к читателю
- МАШИНА ДЛЯ ИГРЫ В ШАХМАТЫ
- СОСТАВЛЕНИЕ ПРОГРАММ ДЛЯ ИГРЫ В ШАХМАТЫ НА ВЫЧИСЛИТЕЛЬНОЙ МАШИНЕ
- 3. Приближенная оценочная функция
- 4. Стратегия, основанная на оценочной функции
- 5. Составление программы для универсальной вычислительной машины для реализации стратегии типа А
- 6. Улучшение стратегии
- 7. Изменения в игре и в стиле
- 8. Другой тип стратегии
- ПРИЛОЖЕНИЕ. ОЦЕНОЧНАЯ ФУНКЦИЯ ДЛЯ ШАХМАТ
- ИГРАЮЩИЕ МАШИНЫ
- СООБЩЕНИЕ О МАШИНЕ, РЕШАЮЩЕЙ ЛАБИРИНТНУЮ ЗАДАЧУ
- ВКЛАД ФОН НЕЙМАНА В ТЕОРИЮ АВТОМАТОВ
- МАТЕМАТИЧЕСКАЯ ТЕОРИЯ СВЯЗИ
- 1. ДИСКРЕТНЫЕ СИСТЕМЫ БЕЗ ШУМОВ
- 2. Дискретный источник сообщений
- 3. Последовательные приближения к английскому языку
- 4. Графическое представление марковского процесса
- 5. Эргодические и смешанные источники
- 6. Выбор, неопределенность и энтропия
- 7. Энтропия источника сообщений
- 8. Представление операций кодирования и декодирования
- 9. Основная теорема для канала без шума
- 10. Рассмотрение полученных результатов и примеры
- 11. Примеры
- II. ДИСКРЕТНЫЙ КАНАЛ С ШУМОМ
- 12. Надежность и пропускная способность канала
- 13. Основная теорема для дискретного канала с шумом
- 14. Рассмотрение полученных результатов
- 15. Пример дискретного канала и его пропускной способности
- 16. Пропускная способность канала в некоторых частных случаях
- 17. Пример эффективного кодирования
- III. ИНФОРМАЦИЯ ДЛЯ НЕПРЕРЫВНЫХ ВЕЛИЧИН
- 19. Ансамбли функций с ограниченной полосой частот
- 20. Энтропия непрерывного распределения
- 21. Энтропия ансамбля функций
- 22. Потеря энтропии в линейных фильтрах
- 23. Энтропия суммы двух ансамблей
- IV. НЕПРЕРЫВНЫЙ КАНАЛ
- 24. Пропускная способность непрерывного канала
- 25. Пропускная способность канала при ограничении средней мощности
- 26. Пропускная способность канала при ограничении пиковой мощности
- V. СКОРОСТЬ СОЗДАНИЯ СООБЩЕНИЙ ДЛЯ НЕПРЕРЫВНОГО ИСТОЧНИКА
- 28. Скорость создания сообщений источником при данной точности воспроизведения
- 29. Вычисление скорости создания сообщений
- Приложение 1. РОСТ ЧИСЛА БЛОКОВ СИМВОЛОВ ПРИ УСЛОВИЯХ, ОПИСЫВАЕМЫХ КОНЕЧНЫМ ЧИСЛОМ СОСТОЯНИЙ
- Приложение 2. ВЫВОД РАВЕНСТВА …
- Приложение 3. ТЕОРЕМА ОБ ЭРГОДИЧЕСКИХ ИСТОЧНИКАХ
- Приложение 4. МАКСИМИЗАЦИЯ СКОРОСТИ ДЛЯ СИСТЕМЫ ОГРАНИЧЕНИЯ
- Приложение 5
- Приложение 6
- Приложение 7
- ТЕОРИЯ СВЯЗИ В СЕКРЕТНЫХ СИСТЕМАХ
- Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ СИСТЕМ
- 3. Способы изображения систем
- 4. Примеры секретных систем
- 5. Оценка секретных систем
- 6. Алгебра секретных систем
- 7. Чистые и смешанные шифры
- 8. Подобные системы
- Часть II. ТЕОРЕТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 10. Совершенная секретность
- 11. Ненадежность
- 12. Свойства ненадежности
- 13. Ненадежность простой подстановки для языка с двухбуквенным алфавитом
- 14. Характеристика ненадежности для «случайного» шифра
- 15. Применение к стандартным шифрам
- 16. Правильность решения криптограммы
- 17. Идеальные секретные системы
- 18. Примеры идеальных секретных систем
- 19. Дополнительные замечания о ненадежности и избыточности
- 20. Распределение ненадежности
- Часть III. ПРАКТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 22. Общие замечания о решении криптограмм
- 23. Статистические методы
- 24. Метод вероятных слов
- 25. Перемешивание
- 26. Шифры типа …
- 27. Несовместимость требований к хорошим системам
- ПРИЛОЖЕНИЕ. Доказательство теоремы 3
- СОВРЕМЕННЫЕ ДОСТИЖЕНИЯ ТЕОРИИ СВЯЗИ
- Измерение информаций
- Кодирование информации
- Пропускная способность канала
- Идеальные и практические системы
- ПРИНЦИПЫ КОДОВО-ИМПУЛЬСНОЙ МОДУЛЯЦИИ
- 2. Условия передачи для КИМ
- 3. Действие системы КИМ
- 4. Сравнение КИМ и ЧМ
- 5. Заключение
- Приложение I
- Приложение II
- СВЯЗЬ ПРИ НАЛИЧИИ ШУМА
- 2. Теорема отсчетов
- 3. Геометрическое представление сигналов
- 4. Геометрическое представление сообщений
- 5. Геометрическое представление передатчика и приемника
- 6. Отображение пространства
- 7. Пропускная способность канала при наличии белого теплового шума
- 8. Обсуждение
- 9. Произвольный гауссовский шум
- 10. Пропускная способность канала при произвольном типе шума
- 11. Дискретные источники информации
- 12. Непрерывные источники информации
- НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ИНФОРМАЦИИ
- ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА С ШУМОМ ПРИ НУЛЕВОЙ ОШИБКЕ
- Пропускная способность канала при нулевой ошибке
- Пропускная способность для суммы и произведения каналов
- Каналы с обратной связью
- ГЕОМЕТРИЧЕСКИЙ ПОДХОД К ТЕОРИИ ПРОПУСКНОЙ СПОСОБНОСТИ. КАНАЛОВ СВЯЗИ
- КАНАЛЫ С ДОПОЛНИТЕЛЬНОЙ ИНФОРМАЦИЕЙ НА ПЕРЕДАТЧИКЕ
- Дискретный канал без памяти с дополнительной информацией о состоянии
- Приложение
- НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ТЕОРИИ КОДИРОВАНИЯ ДЛЯ КАНАЛОВ С ШУМАМИ
- Оценка вероятности ошибки в терминах производящей функции моментов
- Пропускная способность канала с конечным числом состояний, состояние которого вычислимо на обоих концах
- Пропускная способность канала с конечным числом состояний в случае, когда состояние вычислимо на передающем конце и не вычислимо на приемном конце
- ЗАМЕЧАНИЯ О ЧАСТИЧНОМ УПОРЯДОЧИВАНИИ КАНАЛОВ СВЯЗИ
- Дальнейшее обобщение и некоторые предположения
- ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ ОПТИМАЛЬНЫХ кодов В ГАУССОВСКОМ КАНАЛЕ
- 2. Сводка результатов
- 3. Нижняя граница, основанная на соображениях «сферической упаковки»
- 4. Верхняя граница, определяемая методом случайного кодирования
- 5. Формулы для скорости передачи R как функции угла конуса
- 6. Асимптотические формулы для …
- 7. Асимптотическое выражение для верхней границы при случайном кодировании
- 8. Жесткая верхняя граница
- 9. Жесткая нижняя граница
- 10. Поведение границ вблизи пропускной способности канала
- 11. Верхняя граница, полученная методом исчерпывания
- 12. Нижняя граница для гауссовского канала, получаемая исходя из минимального расстояния
- 13. Границы ошибок и другие условия, накладываемые на точки
- 14. Кривые для асимптотических границ
- ТЕОРЕМЫ КОДИРОВАНИЯ ДЛЯ ДИСКРЕТНОГО ИСТОЧНИКА ПРИ ЗАДАННОМ КРИТЕРИИ ТОЧНОСТИ
- Мера искажения отдельной буквы
- Несколько простых примеров
- Скорость при заданном искажении R(d)
- Выпуклость вниз кривой R(d)
- Нахождение R(d) в некоторых простых случаях
- Скорость передачи для произведения источников с мерой, являющейся суммой мер искажения
- Нижняя граница для искажения при заданной пропускной способности канала
- Теоремы кодирования при заданной мере искажения отдельной буквы
- Двойственность источника и канала
- Численные расчеты для некоторых простых каналов
- Обобщение на случаи непрерывных алфавитов
- Разностная мера искажения
- Определение меры локального искажения
- Функции Rn(d) и R(d) для меры локального искажения и эргодического источника
- Прямая теорема кодирования для меры локального искажения
- Обратная теорема кодирования
- Канал с памятью
- ДВУСТОРОННИЕ КАНАЛЫ СВЯЗИ
- 4. Средние взаимные скорости передачи информации
- 5. Распределение информации
- 6. Случайное кодирование для двусторонних каналов
- 7. Вероятность ошибки для ансамбля кодов
- 8. Выпуклая оболочка G как внутренняя граница области пропускной способности
- 9. Внешняя граница для области пропускной способности
- 10. Выпуклость вниз как функций от …
- 11. Приложения свойства выпуклости. Каналы с симметричной структурой
- 12. Характер области, выделяемой внешней границей
- 13. Пример, в котором внутренняя и внешняя границы различны
- 14. Достижимость внешней границы при зависимых источниках
- 15. Общий метод нахождения области пропускной способности двустороннего канала
- 16. Двусторонние каналы с памятью
- 17. Обобщение на каналы с Т концами
- БАНДВАГОН
- ПРЕДСКАЗАНИЕ И ЭНТРОПИЯ ПЕЧАТНОГО АНГЛИЙСКОГО ТЕКСТА
- 2. Вычисление энтропии по статистике английского языка
- 3. Предсказание английского текста
- 4. Идеальное N-граммное предсказывание
- 5. Граница для энтропии на основании частот предсказания
- 6. Результаты эксперимента для английского языка
- УПРОЩЕННЫЙ ВЫВОД ЛИНЕЙНОЙ ТЕОРИИ СГЛАЖИВАНИЯ И ПРЕДСКАЗАНИЯ ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ
- 3. Свойства линейных фильтров
- 4. Основное выражение для среднеквадратичной ошибки
- 5. Чистая проблема сглаживания
- 6. Проблема чистого предсказания
- 7. Предсказание при наличии шума
- 8. Обобщения
- 9. Обсуждение основных предположений
- МАТЕМАТИЧЕСКАЯ ТЕОРИЯ ДИФФЕРЕНЦИАЛЬНОГО АНАЛИЗАТОРА
- Основное условие разрешимости
- Реализация функций
- Системы уравнений
- Аппроксимация множителей с помощью передаточных чисел
- Автоматическое управление скоростью работы устройства
- О МАКСИМАЛЬНОМ ПОТОКЕ ЧЕРЕЗ СЕТЬ
- ТЕОРЕМА О РАСКРАСКЕ РЕБЕР ГРАФА
- УНИВЕРСАЛЬНАЯ МАШИНА ТЬЮРИНГА С ДВУМЯ ВНУТРЕННИМИ СОСТОЯНИЯМИ
- Невозможность создания универсальной машины Тьюринга с одним состоянием
- Моделирование машины Тьюринга с помощью только двух символов на ленте
- ВЫЧИСЛИМОСТЬ НА ВЕРОЯТНОСТНЫХ МАШИНАХ
- Приложение
- БИБЛИОГРАФИЯ РАБОТ ПО ШЕННОНОВСКОЙ ТЕОРИИ ОПТИМАЛЬНОГО КОДИРОВАНИЯ ИНФОРМАЦИИ