| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ЗАМЕЧАНИЯ О ЧАСТИЧНОМ УПОРЯДОЧИВАНИИ КАНАЛОВ СВЯЗИ
В статье определяется понятие частичного упорядочивания для дискретных каналов без памяти. Это упорядочивание транзитивно и сохраняется при таких операциях над каналами, как сложение и умножение.

Рис. 1. Примеры, иллюстрирующие отношение включения,
Основной результат работы состоит в доказательстве того, что если  — два канала и
— два канала и  то для любого кода для канала
то для любого кода для канала  существует по крайней мере такой же хороший код для канала К и если качество кода измерять вероятностью ошибки.
существует по крайней мере такой же хороший код для канала К и если качество кода измерять вероятностью ошибки.
Рассмотрим три дискретных канала без памяти, изображенные на рис. 1. Про первый можно сказать, что он включает второй, так как первый сводится ко второму, если в нем использовать только буквы А, В, С. Все, что можно передавать по второму каналу, можно с помощью такого искусственного сведения передавать и по первому (но по первому каналу можно, конечно, передать больше, используя полный алфавит). Второй в некотором смысле включает третий, так как третий можно получить из второго, объединив буквы А и В на выходе в одну и ту же букву. Можно представить себе как бы некоторое приспособление, поставленное
на выходе второго канала, которое выдает букву А, когда на выходе появляется буква А или В и пропускает букву С без изменения.
Это и есть примеры отношения включения каналов, которое будет определено и рассмотрено ниже. Другой пример представлен на рис. 2 двумя двоичными симметричными каналами.

Рис. 2. Еще один пример включения.
В этом случае первый канал можно свести ко второму не с помощью метода идентификации букв, а с помощью добавления некоторого статистического устройства на входе или на выходе; а именно, если поместить, как показано на рис. 3, перед первым каналом (или после него) двоичный симметричный канал с вероятностью  такой, что
такой, что  то полное устройство будет действовать как второй канал на рис. 2.
то полное устройство будет действовать как второй канал на рис. 2.

Рис. 3. Сведение левого канала, изображенного на рис. 2, к правому с помощью предыдущего канала.
Практически требуемое статистическое устройство можно осуществить с помощью соответствующей схемы со случайным элементом. Приведенные примеры наводят на мысль считать по определению, что канал  с матрицей переходных вероятностей
с матрицей переходных вероятностей  включает канал
включает канал  с матрицей переходных вероятностей
с матрицей переходных вероятностей  если существуют стохастические матрицы А и В, такие, что
если существуют стохастические матрицы А и В, такие, что

Такое определение возможно, но оно допускает в действительности некоторое обобщение, при котором еще сохраняются те свойства, которые желательно получить и для отношения включения каналов. А именно, можно рассматривать «предварительную» и «заключительную» статистические операции, коррелированные между собой. Физически можно представить себе устройства, расположенные на передающем и приемном конце канала и содержащие случайные, но необязательно независимые элементы. Например, статистические устройства могут производить выбор с лент, между которыми имеется некоторая корреляция. Ясно, что такая ситуация вполне реальна. Математически она может быть представлена в простейшем случае следующим образом.
Определение. Пусть  есть вероятности перехода для дискретного канала без памяти
есть вероятности перехода для дискретного канала без памяти  есть такие же вероятности для канала
есть такие же вероятности для канала  Будем говорить, что канал
Будем говорить, что канал  включает канал
включает канал  тогда и только тогда, когда существуют два множества вероятностей перехода
тогда и только тогда, когда существуют два множества вероятностей перехода  и такие, что
и такие, что

и

и, кроме того, существуют

при которых выполняется равенство

Грубо говоря, за этим определением скрывается некоторое множество предшествующих и последующих каналов  и Та для канала
и Та для канала  которые используются попарно, и вероятность для такой пары равна
которые используются попарно, и вероятность для такой пары равна  Когда операции указанного вида производятся над каналом
Когда операции указанного вида производятся над каналом  он действует аналогично каналу
он действует аналогично каналу 
Определим чистый канал требованием, чтобы все переходы имели вероятности либо 0, либо 1; иными словами, в таком канале каждая буква на входе безошибочно переходит в определенную букву на выходе. Любую пару, составленную из предварительного и заключительного каналов  и Та, фигурирующую в (1), можно представить себе как взвешенную сумму чистых каналов, предварительного и заключительного для канала
и Та, фигурирующую в (1), можно представить себе как взвешенную сумму чистых каналов, предварительного и заключительного для канала  и действующих на него. Рассмотрим всевозможные отображения входных букв канала
и действующих на него. Рассмотрим всевозможные отображения входных букв канала  на его выходные буквы и сопоставим каждому отображению вероятность,
на его выходные буквы и сопоставим каждому отображению вероятность,
такую, чтобы в результате получился канал, эквивалентный  Тогда отображение, при котором каждая буква
Тогда отображение, при котором каждая буква  отображается в некоторую букву тк, имеет вероятность
отображается в некоторую букву тк, имеет вероятность  Подобная же операция может быть проделана над заключительным каналом Та и над парой из предварительного и заключительного каналов, причем вероятности берутся равными произведению вероятностей.
Подобная же операция может быть проделана над заключительным каналом Та и над парой из предварительного и заключительного каналов, причем вероятности берутся равными произведению вероятностей.
Указанное сведение к «чистым» компонентам может быть выполнено при каждом а с вероятностями, соответствующими данному а. Таким образом, операции, которые должны быть выполнены в соответствии с формулой (1), могут быть выполнены при помощи только чистых каналов на основании указанного выше сведения. Другими словами, отношение включения между каналами может быть эквивалентным образом переформулировано так, что все  будут соответствовать чистым каналам.
будут соответствовать чистым каналам.
Отношение включения транзитивно. Если  то
то  . В самом деле, пусть
. В самом деле, пусть  Та суть вероятности для предварительного и заключительного каналов для первого включения и
Та суть вероятности для предварительного и заключительного каналов для первого включения и  аналогичные характеристики для второго. Тогда при помощи вероятностей
аналогичные характеристики для второго. Тогда при помощи вероятностей  для предварительного канала
для предварительного канала  и для заключительного канала Та
и для заключительного канала Та  (знак
(знак  означает последовательное использование каналов, соответствующее произведению матриц) получим канал
означает последовательное использование каналов, соответствующее произведению матриц) получим канал  из канала
из канала  Если
Если  будем говорить, что каналы
будем говорить, что каналы  эквивалентны. Обозначим это через
эквивалентны. Обозначим это через  Заметим, что всегда
Заметим, что всегда  Группируя каналы в классы эквивалентности, получаем частичное упорядочение дискретных каналов без памяти. Очевидно, канал с одной входной буквой, с одной выходной буквой и с вероятностью 1 для перехода является общей нижней границей для всех каналов. Общей (конечной) верхней границы не существует. Однако если ограничиться каналами, у которых не больше
Группируя каналы в классы эквивалентности, получаем частичное упорядочение дискретных каналов без памяти. Очевидно, канал с одной входной буквой, с одной выходной буквой и с вероятностью 1 для перехода является общей нижней границей для всех каналов. Общей (конечной) верхней границы не существует. Однако если ограничиться каналами, у которых не больше  входных и выходных символов (или им эквивалентными), то для этого подмножества можно найти верхнюю границу, а именно чистый канал с
входных и выходных символов (или им эквивалентными), то для этого подмножества можно найти верхнюю границу, а именно чистый канал с  входными и
входными и  выходными буквами, взаимно однозначно отображаемыми друг на друга.
выходными буквами, взаимно однозначно отображаемыми друг на друга.
Отношение включения сохраняется при сложении и умножении каналов. Если  — каналы и
— каналы и  то
то

Напомним, что употребляемые здесь понятия суммы и произведения каналов были определены в более ранней работе автора как такие каналы, в которых может использоваться либо канал  либо
либо
 (сумма каналов), или как такие, в которых одновременно используются каналы
(сумма каналов), или как такие, в которых одновременно используются каналы  (произведение каналов). Для доказательства выписанных неравенств для произведения предположим, что канал
(произведение каналов). Для доказательства выписанных неравенств для произведения предположим, что канал  получается из канала
получается из канала  с помощью
с помощью  и канал
и канал  из канала
из канала  с помощью
с помощью  Тогда с помощью
Тогда с помощью  канал
канал  получается из канала
получается из канала  где произведение
где произведение  означает произведение каналов. Для суммы каналов доказательство аналогично. Именно сумма
означает произведение каналов. Для суммы каналов доказательство аналогично. Именно сумма  получается из
получается из  с помощью
с помощью  Та
Та  где знак
где знак  означает сумму каналов, а индексы
означает сумму каналов, а индексы  пробегают по всевозможным значениям.
пробегают по всевозможным значениям.
Если в дискретном канале без памяти рассмотреть слова из  букв, то получим другой канал без памяти, в котором входными буквами будут служить
букв, то получим другой канал без памяти, в котором входными буквами будут служить  -буквенные слова, составленные из выходных букв нашего канала. Очевидно, что такой канал эквивалентен
-буквенные слова, составленные из выходных букв нашего канала. Очевидно, что такой канал эквивалентен  Следовательно, если
Следовательно, если  то канал
то канал  включает канал
включает канал 
Предположим, что  и что
и что  имеют матрицы
имеют матрицы  соответственно. Тогда
соответственно. Тогда  включает канал, матрица которого имеет вид
включает канал, матрица которого имеет вид

Следовательно, если каналы характеризовать матрицами перехода, то совокупность каналов, меньших данного канала  образует в пространстве матриц выпуклое тело. В самом деле, канал с матрицей
образует в пространстве матриц выпуклое тело. В самом деле, канал с матрицей  может быть получен из канала
может быть получен из канала  объединением
объединением  Та) и
Та) и 
Наш основной результат, явившийся главной причиной для рассмотрения отношения включения каналов, связывает высказанные выше соображения с теорией кодирования. Покажем, что для всякого кода для канала  и любого канала
и любого канала  найдется код для канала
найдется код для канала  не худший, чем код для канала
не худший, чем код для канала  в смысле величины вероятности ошибки.
в смысле величины вероятности ошибки.
Теорема. Предположим, что  и что для канала
и что для канала  задано множество кодовых слов длины
задано множество кодовых слов длины  и система декодирования такова, что если слово
и система декодирования такова, что если слово  употребляется с вероятностью
употребляется с вероятностью  то средняя вероятность ошибки равна Ре. Тогда для канала
то средняя вероятность ошибки равна Ре. Тогда для канала  существует множество
существует множество  кодовых слов длины
кодовых слов длины  и такая декодирующая система, что если эти слова употреблять с теми же вероятностями
и такая декодирующая система, что если эти слова употреблять с теми же вероятностями  то средняя вероятность ошибки
то средняя вероятность ошибки  Следовательно, пропускная способность канала
Следовательно, пропускная способность канала  не меньше, чем пропускная способность канала
не меньше, чем пропускная способность канала 
Доказательство. Пусть  и множество
и множество  превращает канал
превращает канал  в канал
в канал  где Т и
где Т и  — чистые каналы.
— чистые каналы.
При каждом а канал  определяет отображение входных слов, из кода
определяет отображение входных слов, из кода  в множество входных слов из словаря канала
в множество входных слов из словаря канала  (т. е. слов, в которые
(т. е. слов, в которые  преобразует вводимый код). Далее Та определяет отображение выходных букв канала
преобразует вводимый код). Далее Та определяет отображение выходных букв канала  на выходные буквы канала
на выходные буквы канала  Из системы кодирования и декодирования для канала
Из системы кодирования и декодирования для канала  можно получить для каждого значения а кодирующую и декодирующую систему для канала
можно получить для каждого значения а кодирующую и декодирующую систему для канала  Возьмем для этого в качестве кода слова полученные при отображении, задаваемом
Возьмем для этого в качестве кода слова полученные при отображении, задаваемом  из кодовых слов для
из кодовых слов для 

Рис. 4. Общий двоичный канал.

Рис. 5. Шестиугольник из двоичных каналов, включенных в типичный двоичный канал.
Декодирование определим следующим образом: слово, выходящее из канала  декодируется так же, как декодируется слово, которое получается из данного при отображении
декодируется так же, как декодируется слово, которое получается из данного при отображении  . Такой код дает среднюю вероятность ошибки
. Такой код дает среднюю вероятность ошибки  для канала
для канала  . Теперь очевидно, что
. Теперь очевидно, что

поскольку канал  действует как бы с построенными нами различными кодами с вероятностью
действует как бы с построенными нами различными кодами с вероятностью  каждый. Так как из последнего уравнения вытекает, что взвешенное среднее вероятностей
каждый. Так как из последнего уравнения вытекает, что взвешенное среднее вероятностей  равно
равно  то должно существовать по крайней мере одно такое
то должно существовать по крайней мере одно такое  которое больше или равно Ре. [Если все
которое больше или равно Ре. [Если все  были бы меньше
были бы меньше  то правая часть (2) необходимо была бы меньше
то правая часть (2) необходимо была бы меньше  ] Система кодирования и декодирования для этого частного значения а и дает доказательство теоремы. В самом деле, величина
] Система кодирования и декодирования для этого частного значения а и дает доказательство теоремы. В самом деле, величина  равная
равная
минимуму вероятности ошибки при передаче М равновероятных слов длины  будет для канала
будет для канала  не больше, чем для канала
не больше, чем для канала  Аналогичным образом пропускная способность канала, определяемая как наибольшая нижняя граница скоростей передачи, для которых
Аналогичным образом пропускная способность канала, определяемая как наибольшая нижняя граница скоростей передачи, для которых  можно заставить стремиться к нулю, будет для канала
можно заставить стремиться к нулю, будет для канала  по крайней мере столь же большой, как и для канала
по крайней мере столь же большой, как и для канала 
Интересно проследить геометрическую интерпретацию отношений включения каналов в том простом случае, когда число входных и выходных букв равно двум (общий двоичный канал). Такой канал определяется двумя вероятностями и  (рис. 4) и может быть представлен точкой единичного квадрата. В связи с этим см. работу Силвермана, в которой пропускная способность канала и другие его параметры были изображены линиями на таком квадрате. На рис. 5 канал, для которого
(рис. 4) и может быть представлен точкой единичного квадрата. В связи с этим см. работу Силвермана, в которой пропускная способность канала и другие его параметры были изображены линиями на таком квадрате. На рис. 5 канал, для которого  изображен вместе с тремя другими, эквивалентными ему каналами с вероятностями
изображен вместе с тремя другими, эквивалентными ему каналами с вероятностями 

Рис. 6. Наибольшая нижняя граница X и наименьшая верхняя граница У двух сравниваемых двоичных каналов.
Добавляя две точки (0,0) и (1,1), получим шесть точек. Внутри шестиугольника, определяемого ими, заключены все каналы, включаемые в данный, В самом деле, непосредственной проверкой легко убедиться, что для каждого канала внутри этого шестиугольника найдется предварительный и заключающий каналы, которые приведут к одному из шести выделенных каналов. Очевидно также, что любая взвешенная сумма каналов с вероятностями  не выведет нас за пределы шестиугольника.
не выведет нас за пределы шестиугольника.
На рис. 5 двоичные симметричные каналы лежат на диагонали, идущей от (1,0) к (0,1). Из этого следует, что взятый нами канал включает, в частности, некоторый двоичный симметричный канал X, изображенный точкой  квадрата, что для нашего примера дает (3/5, 5/8). Кроме того, наш канал включается в двоичный симметричный канал
квадрата, что для нашего примера дает (3/5, 5/8). Кроме того, наш канал включается в двоичный симметричный канал  с координатами
с координатами  что для нашею частного случая превращается в 1/3, 2/3. Такие включения дают простые верхние и нижние оценки для пропускной способности общего двоичного канала через более удобные характеристики подходящим образом подобранных симметричных каналов.
что для нашею частного случая превращается в 1/3, 2/3. Такие включения дают простые верхние и нижние оценки для пропускной способности общего двоичного канала через более удобные характеристики подходящим образом подобранных симметричных каналов.
Случай, когда имеется два канала, ни один из которых не включает другого, представлен на рис. 6 с помощью двух шестиугольников. Здесь существует наибольшая нижняя граница и наименьшая верхняя граница для этих двух каналов, представленная на рис. 6 точками X и  соответственно. Таким образом, в случае двоичных каналов имеется больше, чем простое частичное упорядочение, т. е. имеется структура.
соответственно. Таким образом, в случае двоичных каналов имеется больше, чем простое частичное упорядочение, т. е. имеется структура.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- СИМВОЛИЧЕСКИЙ АНАЛИЗ РЕЛЕЙНЫХ И ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- 2. Параллельно-последовательные двухполюсные схемы. Основные определения и постулаты
- 3. Многополюсные и не параллельно-последовательные схемы
- Преобразование треугольника в звезду и звезды в ячейку
- Функция сопротивления не параллельно-последовательной схемы
- Системы уравнений
- Реле и переключатели специальных типов
- 4. Синтез схем
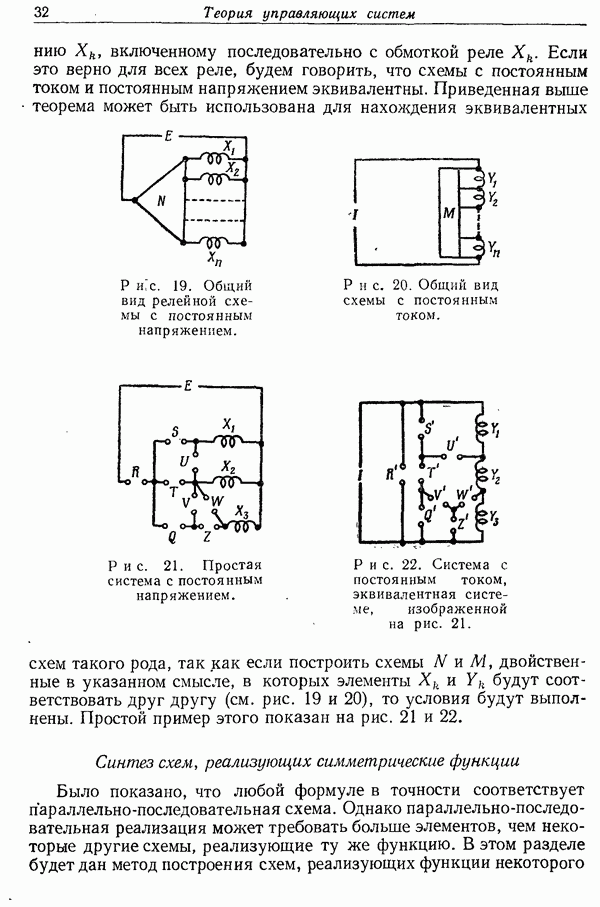
- Двойственные схемы
- Синтез схем, реализующих симметрические функции
- Составление уравнений по рабочим характеристикам
- 5. Примеры
- ЧИСЛО ДВУХПОЛЮСНЫХ ПАРАЛЛЕЛЬНО-ПОСЛЕДОВАТЕЛЬНЫХ СЕТЕЙ
- 1. Получение производящей функции
- 2. Численный подсчет
- 3. Асимптотическое поведение
- 4. Параллельно-последовательная реализация переключательных функций
- СИНТЕЗ ДВУХПОЛЮСНЫХ ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- 2. Основная теорема синтеза
- 3. Синтез схем для произвольных функций.
- Часть II. РАСПРЕДЕЛЕНИЕ НАГРУЗКИ МЕЖДУ РЕЛЕ
- 5. Разделительное дерево
- 6. Другие задачи распределения
- 7. Функция «мю»
- Часть III. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- 9. Частично симметрические функции
- ПРИМЕЧАНИЯ РЕДАКТОРА
- ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К ОБЪЕМУ ПАМЯТИ ТЕЛЕФОННОГО КОММУТАТОРА
- 2. Память, требуемая для S произвольных вызовов от N абонентов
- 3. Условие раздельной памяти
- 4. Связь с теорией информации
- НАДЕЖНЫЕ СХЕМЫ ИЗ НЕНАДЕЖНЫХ РЕЛЕ
- Идеализированные реле
- Общий метод повышения надежности
- Свойства функции h(p)
- Комбинация двух схем
- Оценки функции h'(p)
- Схемы заданной длины и ширины
- Оценки числа контактов в случае, когда реле уже достаточно надежны
- Сравнение с элементами фон Неймана
- Реле с неопределенным временем срабатывания
- Синтез надежных схем в целом
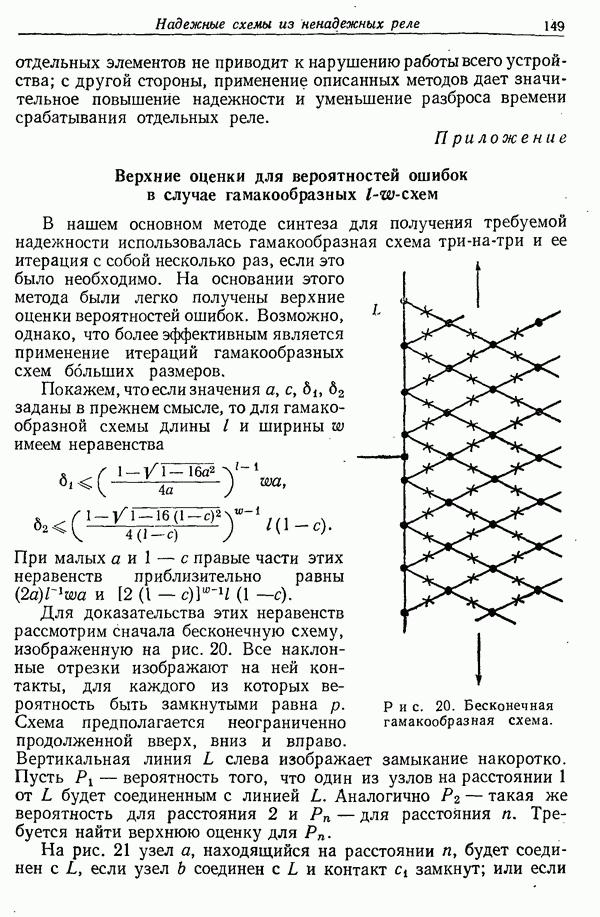
- Приложение. Верхние оценки для вероятностей ошибок в случае гамакообразных l-w-схем
- ИСПОЛЬЗОВАНИЕ МАШИНЫ ДЛЯ ПРОЕКТИРОВАНИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА И АВТОМАТЫ
- Машины Тьюринга
- Логические машины
- «Играющие машины»
- Обучаемые машины
- Самовоспроизводящиеся машины
- Обращение к читателю
- МАШИНА ДЛЯ ИГРЫ В ШАХМАТЫ
- СОСТАВЛЕНИЕ ПРОГРАММ ДЛЯ ИГРЫ В ШАХМАТЫ НА ВЫЧИСЛИТЕЛЬНОЙ МАШИНЕ
- 3. Приближенная оценочная функция
- 4. Стратегия, основанная на оценочной функции
- 5. Составление программы для универсальной вычислительной машины для реализации стратегии типа А
- 6. Улучшение стратегии
- 7. Изменения в игре и в стиле
- 8. Другой тип стратегии
- ПРИЛОЖЕНИЕ. ОЦЕНОЧНАЯ ФУНКЦИЯ ДЛЯ ШАХМАТ
- ИГРАЮЩИЕ МАШИНЫ
- СООБЩЕНИЕ О МАШИНЕ, РЕШАЮЩЕЙ ЛАБИРИНТНУЮ ЗАДАЧУ
- ВКЛАД ФОН НЕЙМАНА В ТЕОРИЮ АВТОМАТОВ
- МАТЕМАТИЧЕСКАЯ ТЕОРИЯ СВЯЗИ
- 1. ДИСКРЕТНЫЕ СИСТЕМЫ БЕЗ ШУМОВ
- 2. Дискретный источник сообщений
- 3. Последовательные приближения к английскому языку
- 4. Графическое представление марковского процесса
- 5. Эргодические и смешанные источники
- 6. Выбор, неопределенность и энтропия
- 7. Энтропия источника сообщений
- 8. Представление операций кодирования и декодирования
- 9. Основная теорема для канала без шума
- 10. Рассмотрение полученных результатов и примеры
- 11. Примеры
- II. ДИСКРЕТНЫЙ КАНАЛ С ШУМОМ
- 12. Надежность и пропускная способность канала
- 13. Основная теорема для дискретного канала с шумом
- 14. Рассмотрение полученных результатов
- 15. Пример дискретного канала и его пропускной способности
- 16. Пропускная способность канала в некоторых частных случаях
- 17. Пример эффективного кодирования
- III. ИНФОРМАЦИЯ ДЛЯ НЕПРЕРЫВНЫХ ВЕЛИЧИН
- 19. Ансамбли функций с ограниченной полосой частот
- 20. Энтропия непрерывного распределения
- 21. Энтропия ансамбля функций
- 22. Потеря энтропии в линейных фильтрах
- 23. Энтропия суммы двух ансамблей
- IV. НЕПРЕРЫВНЫЙ КАНАЛ
- 24. Пропускная способность непрерывного канала
- 25. Пропускная способность канала при ограничении средней мощности
- 26. Пропускная способность канала при ограничении пиковой мощности
- V. СКОРОСТЬ СОЗДАНИЯ СООБЩЕНИЙ ДЛЯ НЕПРЕРЫВНОГО ИСТОЧНИКА
- 28. Скорость создания сообщений источником при данной точности воспроизведения
- 29. Вычисление скорости создания сообщений
- Приложение 1. РОСТ ЧИСЛА БЛОКОВ СИМВОЛОВ ПРИ УСЛОВИЯХ, ОПИСЫВАЕМЫХ КОНЕЧНЫМ ЧИСЛОМ СОСТОЯНИЙ
- Приложение 2. ВЫВОД РАВЕНСТВА …
- Приложение 3. ТЕОРЕМА ОБ ЭРГОДИЧЕСКИХ ИСТОЧНИКАХ
- Приложение 4. МАКСИМИЗАЦИЯ СКОРОСТИ ДЛЯ СИСТЕМЫ ОГРАНИЧЕНИЯ
- Приложение 5
- Приложение 6
- Приложение 7
- ТЕОРИЯ СВЯЗИ В СЕКРЕТНЫХ СИСТЕМАХ
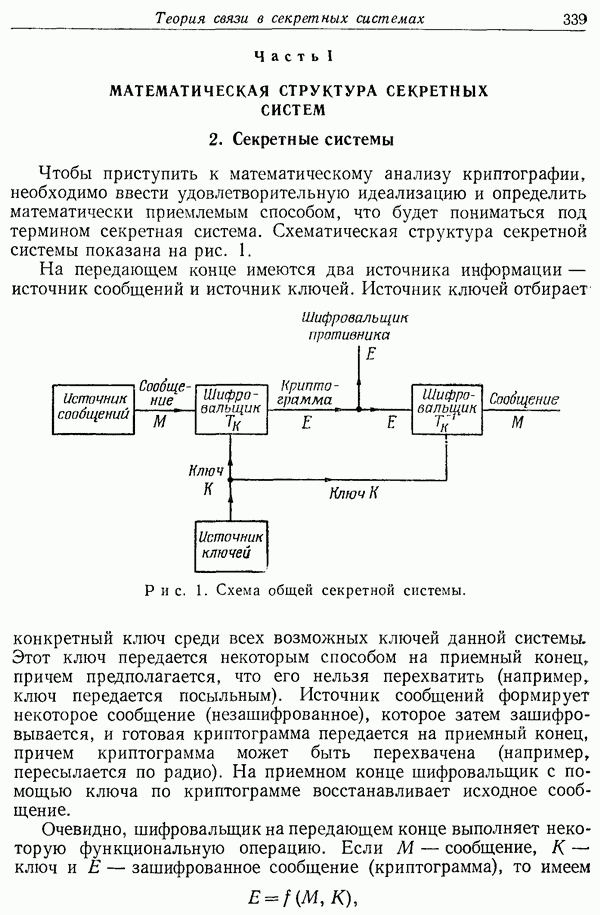
- Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ СИСТЕМ
- 3. Способы изображения систем
- 4. Примеры секретных систем
- 5. Оценка секретных систем
- 6. Алгебра секретных систем
- 7. Чистые и смешанные шифры
- 8. Подобные системы
- Часть II. ТЕОРЕТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 10. Совершенная секретность
- 11. Ненадежность
- 12. Свойства ненадежности
- 13. Ненадежность простой подстановки для языка с двухбуквенным алфавитом
- 14. Характеристика ненадежности для «случайного» шифра
- 15. Применение к стандартным шифрам
- 16. Правильность решения криптограммы
- 17. Идеальные секретные системы
- 18. Примеры идеальных секретных систем
- 19. Дополнительные замечания о ненадежности и избыточности
- 20. Распределение ненадежности
- Часть III. ПРАКТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 22. Общие замечания о решении криптограмм
- 23. Статистические методы
- 24. Метод вероятных слов
- 25. Перемешивание
- 26. Шифры типа …
- 27. Несовместимость требований к хорошим системам
- ПРИЛОЖЕНИЕ. Доказательство теоремы 3
- СОВРЕМЕННЫЕ ДОСТИЖЕНИЯ ТЕОРИИ СВЯЗИ
- Измерение информаций
- Кодирование информации
- Пропускная способность канала
- Идеальные и практические системы
- ПРИНЦИПЫ КОДОВО-ИМПУЛЬСНОЙ МОДУЛЯЦИИ
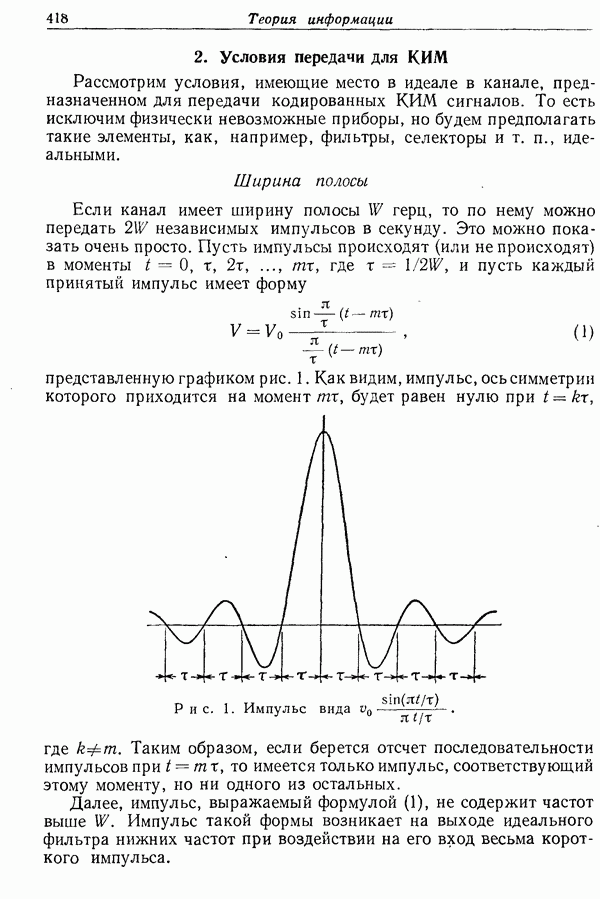
- 2. Условия передачи для КИМ
- 3. Действие системы КИМ
- 4. Сравнение КИМ и ЧМ
- 5. Заключение
- Приложение I
- Приложение II
- СВЯЗЬ ПРИ НАЛИЧИИ ШУМА
- 2. Теорема отсчетов
- 3. Геометрическое представление сигналов
- 4. Геометрическое представление сообщений
- 5. Геометрическое представление передатчика и приемника
- 6. Отображение пространства
- 7. Пропускная способность канала при наличии белого теплового шума
- 8. Обсуждение
- 9. Произвольный гауссовский шум
- 10. Пропускная способность канала при произвольном типе шума
- 11. Дискретные источники информации
- 12. Непрерывные источники информации
- НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ИНФОРМАЦИИ
- ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА С ШУМОМ ПРИ НУЛЕВОЙ ОШИБКЕ
- Пропускная способность канала при нулевой ошибке
- Пропускная способность для суммы и произведения каналов
- Каналы с обратной связью
- ГЕОМЕТРИЧЕСКИЙ ПОДХОД К ТЕОРИИ ПРОПУСКНОЙ СПОСОБНОСТИ. КАНАЛОВ СВЯЗИ
- КАНАЛЫ С ДОПОЛНИТЕЛЬНОЙ ИНФОРМАЦИЕЙ НА ПЕРЕДАТЧИКЕ
- Дискретный канал без памяти с дополнительной информацией о состоянии
- Приложение
- НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ТЕОРИИ КОДИРОВАНИЯ ДЛЯ КАНАЛОВ С ШУМАМИ
- Оценка вероятности ошибки в терминах производящей функции моментов
- Пропускная способность канала с конечным числом состояний, состояние которого вычислимо на обоих концах
- Пропускная способность канала с конечным числом состояний в случае, когда состояние вычислимо на передающем конце и не вычислимо на приемном конце
- ЗАМЕЧАНИЯ О ЧАСТИЧНОМ УПОРЯДОЧИВАНИИ КАНАЛОВ СВЯЗИ
- Дальнейшее обобщение и некоторые предположения
- ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ ОПТИМАЛЬНЫХ кодов В ГАУССОВСКОМ КАНАЛЕ
- 2. Сводка результатов
- 3. Нижняя граница, основанная на соображениях «сферической упаковки»
- 4. Верхняя граница, определяемая методом случайного кодирования
- 5. Формулы для скорости передачи R как функции угла конуса
- 6. Асимптотические формулы для …
- 7. Асимптотическое выражение для верхней границы при случайном кодировании
- 8. Жесткая верхняя граница
- 9. Жесткая нижняя граница
- 10. Поведение границ вблизи пропускной способности канала
- 11. Верхняя граница, полученная методом исчерпывания
- 12. Нижняя граница для гауссовского канала, получаемая исходя из минимального расстояния
- 13. Границы ошибок и другие условия, накладываемые на точки
- 14. Кривые для асимптотических границ
- ТЕОРЕМЫ КОДИРОВАНИЯ ДЛЯ ДИСКРЕТНОГО ИСТОЧНИКА ПРИ ЗАДАННОМ КРИТЕРИИ ТОЧНОСТИ
- Мера искажения отдельной буквы
- Несколько простых примеров
- Скорость при заданном искажении R(d)
- Выпуклость вниз кривой R(d)
- Нахождение R(d) в некоторых простых случаях
- Скорость передачи для произведения источников с мерой, являющейся суммой мер искажения
- Нижняя граница для искажения при заданной пропускной способности канала
- Теоремы кодирования при заданной мере искажения отдельной буквы
- Двойственность источника и канала
- Численные расчеты для некоторых простых каналов
- Обобщение на случаи непрерывных алфавитов
- Разностная мера искажения
- Определение меры локального искажения
- Функции Rn(d) и R(d) для меры локального искажения и эргодического источника
- Прямая теорема кодирования для меры локального искажения
- Обратная теорема кодирования
- Канал с памятью
- ДВУСТОРОННИЕ КАНАЛЫ СВЯЗИ
- 4. Средние взаимные скорости передачи информации
- 5. Распределение информации
- 6. Случайное кодирование для двусторонних каналов
- 7. Вероятность ошибки для ансамбля кодов
- 8. Выпуклая оболочка G как внутренняя граница области пропускной способности
- 9. Внешняя граница для области пропускной способности
- 10. Выпуклость вниз как функций от …
- 11. Приложения свойства выпуклости. Каналы с симметричной структурой
- 12. Характер области, выделяемой внешней границей
- 13. Пример, в котором внутренняя и внешняя границы различны
- 14. Достижимость внешней границы при зависимых источниках
- 15. Общий метод нахождения области пропускной способности двустороннего канала
- 16. Двусторонние каналы с памятью
- 17. Обобщение на каналы с Т концами
- БАНДВАГОН
- ПРЕДСКАЗАНИЕ И ЭНТРОПИЯ ПЕЧАТНОГО АНГЛИЙСКОГО ТЕКСТА
- 2. Вычисление энтропии по статистике английского языка
- 3. Предсказание английского текста
- 4. Идеальное N-граммное предсказывание
- 5. Граница для энтропии на основании частот предсказания
- 6. Результаты эксперимента для английского языка
- УПРОЩЕННЫЙ ВЫВОД ЛИНЕЙНОЙ ТЕОРИИ СГЛАЖИВАНИЯ И ПРЕДСКАЗАНИЯ ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ
- 3. Свойства линейных фильтров
- 4. Основное выражение для среднеквадратичной ошибки
- 5. Чистая проблема сглаживания
- 6. Проблема чистого предсказания
- 7. Предсказание при наличии шума
- 8. Обобщения
- 9. Обсуждение основных предположений
- МАТЕМАТИЧЕСКАЯ ТЕОРИЯ ДИФФЕРЕНЦИАЛЬНОГО АНАЛИЗАТОРА
- Основное условие разрешимости
- Реализация функций
- Системы уравнений
- Аппроксимация множителей с помощью передаточных чисел
- Автоматическое управление скоростью работы устройства
- О МАКСИМАЛЬНОМ ПОТОКЕ ЧЕРЕЗ СЕТЬ
- ТЕОРЕМА О РАСКРАСКЕ РЕБЕР ГРАФА
- УНИВЕРСАЛЬНАЯ МАШИНА ТЬЮРИНГА С ДВУМЯ ВНУТРЕННИМИ СОСТОЯНИЯМИ
- Невозможность создания универсальной машины Тьюринга с одним состоянием
- Моделирование машины Тьюринга с помощью только двух символов на ленте
- ВЫЧИСЛИМОСТЬ НА ВЕРОЯТНОСТНЫХ МАШИНАХ
- Приложение
- БИБЛИОГРАФИЯ РАБОТ ПО ШЕННОНОВСКОЙ ТЕОРИИ ОПТИМАЛЬНОГО КОДИРОВАНИЯ ИНФОРМАЦИИ