| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
СООБЩЕНИЕ О МАШИНЕ, РЕШАЮЩЕЙ ЛАБИРИНТНУЮ ЗАДАЧУ
Лабиринтная машина способна найти путь в лабиринте, применяя метод испытаний и ошибок. Машина запоминает решение, а в случае, когда ситуация меняется и решение оказывается неприемлемым, забывает его. Я думаю, что эта машина может представлять интерес с точки зрения связи ее с задачей обучения (и забывания) систем, содержащих обратные связи и работающих по методу испытаний и ошибок.
Как показано на рис. 1, на верхней панели машины расположен лабиринт, содержащий 5x5 квадратов. Лабиринт можно изменять любым желаемым образом, переставляя перегородки между двадцатью пятью квадратами. В лабиринте помещен чувствительный щуп, который может обнаруживать перегородки, когда он к ним подходит. Этот щуп связан с двумя двигателями, перемещающими его в двух взаимно перпендикулярных направлениях. Условимся считать, что один двигатель перемещает щуп в направлении восток — запад и обратно, а другой в направлении север — юг и обратно. Задачей машины является проведение щупа по лабиринту к цели. Цель укреплена на шпильке, которая может быть вставлена по произволу в одно из гнезд, расположенных в центре каждого из двадцати пяти квадратов. Таким образом, условия задачи могут произвольно изменяться; сохраняется лишь размер лабиринта из 5x5 квадратов. После первого включения машина пытается найти решение лабиринтной задачи. Когда машина выключается, запоминающие реле по существу забывают все, что они запоминали, и после этого начинают работать заново, ничего не зная о лабиринте.
Севидж (Savage). Значит ли это, что реле находятся в нейтральном среднем положении, т. е. ни в правом, ни в левом?

(кликните для просмотра скана)
Шеннон. Они находятся в некоторой исходной позиции, которая не является точно нейтральной позицией, но остается малозначащей. Теперь щуп исследует лабиринт в поисках цели. Когда он достигает центра квадрата, машина принимает новое решение испробовать следующее направление. Если щуп коснется перегородки, двигатель реверсируется, перемещая щуп вновь к центру квадрата, где выбирается новое направление движения. Выбор базируется на предыдущих сведениях и соответствует определенной «стратегии», которая не очень сложна.
Питтс (Pitts). Это стратегия фиксированная, а не случайная?
Шеннон. Да, здесь нет случайного элемента. Вначале предполагалось использовать вероятностный элемент, но потом было решено, что проще иметь дело с чистой стратегией. Когда щуп в своем исследовании достигает цели, двигатели останавливаются, на щупе зажигается лампочка и включается звонок. Машина решила лабиринтную задачу. Теперь можно вручную возвратить щуп обратно в начальное положение, и очевидно, что машина запомнила найденное ею решение, так как, когда машина снова включается, щуп пойдет прямо к цели, не натыкаясь на перегородки и минуя тупики. Он в состоянии пройти прямо к цели из любой части лабиринта, которую он посетил при исследовании. Если теперь передвинуть щуп в ту часть лабиринта, которую он еще не исследовал, он будет продолжать поиск и перемещаться до тех пор, пока не достигнет уже исследованной им зоны. Оттуда он пойдет прямо к цели.
Теперь хотелось бы указать на следующую особенность машины. Можно изменить лабиринт так, что решение, найденное машиной, перестанет действовать. Соответствующей перестановкой перегородок можно получить интересный эффект. В предшествующем лабиринте решение начинается в квадрате А, ведет в квадрат В, затем в С и далее к цели. Перестановкой перегородок можно вынудить машину из квадрата С отправиться в новый квадрат, квадрат!), и оттуда обратно к исходному квадрату А. Когда щуп приходит в квадрат А, он «вспоминает», что по старой программе он должен идти в квадрат В; в результате он начинает совершать путь последовательно по квадратам А, В, С, D, А, В, С, D,... Устанавливается порочный круг или зацикливание.
Джерард (Gerard). Невроз?
Шеннон. Да.
Севидж. Машина не может поступать так, если ее память ничего не хранит, но она может так поступать, если ее поведение обусловлено?
Шеннон. Да, только после того, как это поведение обусловлено заранее. Однако машина имеет антиневротические цепи, предназначенные для предотвращения подобной ситуации.
Мид (Mead). После того как она повторится несколько раз?
Шеннон. После того как машина повторит цикл около 6 раз, он будет прерван. Релейная схема, содержащая счетчик, прекращает цикл на двадцать четвертой попытке.
Франк (Frank). Сколько всего реле в машине?
Шеннон. В общей сложности около 75 реле.
Севидж. Не имеется ли какого-либо способа определить, что имеет место «психическое» расстройство, или только определяется, что процесс перемещения щупа совершается слишком долго?
Шеннон. Да. После выхода из цикла машина возвращается к исследовательской стратегии.
Тойбер (Teuber). Должна ли она снова изучить лабиринт полностью или она может использовать какую-либо информацию о его форме, полученную ранее?
Шеннон. Нет, если машина остановится, она начинает с начала и не может использовать полученную ранее информацию.
Севидж. Но я думаю, она пытается использовать ее. Она двигается, как будто она уже знает, куда следует двигаться.
Шеннон. На самом же деле вся старая информация начинает ей вредить.
Бигелоу (Bigelou). Я думаю это так.
Шеннон. Да, она постепенно начинает продвигаться в направлении цели. Я хотел бы использовать оставшееся у меня время для того, чтобы пояснить некоторые особенности работы машины.
Стратегия, используемая машиной, может быть описана следующим образом: имеется два типа поведения машины, которые я называю «исследовательская стратегия» и «стратегия цели». Обе они достаточно просты. Исследовательская стратегия используется при первых попытках найти цель. Каждому квадрату лабиринта соответствует запоминающее устройство, состоящее из двух реле. Они могут запомнить одно из четырех возможных направлений: север, восток, юг или запад. При этом запоминается то направление, в котором щуп покинул данный квадрат в последнее посещение. В этом состоят все сведения, которые машина запоминает по пути щупа в лабиринте. Существуют некоторые другие функции памяти в вычислительной части схемы, но эти запомненные направления являются теми сведениями, которые позднее позволяют воспроизвести маршрут щупа.
Представим теперь запомненное направление в некотором квадрате D в виде вектора. В исследовательской стратегии, когда щуп входит в квадрат, машина берет вектор D и в качестве первого выбора поворачивает его на 90°. Пусть, например, щуп при своем последнем посещении покинул квадрат в восточном направлении. Если он снова попадет в этот же квадрат, он в качестве первой попытки будет испытывать северное направление. Если
щуп коснется перегородки и вернется обратно, он снова повернется на 90°, так как он только что ввел это северное направление в запоминающее устройство, и будет испытывать западное направление и т. д. Попытки следуют против часовой стрелки, начиная с того направления, в котором щуп покинул квадрат при своем последнем посещении, за одним исключением: щуп запоминает также направление, по которому он вошел в квадрат при данном посещении, но при первом повороте вектора D он пропускает это входное направление. Это предотвращает многократные повторения в траектории щупа. До того как эта особенность была установлена, имелась тенденция продолжать исследование до нового квадрата, возвращаться обратно через весь лабиринт, а затем выбирать следующий квадрат и т. д.; все это требовало очень много времени для решения лабиринтной задачи (приблизительно в три раза больше, чем сейчас).
Когда щуп достигнет цели, сработает реле, замыкающее цепи, и машина будет действовать далее по принципу «стратегии цели», которая также основывается на использовании вектора D.
В стратегии цели машина сразу использует направление D, в котором щуп покинул квадрат в свое последнее посещение. Это очень просто реализуется и очень удобно для решения лабиринтной задачи, так как исключает все тупики и кружения на одном месте. Так как тупик должен быть покинут щупом через тот же квадрат, через который он вошел, направление D, запомненное для данного квадрата, неизбежно поведет щуп к цели скорее, чем при заходе в тупик. Аналогично в случае, если машина следует по замкнутому (циклическому) пути или по незнакомой части, отыскивая путь к цели, направление, запомненное для последнего разветвления пути, должно вести к цели скорее, чем боковые ветви. Следовательно, машина (щуп) следует к цели по кратчайшему пути, который она уже установила.
Последняя особенность — способность забывать — заключается в следующем: предположим, что - после достижения цели щуп переставлен на другое место лабиринта и поиск начался снова. Тогда машина начнет считать число сделанных движений щупа и если он не достигнет цели в течение определенного количества шагов, в данном случае двадцати четырех, машина устанавливает, что лабиринт был изменен или что щуп совершает движение по замкнутому циклу, или что-нибудь в этом роде, и следовательно, предыдущая программа уже не действует. Схема после этого переключается на исследовательскую стратегию, которая математически гарантирует нахождение пути в любом лабиринте, имеющем конечное решение.
Существуют также и другие стороны работы машины, представляющие некоторый интерес. Запоминающее устройство почтц
не различает смысла запоминаемого; так, можно взять группу проводов, идущих от основания системы к запоминающему устройству, и поменять местами группы, соответствующие направлению «север — юг» и направлению «восток — запад», и машина при этом будет продолжать работать - правильно и без заметных изменений, хотя данные, соответствующие некоторому квадрату, будут храниться в других частях запоминающего устройства.
Следующая особенность машины — это, конечно, наличие в ней большого количества цепей обратной связи. Наиболее значительной из них является цепь обратной связи от щупа через всю систему к двигателям и в виде механического перемещения обратно от двигателя к щупу. Обычно если имеется цепь обратной связи, то изменение знака обратной связи полностью нарушает действие всей системы. Существует большая разница между положительной и отрицательной обратной связью. Однако эта машина, решающая лабиринтную задачу, является такой, что можно менять как один, так и оба знака обратной связи, иона будет работать одинаково хорошо.
Это значит, что внутри данной системы понятия «правое» и «левое» взаимозаменяемы; другими словами, воздействие этого явления на стратегию машины заключается в том, что если одна из цепей обратной связи меняет знак, - то это означает, что поворот на  против часовой стрелки заменяется таким же поворотом по часовой стрелке. Если знаки меняются в обеих цепях, стратегия не изменяется.
против часовой стрелки заменяется таким же поворотом по часовой стрелке. Если знаки меняются в обеих цепях, стратегия не изменяется.
Фон Фёрстер (von Foerster). Если существуют два различных пути достижения цели, машина, конечно, способна выбрать только один. Имеется ли у нее при этом возможность выбрать наилучший путь?
Шеннон. Нет, она не обязательно выбирает лучший путь, хотя существует вероятность предпочтения ею более короткого при выборе из двух путей. Кроме того, исследовательская стратегия этой машины позволяет находить решение для любого лабиринта как односвязного, так и многосвязного. Некоторые классические программы решения лабиринтных задач пригодны лишь для односвязных лабиринтов. Примером этого может служить метод правой руки, когда при проходе по лабиринту все время держатся за его правую стенку. Этот способ позволяет решить любой простой лабиринт, но часто оказывается безуспешным, если в лабиринте попадаются замкнутые петли.
Севидж. Не появляется ли указанное явление цикличности вследствие того, что машина не находится в условиях действительного поиска?
Шеннон. Нет, это скорее наблюдается при применении стратегии цели, чем при исследовательской стратегии.
Севидж. Стратегия цели заключается в перемещении по тому пути, по которому щуп прошел ранее, но что должна делать машина, если попытка оказывается тщетной?
Шеннон. Щуп возвращается к центру квадрата, поворачивается на 90° и пробует это направление. Машина при этом остается в состоянии стратегии цели.
Севидж. Понимаю. Когда щуп попадет в следующий квадрат, он пробует идти дальше по уже знакомому направлению?
Шеннон. Правильно. Дело в том, что при поиске решения может быть изучена большая часть лабиринта, но не весь лабиринт полностью. Если же поместить щуп в квадрат, который он не посещал, он будет продолжать поиск методом испытаний и ошибок до тех пор, пока не достигнет знакомого квадрата, откуда и направится прямо к цели. Прежде неизвестные квадраты при этом добавляются к первоначальному решению.
Бигелоу. Можно создать новую петлю на любом известном пути; щуп исследует эту новую петлю немедленно и не делает ошибки. Так ли это?
Шеннон. Правильно.
Бигелоу. Потому что, когда щуп возвращается на основной путь, поиск идет в верном направлении, если он узнает соответствующий квадрат?
Шеннон. Я не убежден, что понял, что вы имеете в виду.
Бигелоу. Щуп совершает направленный путь. Теперь, если предложить новый маршрут, который перенесет щуп с известного пути в неизвестную ему зону, он вновь вернется на правильный путь.
Шеннон. Такой боковой путь полностью исключается, так как действует стратегия цели.
Бигелоу. Но если все начинается где-то внутри данной системы, то процесс идет правильно, начиная от места старта?
Шеннон. Это в случае стратегии цели, но не в исследовательской стратегии.
Бигелоу. Что следует сделать для уменьшения времени поиска решения для того, чтобы обучение путем повторных попыток позволило найти наиболее короткий путь в сложном лабиринте?
Шеннон. Думаю, что это потребовало бы значительно большей памяти в виде реле в связи с необходимостью сохранения в ней разных решений лабиринтной задачи, а также дополнительных вычислительных релейных схем для сравнения и оценки этих решений. Это действительно следовало бы сделать, но это будет очень сложно; это означало бы создание машины гораздо более сложной, чем имеющаяся.
Севидж. К тому же нужно было бы решать, когда следует осуществлять поиски нового пути. Это действительно весьма
важная проблема, возникающая в любом случае фактического обучения человека. Если вы уже можете чистить картофель, почему вы должны заботиться о поиске лучшего способа чистки? Может быть, вы уже чистите правильно? Как вы это узнаете?
Фон Фёрстер. Что происходит, если в лабиринте не оказывается цели?
Шеннон. Если цели нет, машина периодически повторяет путь, разыскивая цель; это значит, что она прорабатывает путь, идущий через каждый квадрат, и исследует каждую перегородку, и если она не находит цели, маршрут повторяется снова и снова. Машина продолжает искать цель в каждом квадрате, чтобы быть уверенной, что она обследовала все квадраты.
Франк. Это все слишком по-человечески.
Брозин (Brosin). Джордж Оруэлл, покойный автор книги «1984», должен был бы это рассмотреть.
Фон Фёрстер. А после этого? Что произойдет, если установить цель на пути после того, как машина начнет такое периодическое движение?
Шеннон. Когда щуп коснется цели, машина остановится и перейдет к стратегии цели, после чего каждый очередной раз она будет выходить на эту цель. Кстати, рассмотрим вопрос с математической точки зрения: для каждого из 25 квадратов запоминающее устройство машины сохраняет в памяти векторные направления — север, восток, юг и запад. Таким образом, в целом запоминающее устройство содержит векторное поле, определенное на лабиринте из 25 клеток. Когда щуп движется по лабиринту, он непрерывно исправляет это запомненное векторное поле таким образом, что векторы направляются вдоль возможных путей в лабиринте, ведущих к месту нахождения щупа в каждый данный момент.
Тойбер. Если повернуть поле на 180°, будет ли оно продолжать правильно функционировать?
Мак-Каллок. Если реверсировать соединения и пустить двигатель в таком состоянии, что направление его вращения изменится, сможет ли при этом машина, как и прежде, найти путь к цели?
Шеннон. Только если переключить те же переключатели в машине, которые сообщают, какой квадрат занят (щупом) в данный момент. Если реверсировать двигатели, то надо для компенсации переключить и эти реле. Иначе щуп будет считать, что он движется одним путем и введет его в запоминающее устройство, а фактически он двигался в другом направлении.
Джерард. Это было бы похоже на перекрестное сшивание двигательных нервов у животного и появление вследствие этого сгибания вместо разгибания.
Бигелоу. Как вы думаете, трудно было бы создать систему, которая, вместо того чтобы забывать, возвращалась бы к началу и, помня все, что она делала в первом квадрате, попыталась бы сделать что-нибудь еще, например вести поиск в обратной последовательности? Если это не приведет к новому решению, вернуться назад и двигаться в обратной последовательности из второго квадрата, что потребует замены в запоминающем устройстве каждого хранящегося в памяти квадрата, через который проходит щуп. Другими словами, это потребует очень небольшого дополнения к запоминающему устройству, поскольку необходимо запомнить только одну последнюю картину (лабиринт). Но когда стратегия цели больше не приводит к решению (это определяется, когда число попыток превысило некоторое число N), можно использовать переключающие схемы, которые возвращают все к началу, и затем повторными проверками искать новое решение.
Шеннон. Этот вопрос не рассматривался, но думаю, что все делалось бы слишком медленно, поскольку при этом большая часть времени уходила бы на возвратные движения, возвращения к началу и исследование разных гипотез.
Бигелоу. Если известно, как идти от начала к цели, всегда ли известно, как возвращаться от цели к началу с помощью простого реверса переключателей?
Шеннон. Нет. Это векторное поле, если хотите, является уникальным при движении в направлении векторов, но при обратном движении появляются точки ветвления, так что машина не знает, откуда она пришла.
Севидж. Ориентировано ли это поле в направлении к цели в каждой своей точке?
Шеннон. Да. Если следовать по направлению векторов, цель будет достигнута, но в обратном направлении можно попасть в точку ветвления, из которой можно идти в любом направлении. В этом случае, изучая запоминающее устройство, нельзя сказать, откуда пришел щуп.
Севидж. Эта неорганизованность, существующая в окрестности любой определенной начальной точки, является одной из особенностей машины. После того как она исследовала лабиринт, если начать работу в точке, где щуп уже был, она продолжает путь; если начать путь там, где щуп еще не был, он сначала найдет место, где он был, а затем будет продолжать путь к цели.
Мак Каллок. Подобно тому, как человек, знающий город, может из какого-нибудь места прийти в любое другое, но не всегда помнит, каким путем он шел.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- СИМВОЛИЧЕСКИЙ АНАЛИЗ РЕЛЕЙНЫХ И ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- 2. Параллельно-последовательные двухполюсные схемы. Основные определения и постулаты
- 3. Многополюсные и не параллельно-последовательные схемы
- Преобразование треугольника в звезду и звезды в ячейку
- Функция сопротивления не параллельно-последовательной схемы
- Системы уравнений
- Реле и переключатели специальных типов
- 4. Синтез схем
- Двойственные схемы
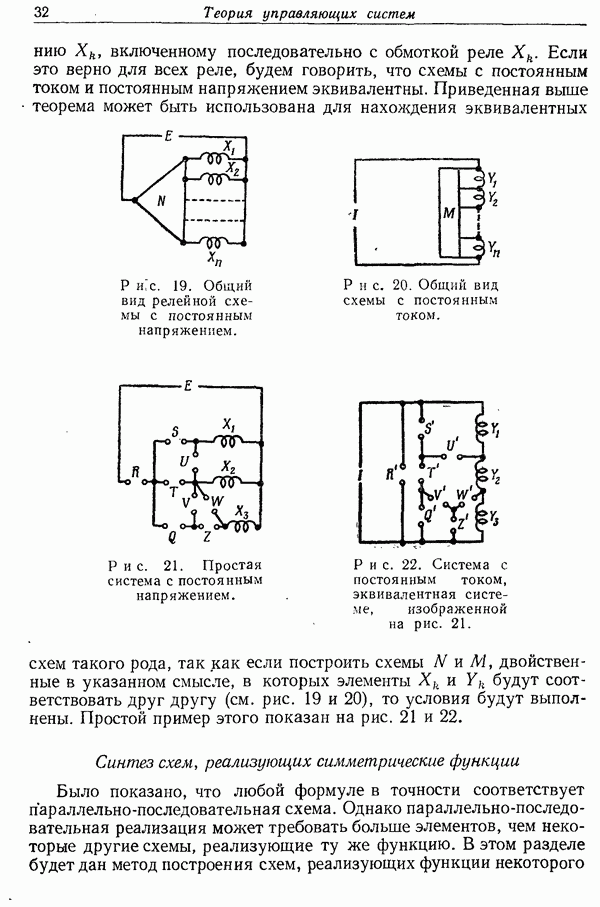
- Синтез схем, реализующих симметрические функции
- Составление уравнений по рабочим характеристикам
- 5. Примеры
- ЧИСЛО ДВУХПОЛЮСНЫХ ПАРАЛЛЕЛЬНО-ПОСЛЕДОВАТЕЛЬНЫХ СЕТЕЙ
- 1. Получение производящей функции
- 2. Численный подсчет
- 3. Асимптотическое поведение
- 4. Параллельно-последовательная реализация переключательных функций
- СИНТЕЗ ДВУХПОЛЮСНЫХ ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- 2. Основная теорема синтеза
- 3. Синтез схем для произвольных функций.
- Часть II. РАСПРЕДЕЛЕНИЕ НАГРУЗКИ МЕЖДУ РЕЛЕ
- 5. Разделительное дерево
- 6. Другие задачи распределения
- 7. Функция «мю»
- Часть III. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- 9. Частично симметрические функции
- ПРИМЕЧАНИЯ РЕДАКТОРА
- ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К ОБЪЕМУ ПАМЯТИ ТЕЛЕФОННОГО КОММУТАТОРА
- 2. Память, требуемая для S произвольных вызовов от N абонентов
- 3. Условие раздельной памяти
- 4. Связь с теорией информации
- НАДЕЖНЫЕ СХЕМЫ ИЗ НЕНАДЕЖНЫХ РЕЛЕ
- Идеализированные реле
- Общий метод повышения надежности
- Свойства функции h(p)
- Комбинация двух схем
- Оценки функции h'(p)
- Схемы заданной длины и ширины
- Оценки числа контактов в случае, когда реле уже достаточно надежны
- Сравнение с элементами фон Неймана
- Реле с неопределенным временем срабатывания
- Синтез надежных схем в целом
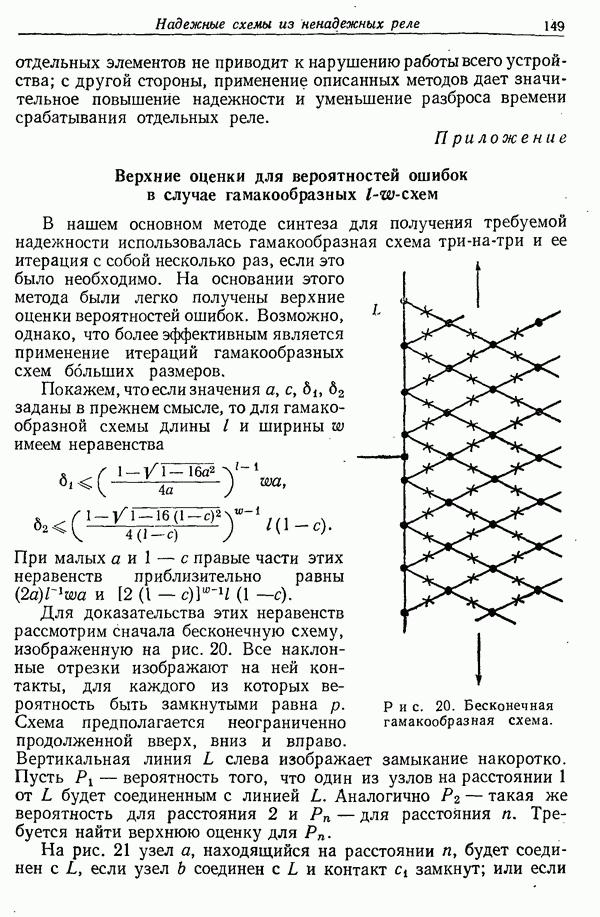
- Приложение. Верхние оценки для вероятностей ошибок в случае гамакообразных l-w-схем
- ИСПОЛЬЗОВАНИЕ МАШИНЫ ДЛЯ ПРОЕКТИРОВАНИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА И АВТОМАТЫ
- Машины Тьюринга
- Логические машины
- «Играющие машины»
- Обучаемые машины
- Самовоспроизводящиеся машины
- Обращение к читателю
- МАШИНА ДЛЯ ИГРЫ В ШАХМАТЫ
- СОСТАВЛЕНИЕ ПРОГРАММ ДЛЯ ИГРЫ В ШАХМАТЫ НА ВЫЧИСЛИТЕЛЬНОЙ МАШИНЕ
- 3. Приближенная оценочная функция
- 4. Стратегия, основанная на оценочной функции
- 5. Составление программы для универсальной вычислительной машины для реализации стратегии типа А
- 6. Улучшение стратегии
- 7. Изменения в игре и в стиле
- 8. Другой тип стратегии
- ПРИЛОЖЕНИЕ. ОЦЕНОЧНАЯ ФУНКЦИЯ ДЛЯ ШАХМАТ
- ИГРАЮЩИЕ МАШИНЫ
- СООБЩЕНИЕ О МАШИНЕ, РЕШАЮЩЕЙ ЛАБИРИНТНУЮ ЗАДАЧУ
- ВКЛАД ФОН НЕЙМАНА В ТЕОРИЮ АВТОМАТОВ
- МАТЕМАТИЧЕСКАЯ ТЕОРИЯ СВЯЗИ
- 1. ДИСКРЕТНЫЕ СИСТЕМЫ БЕЗ ШУМОВ
- 2. Дискретный источник сообщений
- 3. Последовательные приближения к английскому языку
- 4. Графическое представление марковского процесса
- 5. Эргодические и смешанные источники
- 6. Выбор, неопределенность и энтропия
- 7. Энтропия источника сообщений
- 8. Представление операций кодирования и декодирования
- 9. Основная теорема для канала без шума
- 10. Рассмотрение полученных результатов и примеры
- 11. Примеры
- II. ДИСКРЕТНЫЙ КАНАЛ С ШУМОМ
- 12. Надежность и пропускная способность канала
- 13. Основная теорема для дискретного канала с шумом
- 14. Рассмотрение полученных результатов
- 15. Пример дискретного канала и его пропускной способности
- 16. Пропускная способность канала в некоторых частных случаях
- 17. Пример эффективного кодирования
- III. ИНФОРМАЦИЯ ДЛЯ НЕПРЕРЫВНЫХ ВЕЛИЧИН
- 19. Ансамбли функций с ограниченной полосой частот
- 20. Энтропия непрерывного распределения
- 21. Энтропия ансамбля функций
- 22. Потеря энтропии в линейных фильтрах
- 23. Энтропия суммы двух ансамблей
- IV. НЕПРЕРЫВНЫЙ КАНАЛ
- 24. Пропускная способность непрерывного канала
- 25. Пропускная способность канала при ограничении средней мощности
- 26. Пропускная способность канала при ограничении пиковой мощности
- V. СКОРОСТЬ СОЗДАНИЯ СООБЩЕНИЙ ДЛЯ НЕПРЕРЫВНОГО ИСТОЧНИКА
- 28. Скорость создания сообщений источником при данной точности воспроизведения
- 29. Вычисление скорости создания сообщений
- Приложение 1. РОСТ ЧИСЛА БЛОКОВ СИМВОЛОВ ПРИ УСЛОВИЯХ, ОПИСЫВАЕМЫХ КОНЕЧНЫМ ЧИСЛОМ СОСТОЯНИЙ
- Приложение 2. ВЫВОД РАВЕНСТВА …
- Приложение 3. ТЕОРЕМА ОБ ЭРГОДИЧЕСКИХ ИСТОЧНИКАХ
- Приложение 4. МАКСИМИЗАЦИЯ СКОРОСТИ ДЛЯ СИСТЕМЫ ОГРАНИЧЕНИЯ
- Приложение 5
- Приложение 6
- Приложение 7
- ТЕОРИЯ СВЯЗИ В СЕКРЕТНЫХ СИСТЕМАХ
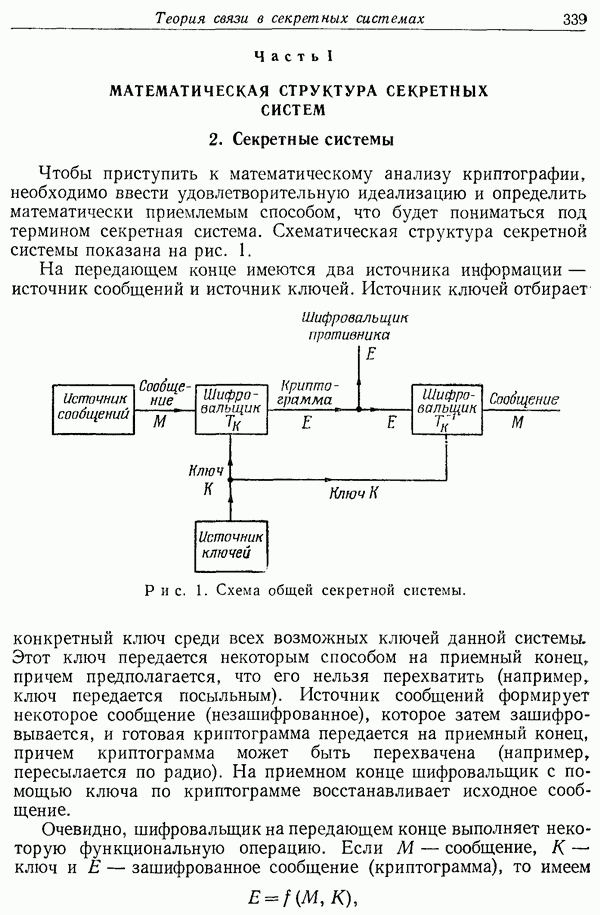
- Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ СИСТЕМ
- 3. Способы изображения систем
- 4. Примеры секретных систем
- 5. Оценка секретных систем
- 6. Алгебра секретных систем
- 7. Чистые и смешанные шифры
- 8. Подобные системы
- Часть II. ТЕОРЕТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 10. Совершенная секретность
- 11. Ненадежность
- 12. Свойства ненадежности
- 13. Ненадежность простой подстановки для языка с двухбуквенным алфавитом
- 14. Характеристика ненадежности для «случайного» шифра
- 15. Применение к стандартным шифрам
- 16. Правильность решения криптограммы
- 17. Идеальные секретные системы
- 18. Примеры идеальных секретных систем
- 19. Дополнительные замечания о ненадежности и избыточности
- 20. Распределение ненадежности
- Часть III. ПРАКТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 22. Общие замечания о решении криптограмм
- 23. Статистические методы
- 24. Метод вероятных слов
- 25. Перемешивание
- 26. Шифры типа …
- 27. Несовместимость требований к хорошим системам
- ПРИЛОЖЕНИЕ. Доказательство теоремы 3
- СОВРЕМЕННЫЕ ДОСТИЖЕНИЯ ТЕОРИИ СВЯЗИ
- Измерение информаций
- Кодирование информации
- Пропускная способность канала
- Идеальные и практические системы
- ПРИНЦИПЫ КОДОВО-ИМПУЛЬСНОЙ МОДУЛЯЦИИ
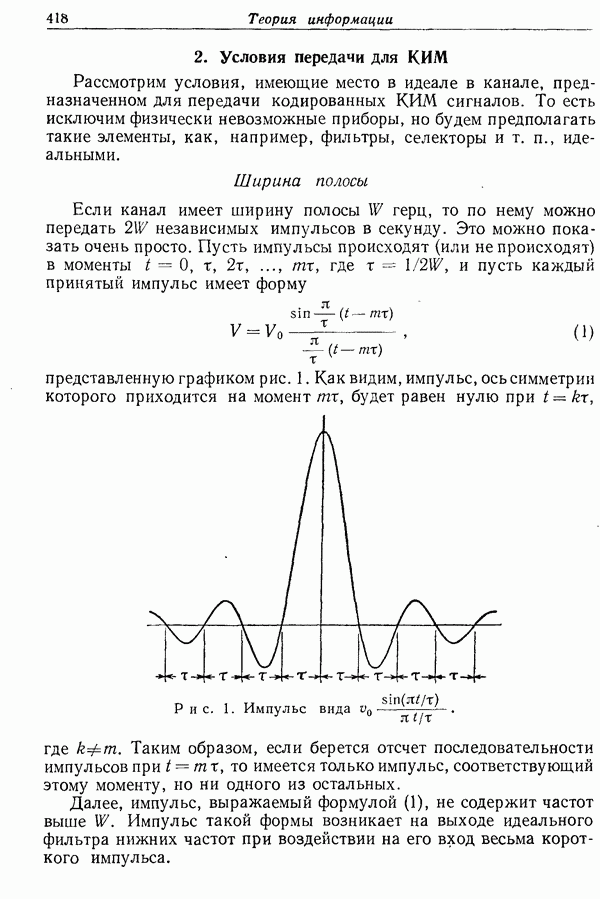
- 2. Условия передачи для КИМ
- 3. Действие системы КИМ
- 4. Сравнение КИМ и ЧМ
- 5. Заключение
- Приложение I
- Приложение II
- СВЯЗЬ ПРИ НАЛИЧИИ ШУМА
- 2. Теорема отсчетов
- 3. Геометрическое представление сигналов
- 4. Геометрическое представление сообщений
- 5. Геометрическое представление передатчика и приемника
- 6. Отображение пространства
- 7. Пропускная способность канала при наличии белого теплового шума
- 8. Обсуждение
- 9. Произвольный гауссовский шум
- 10. Пропускная способность канала при произвольном типе шума
- 11. Дискретные источники информации
- 12. Непрерывные источники информации
- НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ИНФОРМАЦИИ
- ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА С ШУМОМ ПРИ НУЛЕВОЙ ОШИБКЕ
- Пропускная способность канала при нулевой ошибке
- Пропускная способность для суммы и произведения каналов
- Каналы с обратной связью
- ГЕОМЕТРИЧЕСКИЙ ПОДХОД К ТЕОРИИ ПРОПУСКНОЙ СПОСОБНОСТИ. КАНАЛОВ СВЯЗИ
- КАНАЛЫ С ДОПОЛНИТЕЛЬНОЙ ИНФОРМАЦИЕЙ НА ПЕРЕДАТЧИКЕ
- Дискретный канал без памяти с дополнительной информацией о состоянии
- Приложение
- НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ТЕОРИИ КОДИРОВАНИЯ ДЛЯ КАНАЛОВ С ШУМАМИ
- Оценка вероятности ошибки в терминах производящей функции моментов
- Пропускная способность канала с конечным числом состояний, состояние которого вычислимо на обоих концах
- Пропускная способность канала с конечным числом состояний в случае, когда состояние вычислимо на передающем конце и не вычислимо на приемном конце
- ЗАМЕЧАНИЯ О ЧАСТИЧНОМ УПОРЯДОЧИВАНИИ КАНАЛОВ СВЯЗИ
- Дальнейшее обобщение и некоторые предположения
- ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ ОПТИМАЛЬНЫХ кодов В ГАУССОВСКОМ КАНАЛЕ
- 2. Сводка результатов
- 3. Нижняя граница, основанная на соображениях «сферической упаковки»
- 4. Верхняя граница, определяемая методом случайного кодирования
- 5. Формулы для скорости передачи R как функции угла конуса
- 6. Асимптотические формулы для …
- 7. Асимптотическое выражение для верхней границы при случайном кодировании
- 8. Жесткая верхняя граница
- 9. Жесткая нижняя граница
- 10. Поведение границ вблизи пропускной способности канала
- 11. Верхняя граница, полученная методом исчерпывания
- 12. Нижняя граница для гауссовского канала, получаемая исходя из минимального расстояния
- 13. Границы ошибок и другие условия, накладываемые на точки
- 14. Кривые для асимптотических границ
- ТЕОРЕМЫ КОДИРОВАНИЯ ДЛЯ ДИСКРЕТНОГО ИСТОЧНИКА ПРИ ЗАДАННОМ КРИТЕРИИ ТОЧНОСТИ
- Мера искажения отдельной буквы
- Несколько простых примеров
- Скорость при заданном искажении R(d)
- Выпуклость вниз кривой R(d)
- Нахождение R(d) в некоторых простых случаях
- Скорость передачи для произведения источников с мерой, являющейся суммой мер искажения
- Нижняя граница для искажения при заданной пропускной способности канала
- Теоремы кодирования при заданной мере искажения отдельной буквы
- Двойственность источника и канала
- Численные расчеты для некоторых простых каналов
- Обобщение на случаи непрерывных алфавитов
- Разностная мера искажения
- Определение меры локального искажения
- Функции Rn(d) и R(d) для меры локального искажения и эргодического источника
- Прямая теорема кодирования для меры локального искажения
- Обратная теорема кодирования
- Канал с памятью
- ДВУСТОРОННИЕ КАНАЛЫ СВЯЗИ
- 4. Средние взаимные скорости передачи информации
- 5. Распределение информации
- 6. Случайное кодирование для двусторонних каналов
- 7. Вероятность ошибки для ансамбля кодов
- 8. Выпуклая оболочка G как внутренняя граница области пропускной способности
- 9. Внешняя граница для области пропускной способности
- 10. Выпуклость вниз как функций от …
- 11. Приложения свойства выпуклости. Каналы с симметричной структурой
- 12. Характер области, выделяемой внешней границей
- 13. Пример, в котором внутренняя и внешняя границы различны
- 14. Достижимость внешней границы при зависимых источниках
- 15. Общий метод нахождения области пропускной способности двустороннего канала
- 16. Двусторонние каналы с памятью
- 17. Обобщение на каналы с Т концами
- БАНДВАГОН
- ПРЕДСКАЗАНИЕ И ЭНТРОПИЯ ПЕЧАТНОГО АНГЛИЙСКОГО ТЕКСТА
- 2. Вычисление энтропии по статистике английского языка
- 3. Предсказание английского текста
- 4. Идеальное N-граммное предсказывание
- 5. Граница для энтропии на основании частот предсказания
- 6. Результаты эксперимента для английского языка
- УПРОЩЕННЫЙ ВЫВОД ЛИНЕЙНОЙ ТЕОРИИ СГЛАЖИВАНИЯ И ПРЕДСКАЗАНИЯ ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ
- 3. Свойства линейных фильтров
- 4. Основное выражение для среднеквадратичной ошибки
- 5. Чистая проблема сглаживания
- 6. Проблема чистого предсказания
- 7. Предсказание при наличии шума
- 8. Обобщения
- 9. Обсуждение основных предположений
- МАТЕМАТИЧЕСКАЯ ТЕОРИЯ ДИФФЕРЕНЦИАЛЬНОГО АНАЛИЗАТОРА
- Основное условие разрешимости
- Реализация функций
- Системы уравнений
- Аппроксимация множителей с помощью передаточных чисел
- Автоматическое управление скоростью работы устройства
- О МАКСИМАЛЬНОМ ПОТОКЕ ЧЕРЕЗ СЕТЬ
- ТЕОРЕМА О РАСКРАСКЕ РЕБЕР ГРАФА
- УНИВЕРСАЛЬНАЯ МАШИНА ТЬЮРИНГА С ДВУМЯ ВНУТРЕННИМИ СОСТОЯНИЯМИ
- Невозможность создания универсальной машины Тьюринга с одним состоянием
- Моделирование машины Тьюринга с помощью только двух символов на ленте
- ВЫЧИСЛИМОСТЬ НА ВЕРОЯТНОСТНЫХ МАШИНАХ
- Приложение
- БИБЛИОГРАФИЯ РАБОТ ПО ШЕННОНОВСКОЙ ТЕОРИИ ОПТИМАЛЬНОГО КОДИРОВАНИЯ ИНФОРМАЦИИ