| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ВКЛАД ФОН НЕЙМАНА В ТЕОРИЮ АВТОМАТОВ
Теория автоматов возникла сравнительно недавно и, без сомнения, принадлежит к числу наиболее интенсивно развивающихся областей исследования. Она представляет собой науку, граничащую в математике с символической логикой и теорией машин Тьюринга, в инженерном деле — с теорией и применением универсальных вычислительных машин, в особенности к общим проблемам неарифметического характера, а в биологии — с нейрофизиологией, теорией нервных сетей и т. д. Теория автоматов охватывает различные проблемы, начиная с проблем «геделевского типа» (относящихся к машинам Тьюринга и проблемам разрешения) и кончая проблемами размножения, приспособления, самовоспроизведения и самовосстановления и др. применительно к машинам.
Последние несколько лет своей жизни фон Нейман много работал в области теории автоматов, которая соединила его ранние исследования в логике и теории доказательств и его более поздние работы времени второй мировой войны и послевоенного периода, относящиеся к области универсальных вычислительных машин.
Теория автоматов, включающая в себя элементы «чистой» и прикладной математики наряду с элементами других наук, была идеальным полем для разностороннего интеллекта фон Неймана. Он внес в эту теорию много новых идей и положил начало по меньшей мере двум новым направлениям исследования. К сожалению, он не смог довести до конца начатую работу, часть которой осталась в черновиках и неизданных лекциях, а часть нигде не записана и восстановить ее можно только по воспоминаниям его коллег о случайных разговорах.
Здесь не будет рассматриваться его огромной важности вклад в теорию вычислительных машин и их применение; его идеи,
касающиеся логической структуры машин, использования блок-схем для программирования, и методов программирования различных задач, таких, как обращение матриц, метод Монте-Карло и т. д. - ограничимся областью собственно теории автоматов.
Надежные машины и ненадежные элементы. Одна из важных частей работы, проделанной фон Нейманом в теории автоматов, относится к проблеме синтеза надежных машин из ненадежных элементов.
Пусть дано множество элементарных блоков с некоторыми положительными вероятностями неправильного функционирования. Можно ли из этих блоков при помощи соответствующего метода синтеза строить произвольно большие и сложные автоматы, для которых вероятность появления ошибки на выходе поддавалась бы контролю? Можно ли сделать вероятность ошибки сколь угодно малой или хотя бы не превосходящей некоторого фиксированного значения (не зависящего от конкретного автомата)?
Мозг человека и животных дает нам пример очень большой и относительно надежной системы, построенной из индивидуальных компонент, нейронов, которые ненадежны не только в выполнении операций, но и в тонких деталях взаимосвязи. Более того, хорошо известно, что при повреждении, несчастном случае, болезни и т. д. мозг продолжает функционировать замечательно правильно, даже если поражены его большие области.
Эти факты представляют сильный контраст по сравнению с поведением и организацией современных вычислительных машин. Индивидуальные элементы этих машин должны быть выполнены с чрезвычайной надежностью, каждый провод должен быть соединен нужным образом и каждая команда в программе должна быть правильной. Любая ошибка в элементе, в соединении элементов или в программе обычно приводит к полному искажению результатов. Если рассматривать мозг как машину, то очевидно, что предохранение от ошибок организовано в нем совершенно иначе, чем в вычислительных машинах.
Эта проблема аналогична проблеме, возникающей в теории связи, когда требуется построить такие коды для передачи информации, что надежность полного кода высока даже в тех случаях, когда надежность передачи отдельных символов мала. В теории связи эту проблему можно решить соответствующим введением избыточности и в данном случае нужно применить аналогичные приемы. Здесь недостаточно простого выполнения одних и тех же вычислений много раз подряд и выбора значения по большинству. Значение по большинству берется от ненадежных элементов, и так много раз подряд — значение по большинству от значений по большинству и т. д. Здесь возникает ситуация: «кто будет сторожить сторожа».
Исследование этих проблем фон Нейман начал с рассмотрения формальной структуры автомата. Та система, которую он выбрал, аналогична модели Мак Каллока—Питтса; схемы состоят из отдельных элементов относительно простого типа, связанных между собой. Каждый элемент получает двоичные сигналы на входы от множества различных входных линий и выдает выходные двоичные сигналы на некоторую выходную линию. Сигнал на выходе появляется через целое число единиц времени после подачи сигнала на вход. Если бы выходной сигнал был функцией значений входных сигналов, имелся бы надежный элемент, который может выполнять операцию «и», «не», штрих Шеффера и т. д. Однако если выходной сигнал зависит от входных только статистически, например с вероятностью 1—е, на выходе получается штрих Шеффера и с вероятностью  — отрицание этой операции, то имеется ненадежный элемент. Если же дано неограниченное число таких ненадежных элементов, например элементов для реализации штриха Шеффера, то можно ли из них построить надежный вариант любого заданного автомата?
— отрицание этой операции, то имеется ненадежный элемент. Если же дано неограниченное число таких ненадежных элементов, например элементов для реализации штриха Шеффера, то можно ли из них построить надежный вариант любого заданного автомата?
Фон Нейман показал, что это можносделать, и проиллюстрировал это двумя совершенно различными приемами. Первый из них, возможно, более красив математически, так как он тесно связан с описанной проблемой и близко подходит к проблеме «сторожа».
Решение состоит в конструировании из трех ненадежных подсхем и некоторых сравнивающих устройств одной более крупной и более надежной подсхемы, выполняющей ту же функцию, что и исходная подсхема. Проделывая это для каждого элемента схемы с ненадежными элементами, получим схему с тем же поведением, что и у заданной, но состоящую из ненадежных элементов.
Первый прием, как он указывал, страдает двумя недостатками. Во-первых, окончательная надежность не может быть сделана произвольно высокой, а может быть доведена только до определенного уровня  зависит от надежности исходных элементов). Если эти элементы очень низкого качества, то решение едва ли может
зависит от надежности исходных элементов). Если эти элементы очень низкого качества, то решение едва ли может
считаться удовлетворительным. Во-вторых, что более важно с практической точки зрения, требуемая избыточность в большинстве случаев фантастически велика. Число требуемых элементов растет экспоненциально по отношению к числу  элементов, необходимых для создания моделируемого автомата. Так как во всех случаях, представляющих практический интерес,
элементов, необходимых для создания моделируемого автомата. Так как во всех случаях, представляющих практический интерес,  очень велико, то это решение ценно только с точки зрения логической возможности.
очень велико, то это решение ценно только с точки зрения логической возможности.
Второй прием состоит в том, что фон Нейман называл «мультитрюком». Он заключается в том, что двоичный выход в машине представляется не одной линией, а пучком из  линий, и двоичный выходной сигнал определяется в зависимости от того, много линий или, наоборот, очень мало линий несут значения 1. Метод синтеза автоматов, основанный на использовании надежных элементов, в этом случае заменяется методом, в котором каждая линия становится пучком линий, а каждый элемент заменяется подсхемой, которая оперирует соответствующим образом с пучками входных и выходных линий. Фон Нейман показал, каким образом можно сконструировать такие подсхемы. Он также сделал некоторые оценки избыточности, требуемой для достижения определенной надежности. Например, вместо одного ненадежного «мажоритарного» элемента, вероятность ошибки которого равна 1/200, использованием избыточности в
линий, и двоичный выходной сигнал определяется в зависимости от того, много линий или, наоборот, очень мало линий несут значения 1. Метод синтеза автоматов, основанный на использовании надежных элементов, в этом случае заменяется методом, в котором каждая линия становится пучком линий, а каждый элемент заменяется подсхемой, которая оперирует соответствующим образом с пучками входных и выходных линий. Фон Нейман показал, каким образом можно сконструировать такие подсхемы. Он также сделал некоторые оценки избыточности, требуемой для достижения определенной надежности. Например, вместо одного ненадежного «мажоритарного» элемента, вероятность ошибки которого равна 1/200, использованием избыточности в  к 1 можно построить подсхему, представляющую мажоритарный элемент для пучков и с вероятностью ошибки
к 1 можно построить подсхему, представляющую мажоритарный элемент для пучков и с вероятностью ошибки  Произведя соответствующий подсчет, увидим, что этот автомат, обладающий сложностью и быстродействием мозга, может работать в течение ста лет, сделав при этом всего несколько ошибок. Другими словами, нечто родственное этой схеме может обладать по крайней мере такой же надежностью, как мозг.
Произведя соответствующий подсчет, увидим, что этот автомат, обладающий сложностью и быстродействием мозга, может работать в течение ста лет, сделав при этом всего несколько ошибок. Другими словами, нечто родственное этой схеме может обладать по крайней мере такой же надежностью, как мозг.
Самовоспроизводящиеся машины. Другой ветвью теории автоматов, которую развивал фон Нейман, является изучение проблемы самовоспроизведения машин или проблемы — можно ли построить простую и абстрактную систему «машин», которые способны строить другие идентичные машины или даже способные к некоторого рода эволюционному процессу, в котором последующие поколения строят машины более высокой «сложности». Реальная трудность здесь состоит в том, чтобы соответствующим образом сбалансировать простоту формальных построений и легкость обращения, с одной стороны, и степень близости модели к реальным физическим машинам, с другой стороны. Если модель слишком близка к реальности, нам приходится кодировать все сложнейшие аспекты природы, большая часть которых не имеет никакого отношения к вопросу самовоспроизведения. Однако при слишком сильном упрощении модель становится настолько абстрактной и упрощенной, что проблема выглядит почти тривиальной и решение не дает ничего нового с точки зрения выяснения поставленного философского вопроса.
Однажды после продолжительной дискуссии о трудности удовлетворительно сформулировать эту проблему фон Нейман заметил: «Я не собираюсь всерьез возражать тем, кто утверждает: а) каждому известно, что автомат может воспроизвести сам себя, и б) каждому известно, что он этого сделать не может».
Фон Нейман посвятил много времени исследованию вопроса о самовоспроизведении автоматов; краткое изложение его высказываний по этому поводу содержится в материалах Хиксонского симпозиума, и подробное — в более поздних незаконченных рукописях.
Фактически он рассмотрел две различные формулировки проблемы. Модель, о которой он говорил в докладе на Хиксонском симпозиуме и в более ранних работах на эту же тему, состоит из небольшого числа различных исходных элементов. Этими элементами могут быть, например, стойка, датчик (для установления присутствия других частей), соединительный элемент (для скрепления отдельных частей вместе) и т. д. Машины представляют собой комбинации этих частей и существуют в геометрической среде вместе с другими подобными частями, которые могут быть взяты машиной из этой окружающей среды.
Некоторые машины, собранные из таких частей, способны группировать вместе и оперировать отдельными частями из окружающей среды. Можно также сконструировать машину с «программным» управлением, которая выполняет такие же длинные последовательности команд, как и обычная вычислительная машина. Здесь, однако, команды содержат операции над такими отдельными частями, а не над числами в ходе длинных вычислений. Ситуация несколько аналогична той, которая имеет место в случае машин Тьюринга, и действительно существует понятие универсальной конструирующей машины, которая может при наличии соответствующей программы моделировать любую машину. Фон Нейман показал, что такая универсальная машина вместе с устройством, копирующим программы, может быть превращена в самовоспроизводящуюся машину.
Эта модель очень интересна сама по себе, но так как она требует изучения сложных случаев движения частей в действительном
евклидовом пространстве, то выполнить ее во всех подробностях чрезвычайно трудно, даже если не учитывать проблем источников питания, шумов в среде и тому подобное. Во всяком случае, фон Нейман в своих более поздних работах перешел от этой модели к более простой.
Второй тип самовоспроизводящейся системы описан в неоконченной книге, предназначенной для издательства Иллинойского университета. Эта вторая модель, возможно, больше напоминает биологическое размножение на низшем уровне (скажем, на клеточном или даже молекулярном), хотя она и не следует в точности никакой реальной физической системе.
Рассмотрим бесконечное множество квадратов на евклидовой плоскости, каждый квадрат, или «клетка», может находиться в некотором числе состояний. В модели, построенной фон Нейманом, клетки имеют двадцать девять состояний. Время пробегает дискретные моменты. Состояние клетки в данный момент есть функция ее состояния в предыдущий момент и состояний четырех ее ближайших соседей в предыдущий момент. С течением времени состояния всех клеток изменяются в соответствии с этими функциональными соотношениями. Определенное состояние клеток называется «начальным» и соответствует неактивной части плоскости. При соответствующем подборе функциональных уравнений можно получить группы соседних клеток, которые ведут себя подобно живому организму, способному сохранять свою индивидуальность, передвигаться и даже воспроизводить себя в смысле порождения других групп клеток с теми же активными состояниями.
В дополнение к вопросу о самовоспроизведении автоматов фон Нейман в некоторой степени касался проблем «эволюции» в автоматах или проблемы — можно ли построить автоматы, которые будут конструировать последовательные поколения автоматов, могущих в некотором смысле приспосабливаться к окружающей среде. Он указывал на существование критических размеров автомата, построенного из элементов заданного типа, а именно что автоматы, размер которых меньше критического, могут конструировать только автоматы меньшие, чем они сами, в то время, как некоторые автоматы, размер которых равен или больше критического, способны к самовоспроизведению и даже к эволюции (при соответствующем задании условий и требований приспособляемости).
Сравнение вычислительных машин и мозга. Огромный интерес для фон Неймана представлял вопрос о соотношении между центральной нервной системой и современными универсальными вычислительными машинами. В его докладе на Хиксонском симпозиуме этой теме уделено не меньше внимания, чем проблеме самовоспроизводящихся машин. Более широко эти вопросы затронуты
в лекциях на Силимановских чтениях (которые он подготовил, но не смог прочитать).
Выявляя аналогии между вычислительными машинами и нервными сетями, фон Нейман ясно понимал и часто подчеркивал существенные различия между ними. При поверхностном рассмотрении очевидны различия в порядке числа и размеров их элементов и в скорости выполнения ими операций. Нейроны мозга работают гораздо медленнее, чем их искусственные аналоги — транзисторы или электронные лампы, но, с другой стороны, они имеют намного меньшие размеры, расходуют меньше энергии и число их в мозгу на несколько порядков больше, чем в самых больших вычислительных машинах. При более глубоком изучении обнаруживаются, как подчеркивал фон Нейман, различия в логической организации, определяющей функционирование этих двух типов систем. Отчасти эти различия определяются характером решаемых задач, который проявляется в «логической глубине», т. е. в числе элементарных операций, которые должны быть последовательно выполнены для получения решения. В вычислительных машинах это число может иметь порядок  или больше из-за определенной искусственности и «последовательности» метода решения задач. Мозг, обладая большим числом более медленных элементов, по-видимому, работает ближе к параллельному методу при меньшей логической глубине, и, кроме того, задачи, которые он решает, требуют меньшего разнообразия последовательных вычислений.
или больше из-за определенной искусственности и «последовательности» метода решения задач. Мозг, обладая большим числом более медленных элементов, по-видимому, работает ближе к параллельному методу при меньшей логической глубине, и, кроме того, задачи, которые он решает, требуют меньшего разнообразия последовательных вычислений.
В лекциях на Силимановских чтениях фон Нейман кратко коснулся любопытной идеи, относящейся к основаниям математики. Тьюринг в своей хорошо известной работе о вычислимости показал, как одна вычислительная машина может моделировать другую. Команды для второй машины переводятся с помощью сокращенной программы в последовательности команд для первой машины, что заставляет ее выполнять (в общем случае косвенным образом) то, что должна делать вторая машина. С помощью таких переводных программ можно заставить первую машину в конечном итоге делать то же, что вторая машина, хотя в действительности она работает в ином внутреннем коде. Этот прием стал обычным и весьма полезным в повседневном использовании вычислительных машин.
Если принять мозг как некую разновидность вычислительной машины, то вполне возможно предположить, что внешний язык, которым мы пользуемся при общении друг с другом, может быть совершенно отличен от внутреннего языка, используемого при вычислениях (которые включают, разумеется, все логические
и информационные операции наряду с арифметическими вычислениями).
Фон Нейман действительно приводит убедительные аргументы, говорящие о том, что до сих пор нет совершенно никакого представления о природе того первичного языка, который используется при работе мозга. Он говорит: «Логика и математика в центральной нервной системе, рассматриваемые как некоторые языки, должны иметь структуру, существенно отличную от структуры языков, к которым приводит нас повседневный опыт.
Нужно также отметить, что тот язык, о котором идет речь, может скорее соответствовать сокращенным программам в том смысле, как это было сказано выше, чем полным программам: когда мы говорим о математике, то при этом имеется в виду некоторый вторичный язык, построенный на основе первичного языка, используемого в действительности центральной нервной системой. Таким образом, внешняя форма нашей математики не является абсолютно существенной с точки зрения выяснения вопроса, что представляет собой математический или логический язык, в действительности используемый центральной нервной системой. Однако сделанные выше замечания относительно надежности, логической и арифметической глубины показывают, что эта система, чем бы она ни была, не может не отличаться существенным образом от того, что мы сознательно и явно рассматриваем как математику».
В целом вклад фон Неймана в теорию автоматов, так же как и его вклад в другие разделы математики и другие науки, характеризуется открытием совершенно новых областей исследования и прозорливостью в оценке возможностей приложений методов современной математики. Исследования в направлениях, открытые. им для разработки, не будут полностью закончены еще в течение долгих лет. Очень жаль, что часть его замыслов относительно теории автоматов осталась нереализованной.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- СИМВОЛИЧЕСКИЙ АНАЛИЗ РЕЛЕЙНЫХ И ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- 2. Параллельно-последовательные двухполюсные схемы. Основные определения и постулаты
- 3. Многополюсные и не параллельно-последовательные схемы
- Преобразование треугольника в звезду и звезды в ячейку
- Функция сопротивления не параллельно-последовательной схемы
- Системы уравнений
- Реле и переключатели специальных типов
- 4. Синтез схем
- Двойственные схемы
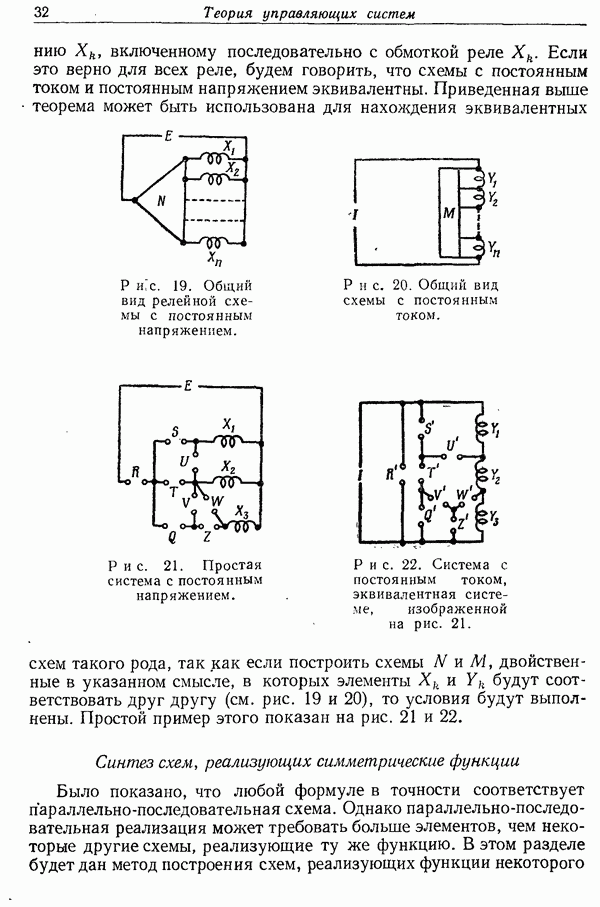
- Синтез схем, реализующих симметрические функции
- Составление уравнений по рабочим характеристикам
- 5. Примеры
- ЧИСЛО ДВУХПОЛЮСНЫХ ПАРАЛЛЕЛЬНО-ПОСЛЕДОВАТЕЛЬНЫХ СЕТЕЙ
- 1. Получение производящей функции
- 2. Численный подсчет
- 3. Асимптотическое поведение
- 4. Параллельно-последовательная реализация переключательных функций
- СИНТЕЗ ДВУХПОЛЮСНЫХ ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- 2. Основная теорема синтеза
- 3. Синтез схем для произвольных функций.
- Часть II. РАСПРЕДЕЛЕНИЕ НАГРУЗКИ МЕЖДУ РЕЛЕ
- 5. Разделительное дерево
- 6. Другие задачи распределения
- 7. Функция «мю»
- Часть III. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- 9. Частично симметрические функции
- ПРИМЕЧАНИЯ РЕДАКТОРА
- ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К ОБЪЕМУ ПАМЯТИ ТЕЛЕФОННОГО КОММУТАТОРА
- 2. Память, требуемая для S произвольных вызовов от N абонентов
- 3. Условие раздельной памяти
- 4. Связь с теорией информации
- НАДЕЖНЫЕ СХЕМЫ ИЗ НЕНАДЕЖНЫХ РЕЛЕ
- Идеализированные реле
- Общий метод повышения надежности
- Свойства функции h(p)
- Комбинация двух схем
- Оценки функции h'(p)
- Схемы заданной длины и ширины
- Оценки числа контактов в случае, когда реле уже достаточно надежны
- Сравнение с элементами фон Неймана
- Реле с неопределенным временем срабатывания
- Синтез надежных схем в целом
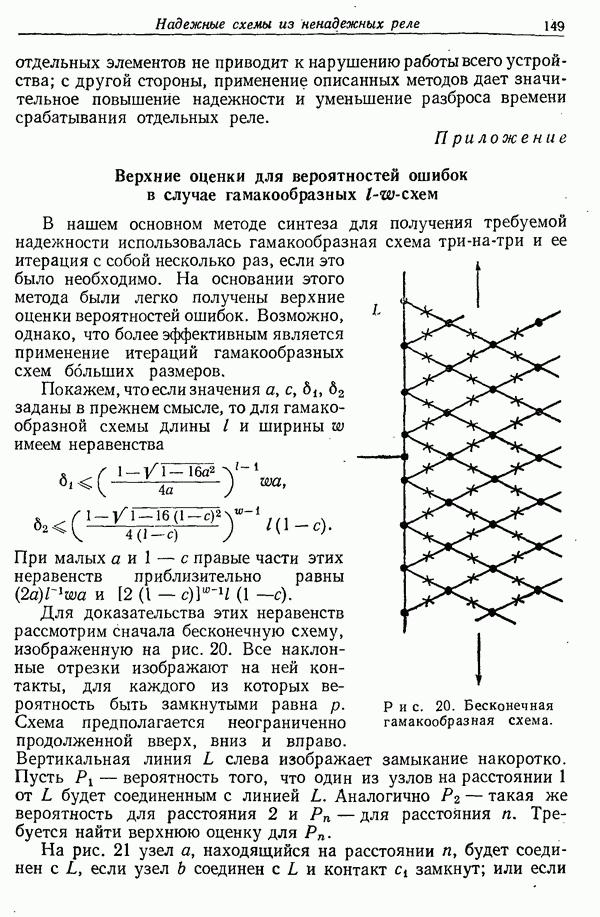
- Приложение. Верхние оценки для вероятностей ошибок в случае гамакообразных l-w-схем
- ИСПОЛЬЗОВАНИЕ МАШИНЫ ДЛЯ ПРОЕКТИРОВАНИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА И АВТОМАТЫ
- Машины Тьюринга
- Логические машины
- «Играющие машины»
- Обучаемые машины
- Самовоспроизводящиеся машины
- Обращение к читателю
- МАШИНА ДЛЯ ИГРЫ В ШАХМАТЫ
- СОСТАВЛЕНИЕ ПРОГРАММ ДЛЯ ИГРЫ В ШАХМАТЫ НА ВЫЧИСЛИТЕЛЬНОЙ МАШИНЕ
- 3. Приближенная оценочная функция
- 4. Стратегия, основанная на оценочной функции
- 5. Составление программы для универсальной вычислительной машины для реализации стратегии типа А
- 6. Улучшение стратегии
- 7. Изменения в игре и в стиле
- 8. Другой тип стратегии
- ПРИЛОЖЕНИЕ. ОЦЕНОЧНАЯ ФУНКЦИЯ ДЛЯ ШАХМАТ
- ИГРАЮЩИЕ МАШИНЫ
- СООБЩЕНИЕ О МАШИНЕ, РЕШАЮЩЕЙ ЛАБИРИНТНУЮ ЗАДАЧУ
- ВКЛАД ФОН НЕЙМАНА В ТЕОРИЮ АВТОМАТОВ
- МАТЕМАТИЧЕСКАЯ ТЕОРИЯ СВЯЗИ
- 1. ДИСКРЕТНЫЕ СИСТЕМЫ БЕЗ ШУМОВ
- 2. Дискретный источник сообщений
- 3. Последовательные приближения к английскому языку
- 4. Графическое представление марковского процесса
- 5. Эргодические и смешанные источники
- 6. Выбор, неопределенность и энтропия
- 7. Энтропия источника сообщений
- 8. Представление операций кодирования и декодирования
- 9. Основная теорема для канала без шума
- 10. Рассмотрение полученных результатов и примеры
- 11. Примеры
- II. ДИСКРЕТНЫЙ КАНАЛ С ШУМОМ
- 12. Надежность и пропускная способность канала
- 13. Основная теорема для дискретного канала с шумом
- 14. Рассмотрение полученных результатов
- 15. Пример дискретного канала и его пропускной способности
- 16. Пропускная способность канала в некоторых частных случаях
- 17. Пример эффективного кодирования
- III. ИНФОРМАЦИЯ ДЛЯ НЕПРЕРЫВНЫХ ВЕЛИЧИН
- 19. Ансамбли функций с ограниченной полосой частот
- 20. Энтропия непрерывного распределения
- 21. Энтропия ансамбля функций
- 22. Потеря энтропии в линейных фильтрах
- 23. Энтропия суммы двух ансамблей
- IV. НЕПРЕРЫВНЫЙ КАНАЛ
- 24. Пропускная способность непрерывного канала
- 25. Пропускная способность канала при ограничении средней мощности
- 26. Пропускная способность канала при ограничении пиковой мощности
- V. СКОРОСТЬ СОЗДАНИЯ СООБЩЕНИЙ ДЛЯ НЕПРЕРЫВНОГО ИСТОЧНИКА
- 28. Скорость создания сообщений источником при данной точности воспроизведения
- 29. Вычисление скорости создания сообщений
- Приложение 1. РОСТ ЧИСЛА БЛОКОВ СИМВОЛОВ ПРИ УСЛОВИЯХ, ОПИСЫВАЕМЫХ КОНЕЧНЫМ ЧИСЛОМ СОСТОЯНИЙ
- Приложение 2. ВЫВОД РАВЕНСТВА …
- Приложение 3. ТЕОРЕМА ОБ ЭРГОДИЧЕСКИХ ИСТОЧНИКАХ
- Приложение 4. МАКСИМИЗАЦИЯ СКОРОСТИ ДЛЯ СИСТЕМЫ ОГРАНИЧЕНИЯ
- Приложение 5
- Приложение 6
- Приложение 7
- ТЕОРИЯ СВЯЗИ В СЕКРЕТНЫХ СИСТЕМАХ
- Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ СИСТЕМ
- 3. Способы изображения систем
- 4. Примеры секретных систем
- 5. Оценка секретных систем
- 6. Алгебра секретных систем
- 7. Чистые и смешанные шифры
- 8. Подобные системы
- Часть II. ТЕОРЕТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 10. Совершенная секретность
- 11. Ненадежность
- 12. Свойства ненадежности
- 13. Ненадежность простой подстановки для языка с двухбуквенным алфавитом
- 14. Характеристика ненадежности для «случайного» шифра
- 15. Применение к стандартным шифрам
- 16. Правильность решения криптограммы
- 17. Идеальные секретные системы
- 18. Примеры идеальных секретных систем
- 19. Дополнительные замечания о ненадежности и избыточности
- 20. Распределение ненадежности
- Часть III. ПРАКТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 22. Общие замечания о решении криптограмм
- 23. Статистические методы
- 24. Метод вероятных слов
- 25. Перемешивание
- 26. Шифры типа …
- 27. Несовместимость требований к хорошим системам
- ПРИЛОЖЕНИЕ. Доказательство теоремы 3
- СОВРЕМЕННЫЕ ДОСТИЖЕНИЯ ТЕОРИИ СВЯЗИ
- Измерение информаций
- Кодирование информации
- Пропускная способность канала
- Идеальные и практические системы
- ПРИНЦИПЫ КОДОВО-ИМПУЛЬСНОЙ МОДУЛЯЦИИ
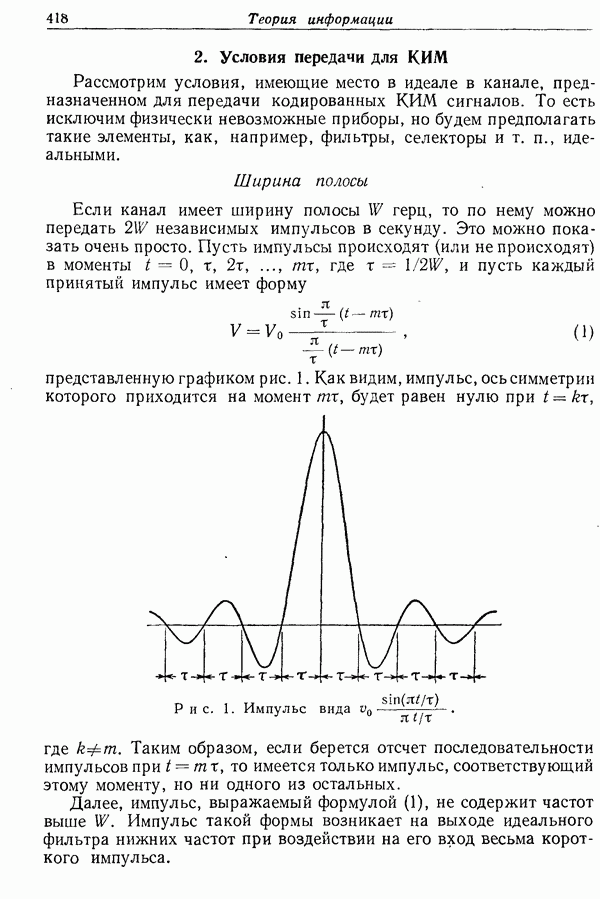
- 2. Условия передачи для КИМ
- 3. Действие системы КИМ
- 4. Сравнение КИМ и ЧМ
- 5. Заключение
- Приложение I
- Приложение II
- СВЯЗЬ ПРИ НАЛИЧИИ ШУМА
- 2. Теорема отсчетов
- 3. Геометрическое представление сигналов
- 4. Геометрическое представление сообщений
- 5. Геометрическое представление передатчика и приемника
- 6. Отображение пространства
- 7. Пропускная способность канала при наличии белого теплового шума
- 8. Обсуждение
- 9. Произвольный гауссовский шум
- 10. Пропускная способность канала при произвольном типе шума
- 11. Дискретные источники информации
- 12. Непрерывные источники информации
- НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ИНФОРМАЦИИ
- ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА С ШУМОМ ПРИ НУЛЕВОЙ ОШИБКЕ
- Пропускная способность канала при нулевой ошибке
- Пропускная способность для суммы и произведения каналов
- Каналы с обратной связью
- ГЕОМЕТРИЧЕСКИЙ ПОДХОД К ТЕОРИИ ПРОПУСКНОЙ СПОСОБНОСТИ. КАНАЛОВ СВЯЗИ
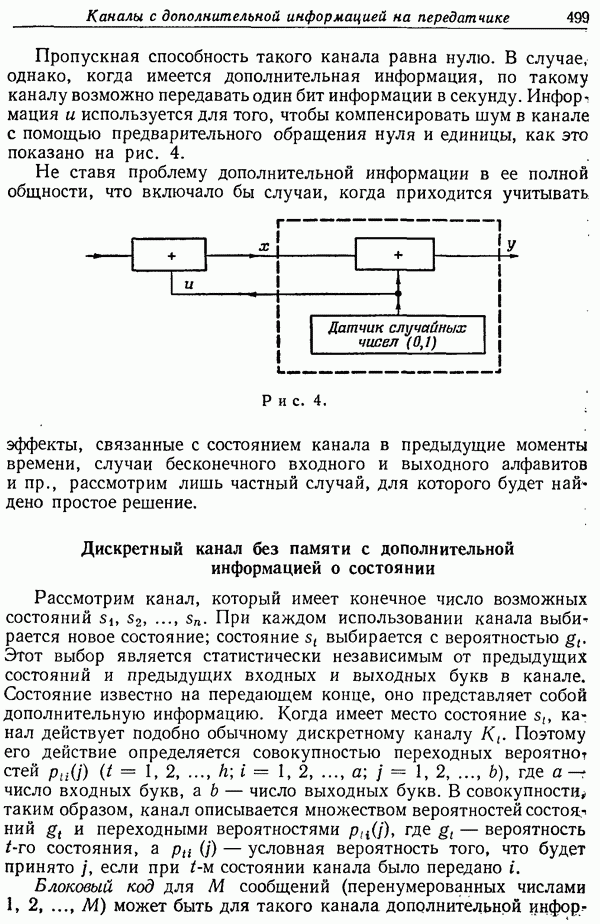
- КАНАЛЫ С ДОПОЛНИТЕЛЬНОЙ ИНФОРМАЦИЕЙ НА ПЕРЕДАТЧИКЕ
- Дискретный канал без памяти с дополнительной информацией о состоянии
- Приложение
- НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ТЕОРИИ КОДИРОВАНИЯ ДЛЯ КАНАЛОВ С ШУМАМИ
- Оценка вероятности ошибки в терминах производящей функции моментов
- Пропускная способность канала с конечным числом состояний, состояние которого вычислимо на обоих концах
- Пропускная способность канала с конечным числом состояний в случае, когда состояние вычислимо на передающем конце и не вычислимо на приемном конце
- ЗАМЕЧАНИЯ О ЧАСТИЧНОМ УПОРЯДОЧИВАНИИ КАНАЛОВ СВЯЗИ
- Дальнейшее обобщение и некоторые предположения
- ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ ОПТИМАЛЬНЫХ кодов В ГАУССОВСКОМ КАНАЛЕ
- 2. Сводка результатов
- 3. Нижняя граница, основанная на соображениях «сферической упаковки»
- 4. Верхняя граница, определяемая методом случайного кодирования
- 5. Формулы для скорости передачи R как функции угла конуса
- 6. Асимптотические формулы для …
- 7. Асимптотическое выражение для верхней границы при случайном кодировании
- 8. Жесткая верхняя граница
- 9. Жесткая нижняя граница
- 10. Поведение границ вблизи пропускной способности канала
- 11. Верхняя граница, полученная методом исчерпывания
- 12. Нижняя граница для гауссовского канала, получаемая исходя из минимального расстояния
- 13. Границы ошибок и другие условия, накладываемые на точки
- 14. Кривые для асимптотических границ
- ТЕОРЕМЫ КОДИРОВАНИЯ ДЛЯ ДИСКРЕТНОГО ИСТОЧНИКА ПРИ ЗАДАННОМ КРИТЕРИИ ТОЧНОСТИ
- Мера искажения отдельной буквы
- Несколько простых примеров
- Скорость при заданном искажении R(d)
- Выпуклость вниз кривой R(d)
- Нахождение R(d) в некоторых простых случаях
- Скорость передачи для произведения источников с мерой, являющейся суммой мер искажения
- Нижняя граница для искажения при заданной пропускной способности канала
- Теоремы кодирования при заданной мере искажения отдельной буквы
- Двойственность источника и канала
- Численные расчеты для некоторых простых каналов
- Обобщение на случаи непрерывных алфавитов
- Разностная мера искажения
- Определение меры локального искажения
- Функции Rn(d) и R(d) для меры локального искажения и эргодического источника
- Прямая теорема кодирования для меры локального искажения
- Обратная теорема кодирования
- Канал с памятью
- ДВУСТОРОННИЕ КАНАЛЫ СВЯЗИ
- 4. Средние взаимные скорости передачи информации
- 5. Распределение информации
- 6. Случайное кодирование для двусторонних каналов
- 7. Вероятность ошибки для ансамбля кодов
- 8. Выпуклая оболочка G как внутренняя граница области пропускной способности
- 9. Внешняя граница для области пропускной способности
- 10. Выпуклость вниз как функций от …
- 11. Приложения свойства выпуклости. Каналы с симметричной структурой
- 12. Характер области, выделяемой внешней границей
- 13. Пример, в котором внутренняя и внешняя границы различны
- 14. Достижимость внешней границы при зависимых источниках
- 15. Общий метод нахождения области пропускной способности двустороннего канала
- 16. Двусторонние каналы с памятью
- 17. Обобщение на каналы с Т концами
- БАНДВАГОН
- ПРЕДСКАЗАНИЕ И ЭНТРОПИЯ ПЕЧАТНОГО АНГЛИЙСКОГО ТЕКСТА
- 2. Вычисление энтропии по статистике английского языка
- 3. Предсказание английского текста
- 4. Идеальное N-граммное предсказывание
- 5. Граница для энтропии на основании частот предсказания
- 6. Результаты эксперимента для английского языка
- УПРОЩЕННЫЙ ВЫВОД ЛИНЕЙНОЙ ТЕОРИИ СГЛАЖИВАНИЯ И ПРЕДСКАЗАНИЯ ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ
- 3. Свойства линейных фильтров
- 4. Основное выражение для среднеквадратичной ошибки
- 5. Чистая проблема сглаживания
- 6. Проблема чистого предсказания
- 7. Предсказание при наличии шума
- 8. Обобщения
- 9. Обсуждение основных предположений
- МАТЕМАТИЧЕСКАЯ ТЕОРИЯ ДИФФЕРЕНЦИАЛЬНОГО АНАЛИЗАТОРА
- Основное условие разрешимости
- Реализация функций
- Системы уравнений
- Аппроксимация множителей с помощью передаточных чисел
- Автоматическое управление скоростью работы устройства
- О МАКСИМАЛЬНОМ ПОТОКЕ ЧЕРЕЗ СЕТЬ
- ТЕОРЕМА О РАСКРАСКЕ РЕБЕР ГРАФА
- УНИВЕРСАЛЬНАЯ МАШИНА ТЬЮРИНГА С ДВУМЯ ВНУТРЕННИМИ СОСТОЯНИЯМИ
- Невозможность создания универсальной машины Тьюринга с одним состоянием
- Моделирование машины Тьюринга с помощью только двух символов на ленте
- ВЫЧИСЛИМОСТЬ НА ВЕРОЯТНОСТНЫХ МАШИНАХ
- Приложение
- БИБЛИОГРАФИЯ РАБОТ ПО ШЕННОНОВСКОЙ ТЕОРИИ ОПТИМАЛЬНОГО КОДИРОВАНИЯ ИНФОРМАЦИИ