| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Дискретный канал без памяти с дополнительной информацией о состоянии
Рассмотрим канал, который имеет конечное число возможных состояний  При каждом использовании канала выбирается новое состояние; состояние
При каждом использовании канала выбирается новое состояние; состояние  выбирается с вероятностью
выбирается с вероятностью  Этот выбор является статистически независимым от предыдущих состояний и предыдущих входных и выходных букв в канале. Состояние известно на передающем конце, оно представляет собой дополнительную информацию. Когда имеет место состояние
Этот выбор является статистически независимым от предыдущих состояний и предыдущих входных и выходных букв в канале. Состояние известно на передающем конце, оно представляет собой дополнительную информацию. Когда имеет место состояние  канал действует подобно обычному дискретному каналу
канал действует подобно обычному дискретному каналу  Поэтому его действие определяется совокупностью переходных вероятнот стей
Поэтому его действие определяется совокупностью переходных вероятнот стей  где
где  число входных букв,
число входных букв,  число выходных букв. В совокупности таким образом, канал описывается множеством вероятностей состояний
число выходных букв. В совокупности таким образом, канал описывается множеством вероятностей состояний  и переходными вероятностями
и переходными вероятностями  где
где  — вероятность
— вероятность  состояния,
состояния,  — условная вероятность того, что будет принято если при
— условная вероятность того, что будет принято если при  состоянии канала было передано
состоянии канала было передано 
Блоковый код для М сообщений (перенумерованных числами  может быть для такого канала дополнительной инфор?
может быть для такого канала дополнительной инфор?
мацией определен следующим образом. Это определение, между прочим, аналогично тому, которое было дано ранее для канала с обратной связью. Пусть  длина блокового кода. Тогда существуют
длина блокового кода. Тогда существуют  функций
функций  . В этих функциях
. В этих функциях  пробегает множество возможных сообщений и поэтому
пробегает множество возможных сообщений и поэтому  . Все
. Все  пробегают все значения алфавита дополнительной информации. В рассматриваемом здесь частном случае каждое из
пробегают все значения алфавита дополнительной информации. В рассматриваемом здесь частном случае каждое из  может принимать значения от 1 до
может принимать значения от 1 до  Каждая функция
Каждая функция  принимает значения в алфавите входных букв канала х. Величина
принимает значения в алфавите входных букв канала х. Величина  является входом
является входом  который следует использовать в коде, если сообщением является
который следует использовать в коде, если сообщением является  а дополнительная информация вплоть до момента, соответствующего
а дополнительная информация вплоть до момента, соответствующего  состоит из
состоит из  Это является математическим эквивалентом утверждения о том, что код представляет собой правило определения следующей передаваемой буквы по каждому сообщению
Это является математическим эквивалентом утверждения о том, что код представляет собой правило определения следующей передаваемой буквы по каждому сообщению  и заданной дополнительной информации о состоянии канала от начала блока до настоящего момента. Существенным здесь является то, что при выборе следующей передаваемой буквы
и заданной дополнительной информации о состоянии канала от начала блока до настоящего момента. Существенным здесь является то, что при выборе следующей передаваемой буквы  могут быть использованы только имеющиеся к данному моменту
могут быть использованы только имеющиеся к данному моменту  (а именно,
(а именно,  а не дополнительная информация
а не дополнительная информация  которая еще не получена.
которая еще не получена.
Система декодирования для такого кода представляет собой отображение, или функцию  принятых блоков длины
принятых блоков длины  значением которых являются сообщения
значением которых являются сообщения  поэтому Л принимает значения от 1 до М. Таков способ выбора декодированного сообщения, которое ставится в соответствие всему принятому блоку
поэтому Л принимает значения от 1 до М. Таков способ выбора декодированного сообщения, которое ставится в соответствие всему принятому блоку 
Для некоторой заданной совокупности вероятностей и для некоторых заданных каналов, кодирующей и декодирующей систем существует поддающаяся вычислению вероятность ошибки  которая является вероятностью того, что некоторое сообщение будет закодировано и принято таким образом, что функция
которая является вероятностью того, что некоторое сообщение будет закодировано и принято таким образом, что функция  даст на выходе сообщение, отличное от переданного. В частности, будем интересоваться случаями, когда сообщения равновероятны; каждое имеет вероятность, равную
даст на выходе сообщение, отличное от переданного. В частности, будем интересоваться случаями, когда сообщения равновероятны; каждое имеет вероятность, равную  Скоростью передачи информации для такого кода является величина
Скоростью передачи информации для такого кода является величина  Нас интересует пропускная способность канала С, т. е. наибольшая скорость
Нас интересует пропускная способность канала С, т. е. наибольшая скорость  такая, что возможно выбрать коды со скоростями, произвольно близкими к скорости
такая, что возможно выбрать коды со скоростями, произвольно близкими к скорости  и с произвольно малой вероятностью ошибки
и с произвольно малой вероятностью ошибки  .
.
Можно отметить, что если бы дополнительная информация о Состоянии канала не поступала бы на передающий конец, то канал
действовал бы подобно каналу без памяти с переходными вероятностями

При этом условии, следовательно, пропускная способность могла бы быть вычислена обычными методами, существующими для каналов без памяти. С другой стороны, если бы дополнительная информация имелась как на передающем, так и на приемном концах, то, как легко показать, пропускная способность в этом случае выражалась бы формулой  где
где  — пропускная способность канала без памяти с переходными вероятностями
— пропускная способность канала без памяти с переходными вероятностями  Рассматриваемый здесь случай является промежуточным: дополнительная информация имеется на передающем, но не имеется на приемном конце.
Рассматриваемый здесь случай является промежуточным: дополнительная информация имеется на передающем, но не имеется на приемном конце.
Теорема. Пропускная способность дискретного канала К без памяти с дополнительной информацией, которая определяется значениями  равна пропускной способности канала К без памяти (и без дополнительной информации) с тем же самым выходным и входным алфавитом, состоящим из
равна пропускной способности канала К без памяти (и без дополнительной информации) с тем же самым выходным и входным алфавитом, состоящим из  входных букв
входных букв  где каждое
где каждое  а. Переходные вероятности
а. Переходные вероятности  для канала К имеют вид
для канала К имеют вид

Любой код и система декодирования для К могут быть переведены в некоторые эквивалентные код и систему декодирования для К с той же самой вероятностью ошибки. Любой код для К имеет неопределенность сообщений (условную энтропию на букву сообщения принятой последовательности) не большую, чем  где С — пропускная способность
где С — пропускная способность  Любой код со скоростью
Любой код со скоростью  обладает вероятностью ошибки, ограниченной снизу неравенством (при произвольной длине блока
обладает вероятностью ошибки, ограниченной снизу неравенством (при произвольной длине блока 

Можно заметить, что эта теорема сводит исследование данного канала К с дополнительной информацией к исследованию канала  без памяти, обладающего большим числом входных букв, но не имеющего дополнительной информации. Для определения пропускной способности этого вновь полученного канала К можно использовать уже известные методы и в результате вычислить пропускную способность исходного канала. Более того, коды для вновь полученного канала могут быть переведены в коды исходного
без памяти, обладающего большим числом входных букв, но не имеющего дополнительной информации. Для определения пропускной способности этого вновь полученного канала К можно использовать уже известные методы и в результате вычислить пропускную способность исходного канала. Более того, коды для вновь полученного канала могут быть переведены в коды исходного
канала без изменения вероятности ошибки. (На самом деле все статистические свойства кодов остаются теми же самыми.)
Покажем сначала, каким образом коды для канала К могут быть переведены в коды для канала К? Кодовое слово для вновь полученного канала К состоит из последовательности  букв, принадлежащих входному алфавиту X канала
букв, принадлежащих входному алфавиту X канала  Любая заданная буква X для этого канала может быть представлена как некоторая функция, определенная на алфавите состояний канала и принимающая значения во входном алфавите х канала К? Весь возможный алфавит X состоит из полного множества
Любая заданная буква X для этого канала может быть представлена как некоторая функция, определенная на алфавите состояний канала и принимающая значения во входном алфавите х канала К? Весь возможный алфавит X состоит из полного множества  всех возможных функций, определенных на алфавите состояний с
всех возможных функций, определенных на алфавите состояний с  элементами, со значениями во входном алфавите с
элементами, со значениями во входном алфавите с  элементами. Таким образом, каждая буква
элементами. Таким образом, каждая буква  кодового слова для канала
кодового слова для канала  может быть интерпретирована как функция от состояния и, принимающая значения во входном алфавите х. Перевод кодов заключается просто в формировании входа х, даваемого этой функцией от состояния канала. Таким образом, если аргумент — состояние и принимает значение 1, то по каналу К передается
может быть интерпретирована как функция от состояния и, принимающая значения во входном алфавите х. Перевод кодов заключается просто в формировании входа х, даваемого этой функцией от состояния канала. Таким образом, если аргумент — состояние и принимает значение 1, то по каналу К передается  если же состояние
если же состояние  то передается
то передается  Другими словами, перевод является простым побуквенным переводом без памяти, привносящей зависимость от предыдущих состояний.
Другими словами, перевод является простым побуквенным переводом без памяти, привносящей зависимость от предыдущих состояний.
Коды для канала К представляют собой просто иной способ описания некоторых из кодов для канала  а именно таких кодов, в которых следующая входная буква х является функцией лишь сообщения
а именно таких кодов, в которых следующая входная буква х является функцией лишь сообщения  и текущего состояния и и не зависит от предыдущих состояний.
и текущего состояния и и не зависит от предыдущих состояний.
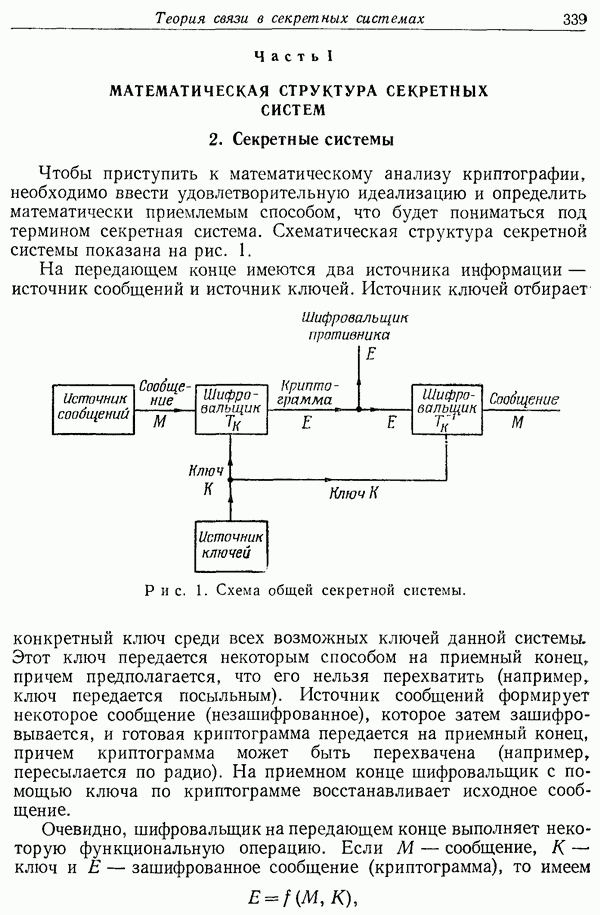
Можно указать также, что не трудно сконструировать простой физический прибор, который, будучи помещенным перед каналом К, сделал бы его сходным с каналом  Этот прибор имел бы алфавит X на одном входе и алфавит состояний на другом (этот вход был бы присоединен к линии и на рис. 1). Его выход принимал бы значения в алфавите х и был бы соединен с линией х на рис. 1. Работа прибора заключалась бы в том, чтобы давать выход х, соответствующий значению функции X от состояния и. Ясно, что если произвести перевод кодов, то статистические характеристики для каналов К, и К окажутся идентичными. Вероятность того, что некоторое входное слово для канала
Этот прибор имел бы алфавит X на одном входе и алфавит состояний на другом (этот вход был бы присоединен к линии и на рис. 1). Его выход принимал бы значения в алфавите х и был бы соединен с линией х на рис. 1. Работа прибора заключалась бы в том, чтобы давать выход х, соответствующий значению функции X от состояния и. Ясно, что если произвести перевод кодов, то статистические характеристики для каналов К, и К окажутся идентичными. Вероятность того, что некоторое входное слово для канала  будет принято как некоторое фиксированное выходное слово, является той же самой для соответствующей операции в канале К.. Это показывает справедливость первой половины теоремы.
будет принято как некоторое фиксированное выходное слово, является той же самой для соответствующей операции в канале К.. Это показывает справедливость первой половины теоремы.
Для того чтобы доказать вторую половину теоремы, покажем, что в первоначальном канале К приращение условной энтропии (неопределенности) сообщения  при приеме на приемном конце одной буквы не может превзойти С (пропускную способность нового канала
при приеме на приемном конце одной буквы не может превзойти С (пропускную способность нового канала  Пусть на рис. 1
Пусть на рис. 1  будет сообщение; х, у и и
будет сообщение; х, у и и
будут следующей входной буквой, выходной буквой и буквой состояния соответственно. Пусть  будет последовательностью предыдущих состояний и, имевших место от начала кодового блока до настоящего момента (точно до и),
будет последовательностью предыдущих состояний и, имевших место от начала кодового блока до настоящего момента (точно до и),  будет последовательностью предыдущих выходных букв вплоть до текущей буквы у. Предположим теперь, что задан блоковый код для кодирования сообщений. Эти сообщения выбираются из некоторого множества с определенными вероятностями (не обязательно равными). При заданных статистике источника сообщений, системе кодирования и статистике канала эти величины
будет последовательностью предыдущих выходных букв вплоть до текущей буквы у. Предположим теперь, что задан блоковый код для кодирования сообщений. Эти сообщения выбираются из некоторого множества с определенными вероятностями (не обязательно равными). При заданных статистике источника сообщений, системе кодирования и статистике канала эти величины  и
и  принадлежат все некоторому вероятностному пространству, и различные вероятности, включенные в последующие вычисления, имеют смысл. Таким образом, неопределенность сообщения
принадлежат все некоторому вероятностному пространству, и различные вероятности, включенные в последующие вычисления, имеют смысл. Таким образом, неопределенность сообщения  при уже принятом
при уже принятом  представляется в виде
представляется в виде

(Символ  здесь и в дальнейшем означает математическое ожидание или среднее значение
здесь и в дальнейшем означает математическое ожидание или среднее значение  по вероятностному пространству.) Приращение неопределенности при приеме следующей буквы у равно
по вероятностному пространству.) Приращение неопределенности при приеме следующей буквы у равно

Последнее неравенство является справедливым в силу того, что член  представляет собой среднюю взаимную информацию и, следовательно, является неотрицательным. Заметим теперь, что из требований независимости в нашей первоначальной системе следует, что
представляет собой среднюю взаимную информацию и, следовательно, является неотрицательным. Заметим теперь, что из требований независимости в нашей первоначальной системе следует, что

Далее, так как  является однозначной функцией
является однозначной функцией  системой кодирования, то его можно опустить при указании переменных в условии
системой кодирования, то его можно опустить при указании переменных в условии

В силу того что новое состояние и не зависит от предыдущего, 
После подстановки и упрощения получим

Суммирование по и дает

Поэтому

Используя это в неравенстве (1), получаем

Покажем теперь, что  Здесь X — случайная величина, описывающая функцию, переводящую
Здесь X — случайная величина, описывающая функцию, переводящую  задаваемая операцией кодирования следующего входного символа х в канале. Или, что то же самое, X соответствует входной букве в новом канале К. Имеем
задаваемая операцией кодирования следующего входного символа х в канале. Или, что то же самое, X соответствует входной букве в новом канале К. Имеем  Более того, из задания системы кодирования вытекает наличие функционального соотношения, определяющего следующую входную букву х по заданным
Более того, из задания системы кодирования вытекает наличие функционального соотношения, определяющего следующую входную букву х по заданным  . Поэтому
. Поэтому  . Если для некоторых двух заданных пар
. Если для некоторых двух заданных пар  при всех и имеет место равенство
при всех и имеет место равенство  , то отсюда следует, что
, то отсюда следует, что  для всех и и у, так как
для всех и и у, так как  и и приводят к тем же самым буквам х, что и
и и приводят к тем же самым буквам х, что и  . Пользуясь этим, получим условие
. Пользуясь этим, получим условие  Иначе говоря, пары
Иначе говоря, пары  приводящие к одной и той же функции
приводящие к одной и той же функции  приводят к одной и той же величине
приводят к одной и той же величине  или, что эквивалентно,
или, что эквивалентно, 
Возвращаясь теперь к неравенству (2), получаем

Это неравенство и требовалось получить для выражения неопределенности. Для каждой принимаемой буквы неопределенность не может уменьшиться более чем на С — пропускную способность нового канала К. В частности, в блоковом коде с равновероятными сообщениями  . Если
. Если  то при окончании блока неопределенность должна еще оставаться по крайней мере равной
то при окончании блока неопределенность должна еще оставаться по крайней мере равной  так как вначале она равна
так как вначале она равна  и может уменьшаться самое большее лишь на величину С для каждой из
и может уменьшаться самое большее лишь на величину С для каждой из  букв.
букв.
Если, как показано в приложении, неопределенность на одну букву равна по крайней мере  то вероятность ошибки при декодировании ограничена следующим неравенством:
то вероятность ошибки при декодировании ограничена следующим неравенством:

Таким образом, в случае, когда делается попытка использовать код со скоростью  то вероятность ошибки оказывается отличной от нуля, какова бы ни была длина блока
то вероятность ошибки оказывается отличной от нуля, какова бы ни была длина блока  Этим заканчивается доказательство теоремы.
Этим заканчивается доказательство теоремы.
В качестве примера рассмотрим канал с двумя выходными буквами, произвольным числом а входных букв и произвольным числом  состояний. При этом новый канал К обладает двумя выходными буквами и
состояний. При этом новый канал К обладает двумя выходными буквами и  входными буквами. Однако в канале, у которого имеются ровно две выходные буквы, для того чтобы достичь пропускной способности, нужно, как показано в работе автора, использовать лишь две входные буквы; именно в канале К использовать только те две буквы, одна из которых обладает максимальной, а другая минимальной вероятностями перехода к одной из выходных букв. Эта пара может быть найдена следующим образом. Переходные вероятности для какой-либо буквы из алфавита канала К являются средними соответствующих переходных вероятностей для множества букв канала К, взятых по одной для каждого состояния. Ясно, что для того, чтобы максимизировать переходную вероятность к одной из выходных букв, требуется выбрать для каждого состояния букву с максимальной вероятностью перехода в эту выходную букву. Подобно этому, для минимизации нужно выбрать для каждого состояния букву с минимальной вероятностью перехода в указанную букву. При использовании лишь этих двух результирующих букв в канале К получим, что соответствующий канал даст желаемую пропускную способность. Формально, в случае, когда данный канал в состоянии
входными буквами. Однако в канале, у которого имеются ровно две выходные буквы, для того чтобы достичь пропускной способности, нужно, как показано в работе автора, использовать лишь две входные буквы; именно в канале К использовать только те две буквы, одна из которых обладает максимальной, а другая минимальной вероятностями перехода к одной из выходных букв. Эта пара может быть найдена следующим образом. Переходные вероятности для какой-либо буквы из алфавита канала К являются средними соответствующих переходных вероятностей для множества букв канала К, взятых по одной для каждого состояния. Ясно, что для того, чтобы максимизировать переходную вероятность к одной из выходных букв, требуется выбрать для каждого состояния букву с максимальной вероятностью перехода в эту выходную букву. Подобно этому, для минимизации нужно выбрать для каждого состояния букву с минимальной вероятностью перехода в указанную букву. При использовании лишь этих двух результирующих букв в канале К получим, что соответствующий канал даст желаемую пропускную способность. Формально, в случае, когда данный канал в состоянии  имеет вероятность
имеет вероятность  перехода входной буквы
перехода входной буквы  в выходную 1 и вероятность
в выходную 1 и вероятность  перехода к другой выходной букве 2, имеем
перехода к другой выходной букве 2, имеем

Канал К, у которого две входные буквы обладают переходными вероятностями  соответственно для двух
соответственно для двух
выходных букв, имеет пропускную способность, совпадающую с пропускной способностью первоначального канала К-
Рассмотрим еще следующий пример канала с тремя выходными буквами, двумя входными буквами и тремя состояниями. Предположим, что вероятность каждого из состояний равна V и матрицы вероятностей для этих трех состояний имеют вид

В этом случае в новом канале К имеются  входных букв. Они образуют следующую матрицу:
входных букв. Они образуют следующую матрицу:

Если имеются лишь три выходные буквы, то нужно использовать только три входные буквы, чтобы достичь пропускной способности канала. В рассматриваемом случае, как легко показать, можно (а фактически и необходимо) использовать первые три буквы. Из-за симметрии эти три буквы должны быть употреблены с равными вероятностями; результирующая пропускная способность канала в этом случае равна 
Нетрудно заметить, что если бы в исходном канале не имелось бы информации о состоянии, то канал работал бы подобно каналу с матрицей вероятностей перехода

Ясно, что такой канал обладает нулевой пропускной способностью. С другой стороны, если бы на приемном конце или и на приемном, и на передающем концах имелась бы информация о предыдущем состоянии, то обе входные буквы могли бы быть полностью различимы и пропускная способность равнялась бы 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- СИМВОЛИЧЕСКИЙ АНАЛИЗ РЕЛЕЙНЫХ И ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- 2. Параллельно-последовательные двухполюсные схемы. Основные определения и постулаты
- 3. Многополюсные и не параллельно-последовательные схемы
- Преобразование треугольника в звезду и звезды в ячейку
- Функция сопротивления не параллельно-последовательной схемы
- Системы уравнений
- Реле и переключатели специальных типов
- 4. Синтез схем
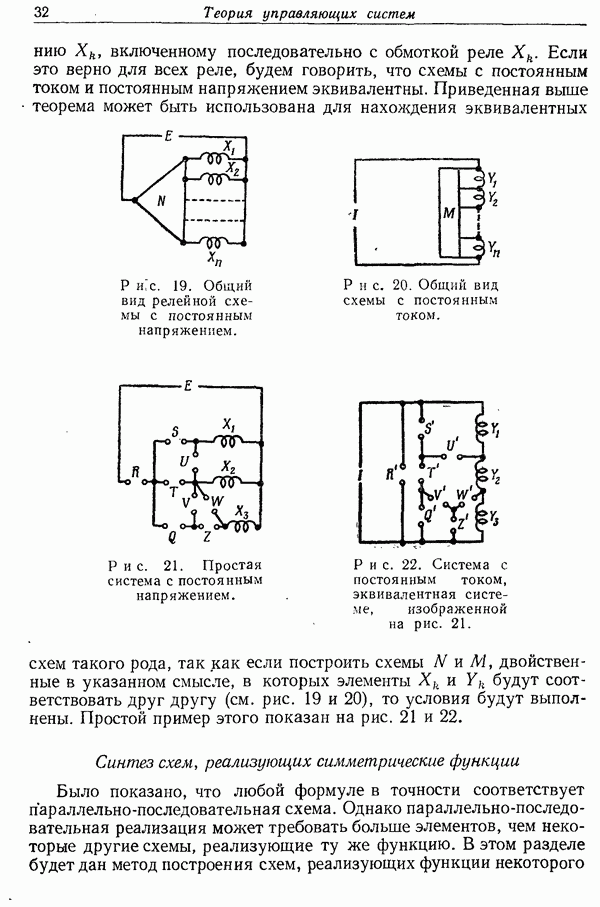
- Двойственные схемы
- Синтез схем, реализующих симметрические функции
- Составление уравнений по рабочим характеристикам
- 5. Примеры
- ЧИСЛО ДВУХПОЛЮСНЫХ ПАРАЛЛЕЛЬНО-ПОСЛЕДОВАТЕЛЬНЫХ СЕТЕЙ
- 1. Получение производящей функции
- 2. Численный подсчет
- 3. Асимптотическое поведение
- 4. Параллельно-последовательная реализация переключательных функций
- СИНТЕЗ ДВУХПОЛЮСНЫХ ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- 2. Основная теорема синтеза
- 3. Синтез схем для произвольных функций.
- Часть II. РАСПРЕДЕЛЕНИЕ НАГРУЗКИ МЕЖДУ РЕЛЕ
- 5. Разделительное дерево
- 6. Другие задачи распределения
- 7. Функция «мю»
- Часть III. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- 9. Частично симметрические функции
- ПРИМЕЧАНИЯ РЕДАКТОРА
- ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К ОБЪЕМУ ПАМЯТИ ТЕЛЕФОННОГО КОММУТАТОРА
- 2. Память, требуемая для S произвольных вызовов от N абонентов
- 3. Условие раздельной памяти
- 4. Связь с теорией информации
- НАДЕЖНЫЕ СХЕМЫ ИЗ НЕНАДЕЖНЫХ РЕЛЕ
- Идеализированные реле
- Общий метод повышения надежности
- Свойства функции h(p)
- Комбинация двух схем
- Оценки функции h'(p)
- Схемы заданной длины и ширины
- Оценки числа контактов в случае, когда реле уже достаточно надежны
- Сравнение с элементами фон Неймана
- Реле с неопределенным временем срабатывания
- Синтез надежных схем в целом
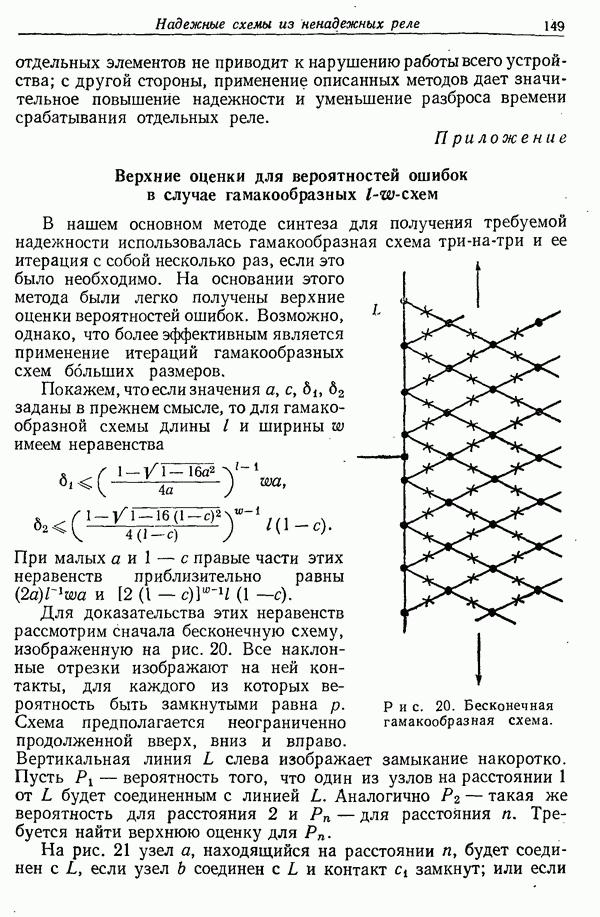
- Приложение. Верхние оценки для вероятностей ошибок в случае гамакообразных l-w-схем
- ИСПОЛЬЗОВАНИЕ МАШИНЫ ДЛЯ ПРОЕКТИРОВАНИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА И АВТОМАТЫ
- Машины Тьюринга
- Логические машины
- «Играющие машины»
- Обучаемые машины
- Самовоспроизводящиеся машины
- Обращение к читателю
- МАШИНА ДЛЯ ИГРЫ В ШАХМАТЫ
- СОСТАВЛЕНИЕ ПРОГРАММ ДЛЯ ИГРЫ В ШАХМАТЫ НА ВЫЧИСЛИТЕЛЬНОЙ МАШИНЕ
- 3. Приближенная оценочная функция
- 4. Стратегия, основанная на оценочной функции
- 5. Составление программы для универсальной вычислительной машины для реализации стратегии типа А
- 6. Улучшение стратегии
- 7. Изменения в игре и в стиле
- 8. Другой тип стратегии
- ПРИЛОЖЕНИЕ. ОЦЕНОЧНАЯ ФУНКЦИЯ ДЛЯ ШАХМАТ
- ИГРАЮЩИЕ МАШИНЫ
- СООБЩЕНИЕ О МАШИНЕ, РЕШАЮЩЕЙ ЛАБИРИНТНУЮ ЗАДАЧУ
- ВКЛАД ФОН НЕЙМАНА В ТЕОРИЮ АВТОМАТОВ
- МАТЕМАТИЧЕСКАЯ ТЕОРИЯ СВЯЗИ
- 1. ДИСКРЕТНЫЕ СИСТЕМЫ БЕЗ ШУМОВ
- 2. Дискретный источник сообщений
- 3. Последовательные приближения к английскому языку
- 4. Графическое представление марковского процесса
- 5. Эргодические и смешанные источники
- 6. Выбор, неопределенность и энтропия
- 7. Энтропия источника сообщений
- 8. Представление операций кодирования и декодирования
- 9. Основная теорема для канала без шума
- 10. Рассмотрение полученных результатов и примеры
- 11. Примеры
- II. ДИСКРЕТНЫЙ КАНАЛ С ШУМОМ
- 12. Надежность и пропускная способность канала
- 13. Основная теорема для дискретного канала с шумом
- 14. Рассмотрение полученных результатов
- 15. Пример дискретного канала и его пропускной способности
- 16. Пропускная способность канала в некоторых частных случаях
- 17. Пример эффективного кодирования
- III. ИНФОРМАЦИЯ ДЛЯ НЕПРЕРЫВНЫХ ВЕЛИЧИН
- 19. Ансамбли функций с ограниченной полосой частот
- 20. Энтропия непрерывного распределения
- 21. Энтропия ансамбля функций
- 22. Потеря энтропии в линейных фильтрах
- 23. Энтропия суммы двух ансамблей
- IV. НЕПРЕРЫВНЫЙ КАНАЛ
- 24. Пропускная способность непрерывного канала
- 25. Пропускная способность канала при ограничении средней мощности
- 26. Пропускная способность канала при ограничении пиковой мощности
- V. СКОРОСТЬ СОЗДАНИЯ СООБЩЕНИЙ ДЛЯ НЕПРЕРЫВНОГО ИСТОЧНИКА
- 28. Скорость создания сообщений источником при данной точности воспроизведения
- 29. Вычисление скорости создания сообщений
- Приложение 1. РОСТ ЧИСЛА БЛОКОВ СИМВОЛОВ ПРИ УСЛОВИЯХ, ОПИСЫВАЕМЫХ КОНЕЧНЫМ ЧИСЛОМ СОСТОЯНИЙ
- Приложение 2. ВЫВОД РАВЕНСТВА …
- Приложение 3. ТЕОРЕМА ОБ ЭРГОДИЧЕСКИХ ИСТОЧНИКАХ
- Приложение 4. МАКСИМИЗАЦИЯ СКОРОСТИ ДЛЯ СИСТЕМЫ ОГРАНИЧЕНИЯ
- Приложение 5
- Приложение 6
- Приложение 7
- ТЕОРИЯ СВЯЗИ В СЕКРЕТНЫХ СИСТЕМАХ
- Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ СИСТЕМ
- 3. Способы изображения систем
- 4. Примеры секретных систем
- 5. Оценка секретных систем
- 6. Алгебра секретных систем
- 7. Чистые и смешанные шифры
- 8. Подобные системы
- Часть II. ТЕОРЕТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 10. Совершенная секретность
- 11. Ненадежность
- 12. Свойства ненадежности
- 13. Ненадежность простой подстановки для языка с двухбуквенным алфавитом
- 14. Характеристика ненадежности для «случайного» шифра
- 15. Применение к стандартным шифрам
- 16. Правильность решения криптограммы
- 17. Идеальные секретные системы
- 18. Примеры идеальных секретных систем
- 19. Дополнительные замечания о ненадежности и избыточности
- 20. Распределение ненадежности
- Часть III. ПРАКТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 22. Общие замечания о решении криптограмм
- 23. Статистические методы
- 24. Метод вероятных слов
- 25. Перемешивание
- 26. Шифры типа …
- 27. Несовместимость требований к хорошим системам
- ПРИЛОЖЕНИЕ. Доказательство теоремы 3
- СОВРЕМЕННЫЕ ДОСТИЖЕНИЯ ТЕОРИИ СВЯЗИ
- Измерение информаций
- Кодирование информации
- Пропускная способность канала
- Идеальные и практические системы
- ПРИНЦИПЫ КОДОВО-ИМПУЛЬСНОЙ МОДУЛЯЦИИ
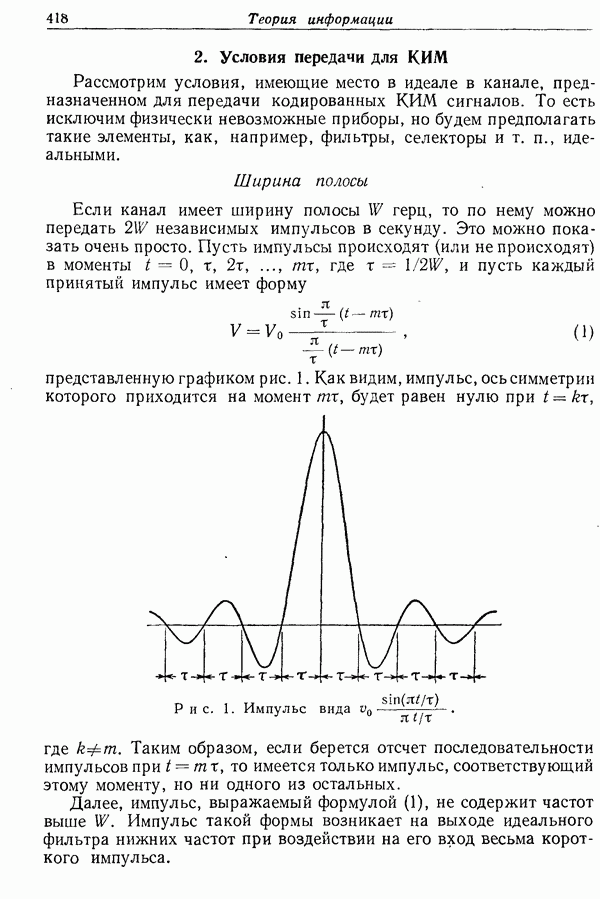
- 2. Условия передачи для КИМ
- 3. Действие системы КИМ
- 4. Сравнение КИМ и ЧМ
- 5. Заключение
- Приложение I
- Приложение II
- СВЯЗЬ ПРИ НАЛИЧИИ ШУМА
- 2. Теорема отсчетов
- 3. Геометрическое представление сигналов
- 4. Геометрическое представление сообщений
- 5. Геометрическое представление передатчика и приемника
- 6. Отображение пространства
- 7. Пропускная способность канала при наличии белого теплового шума
- 8. Обсуждение
- 9. Произвольный гауссовский шум
- 10. Пропускная способность канала при произвольном типе шума
- 11. Дискретные источники информации
- 12. Непрерывные источники информации
- НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ИНФОРМАЦИИ
- ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА С ШУМОМ ПРИ НУЛЕВОЙ ОШИБКЕ
- Пропускная способность канала при нулевой ошибке
- Пропускная способность для суммы и произведения каналов
- Каналы с обратной связью
- ГЕОМЕТРИЧЕСКИЙ ПОДХОД К ТЕОРИИ ПРОПУСКНОЙ СПОСОБНОСТИ. КАНАЛОВ СВЯЗИ
- КАНАЛЫ С ДОПОЛНИТЕЛЬНОЙ ИНФОРМАЦИЕЙ НА ПЕРЕДАТЧИКЕ
- Дискретный канал без памяти с дополнительной информацией о состоянии
- Приложение
- НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ТЕОРИИ КОДИРОВАНИЯ ДЛЯ КАНАЛОВ С ШУМАМИ
- Оценка вероятности ошибки в терминах производящей функции моментов
- Пропускная способность канала с конечным числом состояний, состояние которого вычислимо на обоих концах
- Пропускная способность канала с конечным числом состояний в случае, когда состояние вычислимо на передающем конце и не вычислимо на приемном конце
- ЗАМЕЧАНИЯ О ЧАСТИЧНОМ УПОРЯДОЧИВАНИИ КАНАЛОВ СВЯЗИ
- Дальнейшее обобщение и некоторые предположения
- ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ ОПТИМАЛЬНЫХ кодов В ГАУССОВСКОМ КАНАЛЕ
- 2. Сводка результатов
- 3. Нижняя граница, основанная на соображениях «сферической упаковки»
- 4. Верхняя граница, определяемая методом случайного кодирования
- 5. Формулы для скорости передачи R как функции угла конуса
- 6. Асимптотические формулы для …
- 7. Асимптотическое выражение для верхней границы при случайном кодировании
- 8. Жесткая верхняя граница
- 9. Жесткая нижняя граница
- 10. Поведение границ вблизи пропускной способности канала
- 11. Верхняя граница, полученная методом исчерпывания
- 12. Нижняя граница для гауссовского канала, получаемая исходя из минимального расстояния
- 13. Границы ошибок и другие условия, накладываемые на точки
- 14. Кривые для асимптотических границ
- ТЕОРЕМЫ КОДИРОВАНИЯ ДЛЯ ДИСКРЕТНОГО ИСТОЧНИКА ПРИ ЗАДАННОМ КРИТЕРИИ ТОЧНОСТИ
- Мера искажения отдельной буквы
- Несколько простых примеров
- Скорость при заданном искажении R(d)
- Выпуклость вниз кривой R(d)
- Нахождение R(d) в некоторых простых случаях
- Скорость передачи для произведения источников с мерой, являющейся суммой мер искажения
- Нижняя граница для искажения при заданной пропускной способности канала
- Теоремы кодирования при заданной мере искажения отдельной буквы
- Двойственность источника и канала
- Численные расчеты для некоторых простых каналов
- Обобщение на случаи непрерывных алфавитов
- Разностная мера искажения
- Определение меры локального искажения
- Функции Rn(d) и R(d) для меры локального искажения и эргодического источника
- Прямая теорема кодирования для меры локального искажения
- Обратная теорема кодирования
- Канал с памятью
- ДВУСТОРОННИЕ КАНАЛЫ СВЯЗИ
- 4. Средние взаимные скорости передачи информации
- 5. Распределение информации
- 6. Случайное кодирование для двусторонних каналов
- 7. Вероятность ошибки для ансамбля кодов
- 8. Выпуклая оболочка G как внутренняя граница области пропускной способности
- 9. Внешняя граница для области пропускной способности
- 10. Выпуклость вниз как функций от …
- 11. Приложения свойства выпуклости. Каналы с симметричной структурой
- 12. Характер области, выделяемой внешней границей
- 13. Пример, в котором внутренняя и внешняя границы различны
- 14. Достижимость внешней границы при зависимых источниках
- 15. Общий метод нахождения области пропускной способности двустороннего канала
- 16. Двусторонние каналы с памятью
- 17. Обобщение на каналы с Т концами
- БАНДВАГОН
- ПРЕДСКАЗАНИЕ И ЭНТРОПИЯ ПЕЧАТНОГО АНГЛИЙСКОГО ТЕКСТА
- 2. Вычисление энтропии по статистике английского языка
- 3. Предсказание английского текста
- 4. Идеальное N-граммное предсказывание
- 5. Граница для энтропии на основании частот предсказания
- 6. Результаты эксперимента для английского языка
- УПРОЩЕННЫЙ ВЫВОД ЛИНЕЙНОЙ ТЕОРИИ СГЛАЖИВАНИЯ И ПРЕДСКАЗАНИЯ ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ
- 3. Свойства линейных фильтров
- 4. Основное выражение для среднеквадратичной ошибки
- 5. Чистая проблема сглаживания
- 6. Проблема чистого предсказания
- 7. Предсказание при наличии шума
- 8. Обобщения
- 9. Обсуждение основных предположений
- МАТЕМАТИЧЕСКАЯ ТЕОРИЯ ДИФФЕРЕНЦИАЛЬНОГО АНАЛИЗАТОРА
- Основное условие разрешимости
- Реализация функций
- Системы уравнений
- Аппроксимация множителей с помощью передаточных чисел
- Автоматическое управление скоростью работы устройства
- О МАКСИМАЛЬНОМ ПОТОКЕ ЧЕРЕЗ СЕТЬ
- ТЕОРЕМА О РАСКРАСКЕ РЕБЕР ГРАФА
- УНИВЕРСАЛЬНАЯ МАШИНА ТЬЮРИНГА С ДВУМЯ ВНУТРЕННИМИ СОСТОЯНИЯМИ
- Невозможность создания универсальной машины Тьюринга с одним состоянием
- Моделирование машины Тьюринга с помощью только двух символов на ленте
- ВЫЧИСЛИМОСТЬ НА ВЕРОЯТНОСТНЫХ МАШИНАХ
- Приложение
- БИБЛИОГРАФИЯ РАБОТ ПО ШЕННОНОВСКОЙ ТЕОРИИ ОПТИМАЛЬНОГО КОДИРОВАНИЯ ИНФОРМАЦИИ