| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
3. Предсказание английского текста
В новом методе оценки энтропии английского языка используется тот факт, что каждый, говорящий на этом языке, обладает огромными трудно учитываемыми сведениями о статистике языка. Знакомство со словами, идиомами, стандартными оборотами и грамматикой позволяет выправить неправильные или пополнить пропущенные буквы при чтении корректур или дополнить неоконченную фразу в разговоре. Экспериментальная демонстрация степени возможности предсказания английского текста может быть следующей: выберем короткий отрывок текста, не известный отгадывающему. Затем предложим ему отгадать первую букву
отрывка. Если догадка оказалась правильной, то об этом сообщается отгадывающему и предлагается определить вторую букву. Если первая буква не отгадана правильно, то она также сообщается, и переходят к следующему отгадыванию. Это продолжается до конца текста. По ходу эксперимента отгадывающий выписывает правильный текст вплоть до последней буквы для использования его при отгадывании очередной буквы. Результат эксперимента такого рода приводится ниже. Пробел между словами считается дополнительной буквой, т. е. имеется  -буквенный алфавит. В строках, помеченных (1), написан исходный текст. В строках, помеченных (2), на месте угаданных букв проставляется черта, а в случае неправильного отгадывания выписывается буква исходного текста.
-буквенный алфавит. В строках, помеченных (1), написан исходный текст. В строках, помеченных (2), на месте угаданных букв проставляется черта, а в случае неправильного отгадывания выписывается буква исходного текста.

Из общего числа 129 букв 89 букв, или 69%, были отгаданы правильно. Ошибки, как и следовало ожидать, встречались наиболее часто в начале слов и слогов, где ход мысли может быть наиболее разнообразным. Можно было бы подумать, что вторые строки в (8), которые назовем приведенным текстом, содержат гораздо меньше информации, чем первые. В действительности же обе строки содержат одинаковую информацию в том смысле, что возможно, по крайней мере в принципе, определить первую строку по второй. Для выполнения этого тому, кто отгадывает текст, необходим двойник. Двойник (который если не биологически, то по крайней мере математически идентичен с оригиналом) должен будет отвечать точно так же, как отгадывающий, когда столкнется с аналогичной ситуацией. Предположим теперь, что имеется только приведенный текст (8). Двойнику предлагается отгадать исходный текст. В каждый момент нам известно, правильно выполнено отгадывание или нет, поскольку он отгадывает так же хорошо, как и его предшественник, и присутствие черточки в приведенном тексте соответствует правильному отгадыванию. Буквы, которые он отгадывает неправильно, также доступны, так что на каждом шагу ему может быть предоставлена в точности та информация, которая была получена первым отгадывающим.
От необходимости в двойнике в таком мыслимом эксперименте можно отказаться следующим приемом. Вообще говоря, хорошее предсказание не требует знания более чем  букв предшествующего текста, где
букв предшествующего текста, где  не очень велико. Имеется конечное число
не очень велико. Имеется конечное число
возможных последовательностей из  букв или
букв или  -грамм. Можно предложить кому-либо отгадать следующую букву в каждой возможной
-грамм. Можно предложить кому-либо отгадать следующую букву в каждой возможной  -грамме. Полный список этих предсказаний может быть затем использован как для получения приведенного текста, так и для осуществления обратного восстанавливающего процесса.
-грамме. Полный список этих предсказаний может быть затем использован как для получения приведенного текста, так и для осуществления обратного восстанавливающего процесса.
Для применения такого приема приведенный текст следует рассматривать как закодированную форму исходного, т. е. как результат пропускания текста чёрез обратимый преобразователь.

Рис. 2. Система связи, использующая приведенный текст.
В самом деле, система связи может быть построена таким образом, чтобы только приведенный текст передавался от одного пункта к другому. Для этого достаточно, как показано на рис. 2, системы с двумя одинаковыми предсказывающими устройствами.
Описанный эксперимент может быть обобщен для получения дальнейшей информации о возможности предсказания английского текста. Как и раньше, отгадывающему известен текст до текущего момента и ему предлагается отгадать следующую букву. В случае ошибки ему сообщается об этом и предлагается отгадывать снова. Так продолжается до тех пор, пока не будет найдена правильная буква. Типичный результат такого эксперимента показан ниже. В строках, обозначенных (1), выписан исходный текст, а цифры в строках, обозначенных (2), указывают, сколько отгадываний потребовалось на данную букву.

Из 102 букв 79 букв было отгадано с первого раза, 8 букв со второго, 3 буквы с третьего раза, четыре и пять угадываний понадобилось для трех букв и только восемь букв требовалось отгадывать более пяти раз. Результаты такого характера можно считать типичными при предсказывании хорошо умеющим отгадывать и при
работе с нормативным литературным английским текстом. Статьи из газеты, научные работы или поэзия требуют меньшего числа попыток.
Приведенный текст в этом случае также содержит ту же информацию, что и исходный. Опять, используя двойника, предлагаем ему на каждой стадии отгадывать текст столько раз, сколько единиц соответствует цифре в приведенном тексте, и таким путем обнаружить исходный текст. Для  того чтобы исключить субъективный элемент, можно просить отгадывающего указать для каждой
того чтобы исключить субъективный элемент, можно просить отгадывающего указать для каждой  -граммы текста наиболее вероятную букву, вторую по вероятности букву и т. д. Эта совокупность данных может служить как для предсказания, так и для отгадывания.
-граммы текста наиболее вероятную букву, вторую по вероятности букву и т. д. Эта совокупность данных может служить как для предсказания, так и для отгадывания.
Как и раньше, приведенный текст можно рассматривать как закодированный вариант исходного. Именно английский язык с алфавитом в 27 символов,  пробел, переведен на новый язык с алфавитом
пробел, переведен на новый язык с алфавитом  Перевод выполнен таким образом, что символ 1 имеет теперь наибольшую частоту. Символы 2, 3, 4 имеют последовательно все меньшие и меньшие частоты, и заключительные символы
Перевод выполнен таким образом, что символ 1 имеет теперь наибольшую частоту. Символы 2, 3, 4 имеют последовательно все меньшие и меньшие частоты, и заключительные символы  встречаются вообще очень редко. Таким образом, перевод в значительной степени упростил рассматриваемую статистическую структуру. Избыточность, которая проявлялась вначале в сложных зависимостях между группами букв, теперь свелась к значительной разнице между вероятностями новых, символов. Это, как будет видно позднее, явится основой для оценки энтропии с помощью таких экспериментов.
встречаются вообще очень редко. Таким образом, перевод в значительной степени упростил рассматриваемую статистическую структуру. Избыточность, которая проявлялась вначале в сложных зависимостях между группами букв, теперь свелась к значительной разнице между вероятностями новых, символов. Это, как будет видно позднее, явится основой для оценки энтропии с помощью таких экспериментов.
Для определения того, как возможность предсказания зависит от числа  предшествующих букв, известных отгадывающему, был выполнен более сложный эксперимент. Сотня выборок по 15 букв английского текста была выбрана случайным образом из книги. Отгадывающему было предложено отгадывать текст по одной букве в каждой выборке, как в предыдущем эксперименте. Таким образом, была получена сотня выборок, где отгадывающий знал
предшествующих букв, известных отгадывающему, был выполнен более сложный эксперимент. Сотня выборок по 15 букв английского текста была выбрана случайным образом из книги. Отгадывающему было предложено отгадывать текст по одной букве в каждой выборке, как в предыдущем эксперименте. Таким образом, была получена сотня выборок, где отгадывающий знал  предшествующих букв. Отгадывающему могут быть предоставлены все средства, которые он пожелает, например, различные статистические таблицы, однобуквенные, двухбуквенные и трехбуквенные таблицы, таблицы частот начальных букв в словах, сводка частот наиболее употребительных слов и любой словарь. Выборки для эксперимента были взяты из книги «Виргинец Джефферсон» Дюма Малона. Полученные результаты вместе с аналогичным экспериментом, когда отгадывающему были известны 100 букв, собраны в табл. 1. (см. стр. 678—679). Столбец соответствует числу известных предшествующих букв; номер строки указывает число отгадываний. На пересечении
предшествующих букв. Отгадывающему могут быть предоставлены все средства, которые он пожелает, например, различные статистические таблицы, однобуквенные, двухбуквенные и трехбуквенные таблицы, таблицы частот начальных букв в словах, сводка частот наиболее употребительных слов и любой словарь. Выборки для эксперимента были взяты из книги «Виргинец Джефферсон» Дюма Малона. Полученные результаты вместе с аналогичным экспериментом, когда отгадывающему были известны 100 букв, собраны в табл. 1. (см. стр. 678—679). Столбец соответствует числу известных предшествующих букв; номер строки указывает число отгадываний. На пересечении  столбца и 5-й строки стоит число раз, при которых опознавание правильной буквы произошло при
столбца и 5-й строки стоит число раз, при которых опознавание правильной буквы произошло при  отгадывании, когда известны предыдущие
отгадывании, когда известны предыдущие  букв.
букв.
Например, цифра 19 на пересечении  столбца и 2-й строки означает, что при известных пяти предшествующих буквах правильная буква была получена в девятнадцати случаях из ста при втором угадывании. Первые два столбца этой таблицы были получены не экспериментально, как описано выше, а были вычислены непосредственно с помощью известных частот отдельных букв и диграмм. Таким образом, если ни одна из предшествующих букв не задана, то наиболее вероятным символом является промежуток между словами (вероятность 0,182) в случае, если первое угадывание оказалось ошибочным, следующим должно быть Е (вероятность 0,107) и т. д. Эти вероятности суть частоты, с которыми правильные угадывания произойдут при первом, втором и т. д. эксперименте при наилучшем предсказании. Подобным же образом простое вычисление при помощи таблицы диграмм дает результаты для
столбца и 2-й строки означает, что при известных пяти предшествующих буквах правильная буква была получена в девятнадцати случаях из ста при втором угадывании. Первые два столбца этой таблицы были получены не экспериментально, как описано выше, а были вычислены непосредственно с помощью известных частот отдельных букв и диграмм. Таким образом, если ни одна из предшествующих букв не задана, то наиболее вероятным символом является промежуток между словами (вероятность 0,182) в случае, если первое угадывание оказалось ошибочным, следующим должно быть Е (вероятность 0,107) и т. д. Эти вероятности суть частоты, с которыми правильные угадывания произойдут при первом, втором и т. д. эксперименте при наилучшем предсказании. Подобным же образом простое вычисление при помощи таблицы диграмм дает результаты для  столбца. Поскольку частотные таблицы определены по весьма длинным выборкам из английского текста, то эти два столбца подчинены меньшим статистическим ошибкам, чем остальные.
столбца. Поскольку частотные таблицы определены по весьма длинным выборкам из английского текста, то эти два столбца подчинены меньшим статистическим ошибкам, чем остальные.
Далее будет показано, что предсказание действительно улучшается, если не учитывать статистических флуктуаций, зависящих от знания прошлого; так, это подтверждается большим количеством правильных угадываний и меньшим числом угадываний, требующих много проб.
Был проделан также один эксперимент с «обратным» предсказанием, когда приходилось угадывать букву, предшествующую уже известным. Хотя задача субъективно гораздо более трудная, но результаты были ненамного хуже. Так, для выборки в 101 букву из той же самой книги были получены следующие результаты:

Следует учесть, что  -граммная энтропия
-граммная энтропия  для обратного языка равна
для обратного языка равна  -граммной энтропии для прямого языка, что можно видеть из второго выражения в уравнении (1). Оба члена имеют одно и то же значение в прямом и обратном случаях.
-граммной энтропии для прямого языка, что можно видеть из второго выражения в уравнении (1). Оба члена имеют одно и то же значение в прямом и обратном случаях.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- СИМВОЛИЧЕСКИЙ АНАЛИЗ РЕЛЕЙНЫХ И ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- 2. Параллельно-последовательные двухполюсные схемы. Основные определения и постулаты
- 3. Многополюсные и не параллельно-последовательные схемы
- Преобразование треугольника в звезду и звезды в ячейку
- Функция сопротивления не параллельно-последовательной схемы
- Системы уравнений
- Реле и переключатели специальных типов
- 4. Синтез схем
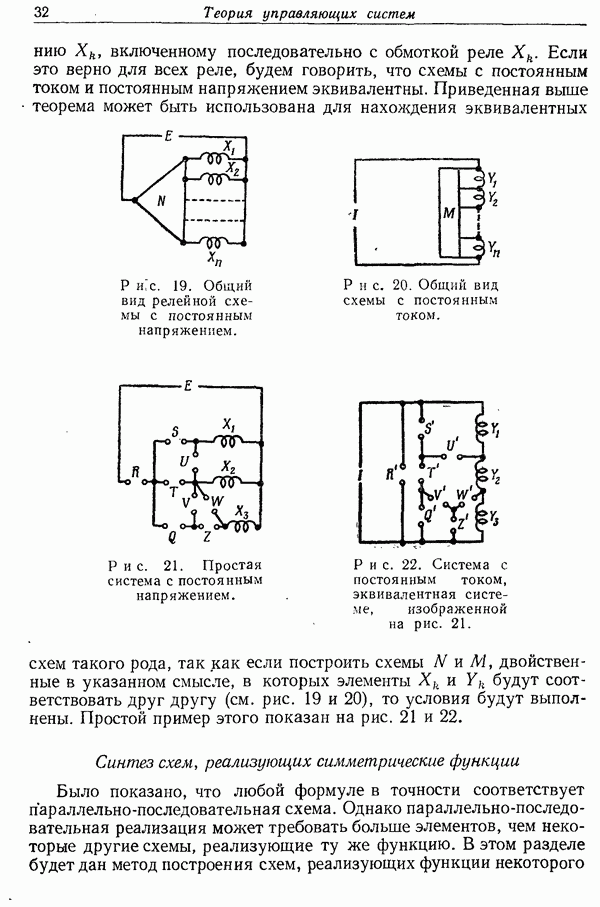
- Двойственные схемы
- Синтез схем, реализующих симметрические функции
- Составление уравнений по рабочим характеристикам
- 5. Примеры
- ЧИСЛО ДВУХПОЛЮСНЫХ ПАРАЛЛЕЛЬНО-ПОСЛЕДОВАТЕЛЬНЫХ СЕТЕЙ
- 1. Получение производящей функции
- 2. Численный подсчет
- 3. Асимптотическое поведение
- 4. Параллельно-последовательная реализация переключательных функций
- СИНТЕЗ ДВУХПОЛЮСНЫХ ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- 2. Основная теорема синтеза
- 3. Синтез схем для произвольных функций.
- Часть II. РАСПРЕДЕЛЕНИЕ НАГРУЗКИ МЕЖДУ РЕЛЕ
- 5. Разделительное дерево
- 6. Другие задачи распределения
- 7. Функция «мю»
- Часть III. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- 9. Частично симметрические функции
- ПРИМЕЧАНИЯ РЕДАКТОРА
- ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К ОБЪЕМУ ПАМЯТИ ТЕЛЕФОННОГО КОММУТАТОРА
- 2. Память, требуемая для S произвольных вызовов от N абонентов
- 3. Условие раздельной памяти
- 4. Связь с теорией информации
- НАДЕЖНЫЕ СХЕМЫ ИЗ НЕНАДЕЖНЫХ РЕЛЕ
- Идеализированные реле
- Общий метод повышения надежности
- Свойства функции h(p)
- Комбинация двух схем
- Оценки функции h'(p)
- Схемы заданной длины и ширины
- Оценки числа контактов в случае, когда реле уже достаточно надежны
- Сравнение с элементами фон Неймана
- Реле с неопределенным временем срабатывания
- Синтез надежных схем в целом
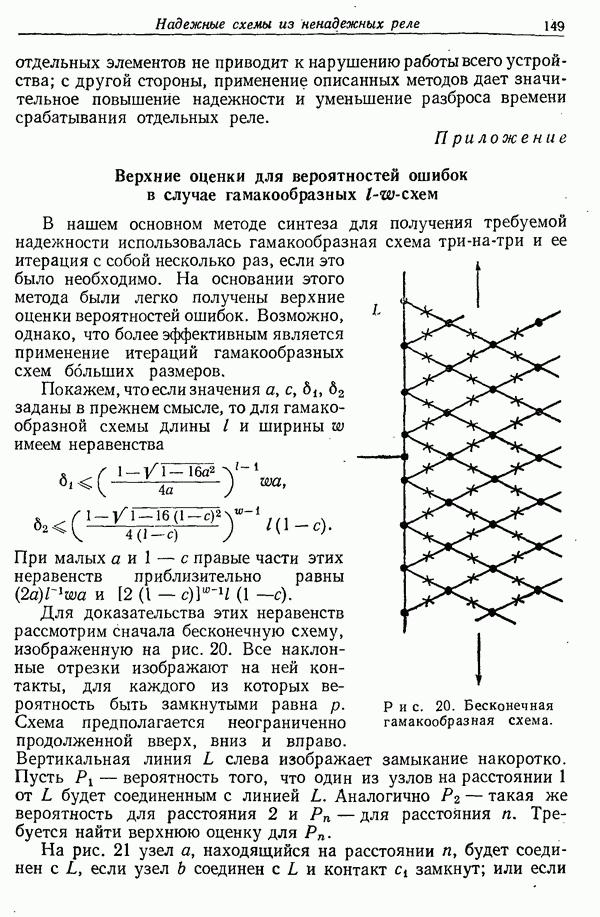
- Приложение. Верхние оценки для вероятностей ошибок в случае гамакообразных l-w-схем
- ИСПОЛЬЗОВАНИЕ МАШИНЫ ДЛЯ ПРОЕКТИРОВАНИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА И АВТОМАТЫ
- Машины Тьюринга
- Логические машины
- «Играющие машины»
- Обучаемые машины
- Самовоспроизводящиеся машины
- Обращение к читателю
- МАШИНА ДЛЯ ИГРЫ В ШАХМАТЫ
- СОСТАВЛЕНИЕ ПРОГРАММ ДЛЯ ИГРЫ В ШАХМАТЫ НА ВЫЧИСЛИТЕЛЬНОЙ МАШИНЕ
- 3. Приближенная оценочная функция
- 4. Стратегия, основанная на оценочной функции
- 5. Составление программы для универсальной вычислительной машины для реализации стратегии типа А
- 6. Улучшение стратегии
- 7. Изменения в игре и в стиле
- 8. Другой тип стратегии
- ПРИЛОЖЕНИЕ. ОЦЕНОЧНАЯ ФУНКЦИЯ ДЛЯ ШАХМАТ
- ИГРАЮЩИЕ МАШИНЫ
- СООБЩЕНИЕ О МАШИНЕ, РЕШАЮЩЕЙ ЛАБИРИНТНУЮ ЗАДАЧУ
- ВКЛАД ФОН НЕЙМАНА В ТЕОРИЮ АВТОМАТОВ
- МАТЕМАТИЧЕСКАЯ ТЕОРИЯ СВЯЗИ
- 1. ДИСКРЕТНЫЕ СИСТЕМЫ БЕЗ ШУМОВ
- 2. Дискретный источник сообщений
- 3. Последовательные приближения к английскому языку
- 4. Графическое представление марковского процесса
- 5. Эргодические и смешанные источники
- 6. Выбор, неопределенность и энтропия
- 7. Энтропия источника сообщений
- 8. Представление операций кодирования и декодирования
- 9. Основная теорема для канала без шума
- 10. Рассмотрение полученных результатов и примеры
- 11. Примеры
- II. ДИСКРЕТНЫЙ КАНАЛ С ШУМОМ
- 12. Надежность и пропускная способность канала
- 13. Основная теорема для дискретного канала с шумом
- 14. Рассмотрение полученных результатов
- 15. Пример дискретного канала и его пропускной способности
- 16. Пропускная способность канала в некоторых частных случаях
- 17. Пример эффективного кодирования
- III. ИНФОРМАЦИЯ ДЛЯ НЕПРЕРЫВНЫХ ВЕЛИЧИН
- 19. Ансамбли функций с ограниченной полосой частот
- 20. Энтропия непрерывного распределения
- 21. Энтропия ансамбля функций
- 22. Потеря энтропии в линейных фильтрах
- 23. Энтропия суммы двух ансамблей
- IV. НЕПРЕРЫВНЫЙ КАНАЛ
- 24. Пропускная способность непрерывного канала
- 25. Пропускная способность канала при ограничении средней мощности
- 26. Пропускная способность канала при ограничении пиковой мощности
- V. СКОРОСТЬ СОЗДАНИЯ СООБЩЕНИЙ ДЛЯ НЕПРЕРЫВНОГО ИСТОЧНИКА
- 28. Скорость создания сообщений источником при данной точности воспроизведения
- 29. Вычисление скорости создания сообщений
- Приложение 1. РОСТ ЧИСЛА БЛОКОВ СИМВОЛОВ ПРИ УСЛОВИЯХ, ОПИСЫВАЕМЫХ КОНЕЧНЫМ ЧИСЛОМ СОСТОЯНИЙ
- Приложение 2. ВЫВОД РАВЕНСТВА …
- Приложение 3. ТЕОРЕМА ОБ ЭРГОДИЧЕСКИХ ИСТОЧНИКАХ
- Приложение 4. МАКСИМИЗАЦИЯ СКОРОСТИ ДЛЯ СИСТЕМЫ ОГРАНИЧЕНИЯ
- Приложение 5
- Приложение 6
- Приложение 7
- ТЕОРИЯ СВЯЗИ В СЕКРЕТНЫХ СИСТЕМАХ
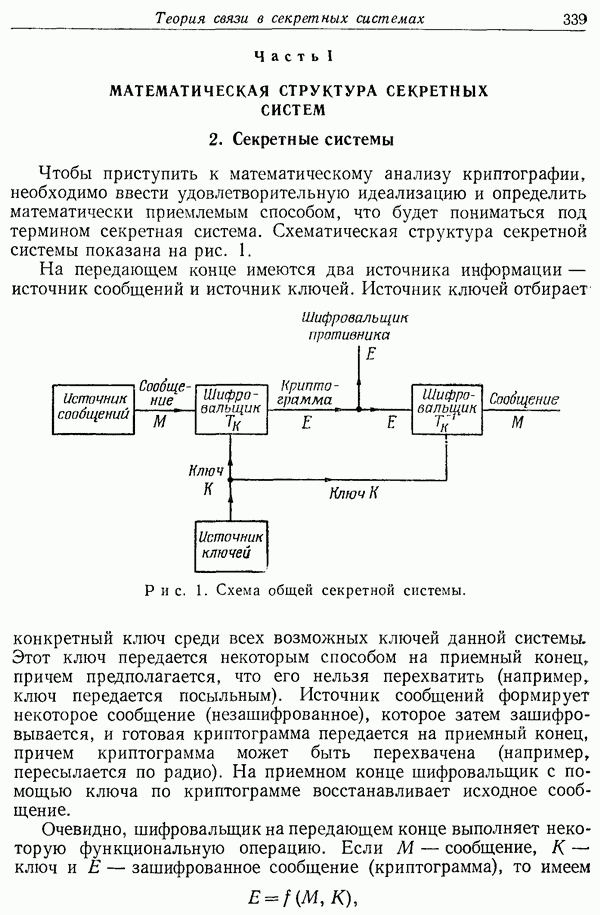
- Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ СИСТЕМ
- 3. Способы изображения систем
- 4. Примеры секретных систем
- 5. Оценка секретных систем
- 6. Алгебра секретных систем
- 7. Чистые и смешанные шифры
- 8. Подобные системы
- Часть II. ТЕОРЕТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 10. Совершенная секретность
- 11. Ненадежность
- 12. Свойства ненадежности
- 13. Ненадежность простой подстановки для языка с двухбуквенным алфавитом
- 14. Характеристика ненадежности для «случайного» шифра
- 15. Применение к стандартным шифрам
- 16. Правильность решения криптограммы
- 17. Идеальные секретные системы
- 18. Примеры идеальных секретных систем
- 19. Дополнительные замечания о ненадежности и избыточности
- 20. Распределение ненадежности
- Часть III. ПРАКТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 22. Общие замечания о решении криптограмм
- 23. Статистические методы
- 24. Метод вероятных слов
- 25. Перемешивание
- 26. Шифры типа …
- 27. Несовместимость требований к хорошим системам
- ПРИЛОЖЕНИЕ. Доказательство теоремы 3
- СОВРЕМЕННЫЕ ДОСТИЖЕНИЯ ТЕОРИИ СВЯЗИ
- Измерение информаций
- Кодирование информации
- Пропускная способность канала
- Идеальные и практические системы
- ПРИНЦИПЫ КОДОВО-ИМПУЛЬСНОЙ МОДУЛЯЦИИ
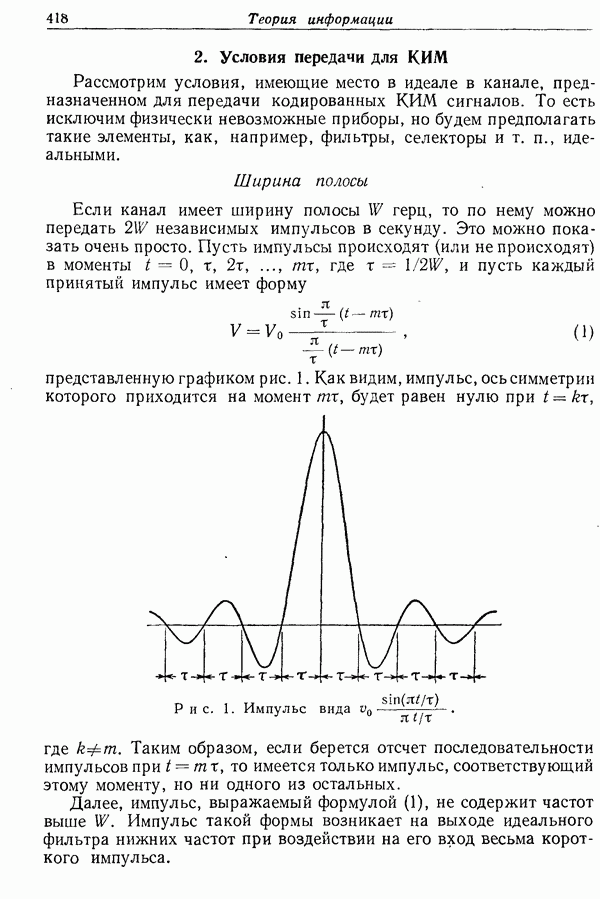
- 2. Условия передачи для КИМ
- 3. Действие системы КИМ
- 4. Сравнение КИМ и ЧМ
- 5. Заключение
- Приложение I
- Приложение II
- СВЯЗЬ ПРИ НАЛИЧИИ ШУМА
- 2. Теорема отсчетов
- 3. Геометрическое представление сигналов
- 4. Геометрическое представление сообщений
- 5. Геометрическое представление передатчика и приемника
- 6. Отображение пространства
- 7. Пропускная способность канала при наличии белого теплового шума
- 8. Обсуждение
- 9. Произвольный гауссовский шум
- 10. Пропускная способность канала при произвольном типе шума
- 11. Дискретные источники информации
- 12. Непрерывные источники информации
- НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ИНФОРМАЦИИ
- ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА С ШУМОМ ПРИ НУЛЕВОЙ ОШИБКЕ
- Пропускная способность канала при нулевой ошибке
- Пропускная способность для суммы и произведения каналов
- Каналы с обратной связью
- ГЕОМЕТРИЧЕСКИЙ ПОДХОД К ТЕОРИИ ПРОПУСКНОЙ СПОСОБНОСТИ. КАНАЛОВ СВЯЗИ
- КАНАЛЫ С ДОПОЛНИТЕЛЬНОЙ ИНФОРМАЦИЕЙ НА ПЕРЕДАТЧИКЕ
- Дискретный канал без памяти с дополнительной информацией о состоянии
- Приложение
- НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ТЕОРИИ КОДИРОВАНИЯ ДЛЯ КАНАЛОВ С ШУМАМИ
- Оценка вероятности ошибки в терминах производящей функции моментов
- Пропускная способность канала с конечным числом состояний, состояние которого вычислимо на обоих концах
- Пропускная способность канала с конечным числом состояний в случае, когда состояние вычислимо на передающем конце и не вычислимо на приемном конце
- ЗАМЕЧАНИЯ О ЧАСТИЧНОМ УПОРЯДОЧИВАНИИ КАНАЛОВ СВЯЗИ
- Дальнейшее обобщение и некоторые предположения
- ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ ОПТИМАЛЬНЫХ кодов В ГАУССОВСКОМ КАНАЛЕ
- 2. Сводка результатов
- 3. Нижняя граница, основанная на соображениях «сферической упаковки»
- 4. Верхняя граница, определяемая методом случайного кодирования
- 5. Формулы для скорости передачи R как функции угла конуса
- 6. Асимптотические формулы для …
- 7. Асимптотическое выражение для верхней границы при случайном кодировании
- 8. Жесткая верхняя граница
- 9. Жесткая нижняя граница
- 10. Поведение границ вблизи пропускной способности канала
- 11. Верхняя граница, полученная методом исчерпывания
- 12. Нижняя граница для гауссовского канала, получаемая исходя из минимального расстояния
- 13. Границы ошибок и другие условия, накладываемые на точки
- 14. Кривые для асимптотических границ
- ТЕОРЕМЫ КОДИРОВАНИЯ ДЛЯ ДИСКРЕТНОГО ИСТОЧНИКА ПРИ ЗАДАННОМ КРИТЕРИИ ТОЧНОСТИ
- Мера искажения отдельной буквы
- Несколько простых примеров
- Скорость при заданном искажении R(d)
- Выпуклость вниз кривой R(d)
- Нахождение R(d) в некоторых простых случаях
- Скорость передачи для произведения источников с мерой, являющейся суммой мер искажения
- Нижняя граница для искажения при заданной пропускной способности канала
- Теоремы кодирования при заданной мере искажения отдельной буквы
- Двойственность источника и канала
- Численные расчеты для некоторых простых каналов
- Обобщение на случаи непрерывных алфавитов
- Разностная мера искажения
- Определение меры локального искажения
- Функции Rn(d) и R(d) для меры локального искажения и эргодического источника
- Прямая теорема кодирования для меры локального искажения
- Обратная теорема кодирования
- Канал с памятью
- ДВУСТОРОННИЕ КАНАЛЫ СВЯЗИ
- 4. Средние взаимные скорости передачи информации
- 5. Распределение информации
- 6. Случайное кодирование для двусторонних каналов
- 7. Вероятность ошибки для ансамбля кодов
- 8. Выпуклая оболочка G как внутренняя граница области пропускной способности
- 9. Внешняя граница для области пропускной способности
- 10. Выпуклость вниз как функций от …
- 11. Приложения свойства выпуклости. Каналы с симметричной структурой
- 12. Характер области, выделяемой внешней границей
- 13. Пример, в котором внутренняя и внешняя границы различны
- 14. Достижимость внешней границы при зависимых источниках
- 15. Общий метод нахождения области пропускной способности двустороннего канала
- 16. Двусторонние каналы с памятью
- 17. Обобщение на каналы с Т концами
- БАНДВАГОН
- ПРЕДСКАЗАНИЕ И ЭНТРОПИЯ ПЕЧАТНОГО АНГЛИЙСКОГО ТЕКСТА
- 2. Вычисление энтропии по статистике английского языка
- 3. Предсказание английского текста
- 4. Идеальное N-граммное предсказывание
- 5. Граница для энтропии на основании частот предсказания
- 6. Результаты эксперимента для английского языка
- УПРОЩЕННЫЙ ВЫВОД ЛИНЕЙНОЙ ТЕОРИИ СГЛАЖИВАНИЯ И ПРЕДСКАЗАНИЯ ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ
- 3. Свойства линейных фильтров
- 4. Основное выражение для среднеквадратичной ошибки
- 5. Чистая проблема сглаживания
- 6. Проблема чистого предсказания
- 7. Предсказание при наличии шума
- 8. Обобщения
- 9. Обсуждение основных предположений
- МАТЕМАТИЧЕСКАЯ ТЕОРИЯ ДИФФЕРЕНЦИАЛЬНОГО АНАЛИЗАТОРА
- Основное условие разрешимости
- Реализация функций
- Системы уравнений
- Аппроксимация множителей с помощью передаточных чисел
- Автоматическое управление скоростью работы устройства
- О МАКСИМАЛЬНОМ ПОТОКЕ ЧЕРЕЗ СЕТЬ
- ТЕОРЕМА О РАСКРАСКЕ РЕБЕР ГРАФА
- УНИВЕРСАЛЬНАЯ МАШИНА ТЬЮРИНГА С ДВУМЯ ВНУТРЕННИМИ СОСТОЯНИЯМИ
- Невозможность создания универсальной машины Тьюринга с одним состоянием
- Моделирование машины Тьюринга с помощью только двух символов на ленте
- ВЫЧИСЛИМОСТЬ НА ВЕРОЯТНОСТНЫХ МАШИНАХ
- Приложение
- БИБЛИОГРАФИЯ РАБОТ ПО ШЕННОНОВСКОЙ ТЕОРИИ ОПТИМАЛЬНОГО КОДИРОВАНИЯ ИНФОРМАЦИИ