| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5. Составление программы для универсальной вычислительной машины для реализации стратегии типа А
Пусть имеется универсальная цифровая машина, изображенная схематично на рис. 3 и обладающая свойствами.

Рис. 3.
1) Имеется большая внутренняя память для хранения чисел. Она разделена на некоторое число ячеек, каждая из которых способна содержать, скажем, десятиразрядное число. Каждой ячейке присвоен адрес в памяти.
2) Машина имеет арифметическое устройство, которое может выполнять элементарные операции сложения, умножения и т. д.
3) Вычислительная машина работает, повинуясь программе. Программа состоит из последовательности элементарных команд. Обычная команда имеет вид:

Это означает: выбрать содержимое ячеек 372 и 451, сложить эти числа и записать их сумму в ячейку 133.
Другой тип команд содержит в себе выбор, например,

По этой команде машина сравнивает содержимое ячеек 291 и 118. Если первое число больше второго, машина выполняет следующую по порядку команду программы, если нет, то следующей выполняется команда из ячейки 345. Этот тип команд дает возможность машине сделать выбор из двух возможностей в зависимости от предыдущих результатов. Будем предполагать, что при помощи команд можно переносить числа из ячейки в ячейку, производить арифметические операции и осуществлять выбор (в только что указанном смысле).
Наша задача состоит в представлении шахматной игры в виде чисел и операций над числами и в записи стратегии в виде последовательности команд. Не приводя детали, опишем в общих чертах программы. Ясно, что конечная программа должна быть записана в виде команд.
Эта, так сказать, прокрустова задача представления шахмат в машине, предназначенной для выполнения математических вычислений, вызвана экономическими соображениями. Лучше всего было бы построить специальную вычислительную машину для шахмат, содержащую вместо арифметического устройства «шахматное устройство», специально сконструированное для выполнения простых шахматных вычислений. Несмотря на то что при этом, несомненно, будет достигнуто большое увеличение скорости выполнения операции, стоимость такой вычислительной машины будет так высока, что ее создание окажется невозможным. Предполагается все же провести ряд экспериментов на одной из цифровых вычислительных машин, которая сейчас конструируется.
Игра в шахматы может быть разделена на три фазы: дебют, середину и окончание. На разных фазах приложимы различные принципы игры. В дебюте, который обычно заканчивается в течение примерно десяти ходов, главной целью является развитие фигур для занятия хороших позиций. В середине игры превалируют тактические удары и комбинации. К концу этой фазы обычно большинство фигур разменивается, остаются только короли, пешки и, может быть, одна или две фигуры с каждой стороны. Эндшпиль в основном связан с пешечными превращениями, где становится важным точное определение таких возможностей, как цугцванг, пат и т. д.
Ясно, что при таком разнообразии стратегических задач на различных стадиях игры должны быть использованы различные программы. Будем в основном касаться середины игры и совсем не будем рассматривать окончания. Не видно, однако, причин, по которым не могла бы быть построена и достаточно хорошо запрограммирована стратегия окончания игры.
Поле на шахматной доске может быть занято тринадцатью различными способами: либо оно пусто (0), либо на нем стоит одна из шести возможных белых фигур 
 либо одна из шести черных фигур
либо одна из шести черных фигур  Таким образом, состояние поля можно охарактеризовать приписыванием ему целого числа
Таким образом, состояние поля можно охарактеризовать приписыванием ему целого числа  поля можно пронумеровать так, как показано на рис. 4. Положение всех фигур тогда задается в виде последовательности 64 чисел, каждое из которых находится между —6 и
поля можно пронумеровать так, как показано на рис. 4. Положение всех фигур тогда задается в виде последовательности 64 чисел, каждое из которых находится между —6 и  Для такого представления достаточно всего 256 двоичных разрядов.
Для такого представления достаточно всего 256 двоичных разрядов.

Рис. 4.
Обозначения фигур

Хотя это кодирование не является оптимальным, оно достаточно удобно для вычислений. Еще одно число X будет иметь значение  или —1 в зависимости оттого, принадлежит ход белым или черным соответственно. Затем необходимо добавить данные, относящиеся к возможности рокировки (двигались ли белые или черные короли и ладьи), а также к взятиям на проходе (т. е. описание последнего
или —1 в зависимости оттого, принадлежит ход белым или черным соответственно. Затем необходимо добавить данные, относящиеся к возможности рокировки (двигались ли белые или черные короли и ладьи), а также к взятиям на проходе (т. е. описание последнего
кода). Однако здесь эта информация опущена. Во введенных обозначениях начальная шахматная позиция имеет вид

Любой ход (кроме рокировки и превращения пешки) можно описать указанием того, с какого поля и на какое переставляется фигура. Всего на доске 64 поля, следовательно, достаточно 6 двоичных разрядов для указания одного поля и всего 12 двоичных разрядов нужно для описания хода. Таким образом, первый ход  записывается в виде 1,4; 3,4. Чтобы закодировать превращение пешки, необходимо добавить 3 двоичных разряда для указания фигуры, в которую она превращается. Рокировку можно определить по движению короля (это единственный случай, когда король может двинуться сразу на два шага). Всякий ход, следовательно, можно задать выражением
записывается в виде 1,4; 3,4. Чтобы закодировать превращение пешки, необходимо добавить 3 двоичных разряда для указания фигуры, в которую она превращается. Рокировку можно определить по движению короля (это единственный случай, когда король может двинуться сразу на два шага). Всякий ход, следовательно, можно задать выражением  , где
, где  обозначают поля, а с указывает фигуру в случае превращения пешки.
обозначают поля, а с указывает фигуру в случае превращения пешки.
Полная программа для стратегии типа А состоит из девяти программ, которые обозначим  и основной программы
и основной программы  Основные функции этих программ следующие.
Основные функции этих программ следующие.
 — выполняет ход
— выполняет ход  в позиции Р, определяя новую позицию.
в позиции Р, определяя новую позицию.
 — составляет список возможных ходов пешек с поля
— составляет список возможных ходов пешек с поля  в позиции Р.
в позиции Р.
 — составляют аналогичные списки для других фигур: коней, слонов, ладей, ферзей и короля.
— составляют аналогичные списки для других фигур: коней, слонов, ладей, ферзей и короля.
 — составляет список всех возможных ходов в данной позиции.
— составляет список всех возможных ходов в данной позиции.
 — вычисляет оценочную функцию
— вычисляет оценочную функцию  для данной позиции Р.
для данной позиции Р.
 — управляющая программа; выполняет вычисления, связанные с выбором максимумов и минимумов для определения искомого хода.
— управляющая программа; выполняет вычисления, связанные с выбором максимумов и минимумов для определения искомого хода.
Имея данную позицию Р и ход  во внутренней памяти, машина может найти следующую позицию, выполняя программу
во внутренней памяти, машина может найти следующую позицию, выполняя программу 
1) В памяти машины отыскивается поле а позиции Р.
2) Число х в этом квадрате заменяется на 0 (пустой квадрат).
3) а) Если  и первая координата а равна 6 (белая пешка достигает поля превращения) или если
и первая координата а равна 6 (белая пешка достигает поля превращения) или если  и первая координата а равна 1 (черная пешка достигает поля превращения), то в поле
и первая координата а равна 1 (черная пешка достигает поля превращения), то в поле  записывается число с (заменяя то число, которое было там записано).
записывается число с (заменяя то число, которое было там записано).
б) Если  (короткая рокировка белых), то в поля
(короткая рокировка белых), то в поля  записывается 0, а в поля 06 и 05 - числа 6 и 4 соответственно. Аналогично делается в случае
записывается 0, а в поля 06 и 05 - числа 6 и 4 соответственно. Аналогично делается в случае  (длинная рокировка белых) и
(длинная рокировка белых) и  (короткая или длинная рокировка черных).
(короткая или длинная рокировка черных).
в) Во всех остальных случаях в поле  записывается х.
записывается х.
4) Изменяется знак К.
Для фигуры каждого типа имеется программа, определяющая ее возможные ходы. Типичным примером является программа  для определения возможных ходов слона, которую кратко можно описать так. Пусть
для определения возможных ходов слона, которую кратко можно описать так. Пусть  координаты поля, на котором стоит слон.
координаты поля, на котором стоит слон.
1) Вычислим  и посмотрим содержимое «этого поля в позиции Р.
и посмотрим содержимое «этого поля в позиции Р.
2) Если  (пустое поле), внесем в список ход
(пустое поле), внесем в список ход  и вернемся в начало, поставив
и вернемся в начало, поставив  вместо
вместо  Если
Если  — положительно (наша фигура в поле), перейдем к 3). Если
— положительно (наша фигура в поле), перейдем к 3). Если  — отрицательно (в поле фигура противника), внесем в список ход и перейдем к 3). Если поля не существует, перейдем к 3).
— отрицательно (в поле фигура противника), внесем в список ход и перейдем к 3). Если поля не существует, перейдем к 3).
3) Вычислим  и проведем аналогичные рассмотрения.
и проведем аналогичные рассмотрения.
4) Аналогично с 
5) Аналогично с 
По такой программе составляется список возможных ходов слона в позиции Р. Подобные программы составят списки возможных ходов для любых других фигур. При этом имеются значительные возможности для упрощения этих программ, например программа  для ферзя может быть комбинацией программ
для ферзя может быть комбинацией программ  для слона и
для слона и  для ладьи.
для ладьи.
Используя программы для фигур  и логическую программу
и логическую программу  машина может составить список всех возможных ходов в любой данной позиции Р. Управляющая программа
машина может составить список всех возможных ходов в любой данной позиции Р. Управляющая программа  коротко может быть описана так (опуская детали).
коротко может быть описана так (опуская детали).
1) Обращаемся к полю (1,1) и определяем его содержимое х.
2) Если  положительно, обращаемся к соответствующей программе
положительно, обращаемся к соответствующей программе  и по окончании ее работы возвращаемся к 1), прибавив 1 к номеру поля. Если
и по окончании ее работы возвращаемся к 1), прибавив 1 к номеру поля. Если  есть нуль или отрицательно, возвращаемся к 1), прибавив 1 к номеру поля.
есть нуль или отрицательно, возвращаемся к 1), прибавив 1 к номеру поля.
3) Проверяем, допустим ли каждый из выписанных ходов, и выбрасываем недопустимые ходы. Это делается путем выполнения каждого хода в позиции Р (по программе  и проверкой, находится ли король под шахом или нет.
и проверкой, находится ли король под шахом или нет.
Машина может играть в шахматы, пользуясь только программами  (т. е. соблюдая правила игры и делая каждый раз просто случайно выбранный допустимый ход). Уровень игры по
(т. е. соблюдая правила игры и делая каждый раз просто случайно выбранный допустимый ход). Уровень игры по
такой стратегии очень низок. Автор сыграл несколько игр против такой случайной стратегии и обычно делал противнику мат в четыре-пять ходов. Следующая партия иллюстрирует полную бесцельность игры по такой стратегии:

Теперь вернемся к стратегии, основанной на оценочной функции  Программа
Программа  производит оценку позиции согласно значению
производит оценку позиции согласно значению  Очевидно, это можно сделать, просматривая поля и суммируя указанные в оценочной функции члены. Нетрудно учесть такие факторы, как сдвоенные пешки и т. д.
Очевидно, это можно сделать, просматривая поля и суммируя указанные в оценочной функции члены. Нетрудно учесть такие факторы, как сдвоенные пешки и т. д.
Последняя управляющая программа  необходима для того, чтобы выбрать ход в соответствии с минимаксным процессом, описанным выше. В случае стратегии, учитывающей по одному ходу с каждой стороны,
необходима для того, чтобы выбрать ход в соответствии с минимаксным процессом, описанным выше. В случае стратегии, учитывающей по одному ходу с каждой стороны,  работает следующим образом:
работает следующим образом:
1) Составляет список допустимых ходов (используя  в данной позиции.
в данной позиции.
2) Делает первый ход в списке по программе  получая позицию
получая позицию 
3) Составляет список ходов черных в позиции 
4) Делает первый ход за черных, получает позицию  и оценивает ее по
и оценивает ее по 
5) Делает второй ход за черных и оценивает полученную позицию.
6) Сравнивает оценки и выбрасывает ход с меньшей оценкой (т. е. остается лучшая оценка за черных).
7) Выполняет для третьего хода сравнение с оставшейся величиной и т. д.
8) Когда ходы черных исчерпаны, будет оставлен один ход с его оценкой. Процесс затем повторяется для второго хода белых.
9) Конечные оценки этих двух вычислений сравниваются, и оставляется тот из ходов белых (вместе с соответствующей оценкой), у которого оценочная функция больше.
10) Этот процесс повторяется для всех ходов белых и выбирается лучший (он остается после перебора всех возможных ходов белых). Это и есть тот ход, который надо сделать.
Эти программы в высокой степени цикличны, следовательно, если они хорошо составлены, не должны занимать много места в памяти машины.
Можно оценить объем памяти для записи позиций и промежуточных результатов, когда просматриваются все варианты на три хода вперед (с каждой стороны). Вероятно, должны запоминаться три позиции: начальная позиция, последняя позиция (которая теперь оценивается) и предшествующая ей. Это потребует около 800 двоичных разрядов. Кроме того, нужно помнить пять списков ходов, каждый из которых требует около  двоичных разрядов, а все они потребуют 1800 двоичных разрядов. Наконец, чтобы сделать выбор и оценку в необходимых вычислениях, требуется около 200 двоичных разрядов. Значит, всего потребуется порядка 3000 двоичных разрядов.
двоичных разрядов, а все они потребуют 1800 двоичных разрядов. Наконец, чтобы сделать выбор и оценку в необходимых вычислениях, требуется около 200 двоичных разрядов. Значит, всего потребуется порядка 3000 двоичных разрядов.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- СИМВОЛИЧЕСКИЙ АНАЛИЗ РЕЛЕЙНЫХ И ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- 2. Параллельно-последовательные двухполюсные схемы. Основные определения и постулаты
- 3. Многополюсные и не параллельно-последовательные схемы
- Преобразование треугольника в звезду и звезды в ячейку
- Функция сопротивления не параллельно-последовательной схемы
- Системы уравнений
- Реле и переключатели специальных типов
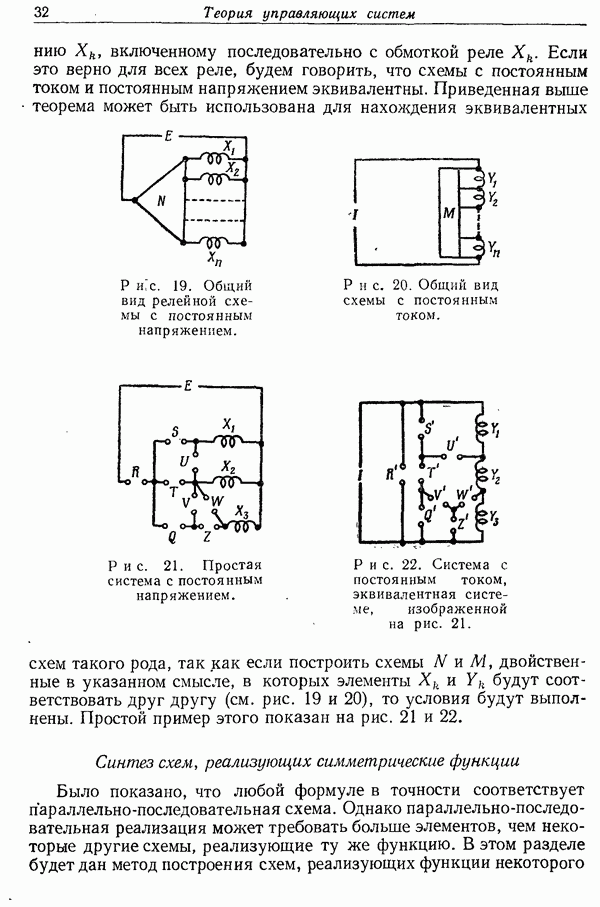
- 4. Синтез схем
- Двойственные схемы
- Синтез схем, реализующих симметрические функции
- Составление уравнений по рабочим характеристикам
- 5. Примеры
- ЧИСЛО ДВУХПОЛЮСНЫХ ПАРАЛЛЕЛЬНО-ПОСЛЕДОВАТЕЛЬНЫХ СЕТЕЙ
- 1. Получение производящей функции
- 2. Численный подсчет
- 3. Асимптотическое поведение
- 4. Параллельно-последовательная реализация переключательных функций
- СИНТЕЗ ДВУХПОЛЮСНЫХ ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- 2. Основная теорема синтеза
- 3. Синтез схем для произвольных функций.
- Часть II. РАСПРЕДЕЛЕНИЕ НАГРУЗКИ МЕЖДУ РЕЛЕ
- 5. Разделительное дерево
- 6. Другие задачи распределения
- 7. Функция «мю»
- Часть III. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- 9. Частично симметрические функции
- ПРИМЕЧАНИЯ РЕДАКТОРА
- ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К ОБЪЕМУ ПАМЯТИ ТЕЛЕФОННОГО КОММУТАТОРА
- 2. Память, требуемая для S произвольных вызовов от N абонентов
- 3. Условие раздельной памяти
- 4. Связь с теорией информации
- НАДЕЖНЫЕ СХЕМЫ ИЗ НЕНАДЕЖНЫХ РЕЛЕ
- Идеализированные реле
- Общий метод повышения надежности
- Свойства функции h(p)
- Комбинация двух схем
- Оценки функции h'(p)
- Схемы заданной длины и ширины
- Оценки числа контактов в случае, когда реле уже достаточно надежны
- Сравнение с элементами фон Неймана
- Реле с неопределенным временем срабатывания
- Синтез надежных схем в целом
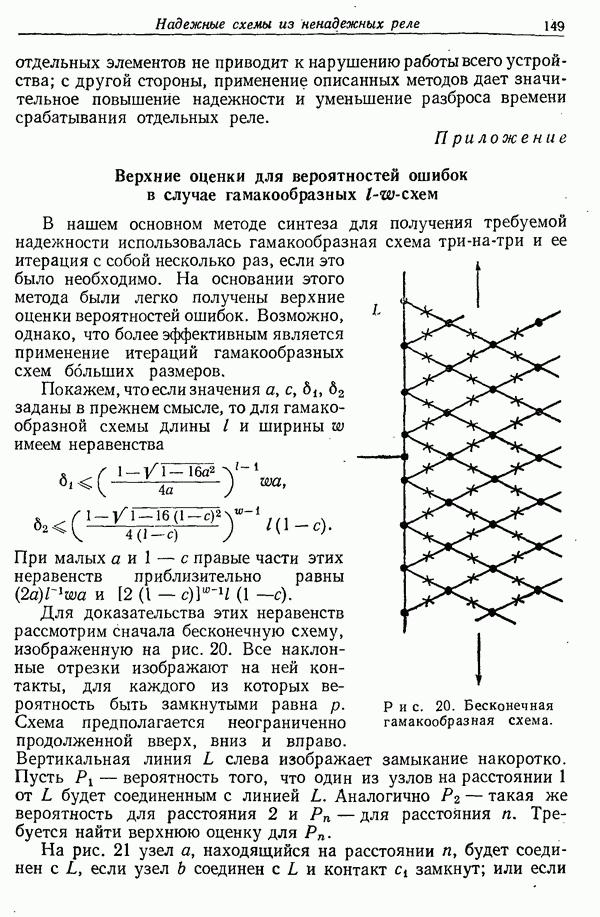
- Приложение. Верхние оценки для вероятностей ошибок в случае гамакообразных l-w-схем
- ИСПОЛЬЗОВАНИЕ МАШИНЫ ДЛЯ ПРОЕКТИРОВАНИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА И АВТОМАТЫ
- Машины Тьюринга
- Логические машины
- «Играющие машины»
- Обучаемые машины
- Самовоспроизводящиеся машины
- Обращение к читателю
- МАШИНА ДЛЯ ИГРЫ В ШАХМАТЫ
- СОСТАВЛЕНИЕ ПРОГРАММ ДЛЯ ИГРЫ В ШАХМАТЫ НА ВЫЧИСЛИТЕЛЬНОЙ МАШИНЕ
- 3. Приближенная оценочная функция
- 4. Стратегия, основанная на оценочной функции
- 5. Составление программы для универсальной вычислительной машины для реализации стратегии типа А
- 6. Улучшение стратегии
- 7. Изменения в игре и в стиле
- 8. Другой тип стратегии
- ПРИЛОЖЕНИЕ. ОЦЕНОЧНАЯ ФУНКЦИЯ ДЛЯ ШАХМАТ
- ИГРАЮЩИЕ МАШИНЫ
- СООБЩЕНИЕ О МАШИНЕ, РЕШАЮЩЕЙ ЛАБИРИНТНУЮ ЗАДАЧУ
- ВКЛАД ФОН НЕЙМАНА В ТЕОРИЮ АВТОМАТОВ
- МАТЕМАТИЧЕСКАЯ ТЕОРИЯ СВЯЗИ
- 1. ДИСКРЕТНЫЕ СИСТЕМЫ БЕЗ ШУМОВ
- 2. Дискретный источник сообщений
- 3. Последовательные приближения к английскому языку
- 4. Графическое представление марковского процесса
- 5. Эргодические и смешанные источники
- 6. Выбор, неопределенность и энтропия
- 7. Энтропия источника сообщений
- 8. Представление операций кодирования и декодирования
- 9. Основная теорема для канала без шума
- 10. Рассмотрение полученных результатов и примеры
- 11. Примеры
- II. ДИСКРЕТНЫЙ КАНАЛ С ШУМОМ
- 12. Надежность и пропускная способность канала
- 13. Основная теорема для дискретного канала с шумом
- 14. Рассмотрение полученных результатов
- 15. Пример дискретного канала и его пропускной способности
- 16. Пропускная способность канала в некоторых частных случаях
- 17. Пример эффективного кодирования
- III. ИНФОРМАЦИЯ ДЛЯ НЕПРЕРЫВНЫХ ВЕЛИЧИН
- 19. Ансамбли функций с ограниченной полосой частот
- 20. Энтропия непрерывного распределения
- 21. Энтропия ансамбля функций
- 22. Потеря энтропии в линейных фильтрах
- 23. Энтропия суммы двух ансамблей
- IV. НЕПРЕРЫВНЫЙ КАНАЛ
- 24. Пропускная способность непрерывного канала
- 25. Пропускная способность канала при ограничении средней мощности
- 26. Пропускная способность канала при ограничении пиковой мощности
- V. СКОРОСТЬ СОЗДАНИЯ СООБЩЕНИЙ ДЛЯ НЕПРЕРЫВНОГО ИСТОЧНИКА
- 28. Скорость создания сообщений источником при данной точности воспроизведения
- 29. Вычисление скорости создания сообщений
- Приложение 1. РОСТ ЧИСЛА БЛОКОВ СИМВОЛОВ ПРИ УСЛОВИЯХ, ОПИСЫВАЕМЫХ КОНЕЧНЫМ ЧИСЛОМ СОСТОЯНИЙ
- Приложение 2. ВЫВОД РАВЕНСТВА …
- Приложение 3. ТЕОРЕМА ОБ ЭРГОДИЧЕСКИХ ИСТОЧНИКАХ
- Приложение 4. МАКСИМИЗАЦИЯ СКОРОСТИ ДЛЯ СИСТЕМЫ ОГРАНИЧЕНИЯ
- Приложение 5
- Приложение 6
- Приложение 7
- ТЕОРИЯ СВЯЗИ В СЕКРЕТНЫХ СИСТЕМАХ
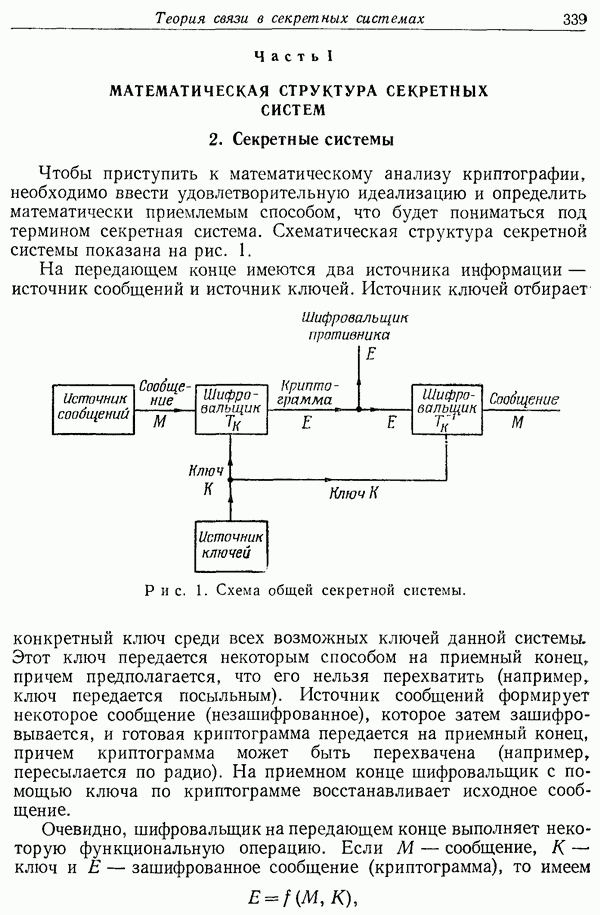
- Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ СИСТЕМ
- 3. Способы изображения систем
- 4. Примеры секретных систем
- 5. Оценка секретных систем
- 6. Алгебра секретных систем
- 7. Чистые и смешанные шифры
- 8. Подобные системы
- Часть II. ТЕОРЕТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 10. Совершенная секретность
- 11. Ненадежность
- 12. Свойства ненадежности
- 13. Ненадежность простой подстановки для языка с двухбуквенным алфавитом
- 14. Характеристика ненадежности для «случайного» шифра
- 15. Применение к стандартным шифрам
- 16. Правильность решения криптограммы
- 17. Идеальные секретные системы
- 18. Примеры идеальных секретных систем
- 19. Дополнительные замечания о ненадежности и избыточности
- 20. Распределение ненадежности
- Часть III. ПРАКТИЧЕСКАЯ СЕКРЕТНОСТЬ
- 22. Общие замечания о решении криптограмм
- 23. Статистические методы
- 24. Метод вероятных слов
- 25. Перемешивание
- 26. Шифры типа …
- 27. Несовместимость требований к хорошим системам
- ПРИЛОЖЕНИЕ. Доказательство теоремы 3
- СОВРЕМЕННЫЕ ДОСТИЖЕНИЯ ТЕОРИИ СВЯЗИ
- Измерение информаций
- Кодирование информации
- Пропускная способность канала
- Идеальные и практические системы
- ПРИНЦИПЫ КОДОВО-ИМПУЛЬСНОЙ МОДУЛЯЦИИ
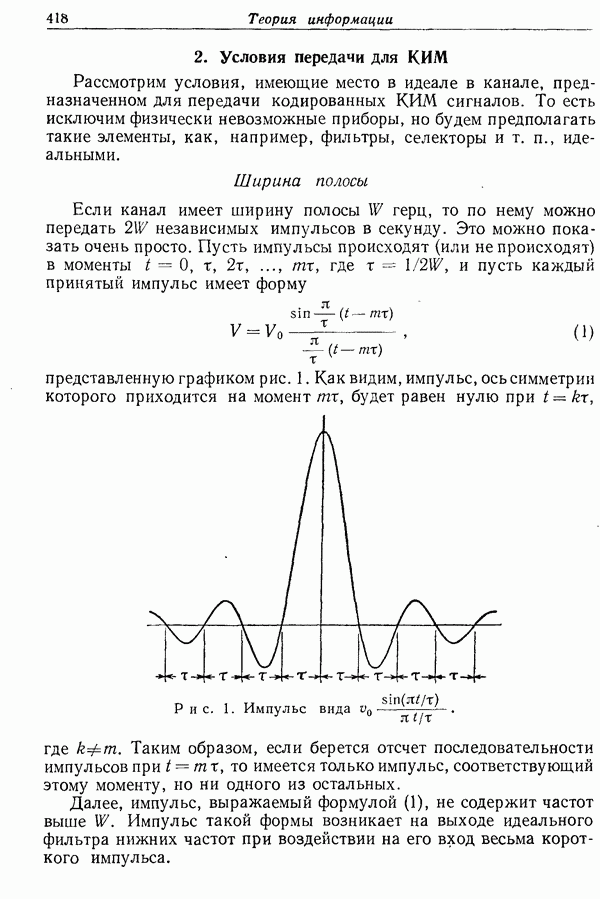
- 2. Условия передачи для КИМ
- 3. Действие системы КИМ
- 4. Сравнение КИМ и ЧМ
- 5. Заключение
- Приложение I
- Приложение II
- СВЯЗЬ ПРИ НАЛИЧИИ ШУМА
- 2. Теорема отсчетов
- 3. Геометрическое представление сигналов
- 4. Геометрическое представление сообщений
- 5. Геометрическое представление передатчика и приемника
- 6. Отображение пространства
- 7. Пропускная способность канала при наличии белого теплового шума
- 8. Обсуждение
- 9. Произвольный гауссовский шум
- 10. Пропускная способность канала при произвольном типе шума
- 11. Дискретные источники информации
- 12. Непрерывные источники информации
- НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ИНФОРМАЦИИ
- ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА С ШУМОМ ПРИ НУЛЕВОЙ ОШИБКЕ
- Пропускная способность канала при нулевой ошибке
- Пропускная способность для суммы и произведения каналов
- Каналы с обратной связью
- ГЕОМЕТРИЧЕСКИЙ ПОДХОД К ТЕОРИИ ПРОПУСКНОЙ СПОСОБНОСТИ. КАНАЛОВ СВЯЗИ
- КАНАЛЫ С ДОПОЛНИТЕЛЬНОЙ ИНФОРМАЦИЕЙ НА ПЕРЕДАТЧИКЕ
- Дискретный канал без памяти с дополнительной информацией о состоянии
- Приложение
- НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ТЕОРИИ КОДИРОВАНИЯ ДЛЯ КАНАЛОВ С ШУМАМИ
- Оценка вероятности ошибки в терминах производящей функции моментов
- Пропускная способность канала с конечным числом состояний, состояние которого вычислимо на обоих концах
- Пропускная способность канала с конечным числом состояний в случае, когда состояние вычислимо на передающем конце и не вычислимо на приемном конце
- ЗАМЕЧАНИЯ О ЧАСТИЧНОМ УПОРЯДОЧИВАНИИ КАНАЛОВ СВЯЗИ
- Дальнейшее обобщение и некоторые предположения
- ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ ОПТИМАЛЬНЫХ кодов В ГАУССОВСКОМ КАНАЛЕ
- 2. Сводка результатов
- 3. Нижняя граница, основанная на соображениях «сферической упаковки»
- 4. Верхняя граница, определяемая методом случайного кодирования
- 5. Формулы для скорости передачи R как функции угла конуса
- 6. Асимптотические формулы для …
- 7. Асимптотическое выражение для верхней границы при случайном кодировании
- 8. Жесткая верхняя граница
- 9. Жесткая нижняя граница
- 10. Поведение границ вблизи пропускной способности канала
- 11. Верхняя граница, полученная методом исчерпывания
- 12. Нижняя граница для гауссовского канала, получаемая исходя из минимального расстояния
- 13. Границы ошибок и другие условия, накладываемые на точки
- 14. Кривые для асимптотических границ
- ТЕОРЕМЫ КОДИРОВАНИЯ ДЛЯ ДИСКРЕТНОГО ИСТОЧНИКА ПРИ ЗАДАННОМ КРИТЕРИИ ТОЧНОСТИ
- Мера искажения отдельной буквы
- Несколько простых примеров
- Скорость при заданном искажении R(d)
- Выпуклость вниз кривой R(d)
- Нахождение R(d) в некоторых простых случаях
- Скорость передачи для произведения источников с мерой, являющейся суммой мер искажения
- Нижняя граница для искажения при заданной пропускной способности канала
- Теоремы кодирования при заданной мере искажения отдельной буквы
- Двойственность источника и канала
- Численные расчеты для некоторых простых каналов
- Обобщение на случаи непрерывных алфавитов
- Разностная мера искажения
- Определение меры локального искажения
- Функции Rn(d) и R(d) для меры локального искажения и эргодического источника
- Прямая теорема кодирования для меры локального искажения
- Обратная теорема кодирования
- Канал с памятью
- ДВУСТОРОННИЕ КАНАЛЫ СВЯЗИ
- 4. Средние взаимные скорости передачи информации
- 5. Распределение информации
- 6. Случайное кодирование для двусторонних каналов
- 7. Вероятность ошибки для ансамбля кодов
- 8. Выпуклая оболочка G как внутренняя граница области пропускной способности
- 9. Внешняя граница для области пропускной способности
- 10. Выпуклость вниз как функций от …
- 11. Приложения свойства выпуклости. Каналы с симметричной структурой
- 12. Характер области, выделяемой внешней границей
- 13. Пример, в котором внутренняя и внешняя границы различны
- 14. Достижимость внешней границы при зависимых источниках
- 15. Общий метод нахождения области пропускной способности двустороннего канала
- 16. Двусторонние каналы с памятью
- 17. Обобщение на каналы с Т концами
- БАНДВАГОН
- ПРЕДСКАЗАНИЕ И ЭНТРОПИЯ ПЕЧАТНОГО АНГЛИЙСКОГО ТЕКСТА
- 2. Вычисление энтропии по статистике английского языка
- 3. Предсказание английского текста
- 4. Идеальное N-граммное предсказывание
- 5. Граница для энтропии на основании частот предсказания
- 6. Результаты эксперимента для английского языка
- УПРОЩЕННЫЙ ВЫВОД ЛИНЕЙНОЙ ТЕОРИИ СГЛАЖИВАНИЯ И ПРЕДСКАЗАНИЯ ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ
- 3. Свойства линейных фильтров
- 4. Основное выражение для среднеквадратичной ошибки
- 5. Чистая проблема сглаживания
- 6. Проблема чистого предсказания
- 7. Предсказание при наличии шума
- 8. Обобщения
- 9. Обсуждение основных предположений
- МАТЕМАТИЧЕСКАЯ ТЕОРИЯ ДИФФЕРЕНЦИАЛЬНОГО АНАЛИЗАТОРА
- Основное условие разрешимости
- Реализация функций
- Системы уравнений
- Аппроксимация множителей с помощью передаточных чисел
- Автоматическое управление скоростью работы устройства
- О МАКСИМАЛЬНОМ ПОТОКЕ ЧЕРЕЗ СЕТЬ
- ТЕОРЕМА О РАСКРАСКЕ РЕБЕР ГРАФА
- УНИВЕРСАЛЬНАЯ МАШИНА ТЬЮРИНГА С ДВУМЯ ВНУТРЕННИМИ СОСТОЯНИЯМИ
- Невозможность создания универсальной машины Тьюринга с одним состоянием
- Моделирование машины Тьюринга с помощью только двух символов на ленте
- ВЫЧИСЛИМОСТЬ НА ВЕРОЯТНОСТНЫХ МАШИНАХ
- Приложение
- БИБЛИОГРАФИЯ РАБОТ ПО ШЕННОНОВСКОЙ ТЕОРИИ ОПТИМАЛЬНОГО КОДИРОВАНИЯ ИНФОРМАЦИИ