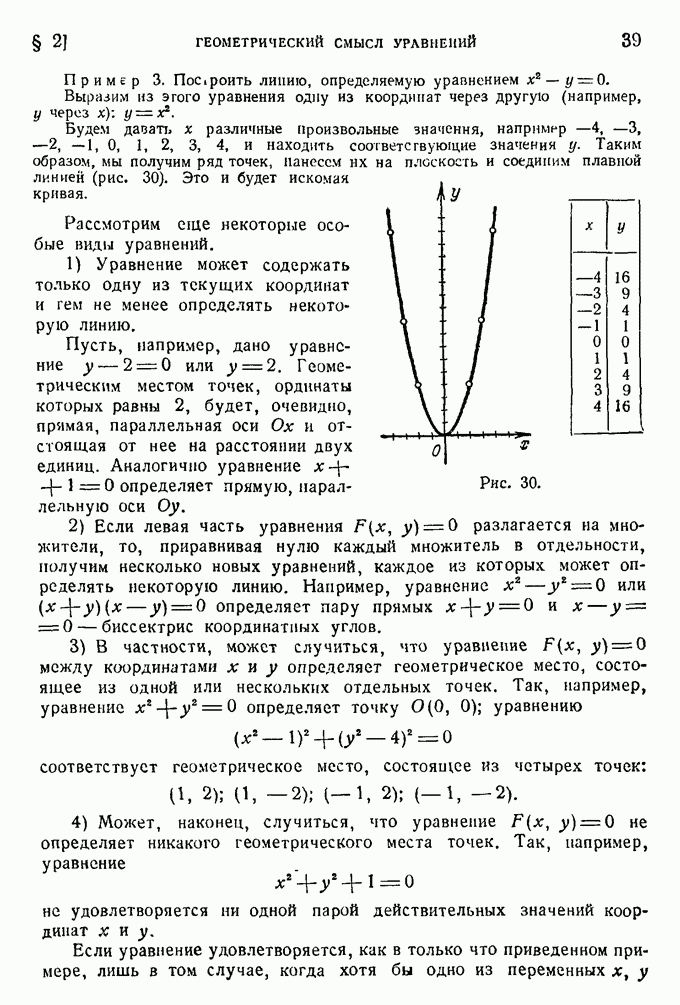
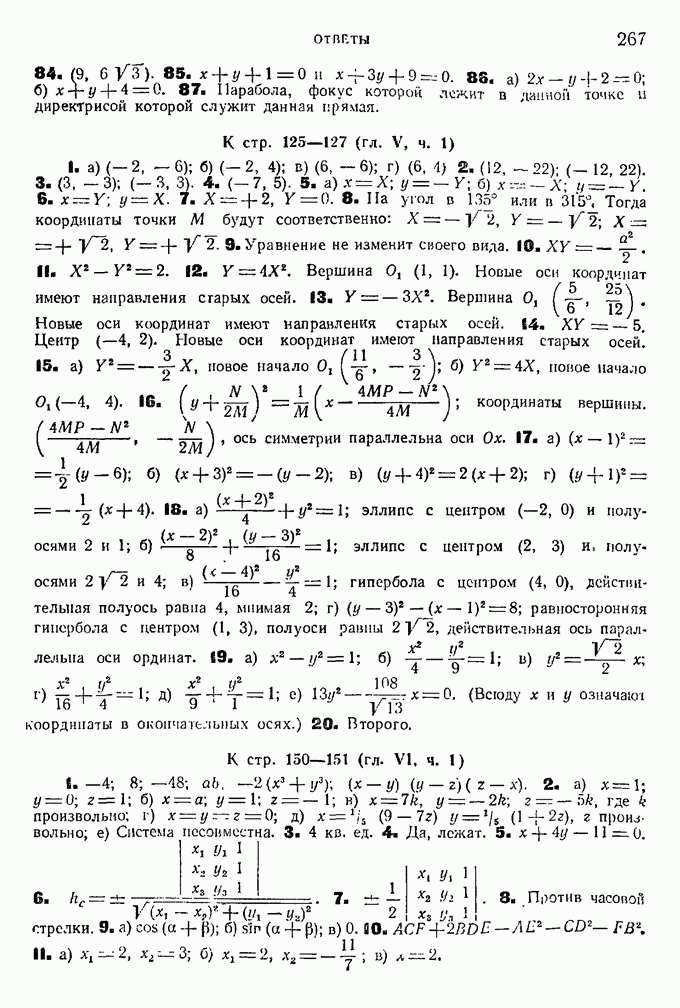| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 6. Уравнения линий в полярных координатах.
Ранее мы рассматривали уравнения линий в декартовых координатах, но аналогично можно говорить и об уравнениях линий в полярных координатах. Уравнением линии в полярной системе координат мы будем называть такое уравнение между переменными  которому удовлетворяют координаты любой точки, лежащей на линии, и не удовлетворяют
которому удовлетворяют координаты любой точки, лежащей на линии, и не удовлетворяют
координаты точек, не принадлежащих ей. Рассмотрим пример на нахождение уравнении данной линии в полярных координатах.
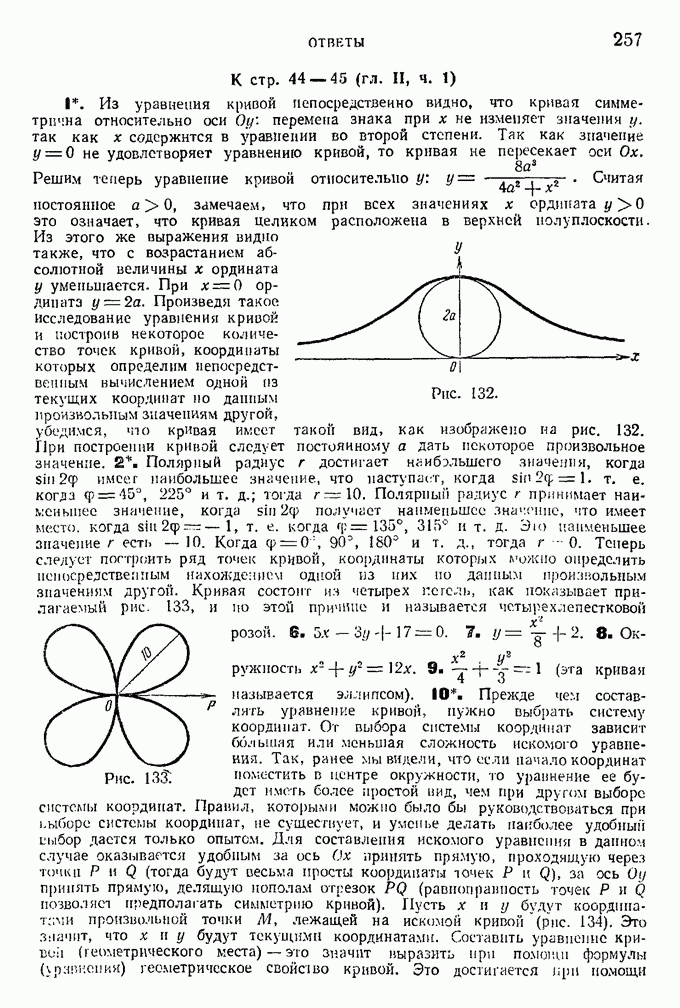
Пусть требуется найти уравнение окружности, проходящей через полюс, центр которой С лежит на полярной оси, а радиус равен а. Соединим отрезками прямой произвольную точку М окружности с полюсом и с конечной точкой D диаметра, проходящего через полюс (рис. 32). Координатами точки М будут угол  и длина
и длина  отрезка ОМ. Припомним, что окружность есть геометрическое место вершин прямых углов, опирающихся на ее диаметр. Следовательно, треугольник OMD — прямоугольный.
отрезка ОМ. Припомним, что окружность есть геометрическое место вершин прямых углов, опирающихся на ее диаметр. Следовательно, треугольник OMD — прямоугольный.
Отсюда получаем:

Это и есть искомое уравнение окружности.

Рис. 32.
Заметим, что вид уравнения данной линии зависит от выбора полюса и полярной оси. Так, если мы выберем полюс в центре окружности радиуса а, то для всех точек окружности (и только для этих точек) полярный радиус будет иметь одно и то же значение  это равенство будет, следовательно, уравнением окружности радиуса а с центром в полюсе. Полярный угол
это равенство будет, следовательно, уравнением окружности радиуса а с центром в полюсе. Полярный угол  в это уравнение не входит, оставаясь произвольным.
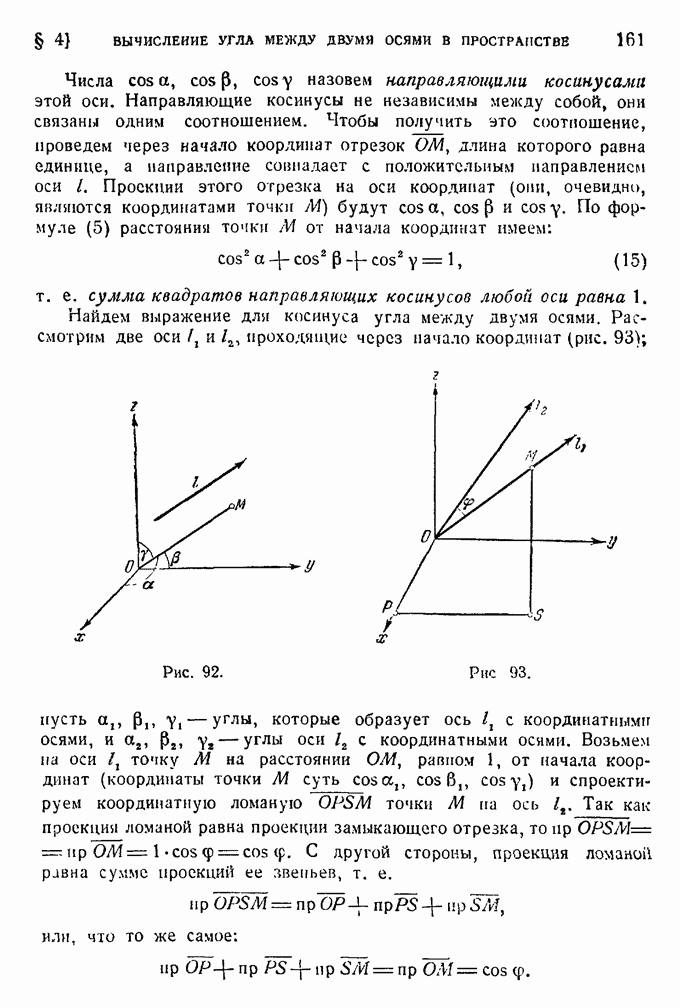
в это уравнение не входит, оставаясь произвольным.
При исследовании формы линии на основании ее уравнения приходится часто пользоваться полярными координатами. Это удобно делать всякий раз, когда уравнение линии в полярных координатах проще, чем в декартовых. В качестве примеров мы рассмотрим две линии, часто встречающиеся в приложениях.
Пример 1. Линия, называемая спиралью Архимеда, определяется в полярных координатах уравнением

где а есть положительная постоянная. Чтобы начертить эту линию, будем давать  произвольные значения и определять соответствующие значения
произвольные значения и определять соответствующие значения  . Приводимая таблица значений
. Приводимая таблица значений  удовлетворяющих данному уравнению, показывает, что при возрастании угла
удовлетворяющих данному уравнению, показывает, что при возрастании угла  в арифметической прогрессии с разностью полярный радиус
в арифметической прогрессии с разностью полярный радиус  возрастает тоже в арифметической прогрессии с разностью
возрастает тоже в арифметической прогрессии с разностью  . Кроме того, заметим, что всякой точке этой линии с положительными координатами
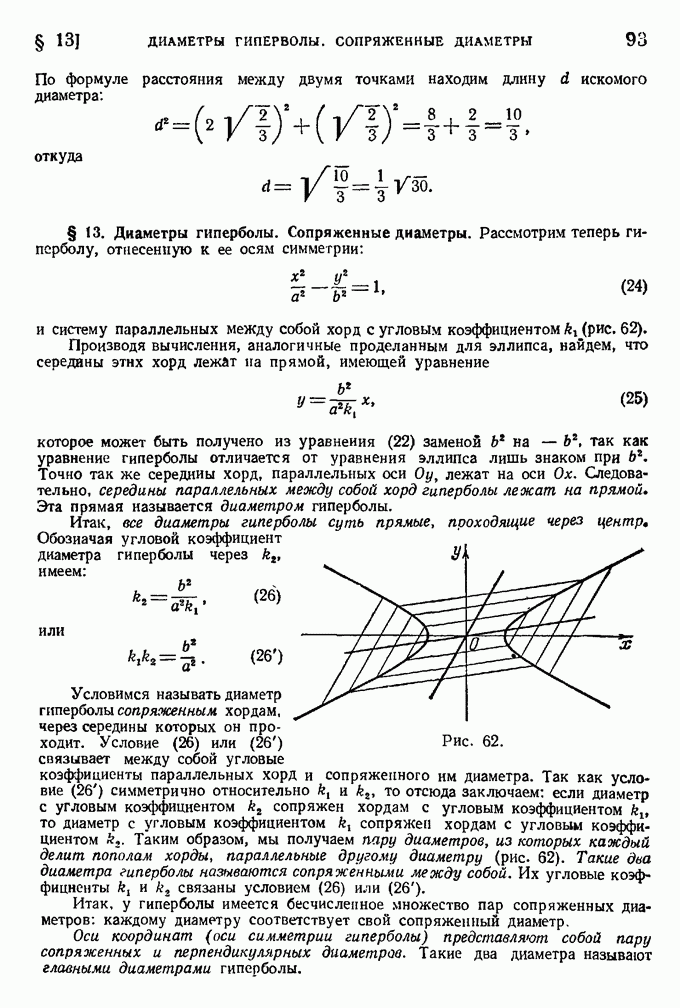
. Кроме того, заметим, что всякой точке этой линии с положительными координатами  соответствует на этой же линии точка
соответствует на этой же линии точка 
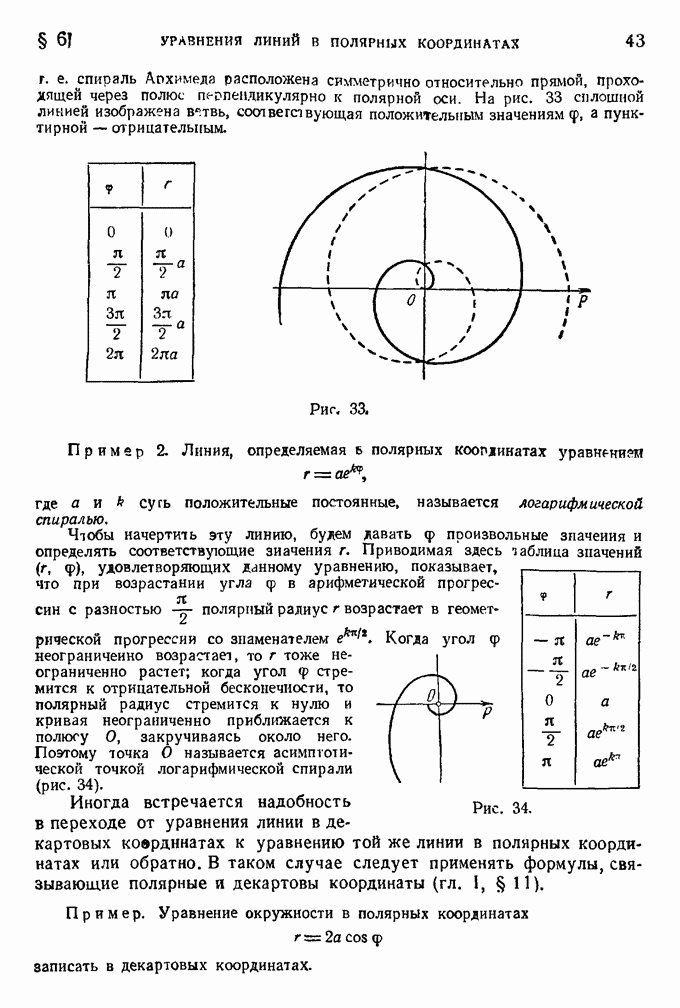
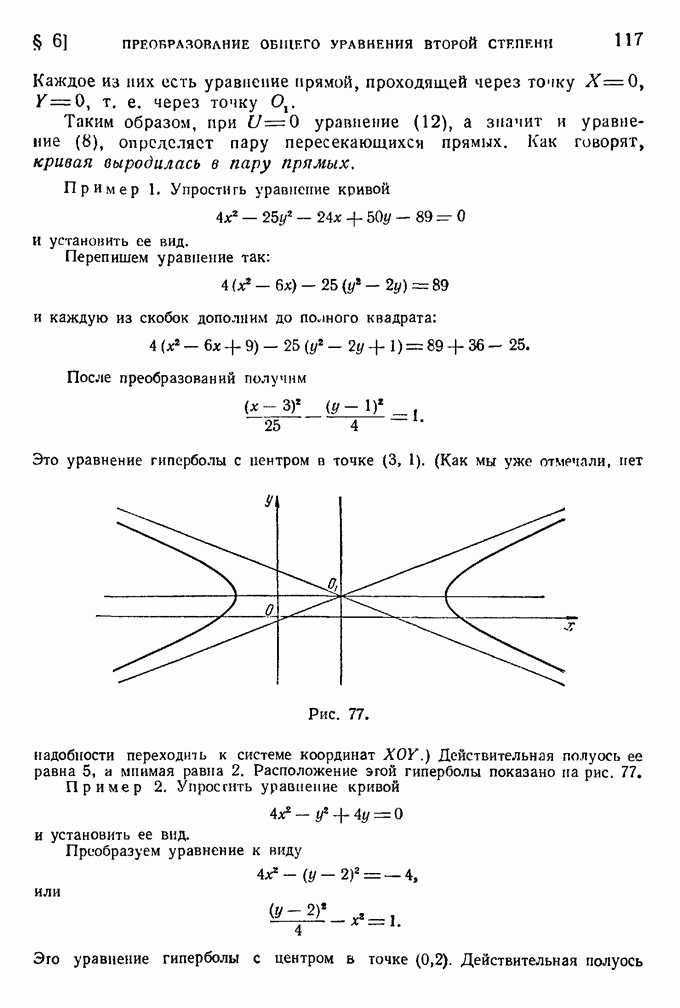
т. е. спираль Архимеда расположена симметрично относительно прямой, проходящей через полюс перпендикулярно к полярной оси. На рис. 33 сплошной линией изображена ветвь, соответствующая положительным значениям  а пунктирной — отрицательным.
а пунктирной — отрицательным.

Рис. 33.
Пример 2. Линия, определяемая в полярных координатах уравнением

где а и k суть положительные постоянные, называется логарифмической спиралью.
(см. скан)
Рис. 34.
Чтобы начертить эту линию, будем давать  произвольные значения и определять соответствующие значения
произвольные значения и определять соответствующие значения  . Приводимая здесь таблица значений
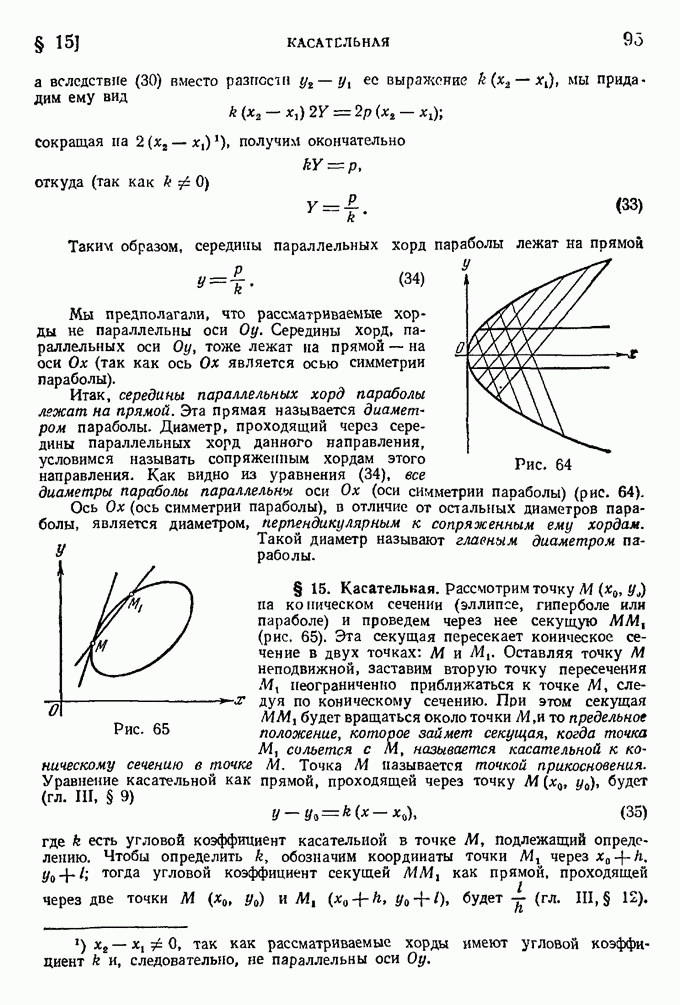
. Приводимая здесь таблица значений  удовлетворяющих данному уравнению, показывает, что при возрастании угла
удовлетворяющих данному уравнению, показывает, что при возрастании угла  в арифметической прогрессии с разностью
в арифметической прогрессии с разностью  полярный радиус
полярный радиус  возрастает в геометрической прогрессии со знаменателем Когда угол
возрастает в геометрической прогрессии со знаменателем Когда угол  неограниченно возрастает, то
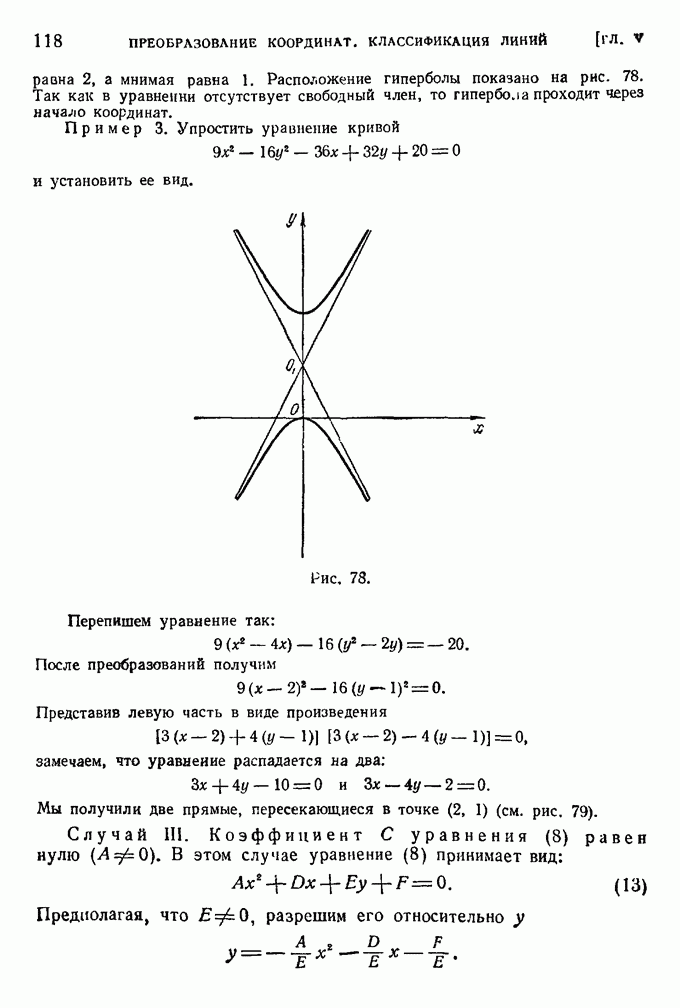
неограниченно возрастает, то  тоже неограниченно растет; когда угол Ф стремится к отрицательной бесконечности, то полярный радиус стремится к нулю и кривая неограниченно приближается к полюсу О, закручиваясь около него.
тоже неограниченно растет; когда угол Ф стремится к отрицательной бесконечности, то полярный радиус стремится к нулю и кривая неограниченно приближается к полюсу О, закручиваясь около него.
Поэтому точка О называется асимптотической точкой логарифмической спирали (рис. 34).
Иногда встречается надобность в переходе от уравнения линии в декартовых коврдннатах к уравнению той же линии в полярных координатах или обратно. В таком случае следует применять формулы, связывающие полярные и декартовы координаты (гл. 1, § 11).
Пример. Уравнение окружности в полярных координатах

записать в декартовых координатах.
Выражаем  через
через 

Подставляя эти выражения в данное уравнение, после упрощений получим:

Упражнения
1. Построить кривую, заданную уравнением  (Эта кривая носит название локона Аньези.)
(Эта кривая носит название локона Аньези.)
2. Построить кривую, заданную уравнением  (Эта кривая называв]
(Эта кривая называв]  четырехлепестковой розой.)
четырехлепестковой розой.)
3. Построить кривые, заданные уравнениями:

4. Построить кривые, которым в полярных координатах соответствуют уравнения:

5. Построить кривые, заданные в полярных координатах уравнениями:

6. Составить уравнение геометрического места точек, одинаково удаленных от начала координат и от точки 
7. Составить уравнение геометрического места точек, одинаково удаленных от оси Ох и от точки  Построить кривую.
Построить кривую.
8. Определить траекторию точки М, которая движется так, что ее расстояние от точки  остается вдвое меньше расстояния от точки
остается вдвое меньше расстояния от точки 
9. Определить траекторию точки М, которая движется так, что ее расстояние от точки  остается вдвое меньше расстояния
остается вдвое меньше расстояния  прямой
прямой 

Рис. 35.
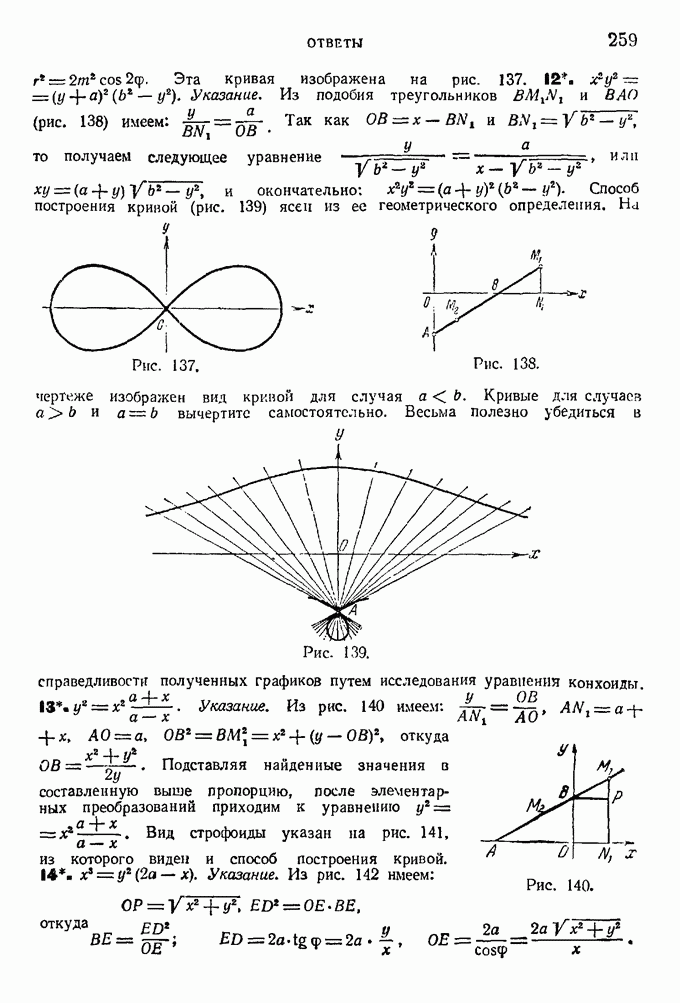
10. Найти уравнение геометрического места точек, произведение расстояний которых до двух данных точек Р и Q есть величина постоянная, оавиая  Расстояние между Р и Q равно
Расстояние между Р и Q равно  (Это геометрическое место точек называется овалом Кассини.) Построить эту линию.
(Это геометрическое место точек называется овалом Кассини.) Построить эту линию.
11. Овал Кассини (см. упражнение 10) для случая, когда  , называется лемнискатой Бернулли. Найти уравнение лемнискаты: а) в декартовых координатах и б) в полярных координатах. Построй
, называется лемнискатой Бернулли. Найти уравнение лемнискаты: а) в декартовых координатах и б) в полярных координатах. Построй  эту кривую.
эту кривую.
12. Даны прямая Ох и на расстоянии а от нее точка А (рис. 35). Если прямая  будет вращаться около точки А, то точки
будет вращаться около точки А, то точки  лежащие на этой прямой и отстоящие от точки В пересечения прямой АВ с основной прямой Ох на данное расстояние b, опишут некоторую линию. Она называется конхоидой Никомеда. Найти уравнение конхоиды и построить ее для случаев
лежащие на этой прямой и отстоящие от точки В пересечения прямой АВ с основной прямой Ох на данное расстояние b, опишут некоторую линию. Она называется конхоидой Никомеда. Найти уравнение конхоиды и построить ее для случаев 

Рис. 36.
13. Даны прямая Оу и точка А на расстоянии а от нее (рис. 36). Вокруг точки А вращается луч А В и на нем в обе стороны от точки В (точки пересечения луча с осью Оу) отложены переменные отрезки ВМ, и  равные по длине ОВ. При вращении луча АВ точки М, и
равные по длине ОВ. При вращении луча АВ точки М, и  описывают кривую, называемую строфоидой. Составить уравнение этой кривой
описывают кривую, называемую строфоидой. Составить уравнение этой кривой  построить ее.
построить ее.
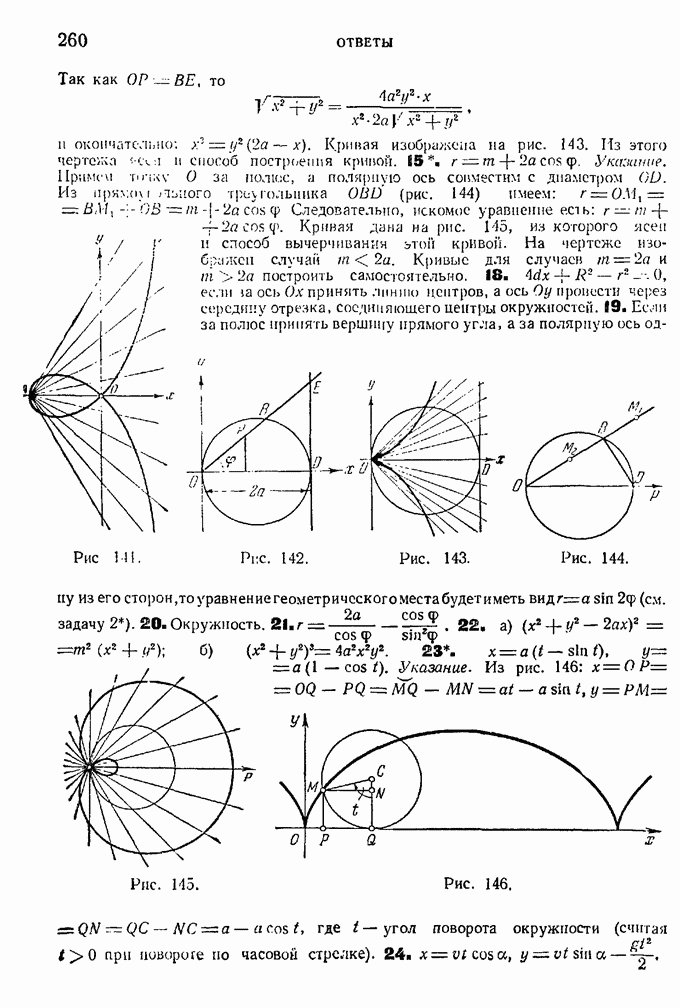
14. Даны окружность диаметра  и касательная к ней РЕ (рис. 37). Через точку О, диаметрально противоположную точки D, проведен луч ОЕ и на нем отложен отрезок ОР, равный отрезку BE, заключающемуся между окружностью и касательной.
и касательная к ней РЕ (рис. 37). Через точку О, диаметрально противоположную точки D, проведен луч ОЕ и на нем отложен отрезок ОР, равный отрезку BE, заключающемуся между окружностью и касательной.
Если луч ОЕ будет вращаться около точки О, то точка Р опишет кривую, называемую циссоидой Диоклеса. Найти уравнение этой кривой и построить ее.

Рис. 37.

Рис. 38.
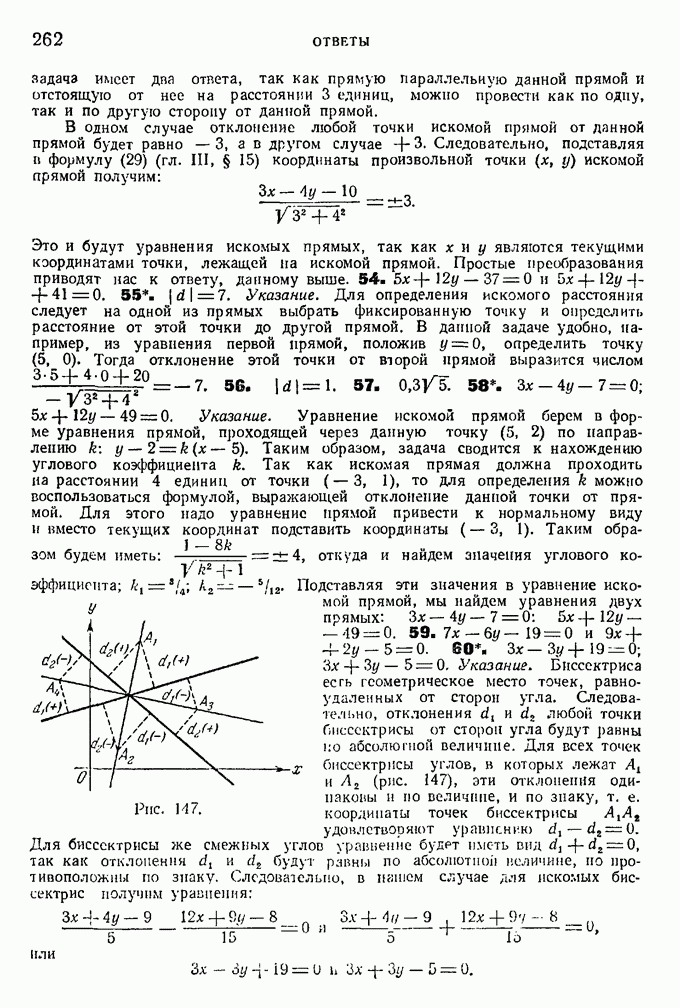
15. Даны окружность радиуса а и на ней точка О (рис. 38). Если прямая О В будет вращаться около тчки О, то точки М, и  находящиеся на данной прямой и отстоящие на данное расстояние
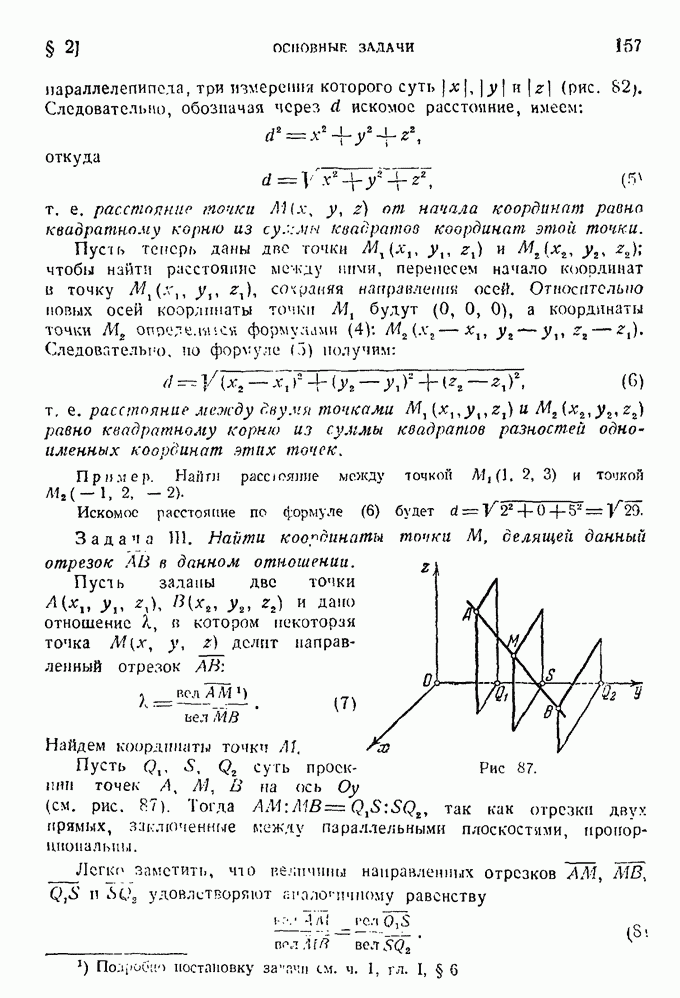
находящиеся на данной прямой и отстоящие на данное расстояние  от точки В пересечения прямой с окружностью, опишут кривую, называемую улиткой Паскаля. Найти уравнение этой кривой в полярных координатах и построить ее. (Кривые вычертить для случаев
от точки В пересечения прямой с окружностью, опишут кривую, называемую улиткой Паскаля. Найти уравнение этой кривой в полярных координатах и построить ее. (Кривые вычертить для случаев  )
)
16. Составить уравнение геометрического места точек, равноудаленных от двух данных точек.
17. Две прямые вращаются вокруг двух неподвижных точек, оставаясь все время перпендикулярными друг к Другу. Найги уравнение линии, описываемой точкой их пересечения.
18. Из точки М проведены к двум окружностям радиусов R и  две равные касательные. Найти уравнение геометрического места точек М при условии, что расстояние между центрами окружностей равно
две равные касательные. Найти уравнение геометрического места точек М при условии, что расстояние между центрами окружностей равно 
19. Отрезок постоянной длины 2а скользит своими концами по сторонам прямого угла. Из вершины прямого угла на этот отрезок опущен перпендикуляр ОМ. Найти уравнение геометрического места оснований этих перпендикуляров в полярных координатах и построить эту линию.
20. Найтн геометрическое место точек, сумма квадратов расстояний которых от сторон квадрата равьа постоянной величине.
21. Написать уравнение циссоиды  в полярных координатах.
в полярных координатах.
22. Нанисать уравнения кривых:
а)  (улитка Паскаля);
(улитка Паскаля);
б)  (четырехлепестковая роза) в декартовых координатах.
(четырехлепестковая роза) в декартовых координатах.
23. Круг радиуса а катится без скольжения по оси абсцисс. Найти параметрические уравнения линии, описываемой при указанном движении той точкой окружности, которая при начальном положении окружности находилась в начале координат.
24. Тело брошено вверх со скоростью v под углом а к горизонту. Найти, пренебрегая сопротивлением воздуха, параметрические уравнения траектории тела (за параметр принять время).
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ЧАСТЬ ПЕРВАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
- ГЛАВА I. МЕТОД КООРДИНАТ
- § 2. Координаты на прямой линии.
- § 3. Расстояние между двумя точками на прямой линии.
- § 4. Прямоугольные координаты на плоскости.
- § 5. Расстояние между двумя точками на плоскости.
- § 6. Деление отрезка в данном отношении.
- § 7. Угол между двумя осями.
- § 8. Основные положения теории проекций.
- § 9. Проекции направленного отрезка на оси координат.
- § 10. Площадь треугольника.
- § 11. Полярные координаты.
- Упражнения
- ГЛАВА II. ЛИНИИ И ИХ УРАВНЕНИЯ
- § 1. Составление уравнений заданных линий.
- § 2. Геометрический смысл уравнений.
- § 3. Две основные задачи.
- § 4. Пересечение двух линий.
- § 5. Параметрические уравнения линий.
- § 6. Уравнения линий в полярных координатах.
- ГЛАВА III. ПРЯМАЯ ЛИНИЯ
- § 1. Угловой коэффициент прямой.
- § 2. Уравнение прямой линии с угловым коэффициентом.
- § 3. Геометрический смысл уравнения первой степени между двумя переменными.
- § 4. Исследование общего уравнения первой степени Ах + Ву + С = 0.
- § 5. Уравнение прямой линии в отрезках.
- § 6. Построение прямой линии по ее уравнению.
- § 7. Угол между двумя прямыми.
- § 8. Условия параллельности и перпендикулярности двух прямых.
- § 9. Уравнение прямой, проходящей через данную точку в данном направлении.
- § 10. Взаимное расположение двух прямых на плоскости.
- § 11. Уравнение пучка прямых.
- § 12. Уравнение прямой, проходящей через две данные точки.
- § 13. Условие, при котором три данные точки лежат на одной прямой.
- § 14. Нормальное уравнение прямой линии.
- § 15. Приведение общего уравнения первой степени к нормальному виду.
- § 16. Расстояние от дайной точки до данной прямой.
- § 17. Уравнение прямой в полярной системе координат.
- Упражнения
- ГЛАВА IV. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ КОНИЧЕСКИХ СЕЧЕНИЙ
- § 2. Окружность.
- § 3. Эллипс.
- § 4. Гипербола и ее асимптоты.
- § 5. Парабола.
- § 6. Построение точек эллипса, гиперболы и параболы посредством циркуля и линейки.
- § 7. Эллипс, гипербола и парабола как конические сечения.
- § 8. Эксцентриситет и директрисы эллипса.
- § 9. Эксцентриситет и директрисы гиперболы.
- § 10. Эксцентриситет и директриса параболы.
- § 11. Уравнение конического сечения в полярных координатах.
- § 12. Диаметры зллипса. Сопряженные диаметры.
- § 13. Диаметры гиперболы. Сопряженные диаметры.
- § 14. Диаметры параболы.
- § 15. Касательная.
- § 16. Эллипс как проекция окружности.
- § 17. Параметрические уравнения эллипса.
- Упражнения
- ГЛАВА V. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. КЛАССИФИКАЦИЯ ЛИНИЙ
- § 2. Перенос начала координат.
- § 3. Поворот осей координат.
- § 4. Общий случай.
- § 5. Некоторые приложения формул преобразования координат.
- § 6. Преобразование общего уравнения второй степени, не содержащего произведения переменных.
- § 7. Преобразование общего уравнения второй степени.
- § 8. Классификация линий.
- Упражнения
- ГЛАВА VI. ОПРЕДЕЛИТЕЛИ 2-го и 3-го ПОРЯДКА
- § 2. Однородная система двух уравнений с тремя неизвестными.
- § 3. Определители 3-го порядка.
- § 4. Основные свойства определителей 3-го порядка.
- § 5. Система трех уравнений первой степени с тремя неизвестными.
- § 6. Однородная система.
- § 7. Общее исследование системы трех уравнений первой степени с тремя неизвестными.
- § 8. Некоторые приложения определителей к аналитической геометрии.
- Упражнения
- ЧАСТЬ ВТОРАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
- ГЛАВА I. МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ
- § 2. Основные задачи.
- § 3. Основные положения теории проекций в пространстве.
- § 4. Вычисление угла между двумя осями в пространстве.
- Упражнения
- ГЛАВА II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
- § 2. Сложение векторов.
- § 3. Вычитание векторов.
- § 4. Умножение вектора на число.
- § 5. Проекции вектора.
- § 6. Действия над векторами, заданными своими проекциями.
- § 7. Скалярное произведение векторов.
- § 8. Основные свойства скалярного произведения.
- § 9. Скалярное произведение векторов, заданных проекциями.
- § 10. Направление вектора.
- § 11. Векторное произведение.
- § 12. Основные свойства векторного произведения.
- § 13. Векторное произведение векторов, заданных проекциями.
- § 14. Векторно-скалярное произведение.
- § 15. Векторно-скалярное произведение в проекциях.
- § 16. Двойное векторное произведение.
- Упражнения
- ГЛАВА III. ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ
- § 1. Уравнение поверхности.
- § 2. Геометрический смысл уравнений.
- § 3. Две основные задачи.
- § 4. Сфера.
- § 5. Цилиндрические поверхности.
- § 6. Уравнения линии в пространстве.
- § 7. Пересечение трех поверхностей.
- Упражнения
- ГЛАВА IV. ПЛОСКОСТЬ
- § 1. Нормальное уравнение плоскости.
- § 2. Геометрический смысл уравнения первой степени между тремя переменными. Приведение общего уравнения первой степени к нормальному виду.
- § 3. Исследование общего уравнения плоскости.
- § 4. Уравнение плоскости в отрезках.
- § 5. Уравнение плоскости, проходящей через данную точку.
- § 6. Уравнение плоскости, проходящей через три данные точки.
- § 7. Угол между двумя плоскостями.
- § 8. Условия параллельности и перпендикулярности двух плоскостей.
- § 9. Точка пересечения трех плоскостей.
- § 10. Расстояние от точки до плоскости.
- Упражнения
- ГЛАВА V. ПРЯМАЯ ЛИНИЯ
- § 1. Уравнения прямой линии.
- § 2. Прямая как линия пересечения двух плоскостей. Общие уравнения прямой.
- § 3. Угол между двумя прямыми линиями.
- § 4. Условия параллельности и перпендикулярности двух прямых.
- § 5. Уравнения прямой, проходящей через две данные точки.
- § 6. Угол между прямой и плоскостью.
- § 7. Условия параллельности и перпендикулярности прямой и плоскости.
- § 8. Уравнение пучка плоскостей.
- § 9. Пересечение прямой с плоскостью.
- § 10. Условие, при котором две прямые лежат в одной плоскости.
- Упражнения
- ГЛАВА VI. ЦИЛИНДРИЧЕСКИЕ И КОНИЧЕСКИЕ ПОВЕРХНОСТИ. ПОВЕРХНОСТИ ВРАЩЕНИЯ. ПОВЕРХНОСТИ 2-го ПОРЯДКА
- § 1. Классификация поверхностей.
- § 2. Цилиндрические поверхности (общий случай).
- § 3. Конические поверхности.
- § 4. Поверхности вращения.
- § 5. Эллипсоид.
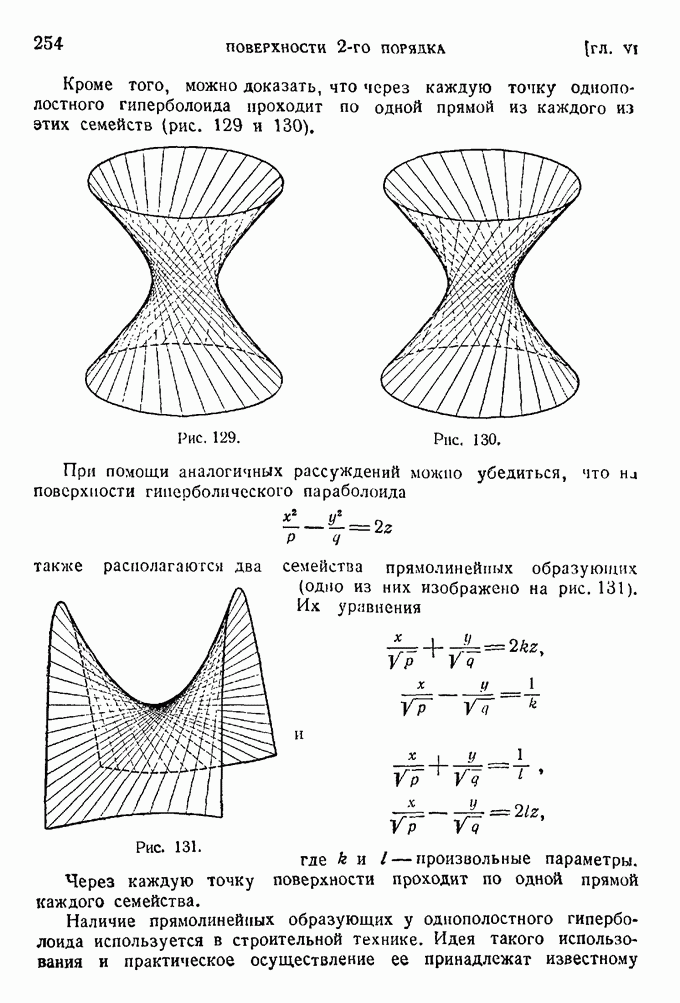
- § 6. Однополостный гиперболоид.
- § 7. Двуполостный гиперболоид.
- § 8. Эллиптический параболоид.
- § 9. Гиперболический параболоид.
- § 10. Конус 2-го порядка.
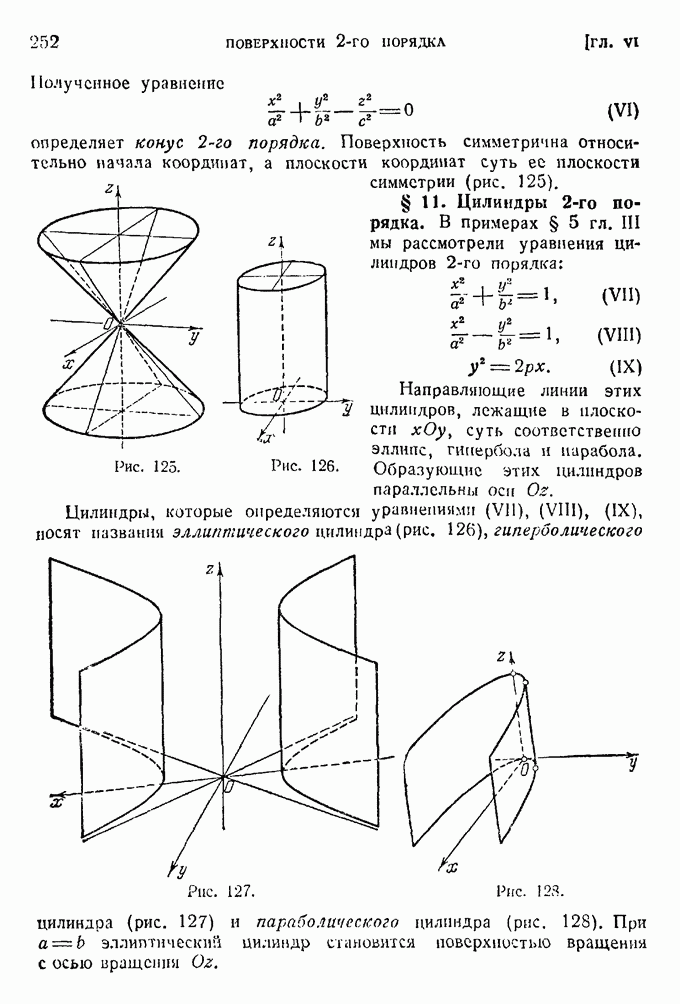
- § 11. Цилиндры 2-го порядка.
- § 12. Прямолинейные образующие поверхностей 2-го порядка. Конструкции В. Г. Шухова.
- Упражнения
- Ответы