| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 14. Векторно-скалярное произведение.
Выясним, что можно сказать о произведении трех векторов. Если мы умножим скалярно два вектора А и В, то их произведение будет скаляром. При умножении третьего вектора С на этот скаляр мы получим вектор, коллинсарный вектору С.
Совсем иное дело будет, если мы перемножим два вектора векторно; в результате мы получим снова вектор А X В. Представляется интересным исследовать дальнейшие произведения, как скалярное, так и векторное, этого вектора на новый вектор С. В первом случае мы будем иметь векторно-скалярное произведение  а во втором случае двойное векторное произведение
а во втором случае двойное векторное произведение 

Рис. 107.
Векторно-скалярное произведение  называется также смешанным произведением и обозначается (ABC) или
называется также смешанным произведением и обозначается (ABC) или 
Для приложения векторно-скалярного произведения весьма важным является уяснить себе его геометрический смысл. Пусть рассматриваемые векторы А, В и С некомпланарны. Векторное произведение  есть вектор Е, по длине численно равный площади параллелограмма OADB, построенного на векторах А и В, и направленный перпендикулярно к плоскости параллелограмма (рис. 107).
есть вектор Е, по длине численно равный площади параллелограмма OADB, построенного на векторах А и В, и направленный перпендикулярно к плоскости параллелограмма (рис. 107).
Скалярное произведение  есть произведение длины Е первого множителя на проекцию второго вектора С на первый. Эта проекция
есть произведение длины Е первого множителя на проекцию второго вектора С на первый. Эта проекция  как проекция вектора С на перпендикуляр к плоскости равна расстоянию точки С (конца вектора С) от плоскости параллелограмма OADB, взятому со знаком
как проекция вектора С на перпендикуляр к плоскости равна расстоянию точки С (конца вектора С) от плоскости параллелограмма OADB, взятому со знаком  или
или 
Построим параллелепипед на векторах А, В, С как на ребрах. Высота этого параллелепипеда есть абсолютная величина нашей проекции  а площадь основания — параллелограмма OADB — численно равна длине вектора Е.
а площадь основания — параллелограмма OADB — численно равна длине вектора Е.
Итак, произведение  по абсолютной величине равно произведению площади основания параллелепипеда на его высоту, т. е. измеряет объем параллелепипеда.
по абсолютной величине равно произведению площади основания параллелепипеда на его высоту, т. е. измеряет объем параллелепипеда.
При этом важно отметить, что наше скалярное произведение дает объем параллелепипеда иногда с положительным, а иногда
с отрицательным знаком. Положительный знак получается, если угол между векторами Е и С острый; отрицательный — если он тупой. При остром угле между Е и С вектор С расположен по ту же сторону плоскости OADB, что и вектор Е, и, следовательно, из его конца С вращение от А к В будет видно так же, как и из точки Е, т.е. в положительном направлении (против часовой стрелки).
При тупом угле между Е и С вектор С расположен по другую сторону плоскости OADB, чем вектор Е, и, следовательно, из его конца С вращение от А к В будет видно в отрицательном направлении (по часовой стрелке). Иными словами, произведение (ABC) положительно, если векторы А, В и С образуют систему, одноименную с основной (взаимно расположены так же, как оси х, у, z), и оно отрицательно, если векторы А, В и С образуют систему, разноименную с основной.
Итак, мы получили следующую теорему:
Векторно-скалярное произведение  трех некомпланарных векторов есть число, абсолютная величина которого выражает объем параллелепипеда, построенного на векторах А, В, С, как на ребрах. Знак произведения положителен, если векторы А, В, С образуют систему, одноименную с основной, и отрицателен в противном случае.
трех некомпланарных векторов есть число, абсолютная величина которого выражает объем параллелепипеда, построенного на векторах А, В, С, как на ребрах. Знак произведения положителен, если векторы А, В, С образуют систему, одноименную с основной, и отрицателен в противном случае.

Рис. 108.
Из этой теоремы следует, что абсолютная величина произведения  . С останется та же, в каком бы порядке мы ни брали сомножители А, В, С. Что касается знака, то он будет в одних случаях положительным, в других — отрицательным; это зависит от того, образуют ли наши три вектора, взятые в определенном порядке, систему, одноименную с основной, или нет. Заметим, что у нас оси координат расположены так, что они следуют одна за другой против часовой стрелки, если смотреть во внутреннюю часть трехгранного угла (рис. 108).
. С останется та же, в каком бы порядке мы ни брали сомножители А, В, С. Что касается знака, то он будет в одних случаях положительным, в других — отрицательным; это зависит от того, образуют ли наши три вектора, взятые в определенном порядке, систему, одноименную с основной, или нет. Заметим, что у нас оси координат расположены так, что они следуют одна за другой против часовой стрелки, если смотреть во внутреннюю часть трехгранного угла (рис. 108).
Порядок следования не нарушится, если мы начнем обход со второй оси или с третьей, лишь бы он совершался в том же направлении, т. е. против часовой стрелки. При этом наши множители переставляются в круговом порядке. Таким образом, получаем теорему:
Круговая перестановка трех сомножителей векторно-скалярного произведения не меняет его величины. Перестановка двух соседних сомножителей меняет знак произведения:

При каких условиях векторно-скалярное произведение может обратиться в нуль? Очевидно: а) если среди сомножителей есть
хотя бы один нулевой вектор; б) если по крайней мере два из перемножаемых векторов коллинеарны (и, следовательно, их векторное произведение равно нулевому вектору), в частности:

в) если три вектора А, В, С компланарны (параллельны одной и той же плоскости), потому что тогда  и, следовательно:
и, следовательно:

Объединяя все три случая, можем сказать, что (АВС)  если векторы А, В, С компланарны. Обратно, пусть (АВС)
если векторы А, В, С компланарны. Обратно, пусть (АВС)  Тогда, если никакой из векторов не является нулевым и иикакие два из векторов не коллинеарны, АХ В и С должны быть перпендикулярны, так как их скалярное произведение равно нулю, а так как, кроме того,
Тогда, если никакой из векторов не является нулевым и иикакие два из векторов не коллинеарны, АХ В и С должны быть перпендикулярны, так как их скалярное произведение равно нулю, а так как, кроме того,  перпендикулярен к А и В, то векторы А, В, С компланарны. Следовательно, можно утверждать, что равенство
перпендикулярен к А и В, то векторы А, В, С компланарны. Следовательно, можно утверждать, что равенство

есть необходимое и достаточное условие компланарности векторов А, В, С.
Отсюда, в частности, следует, что формулы (33), доказанные для нскомпланарных векторов, остаются справедливыми и в случае их компланарности.
Пример 1. Показать, что объем треугольной пирамиды равен -i- абсолютной величины векторно-скаляриого произведения, составленного из трех векторов-ребер, выходящих из одной вершины.
В самом деле, объем треугольной пирамиды ABCD можно рассматривать как  объема параллелепипеда, построенного на векторах АВ, AC, AD, как на ребрах:
объема параллелепипеда, построенного на векторах АВ, AC, AD, как на ребрах:

Пример 2, Раскрыть скобки в выражении

Это выражение представляет  . Векторное произведение будет равно:
. Векторное произведение будет равно:

Умножая его скалярно на (С А), получим:

| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ЧАСТЬ ПЕРВАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
- ГЛАВА I. МЕТОД КООРДИНАТ
- § 2. Координаты на прямой линии.
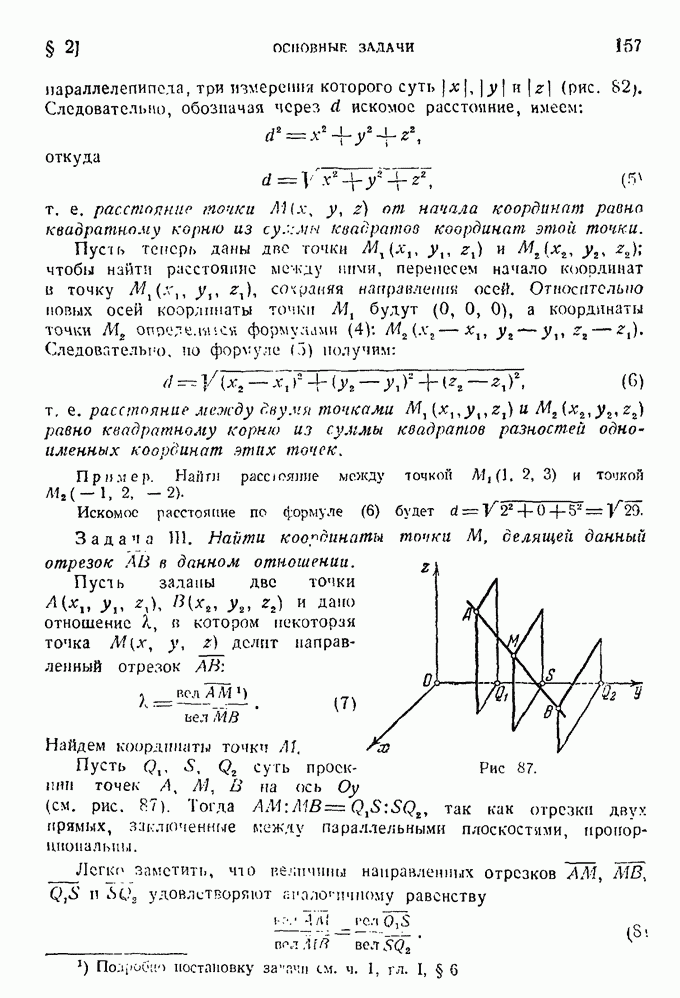
- § 3. Расстояние между двумя точками на прямой линии.
- § 4. Прямоугольные координаты на плоскости.
- § 5. Расстояние между двумя точками на плоскости.
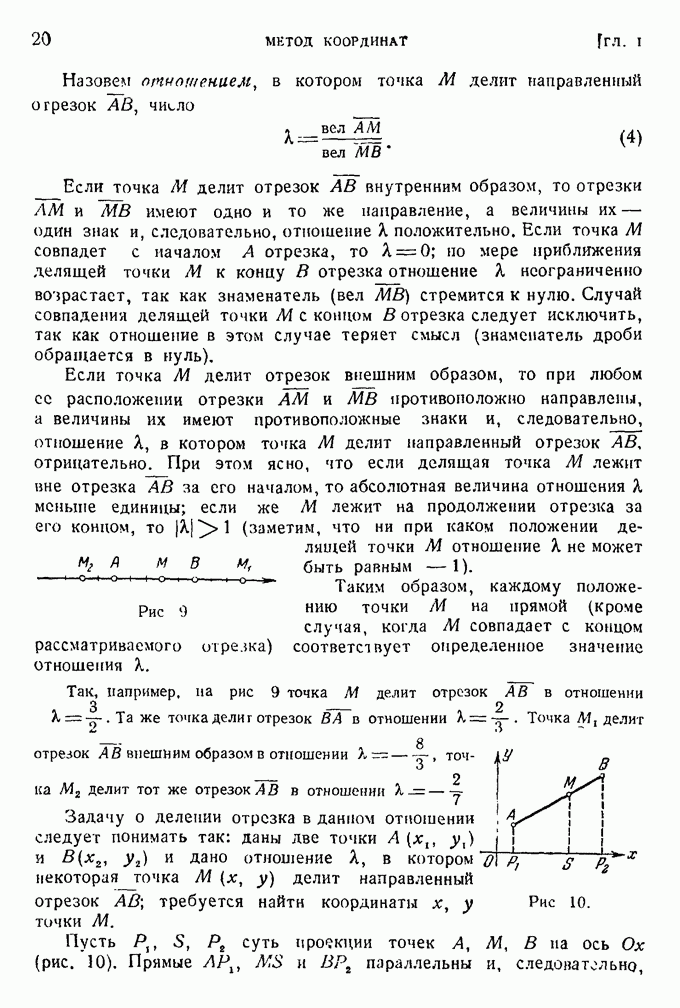
- § 6. Деление отрезка в данном отношении.
- § 7. Угол между двумя осями.
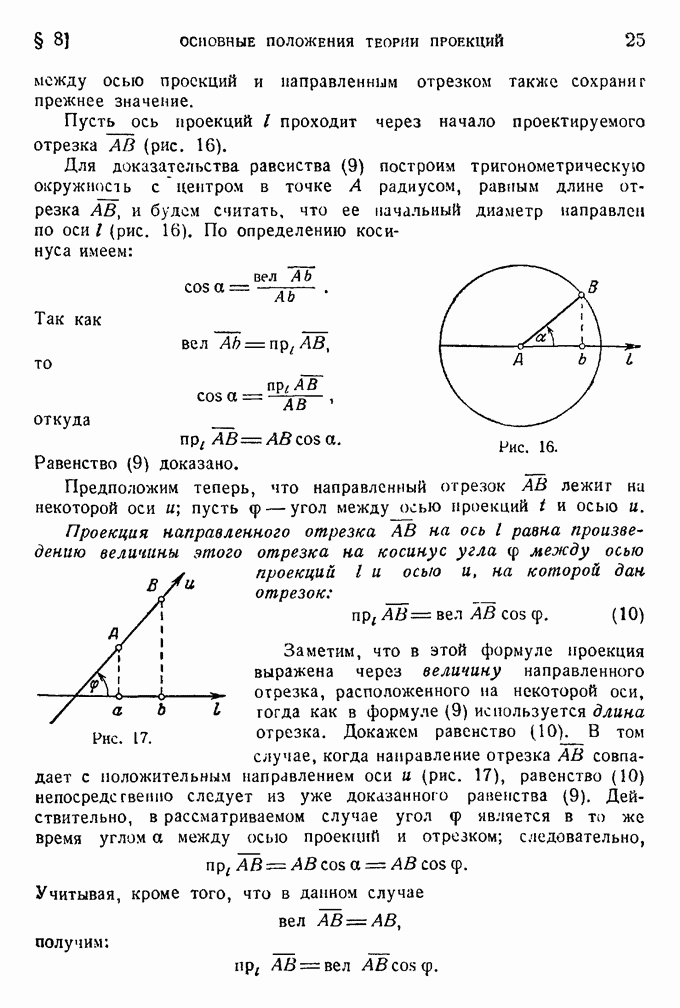
- § 8. Основные положения теории проекций.
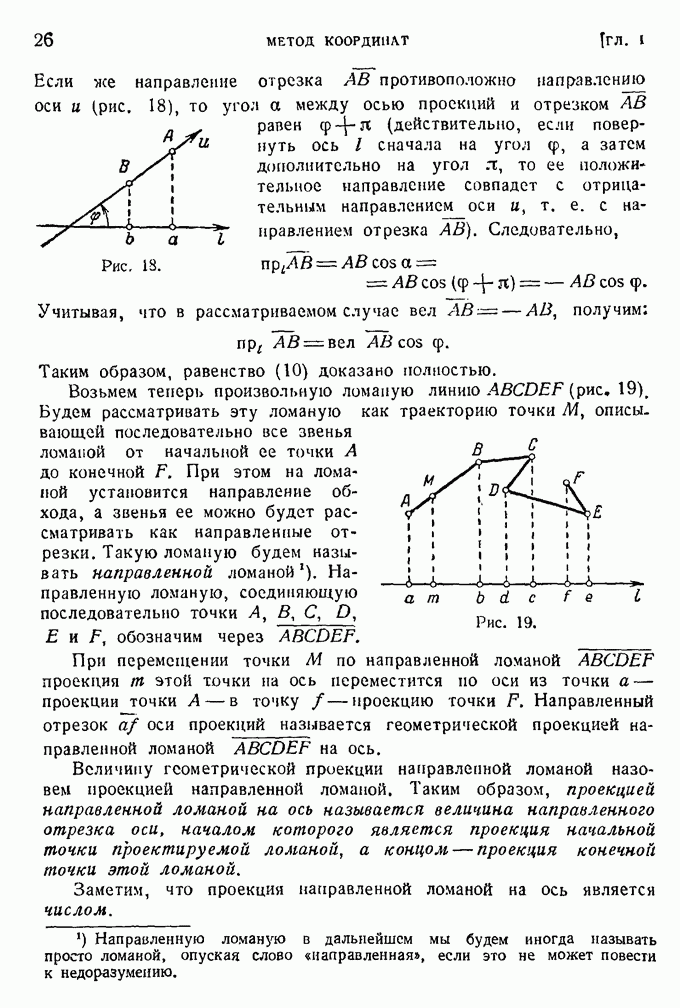
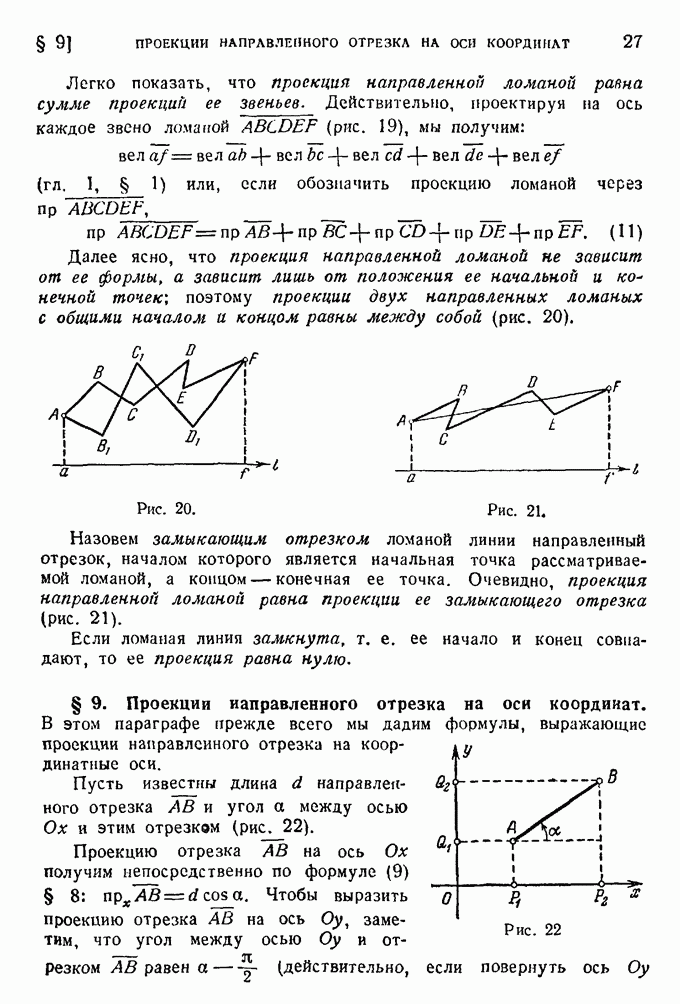
- § 9. Проекции направленного отрезка на оси координат.
- § 10. Площадь треугольника.
- § 11. Полярные координаты.
- Упражнения
- ГЛАВА II. ЛИНИИ И ИХ УРАВНЕНИЯ
- § 1. Составление уравнений заданных линий.
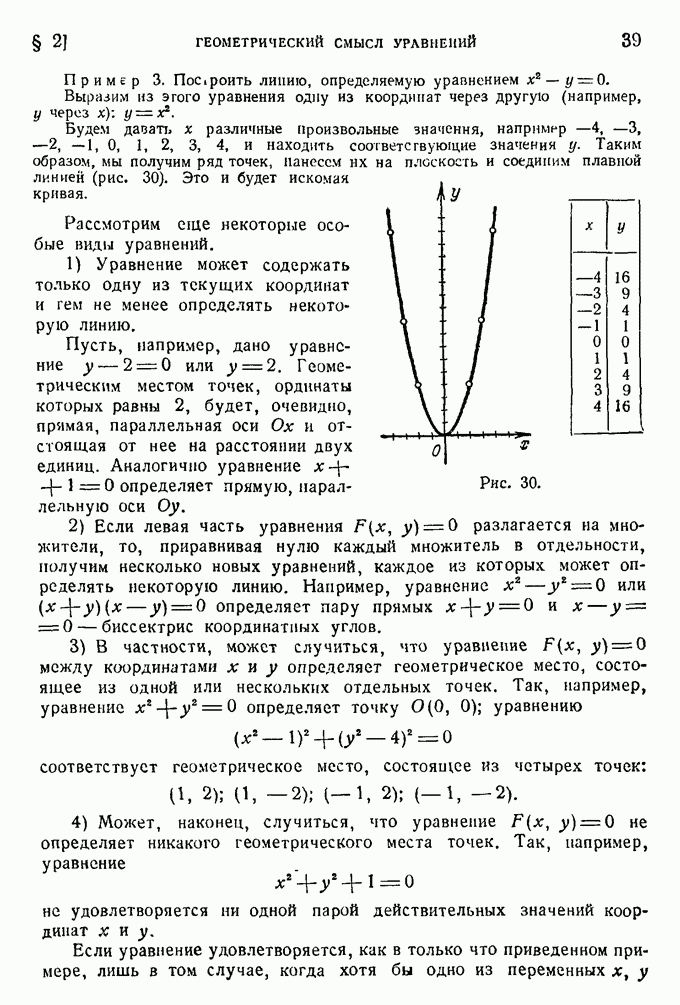
- § 2. Геометрический смысл уравнений.
- § 3. Две основные задачи.
- § 4. Пересечение двух линий.
- § 5. Параметрические уравнения линий.
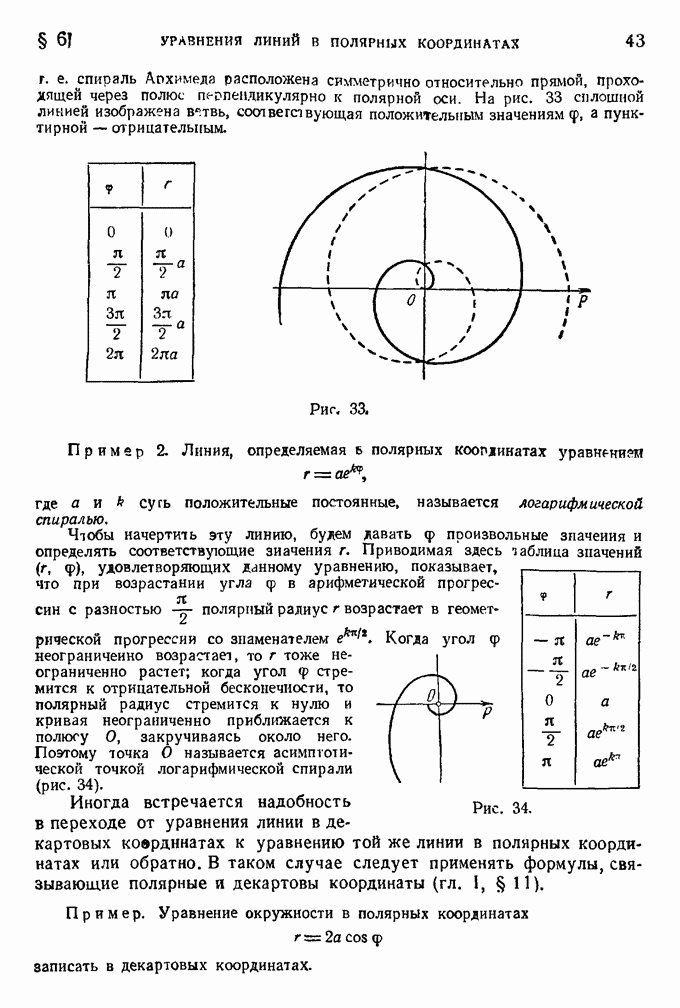
- § 6. Уравнения линий в полярных координатах.
- ГЛАВА III. ПРЯМАЯ ЛИНИЯ
- § 1. Угловой коэффициент прямой.
- § 2. Уравнение прямой линии с угловым коэффициентом.
- § 3. Геометрический смысл уравнения первой степени между двумя переменными.
- § 4. Исследование общего уравнения первой степени Ах + Ву + С = 0.
- § 5. Уравнение прямой линии в отрезках.
- § 6. Построение прямой линии по ее уравнению.
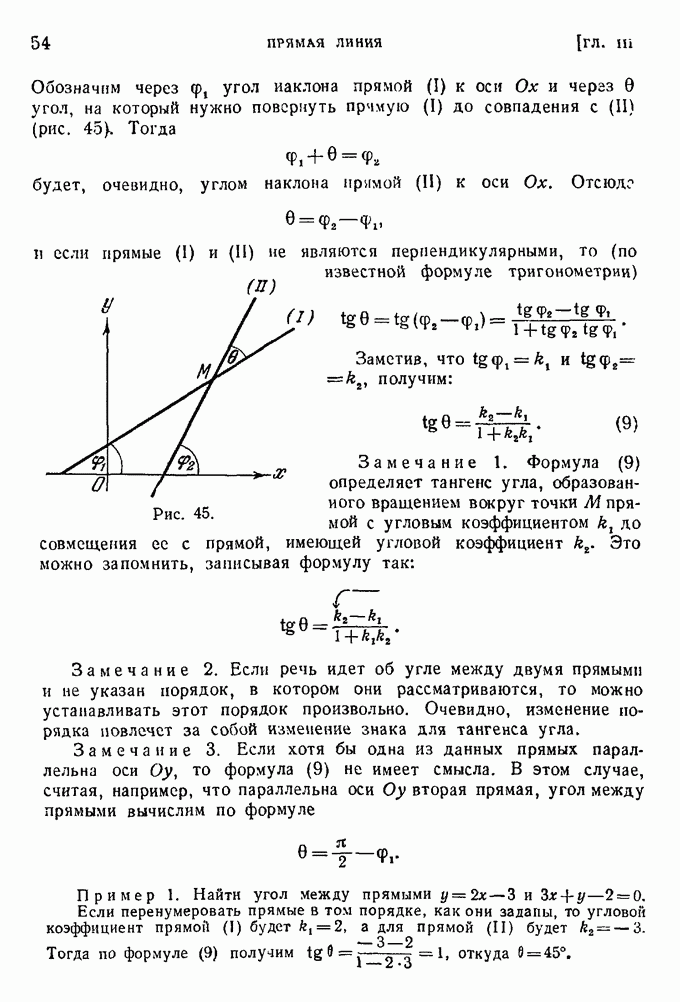
- § 7. Угол между двумя прямыми.
- § 8. Условия параллельности и перпендикулярности двух прямых.
- § 9. Уравнение прямой, проходящей через данную точку в данном направлении.
- § 10. Взаимное расположение двух прямых на плоскости.
- § 11. Уравнение пучка прямых.
- § 12. Уравнение прямой, проходящей через две данные точки.
- § 13. Условие, при котором три данные точки лежат на одной прямой.
- § 14. Нормальное уравнение прямой линии.
- § 15. Приведение общего уравнения первой степени к нормальному виду.
- § 16. Расстояние от дайной точки до данной прямой.
- § 17. Уравнение прямой в полярной системе координат.
- Упражнения
- ГЛАВА IV. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ КОНИЧЕСКИХ СЕЧЕНИЙ
- § 2. Окружность.
- § 3. Эллипс.
- § 4. Гипербола и ее асимптоты.
- § 5. Парабола.
- § 6. Построение точек эллипса, гиперболы и параболы посредством циркуля и линейки.
- § 7. Эллипс, гипербола и парабола как конические сечения.
- § 8. Эксцентриситет и директрисы эллипса.
- § 9. Эксцентриситет и директрисы гиперболы.
- § 10. Эксцентриситет и директриса параболы.
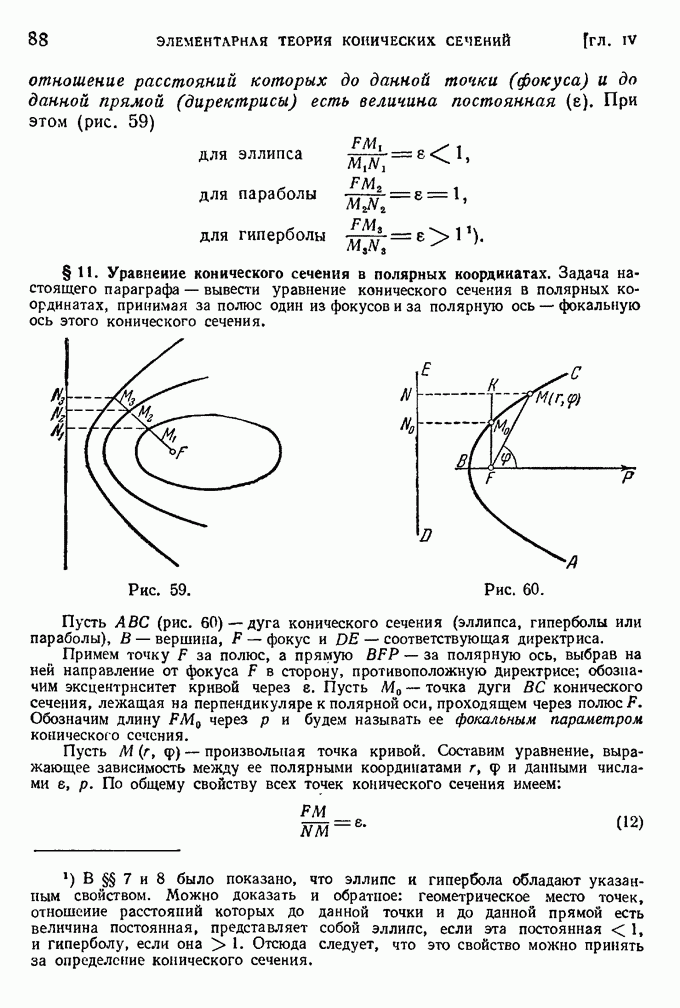
- § 11. Уравнение конического сечения в полярных координатах.
- § 12. Диаметры зллипса. Сопряженные диаметры.
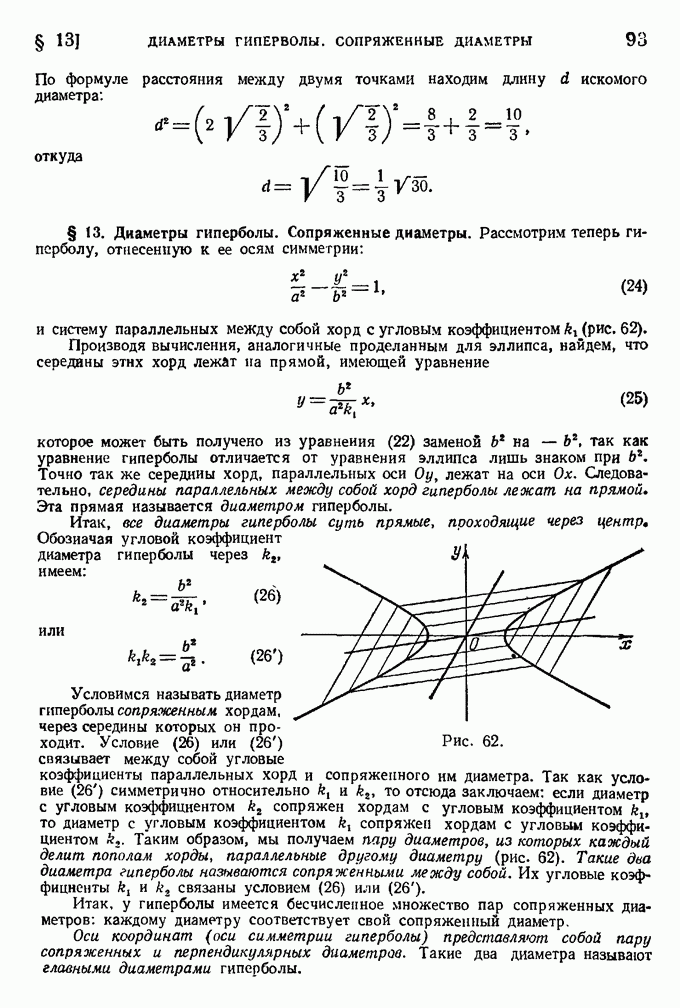
- § 13. Диаметры гиперболы. Сопряженные диаметры.
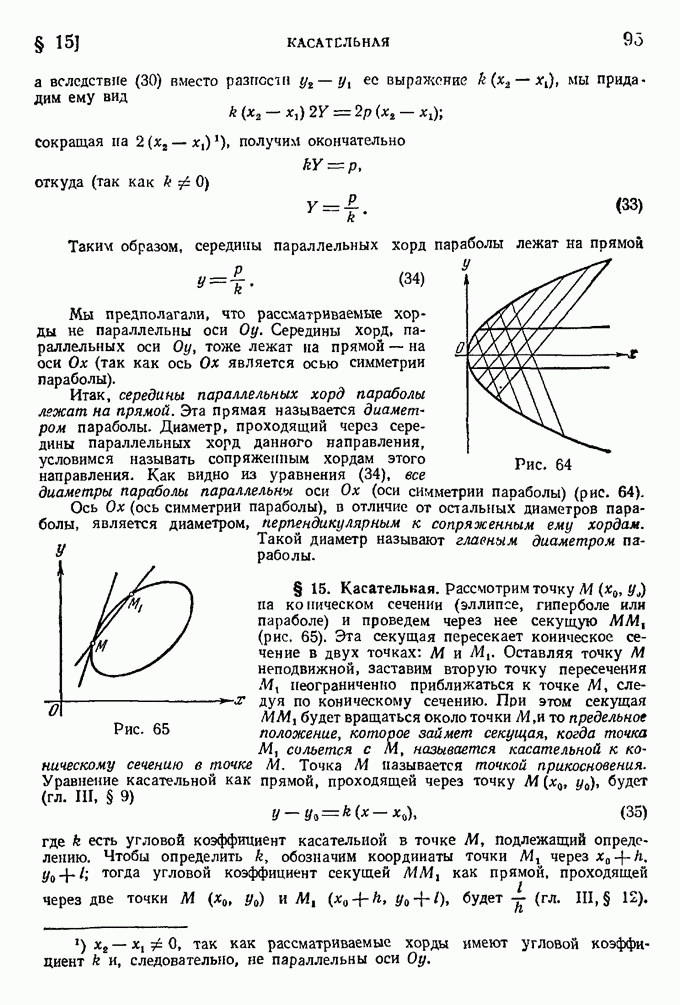
- § 14. Диаметры параболы.
- § 15. Касательная.
- § 16. Эллипс как проекция окружности.
- § 17. Параметрические уравнения эллипса.
- Упражнения
- ГЛАВА V. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. КЛАССИФИКАЦИЯ ЛИНИЙ
- § 2. Перенос начала координат.
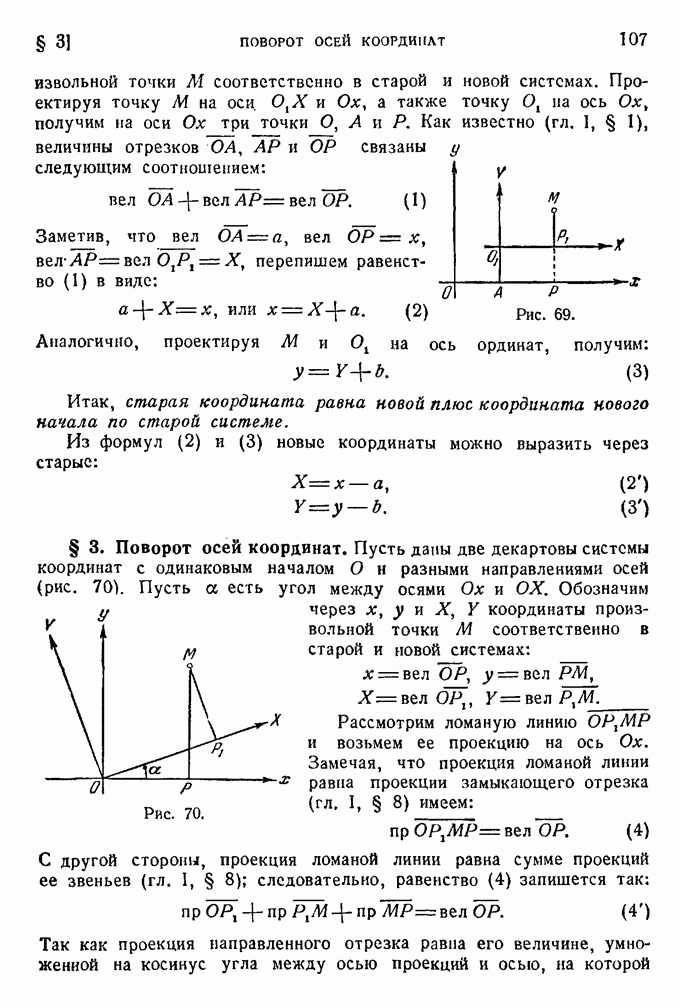
- § 3. Поворот осей координат.
- § 4. Общий случай.
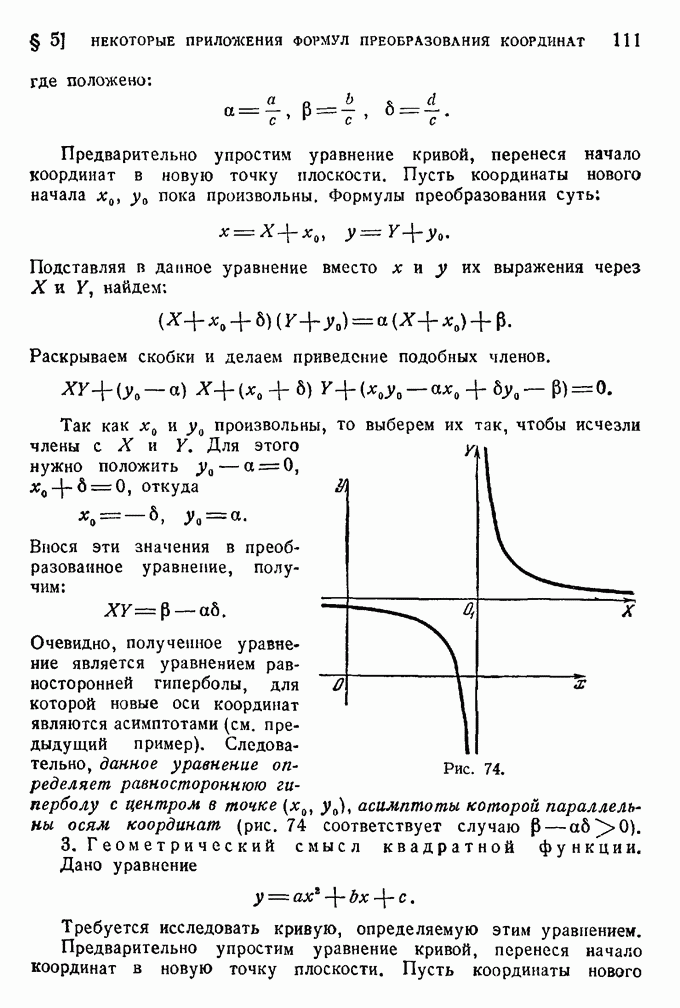
- § 5. Некоторые приложения формул преобразования координат.
- § 6. Преобразование общего уравнения второй степени, не содержащего произведения переменных.
- § 7. Преобразование общего уравнения второй степени.
- § 8. Классификация линий.
- Упражнения
- ГЛАВА VI. ОПРЕДЕЛИТЕЛИ 2-го и 3-го ПОРЯДКА
- § 2. Однородная система двух уравнений с тремя неизвестными.
- § 3. Определители 3-го порядка.
- § 4. Основные свойства определителей 3-го порядка.
- § 5. Система трех уравнений первой степени с тремя неизвестными.
- § 6. Однородная система.
- § 7. Общее исследование системы трех уравнений первой степени с тремя неизвестными.
- § 8. Некоторые приложения определителей к аналитической геометрии.
- Упражнения
- ЧАСТЬ ВТОРАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
- ГЛАВА I. МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ
- § 2. Основные задачи.
- § 3. Основные положения теории проекций в пространстве.
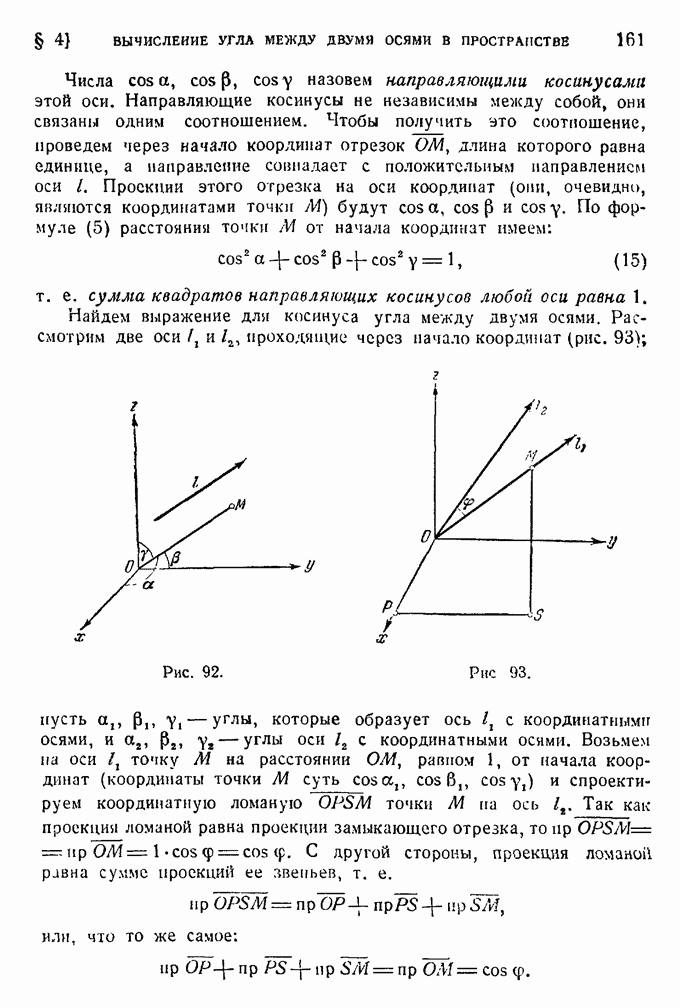
- § 4. Вычисление угла между двумя осями в пространстве.
- Упражнения
- ГЛАВА II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
- § 2. Сложение векторов.
- § 3. Вычитание векторов.
- § 4. Умножение вектора на число.
- § 5. Проекции вектора.
- § 6. Действия над векторами, заданными своими проекциями.
- § 7. Скалярное произведение векторов.
- § 8. Основные свойства скалярного произведения.
- § 9. Скалярное произведение векторов, заданных проекциями.
- § 10. Направление вектора.
- § 11. Векторное произведение.
- § 12. Основные свойства векторного произведения.
- § 13. Векторное произведение векторов, заданных проекциями.
- § 14. Векторно-скалярное произведение.
- § 15. Векторно-скалярное произведение в проекциях.
- § 16. Двойное векторное произведение.
- Упражнения
- ГЛАВА III. ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ
- § 1. Уравнение поверхности.
- § 2. Геометрический смысл уравнений.
- § 3. Две основные задачи.
- § 4. Сфера.
- § 5. Цилиндрические поверхности.
- § 6. Уравнения линии в пространстве.
- § 7. Пересечение трех поверхностей.
- Упражнения
- ГЛАВА IV. ПЛОСКОСТЬ
- § 1. Нормальное уравнение плоскости.
- § 2. Геометрический смысл уравнения первой степени между тремя переменными. Приведение общего уравнения первой степени к нормальному виду.
- § 3. Исследование общего уравнения плоскости.
- § 4. Уравнение плоскости в отрезках.
- § 5. Уравнение плоскости, проходящей через данную точку.
- § 6. Уравнение плоскости, проходящей через три данные точки.
- § 7. Угол между двумя плоскостями.
- § 8. Условия параллельности и перпендикулярности двух плоскостей.
- § 9. Точка пересечения трех плоскостей.
- § 10. Расстояние от точки до плоскости.
- Упражнения
- ГЛАВА V. ПРЯМАЯ ЛИНИЯ
- § 1. Уравнения прямой линии.
- § 2. Прямая как линия пересечения двух плоскостей. Общие уравнения прямой.
- § 3. Угол между двумя прямыми линиями.
- § 4. Условия параллельности и перпендикулярности двух прямых.
- § 5. Уравнения прямой, проходящей через две данные точки.
- § 6. Угол между прямой и плоскостью.
- § 7. Условия параллельности и перпендикулярности прямой и плоскости.
- § 8. Уравнение пучка плоскостей.
- § 9. Пересечение прямой с плоскостью.
- § 10. Условие, при котором две прямые лежат в одной плоскости.
- Упражнения
- ГЛАВА VI. ЦИЛИНДРИЧЕСКИЕ И КОНИЧЕСКИЕ ПОВЕРХНОСТИ. ПОВЕРХНОСТИ ВРАЩЕНИЯ. ПОВЕРХНОСТИ 2-го ПОРЯДКА
- § 1. Классификация поверхностей.
- § 2. Цилиндрические поверхности (общий случай).
- § 3. Конические поверхности.
- § 4. Поверхности вращения.
- § 5. Эллипсоид.
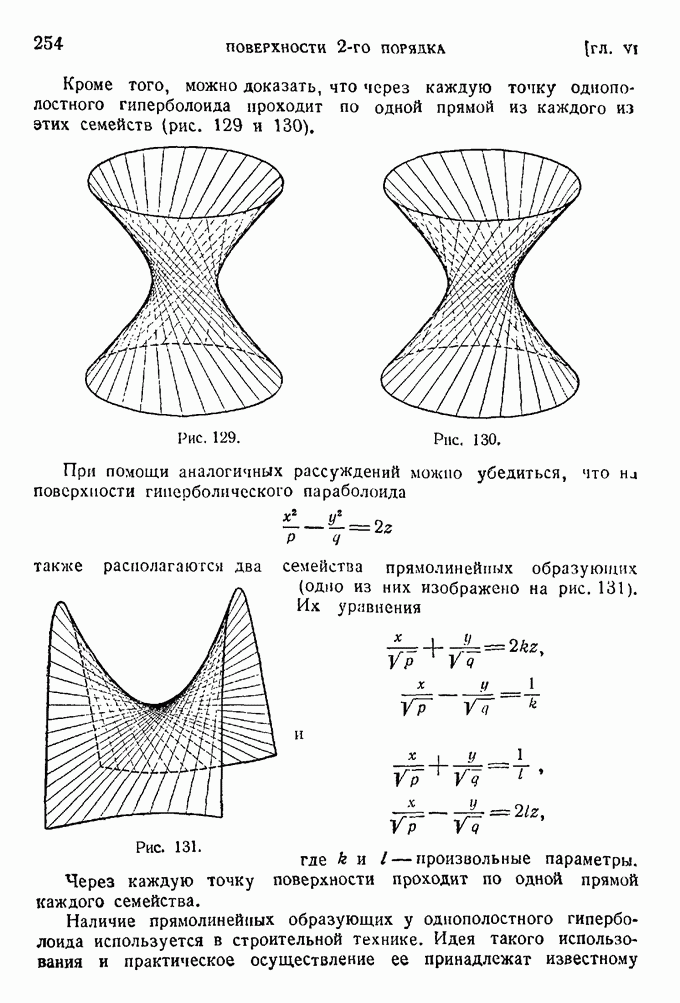
- § 6. Однополостный гиперболоид.
- § 7. Двуполостный гиперболоид.
- § 8. Эллиптический параболоид.
- § 9. Гиперболический параболоид.
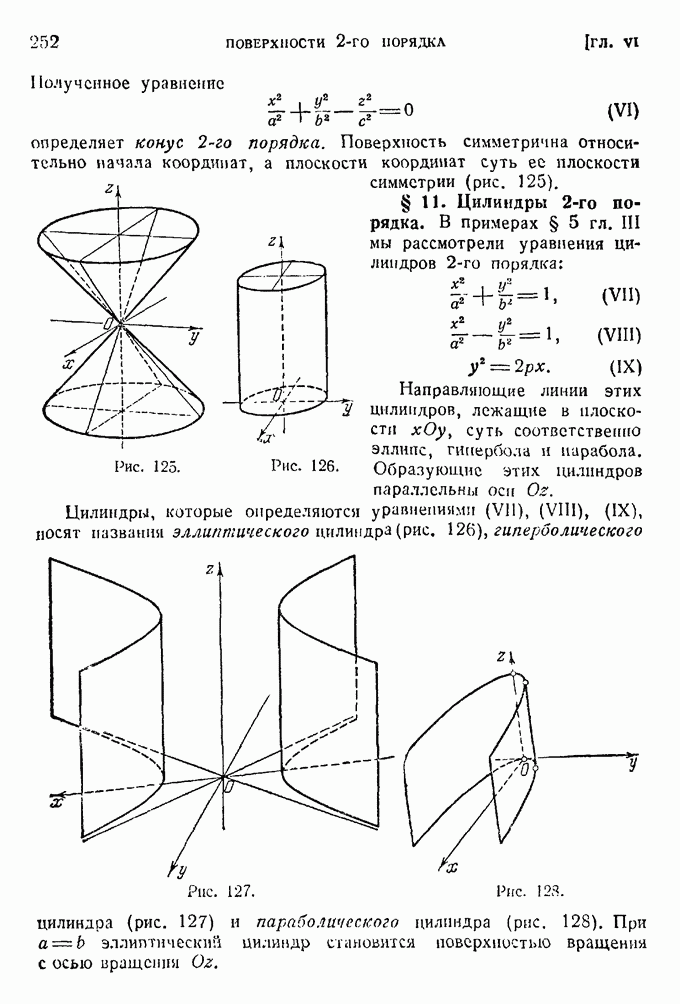
- § 10. Конус 2-го порядка.
- § 11. Цилиндры 2-го порядка.
- § 12. Прямолинейные образующие поверхностей 2-го порядка. Конструкции В. Г. Шухова.
- Упражнения
- Ответы