| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Упражнения
1. Найти уравнение прямой, отсекающей на оси Оу отрезок, величина которого равна 5, и наклоненной к оси Ох под углом: а) 45°; б) 60°; в) 135°; г) 180°.
2. Написагь уравнение прямой, наклоненной к оси Ох под углом в 30° и отсекающей на оси Оу отрезок, величина которого равна —3.
3. Найти уравнение прямой, проходящей через начало координат и наклоненной к оси Ох под углом: а) 45°; б) 135°; в) 180°.
4. Привести к виду уравнений с угловым коэффициентом уравнения прямых:

5. Написать уравнение прямой, отсекающей на осях  отрезки, величины которых соответственно равны и - 4.
отрезки, величины которых соответственно равны и - 4.
6. Написать уравнения прямых

в фооме уравнений в отрезках.
7. Найти угол наклона прямой  к оси
к оси 
8. Построить прямые, определяемые уравнениями

9. Какое расположение относительно осей координат имеют прямые, выражаемые уравнениями

10. Диагонали ромба, равные 8 и 6 единицам длины, приняты за оси координат. Найти уравнения сторон этого ромба.
11. Определить площадь треугольника, заключенного между осями координат и прямой 
12. Найти площадь треугольника, ограниченного прямыми

13. Какая зависимость должна быть между коэффициентами а и b, чтобы прямая  была наклонена к оси Ох под углом: а) 45°;б) 60°; в) 135°?
была наклонена к оси Ох под углом: а) 45°;б) 60°; в) 135°?
14. Исследовать, как расположены относительно осей координат следующие прямые:  Построить эти прямые.
Построить эти прямые.
15. Найти уравнение прямой, проходящей через точку (2, 3) и наклоненной к оси абсцисс под углом в 45°.
16. Найти уравнение прямой, проходящей через точку (2, — 3) параллельно прямой, Соединяющей точки (1, 2) и  .
.
17. Найти уравнение прямой, проходящей через точку (1, 2) и перпендикулярной к прямой, соединяющей точки (4, 3) и 
18. Даны вершины четырехугольника  . Найтн точку пересечения его диагоналей.
. Найтн точку пересечения его диагоналей.
19. Вычислить угол между прямыми:

20. Найти угол между прямыми: 
21. Провести через точку (3, 3) прямые, составляющие углы в 45° с прямой 
22. Найти внутренние углы треугольника, стороны которого выражены уравнениями

23. Найти длины сторон и внутренние углы треугольника с вершинами 
24. Даны две вершины треугольника  и гочка пересечения его медиан
и гочка пересечения его медиан  Найти третью вершину С.
Найти третью вершину С.
25. Найти уравнение прямой, которая проходит через начало координат и а) параллельна прямой  ; б) перпендикулярна к прямой
; б) перпендикулярна к прямой  в) образует угол в
в) образует угол в  с прямой
с прямой  .
.
26. Найти уравнение прямой, которая проходит через точку  и а) параллельна оси
и а) параллельна оси  параллельна биссектрисе I координатного угла; в) параллельна прямой
параллельна биссектрисе I координатного угла; в) параллельна прямой  образует угол в 60° с прямой
образует угол в 60° с прямой 
д) перпендикулярна к прямой 
27. Найти уравнения двух перпендикуляров к прямой  восставленных в точках пересечения ее с осями координат.
восставленных в точках пересечения ее с осями координат.
28. Провести через точку пересечения прямых  прямую, параллельную прямой
прямую, параллельную прямой 
29. Провести через точку пересечения прямых  прямую, перпендикулярную к первой из них.
прямую, перпендикулярную к первой из них.
30. Провести прямую, соединяющую точку пересечения прямых

с началом координат.
31. Через точку пересечения прямых  провести прямую под углом в 45° к прямой
провести прямую под углом в 45° к прямой 
32. Найти прямую, проходящую через точку (2, —3) и образующую с осью Ох угол, вдвое больший угла, образуемого с той же осью прямою 
33. Через точку пересечения прямых  провести прямую, параллельную прямой
провести прямую, параллельную прямой 
34. Через точку пересечения прямых  провести прямую под углом в 45° к прямой
провести прямую под углом в 45° к прямой  (угол отсчитывается от прямой
(угол отсчитывается от прямой 
35. Стороны треугольника выражаются уравнениями

Найти уравнения иысот этого треугольника.
36. Вершины треугольника суть (0, 5), (1, —2), (-6, 5). Найти уравнения перпендикуляров, восставленных в серединах его сторон, а также точку пересечения этих перпендикуляров.
37. Вершины треугольника суть (0, 1), (1, 0), (1, 1). Найти уравнения медиан.
38. Вершины треугольника суть  Найти уравнения медиан и точку их пересечения.
Найти уравнения медиан и точку их пересечения.
39. Найти уравнение прямой, проходящей через начало координат и через точку пересечения медиан треугольника, стороны которого выражаются уравнениями 
40. Найти уравнение прямой, проходящей через начало координат и через точку пересечения медиан треугольника, стороны которого выражаются уравнениями 
41. На прямой  найти точку, равноудаленную от точек
найти точку, равноудаленную от точек  и (1, 4).
и (1, 4).
42. На прямой  иайти точку, равноудаленную от точек
иайти точку, равноудаленную от точек  .
.
43. Найти точку, равноудаленную от точек 
44. Даны уравнения двух сторон параллелограмма:

и точка пересечения его диагоналей (3, 3). Найти уравнения двух других сторон.
45. Даны две вершины равностороннего треугольника  и
и  Найти третью вершину С.
Найти третью вершину С.
46. Даны уравнения прямых: а)  Какие из этих уравнений являются уравнениями в нормальном виде?
Какие из этих уравнений являются уравнениями в нормальном виде?
47. Найти уравнение прямой по следующим условиям: ее расстояние от начала координат равно 7 едшшцам длины и угол между осью Ох и перпендикуляром к искомой прямой, проведенным из начала координат, равен 120°.
48. Написать уравнение прямой, если известно, что ее расстояние от начала координат равно 5 и что перпендикуляр, опущенный на нее  начала координат, составляет с осью Ох угол в 60°.
начала координат, составляет с осью Ох угол в 60°.
49. Привести к нормальному виду уравнения следующих прямых:

50. Найти длины перпендикуляров, опущенных из начала координат на прямые  Найти также координаты оснований этих перпендикуляров.
Найти также координаты оснований этих перпендикуляров.
51. Вершиной треугольника служит точка (5, —3), а основанием — огрезок, соединяющий точки (0, —1) и (3, 3). Найти длину высоты треугольника.
52. На прямой  найти точку, равноудаленную от начала координат и от прямой
найти точку, равноудаленную от начала координат и от прямой 
53. Дана прямая  Найги уравнение прямой, параллельной данной и отстоящей от нее на расстоянии 3 единиц.
Найги уравнение прямой, параллельной данной и отстоящей от нее на расстоянии 3 единиц.
54. Дана прямая  Найти уравнение прямой, параллельной данной и отстоящей от нее на расстоянии 3 единиц.
Найти уравнение прямой, параллельной данной и отстоящей от нее на расстоянии 3 единиц.
55. Найги расстояние между параллельными прямыми

56. Найти расстояние между параллельными прямыми

57. Даны уравнения оснований трапеции:  Найти ее высоту.
Найти ее высоту.
58. Написать уравнение прямой, проходящей через точку  на расстоянии 4 единиц от точки
на расстоянии 4 единиц от точки 
59. Из точки (1, —2) провести касательные к окружности радиуса  центр которой лежит в точке (3, 6).
центр которой лежит в точке (3, 6).
60. Найти биссектрисы углов, образуемых прямыми  Проверить, что эти биссектрисы перпендикулярны друг к другу.
Проверить, что эти биссектрисы перпендикулярны друг к другу.
61. Найти биссектрисы углов, образуемых прямыми

62. Найти уравнение биссектрисы внешнего угла А треугольника с вершинами 
63. Найти точку, равноудаленную от точек  и отстоящую от прямой
и отстоящую от прямой  на расстоянии, равном 2.
на расстоянии, равном 2.
64. Даны центр квадрата  и уравнение стороны
и уравнение стороны

Составить уравнения остальных трех сторон.
65. В прямоугольном равнобедренном треугольнике даны уравнение катета  и середина гипотенузы
и середина гипотенузы  Найти уравнения двух других его сторон.
Найти уравнения двух других его сторон.
66. Найти геометрическое место точек, разность квадратов расстояний которых от двух данных точек равна постоянной величине.
67. Основание треугольника неподвижно, а вершина движется по данной прямой. Найти уравнение линии, описываемой центром тяжести этого треугольника.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ЧАСТЬ ПЕРВАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
- ГЛАВА I. МЕТОД КООРДИНАТ
- § 2. Координаты на прямой линии.
- § 3. Расстояние между двумя точками на прямой линии.
- § 4. Прямоугольные координаты на плоскости.
- § 5. Расстояние между двумя точками на плоскости.
- § 6. Деление отрезка в данном отношении.
- § 7. Угол между двумя осями.
- § 8. Основные положения теории проекций.
- § 9. Проекции направленного отрезка на оси координат.
- § 10. Площадь треугольника.
- § 11. Полярные координаты.
- Упражнения
- ГЛАВА II. ЛИНИИ И ИХ УРАВНЕНИЯ
- § 1. Составление уравнений заданных линий.
- § 2. Геометрический смысл уравнений.
- § 3. Две основные задачи.
- § 4. Пересечение двух линий.
- § 5. Параметрические уравнения линий.
- § 6. Уравнения линий в полярных координатах.
- ГЛАВА III. ПРЯМАЯ ЛИНИЯ
- § 1. Угловой коэффициент прямой.
- § 2. Уравнение прямой линии с угловым коэффициентом.
- § 3. Геометрический смысл уравнения первой степени между двумя переменными.
- § 4. Исследование общего уравнения первой степени Ах + Ву + С = 0.
- § 5. Уравнение прямой линии в отрезках.
- § 6. Построение прямой линии по ее уравнению.
- § 7. Угол между двумя прямыми.
- § 8. Условия параллельности и перпендикулярности двух прямых.
- § 9. Уравнение прямой, проходящей через данную точку в данном направлении.
- § 10. Взаимное расположение двух прямых на плоскости.
- § 11. Уравнение пучка прямых.
- § 12. Уравнение прямой, проходящей через две данные точки.
- § 13. Условие, при котором три данные точки лежат на одной прямой.
- § 14. Нормальное уравнение прямой линии.
- § 15. Приведение общего уравнения первой степени к нормальному виду.
- § 16. Расстояние от дайной точки до данной прямой.
- § 17. Уравнение прямой в полярной системе координат.
- Упражнения
- ГЛАВА IV. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ КОНИЧЕСКИХ СЕЧЕНИЙ
- § 2. Окружность.
- § 3. Эллипс.
- § 4. Гипербола и ее асимптоты.
- § 5. Парабола.
- § 6. Построение точек эллипса, гиперболы и параболы посредством циркуля и линейки.
- § 7. Эллипс, гипербола и парабола как конические сечения.
- § 8. Эксцентриситет и директрисы эллипса.
- § 9. Эксцентриситет и директрисы гиперболы.
- § 10. Эксцентриситет и директриса параболы.
- § 11. Уравнение конического сечения в полярных координатах.
- § 12. Диаметры зллипса. Сопряженные диаметры.
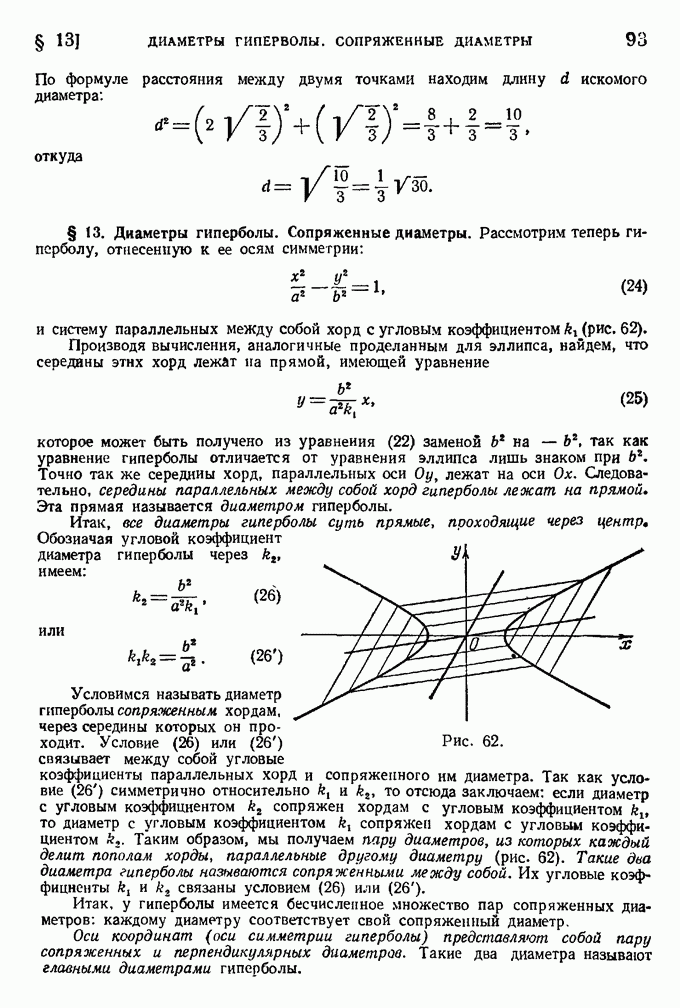
- § 13. Диаметры гиперболы. Сопряженные диаметры.
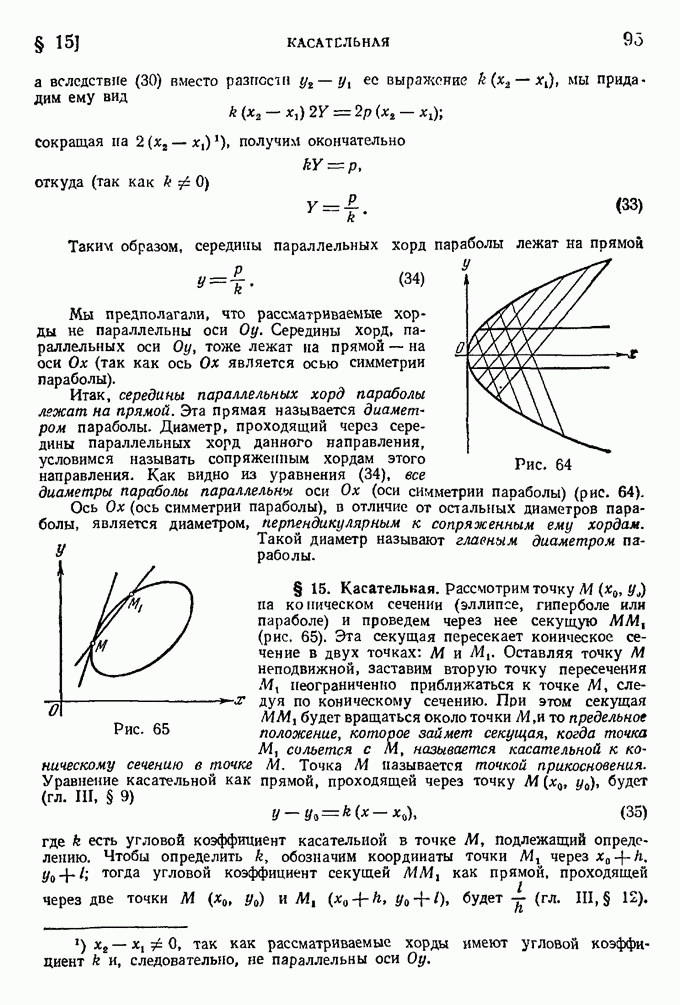
- § 14. Диаметры параболы.
- § 15. Касательная.
- § 16. Эллипс как проекция окружности.
- § 17. Параметрические уравнения эллипса.
- Упражнения
- ГЛАВА V. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. КЛАССИФИКАЦИЯ ЛИНИЙ
- § 2. Перенос начала координат.
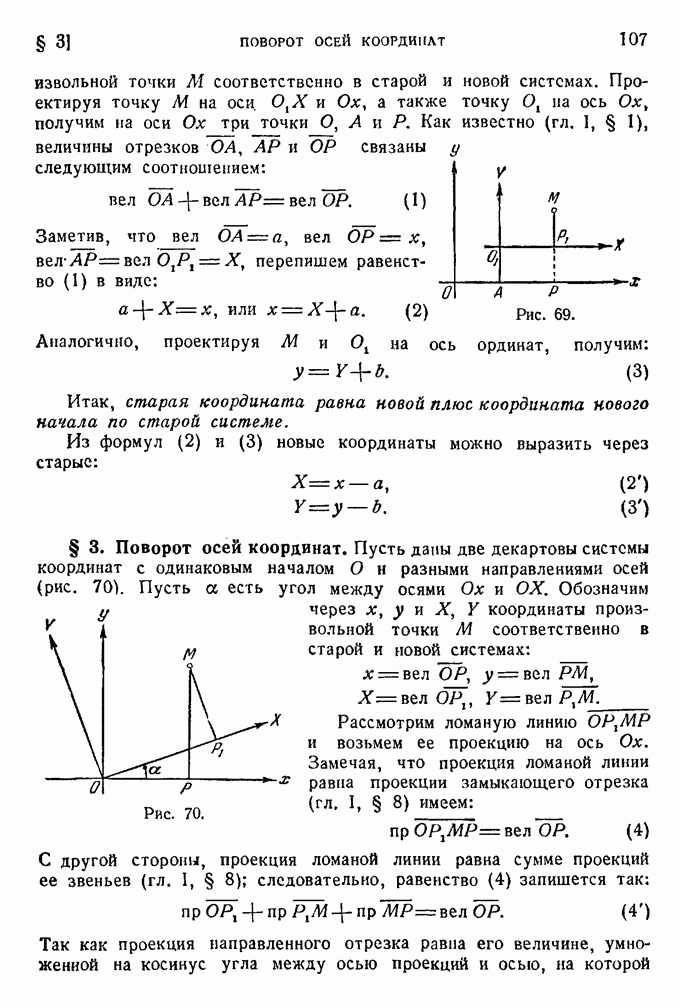
- § 3. Поворот осей координат.
- § 4. Общий случай.
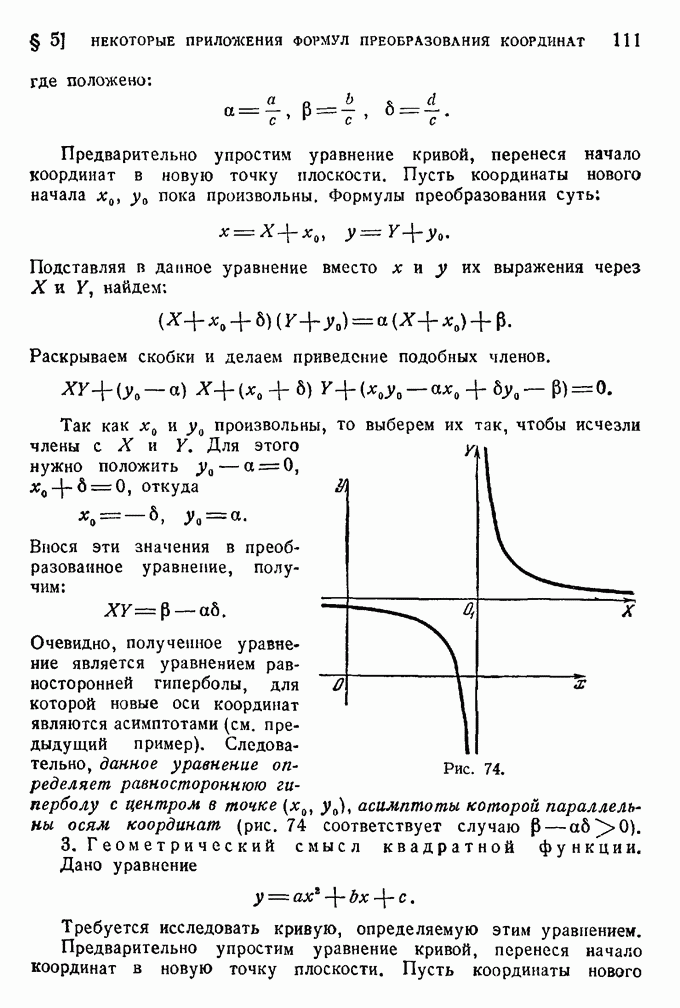
- § 5. Некоторые приложения формул преобразования координат.
- § 6. Преобразование общего уравнения второй степени, не содержащего произведения переменных.
- § 7. Преобразование общего уравнения второй степени.
- § 8. Классификация линий.
- Упражнения
- ГЛАВА VI. ОПРЕДЕЛИТЕЛИ 2-го и 3-го ПОРЯДКА
- § 2. Однородная система двух уравнений с тремя неизвестными.
- § 3. Определители 3-го порядка.
- § 4. Основные свойства определителей 3-го порядка.
- § 5. Система трех уравнений первой степени с тремя неизвестными.
- § 6. Однородная система.
- § 7. Общее исследование системы трех уравнений первой степени с тремя неизвестными.
- § 8. Некоторые приложения определителей к аналитической геометрии.
- Упражнения
- ЧАСТЬ ВТОРАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
- ГЛАВА I. МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ
- § 2. Основные задачи.
- § 3. Основные положения теории проекций в пространстве.
- § 4. Вычисление угла между двумя осями в пространстве.
- Упражнения
- ГЛАВА II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
- § 2. Сложение векторов.
- § 3. Вычитание векторов.
- § 4. Умножение вектора на число.
- § 5. Проекции вектора.
- § 6. Действия над векторами, заданными своими проекциями.
- § 7. Скалярное произведение векторов.
- § 8. Основные свойства скалярного произведения.
- § 9. Скалярное произведение векторов, заданных проекциями.
- § 10. Направление вектора.
- § 11. Векторное произведение.
- § 12. Основные свойства векторного произведения.
- § 13. Векторное произведение векторов, заданных проекциями.
- § 14. Векторно-скалярное произведение.
- § 15. Векторно-скалярное произведение в проекциях.
- § 16. Двойное векторное произведение.
- Упражнения
- ГЛАВА III. ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ
- § 1. Уравнение поверхности.
- § 2. Геометрический смысл уравнений.
- § 3. Две основные задачи.
- § 4. Сфера.
- § 5. Цилиндрические поверхности.
- § 6. Уравнения линии в пространстве.
- § 7. Пересечение трех поверхностей.
- Упражнения
- ГЛАВА IV. ПЛОСКОСТЬ
- § 1. Нормальное уравнение плоскости.
- § 2. Геометрический смысл уравнения первой степени между тремя переменными. Приведение общего уравнения первой степени к нормальному виду.
- § 3. Исследование общего уравнения плоскости.
- § 4. Уравнение плоскости в отрезках.
- § 5. Уравнение плоскости, проходящей через данную точку.
- § 6. Уравнение плоскости, проходящей через три данные точки.
- § 7. Угол между двумя плоскостями.
- § 8. Условия параллельности и перпендикулярности двух плоскостей.
- § 9. Точка пересечения трех плоскостей.
- § 10. Расстояние от точки до плоскости.
- Упражнения
- ГЛАВА V. ПРЯМАЯ ЛИНИЯ
- § 1. Уравнения прямой линии.
- § 2. Прямая как линия пересечения двух плоскостей. Общие уравнения прямой.
- § 3. Угол между двумя прямыми линиями.
- § 4. Условия параллельности и перпендикулярности двух прямых.
- § 5. Уравнения прямой, проходящей через две данные точки.
- § 6. Угол между прямой и плоскостью.
- § 7. Условия параллельности и перпендикулярности прямой и плоскости.
- § 8. Уравнение пучка плоскостей.
- § 9. Пересечение прямой с плоскостью.
- § 10. Условие, при котором две прямые лежат в одной плоскости.
- Упражнения
- ГЛАВА VI. ЦИЛИНДРИЧЕСКИЕ И КОНИЧЕСКИЕ ПОВЕРХНОСТИ. ПОВЕРХНОСТИ ВРАЩЕНИЯ. ПОВЕРХНОСТИ 2-го ПОРЯДКА
- § 1. Классификация поверхностей.
- § 2. Цилиндрические поверхности (общий случай).
- § 3. Конические поверхности.
- § 4. Поверхности вращения.
- § 5. Эллипсоид.
- § 6. Однополостный гиперболоид.
- § 7. Двуполостный гиперболоид.
- § 8. Эллиптический параболоид.
- § 9. Гиперболический параболоид.
- § 10. Конус 2-го порядка.
- § 11. Цилиндры 2-го порядка.
- § 12. Прямолинейные образующие поверхностей 2-го порядка. Конструкции В. Г. Шухова.
- Упражнения
- Ответы