| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
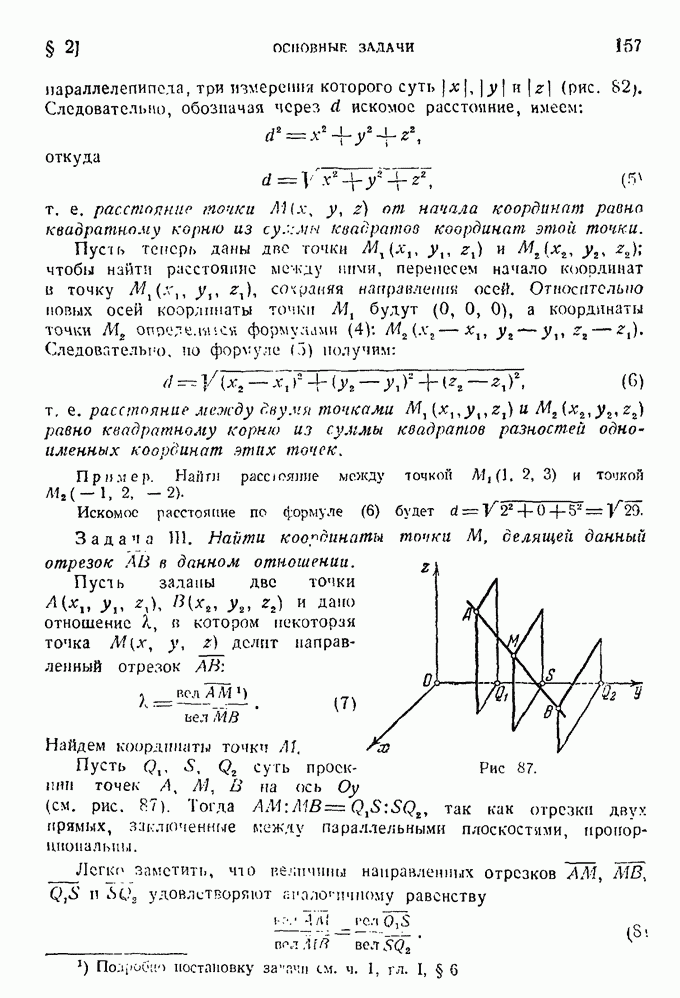
§ 8. Эллиптический параболоид.
Параболоид вращения получается вращением параболы

вокруг оси  Его уравнение будет (гл. VI, § 4):
Его уравнение будет (гл. VI, § 4):

В сечении его плоскостью  перпендикулярной к оси вращения
перпендикулярной к оси вращения  получается окружность, уравнения которой будут:
получается окружность, уравнения которой будут:

и радиус которой равен

Следовательно, при изменении h от 0 до со окружность (22) описывает параболоид вращения.
Возьмем вместо окружности (22) эллипс

( положительные числа), лежащий в плоскости
положительные числа), лежащий в плоскости  параллельной плоскости
параллельной плоскости  полуоси которого суть;
полуоси которого суть;

При изменении  от 0 до
от 0 до  этот эллипс описывает поверхность 2-го порядка, называемую эллиптическим параболоидом, уравнение которой получим, исключив h из двух уравнений (24):
этот эллипс описывает поверхность 2-го порядка, называемую эллиптическим параболоидом, уравнение которой получим, исключив h из двух уравнений (24):


Рис. 123.
Пересекая эту поверхность плоскостями координат  получим в сечении соответственно точку и две параболы:
получим в сечении соответственно точку и две параболы:

Из предыдущего усматриваем, что эллиптический параболоид можно рассматривать как поверхность, образованную движущимся эллипсом, который остается себе подобным и концы осей которого скользят по параболам (26) (рис. 123); плоскость эллипса при движении остается параллельной плоскости хОу.
Уравнение (IV) содержит только квадраты координат х и у, а потому плоскости xOz и yOz являются плоскостями симметрии поверхности. При  уравнение (IV) определяет параболоид вращения с осью вращения
уравнение (IV) определяет параболоид вращения с осью вращения 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ
- ЧАСТЬ ПЕРВАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
- ГЛАВА I. МЕТОД КООРДИНАТ
- § 2. Координаты на прямой линии.
- § 3. Расстояние между двумя точками на прямой линии.
- § 4. Прямоугольные координаты на плоскости.
- § 5. Расстояние между двумя точками на плоскости.
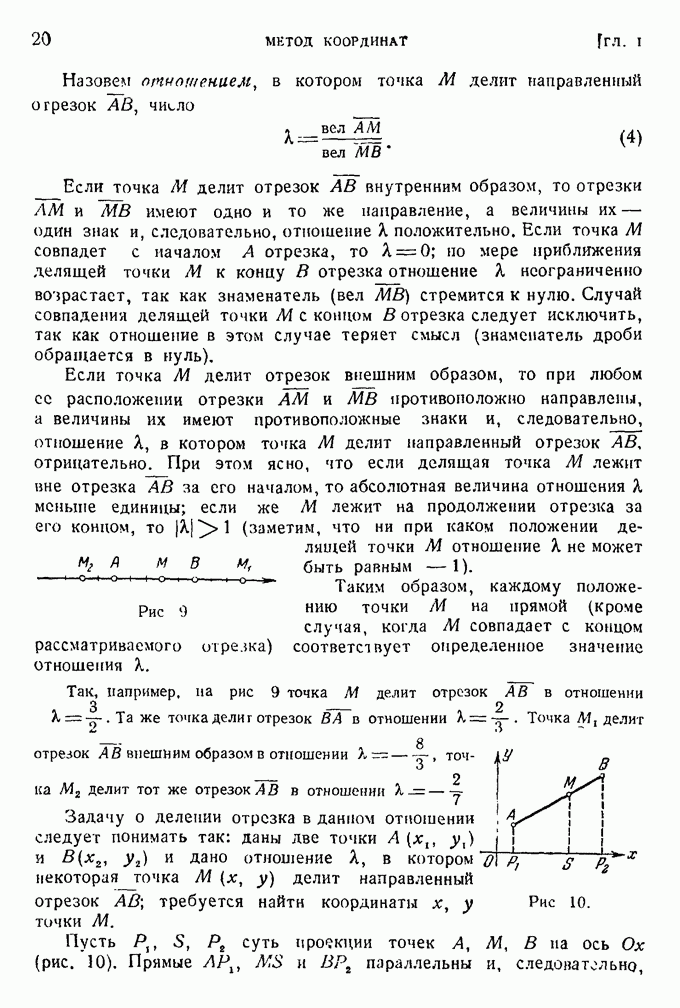
- § 6. Деление отрезка в данном отношении.
- § 7. Угол между двумя осями.
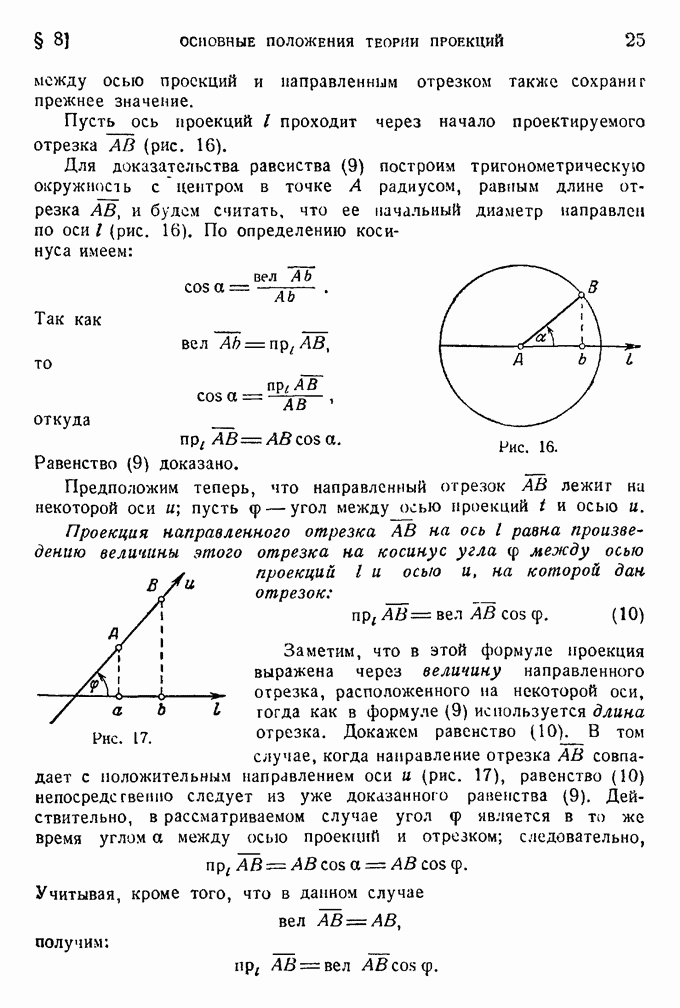
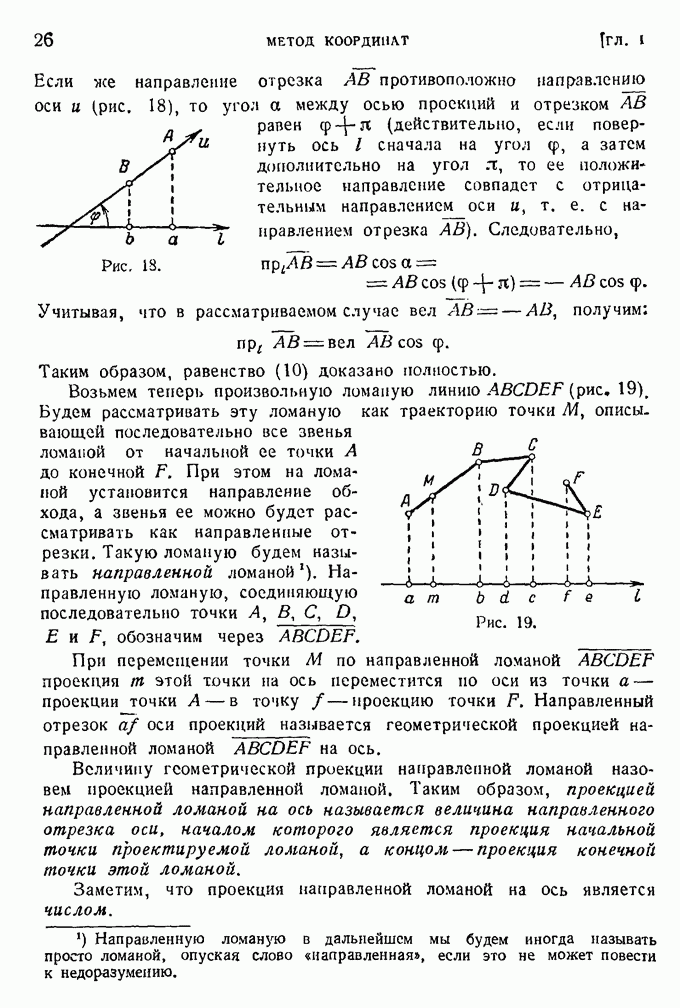
- § 8. Основные положения теории проекций.
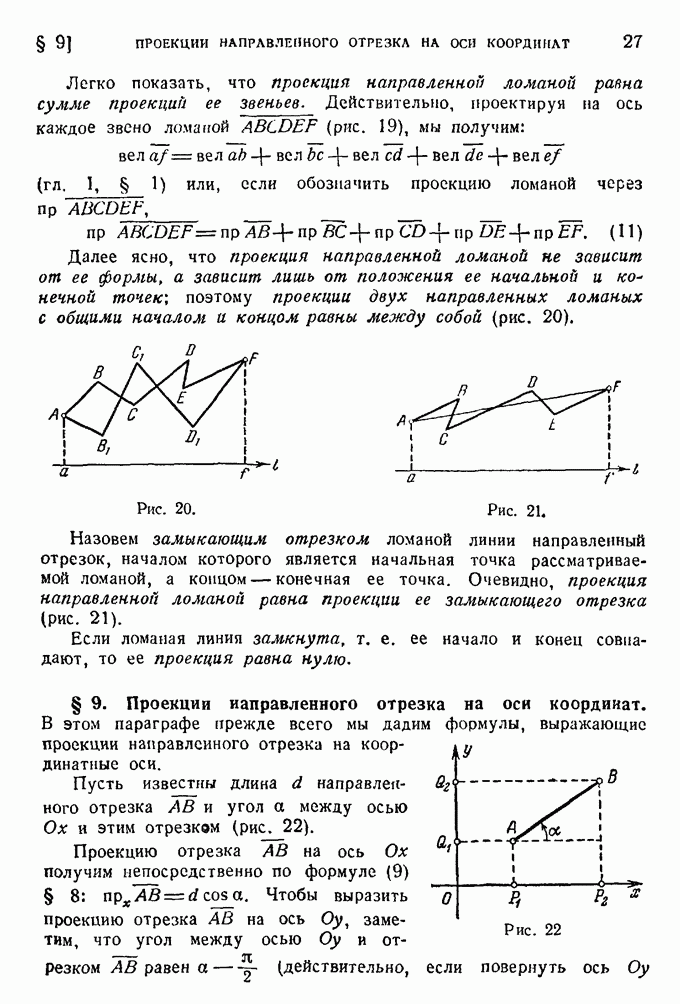
- § 9. Проекции направленного отрезка на оси координат.
- § 10. Площадь треугольника.
- § 11. Полярные координаты.
- Упражнения
- ГЛАВА II. ЛИНИИ И ИХ УРАВНЕНИЯ
- § 1. Составление уравнений заданных линий.
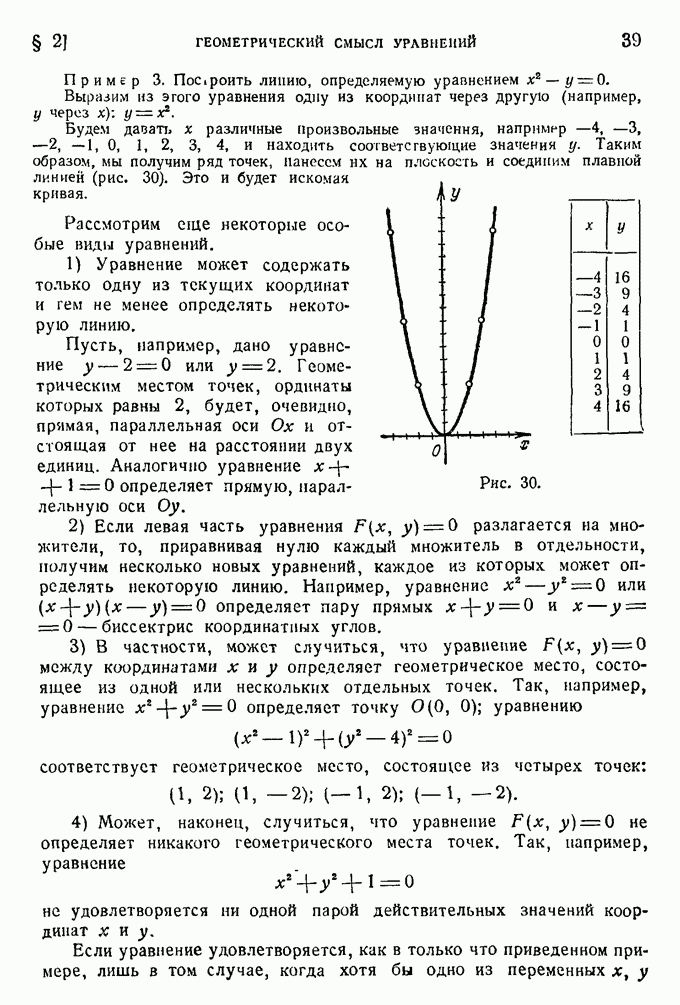
- § 2. Геометрический смысл уравнений.
- § 3. Две основные задачи.
- § 4. Пересечение двух линий.
- § 5. Параметрические уравнения линий.
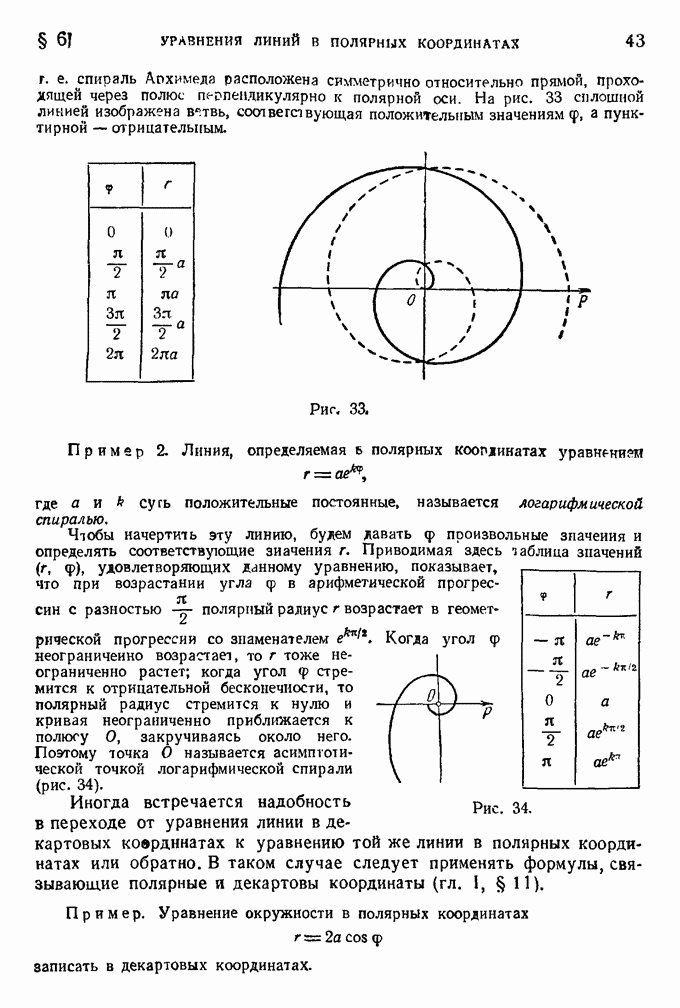
- § 6. Уравнения линий в полярных координатах.
- ГЛАВА III. ПРЯМАЯ ЛИНИЯ
- § 1. Угловой коэффициент прямой.
- § 2. Уравнение прямой линии с угловым коэффициентом.
- § 3. Геометрический смысл уравнения первой степени между двумя переменными.
- § 4. Исследование общего уравнения первой степени Ах + Ву + С = 0.
- § 5. Уравнение прямой линии в отрезках.
- § 6. Построение прямой линии по ее уравнению.
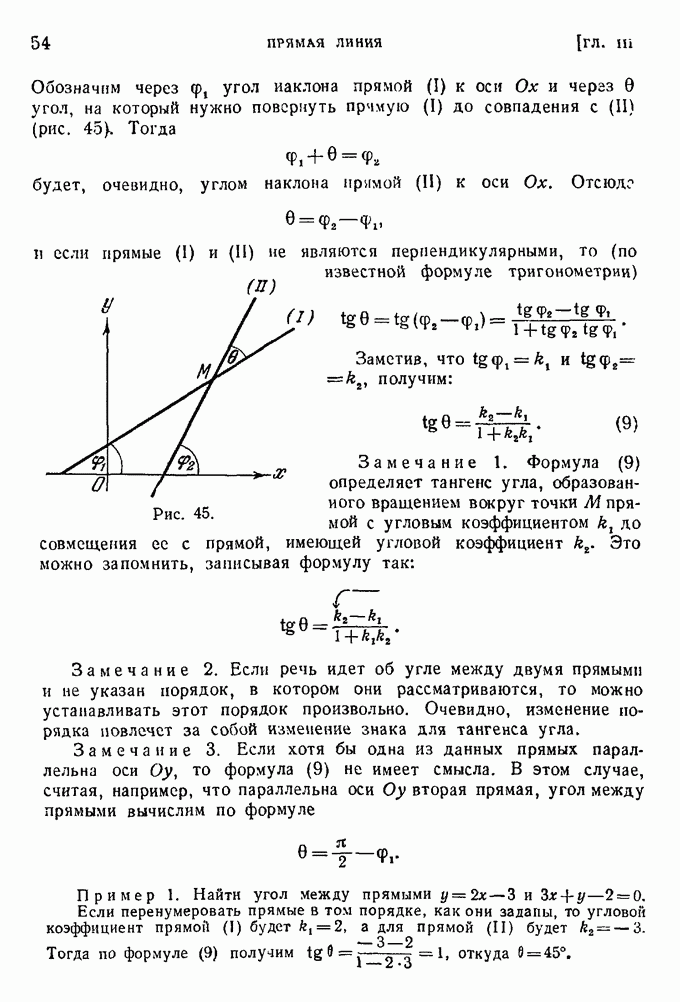
- § 7. Угол между двумя прямыми.
- § 8. Условия параллельности и перпендикулярности двух прямых.
- § 9. Уравнение прямой, проходящей через данную точку в данном направлении.
- § 10. Взаимное расположение двух прямых на плоскости.
- § 11. Уравнение пучка прямых.
- § 12. Уравнение прямой, проходящей через две данные точки.
- § 13. Условие, при котором три данные точки лежат на одной прямой.
- § 14. Нормальное уравнение прямой линии.
- § 15. Приведение общего уравнения первой степени к нормальному виду.
- § 16. Расстояние от дайной точки до данной прямой.
- § 17. Уравнение прямой в полярной системе координат.
- Упражнения
- ГЛАВА IV. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ КОНИЧЕСКИХ СЕЧЕНИЙ
- § 2. Окружность.
- § 3. Эллипс.
- § 4. Гипербола и ее асимптоты.
- § 5. Парабола.
- § 6. Построение точек эллипса, гиперболы и параболы посредством циркуля и линейки.
- § 7. Эллипс, гипербола и парабола как конические сечения.
- § 8. Эксцентриситет и директрисы эллипса.
- § 9. Эксцентриситет и директрисы гиперболы.
- § 10. Эксцентриситет и директриса параболы.
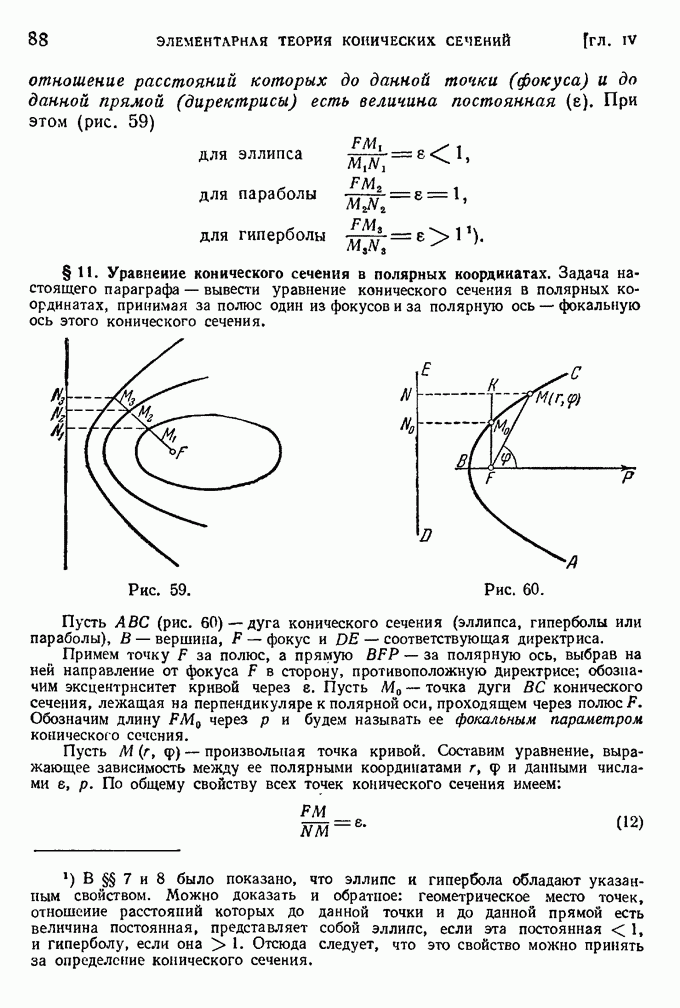
- § 11. Уравнение конического сечения в полярных координатах.
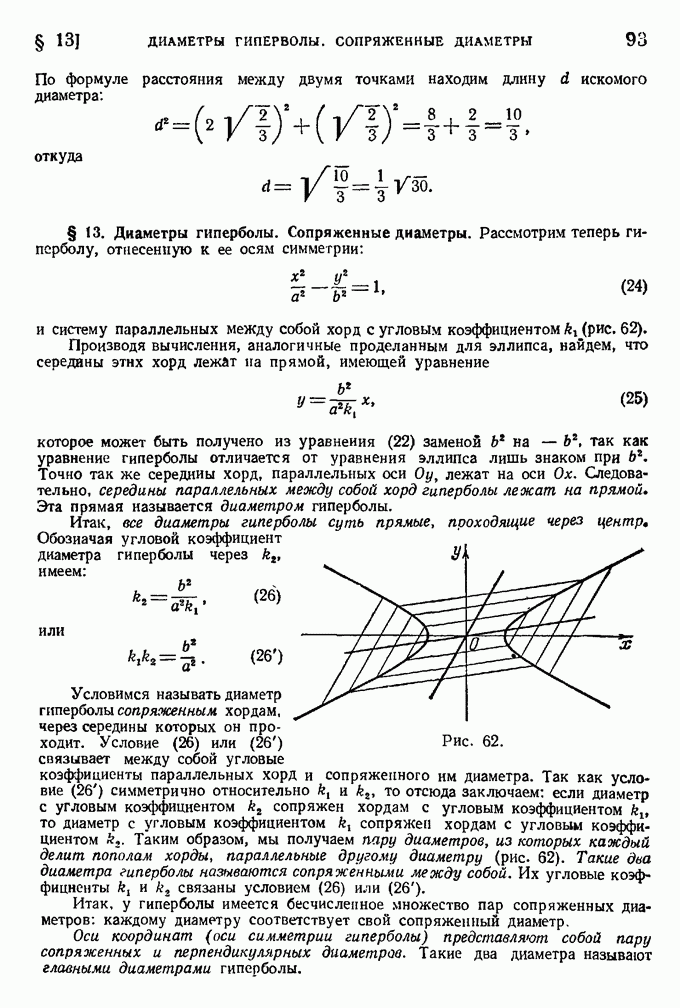
- § 12. Диаметры зллипса. Сопряженные диаметры.
- § 13. Диаметры гиперболы. Сопряженные диаметры.
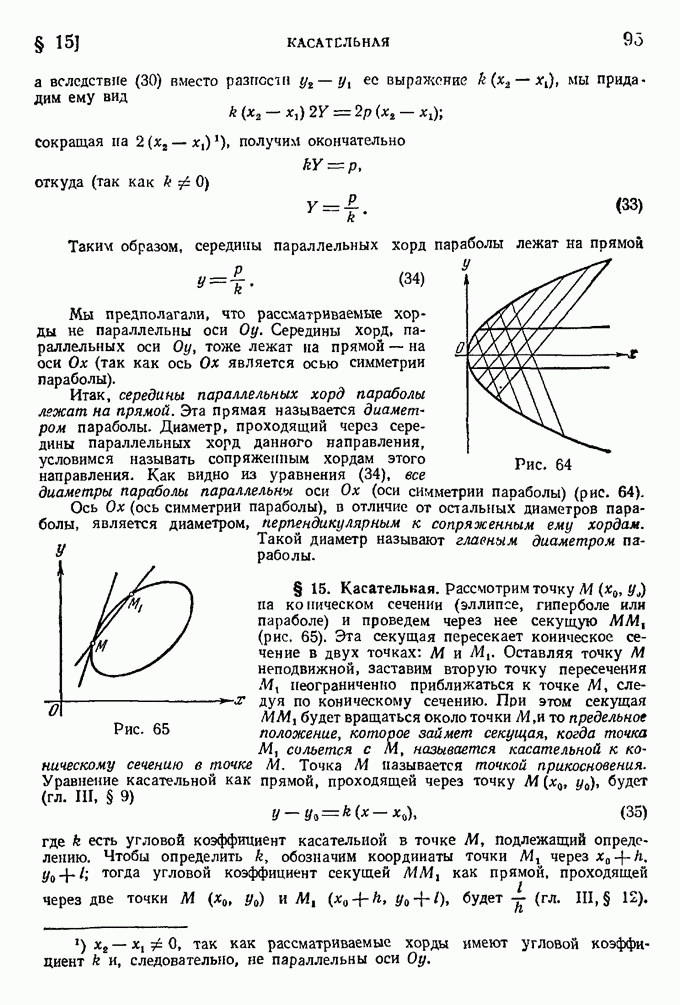
- § 14. Диаметры параболы.
- § 15. Касательная.
- § 16. Эллипс как проекция окружности.
- § 17. Параметрические уравнения эллипса.
- Упражнения
- ГЛАВА V. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. КЛАССИФИКАЦИЯ ЛИНИЙ
- § 2. Перенос начала координат.
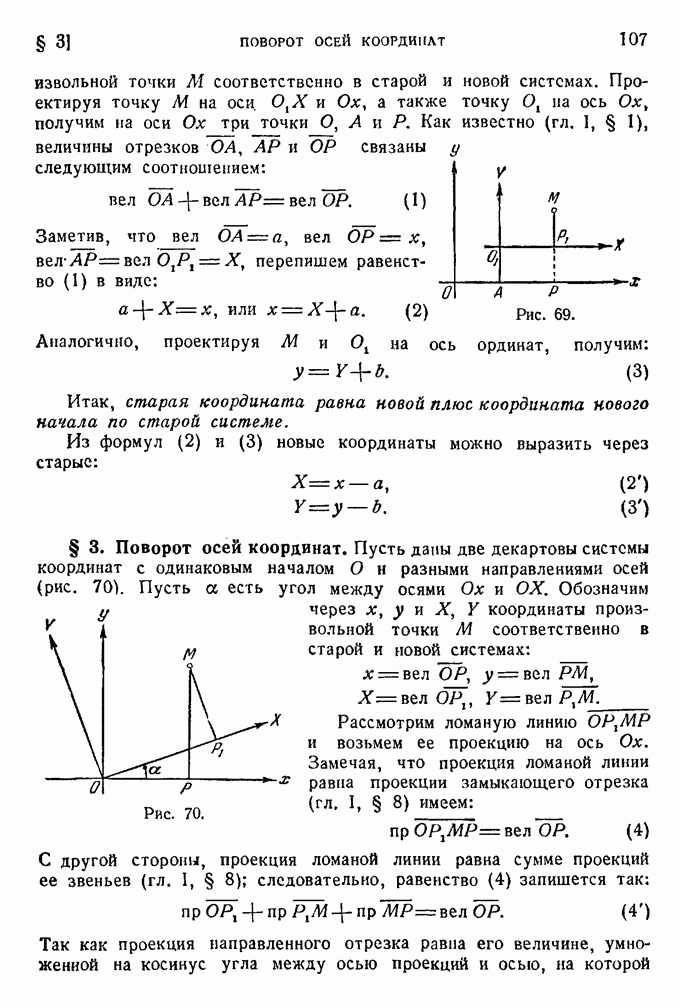
- § 3. Поворот осей координат.
- § 4. Общий случай.
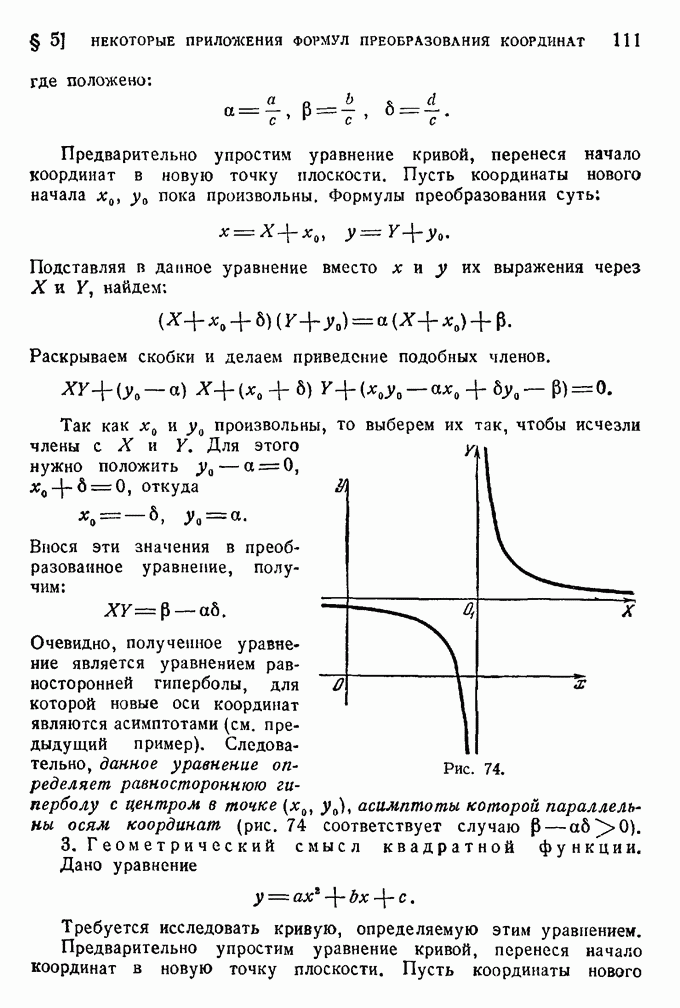
- § 5. Некоторые приложения формул преобразования координат.
- § 6. Преобразование общего уравнения второй степени, не содержащего произведения переменных.
- § 7. Преобразование общего уравнения второй степени.
- § 8. Классификация линий.
- Упражнения
- ГЛАВА VI. ОПРЕДЕЛИТЕЛИ 2-го и 3-го ПОРЯДКА
- § 2. Однородная система двух уравнений с тремя неизвестными.
- § 3. Определители 3-го порядка.
- § 4. Основные свойства определителей 3-го порядка.
- § 5. Система трех уравнений первой степени с тремя неизвестными.
- § 6. Однородная система.
- § 7. Общее исследование системы трех уравнений первой степени с тремя неизвестными.
- § 8. Некоторые приложения определителей к аналитической геометрии.
- Упражнения
- ЧАСТЬ ВТОРАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
- ГЛАВА I. МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ
- § 2. Основные задачи.
- § 3. Основные положения теории проекций в пространстве.
- § 4. Вычисление угла между двумя осями в пространстве.
- Упражнения
- ГЛАВА II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
- § 2. Сложение векторов.
- § 3. Вычитание векторов.
- § 4. Умножение вектора на число.
- § 5. Проекции вектора.
- § 6. Действия над векторами, заданными своими проекциями.
- § 7. Скалярное произведение векторов.
- § 8. Основные свойства скалярного произведения.
- § 9. Скалярное произведение векторов, заданных проекциями.
- § 10. Направление вектора.
- § 11. Векторное произведение.
- § 12. Основные свойства векторного произведения.
- § 13. Векторное произведение векторов, заданных проекциями.
- § 14. Векторно-скалярное произведение.
- § 15. Векторно-скалярное произведение в проекциях.
- § 16. Двойное векторное произведение.
- Упражнения
- ГЛАВА III. ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ
- § 1. Уравнение поверхности.
- § 2. Геометрический смысл уравнений.
- § 3. Две основные задачи.
- § 4. Сфера.
- § 5. Цилиндрические поверхности.
- § 6. Уравнения линии в пространстве.
- § 7. Пересечение трех поверхностей.
- Упражнения
- ГЛАВА IV. ПЛОСКОСТЬ
- § 1. Нормальное уравнение плоскости.
- § 2. Геометрический смысл уравнения первой степени между тремя переменными. Приведение общего уравнения первой степени к нормальному виду.
- § 3. Исследование общего уравнения плоскости.
- § 4. Уравнение плоскости в отрезках.
- § 5. Уравнение плоскости, проходящей через данную точку.
- § 6. Уравнение плоскости, проходящей через три данные точки.
- § 7. Угол между двумя плоскостями.
- § 8. Условия параллельности и перпендикулярности двух плоскостей.
- § 9. Точка пересечения трех плоскостей.
- § 10. Расстояние от точки до плоскости.
- Упражнения
- ГЛАВА V. ПРЯМАЯ ЛИНИЯ
- § 1. Уравнения прямой линии.
- § 2. Прямая как линия пересечения двух плоскостей. Общие уравнения прямой.
- § 3. Угол между двумя прямыми линиями.
- § 4. Условия параллельности и перпендикулярности двух прямых.
- § 5. Уравнения прямой, проходящей через две данные точки.
- § 6. Угол между прямой и плоскостью.
- § 7. Условия параллельности и перпендикулярности прямой и плоскости.
- § 8. Уравнение пучка плоскостей.
- § 9. Пересечение прямой с плоскостью.
- § 10. Условие, при котором две прямые лежат в одной плоскости.
- Упражнения
- ГЛАВА VI. ЦИЛИНДРИЧЕСКИЕ И КОНИЧЕСКИЕ ПОВЕРХНОСТИ. ПОВЕРХНОСТИ ВРАЩЕНИЯ. ПОВЕРХНОСТИ 2-го ПОРЯДКА
- § 1. Классификация поверхностей.
- § 2. Цилиндрические поверхности (общий случай).
- § 3. Конические поверхности.
- § 4. Поверхности вращения.
- § 5. Эллипсоид.
- § 6. Однополостный гиперболоид.
- § 7. Двуполостный гиперболоид.
- § 8. Эллиптический параболоид.
- § 9. Гиперболический параболоид.
- § 10. Конус 2-го порядка.
- § 11. Цилиндры 2-го порядка.
- § 12. Прямолинейные образующие поверхностей 2-го порядка. Конструкции В. Г. Шухова.
- Упражнения
- Ответы