| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Упражнения
Окружность
1. Написать уравнение окружности, зная, что:
а) центр окружности лежит в точке (-2,-3) и радиус ее равен 3 единицам длины;
б) центр лежит в точке (2, —3) и окружность проходит через точку (5, 1);
в) концы одного из диаметров имеют координаты (3, 9) и (7, 3).
2. Найти уравнение окружности, проходящей через точки  .
.
3. Какие значения должны иметь коэффициенты уравнения

чтобы оно определяло окружность радиуса 5 с центром в точке  ?
?
4. Определить координаты центра и радиус окружности, выражаемой уравнением:

5. Найти уравнение окружности, касающейся осей координат на расстояниях а единиц от начала координат.
6. Найти уравнение окружности, касающейся оси Оу в начале координат и пересекающей ось Ох в точке (6, 0).
7. Найти уравнение окружности, касающейся оси Ох в начале координат и пересекающей ось Оу в точке (0, — 8).
8. Найти уравнение окружности, касающейся оси Ох в точке  и имеющей радиус, равный 3 единицам длины.
и имеющей радиус, равный 3 единицам длины.
9. Найти уравнение окружности, центр которой лежит в точке (4, 7) и которая касается прямой 
10. Вывести уравнение касательной к окружности  в точке
в точке 
11. Составить уравнение касательной к окружности  в точке
в точке 
12. Написать уравнение касательной к окружности  в точке (3, 6).
в точке (3, 6).
13. Найти уравнения касательных к окружности  проходящих через точку
проходящих через точку 
14. Найти уравнения касательных к окружности  проходящих через точку
проходящих через точку  .
.
15. а) Найти касательные к окружности  параллельные прямой
параллельные прямой  Найти касательные к окружности
Найти касательные к окружности  перпендикулярные к прямой
перпендикулярные к прямой 
16. Найти длину  касательной, проведенной
касательной, проведенной  точки
точки  к окружности
к окружности 
17. а) Даны точки  Найти геометрическое место точек, из которых отрезки ОА и ОВ видны под равными углами, б) Все хорды ON окружности
Найти геометрическое место точек, из которых отрезки ОА и ОВ видны под равными углами, б) Все хорды ON окружности  проведенные из начала координат, продолжены за точку N на расстояние
проведенные из начала координат, продолжены за точку N на расстояние  Найти геометрическое место точек М..
Найти геометрическое место точек М..
Эллипс
18. Составить простейшее уравнение эллипса, зная, что:
а) полуоси его равны соответственно 5 и 4;
б) расстояние между фокусами равно 8 и большая ось равна 10;
в) малая полуось равна 2 и расстояние между фокусами равно 6;
г) большая полуось равна 10 и эксцентриситет равен 0,6;
д) малая полуось равна 6 и эксцентриситет равен 0,8;
е) эксцентриситет равен 0,8 и расстояние между фокусами равно 8;
ж) сумма полуосей равна 10 и расстояние между фокусами равно 45.
19. Найти длины осей, координаты фокусов и эксцентриситет эллипса, заданного уравнением:

20. Определить эксцентриситет эллипса, если:
а) отрезок, соединяющий его фокусы, виден из конца малой оси под прямым углом;
б) расстояние между фокусами равно расстоянию между концами большой и малой осей;
в) его большая ось втрое больше малой;
г) ею оси относятся, как 
21. Дан эксцентриситет эллипса  . Найти отношение его полуосей.
. Найти отношение его полуосей.
Как величина эксцентриситета характеризует форму эллипса?
22. Эллипс касается оси ординат в начале координат, а центр его находится в точке (5, 0). Составить уравнение эллипса, зная, что эксцентриситет его равен  .
.
23. Эллипс касается оси абсцисс в точке (8, 0) и оси ординат в точке (0, — 5). Написать уравнение эллипса, если известно, что оси его параллельны осям координат.
24. Эллипс касается оси ординат в точке (0, 5) и пересекает ось абсцисс в точках (5, 0) и (11, 0). Составить уравнение эллипса, если известно, что оси его параллельны осям координат.
25. Сколько касательных к эллипсу  можно провести из точки О, 1). сколько из точки (3, 1) и сколько из точки
можно провести из точки О, 1). сколько из точки (3, 1) и сколько из точки  ?
?
26. Написать уравнение касательной к эллипсу  в точке
в точке 
27. Известно, что прямая  касается эллипса
касается эллипса  Найти точку касания.
Найти точку касания.
28. Найти уравнения касательных, проведенных из точки (4, — 1) к эллипсу 
29. Найти касательные к эллипсу  проходящие через точку
проходящие через точку 
30. Найти касательные к эллипсу  параллельные прямой
параллельные прямой 
31. Найти касательные к эллипсу  перпендикулярные к прямой
перпендикулярные к прямой 
32. Написать уравнения директрис эллипса 
33. Написать уравнение эллипса, малая полуось которого равна  и директрисами которого служат прямые
и директрисами которого служат прямые  ±10.
±10.
34. Найти уравнение эллипса, расстояние между фокусами которого равняется 2 и расстояние между директрисами 10.
35. Найти эксцентриситет эллипса, если расстояние между его директрисами в три раза больше расстояния между фокусами.
36. Расстояние между директрисами эллипса равняется 36. Найти уравнение этого эллипса, зная, что фокальные радиусы некоторой его точки равны 9 и 15.
37. Расстояние между фокусами эллипса равно 8, расстояние между его директрисами равно 12,5. Найти простейшее уравнение этого эллипса.
38. Дан эллипс  Через точку (1, 1) провести хорду, делящуюся в этой точке пополам.
Через точку (1, 1) провести хорду, делящуюся в этой точке пополам.
39. Дан эллипс  Через точку
Через точку  провести хорду, делящуюся в этой точке пополам.
провести хорду, делящуюся в этой точке пополам.
40. Найти длину диаметра эллипса  направленного по биссектрисе второго координатного угла.
направленного по биссектрисе второго координатного угла.
41. Доказать, что касательные к эллипсу  проведенные в концах одною и того же диаметра, параллельны.
проведенные в концах одною и того же диаметра, параллельны.
42. Найти уравнения диаметров эллипса  длины которых равны 2/5.
длины которых равны 2/5.
43. Найти угол между двумя сопряженными диаметрами эллипса  из которых один наклонен к большой оси иод углом в 30°.
из которых один наклонен к большой оси иод углом в 30°.
44. Найти для эллипса  направления и длины двух сопряженных диаметров, из которых один проходит через точку (4, 2).
направления и длины двух сопряженных диаметров, из которых один проходит через точку (4, 2).
45. Определить длины сопряженных диаметров эллипса  которые образуют между собой угол в 60°.
которые образуют между собой угол в 60°.
46. Найти уравнения равных сопряженных диаметров эллипса — 
47. Написать уравнения двух равных сопряженных диаметров эллипса

48. Найти угол между двумя равными сопряженными диаметрами эллипса

49. Отрезок постоянной длины скользит своими концами по сторонам прямого угла. Определить кривую, описываемую любой точкой М, лежащей на этом отрезке.
50. Найти простейшее полярное уравнение эллипса 
Гипербола
51. Составить простейшее уравнение гиперболы, зная, что:
а) полуоси ее равны соответственно 5 и 4 единицам длины;
б) расстояние между фокусами равно 14, а расстояние между вершинами 12;
в) действительная полуось равна 5 и эксцентриситет равен 1,4;
г) расстояние между фокусами равно 16 и эксцентриситет равен 
д) действительная полуось равна  и гипербола проходит через точку
и гипербола проходит через точку 
е) гипербола проходит через точки 
52. Найти длины осей, координаты фокусов и эксцентриситет гиперболы, заданной уравнением:

53. а) Найти зависимость между эксцентриситетом гиперболы и углом между ее асимптотами; б) выразить отношение полуосей гиперболы через эксцентриситет. Как влияет величина эксцентриситета на форму гиперболы?
54. Дана гипербола  уравнение диаметра, длина которого равна
уравнение диаметра, длина которого равна 
55. На гиперболе  взята точка, абсцисса которой равна
взята точка, абсцисса которой равна  ордината положительна. Вычислить фокальные радиусы этой точки,
ордината положительна. Вычислить фокальные радиусы этой точки,
56. Дан эллипс  . Найтн уравнение гиперболы, вершины которой находятся в фокусах, а фокусы — в вершинах данного эллипса.
. Найтн уравнение гиперболы, вершины которой находятся в фокусах, а фокусы — в вершинах данного эллипса.
57. Найти касательные к гиперболе  в точках пересечения ее с прямой
в точках пересечения ее с прямой 
Найти касательные к гиперболе  проходящие через точку
проходящие через точку 
59. Найти касательные к гиперболе  параллельные прямой
параллельные прямой 
60. Доказать, что для гиперболы  произведение расстояний от фокусов до касательной равно
произведение расстояний от фокусов до касательной равно 
61. Доказать, что асимптоты равнобочной гиперболы делят пополам углы между ее сопряженными диаметрами.
62. 1) Найти отклонение фокуса гиперболы  от асимптоты.
от асимптоты.
2) Доказать, что произведение расстояний любой точки гиперболы до асимптот есть величина постоянная,
63. Даны фокальный параметр  и эксцентриситет
и эксцентриситет  гиперболы. Найти полуоси.
гиперболы. Найти полуоси.
64. Гипербола касается прямой  в точке (5, 2). Составить уравнение этой гиперболы.
в точке (5, 2). Составить уравнение этой гиперболы.
65. Найти касательные к гиперболе  , перпендикулярные к прямой
, перпендикулярные к прямой 
66. Найти уравнение гиперболы, зная, что расстояние между ее директрисами равно 6, а расстояние между фокусами 10.
67. Найти эксцентриситет гиперболы, если известно, что расстояние между ее директрисами в три раза меньше расстояния между фокусами.
68. Найти уравнения двух сопряженных диаметров гиперболы  , угол между которыми равен
, угол между которыми равен  ,
,
69. Найти уравнения диаметров гиперболы —  длина которых равна 2 1/5.
длина которых равна 2 1/5.
70. Дана гипербола  Написать уравнения асимптот.
Написать уравнения асимптот.
71. Найти уравнение гиперболы, если известно, что:
а)  и директрисы даны уравнениями
и директрисы даны уравнениями 
б) асимптоты даны уравнениями  и расстояние между фокусами равно 10;
и расстояние между фокусами равно 10;
в) асимптоты даны уравнениями  и гипербола проходит через точку
и гипербола проходит через точку  .
.
72. Даны точки  Точка М движется так, что в треугольнике АМВ угол В остается вдвое больше угла А. Определить траекторию движения.
Точка М движется так, что в треугольнике АМВ угол В остается вдвое больше угла А. Определить траекторию движения.
73. Две прямые вращаются около двух неподвижных точек в противоположных направлениях и с одинаковой угловой скоростью. При начале движения одна из этих прямых совпадает с прямой, соединяющей данные точки, а другая перпендикулярна к этой прямой. Найти геометрическое место точек пересечения этих прямых.
74. Составить уравнение касательной к гиперболе  в точке
в точке 
Парабола
75. Составить уравнение параболы, зная, что:
а) осью симметрии параболы служит ось Ох, вершина лежит в начале координат и расстояние от фокуса до вершины равно 4 единицам длины;
б) парабола симметрична относительно оси Ох, проходит через точку (2, — 4) и вершина ее лежит в начале координат;
в) парабола симметрична относительно оси Ох, проходит через точку  и вершина ее лежит в начале координат;
и вершина ее лежит в начале координат;
г) парабола симметрична относительно оси Оу, фокус лежит в точке (0, 3) и вершина совпадает с началом координат;
д) парабола симметрична относительно оси Оу, проходит через точку (4, 2) и вершина ее лежит в начале координат;
е) парабола симметрична относительно оси Оу, проходит через точку  и вершина совпадает с началом координат;
и вершина совпадает с началом координат;
ж) фокус имеет координаты (3,0), директриса служит осью ординат и ось симметрии — осью абсцисс;
з) фокус имеет координаты (0, 3), директриса служит осью абсцисс и ось симметрии — осью ординат.
76. Составить уравнение параболы, зная, что вершина ее лежит в точке  , параметр равен
, параметр равен  и направление оси симметрии совпадает;
и направление оси симметрии совпадает;
а) с положительным направлением оси 
б) с отрицательным направлением оси 
в) с положительным направлением оси 
г) с отрицательным направлением оси 
77. Составить уравнение параболы, зная, что вершина ее лежит в начале координат-, направление оси симметрии совпадает с отрицательным направлением оси Ох, а параметр  равен расстоянию от фокусов гиперболы
равен расстоянию от фокусов гиперболы  до асимптот.
до асимптот.
78. Составить уравнение параболы, зная, что вершина ее лежит в точке  направление оси симметрии совпадает с отрицательным направлением оси Оу, а параметр
направление оси симметрии совпадает с отрицательным направлением оси Оу, а параметр  равен расстоянию между директрисами эллипса
равен расстоянию между директрисами эллипса 
79. Найти длину хорды, проходящей через фокус параболы  и перпендикулярной к ее оси симметрии.
и перпендикулярной к ее оси симметрии.
80. Дана парабола  Через точку (4, 1) провести такую хорду, которая делилась бы в этой точке пополам.
Через точку (4, 1) провести такую хорду, которая делилась бы в этой точке пополам.
81. Дана парабола  Через точку
Через точку  провести такую хорду, которая в этой точке делилась бы пополам.
провести такую хорду, которая в этой точке делилась бы пополам.
82. Найти уравнения диаметров параболы  сопряженных с хордами, наклоненными к
сопряженных с хордами, наклоненными к  под углом в 45°.
под углом в 45°.
83. Дана парабола  Найти к этой параболе касательные в точках, в которых она пересекается с прямой
Найти к этой параболе касательные в точках, в которых она пересекается с прямой 
84. Найти такую точку на параболе  чтобы касательная в ней образовывала с осью симметрии параболы угол в 30°.
чтобы касательная в ней образовывала с осью симметрии параболы угол в 30°.
85. Найти касательные к параболе  проходящие через точку (3, —4).
проходящие через точку (3, —4).
86. Найти уравнение касательной к параболе  которая была бы: а) параллельна прямой
которая была бы: а) параллельна прямой  перпендикулярна к прямой
перпендикулярна к прямой 
87. Найти геометрическое место центров кругов, проходящих через данную точку и касающихся данной прямой.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ЧАСТЬ ПЕРВАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
- ГЛАВА I. МЕТОД КООРДИНАТ
- § 2. Координаты на прямой линии.
- § 3. Расстояние между двумя точками на прямой линии.
- § 4. Прямоугольные координаты на плоскости.
- § 5. Расстояние между двумя точками на плоскости.
- § 6. Деление отрезка в данном отношении.
- § 7. Угол между двумя осями.
- § 8. Основные положения теории проекций.
- § 9. Проекции направленного отрезка на оси координат.
- § 10. Площадь треугольника.
- § 11. Полярные координаты.
- Упражнения
- ГЛАВА II. ЛИНИИ И ИХ УРАВНЕНИЯ
- § 1. Составление уравнений заданных линий.
- § 2. Геометрический смысл уравнений.
- § 3. Две основные задачи.
- § 4. Пересечение двух линий.
- § 5. Параметрические уравнения линий.
- § 6. Уравнения линий в полярных координатах.
- ГЛАВА III. ПРЯМАЯ ЛИНИЯ
- § 1. Угловой коэффициент прямой.
- § 2. Уравнение прямой линии с угловым коэффициентом.
- § 3. Геометрический смысл уравнения первой степени между двумя переменными.
- § 4. Исследование общего уравнения первой степени Ах + Ву + С = 0.
- § 5. Уравнение прямой линии в отрезках.
- § 6. Построение прямой линии по ее уравнению.
- § 7. Угол между двумя прямыми.
- § 8. Условия параллельности и перпендикулярности двух прямых.
- § 9. Уравнение прямой, проходящей через данную точку в данном направлении.
- § 10. Взаимное расположение двух прямых на плоскости.
- § 11. Уравнение пучка прямых.
- § 12. Уравнение прямой, проходящей через две данные точки.
- § 13. Условие, при котором три данные точки лежат на одной прямой.
- § 14. Нормальное уравнение прямой линии.
- § 15. Приведение общего уравнения первой степени к нормальному виду.
- § 16. Расстояние от дайной точки до данной прямой.
- § 17. Уравнение прямой в полярной системе координат.
- Упражнения
- ГЛАВА IV. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ КОНИЧЕСКИХ СЕЧЕНИЙ
- § 2. Окружность.
- § 3. Эллипс.
- § 4. Гипербола и ее асимптоты.
- § 5. Парабола.
- § 6. Построение точек эллипса, гиперболы и параболы посредством циркуля и линейки.
- § 7. Эллипс, гипербола и парабола как конические сечения.
- § 8. Эксцентриситет и директрисы эллипса.
- § 9. Эксцентриситет и директрисы гиперболы.
- § 10. Эксцентриситет и директриса параболы.
- § 11. Уравнение конического сечения в полярных координатах.
- § 12. Диаметры зллипса. Сопряженные диаметры.
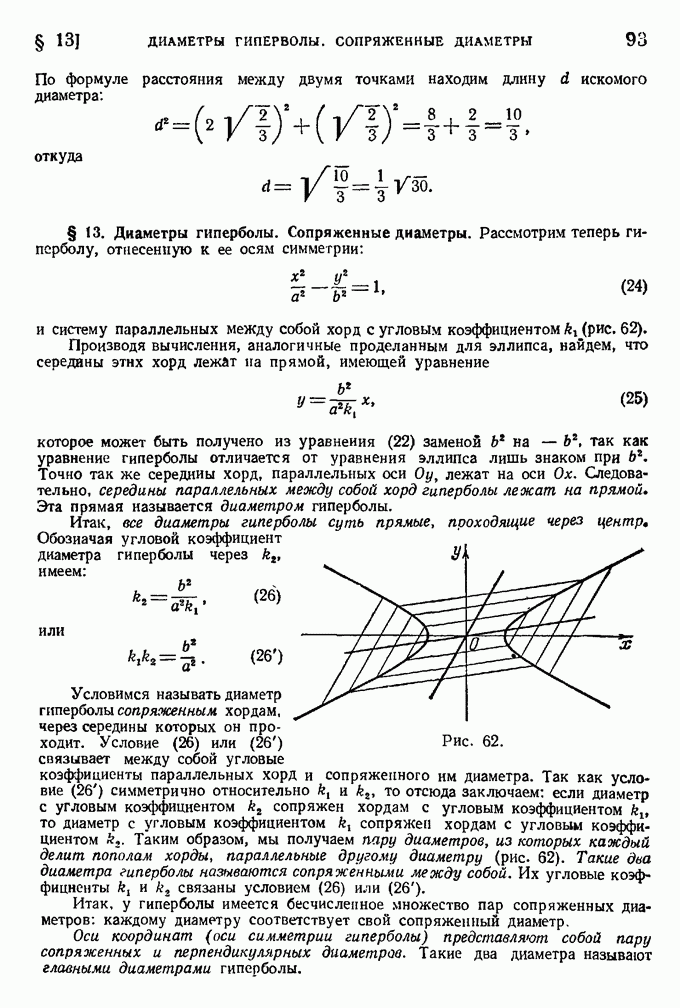
- § 13. Диаметры гиперболы. Сопряженные диаметры.
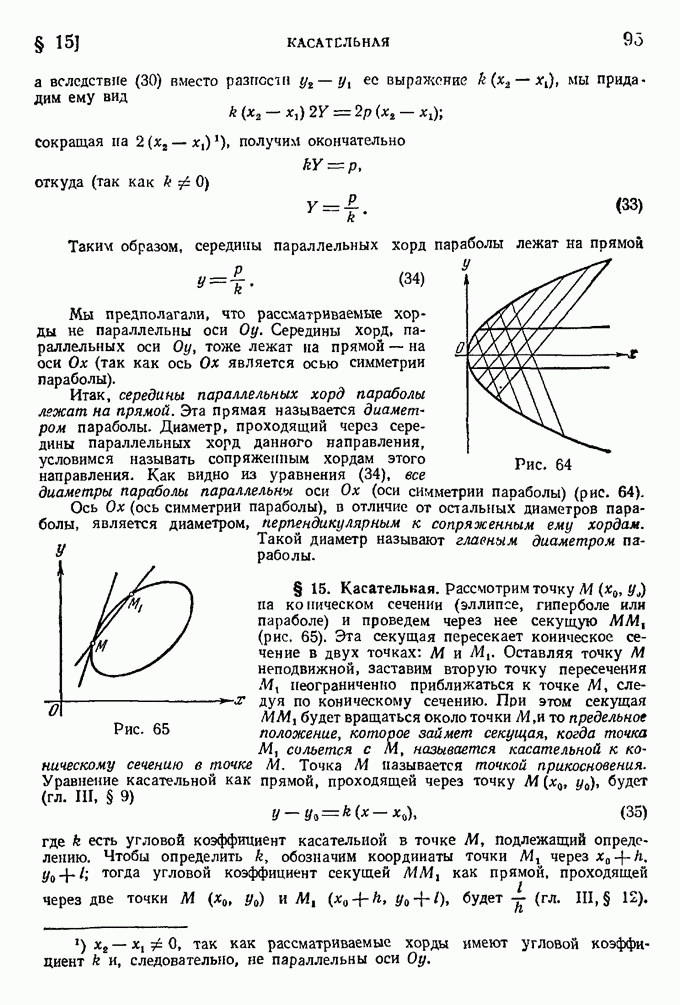
- § 14. Диаметры параболы.
- § 15. Касательная.
- § 16. Эллипс как проекция окружности.
- § 17. Параметрические уравнения эллипса.
- Упражнения
- ГЛАВА V. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. КЛАССИФИКАЦИЯ ЛИНИЙ
- § 2. Перенос начала координат.
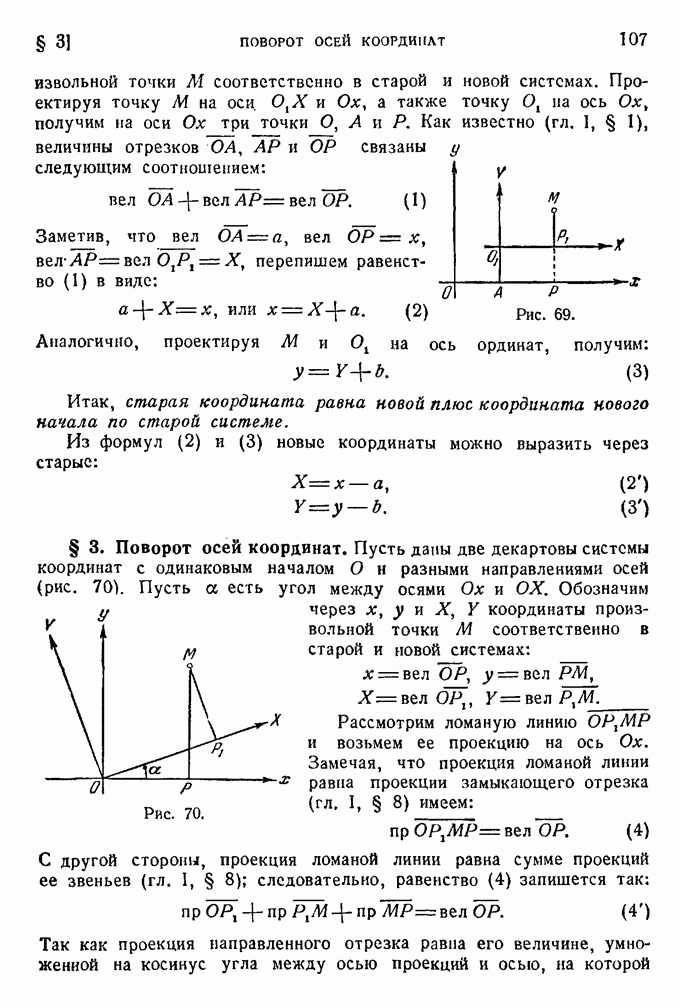
- § 3. Поворот осей координат.
- § 4. Общий случай.
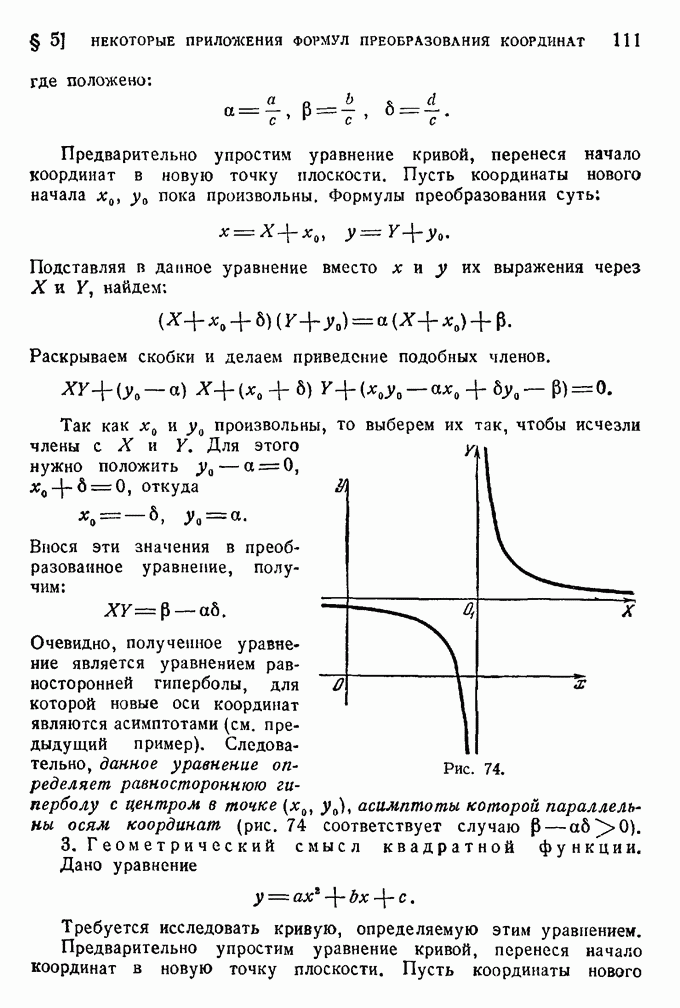
- § 5. Некоторые приложения формул преобразования координат.
- § 6. Преобразование общего уравнения второй степени, не содержащего произведения переменных.
- § 7. Преобразование общего уравнения второй степени.
- § 8. Классификация линий.
- Упражнения
- ГЛАВА VI. ОПРЕДЕЛИТЕЛИ 2-го и 3-го ПОРЯДКА
- § 2. Однородная система двух уравнений с тремя неизвестными.
- § 3. Определители 3-го порядка.
- § 4. Основные свойства определителей 3-го порядка.
- § 5. Система трех уравнений первой степени с тремя неизвестными.
- § 6. Однородная система.
- § 7. Общее исследование системы трех уравнений первой степени с тремя неизвестными.
- § 8. Некоторые приложения определителей к аналитической геометрии.
- Упражнения
- ЧАСТЬ ВТОРАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
- ГЛАВА I. МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ
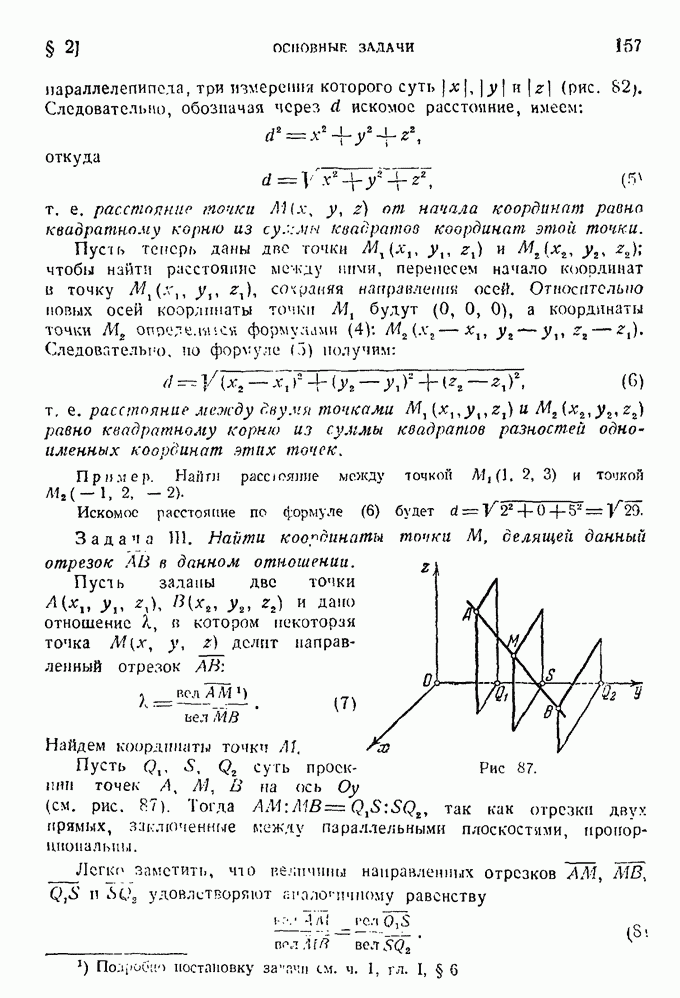
- § 2. Основные задачи.
- § 3. Основные положения теории проекций в пространстве.
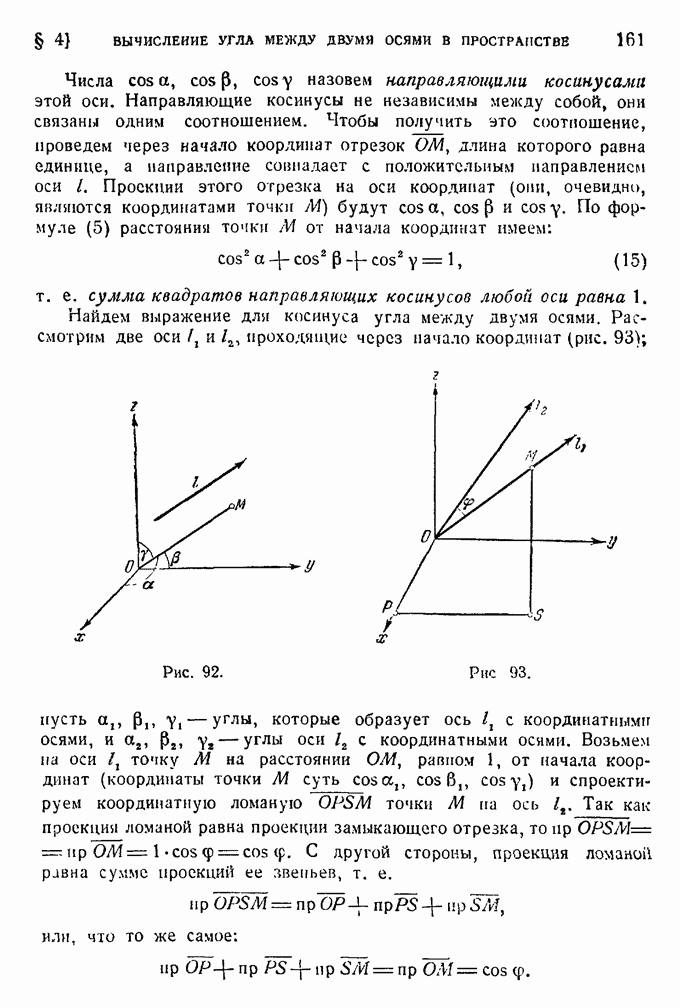
- § 4. Вычисление угла между двумя осями в пространстве.
- Упражнения
- ГЛАВА II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
- § 2. Сложение векторов.
- § 3. Вычитание векторов.
- § 4. Умножение вектора на число.
- § 5. Проекции вектора.
- § 6. Действия над векторами, заданными своими проекциями.
- § 7. Скалярное произведение векторов.
- § 8. Основные свойства скалярного произведения.
- § 9. Скалярное произведение векторов, заданных проекциями.
- § 10. Направление вектора.
- § 11. Векторное произведение.
- § 12. Основные свойства векторного произведения.
- § 13. Векторное произведение векторов, заданных проекциями.
- § 14. Векторно-скалярное произведение.
- § 15. Векторно-скалярное произведение в проекциях.
- § 16. Двойное векторное произведение.
- Упражнения
- ГЛАВА III. ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ
- § 1. Уравнение поверхности.
- § 2. Геометрический смысл уравнений.
- § 3. Две основные задачи.
- § 4. Сфера.
- § 5. Цилиндрические поверхности.
- § 6. Уравнения линии в пространстве.
- § 7. Пересечение трех поверхностей.
- Упражнения
- ГЛАВА IV. ПЛОСКОСТЬ
- § 1. Нормальное уравнение плоскости.
- § 2. Геометрический смысл уравнения первой степени между тремя переменными. Приведение общего уравнения первой степени к нормальному виду.
- § 3. Исследование общего уравнения плоскости.
- § 4. Уравнение плоскости в отрезках.
- § 5. Уравнение плоскости, проходящей через данную точку.
- § 6. Уравнение плоскости, проходящей через три данные точки.
- § 7. Угол между двумя плоскостями.
- § 8. Условия параллельности и перпендикулярности двух плоскостей.
- § 9. Точка пересечения трех плоскостей.
- § 10. Расстояние от точки до плоскости.
- Упражнения
- ГЛАВА V. ПРЯМАЯ ЛИНИЯ
- § 1. Уравнения прямой линии.
- § 2. Прямая как линия пересечения двух плоскостей. Общие уравнения прямой.
- § 3. Угол между двумя прямыми линиями.
- § 4. Условия параллельности и перпендикулярности двух прямых.
- § 5. Уравнения прямой, проходящей через две данные точки.
- § 6. Угол между прямой и плоскостью.
- § 7. Условия параллельности и перпендикулярности прямой и плоскости.
- § 8. Уравнение пучка плоскостей.
- § 9. Пересечение прямой с плоскостью.
- § 10. Условие, при котором две прямые лежат в одной плоскости.
- Упражнения
- ГЛАВА VI. ЦИЛИНДРИЧЕСКИЕ И КОНИЧЕСКИЕ ПОВЕРХНОСТИ. ПОВЕРХНОСТИ ВРАЩЕНИЯ. ПОВЕРХНОСТИ 2-го ПОРЯДКА
- § 1. Классификация поверхностей.
- § 2. Цилиндрические поверхности (общий случай).
- § 3. Конические поверхности.
- § 4. Поверхности вращения.
- § 5. Эллипсоид.
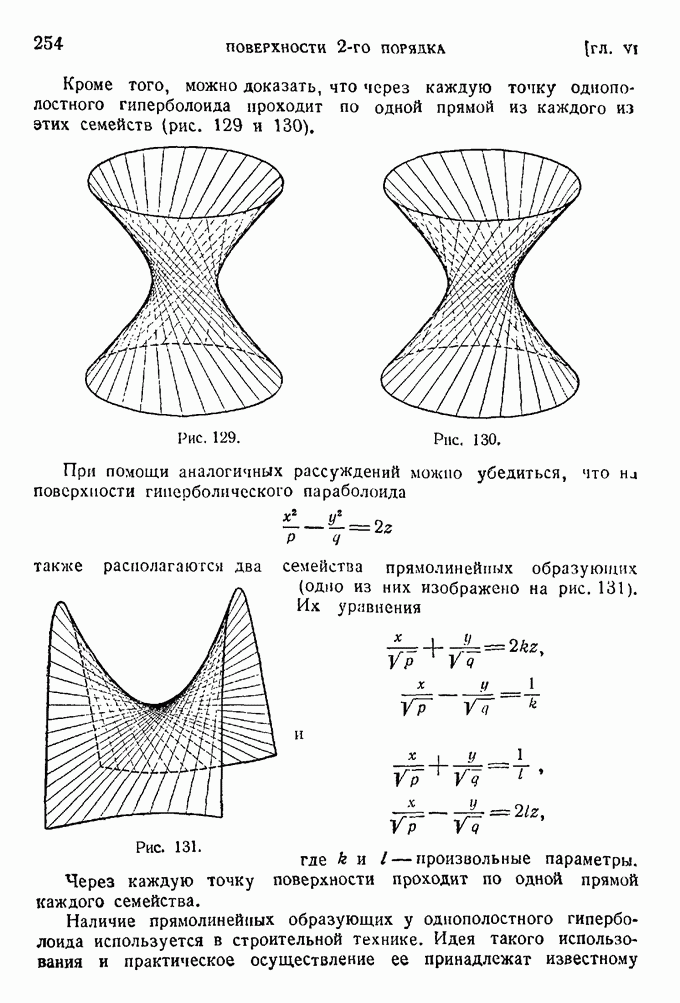
- § 6. Однополостный гиперболоид.
- § 7. Двуполостный гиперболоид.
- § 8. Эллиптический параболоид.
- § 9. Гиперболический параболоид.
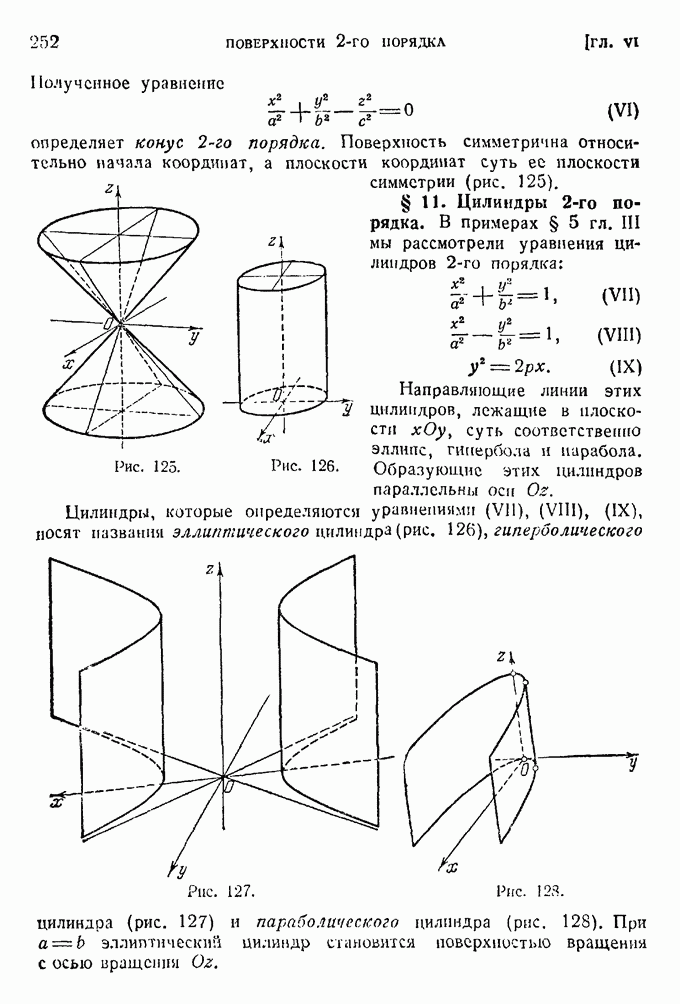
- § 10. Конус 2-го порядка.
- § 11. Цилиндры 2-го порядка.
- § 12. Прямолинейные образующие поверхностей 2-го порядка. Конструкции В. Г. Шухова.
- Упражнения
- Ответы